- 1Department of Physics and Astronomy, Virginia Military Institute, Lexington, VA, United States
- 2Department of Physics and Center for Accelerator Science, Old Dominion University, Norfolk, VA, United States
We report calculations of a DC superheating field Hsh in superconductors with nanostructured surfaces. Numerical simulations of the Ginzburg–Landau (GL) equations were performed for a superconductor with an inhomogeneous impurity concentration, a thin superconducting layer on top of another superconductor, and superconductor–insulator–superconductor (S-I-S) multilayers. The superheating field was calculated taking into account the instability of the Meissner state with a non-zero wavelength along the surface, which is essential for the realistic values of the GL parameter κ. Simulations were performed for the material parameters of Nb and Nb3Sn at different values of κ and the mean free paths. We show that the impurity concentration profile at the surface and thicknesses of S-I-S multilayers can be optimized to enhance Hsh above the bulk superheating fields of both Nb and Nb3Sn. For example, an S-I-S structure with a 90-nm-thick Nb3Sn layer on Nb can boost the superheating field up to ≈500 mT, while protecting the superconducting radio-frequency (SRF) cavity from dendritic thermomagnetic avalanches caused by local penetration of vortices.
1 Introduction
The superconducting radio-frequency (SRF) resonant cavities in particle accelerators enable high accelerating gradients with low power consumption. The best Nb cavities can have high quality factors Q ∼ 1010–1011 and sustain accelerating fields up to 50 MV/m at T = 1.5–2 K and 0.6–2 GHz (Padamsee et al., 2018; Gurevich, 2023). The peak RF fields B0 ≃ 200 mT at the equatorial surface of Nb cavities can approach the thermodynamic critical field Bc ≈ 200 mT at which the screening current density flowing at the inner cavity surface is close to the depairing current density Jc ≃ Bc/μ0λ—the maximum DC current density a superconductor can carry in the Meissner state (Tinkham, 2004), where λ is the penetration depth of the magnetic field. Thus, the breakdown fields of the best Nb cavities have nearly reached the DC superheating field Bsh ≃ Bc (Galaiko, 1966; Matricon and Saint-James, 1967; Christiansen, 1969; Chapman, 1995; Catelani and Sethna, 2008; Transtrum et al., 2011; Lin and Gurevich, 2012). The Q factors can be increased by material treatments such as high-temperature annealing followed by low-temperature baking which not only increase Q (B0) and the breakdown field but also reduce the deterioration of Q at high fields (Ciovati et al., 2010; Posen et al., 2020). High-temperature treatments combined with the infusion of nitrogen, titanium, or oxygen can produce an anomalous increase of Q (B0) with RF field amplitude B0 = μ0H0 (Ciovati et al., 2016; Grassellino et al., 2017; Dhakal, 2020; Lechner et al., 2021). These advances raise the question about the fundamental limit of the breakdown fields of SRF cavities and the extent to which it can be pushed by surface nanostructuring and impurity management (Gurevich and Kubo, 2017; Gurevich, 2023).
Several ways of increasing the SRF breakdown fields by surface nanostructuring have been proposed. They include depositing high-Tc superconducting multilayers with thin dielectric interlayers (Gurevich, 2006; Gurevich, 2015; Kubo et al., 2014; Liarte et al., 2017; Kubo, 2021) or a dirty overlayer with a higher impurity concentration at the surface (Ngampruetikorn and Sauls, 2019). The DC superheating field of such structures has been evaluated using the London, Ginzburg–Landau (GL), and quasiclassical Usadel and Eilenberger equations in the limit of an infinite GL parameter κ = λ/ξ → ∞ in which the breakdown of the Meissner state at H0 = Hsh occurs once the current density at the surface reaches the depairing limit (Gurevich, 2006; Gurevich, 2015; Kubo et al., 2014; Liarte et al., 2017; Kubo, 2021; Ngampruetikorn and Sauls, 2019). Yet, it has been well-established that in a more realistic case of a finite κ, the breakdown of the Meissner state at H = Hsh occurs due to the exponential growth of periodic perturbations of the order parameter and the magnetic field with a wavelength
We present the results of numerical calculations of a DC superheating field for different superconducting geometries in materials with finite κ and determine optimal surface nanostructures that can withstand the maximum magnetic field in the vortex-free Meissner state. In particular, we consider a bulk superconductor with a thin impurity diffusion layer, a clean superconducting overlayer separated by an insulating layer from the bulk (e.g., Nb3Sn-I-Nb3Sn), a thin dirty superconducting layer on the top of the same superconductor (e.g., dirty Nb3Sn-I-clean Nb3Sn), and a thin high-Tc superconducting layer on the top of a low-Tc superconductor (e.g., Nb3Sn-I-Nb). We calculate Hsh and determine an optimal layer thickness for each geometry by numerically solving the GL equations, taking into account both the non-linear screening of the applied magnetic field and the periodic instability of the Meissner state in a nanostructured superconductor.
The paper is organized as follows. The GL equations and methods of numerical detection of Hsh and the wavelength λc of a critical perturbation causing the instability of the Meissner state are presented in Section 2. The results of numerical calculations of Hsh for impurity diffusion layers and various S-I-S structures are given in Section 3 and Section 4, respectively. Section 5 contains discussion of the results, and Section 6 provides the conclusion with a summary. Computational details are given in Section Method and other technical details are given in Supplementary Appendices A, B.
2 GL equations and numerical detection of Hsh and kc
We first consider a semi-infinite uniform superconductor in a magnetic field H0 applied along the z-axis, parallel to the planar surface. In this case, the induced supercurrents flow in the xy plane and GL equations for the complex order parameter ψ = Δeiφ, and two components of the vector potential Ax and Ay can be reduced to two coupled partial differential equations for the amplitude Δ(x, y, t) and the z-component of the magnetic field H (x, y, t). As shown in Supplementary Appendix A, these equations can be written in the following dimensionless form:
Here, f (x, y) = Δ(x, y)/Δ0, Δ0(T) is the equilibrium order parameter in the bulk,
where
Shown in Figures 1A,B are f (x, y) calculated at κ = 10 and the applied fields H0 slightly below and above Hsh. At H0 < Hsh, the order parameter f(x) is reduced at the surface by the flowing screening currents. At H0 > Hsh, the stationary f(x) becomes unstable with respect to spontaneously growing periodic perturbations δf (x, y, t) along the surface, as shown in Figure 1B. This Turing instability (Cross and Hohenberg, 1993) occurs with respect to a small disturbance δf (x, y, t) ∝ δf(x)eiky+Γt, where the increment Γ(H0, k) depends on the wave vector k of spatial oscillations of f (x, y) along the surface as shown in Figure 2A. Below the superheating field, Γ(k) is negative so perturbations with all k decay exponentially and the Meissner state is stable. At the superheating field, Γ(k) first vanishes at a critical wave number k = kc at which Γ(k) is maximum. At H0 = Hsh + 0, the increment Γ(k) becomes positive at k = kc, making the Meissner state unstable with respect to a growing critical perturbation
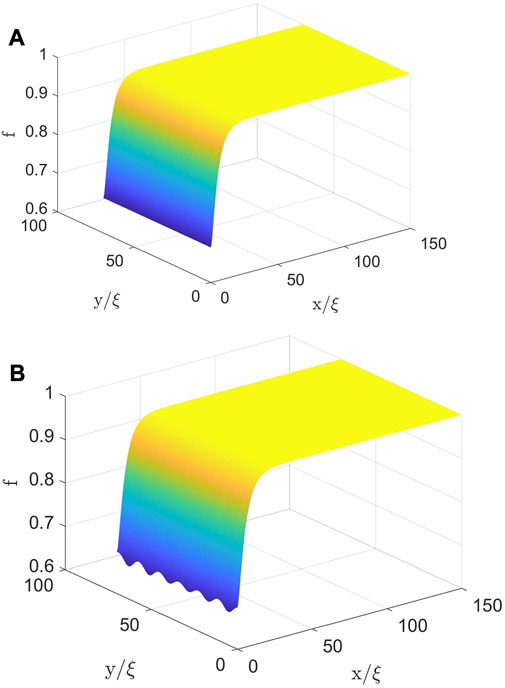
FIGURE 1. Spatial distribution of the order parameter calculated at κ =10, H0= Hsh −0 (A), and H0= Hsh +0 (B).
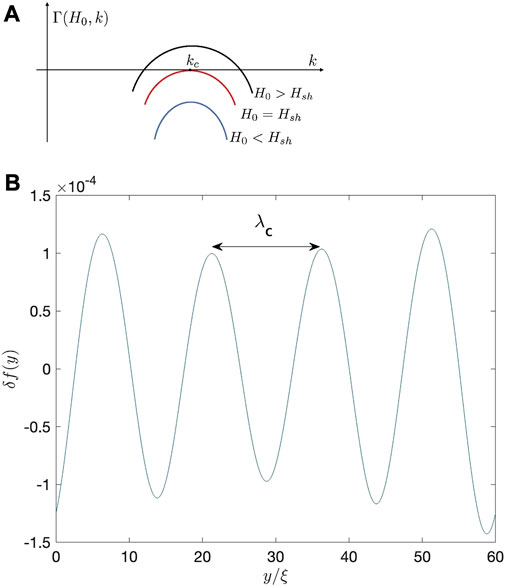
FIGURE 2. (A) Qualitative dependence of the instability increment Γ(H0, k) on the wave vector of perturbation k at different applied fields H0. (B) Snapshot of δf(y) at x =0, and H0= Hsh +0 calculated at κ =10.
We then compare some of our numerical results with the known analytical approximations for Hsh and kc at κ ≫ 1, given as follows (Christiansen, 1969; Chapman, 1995; Transtrum et al., 2011; Liarte et al., 2017).
At κ = 10–20, Eqs (4, 5) give the instability wavelength
3 Superconductor with an impurity diffusion layer
We consider a dirty layer at the surface with a higher impurity concentration, as shown in Figure 3A. In our simulations, such a layer was modeled by a spatially varying coherence length and penetration depths
where κ = λ∞/ξ∞,
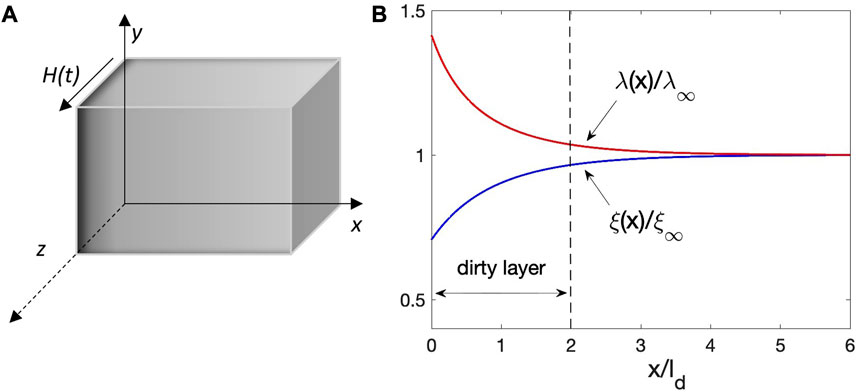
FIGURE 3. (A) Impurity diffusion layer at the surface shown by the dark gray contrast. (B) Variations of normalized coherence length and penetration depth across a dirty layer with α =0.5.
The calculated dependencies of Hsh(ld) on the diffusion layer thickness at different α for κ = 2 and κ = 10 are shown in Figures 4A, B, respectively. One can see that Hsh(ld) first increases with ld, reaches a maximum, and then decreases with ld approaching a lower value of Hsh at ld ≫ ξ∞. At κ = 2, Hsh(ld) is maximum at ld/ξ∞ = 0.8, 0.9, 1.5 for α = 0.2, 0.5, 0.8. Similarly, at κ = 10, Hsh(ld) is maximum at ld/ξ∞ = 4, 5, 10. Here, the diffusion layer can increase Hsh by
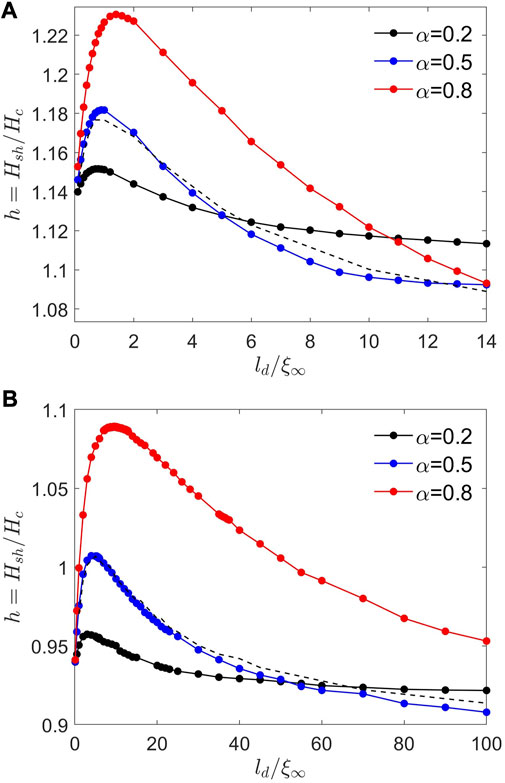
FIGURE 4. Superheating field Hsh(ld) as a function of the dirty layer thickness calculated at (A) κ =2 (B) κ =10 for different α. The dashed line shows Hsh(ld) calculated from the condition δ2F =0 and ∂kδ2F =0 at (A) κ =2 and (B) κ =10 at α =0.5.
The direct numerical calculation of Hsh involves detecting the instability of the Meissner state with respect to an infinitesimal perturbation
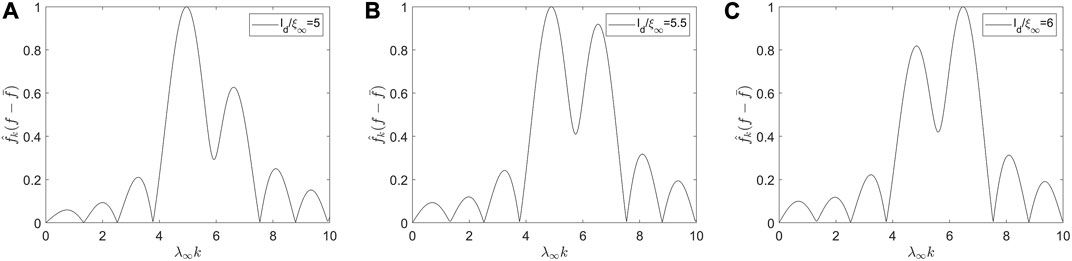
FIGURE 5. Discrete fast Fourier transform of δf (0, y) at H0= Hsh +0, α =0.5, and κ =10; (A) ld/ξ∞=5, (B) ld/ξ∞=5.5, and (C) ld/ξ∞=6. Evolution of these peaks with ld/ξ∞ is shown in “Fourier Transform.gif” in Supplementary Video S1.
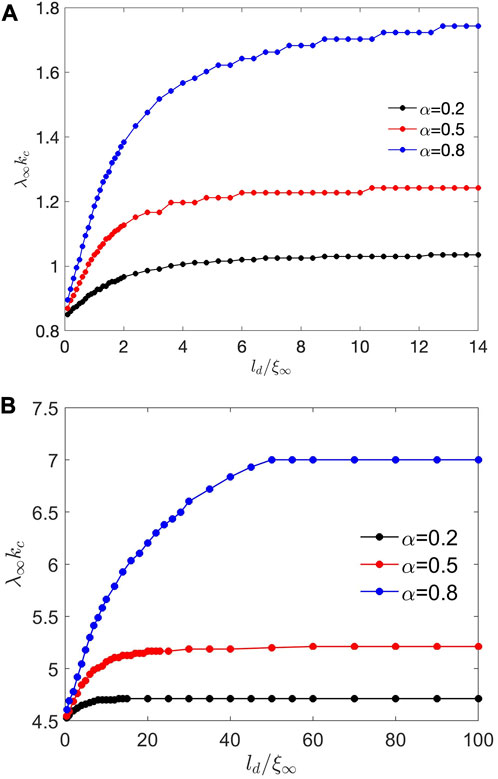
FIGURE 6. Dependencies of λkc on ld calculated from the conditions δ2F =0 and ∂kδ2F =0 at (A) κ =2 and (B) κ =10 for different α.
4 S-I-S structures
Using the direct simulation method outlined in Section 2, we have calculated Hsh(d) and the critical wave number kc(d) for various S-I-S structures: the S layer of thickness d is separated by an insulator from the S substrate of the same material, a dirty S layer on the top of a cleaner superconductor (e.g., dirty Nb-I-clean Nb), and a thin high Tc overlayer on the top of a low Tc superconductor (e.g., Nb3Sn-I-Nb). Here, the I layer is assumed to be thick enough to fully suppress the Josephson coupling between the S overlayer and the bulk, but thinner than the S overlayer. The screening of the applied field in an S-I-S multilayer is shown in Figure 7.
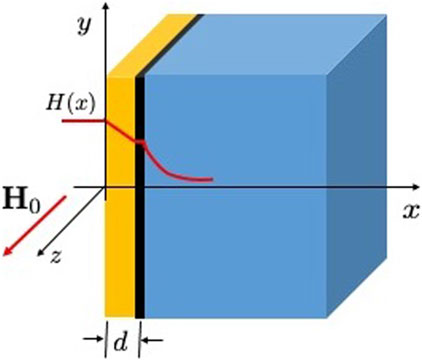
FIGURE 7. Superconductor–insulator–superconductor structure. The vertical black line represents the insulating layer, and the red line shows the screened magnetic field profile H(x).
4.1 S overlayer on the top of the S-substrate
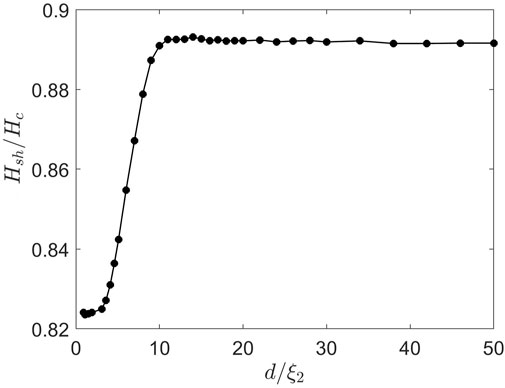
The GL Eqs (1, 2) for the S overlayer separated by the I layer from the substrate made of the same superconductor were solved in both S-domains with the boundary conditions given by Eq. (3) supplemented by the conditions of continuity of h (d + 0, y) = h (d − 0, y), parallel electric field Ey (d + 0, y) = Ey (d − 0, y), and zero current ∂yh (d + 0) = ∂yh (d − 0) = 0 through the I layer. Figure 8 shows that Hsh is a function of the thickness of the S overlayer d calculated at κ = 17 representing Nb3Sn. Here, a very thin S overlayer reduces Hsh(d), which then gradually increases with d, reaching a higher bulk value of Hsh at d > 9ξ2, where ξ2 is the coherence length in the S-substrate. The reduction of Hsh(d) at small d results from the I layer blocking the perpendicular currents produced by the critical perturbation and reducing its decay length in the bulk from
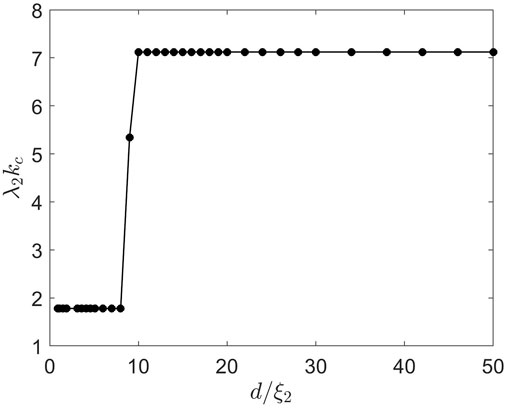
FIGURE 9. Critical wave number kc(d) calculated for the Nb3Sn-I-Nb3Sn structure by solving the quasistatic GL equations directly as described in Section 2.
4.2 Dirty S overlayer on a cleaner S-substrate
A dirty S overlayer with a higher concentration of non-magnetic impurities on a cleaner S substrate of the same material is considered, assuming that both have the same Tc unaffected by non-magnetic impurity scattering (Tinkham, 2004). Superconductivity in the bulk is described by the following GL equations
where index 2 corresponds to the substrate parameters in which the lengths and f2 are in units of their respective bulk values of ξ2 and Δ2. In turn, the GL equations in the overlayer are as follows:
Equations (8–11) were solved for a dirty Nb3Sn overlayer on a cleaner Nb3Sn with a mean free path l = 2 nm,
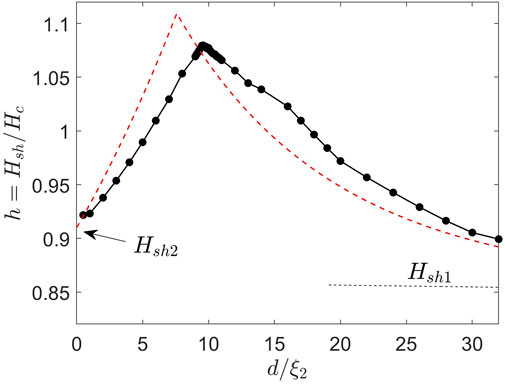
FIGURE 10. Superheating field Hsh(d) calculated for the Nb3Sn(dirty)-I-Nb3Sn structure. The red dashed line shows Hsh(d) calculated from the London Eqs (15–17) with Hsh1=0.855Hc and Hsh2=0.91Hc taken from the asymptotic limits of Hsh(d) at d ≫ λ1 and d =0, respectively.
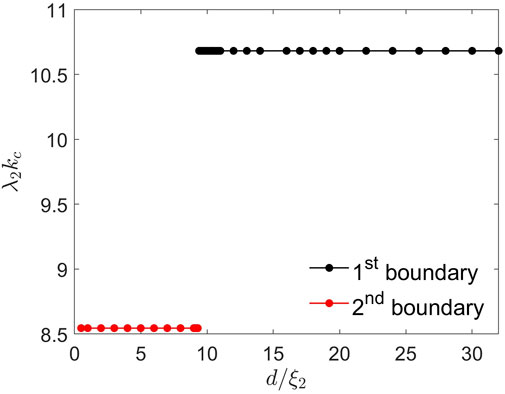
FIGURE 11. The critical wave number kc(d) calculated for the Nb3Sn(dirty)-I-Nb3Sn structure by solving the quasi-static GL equations directly as described in Section 2.
4.3 High-Tc superconducting overlayer
Finally, we consider an S-I-S structure comprising a high-Tc layer on the top of a lower-Tc substrate. The order parameter f2 and the field h2 in the substrate are described in Eqs (8, 9), and the GL equations for f1 and h1 in the overlayer are given by
where Tc1 and Tc2 are the critical temperatures of the overlayer and the substrate, respectively, and the order parameter and lengths are normalized to the respective parameters of the substrate. Equations (12–14) are supplemented by the boundary conditions given by Eq. (3) and the conditions of field continuity and zero current through the I layer.
We solved the GL equations for a clean Nb3Sn overlayer on a bulk Nb using κ2 = 50/22 and κ1 = 17 (Orlando et al., 1979; Posen and Hall, 2017). The calculated superheating field Hsh(d) shown in Figure 12 has a maximum at dm ≈ 4ξ2. This behavior of Hsh(d) is similar to that of Hsh(d) considered in the previous section: Hsh(d) at d < dm is limited by the instability of the Meissner state in the Nb substrate partly screened by the Nb3Sn overlayer, while Hsh at d > dm is determined by the superheating field of Nb3Sn enhanced at d ≈ dm by the current counterflow caused by the Nb substrate. The corresponding dependence of kc(d) on the overlayer thickness is shown in Figure 13. The jumpwise change of kc(d) reflects the switch from the instability of the Meissner state at the inner surface of the low-Tc substrate at d < dm to the instability at the outer surface in the high-Tc overlayer at d > dm, which is similar to that shown in Figure 11. For the parameters used in the simulations, such Nb3Sn-I-Nb structures with d ≈ dm can boost the superheating field up to
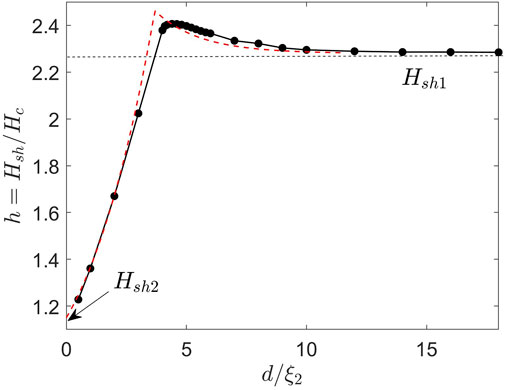
FIGURE 12. Superheating field Hsh(d) calculated for the Nb3Sn-I-Nb structure. The red dashed line shows Hsh(d) calculated from the London Eqs (15–17) with Hsh1=2.28Hc and Hsh2=1.08Hc taken from the asymptotic limits of Hsh(d) at d ≫ λ1 and d =0, respectively.
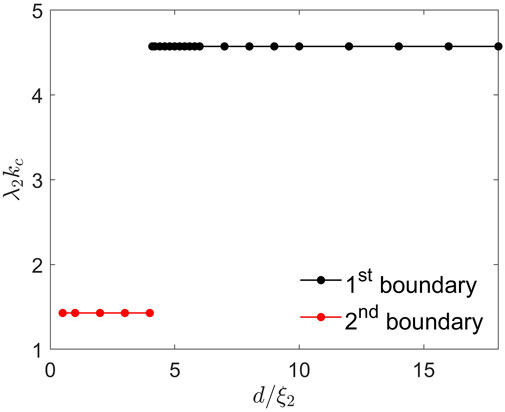
FIGURE 13. The critical wave number kc(d) calculated for the Nb3Sn-I-Nb structure by solving the quasistatic GL equations directly as described in Section 2.
5 Discussion
The GL calculations of the DC superheating field at T ≈ Tc self-consistently take into account the essential non-linear field screening and the periodic instability of the Meissner state in the entire range of the GL parameters which can be tuned by the impurities. This approach shows that the thicknesses of the impurity diffusion layer or S-I-S layers can be optimized to increase Hsh above the superheating fields of individual components. For instance, optimizing the diffusion length can enhance Hsh by ≃ 5–20% at κ = 10 and by ≃ 2–9% at κ = 2. An optimized dirty Nb3Sn overlayer deposited onto the Nb3Sn field by ≃ 10% as compared to Hsh of a clean Nb3Sn. This effect manifests itself in a non-monotonic dependence of Hsh on the dirty layer thickness due to the current counterflow induced at the surface by a superconducting substrate with a shorter field penetration depth. Such behavior of Hsh(d) is consistent with the previous calculations of Hsh based on the London (Gurevich, 2006; Gurevich, 2015; Kubo et al., 2014) or Usadel (Kubo, 2021) and Eilenberger (Ngampruetikorn and Sauls, 2019) theories at κ → ∞. To see the extent to which the London model is consistent with the GL results, we consider Hsh(d) calculated for an S-I-S multilayer in the London limit (Gurevich, 2015).
where Hsh1 and Hsh2 are the bulk superheating fields of the overlayer and the substrate, respectively. Equation (15) describes Hsh(d) of S-I-S structures with thin overlayers (d < dm), where the Meissner state first breaks down at the surface of the substrate. Here, the high-Hc overlayer partly screens the substrate, allowing it to stay in the Meissner state at a higher applied field H0 = Hsh(d) than the bare substrate. If d > dm, the Meissner state first breaks down at the outer surface of the overlayer so that Hsh(d) → Hsh1 at d ≫ λ1. The maximum Hsh(dm) is given by:
The maximum
Equations (15–17) do not take into account the reduction of the superfluid density by current, non-linear field screening and the periodic instability of the Meissner state at a finite κ. The London model does not account for the size effect of reducing Hsh(d) if the overlayer thickness is smaller than the decay length
In the GL region T ≈ Tc2, Eqs (15–17) predict a significant change in the temperature dependence of Hsh(T) of the S-I-S multilayer with a higher-Tc overlayer as compared to Hsh2(T) of the bare substrate. If T → Tc2, the penetration depth
Hence, Hsh(T) can be significantly higher than Hsh2(T) ∝ Tc2 − T at T ≈ Tc2, particularly if d > λ1. As an illustration, Figure 14 shows Hsh(T) calculated from Eqs (15–17) for different ratios d/λ1 and the parameters of Nb3Sn-I-Nb specified in Section 4.3. One can see both the square root temperature dependence given by Eq. (19) at T ≈ Tc2 and a sharp change in Hsh(T) upon decreasing T as dm(T) becomes shorter than d and Hsh(T) crosses over to a nearly constant Hsh1(T) of the overlayer. For d/λ1 < 2, such a transition in Hsh(T) happens at lower T outside the GL temperature range shown in the figure.
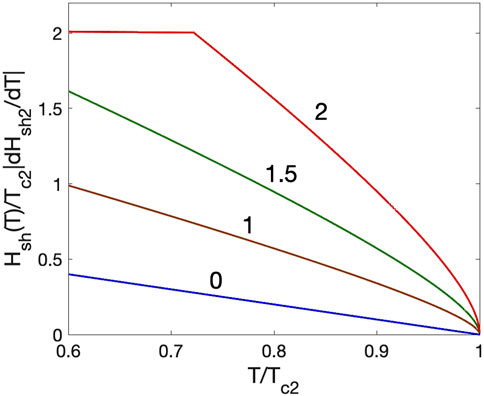
FIGURE 14. Temperature dependencies of Hsh(T) calculated from Eqs (15–17) for different ratios d/λ1 and the superconducting parameters of Nb3Sn-I-Nb specified in the text. The sharp change in the behavior of Hsh(T) upon decreasing T at d/λ1=2 occurs as dm(T) becomes shorter than d and Hsh(T) crosses over to a nearly constant Hsh1(T) of the overlayer. For smaller d/λ1, such a transition in Hsh(T) takes place at lower T outside the GL temperature range shown in the figure. Here, the blue line with d/λ1=0 represents Hsh2(T) of the bare substrate.
The relation between the static Hsh calculated here and the dynamic superheating field Hsd (T, ω) representing the fundamental field limit of superconductivity breakdown in SRF cavities depends on the rf frequency ω, temperature, and the material purity (Gurevich, 2023). The calculation of Hsd for S-I-S structures generally requires solving complex equations of non-equilibrium superconductivity, which in some cases can be reduced to TDGL equations at T ≈ Tc (Watts-Tobin et al., 1981). The dynamic superheating field of an alloyed superconductor with an ideal surface at T ≈ Tc was calculated from the microscopic theory (Sheikhzada and Gurevich, 2020), where it was shown that Hsd(T) approaches the static Hsh(T) at low frequencies ω ≪ ωc but can be by a factor
In this work, Hsh was calculated for S-I-S structures with ideal surfaces and interfaces without topographical and material defects or weakly coupled grain boundaries in the overlayer and the substrate. Topographical and other surface defects can locally reduce the field onset of the dissipative penetration of vortices and reduce the global Hsh, as was shown by TDGL simulations (Vodolazov, 2000; Pack et al., 2020; Wang et al., 2022). Likewise, Hsh(T) can be reduced by weakly coupled grain boundaries causing premature proliferation of mixed Abrikosov–Josephson vortices or phase slips (Sheikhzada and Gurevich, 2017). The I interlayer in S-I-S coating can mitigate these detrimental effects by the following: 1. increasing the cavity breakdown field by thin high-Hc overlayers and 2. confining vortices penetrating at surface defects in a thin overlayer and blocking flux penetration in the cavity wall, where it can trigger thermo-magnetic avalanches, causing global superconductivity breakdown (Gurevich, 2015; Gurevich, 2023). The S-I-S coating can provide these two goals if the overlayer thickness does not exceed λ1 (Gurevich, 2006). In this work, we calculated the upper limit of Hsh and showed how the S-I-S geometry can be optimized to increase Hsh at d ≲ λ1.
6 Conclusion
Our numerical GL calculations of the DC superheating field in superconductors with nanostructured surfaces cover the entire range of 1 < κ < ∞ and account for both the non-linear Meissner screening and the instability with a finite wave number kc at H0 = Hsh. We showed that there are optimum thicknesses of the impurity diffusion layer and the superconducting overlayer which maximize Hsh. These results suggest the possible ways of increasing the breakdown fields by surface nanostructuring and can help understand the ways of optimizing SRF cavities to achieve higher accelerating gradients.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
WP performed all numerical simulations, analyzed the results, and wrote the first draft of the manuscript. AG initiated and supervised the project and wrote the revised manuscript. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by DOE under grant DE-SC 100387–020 (ODU) and by the Virginia Military Institute (VMI).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/femat.2023.1246016/full#supplementary-material
References
Catelani, G., and Sethna, J. P. (2008). Temperature dependence of the superheating field for superconductors in the high-κ London limit. Phys. Rev. B 78, 224509. doi:10.1103/PhysRevB.78.224509
Chapman, S. J. (1995). Superheating field of type II superconductors. SIAM J. Appl. Math. 55 (5), 1233–1258. doi:10.1137/S0036139993254760
Christiansen, P. V. (1969). Magnetic superheating field in high-κ superconductors. Solid State Commun. 7 (10), 727–729. doi:10.1016/0038-1098(69)90652-8
Ciovati, G., Myneni, G., Stevie, F., Maheshwari, P., and Griffis, D. (2010). High field Q slope and the baking effect: review of recent experimental results and new data on Nb heat treatments. Phys. Rev. St. Accel. Beams 13, 022002. doi:10.1103/PhysRevSTAB.13.022002
Ciovati, G., Dhakal, P., and Myneni, G. (2016). Superconducting radio-frequency cavities made from medium and low-purity niobium ingots. Supercond. Sci. Technol. 29, 064002. doi:10.1088/0953-2048/29/6/064002
COMSOL COMSOL Multiphysics modeling software. Available at: https://www.comsol.com (Accessed March 15, 2017).
Cross, M. C., and Hohenberg, P. C. (1993). Pattern formation outside of equilibrium. Rev. Mod. Phys. 65, 851–1112. doi:10.1103/RevModPhys.65.851
Dhakal, P. (2020). Nitrogen doping and infusion in SRF cavities: A review. Open Phys. J. 5, 100034. doi:10.1016/j.physo.2020.100034
Galaiko, V. P. (1966). Stability limits of the superconducting state in a magnetic field for superconductors of the second kind. Zh. Exp. Teor. Fiz. 50, 717–723.
Grassellino, A., Romanenko, A., Trenikhina, Y., Checchin, M., Martinello, M., Melnychuk, P., et al. (2017). Unprecedented quality factors at accelerating gradients up to 45 MVm-1 in niobium superconducting resonators via low temperature nitrogen infusion. Supercond. Sci. Technol. 30, 094004. doi:10.1088/1361-6668/aa7afe
Gurevich, A. (2006). Enhancement of rf breakdown field of superconductors by multilayer coating. Appl. Phys. Lett. 88 (1), 012511. doi:10.1063/1.2162264
Gurevich, A., and Kubo, T. (2017). Surface impedance and optimum surface resistance of a superconductor with an imperfect surface. Phys. Rev. B 96, 184515. doi:10.1103/PhysRevB.96.184515
Gurevich, A. (2015). Maximum screening fields of superconducting multilayer structures. AIP Adv. 5 (1), 017112. doi:10.1063/1.4905711
Gurevich, A. (2023). Tuning microwave losses in superconducting resonators. Supercond. Sci. Technol. 36, 063002. doi:10.1088/1361-6668/acc214
Kubo, T., Iwashita, Y., and Saeki, T. (2014). Radio-frequency electromagnetic field and vortex penetration in multilayered superconductors. Appl. Phys. Lett. 104, 032603. doi:10.1063/1.4862892
Kubo, T. (2021). Superheating fields of semi-infinite superconductors and layered superconductors in the diffusive limit: structural optimization based on the microscopic theory. Supercond. Sci. Technol. 34, 045006. doi:10.1088/1361-6668/abdedd
Lechner, E. M., Angle, J. W., Stevie, F. A., Kelley, M. J., Reece, C. E., and Palczewski, A. D. (2021). RF surface resistance tuning of superconducting niobium via thermal diffusion of native oxide. Appl. Phys. Lett. 119, 082601. doi:10.1063/5.0059464
Liarte, D. B., Posen, S., Transtrum, M. K., Catelani, G., Liepe, M., and Sethna, J. P. (2017). Theoretical estimates of maximum fields in superconducting resonant radio frequency cavities: stability theory, disorder, and laminates. Supercond. Sci. Technol. 30, 033002. doi:10.1088/1361-6668/30/3/033002
Lin, F. P. J., and Gurevich, A. (2012). Effect of impurities on the superheating field of type-II superconductors. Phys. Rev. B 85 (5), 054513. doi:10.1103/PhysRevB.85.054513
Matricon, J., and Saint-James, D. (1967). Superheating fields in superconductors. Phys. Lett. A 24 (5), 241–242. doi:10.1016/0375-9601(67)90412-4
MATLAB Matlab. Available at: https://www.mathworks.com/products/matlab.html (Accessed March 15, 2017).
Ngampruetikorn, V., and Sauls, J. A. (2019). Effect of inhomogeneous surface disorder on the superheating field of superconducting RF cavities. Phys. Rev. Res. 1, 012015. doi:10.1103/PhysRevResearch.1.012015
Orlando, T. P., McNiff, E. J., Foner, S., and Beasley, M. R. (1979). Critical fields, Pauli paramagnetic limiting, and material parameters of Nb3Sn and V3Si. Phys. Rev. B 19, 4545–4561. doi:10.1103/physrevb.19.4545
Pack, A. R., Carlson, J., Wadsworth, S., and Transtrum, M. K. (2020). Vortex nucleation in superconductors within time-dependent Ginzburg-Landau theory in two and three dimensions: role of surface defects and material inhomogeneities. Phys. Rev. B 101, 144504. doi:10.1103/PhysRevB.101.144504
Padamsee, H., Knobloch, J., and Hays, T. (2018). RF superconductivity for accelerators. 2nd ed. Germany: Wiley-VCH Verlag GmbH and Co. KGaA.
Posen, S., and Hall, D. L. (2017). Nb3Sn superconducting radiofrequency cavities: fabrication, results, properties, and prospects. Supercond. Sci. Technol. 30, 033004. doi:10.1088/1361-6668/30/3/033004
Posen, S., Romanenko, A., Grassellino, A., Melnychuk, O. S., and Sergatskov, D. A. (2020). Ultralow surface resistance via vacuum heat treatment of superconducting radio-frequency cavities. Phys. Rev. Appl. 13, 014024. doi:10.1103/PhysRevApplied.13.014024
Sheikhzada, A., and Gurevich, A. (2020). Dynamic pair-breaking current, critical superfluid velocity, and nonlinear electromagnetic response of nonequilibrium superconductors. Phys. Rev. B 102, 104507. doi:10.1103/PhysRevB.102.104507
Sheikhzada, A., and Gurevich, A. (2017). Dynamic transition of vortices into phase slips and generation of vortex-antivortex pairs in thin film Josephson junctions under dc and ac currents. Phys. Rev. B 95, 214507. doi:10.1103/PhysRevB.95.214507
Transtrum, M. K., Catelani, G., and Sethna, J. P. (2011). Superheating field of superconductors within Ginzburg-Landau theory. Phys. Rev. B 83 (9), 094505. doi:10.1103/PhysRevB.83.094505
Vodolazov, D. Yu. (2000). Effect of surface defects on the first field for vortex entry in type-II superconductors. Phys. Rev. B 62, 8691–8694. doi:10.1103/PhysRevB.62.8691
Wang, Q-Y., Xue, C., Dong, C. C., and Zhou, Y-H. (2022). Effects of defects and surface roughness on the vortex penetration and vortex dynamics in superconductor–insulator–superconductor multilayer structures exposed to RF magnetic fields: numerical simulations within TDGL theory. Supercond. Sci. Technol. 35, 045004. doi:10.1088/1361-6668/ac4ad1
Watts-Tobin, R. J., Krähenbühl, Y., and Kramer, L. (1981). Nonequilibrium theory of dirty, current-carrying superconductors: phase-slip oscillators in narrow filaments near Tc. J. Low. Temp. Phys. 42, 459–501. doi:10.1007/BF00117427
Keywords: superheating field, superconductors, multilayered superconductors, vortices, Ginzburg–Landau theory
Citation: Pathirana WPMR and Gurevich A (2023) Superheating field in superconductors with nanostructured surfaces. Front. Electron. Mater. 3:1246016. doi: 10.3389/femat.2023.1246016
Received: 24 June 2023; Accepted: 15 August 2023;
Published: 07 September 2023.
Edited by:
Pashupati Dhakal, Jefferson Lab (DOE), United StatesReviewed by:
Akira Miyazaki, UMR9012 Laboratoire de Physique des 2 infinis Irène Joliot-Curie (IJCLab), FranceGianluigi Catelani, Forschungszentrum Jülich, Germany
Copyright © 2023 Pathirana and Gurevich. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: W. P. M. R. Pathirana, d2FsaXZlcGF0aGlyYW5hZ2VtckB2bWkuZWR1
 W. P. M. R. Pathirana
W. P. M. R. Pathirana A. Gurevich2
A. Gurevich2