Optimal limb regeneration strategies in Hemigrapsus sanguineus

Non-lethal injury in animals is both common and costly. The cost of regenerating autotomized limbs may leave less energy available for processes such as reproduction and growth, leading to trade-offs. Such trade-offs are context-dependent, and an individual’s energy allocation strategies may vary widely based on its condition and the environment. However, many traditional bioenergetics models have relied on fixed energy allocation rules, such as the -rule of dynamic energy budget theory, which assumes a fixed proportion (κ) of assimilated energy is always allocated to growth and maintenance. To determine whether incorporating optimality approaches into bioenergetics models improves the ability to predict energy allocation, we developed a dynamic state variable model that identifies optimal limb regeneration strategies in a model system, the Asian shore crab Hemigrapsus sanguineus. Our model predictions align with known patterns for this species, including increased regeneration effort with injury severity, a shift from reproduction to growth as consumption amount increases, and an increase in regeneration effort as regeneration progresses. Lastly, Monte Carlo simulations of individuals from a previous experiment demonstrate that flexible energy allocation successfully predicts reproductive effort, suggesting that this approach may improve the accuracy of bioenergetics modeling.

1 Introduction

Non-lethal injury is prevalent in both vertebrate and invertebrate animals (Lindsay, 2010) and exacts high energetic costs in the form of wound healing (Archie, 2013), reduced locomotive ability (Escalante et al., 2021), and decreased foraging ability (Smith and Hines, 1991). For those taxa which regenerate autotomized appendages, the energetic demands of regeneration leave even less energy available for other processes (Maginnis, 2006; Fleming et al., 2007). Indeed, individuals undergoing regeneration often exhibit reduced reproductive output (Griffen et al., 2020a; Prestholdt et al., 2022) and growth (Smith, 1990). This suggests the existence of energetic trade-offs between regeneration, growth, and reproduction, with important implications for fitness. Injured individuals are expected to have higher rates of mortality (Smith, 1995), so regeneration should increase survival and lifetime fecundity. On the other hand, allocating energy to growth should increase body size and the number of offspring that may be produced, and may also reduce mortality, as larger individuals are often less susceptible to predation (Marshall et al., 2005). Finally, allocating energy to reproduction will directly increase reproductive output and fitness. However, the relative benefits of each of these processes are context-dependent (Juanes and Smith, 1995; Maginnis, 2006), and are influenced by factors such as body size and age (Cheng and Chang, 1993), injury severity (Kuris and Mager, 1975), energetic state (Ballinger and Tinkle, 1979), and habitat quality (Griffen et al., 2020b). Therefore, to successfully predict how an organism should allocate its energy following injury, trade-offs and context must be considered.

There is a rich framework for modeling energetics based on energy budgets (Kitchell et al., 1977), the metabolic theory of ecology (Brown et al., 2004), and dynamic energy budget theory (Kooijman, 2010). These modeling approaches highlight the importance of individual-based ecology and have yielded valuable predictions. For example, dynamic energy budget theory has been used to successfully predict growth patterns in blue mussels (Mytilus edulis; Saraiva et al., 2012) and green sea turtles (Chelonia mydus; Stubbs et al., 2020), among other systems. However, there is often a disconnect between model energetic predictions and empirical observations (Chipps and Wahl, 2008). One reason for the relatively low accuracy of model predictions may be that incorrect parameters are used, or that parameters are not adjusted correctly based on spatial and temporal variation (Chipps and Wahl, 2008). Model predictions may also fall short when they rely on fixed energy allocation rules. For example, dynamic energy budget theory assumes that a fixed amount of energy is allocated to growth and maintenance, while the rest is allocated to reproduction and other non-essential processes (Kooijman, 2010). However, as stated above, energy allocation is subject to trade-offs and is often context-dependent (Stearns, 1989). The optimal energy allocation strategy may therefore vary over time and space, inconsistent with models that assume a fixed allocation strategy.

Optimality theory, flexible energy allocation, and bioenergetics models have not been widely integrated. To date, only two empirical studies have examined the efficacy of flexible energy allocation in the context of bioenergetics models, and both found that flexible allocation was an improvement over fixed allocation rules (Shertzer and Ellner, 2002; Lee et al., 2011). Shertzer and Ellner (2002) modified a dynamic energy budget model to enable flexible allocation to growth, while Lee et al. (2011) found that more complex models which incorporated variable allocation strategies matched observed patterns more closely than simpler models. Incorporating flexible energy allocation with bioenergetics and optimality theory may therefore improve energy allocation predictions. This approach is possible with dynamic models such as dynamic state variable models (Mangel and Clark, 1988; Clark and Mangel, 2000). These models have been used to predict a variety of optimal behavior strategies, including those pertaining to mate desertion (Kelly and Kennedy, 1993), migration (Farmer and Wiens, 1998; Weber et al., 1998; Clark and Butler, 1999; Pirotta et al., 2018), food-caching (Pravosudov and Lucas, 2001), reproductive strategies (Yerkes and Koops, 1999; Isvaran and St. Mary, 2003), and egg-laying in parasitoid wasps (Collier, 1995), and others. In contrast to static models, dynamic state variable models assume that individuals make decisions to optimize lifetime fitness, and optimal behaviors change based on the organism’s physiological state and the environment (Houston and McNamara, 1999; Clark and Mangel, 2000). Plumb et al. (2014) successfully incorporated one such dynamic model with bioenergetics modeling to predict depth selection in lake trout (Salvelinus namaycush); however, they did not determine whether this method yielded more accurate predictions than a simpler model with fixed energy allocation rules.

We developed a dynamic state variable model to predict optimal energy allocation strategies following nonlethal injury via lost limbs, using a basic bioenergetics model as its base. We validated the model by comparing its predictions to patterns established in the literature. To test whether the optimality model more accurately predicts reproductive effort than fixed energy allocation, we ran Monte Carlo simulations of individuals following either the optimal energy allocation strategies predicted by the model or fixed energy allocation strategies. We hypothesized that model-predicted energy allocation strategies to injury recovery vs. to growth or reproduction would vary with body size, time since maturity, energetic condition, habitat quality, injury severity, and regeneration progress. We further hypothesized that model-predicted regeneration strategies would match existing patterns in modeled systems (i.e., pattern-oriented modeling, Gallagher et al., 2021), consistent with evolutionary adaptations in model systems that increase fitness. Lastly, we hypothesized that simulations of individuals following the optimal energy allocation strategy would yield more accurate predictions of reproductive effort than simulations of individuals following fixed energy allocation strategies.

2 Materials and methods

2.1 Study system

As an example model system to explore the use of optimality in a bioenergetics model, we used the Asian shore crab, Hemigrapsus sanguineus. H. sanguineus is an abundant invader on the east coast of the US (Kraemer et al., 2007) and exhibits trade-offs between growth, regeneration of lost limbs, and reproduction (Vernier and Griffen, 2019; Griffen et al., 2020b, 2022, 2023; Prestholdt et al., 2022). Native to the western Pacific, it was first introduced to the New Jersey Coast in 1988 (Williams and McDermott, 1990; McDermott, 1991). To date, it has colonized much of the east coast, and established populations can be found from Maine to North Carolina (~ 45°N - 35°N; Epifanio, 2013). Like many other brachyurans, H. sanguineus experiences a high degree of non-lethal injury (limb loss) throughout its invaded range. Injury prevalence tends to hover around 40-50% for most populations (Davis et al., 2005; Delaney et al., 2011). Regeneration rates are also high in this species, with an average of 15.8% of all existing limbs still undergoing regeneration from historical injury (Griffen et al., 2023) and 63.8% of recently lost limbs developing limb buds, leading to reduced growth and reproductive output due to trade-offs (Griffen et al., 2022).

Work on other crabs shows that the regeneration process also depends on injury severity, or the number of limbs an individual has lost (Kuris and Mager, 1975; Pringle, 1990; He et al., 2016). Increased injury severity may trigger the molting process early, resulting in shorter intermolt periods and faster regeneration (Pringle, 1990; He et al., 2016); however, an increase in reproductive effort following loss of multiple limbs is also associated with smaller post-molt body sizes (Kuris and Mager, 1975). Therefore, regeneration effort is influenced by a range of factors, including energetic state, body size, severity of injury, etc. Like other crustaceans, crabs store their long-term energy reserves in lipids within the hepatopancreas, a digestive organ (Vogt, 2019). These reserves may be used to finance reproduction in combination with energy acquired via daily foraging (Griffen, 2018). Reproduction is thus influenced by available energy reserves and energy intake, and energy used for regeneration cannot be used in reproduction.

2.2 Model overview

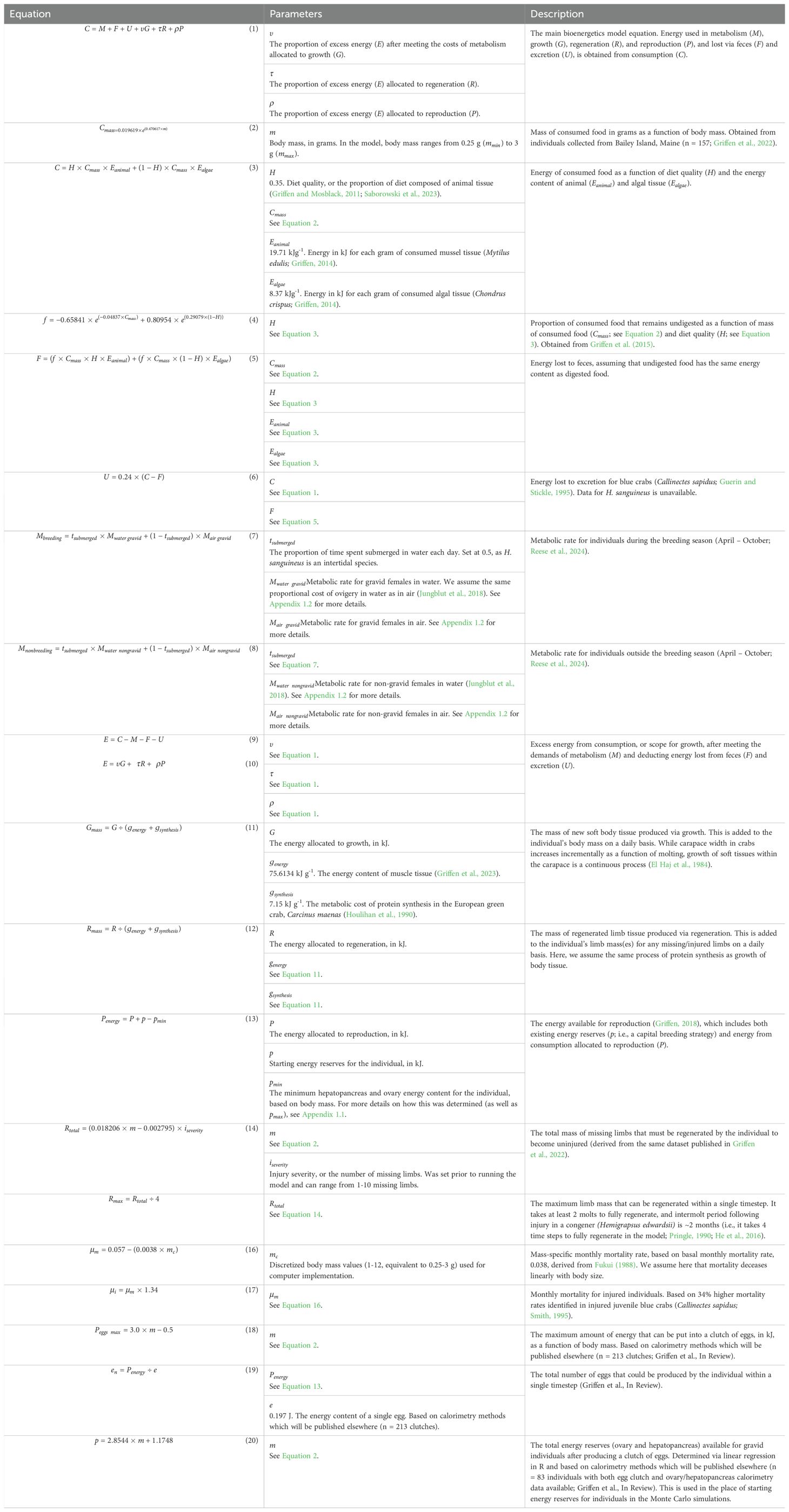
We developed a dynamic state variable model that determines optimal energy allocation decisions which maximize fitness in adult female individuals in R (v.4.1.2; R Core Team, 2021). We define fitness as the number of eggs produced by the female over her lifetime. We assume that the adult lifespan of H. sanguineus is 36 months (Fukui, 1988), and use this as the total time horizon (T) of the model. We used backward iteration and stochastic dynamic programming (following Clark and Mangel, 2000) to determine optimal energy allocation strategies (Table 1) over monthly model timesteps, which is long enough to match the resolution of field data, facilitating comparison between model predictions and observed field patterns. For an overview of the steps taken by the model within each time step, refer to Figure 1.

Table 1

Table 1. The ten possible energy allocation strategies.

Figure 1

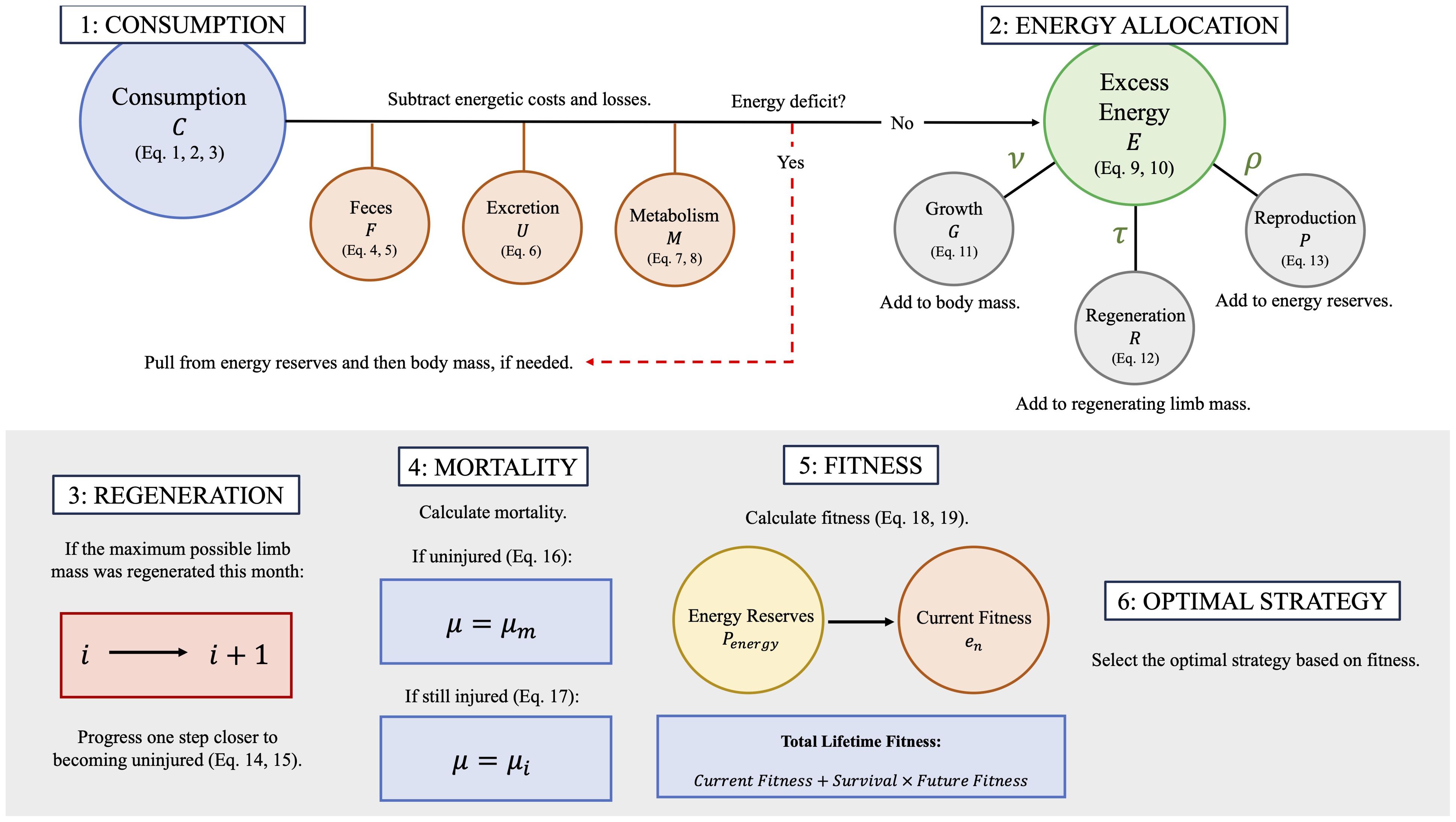
Figure 1. Diagram depicting the steps taken by the model for each iteration. Steps 1 and 2 are repeated 30 times, once for each day of the month. Steps 3-5 (gray box) are implemented at the end of each monthly time step. Lastly, this entire process is repeated ten times, once for each energy allocation strategy, and the strategy that produces the highest fitness is selected as the optimal strategy for that month and combination of state variables in Step 6. See Table 2 for corresponding equations.

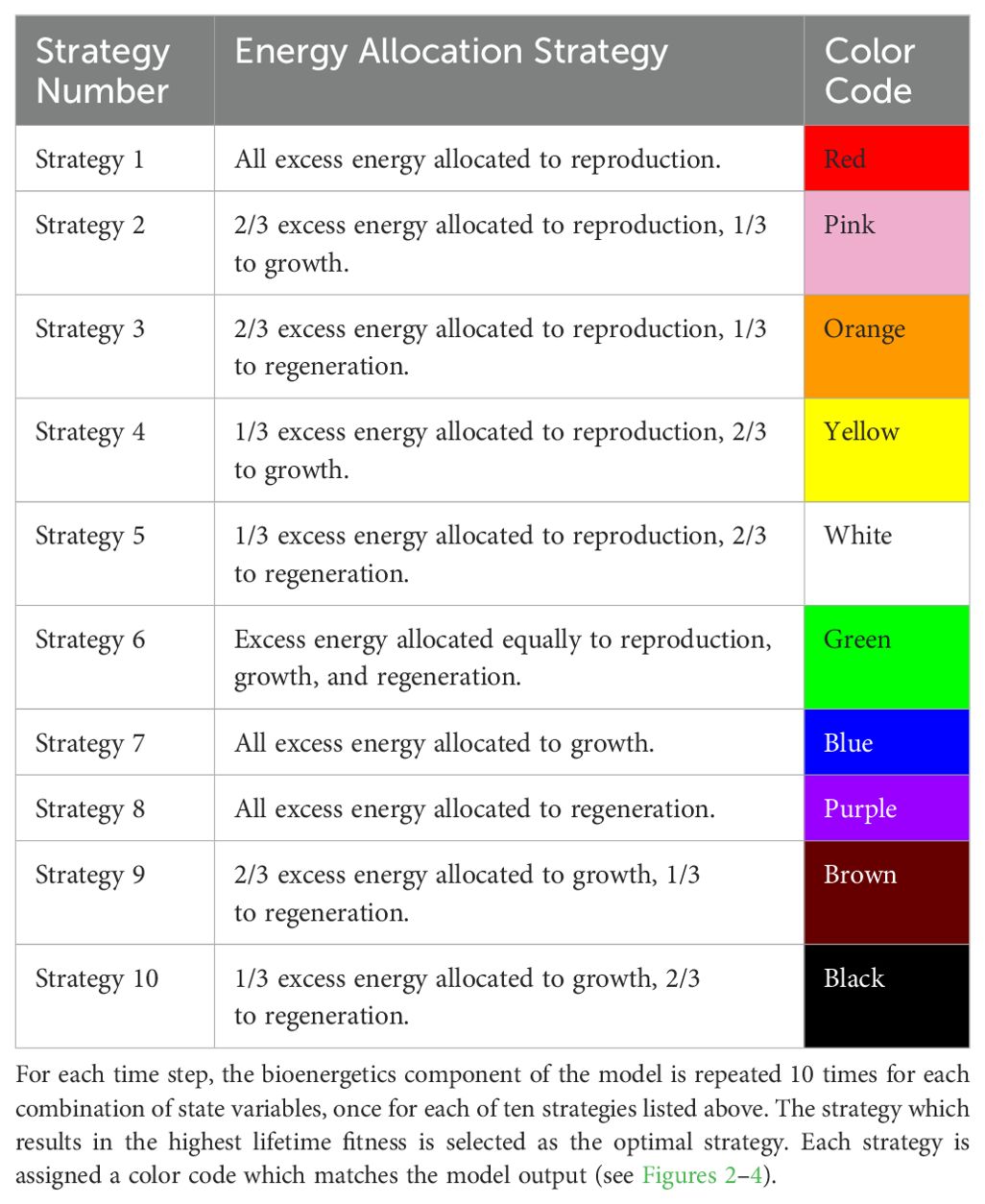
The dynamic state variable model centers around a basic bioenergetics model that tracks daily energy gains and losses in kJ (Table 2; Equation 1) using a Monte Carlo process within each monthly time step. For each of the 30 days, consumption (C; Table 2; Equations 2, 3) is calculated for the individual, and the energy lost to feces (F; Table 2; Equations 4, 5) and excretion (U; Table 2; Equation 6) and the costs of metabolism (M; Table 2; Equations 7, 8) are deducted from the individual’s energy intake (Figure 1, Step 1). Any remaining energy (E; Table 2; Equations 9, 10) is allocated to growth (G; Table 2; Equation 11), regeneration (R; Table 2; Equation 12), or reproduction (P; Table 2; Equation 13) based on each of ten possible energy allocation strategies (Table 1; Figure 1, Step 2). At the end of the month (t), the individual may progress to the next stage of regeneration and potentially become uninjured based on the total limb mass that must be regenerated ($R_{total}$; Table 2; Equation 14) and the maximum mass which can be regenerated in a single month ($R_{max}$; Table 2; Equation 15; Figure 1, Step 3). Next, the mortality is calculated based on the individual’s body mass (Table 2; Equation 16) and injury status (Table 2; Equation 17; Figure 1, Step 4). Lastly, the maximum number of eggs that may be produced by the female is calculated based on her available energy reserves and body size and added to her total lifetime fitness (Table 2; Equations 18, 19; Figure 1, Step 5). This process (Figure 1, Steps 1-5) is repeated for each of the ten possible energy allocation strategies (Table 1), and the strategy which results in the highest lifetime fitness is the optimal strategy for that month and combination of state variables (Figure 1, Step 6). For details on how each component of the bioenergetics model was calculated, see Table 2.

Table 2

Table 2. A compilation of equations and corresponding parameters used in the model.

2.3 State variables

The dynamic state variable model includes five state variables. The first is age, or time since sexual maturity in months (t). We assumed that age begins at the start of the breeding season, which varies based on latitude but typically lasts from April through October for invasive populations along the east coast of the US (Reese et al., 2024). Therefore, we also use this state variable to track temperature changes with time of year. The maximum age in months (T) is 36, or three years.

The second state variable is body mass (m), which does not include hepatopancreas or ovary mass. An individual may enter a time step with one of 12 possible body masses, ranging from 0.25 g (m_min) to 3 g (m_max) in increments of 0.25 g. The minimum and maximum values were determined from data collected throughout the invasive range of H. sanguineus (Griffen et al., 2022). Body mass changes during daily Monte Carlo periods within each monthly time step as the individual produces new mass with energy allotted to growth (G; Table 2; Equation 11) or loses mass due to an energy deficit.

The third state variable is energy reserves (p), and is also treated as a continuous variable within time steps. However, an individual may begin each time step with one of four possible discrete starting energy reserve levels, with an energy reserve (p) of 1 being the lowest and 4 being the highest. Starting energy reserves are then converted to continuous energy values (in kJ) with equation 2.3 from Clark and Mangel (2000). Maximum and minimum energy reserves were determined by plotting hepatopancreas and ovary mass against body mass, manually fitting upper and lower trend lines to the data, and converting from grams to kJ. For more details, see Appendix 1.1. The individual may add to their starting energy reserves each day (Table 2; Equation 13) depending on the energy allocation strategy (Table 1). To convert between continuous energy and mass values (kJ; g) and discrete values for these two state variables (1-4; 1-12) for computer implementation, we used equations 2.3, 2.4, 2.7, 2.9, and 2.10 from Clark and Mangel (2000) for two-dimensional linear interpolation.

The fourth state variable is regeneration stage (i), which is split into five states: newly injured, 1/4 regenerated, 1/2 regenerated, 3/4 regenerated, and completely regenerated. The fifth and final state variable is resource availability, or energy intake (c). Energy intake (c) is a multiplier which modifies basal consumption calculated from body mass (C; Table 2; Equation 3). Total energy intake may be 0.5x, 1x, or 2x basal consumption.

2.4 Model constants and parameters

Injury severity (i_severity), or the number of missing limbs that must be regenerated, is set prior to running the model, and can range from 1-10. Although each of the ten limbs may vary in terms of mass and contributions to foraging ability or movement (i.e., claws versus walking limbs), we chose to treat each limb equally by using the average walking limb mass for an individual of a given body size (Table 2; Equation 14). It may also be valuable to examine the optimal limb to regenerate using a similar dynamic programming approach; however, this lies outside the scope of this study, as our model was focused on whether an individual should allocate energy to regeneration, growth, or reproduction. Low injury severity (1-3 missing limbs) is most common in H. sanguineus (Davis et al., 2005), so we chose to report most of our results at the lowest level of injury (i_severity = 1), To capture moderate and severe levels of injury, we also ran the model for individuals missing 2, 3, 4, and 6 missing limbs. It is rare for individuals to be missing more than 6 limbs at any given time (Davis et al., 2005).

Basal monthly mortality (μ_base) was derived from Fukui (1988), and is 0.038. Mortality is also expected to decrease with body size (Marshall et al., 2005) and increase with injury (Smith, 1995). While the precise effects of body size and injury on mortality are unknown for H. sanguineus, we assumed for the purpose of the model that mortality decreases linearly with body size (Table 2; Equation 16). To account for the effects of injury on mortality, we then multiplied body mass specific mortality (μ_m) by 1.34 (Table 2; Equation 17) for all injured individuals, resulting in 34% higher mortality rates for injured individuals compared to uninjured individuals. This is based on the 34% higher mortality rates reported for juvenile blue crabs (Callinectes sapidus) missing walking limbs compared to intact individuals (Smith, 1995), as no data are currently available for Hemigrapsus spp. For additional constants and parameters, see Table 2.

2.5 State dynamics and stochastics

The energy reserves (p), body mass (m), and injury status (i) of an individual may change within each time step according to energy allocation strategy (Table 1) and the bioenergetics model (Table 2; Equation 1). If an individual experiences an energy deficit based on energy consumed, this deficit is financed first by energy reserves, and then by muscle tissue, if needed (Figure 1, Step 1). There are currently no data available on the percentage of total muscle tissue that may be metabolized, or the proportion of body mass comprised of carapace versus muscle tissue, for H sanguineus or related species. However, given that individuals likely rely on mobility for foraging and evading predators, it is not probable that an individual would survive with less than half of their muscle tissue. We conservatively assume that an individual may only use half of their available muscle tissue to meet energy demands, and that muscle tissue makes up half of the individual’s total body mass (with carapace comprising the other half). Thus, if the energy deficit exceeds a quarter of the individual’s body mass, then the individual is considered dead, and the time step ends with a fitness value of 0. Any excess energy (E; Table 2; Equation 10) is divided according to energy allocation strategy (Table 1). Body mass (m), energy reserves (p), and the mass of regenerated tissue (R_mass) are updated for the day based on the proportion of available energy allocated to each (ν, τ, and ρ; Figure 1, Step 2).

To determine whether an individual’s regeneration stage (i) should change, the total mass of regenerated tissue that must be regenerated (R_total) is calculated based on the number of missing limbs and body mass (Table 2, Equation 14). Consistent with data from injured congeners (Hemigrapsus edwardsii; Pringle, 1990), we assumed that the intermolt period is 2 months, and that two molts are required to fully regenerate limbs. Thus, the maximum mass that may be regenerated each month ($R_{max}$; Table 2; Equation 15) is 1/4 the total mass that must be regenerated ($R_{total}$). If the individual reaches this point within the timestep, at the end of the month, they progress to the next regeneration stage.

Once m, p, and i have been updated based on the bioenergetics model, potential reproductive output is calculated based on how much energy was allocated to energy reserves that month and whether it is during the breeding season (April through October; Reese et al., 2024). To determine fitness for the current timestep (t) within the breeding season, the energy reserves available for reproduction are determined based on the maximum clutch mass that can be produced for a given body size (Table 2; Equation 18). If total energy reserves exceed this amount, then only the maximum amount is used to produce eggs, and the rest remains in the energy reserves for use in future reproduction. The number of eggs that may be produced for a given month (e_n(t)) is calculated by dividing available energy reserves by the energy content of a single egg (e, obtained calorimetrically; Griffen et al., In review; Table 2; Equation 19). For months falling outside the breeding season, total lifetime fitness consists only of future fitness based on the current stored energy reserves and probability of survival.

2.6 Decision variables

The model includes only one decision variable to maximize fitness: the relative proportions (ν, τ, and ρ) of excess energy (E) allocated to growth (G), regeneration (R), and reproduction (P), respectively. These proportions are likely continuous in real populations, ranging from 0-1, with all three summing to 1. However, for computer implementation, we discretized these values by splitting excess energy (E) into thirds, assuming that each third may be allocated independently to growth (tG), regeneration (R), or reproduction (P). This results in 10 possible energy allocation strategies (Table 1). The strategy which produced the highest fitness was then selected as the optimal strategy for that timestep and combination of state variables.

2.7 Fitness function and dynamic programming equation

The fitness function (V_z) is based on the daily bioenergetics model used within monthly timesteps, and is solved for each of the 10 possible energy allocation strategies (z). It is represented by the following function:

$\begin{array}{ll}{V}_z(m,p,i,t,c)=e_n(t)+(1-\mu )(F(m,p,i,t+1,c))& (21)\end{array}$

Where $e_n$(t) represents current fitness, ($1-\mu$) represents the probability of surviving to the next time step, and F($m, p, i, t+1, c$) represents future fitness. We assume that no reproduction occurs at the end of the individual’s life ($t=36$); thus, terminal fitness is 0.

The dynamic programming equation identifies optimal energy allocation, or the allocation strategy which maximizes fitness (F), for each combination of the five state variables. It can be written as:

$\begin{array}{ll}F(m,p,i,t,c)=\text{max}\left\{V_1(m,p,i,t,c), V_2(m,p,i,t,c)\dots V_{10}(m,p,i,t,c)\right\}& (22)\end{array}$

2.8 Model validation

To validate our model, we compared its output to the three following patterns established in the literature for H. sanguineus and closely related congeners. 1) Regeneration effort should increase with injury severity, while growth should decrease (Kuris and Mager, 1975; He et al., 2016). 2) Individuals consuming higher energy diets should allocate more energy to growth, and individuals consuming lower energy diets should allocate more energy to reproduction (Griffen et al., 2020b). 3) Regeneration effort should increase as individuals get closer to fully regenerating their limbs, while growth and reproductive effort should decrease (Griffen et al., 2023; Prestholdt et al., 2022).

While the model was run for all combinations of state variables, Figures 2–4 graphically depict predictions for individuals at basal consumption, with a starting energy reserve value of 3 and one missing limb which is 3/4 regenerated. We chose to focus on this specific combination of state variables because it yielded clear patterns for comparison with published literature; however, the patterns we discuss in the results below are present at most if not all possible state variable combinations. Model code and files are included as Supplementary Materials and may be run to produce graphs for all combinations of state variables.

2.9 Monte Carlo simulations

To determine whether incorporating optimality modeling into bioenergetics models improves predictions, we ran Monte Carlo simulations of individuals following both optimal and fixed energy allocation strategies. The κ-rule of dynamic energy budget theory assumes that a fixed proportion of assimilated energy (κ) is allocated to growth and somatic maintenance (i.e., regeneration), while the rest is allocated to reproduction (1–κ). While κ has not been estimated for H. sanguineus, it can vary widely based on the system, from 0.437 in the earthworm Eisenia fetida (Rakel et al., 2020) to 0.9 in the European green crab, Carcinus maenas (Talbot et al., 2019). In our simulations, individuals could follow two different fixed energy allocation strategies: 1) energy is divided equally between growth, regeneration, and reproduction (i.e., a third of excess energy is allocated to each; $\kappa =0.67$), or 2) 45% of available energy is allocated to growth, 45% of available energy is allocated to regeneration, and 10% of available energy is allocated to reproduction ($\kappa =0.9$). We chose to use a value of 0.9 for the second fixed strategy because this is the value empirically determined for another brachyuran crab, C. maenas (Talbot et al., 2019). These two κ-rule options were then compared to the third option, where individuals followed the optimal energy allocation strategy as predicted by the dynamic state variable model.

We simulated individuals from an experimental dataset first published (and described in full) in Griffen et al. (2015). Briefly, forty gravid adult female individuals were captured and egg release was stimulated using temperature modulation. After this, crabs were kept submerged in a lab setting for ~ 8 weeks, during which they were fed differing amounts of algae (Chondrus crispus) and mussel (Mytilus edulis) two times a week depending on their experimental treatment. At the conclusion of the experiment, individuals were dissected and energy allocation to reproduction was measured.

We simulated this experiment by starting each individual with the body mass and number of missing limbs that were measured at the beginning of the experiment. Energy reserves for each individual were not measurable at the start of the experiment, so we calculated starting energy reserves as a function of body size for gravid individuals (Table 2; Equation 20) and used this for the starting energy reserves. Each day of the experiment was then simulated. For each individual and on each feeding day, the dynamic state variable model was run for that day’s measured diet quality and consumption amount to determine the optimal energy allocation strategy, and energy from consumption was divided accordingly. On non-feeding days, metabolic costs in water (Jungblut et al., 2018; Appendix 1.2) were deducted from the individual’s energy reserves. At the end of the eight-week simulation period, we calculated the number of eggs that could be produced by each individual based on existing energy reserves (Table 2; Equation 19) for each of the three possible energy allocation strategies described above.

We determined model fit by comparing the model-predicted and observed allometric relationship between possible clutch size and final body size. Specifically, we used linear regression and ANCOVA in R (v.4.1.2; R Core Team, 2021) to identify significant differences in slope and intercept between the observed relationship and each of the three energy allocation models. First, we tested the relationship between clutch size and body size for the observed and simulated data with linear regression, with clutch size as the response variable and body size as the explanatory variable. Next, we ran a separate ANCOVA test for each of the three energy allocation strategies, with clutch size as the response variable and body size, data type (simulated or observed), and the interaction between the two as explanatory variables. A significant main effect of data type or its interaction would indicate a lack of similarity between simulated and observed clutch size.

3 Results

As we hypothesized, each of the five state variables (body size, starting energy reserves, energy intake, time since maturity, and regeneration stage) influenced optimal energy allocation strategies, though the results were heavily context dependent, and each of the state variables interacted with each other. Regeneration occurred most frequently in small (0.25 - 1 g) and large (2 -3 g) individuals, reproduction dominated at low starting energy reserves, while growth dominated at higher starting energy reserves, and seasonal effects on energy allocation were strongest at low energy intake. See Appendix 2 for more details and discussion of these results. It should also be noted that while we ran the model over all possible combinations of state variables, not all combinations are biologically realistic. For instance, in nature, we would not expect to see a newly matured individual with a body mass of 3 grams, as age and body size are tightly linked in species with indeterminate growth. Results should therefore be interpreted carefully with this in mind. Below, we compare the model predictions to patterns that have been empirically observed.

3.1 Pattern #1: the effect of injury severity on energy allocation

In line with the findings of Kuris and Mager (1975) for the congener H. oregonensis, and the findings of He et al. (2016) for the Chinese mitten crab Eriocheir sinensis, our model predicted that as injury severity increased, regeneration effort, or the proportion of available energy allocated to regeneration, should increase (Figure 2). However, the model also predicted that regeneration effort should not change between one and three missing limbs, and should only increase once four or more limbs are missing. Additionally, when this increase in regeneration effort occurred, we observed a shift away from growth-dominated strategies in favor of regeneration-dominated strategies (Figure 2), indicating a trade-off between growth and regeneration that may be instigated as the extent of injury increases. Increasing injury severity at low energy intake (0.5x basal consumption) was the exception to these patterns. The model did not predict an increase in regeneration effort for individuals with moderate and high injury severity at low consumption; instead, regeneration effort was often lower relative to individuals with low injury severity.

Figure 2

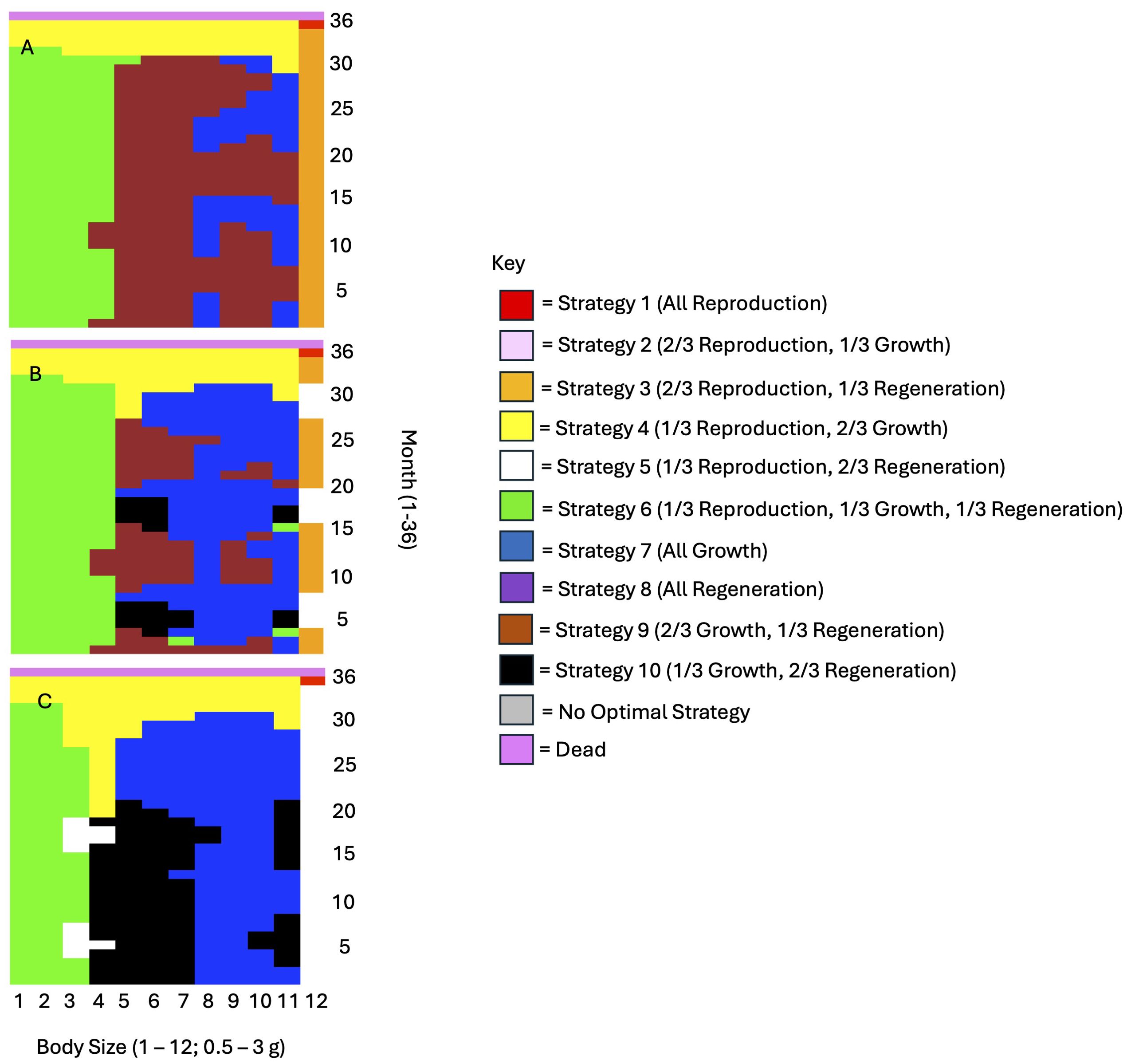
Figure 2. Kuris and Mager (1975) empirically demonstrated that regeneration effort should increase with injury severity. This figure depicts optimal energy allocation strategies as a function of injury severity for (A) 1 missing limb, (B) 4 missing limbs, and (C) 6 missing limbs. The graphs shown here are for individuals consuming the basal consumption amount, with a starting energy reserve value of 3, and 3/4 regenerated limbs.

3.2 Pattern #2: the effect of energy intake on energy allocation

Griffen et al. (2020b) empirically found that higher energy intake (in terms of total energy consumed, but not nutrient content) should increase energy allocation to growth. Similarly, our model predicted that higher energy intake should increase energy allocation to growth and regeneration, and lower energy intake should increase energy allocation to reproduction (Figure 3). This pattern consistently held true across all levels of injury severity, regeneration stage, and starting energy reserves. Additionally, while the prevalence of energy allocation strategies involving regeneration did not necessarily change with energy intake, the proportion of energy allocated to regeneration was higher at low energy intake compared to basal and high energy intake (see the change from regeneration-dominated Strategy 8 in Figure 3A to reproduction and growth dominated strategies in Figures 3B, C).

Figure 3

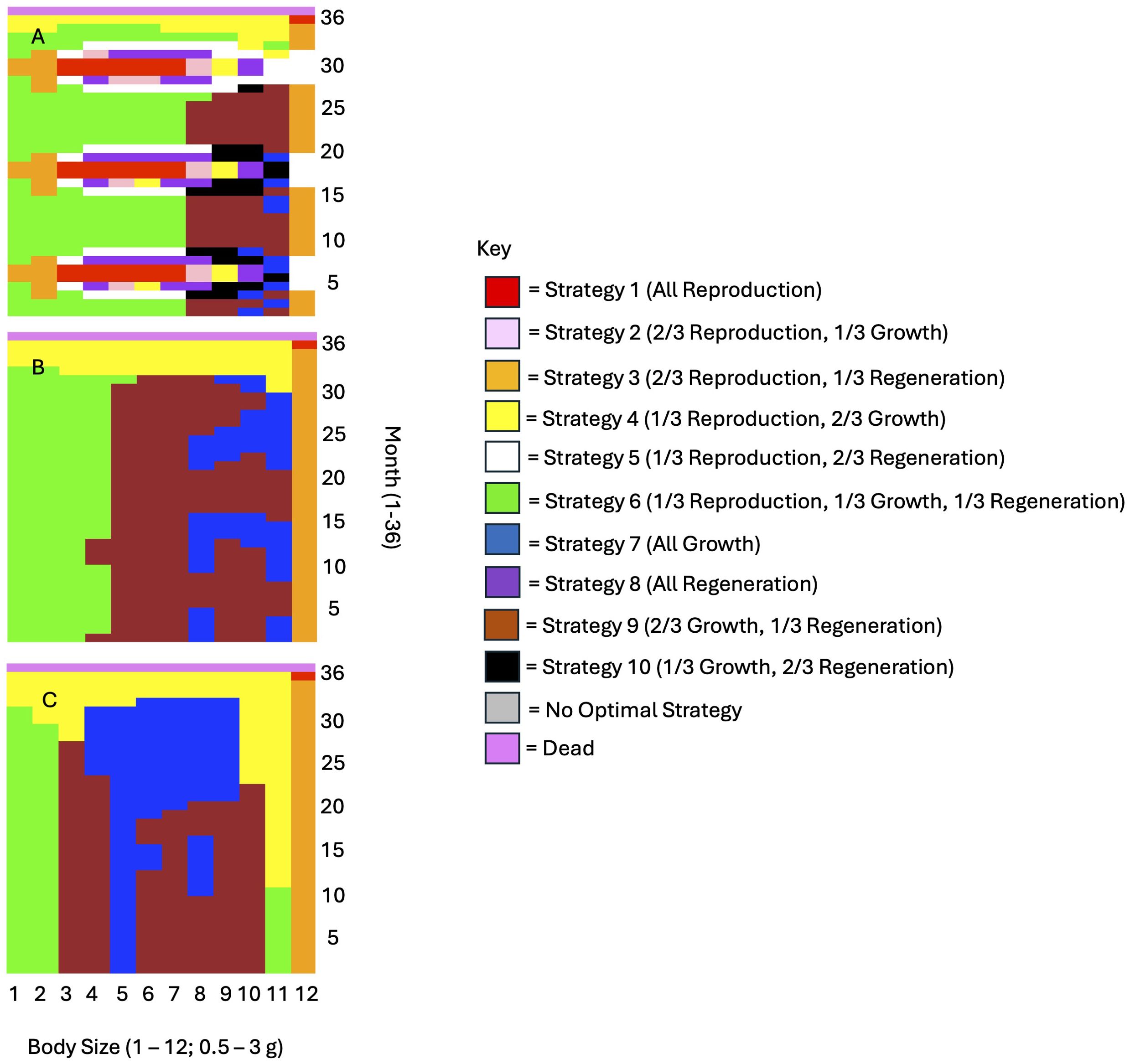
Figure 3. According to Griffen et al. (2020b), higher energy intake (in terms of total energy consumed, but not nutrient content) should increase energy allocation to growth and decrease energy allocation to reproduction. This figure depicts optimal energy allocation strategies as a function of energy intake for (A) half the basal consumption amount calculated from body mass, (B) the basal consumption amount, and (C) 2x the basal consumption amount. The graphs shown here are for individuals with a starting energy reserve value of 3, 3/4 regenerated limbs, and 1 missing limb.

3.3 Pattern #3: the effect of regeneration stage on energy allocation

As we expected based on the findings of Griffen et al. (2023), regeneration effort increased as regeneration neared completion (Figure 4). However, the strength of this increase varied with other state variables. For instance, the increase in regeneration was strongest at high starting energy reserves (p = 3 or 4) and high energy intake (1x and 2x basal consumption). It was weaker with severe injury (6 missing limbs). Lastly, energy allocation to growth and reproduction both decreased as missing limbs became closer to being fully regenerated.

Figure 4

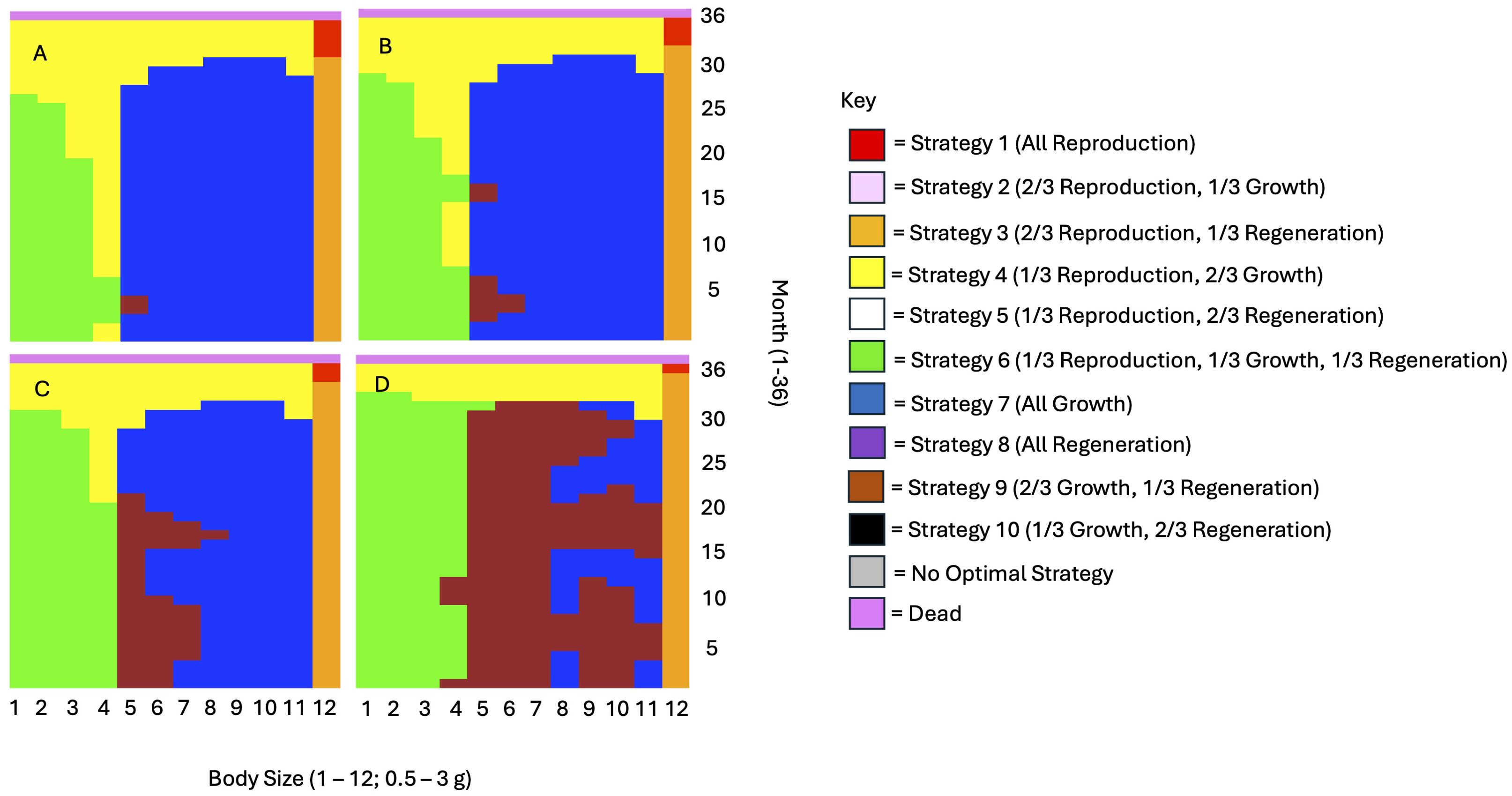
Figure 4. Regeneration effort is known to increase the closer a missing limb is to being fully regenerated (Griffen et al., 2023). This figure depicts optimal energy allocation strategies as a function of regeneration stage for (A), newly injured individuals, (B) individuals with 1/4 regenerated limbs, (C) individuals with 1/2 regenerated limbs, and (D) individuals with 3/4 regenerated limbs. The graphs shown here are for individuals consuming the basal consumption amount, with a starting reserve value of 3, and 1 missing limb.

3.4 Monte Carlo simulations

We hypothesized that the optimal energy allocation strategy would produce more accurate predictions than the fixed energy allocation strategies when making individual-level predictions. While only one of the fixed strategies differed significantly from the observed data, the flexible energy allocation model produced the closest match (Figure 5A), and the fixed allocation models appeared to underestimate reproductive effort (Figures 5B, C). Specifically, observed clutch size increased by 10676 ± 3309 eggs for every gram of body mass (t = 3.227, p = 0.0026), with an intercept of -1978. Optimal clutch size increased by 7598 ± 3248 eggs for every gram of body mass (t = 2.339, p = 0.0247), with an intercept of 2148. Neither the interaction term (t = 0.664, p = 0.5089) nor the main effect of data type (t = - 0.658, p = 0.5125) had a significant impact on clutch size, indicating that the slope and intercept of the optimal model did not differ from the observed.

Figure 5

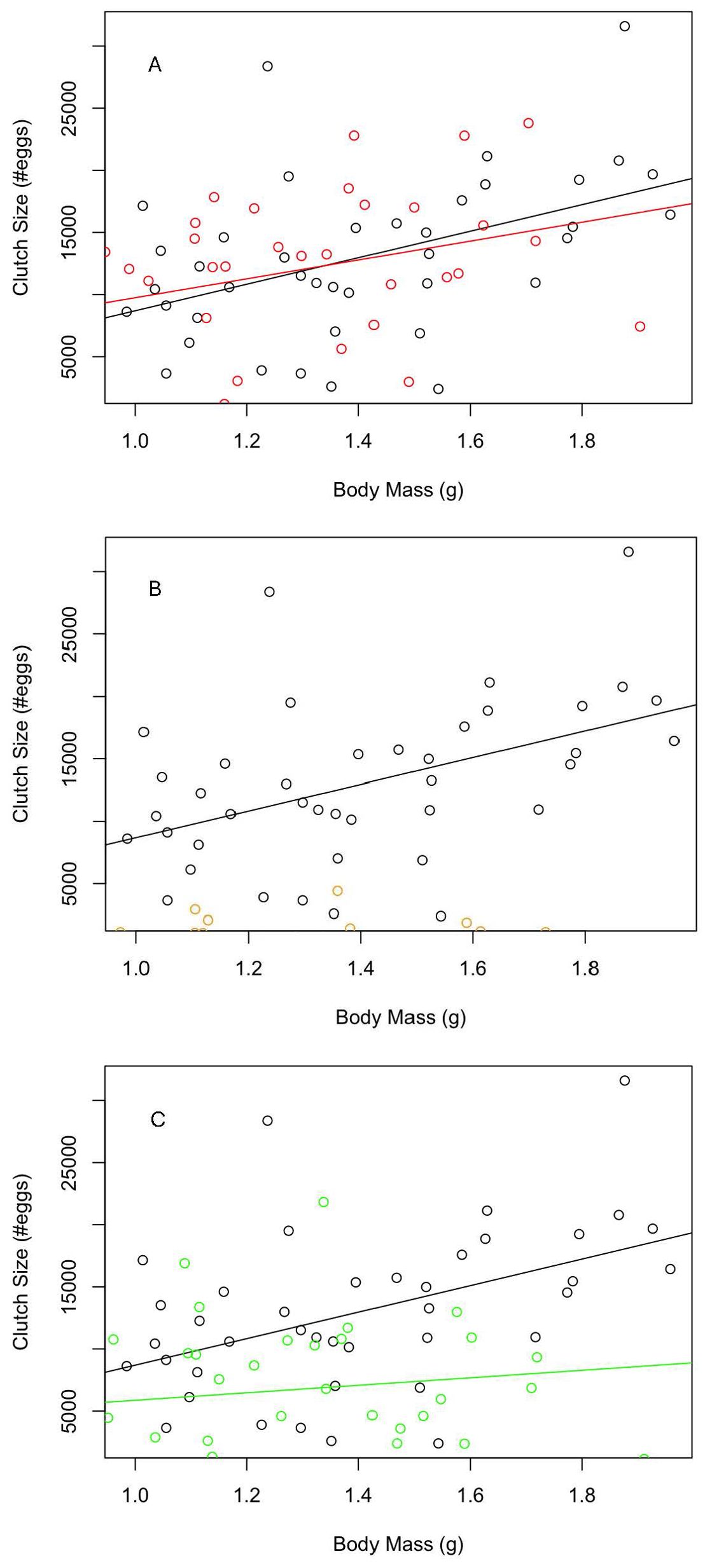
Figure 5. Simulation-predicted clutch size as a function of body size for (A) individuals following the optimal strategy as determined by the dynamic state variable model (in red), (B) individuals following a fixed energy allocation strategy with a κ value of 0.2 (in blue), and (C), individuals following a fixed energy allocation strategy where they always divide energy equally between growth, regeneration, and reproduction (in green; κ = 0.67). Colored points denote model-predicted clutch size, while black points denote observed clutch size for the experimental individuals (Griffen et al., 2015).

Clutch size for the first fixed allocation model (=0.2) increased by 5432.3 ± 1661.7 eggs for every gram of body mass (t = 3.269, p = 0.0.0016), with an intercept of -798.6. Its slope did not differ significantly from the observed, as demonstrated by the non-significant interaction term (t = - 0.005, p = 0.9958). However, its intercept did differ significantly from the observed based on a significant effect of data type on clutch size (t = 3.156, p = 0.0023). Lastly, clutch size for the second fixed allocation model (energy divided evenly) increased by 3015 ± 2897 eggs for every gram of body mass, though not significantly (t = 1.041, p = 0.3050), with an intercept of 2957. Despite no significant increase in clutch size with body size, the slope for this model did not differ from the observed, as the interaction between data type and body size was not significant (t = 1.744, p = 0.0853). Its intercept also did not differ significantly from the observed (t = - 0.816, p = 0.4171).

4 Discussion

To examine whether incorporating optimality into bioenergetic models produces more accurate predictions than fixed energy allocation models, we designed a dynamic state variable model using H. sanguineus as a study system. We tested the model’s predictive ability by comparing its results to patterns established in the literature and by running Monte Carlo simulations for individuals following fixed and optimal energy allocation strategies. The optimal energy allocation strategies predicted by the dynamic state variable model differed based on each of the state variables, which also interacted with each other. Overall, the model predicted that regeneration effort should increase with the number of missing limbs, growth should be favored over reproduction at high energy intake and vice versa, and that regeneration effort increases as individuals become closer to fully regenerating their limbs. These predictions largely matched patterns established in the literature, supporting the accuracy of our model predictions. Similarly, our Monte Carlo simulations demonstrated that flexible energy allocation accurately predicts reproductive effort as a function of body size, suggesting that this approach may improve bioenergetics modeling.

The first pattern we examined with our model was energy allocation as a function of non-lethal injury severity, or the number of missing appendages an individual has. Our model predicted that as injury increases, the energy allocated to regeneration should increase. In some systems, the loss of multiple appendages is indeed associated with shorter molt intervals following injury compared to loss of only a single limb (Pringle, 1990; Smith, 1990; He et al., 2016), demonstrating that our model is capable of accurately predicting energy allocation strategies in response to non-lethal injury. Curiously, the increase in regeneration predicted by the model was not uniform. Our model predicted that an increase in regeneration effort should only occur once an individual is missing 4 or more limbs, demonstrating the potential presence of an energetic threshold below which minimal regeneration effort is acceptable, and above which regeneration effort must increase to meet the demands of regenerating additional limbs. In H. sanguineus, our model system, the loss of four or more limbs is uncommon (Davis et al., 2005), and our results suggest adaptive resilience to lower levels of injury that are more common. Similarly, in harvestmen (Nelima paessleri), active metabolic rate only increases after losing three or more limbs (Escalante et al., 2021). Given this evidence and our model’s predictions, it is possible that such an energetic threshold exists for any organism which experiences limb autotomy, and may depend on the frequency of non-lethal injury in each species or population. However, additional research is needed to confirm this hypothesis.

The second pattern we examined to test the efficacy of our model was energy allocation as a function of energy intake. The model predicted that at higher energy intake, individuals should prioritize growth, while at lower energy intake, individuals should prioritize reproduction. This occurs in the model due to energetic limitations; the costs of growth likely outweigh the benefits for individuals with low energy intake. In general, this prediction matches trends established in the literature for arthropods. For example, female yellow dung flies (Scathophaga stercoraria) reach smaller adult body sizes and produce larger clutches relative to body mass in response to low food availability, and vice versa (Reim et al., 2006). Conversely, in our model species, H. sanguineus, individuals consuming higher quality diets prioritize reproduction over growth (Griffen et al., 2020b). In this specific example, however, energy may be less important than nutrient intake, as many herbivorous crabs are nitrogen-limited (Kennish, 1997; Linton and Greenaway, 2000). It is therefore possible that in some species, nutrient availability, not energy, is the primary limiting factor when it comes to trade-offs between growth and reproduction. In yet other species, such as the seed beetle Callosobruchus maculatus, where growth and reproduction are temporally isolated, high food availability may eliminate a trade-off between the two processes altogether and lead to a direct positive correlation between growth and fecundity (Messina and Slade, 1999). Thus, depending on the species, reproductive timing, energy intake, and nutrient availability may each play a role in driving trade-offs between growth and reproduction.

The third and final pattern used to test our model was energy allocation as a function of regeneration progress. According to the model, regeneration effort should increase the closer an individual is to completing the regeneration process, representing a final push toward becoming uninjured and reducing mortality risk. While direct measurements of regeneration effort over time for many systems are unavailable, Griffen et al. (2023) demonstrated that trade-offs between growth and regeneration and energy storage and regeneration are strongest at later stages of regeneration in H. sanguineus, when previously lost limbs are nearly fully formed. This finding seems to support the model’s predictions. The exception to this pattern occurs at lower consumption and energy reserves and with more severe injury. In these cases, energy is more limited, preventing individuals from allocating more energy to regeneration as regeneration approaches completion. Therefore, depending on energy availability, individuals closer to fully regenerating their limbs should be expected to increase the energy they allocate to limb regeneration and decrease reproductive effort. Future studies should empirically investigate whether regeneration effort increases as the regeneration process proceeds, both in H. sanguineus and other species of arthropods which undergo limb regeneration.

All ecological models are based on assumptions, and the utility of a model largely depends on how realistic its assumptions are. For example, one important assumption we made was that energy reserves are devoted solely to future reproduction, and are not used to finance growth or regeneration. In many systems, this assumption may not reflect reality; however, when we attempted to divide energy reserves between the three processes according to the ten possible strategies (Table 1), the model predicted that it was never optimal to regenerate. This could indicate one of two things: either some species do not finance regeneration with energy reserves, or there are additional benefits to regeneration not captured by our model, such as restoring mobility (Dorrance et al., 2021) or foraging ability (Smith and Hines, 1991; Davis et al., 2005). Future research should evaluate whether regeneration is financed by energy reserves, daily consumption, or both. Regardless, our model still produces realistic predictions in general, implying that the assumption we made here was either unimportant for optimal energy allocation or realistic for our model species.

When parameterizing an ecological model, it is important to use parameters for the specific model system whenever possible. Dynamic state variable models depict the optimization of fitness, an evolutionary process; thus, by borrowing parameters from other species, however closely related they may be, an ecologist may unintentionally ignore aspects of the species’ unique evolutionary history. Despite this, limited data availability sometimes necessitates the use of parameters from closely related species. For example, for parameters which were unknown for H. sanguineus, we had to rely on congeners or other species of crabs. We used data from the congener H. edwardsii to determine that it should take at least four time steps to fully regenerate a limb (Pringle, 1990) and we used data from the congeners H. oregonensis (Kuris and Mager, 1975) and H. nudus (Prestholdt et al., 2022) to validate our model’s predictions. We also used data for the Chinese mitten crab (E. sinensis), which belongs to the same family, Varunidae, to validate our model’s predictions (He et al., 2016). For injury specific mortality (Smith, 1995) and energy lost to excretion (Guerin and Stickle, 1995), we had to rely on data from the blue crab (Callinectes sapidus), a brachyuran from a different family (Portunidae). Similarly, we had to use data for European green crabs (Carcinus maenas; family Portunidae) for the metabolic cost of protein synthesis (Houlihan et al., 1990).We would expect this to lead to some incongruence between our model’s predictions and patterns observed in nature. However, given that several predictions made by the dynamic state variable model qualitatively align with patterns in nature, and that the vast majority of the parameters and variables we use come from our focal species, we are confident that any incongruences of this nature are minimal for our model. While our model may be adjusted to make predictions for any crab which experiences trade-offs between growth, regeneration, and reproduction, we caution against using a species for which few data are available.

One of the hypotheses we chose to test was that incorporating optimality into bioenergetics models would yield more accurate predictions than traditional bioenergetics models with fixed energy allocation. The Monte Carlo simulations supported this hypothesis. Only one of the three models differed significantly from the observed (fixed, $\kappa =0.9$), indicating that either the optimality model or the second fixed strategy ($\kappa =0.67$) could be used to predict reproductive effort, but the optimal energy allocation model produced the closest match (Figure 5). This suggests that while fixed energy allocation models are still relatively successful at making predictions, flexible energy allocation models provide heightened accuracy and may improve bioenergetics modeling, consistent with our hypothesis. However, differences between model-predicted and observed reproductive effort for specific individuals occurred frequently in the simulations, suggesting that making one-to-one comparisons between an individual animal and its model-predicted traits is not always possible. Thus, this approach is likely most effective at predicting general trends in life-history traits across individuals, and has the potential to improve the accuracy of bioenergetics modeling.

The purpose of this study was to develop a dynamic state variable model to examine optimal regeneration strategies and the utility of incorporating optimality with bioenergetics modeling. We have demonstrated that our dynamic state variable model is capable of making general qualitative predictions about optimal energy allocation, but the model has other potential applications which we have not yet explored. For instance, it may be altered to examine how optimal energy allocation strategies change based on the type of missing appendage (walking limbs, feeding appendages, etc.), or how optimal strategies change across latitudes for species with wide geographical ranges. Furthermore, while the model may not be directly applied to some taxa (i.e., taxa which do not need to molt to regenerate, or taxa which lose their energy reserves along with autotomized appendages, such as lizards or sea stars), it may be adapted to make predictions for species which share similar behaviors, physiology, and life history traits with H. sanguineus. Despite this, many of the trade-offs predicted by our model are broadly applicable to all systems which undergo autotomy, including decreased growth and reproduction as a result of regeneration (Maginnis, 2006). A similar modeling approach could be used to examine when it is optimal to drop a limb, as many factors are known to influence the likelihood of injury, such as the reproductive status of females (Hobbs et al., 2017) and latitude (Griffen et al., 2022). As it is, our model’s predictions match patterns established in the literature, and simulations demonstrated that flexible energy allocation accurately predicts patterns of reproductive effort across individuals. Therefore, this approach has promise for other systems as a method of incorporating trade-offs and optimal strategies into bioenergetics modeling, consistent with life history theory.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Ethics statement

The manuscript presents research on animals that do not require ethical approval for their study.

Author contributions

LF: Data curation, Formal analysis, Methodology, Visualization, Writing – original draft, Writing – review & editing. BG: Conceptualization, Funding acquisition, Methodology, Writing – review & editing, Supervision.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was funded by National Science Foundation grant 2052246.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2024.1462916/full#supplementary-material

References

Archie E. A. (2013). Wound healing in the wild: stress, sociality and energetic costs affect wound healing in natural populations. Parasite Immunol. 35, 374–385. doi: 10.1111/pim.12048

PubMed Abstract | Crossref Full Text | Google Scholar

Ballinger R. E., Tinkle D. W. (1979). On the cost of tail regeneration to body growth in lizards. J. Herpetology. 13, 374–375. doi: 10.2307/1563343

Crossref Full Text | Google Scholar

Brown J. H., Gillooly J. F., Allen A. P., Savage V. M., West G. B. (2004). Toward a metabolic theory of ecology. Ecology. 85, 1771–1789. doi: 10.1890/03-9000

Crossref Full Text | Google Scholar

Cheng J. H., Chang E. S. (1993). Determinants of postmolt size in the American lobster (Homarus americanus). I. D13 is the critical stage. Can. J. Fisheries Aquat. Sci. 50, 2106–2111. doi: 10.1139/f93-235

Crossref Full Text | Google Scholar

Chipps S. R., Wahl D. H. (2008). Bioenergetics modeling in the 21st century: reviewing new insights and revisiting old constraints. Trans. Am. Fisheries Society. 137, 298–313. doi: 10.1577/T05-236.1

Crossref Full Text | Google Scholar

Clark C. W., Butler R. W. (1999). Fitness components of avian migration: a dynamic model of Western Sandpiper migration. Evolutionary Ecol. Res. 1, 443–457.

Google Scholar

Clark C. W., Mangel M. (2000). Dynamic state variable models in ecology: methods and applications (Oxford University Press, New York, USA).

Google Scholar

Collier T. R. (1995). Adding physiological realism to dynamic state variable models of parasitoid host feeding. Evolutionary Ecology. 9, 217–235. doi: 10.1007/BF01237769

Crossref Full Text | Google Scholar

Davis J. L., Dobroski N. A., Carlton J. T., Prevas J., Parks S., Hong D., et al. (2005). Autotomy in the Asian shore crab (Hemigrapsus sanguineus) in a non-native area of its range. J. Crustacean Biol. 25, 655–660. doi: 10.1651/C-2586.1

Crossref Full Text | Google Scholar

Delaney D. G., Griffen B. D., Leung B. (2011). Does consumer injury modify invasion impact? Biol. Invasions. 13, 2935–2945. doi: 10.1007/s10530-011-9975-0

Crossref Full Text | Google Scholar

Dorrance A. N., Goldstein J. S., Carloni J. T., Gutzler B. C., Watson W. H. III (2021). Sublethal behavioral and physiological effects of claw removal on Jonah crabs (Cancer borealis). J. Exp. Mar. Biol. Ecol. 545, 151642. doi: 10.1016/j.jembe.2021.151642

Crossref Full Text | Google Scholar

El Haj A. J., Govind C. K., Houlihan D. F. (1984). Growth of lobster leg muscle fibers over intermolt and molt. J. Crustacean Biol. 4, 536–545. doi: 10.2307/1548067

Crossref Full Text | Google Scholar

Epifanio C. E. (2013). Invasion biology of the Asian shore crab Hemigrapsus sanguineus: a review. J. Exp. Mar. Biol. Ecology. 441, 33–49. doi: 10.1016/j.jembe.2013.01.010

Crossref Full Text | Google Scholar

Escalante I., Ellis V. R., Elias D. O. (2021). Leg loss decreases endurance and increases oxygen consumption during locomotion in harvestmen. J. Comp. Physiol. A. 207, 257–268. doi: 10.1007/s00359-020-01455-1

PubMed Abstract | Crossref Full Text | Google Scholar

Farmer A. H., Wiens J. A. (1998). Optimal migration schedules depend on the landscape and the physical environment: a dynamic modeling view. J. Avian Biol. 29, 405–415. doi: 10.2307/3677159

Crossref Full Text | Google Scholar

Fleming P. A., Muller D., Bateman P. W. (2007). Leave it all behind: a taxonomic perspective of autotomy in invertebrates. Biol. Rev. 82, 481–510. doi: 10.1111/j.1469-185X.2007.00020.x

PubMed Abstract | Crossref Full Text | Google Scholar

Fukui Y. (1988). Comparative studies on the life history of the grapsid crabs (Crustacea, Brachyura) inhabiting intertidal cobble and boulder shores. Publications Seto Mar. Biol. Laboratory. 33, 121–162. doi: 10.5134/176156

Crossref Full Text | Google Scholar

Gallagher C. A., Chudzinska M., Larsen-Gray A., Pollock C. J., Sells S. N., White P. J., et al. (2021). From theory to practice in pattern-oriented modelling: identifying and using empirical patterns in predictive models. Biol. Rev. 96, 1868–1888. doi: 10.1111/brv.12729

PubMed Abstract | Crossref Full Text | Google Scholar

Griffen B. D. (2014). Linking individual diet variation and fecundity in an omnivorous marine consumer. Oecologia. 174, 121–130. doi: 10.1007/s00442-013-2751-3

PubMed Abstract | Crossref Full Text | Google Scholar

Griffen B. D. (2018). The timing of energy allocation to reproduction in an important group of marine consumers. PloS One 13, 6. doi: 10.1371/journal.pone.0199043

PubMed Abstract | Crossref Full Text | Google Scholar

Griffen B. D., Alder J., Anderson L. III, Asay E. G., Blakeslee A., Bolander M., et al. (2022). Latitudinal and temporal variation in injury and its impacts in the invasive Asian shore crab Hemigrapsus sanguineus. Sci. Rep. 12, 16557. doi: 10.1038/s41598-022-21119-1

PubMed Abstract | Crossref Full Text | Google Scholar

Griffen B. D., Bailey J., Carver J., Vernier A., DiNuzzo E. R., Anderson L. III, et al. (2020b). Mechanisms of possible self-limitation in the invasive Asian shore crab Hemigrapsus sanguineus. Sci. Rep. 10, 16908. doi: 10.1038/s41598-020-74053-5

PubMed Abstract | Crossref Full Text | Google Scholar

Griffen B. D., Bolander M., Blakeslee A., Crane L. C., Repetto M. F., Tepolt C. K., et al. (2023). Past energy allocation overwhelms current energy stresses in determining energy allocation trade-offs. Ecol. Evolution. 13, 8. doi: 10.1002/ece3.10402

PubMed Abstract | Crossref Full Text | Google Scholar

Griffen B. D., Cannizzo Z. J., Carver J., Meidell M. (2020a). Reproductive and energetic costs of injury in the mangrove tree crab. Mar. Ecol. Prog. Series. 640, 127–137. doi: 10.3354/meps13280

Crossref Full Text | Google Scholar

Griffen B. D., Mosblack H. (2011). Predicting diet and consumption rate differences between and within species using gut ecomorphology. J. Anim. Ecology. 80, 854–863. doi: 10.1111/j.1365-2656.2011.01832.x

PubMed Abstract | Crossref Full Text | Google Scholar

Griffen B. D., Vogel M., Goulding L., Hartman R. (2015). Energetic effects of diet choice by invasive Asian shore crabs: Implications for persistence when prey are scarce. Mar. Ecol. Prog. Series. 522, 181–192. doi: 10.3354/meps11160

Crossref Full Text | Google Scholar

Guerin J. L., Stickle W. B. (1995). Effects of cadmium on survival, osmoregulatory ability and bioenergetics of juvenile blue crabs Callinectes sapidus at different salinities. Mar. Environ. Res. 40, 227–246. doi: 10.1016/0141-1136(94)00148-I

Crossref Full Text | Google Scholar

He J., Wu X., Cheng Y. (2016). Effects of limb autotomy on growth, feeding and regeneration in the juvenile Eriocheir sinensis. Aquaculture 457, 79–84. doi: 10.1016/j.aquaculture.2016.02.004

Crossref Full Text | Google Scholar

Hobbs N. V. S., Cobb J. S., Thornber C. S. (2017). Injury, reproductive status, and distribution of Hemigrapsus sanguineus (De Haan 1835) (Brachyura: Varunidae) on the rocky intertidal shores of Rhode Island, USA. J. Crustacean Biol. 37, 16–20. doi: 10.1093/jcbiol/ruw002

Crossref Full Text | Google Scholar

Houlihan D. F., Waring C. P., Mathers E., Gray C. (1990). Protein synthesis and oxygen consumption of the shore crab Carcinus maenas after a meal. Physiol. Zoology. 63, 735–756. doi: 10.1086/physzool.63.4.30158174

Crossref Full Text | Google Scholar

Houston A. I., McNamara J. M. (1999). Models of adaptive behaviour: an approach based on state (Cambridge University Press: Cambridge, UK).

Google Scholar

Isvaran K., St. Mary C. M. (2003). When should males lek? Insights from a dynamic state variable model. Behav. Ecology. 14, 876–886. doi: 10.1093/beheco/arg066

Crossref Full Text | Google Scholar

Juanes F., Smith L. D. (1995). The ecological consequences of limb damage and loss in decapod crustaceans: a review and prospectus. J. Exp. Mar. Biol. Ecology. 193, 197–223. doi: 10.1016/0022-0981(95)00118-2

Crossref Full Text | Google Scholar

Jungblut S., Boos K., McCarthy M. L., Saborowski R., Hagen W. (2018). Invasive versus native brachyuran crabs in a European rocky intertidal: respiratory performance and energy expenditures. Mar. Biol. 165, 1–14. doi: 10.1007/s00227-018-3313-3

Crossref Full Text | Google Scholar

Kelly E. J., Kennedy P. L. (1993). A dynamic state variable model of mate desertion in Cooper’s hawks. Ecology. 74, 351–366. doi: 10.2307/1939298

Crossref Full Text | Google Scholar

Kennish R. (1997). Seasonal patterns of food availability: influences on the reproductive output and body condition of the herbivorous crab Grapsus albolineatus. Oecologia. 109, 209–218. doi: 10.1007/s004420050075

PubMed Abstract | Crossref Full Text | Google Scholar

Kitchell J. F., Stewart D. J., Weininger D. (1977). Applications of a bioenergetics model to yellow perch (Perca flavescens) and walleye (Stizostedion vitreum vitreum). J. Fisheries Board Canada. 34, 1922–1935. doi: 10.1139/f77-258

Crossref Full Text | Google Scholar

Kooijman S. A. L. M. (2010). Dynamic energy budget theory for metabolic organisation (Cambridge University Press, Cambridge, UK).

Google Scholar

Kraemer G. P., Sellberg M., Gordon A., Main J. (2007). Eight-year record of Hemigrapsus sanguineus (Asian shore crab) invasion in western Long Island Sound estuary. Northeastern Naturalist. 14, 207–224. doi: 10.1656/1092-6194(2007)14[207:EROHSA]2.0.CO;2

Crossref Full Text | Google Scholar

Kuris A. M., Mager M. (1975). Effect of limb regeneration on size increase at molt of the shore crabs Hemigrapsus oregonensis and Pachygrapsus crassipes. J. Exp. Zoology. 193, 353–359. doi: 10.1002/jez.1401930311

PubMed Abstract | Crossref Full Text | Google Scholar

Lee W. S., Metcalfe N. B., Monaghan P., Mangel M. (2011). A comparison of dynamic-state-dependent models of the trade-off between growth, damage, and reproduction. Am. Naturalist. 178, 774–786. doi: 10.1086/662671

PubMed Abstract | Crossref Full Text | Google Scholar

Lindsay S. M. (2010). Frequency of injury and the ecology of regeneration in marine benthic invertebrates. Integr. Comp. Biol. 50, 479–493. doi: 10.1093/icb/icq099

PubMed Abstract | Crossref Full Text | Google Scholar

Linton S. M., Greenaway P. (2000). The nitrogen requirements and dietary nitrogen utilization for the gecarcinid land crab Gecarcoidea natalis. Physiol. Biochem. Zoology. 73, 209–218. doi: 10.1086/316735

PubMed Abstract | Crossref Full Text | Google Scholar

Maginnis T. L. (2006). The costs of autotomy and regeneration in animals: a review and framework for future research. Behav. Ecology. 17, 857–872. doi: 10.1093/beheco/arl010

Crossref Full Text | Google Scholar

Mangel M., Clark C. W. (1988). Dynamic modeling in behavioral ecology (Princeton University Press, New Jersey, USA).

Google Scholar

Marshall S., Warburton K., Paterson B., Mann D. (2005). Cannibalism in juvenile blue-swimmer crabs Portunus pelagicus (Linnaeus 1766): effects of body size, moult stage and refuge availability. Appl. Anim. Behav. Science. 90, 65–82. doi: 10.1016/j.applanim.2004.07.007

Crossref Full Text | Google Scholar

McDermott J. J. (1991). A breeding population of the western Pacific crab Hemigrapsus sanguineus (Crustacea: Decapoda: Grapsidae) established on the Atlantic coast of North America. Biol. Bulletin. 181, 195–198. doi: 10.2307/1542503

PubMed Abstract | Crossref Full Text | Google Scholar

Messina F. J., Slade A. F. (1999). Expression of a life-history trade-off in a seed beetle depends on environmental context. Physiol. Entomology 24, 358–363. doi: 10.1046/j.1365-3032.1999.00151.x

Crossref Full Text | Google Scholar

Pirotta E., Mangel M., Costa D. P., Mate B., Goldbogen J. A., Palacios D. M., et al. (2018). A dynamic state model of migratory behavior and physiology to assess the consequences of environmental variation and anthropogenic disturbance on marine vertebrates. Am. Naturalist. 191, 40–56. doi: 10.1086/695135

PubMed Abstract | Crossref Full Text | Google Scholar

Plumb J. M., Blanchfield P. J., Abrahams M. V. (2014). A dynamic-bioenergetics model to assess depth selection and reproductive growth by lake trout (Salvelinus namaycush). Oecologia. 175, 549–563. doi: 10.1007/s00442-014-2934-6

PubMed Abstract | Crossref Full Text | Google Scholar

Pravosudov V. V., Lucas J. R. (2001). Daily patterns of energy storage in food-caching birds under variable daily predation risk: a dynamic state variable model. Behav. Ecol. Sociobiology. 50, 239–250. doi: 10.1007/s002650100361

Crossref Full Text | Google Scholar

Prestholdt T., White-Toney T., Bates K., Termulo K., Reid S., Kennedy K., et al. (2022). Tradeoffs associated with autotomy and regeneration and their potential role in the evolution of regenerative abilities. Behav. Ecology. 33, 518–525. doi: 10.1093/beheco/arac004

Crossref Full Text | Google Scholar

Pringle J. M. (1990). Growth and regeneration in the purple rock crab, Hemigrapsus edwardsi. [master’s thesis]. University of Canterbury, Christchurch (NZ.

Google Scholar

Rakel K. J., Preuss T. G., Gergs A. (2020). Individual-based dynamic energy budget modelling of earthworm life-histories in the context of competition. Ecol. Modelling. 432, 109222. doi: 10.1016/j.ecolmodel.2020.109222

Crossref Full Text | Google Scholar

R Core Team (2021). R: A language and environment for statistical computing (Vienna, Austria: R Foundation for Statistical Computing). Available at: https://www.R-project.org/.

Google Scholar

Reese T. C., Blakeslee A. M., Crane L. C., Fletcher L. S., Repetto M. F., Smith N., et al. (2024). Shift from income breeding to capital breeding with latitude in the invasive Asian shore crab Hemigrapsus sanguineus. Sci. Rep. 14, 6654. doi: 10.1038/s41598-024-57434-y

PubMed Abstract | Crossref Full Text | Google Scholar

Reim C., Teuschl Y., Blanckenhorn W. U. (2006). Size-dependent effects of larval and adult food availability on reproductive energy allocation in the yellow dung fly. Funct. Ecology. 20, 1012–1021. doi: 10.1111/j.1365-2435.2006.01173.x

Crossref Full Text | Google Scholar

Saborowski R., Bartolin P., Koch M., Jungblut S. (2023). Trophic ecophysiology of the native green shore crab, Carcinus maenas, and the invasive Asian shore crab, Hemigrapsus sanguineus, in the rocky intertidal of Helgoland (North Sea). Front. Mar. Science. 10. doi: 10.3389/fmars.2023.1247263

Crossref Full Text | Google Scholar

Saraiva S., van der Meer J., Kooijman S. A. L. M., Witbaard R., Philippart C. J. M., Hippler D., et al. (2012). Validation of a Dynamic Energy Budget (DEB) model for the blue mussel Mytilus edulis. Mar. Ecol. Prog. Ser. 463, 141–158. doi: 10.3354/meps09801

Crossref Full Text | Google Scholar

Shertzer K. W., Ellner S. P. (2002). State-dependent energy allocation in variable environments: life history evolution of a rotifer. Ecology. 83, 2181–2193. doi: 10.1890/0012-9658(2002)083[2181:SDEAIV]2.0.CO;2

Crossref Full Text | Google Scholar

Smith L. D. (1990). Patterns of limb loss in the blue crab, Callinectes sapidus Rathbun, and the effects of autotomy on growth. Bull. Mar. Science. 46, 23–36.

Google Scholar

Smith L. D. (1995). Effects of limb autotomy and tethering on juvenile blue crab survival from cannibalism. Mar. Ecol. Prog. Series. 116, 65–74. doi: 10.3354/meps116065

Crossref Full Text | Google Scholar

Smith L. D., Hines A. H. (1991). The effect of cheliped loss on blue crab Callinectes sapidus Rathbun foraging rate on soft-shell clams Mya arenaria L. J. Exp. Mar. Biol. Ecology. 151, 245–256. doi: 10.1016/0022-0981(91)90127-I

Crossref Full Text | Google Scholar

Stearns S. C. (1989). Trade-offs in life-history evolution. Funct. Ecology. 3, 259–268. doi: 10.2307/2389364

Crossref Full Text | Google Scholar

Stubbs J. L., Marn N., Vanderklift M. A., Fossette S., Mitchell N. J. (2020). Simulated growth and reproduction of green turtles (Chelonia mydas) under climate change and marine heatwave scenarios. Ecol. Model. 431, 109185. doi: 10.1016/j.ecolmodel.2020.109185

Crossref Full Text | Google Scholar

Talbot S. E., Widdicombe S., Hauton C., Bruggeman J. (2019). Adapting the dynamic energy budget (DEB) approach to include non-continuous growth (moulting) and provide better predictions of biological performance in crustaceans. ICES J. Mar. Science. 76, 192–205. doi: 10.1093/icesjms/fsy164

Crossref Full Text | Google Scholar

Vernier A., Griffen B. D. (2019). Physiological effects of limb loss on the Asian Shore Crab, Hemigrapsus sanguineus. Northeastern Naturalist. 26, 761–771. doi: 10.1656/045.026.0407

Crossref Full Text | Google Scholar

Vogt G. (2019). Functional cytology of the hepatopancreas of decapod crustaceans. J. Morphology. 280, 1405–1444. doi: 10.1002/jmor.21040

PubMed Abstract | Crossref Full Text | Google Scholar

Weber T. P., Ens B. J., Houston A. I. (1998). Optimal avian migration: a dynamic model of fuel stores and site use. Evolutionary Ecology. 12, 377–401. doi: 10.1023/A:1006560420310

Crossref Full Text | Google Scholar

Williams A. B., McDermott J. J. (1990). An eastern United States record for the western Indo-Pacific crab, Hemigrapsus sanguineus (Crustacea: Decapoda: Grapsidae). Proc. Biol. Soc. Washington. 103, 108–109.

Google Scholar

Yerkes T., Koops M. A. (1999). Redhead reproductive strategy choices: a dynamic state variable model. Behav. Ecology. 10, 30–40. doi: 10.1093/beheco/10.1.30

Crossref Full Text | Google Scholar