Path-dependent selection—a bridge between natural selection and neutral selection

Path-dependent selection follows the premise of complete symmetry in the neutral theory of selection; mutations in the natural world are entirely based on statistical randomness, lack directionality, and thus do not exhibit differences in fitness. Under specific spatiotemporal conditions, however, evolutionary positive feedback effects resulting from the specific environment will result in the breakdown of symmetry pre-assumed in neutral selection. This evolutionary positive feedback, a recursive effect, is of Lamarckian active selection or inheritance of acquired characteristics. The mutual antagonistic interactions between the positive selection of recursive effect and the passive selection under natural selection pressure of the environment in multidimensional conditions will result in evolutionary paths. Path-dependent selection proposes that the evolutionary process of organisms is a selection process based on path frequencies rather than an increase in fitness, with a strong reliance on the paths that it has taken in the past. Because of the existence of transition probabilities between different paths or within the same path (such as plasmid transfer, transposons, and function transfer in ecological interactions), path formation will exhibit acceleration or deceleration effects, explaining Gould’s principles such as punctuated equilibrium. When environmental selection pressure is weak or zero, most or all paths (like neutral selection outcomes) may be possible. The frequencies of different paths will differentiate as environmental selection increases, and the paths with higher frequencies will be more easily selected. When the evolutionary process or history has no impact on the evolution of the paths themselves (a static, equilibrium state), the path with the highest frequency is the shortest or optimal path used by evolution—a result consistent with Darwin’s theory of natural selection. Path-dependent selection, which draws inspiration from modern physics, particularly path integral methods in quantum mechanics, may provide us with a new perspective and approach to explaining the evolution of life.

1 Introduction

A Roman proverb expresses a sentiment that “All roads lead to Rome.” Whereas, a very ancient Chinese book, Book of Changes (Yijing), has a very similar idea, which is “under heaven, paths diverge, yet ultimately converge; diverse routes lead to the same destination; unity amid myriad concerns.” These proverbs convey the idea that, even if the starting points are the same, different paths can lead to the same destination. This concept encapsulates the most basic concept of path dependence. There is a critical scientific question in this simple concept of paths: given a starting point and a destination, which path should be chosen to reach the end point? This is not only a common question in our daily social and economic lives, but it was also posed early on by physicists. If we believe that the evolution of life processes is governed by the same principles as the natural physical world, the question becomes a central issue in evolutionary biology.

A similar question has been posed by physicists (Guan, 1994): for two points not on the same vertical line on a vertical plane, there are an infinite number of possible paths for a particle to move from one position to another under the influence of gravity. The question becomes, which path minimizes the time of motion? This is known in physics as the Brachistochrone problem (Boxes 1, 2) (Rouse Ball, 1960). The renowned palaeontologist Stephen Jay Gould of Harvard University raised a similar path-related question in his book The Panda’s Thumb: when water flows down an inclined plane, the resulting groove can take countless forms, suggesting that biological evolution is like the grooves formed by flowing water, evolving along numerous paths (Gould, 1992). On the basis of the least action principle (Box 1), Traulsen et al. (2007) argue that, for a gene mutation from A to B, only the path with the shortest selection time aligns exactly with Darwin’s theory of natural selection (Darwin, 1859; Traulsen et al., 2007). Importantly, natural evolution does not always take the shortest path in terms of selection time in both the physical and biological worlds (Poelwijk et al., 2007; Mustonen and Lassig, 2010; Steinberg and Ostermeier, 2016; Sohail et al., 2021).

Box 1. Least action principle
The least action principle is a fundamental principle of mechanics that describes a system’s laws of motion. It is primarily concerned with the reduction of an action for a moving object. In classical mechanics, if $q(t)$ represents the arbitrary path of an object in motion, then a system can be characterized by a Lagrange function, denoted as $L(t,q(t),\dot{q}(t))$, where $L(t)$ is the Lagrange function evolving with time as $q(t)$ varies. A definite integral can be used to calculate the object’s total action $S[x(t)]$ along this path $S[x(t)]={\displaystyle \underset{t_1}{\overset{t_2}{\int }}L(t,q(t),\dot{q}(t))}dt$,

where t₁ and t₂ denote the initial and final times of the object’s motion, respectively, and the Lagrange function $L(t,q(t),\dot{q}(t))$ is determined by the moving object’s generalized coordinates and generalized velocities $q(t)$ and $\dot{q}(t)$. Clearly, different paths correspond to different actions, and the variational method can be used to calculate the path that minimizes the action. A typical example is the phenomenon of refraction of light. When light transitions from one medium to another, its propagation direction changes. Fermat’s theorem, which states that the path of light is the one that minimizes (shortens) the action, which is often interpreted as minimizing the time taken, can explain this phenomenon.

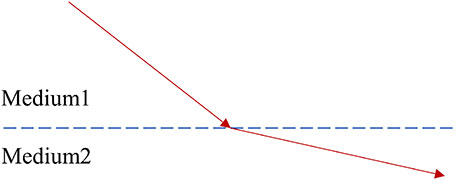
Caption 1: The path of light (shown in red) as it enters medium 2 from medium 1. According to the least action principle, this path is the one that minimizes action, implying that it is the shortest time path.

Box 2. Brachistochrone problem
When considering all the plane curves that connect two points A and B that are not on the same vertical line within a vertical plane, there may exist multiple paths in the real world. The Brachistochrone problem is concerned with determining the path that a particle should take from point A to point B, influenced only by gravity and initially at rest, to minimize the time of descent. The calculus of variations can be used to obtain the expression for this curved path, and it is discovered that the path is not a straight line, as shown in Caption 2A. Similarly, Traulsen and his colleagues argue that, if the principle of the shortest evolutionary time is considered, then the results of Darwin’s theory of natural selection are exactly aligned to the Brachistochrone principle (Traulsen et al., 2007).

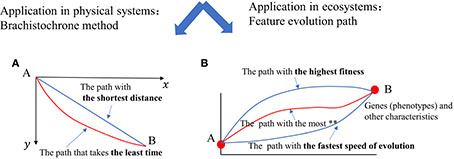
Caption 2: In (A), the red curve represents the path taken by a small ball to get from point A to point B in the shortest amount of time, despite the fact that the path itself is longer. In (B), when different quantities in the evolutionary process are considered, the transition from feature A to feature B involves different paths. Natural selection frequently involves multiple attempts, with the most advantageous path or the path with the highest probability being chosen. If evolution takes the path with shortest time, then it is completely consistent with Darwin’s theory of natural selection (Traulsen et al., 2007).

If we assume that mutations in genes, traits, or behaviors are entirely random and lack directionality in the evolutionary process of living systems, then this aligns with a widely validated conclusion in modern molecular biology—the theoretical assumption of neutral selection (Kimura, 1955). This, however, contradicts the observed orderliness in macroscopic ecological systems, such as heterogeneity of species functions and its distribution, community structures, and social hierarchies within population. Path-dependent selection, which is well-developed in the evolution of technology and in quantum physics through path integral principles, might be able to solve the paradox of neutral selection. Several theoretical research articles (e.g., Svirezhev, 1972; Traulsen et al., 2007; Mustonen and Lassig, 2010; Li et al., 2021; Wang et al., 2022a; Wang et al., 2022b; Li et al., 2023) and the book The End of Rationality and Selfishness (Wang, 2023) have proposed that a process similar to path-dependent evolution in physics may exist in the biological evolution process. Path-dependent selection holds that, rather than attempting to provide a stable landscape of species or traits, we can only depict the transient evolutionary process of species or trait features. Path-dependent selection, as described by taxonomists, implies that species evolution is a continuous process with no fixed goal or end point (e.g., Metz et al., 1992; Liu, 2016).

Path-dependent selection assumes that mutations in the natural world are completely random and lack directionality. However, in certain spatiotemporal environments, positive feedback effects cause recursive effects to emerge in these mutations, forming paths. Biological evolution is viewed as a process of selection based on path frequencies rather than an increase in fitness. The species or character path evolution is very similar to path formation of water grooves on an inclined plane (Gould, 1992). In the case that plane is almost vertical, the path number of water grooves will be much fewer than that in inclined plane. However, when the plane is almost parallel with the ground, the path distribution of water grooves will be randomly evolved, and any environmental accidents might change the direction of path evolution (Figure 1). The path diversity in biological evolution, namely, the species or character diversity, will strongly depend on the counterbalance between the interacted forces. In biological evolution, the species or character diversity might greatly depend on game or balance between the passive selection force of natural selection and positive selection force of Landmark’s inheritance of acquired characters (positive feedback from environment). In the case that the natural selection is weak, the intrinsic positive selection will benefit the more path evolution and any environmental accidents might lead to different path evolution (Figure 1A), whereas in the case that the natural selection becomes stronger, the less paths will be selected (Figures 1B, C).

Figure 1

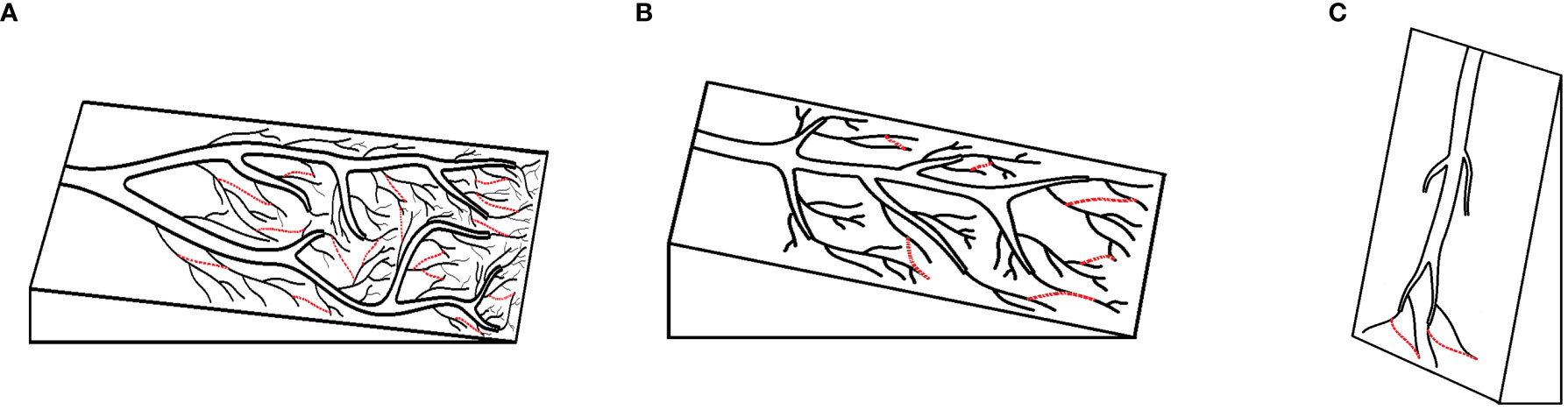
Figure 1 The web of water grooves or tidal tree analogy to the web of species (see Lawton, 2009), and the paths of water grooves or tidal tree under different counterbalances of interacted forces. (A) The force of gravity is weak. (B) The force of gravity is middling. (C) The force of gravity is strong.

Path formation will exhibit acceleration or deceleration effects due to the existence of transition probabilities between different paths and within the same path. In the biological evolution process, transition probabilities are realized through processes such as plasmid transfer, transposons, and ecological interactions such as mutualism, cooperation, competition, and synchrony. These transition probabilities cause differences in the environmental feedback effects on existing paths, resulting in acceleration or deceleration effects in path evolution (fitness flux). Transition probabilities imply that different levels or units of life entities, such as species, individuals, and genes, will be inextricably linked, forming a path web and challenging the traditional Darwinian natural selection theory, which emphasizes the separation of species, individuals, and genes (Lawton, 2009). As a result, selection will take place at various levels or units.

2 The breakdown of neutral selection symmetry—path-dependent selection

Path-dependent selection assumes that the probability of any mutation occurring, whether in genes or phenotypic traits, is completely random, with no fitness differences associated with gene or trait mutations. This assumption is consistent with the central premise of neutral selection theory. Certain mutations, on the other hand, exhibit recursive effects in specific spatiotemporal environments, implying that these environments generate positive feedback effects on these mutations. Gene or trait mutations are like seeds that fall randomly in the wind. Some seeds, on the other hand, may fall into specific environments, such as cow dung, accelerating their growth and reproduction. Plants that grow in cow dung improve their surroundings, making it more conducive to the germination and growth of other seeds, eventually forming a forest. This is referred to as the recursive effect or the positive feedback effect caused by the environment (Nowak and Sigmund, 2004; Wang, 2023).

Kimura proposed the neutral theory in 1968, based on statistical physics theory, as a doctrine distinct from Darwin’s theory of natural selection. It is also known as the theory of neutral mutation and random genetic drift, and it has been supported by extensive molecular biology research. There are some important points. Firstly, most molecular mutations are neutral or nearly neutral, with no significant advantages or disadvantages. As a result, natural selection has no effect on them. Secondly, through genetic drift, neutral mutations become fixed or disappear. Mutations provide random evolutionary raw materials, and the path and direction of evolution are largely determined by chance. This is influenced by a random, free combination of biomolecules that is unaffected by the surrounding environment. Thirdly, the rate of neutral mutations is equal to and constant with the rate of molecular evolution. The main characteristics of molecular evolution are consistency and constancy of the rate of biological evolution. The rate of each large molecule in any organism is roughly constant, unrelated to population size, species life span, or reproductive capacity, and unaffected by environmental factors.

The neutrality theory proposed by ecologist Hubbell and the near-neutrality neutral theory proposed by Zhou and Zhang share a fundamental theoretical and logical framework that is nearly identical to Kimura’s neutrality theory (Hubbell and Borda-De-Agua, 2004; Zhou and Zhang, 2006). From a physical standpoint, the basic premise of the neutral selection theories assumes symmetry among species, individuals, and genes within their ecological systems, population structures, or gene networks. This means that individual units within these systems can swap states and evolve over time without changing their function or role (Wang, 2023). Such symmetry in physics leads to system stability, resulting in predictable deterministic behavior or evolution (Noether’s theorem).

Modern physics has revealed that perfect symmetry is almost nonexistent in the real world, and symmetry breakdown is widely confirmed in modern physics (Prigogine, 1997). The evolution of life sciences has paralleled that of physics, and real-life biological systems, like the physical world, exhibit little to no complete symmetry. Different species perform vastly different ecological functions in ecological systems. Changing a species’ ecological functions or evolutionary processes could result in completely different ecological system structures. Similarly, different individuals within a biological population may have completely different functions in the population, and their spatial or evolutionary positions cannot be interchanged. A queen ant and a worker ant, for example, serve entirely different functions in the population and cannot be interchanged (Wang and Shi, 2010; Wang, 2023). The same is true at the genetic level, where genes in different chromosomal positions may have entirely different functions, and different position of a gene might play vastly different roles in chromosomes.

Path-dependent selection provides a mechanism for neutral selection symmetry breakdown. According to neutral selection theory, the generation of mutations is completely random, with the probability distribution being equivalent. In neutral selection, any invariants in spatial and temporal scales can be swapped out without changing the overall nature of the system (Figure 2A). The premise of neutral selection theory is supported by path-dependent selection. However, in path-dependent selection, the mutations may exhibit recursive effects in specific environmental conditions, although mutations are assumed to be random. In ecology, this phenomenon is analogous to the Allee effect, in which environmental feedback produces positive feedback effects. The genes or traits associated with this mutation spread more than other mutations as a result of the positive feedback effects of the environment, and the evolutionary path of the species, trait, or behavior is formed. These different species or phenotypic features will exhibit continuity due to the existence of transition probabilities between different paths, such as plasmid transfer, transposons, and ecological interactions. This continuity extends beyond the classical separateness of species or phenotypic features, resulting in a fitness landscape of peaks and valleys due to species or phenotypic feature continuity (Figure 2B). Transition probabilities between different paths, or in different times and spaces, will cause path evolution to accelerate. The acceleration caused by probability transition, such as plasmid transfer, can vary significantly in different spatial and temporal contexts during the process of biological evolution. In other words, the rate of evolution of species or phenotypic features caused by plasmid transfer may vary greatly across evolutionary histories or spatial locations.

Figure 2

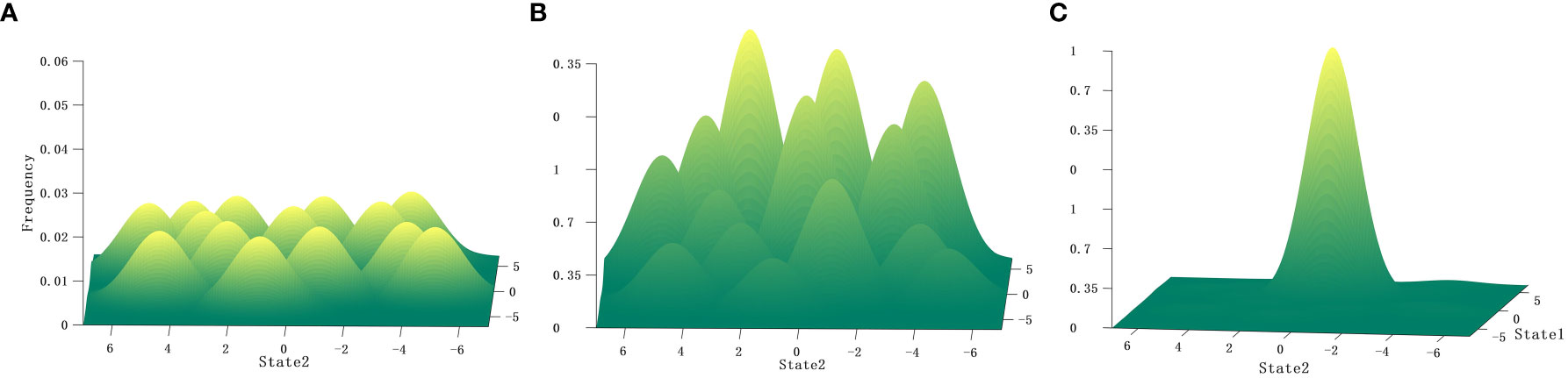
Figure 2 Schematic diagrams corresponding to different selection mechanisms. (A) Neutral selection mutation is completely random and equivalent, i.e., entirely symmetrical. (B) Path-dependent selection conditions, where some mutations exhibit recursive effects due to positive feedback from the environment, resulting in differences in path frequencies between mutations, breaking the symmetry of randomness. (C) Conditions of Darwinian natural selection theory, representing infinitely high pressure, static conditions without considering the influence of historical imprints. Species or trait features will choose the optimal path, as predicted by Darwinian natural selection theory.

When the Fokker–Planck equation (which is also the basis for Kimura’s neutral selection) is path-integrated, the equation returns to neutral selection when the selection pressure equals zero. In other words, when there is no environmental selection pressure, the neutral theory’s theoretical premise of random mutation holds true (Box 3). For example, in environments where organisms’ internal conditions or external conditions in tropical rainforests are relatively stable, the intricate relationships within the organism’s gene network or the complex tropical rainforest species network result in little pressure on low-frequency mutations or small populations. In such cases, the system approaches neutrality according to the principles of neutral selection.

Box 3. Model
Consider a finite population N in a dynamic evolutionary game with two phenotypes A and B. $\begin{array}{cc}& AB\\ \begin{array}{c}A\\ B\end{array}& \left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\end{array}$ is the payoff matrix. After random pairing interactions, the expected payoffs for A and B are given by ${\varphi }_A=xa+(1-x)b$ and ${\varphi }_B=xc+(1-x)d$ for a large population size N. Furthermore, the fitness functions for individuals with phenotypes A and B are defined as $f_A=1-\omega +\omega {\varphi }_A$ and $f_B=1-\omega +\omega {\varphi }_B$. The Moran process gives the transition probabilities from x to $x+\frac{1}{N}$ and from x to $x-\frac{1}{N}$ at each time step as ${\pi }^{+}(x)=\frac{x(1-x)f_A(x)}{x{f}_A(x)+(1-x)f_B(x)}$ and ${\pi }^{-}(x)=\frac{x(1-x)f_B(x)}{x{f}_A(x)+(1-x)f_B(x)}$, respectively. Let $p(x,t|x_0,t_0)$ be the transition probability density when A’s initial frequency is $x_0$ and its frequency at time $t$ is $x$. $p(x,t|x_0,t_0)$ can be calculated from the Fokker–Planck equation using the diffusion approximation (Zheng et al., 2011): $\frac{\partial p(x,t|x_0,t_0)}{\partial t}=-\frac{\partial }{\partial x}{D}^{(1)}(x)p(x,t|x_0,t_0)+\frac{{\partial }^2}{\partial x^2}{D}^{(2)}(x)p(x,t|x_0,t_0),$ with $D^{(1)}(x)={\pi }^{+}(x)-{\pi }^{-}(x)$ and $D^{(2)}(x)=\frac{{\pi }^{+}(x)+{\pi }^{-}(x)}{2N}$.

Conclusion: Simplified calculations reveal $D^{(1)}(x)=\omega x(1-x)\left((a-b-c+d)x+b-d\right)$ and $D^{(2)}(x)=\frac{x(1-x)}{N}$ under weak selection. When selection strength $\omega =0$, $D^{(1)}(x)=0$ and $D^{(2)}(x)=\frac{x(1-x)}{N},$ precisely corresponding to the Fokker–Planck equation under neutral selection $\frac{\partial \tilde{p}(x,t|x_0,t_0)}{\partial t}=\frac{{\partial }^2}{\partial x^2}{D}^{(2)}(x)\tilde{p}(x,t|x_0,t_0).$

Under weak selection, the path integral form of the probability density function takes the following form: $p(x,t|x_0,t_0)=e^{\frac{Nw}{2}\underset{x_0}{\overset{x}{\int }}((a-b-c+d)y+b-d)dy}\dot{p}(x,t|x_0,t_0),$where $\dot{\text{p}}(x,t|x_0,t_0)=\underset{(0,x_0)}{\overset{(t,x)}{\int }}{\prod }_{i=1}^n\frac{e^{-\frac{N}{4}{\int }_0^t\frac{{\dot{x}}^2}{x(1-x)}ds}}{2\sqrt{\pi x_{i-1}(1-x_{i-1})\tau /N}}\mathcal{D}x(t)$. It is worth noting that when selection strength $\omega =0$, the form exactly matches $\tilde{p}(x,t|x_0,t_0)=\dot{p}(x,t|x_0,t_0).$

3 Generation of species or character diversity

Positive feedback in specific historical stages or spatial environments causes a recursive effect for a specific mutation in the path-dependent selection process. In path-dependent selection, the existence of mutations is not because of their fitness advantage than other mutations but because of their inherent recursive effects and inertia in trajectory. This is similar to a toddler growing up, where a child becomes captivated and develops a fascination for such music or dance after hearing a beautiful piece of music or witnessing a graceful dance. As a result of learning more about music or dance, their physical and mental well-being improves, and they eventually adopt this music or dance as a lifelong pursuit. Clearly, the choice of music or dance is not based on superior competitiveness to studying science or engineering; rather, environmental factors unintentionally stimulate the child’s inner interests and potential. Because the environmental factors influencing the replication of their genes or phenotypic traits are hierarchical or multidimensional in the evolutionary process of living organisms, the intrinsic forces of replication will also be diverse. Transitioning to other paths will be costly once such a path is established due to the inertia involved. In some ways, biological evolution’s inheritance is a biological understanding of inertia.

Different species or phenotypic traits may coexist completely in the context of path-dependent selection under conditions where ecological niches or resource sharing are identical. Different mutations may form distinct paths in different historical contexts in a homogeneous environment and continue to evolve along those paths due to inertia. Both can coexist even in a completely same environment. Only when there is significant selection pressure will the majority of individuals evolve along the path with greater frequency. According to Darwin’s theory of natural selection, the path with the highest frequency may also be considered the optimal path (Figures 2A–C, 3A–C).

Figure 3

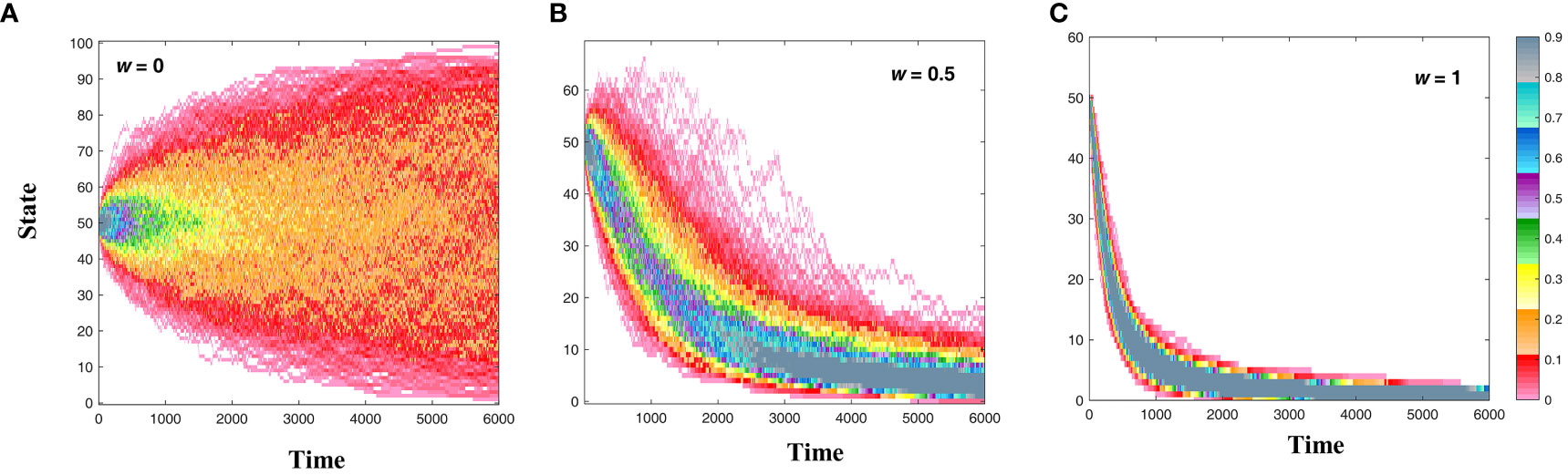
Figure 3 Evolutionary paths under different selection pressures (Li et al., 2023), where (A–C) correspond to selection intensities of 0, 0.5, and 1, respectively. When w = 0, there is no selection pressure, and population evolution is only affected by random drift, resulting in an outcome closer to neutral selection. However, when w = 1, the selection pressure is very high, resulting in an outcome closer to Darwinian natural selection.

4 Path-dependent selection vs. Darwinian natural selection—uncertainty vs. certainty

According to Kimura’s neutral theory, mutations are entirely random and equivalent (Kimura, 1983). Its ecological implications are inextricably linked to Hubbell’s neutral theory, which states that species distribution is random and equivalent (Hubbell and Borda-De-Agua, 2004). In contrast, Darwin’s theory of natural selection proposes that the selection of traits in any organism is directional, with the goal of increasing biological individuals’ fitness. Following Darwin’s theory of natural selection would, in theory, inevitably result in the optimal, or even maximal, final benefits of traits or individuals (Wang, 2022). In biology, the issue of directionality is analogous to the issue of determinism and certainty in physics.

According to neutral theory, whether a mutation occurs is entirely random, as is the formation of a specific species. Individual mutations are completely unpredictable, but the probability of their occurrence is deterministic (Niu et al., 2009). However, in Darwin’s natural selection, the trait with higher fitness will be deterministically spread and maintained within the population via inheritance. In natural selection, the probability of mutation is treated as a constant on both temporal and spatial scales, implying that random variation error is treated as a constant. The assumption of perpetual randomness of mutation, both in time and space, is a highly specific and potentially unreliable theoretical proposition.

Path-dependent selection exists at the intersection of determinism and uncertainty, directionality, and non-directionality. The stronger the positive feedback from the environment, the higher the frequency of the path in path-dependent selection. It is relatively difficult to change paths once one has been chosen. This is analogous to physics’ inertia, also known as genetic inertia in biology. Walking or evolving along the same path, or copying the same genes, with constant environmental or external conditions should be the most energy-efficient, which Richard Dawkins, author of The Selfish Gene, calls inertia. In this sense, in path-dependent selection, individuals tend to choose the original or more frequent path, which is directional. Path-dependent selection, on the other hand, assumes the existence of transition probabilities between paths. The probability of mutations occurring on different paths varies significantly under different spatiotemporal conditions due to the influence of transition probabilities, and this alters the distribution of the entire path frequency. Because of the presence of transition probabilities in the fitness landscape of species, the main peak may collapse, and other peaks may evolve into the main peak in different spatiotemporal environments. In ecosystems, dominant species may evolve into rare species due to differences in evolutionary histories or spatial distributions, whereas rare species may evolve into dominant ones. Transfers occurring at different evolutionary times and spatial scales will result in different mutation rates or error values, resulting in distinct paths and path distributions.

Path-dependent selection proposes that, during biological evolution, species or individuals prefer the frequency of paths over an increase in fitness. This is analogous to having a large lawn in front of an office building and a bus stop across the lawn. On the lawn, multiple paths lead to the bus stop over time. Because of historical or random factors, the path that most people take is not always the best (shortest or fastest). However, the imprints left on each path differ; some paths are more frequently crossed than others. In a leisurely park, most people are likely to walk a rough and winding path. The distribution of path probabilities becomes diffuse as the destination, the bus stop, evolves over time, similar to the branching tree diagram in species evolution (Figure 4).

Figure 4

Figure 4 Schematic diagram of the evolutionary paths from the initial point to the target location, or from species (gene) A to species (gene) B In the evolutionary process of life, paths may represent the shortest time, the shortest distance, or the highest resource utilization efficiency, among other factors. Especially when evolution is influenced by historical imprints, paths can be highly diverse. (A) The target location or fitness is static and fixed. (B) The target location or fitness is dynamic and not fixed.

However, as selection pressure increases, the incentive to improve efficiency grows stronger. The most frequently taken path among the various paths may be the shortest route, the optimal path. As a result, natural selection may be a process of selecting path frequencies rather than the highest benefits or fitness. Some path frequencies may be selected more frequently, whereas others may be selected less frequently. Although all paths have the potential to be chosen in a static environment or when the path’s destination is fixed and stationary at a specific location, the frequency of selecting the optimal path will increase with increasing evolutionary pressure. The majority of individuals will likely choose this path in the end. When we define a path as the one with the shortest time or the fastest increase in fitness, it will be idea of Darwin’s natural selection. In such cases, the optimal path is a completely deterministic outcome (Figure 3).

Path-dependent selection emphasizes how history and the evolutionary process influence the evolution of paths. Like the paths formed when crossing a park from an office building to an opposing bus stop, perhaps in history, the bus stop was right in front of the office building’s entrance. As a result, from the entrance to the bus stop, a relatively straight path was formed. However, the bus stops later moved forward a short distance, and the path between the office entrance and the bus stop may have taken on a zigzag shape as a result, no longer representing the shortest straight line between two points. Historical events may leave imprints on the evolutionary process, whether in the evolution of species or traits (Arthur et al., 1987), potentially influencing the paths of their evolution.

5 Path-dependent selection—punctuated equilibrium theory

In path-dependent selection, the evolution along the inertia of the original path could be understood as the variable of inheritance of Darwinian natural selection, whereas the deviation from the original path or generation of new paths could be understood as the variation of natural selection. The parameter of variation in path-dependent selection is no longer a fixed parameter measuring randomness but rather a parameter that changes over time or space. This means that the rate of variation will differ depending on the temporal or spatial environment. The evolution or mutation rate of the same gene in different evolutionary stages of the chromosome, that is, different historical stages of the same path, will differ in terms of the historical process of evolution. In terms of space, the transition probabilities among different paths, such as plasmid transfer, can result in different evolutionary or mutation rates for the original path.

The probability transition of path-dependent selection, which could result in rapid or slow evolution of species or phenotype, might well interpret punctuated equilibrium. The “punctuated equilibrium hypothesis” was proposed by palaeontologists Gould and Eldredge in 1972 (Eldredge and Gould, 1972; Gould and Eldredge, 1977). According to this theory, there is both gradual slow evolution and rapid, explosive species formation during the evolutionary process of species. As information accumulates in a specific state, biological systems may transition from continuous equilibrium to discontinuous non-equilibrium. Rapid evolution coexists with gradual change, and the simultaneous existence of rapid evolution is the core idea of punctuated equilibrium theory.

Because of the presence of transition probabilities between paths, the evolution rate of different paths varies significantly at different spatial and temporal scales when the modern physics principle of path integration (a mathematical method used in quantum physics) is introduced. In other words, the fitness itself changes (Box 4) (referred to in the literature as fitness flux). When the system is in an equilibrium, stable state, the classical concept of population fitness, like the concept of physics velocity used to measure the parameter of population growth speed, reaches its maximum and remains unchanged (Metz et al., 1992). Because transition probabilities exist in path-dependent evolution and because transition probabilities may cause changes in the original gene space structure and function, biological population structure, ecological system interactions, and so on, fitness may change due to different effects on environmental feedback. This is like the concept of velocity in physics, but it incorporates the variable of velocity change as an acceleration factor. When the fitness flux, or acceleration parameter, is zero, it corresponds to the traditional definition of fitness in population biology. When the fitness flux is positive, it corresponds to Gould’s advocated rapid evolution. When the fitness flux is negative, species may decelerate their evolution, resulting in situations such as degeneration or a gradual loss of features.

Box 4. Fitness flux
Assuming that the frequency of a certain genotype in a population evolves over continuous time $(t_0,t_1,\cdots ,t_n)$ as $x=(x_0,x_1,\cdots ,x_n)$, and the selection coefficient is $s(x,t)$, the fitness flux at a given point $t_i$ can be defined as $\varphi (t_i)=\frac{s(x_i,t_i)\text{Δ}{x}_i}{\text{Δ}{t}_i}$, where the cumulative fitness flux of the evolutionary process is defined as $\varphi (x)={\sum }_{t=0}^{n-1}\varphi (t_i)\text{Δ}{t}_i={\sum }_{t=0}^{n-1}s(x_i,t_i)\text{Δ}{x}_i$, describing the selection effects on changes in genotype frequency. When the selection coefficient $s(x)=\nabla F(x)$ is the gradient of the fitness $F(x)$ and does not depend on time, the cumulative fitness flux (fitness flux) of genotype frequency $x$ can be expressed as $\varphi (x)=F(x_n)-F(x_0)$, meaning that the fitness flux equals the change in fitness between the initial and final states of the population (Mustonen and Lassig, 2010).

Transition probability refers to the probability of transitioning from one state to another in a Markov chain. In the evolutionary process of biological populations, the transition probability of genotype frequency is influenced by factors such as selection, mutation, and genetic drift. Moreover, biological phenomena such as plasmid transfer that occur during evolution may also affect the transition probability of genotype frequency. There is a certain connection between transition probability, fitness, and fitness flux. For the evolutionary process of genotype frequency $x=(x_0,x_1,\cdots ,x_n)$, when the selection coefficient is $s(x)=\nabla F(x)$ and the fitness flux is $\varphi (x)=F(x_n)-F(x_0)$, the equilibrium transition probability $P_{eq}(x)$ is also related to the fitness function $F(x)$, i.e., $P_{eq}(x)=P_0(x)e^{NF(x)}$, where $N$ is the population size and $P_0(x)$ is (approximate) equilibrium that the mutation-drift process in the absence of selection. In the state of evolutionary equilibrium, the fitness flux is zero, whereas, in non-equilibrium states, the fitness flux is non-zero. Mathematically, changes in the transition probability $P_{eq}(x)$ can be observed to affect the fitness function $F(x)$ and, consequently, the values of the fitness flux $\varphi (x)$.

6 Path-dependent selection—multi-level selection

A fundamental and unquestioned concept in classical socioeconomics and evolutionary biology is that the unit of selection is the individual. The concept of genes as a unit of selection was first proposed in evolutionary biology with the introduction of kin selection. A species becomes a unit of selection at the level of species differentiation, in the process of species formation. Can ecological communities at the species level or populations at the population level evolve into selection units? From a path-dependent standpoint, it appears possible.

As a fundamental unit of selection, it cannot be further subdivided internally, and the smaller units below it lack the unit’s main characteristics. In biological individuals, for example, units that decompose further, such as organs, no longer exhibit the characteristics of independent evolution. Similarly, when genes are further subdivided into smaller molecular units, they lose their genetic characteristics.

Path-dependent selection proposes not only a mechanism of separation between paths or between species and trait features (i.e., a mechanism by which one species or trait differs from others) but also a mechanism of continuity between species or trait features, which is theoretically represented by transition probabilities. Well-known mechanisms in biological evolution, such as interspecific hybridization, cell fusion, and sexual reproduction, increase the similarity between species or individual traits. The now widely reported plasmid transfer between species and the information flow caused by ecological processes between species may also improve species continuity. If the continuity between species is greater than the separation between species in certain specific environments, then the selection level based on the ecological community above the species level may be established (Li et al., 2021; Wang, 2022). This is demonstrated in the fitness landscape (Figures 3, 5), where measuring the continuity between species peaks is less than measuring their separation, resulting in the continuity between species gluing different species together into a whole. Other levels of selection, such as gene or group selection, use similar mechanisms.

Figure 5

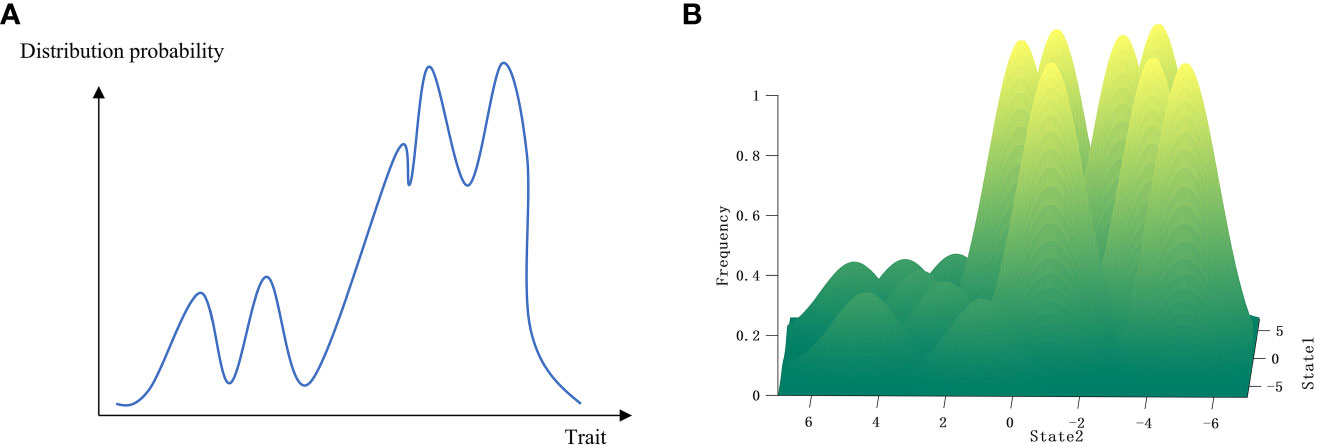
Figure 5 Schematic diagrams of multi-level selection in species or traits. (A) The planar view of species or traits at different selection levels. (B) The three-dimensional representation of species or traits in fitness landscape at different selection levels.

Transition probabilities occurring in different evolutionary processes between paths may result in completely different rates of evolution or mutation rates in the process of path-dependent selection. Plasmid transfer at more primitive or conservative loci, for example, may have no effect on the original chromosome, whereas transfer to relatively new or sensitive loci may result in rapid evolution or mutation. Species mountain ranges can form in low-altitude areas, similar to the uplift of plateaus in geology, and, after being uplifted to a plateau, new mountain ranges can form. The formation of gene mountains at the gene level can be explained by the mechanism of transition probabilities, and, after genes are cohered into a selection unit, new paths can emerge on the gene mountain, forming the species mountain. Species are cohered into a selection unit due to their continuity, forming a selection unit at the community level, and new paths can then be formed on this basis (Figure 5).

7 Environmental positive feedback—Lamarckism

Path-dependent selection assumes that mutations are random, but, in certain environments, some mutations may exhibit positive feedback effects. Because of the positive feedback effect of the environment, these mutations have recursive effects. The inherent recursive effects are analogous to Lamarck’s use and disuse principle and the inheritance of acquired characteristics. Under the influence of the external environment, these intrinsic mutations accelerate their own evolution. This represents a scenario in which the process of life evolution actively accelerates the rate of mutation or evolution. In terms of dynamics, this is fundamentally different from Darwin’s theory of natural selection. According to Darwin’s theory of natural selection, the rate of evolution or mutation is constant. The environment selects favorable mutations, and the selected mutations spread within the population. The types of species or trait mutations are thought to be passive results of the environment.

The frequency of paths varies as the environmental selection pressure increases in the path-dependent selection model. Paths with higher frequencies are more likely to be chosen when environmental pressure is high. When the pressure is extremely high, most individuals will choose the optimal path or the path with the highest frequency. The path with the highest frequency may not be the optimal path due to the influence of historical imprints on path evolution. In other words, the most frequent path may not be the shortest or fastest path in terms of time. When the pressure is absent or extremely weak, all paths can be chosen, and the frequency of paths is almost identical.

8 Conclusion and discussion

The evolution of a technological or institutional system based on path dependence has received widespread recognition in economic and social sciences. The development of these paths, however, remains rooted in the equilibrium deterministic perspective, in which the paths of technologies or institutions are considered stable and deterministic. Historical imprints play an important role in the formation of technological or institutional paths, and the evolution process locks these paths in place, making transitioning to other paths expensive. The longer the path, the more difficult it is to switch to a different path. The transfer of technologies or institutions between paths is frequently regarded as completely random.

We introduce the path integral principle, a modern physics-based theory of path evolution that builds on classical theories of technological and institutional path evolution. In addition, the concept of transition probabilities is incorporated into the existing framework. The occurrence of transition probabilities causes changes in fitness (fitness flux), which is analogous to acceleration in physics, whereas fitness itself is analogous to the concept of velocity in physics. In life sciences, transition probabilities may be associated with phenomena such as plasmid transfer, transposons, and ecological interactions. Different rates of evolution or variation will result from transition probabilities occurring in different evolutionary histories or spatial locations of paths, causing changes in fitness.

Transition probabilities are frequently treated as having a continuous distribution in current theoretical models of path evolution, and their trajectories are considered paths. However, in the evolution of life, whether through plasmid transfer or transposons, these transition probabilities are inherently discontinuous and non-continuous along different paths. The mathematical structures of these problems in life sciences will place new demands on physics and mathematical methods, potentially opening up new avenues for physics advancement.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding authors.

Author contributions

RW: Conceptualization, Funding acquisition, Supervision, Writing – original draft, Writing – review & editing. YY: Conceptualization, Validation, Writing – original draft. AS: Writing – review & editing. QZ: Visualization, Writing – review & editing. ML: Conceptualization, Methodology, Visualization, Writing – original draft. CW: Conceptualization, Supervision, Writing – original draft. YT: Conceptualization, Supervision, Writing – original draft. JH: Conceptualization, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study was supported by NSFC-Yunnan United fund (No. U2102221), the National Science Fund for Distinguished Young Scholars (No. 31325005), National Natural Science Foundation of China (No. 32171482) and Natural Science Basic Research Program of Shaanxi (Program No.2022JQ-897).

Acknowledgments

Professors Shu-Cun Sun and Ke-Chang Niu from Nanjing University and Researcher Feng Zhang from Xishuangbanna Tropical Botanical Garden of the Chinese Academy of Sciences have discussed and revised the paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arthur W. B., Ermoliev Y. M., Kaniovski Y. M. (1987). Path-dependent processes and the emergence of macro-structure. Eur. J. Operational Res. 30 (3), 294–303. doi: 10.1016/0377-2217(87)90074-9

CrossRef Full Text | Google Scholar

Darwin C. R. (1859). On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life (London: John Murray).

Google Scholar

Eldredge N., Gould S. J. (1972). “Punctuated equilibria: An alternative to phyletic gradualism,” in Models in Paleobiology (San Francisco: Freeman Cooper & Company), 82–115.

Google Scholar

Gould S. J. (1992). The Panda’s Thumb: More Reflections in Natural History (New York: W. W. Norton & Company).

Google Scholar

Gould S. J., Eldredge N. (1977). Punctuated equilibria: The tempo and mode of evolution reconsidered. Paleobiology 3, 115–151. doi: 10.1017/S0094837300005224

CrossRef Full Text | Google Scholar

Guan H. (1994). Selected Lectures on the History of Physics (Beijing: Higher Education Press).

Google Scholar

Hubbell S. P., Borda-De-Agua L. (2004). The unified neutral theory of biodiversity and biogeography: Reply. Ecology 85 (11), 3175–3178. doi: 10.1890/04-0808

CrossRef Full Text | Google Scholar

Kimura M. (1955). Solution of a process of random genetic drift with a continuous model. Genetics 41, 144–150. doi: 10.1073/pnas.41.3.144

CrossRef Full Text | Google Scholar

Kimura M. (1983). The Neutral Theory of Molecular Evolution (Cambridge: Cambridge University Press).

Google Scholar

Lawton G. (2009). Axing Darwin's tree. New Scientist 201 (2692), 34–39. doi: 10.1016/s0262-4079(09)60231-1

CrossRef Full Text | Google Scholar

Li M. L., Wang C., Wang R. W. (2021). Path-dependent speciation in the process of evolution. Biodiversity Sci. 29 (3), 409–418. doi: 10.17520/biods.2020276

CrossRef Full Text | Google Scholar

Li ML A. K., Liu C., Tao Y., Wang C., Wang R. W. (2023). The path integral formula for the stochastic evolutionary game dynamics. EPL 142 (6), 1–7. doi: 10.1209/0295-5075/acd9eb

CrossRef Full Text | Google Scholar

Liu J. Q. (2016). The integrative species concept” and “species on the speciation way. Biodiversity Sci. 24, 1004–1008. doi: 10.17520/biods.2016222

CrossRef Full Text | Google Scholar

Metz J. A. J., Nisbet R. M., Geritz S. A. H. (1992). How should we define ‘fitness’ for general ecological scenarios? Trends Ecol. Evol. 7 (6), 198–202. doi: 10.1016/0169-5347(92)90073-K

PubMed Abstract | CrossRef Full Text | Google Scholar

Mustonen V., Lassig M. (2010). Fitness flux and ubiquity of adaptive evolution. Proceedings of the National Academy of Sciences, 107(9), 4248–4251. doi: 10.1073/pnas.0907953107

CrossRef Full Text | Google Scholar

Niu K. C., Liu Y. N., Shen Z. H., He F. L., Fang J. Y. (2009). Community assembly: the relative importance of neutral theory and niche theory. Biodiversity Sci. 17 (6), 579–593. doi: 10.3724/SP.J.1003.2009.09142

CrossRef Full Text | Google Scholar

Nowak M. A., Sigmund K. (2004). Evolutionary dynamics of biological games. Science 303 (5659), 793–799. doi: 10.1126/science.1093411

PubMed Abstract | CrossRef Full Text | Google Scholar

Poelwijk F. J., Kiviet D. J., Weinreich D. M., Tans S. J. (2007). Empirical fitness landscapes reveal accessible evolutionary paths. Nature 445 (7126), 383–386. doi: 10.1038/nature05451

PubMed Abstract | CrossRef Full Text | Google Scholar

Prigogine I. (1997). The end of certainty: times, chaos, and the new laws of nature (Free Press, New York).

Google Scholar

Rouse Ball W. W. (1960). A Short Account of the History of Mathematics (New York: Dover).

Google Scholar

Sohail M. S., Louie R. H. Y., McKay M. R., Barton J. P. (2021). MPL resolves genetic linkage in fitness inference from complex evolutionary histories. Nat. Biotechnol. 39 (4), 472–479. doi: 10.1038/s41587-020-0737-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Steinberg B., Ostermeier M. (2016). Environmental changes bridge evolutionary valleys. Sci. Adv. 2 (1), e1500921. doi: 10.1126/sciadv.1500921

PubMed Abstract | CrossRef Full Text | Google Scholar

Svirezhev Y. M. (1972). “Optimum principles in population genetics,” in Studies on theoretical genetics. Ed. Ratner V. A. (Novosibirsk, Russia: Academy of Sciences of the USSR), 86–102.

Google Scholar

Traulsen A., Iwasa Y., Nowak M. A. (2007). The fastest evolutionary trajectory. J. Theor. Biol. 249, 617–623. doi: 10.1016/j.jtbi.2007.08.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang R. W. (2022). On the methodology of Darwinism and non-Darwinism. Biodiversity Sci. 30 (9), 1–4. doi: 10.17520/biods.2022482

CrossRef Full Text | Google Scholar

Wang R. W. (2023). The End of Rationality and Selfishness: A story on the asymmetry, uncertainty and the evolution of cooperation (Springer press, New York).

Google Scholar

Wang R. W., Li M. L., Han J. X., Wang C. (2022b). Fitness relativity and path-dependent selection. Biodiversity Sci. 30 (1), 1–12. doi: 10.17520/biods.2021323

CrossRef Full Text | Google Scholar

Wang C., Li M. L., Wang R. W. (2022a). Path probability selection in nature and path integral. Sci. Rep. 12, 1–9. doi: 10.1038/s41598-022-20235-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang R. W., Shi L. (2010). The evolution of cooperation in asymmetric systems. Sci. China: Life Sci. 53, 139–149. doi: 10.1007/s11427-010-0007-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng X. D., Cressman R., Tao Y. (2011). The diffusion approximation of stochastic evolutionary game dynamics: Mean effective fixation time and the significance of the one-third law. Dynamic Games Appl. 1 (3), 462–477. doi: 10.1007/s13235-011-0025-4

CrossRef Full Text | Google Scholar

Zhou S. R., Zhang D. Y. (2006). Neutral theory in community ecology. Chin. J. Plant Ecol. 30 (5), 868–877. doi: 10.1007/s11515-008-0008-z

CrossRef Full Text | Google Scholar