Numerical investigation of the influence of mineral mesostructure on quasi-static compressive behaviors of granite using a breakable grain-based model

The mesostructure of brittle rocks, such as granite, plays a vital role in determining their mechanical properties and failure mode. Understanding the influence of rock mesostructure on mechanical behavior requires a realistic representation of grain size distribution, grain shape, and average grain size. In this study, we developed a breakable polygonal discrete element model that incorporates mineralogical composition, grain size distributions, and grain shape to simulate the rock mesostructure. Numerical specimens with varying mesostructures were created to represent different grain size, shape, and distribution characteristics. Quasi-static uniaxial compressive loading tests were conducted on these specimens to analyze their peak strength and macroscopic failure modes. The results revealed a strong linear relationship between the quasi-static compressive strength of the rock and mesostructure parameters, including average grain size, grain size coefficient, and grain roundness. Additionally, the simulation results demonstrated that the rock mesostructure significantly influenced the quasi-static compression failure mode. The proposed breakable polygonal discrete element model has the potential to predict the macroscopic behavior of brittle rocks accurately. It provides a reliable method for studying the effect of mesostructure on the quasi-static compressive mechanical behavior of rocks.

1 Introduction

Rocks, composed of one or more minerals, are inherently heterogeneous due to their diverse composition, type, size, shape, and spatial distribution. Previous research has indicated that the mechanical characteristics and deformation behavior of rocks are primarily controlled by their internal mesostructures, especially crystalline rocks (Wang et al., 2022). Granite, a typical crystalline rock, is a common host rock for a variety of engineering and geologic applications due to its widespread occurrence and desirable mechanical properties (e.g., durability and high strength). Hence, a comprehensive analysis of the influence of mesostructure characteristics, including grain size, distribution, shape, and mineral composition, on the mechanical response of granite is crucial.

In recent decades, numerous laboratory experiments have been conducted to explore the impact of mesostructure on the macroscopic mechanical behavior of rocks (Fredrich et al., 1990; Eberhardt et al., 1999; Keikha and Keykha, 2013; Li et al., 2020). The findings indicate that the mechanical characteristics of granite are generally a function of mineralogical parameters. For instance, Fredrich et al. (1990) carried out triaxial compression experiments on rock with various grain sizes and observed an inverse relationship between the confining pressure needed for the rock to transform from brittle to plastic and the grain size. Eberhardt et al. (1999) conducted an analysis of the impact of grain size on crack initiation and propagation in Lac du Bonnet granite. Their findings revealed a decrease in rock strength as grain size increases. Keikha and Keykha (2013) conducted a study on two types of granites and observed a correlation between the mechanical characteristics of the rocks and their petrological parameters. Recently, Cowie and Walton (2018) analyzed the mechanical properties and mineralogical parameters of 58 different granite types from 12 countries to gain a complete understanding of their interrelationships. The study demonstrated that incorporating both grain size parameters and mica modal percentage led to improved predictions of critical mechanical properties in granitic rock. Furthermore, they also identified that previous correlations proposed in the literature may be spurious due to the presence of unknown additional variables that are correlated with both the dependent and independent variables used in establishing those correlations. As we know, the randomness of rock formation processes, including mineral crystallization and subsequent deformation events, leads to inherent variability in the mesostructure of rocks. Even within the same rock type, variations in mineral grain sizes, their spatial distribution, and the overall mineral content can be significant. This natural variability poses difficulties in conducting laboratory experiments that precisely replicate the exact mesostructure parameters of rocks. Furthermore, Laboratory experiments typically involve a limited number of samples, and the variations in mesostructure among these samples can introduce uncertainties and hinder the establishment of robust correlations.

To overcome these challenges, numerical simulations have become an effective method to study the influence of rock mesostructure due to their high repeatability and low cost. In order to accurately model the interactions at the grain-scale level, grain-based models (GBMs) have been proposed and employed in combination with various numerical methods, including the finite difference method (FDM) (Xiao et al., 2022), finite-discrete element method (FDEM) (Abdelaziz et al., 2018; Fukuda et al., 2020; Zhou et al., 2020), discrete element method (DEM) (Zhang et al., 2020; Pan et al., 2021a; Kong et al., 2022). Among them, the DEM method can explicitly simulate crack initiation and propagation, making it an ideal method for modeling the mechanical characteristics and failure process of rocks (Wang and Yan, 2022). The current mainstream grain-based discrete element models mainly include the particle flow code grain-based model (PFC-GBM) (Zhang et al., 2020; Quan et al., 2023) and the universal distinct element code grain-based model (UDEC-GBM) (Gao et al., 2016; Wang et al., 2021; Huang et al., 2023). Some researchers have used PFC-GBM to examine the effect of grain size on the strength of granite and found that rock strength increases with the increase of grain size (Han et al., 2021; Peng et al., 2021). Gui et al. (2016a) employed the UDEC model with unbreakable grains and also observed that rock strength increases with grain size. However, conflicting results regarding the influence of grain size on granite strength have been observed in existing numerical simulations. For instance, Wang et al. (2021) employed the breakable UDEC-GBM model and reported a decrease in the strength of granite with increasing grain size. Moreover, previous investigations have primarily focused on grain size and distribution, overlooking the potential effect of mineral spatial distribution and grain shape on the mechanical properties of granite. These factors remain largely unexplored and warrant further investigation to comprehensively understand their impact on the mechanical behavior of granite.

According to Gao et al. (2016), the PFC-GBM approach has been identified to have a drawback of high inherent porosity resulting from the spherical shape of its particles. This characteristic poses challenges in accurately modeling low porosity rocks such as granite using this method. Conversely, UDEC-GBM has a tightly interlocked block structure and does not have a porosity issue. Therefore, the UDEC-GBM is considered more suitable for modeling rocks with low porosity. Furthermore, it is widely recognized that the microscopic cracking process in rocks involves both intergranular and transgranular failure mechanisms (Gulizzi et al., 2018; Ghasemi et al., 2020; Li et al., 2023). In this study, the breakable UDEC-GBM model will be utilized to analyze the influence of mesostructure characteristics on the quasi-static compression behavior of granite. This model takes into account the breakability of grains and allows for a more accurate representation of the mechanical response of granite under compression. By considering the specific mesostructure parameters of the rock, such as grain size, shape, and distribution, the model can provide insights into how these factors affect the overall behavior of granite under compression.

2 Numerical methodology

2.1 Breakable grain-based model in UDEC

The grain-based model is a technique that utilizes a polygonal structure to represent grain topology. By analyzing optical microscopy images of granite (Figure 1A), two-dimensional grain structures can be described by polygonal boundaries (Ghasemi et al., 2020). In the UDEC-GBM approach, the behavior of polygonal grains can be classified into different categories: deformable or rigid, and breakable or unbreakable. It is important to note that unbreakable grains, whether they are deformable or rigid, limit the development of intra-granular cracks. This is because there are no potential pathways within the grains to accommodate the propagation of such cracks. As a result, only intergranular cracks along the grain interfaces are allowed to propagate in the simulation. Previous research has demonstrated that rocks subjected to external loads generate both intergranular and transgranular fractures, as depicted in Figure 1B (Ghasemi et al., 2020).

FIGURE 1

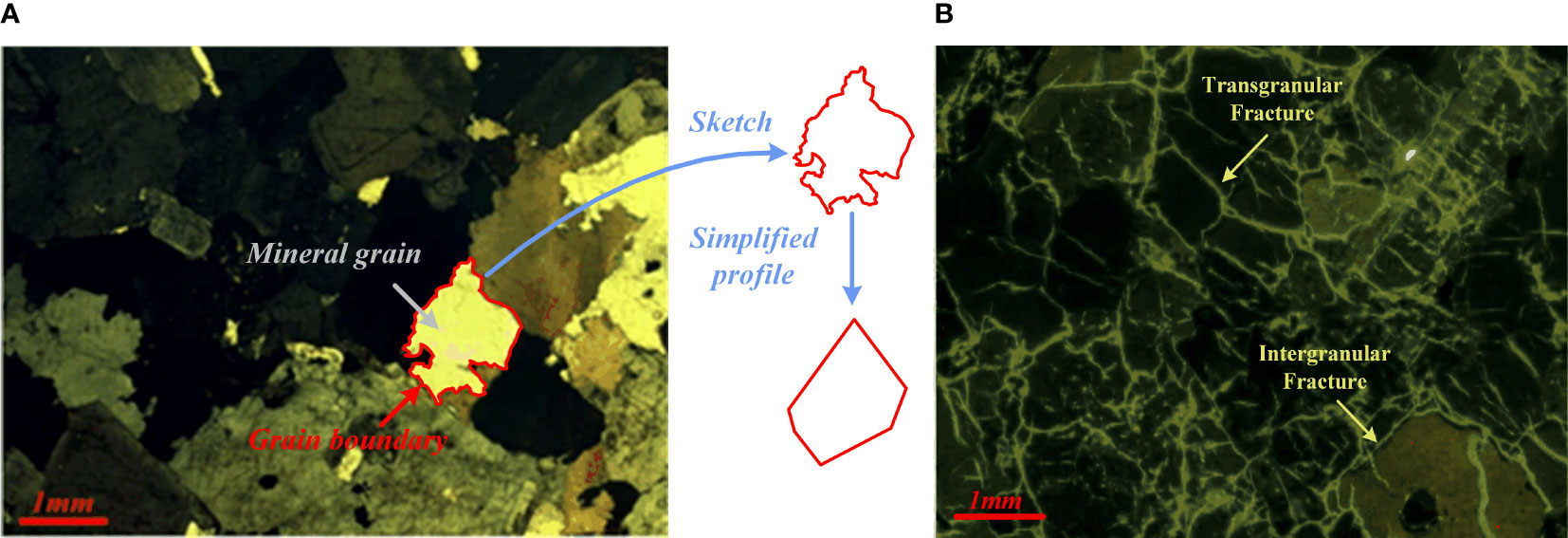
Figure 1 Micrograph image of granite (A) Fresh sample, (B) Crack initiation sample (Ghasemi et al., 2020).

The breakable UDEC-GBM method proposes subdividing each grain into multiple small triangular or polygonal sub-grains to achieve grain breaking. Previous research has shown that the heterogeneity in shape and size of polygonal blocks, resembling natural mineral grains, can induce axial splitting, while triangular blocks with greater kinematic freedom tend to exhibit shear failure mechanisms (Mayer and Stead, 2017). As crystalline rocks are more prone to experiencing tensile failure under uniaxial loading, this study utilizes a dual-layer discretization method with sub-polygonal blocks to model intra-granular and inter-granular fractures. As depicted in Figure 2, the breakable GBM generation process using UDEC can be described as follows: (a) Generating polycrystals as Voronoi tessellations in square domains using Neper, as shown in Figure 2A. Indeed, Neper is a widely used open-source software package for generating and meshing polycrystals (Quey et al., 2011; Quey and Renversade, 2018). It allows for the generation of grain sizes and grain shape distributions that can mimic real cell morphology properties or random distributions, such as lognormal, normal, or Weibull. (b) Further dividing the primary grains (first discrete layer) produced by Neper into multiple sub-grains to form a multiscale Voronoi tessellation. Neper’s multiscale tessellation scheme makes it possible to consider intergranular and transgranular fractures, as illustrated in Figure 2B. (c) Exporting the multiscale Voronoi diagram from Neper and converting the multiscale Voronoi tessellation file (comprising geometric data such as points, edges, and polygons) into a data format recognizable by UDEC using C++. The mesoscopic structure in Figure 2B was imported into UDEC via the embedded FISH language as the basis for establishing a breakable GBM (Figure 2C). (d) Discretizing the sub-grains into finite-difference triangular elements to account for block deformability. Then, assign mesoscopic parameters for mineral grains and contacts. Ultimately, a completely breakable UDEC-GBM model is formed (Figure 2D).

FIGURE 2

Figure 2 Procedure of generating the breakable UDEC-GBM model (A) Polygonal grains generated by Voronoi tessellation in Neper, (B) Sub-grains generated by dual-scale tessellation in Neper, (C) Exporting the geometry of grains and sub-grains from Neper to UDEC, (D) Breakable UDEC-GBM generation.

2.2 Contact models used in GBM

In this paper, the polygonal blocks are assumed to behave linear elastically, indicating that the failure governed by the contact constitutive law. Experimental results demonstrate that the fracture behavior of brittle materials is a gradual phenomenon, namely crack surface separation that takes place at the propagating crack tip, hindered by cohesive forces (Fathipour-Azar et al., 2020). To capture the nonlinear fracture behavior at the crack tip, Dugdale (1960) and Barenblatt (1962) proposed the cohesive zone model. Recently, various cohesive zone models have found successful applications in studying the mechanical behavior of rocks under static (Kazerani, 2013; Gui et al., 2015; Saadat and Taheri, 2020; Pan et al., 2021b) and dynamic loading conditions (Wu et al., 2015; Gui et al., 2016b).

The cohesive zone contact model encompasses three essential components: the traction-separation criterion, the initial damage criterion, and the damage evolution law. Various mathematical expressions can be employed to describe the traction-separation relationship, such as the bilinear, polynomial, trapezoidal, or exponential forms (Elices et al., 2002). In the realm of simulating brittle fracture, Alfano (2006) have demonstrated that the specific mathematical form of the traction-separation function holds relatively less significance compared to the fracture energy and cohesive strength. Thus, this investigation adopts the bilinear form of the cohesive contact model, as illustrated in Figure 3, due to its simplicity without compromising the accuracy of the simulation. The detailed description and mathematical formulation of this constitutive model can be found in our previous work (Pan et al., 2021b).

FIGURE 3

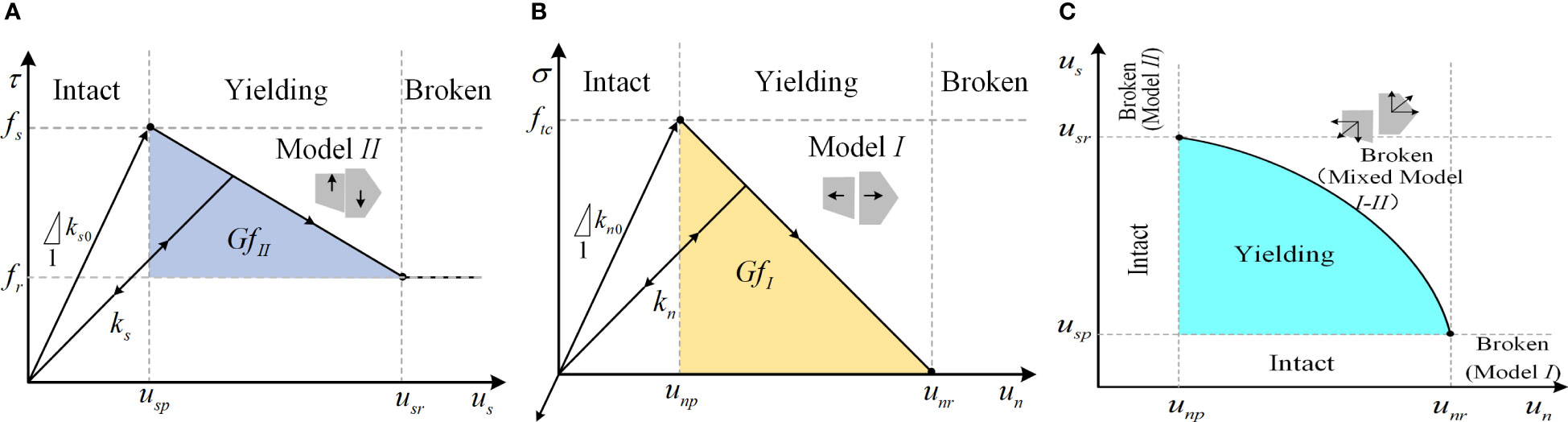
Figure 3 Cohesive contact model (A) Shear model, (B) Tensile model, (C) Mixed model (Pan et al., 2021b).

2.3 Parameter calibration

Barre granite, as a representative brittle rock, has undergone extensive laboratory testing to investigate its mesostructure and mechanical properties. According to reports, Barre granite approximately consists of 3% muscovite, 8% biotite, 18% K-feldspar, 32% quartz, and 36% plagioclase (Morgan et al., 2013). The granite samples exhibit a grain size distribution spanning from 0.87 to 2.54 mm, with an average grain size of 1.7 mm (Pan et al., 2021a). For the purpose of configuring the UDEC-GBM model and calibrating the mesoscopic parameters, the test data of Barre granite were specifically selected in this investigation. By implementing the UDEC-GBM generation approach described in section 2.1, a breakable GBM model was generated with dimensions of 50 mm (height) and 25 mm (width), as depicted in Figure 4A. This model contains 507 blocks and 1521 sub-blocks. The average block size is 1.5 mm, which is close to the average grain size of Barre granite. During the model generation process, it is important to note that muscovite was categorized as biotite due to its small proportion. Therefore, the model only includes four minerals: quartz, plagioclase, K-feldspar, and biotite. Furthermore, the mineral proportions in the model are determined by the block area ratio. Figure 4B provides a comparative analysis of the mineral contents between the real granite and the UDEC-GBM model. The figure clearly demonstrates the similarity in mineral contents between the two.

FIGURE 4

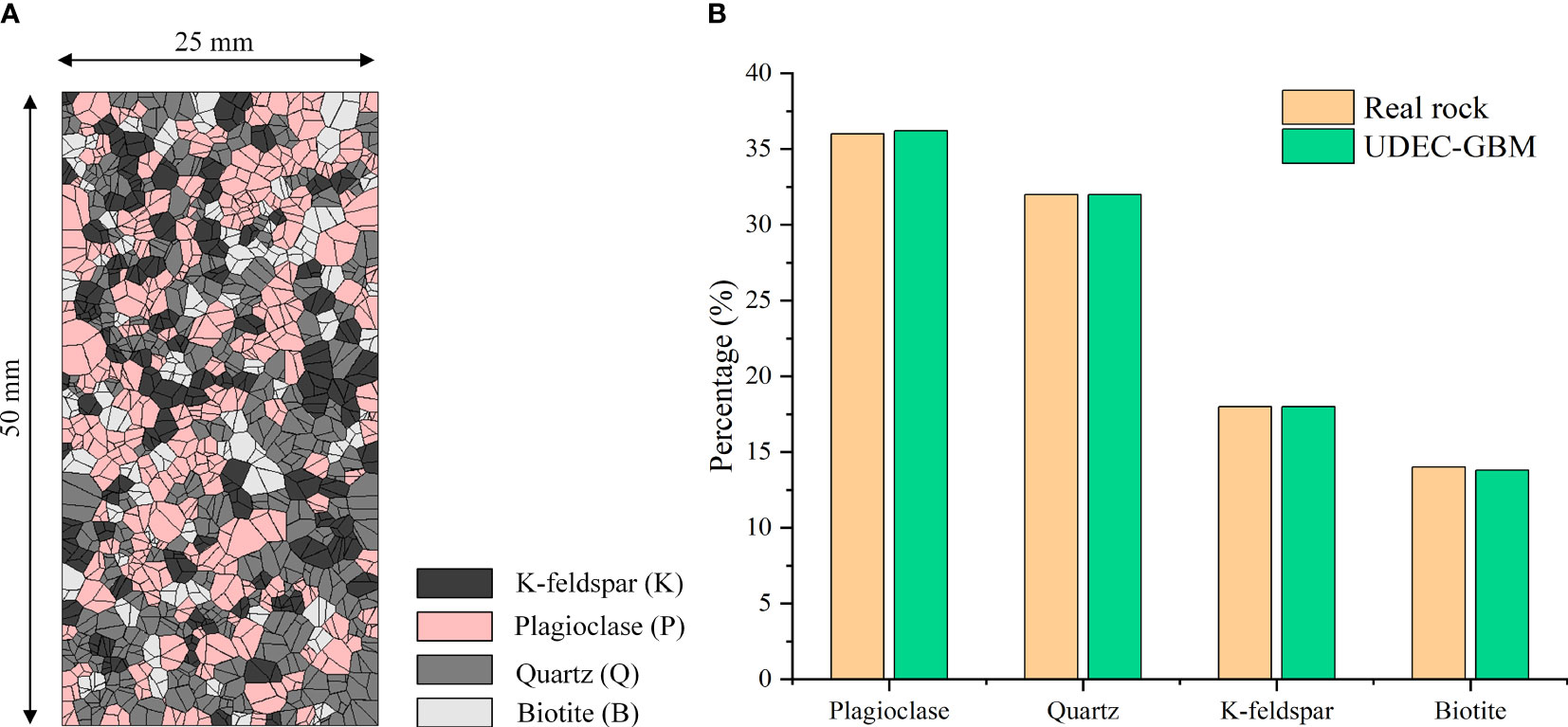
Figure 4 UDEC-GBM model of Barre granite (A) UDEC-GBM model, (B) Comparison of mineral content of UDEC-GBM model with real rock.

Accurate simulation of the macroscopic mechanical behavior of rock requires the calibration of mesoscopic parameters associated with mineral blocks and interfaces. In UDEC, there is no one-to-one correspondence between rock macroscopic and mesoscopic parameters. Therefore, the calibration of mesoscopic parameters is typically achieved through a trial-and-error approach. This involves comparing the simulation results with the actual experimental data and making iterative adjustments to the mesoscopic parameters until a satisfactory match is obtained. However, the traditional trial-and-error method for parameter calibration faces challenges such as non-uniqueness of GBM model parameters and time-consuming processes. To address these issues, this study adopts the model parameter calibration procedure proposed by Pan et al. (2021b), which offers an efficient approach to correct the mesoscopic parameters. The parameter calibration procedure involves several steps. Firstly, the Plackett-Burman test design is utilized to assess the sensitivity of the mesomechanical parameters to the macroscopic response. This analysis identifies the influential mesoscopic parameters that significantly affect each macroscopic response value. Next, the response surface method is employed to investigate the interaction between the mesoscopic parameters and macroscopic responses. This methodology enables the establishment of a nonlinear relationship that captures the interaction between the significant mesoscopic parameters and macroscopic response values. Lastly, through the particle swarm optimization algorithm, the parameters of the GBM model can be effectively optimized. This optimization process aims to attain optimal parameter values that yield the highest level of agreement between the model predictions and the observed macroscopic mechanical behavior.

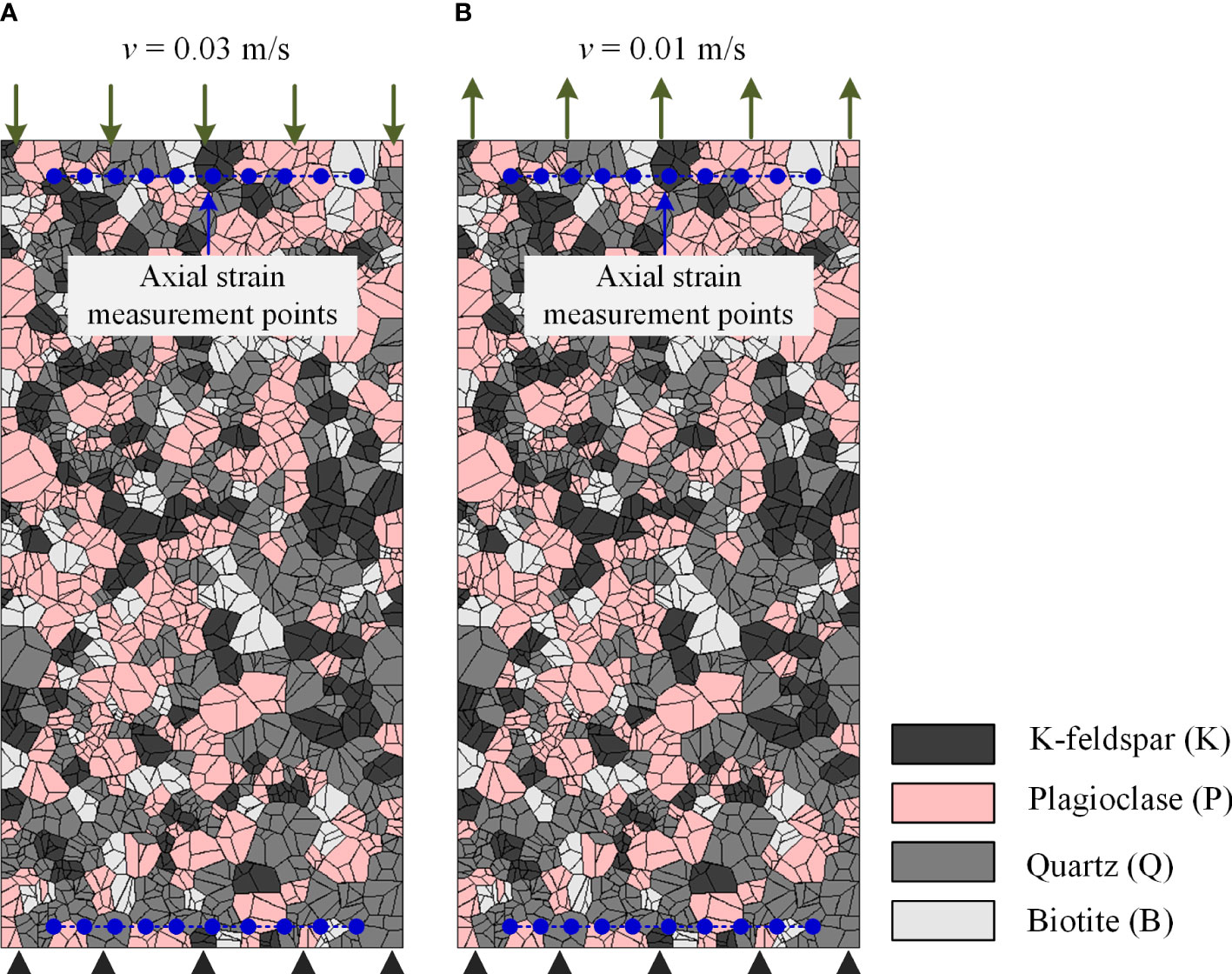
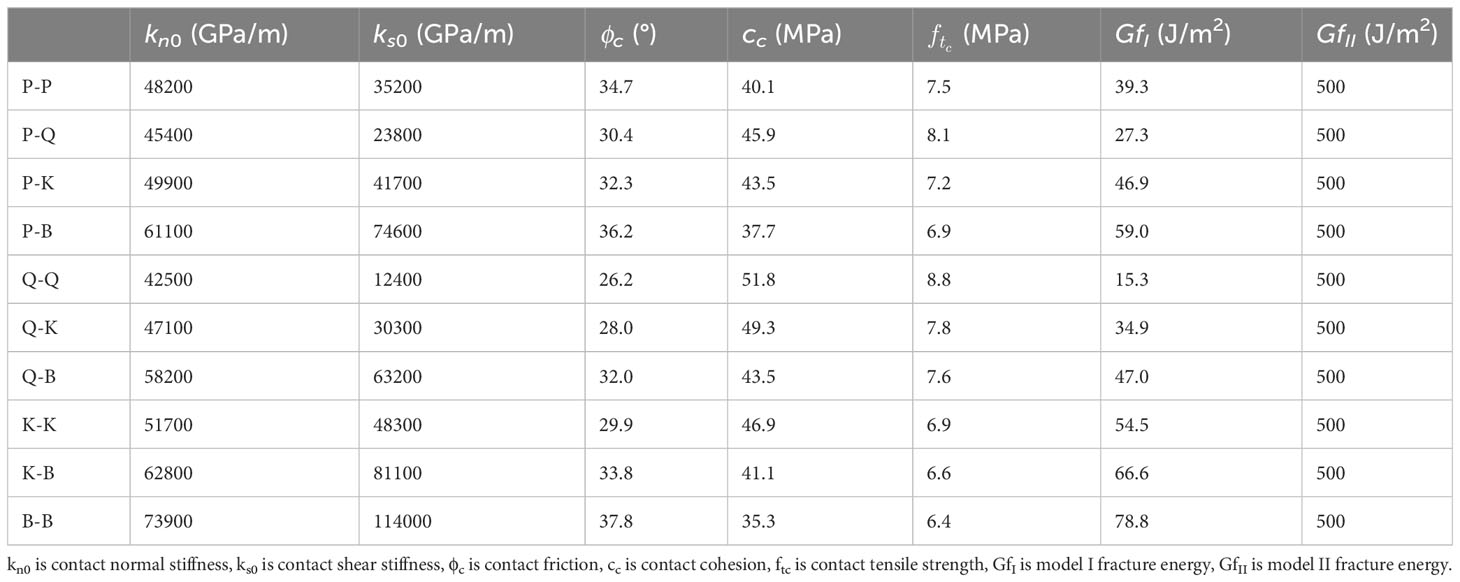
Using the above calibration procedure, mesoscopic parameters were determined through uniaxial compression and direct tensile tests conducted on the numerical specimens. In the numerical models, the loading conditions for the specimens were simulated by fixing the lower boundary of the model and applying vertical velocities to the upper boundary. For the uniaxial compression model, a loading velocity of 0.03 m/s, directed downward, was employed. In the case of the direct tensile model, a loading velocity of 0.01 m/s, directed upward, was used. Although these values are large compared to typical loading rates in laboratory tests, since the time steps in UDEC are very small, about 10⁻⁶ mm/step, this means that a large number of computational steps are required to move the upper boundary 1mm. Therefore, the speed selected in this study is sufficient to simulate quasi-static loading conditions. During the calculation process, the axial strain of the sample is determined by calculating the ratio of the average displacement in the y-direction at multiple monitoring points to the height of the sample. Figure 5 shows the locations of these monitoring points. Axial stress was determined by computing the average stress of the top monitoring elements using the Fish language. Tables 1, 2 present the mineral and mineral boundary parameters of the calibrated Barre granite. It is noteworthy that in Table 2, the entries P-P, Q-Q, K-K, and B-B correspond to contacts between Plagioclase-Plagioclase, Quartz-Quartz, K-feldspar-K-feldspar, and Biotite-Biotite, respectively. These parameters were determined through the aforementioned calibration procedure. On the other hand, the entries P-Q, P-K, P-B, Q-K, Q-B, and K-B denote contacts between Plagioclase-Quartz, Plagioclase-K-feldspar, Plagioclase-Biotite, Quartz-K-feldspar, Quartz-Biotite, and K-feldspar-Biotite, respectively. These parameters are defined as the averages of the properties of adjacent mineral grains. The stress-strain curves resulting from uniaxial compression and tension simulations are depicted in Figures 6A, B. Table 3 presents a summary of the comparison between simulated and experimental values for Poisson’s ratio, elastic modulus, direct tensile strength, and uniaxial compressive strength. The high degree of agreement observed between the simulated and experimental values (Dehghan Banadaki and Mohanty, 2012; Pan et al., 2021a) further validates the accuracy and reliability of the calibrated GBM model in accurately capturing the macroscopic mechanical responses of the material.

FIGURE 5

Figure 5 Numerical model setup (A) Uniaxial compression test, (B) Direct tensile test.

TABLE 1

Table 1 Calibrated properties of Granite minerals.

TABLE 2

Table 2 Calibrated properties of the contacts between mineral grains.

FIGURE 6

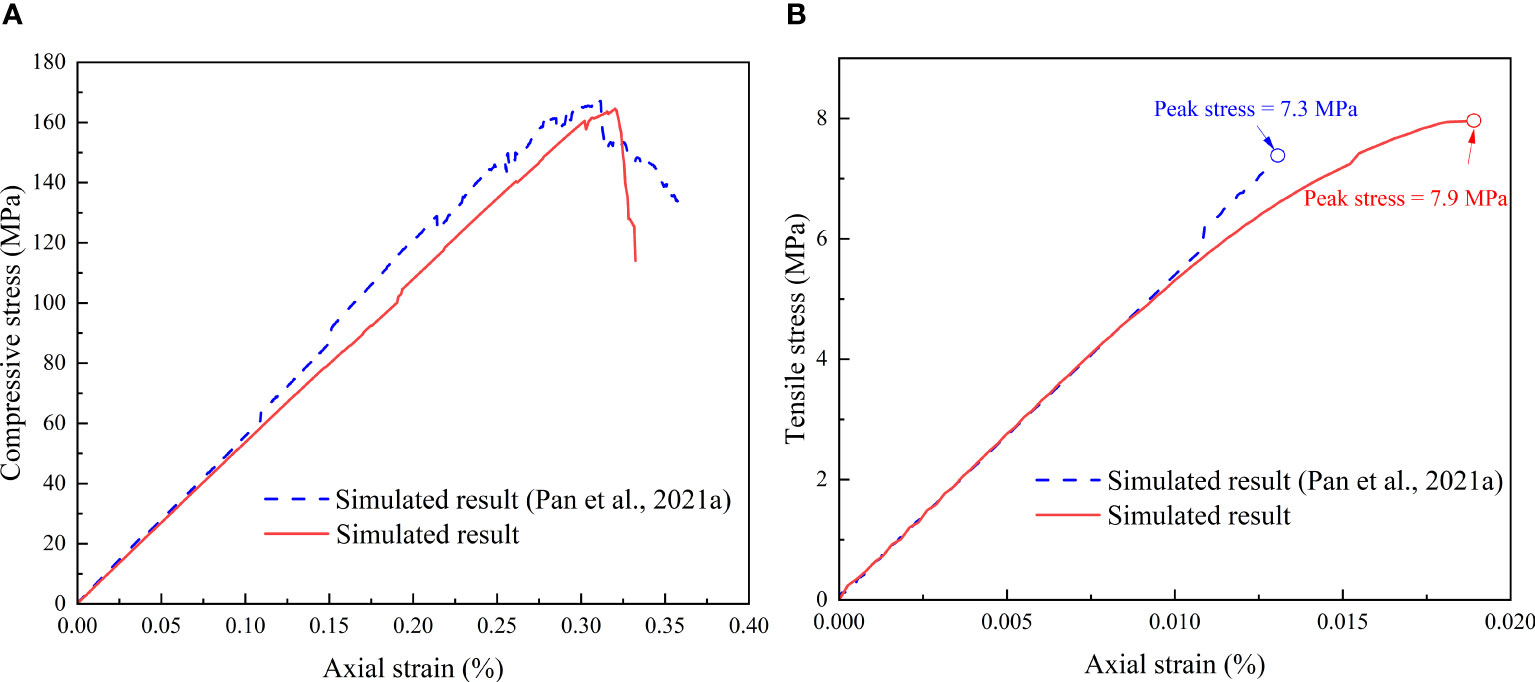
Figure 6 Numerical simulation stress-strain curves (A) Uniaxial compression test, (B) Direct tensile test.

TABLE 3

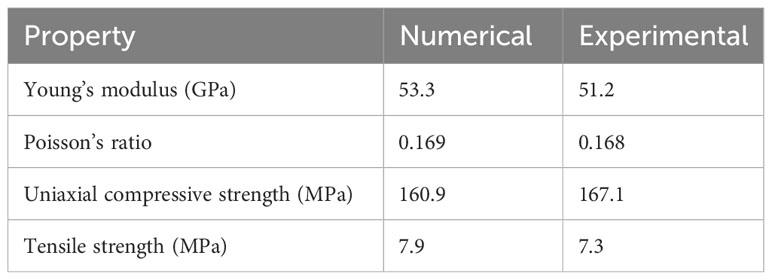
Table 3 Comparison between numerical and experimental results (Dehghan Banadaki and Mohanty, 2012) for the calibration example.

3 Factors affecting the rock strength and failure mode

The previous section presented the methodology employed for generating the breakable grain-based discrete element model. In this section, we apply this method to generate samples exhibiting various grain sizes, distributions, and shapes. The objective is to study the impact of mesostructure on the quasi-static compressive strength and failure mode of granite.

3.1 Grain size distribution

This study assumes a logarithmic normal distribution for the grain size of minerals within the rock. To generate samples with varying grain size distributions, the standard deviation of the mean grain size is modified, allowing for the desired adjustments in the overall distribution characteristics. A larger standard deviation results in a wider distribution, indicating a greater variation in grain sizes within the sample. Conversely, a smaller standard deviation leads to a narrower distribution, indicating a more uniform grain size distribution. The grain size coefficient So, which quantifies the impact of grain size distribution on rock homogeneity, is defined as follows (Nicksiar and Martin, 2014):

$\begin{array}{ll}So=\sqrt{Q_{25\%}/Q_{75\%}}& (1)\end{array}$

where Q_75% and Q_25% represent the grain diameters on the grain size cumulative frequency plot at which 75% and 25% of the grains, respectively, have diameters larger than the corresponding values. The grain size coefficient is commonly greater than 1, and a value approaching 1 indicates a more uniform distribution of grain sizes within the rock.

This section focuses on the investigation and analysis of the effect of grain size distribution on the quasi-static compressive strength and failure mode of rocks. To accomplish this, four groups of models were generated with grain size coefficients 1.07, 1.14, 1.22, and 1.30, respectively. Considering the differences in the spatial distribution of blocks caused by different numbers of random seeds, three samples were generated for each group of models simultaneously. In total, 12 models were generated for analysis, and all models had dimensions of 25 mm (width) × 50 mm (height). It is worth noting that the average grain size, grain circularity, and mineral content were maintained constant for all four groups of models. Specifically, the average grain diameter was fixed at 1.5 mm, while the grain circularity (Ro) was set to 0.9. Figure 7 presents the generated representative grain models.

FIGURE 7

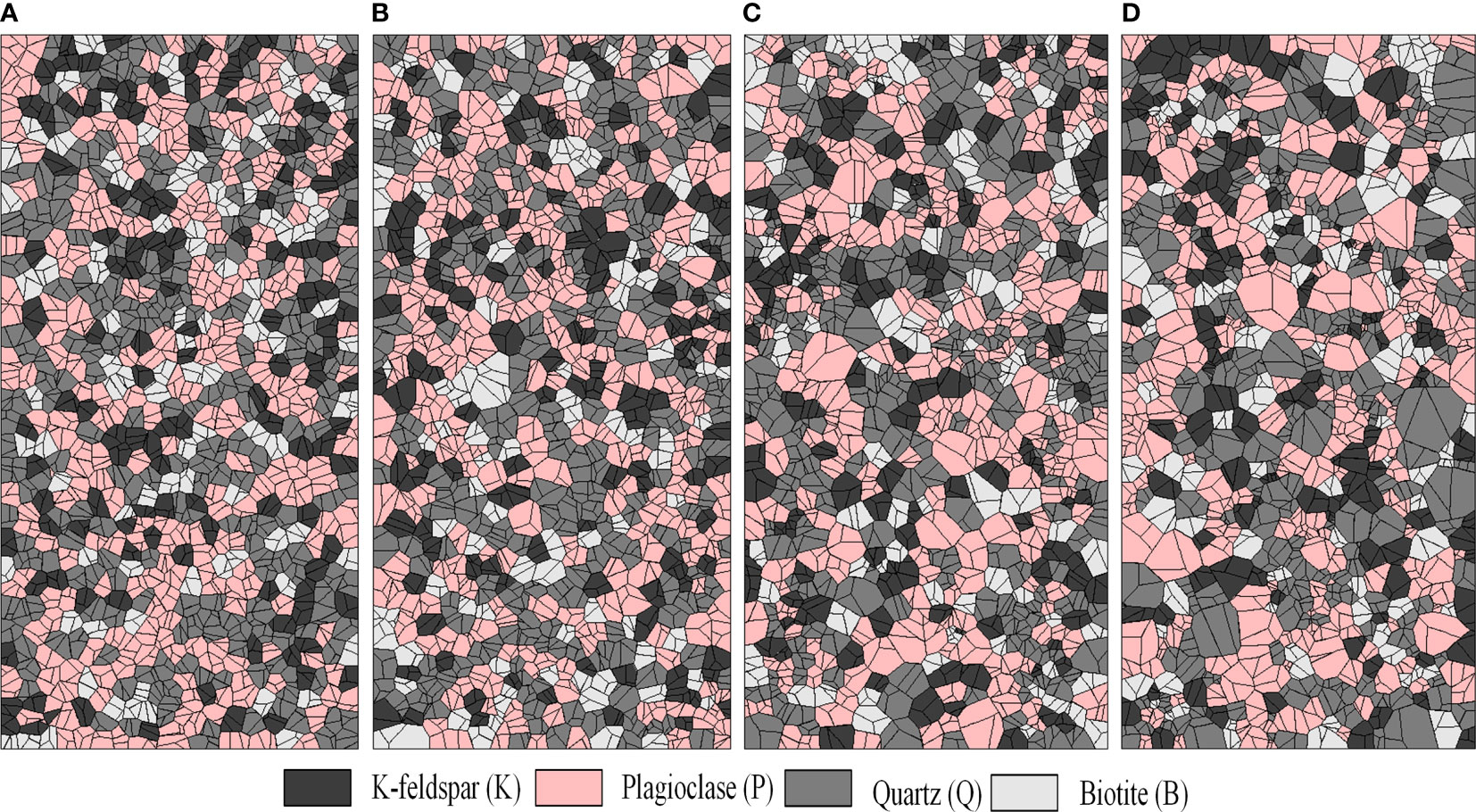
Figure 7 UDEC-GBM models with different grain size coefficients (A) So = 1.07, (B) So = 1.14, (C) So = 1.22, (D) So = 1.30.

Figure 8A illustrates the stress-strain curves under quasi-static uniaxial compression for samples with varying grain size distributions. It can be observed that these curves exhibit similar characteristics, all going through three stages of elasticity, yield, and fracture. However, it should be noted that the simulated stress-strain curves do not include an initial compaction stage. This limitation arises from the inherent characteristics of the Voronoi block model, which does not account for the existence of initial cracks or pores. Furthermore, Figure 8 demonstrates the significant influence of the value of So on the quasi-static uniaxial compressive strength of granite. Through data fitting, it is found that the quasi-static peak strength decreases linearly with the increase of So (Figure 8B). Specifically, for the tested rock samples, the uniaxial compression strength decreased from 165.7 MPa to 143.7 MPa (mean value) with an increase in the value of So from 1.07 to 1.30. This observed trend can be attributed to the enhanced inhomogeneity of the grain size distribution, leading to amplified local stress concentrations within the samples. These stress concentration areas contribute to the failure of heterogeneous samples at lower stress levels, consequently reducing the overall peak strength of the rock.

FIGURE 8

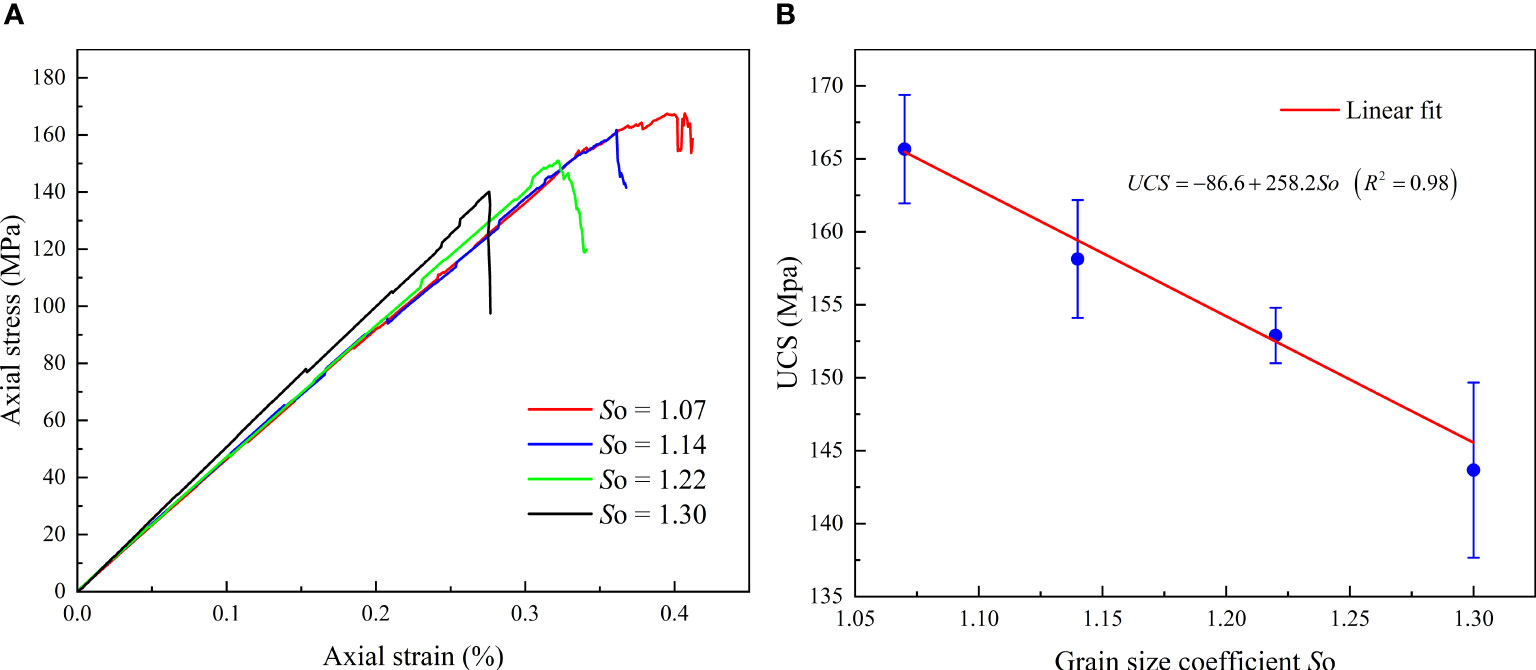
Figure 8 Uniaxial compression strength of numerical rock specimens with varying grain size coefficient (A) Stress-strain curves, (B) Fitting relationship between UCS and So.

Figure 9 presents the failure modes of samples with varying grain size distributions under quasi-static uniaxial compression. The results indicate a close relationship between the crack propagation path and the rock mesostructure. In cases where the rock structure exhibits relative homogeneity (e.g., So = 1.07), cracks tend to propagate along the axial direction, parallel to the direction of maximum compressive stress, ultimately forming one or more vertical macro-fracture planes (as depicted in Figure 9A). This corresponds to a typical splitting failure mode. As the grain size distribution coefficient increases (e.g., So = 1.30), the likelihood of forming inclined macroscopic cracks in the sample becomes more prominent (as shown in Figure 9D). This can be attributed to the widening distribution range of grains within the sample as rock heterogeneity increases. Under axial loading, minerals with larger grain sizes not only experience stress concentration but also possess longer mineral boundaries that serve as preferential paths for crack propagation. Furthermore, Figure 9 reveals a notable “wrapping around the core” phenomenon during the process of crack expansion. Specifically, cracks preferentially propagate along mineral boundaries, and this phenomenon becomes more pronounced with increasing rock heterogeneity.

FIGURE 9

Figure 9 Quasi-static uniaxial compression failure modes of different grain size distribution models (A) So = 1.07, (B) So = 1.14, (C) So = 1.22, (D) So = 1.30.

3.2 Average grain size

Granite typically has a crystalline structure of 1-5 mm interlocking mineral grains. To examine the impact of average grain size on failure modes and quasi-static compressive strength of granite, this research employed four numerical models featuring distinct average grain sizes: 4.5 mm, 3.5 mm, 2.5 mm, and 1.5 mm. To account for the spatial distribution variations caused by different random seed numbers, three samples were generated for each grain size model simultaneously. The size of the model was maintained at 25 mm × 50 mm. It is important to emphasize that the grain size coefficient, grain circularity, and mineral content were kept constant across all models. In this particular study, the values of So and Ro were set to 1.07, and 0.9, respectively. The typical numerical models generated for each average grain size are depicted in Figure 10.

FIGURE 10

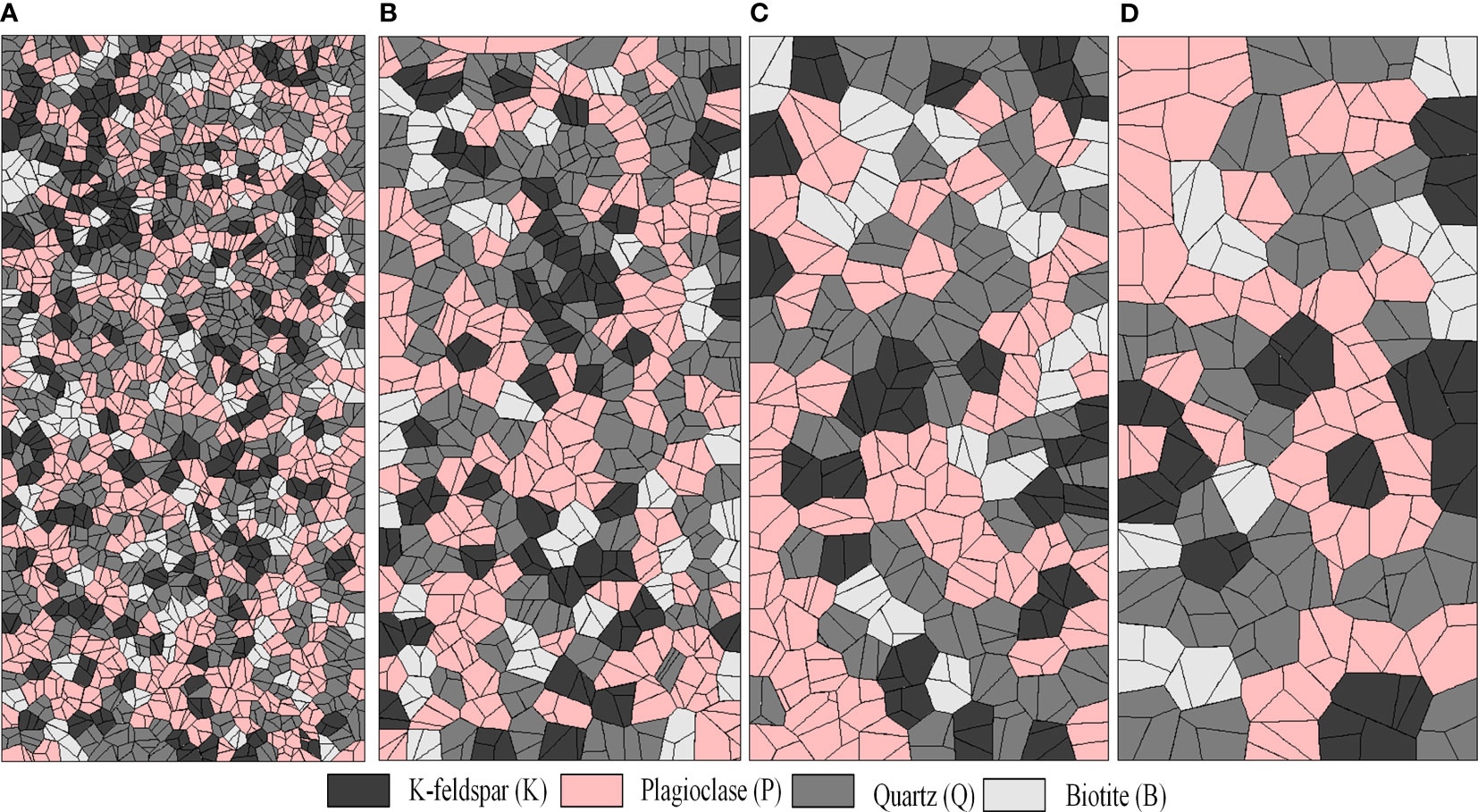
Figure 10 UDEC-GBM models with different average grain sizes (A) D = 1.5 mm, (B) D = 2.5 mm, (C) D = 3.5 mm, (D) D = 4.5 mm.

Figure 11A depicts the stress-strain curves of representative models with varying average grain sizes. The findings reveal a notable reduction in the peak strain as the average grain size increases. Specifically, when the average grain size is 1.5 mm, the peak strain reaches approximately 0.36%. In contrast, with an average grain size of 4.5 mm, the peak strain decreases to 0.19%. This phenomenon can be attributed to the increased contact surfaces between grains in rocks with smaller grain sizes compared to those with larger grain sizes, assuming the sample size remains constant. With more contact surfaces, the deformation modulus of the rock sample during loading is lower, resulting in higher strain values. Furthermore, Figure 11B illustrates the correlation between the average grain size and peak strength. The findings reveal a decline in compressive strength as the average grain size increases. Moreover, a good linear fitting relationship between the two variables is identified, indicating a predictable correlation between average grain size and compressive strength. This finding aligns with the results of experimental tests conducted by other researchers (Tuğrul and Zarif, 1999; Sajid et al., 2016). The observed phenomenon can be attributed to the elongation of grain boundaries that occurs with larger grain sizes. Rock samples with larger average grain sizes exhibit a higher susceptibility to fracture due to the presence of longer grain boundaries, which provide a more continuous path for the growth and propagation of fractures.

FIGURE 11

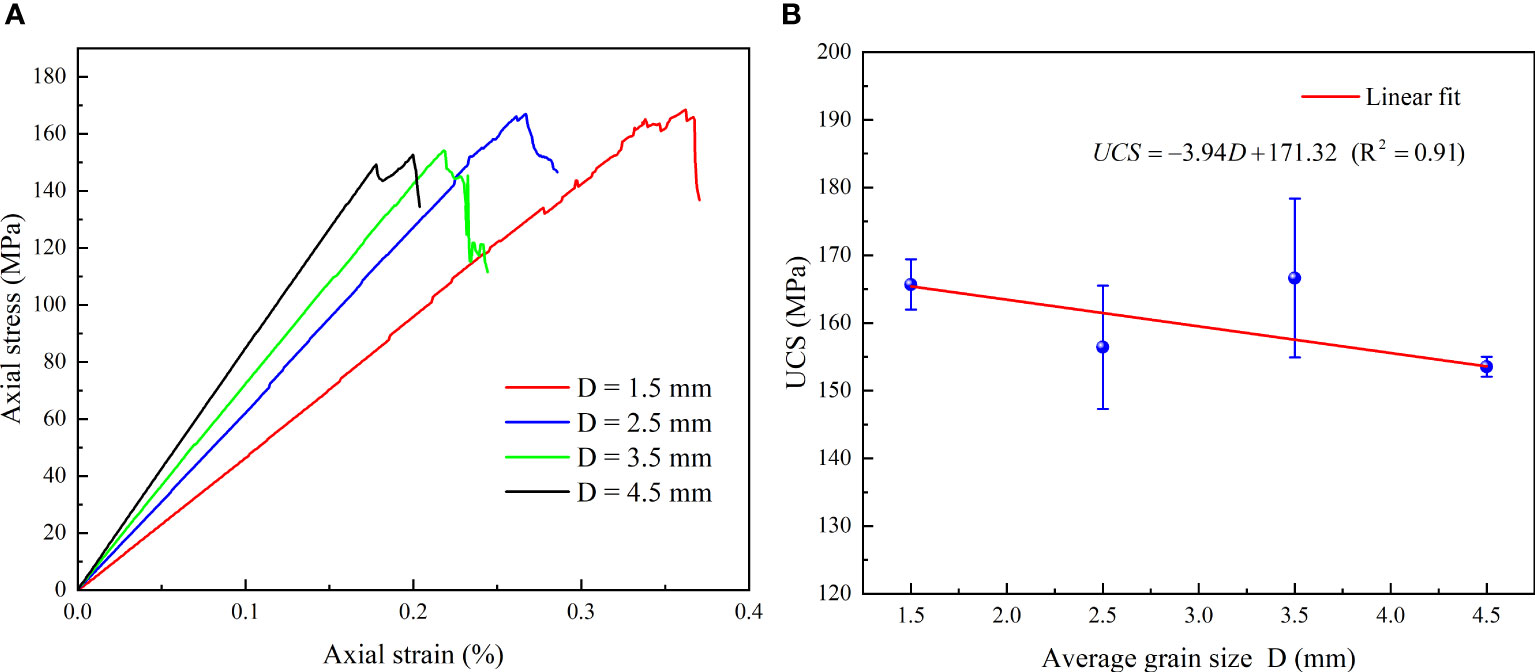
Figure 11 Uniaxial compression strength of numerical rock specimens with varying average grain size (A) Stress-strain curves of different average grain size models, (B) Fitting relationship between UCS and D.

Figure 12 illustrates the macroscopic fracture modes under quasi-static uniaxial compression for four different average grain size models. It can be seen from the figure that numerical specimens exhibit two distinct fracture modes as the average grain size changes. When the grain average diameter is 1.5 mm, the rock specimen displays some tensile fractures oriented parallel to the loading direction, accompanied by shear plane failure across the specimen. However, When the average grain size reaches 3.5 mm, the shear band becomes almost imperceptible, and the primary failure mechanism shifts to a significant number of tensile fractures parallel to the axial loading direction. Consequently, as the average grain size increases, the dominant failure mode transitions from shear and axial splitting to primarily axial splitting. Furthermore, it is observable that as the average grain size increases from 1.5 mm to 4.5 mm, the length or width of the tensile fractures also increases.

FIGURE 12

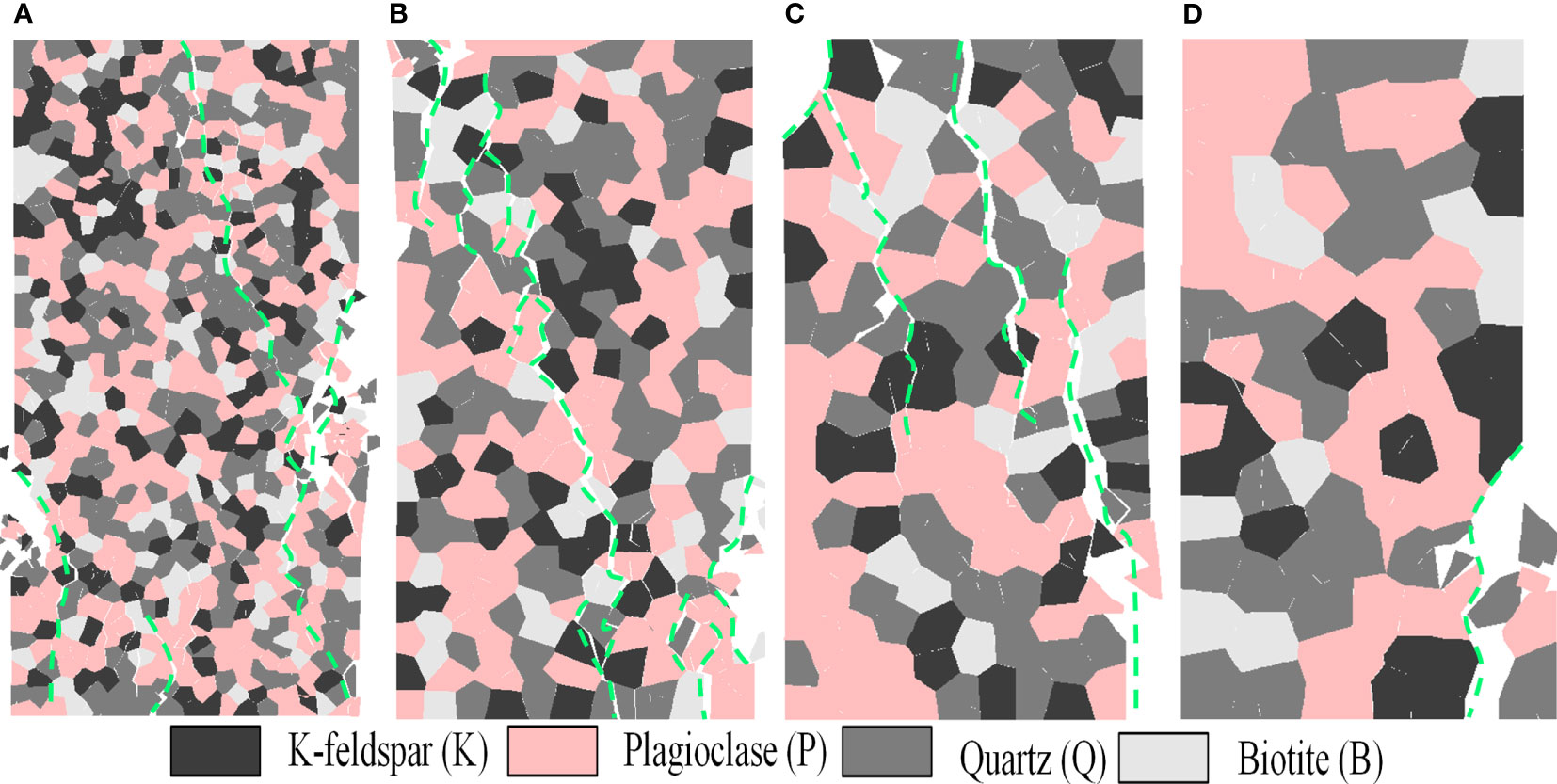
Figure 12 Quasi-static uniaxial compression failure modes of different average grain size models (A) D = 1.5 mm, (B) D = 2.5 mm, (C) D = 3.5 mm, (D) D = 4.5 mm.

3.3 Grain shape

For two-dimensional models, Neper uses circularity to describe particle shape, defined as the ratio of the circumference of a circle of equal area to the circumference of the grain. According to Contreras et al. (2021), the roundness of granite grains typically falls within the range of 0.55 to 0.96, with an average roundness of 0.83. Therefore, four groups of numerical samples with different grain roundness (Ro), namely 0.9, 0.85, 0.8, and 0.75, were generated in this research. It is worth mentioning that throughout the models, the average grain size, grain size coefficient, and mineral content were kept constant. Here, the grain size coefficient (So) was set to 1.07, and the average grain size was fixed at 1.5 mm. Considering the differences in block spatial distribution caused by different numbers of random seeds, three samples were generated for each group of models at the same time for calculation. Figure 13 illustrates the typical numerical models of different grain roundness. All of these samples have dimensions of 25 mm × 50 mm.

FIGURE 13

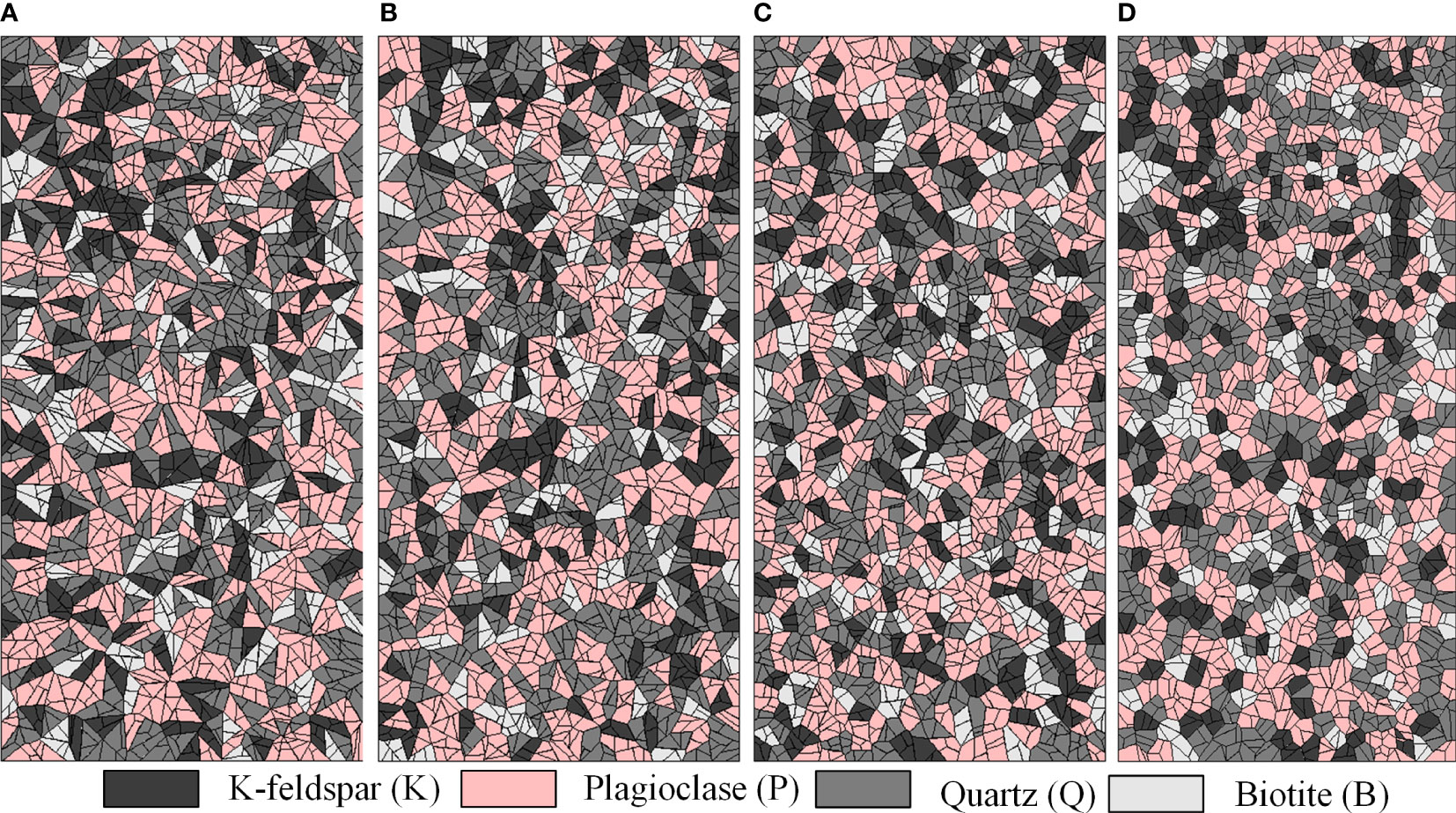
Figure 13 UDEC-GBM models with different grain roundness (A) Ro = 0.75, (B) Ro = 0.80, (C) Ro = 0.85, (D) Ro = 0.90.

Figure 14A presents the stress-strain curves obtained from samples with varying grain roundness under quasi-static uniaxial compression. The results reveal the considerable influence of grain roundness on both peak strength and peak strain. As depicted in the figure, an increase in grain roundness corresponds to higher values of uniaxial compressive strength (UCS) and peak strain. As an example, when the grain roundness is 0.75, the peak strength is measured at 119.2 MPa, and the corresponding peak strain is 0.29%. However, when the grain roundness increases to 0.9, the peak strength significantly rises to 168.2 MPa, accompanied by a corresponding peak strain of 0.36%. The reason for this phenomenon is related to the level of interlocking within the grain structure. The observed trend in Figure 13 indicates that as the roundness of the grains decreases, the shape of the grains becomes more triangular. However, studies by Mayer and Stead (2017) indicate that triangular particles tend to favor interparticle shear failure. Compared with triangular grains, polygonal grains tend to provide a high degree of interlocking within the grain, which will facilitate interparticle tensile failure and lead to higher peak strength. Furthermore, Figure 14B presents the fitted relationship between grain roundness and the average value of UCS. The fitting results exhibit a strong linear relationship when the grain distribution coefficient, average grain size, and mineral content are kept constant. The fitting correlation coefficient (R²) reaches 0.99.

FIGURE 14

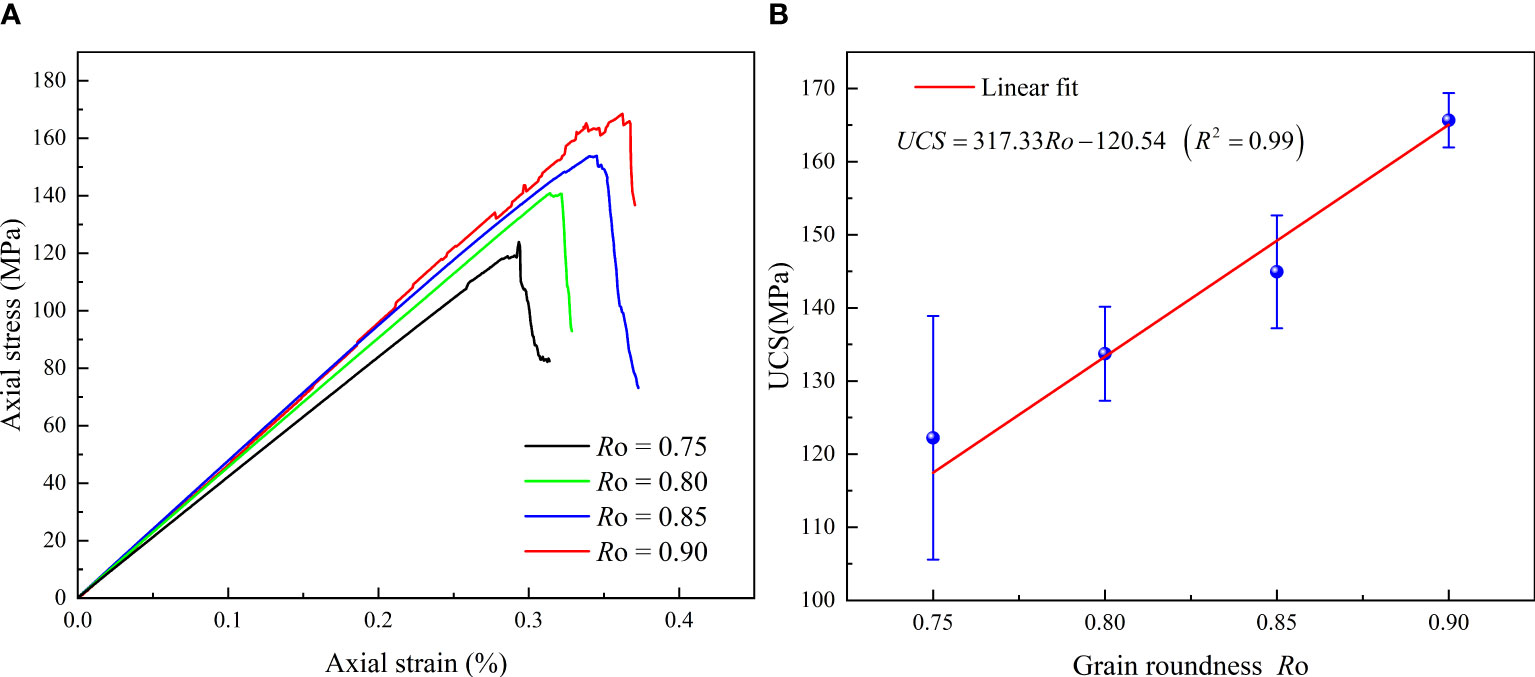
Figure 14 Uniaxial compression strength of numerical rock specimens with varying grain roundness (A) Stress-strain curves of different grain roundness models, (B) Fitting relationship between grain roundness and uniaxial compressive strength.

Figure 15 illustrates the distinctive failure modes observed in quasi-static uniaxial compression for various grain roundness models. It is evident that the failure mode of the rock is intricately linked to the roundness characteristics of the grains. As mentioned earlier, when the roundness of the grains decreases, their shape tends to be closer to triangular (e.g., Ro = 0.75). In such cases, the model is more prone to shear failure, resulting in the development of oblique macroscopic cracks, as depicted in Figure 15D. On the other hand, the GBM model with high roundness (e.g., Ro = 0.9) has a high degree of interlocking, and tensile failure between particles is easy to occur, so that macroscopic axial splitting damage is more likely to occur, as shown in Figure 15A.

FIGURE 15

Figure 15 Quasi-static uniaxial compression failure modes of different grain roundness models (A) Ro = 0.75, (B) Ro = 0.80, (C) Ro = 0.85, (D) Ro = 0.90.

4 Conclusions

This study presents a developed breakable grain-based model to examine the impacts of grain size coefficient (1.07 to 1.3), average grain size (1.5 mm to 4.5 mm), and grain roundness (0.75 to 0.9) on the quasi-static uniaxial compressive strength and failure modes of rocks. Based on the numerical simulation results, the following conclusions can be drawn:

1. The successful replication of granite behavior using the breakable polygonal grain-based discrete element model demonstrates its applicability for studying the mechanical response and failure mechanisms of rock materials. In addition, with the help of multi-scale Voronoi tessellation technology, the model can effectively capture both inter-granular and trans-granular cracks that occur during the compression process.

2. The quasi-static compressive strength of the rock exhibits a good linear relationship with the average grain size (D), grain size coefficient (So), and grain roundness (Ro). Specifically, the compressive strength of the rock exhibits a negative correlation with both the D and So, indicating that as rock heterogeneity and the average grain size increases, the compressive strength tends to decrease. Conversely, the compressive strength shows a positive correlation with the Ro (degree of interlocking) of the grains. This implies that there is a tendency for the compressive strength to rise as the degree of interlocking among the grains increases.

3. The mesostructure of rock significantly influences the observed failure modes in compression tests. The degree of heterogeneity within the rock model has a pronounced impact on the resulting failure mode. In relatively homogeneous models, the dominant failure mode is splitting. As the heterogeneity of the rock model increases, the failure mode transitions to shear failure. The grain size of the rock also influences the failure mode. Fine-grained rocks tend to fracture in single shear bands, while coarse-grained rocks tend to fracture axially. The shape of the grains, characterized by roundness, also affects the failure mode. Rocks with lower roundness values are more prone to shear failure, while rocks with higher roundness values tend to exhibit axial splitting.

In this paper, the breakable UDEC-GBM model is employed to investigate the macroscopic compressive mechanical behavior of rocks. However, the model exhibits certain limitations, such as the absence of consideration for internal microcracks within the rock during modeling. Consequently, this model is suitable for hard and dense rocks, while for soft or microcrack-laden rocks, more nuanced meso features should be taken into account. Subsequent research will further address the influence of pore and crack defect structures, leading to the development of more refined numerical models.

Data availability statement

The original contributions presented in the study are included in the article/supplementary files, further inquiries can be directed to the corresponding author.

Author contributions

CP: Conceptualization, Funding acquisition, Writing – original draft. GZ: Funding acquisition, Writing – review & editing. XM: Writing – review & editing. CD: Formal Analysis, Funding acquisition, Writing – review & editing. PG: Data curation, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was financially supported by the Scientific Research Foundation for High-level Talents of Anhui University of Science and Technology (No. 2022yjrc80), the National Natural Science Foundation of China (No. 51974009, 52074006, 52304075), the National Talent Project (T2021137), the Anhui Provincial Major Science and Technology Project (202203a07020011), the Leading Talents Project of Anhui Province’s “Special Support Plan” (T000508), the Anhui Province Academic and Technical Leaders Research Activity Fund (2021), and the University Synergy Innovation Program of Anhui Province (No. GXXT-2021-075).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdelaziz A., Zhao Q., Grasselli G. (2018). Grain based modelling of rocks using the combined finite-discrete element method. Comput. Geotech. 103, 73–81. doi: 10.1016/J.COMPGEO.2018.07.003

CrossRef Full Text | Google Scholar

Alfano G. (2006). On the influence of the shape of the interface law on the application of cohesive-zone models. Compos. Sci. Technol. 66, 723–730. doi: 10.1016/J.COMPSCITECH.2004.12.024

CrossRef Full Text | Google Scholar

Barenblatt G. I. (1962). The mathematical theory of equilibrium cracks in brittle fracture. Adv. Appl. Mechanics. 7, 55–129. doi: 10.1016/S0065-2156(08)70121-2

CrossRef Full Text | Google Scholar

Contreras I. C.E., Walton G., Holley E. (2021). Statistical assessment of the effects of grain-structure representation and micro-properties on the behavior of bonded block models for brittle rock damage prediction. Sustainability 13, 147889. doi: 10.3390/su13147889

CrossRef Full Text | Google Scholar

Cowie S., Walton G. (2018). The effect of mineralogical parameters on the mechanical properties of granitic rocks. Eng. Geol. 240, 204–225. doi: 10.1016/J.ENGGEO.2018.04.021

CrossRef Full Text | Google Scholar

Dehghan Banadaki M. M., Mohanty B. (2012). Numerical simulation of stress wave induced fractures in rock. Int. J. Impact. Eng. 40–41, 16–25. doi: 10.1016/J.IJIMPENG.2011.08.010

CrossRef Full Text | Google Scholar

Dugdale D. S. (1960). Yielding of steel sheets containing slits. J. Mech. Phys. Solids. 8, 100–104. doi: 10.1016/0022-5096(60)90013-2

CrossRef Full Text | Google Scholar

Eberhardt E., Stimpson B., Stead D. (1999). Effects of grain size on the initiation and propagation thresholds of stress-induced brittle fractures. Rock. Mech. Rock. Eng. 32, 81–99. doi: 10.1007/s006030050026

CrossRef Full Text | Google Scholar

Elices M., Guinea G. V., Gómez J., Planas J. (2002). The cohesive zone model: advantages, limitations and challenges. Eng. Fract. Mech. 69, 137–163. doi: 10.1016/S0013-7944(01)00083-2

CrossRef Full Text | Google Scholar

Fathipour-Azar H., Wang J., Jalali S.-M. E., Torabi S. R. (2020). Numerical modeling of geomaterial fracture using a cohesive crack model in grain-based DEM. Comput. Part Mech. 7, 645–654. doi: 10.1007/s40571-019-00295-4

CrossRef Full Text | Google Scholar

Fredrich J. T., Evans B., Wong T.-F. (1990). Effect of grain size on brittle and semibrittle strength: Implications for micromechanical modelling of failure in compression. J. Geophys. Res. Solid. Earth 95, 10907–10920. doi: 10.1029/JB095iB07p10907

CrossRef Full Text | Google Scholar

Fukuda D., Mohammadnejad M., Liu H., Zhang Q., Zhao J., Dehkhoda S., et al. (2020). Development of a 3D hybrid finite-discrete element simulator based on GPGPU-parallelized computation for modelling rock fracturing under quasi-static and dynamic loading conditions. Rock. Mech. Rock. Eng. 53, 1079–1112. doi: 10.1007/s00603-019-01960-z

CrossRef Full Text | Google Scholar

Gao F., Stead D., Elmo D. (2016). Numerical simulation of microstructure of brittle rock using a grain-breakable distinct element grain-based model. Comput. Geotech. 78, 203–217. doi: 10.1016/J.COMPGEO.2016.05.019

CrossRef Full Text | Google Scholar

Ghasemi S., Khamehchiyan M., Taheri A., Nikudel M. R., Zalooli A. (2020). Crack evolution in damage stress thresholds in different minerals of granite rock. Rock. Mech. Rock. Eng. 53, 1163–1178. doi: 10.1007/s00603-019-01964-9

CrossRef Full Text | Google Scholar

Gui Y., Bui H. H., Kodikara J. (2015). An application of a cohesive fracture model combining compression, tension and shear in soft rocks. Comput. Geotech. 66, 142–157. doi: 10.1016/J.COMPGEO.2015.01.018

CrossRef Full Text | Google Scholar

Gui Y. L., Bui H. H., Kodikara J., Zhang Q. B., Zhao J., Rabczuk T. (2016b). Modelling the dynamic failure of brittle rocks using a hybrid continuum-discrete element method with a mixed-mode cohesive fracture model. Int. J. Impact. Eng. 87, 146–155. doi: 10.1016/J.IJIMPENG.2015.04.010

CrossRef Full Text | Google Scholar

Gui Y. L., Zhao Z. Y., Ji J., Wang X. M., Zhou K. P., Ma S. Q. (2016a). The grain effect of intact rock modelling using discrete element method with Voronoi grains. Géotechnique. Lett. 6, 136–143. doi: 10.1680/jgele.16.00005

CrossRef Full Text | Google Scholar

Gulizzi V., Rycroft C. H., Benedetti I. (2018). Modelling intergranular and transgranular micro-cracking in polycrystalline materials. Comput. Methods Appl. Mech. Eng. 329, 168–194. doi: 10.1016/J.CMA.2017.10.005

CrossRef Full Text | Google Scholar

Han Z., Zhang L., Azzam R., Zhou J., Wang S. (2021). A statistical index indicating the degree and mechanical effects of grain size heterogeneity in rocks. Eng. Geol. 293, 106292. doi: 10.1016/J.ENGGEO.2021.106292

CrossRef Full Text | Google Scholar

Huang X., Xu L., Zhao T., Lu S., Sun Z., Ding D. (2023). Characterization of the negative Poisson's ratio effect of the thermal-damaged crystalline rock by the grain-based model. Int. J. Rock. Mech. Min. Sci. 170, 105553. doi: 10.1016/J.IJRMMS.2023.105553

CrossRef Full Text | Google Scholar

Kazerani T. (2013). Effect of micromechanical parameters of microstructure on compressive and tensile failure process of rock. Int. J. Rock. Mech. Min. Sci. 64, 44–55. doi: 10.1016/J.IJRMMS.2013.08.016

CrossRef Full Text | Google Scholar

Keikha T., Keykha H. A. (2013). Correlation between mineralogical characteristics and engineering properties of granitic rocks. Electronic. J. Geotechnical. Eng. 18, 4055–4065.

Google Scholar

Kong L., Ranjith P. G., Li Q. B., Song Y. (2022). Rock grain-scale mechanical properties influencing hydraulic fracturing using Hydro-GBM approach. Eng. Fract. Mech. 262, 108227. doi: 10.1016/J.ENGFRACMECH.2021.108227

CrossRef Full Text | Google Scholar

Li D., Liu Z., Zhu Q., Zhang C., Xiao P., Ma J. (2023). Quantitative identification of mesoscopic failure mechanism in granite by deep learning method based on SEM images. Rock. Mech. Rock. Eng. 56, 4833–4854. doi: 10.1007/s00603-023-03307-1

CrossRef Full Text | Google Scholar

Li M., Zuo J., Hu D., Shao J., Liu D. (2020). Experimental and numerical investigation of microstructure effect on the mechanical behavior and failure process of brittle rocks. Comput. Geotech. 125, 103639. doi: 10.1016/J.COMPGEO.2020.103639

CrossRef Full Text | Google Scholar

Mayer J. M., Stead D. (2017). Exploration into the causes of uncertainty in UDEC Grain Boundary Models. Comput. Geotech. 82, 110–123. doi: 10.1016/J.COMPGEO.2016.10.003

CrossRef Full Text | Google Scholar

Morgan S. P., Johnson C. A., Einstein H. H. (2013). Cracking processes in Barre granite: fracture process zones and crack coalescence. Int. J. Fract. 180, 177–204. doi: 10.1007/s10704-013-9810-y

CrossRef Full Text | Google Scholar

Nicksiar M., Martin C. D. (2014). Factors affecting crack initiation in low porosity crystalline rocks. Rock. Mech. Rock. Eng. 47, 1165–1181. doi: 10.1007/s00603-013-0451-2

CrossRef Full Text | Google Scholar

Pan C., Li X., He L., Li J. (2021b). Study on the effect of micro-geometric heterogeneity on mechanical properties of brittle rock using a grain-based discrete element method coupling with the cohesive zone model. Int. J. Rock. Mech. Min. Sci. 140, 104680. doi: 10.1016/J.IJRMMS.2021.104680

CrossRef Full Text | Google Scholar

Pan C., Li X., Li J., Zhao J. (2021a). Numerical investigation of blast-induced fractures in granite: insights from a hybrid LS-DYNA and UDEC grain-based discrete element method. Geomech. Geophys. Geo-Energy. Geo-Resour. 7, 49. doi: 10.1007/s40948-021-00253-6

CrossRef Full Text | Google Scholar

Peng J., Wong L. N. Y., The C. I. (2021). Influence of grain size on strength of polymineralic crystalline rock: New insights from DEM grain-based modeling. J. Rock. Mech. Geotech. Eng. 13, 755–766. doi: 10.1016/J.JRMGE.2021.01.011

CrossRef Full Text | Google Scholar

Quan J., Rong G., Xu L., Chen Z. (2023). A three-dimensional grain-based model for studying the microscopic fracture behaviour of granite. Comput. Geotech. 159, 105427. doi: 10.1016/J.COMPGEO.2023.105427

CrossRef Full Text | Google Scholar

Quey R., Dawson P. R., Barbe F. (2011). Large-scale 3D random polycrystals for the finite element method: Generation, meshing and remeshing. Comput. Methods Appl. Mech. Eng. 200, 1729–1745. doi: 10.1016/J.CMA.2011.01.002

CrossRef Full Text | Google Scholar

Quey R., Renversade L. (2018). Optimal polyhedral description of 3D polycrystals: Method and application to statistical and synchrotron X-ray diffraction data. Comput. Methods Appl. Mech. Eng. 330, 308–333. doi: 10.1016/J.CMA.2017.10.029

CrossRef Full Text | Google Scholar

Saadat M., Taheri A. (2020). A cohesive grain based model to simulate shear behaviour of rock joints with asperity damage in polycrystalline rock. Comput. Geotech. 117, 103254. doi: 10.1016/J.COMPGEO.2019.103254

CrossRef Full Text | Google Scholar

Sajid M., Coggan J., Arif M., Andersen J., Rollinson G. (2016). Petrographic features as an effective indicator for the variation in strength of granites. Eng. Geol. 202, 44–54. doi: 10.1016/J.ENGGEO.2016.01.001

CrossRef Full Text | Google Scholar

Tuğrul A., Zarif I. H. (1999). Correlation of mineralogical and textural characteristics with engineering properties of selected granitic rocks from Turkey. Eng. Geol. 51, 303–317. doi: 10.1016/S0013-7952(98)00071-4

CrossRef Full Text | Google Scholar

Wang F., Konietzky H., Herbst M., Chen W. (2022). Mechanical responses of grain-based models considering different crystallographic spatial distributions to simulate heterogeneous rocks under loading. Int. J. Rock. Mech. Min. Sci. 151, 105036. doi: 10.1016/J.IJRMMS.2022.105036

CrossRef Full Text | Google Scholar

Wang S., Yan Y. (2022). Numerical study of dynamic fracture behaviors of rock containing double pre-existing flaws under different confined stress and flaw geometry. Eur. J. Environ. Civil. Eng. 27, 3363–3379. doi: 10.1080/19648189.2022.2136248

CrossRef Full Text | Google Scholar

Wang Z., Wang T., Wu S., Hao Y. (2021). Investigation into the effects of grain size on strength and failure behaviors of granites using a breakable polygonal grain–based model. Bul. Eng. Geol. Environ. 80, 6989–7007. doi: 10.1007/s10064-021-02354-8

CrossRef Full Text | Google Scholar

Wu Z., Liang X., Liu Q. (2015). Numerical investigation of rock heterogeneity effect on rock dynamic strength and failure process using cohesive fracture model. Eng. Geol. 197, 198–210. doi: 10.1016/J.ENGGEO.2015.08.028

CrossRef Full Text | Google Scholar

Xiao H., He L., Zheng Y., Yan S. (2022). 3D solid digital and numerical modeling of multimineral heterogeneous rocks based on deep learning. Geomech. Geophys. Geo-Energy. Geo-Resour. 8, 188. doi: 10.1007/s40948-022-00495-y

CrossRef Full Text | Google Scholar

Zhang X. P., Ji P. Q., Peng J., Wu S. C., Zhang Q. (2020). A grain-based model considering pre-existing cracks for modelling mechanical properties of crystalline rock. Comput. Geotech. 127, 103776. doi: 10.1016/J.COMPGEO.2020.103776

CrossRef Full Text | Google Scholar

Zhou W., Ji X., Ma G., Chen Y. (2020). FDEM simulation of rocks with microstructure generated by Voronoi grain-based model with particle growth. Rock. Mech. Rock. Eng. 53, 1909–1921. doi: 10.1007/s00603-019-02014-0

CrossRef Full Text | Google Scholar