Numerical simulation of the Oncomelania snails transport attached to floating objects under different wind conditions

The long-distance migration of Oncomelania snails mainly occurs by attaching to floating objects during floods. However, the processes, characteristics and effects of migration are not fully understood. Here, a motion equation for floating objects with attached Oncomelania snails was constructed using the Lagrangian method. The equation can be numerically solved to simulate the movement of floating objects after parameter calibration. Then, the calibrated parameters were used to simulate the migration of Oncomelania snails in the lower Jingjiang River, where they had spread over a large area. The effects of flood conditions on the migration and spread of Oncomelania snails have been studied to a certain extent, but the impact of wind conditions on snail migration has rarely been reported. Therefore, based on the distribution of Oncomelania snails in China, the difficulties and key areas for the control of schistosomiasis and Oncomelania snails, and the morphological characteristics of the river reach, the Lower Jingjiang River section was selected as a practical application case. A theoretical model of the migration and spread of Oncomelania snails was established, and the characteristics of the Oncomelania snail migration were simulated and analyzed based on flood and distribution patterns under different wind conditions. The results indicate that wind conditions have little influence on the longitudinal spreading of Oncomelania snails but have a relatively large influence on the lateral spreading of snails. Compared with calm wind conditions, both northeasterly and southerly wind conditions can lead to longer longitudinal migration distances of snails, thereby increasing the risk of snail spreading and schistosomiasis transmission.

1 Introduction

Schistosomiasis is a contagious disease that seriously endangers human health and harms socioeconomic development (Jean et al., 2022; Lo et al., 2022). Due to its high contagiousness, long communication links and wide endemic distribution (Song et al., 2017; Ghazy et al., 2022; Lv et al., 2022), schistosomiasis is listed by the World Health Organization as one of the most widely distributed parasitic diseases (Li et al., 2016; Liu et al., 2021). Schistosomiasis mainly infects people who have come into contact with infected water through skin and mucous membranes (Yuan et al., 2017; Zhang and Zhao, 2023). The infected water contains the cercariae of schistosomiasis, which are released from Oncomelania snails. As the only intermediate host of Schistosoma japonicum (Sokolo et al., 2017; Agola et al., 2021), the migration of Oncomelania snails is directly linked to the distribution of schistosomiasis (Wang et al., 2016; Wang et al., 2017). Therefore, controlling the migration of Oncomelania snails is the most important and effective way to control the spread of schistosomiasis.

The migration and diffusion behaviors of Oncomelania snails are complex because they are related not only to the physical properties of the snails, including the geometry and density of their bodies, but also to water flow and meteorological conditions and are further affected by the survival activities of the snails (Belizario et al., 2017). Yang et al. (2005), He et al., 2016 and Zhang et al. (2004) studied the settlement and incipient motion of Oncomelania snails in laboratory flumes and proposed formulas for the settling velocity and incipient velocity. Field surveys and sampling have commonly been used to explore the spatiotemporal distribution patterns of Oncomelania snails in the Changjiang River basin (Liu et al., 2011; Liu, 2013) and to assess the effect of various water projects, such as water system connection projects and water diversion projects, on snail migration and diffusion (Perez Saez et al., 2016; Hu et al., 2017; Hu et al., 2019).

Studies have shown that floods and floating debris play an important role in the migration of Oncomelania snails (Yang et al., 2009). Chen et al. (2007) investigated the schistosomiasis epidemic in Fengyizhou Township, Zongyang County, Anhui Province, where the river burst its bank during a flood, and found that flooding had a significant impact on the spread of Oncomelania snails. The density of live snails, the density of infected downstream snails and the infection rate of humans and animals increased after the breach of the bank. Based on a long-term field survey and on-site observations of the Dongting Lake area, Ma et al (Maszle et al., 1998). found that in July and August, when the water level increased, Oncomelania snails outside the polders could attach to floating objects and drift long distances with the water current, which resulted in the spread of snails to nonsnail areas inside the polders. Through field surveys, Zhang et al. (2008) found that Oncomelania snails were first spotted on floating debris in lowland areas at the northeast corner of the Chenjiazhounan shoal in the Anhui section of the Changjiang River. This corner served as a snail source, and the Oncomelania snails quickly spread throughout the shoal.

Despite the abundance of studies and surveyed data, most studies of Oncomelania snails have been based on field observations and qualitative analyses. Some scholars have used mathematical and statistical methods for further analysis and established functional relationships between the Oncomelania snail distribution and environmental factors. For example, Li et al. (1997) generalized the vertical migration of Oncomelania snails in a shoal after changes in the water level and described the functional relationship between the distribution of snails and the water level. Only a few studies have simulated the trajectory of Oncomelania snails based on motion equations. Xue (Xue et al., 2015) used a 3D Reynolds-averaged numerical simulation (RANS) model to simulate the flow field in a spiral flow snail elimination device and derived the speed of individual snail particles based on a force balance; then, the trajectory of the snails was calculated. In that study, the snails were not controlled, and the simulation of their trajectories considered only the influence of the mean flow velocity and not the random effect of turbulence. In natural conditions, uncontrolled movement is not the primary mode of snail migration. In contrast, Oncomelania snails proactively attach to floating objects, which could result in large-scale migrations of Oncomelania snails. The drifting process of floating objects is affected not only by the mean flow and turbulent water flows but also by the wind.

Numerical simulation is one of the main methods used to study the motion of substances. Currently, numerical simulation methods can be roughly divided into two types: Eulerian methods and Lagrangian methods (also known as particle tracking methods). Eulerian methods are based on a field view and are suitable for simulating the movement of spatially and continuously distributed substances. Lagrangian methods directly describe the motion of particles and are suitable for simulating the motion of discrete objects. As the temporal and spatial distributions of Oncomelania snails are obviously discontinuous, Lagrangian methods based on particle tracking are naturally more suitable than Eulerian methods for simulating the migration of Oncomelania snails.

Lagrangian methods have been widely applied in studies of the surface water environment, such as the transport of soluble pollutants (Xue et al., 2021), fish eggs (Li et al., 2016; Sun et al., 2017), and oil substances (Hata et al., 2017; Moendeg et al., 2017); water exchange (Song et al., 2016);and vegetated flows (Yang et al., 2018). However, considering the current understanding of Oncomelania snails and the professional backgrounds of schistosomiasis researchers, to the authors knowledge, no study has been conducted using Lagrangian methods to simulate the migration of Oncomelania snails in natural environments.

To better understand the migration behavior and physical mechanism of snail movement, a governing equation of snail migration is established in this work. The equation is based on the Lagrangian method, and numerical solution techniques are applied to build a numerical model. The effects of the mean and turbulent water flow velocities are considered, as are the effects of wind forces. Then, the numerical model is used to study the migration of snails.

The main objective of this study is to develop a tool capable of evaluating the influences of advection and turbulent diffusion for water and wind forces on the transport and dispersal pattern of Oncomelania snails. Therefore, a Lagrangian numerical model that considers the effects of mean and turbulent water flow velocities and wind speed on the movement of Oncomelania snails is formulated and applied. This model can be used to not only evaluate the migration of Oncomelania snails but also to simulate the transport of other passive particles.

2 Materials and methods

The symbols and units used in this paper are shown in Table 1.

Table 1

Table 1 Symbols and units used in this paper.

2.1 Motion equation for an individual particle

As stated, Oncomelania snails mainly migrate on large spatial scales by attaching to floating objects. Therefore, the migration of snails can be described by the displacement of floating objects. By treating a floating object as an individual floating particle, its motion can be determined by the water flow and wind patterns. The motion of a floating particle caused by the actions of wind and water can eventually be decomposed into mean motion and random motion. The position of a floating particle S_i is set at time t_i. The particle moves to a new position S_i+1 after a time step Δt. Thus,

$\begin{array}{ll}{S}_{i+1}=S_i+\Delta {\overline{\text{X}}}_{{}_i}+\Delta {\text{X}}_d{}_{{}_i}& (1)\end{array}$

where $\Delta {\overline{X}}_{{}_i}$ denotes the displacement caused by the mean velocity during Δt and $\Delta X_d{}_{{}_i}$ is the random displacement during Δt.

2.1.1 Mean velocity

The displacement caused by the mean velocity during Δt can be obtained from

$\begin{array}{ll}\Delta {\overline{\text{X}}}_{{}_i}={\overrightarrow{v}}_i\Delta t& (2)\end{array}$

where ${\overrightarrow{v}}_i$ denotes the mean velocity of the snail at time t_i. Because all analyses are based on time step i, all subscripts i here and later are omitted for convenience. Thus, Equation (2) is rewritten as Equation (3).

$\begin{array}{ll}\Delta \overline{\text{X}}=\overrightarrow{v}\Delta t& (3)\end{array}$

The floating object moves under the effects of wind and water. The drag forces of wind and flowing water can be described Equation (4) and Equation (5).

$\begin{array}{ll}{\overrightarrow{F}}_w=\frac{1}{2}{S}_a{D}_a{\rho }_a({\overrightarrow{v}}_w-\overrightarrow{v})\left|{\overrightarrow{v}}_{w_i}-\overrightarrow{v}\right|& (4)\end{array}$

$\begin{array}{ll}{\overrightarrow{F}}_c=\frac{1}{2}{S}_c{D}_c{\rho }_c({\overrightarrow{v}}_c-\overrightarrow{v})\left|{\overrightarrow{v}}_c-\overrightarrow{v}\right|& (5)\end{array}$

where i represents the time step, ${\overrightarrow{F}}_w$ and ${\overrightarrow{F}}_c$ are the drag forces exerted by the wind and water flow, respectively; S_a and S_c represent the sectional areas of the floating object above and below the water surface; ρ_a and ρ_c denote the densities of air and water; D_a and D_c are the resistance coefficients of the air and water flow; and ${\overrightarrow{v}}_w$, ${\overrightarrow{v}}_c$ and $\overrightarrow{v}$ are the mean velocities of the wind, water flow and floating object, respectively.

The water flow information, including the mean flow velocity and turbulence intensity, can be obtained from computational fluid dynamics (CFD) models. The wind speed and direction can be derived from observations.

It is assumed that the floating particle is always in a state of approximate force equilibrium. From the horizontal force balance, the Equation (6) can be obtained:

$\begin{array}{ll}{\overrightarrow{F}}_c+{\overrightarrow{F}}_w=0& (6)\end{array}$

We take the direction of water flow as the positive direction of the x-axis and the direction perpendicular to the x-Axis s in the horizontal plane as the y-axis.

The force balance in the x direction gives

$\begin{array}{ll}{F}_{wx}+F_{cx}=\frac{1}{2}{S}_a{D}_a{\rho }_a(v_{wx}-v_x)\left|{\overrightarrow{v}}_w-\overrightarrow{v}\right|+\frac{1}{2}{S}_c{D}_c{\rho }_c(v_{cx}-v_x)\left|{\overrightarrow{v}}_c-\overrightarrow{v}\right|=0& (7)\end{array}$

where the symbols with x subscripts (and y below) represent the components in the x (and y below) direction.

Based on the definitions of directions x and y, the water flow velocity of the component in the y direction is 0, which suggests that v_cx = v_c and v_cy = 0. Because the density of air is much smaller than the density of water, it is reasonable to assume that the difference between the velocities of the floating object and the water flow is relatively small and that the y component of the velocity of the floating object is much smaller than that of the wind speed. This assumption means that $v_y\ll v_x\approx v\approx v_c=v_{cx}$ and $v_y\ll v_{wy}$. Therefore,

$\begin{array}{ll}{v}_{wx}-v_x\approx v_{wx}-v_c& (8)\end{array}$

$\begin{array}{ll}\left|{\overrightarrow{v}}_w-\overrightarrow{v}\right|=\sqrt{{(v_{wx}-v_x)}^2+{(v_{wy}-v_y)}^2}\approx \sqrt{{(v_{wx}-v_c)}^2+v_{wy}{}^2}& (9)\end{array}$

$\begin{array}{ll}\left|{\overrightarrow{v}}_c-\overrightarrow{v}\right|=\sqrt{{(v_{cx}-v_x)}^2+{(v_{cy}-v_y)}^2}\approx \sqrt{{(v_c-v_x)}^2+v_y{}^2}& (10)\end{array}$

Substituting Equations (8)–(10) into Equation (7) results in

$\begin{array}{ll}{S}_a{D}_a{\rho }_a(v_{wx}-v_c)\sqrt{{(v_{wx}-v_c)}^2+v_{wy}{}^2}+S_c{D}_c{\rho }_c(v_c-v_x)\sqrt{{(v_c-v_x)}^2+v_y{}^2}=0& (11)\end{array}$

In the y direction, the Equation (12) can be obtained:

$\begin{array}{ll}{F}_{wy}+F_{cy}=\frac{1}{2}{S}_a{D}_a{\rho }_a(v_{wy}-v_y)\left|{\overrightarrow{v}}_w-\overrightarrow{v}\right|+\frac{1}{2}{S}_c{D}_c{\rho }_c(v_{cy}-v_y)\left|{\overrightarrow{v}}_c-\overrightarrow{v}\right|=0& (12)\end{array}$

Under the same assumption, the above equation can be simplified to

$\begin{array}{ll}{S}_a{D}_a{\rho }_a(v_{wy})\sqrt{{(v_{wx}-v_c)}^2+v_{wy}{}^2}+S_c{D}_c{\rho }_c(-v_y)\sqrt{{(v_c-v_x)}^2+v_y{}^2}=0& (13)\end{array}$

The following equations are set:

$c_1=S_a{D}_a{\rho }_a(v_{wx}-v_c)\sqrt{{(v_{wx}-v_c)}^2+v_{wy}{}^2}$ and

$$c_2=S_a{D}_a{\rho }_a(v_{wy})\sqrt{{(v_{wx}-v_c)}^2+v_{wy}{}^2}$$

Additionally, $v_x-v_c=\mathrm{Acos}\theta$ is set so that

$\begin{array}{ll}{v}_x=v_c+A\cos \theta & (14)\end{array}$

and

$\begin{array}{ll}{v}_y=A\sin \theta & (15)\end{array}$

By substituting Equations (14) and (15) into Equations (11) and (13), we can obtain

$\begin{array}{ll}{S}_c{D}_c{\rho }_c(A\cos \theta )A=c_1& (16)\end{array}$

and

$\begin{array}{ll}{S}_c{D}_c{\rho }_c(A\sin \theta )A=c_2& (17)\end{array}$

By combining these two equations, we can obtain Equation (18):

$\begin{array}{ll}{(S_c{D}_c{\rho }_c)}^2{A}^4=c_1{}^2+c_2{}^2& (18)\end{array}$

Therefore,

$\begin{array}{ll}A=\frac{{(c_1{}^2+c_2{}^2)}^{0.25}}{{(S_c{D}_c{\rho }_c)}^{0.5}}& (19)\end{array}$

Dividing Equation (17) by Equation (16) results in Equation (20):

$\begin{array}{ll}\tan \theta =\frac{c_2}{c_1}& (20)\end{array}$

Assuming c₁>0,

$\begin{array}{ll}\theta =\{\begin{array}{}\arctan \frac{c_2}{c_1},\text{for }{c}_2>0\\ \arctan \frac{c_2}{c_1}\pm \pi \text{ and }\theta \in (-\pi ,\pi ),\text{for }{c}_2<0\end{array}& (21)\end{array}$

By substituting Equations (19) and (21) into Equations (14) and (15), we obtain v_x and v_y, which are expressed as

$\begin{array}{ll}\{\begin{array}{}{v}_x=v_c+A\cos \theta \\ v_y=A\sin \theta \end{array}& (22)\end{array}$

To solve Equation (22), we need to know the value of S_c, which is related to the shape of the floating object. Because several parameters are involved in force analysis, the floating object is assumed to be an ellipsoid to keep the modeling process from being overly complicated. In the vertical direction, the floating object is mainly affected by gravity G and buoyancy F_buoy, which are expressed as Equation (23) and Equation (24).

$\begin{array}{ll}G={\rho }_f{V}_{f}g={\rho }_{f}g·\frac{4}{3}b(S_a+S_c)& (23)\end{array}$

$\begin{array}{ll}{F}_{bouy}={\rho }_c{V}_{c}g={\rho }_{c}g·\frac{4}{3}b{S}_c& (24)\end{array}$

where ρ_f is the density of the floating object; V_f and V_c are the total and submerged volumes of the floating object, respectively; and b is the semimajor axis of the ellipsoid.

Based on the force balance of G and F_buoy, we can obtain the following formula.

$\begin{array}{ll}\frac{S_a}{S_c}=\frac{{\rho }_c-{\rho }_f}{{\rho }_f}& (25)\end{array}$

In addition, we have

$\begin{array}{ll}S=S_c+S_a& (26)\end{array}$

where S is the sectional area of the floating object. Based on Equations (25) and (26), we obtain Equation (27).

$\begin{array}{ll}{S}_c=\frac{{\rho }_f}{{\rho }_c}S& (27)\end{array}$

2.1.2 Random velocity

Random displacement is caused by turbulence and can be expressed as follows (Zhang et al., 2020):

$\begin{array}{ll}\Delta X_d=R\sqrt{2k\Delta t}& (28)\end{array}$

where R is a standard normally distributed random number in the range of (-1, 1) with a mean = 0 and a variance = 1 and k is the turbulence diffusion coefficient.

The random velocity is purely for horizontal motion and not vertical. Similarly, the turbulent diffusion coefficient is a function of the horizontal position only in this study.

We do not consider the random effects of wind because (1) in inland rivers, the water surface is relatively narrow, and a floating object is mostly submerged in the water; thus, the wind has a limited effect on the floating object. Additionally, (2) there is no widely recognized expression for the effects of wind on the random motion of floating objects.

2.2 Numerical calculation

The numerical calculation includes the following steps.

(1) Select a study area, and divide it using an unstructured triangular mesh. The grid size should be determined according to the water flow and wind conditions and the expected accuracy.

(2) Set the initial conditions and parameter values, including the simulation time interval, the calculation time step, and the initial position of each snail. River flow information, such as the velocity, depth and turbulence diffusion coefficient, should be obtained in advance. Other information, such as the resistance coefficients of the wind and water flow and densities of air and water, should also be known before conducting the calculation.

(3) Calculate the displacement $\Delta \overline{\text{X}}$ caused by the mean velocity and the random displacement ΔX_d during the ith time step according to Equations (2) and (28).

(4) Substitute $\Delta \overline{X}$, ΔX_d and the snail’s position S_i at the present time t_i into Equation (1) to obtain the new position S_i+1 at time t_i+1. The time step Δt should be determined based on the hydrodynamic conditions, the geometric and mechanical characteristics of the floating object and numerical experience.

(5) Repeat steps (4) and (5) until the end of the calculation.

2.3 Model validation

2.3.1 Determination of k

It is difficult to determine k exactly. Here, we used the inverse method to determine a reasonable value for k based on the guaranteed rate and the confidence region. The confidence region refers to the estimated region of the overall parameter constructed by the sample statistics and shows the degree to which the true value of this parameter has a certain probability of falling around the measurement result. For example, (1) assume that 10,000 particles were released at the start of a numerical simulation at the location where the in situ experimental floating objects were released. (2) Apply the numerical model to simulate the trajectories of the particles under the effects of the mean flow, turbulence and wind. (3) Set the confidence level to 95%. (4) For each time step, check whether the experimental floating object is inside the area that includes 95% of the densely populated released particles. Using 10,000 particles as an example, the area is the one that includes the 9500 densely populated particles. If the probability that the experimental floating object falls within the corresponding confidence region, i.e., the guarantee rate, is greater than 95%, then k is reasonable. In other words, the greater the guarantee rate, the more reasonable the value of k is.

The 95% confidence region is where the particle concentration is greater than 5 × 10^-2/km², and this region is shown by the dark blue areas in Figure 1. Figure 1 illustrates the distribution of the particles at the end of 5 h. As shown, as time progresses, the role of random movement becomes apparent, and the distribution region of the 10,000 particles is extended. Meanwhile, the highest concentration decreased to 7.1 × 10^-2/km².

Figure 1

Figure 1 Particle concentration distribution at the end of 5 h.

Table 2 lists the validation results for k. The total simulation time was 40 h. Table 2 indicates that as the confidence level increased, the included confidence region also increased; thus, the length of time that the experimental floating object remained inside the confidence region increased. On the other hand, with the same confidence level, the longest time a floating object remained in the confidence region was also when the largest guarantee rate occurred, i.e., when k = 1.2 m²/s. Therefore, k = 1.2 m²/s is a more reasonable value.

Table 2

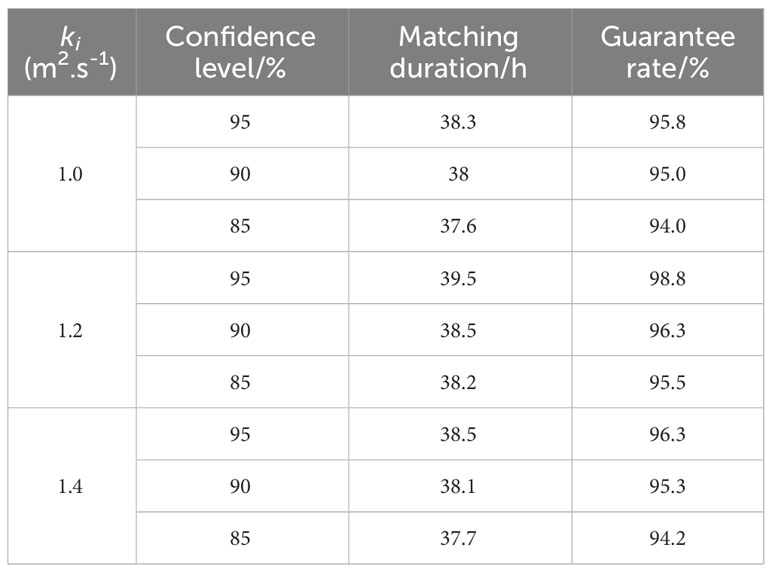
Table 2 Statistical results of the experimental floating object in the confidence region with various k values.

2.3.2 Comparison of experimental and simulated trajectories

We conducted a field test of floating objects in the middle Changjiang River to validate the proposed model. The experiment was conducted during the flood season. Common floating branches were collected, and GPS positioning modules were attached. Then, the floating objects were released into the river. The drifting trajectories of these objects were recorded through a GIS platform. Environmental information, such as the flow discharge, water level, wind, and water temperature, was recorded.

The corresponding numerical simulations were conducted. The parameters used in the simulations are given as follows: the air is at the standard atmospheric pressure, the air temperature is 20°C, the air density is 1.205 kg/m³, the water temperature is 23°C, and the water density is 997 kg/m³. The density of the floating branches is approximately 556 kg/m³. The resistance coefficients of the wind and water flow should be related to the configuration of the floating object. However, in this work, they were set to 1.

The sectional areas of the floating object above and below the water surface were assumed to be equal. The error of the simulation results relative to the experimental data was assessed based on the averaged deviation E defined below Equation (29). The smaller the value of E was, the closer the simulated trajectory was to the field test, and vice versa.

$\begin{array}{ll}E=\frac{1}{10}{\displaystyle \sum _{j=1}^{10}{\displaystyle \sum _{i=1}^n\sqrt{{(x_{s_{ij}}-x_{e_{ij}})}^2+{(y_{s_{ij}}-y_{e_{ij}})}^2}}/n}& (29)\end{array}$

where j is the ID of the floating object being investigated, $x_{s_{ij}}$ and $y_{s_{ij}}$ represent the simulated position of object j at time t_i, and $x_{e_{ij}}$ and $y_{e_{ij}}$ represent the experimental position of object j at time t_i.

Figure 2 illustrates a comparison between the simulated and experimental trajectories. Although the simulated trajectory generally matches the experimental data, some errors remain. The average deviation (E) is 1.3 km according to Equation (26), which is quite small relative to the scale of the experiment.

Figure 2

Figure 2 Trajectories of the experiment and simulation.

3 Model application

Initial conditions of the river currents modeling included water surface elevations, flow discharge and bed elevation, while boundary conditions consisted of atmospheric forcing, surface wind stress and inflows and outflows. Flow discharge and water surface elevations were initialized with observed values obtained at The Jianli Station and The Chenglingjin Station. Meteorological data were also obtained from the Jingzhou monitoring platforms and included wind speed and direction, relative humidity, air temperature and barometric pressure. This derive from the same wind field also used to advect the Virtual snails.

The Lagrangian modeling includes invirtual individuals (snails) and fluvial environmental and hydraulic characteristics. Virtual snails are characterized by the state variables: location (x, y) in [m] and total number. The hydraulic state variables include: water depth [m], the velocities of water flow in the x direction [m/s] and the y direction [m/s] which were obtained from the river currents model. The fluvial environmental state variables include wind speed[m/s] and direction[°].

According to the distribution of Oncomelania snails and considering the key area of snail control and schistosomiasis prevention, the lower Jingjiang reach of the Changjiang River was selected as the application zone. The reach is 78 km long and covers the distance from the Jianli hydrological station to the Chenglingji hydrological station. To study the effects of wind conditions on the migration and spreading of Oncomelania snails with floating objects during the flooding period, calm winds, namely, the dominant summer southerly wind (2.4 m/s) and the dominant usual northeasterly wind (2.6 m/s), were selected to establish free surface conditions and typical floods were used to established hydrodynamic conditions. It was assumed that 200 floating objects were located on the beach at the right bank of the upper reach of the test zone (as shown in Figure 3) at the beginning of the simulation. The time step Δt=3s, the densities of air was ρ_a=1.29Kg/m³, the densities of water was ρ_c= 999.87kg/m³.

Figure 3

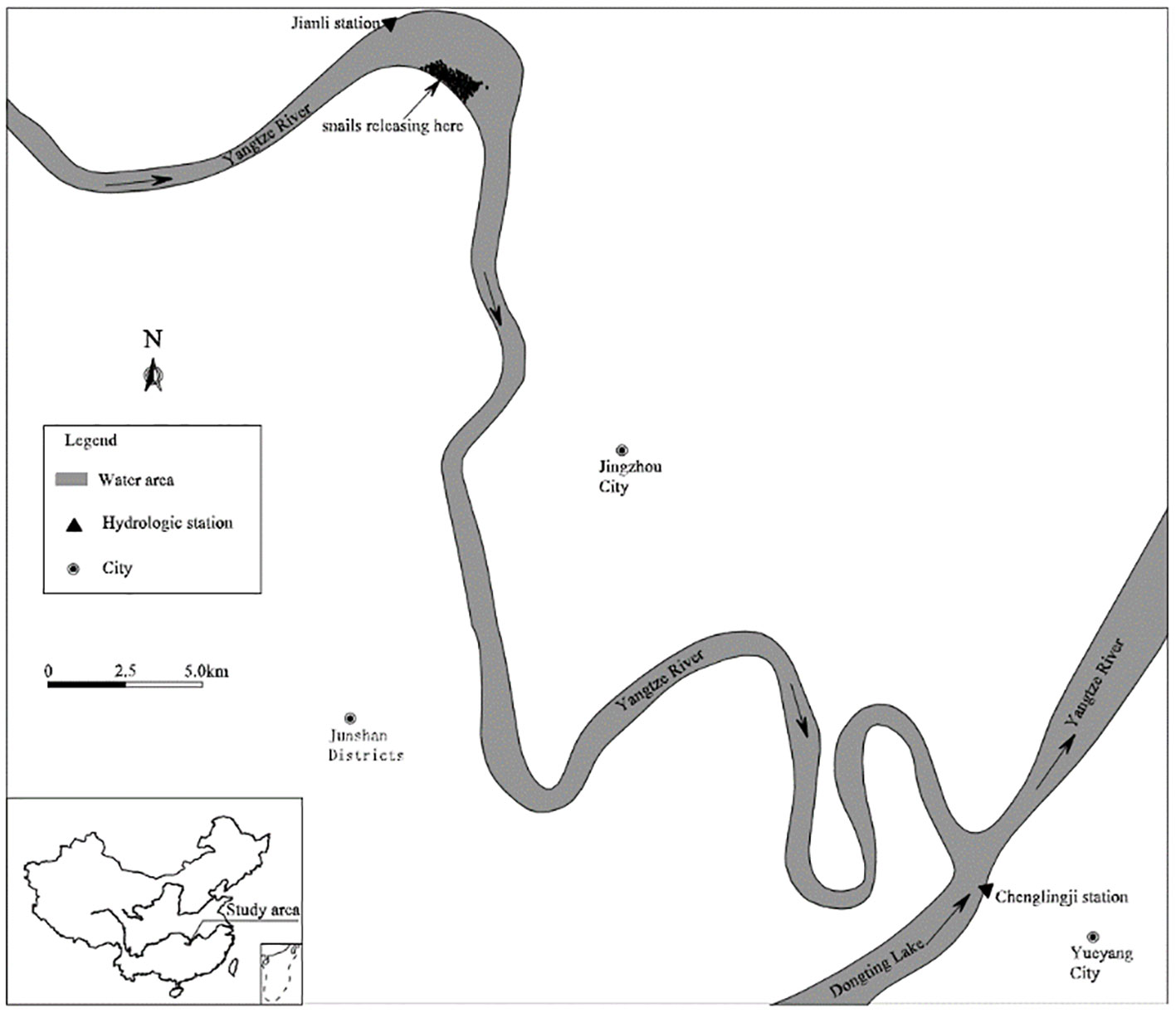
Figure 3 A geographical sketch of the study area located in the lower Jingjiang River and the bottomland with snails.

Based on previous research, snails can stick to floating objects for as long as 4 days. Although our simulation lasted only 3 days, the snails were assumed to not fall from the objects to which they were attached.

4 Results and discussion

As the water level of the Yangtze River rises, the dead branches and leaves on the beach become objects floating on the water surface, snails adhering to the floating objects are transported through drifting and spreading, and snails mainly migrate with the water current or randomly.

4.1 Analysis of longitudinal migration and the spreading characteristics of snails

4.1.1 Characteristics of the snail migration trajectory

The migration trajectories of snails under different wind conditions are shown in Figures 4–7. Figures 4–7 show that during the flooding period, snail movement is mainly driven by the flood dynamics, and the longitudinal migration trajectory is generally consistent with the mainstream trend. The Oncomelania snails inhabiting the beach on the opposite bank of Wuguizhou are transported by the flood and migrate downstream with floating objects. When reaching the bend near Yinmazhou, the water flow is divided into two branches (left and right) by Jiangxinzhou in the middle of the river; the right branch is the mainstream, which is first close to the left bank and then close to the right convex bank, and the left branch is close to the left bank and moves at relatively low speeds. Under the action of the two currents, most of the snails move with the mainstream from the left bank to the right bank, and some of the snails migrate downstream with the current close to the left bank. As the two currents converge at the next bend, the snails migrating separately on the left and right banks also converge at the bend and gradually migrate downstream with the mainstream. Because the studied river reach is a typical continuous curved river reach, the mainstream is sometimes close to the left bank and sometimes close to the right bank; therefore, the snails transported by the mainstream migrate close to the left bank at times and close to the right bank at other times.

Figure 4

Figure 4 Oncomelania snail migration trajectory (full studied reach).

Figure 5

Figure 5 Oncomelania snail migration trajectory under the calm wind [(A) reach and (B) reach].

Figure 6

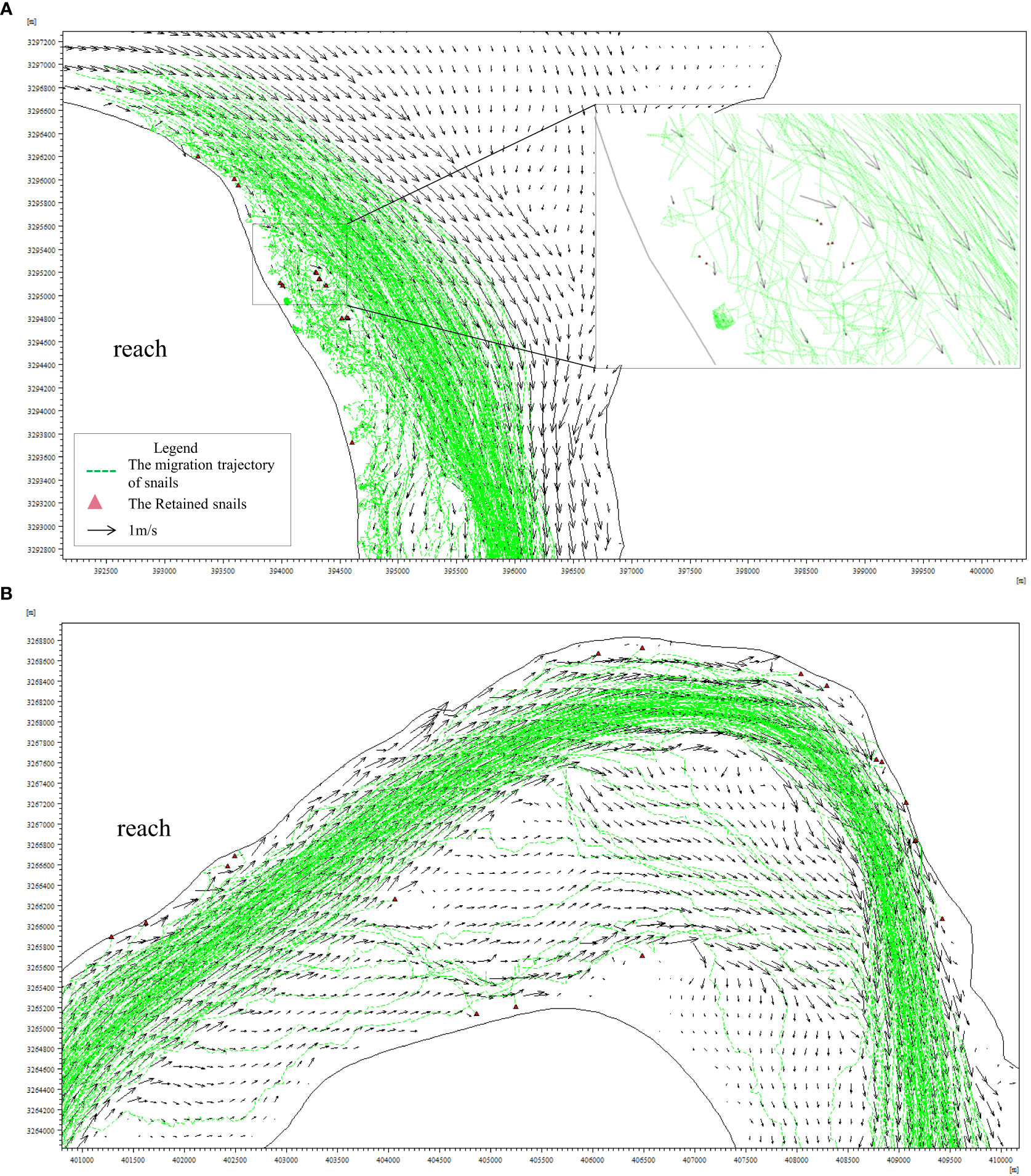
Figure 6 Oncomelania snail migratory trajectory under the northeasterly wind [(A) reach and (B) reach].

Figure 7

Figure 7 Oncomelania snail migratory trajectory under the southerly wind [(A) reach and (B) reach].

4.1.2 Spatial distribution characteristics of snails

Figure 8 shows the distribution map of the retained snails in the studied river reach. Notably, under calm wind conditions, approximately 41% of the snails stay in the river reach from the snail breeding site to within 40 km downstream, and approximately 78% of the snails stay in the river reach from the snail breeding site to within 78 km downstream; under northeasterly wind conditions, approximately 39% of the snails stay in the river reach from the snail breeding site to within 40 km downstream, approximately 76.5% of the snails stay in the river reach from the snail breeding site to the to within 78 km downstream, and approximately 23.5% of snails migrate and spread farther downstream; and under southerly wind conditions, approximately 38% of the snails stay in the river reach from the snail breeding site to within 40 km downstream, approximately 75.5% of the snails stay in the river reach from the snail breeding site to within 78 km downstream, and approximately 24.5% of snails migrate and spread farther downstream. Both northeasterly and southerly winds increase the risk of snail spreading downstream to a certain extent, which is mainly due to the drag effect of the wind.

Figure 8

Figure 8 Schematic diagram of the positions of the retained snails under different wind.

In the horizontal direction, Oncomelania snail migration is mainly affected by wind and water flow. To analyze the influence of wind drag on the migration of snails, the mainstream direction is selected as the positive vertical axis and the direction perpendicular to the mainstream direction is aligned with the horizontal axis to decompose the wind force. Figure 9 shows the decomposition of the southerly wind. Figure 9 shows that the southerly wind creates a drag force in the horizontal direction toward the middle line of the river, which obviously causes the Oncomelania snails that originally inhabit the right bank to spread to the left bank; i.e., the snails that originally gathered on the shore spread to the mainstream area at high flow velocities. Therefore, the snails easily move positions, which increases the risk of the downstream migration of snails. Figure 10 shows the decomposition of the northeasterly wind. Since the studied river reach is generally southeast trending, the northeasterly wind has a longitudinal drag component in the same direction as the main flow. Compared with the calm wind condition, under the northeasterly wind, the speed of snail spreading in the longitudinal direction is increased, so snails are less likely to stay on the shoreline, which increases the probability of spreading to the lower reaches of the river.

Figure 9

Figure 9 Distribution of the percentage of retained particles along the river.

Figure 10

Figure 10 Decomposition of the southerly wind.

Existing studies have shown that Oncomelania snails are the only intermediate host of schistosomiasis, the release of tailed larvae from the Oncomelania snails into the water creates schistosome-infested water, and humans and mammals may be infected when they come into contact with the schistosome-infested water. Both the northeasterly and southerly winds increase the risk of downstream spreading of Oncomelania snails to a certain extent and thus increase the risk of schistosomiasis spreading in the downstream direction to a certain extent.

4.1.3 Time distribution characteristics of snails

Table 3 shows that under calm wind conditions, the shortest time required for the Oncomelania snails to move 20 km, 50 km, and 78 km downstream is 27.65 h, 33.20 h, and 37.70 h, respectively; under the northeasterly wind condition, the shortest time required for the Oncomelania snails to move 20 km, 50 km, and 78 km downstream is 27.60 h, 33.00 h, and 37.25 h, respectively; under the southerly wind, the shortest time required for the Oncomelania snails to move 20 km, 50 km, and 78 km downstream is 27.60 h, 33.05 h, and 37.85 h, respectively. Compared with the calm wind, the southerly wind reduces the speed of snail spreading from upstream to downstream to a certain extent, and the northeasterly wind increases the speed of snail spreading from upstream to downstream to a certain extent, which is mainly due to the drag effect of the wind. Oncomelania snail migration in the horizontal direction is mainly affected by wind and water flow. To analyze the influence of wind drag on Oncomelania snail migration, the mainstream direction is set as the positive vertical axis, and the direction perpendicular to the mainstream direction is set as the horizontal axis to decompose the wind force. Figure 10 shows the decomposition of the southerly wind. Since the studied river reach is generally south-east trending, the southerly wind has a drag component in the mainstream direction opposite that of the water flow. Therefore, compared that under calm wind conditions, the speed of snail spreading in the longitudinal direction is reduced under southerly wind conditions. Figure 11 shows the decomposition of the northeasterly wind. Since the studied river reach is generally southeast trending, the northeasterly wind has a drag component in the same direction as the water flow in the mainstream direction. Therefore, compared to that under calm wind conditions, the speed of snail spreading in the longitudinal direction is increased under the southerly wind condition.

Table 3

Table 3 The shortest time required for the Oncomelania snail to migrate each distance.

Figure 11

Figure 11 Decomposition of the northeasterly wind.

4.2 Characteristics of the lateral migration and spreading of Oncomelania snails

4.2.1 Characteristics of the snail migration trajectory

The water flow in the river channel is characterized by a large mainstream flow velocity and a small flow velocity on both sides of the river; therefore, the Oncomelania snails located close to the mainstream mainly migrate with the current and move downstream at a relatively fast speed under the influence of the large mainstream flow velocity. In this case, the migration trajectory is basically the same as that of the mainstream, i.e., a smooth curve. Oncomelania snails along the shoreline mainly randomly spread and move slowly along the continental beach at a slower speed, and the trajectory reflects an irregular zigzag line with a high degree of randomness (Figures 6–8).

4.2.2 Spatial distribution characteristics of snails

The distribution map of the snails that stay in the studied river reach shows that the snails mainly remain on the concave bank in the second half of each bend, such as near Wuguizhou, Yinmazhou, Xionghuangzhou, and Baxingzhou, or on the beach at wide parts of river reaches; notably, the flow velocity is relatively low in these areas. When snails reach a location with a low water depth and a slow flow velocity along the shore, they easily swirl, spin, or become stranded and stay on the beach, which could potentially increase the distribution of snails along the river and the risk of schistosomiasis infection. According to records, the snails at Chenjiazhou South Beach in the Jingjiang reach are carried by floating objects in the Yangtze River, and the snails were first discovered on floating objects in the low-lying river water at the northeast corner of the beach. The density of Oncomelania snails was low when they were first found, and distribution areas were points or small patches; however, as the area and density of snails expand over the years, the infected snails eventually appear.

The total number of snails that remain in the studied river section, the number of snails on the left bank and the right bank, and the percentages under different conditions are counted, as shown in Table 4. Table 4 shows that snails are more likely to stay on the right bank under northeasterly wind conditions than under calm wind conditions and on the left bank under southerly wind conditions than under calm wind conditions, which is mainly due to wind drag. According to the wind decomposition diagram, the southerly wind includes a drag component in the lateral direction pointing to the left bank. Therefore, the snails are more likely to spread to the left bank under southerly wind conditions than under calm wind conditions, thus increasing the probability of snails being retained on the left bank of the river. Additionally, the northeasterly wind has a drag component in the lateral direction pointing to the right bank. Therefore, compared with calm wind conditions, the northeasterly wind increases the probability of snails staying on the right bank of the river channel.

Table 4

Table 4 Statistics for the distribution of retained snails.

The results show that for northeasterly winds, the chance of Oncomelania snails remaining on the right bank is high, and for southerly winds, the chance of them remaining on the left bank is high. Therefore, northeasterly winds increase the risk of schistosomiasis in the right bank area, and southerly winds increase the risk of schistosomiasis in the left bank area since Oncomelania snails are the only intermediate host of schistosomiasis.

5 Conclusion

Based on in-depth research on the behavior and movement mechanism of Oncomelania snails, a control equation for snail movement is proposed by integrating ecology, hydraulics, and river dynamics, and a theoretical model of the migration and spreading of snails is established based on the Lagrangian method. The impact of flooding conditions on the migration and spreading of snails has been studied to a certain extent, but the impact of wind conditions has rarely been reported. Therefore, according to the distribution of snails in China, the difficulties and key areas for the control of schistosomiasis and Oncomelania snails, and the morphological characteristics of river reaches, the Lower Jingjiang River section was selected as a practical application case, the theoretical model of the migration and spreading of Oncomelania snails was established, and the characteristics of the Oncomelania snail migration were simulated and analyzed considering the water flow and distribution patterns under different wind conditions. The conclusions are as follows:

(1) Wind conditions have little influence on the longitudinal spreading of Oncomelania snails but have a relatively large influence on the lateral spreading of snails.

(2) Compared with calm wind conditions, both northeasterly and southerly wind conditions can lead to longer longitudinal migration distances of snails, thereby increasing the risk of snail spreading and schistosomiasis transmission. In addition, compared with those of natural rivers, the hydrodynamics of lakes and reservoirs are greatly affected by wind conditions; thus, the influence of wind conditions on the migration and spreading of snails in lakes and reservoirs should be further studied in the future.

(3) The studied reach is generally southeast trending, so the northeasterly wind is inconsistent with the water flow direction. Under the northeasterly wind condition, the wind hinders the migration process of Oncomelania snails from the right bank to the left bank of the studied reach, resulting in a relative reduction in the probability of snails migrating to and staying on the left bank; because the southerly wind includes a component in the same direction as the lateral velocity of the water flow, the migration process of snails from the right bank to the left bank of the studied reach is promoted under the southerly wind condition, resulting in a relative increase in the probability of snails migrating to and staying on the left bank.

(4) Floods in areas with snail breeding could lead to the horizontal and vertical spreading of snails. Once they reach downstream land and if the natural conditions are suitable, new snail-bearing areas are created, potentially increasing the area of snails along the river and the risk of schistosomiasis infection. Therefore, to eliminate the remaining snails, it is necessary to strengthen the monitoring and protection of areas with few or no snails.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

LZ: Conceptualization, Data curation, Project administration, Writing – original draft, Writing – review & editing. ZC: Data curation, Writing – review & editing. QY: Data curation, Writing – review & editing. JZ: Conceptualization, Data curation, Formal Analysis, Methodology, Project administration, Writing – original draft, Writing – review & editing. ZJ: Data curation, Writing – review & editing..

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by the Jiangsu Provincial Project of Invigorating Health Care through Science, Technology and Education, the National Key Research and Development Plan (2022YFC3202601), the Natural Science Foundation of China (51679009), the Innovation Team of River and Lake Protection and Governance in the Middle and Lower Reaches of the Yangtze River, and the Innovation Team of River Basin Water Environment Protection and Governance in Changjiang Water Resource Commission.

Acknowledgments

Throughout the writing of this dissertation, a great deal of support and assistance was received. Professor Longxi Han is acknowledged for the discussions and English review.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agola E. L., Mwangi I. N., Maina G. M., Kinuthia J. M. (2021). Mutuku MW.Transmission sites for Schistosoma hematobium and Schistosoma bovis identified in localities within the Athi River basin of Kenya using a PCR-RFLP assay. Heliyon 7 (2), e06114. doi: 10.1016/j.heliyon.2021.e06114

PubMed Abstract | CrossRef Full Text | Google Scholar

Belizario V. Y., delos Trinos J. P. C. R., Silawan B., De Veyra C. M., Hornido A., Amoguis H., et al. (2017). The use of geographic information system as a tool for schistosomiasis surveillance in the province of Davao del Norte the Philippines. Geospatial Health 12 (2), 199–209. doi: 10.4081/gh.2017.540

CrossRef Full Text | Google Scholar

Chen J. S., Wang X. K., Zhou W., Shi H. F., Zhou M., Wu Y. S. (2007). Studies on the impact of flood water on Oncomelania snails diffusion and schistosom oasis transmission in Zongyang county,Anhui province. J. Trop. Dis. Parasitol. 5 (1), 43–45.

Google Scholar

Ghazy R. M., Ellakany W. I., Badr M. M., Taktak N. E. M., Elhadad H., Abdo S. M., et al. (2022). Determinants of Schistosoma mansoni transmission in hotspots at the late stage of elimination in Egypt. Infect. Dis. Poverty 11 (5), 102. doi: 10.1186/s40249-022-01026-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Hata N., Yasukawa A., Sei E., Kawasumi K., Miya N., Yamaguchi H., et al. (2017). Comparative analysis of knowledge on schistosomiasis japonica in the local people in the former endemic area in Yamanashi Prefecture, Japan: comparisons among the background of age and occupation. J. Veterinary Med. Sci. 79 (3), 608–617. doi: 10.1292/jvms.16-0579

CrossRef Full Text | Google Scholar

He J., Li W., Bergquist R., Zhang J. F., Shi L., Zhao S., et al. (2016). The spatiotemporal distribution of Oncomelania hupensis along Yangtze river in Jiangsu Province, China after implementation of a new integrated schistosomiasis control strategy. Geospatial Health 11 (3), 324–334. doi: 10.4081/gh.2016.480

CrossRef Full Text | Google Scholar

Hu F., Ge J., Lv S. B., Li Y. F., Li Z. J., Yuan M., et al. (2019). Distribution pattern of the snail intermediate host of schistosomiasis japonica in the poyang lake region of China. Infect. Dis. Poverty 8 (2), 61–69. doi: 10.1186/s40249-019-0534-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu Y., Xia C., Li S., Ward M. P., Luo C., Gao F., et al. (2017). Assessing environmental factors associated with regional schistosomiasis prevalence in Anhui Province, Peoples' Republic of China using a geographical detector method. Infect. Dis. Poverty 6 (1), 87. doi: 10.1186/s40249-017-0299-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Jean C. D., Edoa J. R., Adegnika A. A., Grobusch M. P. (2022). Schistosomiasis in Gabon from 2000 to 2021 - A review. Acta Tropica 4 (228), 106317. doi: 10.1016/j.actatropica.2022.106317

CrossRef Full Text | Google Scholar

Li L. Y., Lu J. Y., Fan B. L., Wang J. S., Zheng S. (2016). Delayed response of Snails’Vertical migration on the bottomland to the changed water level. J. Yangtze River Sci. Res. Institute 33 (8), 1–5.

Google Scholar

Li Z., Nie X., Zhang Y., Huang J., Huang B., Zeng G. (2016). Assessing the influence of water level on schistosomiasis in Dongting Lake region before and after the construction of Three Gorges Dam. Environ. Monit. Assess. 188 (1), 28–38. doi: 10.1007/s10661-015-5033-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Li D. M., Zhan C. H., Hu Z. M. (1997). Studies on moving of oncomelania in water. Adv. Water Sci. 8 (3), 270–274.

Google Scholar

Liu D. N. (2013). Discussion on water conservancy projects and schistosomiasis control in Poyang Lake area. Chin. J. Schistosomiasis Control 25 (1), 93–95+97.

Google Scholar

Liu M. M., Feng Y., Yang K. (2021). Impact of microenvironmental factors on survival, reproduction and distribution of Oncomelania hupensis snails. Infect. Dis. Poverty 10 (2), 73.

PubMed Abstract | Google Scholar

Liu Y., Yu X. L., Zhong Y. Z., Mo X. Y., Hu F., Yin K. (2011). Analysis of spatial and temporal characteristics of the epidemic of schistosomiasis in Poyang Lake Region. Procardia Environ. Sci. 10, 2760–2768. doi: 10.1016/j.proenv.2011.09.428

CrossRef Full Text | Google Scholar

Lo N. C., Bezerra F. S. M., Colley D. G. (2022). Review of 2022 WHO guidelines on the control and elimination of schistosomiasis. Lancet Infect. Dis. 22 (11), 327–335. doi: 10.1016/S1473-3099(22)00221-3

CrossRef Full Text | Google Scholar

Lv W., Zhuang S. J., Yu C. (2022). Robust biobjective optimal control of tungiasis diseases. Chaos Solitons Fractals 156, 111829–111841. doi: 10.1016/j.chaos.2022.111829

CrossRef Full Text | Google Scholar

Maszle D. R., Whitehead P. G., Johnson R. C., Spear R. C. (1998). Hydrological studies of schistosomiasis transport in Sichuan Province, China. Sci. total Environ. 216 (3), 193–203. doi: 10.1016/S0048-9697(98)00152-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Moendeg K. J., Angeles J. M. M., Nakao R., Leonardo L. R., Fontanilla I. K. C., Goto Y., et al. (2017). Geographic strain differentiation of Schistosoma japonicum in the Philippines using microsatellite markers. PloS Negl. Trop. Dis. 11 (7), e0005749. doi: 10.1371/journal.pntd.0005749

PubMed Abstract | CrossRef Full Text | Google Scholar

Perez Saez J., Mande T., Ceperley N., Bertuzzo E., Mari L., Gatto M. (2016). Hydrology and density feedbacks control the ecology of intermediate hosts of schistosomiasis across habitats in seasonal climates. Proc. Natl. Acad. Sci. 113 (23), 6427–6432. doi: 10.1073/pnas.1602251113

CrossRef Full Text | Google Scholar

Sokolo S. H., Jones I. J., Jocque M., La D., Cords O., Knight A., et al. (2017). Nearly 400 million people are at higher risk of schistosomiasis because dams block the migration of snail-eating river prawns. Philos. Trans. R. Soc. B: Biol. Sci. 4 (24), 1–12. doi: 10.1098/rstb.2016.0127

CrossRef Full Text | Google Scholar

Song L., Wu X., Ning A., Wu Z. (2017). Lessons from a 15-year-old boy with advanced schistosomiasis japonica in China: a case report. Parasitol. Res. 116 (7), 1787–1791. doi: 10.1007/s00436-017-5473-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Song L. G., Wu X. Y., Sacko M., Wu Z. D. (2016). History of schistosomiasis epidemiology, current status and challenges in China: on the road to schistosomiasis elimination. Parasitol. Res. 115 (11), 4071–4081. doi: 10.1007/s00436-016-5253-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun D., Li Q., Wang Q. (2017). Study on surveillance and forecast scheme of schistosomiasis in upper section of Huaihe River outfall water way. China Trop. Med. 17 (5), 477–484.

Google Scholar

Wang J. L., Li T. T., Huang S. Y., Cong W., Zhu X. Q. (2016). Major parasitic diseases of poverty in mainland China: perspectives for better control. Infect. Dis. poverty 5 (1), 67. doi: 10.1186/s40249-016-0159-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang X., Wang W., Wang P. (2017). Long-term effectiveness of the integrated schistosomiasis control strategy with emphasis on infectious source control in China: a 10-year evaluation from 2005 to 2014. Parasitol. Res. 116 (2), 521–528. doi: 10.1007/s00436-016-5315-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue J., Ma Y. L., Zeng Y., Liu S. H. (2015). Numerical simulation of oncomelania motion in spiral flow. Chin. J. Hydrodynamics 30 (4), 440–445.

Google Scholar

Xue J. B., Wang X. Y., Zhang L. J., Hao Y. W., Li S. Z. (2021). Potential impact of flooding on schistosomiasis in poyang lake regions based on multi-source remote sensing images. Parasites Vectors 14 (1), 116. doi: 10.1186/s13071-021-04576-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang Y., Gao J., Cheng W., Pan X., Yang Y., Chen Y., et al. (2018). Three gorges dam: polynomial regression modeling of water level and the density of schistosome-transmitting snails oncomelania hupensis. Parasites Vectors 11 (1), 183. doi: 10.1186/s13071-018-2687-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang G. J., Vounatsou P., Xiao Nong Z., Utzinger J., Tanner M. (2005). A review of geographic information system and remote sensing with applications to the epidemiology and control of schistosomiasis in China. Acta tropica 96 (2), 117–129. doi: 10.1016/j.actatropica.2005.07.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang K., Zhou X. N., Steinmann P., Wang X. H., Wu X. H., Yang G. J., et al. (2009). Landscape pattern analysis and bayesian modeling for predicting oncomelania hupesis distribution in eryuan county, people's republic of China. Am. J. Trop. Med. Hygiene 81 (3), 416–423.

Google Scholar

Yuan Y. S., Juan Q., Rendong L., Qiang S., Duan H. (2017). Identification of Potential High-Risk Habitats within the Transmission Reach of Oncomelania hupensis after Floods Based on SAR Techniques in a Plane Region in China. Int. J. Environ. Res. Public Health 14 (9), 986. doi: 10.3390/ijerph14090986

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang L., Chen L. N., Zhou J. Y., Wang J. S., Yang Q. H., Han L. X. (2020). Development and application of a new random walk model to simulate the transport of degradable pollutants. J. Hydrodynamics 32 (4), 784–789. doi: 10.1007/s42241-020-0048-7

CrossRef Full Text | Google Scholar

Zhang Z., Ong S., Peng W., Zhou Y., Zhuang J., Zhao G. (2008). A model for the prediction of Oncomelania hupensis in the lake and marshland regions China. Parasitol. Int. 57 (2), 121–131. doi: 10.1016/j.parint.2007.09.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang S. Q., Wang T. P., Ge J. H. (2004). Influence on the diffusion of snail by flooding in Anhui Province. J. Trop. Dis. Parasitol. 2 (2), 90–94.

Google Scholar

Zhang T., Zhao X. Q. (2023). A multihost schistosomiasis model with seasonality and time-dependent delays. Discrete Continuous Dynamical Systems-B 28 (5), 2927–2959. doi: 10.3934/dcdsb.2022198

CrossRef Full Text | Google Scholar