- 1School of Civil and Transportation Engineering, Ningbo University of Technology, Ningbo, China
- 2College of Civil Engineering, Chongqing University, Chongqing, China
- 3Key Laboratory of New Technology for Construction of Cities in Mountain Area (Chongqing University), Ministry of Education, Chongqing, China
The study conducted a pure rotation test of 720° for saturated remolded Q2 loess under principal stress axis (PSA) rotation when deviatoric stress and the intermediate principal stress ratio are different, also paying attention to examining the changes of strain accumulation and pore pressure of such loess. According to the test, as the PSA rotates continuously, the pore water pressure exhibited by saturated remolded loess presents a normal cyclic accumulation elevation, and under the same deviatoric stress conditions, the pore water pressure accumulation trend of different principal stress ratios is the same; however, the magnitude is different. The increment of pore water pressure becomes smaller as the number of cycles increases. When the deviatoric stress level is low, the material hardening is in a cyclic stable state, the strain component remains stable with the continuous rotation of the PSA, and the strain path area is reduced, together with a stable final size. In case of higher deviatoric stress, the material strength cycle becomes weaker and the strain component accumulates slowly as the PSA (the spiral line of the strain path) continuously rotates in the γzθ−(ϵz−ϵθ) plane, and gradually expands until failure. The increased intermediate principal stress is accompanied by accelerated strain development speed and advanced failure.
1 Introduction
With China’s western development and “the Belt and Road initiative” strategy, the transportation network construction in the western region has been developing vigorously, in order to meet the needs of the western economy’s prosperity and development and to strengthen the need for exchanges and cooperation between East and West. In Western China, especially in Northwest China, the coverage area of structural loess is more than 60 × 104 km2, which spans Gansu, Ningxia, Shaanxi, Shanxi, Qinghai, Inner Mongolia, Henan, and other provinces. The loess distribution area is rich in energy and mineral resources, undertakes the strategic task of transporting resources to the East, and has built many important transportation roads.
In subgrade engineering, most of the loads appear in the form of cyclic dynamic loads, especially traffic loads. Therefore, the properties of the sample under cyclic torsional shear load are closer to the actual engineering conditions. Cyclic rotation tests regarding the main stress axis have been conducted (Miura et al., 1986; Brown, 1996; Chazallon et al., 2006; Kumruzzaman and Yin, 2010; Ishikawa et al., 2011; Cai et al., 2016; Guo et al., 2016; Qian et al., 2016; Wang et al., 2016; Shen et al., 2017) and obtained useful test results. Grabe (2009) carried out three kinds of principal stress direction change path tests in principal stress space, namely, axial rotation, circular rotation, and directional shear of principal stress, and investigated the long-term dynamic characteristics exhibited by saturated soft clay under traffic load. By virtue of the hollow torsional shear system, Yang et al. (2007) carried out the rotation test regarding the pure principal stress axis (PSA) in case of unchanged intermediate principal stress coefficient. According to the test, in the face of unchanged generalized shear stress, pure PSA rotation will result in pore pressure accumulation and strain development and even lead to the generation of liquefaction. Tong et al. (2010) carried out a test similar to Yang’s and studied the evolution of the sample strain component and volumetric strain when the number of cycles changes under PSA rotation. Zhou et al. (2014) analyzed the law, internal mechanism, and influencing factors of plastic strain increment direction of clay under the condition of PSA rotation. However, scholars such as Ishikawa et al. (2011) and Cai et al. (2015) found that the rotation of the principal stress involved in the stress path of traffic load will accelerate the accumulation of transverse strain and weaken the vertical rebound modulus. Uthayakumar and Vaid (1998) carried out a series of monotonic shear tests with different principal stress direction angles on different sands by using a hollow torsional shear instrument. According to the test, the direction angle of principal stress remarkably impacts sand strength and deformation, and the softening and hardening degrees of sands are different. Symes et al. (1984) conducted the torsional shear test of the hollow cylinder test under undrained conditions on the remolded ham river sand, finding the obviously different pore pressure characteristics when the PSA rotates positively and reversely, in the case of constant shear stress. Ishihara and Towhata (1983) used Toyoura sand from Japan to conduct the cyclic rotation test of the PSA with the constant shear stress value under undrained conditions. The results also show that compared with the triaxial cyclic shear test, the generation rate of pore water pressure under the rotation of the PSA is significantly faster. As found by Wong and Arthur (1986), the cyclic PSA rotation strengthens the production of pore pressure, thereby lowering the soil resilience modulus.
It can be seen from the above research that many scholars have carried out extensive experimental research on the principal stress rotation of soil. The experimental research with regard to the continuous PSA rotation mainly pays attention to sandy soil and soft clay, and there is basically no research that examines the principal stress of loess, let alone the non-coaxial properties exhibited by loess under the continuous PSA rotation. Geotechnical materials with directional PSA shear and pure rotation PSA present a strong non-coaxiality, which is caused by anisotropy as it can weaken the soil strength. In addition, existing experimental research on the continuous PSA rotation of sand or soft clay only focuses on small rotation and seldom pay attention to the soil non-coaxial and strain accumulation characteristics with large PSA rotation. Hence, our study employs the hollow cylinder torsional shear instrument for conducting the undrained test on saturated loess under the complicated stress path of cyclic rotation PSA under different intermediate principal stress ratios (IPSRs) and generalized shear stress. Compared with the cyclic triaxial test, the cumulative pore pressure and deformation caused by the rotation of the PSA are analyzed. In addition, the anisotropy and non-coaxiality of stiffness weakening under this cyclic stress path are analyzed. It provides a direct experimental basis for establishing the non-coaxial constitutive model of clay and simulating the deformation characteristics of saturated soft clay under traffic load.
2 Stress path of continuous PSA rotation and test scheme
2.1 Stress path
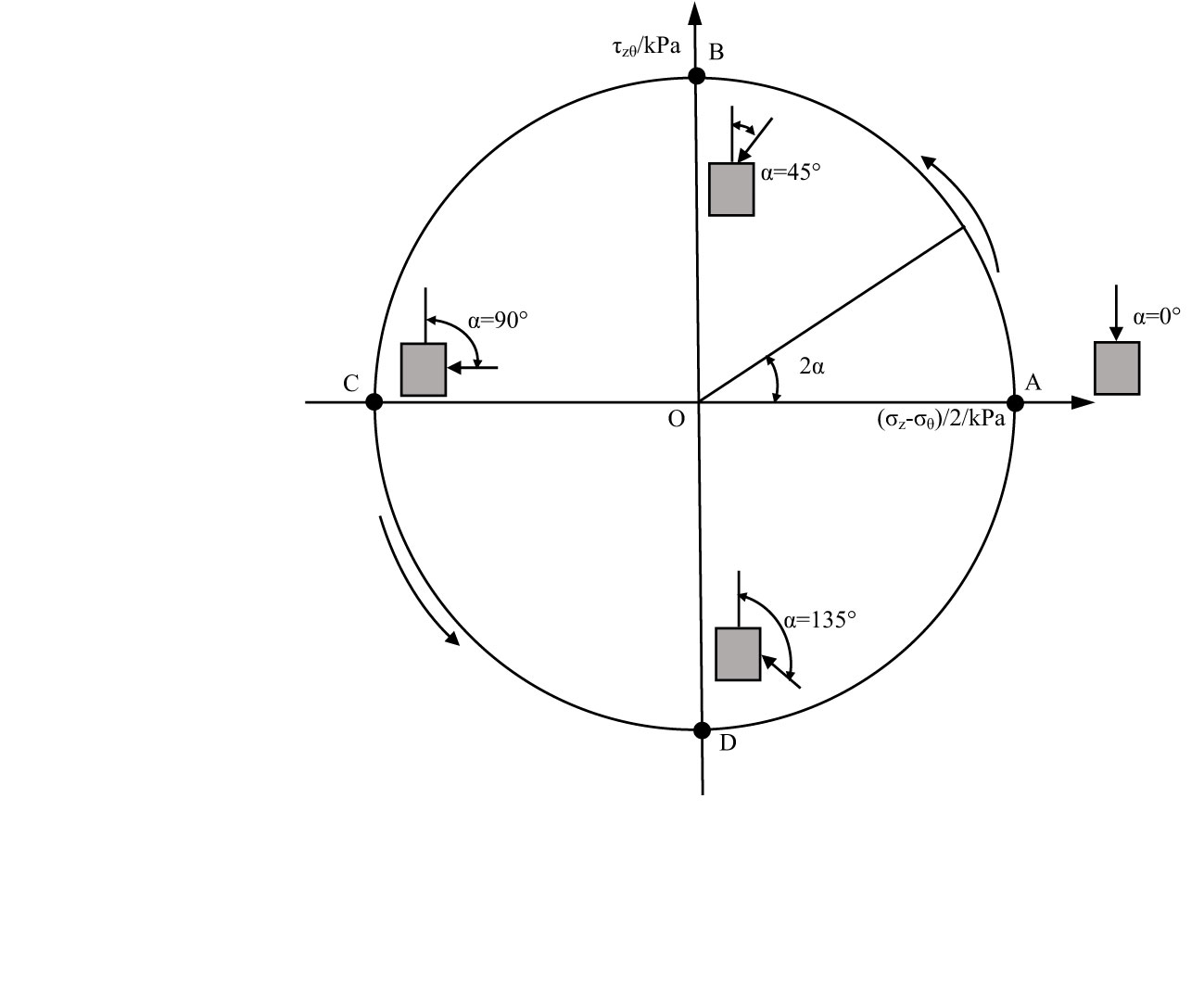
Figure 1 demonstrates the stress path of pure PSA rotation. The pure rotation test falls into consolidation and rotation, with the former falling into isotropic consolidation and anisotropic consolidation. O and OA of Figure 1 display the isotropic and anisotropic consolidation, respectively. The purpose of anisotropic consolidation is to ensure that p remains unchanged and increases to the required q value by adjusting internal and external confining pressures or axial forces, after consolidation rotating from point A and counterclockwise along A-B-C-D-A; the rotation angle in stress space is 2α. Hence, 180° is taken as a cycle (Figure 1).
In the process of testing, the internal and external confining pressures were controlled; axial stress and torsional shear stress were also controlled to make the average stress p, deviatoric stress q, and the ratio of intermediate principal stress b constant. The rotation rate of principal stress is controlled by controlling the cycle of the above four loading components. In this paper, the rotation rate is controlled by 0.2°/min.
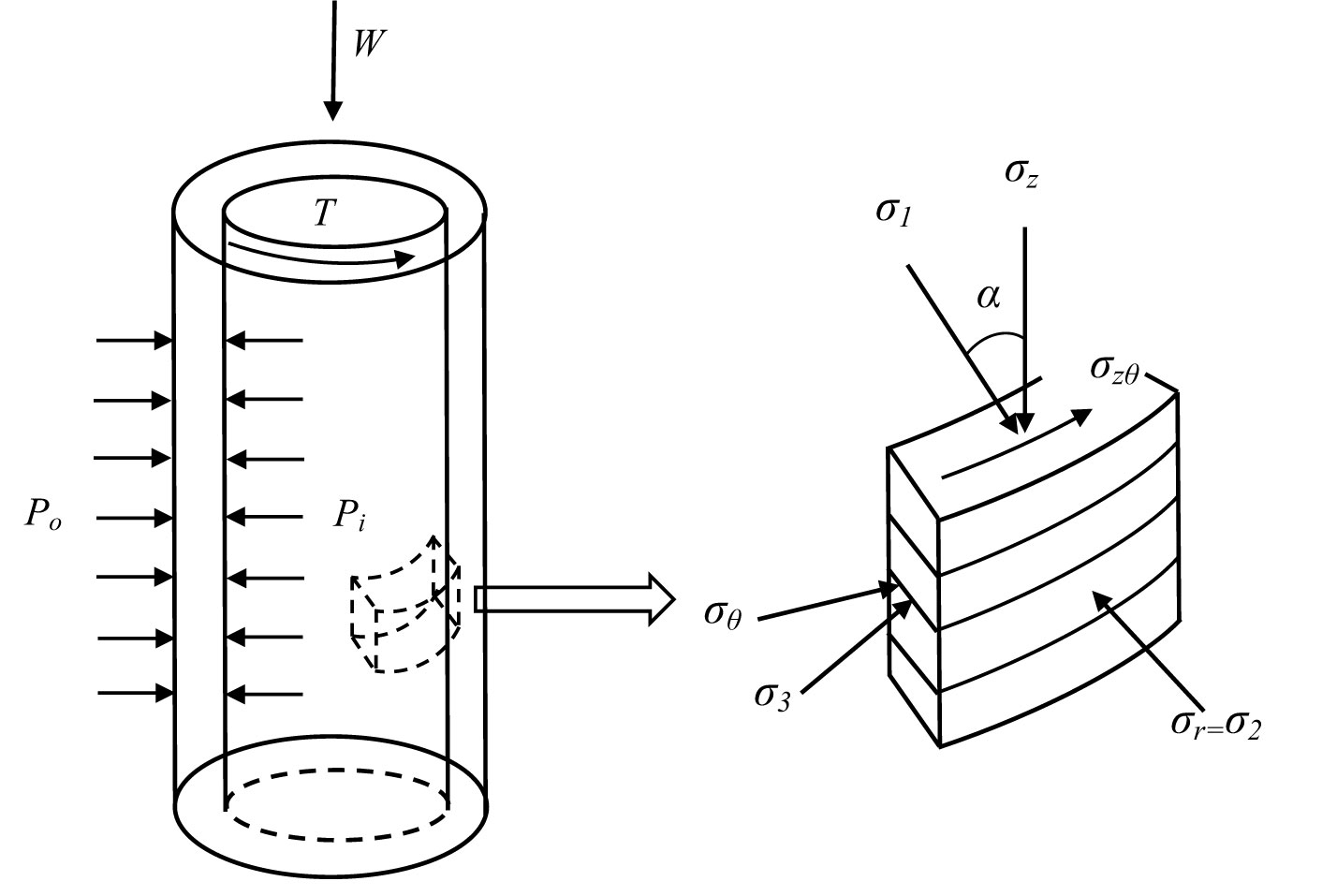
Figure 2 displays the stress state of the hollow cylindrical sample and soil element. Notably, the PSA rotation is the rotation in the plane that includes the angle α between the PSA in the sample’s vertical plane and circumferential plane. The unit body is composed of four independent stress components (torsional shear stress τzθ, radial stress σr, circumferential stress σθ, axial stress σz), which have three main directions. In the vertical, circumferential, and radial planes, they are the first, the third, and the second principal stresses. The four stress components are generated by torque M, internal and external confining pressures (pi,po), and axial force W.
2.2 Sample preparation and test scheme
2.2.1 Preparation of remolded samples
The soil is crushed, sieved according to the standard, dried, weighed, and prepared into wet soil with moisture content of 16.4%, and then sealed and stored in plastic bags for more than 2 days to make the soil fully uniform. According to the sample size, the dry density is controlled to 1.69 g/cm3, the weight of the required wet soil is calculated, and the wet soil pressed uniformly in 10 layers (Figure 3).

Figure 3 Preparation of remolded sample (Wang et al., 2019).
2.2.2 Test scheme
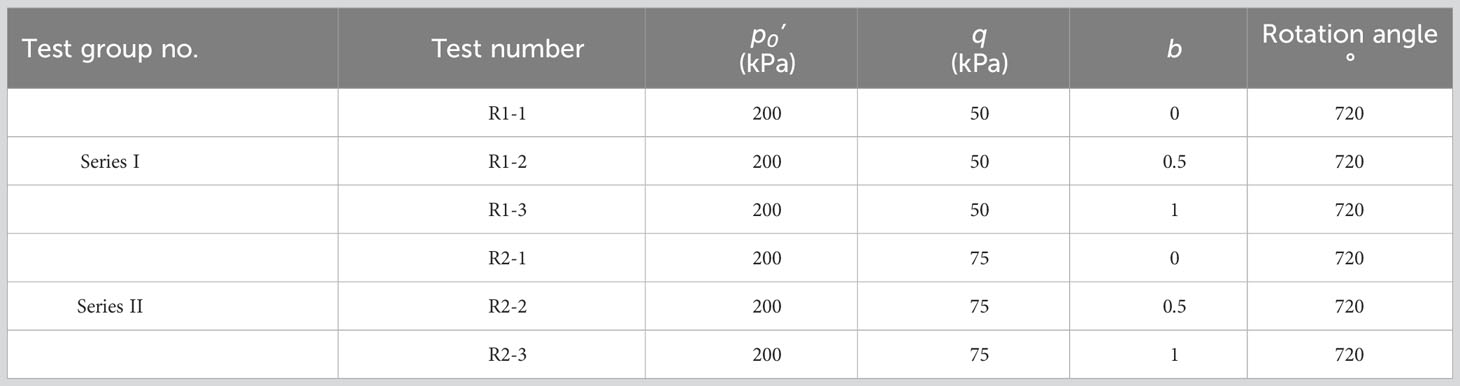
The pure rotation test in this paper mainly studies the pure rotation test of saturated remolded loess under different deviatoric stresses and different intermediate principal stress ratios (IPSRs). The consolidation pressure is uniformly selected as 200 kPa. The consolidation is divided into equal consolidation and pressure bias consolidation, and the rotation rate is 0.2°/min. The pure rotation tests involved six samples, setting the deviatoric stress at 50 kPa and 75 kPa and the IPSR b at 0, 0.5, and 1, respectively. The sample is undrained in the testing process, and Table 1 lists the specific test scheme.
3 Test results and analysis
3.1 Test load and stress
The pure rotation test regarding the PSA is a relatively complicated stress path in the current geotechnical test. Due to the constant equivalence of p, q, and b during the test and only changing the direction of the principal stress, it is necessary to better control the loading mode of four external force inputs. In the pure rotation test of the PSA, the application of internal and external confining pressures, axial force, and torque adopts sine wave input, and the cycle is the same; also the same as that of the PSA rotation, the specific scheme shall be set before the test and realized by the operation program of GCTS.
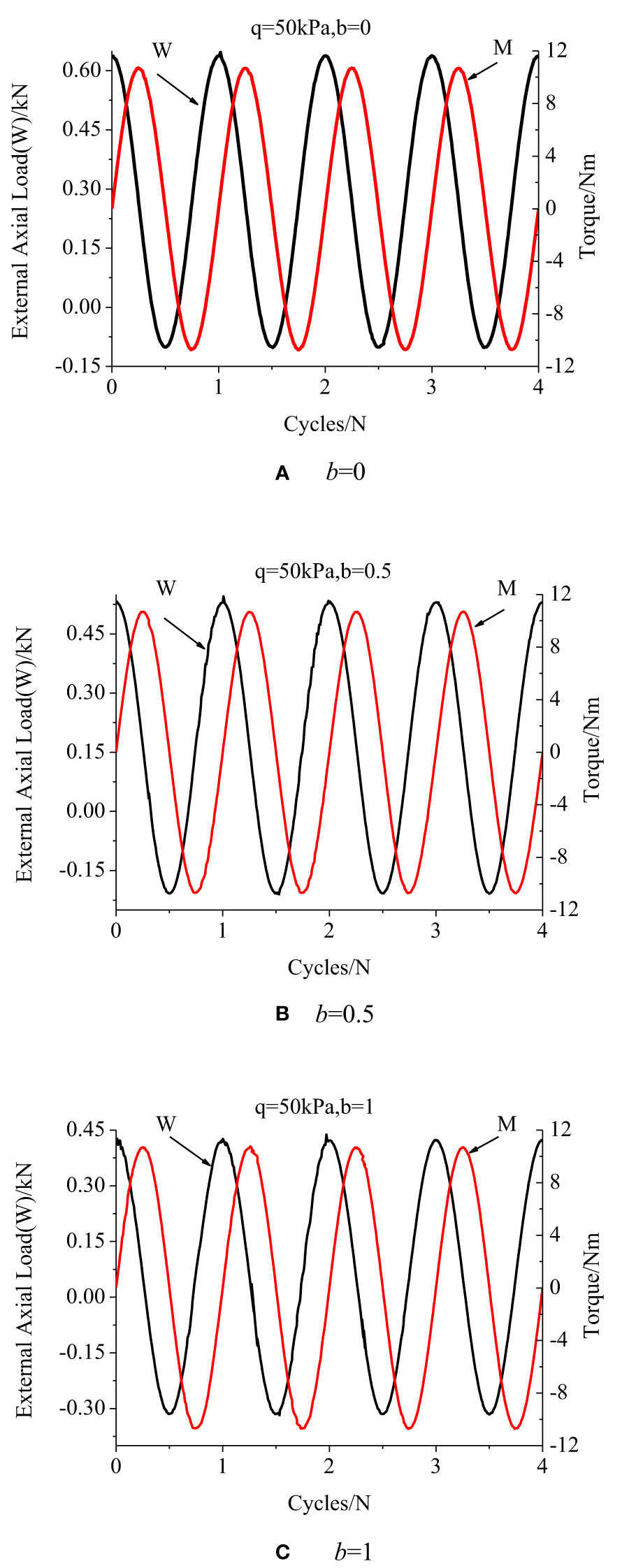
Taking q = 50 kPa as an example, Figure 4 shows the loading mode of axial force and torque components with increasing of the cycle under different IPSRs. According to the figure, for achieving the above stress path, axial force and torque under different IPSRs have consistent loading waveform laws, but the amplitude differs, each input stress component can be controlled independently, and the control result is relatively stable; therefore, the above path can be realized.
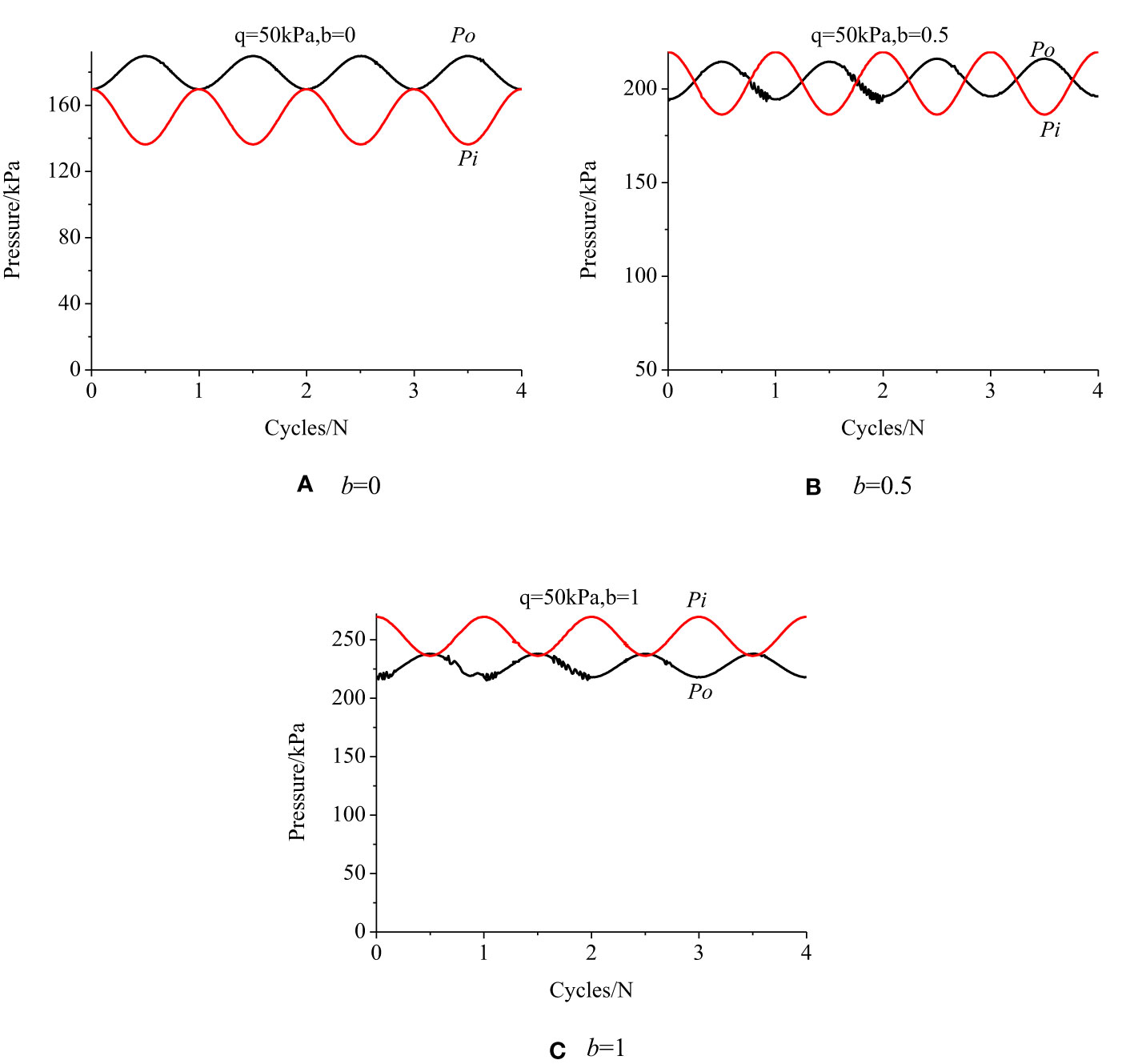
Figure 5 shows the actual loading waveforms of internal and external confining pressure with the number of cycles under different IPSRs. For realizing the above stress path, axial force and torque under different IPSRs have different loading waveforms, and their amplitudes also differ. It is allowed to independently control the internal and external confining pressures. The control results are relatively stable, and the peripheral pressure deviates slightly on the control path; however, the above path can be realized within the error range.
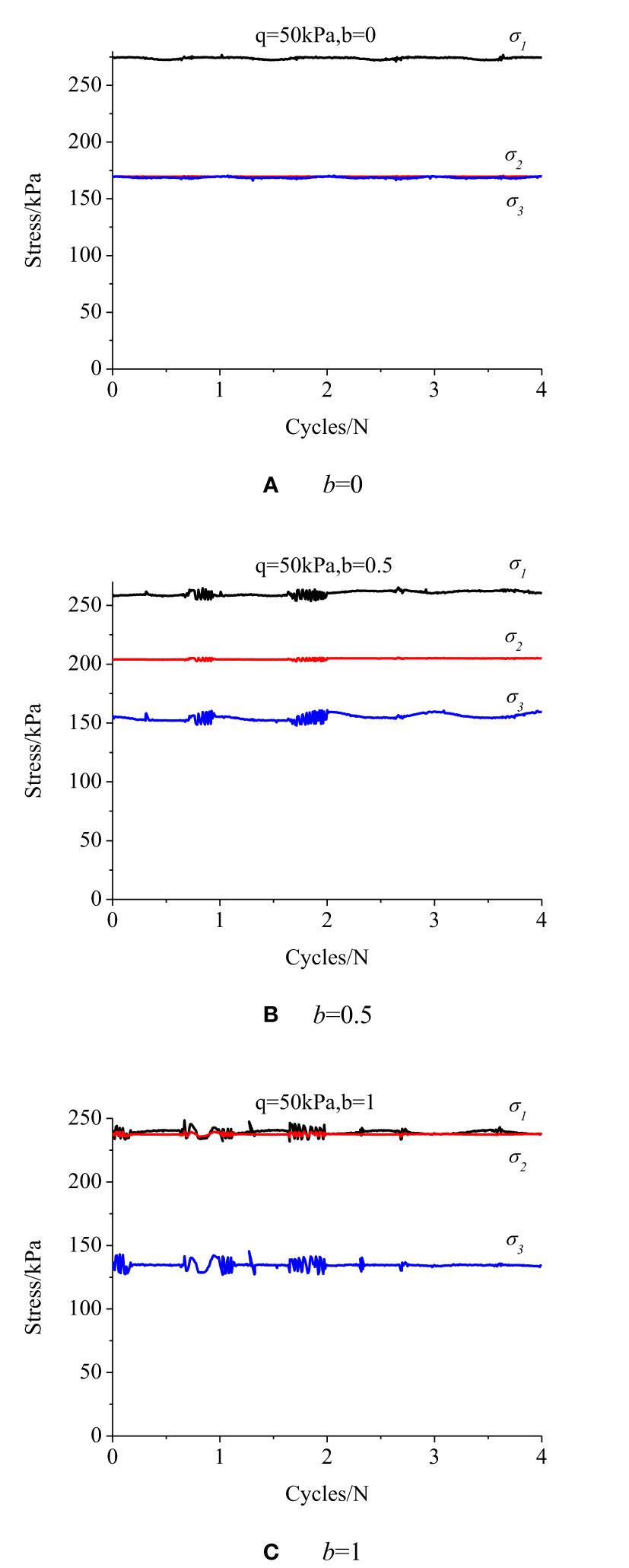
Figure 6 displays the principal stress variation as cycle changes under different IPSRs. Relying on the above loading method regarding axial force and torque under internal and external pressures, the principal stress is relatively stabilized under different IPSRs.
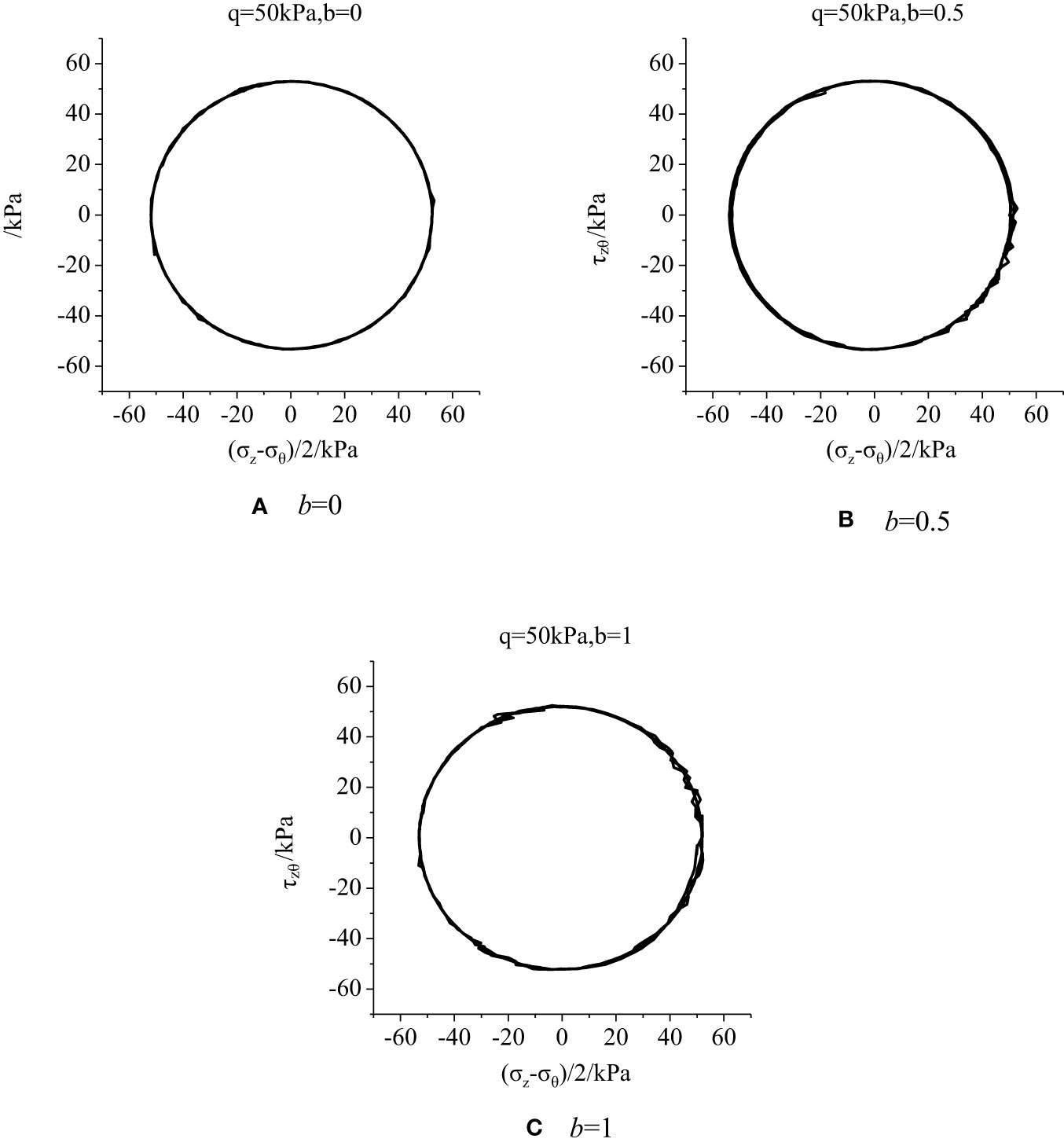
Figure 7 shows the stress paths in the deviatoric plane under different principal stress ratios, which are consistent with the ideal stress path in Figure 1.
3.2 The development of pore pressure
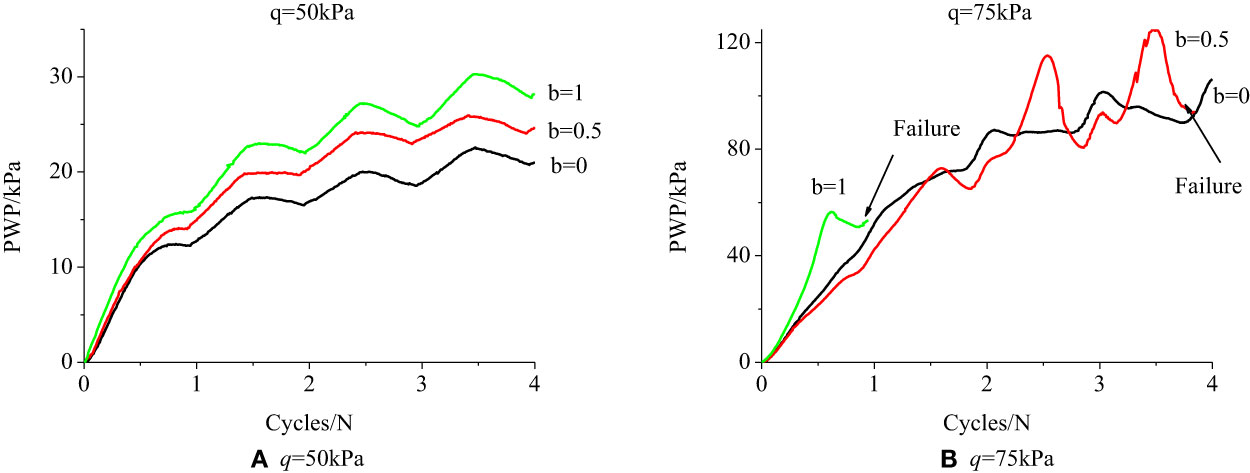
Figure 8 demonstrates the pore water pressure cumulative law with rotation number under different IPSRs and deviatoric stresses. As the PSA rotates continuously, the pore water pressure presents a normal cyclic cumulative growth. When the deviatoric stress is the same, pore water pressure presents a similar cumulative law regardless of IPSRs, but the size differs. IPSR increase leads to increased final stable pore water pressure when b = 0. The development of the principal shrinkage stress is similar to that of the material with the principal shrinkage stress of 0.5; therefore, the development of the principal shrinkage stress is smaller than that of the material with the principal shrinkage stress of 0.5 in the process of deposition. Accordingly, increment of pore water pressure becomes smaller as the number of cycles increases, and the cumulative pore water pressure takes up the largest proportion of the total following the first cycle. According to Figures 8, B, greater deviatoric stress reports rapid pore water pressure accumulation and larger stable pore water pressure. Also, when deviatoric stress is the same, larger intermediate principal stress denotes less rotation failure, revealing the smaller strength.
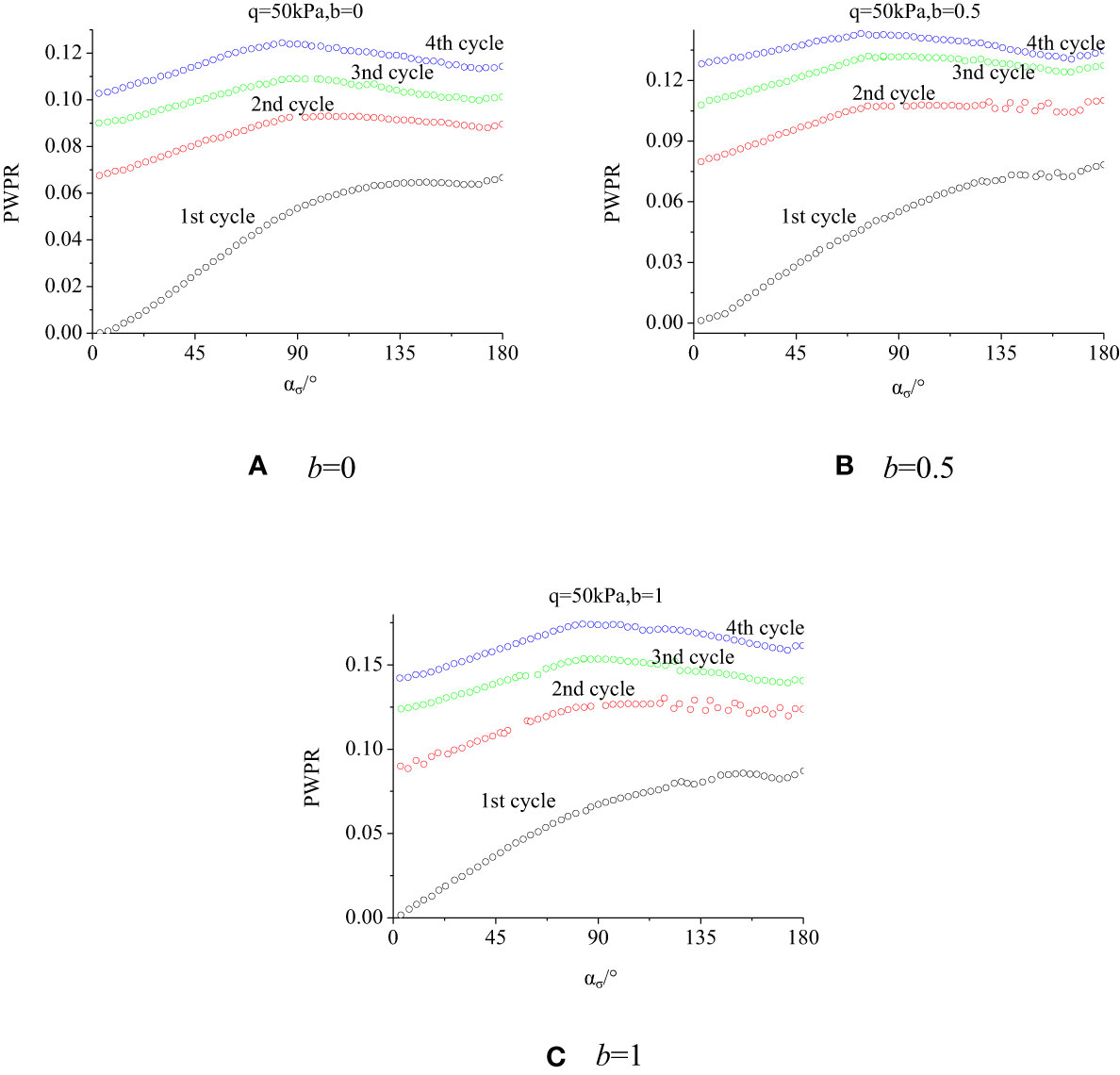
The ratio of pore water pressure to effective stress is the pore water pressure ratio (PWPR = uw/p’). The variation of PWPR with the rotation angle of principal stress for different cycles under different deviatoric stresses and IPSRs is shown in Figure 9. In the case of q = 50 kPa, the PWPR under different IPSRs changes in the same way. In the first cycle, the PWPR grows slowly with the rotation angle. After the second cycle, the PWPR presents an increasing-to-decreasing trend as the rotation angle increases; however, on the whole, the PWPR increases from accumulation after each cycle, i.e., faster pore pressure accumulation rate at the initial rotation stage. The pore pressure accumulates more slowly due to increased rotation cycles. If the sample is not damaged, the pore pressure will develop toward a gradually stable direction.
Clearly, the relationship between the principal stress direction angle and the included angle between the principal stress direction and the transverse axis in the deviatoric plane is twice (Figure 1). Hence, the direction angle of 180° denotes a cycle in the deviatoric plane and the development of pore water pressure is one cycle when the direction angle range is 0–180° (uσ=0°=uσ=180°); the pore water pressure presents a continuous change trend as the principal stress direction angle increases. Considering the massive data points, Figure 9 is the pore water pressure development diagram for selecting some points in the test process, and the midpoint fluctuates in the diagram because of the measurement error of the test instrument.
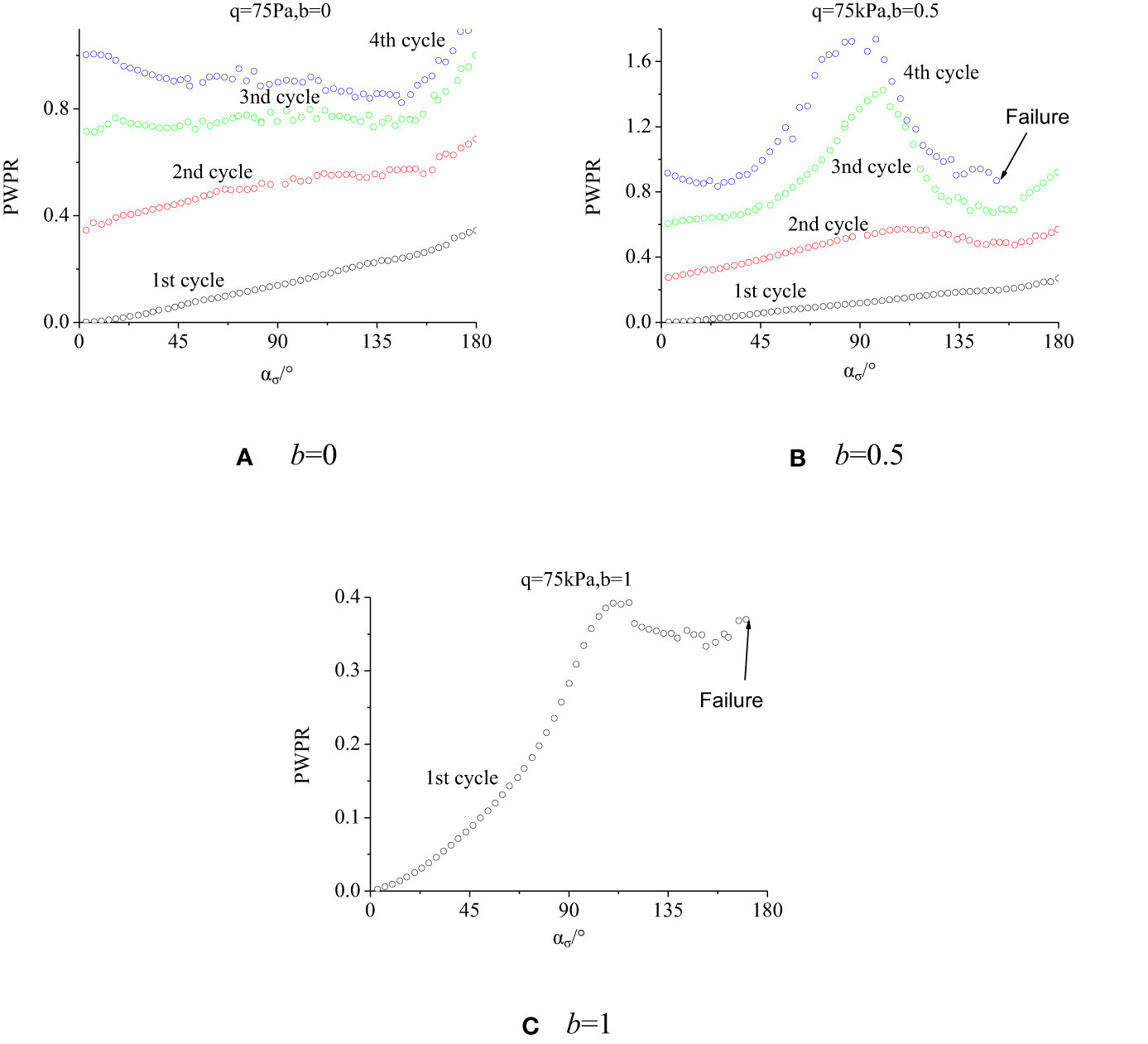
When the deviatoric stress increases to q = 75 kPa, the pore pressure accumulation rate accelerates and the sample will be in an unstable state. Figure 10 displays how the pore pressure ratio changes with the principal stress rotation angle. b = 0, the pore pressure ratio increases gradually in the first and second cycles, decreases first and then increases in the third and fourth cycles, and finally accumulates; b = 0.5, the pore pressure ratio grows in the first and second cycles and presents an increasing-to-decreasing trend in the third and fourth cycles till the damage of the sample but eventually accumulates, as shown in Figure 10B. The pore pressure ratio development is associated with the pore pressure development law, because pore pressure increases and decreases suddenly, as shown in Figure 10B. In the case of b = 1, the same damage occurs in the first cycle, the pore pressure ratio grows with the principal stress rotation angle, and the pore pressure accumulation is small.
3.3 The development of strain
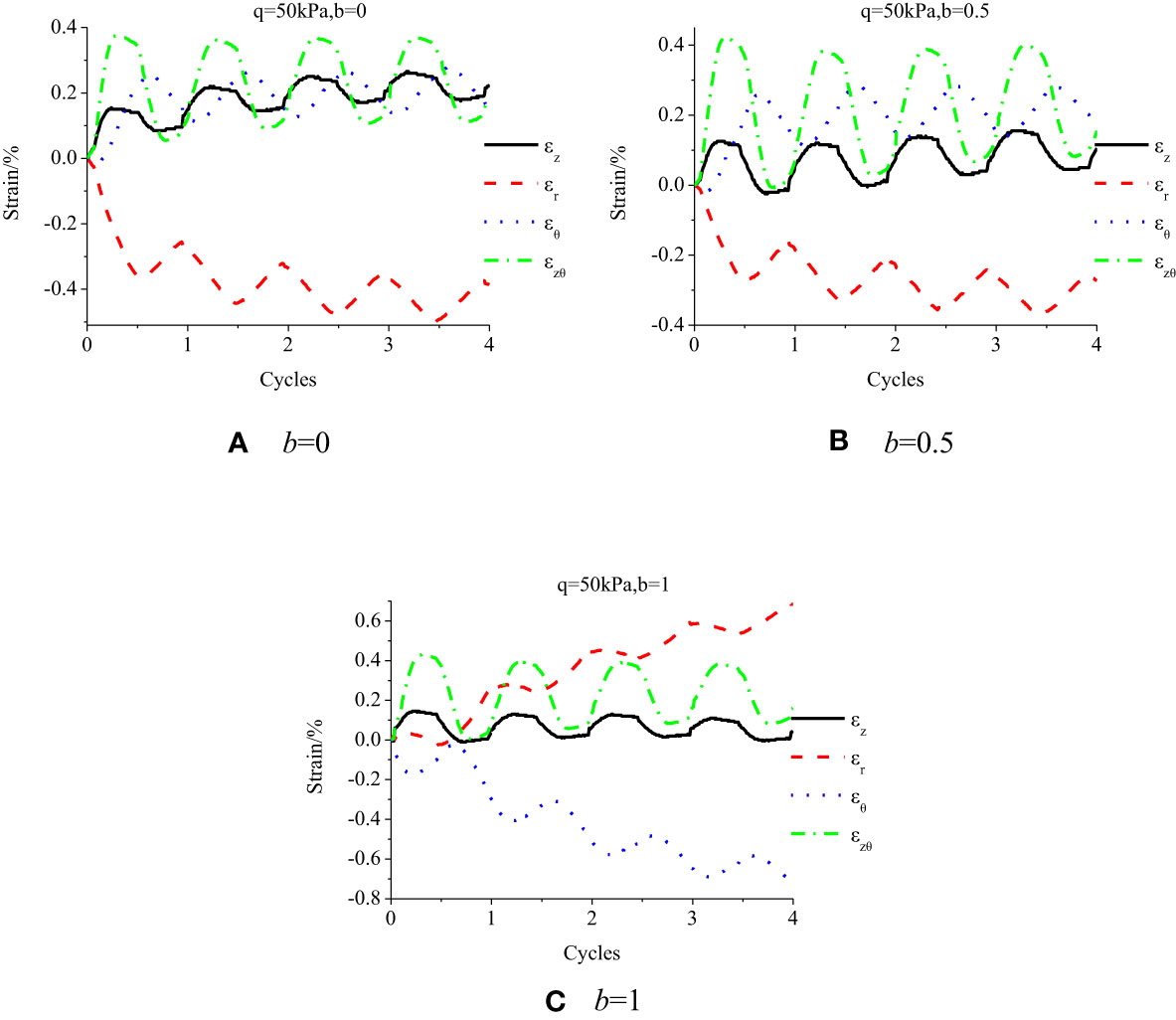
Figures 11, 12 demonstrate the strain component variation under various stress paths when the principal stress rotation number changes. In the case of q = 50 kPa and b = 0 (Figure 11A), the axial strain ϵz and radial strain ϵr with the increase of the number of cycles first accumulate a small amount and then remains stable. The other strain components do not change as the cycle increases. The main reason is that at the beginning, with the application of stress, the soil is compressed and deformed, causing partial strain, followed by elastic strain, i.e., soil hardening. When b = 0.5, as shown in Figure 11B, the radial strain ϵr with the increase of cycles first accumulates a small amount and then remains stable. The other component has stable strains with cycle increase, and the strains are within the range of elastic deformation, and the soil is hardened. When b = 1, as shown in Figure 11C, the circumferential strain ϵθ and radial strain ϵr gradually increase and accumulate with the increase of cycles and then remains stable. Other components have stable strains regardless of the cycle change. In the pure rotation test regarding principal stress, upon the same deviatoric stress, IPSR greatly impacts the strain component development.
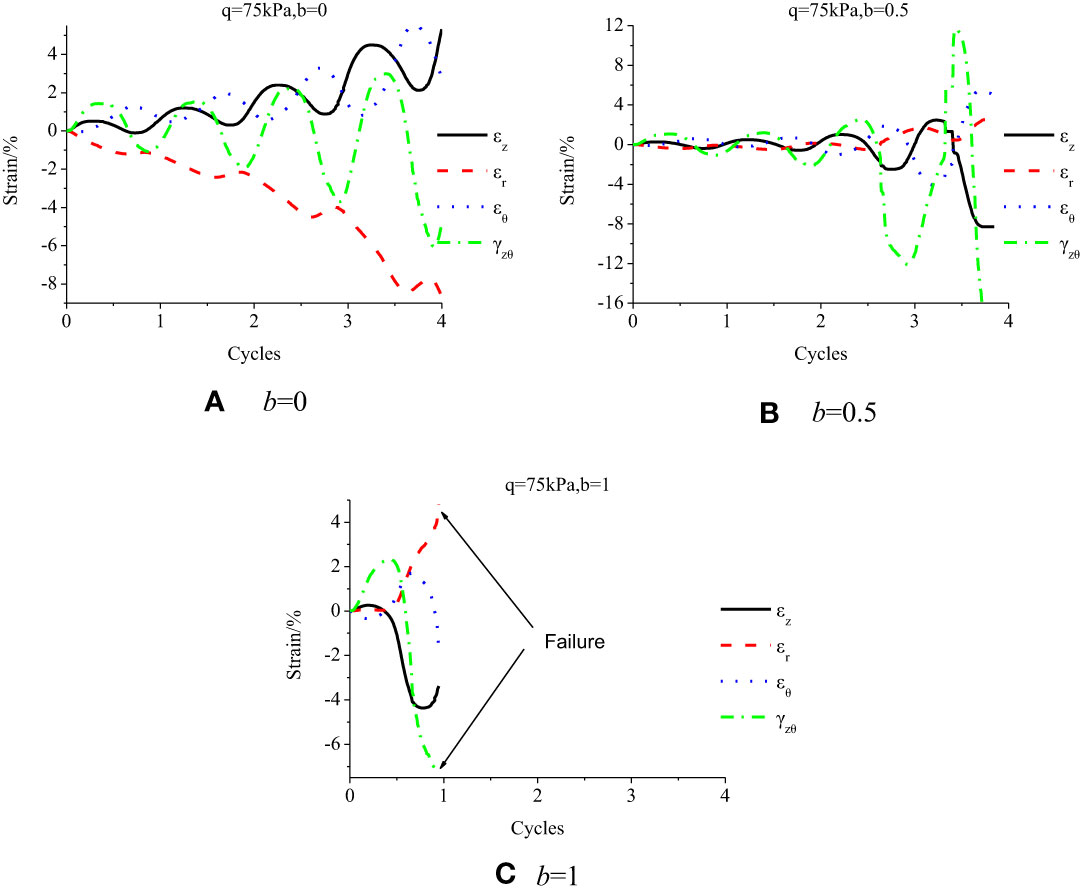
When q = 75 kPa, as shown in Figure 12, the strain component undergoes a gradual accumulation as rotation cycles increase. The accumulation degree changes with IPSR and increases slowly with IPSR before the occurrence of a large strain accumulation. Figures 12B, C show the sample failure. Due to the large deviation stress q, there is a large plastic strain accumulation and then the sample is damaged. The strain component shows different developments and degrees under different IPSRs. When the conditions are same, the IPSR remarkably impacts the strain component development.
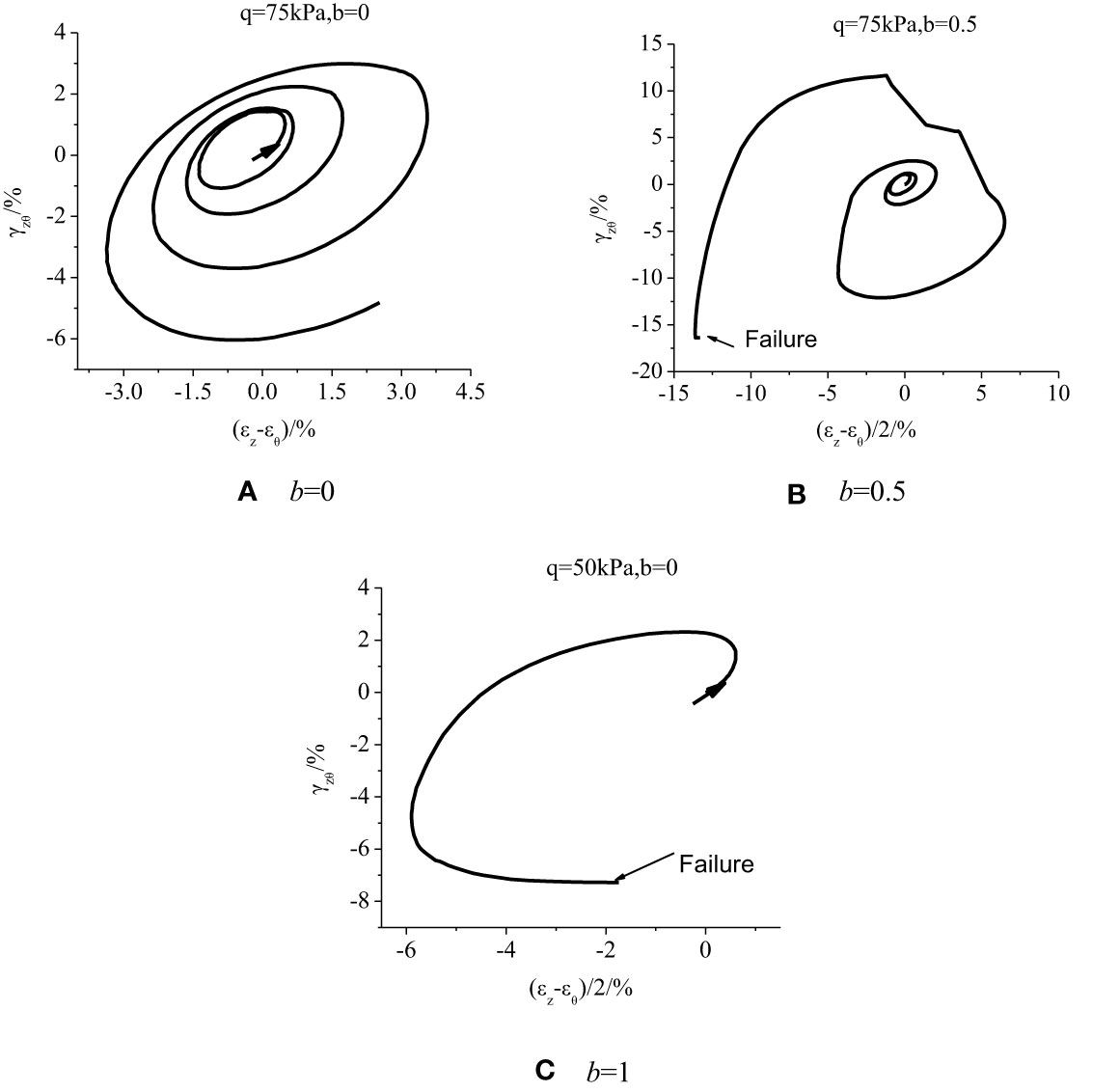
Figures 13, 14 demonstrate the strain path developments in the γzθ−(ϵz−ϵθ) plane. When q = 50 kPa, the strain development is small and within the elastic range. As the principal stress rotates cyclically, the strain path area is reduced, the final size becomes stable, and the strain surface area is along the (ϵz−ϵθ) plane. When b = 0 and b = 0.5, it moves to the left; when b = 1, it moves to the right and is finally in a stable state. Therefore, when q = 50 kPa, the failure stress is not reached and the material hardening is in a cyclic stable state.
With the deviatoric stress reaching q = 75 kPa, (Figure 14), the spiral line of the strain path gradually expands in the plane until failure, indicating the expansion and failure of the plastic strain accumulation cycle, impacted by the deviatoric stress. Strain exhibits a similar development trend under different IPSRs; nevertheless, intermediate principal stress increase leads to accelerated strain development speed and advanced failure time.
In order to further illustrate the cyclic strengthening or weakening properties of the above saturated remolded loess under the pure rotation of the PSA with different deviatoric stresses, according to the definition of reference (Desrues and Chambon, 2002), we take the secant modulus of the ith cycle as the shear stiffness Gi of the remolded loess and the cycle-based Gi/G1 variation as the shear stiffness evolution in the process of PSA rotation. In the case of q = 50 kPa, the stiffness ratio >1 and the stiffness ratio elevates slowly with the cycles; the process is called stiffness strengthening (Figure 15). In the case of q = 75 kPa, the stiffness ratio <1 and the stiffness ratio presents a downtrend as the number of cycles increases, showing the phenomenon of stiffness weakening. In both cases, the IPSR and stiffness ratio change more slightly and there is a negative relation between the two ratios. In conclusion, for the remolded loess in this paper, its stiffness ratio has both strengthening and weakening with the increase of cycles, which is related to the magnitude of deviatoric stress, whereas for sandy soil (Yang et al., 2007), there is cyclic weakening, which is independent of the magnitude of deviatoric stress, which is an important difference from sandy soil.
4 Conclusion
The continuous pure rotation tests of PSA are carried out on the saturated sample of Q2 remolded loess by a GCTS hollow cylinder instrument. After studying the pore pressure variation, strain accumulation, and stress-strain evolution regarding remolded loess, the main conclusions are as follows:
(1) As the PSA continuously rotates, the cumulative pore pressure following the first cycle occupies the largest proportion of the total. Greater deviator stress reports rapid pore pressure accumulation and larger stable pore pressure value.
(2) The pore water pressure of saturated remolded loess shows a regular cyclic accumulation increase, and under the same deviatoric stress conditions, different IPSRs exhibit the same pore water pressure accumulation law, whereas the degree differs. The increment of pore water pressure becomes smaller as the number of cycles increases.
(3) The strain component presents different developments and degrees upon different IPSRs. The IPSR can remarkably affect strain component development when conditions are the same. Intermediate principal stress increase is accompanied by accelerated strain development speed and advanced failure.
(4) When the deviatoric stress level is low, the material hardening is in a cyclic stable state, the strain component remains stable with the rotation of the PSA, and the strain path area is reduced, together with a stable final size. When the deviatoric stress level is high, the material strength cycle weakens, the strain component gradually accumulates with the rotation of the PSA, and the strain path is a spiral line in the γzθ−(ϵz−ϵθ) plane and gradually expands until it is damaged.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.
Author contributions
SW: Data curation, Methodology, Writing – original draft. ZZ: Conceptualization, Methodology, Writing – review & editing. BC: Software, Supervision, Writing – review & editing. BW: Data curation, Investigation, Methodology, Writing – review & editing. DZ: Writing – review & editing. FN: Data curation, Writing – review & editing.
Funding
The authors declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Brown S. F. (1996). Soil mechanics in pavement engineering. Géotechnique 46 (3), 383–426. doi: 10.1680/geot.1996.46.3.383
Cai Y. Q., Guo L., Jardine R. J., Yang Z., Wang J. (2016). Stress–strain response of soft clay to traffic loading. Géotechnique. doi: 10.1680/jgeot.15.P.224
Cai Y., Sun Q., Guo L., Juang C. H., Wang J. (2015). Permanent deformation characteristics of saturated sand under cyclic loading. Can. Geotech. J. 52 (6), 1–13. doi: 10.1139/cgj-2014-0341
Chazallon C., Hornych P., Mouhoubi S. (2006). Elastoplastic model for the long-term behavior modeling of unbound granular materials in flexible pavements. Int. J. Geomech. 6 (4), 279–289. doi: 10.1061/(ASCE)1532-3641(2006)6:4(279)
Desrues J., Chambon R. (2002). Shear band analysis and shear moduli calibration. Int. J. Solids Struct. 39 (13), 3757–3776. doi: 10.1016/S0020-7683(02)00177-4
Grabe P. J. (2009). Effects of principal stress rotation on permanent deformation in rail track foundations. J. Getech. Geoenviron. Eng. 135 (4), 555–565. doi: 10.1061/(ASCE)1090-0241(2009)135:4(555)
Guo L., Chen J., Wang J., Cai Y., Deng P. (2016). Influences of stress magnitude and loading frequency on cyclic behavior of K0-consolidated marine clay involving principal stress rotation. Soil Dyn. Earthq. Eng. 84, 94–107. doi: 10.1016/j.soildyn.2016.01.024
Ishihara K., Towhata I. (1983). Sand response to cyclic rotation of principal stress directions as induced by wave loads. Soils Foundations 23 (4), 11–26. doi: 10.3208/sandf1972.23.4_11
Ishikawa T., Sekine E., Miura S. (2011). Cyclic deformation of granular material subjected to moving wheel loads. Can. Geotech. J. 48 (5), 691–703. doi: 10.1139/t10-099
Kumruzzaman Md., Yin J.-H. (2010). Influence of principal stress direction and intermediate principal stress on the stress-strain-strength behavior of completely decomposed granite. Can. Geotech. J. 47 (2), 164–179. doi: 10.1139/T09-079
Miura K., Miura S., Toki S. (1986). Deformation behavior of anisotropic dense sand under principal stress axes rotation. Soils Found 26 (1), 36–52. doi: 10.3208/sandf1972.26.36
Qian J. G., Wang Y. G., Yin Z. Y., Huang M. S. (2016). Experimental identification of plastic shakedown behavior of saturated clay subjected to traffic loading with principal stress rotation. Eng. Geol. 214, 29–42. doi: 10.1016/j.enggeo.2016.09.012
Shen Y., Wang X., Liu H. L., Du W. H., Wang B. G. (2017). Influence of principal stress rotation of unequal tensile and compressive stress amplitudes on characteristics of soft clay. J. Mt. Sci. 14 (2), 369–381. doi: 10.1007/s11629-016-4000-9
Symes M. J., Gens A., Hight D. W. (1984). Undrained anisotropy and principal stress rotation in saturated sand. Geotechnique 34 (1), 11–27. doi: 10.1680/geot.1984.34.1.11
Tong Z. X., Zhang J. M., Yu Y. L., Zhang G. (2010). Drained deformation behavior of anisotropic sands during cyclic rotation of Principal Stress Axes. J. Geotech. Geoenviron. Eng. 31 (6), 1509–1518. doi: 10.1061/(ASCE)GT.1943-5606.0000378
Uthayakumar M., Vaid Y. P. (1998). Static liquefaction of sands under multiaxial loading. Can. Geotech. J. 35, 273–283. doi: 10.1139/t98-007
Wang Y. K., Guo L., Gao Y. F., Qiu Y., Hu X. Q., Zhang Y. (2016). Anisotropic drained deformation behavior and shear strength of natural soft marine clay. Mar. Georesour Geotechnol. 34 (5), 493–502. doi: 10.1080/1064119X.2015.1081653
Wang S., Zhong Z., Liu X., Tu Y. (2019). Influences of principal stress rotation on the deformation of saturated loess under traffic loading. KSCE J. Civil Eng. 23 (5), 2036–2048. doi: 10.1007/s12205-019-0474-7
Wong R. K. S., Arthur J. R. F. (1986). Sand sheared by stresses with cyclic variation in direction. Geotechnique 36 (2), 215–226. doi: 10.1680/geot.1986.36.2.215
Yang Z. X., Li X. S., Yang J. (2007). Undrained anisotropy and rotational shear in granular soil. Geotechnique 57 (4), 378–384. doi: 10.1680/geot.2007.57.4.371
Keywords: saturated loess, principal stress axis rotation, cyclic degradation, strain accumulation, pore pressure accumulation
Citation: Wang S, Zhong Z, Chen B, Wu B, Zhang D and Ni F (2023) Experimental study on strain accumulation characteristics of saturated remolded loess under pure rotation of the principal stress axis. Front. Ecol. Evol. 11:1275648. doi: 10.3389/fevo.2023.1275648
Received: 10 August 2023; Accepted: 07 September 2023;
Published: 09 October 2023.
Edited by:
Yongqiang Zhou, Chinese Academy of Sciences (CAS), ChinaReviewed by:
Juehao Huang, Chinese Academy of Sciences (CAS), ChinaYiliang Tu, Chongqing Jiaotong University, China
Copyright © 2023 Wang, Zhong, Chen, Wu, Zhang and Ni. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sui Wang, d2FuZ3N1aTEwNjEwQDE2My5jb20=
 Sui Wang
Sui Wang Zuliang Zhong2,3
Zuliang Zhong2,3