A quantitative description method for the mechanical behavior of soil-rock mixture as affected by water content

The mechanical properties of soil rock mixture (S-RM) are complex, especially the strength deterioration after encountering water, which readily leads to engineering instability. A series of large triaxial tests of S-RM with different water contents under various confining pressures were performed, the mechanical properties of S-RM were explored from a macroscopic perspective. The constitutive model of S-RM – an extended Duncan-Chang (DC) model considering water content – was developed. The results show that: (a) the stress-strain curves of S-RM are strain hardening type, the peak strength decreases non-linearly with the increase of water content, the higher the water content of sample, the more significant the bulging phenomenon and the more numerous and extensive the surface cracks; (b) the cohesion c and internal friction angle φ of S-RM both decrease approximately linearly with the increase of water content, and the secant modulus decreases significantly with the increase of water content, the reason of which can be attributed to the porosity and compression characteristics of S-RM; (c) the extended DC model can be used to describe the mechanical behavior of S-RM affected by water under triaxial test conditions. The material constant K, failure ratio R_f, c, and φ are all related to water content ω, while material constant n is independent, only ω, n, maximum principal stress σ₁, and minimum principal stress σ₃ are needed to determine the tangent modulus of the DC model of S-RM. The results can provide an experimental basis and mechanical understanding applicable to engineering practice in an S-RM formation.

Introduction

Many geological hazards have been induced in geological materials, which are extremely inhomogeneous and composed of rock blocks with high strength, fine soils, and pores, called “soil-rock mixture” (S-RM) by scholars (Gao et al., 2018; Senthilkumar et al., 2018; Fu et al., 2020; Gao et al., 2021). Due to its very nature, S-RM usually exhibits very complex physical and mechanical behaviors (Xu et al., 2015; Zhang et al., 2015; Zhang Z. L. et al., 2016; Zhao and Liu, 2019).

Many scholars believe that the content of “rock blocks” and their size distribution are the main structural characteristic features of S-RM, which mainly control its mechanical properties (Casagli et al., 2003; Zhang H. Y. et al., 2016; He et al., 2020). In-situ and laboratory tests show that the shear strength of S-RM is akin to that of the rock blocks alone when the proportion of rock blocks is higher than a certain threshold, and is basically that of the fine soils when the proportion of rock blocks is less than a certain threshold, the friction angle of S-RM increases with the increase of proportion of rock blocks (Donaghe and Torrey, 1979; Vallejo and Mawby, 2000; Cen et al., 2017; Gao et al., 2018; Wang et al., 2018; Song et al., 2020; Dong et al., 2021). The size distribution of rock block determines the mesoscopic deformation characteristic and fracture form and is an important factor affecting the mechanical properties of S-RM (Buffington et al., 1992; Wickland et al., 2006; Hamidi et al., 2009; Xu and Zhang, 2022). The complex structural characteristics are the root causes of geological hazards in an S-RM formation. In addition to the complex structural characteristics of S-RM, scholars have explored other reasons for its susceptibility to geological hazards. The geological origin, distribution, and occurrence environment of S-RM have been investigated. The geological origins indicate that S-RM is mostly formed by collapses, landslides, and debris flows (Arikan et al., 2007; Hiruma et al., 2013; Viles, 2013; Leigh et al., 2016; Du et al., 2019; Xiang and Song, 2020), which show S-RM formations are mainly distributed in valleys. Geological hazards such as landslides are frequent in valleys, especially after rainfall and changes in reservoir water level (Casagli et al., 2003; Xu et al., 2016; Li et al., 2020; Pan et al., 2020). It is indicated that water plays an important role in the geological hazards of S-RM formation.

The influence of water on the mechanical properties of S-RM has been studied over the past few years. Xu et al. (2007) conducted in-situ shear tests of natural and saturated S-RM in the Hutiao Gorge reservoir area, found that the cohesion and internal friction of S-RM are sensitive to water. Wang et al. (2019) performed large-scale direct shear tests to study the change in water content on the strength of S-RM under the influence of rainfall, revealing that internal friction is the main controlling factor therein. Zhang et al. (2021) discussed the instability mechanism of S-RM slope under the effect of rainfall, which is mainly due to the expansion of infiltration cracks and weakening of mechanical parameters of S-RM caused by the increase of water content. The same conclusion was reached in the study of the stability of S-RM slope under the fluctuation of reservoir water level by numerical simulation (Fan et al., 2021). In terms of deformation characteristics of S-RM, Xing et al. (2019) found that the S-RM samples exhibit slight strain softening and strain hardening under low and high water contents, respectively. The mechanism of influence of water content on the deformation and strength of S-RM has also been studied, Zhao et al. (2019) studied the fracture mechanism of rock blocks of S-RM with different water contents, and investigated the strength deterioration of S-RM. Wei et al. (2018) conducted a series of large-scale direct shear tests with different water contents. They found that the main reason for the strength deterioration of S-RM is the decreasing strength of the rock block with increasing water content. At present, most of the studies on the mechanical properties of S-RM mainly focus on the content of “rock blocks” and their size distribution. The experimental method mainly adopts the direct shear test, and the shear failure surface is determined, which cannot fully reflect the mechanical properties of materials. Moreover, there are few studies on quantitative analysis of deformation and strength parameters and constitutive modelling of S-RM as affected by water.

This present research focuses on the effect of water content on the mechanical properties of S-RM. The better to understand the influence of water on mechanical behavior of S-RM, a certain rock content in the S-RM was selected in this study, and a series of large triaxial tests of S-RM with different water contents under various confining pressures were performed. The influence of water content on the macroscopic mechanical properties of S-RM was investigated and the stress-strain relationship of S-RM were analyzed. The variation characteristics of shear strength and deformation indices with water content were studied. The extended DC model of S-RM considering water content was established, and the variations of model parameters with water content were revealed. The results can provide an experimental basis and constitutive model for the engineering design and application of S-RM affected by environmental water.

Experimental method

Test device and materials

The tests were performed using TAJ-2000 large multifunctional triaxial experimental system. The size of the specimen for testing was Φ 300 mm × 600 mm; the maximum axial load was 1500 kN; the axial displacement ranged from 0 to 300 mm with a resolution of 0.01 mm; the maximum confining pressure was 10 MPa. The S-RM samples were collected from a colluvium bank slope of Jinsha River in Taoyuan, Yunnan Province, China (Figure 1). The physical indices of S-RM were measured and are listed in Table 1. The particle size distribution of S-RM for test is shown in Figure 2. The results show that the grading of S-RM in Taoyuan is continuous and inhomogeneous.

FIGURE 1

Figure 1 Photograph of S-RM in-situ field in Taoyuan.

TABLE 1

Table 1 Physical indices of S-RM in Taoyuan.

FIGURE 2

Figure 2 Particle size distribution of S-RM in Taoyuan.

Test procedures

The saturated water content of S-RM was 16% (as measured). Four different water contents of 4%, 8%, 12%, and 16% were designed in these tests, and remolded samples with different water contents were prepared, and the dry densities of S-RM samples were kept constant (1.652 g/cm³).

The test conditions were unconsolidated and undrained. Four different confining pressures of 200 kPa, 300 kPa, 400 kPa, and 600 kPa were applied. The test scheme is shown in Table 2. The sample was compacted and roughened after each of three layers added to the test cylinder. The test loading rate was 0.6 mm/min, and the test was terminated when the axial strain reached 15%.

TABLE 2

Table 2 Test scheme.

Results and discussions

Stress-strain relationship

Figure 3 presents the stress-strain curves of S-RM samples with different water contents (4%, 8%, 12%, and 16%) under various confining pressures. The results show that the stress-strain curves are all of the strain-hardening type with different water contents under various confining pressures during loading, indicating that the S-RM in Taoyuan has porous characteristics similar to loose sand or normally consolidated soil. The stress-strain curves show significant fluctuations throughout the loading process, which is not as smooth as the stress-strain curves of more general, homogeneous soils. The reason for this is described as follows: during the loading process, the occlusion, dislocation and overturning of the coarse particles of S-RM cause unstable changes of the local contact stress, showing the fluctuation of the statistical average stress-strain curve in macroscopic terms.

FIGURE 3

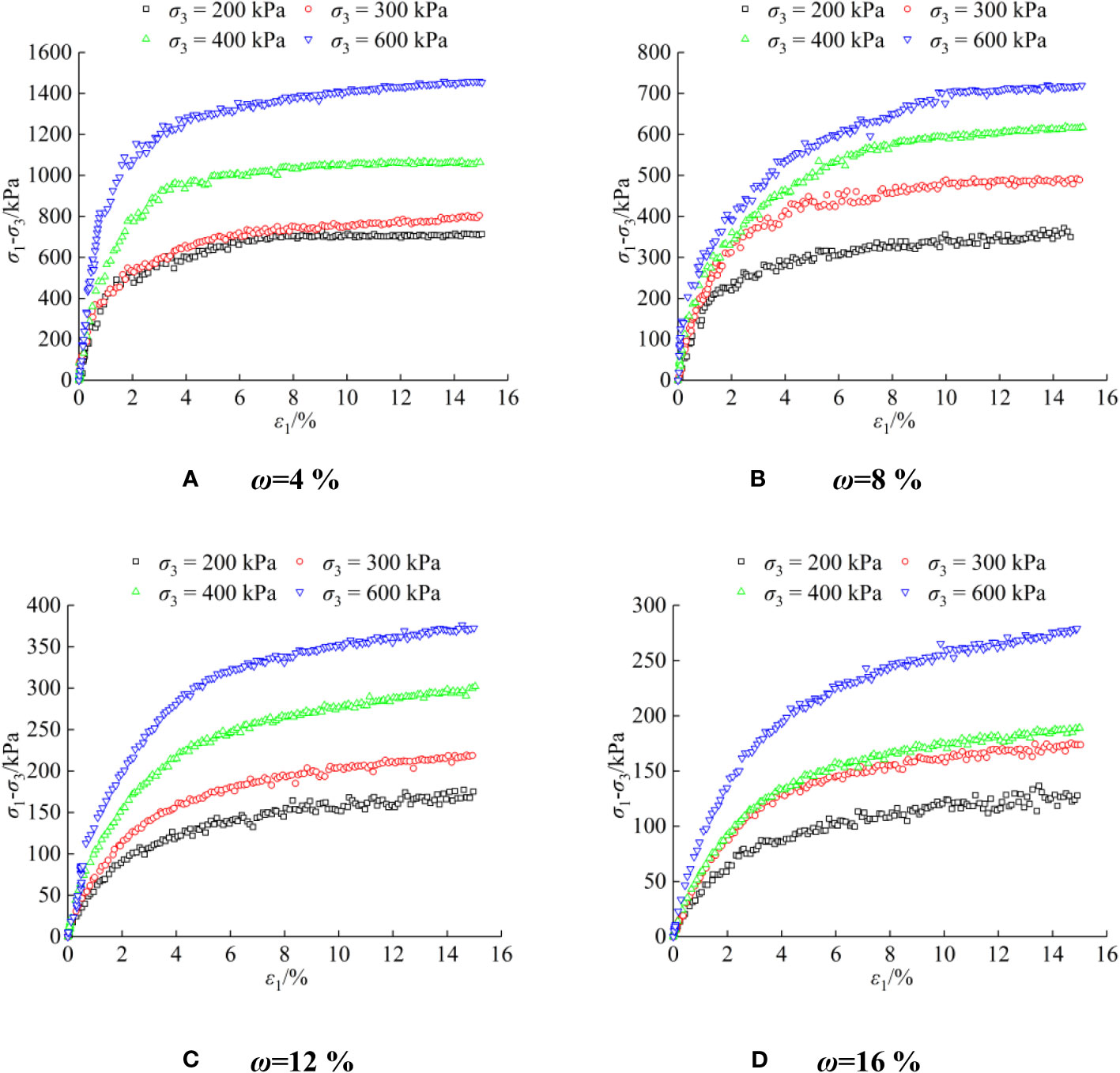
Figure 3 Stress-strain curves of S-RM samples with different water contents: (A) ω = 4%; (B) ω = 8%; (C) ω = 12%; (D) ω = 16%.

The stress-strain curves of S-RM samples with different confining pressures (200 kPa, 300 kPa, 400 kPa, and 600 kPa) under various water contents are illustrated in Figure 4, the results indicate that the linear elastic development stages of stress-strain curves are more significant with the decrease of water content. Figure 5 shows the failure modes of S-RM samples with different water contents when σ₃ is 200 kPa (the failure modes of samples under different confining pressures are similar), the results show that the S-RM sample is unlikely to maintain its original intact cylindrical shape and collapses into a mass with a water content of 4%, which shows an inclined plane shear failure mode, and the sample can maintain a complete shape and show slight bulging failure mode with surface cracks when the water content is between 8% and 16%, the higher the water content, the more significant the bulging and the more numerous and extensive the surface cracks. The bulging failure mode of the sample also reflects the high porosity and low density of S-RM.

FIGURE 4

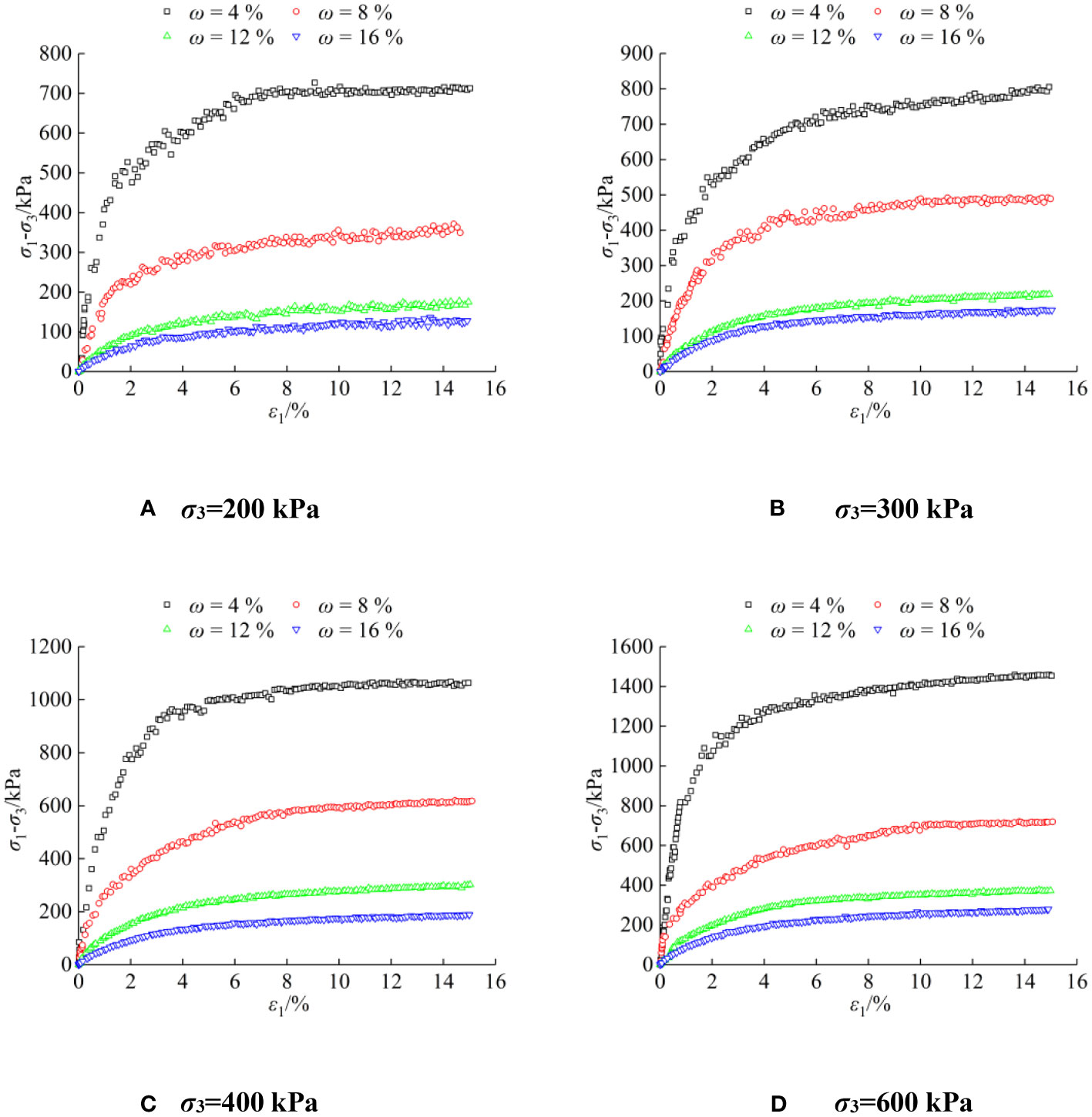
Figure 4 Stress-strain curves of S-RM samples with different confining pressures: (A) σ₃ = 200 kPa; (B) σ₃ = 300 kPa; (C) σ₃ = 400 kPa; (D) σ₃ = 600 kPa.

FIGURE 5

Figure 5 Failure modes of S-RM samples with different water contents (σ₃ = 200 kPa).

The stress-strain curve of S-RM is of the strain-hardening type, and the axial stress at the end-point of loading (axial stress corresponding to axial strain of 15%) is taken as the peak strength of S-RM. Figure 6 shows that the peak strength of S-RM increases in a quasi-linear manner with increasing confining pressure when the water content is constant, for example, when the confining pressure increases from 200 kPa to 600 kPa, and the peak strength of S-RM linearly increases from 912.91 kPa to 2053.53 kPa with a water content of 4%. Figure 7 illustrates that with the increase of water content of S-RM, the peak strength decreases in a non-linear manner, and the rate of change of peak strength decreases continuously, for example, when the water content of S-RM increases from 4% to 16%, and the peak strength decreases from 912.91 kPa to 327.82 kPa under a confining pressure of 200 kPa.

FIGURE 6

Figure 6 The relationship between peak strength and confining pressure.

FIGURE 7

Figure 7 The relationship between peak strength and water content.

Shear strength and deformation index

The Mohr’s circles of stress corresponding to the peak strengths of S-RM with different water contents are drawn, as shown in Figure 8. The results indicate that the peak strength of S-RM approximately meets the Mohr-Coulomb criterion within the test range of water content. The cohesion c and internal friction angle φ of S-RM with different water contents were obtained (Table 3). Figure 9 shows that c and φ of S-RM both decrease in a quasi-linear manner with the increase of water content.

FIGURE 8

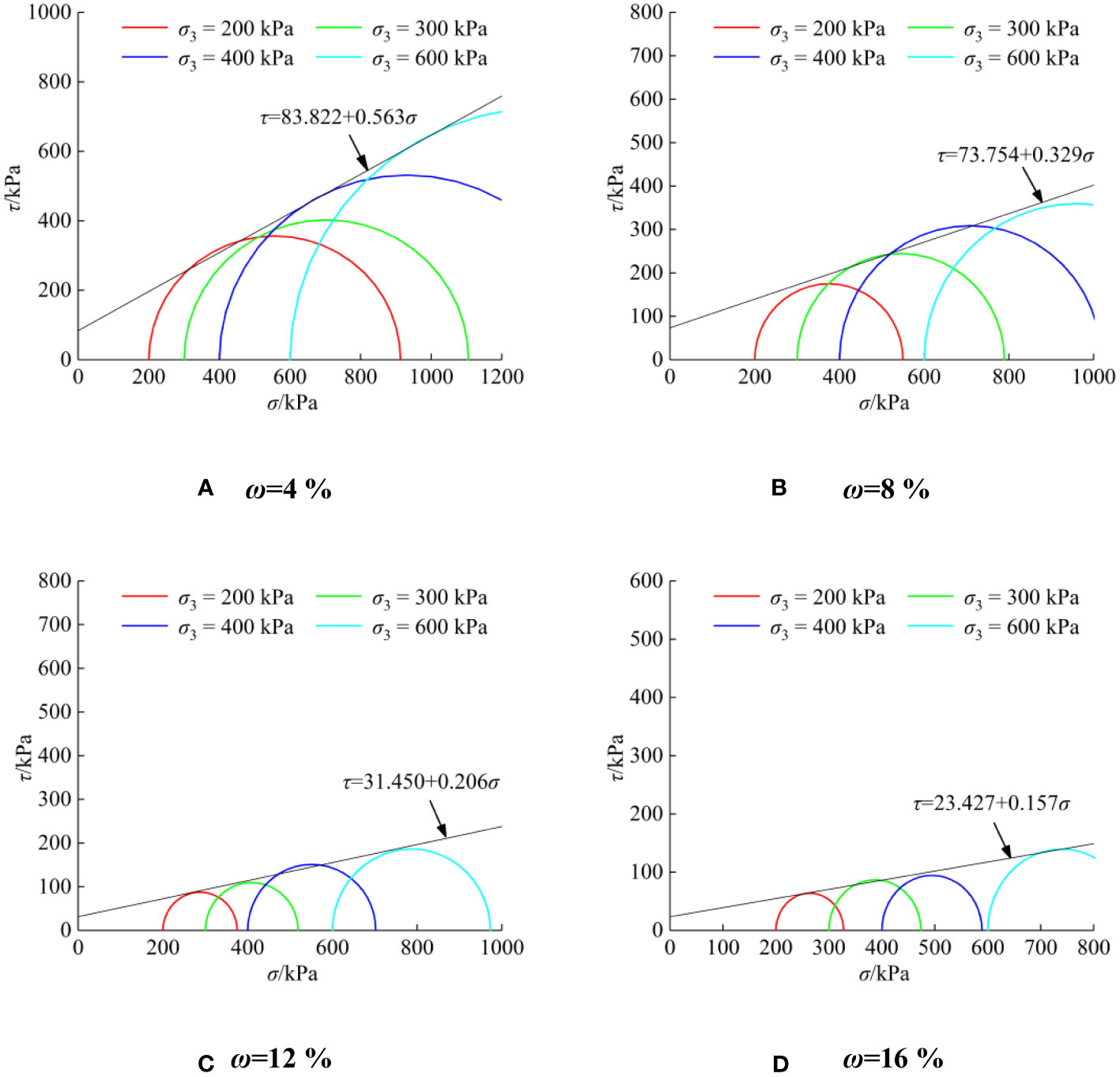
Figure 8 Mohr-Coulomb criterion strength envelope: (A) ω = 4%; (B) ω = 8%; (C) ω = 12%; (D) ω = 16%.

TABLE 3

Table 3 Shear strength indices of S-RM with different water contents.

FIGURE 9

Figure 9 Relationships between shear strength indices and water content.

According to the generalized form of Hooke’s law, the elastic modulus is constant and independent of confining pressure, however, the triaxial tests of geological materials show that the stress-strain curve is non-linear, and the tangent or secant slope is related to the physico-mechanical properties of geological materials. Therefore, the selection methods of tangent modulus, secant modulus and average modulus were developed for the deformation modulus of geological materials under triaxial compression (You, 2003). There is no significant linear elastic stage in the stress-strain curve of S-RM, the secant modulus is used as the deformation modulus for analysis herein, and the point where the deviatoric stress is 0 and the point of 50% of peak strength are taken as the starting and ending points respectively. The calculated results are summarized in Table 4.

TABLE 4

Table 4 Secant modulus of S-RM samples under different test conditions.

The relationship between secant modulus and confining pressure is shown in Figure 10. The results show that when the water content is low, secant modulus increases significantly with the increase of confining pressure, for example, when the confining pressure is increased from 200 kPa to 600 kPa, the secant modulus increases from 42.13 MPa to 105.91 MPa with a water content of 4%. When the water content is high (ω > 8%), the secant modulus increases slowly with the increase of confining pressure. The reasons for the change in secant modulus of S-RM affected by confining pressure can be ascertained: in the process of applying confining pressure, the pore gas in the sample is readily compressed, and the pore water is practically incompressible under unconsolidated and undrained conditions, therefore, when the water content is low, the higher the confining pressure, the greater the primary compaction of the pores, the smaller the secondary compaction of the pores during the application of deviatoric stress, and the greater the secant modulus at the macroscopic level; when the water content is high or in a saturated state, the pores are not readily compressed, the confining pressure exerts little influence on the secondary compaction of the pores caused by deviatoric stress, macroscopically, the confining pressure has little influence on the secant modulus.

FIGURE 10

Figure 10 The relationship between secant modulus and confining pressure.

The relationship between secant modulus and water content is shown in Figure 11. The results indicate that the secant modulus decreases significantly as the water content increases, for example, when the water content increases from 4% to 16%, the secant modulus decreased from 42.13 MPa to 2.97 MPa under a confining pressure of 200 kPa. The reason for this is explored: the lubrication of the pore water between the particles and the water film outside the particles causes slippage and adjustment of the position of particles. Macroscopically, the higher the water content, the more easily the S-RM sample is compressed, and the smaller the secant modulus.

FIGURE 11

Figure 11 The relationship between secant modulus and water content.

Extended DC model for S-RM

The stress-strain curves of S-RM with different water contents have significant strain hardening characteristics. The Duncan-Chang (DC) model is especially suitable for the description of the non-linear hardening type stress-strain relationship. The extended DC model was developed herein, the determination process of the model parameters and the relationship between model parameters and water content were discussed in detail.

Kondner (1963) proposed the hyperbolic function to describe the stress-strain relationship of soils obtained from triaxial tests:

$\begin{array}{ll}{\sigma }_1-{\sigma }_3=\frac{{\epsilon }_1}{a+b{\epsilon }_1}& (1)\end{array}$

where σ₁ represents maximum principal stress; σ₃ is minimum principal stress; ε₁ denotes maximum principal strain; a and b are model constants.

Duncan and Chang (1970) developed an incremental elasticity model based on Eq. (1):

$\begin{array}{ll}\frac{{\epsilon }_1}{{\sigma }_1-{\sigma }_3}=a+b{\epsilon }_1& (2)\end{array}$

In the triaxial test, the tangent modulus is expressed as:

$\begin{array}{ll}{E}_{\text{t}}=\frac{\text{d}\left({\sigma }_1-{\sigma }_3\right)}{\text{d}\left({\epsilon }_1\right)}=\frac{a}{{\left(a+b{\epsilon }_1\right)}^2}& (3)\end{array}$

where E_t is the tangent modulus of soil.

At the origin of coordinates (ε₁ = 0), the initial tangent modulus is expressed as

$\begin{array}{ll}{E}_{\text{i}}=\frac{1}{a}& (4)\end{array}$

The ultimate deviatoric stress of the fitted hyperbola is written as

$\begin{array}{ll}{\left({\sigma }_1-{\sigma }_3\right)}_{\text{ult}}=\frac{1}{b}& (5)\end{array}$

where (σ₁ − σ₃)_ult represents the ultimate deviatoric stress.

Much of the shows that the initial tangent modulus is related to the confining pressure, the form can be expressed thus (Janbu, 1963):

$\begin{array}{ll}{E}_{\text{i}}=K{P}_{\text{a}}{\left(\frac{{\sigma }_3}{P_{\text{a}}}\right)}^n& (6)\end{array}$

where K and n are material constants, reflecting material properties; P_a is the atmospheric pressure.

Since there is no peak strength in the stress-strain curve when using a hyperbolic function to represent it, generally, the stress corresponding to a certain strain value is taken as the strength of soil, and the failure ratio is defined as:

$\begin{array}{ll}{R}_{\text{f}}=\frac{{\left({\sigma }_1-{\sigma }_3\right)}_{\text{f}}}{{\left({\sigma }_1-{\sigma }_3\right)}_{\text{ult}}}& (7)\end{array}$

where R_f is the failure ratio; (σ₁-σ₃)_f represents the peak strength of soil.

According to the Mohr-Coulomb criterion, the strength of soil can be expressed as:

$\begin{array}{ll}{\left({\sigma }_1-{\sigma }_3\right)}_{\text{f}}=\frac{2c\cos \phi +2{\sigma }_3\sin \phi }{1-\sin \phi }& (8)\end{array}$

The tangent modulus of soil can be obtained from Eqs. (3)~(8):

$\begin{array}{ll}{E}_{\text{t}}=K{P}_{\text{a}}{\left(\frac{{\sigma }_3}{P_{\text{a}}}\right)}^n{[1-\frac{R_{\text{f}}\left({\sigma }_1-{\sigma }_3\right)\left(1-\sin \phi \right)}{2c\cos \phi +2{\sigma }_3\sin \phi }]}^2& (9)\end{array}$

The expression for the tangent modulus in the DC model includes five material constants: K, n, R_f, c, and φ.

In order to compare the mechanical properties of S-RM in unsaturated and saturated states, the experimental conditions were set as non-consolidated and undrained, resulting in only obtaining the axial stress-strain relationship. Consequently, the measurement of volumetric strain and lateral strain was not possible, thus preventing the determination of the Poisson’s ratio. This study only investigated the tangent modulus of the D-C model, providing a reference for determining the Poisson’s ratio. The determination process of material constants in the expression of the tangent modulus of the DC model is as follows.

a. The model constants a and b are determined. The test data of S-RM with different confining pressures under various water contents are processed according to Eq. (1), a and b are obtained by data fitting. The fitting hyperbolic curves of test data are shown in Figure 12, the stress-strain curves of S-RM under triaxial compression test with different water contents are in good agreement with the DC model.

b. The initial tangent modulus E_i is calculated using Eq. (4). The ultimate deviatoric stress (σ₁ − σ₃)_ult is determined using Eq. (5).

c. The peak strength (σ₁ − σ₃)_f is determined. There are three ways to determine (σ₁ − σ₃)_f, the first is to take the test value as (σ₁ − σ₃)_f (the deviatoric stress corresponding to 15% axial strain); the second is to take the value in the fitting hyperbolic curve; the third is to recalculate (σ₁ − σ₃)_f by Mohr-Coulomb criterion according to the shear strength indices c and φ determined by test. Because the model finally given is based on the fitted curve, the model curves determined using the second method is in better agreement with the experimental results.

d. The failure ratio R_f is determined. The ultimate deviatoric stress (σ₁ − σ₃)_ult under each confining pressure determined by step (b) and the peak strength (σ₁ − σ₃)_f under each confining pressure determined by step (c) are substituted into Eq. (7). The failure ratios under various confining pressures can be obtained, and the average value can be used as the failure ratio of S-RM with a certain water content.

e. The material constants K and n are determined. The relationship between lg(E_i/P_a) and lg(σ₃/P_a) is fitted by a straight line, the material constants K and n are then obtained.

FIGURE 12

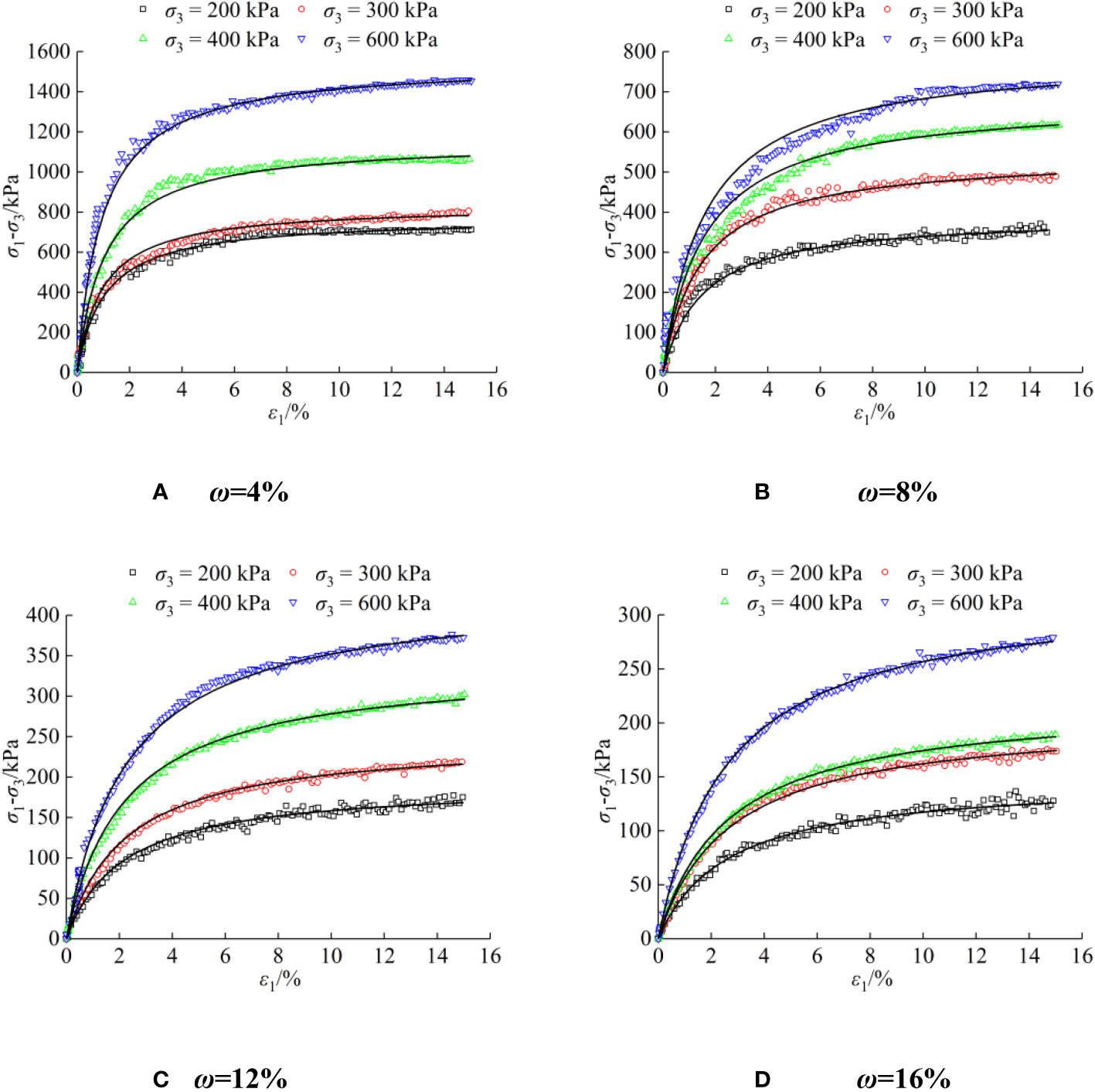
Figure 12 Fitting curves of the (σ₁ − σ₃) − ε₁ relationship: (A) ω = 4%; (B) ω = 8%; (C) ω = 12%; (D) ω = 16%.

The process parameters determined using steps (a)~(e) are listed in Table 5. Combined with the determined shear strength indices c and φ, all five material constants of S-RM with different water contents to obtain the tangent modulus are determined, as listed in Table 6.

TABLE 5

Table 5 Process parameters of the D-C model of S-RM.

TABLE 6

Table 6 Material constants of the D-C model of S-RM with different water contents.

The relationship between the material constants of S-RM and water content is illustrated in Figure 13. The results indicate that the failure ratio decreases approximately linearly with the increase of water content. As the water content increases from 4% to 16% and the failure ratio decreases from 0.9347 to 0.8509. The explanation may be that the higher the water content, the smaller the modulus of S-RM under the same confining pressure, and the stress develops more slowly with the increasing strain, the stress is far from reaching limiting value when the strain reaches 15%, so the smaller the failure ratio. The material constant K decreases with the increase of water content, which is approximately exponential. The correlation between material constant n and water content is not significant.

FIGURE 13

Figure 13 The relationship between material constants and ω: (A) R_f vs. ω; (B) K vs. ω.

The research results indicate that the material constants K and R_f of S-RM in the DC model are the same as the shear strength indices c and φ, which are all related to the water content. The functional relationships are shown in Eqs. (10) to (13). The material constant n is an independent material constant, which has no significant correlation with the water content.

$\begin{array}{ll}K=a_1·e^{b_1\times 100\omega }& (10)\end{array}$

$\begin{array}{ll}c=a_2\times 100\omega +b_2& (11)\end{array}$

$\begin{array}{ll}\phi =a_3\times 100\omega +b_3& (12)\end{array}$

$\begin{array}{ll}{R}_{\text{f}}=a_4\times 100\omega +b_4& (13)\end{array}$

The fitting coefficients of material constants determined according to the triaxial compression test of S-RM are listed in Table 7. The material constant n is taken as the average of the test results under different water contents. Finally, only n, ω, σ₁ and σ₃ are needed to determine the tangent modulus E_t of the DC model of S-RM.

TABLE 7

Table 7 Fitting coefficients of material constants of S-RM.

Conclusions

Large triaxial tests of S-RM with different water contents under various confining pressures were conducted in this study. The stress-strain relationship of S-RM under different conditions was analyzed. The variations in shear strength and deformation indices with water content were studied. The extended DC model of S-RM considering water content was established, the variation law of model parameters with water content was revealed. The main conclusions are drawn as follows:

a. Within the range of test water content and confining pressure, the stress-strain curves of S-RM are all of the strain-hardening type, indicating that the S-RM has porous characteristics similar to loose sand or normally consolidated soil. The failure mode of the sample reflects that the higher the water content, the more significant the bulging phenomenon and the more numerous and extensive the surface cracks. The peak strength of S-RM increases in a quasi-linear manner with the increase of confining pressure, and decreases non-linearly with the increase of water content.

b. The peak strength of S-RM approximately satisfies the Mohr Coulomb criterion within the range of water contents investigated in the present work, and the cohesion c and internal friction angle φ of this S-RM both decrease in a quasi-linear manner with the increase of water content. The secant modulus is used as the deformation index for analysis, the results show that the secant modulus increases with the increase of confining pressure, and decreases significantly with the increase of water content, the reason for this can be attributed to the porosity and compression characteristics of S-RM.

c. The DC model was introduced and its applicability to S-RM was studied, the extended DC model of S-RM considering water content was further established. The results indicate that the stress-strain curves of S-RM under triaxial compression test with different water contents are in good agreement with the DC model which can reflect the strain-hardening characteristics of S-RM. The functional relationships of model parameters with water content were determined as Eqs. (10) to (13), thus, only n, ω, σ₁ and σ₃ are needed to determine the tangent modulus E_t of the DC model of S-RM.

This study focuses on the macroscopic mechanical properties and the mechanical model of S-RM. The conclusions can be applied to engineering of S-RM. The microscopic mechanism of the influence of water condition on the mechanical behavior of S-RM will be further explored in future, and the essential reason of the influence of water condition on its macroscopic mechanical behavior will be revealed.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

YD: Investigation, Numerical simulation, Methodology, Writing original draft. XF: Numerical simulation, Methodology, Review and editing. QS: Numerical simulation, Review and editing. ZZ: Experiment, Review and editing. WD: Numerical simulation, Review and editing. HD: Experiment, Review and editing. TL: Experiment, Review and editing. All authors contributed to the article and approved the submitted version.

Funding

The work reported in this paper is financially supported by the Natural Science Foundation of Hubei Province, China (No. 2022CFB874), the National Natural Science Foundation of China (No. 52209131, No. 52179117), the Youth Innovation Promotion Association CAS (No. 2021325), the Scientific Research Project of Hubei Education Department (No. B2022282), Wuhan Knowledge innovation special project (No. 2023020201020444), and Open Research Fund of Hubei Key Laboratory of Blasting Engineering (No. HKLBEF202006).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Arikan F., Ulusay R., Aydin N. (2007). Characterization of weathered acidic volcanic rocks and a weathering classification based on a rating system. Bull. Eng. Geol. Environ. 66 (4), 415–430. doi: 10.1007/s10064-007-0087-0

CrossRef Full Text | Google Scholar

Buffington J. M., Dietrich W. E., Kirchner J. W. (1992). Friction angle measurements on a naturally formed gravel streambed - implications for critical boundary shear-stress. Water Resour. Res. 28 (2), 411–425. doi: 10.1029/91WR02529

CrossRef Full Text | Google Scholar

Casagli N., Ermini L., Rosati G. (2003). Determining grain size distribution of the material composing landslide dams in the Northern Apennines: sampling and processing methods. Eng. Geol. 69 (1-2), 83–97. doi: 10.1016/S0013-7952(02)00249-1

CrossRef Full Text | Google Scholar

Cen D., Huang D., Ren F. (2017). Shear deformation and strength of the interphase between the soil–rock mixture and the benched bedrock slope surface. Acta Geotech. 12, 391–413. doi: 10.1007/s11440-016-0468-2

CrossRef Full Text | Google Scholar

Donaghe R. T., Torrey V. H. (1979). Scalping and replacement effects on strength parameters of earth-rock mixtures. Proc. Conf. Design Parameters Geotech. Eng. 2, 29–34.

Google Scholar

Dong H., Peng B., Gao Q. F., Hu Y., Jiang X. Z. (2021). Study of hidden factors affecting the mechanical behavior of soil–rock mixtures based on abstraction idea. Acta Geotech. 16, 595–611. doi: 10.1007/s11440-020-01045-0

CrossRef Full Text | Google Scholar

Du Y. X., Sheng Q., Fu X. D., Tang H., Zhang Z. P., Zhao X. (2019). Risk evaluation of colluvial cutting slope based on fuzzy analytic hierarchy process and multilevel fuzzy comprehensive evaluation. J. Intell. Fuzzy Syst. 37 (3), 4253–4271. doi: 10.3233/JIFS-190367

CrossRef Full Text | Google Scholar

Duncan J. M., Chang C. Y. (1970). Nonlinear analysis of stress and strain in soils. J. Soil Mech. Found Div. 96 (5), 1629–1653. doi: 10.1061/JSFEAQ.0001458

CrossRef Full Text | Google Scholar

Fan H. T., Sun S. R., Wei J. H., Le H. L., Zhu F., Wang W. C., et al. (2021). Shear behavior of soil-rock mixture composed of diorite-porphyrite considering weathering sequence. Int. J. Geomech. 21 (7), 04021122. doi: 10.1061/(ASCE)GM.1943-5622.0002100

CrossRef Full Text | Google Scholar

Fu X. D., Sheng Q., Du W. J., Mei H. R., Chen H., Du Y. X. (2020). Evaluation of dynamic stability and analysis of reinforcement measures of a landslide under seismic action: a case study on the Yanyangcun landslide. Bull. Eng. Geol. Environ. 79 (6), 2847–2862. doi: 10.1007/s10064-020-01745-7

CrossRef Full Text | Google Scholar

Gao W. W., Gao W., Hu R. L., Xu P. F., Xia J. G. (2018). Microtremor survey and stability analysis of a soil-rock mixture landslide: a case study in Baidian town, China. Landslides 15 (10), 1951–1961. doi: 10.1007/s10346-018-1009-x

CrossRef Full Text | Google Scholar

Gao W., Iqbal J., Hu R. L. (2021). Investigation of geomechanical characterization and size effect of soil-rock mixture: a case study. Bull. Eng. Geol. Environ. 80 (8), 6263–6274. doi: 10.1007/s10064-021-02289-0

CrossRef Full Text | Google Scholar

Hamidi A., Alizadeh M., Soleimani S. M. (2009). Effect of particle crushing on shear strength and dilation characteristics of sand-gravel mixtures. Int. J. Civ. Eng. 7 (1), 61–71.

Google Scholar

He Z. L., Zhang J. Y., Sun T. (2020). Influence of maximum particle diameter on the mechanical behavior of soil-rock mixtures. Adv. Civ. Eng. 2020 (3), 1–9. doi: 10.1155/2020/8850221

CrossRef Full Text | Google Scholar

Hiruma S. T., Modenesi-Gauttieri M. C., Riccomini C. (2013). Late Quaternary colluvial deposits in the Bocaina Plateau, southeastern Brazil highlands: age and palaeoenvironmental consequences. Boreas 42 (2), 306–316. doi: 10.1111/j.1502-3885.2012.00272.x

CrossRef Full Text | Google Scholar

Janbu N. (1963). Soil compressibility as determined by oedometer and triaxial tests. Proc. Eur. Conf. SMFE Wiesbaden. 1, 19–25.

Google Scholar

Kondner R. L. (1963). Hyperbolic stress-strain response: cohesive soils. J. Soil Mech. Found Div. 89 (1), 115–143. doi: 10.1061/JSFEAQ.0000479

CrossRef Full Text | Google Scholar

Leigh D. S., Gragson T. L., Coughlan M. R. (2016). Colluvial legacies of millennial landscape change on individual hillsides, place-based investigation in the western Pyrenees Mountains. Quatern. Int. 402, 61–71. doi: 10.1016/j.quaint.2015.08.031

CrossRef Full Text | Google Scholar

Li Z. Q., Hu F., Qi S. W., Hu R. L. (2020). Strain-softening failure mode after the post-peak as a unique mechanism of ruptures in a frozen soil-rock mixture. Eng. Geol. 274, 105725. doi: 10.1016/j.enggeo.2020.105725

CrossRef Full Text | Google Scholar

Pan Y., Wu G., Zhao Z. M., He L. (2020). Analysis of rock slope stability under rainfall conditions considering the water-induced weakening of rock. Comput. Geotech. 128, 103806. doi: 10.1016/j.compgeo.2020.103806

CrossRef Full Text | Google Scholar

Senthilkumar V., Chandrasekaran S. S., Maji V. B. (2018). Rainfall-induced landslides: case study of the Marappalam Landslide, Nilgiris District, Tamil Nadu, India. Int. J. Geomech. 18 (9), 05018006. doi: 10.1061/(ASCE)GM.1943-5622.0001218

CrossRef Full Text | Google Scholar

Song D. Q., Chen Z., Dong L. H. (2020). Monitoring analysis of influence of extra-large complex deep foundation pit on adjacent environment: A case study of Zhengzhou City, China. Geomat. Nat. Haz. Risk 11 (1), 2036–2057. doi: 10.1080/19475705.2020.1823492

CrossRef Full Text | Google Scholar

Vallejo L. E., Mawby R. (2000). Porosity influence on the shear strength of granular material-clay mixtures. Eng. Geol. 58 (2), 125–136. doi: 10.1016/S0013-7952(00)00051-X

CrossRef Full Text | Google Scholar

Viles H. A. (2013). Linking weathering and rock slope instability: non-linear perspectives. Earth Surf. Proc. Land 38 (1), 62–70. doi: 10.1002/esp.3294

CrossRef Full Text | Google Scholar

Wang Y., Li C. H., Hu Y. Z. (2018). X-ray computed tomography (CT) observations of crack damage evolution in soil-rock mixture during uniaxial deformation. Arab. J. Geosci. 11 (9), 1–13. doi: 10.1007/s12517-018-3561-z

CrossRef Full Text | Google Scholar

Wang Y. H., Li J. L., Jiang Q., Huang Y. S., Li X. Z. (2019). Study on spatial variation of shear mechanical properties of soil-rock mixture. Period Polytech-Civ 63 (4), 1080–1091. doi: 10.3311/PPci.14769

CrossRef Full Text | Google Scholar

Wei H. Z., Xu W. J., Wei C. F., Meng Q. S. (2018). Influence of water content and shear rate on the mechanical behavior of soil-rock mixtures. Sci. China Technol. Sc. 61 (8), 1127–1136. doi: 10.1007/s11431-017-9277-5

CrossRef Full Text | Google Scholar

Wickland B. E., Wilson G. W., Wijewickreme D., Klein B. (2006). Design and evaluation of mixtures of mine waste rock and tailings. Can. Geotech. J. 43 (9), 928–945. doi: 10.1139/t06-058

CrossRef Full Text | Google Scholar

Xiang G. S., Song D. Q. (2020). Experimental study on the strength behaviors of municipal solid waste incineration bottom ash using ultrasonic wave velocity tests. Geomat. Nat. Haz. Risk 11 (1), 1581–1598. doi: 10.1080/19475705.2020.1805516

CrossRef Full Text | Google Scholar

Xing H. F., Liu L. L., Luo Y. (2019). Water-induced changes in mechanical parameters of soil-rock mixture and their effect on talus slope stability. Geomech. Eng. 18 (4), 353–362. doi: 10.12989/gae.2019.18.4.353

CrossRef Full Text | Google Scholar

Xu W. J., Hu L. M., Gao W. (2016). Random generation of the meso-structure of a soil-rock mixture and its application in the study of the mechanical behavior in a landslide dam. Int. J. Rock Mech. Min. 86, 166–178. doi: 10.1016/j.ijrmms.2016.04.007

CrossRef Full Text | Google Scholar

Xu W. J., Hu R. L., Tan R. J. (2007). Some geomechanical properties of soil-rock mixtures in the Hutiao Gorge area, China. Geotechnique 57 (3), 255–264. doi: 10.1680/geot.2007.57.3.255

CrossRef Full Text | Google Scholar

Xu W. J., Li C. Q., Zhang H. Y. (2015). DEM analyses of the mechanical behavior of soil and soil-rock mixture via the 3D direct shear test. Geomech. Eng. 9 (6), 815–827. doi: 10.12989/gae.2015.9.6.815

CrossRef Full Text | Google Scholar

Xu W. J., Zhang H. Y. (2022). Meso and macroscale mechanical behaviors of soil–rock mixtures. Acta Geotech. 17, 3765–3782. doi: 10.1007/s11440-022-01449-0

CrossRef Full Text | Google Scholar

You M. Q. (2003). Effect of confining pressure on the Young’s modulus of rock specimen and the friction in fissures. Rock Soil Mech. 24 (Sup 1), 167–170. (In Chinese).

Google Scholar

Zhang Z. P., Fu X. D., Sheng Q., Du Y. X., Zhou Y. Q., Huang J. H. (2021). Stability of cracking deposit slope considering parameter deterioration subjected to rainfall. Int. J. Geomech. 21 (7), 05021001. doi: 10.1061/(ASCE)GM.1943-5622.0002045

CrossRef Full Text | Google Scholar

Zhang S., Tang H. M., Zhan H. B., Lei G. P., Cheng H. (2015). Investigation of scale effect of numerical unconfined compression strengths of virtual colluvial-deluvial soil-rock mixture. Int. J. Rock Mech. Min. 77, 208–219. doi: 10.1016/j.ijrmms.2015.04.012

CrossRef Full Text | Google Scholar

Zhang Z. L., Xu W. J., Xia W., Zhang H. Y. (2016). Large-scale in-situ test for mechanical characterization of soil-rock mixture used in an embankment dam. Int. J. Rock Mech. Min. 86, 317–322. doi: 10.1016/j.ijrmms.2015.04.001

CrossRef Full Text | Google Scholar

Zhang H. Y., Xu W. J., Yu Y. Z. (2016). Triaxial tests of soil-rock mixtures with different rock block distributions. Soils Found 56 (1), 44–56. doi: 10.1016/j.sandf.2016.01.004

CrossRef Full Text | Google Scholar

Zhao Y., Fang J. N., Fan C. B., Liu P. H., Huang Z. Q. (2019). Particle crushing and its influence on a compacted cataclasite under different water content conditions. Environ. Earth Sci. 78 (14), 1–9. doi: 10.1007/s12665-019-8403-0

CrossRef Full Text | Google Scholar

Zhao Y. X., Liu Z. X. (2019). Numerical experiments on triaxial compression strength of soil-rock mixture. Adv. Civ. Eng. 2019 (PT.2), 1–15. doi: 10.1155/2019/8763569

CrossRef Full Text | Google Scholar