Sustained beneficial infections: priority effects, competition, and specialization drive patterns of association in intracellular mutualisms

Intracellular symbioses provide a useful system for exploring evolutionary and ecological forces that shape mutualistic partnerships. Within- and among-host competitiveness driven by different strategies that symbionts adopt as they transfer materials to the host across a sub-cellular membrane might explain patterns of host:symbiont association observed in natural systems. We tested the hypothesis that different translocation strategies employed by symbionts affect their ability to occupy host habitats using two distinct modeling approaches. The first involved constructing a deterministic, Lotka-Volterra-type model with two symbiont species competing for access to a single host. The model recovered expected behaviors of co-occupancy/coinfection as well as competitive exclusion. However, a specialization coefficient allowed advantages to accrue to one of the symbionts and permitted otherwise inferior competitors to displace superior competitors. The second approach involved developing and implementing a detailed, highly configurable, and realstic agent-based model (ABM), facilitating experimentation of multiple symbiont strategies in competition simultaneously. The ABM emphasizes bidirectional movement of materials between symbiont and host (e.g., photosynthate from algae to heterotrophic host). Competitive interactions between symbionts based on simple strategies led to exclusion of the inferior symbiont or co-occupancy of the host. As in the first model, inferior competitors could overtake superior competitors when “affinity” terms (i.e., specialization) were included in the model. Both models lay bare the importance of coevolutionary specialization as a selectively advantageous strategy, and they offer a new conceptual framework for interpreting the dynamic patterns observed in extant host and mutualist associations by challenging the idea of “host control” of outcomes, and identifying specific points where coevolutionary specialization might accrue.

1 Introduction

Coevolutionary specialization between species has long been a source of fascination. Intricate co-adaptation between partners is the product of ecological interactions generating reciprocal selective pressures (e.g., mycorrhizal symbiosis, bacteria in light organs of Euprymna squid; Kiers et al., 2011; McFall-Ngai, 2014; Nawroth et al., 2017). Charismatic examples of coevolution often involve intimately coadapted partners (e.g., Darwin’s hawkmoth:Star-of-Bethlehem orchid; Acacia:ant), but these represent later-stage outcomes of iterative interactions extrapolated over many generations. The earliest stages of coevolutionary partnerships were unlikely to have adaptations specific to the partnership, and interactions between species likely varied in terms of the degree of reciprocity and specialization (Kaltenpoth et al., 2014; Nelson and May, 2017).

Connor (1995) posited conditions that favored the evolution of mutualisms from initially amutualistic interactions at the earliest stages of partnerships. Connor’s framework offers an opportunity to explore evolutionary and ecological forces that shape nascent partnerships without assuming any a priori specialization or reciprocity between partners. He defined three mechanisms by which partners might acquire benefit from each other (by-product benefits, purloined benefits, and investment), and then characterized basal mutualisms according to strategies adopted by both partners. Connor’s (1995) “Basal-2” mutualism (purloined, by-product) likely applies to intracellular symbioses. Potential symbionts may purloin space within host cells through direct capture employing nothing more than the typical heterotrophic host cell’s phagocytotic processes (see Figure 1). A potential by-product benefit to host cells is represented by the materials that are transferred (i.e., translocated) from symbiont to host and host to symbiont across sub-cellular membranes (e.g., the symbiosome, parasitophorous vacuole) by the proto-symbiotic organism once inside the cell.

Figure 1

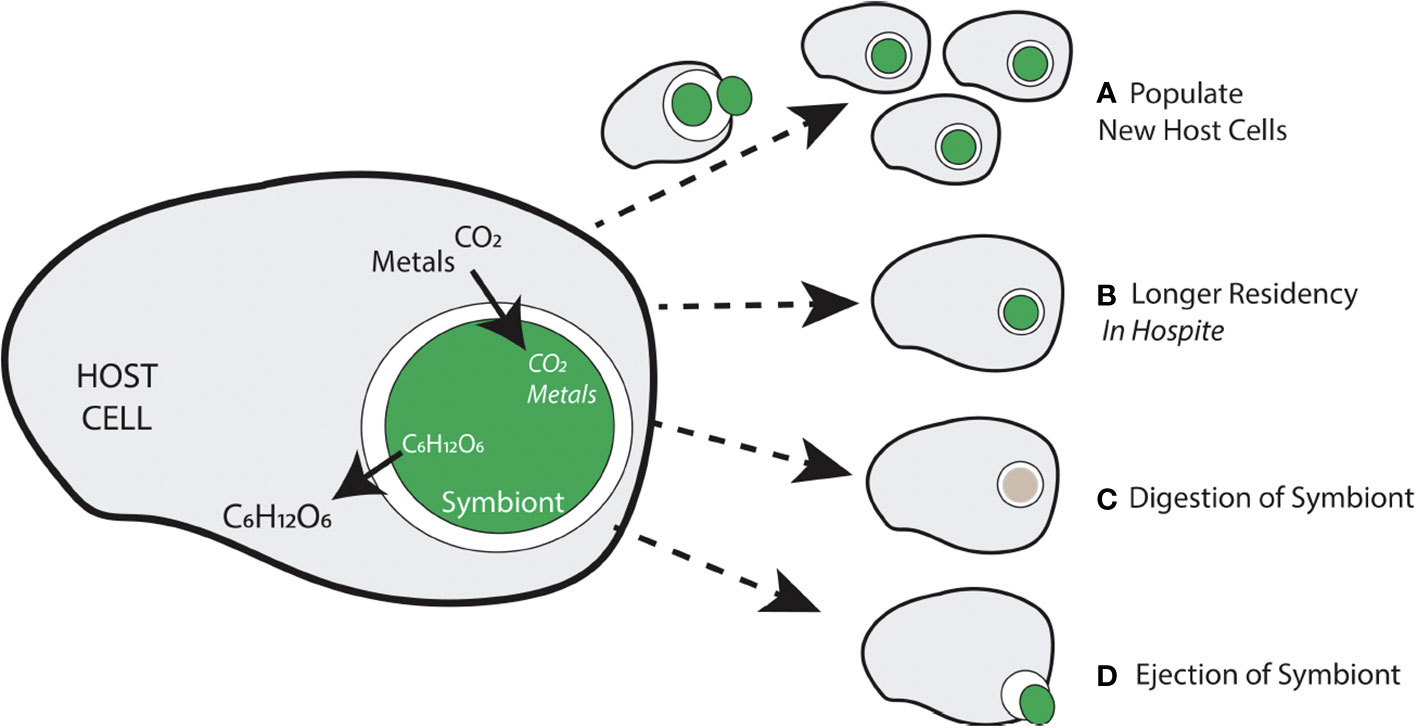
Figure 1 Generalized overview of the nature of the relationship (in terms of materials exchanged) between an intracellular symbiont and the host in which it resides, and some potential outcomes of the relationship. (A) If a symbiont is able to reproduce, a newly derived symbiont cell must be able to populate new host cells. (B) Symbionts can procure longer residency depending on how bidirectional movement of materials matches host and symbiont needs. (C) If a symbiont cannot meet host cell demands or some other dysregulation of the symbiosis occurs, digestion of the symbiont by the host cell may occur. (D) Another potential scenario occurs when a symbiont leaves the intracellular space by its own accord or through host-generated exocytosis.

A common feature of intracellular symbiotic interactions is the bidirectional movement of materials between partners, and these may be an important target of natural selection. Dinoflagellate symbionts translocate significant percentages of photosynthetically fixed carbon to coral hosts and appear to gain essential nutrients from the host (Davy et al., 2012; Hill and Hill, 2012). In freshwater systems, green algae (e.g., Chlorella) are often found in cells of the protozoan Paramecium and cnidarian Hydra, and in both cases bidirectional transfer of nutrients and materials occurs (Kodama and Fujishima, 2010; Kovacevic, 2012; Hamada et al., 2018). Even for protozoan parasites (e.g., those causing malaria, leishmaniasis, and toxoplasmosis), intracellular survival and virulence requires subversion of host cell detection and transport of materials across the vacuolar membrane (e.g., nutrient import, purine auxotrophy, waste efflux, effector protein export, and uptake of host cell cytosol; Beck and Ho, 2021; Piro et al., 2021). Bidirectional transfer of material also occurs in arbuscular mycorrhizal fungi (AMF) that are not intracellular per se. The arbuscules form between the cell wall and cell membrane, and are sites of transfer of micro- and macro-nutrients to their plant hosts (Chen et al., 2017; Mitra et al., 2019) and organic carbon in the form of lipids and sugars from the plant to the AMF (Jiang et al., 2017; Luginbuehl et al., 2017). Extracellular lichen associations rely on carbohydrate transfer from the photosynthesizer to the fungus, and Azolla:cyanobacteria partnerships involve carbohydrate transfer from host to symbiont and ammonium transfer from cyanobacteria to plant partner (Roy et al., 2020). Transfer of materials from symbiont to host (and vice versa) represents a common strategy that might permit extended encounters with a potential partner leading to mutualism.

If multiple symbionts can occupy a single host, within-host competitive ability may be a function of different material transfer strategies, and different strategies may place constraints on energy budgets available for cellular division/growth with significant consequences for the evolutionary potential of these symbioses (Hill and Hill, 2012; Hill, 2014). Natural selection would favor symbiont strategies that optimally balance needs of material transfer and population growth (Figure 1). Many symbiotic associations are facultative given that hosts and symbionts require that a portion of their life cycle be completed in the absence of the other partner. For example, >70% of corals must be reinfected by their phototrophic symbionts at the larval stage each generation (Hartmann et al., 2017).

Furthermore, the degree of specialization of a symbiont for its host (and vice versa) is highly variable with evidence of specificity and promiscuity in different symbiotic systems (e.g., Goulet, 2006; Baker and Romanski, 2007; Ulstrup et al., 2007; Hill et al., 2011; Fujishima and Kodama, 2012; McGinley et al., 2012; Silverstein et al., 2012; Thornhill et al., 2013; Thornhill et al., 2014; Kodama and Fujishima, 2016; Bongrand and Ruby, 2019). The range of promiscuous relationships are varied and can involve coinfection of one host by several symbiont species (Griffiths et al., 2014; Brener-Raffalli et al., 2018). Thus, competition among symbionts within a host is bound to be an important feature of many of these types of partnerships. Symbionts that transfer at higher rates might be at a disadvantage (e.g., through slower infection of host cells) when competing against symbionts who devote more energy towards population growth (e.g., mitosis). Symbionts that release materials at lower rates may face greater rates of detection, digestion, or ejection because they do not meet host cell demand. Host partners might release materials to the symbiont that facilitate one partner’s successful residency over others. Archetti et al. (2011) offer a game theoretic perspective on similar questions about the evolution of cooperation and mutualism incorporating the microeconomic concept of screening. The parallels between models like theirs and the two models presented here are compelling. How might competitive interactions between symbionts in the absence of any host:symbiont specialization (i.e., a naïve host and stealth symbiont) explain patterns of host occupancy (e.g., coinfection/co-occupancy, promiscuity, single-species specialization)? How much does host:symbiont specialization influence the outcome of interspecific competition between symbionts?

2 Deterministic model

We build upon previous work that emphasized the importance of ecological interactions as factors influencing the evolution of stable symbiotic partnerships (e.g., Rahat, 1985; Huss et al., 1993; Frank, 1996; Ware et al., 1996; Zhang, 2003). As a first step towards developing a more sophisticated model (see the ABM section below) for single-host, multiple-symbiont systems, we formulate a simple deterministic model (DM) by adapting and generalizing the classical work of Lotka and Volterra. The DM is a useful stepping stone in several respects. First, it enables the use of routine mathematical analysis to explore how varying a parameter might elicit dramatic changes in the eventual balance of power within an ecosystem. Second, given that the DM and ABM are fundamentally different types of models, any commonalities in their predictions are especially noteworthy. Finally, the simulations and limitations of the DM inform the development of the ABM, by highlighting the need for more detailed descriptions of energy transfer and the tradeoffs between translocation and mitosis.

2.1 Description of the model

Here, we present a brief overview of the DM; for a careful development, please refer to the Supplementary Material. Suppose that two different algal symbionts compete for access to cells within the host environment. Let u₁(t), u₂(t), and u₃(t) denote scaled population densities of the first symbiont, second symbiont, and host cells (respectively) at time t. The DM is presented as a system of three ordinary differential equations containing a total of eight non-negative parameters:

$\begin{array}{ll}\begin{array}{ll}\frac{d{u}_1}{dt}\hfill & ={\rho }_1{u}_1[1-u_1-{\alpha }_{12}{u}_2+{\alpha }_{13}{u}_3]\hfill \\ \frac{d{u}_2}{dt}\hfill & ={\rho }_2{u}_2[1-u_2-{\alpha }_{21}{u}_1+{\alpha }_{23}{u}_3]\hfill \\ \frac{d{u}_3}{dt}\hfill & =u_3[1-u_3+{\alpha }_{31}{u}_1+{\alpha }_{32}{u}_2].\hfill \end{array}& (1)\end{array}$

The model presumes that the populations are spatially well-mixed and that each species, in the absence of the other two, obeys a logistic growth model (Murray, 2002).

The interpretations of the parameters are as follows: ρ₁ and ρ₂ are scaled reproduction rate constants for the two algal symbionts; α₁₂ and α₂₁ indicate the extent to which symbionts are adversely affected by interspecific competition with one another; α₁₃ and α₂₃ indicate the extent to which the first and second symbionts (respectively) benefit from interactions with the host; and α₃₁ and α₃₂ indicate the extent to which the host benefits from interactions with the first and second symbionts, respectively. Boucher (1988) discusses several of the evolutionary challenges presented by mutualism where “public goods” mediated by the host influence the terms of cooperation and altruism.

2.2 Results of the DM

The coefficients of host-symbiont interaction terms (i.e., the parameters α₁₃, α₂₃, α₃₁ and α₃₂) profoundly influence the eventual steady-state populations. We illustrate some of the most interesting possibilities via two examples, one concerning the effects of a host on the symbionts, and the other concerning the effects of the symbionts on the host.

2.3 Effects of a host on competing symbionts

The capacities of the first and second symbionts to derive benefit from the host (the parameters α₁₃ and α₂₃, respectively) significantly affect long-term dynamical behavior. The model predicts that if symbiont 1 is competitively inferior to symbiont 2 in the sense that α₁₂ > α₂₁ but enjoys a more favorable relationship with the host, then symbiont 1 may be able to exclude the competitively superior symbiont 2. Figure 2 illustrates the effects of varying the parameter α₁₃ while holding the other seven parameters fixed, using parameter Set 1 in Table 1.

Figure 2

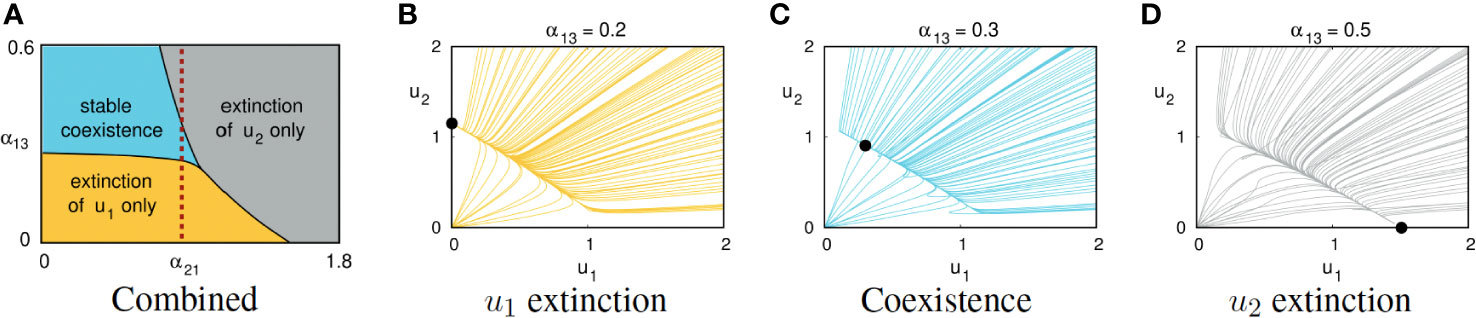
Figure 2 (A) Combined effects of the host:symbiont interaction coefficient α₁₃ and the interspecific competition coefficient α₂₁ on the generic long-term behavior of solutions of (1). The other six parameters are fixed, using values from Set 1 of Table 1. The dashed vertical reference line at α₂₁ = 0.8 crosses three regions, each corresponding to behaviors illustrated in the other three panels. Panels (B–D) show projections of solution trajectories of Equations (1) onto the u₁, u₂-plane, using parameter Set 1 from Table 1. Bold dots indicate long-term equilibrium behavior. (B) If α₁₃ = 0.2, symbiont u₁ is eliminated and symbiont u₂ survives. (C) If α₁₃ = 0.3, the two symbionts exhibit stable coexistence with the host. (D) If α₁₃ = 0.5, symbiont u₂ is eliminated and symbiont u₁ survives.

Table 1

Table 1 Two sample parameter sets for the DM.

Routine mathematical analysis (see Supplementary Material) allows one to characterize parameter regimes for which the DM predicts eventual (i) extinction of only the first symbiont, (ii) extinction of only the second symbiont, or (iii) three-way coexistence. For instance, using parameter Set 1 from Table 1, coexistence occurs only if 0.264 < α₁₃ < 0.434 (see Figure 2). Figure 2A shows regions of the α₁₃, α₂₁ parameter space associated with each of these three outcomes, presuming that the other six parameters are fixed using the values from Set 1 in Table 1.

Figures 2B–D illustrate the effect of gradually increasing α₁₃ while holding the other parameters fixed, using Set 1 from Table 1. For suitably small α₁₃, the second symbiont’s competitive advantage drives the first symbiont to extinction regardless of their initial populations; see Figure 2B. As α₁₃ is increased, the equilibrium corresponding to extinction of the first symbiont loses stability while an equilibrium corresponding to stable coexistence of all three species emerges; see Figure 2C. Further increasing α₁₃ causes another threshold phenomenon: the three-way coexistence equilibrium loses stability and the generic outcome is extinction of the second symbiont; see Figure 2D. Even though the second symbiont was competitively superior, the first symbiont is able to exclude the second because of the strong benefits conferred by the host: α₁₃/α₂₃ is significantly larger than 1.

2.4 Effects of competing symbionts on the host

The benefits that the host extracts from each symbiont (indicated by the parameters α₃₁ and α₃₂) also play a role in dictating outcomes. Consider, for example, Equations (1) with parameter Set 2 appearing in Table 1. If both α₃₁ and α₃₂ are small, one may show (see Example 3 and Figure S2 in the Supplementary Material) that the generic outcome is competitive exclusion of the first symbiont. Phrased mathematically, there is a stable equilibrium of the form (0,u₂,u₃) where u₂ and u₃ are positive. If α₃₂ is small and held fixed, then the equilibrium corresponding to exclusion of u₁ remains stable if α₃₁ is increased. By contrast, if α₃₁ is small and held fixed while α₃₂ is gradually increased, three-way coexistence emerges as the generic outcome once α₃₂ exceeds some threshold (right panel of Figure S2 in the Supplementary Material).

It may seem counterintuitive that increasing α₃₂, an indicator of how much benefit the host derives from interactions with the second symbiont, could save the competitively inferior first symbiont. However, inspection of the DM equations (1) offers some insight. Near the equilibrium for which only u₁ is zero, the variables u₁ and u₂ are of different orders of magnitude. Increasing α₃₁ has a small effect on the α₃₁u₁ term in the du₃/dt equation, but increasing α₃₂ has a much larger effect on the α₃₂u₂ term, and may elevate the steady-state host population. While boosting the host population density u₃ may seem to help both symbionts, for parameter Set 2 in Table 1 note that u₁ receives more of a benefit because α₁₃ is twice as large as α₂₃. Importantly, if α₁₃ is appropriately large, then symbiont u₁ may be saved from extinction.

3 Agent-based model

To complement the DM, we also built an agent-based model (ABM) (Macal and North, 2010) to simulate interactions among different types of symbionts competing for access to cells within a host. Our ABM emphasized energetic aspects of the association including assumptions about the translocation of photosynthate (Tremblay et al., 2014), energetic demands of host cells, and the energetic costs of symbiont cellular division. The structure of our model is based heavily on the work of Lawson et al. (2015), but substantially expanded and refined for the current context to include (a) biologically relevant probabilistic models to drive various stochastic components in the model, (b) a capacity to generate phenotypic mutation so that we could select emergent competitive strategies for our competition experiments, and (c) affinity terms to allow parameterization of symbiont-to-host specialization, which parallels the mutualism coefficients (α₁₃,α₂₃,α₃₁,α₃₂) in the DM.

3.1 Modeling the life cycle of the symbiosis

In our ABM, the host is modeled using an M × N grid of square cells, wrapping from left to right but not top to bottom, representing a slice of host cells located in proximity to passing water where symbiont infection/capture occurs (see Figures 3A, B). For the current work, only a single symbiont can occupy a host cell at any point in time. We follow the fate of algal cells from phagocytosis through the entire process of engagement with a host (see Figure 3C, and compare to Figure 1). We frame the model in terms of trade-offs between translocation and mitosis. Our symbioses are governed by the material exchanges that occur between partners once the symbiosis is established and intracellular residency has begun. In the model, symbionts produce and accumulate photosynthate that can be used for mitosis or energetic exchange with the host. In the event that a symbiont cannot produce sufficient photosynthate to meet the demands of mitosis and/or host cell requirements, the symbiont either escapes the host cell or is digested. Parameter descriptions and initial values for the model are shown in Table 2.

Figure 3

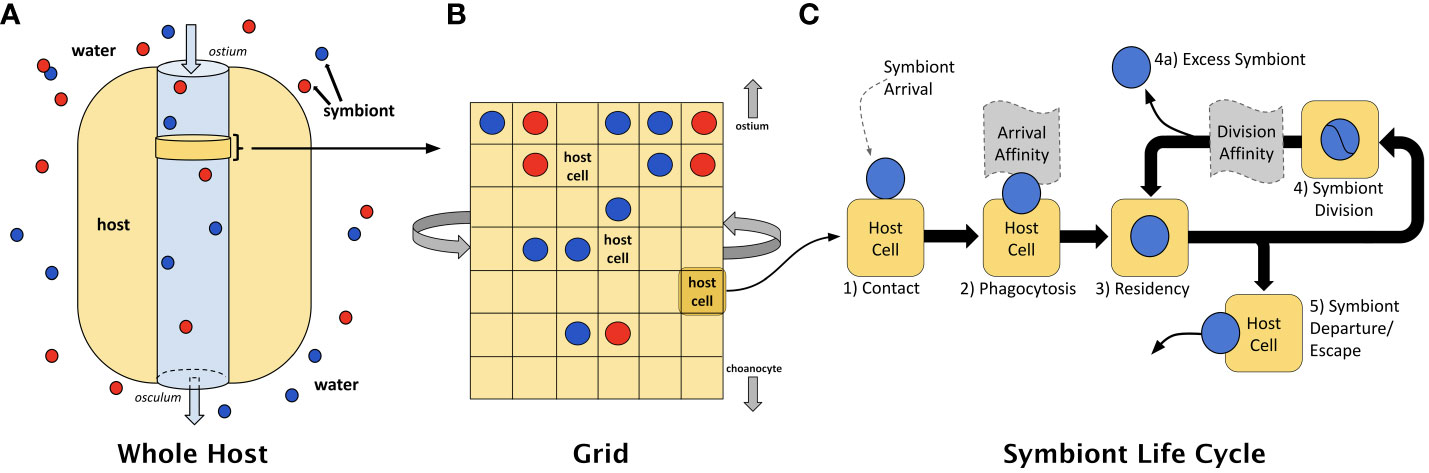
Figure 3 (A) The ABM models a slice of host cells located in proximity to passing water where symbiont infection/capture occurs. (B) This slice is represented as a 2-D grid of host cells, each of which may contain a single symbiont. (C) A dynamic interaction occurs between symbiont and host cell whereby materials are exchanged in a manner that permits long-term residency by symbionts within the host. Within any one of those host cells, the life cycle of an intracellular symbiont is modeled using key events that may be subject to natural selection: (1) contact, (2) phagocytosis, (3) intracellular residency, (4) symbiont mitosis, (4a) loss of symbiont from host, and (5) departure from the host; modified from Lawson et al., 2015. The ABM considers two portions of the symbiont life cycle where affinity might emerge — at the point of contact and phagocytosis (i.e., arrival affinity) and during residency within the specific host cell (i.e., division affinity).

Table 2

Table 2 Primary parameters for the agent-based model.

In the $M\times N$ grid of host cells, each cell $(m,n)$ has an energetic demand ${\delta }_{(m,n)}$ modeled as follows: given a mean host cell demand of $\text{Δ}$ units of photosynthate per unit time and a “tolerance” parameter ${\nu }_{\text{Δ}}$, the value of ${\delta }_{(m,n)}$ is drawn from a positively-truncated normal distribution with approximately 95% of the mass between $\text{Δ}\pm (\text{Δ}·{\nu }_{\text{Δ}})$. For example, $\text{Δ}=1.0$ and ${\nu }_{\text{Δ}}=0.10$ indicates that host cell demands will be normally distributed with $\approx$ 95% of the demands within 10% of 1.0 unit photosynthate per unit time.

Algal symbionts arrive at random from the pool, modeled using a stationary Poisson process with a rate of $\lambda$ symbionts per unit time. For competition experiments, the relative proportions of competing symbiont types that arrive are determined by $p_{{\text{s}}_1},p_{{\text{s}}_2},\dots$ We consider the hypothesis that affinity between the host and the symbiont might elevate the capture rate of one symbiont type over another. Initial phagocytotic capture of an arriving symbiont by an empty host cell occurs with probability equal to the symbiont’s arrival affinity ${\alpha }_{\text{a}}$ (with $0\le {\alpha }_{\text{a}}\le 1$). This allows us to influence the likelihood that a host would engage phagocytosis machinery to allow symbiont entry into the intracellular habitat. This is the first of our ABM “affinity” terms, which are captured by the mutualism terms in the DM.

Upon phagocytotic capture, a symbiont enters residency in the host cell with an initial accumulation of photosynthate, modeled using a gamma distribution with shape parameter k and scale parameter θ, truncated to a maximum value of P_max units of photosynthate. This banked energy allows the symbiont to navigate any initial costs imposed by the host. The symbiont immediately enters the G₀ phase of mitosis for a random length of time, modeled using a positively-truncated normal distribution with mean and tolerance parameters $t_{{\text{G}}_0},{\nu }_{{\text{G}}_0}$, similar to the host cell demand model above. While in G₀, the symbiont produces photosynthate at a rate of ρ units per unit time, while simultaneously transferring photosynthate to the host cell at a rate of ${\delta }_{(m,n)}$ units per unit time, accumulating any excess. If the symbiont cannot meet the energetic requirements of the host cell, the symbiont either escapes the host cell with probability $p_{\text{e}:{\text{G}}_0}$ or is digested with probability $(1-p_{\text{e}:{\text{G}}_0})$.

Once the symbiont successfully completes G₀, it enters a combined G₁/S/G₂/M phase for a random length of time, modeled using a positively-truncated normal distribution with mean and tolerance parameters $t_{{\text{G}}_1},{\nu }_{{\text{G}}_1}$. While in G₁/S/G₂/M, the symbiont continues to produce, accumulate, and transfer photosynthate under the same rates and energetic requirements as in G₀. Additionally, throughout the phase, the symbiont is subject to a mitotic cost of γ units of photosynthate per unit time. If the symbiont cannot meet the combined energetic requirements of the host cell and mitosis, the symbiont either escapes the host cell with probability $p_{\text{e}:{\text{G}}_1}$ or is digested with probability $(1-p_{\text{e}:{\text{G}}_1})$.

Once the symbiont successfully completes G₁/S/G₂/M, a new symbiont is produced. The new symbiont inherits parameter values from the original symbiont according to the following:

● The accumulation of photosynthate will typically be exactly one-half of the original symbiont’s accumulation at the time of the division.

● All other symbiont-level parameter values (see Table 2) are identical to those in the original symbiont.

● Upon division, phenotypic mutation (discussed below) may result in the amount of inherited photosynthate, the photosynthetic production rate ρ, and the mitotic cost rate γ each individually being either slightly more or slightly less than the values discussed above.

The original symbiont will remain in residence in its host cell with probability p_r, in which case the new symbiont must seek residence in a neighboring cell (see below). Therefore, with probability (1 − p_r), the new symbiont will remain in residence in the original symbiont’s host cell, and the original symbiont must seek residence in a neighboring cell. If there are no empty host cells within the eight surrounding cells defining the Moore neighborhood, the migrating symbiont will be evicted into the pool. We do not model individual symbionts in the pool and therefore the evicted symbiont is outside the scope of our model. For a host cell in the top or bottom row of the two-dimensional grid of cells, three of the eight cells in its neighborhood are outside the scope of the grid. If there is an open cell among the remaining five cells within the grid, the migrating symbiont finds residence inside the grid with probability 5/8, or outside the grid — and outside the scope of our model — with probability 3/8. Given these considerations, one of the open cells is chosen at random and phagocytotic capture of the symbiont seeking new residence occurs stochastically according to the symbiont’s division (mitosis) affinity α_d (with 0 ≤ α_d ≤ 1). This term allows us to influence the likelihood that a symbiont cell produced through mitosis preferentially gains entry into the intracellular habitat, i.e., whether favoring one symbiont over another might influence the outcome of competitive interactions (Pool and Muscatine, 1980; Pasternak et al., 2006). This is the second of our ABM “affinity” terms, captured by the mutualism terms in the DM. Each remaining symbiont then immediately enters the G₀ phase of mitosis (see above), and the process repeats.

Our model also implements an average time of residency for symbionts based on the observation that symbionts often have constant population sizes under benign environmental conditions but still undergo mitotic division (Hill and Hill, 2012). Thus, our model assumes that each symbiont has a maximum residence time of τ time units, modeled using a positively-truncated normal distribution with mean and tolerance parameters T,ν_T.

3.2 Model considerations

As part of ongoing/future work, we are investigating the competitive interactions that occur when two symbionts can occupy the same host cell. Our initial approach, presented here, involved creating a simpler system to explore the dynamics of host:symbiont behaviors. In the ABM, if all the host cells in our grid are occupied, then external symbionts (e.g., those banished from the host symbiont or new symbionts arriving from the outside) would not be able to infect the host. This situation is analogous to the situations described in Figure 2 where u₁ and u₂ are excluded from the host. The ABM assumes no synchronicity between host-symbiont cell cycles because the host cells are not replicating. In future work, it would be interesting to explore how host cell behaviors/growth are driven by symbiont translocation strategies. We are assuming that the interaction between the host and symbionts is always positive (i.e., mutualism) in the sense that the host always gains materials from the symbiont, though in reality what we are examining is akin to the amutualistic framing of Connor (1995). Our ABM is distinct from other attempts to understand mutualism because it focuses on nutritive exchanges as being the mechanism that permits long term residence of the symbiont in the host tissue, i.e., the “arrested phagosome hypothesis” (Hill and Hill, 2012).

3.3 Generating distinct symbiont phenotypes

To generate different symbiont competitive strategies used throughout our experiments, our approach involved two steps. We first allowed dominant strategies to naturally emerge in the model via mutation, documenting their resulting characteristics. Then, guided by the most important factors for driving competitive exclusion as evidenced in those results, we conducted a sensitivity analysis to carefully explore the stability and predictability of the model under parameter value perturbation. We will describe each step in more detail next.

In the first step, we initialized the simulation starting with the parameter values given in Table 2, and then allowed agents to “evolve” naturally within the host. Infections were initiated and at mitosis we allowed phenotypic mutation to occur individually for photosynthetic production rate ρ, mitotic cost rate γ, and inherited photosynthate accumulation. For each characteristic, we modeled mutation with probability p_m. “Deleterious mutations” (i.e., mutations that decreased the value of a trait), occurred with probability p_m:d, while “beneficial mutations” (i.e., mutations that increased the value of a trait), occurred with probability (1 − p_m:d). Beneficial mutations were modeled using a gamma distribution having shape and scale parameters such that 75% of the mutations were a 1.5% improvement or less relative to the original symbiont’s value, with a maximum relative beneficial mutation of 10%. Deleterious mutations were modeled using a gamma distribution such that 50% of the mutations were a 2% decline or less relative to the original symbiont’s value, with no maximum decline (subject to non-negative constraints).

Depending on the specific values for initial parameter values (e.g., relatively higher ρ), we observed a dominant strategy resulting from mutation that would quickly occupy the entire host space, driving a fast-growth logistic curve that approached maximum capacity of the host. This dominant strategy would exclude any novel “mutant” symbionts (even numerically superior in characteristics) if they appeared. Occasionally, a slower-growth logistic growth curve indicated that more complicated internal dynamics were occurring. This was due to the production of competitively viable mutants that were capable of temporarily dominating the cellular habitat within the host, before being outcompeted by even stronger mutants. We documented the characteristics of symbiont strategies produced via these mutational processes and cataloged those that were capable of competitive exclusion of other symbiont types. (See Figure S3 in the Supplementary Material and the accompanying discussion there.) From these results, we recognize photosynthetic production rate (ρ) and mitotic cost rate (γ) as primary factors in driving competitive exclusion.

In the second step, based on the above results, we then conducted a sensitivity analysis of the agent-based model, allowing for pairwise competition in the absence of phenotypic mutation. Our goals were to assess the model’s stability and predictability under perturbation of selected parameter values, and to identify representative strategies to use in subsequent competition experiments. Based on identifying ρ and γ as primary factors in driving competitive exclusion (i.e., small changes in the value of one of those parameters via mutation could lead to a strategy resulting in competitive exclusion), we conducted a multidimensional sweep of ρ and γ parameter values as follows:

● The host was initially filled to 95% capacity. We equally divided that initial population into an experimental group (labeled S_E) and a control group (labeled S_C). Both groups started with the same initial ρ and γ values as given in Table 2. The two symbiont types were placed at random with respective proportions (0.5,0.5).

● For the S_E population, we systematically varied the values of ρ and γ relative to the original values, while keeping the ρ and γ values fixed for S_C.

● For each different ρ and γ value for S_E, we simulated pairwise competition of the two resulting strategies (S_E versus S_C), sampling the population of each at year 4, and recording the ratio of S_E population to that of S_C.

● Each such simulation was replicated 30 times, changing only the initial seed to the random number generator. Hence, each presented ratio of S_E population to S_C population is the average of 30 replications.

The results are shown in Figure 4. In this figure, the origin corresponds to competitive strategies that are identical in phenotype, and therefore the ratio of populations S_E/S_C is 1 (subject to random sampling variability in the simulation replications). In general, as ρ is decreased and γ increased for the experimental strategy (upper-left quadrant of the figure), the ratio S_E/S_C tends toward 0, as lower ρ and higher γ for the experimental strategy allow the control strategy to dominate numerically in population. Conversely, as ρ is increased and γ decreased for the experimental strategy (lower-right quadrant), the ratio S_E/S_C grows significantly, as higher ρ and lower γ allow the experimental strategy to dominate. The other two quadrants exhibit similarly expected behavior, even though the change in population ratio is not perfectly linear under these conditions. (Exploration of this non-linearity is the subject of future work.) These results suggest that our model is indeed predictable and stable in the presence of significant changes in important parameter values.

Figure 4

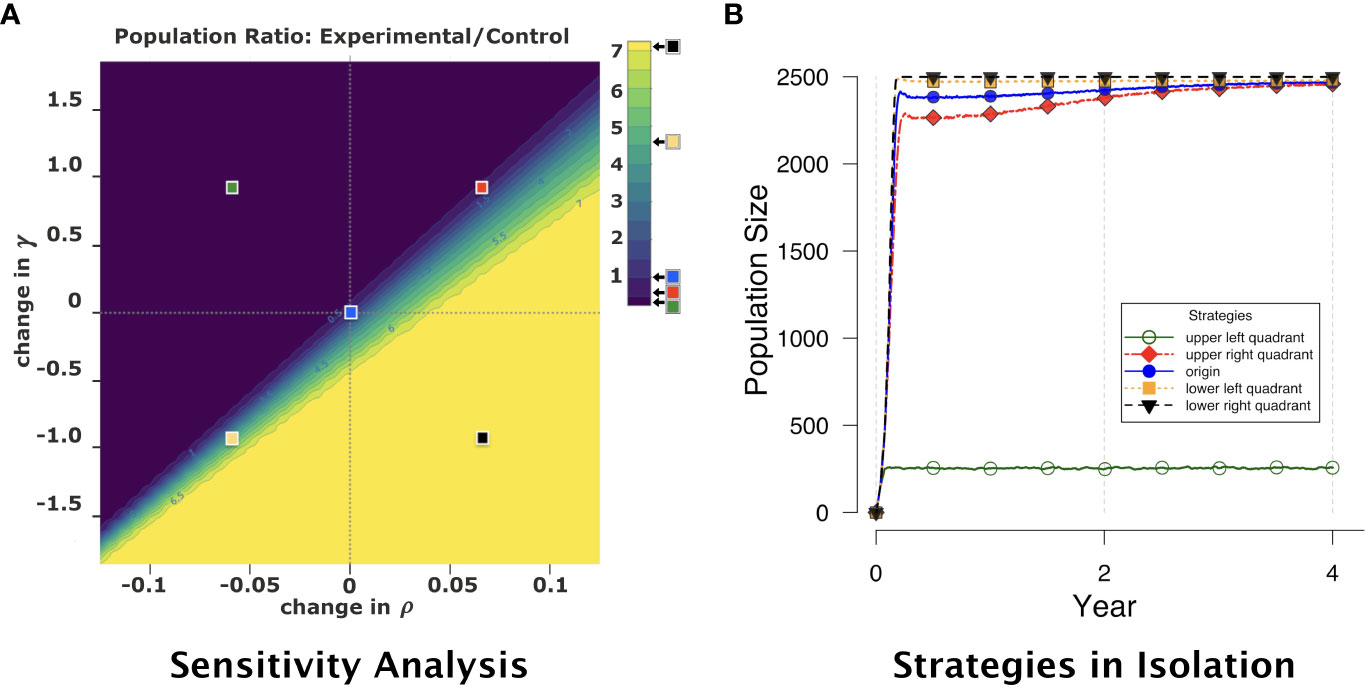
Figure 4 (A) Colored heatmap representing a sensitivity analysis of pairwise competition results from the agent-based model. The photosynthetic production rate ρ and mitotic cost rate γ are varied for the experimental strategy relative to baseline values given in Table 2: ρ is modified relative to its baseline value by minimum and maximum changes respectively of −0.125 and 0.125, varied in increments of 0.0025; γ is modified relative to its baseline value by minimum and maximum changes respectively of −1.833 and 1.833, varied in increments of 0.083 (1/12). For the control strategy (blue square), ρ and γ are held constant. Each color in the heatmap spectrum from dark to light depicts increasing ratio of experimental-strategy population (particular ρ and γ values) to control-strategy population (blue square) at year 4. Darker colors (upper-left quadrant) correspond to ratios closer to 0, where the control strategy is numerically dominant. Lighter colors (lower-right quadrant) correspond to the experimental strategy being numerically dominant, with experimental-to-control population ratios as high as 7. Each point in the figure is the average of 30 replications. The five colored squares (at the centers of the four quadrants and at the origin) represent (ρ, γ) for strategies considered for subsequent pairwise competition experiments. Four were selected due to their strength in isolation. From weakest to strongest: strategy #0 (upper-right quadrant, red); #1 (origin, blue); #2 (lower-left quadrant, gold); #3 (lower-right quadrant, black). (B) Population across time for each of the five strategies selected from the sensitivity analysis. Note that the strategy from the upper-left quadrant of the sensitivity analysis (green, open circles) survives in isolation but does not fill the host, and therefore is not included in our competition experiments.

From these same results, we systematically selected five distinct but representative strategies. These strategies are defined by the ρ-change and γ-change values at the origin and in the centers of the four quadrants — see the superimposed squares in Figure 4A. The center of the upper-left quadrant corresponds to a sufficiently weak symbiont that cannot fill the host in isolation (see curve with open circles in Figure 4B), and therefore is not included in our competition experiments. All the other four strategies could successfully fill the host in isolation (again, see Figure 4B), and are the strategies we use in subsequent competition experiments. We label these strategies from relative weakest to strongest, as #0 (red, upper-right quadrant), #1 (blue, origin), #2 (gold, lower-left quadrant), and #3 (black, lower-right quadrant). We then experimented with these four strategies in isolation and in pairwise competitions, as described in the next section.

3.4 Description of ABM experiments

As discussed above, the four selected phenotypes’ relative competitive abilities ranged from relatively weak to very strong (#0–#3; see Figure 4A). Phenotypes for those four symbiont strategies are provided in the Supplementary Material, where differences in ρ and γ can be compared.

Experiment 1: The first set of experiments allowed us to examine the growth trajectories of each symbiont strategy within the host in the absence of any potential competitor. Furthermore, no further phenotypic mutations were allowed nor were arrivals of any competing strategy allowed. The experiments used two different initial-population approaches, mimicked later in pairwise competition experiments: 10 symbionts of the selected strategy were placed at random within the host; or the host was initially filled to half of 95% capacity, with individual symbionts placed at random. We then varied the symbiont arrival affinity α_a and division affinity α_d, together and individually, and observed the resulting population across time. Each variation of the experiment was replicated 30 times, changing only the initial seed to the random number generator.

Experiment 2: The second set of experiments allowed us to examine the dynamics of population trajectories of symbiont strategies with different competitive abilities when competing for cellular occupancy within a single host. We paired “superior” and “inferior” symbiont strategies in a manner analogous to the strong:strong and strong:weak scenarios described in the DM, and followed the behavior of the competitive encounters. Of the six possible combinations when choosing from among four different strategies, we have selected four combinations to consider: the two weakest strategies in competition (#0 vs. #1), the two strongest strategies (#2 vs. #3), the weakest versus the strongest (#0 vs. #3), and the two middle strategies (#1 vs. #2). The experiments used four different initial-population approaches: 10 symbionts of each of the paired symbiont types were placed at random within the host; or the host was initially filled to 95% capacity, with the paired symbiont types placed at random with symbiont proportions (0.25, 0.75), (0.5,0.5), and (0.75,0.25) respectively. The proportions of the arriving symbiont strategies were $p_{{\text{s}}_1}=p_{{\text{s}}_2}=0.5$. For the superior strategy, we then varied the arrival affinity α_a and division affinity α_d together and individually, and observed the resulting populations of both strategies across time. The goal was to examine how “affinity” might influence the competitive outcomes, as well as to examine transient changes in population dynamics across time. Each variation of the experiment was replicated 30 times, changing only the initial seed to the random number generator.

3.5 ABM results

Experiment 1: In each variation of this experiment, we sampled the population size at year 4 in each of 30 replications, and found that the division affinity term in general had a more significant effect on population size (Figure 5C) than did the arrival affinity term (Figure 5B). Changes to the affinity terms influenced the ability of some of the symbionts to successfully invade host cells — even in the absence of competitors. For example, when the arrival and division affinities were both set to 0.25 for strategy #0 or #1 (rightmost triangles and squares respectively in Figure 5A), both symbiont types occupied the host at a significantly reduced fraction of the population size compared to when affinities were set to 1. Symbiont strategy #3, and to a lesser extent #2, were unaffected by the affinity terms when grown in isolation (Figures 5A–C). In all of the isolation scenarios, with no differential affinities at arrival or upon division (i.e., all affinities set to 1), the four symbiont strategies (#0, #1, #2, and #3) quickly reached their carrying capacities within the host and occupied nearly all of the cells in the host environment. (See Figure S3 in the Supplementary Material for corresponding time series populations).

Figure 5

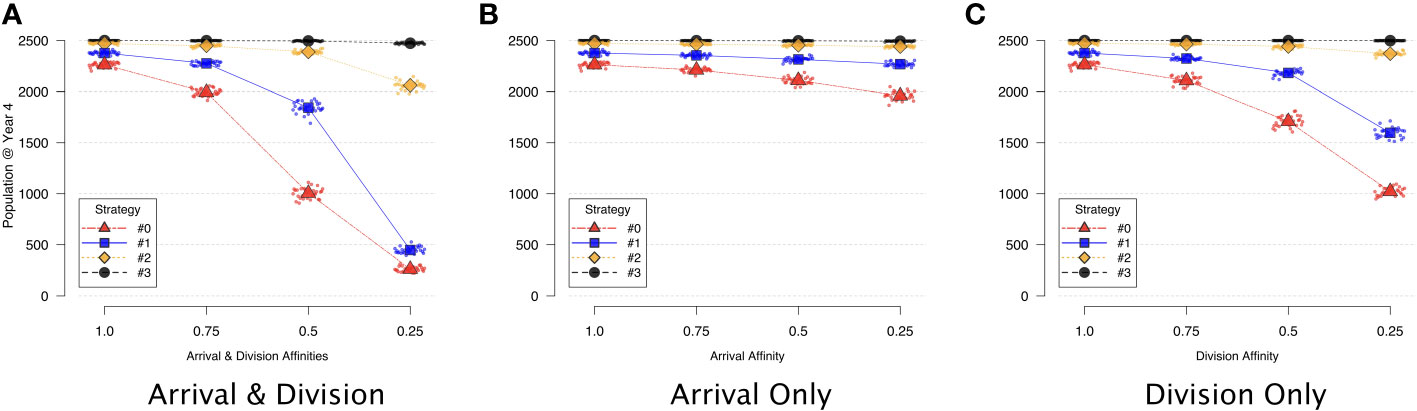
Figure 5 Symbiont strategies in isolation, depicting decrease in population vs. decreasing affinity. Symbionts are initially placed at random, initially filling the host to half of 95% capacity. The population at year 4 from each of 30 different replications is sampled (small points) and then averaged (larger shapes). (A) Effect of decreasing arrival and division affinity together. (B) Effect of decreasing only arrival affinity. (C) Effect of decreasing only division affinity.

Experiment 2: For the figures presented and discussed for this experiment, we show only the 95%-(0.5,0.5) initial-population approach discussed above. When 10 symbionts of each strategy were initially placed at random, as well as in the 95%-(0.25,0.75) and 95%-(0.75,0.25) approaches, population results in equilibrium were qualitatively similar to the 95%-(0.5,0.5) approach. Therefore, the 95%-(0.5,0.5) is reasonably representative of all four approaches. (See Figure S4 in the Supplementary Material).

In our competition experiments, we observed three types of outcomes. The first was when near competitive exclusion was always observed when arrival and division affinities were set to 1. This situation occurred when one very strong competitor (e.g., #3) was pitted against a much weaker competitor (e.g., #0), and the superior competitor was always able to numerically dominate the inferior competitor regardless of the strength of the affinity terms and whether the affinity terms were applied individually or together (Figure 6A).

Figure 6

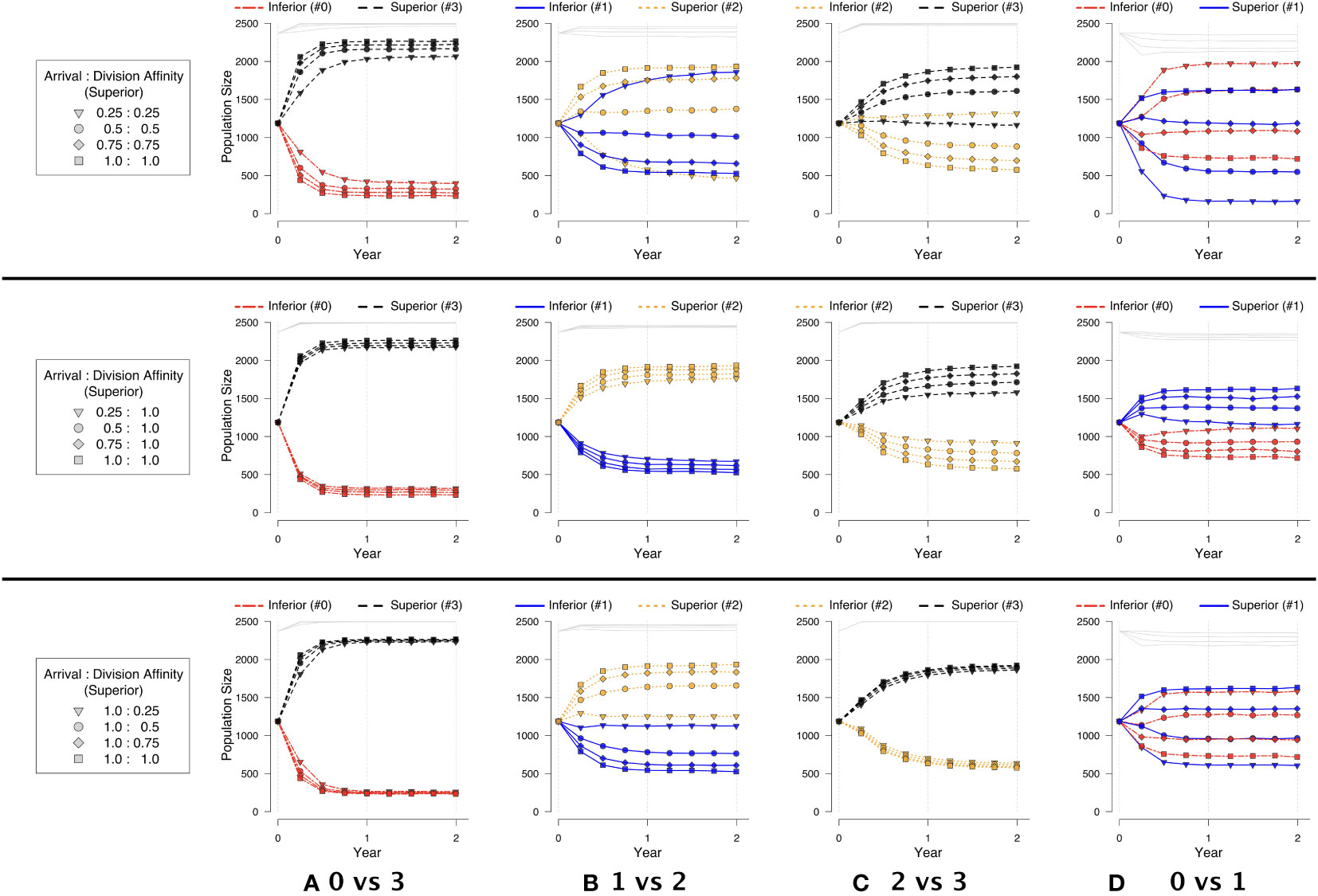
Figure 6 Symbiont strategies in pairwise competition, depicting population across time. An equal number of each strategy is initially placed at random, filling to 95% capacity. Each row respectively corresponds to: (top) decreasing arrival and division affinity together; (middle) decreasing only arrival affinity; (bottom) decreasing only division affinity. Each column corresponds to two of the strategies in pairwise competition, as identified in Experiment 2: (A) 0 vs. 3, (B) 1 vs. 2, (C) 2 vs. 3, and (D) 0 vs. 1.

In the second type of outcome (involving strategy pairings #1 vs. #2 and #2 vs. #3), the superior competitor was numerically dominant except when the arrival and division affinities were strongly biased against the superior competitor (0.25:0.25; triangles in Figures 6B, C). In this case, division affinity had the strongest effect when adjusted individually, but the combination of the two affinities worked together to benefit the inferior competitor. We note however that division affinity had the strongest effect for one of the pairings (#1 vs. #2, in the second and third rows of Figure 6B) while arrival affinity had the strongest effect for the other pairing (#2 vs. #3, in the second and third rows of Figure 6C). On closer inspection, the reason for the relative lack of effect from division affinity when pairing the two strongest competitors (#2 vs. #3) becomes evident. The two strategies are so strong relatively that, even in the face of varying affinities, the combined populations of the two strategies completely fill the host across time, leaving little room for division affinity to have any effect. (See the superimposed gray lines at the very top of the population graphs in Figure 6C) That is, the majority of divisions in this case result in a symbiont eviction as there is insufficient room in the host. Both scenarios (#2 vs. #3 and #1 vs. #2) suggest that an inferior competitor that could otherwise be excluded from a host habitat can be maintained in the host if there are features that benefit the inferior over superior competitors.

For each of the first two types of outcomes, arrival and division affinities individually could not change the ultimate outcome of competition, but could modify population sizes (rows 2–3 of Figures 6A–C). That is, the superior competitor always maintained its population dominance, even if slight, relative to the inferior competitor when coexistence was possible. However, in the final type of outcome involving two relatively weak competitors (#0 vs. #1), division affinity could create a situation where the “inferior” competitor (#0) could numerically dominate the “superior” competitor (#1). Arrival affinity individually resulted in nearly equal coexistence (second row of Figure 6D). Furthermore, a superior competitor (#1) could be nearly completely excluded from the host when both the arrival and division affinities sufficiently favored the inferior competitor (#0) (first row of Figure 6D). As the inferior symbiont accrued relative arrival and/or division benefits, it was able to occupy a greater percentage of the host space and hold it for a longer period of time.

Figure 7 depicts a two-dimensional spatial representation of competing symbiont strategies at two snapshots across time. For each pairing of strategies, we show the initial random placement of symbionts, followed by the dispersion at year 1 when the superior strategy has arrival and division affinities of (1.0,1.0) and (0.5,0.5) respectively. (These correspond to one replication from the ensemble of replications used in the first row of Figures 6A–D.) In some cases, when the superior competitor is disadvantaged, the inferior competitor shows obvious numerical gains, even dominance (see Figures 7B, D), consistent with the results presented in the first row of Figure 6. For future work, we will explore priority effects and clustering as a means for inferior competitors to benefit from exploitative competition, as suggested by the spatial results in Figures 7B, D. (See Supplementary Material for time-lapsed videos of these static figures).

Figure 7

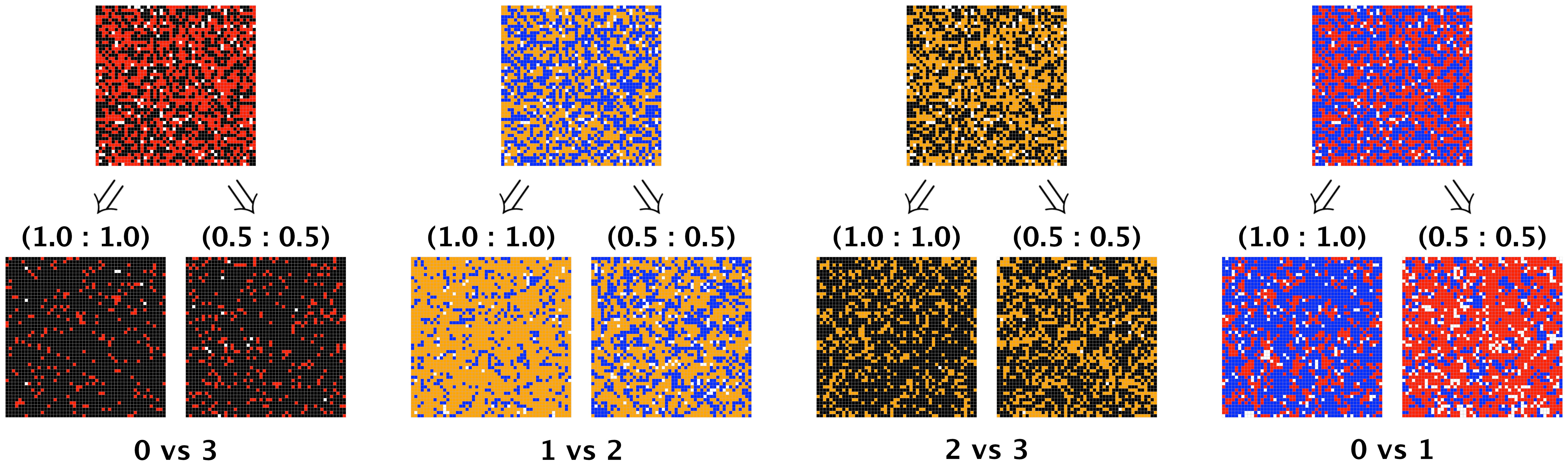
Figure 7 Spatial depiction of symbiont strategies in pairwise competition within the host. For each pairing, the top row shows the host initially filled to 95% capacity, half from the inferior strategy and half from the superior, with symbionts placed into host cells at random. For each pairing, the two figures in the bottom row show the dispersion of symbionts at year 1, with the superior strategy having arrival and division affinities respectively of (left) 1.0 and 1.0, (right) 0.5 and 0.5. Populations in the bottom row are consistent with those shown in row 1 of Figure 6 at year 1 for the 1.0:1.0 and 0.5:0.5 superior strategy affinities.

Across all types of outcomes, we highlight the potential for investigating the rate of growth of the population, as demonstrated by the presented time series. That is, focusing on the early portions of these time series suggests an avenue for future work, involving comparisons of the rates of change exhibited by the population curves, both within a competitive pairing (across affinities) and across pairings.

4 General observations

Several key findings emerged from the models. The first was that superior competitors could competitively exclude inferior competitors in the absence of host influence in both models. This is not a surprising ecological outcome, but does present a different explanatory framework for thinking about intracellular symbioses. Extant partnerships that involve one numerically dominant symbiont may not indicate a high degree of co-evolutionary specialization between the host and symbiont. That is, a naïve host could be nothing more than a competitive arena for the symbionts with the superior competitor excluding all other potential symbionts, which represents a null hypothesis of symbiont numerical dominance that does not presuppose co-adaptation or host control (Dean et al., 2016; Lowe et al., 2016).

The second outcome of both models was that they identified many conditions whereby co-occupancy (i.e., coinfection) of a host by different symbionts was possible. According to the DM, coexistence of symbionts was possible, in fact expected, when competitive coefficients are less than one (intraspecific competition was stronger than interspecific competition), and interactions between host and symbiont is non-existent or limited. The ABM achieved similar results when the two symbionts had similar competitive strategies (i.e., based primarily on photosynthate-release). Results from the ABM demonstrated that two different symbionts can form long-term, stable residence within a particular host — a function of photosynthate translocation absent any influence of the host. Furthermore, sensitivity analysis demonstrated that the model is stable and predictable under parameter-value perturbation, and that competitive outcomes follow anticipated trajectories despite subtle changes in phenotype. Shifts in competitive outcomes may be more strongly influenced if the initial differences between competitors are large.

A third key outcome made apparent by the explicit spatial perspective of the ABM was that exploitative competition made it difficult to dislodge a symbiont from a host cell once it has taken up occupancy. Thus, a symbiont’s ability to occupy a host cell can be a successful competitive strategy because the simple act of colonization affords even inferior competitors the chance to persist within the host for extended periods. While the dynamics of establishment within a host may be complicated, e.g., Bucher et al. (2016), long-term persistence of two or more symbiont types within a single host due to exploitative competition could look like coexistence. This may help explain the low-level residency that is observed in many hosts in natural environments, e.g., Bongrand and Ruby (2019), may produce the tissue-level heterogeneity of distribution observed within hosts, and opens the possibility that the tissue-level landscape of the host may be a mosaic of a diversity of symbionts.

Finally, both models converged on the outcome that “affinity” between partners (whether host or symbiont derived) can favor a single symbiont’s access to the host, even if that symbiont is not a superior competitor. The finding that “affinity” could drive host:symbiont associations is likely an essential step in changing symbiotic partnerships from promiscuous coinfections with high degrees of co-occupancy to symbioses that favor more specific partnerships, e.g., Nawroth et al. (2017). The work of Jacobovitz et al. (2021) is particularly interesting because successful symbionts in Exaptasia hosts induce host cell innate immune suppression through a particular genetic switch that involves LAMP-1, which allows for long-term residency. Once particular combinations of hosts and symbionts are favored, subsequent reciprocal coevolutionary processes may fine tune the partnership to achieve ever greater levels of co-specialization. A host might benefit if a mutation appeared that somehow favored those symbionts that grew more slowly and translocated more material, which are conditions that might make a symbiont a poorer competitor. However, it is also possible that a symbiont that translocates less material might end up becoming specialized for a particular host before a “better” symbiont partner could become entrained in the host’s biology. Recent observations that more diverse symbiont communities are found in holobionts less resistant to environmental stressors (Howe-Kerr et al., 2020) might be explained by a lack of tight specialization between host and symbiont.

Our results offer an explanation for patterns of host:symbiont interaction in extant symbioses. For example, Anthopleura spp. form symbioses involving dinoflagellate and green algal partners that coexist and have different densities depending on the environment (Muscatine, 1971). Anemones dominated by the dinoflagellate tend to be in the high intertidal and upper regions of tide pools, anemones harboring mostly green algae occur in the low shore and deeper regions of tide pools, and anemones harboring mixed populations are found at intermediate shore heights (Bates, 2000; Secord and Augustine, 2000). Experimental changes in environmental conditions (e.g., temperature and light) can shift the composition of the symbiont communities such that the dinoflagellate is favored under low light and the green alga is favored at lower temperatures (Sanders and Muller-Parker, 1997). Our models offer potential explanations for these outcomes by framing the shifts in symbiont populations in terms of competitive capabilities (i.e., competitive coefficients α₁₂ and α₂₁ in the DM or photosynthetic capability/host-cell demand in the ABM) that are influenced by environmental characteristics. Thinking of dinoflagellate and green alga encounters in this way recovers classic features of models describing competitive exclusion, without any assumptions about co-adaptation between hosts and their symbionts.

The symbiont population behaviors observed in our models may apply to associations found on coral reefs involving (mostly) invertebrate hosts and algae belonging to the Symbiodiniaceae (LaJeunesse et al., 2018). Symbiodiniaceae-based symbioses can be disrupted following environmental stress — a process known as coral bleaching. While not restricted to corals (Hill et al., 2016), bleaching occurs when algal cell density decreases (or algal pigment is lost) within a particular host, which has raised questions about the fidelity and specificity of the partnership. Some attempts to explain coral bleaching envision an “adaptive bleaching” process (Buddemeier and Fautin, 1993) employed by hosts to flexibly associate with algal partners that are better suited to the changing environment. The within host shift in symbiont population composition arises after a bleaching event when rarer symbionts that had resided within the host increase in frequency or when the entire symbiont community changes as heterologous symbionts are acquired from the environment (Baker et al., 2004; Fautin and Buddemeier, 2004; Rowan, 2004; Chen et al., 2005; Baker and Romanski, 2007; Jones et al., 2008; Stat and Gates, 2011; Boulotte et al., 2016; Matthews et al., 2017). Rather than invoking adaptationist perspectives, our models may help explain patterns observed among Symbiodiniaceae-based symbioses as context dependent shifts in symbiont competitive ability. For example, thermal stress caused increases in Durusdinium trenchi before bleaching was observed in five species of coral during a mass bleaching event in the Caribbean (LaJeunesse et al., 2009b), but the typical symbiont regained their numerical dominance once the stress was removed — see Figure 4 of (LaJeunesse et al., 2009b). Reductions in the translocation of carbon have been found to precede breakdown of coral-algal symbioses in corals (Rädecker et al., 2021), and the DM and ABM would suggest that D. trenchi was able to expand host occupancy after thermally sensitive symbionts that could no longer afford host cell demands were lost from the host.

Work on the distribution of Symbiodiniaceae symbionts across hosts has focused on the spatial distribution of algal types on the order of centimeters, meters, and kilometers (e.g., Pettay et al., 2011; Baums et al., 2014; Wall et al., 2020). The ABM revealed that tissue-level landscapes of the host (at micrometer scales) may be an important feature of phototroph:heterotroph symbioses where priority effects are important. The vast majority of corals must be reinfected by their phototrophic symbionts at the larval stage each generation, which may protect fertilization (Hartmann et al., 2017) but also creates opportunities for rampant mixing of host and symbiont lineages. While most studies point to remarkable specificity between particular hosts and symbionts in these systems (e.g., LaJeunesse et al., 2005; Goulet, 2006; LaJeunesse et al., 2009b; LaJeunesse et al., 2009a; Stat et al., 2009; LaJeunesse et al., 2010; McGinley et al., 2012; Thornhill et al., 2013; Thornhill et al., 2014), low background symbiont presence (i.e., the “rare-biosphere”) distinct from the major symbiont partner has been discovered within many hosts (Silverstein et al., 2012; Boulotte et al., 2016). Our models predict numerical dominance of one symbiont type when coevolutionary specialization was present or a competitively dominant symbiont occupied the host, but low levels of other symbionts are possible due to priority effects. Rather than seeing rare symbionts as accidental, transitory, and minimally important to the host (Lee et al., 2016), the ABM indicates that that poorer competitors can persist at low levels for significant periods due to exploitative competitive strategies, which might be a successful strategy from the algae’s perspective.

The models we present may be usefully applied to symbioses beyond marine and aquatic systems. In terrestrial habitats, lichens represent the holobiont phenotype of successful partnerships between mycobiont hosts and cyanobacterial or green algal symbionts (Honegger, 1998). Representing more than 20% of all fungal species, this polyphletic host and symbiont partnership is a common nutritional strategy involving translocation of photosynthates whereby extracellular photobiont cells are integrated with fungal partners via complex haustorial or appressorial structures (Honegger, 1998). These associations range from low to high degrees of partner specificity with examples of coinfection with multiple phycobiont lineages within single thalli (e.g., Blaha et al., 2006; Mansournia et al., 2012; Molins et al., 2013; Kosecka et al., 2020; Piercey-Normore and Athukorala, 2017; Yahr et al., 2004). “Algal switching” has also been observed (Ohmura et al., 2019). Our theoretical analyses may be useful for understanding observed patterns in lichen symbioses.

5 Discussion

The models presented here assume no a priori coadapted benefits of the association, and offer an alternative to the often unstated assumption that intracellular symbioses are governed by “host control” of the interactions (e.g., Fautin and Buddemeier, 2004; Frean and Abraham, 2004; Dimond and Carrington, 2008; Yellowlees et al., 2008; Wooldridge, 2010; Damore and Gore, 2011; Dean et al., 2016; Lowe et al., 2016). Our models complement work that explains the maintenance of biodiversity as a result of adaptive niche specialization operating at a local scale that manifests as neutrality at regional/landscape scales (Leibold et al., 2019). Mechanisms of local adaptation between symbionts and hosts (i.e., the affinity terms or mutualism coefficients in our models) could influence patterns of specialization at local scales, which then lead to complicated biodiversity patterns at more expansive spatial scales. Potential connections between our models and those involving metacommunities, where regional and local forces (operating at multiple scales) are simultaneously considered, deserves further attention (Leibold and Chase, 2018). The behavior of our models is also in line with ideas that indicate that symbionts lock hosts into symbiotic dependency due to demanding nutrient lifestyles (Werner et al., 2015).

We would like to highlight a final point. We have previously argued (Hill, 2014) that adopting an explicitly comparative perspective that contrasts findings from different symbioses may elucidate shared characteristics of intracellularity that deserve further attention (i.e., potential symplesiomorphies associated with normal endomembrane processes that produce the parasitophorous vacuole, symbiosome, and digestive vacuole in mutualisms and parasitisms). Our two distinct modeling approaches are focused on intracellular symbioses involving multiple infections that are mutually beneficial to the partners. We recognize parallels between our mutualist-focus and modeling focused on parasitic systems. Parasite models have more than a century of development (e.g., Ross, 1916), predominantly using DM-based susceptible, infected, and recovered (SIR) approaches (but see Ramesh and Hall, 2023 who used food web modules and feedback loops to understand within-host parasite dynamics). While the focus of SIR models is often on the evolution of virulence (e.g., Alizon et al., 2013), the population dynamics they uncover include superinfection, competitive exclusion, and coinfection (Dobson, 1985; Nowak and Sigmund, 2002). Inhibitory or exploitative competition typically drive these outcomes, and the parallels, in terms of population dynamics we observed, raise the intriguing possibility that mutualists and parasites exhibit similar patterns of host occupancy. Agent based models have also been used to examine several parasite-caused diseases (e.g., malaria (Amadi et al., 2021; reviewed in Smith et al., 2018); leishmaniasis (Tabasi et al., 2011); chlamydia (Azizi et al., 2021)). The approach we offer represents a novel application of ABMs to intracellular symbioses that involve reciprocal mutual benefits between interacting partners. Our ABM is squarely focused on exploitative competition, but adding the possibility of inhibitory competition, as seen in some parasite systems, is a worthy avenue to explore.

The pathways to cooperation and coevolution are complex and often poorly understood (Fumagalli and Rice, 2019), and our objective was to build models that offer an alternative conceptual paradigm to understand dynamical relationships among mutualistic hosts and symbionts. We cross-validated the robustness of our model conclusions by considering analytically derived equations along with more complex simulation experiments. The DM framework allowed us to determine all future populations with each specific set of parameter values and initial populations. The ABM provides a detailed, highly configurable, and realistic model of heterogeneous symbiont populations and asynchronous behavior, using empirical and theoretical knowledge of heterotroph:phototroph symbioses. The ABM also facilitates a spatially explicit exploration of conditions that affect symbiont behavior. While our focus was on endosymbiotic phototroph:heterotroph interactions, these models are likely to apply to many different types of mutualistic and amutualistic symbioses (e.g., Romano et al., 2013; Septer, 2019). We found that coexistence of two or more symbiont types within a single host was common as were examples of host:symbiont specificity. Indeed, “coexistence” and colonization may be two distinct ways of looking at symbiotic partnerships (Nylin et al., 2018). Our models suggest that many patterns of coinfection/cooccupancy and specificity observed in nature can be explained from ecological principles alone. However, coevolutionary specialization is clearly important and shifts the nature of competitive encounters between symbionts — competitively inferior symbionts could convert losing strategies into winning strategies with coevolutionary specialization.

Data availability statement

Fully-documented Python source code, along with descriptions of each source file and instructions for executing the agent-based simulation model, are provided at the following GitHub link: https://github.com/blawson-bates/Hill_et_al_2023_ABM_software. The raw data used to generate any of the figures will be made available by the authors, without undue reservation.

Author contributions

JC and MH conceived of and designed the deterministic model. JC, NR, ST, and TW contributed to mathematical analyses of the deterministic model. MH, BL, SG, and AH contributed to conception and design of the agent-based model (ABM). BL, SG, and ER contributed to implementation, testing, modification, and experimentation related to the ABM. MH, BL, JC, SG, and AH conducted analyses of ABM results. MH, BL, JC, and AH wrote sections of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

Portions of this work were funded by grants from the National Science Foundation (OCE-1617255 to MH, OCE-0647119 and IOS-1555440 to MH and AH) and the Gordon and Betty Moore Foundation (9332 to AH).

Acknowledgments

We would like to thank Dan Thornhill for sharing his insights and perspectives at early stages of model development. We also thank Garrett Fundakowski, Melissa Gu, Tyler Heist, and Connor Hughes who worked on aspects of model development. This work was partially supported by a grant from the Gordon and Betty Moore Foundation (#9332).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2023.1221012/full#supplementary-material

References

Alizon S., de Roode J., Michalakis Y. (2013). Multiple infections and the evolution of virulence. Ecol. Lett. 16, 556–567. doi: 10.1111/ele.12076

PubMed Abstract | CrossRef Full Text | Google Scholar

Amadi M., Shcherbacheva A., Haario H. (2021). Agent-based modelling of complex factors impacting malaria prevalence. Malaria J. 20, 185. doi: 10.1186/s12936-021-03721-2

CrossRef Full Text | Google Scholar

Archetti M., Scheuring I., Hoffman M., Frederickson M., Pierce N., Yu D. (2011). Economic game theory for mutualism and cooperation. Ecol. Lett. 14, 1300–1312. doi: 10.1111/j.1461-0248.2011.01697.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Azizi A., Dewar J., Qu Z., Hyman J. (2021). Using an agent-based sexual-network model to analyze the impact of mitigation efforts for controlling chlamydia. Epidemics 35, 100456. doi: 10.1016/j.epidem.2021.100456

PubMed Abstract | CrossRef Full Text | Google Scholar

Baker A., Romanski A. (2007). Multiple symbiotic partnerships are common in scleractinian corals, but not in octocorals: Comment on Goulet, (2006). Mar. Ecol. Prog. Ser. 335, 237–242. doi: 10.3354/meps335237

CrossRef Full Text | Google Scholar

Baker A., Starger C., McClanahan T., Glynn P. (2004). Corals’ adaptive response to climate change: Shifting to new algal symbionts may safeguard devastated reefs from extinction. Nature 430, 741. doi: 10.1038/430741a

PubMed Abstract | CrossRef Full Text | Google Scholar

Bates A. (2000). The intertidal distribution of two algal symbionts hosted by Anthopleura xanthogrammica (Brandt 1835). J. Exp. Mar. Biol. Ecol. 249, 249–262. doi: 10.1016/S0022-0981(00)00203-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Baums I., Devlin-Durante M., LaJeunesse T. (2014). New insights into the dynamics between reef corals and their associated dinoflagellate endosymbionts from population genetic studies. Mol. Ecol. 23, 4203–4215. doi: 10.1111/mec.12788

PubMed Abstract | CrossRef Full Text | Google Scholar

Beck J., Ho C.-M. (2021). Transport mechanisms at the malaria parasite-host cell interface. PloS Pathog. 17, e1009394. doi: 10.1371/journal.ppat.1009394

PubMed Abstract | CrossRef Full Text | Google Scholar

Blaha J., Baloch E., Grube M. (2006). High photobiont diversity in symbioses of the euryoecious lichen Lecanora rupicola (Lecanoraceae, Ascomycota). Biol. J. Linn. Soc. 88, 283–293. doi: 10.1111/j.1095-8312.2006.00640.x

CrossRef Full Text | Google Scholar

Bongrand C., Ruby E. (2019). Achieving a multi-strain symbiosis: Strain behavior and infection dynamics. ISME J. 13, 698–706. doi: 10.1038/s41396-018-0305-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Boucher D. (1988). The Biology of Mutualism: Ecology and Evolution (New York, NY: Oxford University Press), 9780195053920, ISBN: ISBN 13.

Google Scholar

Boulotte N., Dalton S., Carroll A., Harrison P., Putnam H., Peplow L., et al. (2016). Exploring the Symbiodinium rare biosphere provides evidence for symbiont switching in reef-building corals. ISME J. 10, 2693-2701. doi: 10.1038/ismej.2016.54

PubMed Abstract | CrossRef Full Text | Google Scholar

Brener-Raffalli K., Clerissi C., Vidal-Dupiol J., Adjeroud M., Bonhomme F., Pratlong M., et al. (2018). Thermal regime and host clade, rather than geography, drive symbiodinium and bacterial assemblages in the scleractinian coral pocillopora damicornis sensu lato. Microbiome 6, 39. doi: 10.1186/s40168-018-0423-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Bucher M., Wolfowicz I., Voss P., Hambleton E., Guse A. (2016). Development and symbiosis establishment in the cnidarian endosymbiosis model Aiptasia sp. Sci. Rep. 6, 320-326. doi: 10.1038/srep19867

CrossRef Full Text | Google Scholar

Buddemeier R., Fautin D. (1993). Coral bleaching as an adaptive mechanism: A testable hypothesis. Bioscience 43. doi: 10.2307/1312064

CrossRef Full Text | Google Scholar

Chen C., Wang J., Fang L., Yang Y. (2005). Fluctuating algal symbiont communities in Acropora palifera (Scleractinia: Acroporidae) from Taiwan. Mar. Ecol. Prog. Ser. 295, 113–121. doi: 10.3354/meps295113

CrossRef Full Text | Google Scholar

Chen S., Zhao H., Zou C., Li Y., Chen Y., Wang Z. (2017). Combined inoculation with multiple arbuscular mycorrhizal fungi improves growth, nutrient uptake and photosynthesis in cucumber seedlings. Front. Microbiol. 8. doi: 10.3389/fmicb.2017.02516. e. a.

CrossRef Full Text | Google Scholar

Connor R. (1995). The benefits of mutualism: A conceptual framework. Biol. Rev. 70, 427–457. doi: 10.1111/j.1469-185X.1995.tb01196.x

CrossRef Full Text | Google Scholar

Damore J., Gore J. (2011). A slowly evolving host moves first in symbiotic interactions. Evolution 65, 2391–2398. doi: 10.1111/j.1558-5646.2011.01299.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Davy S., Allemand D., Weis V. (2012). Cell biology of cnidarian-dinoflagellat symbiosis. Microbiol. Mol. Biol. Rev. 76, 229–261. doi: 10.1128/MMBR.05014-11

PubMed Abstract | CrossRef Full Text | Google Scholar

Dean A., Minter E., Sørensen M., Lowe C., Cameron D., Brockhurst M., et al. (2016). Host control and nutrient trading in a photosynthetic symbiosis. J. Theor. Biol. 405, 82–93. doi: 10.1016/j.jtbi.2016.02.021

PubMed Abstract | CrossRef Full Text | Google Scholar

Dimond J., Carrington E. (2008). Symbiosis regulation in a facultatively symbiotic temperate coral: Zooxanthellae division and expulsion. Coral Reefs 27, 601–604. doi: 10.1007/s00338-008-0363-x

CrossRef Full Text | Google Scholar

Dobson A. (1985). The population dynamics of competition between parasites. Parasitology 91, 317–347. doi: 10.1017/s0031182000057401

PubMed Abstract | CrossRef Full Text | Google Scholar

Fautin D., Buddemeier R. (2004). Adaptive bleaching: A general phenomenon. Hydrobiologia 530, 459–467. doi: 10.1007/s10750-004-2642-z

CrossRef Full Text | Google Scholar

Frank S. (1996). Host-symbiont conflict over the mixing of symbiotic lineages. Proc. R. Soc. London. Ser. B: Biol. Sci. 263, 339–334. doi: 10.1098/rspb.1996.0052

CrossRef Full Text | Google Scholar

Frean M., Abraham E. (2004). Adaptation and enslavement in endosymbiont-host associations. Phys. Rev. E 69, 051913. doi: 10.1103/PhysRevE.69.051913

CrossRef Full Text | Google Scholar

Fujishima M., Kodama Y. (2012). Endosymbionts in Paramecium. Eur. J. Protistology 48, 124–137. doi: 10.1016/j.ejop.2011.10.002

CrossRef Full Text | Google Scholar

Fumagalli S., Rice S. (2019). Stochasticity and non-additivity expose hidden evolutionary pathways to cooperation. PloS One 14, e0225517. doi: 10.1371/journal.pone.0225517

PubMed Abstract | CrossRef Full Text | Google Scholar

Goulet T. (2006). Most corals may not change their symbionts. Mar. Ecol. Prog. Ser. 321, 1–7. doi: 10.3354/meps321001

CrossRef Full Text | Google Scholar

Griffiths E., Pedersen A., Fenton A., Petchey O. (2014). Analysis of a summary network of co-infection in humans reveals that parasites interact most via shared resources. Proc. Biol. Sci 281, 20132286. doi: 10.1098/rspb.2013.2286

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamada M., Schröder K., Bathia J., Kürn U., Fraune S., Khalturina M., et al. (2018). Metabolic co-dependence drives the evolutionarily ancient Hydra-Chlorella symbiosis. Elife 7, e35122. doi: 10.7554/eLife.35122

PubMed Abstract | CrossRef Full Text | Google Scholar

Hartmann A., Baird A., Knowlton N., Huang D. (2017). The paradox of environmental symbiont acquisition in obligate mutualisms. Curr. Biol. 27, 3711–3716. doi: 10.1016/j.cub.2017.10.036

PubMed Abstract | CrossRef Full Text | Google Scholar

Hill M. (2014). Production possibility frontiers in phototroph:heterotroph symbioses: Trade-offs in allocating fixed carbon pools and the challenges these alternatives present for understanding the acquisition of intracellular habitats. Front. Microbiol. 5. doi: 10.3389/fmicb.2014.00357

CrossRef Full Text | Google Scholar

Hill M., Allenby A., Ramsby B., Schönberg C., Hill A. (2011). Symbiodinium diversity among host clionaid sponges from Caribbean and Pacific reefs: Evidence of heteroplasmy and putative host-specific symbiont lineages. Mol. Phylogenet. Evol. 59, 81–88. doi: 10.1016/j.ympev.2011.01.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Hill M., Hill A. (2012). The magnesium inhibition and arrested phagosome hypotheses: New perspectives on the evolution and ecology of Symbiodinium symbioses. Biol. Rev. 87, 804–821. doi: 10.1111/j.1469-185X.2012.00223.x

CrossRef Full Text | Google Scholar

Hill M., Walter C., Bartels E. (2016). A mass bleaching event involving clionaid sponges. Coral Reefs 35:153 35, 153.

Google Scholar

Honegger R. (1998). The lichen symbiosis—what is so spectacular about it. Lichenologist 30, 193–121. doi: 10.1006/lich.1998.0140

CrossRef Full Text | Google Scholar

Howe-Kerr L., Bachelot B., Wright R., Kenkel C., Bay L., Correa A. (2020). Symbiont community diversity is more variable in corals that respond poorly to stress. Global Change Biol. 26, 2220–2234. doi: 10.1111/gcb.14999

CrossRef Full Text | Google Scholar

Huss V., Holweg C., Seidel B., Reich V., Rahat M., Kessler E. (1993). There is an ecological basis for host/symbiont specificity in Chlorella/Hydra symbioses. Endocytobiosis Cell Res. 10, 35–46.

Google Scholar

Jacobovitz M., Rupp S., Voss P., Maegele I., Gornik S., Guse A. (2021). Dinoflagellate symbionts escape vomocytosis by host cell immune suppression. Nat. Microbiol. 6, 769–782. doi: 10.1038/s41564-021-00897-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang Y., Wang W., Xie Q., Liu N., Liu L., Wang D. P. (2017). Plants transfer lipids to sustain colonization by mutualistic mycorrhizal and parasitic fungi. Science 356, 1172–1175. doi: 10.1126/science.aam9970

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones A., Berkelmans R., Oppen M., Mieog J., Sinclair W. (2008). A community change in the algal endosymbionts of a scleractinian coral following a natural bleaching event: Field evidence of acclimatization. Proc. R. Soc. B: Biol. Sci. 275, 1359–1365. doi: 10.1098/rspb.2008.0069

CrossRef Full Text | Google Scholar

Kaltenpoth M., Roeser-Mueller K., Koehler S., Peterson A., Nechitaylo T. Y., Stubblefield J. W., et al. (2014). Partner choice and fidelity stabilize coevolution in a cretaceous-age defensive symbiosis. Proc. Natl. Acad. Sci. U.S.A. 111, 6359–6364. doi: 10.1073/pnas.1400457111

PubMed Abstract | CrossRef Full Text | Google Scholar

Kiers E., Duhamel M., Beesetty Y., Mensah J. A., Franken O., Verbruggen E., et al. (2011). Reciprocal rewards stabilize cooperation in the mycorrhizal symbiosis. Science 333, 880–882. doi: 10.1126/science.1208473

PubMed Abstract | CrossRef Full Text | Google Scholar

Kodama Y., Fujishima M. (2010). Secondary symbiosis between Paramecium and Chlorella cells. Int. Rev. Cell Mol. Biol. 279, 33–77. doi: 10.1016/S1937-6448(10)79002-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Kodama Y., Fujishima M. (2016). Differences in infectivity between endosymbiotic Chlorella variabilis cultivated outside host Paramecium bursaria for 50 years and those immediately isolated from host cells after one year of reendosymbiosis. Biol. Open 5, 55–61. doi: 10.1242/bio.013946

CrossRef Full Text | Google Scholar

Kosecka M., Jabłońska A., Flakus A., Rodriguez-Flakus P., Kukwa M., Guzow-Krzemińska B. (2020). Trentepohlialean algae (trentepohliales, ulvophyceae) show preference to selected mycobiont lineages in lichen symbioses. J. Phycology 56, 979–993. doi: 10.1111/jpy.12994

CrossRef Full Text | Google Scholar

Kovacevic G. (2012). Value of the Hydra model system for studying symbiosis. Int. J. Dev. Biol. 56, 627–635. doi: 10.1387/ijdb.123510gk

PubMed Abstract | CrossRef Full Text | Google Scholar

LaJeunesse T., Lee S., Bush S., Bruno J. (2005). Persistence of non-Caribbean algal symbionts in Indo-Pacific mushroom corals released to Jamaica 35 years ago. Coral Reefs 24, 157–159. doi: 10.1007/s00338-004-0436-4

CrossRef Full Text | Google Scholar

LaJeunesse T., Loh W., Trench R. (2009a). Do introduced endosymbiotic dinoflagellates ‘take’ to new hosts. Biol. Invasions 11, 995–100. doi: 10.1007/s10530-008-9311-5

CrossRef Full Text | Google Scholar

LaJeunesse T., Parkinson J. E., Gabrielson P. W., Jeon H. J., Reimer J. D., Voolstra C. R., et al. (2018). Systematic revision of Symbiodiniaceae highlights the antiquity and diversity of coral endosymbionts. Curr. Biol. 28, 2570–2580. doi: 10.1016/j.cub.2018.07.008

PubMed Abstract | CrossRef Full Text | Google Scholar

LaJeunesse T., Smith R., Finney J., Oxenford H. (2009b). Outbreak and persistence of opportunistic symbiotic dinoflagellates during the 2005 Caribbean mass coral ‘bleaching’ event. Proc. R. Soc. B: Biol. Sci. 276, 4139–4148. doi: 10.1098/rspb.2009.1405

CrossRef Full Text | Google Scholar

LaJeunesse T., Smith R., Walther M., Pinzón J., Pettay D. T., McGinley M., et al. (2010). Host-symbiont recombination versus natural selection in the response of coral-dinoflagellate symbioses to environmental disturbance. Proc. R. Soc. B: Biol. Sci. 277, 2925–2934. doi: 10.1098/rspb.2010.0385

CrossRef Full Text | Google Scholar

Lawson B., Hill M., Hill A., Heist T., Hughes C. (2015). “An agent-based simulation model of sponge:algae symbiotic relationships,” in Proceedings of the 2015 Winter Simulation Conference (WSC ‘15). Eds. Yilmaz L., Chan W. K.-V., Moon I., Roeder T., Macal C., Rossetti M. (Piscataway, NJ: IEEE Press), 1012–1023. doi: 10.1007/s00338-016-1402-7

CrossRef Full Text | Google Scholar

Lee M., Jeong H., Jang S., Lee S., Kang N., Lee K., et al. (2016). Most low-abundance “background” Symbiodinium spp. are transitory and have minimal functional significance for symbiotic corals. Microbial Ecol. 71, 771–783. doi: 10.1007/s00248-015-0724-2

CrossRef Full Text | Google Scholar

Leibold M., Chase J. (2018). Metacommunity Ecology Vol. 59 (Princeton, NJ: Princeton University Press). doi: 10.2307/j.ctt1wf4d24

CrossRef Full Text | Google Scholar

Leibold M., Urban M., Meester L. D., Klausmeier C., Vanoverbeke J. (2019). Regional neutrality evolves through local adaptive niche evolution. Proc. Natl. Acad. Sci. U.S.A. 116, 2612–2617. doi: 10.1073/pnas.1808615116

PubMed Abstract | CrossRef Full Text | Google Scholar

Lowe C., Minter E., Cameron D., Brockhurst M. (2016). Shining a light on exploitative host control in a photosynthetic endosymbiosis. Curr. Biol. 26, 207–221. doi: 10.1016/j.cub.2015.11.052

PubMed Abstract | CrossRef Full Text | Google Scholar

Luginbuehl L., Menard G., Kurup S., Erp H. V., Radhakrishnan G., Breakspear A. (2017). Fatty acids in arbuscular mycorrhizal fungi are synthesized by the host plant. Science 356, 1175–1178. doi: 10.1126/science.aan0081. e. a.

PubMed Abstract | CrossRef Full Text | Google Scholar

Macal C., North M. (2010). Tutorial on agent-based modelling and simulation. J. Simulation 4, 151–162. doi: 10.1057/jos.2010.3

CrossRef Full Text | Google Scholar

Mansournia M., Wu B., Matsushita N., Hogetsu T. (2012). Genotypic analysis of the foliose lichen Parmotrema tinctorum using microsatellite markers: Association of mycobiont and photobiont, and their reproductive modes. Lichenologist 44, 419–440. doi: 10.1017/S0024282911000909

CrossRef Full Text | Google Scholar

Matthews J., Crowder C., Oakley C., Lutz A., Roessner U., Meyer E., et al. (2017). Optimal nutrient exchange and immune responses operate in partner specificity in the cnidarian-dinoflagellate symbiosis. Proc. Natl. Acad. Sci. U.S.A. 114, 13194–13199. doi: 10.1073/pnas.1710733114

PubMed Abstract | CrossRef Full Text | Google Scholar

McFall-Ngai M. (2014). Divining the essence of symbiosis: Insights from the squid-vibrio model. PloS Biol. 12, e1001783. doi: 10.1371/journal.pbio.1001783

PubMed Abstract | CrossRef Full Text | Google Scholar

McGinley M., Aschaffenburg M., Pettay D., Smith R., LaJeunesse T., Warner M. (2012). Symbiodinium spp. in colonies of eastern Pacific Pocillopora spp. are highly stable despite the prevalence of low-abundance background populations. Mar. Ecol. Prog. Ser. 462, 1–7. doi: 10.3354/meps09914

CrossRef Full Text | Google Scholar

Mitra D., Navendra U., Panneerselvam U., Ansuman S., Ganeshamurthy A., Divya J. (2019). Role of mycorrhiza and its associated bacteria on plant growth promotion and nutrient management in sustainable agriculture. Int. J. Life Sci. Appl. Sci. 1, 1–10.

Google Scholar

Molins A., García-Breijo F. J., Reig-Armiñana J., Campo E. M., Casano L. M., Barreno E. (2013). Coexistence of different intrathalline symbiotic algae and bacterial biofilms in the foliose Canarian lichen Parmotrema pseudotinctorum. Vieraea. Folia Scientarum Biologicarum Canariensium 41, 349–370. doi: 10.31939/vieraea.2013.41.23

CrossRef Full Text | Google Scholar

Murray J. (2002). Mathematical biology: I. An Introduction Vol. 3 (New York: Springer).

Google Scholar

Muscatine L. (1971). Experiments on green algae coexistent with zooxanthellae in sea anemones. Pacific Sci. 25, 13–21.

Google Scholar

Nawroth J., Guo H., Koch E., Heath-Heckman E., Hermanson J., Ruby E., et al. (2017). Motile cilia create fluid-mechanical microhabitats for the active recruitment of the host microbiome. Proc. Natl. Acad. Sci. U.S.A. 114, 9510–9516. doi: 10.1073/pnas.1706926114

PubMed Abstract | CrossRef Full Text | Google Scholar

Nelson P., May G. (2017). Coevolution between mutualists and parasites in symbiotic communities may lead to the evolution of lower virulence. Am. Nat. 190, 803–817. doi: 10.1086/694334

PubMed Abstract | CrossRef Full Text | Google Scholar

Nowak M., Sigmund K. (2002). “Super- and coinfection: The two extremes,” in Adaptive Dynamics of Infectious Diseases: In Pursuit of Virulence Management. Eds. U. D. U., Metz J., Sabelis M., Sigmund K. (Cambridge, UK: Cambridge University Press), 124–137.

Google Scholar

Nylin S., Agosta S., Bensch S., Boeger W., Braga M., Brooks D., et al. (2018). Embracing colonizations: A new paradigm for species association dynamics. Trends Ecol. Evol. 33, 4–14. doi: 10.1016/j.tree.2017.10.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohmura Y., Takeshita S., Kawachi M. (2019). Photobiont diversity within populations of a vegetatively reproducing lichen, Parmotrema tinctorum, can be generated by photobiont switching. Symbiosis 77, 59–72. doi: 10.1007/s13199-018-0572-1

CrossRef Full Text | Google Scholar

Pasternak Z., Blasius B., Abelson A., Achituv Y. (2006). Host-finding behaviour and navigation capabilities of symbiotic zooxanthellae. Coral Reefs 25, 201–207. doi: 10.1007/s00338-005-0085-2

CrossRef Full Text | Google Scholar

Pettay D., Wham D., Pinzon J., LaJeunesse T. (2011). Genotypic diversity and spatial-temporal distribution of Symbiodinium clones in an abundant reef coral. Mol. Ecol. 20, 5197–5212. doi: 10.1111/j.1365-294X.2011.05357.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Piercey-Normore M., Athukorala S. (2017). Interface between fungi and green algae in lichen associations. Botany 95, 1005–1014. doi: 10.1139/cjb-2017-0037

CrossRef Full Text | Google Scholar

Piro F., Focaia R., Dou Z., Masci S., Smith D., Cristina M. D. (2021). An uninvited seat at the dinner table: How Apicomplexan parasites scavenge nutrients from the host. Microorganisms 9, 2592. doi: 10.3390/microorganisms9122592

PubMed Abstract | CrossRef Full Text | Google Scholar

Pool R., Muscatine L. (1980). “Phagocytic recognition and the establishment of the Hydra viridis – Chlorella symbiosis,” in Endosymbiosis and Cell Biology. Eds. Schenk H., Schwemmler W. (Amsterdam: De Gruyter), 223–240.

Google Scholar

Rädecker N., Pogoreutz C., Gegner H., Cardenas A., Roth F., Bougoure J., et al. (2021). Heat stress destabilizes symbiotic nutrient cycling in corals. Proc. Natl. Acad. Sci. U.S.A. 118, e2022653118. doi: 10.1073/pnas.2022653118

PubMed Abstract | CrossRef Full Text | Google Scholar

Rahat M. (1985). Competition between Chlorellae in chimeric infections of Hydra viridis: The evolution of stable symbiosis. J. Cell Sci. 77, 87–92. doi: 10.1242/jcs.77.1.87

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramesh A., Hall S. (2023). Niche theory for within-host parasite dynamics: Analogies to food web modules via feedback loops. Ecol. Lett. 26, 351–368. doi: 10.1111/ele.14142

PubMed Abstract | CrossRef Full Text | Google Scholar

Romano J., Beaumont C., Carrasco J., Ehrenman K., Bavoil P., Coppens I. (2013). Fierce competition between Toxoplasma and Chlamydia for host cell structures in dually infected cells. Eukaryotic Cell 12, 265–277. doi: 10.1128/EC.00313-12

PubMed Abstract | CrossRef Full Text | Google Scholar

Ross R. (1916). An application of the theory of probabilities to the study of a priori pathometry (part i). Proc. R. Soc. A: Mathematical Phys. Eng. Sci. 92, 204–226. doi: 10.1098/rspa.1916.0007

CrossRef Full Text | Google Scholar

Rowan R. (2004). Thermal adaptation in reef coral symbionts. Nature 430, 742. doi: 10.1038/430742a

PubMed Abstract | CrossRef Full Text | Google Scholar

Roy R., Reinders A., Ward J., McDonald T. (2020). Understanding transport processes in lichen, azolla-cyanobacteria, ectomycorrhiza, endomycorrhiza, and rhizobia-legume symbiotic interactions. F1000 Res. 9, 39. doi: 10.12688/f1000research.19740.1

CrossRef Full Text | Google Scholar

Sanders B., Muller-Parker G. (1997). The effects of temperature and light on two algal populations in the temperate sea anemone Anthopleura elegantissima (Brandt 1835). J. Exp. Mar. Biol. Ecol. 211, 213–224. doi: 10.1016/S0022-0981(96)02723-2

CrossRef Full Text | Google Scholar

Secord D., Augustine L. (2000). Biogeography and microhabitat variation in temperate algalinvertebrate symbioses: Zooxanthellae and zooChlorellae in two Pacific intertidal sea anemones, Anthopleura elegantissima and A. xanthogrammica. Invertebrate Biol. 119, 139–114. doi: 10.1111/j.1744-7410.2000.tb00002.x

CrossRef Full Text | Google Scholar

Septer A. (2019). The Vibrio-squid symbiosis as a model for studying interbacterial competition. mSystems 4, e00108-19. doi: 10.1128/mSystems.00108-19

PubMed Abstract | CrossRef Full Text | Google Scholar

Silverstein R., Correa A., Baker A. (2012). Specificity is rarely absolute in coral–algal symbiosis: Implications for coral response to climate change. Proc. R. Soc. B: Biol. Sci. 279, 2609–2618.

Google Scholar

Smith N., Trauer J., Gambhir M., Richards J., Maude R., J.M J. K., et al. (2018). Agent-based models of malaria transmission: a systematic review. Malaria J. 17, 299. doi: 10.1186/s12936-018-2442-y

CrossRef Full Text | Google Scholar

Stat M., Gates R. (2011). Clade D Symbiodinium in Scleractinian corals: A “nugget” of hope, a selfish opportunist, an ominous sign, or all of the above. J. Mar. Biol. 2011, 1–9. doi: 10.1155/2011/730715

CrossRef Full Text | Google Scholar

Stat M., Loh W., LaJeunesse T., Hoegh-Guldberg O., Carter D. (2009). Coral-endosymbiont stability following a natural bleaching event. Coral Reefs 28, 709–713. doi: 10.1007/s00338-009-0509-5

CrossRef Full Text | Google Scholar

Tabasi M., Alesheikh A., Sofizadeh A., Saeidian B., Pradhan B., Alamri A. (2011). A spatio-temporal agent-based approach for modeling the spread of zoonotic cutaneous leishmaniasis in northeast Iran. Parasites Vectors 13, 572. doi: 10.1186/s13071-020-04447-x

CrossRef Full Text | Google Scholar

Thornhill D., Lewis A., Wham D., LaJeunesse T. (2014). Host specialist lineages dominate the adaptive radiation of reef coral endosymbionts. Evolution 68, 352–367. doi: 10.1111/evo.12270

PubMed Abstract | CrossRef Full Text | Google Scholar

Thornhill D., Xiang Y., Pettay D., Zhong M., Santos S. (2013). Population genetic data of a model symbiotic cnidarian system reveal remarkable symbiont specificity and vectored introduction across ocean basins. Mol. Ecol. 22, 4499–4515. doi: 10.1111/mec.12416

PubMed Abstract | CrossRef Full Text | Google Scholar

Tremblay P., Grover R., Maguer J., Hoogenboom M., Ferrier-Pages C. (2014). Carbon translocation from symbiont to host depends on irradiance and food availability in the tropical coral Stylophora pistillata. Coral Reefs 33, 1–13. doi: 10.1007/s00338-013-1100-7

CrossRef Full Text | Google Scholar

Ulstrup K., Oppen M., Kühl M., Ralph P. (2007). Inter-polyp genetic and physiological characterisation of Symbiodinium in an Acropora valida colony. Mar. Biol. 153, 225–234. doi: 10.1007/s00227-007-0806-x

CrossRef Full Text | Google Scholar

Wall C., Kaluhiokalani M., Popp B., Donahue M., Gates R. (2020). Divergent symbiont communities determine the physiology and nutrition of a reef coral across a light-availability gradient. ISME J. 14, 945–958. doi: 10.1038/s41396-019-0570-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Ware F., Fautin D. G., Buddemeier R. W. (1996). Patterns of coral bleaching: Modeling the adaptive bleaching hypothesis. Ecol. Model. 84, 199–121. doi: 10.1016/0304-3800(94)00132-4

CrossRef Full Text | Google Scholar

Werner G., Cronwell W., Cornelissen J., Kiers E. (2015). Evolutionary signals of symbiotic persistence in the legume–rhizobia mutualism. Proc. Natl. Acad. Sci. U.S.A. 112, 10262–10269. doi: 10.1073/pnas.1424030112

PubMed Abstract | CrossRef Full Text | Google Scholar

Wooldridge S. (2010). Is the coral-algae symbiosis really “mutually beneficial” for the partners. BioEssays 32, 615–625. doi: 10.1002/bies.200900182

PubMed Abstract | CrossRef Full Text | Google Scholar

Yahr R., Vilgalys R., DePriest P. (2004). Strong fungal specificity and selectivity for algal symbionts in Florida scrub Cladonia lichens. Mol. Ecol. 13, 3367–3378. doi: 10.1111/j.1365-294X.2004.02350.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Yellowlees D., Rees T., Leggat W. (2008). Metabolic interactions between algal symbionts and invertebrate hosts. Plant Cell Environ. 31, 679–694. doi: 10.1111/j.1365-3040.2008.01802.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang Z. (2003). Mutualism or cooperation among competitors promotes coexistence and competitive ability. Ecol. Model. 164, 271–282. doi: 10.1016/S0304-3800(03)00069-3

CrossRef Full Text | Google Scholar