Seasonal variation of ecosystem photosynthetic capacity and its environmental drivers in global grasslands

Ecosystem maximum photosynthetic rate (Amax) is an important ecosystem functional property, as it is critical for ecosystem productivity modeling. However, little is known about the mechanisms that regulate the seasonal variation of Amax in grasslands, one of the dominant vegetation types worldwide. In this study, we analyzed the seasonal variability of Amax of grassland sites across the globe and its environmental drivers. We found that grassland Amax had strong seasonal variations, which were influenced by the climate and agricultural management, such as grass cutting and grazing. Second, the seasonal variation of Amax at all arid grasslands [mean annual vapor pressure deficit (VPD) > 10 hPa] was driven more by changes in canopy physiological property (i.e., maximum photosynthetic rate per leaf area Amax_a) than canopy structural property (i.e., leaf area, presented by LAI), because Amax_a had stronger temporal variability than LAI in these ecosystems. Third, temperature and VPD were the most influential factors for the seasonal variability of Amax and LAI, but environmental variables only explained a small proportion of the seasonal variation of Amax_a, which was probably because Amax_a was more related to plant traits. Our findings provide new ideas for better parameterizations of Amax in terrestrial ecosystem models.

1. Introduction

Amax refers to ecosystem light-saturated CO₂ assimilation rates and represents the potential of an ecosystem’s photosynthetic capacity. It is an important ecosystem functional property (Reichstein et al., 2014), determining ecosystem carbon assimilation. Seasonal variations in Amax are critical in determining the seasonality and magnitude of gross primary productivity (GPP) in terrestrial ecosystem modeling (Wilson et al., 2001; Medvigy et al., 2013). Therefore, understanding the seasonal variability of Amax and its drivers is vital for improving the understanding of the variability of GPP and the impact of climate change on the terrestrial ecosystem carbon cycle (Luo and Schuur, 2020).

Many studies have shown that Amax has strong seasonal variability in many ecosystem types (Hollinger et al., 1999; Zhang et al., 2006; Polley et al., 2010). Evidence suggests that environmental factors, such as light, temperature, and water, impact the seasonal variations of Amax (Zhang et al., 2006; Polley et al., 2010; Ryan et al., 2017). For example, water stress can directly affect stomatal conductance and the availability of the CO₂ substrate and thus reduce plant photosynthetic capacity (Reich et al., 2018). Leaves can adjust their photosynthetic rates to acclimate or adapt to changes in air temperature and solar radiation on intermediate to long-term timescales (Way and Yamori, 2014; Luo and Keenan, 2020). These environmental variables impact vegetation photosynthetic capacity through two different mechanisms. One is through influencing the canopy’s physiological properties (i.e., the maximum photosynthesis rate per leaf area Amax_a) (Joswig et al., 2021), and the other is through affecting the canopy’s structural properties (i.e., leaf area) (Hu et al., 2018; Li et al., 2019). Nevertheless, little literature has investigated to what extent the two mechanisms contribute to Amax.

Grasslands cover approximately 20–30% of the global land area (O’Mara, 2012), and have a great impact on the inter-annual variations in the global terrestrial carbon cycle (Poulter et al., 2014; Ahlström et al., 2015), thus it is important to understand grassland photosynthetic processes. However, knowledge of the mechanisms behind the seasonal variations in Amax of grassland ecosystems is limited. Therefore, in this study, we investigated the seasonal variations of grassland Amax. First, we derived the time series of Amax from flux measurements for 15 grassland sites in the FLUXNET 2015 dataset and analyzed its seasonal variations. Second, Amax was decomposed into leaf area index (LAI) and Amax_a (Amax = LAI × Amax_a), and their relative contributions to the variations of Amax were quantified. Third, we investigated the effect of environmental variables on the seasonal variations of Amax, Amax_a, and LAI.

2. Data and methods

2.1. Site information and meteorological data

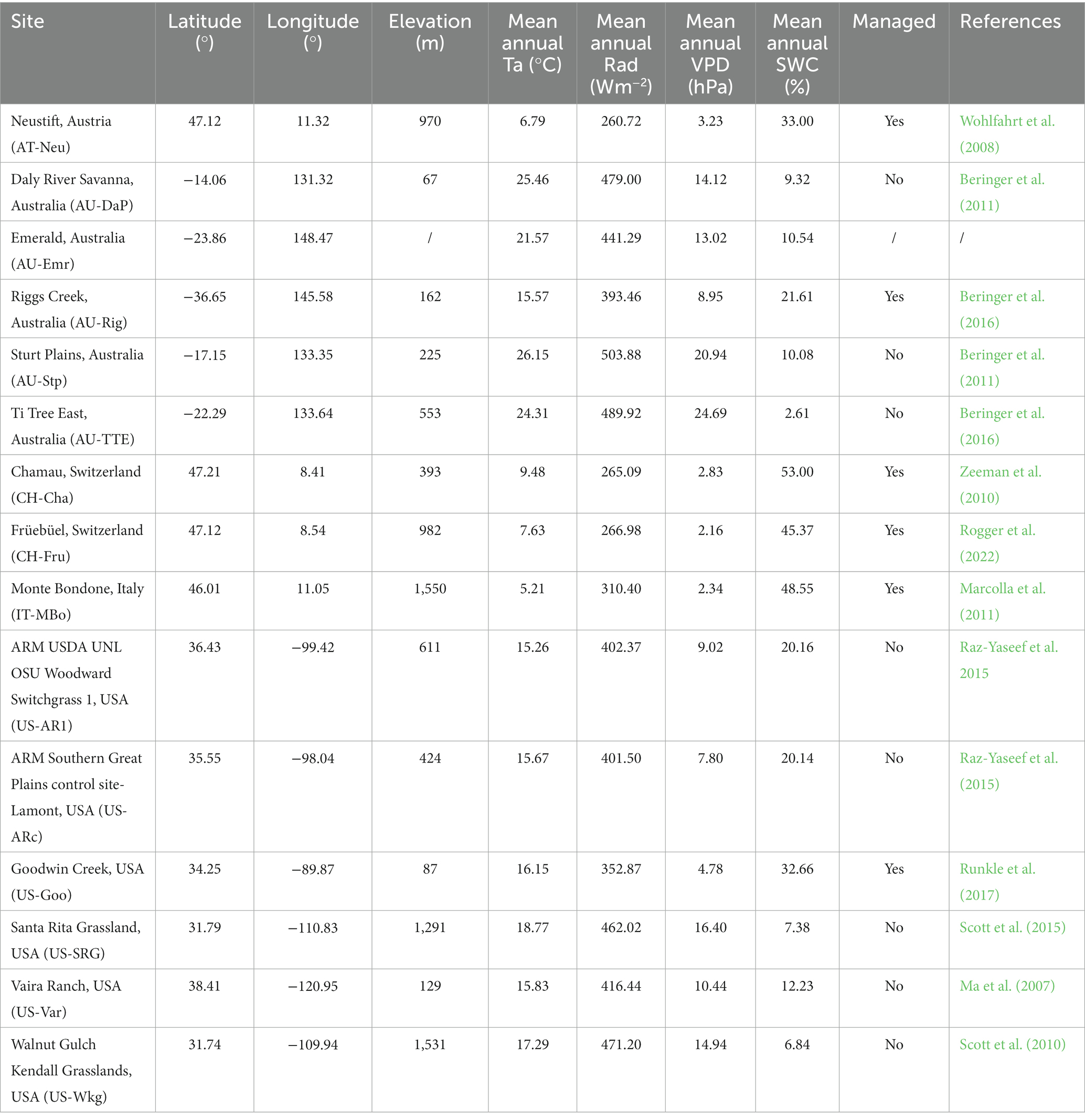
Half-hourly eddy covariance (EC) flux data were used in this study to estimate the Amax of global grasslands. Data were retrieved from the FLUXNET 2015 Tier 1 dataset.¹ Intotal, 15 EC flux sites were analyzed in this study. These sites were selected based on the data availability (i.e., sites with more than 60% of Amax_a data over the available years). Meteorological data measured alongside the flux data were also used, including soil water content (SWC), vapor pressure deficit (VPD), air temperature (Ta), and solar shortwave radiation (Rad). Detailed information for the sites used in this study is listed in Table 1.

TABLE 1

Table 1. Grasslands used in this study.

2.2. Remote sensing data

Leaf area index data (LAI) were extracted from the moderate resolution imaging spectroradiometer (MODIS) Leaf Area Index/FPAR Products version 6.1 (MOD15A2H v061). This product was an 8-day composite dataset with a spatial resolution of 500 m. We filtered out those data points where significant clouds or snow were present, or where the data quality was poor according to the quality flags (FparLai_QC and FparExtra_QC) provided by this dataset. The average LAI of pixels within a 500 m radius around the flux tower was used to represent the LAI of the site, because Chu et al., 2021 suggested that target areas with a smaller radial distance from the flux tower tend to be less biased in representing the land surface characteristics as covered by the flux footprint climatology. Then, the LAI time series were smoothed using the Savitzky–Golay (SG) filter, which has widely been used to remove the noises in MODIS LAI data (Zhu et al., 2016; Huang et al., 2021).

Normalized difference vegetation index (NDVI) data were downloaded from the MODIS C6 (MOD13C1) which had a resolution of 16-day and 500 m. The average NDVI of pixels that are within a 500 m radius around the flux tower was used to represent the NDVI of the site. To match the temporal resolution of LAI, we interpolated the NDVI time series to the LAI dates using linear interpolation.

2.3. Estimation of ecosystem maximum photosynthetic rate

We used the daytime flux partitioning method to derive the parameters of photosynthesis and respiration. The daytime flux partitioning method uses a light response curve to fit the flux of CO₂. We followed the method proposed by Lasslop et al. (2010), with a small modification of separately estimating day-time and night-time reference respiration rates to account for light inhibition of leaf respiration (Keenan et al., 2019):

$\begin{array}{ll}{F}_c=\frac{\alpha \beta R_g}{\alpha R_g+\beta }+F_r& (1)\end{array}$

where α (μmol C J⁻¹) is the canopy-scale quantum yields; β (μmol C m⁻² s⁻¹) is canopy light-saturated CO₂ assimilation rate; R_g (W m⁻²) is incoming shortwave radiation; and F_r (μmol C m⁻² s⁻¹) is the ecosystem respiration term. Parameter β is estimated as an exponentially decreasing function of VPD, to account for the effect of VPD on apparent photosynthesis:

$\beta =\{\begin{array}{c}{\beta }_0\exp \left(-k\left(VPD-VP{D}_0\right)\right),VPD>VP{D}_0\\ {\beta }_0,VPD<VP{D}_0\end{array}\text{ (2)}$

where β₀ and k are fitted parameters and VPD₀ is set to 10 hPa, as in Lasslop et al., (2010). β₀ is the canopy light-saturated CO₂ assimilation rate after removing the influence of VPD, which is equivalent to Amax.

Ecosystem respiration F_r is described by the Lloyd and Taylor model as

$\begin{array}{ll}{F}_r=R_{ref}\exp \left(E_0\left(\frac{1}{T_{ref}-T_0}-\frac{1}{T_{air}-T_0}\right)\right)& (3)\end{array}$

where R_ref (μmol C m⁻² s⁻¹) is the reference respiration rate at the reference temperature (T_ref = 15°C) and E₀ (°C) is the temperature sensitivity. T_air is the air temperature and the parameter T₀ (°C) is set to a constant of −46.02°C following Lloyd and Taylor (1994).

To get the seasonal variations of the parameters in the above model, we fitted the equations above to a dynamic window of 2–14 days of Fc depending on the availability of flux measurements, and assumed that every day in the same time window has the same daily parameters. We retrieved the time series of all parameters in the above model (i.e., α, β₀, k, R_ref, and E₀) for each site by implementing Equations (1)–(3) using the REddyProc R package.² The estimated Amax time series were smoothed with a nonparametric method for estimating regression surfaces (LOESS).

The light-saturated photosynthetic rate per unit leaf area (Amax_a) was calculated as the ratio of Amax to LAI. The unit of Amax is μmol m⁻² ground area s⁻¹ and the unit of Amax_a is μmol m⁻² leaf area s⁻¹. Then, the reason why the ratio of Amax to LAI is Amax_a is demonstrated in Equation (4):

$\begin{array}{c}\begin{array}{l}\frac{Amax}{LAI}=\frac{\mu mol{m}^{-2}ground\mathrm{}area{s}^{-1}}{\frac{m^{2}leaf\mathrm{}area}{m^{2}ground\mathrm{}area}}\\ =\frac{\mu mol{m}^{-2}ground\mathrm{}area{s}^{-1}\times m^{2}ground\mathrm{}area}{m^{2}leafarea}\end{array}\\ =\frac{\mu mol{s}^{-1}}{m^{2}leaf\mathrm{}area}=\mu mol{m}^{-2}leaf\mathrm{}area{s}^{-1}=Ama{x}_a\end{array}\text{ (4)}$

2.4. Statistical analyses

We used linear regression coefficients to quantify the environmental control on the seasonal variations in Amax, Amax_a, and LAI. Environmental variables included air temperature (Ta), solar radiation (Rad), SWC, VPD, and day length (Dlen). Day length was defined as the number of hours with Rad >4 W m⁻² each day. The effects of other environmental factors were also analyzed, but the other environmental factors did not show significant effects on Amax, Amax_a, or LAI. For Amax_a, we also added NDVI into the independent variables, because environmental variables had little explanatory power for Amax_a.

Data used for the seasonal analysis were integrated for every adjacent and non-overlapped eight-day window. Because the time series were multiyear, we divided the 8-day time series each year by the annual mean of that year to remove the inter-annual variations in the variables (Baldocchi et al., 2021). To make the regression coefficients of different variables comparable, we applied z-score standardization to the normalized time series before we conducted the linear regression.

The log–log scaling slope analysis was used to quantify the relative contribution of Amax_a and LAI to variations in Amax because Amax_a and LAI are related to Amax in a multiplicative manner (i.e., Amax = Amax_a × LAI) (Renton and Poorter, 2011). The relative contributions of Amax_a and LAI can be calculated as the regression coefficient of log(Amax) in the following equations:

$\begin{array}{ll}\log \left(Ama{x}_a\right)=a_{Ama{x}_a}+b_{Ama{x}_a}\ast \log \left(Amax\right)& (5)\end{array}$

$\begin{array}{ll}\log \left(LAI\right)=a_{LAI}+b_{LAI}\ast \log \left(Amax\right)& (6)\end{array}$

where a_Amaxa, a_LAI, b_Amaxa, and b_LAI are coefficients of the linear regression between Amax and Amax_a and LAI, in which b_Amaxa and b_LAI represent the relative contribution of Amax_a and LAI to the variations of Amax. b_Amaxa + b_LAI will always equal 1. If b_Amaxa is close to 1 and b_LAI is close to 0, then Amax_a is largely responsible for variations in Amax, whereas if b_Amaxa is close to 0 and b_LAI is close to 1, then LAI is largely responsible for variations in Amax. If b_Amaxa and b_LAI are both close to 0.5, then Amax_a and LAI are similarly responsible. More information about the derivation and effectiveness of this method can be found in Renton and Poorter (2011).

3. Results

3.1. Seasonal patterns of Amax, Amax_a, and LAI

The seasonal dynamics of Amax, Amax_a, and LAI and their multiyear averages for each site are shown in Figure 1 and Table 2, respectively. Amax had strong seasonal variations, mainly showing unimodal curves over the season. Amax at North Hemisphere sites usually exhibited a cyclical character each year, but some grasslands in Australia had variable temporal patterns of Amax, which were different for each year, such as at AU-Emr, AU-Stp, and AU-TTE. The seasonal pattern of Amax_a varied substantially among sites. CH-Cha and IT-MBo did not exhibit any clear seasonal trend in Amax_a, while Amax_a at other sites had strong seasonal variations, and often had a similar trend with Amax over the growing season. LAI also varied a lot over the season.

FIGURE 1

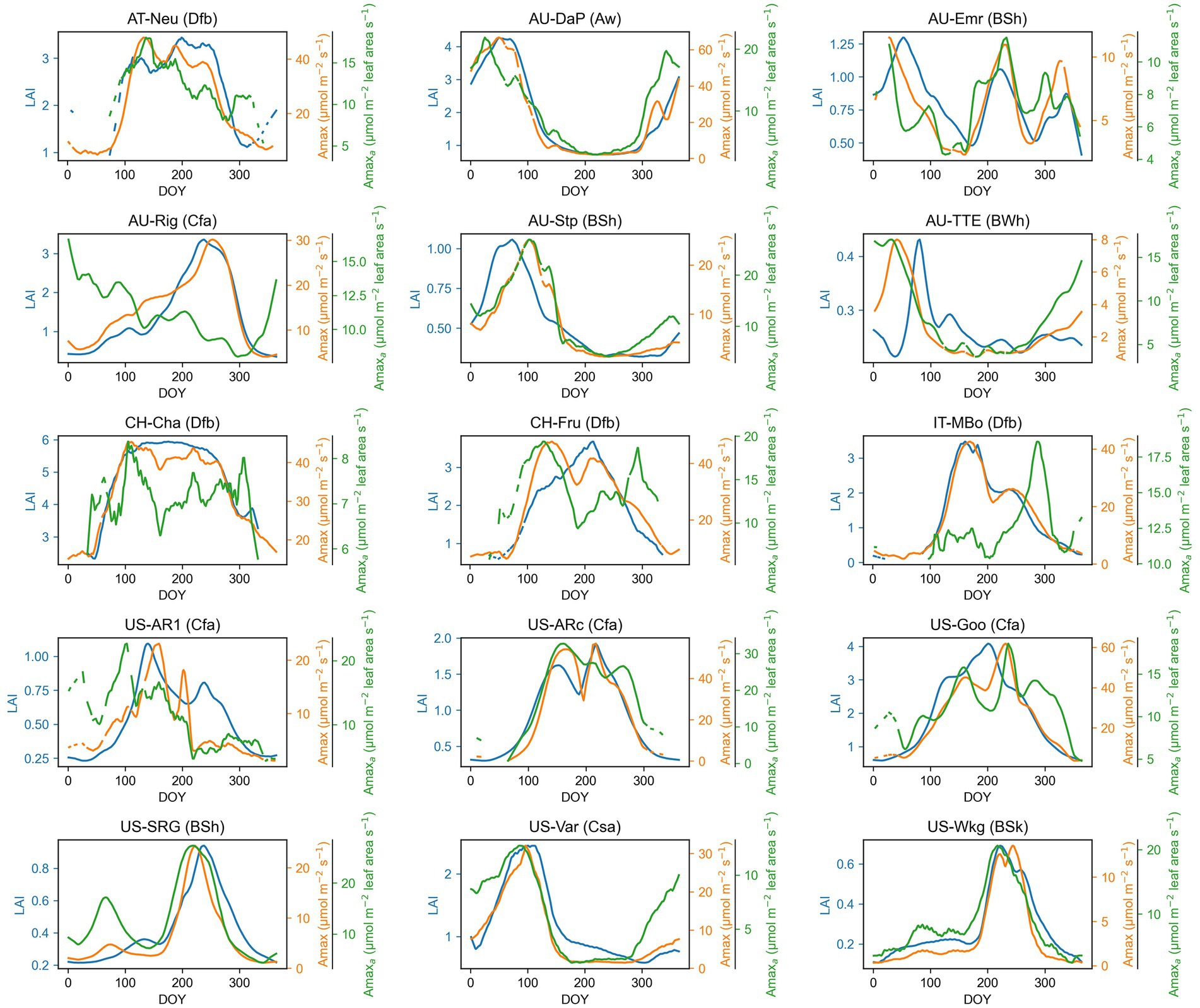
Figure 1. Seasonal patterns of maximum photosynthetic capacity (Amax), maximum photosynthetic capacity per leaf area (Amax_a), and leaf area index (LAI) for each grassland site. The time series presented in the graph are smoothed with a nonparametric method for estimating regression surfaces (LOESS). The abbreviation after each site name is the Köppen-Geiger climate classification dataset (Beck et al., 2018). Aw, Tropical, savannah; BSh, Arid, steppe, hot; BSk, Arid, steppe, cold; BWh, Arid, desert, hot; Cfa, Temperate, no dry season, hot summer; Csa, Temperate, dry summer, hot summer; Dfb, Cold, no dry season, warm summer.

TABLE 2

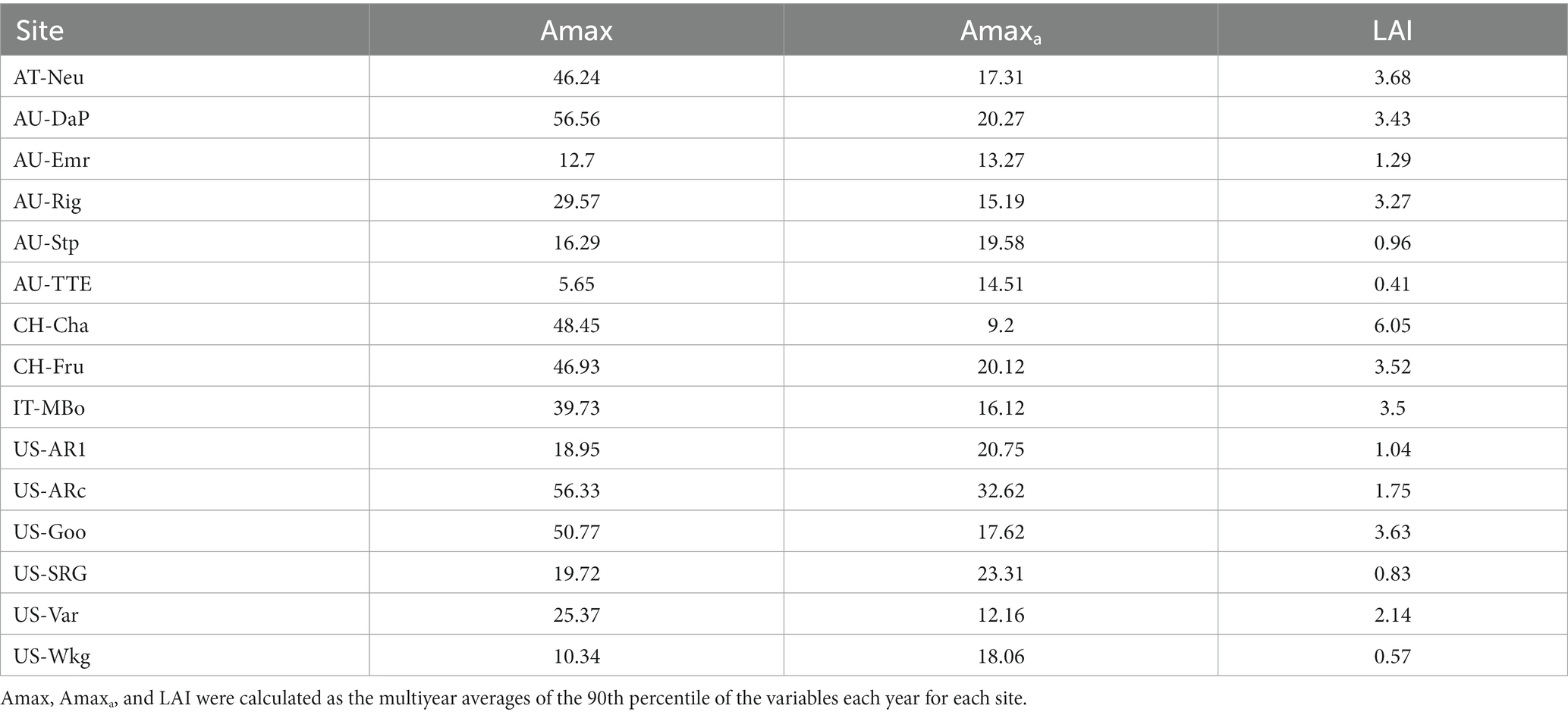
Table 2. Ecosystem maximum photosynthetic capacity (Amax), maximum photosynthetic capacity per leaf area (Amax_a), and leaf area index (LAI) for each grassland.

The climate influenced the seasonal patterns of Amax, Amax_a, and LAI. In grasslands located in no dry season climate according to Köppen-Geiger climate classification (e.g., AT-Neu, CH-Cha, CH-Fru, IT-MBo, US-AR1, US-ARc, and US-Goo), Amax, Amax_a, and LAI were higher in higher temperature and radiation season. In contrast, in arid or dry summer sites, the seasonal pattern of Amax, Amax_a, and LAI was driven more by water availability (Figure 2). For example, at the US-SRG, US-Var, and US-Wkg sites, Amax was significantly greater during higher water availability periods, but lower in high temperature and radiation periods because of the associated low water availability.

FIGURE 2

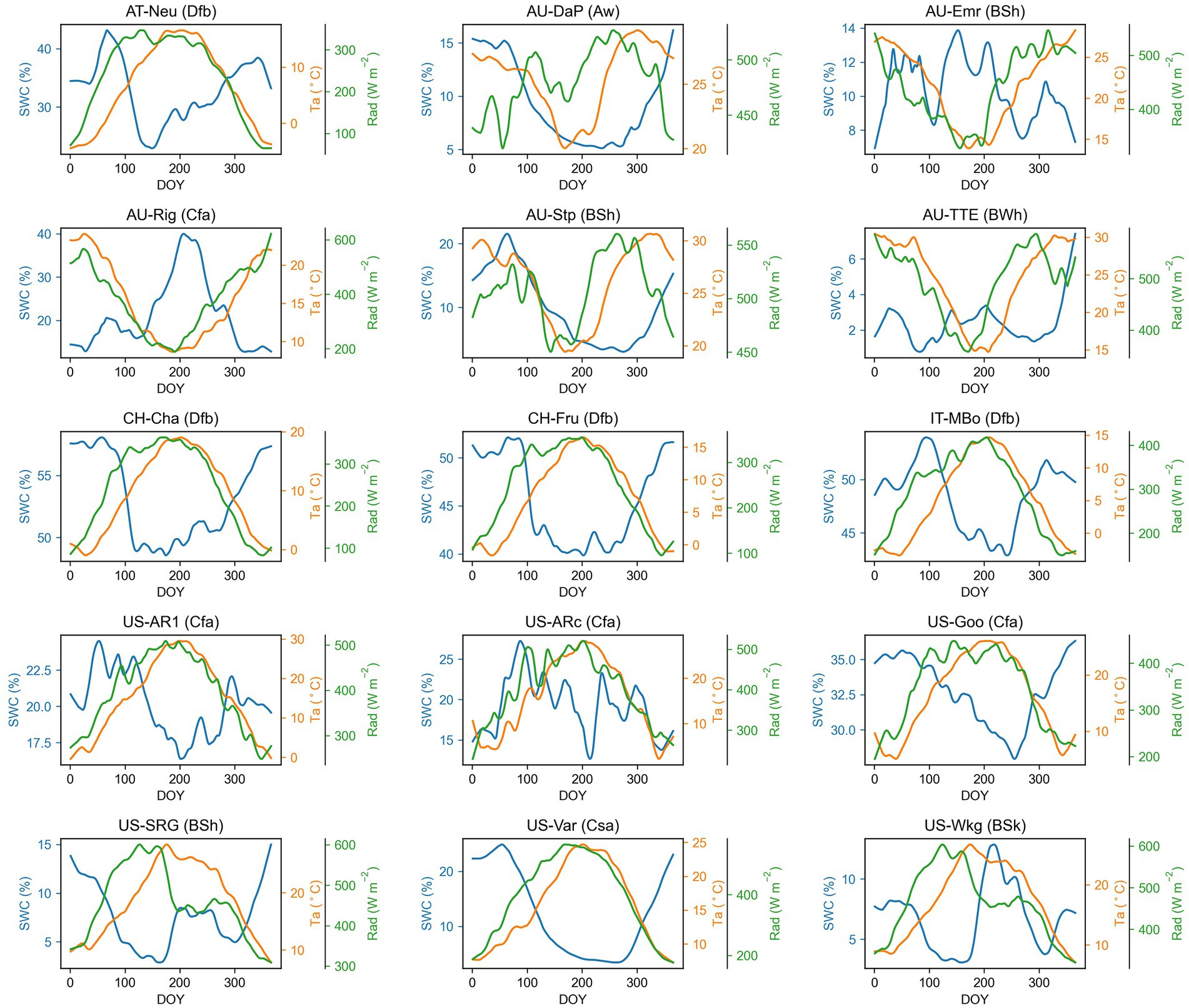
Figure 2. Seasonal patterns of air temperature (Ta), solar radiation (Rad), and soil water content (SWC) for each grassland site. The time series presented in the graph are smoothed with a nonparametric method for estimating regression surfaces (LOESS). The abbreviation after each site name is the Köppen-Geiger climate classification dataset (Beck et al., 2018). Aw, Tropical, savannah; BSh, Arid, steppe, hot; BSk, Arid, steppe, cold; BWh, Arid, desert, hot; Cfa, Temperate, no dry season, hot summer; Csa, Temperate, dry summer, hot summer; Dfb, Cold, no dry season, warm summer.

In addition to climate, agricultural management practices also impacted the seasonal variation of Amax, Amax_a, and LAI. At sites under intensive management practices (i.e., AT-Neu, CH-Cha, CH-Fru, IT-MBo, US-Goo), the unimodal curve of Amax and LAI changed by grass cutting and grazing, which can reduce Amax and LAI. As shown in the seasonal patterns of Amax at these sites, Amax decreased after each cutting or grazing event and later gradually recovered, which added fluctuation into the unimodal seasonal pattern of Amax (Figure 1). For example, at the AT-Neu site, the meadow was cut three times a year, the three cuts taking place between DOY 153 ~ 167, DOY 204 ~ 224, and DOY 264 ~ 301 (Wohlfahrt et al., 2008). We can observe decreases and recovery of Amax and Amax_a around the three cutting periods in our estimated Amax and Amax_a time series (Figure 1). After each cutting, the grassland could not recover to the same level of Amax as before cutting. Therefore, Amax was decreasing with each of the three cuttings. A similar pattern was also observed in IT-MBo, CH-Cha, and CH-Fru.

3.2. Relative contribution of Amax_a and LAI to the seasonal variation in Amax

Amax_a and LAI jointly influenced the seasonal variations of Amax (b_Amaxa and b_LAI ≠ 0) at all sites (Table 3). b_LAI > 0.5 at all managed sites, except CH-Cha, meaning that LAI contributed more to the seasonal variations in Amax than Amax_a at these sites, which might be because cutting and grazing caused more changes in LAI than in Amax_a.

TABLE 3

Table 3. Relative contribution of Amax_a and LAI to the seasonal variation in Amax.

We investigated the effect of air dryness on the relative contribution of LAI to Amax, and we found that b_LAI < 0.5 and b_Amaxa > 0.5 in all arid grasslands (mean annual VPD > 10 hPa), which indicated that Amax_a had more influence on Amax than LAI in these sites. In comparison, among moist grassland sites (mean annual VPD < 10 hPa), there were LAI-driven sites and Amax_a-driven sites (Figure 3).

To explain the difference between arid and moist grasslands in the relative contribution of LAI and Amax_a to Amax, we further investigated the relationship of b_Amaxa with the relative magnitude of the seasonal variability of Amax_a and LAI and the relationship of mean annual VPD and SWC with the seasonal variability of Amax_a and LAI (Figure 4). We found that at sites where CV_Amaxa > CV_LAI, Amax_a contributed more to the seasonal variations of Amax than LAI (b_Amaxa > 0.5), and b_Amaxa < 0.5 at sites where CV_Amaxa < CV_LAI (Figure 4). Sites with CV_Amaxa > CV_LAI tended to have higher mean annual VPD (Figure 4A). Therefore, Amax_a dominated the seasonal variation of Amax at sites with higher mean annual VPD. Mean annual SWC did not show any correlation with the relative magnitude of CV_Amaxa and CV_LAI, but grasslands with higher mean annual SWC had lower absolute CV_Amaxa (Figure 4B).

FIGURE 3

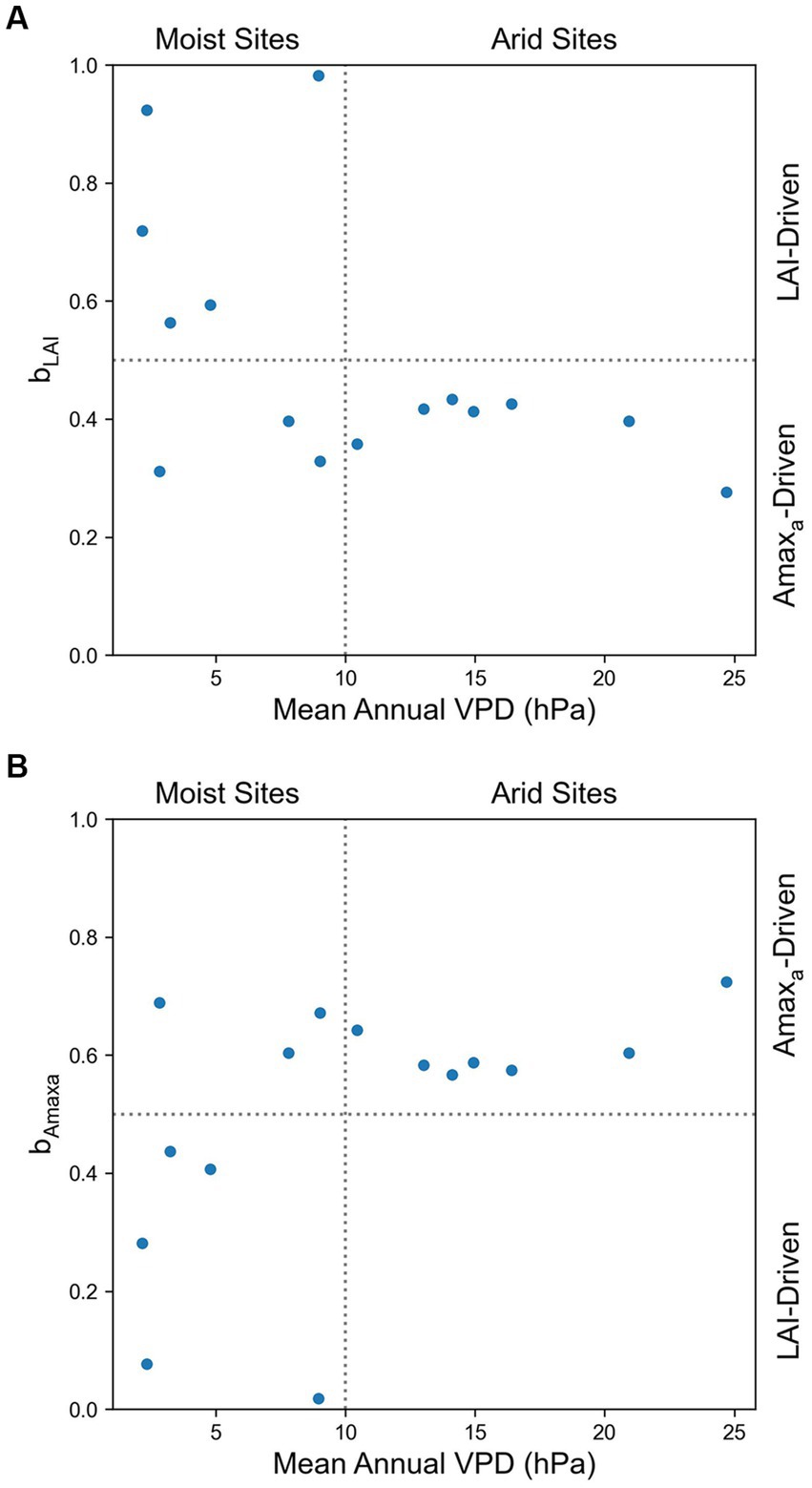
Figure 3. Effects of mean annual VPD on the relative contribution of (A) LAI (b_LAI) and (B) Amax_a (b_Amaxa) to the seasonal variation of Amax. b_LAI + b_Amaxa = 1.

3.3. Effects of environmental factors on the seasonal variations of Amax and its components Amax_a and LAI

Among the environmental variables, air temperature (Ta) showed strong control effects for the seasonal variations of Amax_a, LAI, and Amax (Table 4), with Ta having the largest absolute regression coefficient with them in most sites. Air dryness (VPD) also greatly influenced the seasonal variations of Amax_a, LAI, and Amax, especially for grasslands with a mean annual VPD > 10 hPa. It was consistently negatively associated with them at all sites. However, SWC, representing soil water condition, had a much smaller impact on Amax_a, LAI, and Amax. It positively correlated with them at all arid sites, but negatively correlated with them at some moist sites. Solar radiation and photoperiod were positively correlated with Amax_a, LAI, and Amax at many sites.

TABLE 4

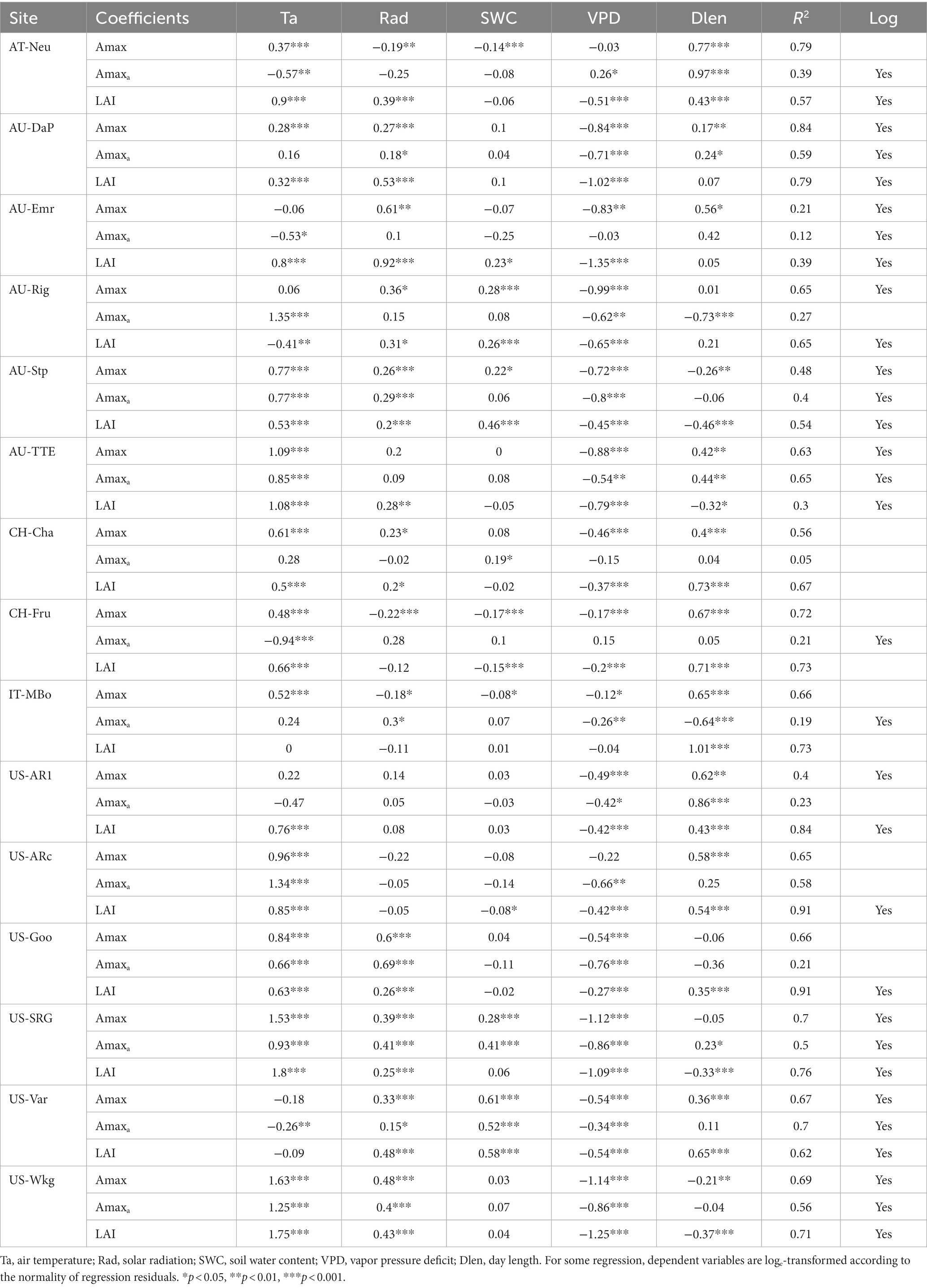
Table 4. Results (regression coefficients) of linear regression analysis with 8-day average Amax, Amax_a, and LAI as dependent and 8-day average Ta, Rad, SWC, VPD, and Dlen as independent variables.

Environmental variables explained on average 38, 70, and 62% of the seasonal variations in Amax_a, LAI, and Amax, respectively, which suggested environmental variables had a greater impact on LAI than on Amax_a. Therefore, environmental factors affected the seasonal variations of Amax mainly through its impact on LAI rather than through its impact on Amax_a.

Environmental variables had little explanatory power for Amax_a, except a few arid grasslands (i.e., AU-DaP, AU-TTE, US-Var, US-Wkg) where environmental factors can account for over 50% variance of Amax_a. The low average R² across sites suggested that environmental factors could affect Amax_a, but were not the main drivers for the seasonal variations of Amax_a. We further investigated whether vegetation greenness (represented by NDVI) was better correlated with Amax_a and found that the average R² for Amax_a with NDVI as one of the independent variables was 0.44, which was slightly greater than without NDVI. Coefficients of NDVI for Amax_a were significant at 11 of the 15 sites. These results suggested that the seasonal variations of Amax_a cannot be well explained by classical environmental factors, but may be more correlated with variations in plant traits such as pigment contents.

4. Discussion

4.1. Relative contribution of Amax_a and LAI to the seasonal variation in Amax

Our results suggested that Amax_a and LAI jointly determined the seasonal dynamics of Amax. The seasonal variation of Amax at all arid grasslands (mean annual VPD > 10 hPa) was driven more by changes in Amax_a than LAI, but the drivers of Amax for the moist grasslands (mean annual VPD < 10 hPa) were bimodal in that some sites were Amax_a-driven and others LAI-driven. The relative contribution of Amax_a and LAI to Amax was related to the relative magnitude of the temporal variability (CV) of Amax_a and LAI, which in turn, was influenced by mean annual VPD.

Annual air dryness influenced the relative magnitude of CV_Amaxa and CV_LAI from two aspects. On one hand, mean annual VPD was negatively correlated with LAI (the correlation coefficient between them was-0.77, p < 0.001), suggesting that drier grasslands tended to have lower LAI, and hence the magnitude of temporal variation in LAI would be smaller. On the other hand, VPD could affect leaf photosynthetic capacity directly by its control on leaf stomatal conductance (Fu et al., 2022), and indirectly by its impact on leaf traits. Moreover, environmental variables explained a large proportion of the variance in Amax_a in arid grasslands (Table 4) compared with wetter grasslands, which also suggested Amax_a in arid grasslands were more sensitive to changes in the environment. Therefore, lesser LAI and greater sensitivity of Amax_a to environmental variables in arid grasslands resulted in a greater contribution of Amax_a to Amax.

4.2. Effects of environmental factors on the seasonal variations of Amax, Amax_a, and LAI

At the seasonal scale, air temperature and air dryness were the driving factors for the variation in Amax. Other studies also identified the two factors as the most important factors to regulate grassland C fluxes (Polley et al., 2010; Scott et al., 2015; Wang et al., 2019). We also found that VPD was more correlated with Amax than SWC at the seasonal scale, which was also observed in previous studies (Ryan et al., 2017; Fu et al., 2022). The possible reason for this higher correlation of VPD and Amax at the seasonal scale could be related to the non-linear relationship between SWC and Amax, as suggested by previous studies (Xu and Zhou, 2011; Fu et al., 2022). Xu and Zhou (2011) found that the Amax of two grass species was enhanced under moderate soil moisture with reductions under both severe water deficit and excessive water conditions. Fu et al. (2022) suggested that Amax was also non-linearly correlated with soil moisture at the ecosystem scale, while VPD was consistently negatively related to Amax.

The environmental factors used in our study can explain the variances in LAI better than Amax and Amax_a. The explanatory power (R²) of linear regression can be impacted by intensive management practices or other irregular natural events, such as fire and extreme temperatures (Moore et al., 2016). For some sites, such as AT-Neu, IT-MBo, CH-Cha, and CH-Fru, previous studies at these sites have demonstrated that management practices, like cutting, grazing, and fertilization, can obscure the response of photosynthesis to environmental variables (Wohlfahrt et al., 2008; Zeeman et al., 2010; Marcolla et al., 2011; Rogger et al., 2022).

In our study, environmental variables only explained a small proportion of variance in Amax_a on the 8-day scale, much less than that of Amax and LAI, which is probably because canopy photosynthetic capacity per leaf area (Amax_a) was controlled more by leaf traits, such as nitrogen (N) and chlorophyll (Chl) content, than by environmental factors, compared with Amax and LAI. According to its definition in our study, Amax_a is the average of the maximum photosynthetic rate per leaf area of individual plants in the ecosystem, or more precisely, all plants within the footprint of the flux tower, a variable independent of the ecosystem structure embedded in LAI and intrinsically related to individual plants. Reichstein et al. (2014) have summarized that environmental variables can account for only a fraction of the temporal and spatial variance of flux-derived ecosystem functional properties (EFP), e.g., seasonal carbon-use efficiency and light-saturated gross primary production (similar to Amax), and suggested that a substantial part of the variation in EFP would be explained by plant traits. Furthermore, Feng and Dietze (2013) examined the relationship between the seasonal variation of Amax and leaf traits on 25 grassland species. They found that leaf N and Chl content significantly correlated with leaf Amax in both mass-and area-based manner. Therefore, we thought that the large unexplained variance in Amax_a was related to plant traits.

FIGURE 4

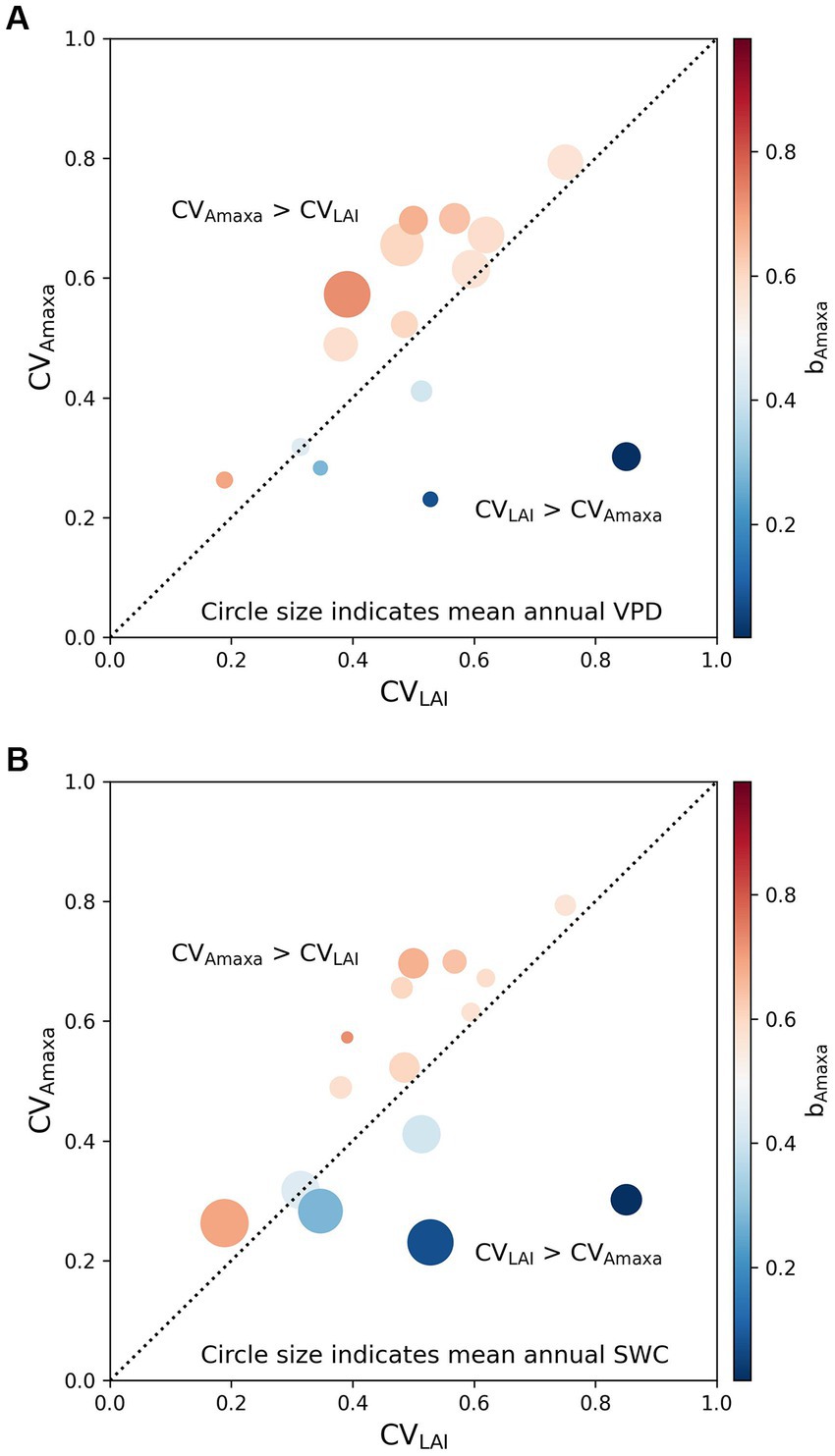
Figure 4. Effects of the relative magnitude of the temporal variability of Amax_a (CV_Amaxa) and LAI (CV_LAI) on the contribution of Amax_a to Amax (b_Amaxa) with circle size indicates (A) mean annual VPD and (B) mean annual SWC. The color indicates the contribution of Amax_a to Amax (b_Amaxa). b_Amaxa > 0.5 represents the seasonal variation of Amax is driven more by Amax_a, while b_Amaxa < 0.5 represents the seasonal variation of Amax is driven more by LAI. The black dotted line is a 1:1 line.

4.3. Uncertainties

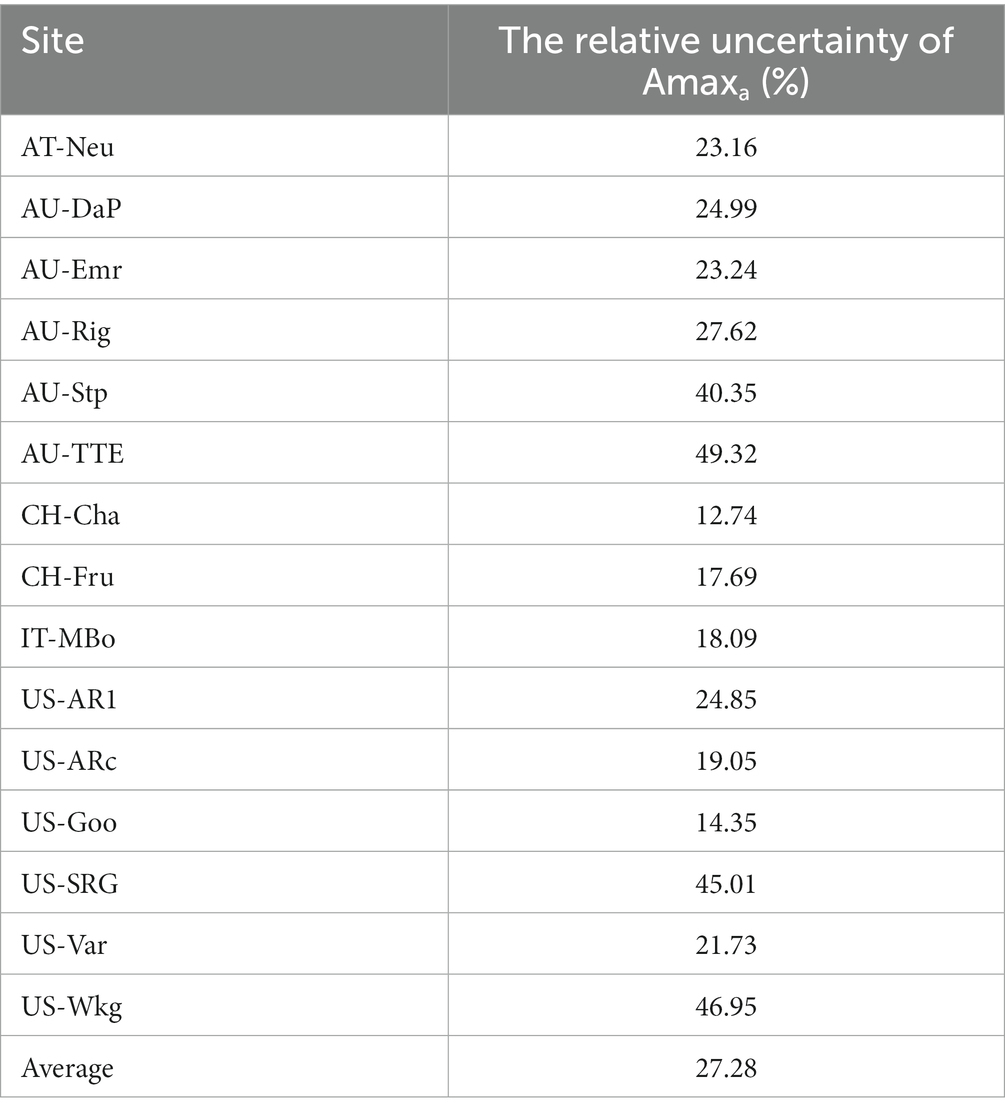
There are still some uncertainties in our estimation and analysis. The LAI data and Amax estimates used in this study had some uncertainty, which could propagate into Amax_a. To reduce the uncertainty of LAI, we tested whether the radius we used to extract LAI from the MODIS LAI dataset could have impacted the temporal dynamics of LAI. We extracted the average LAI of pixels within a 250, 500, 1,000, and 3,000 m radius centered at the flux tower. We found that these buffer sizes did not have much impact on the temporal dynamics in LAI. Then we assessed the influence of the uncertainty of the LAI dataset on Amax_a. Following He et al. (2014), we calculated the relative uncertainty in Amax_a induced by the uncertainty in LAI, which was expressed as the standard deviation for each LAI observation provided by the MODIS LAI dataset. The result (Table 5) showed that on average, the uncertainty in LAI could introduce 27.28% of uncertainty in Amax_a.

TABLE 5

Table 5. The uncertainty in Amax_a induced by the uncertainty in LAI.

The uncertainty of Amax estimates was assessed by the fitting quality flag provided by the REddyProc package. The results were shown in Figure 5. On average, each site had 52% of the Amax estimates that were of good quality, 48% of moderate quality, and no bad quality estimates.

FIGURE 5

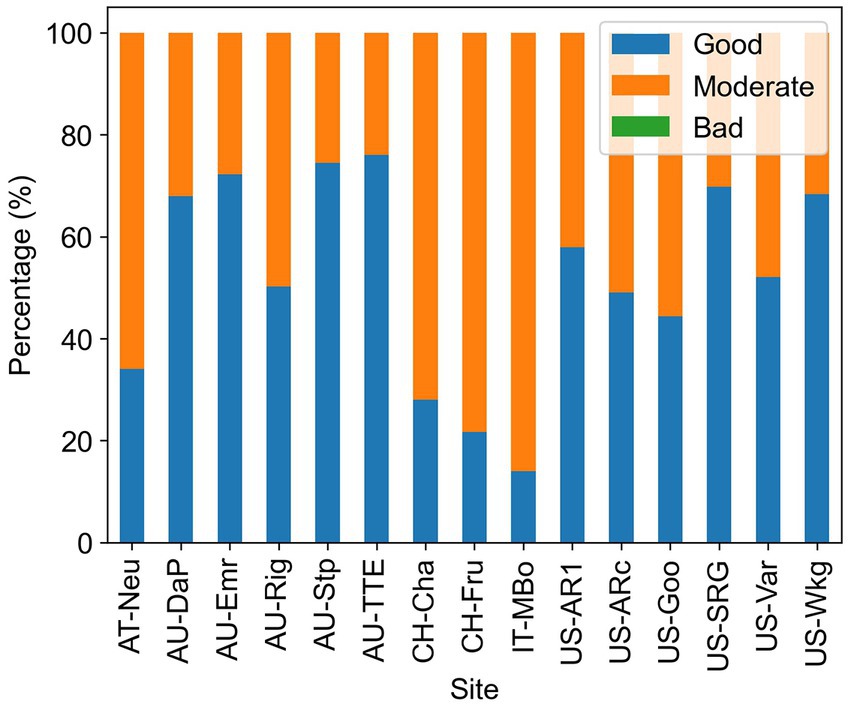
Figure 5. Percentage of the different qualities of the Amax estimates. High quality means all parameters in the fitted curve are within a reasonable range, moderate quality means the light response curve is fitted but some of the parameters are out of the reasonable range, and low quality means the light response curve cannot be well constrained using available data in 2 weeks.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XC: conceptualization, methodology, formal analysis, and writing (original draft). XR: conceptualization and editing. HH: conceptualization. LZ and YL: editing. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (No. 42030509) and the Special Project on National Science and Technology Basic Resources Investigation of China (No. 2021FY100705).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^ http://www.fluxnet.org/

2. ^ https://github.com/bgctw/REddyProc

References

Ahlström, A., Raupach, M. R., Schurgers, G., Smith, B., Arneth, A., Jung, M., et al. (2015). The dominant role of semi-arid ecosystems in the trend and variability of the land CO₂ sink. Sci. 348, 895–899. doi: 10.1126/science.aaa1668

CrossRef Full Text | Google Scholar

Baldocchi, D., Ma, S., and Verfaillie, J. (2021). On the inter-and intra-annual variability of ecosystem evapotranspiration and water use efficiency of an oak savanna and annual grassland subjected to booms and busts in rainfall. Glob. Chang. Biol. 27, 359–375. doi: 10.1111/gcb.15414

PubMed Abstract | CrossRef Full Text | Google Scholar

Beck, H. E., Zimmermann, N. E., McVicar, T. R., Vergopolan, N., Berg, A., and Wood, E. F. (2018). Present and future Koppen-Geiger climate classification maps at 1-km resolution. Sci. Data 5:180214. doi: 10.1038/sdata.2018.214

PubMed Abstract | CrossRef Full Text | Google Scholar

Beringer, J., Hutley, L. B., Hacker, J. M., Neininger, B., and Paw U, K. T. (2011). Patterns and processes of carbon, water and energy cycles across northern Australian landscapes: from point to region. Agric. For. Meteorol. 151, 1409–1416. doi: 10.1016/j.agrformet.2011.05.003

CrossRef Full Text | Google Scholar

Beringer, J., Hutley, L. B., McHugh, I., Arndt, S. K., Campbell, D., Cleugh, H. A., et al. (2016). An introduction to the Australian and New Zealand flux tower network – OzFlux. Biogeosciences 13, 5895–5916. doi: 10.5194/bg-13-5895-2016

CrossRef Full Text | Google Scholar

Chu, H., Luo, X., Ouyang, Z., Chan, W. S., Dengel, S., Biraud, S. C., et al. (2021). Representativeness of Eddy-Covariance flux footprints for areas surrounding AmeriFlux sites. Agric. For. Meteorol. 301-302:108350. doi: 10.1016/j.agrformet.2021.108350

CrossRef Full Text | Google Scholar

Feng, X., and Dietze, M. (2013). Scale dependence in the effects of leaf ecophysiological traits on photosynthesis: Bayesian parameterization of photosynthesis models. New Phytol. 200, 1132–1144. doi: 10.1111/nph.12454

PubMed Abstract | CrossRef Full Text | Google Scholar

Fu, Z., Ciais, P., Prentice, I. C., Gentine, P., Makowski, D., Bastos, A., et al. (2022). Atmospheric dryness reduces photosynthesis along a large range of soil water deficits. Nat. Commun. 13:989. doi: 10.1038/s41467-022-28652-7

PubMed Abstract | CrossRef Full Text | Google Scholar

He, H., Liu, M., Xiao, X., Ren, X., Zhang, L., Sun, X., et al. (2014). Large-scale estimation and uncertainty analysis of gross primary production in Tibetan alpine grasslands. J. Geophys. Res. Biogeo. 119, 466–486. doi: 10.1002/2013jg002449

CrossRef Full Text | Google Scholar

Hollinger, D. Y., Goltz, S. M., Davidson, E. A., Lee, J. T., Tu, K., and Valentine, H. T. (1999). Seasonal patterns and environmental control of carbon dioxide and water vapour exchange in an ecotonal boreal forest. Glob. Chang. Biol. 5, 891–902. doi: 10.1046/j.1365-2486.1999.00281.x

CrossRef Full Text | Google Scholar

Huang, A., Shen, R., Di, W., and Han, H. (2021). A methodology to reconstruct LAI time series data based on generative adversarial network and improved Savitzky-Golay filter. Int. J. Appl. Earth Obs. Geoinf. 105:102633. doi: 10.1016/j.jag.2021.102633

CrossRef Full Text | Google Scholar

Hu, Z., Shi, H., Cheng, K., Wang, Y. P., Piao, S., Li, Y., et al. (2018). Joint structural and physiological control on the interannual variation in productivity in a temperate grassland: A data-model comparison. Glob. Chang. Biol. 24, 2965–2979. doi: 10.1111/gcb.14274

CrossRef Full Text | Google Scholar

Joswig, J. S., Wirth, C., Schuman, M. C., Kattge, J., Reu, B., Wright, I. J., et al. (2021). Climatic and soil factors explain the two-dimensional spectrum of global plant trait variation. Nat. Ecol. Evol. 6, 36–50. doi: 10.1038/s41559-021-01616-8

CrossRef Full Text | Google Scholar

Keenan, T. F., Migliavacca, M., Papale, D., Baldocchi, D., Reichstein, M., Torn, M., et al. (2019). Widespread inhibition of daytime ecosystem respiration. Nat. Ecol. Evol. 3, 407–415. doi: 10.1038/s41559-019-0809-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Lasslop, G., Reichstein, M., Papale, D., Richardson, A. D., Arneth, A., Barr, A., et al. (2010). Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: critical issues and global evaluation. Glob. Chang. Biol. 16, 187–208. doi: 10.1111/j.1365-2486.2009.02041.x

CrossRef Full Text | Google Scholar

Li, F., Peng, Y., Zhang, D., Yang, G., Fang, K., Wang, G., et al. (2019). Leaf Area Rather Than Photosynthetic Rate Determines the Response of Ecosystem Productivity to Experimental Warming in an Alpine Steppe. J. Geophys. Res. Biogeosci. 124, 2277–2287. doi: 10.1029/2019jg005193

CrossRef Full Text | Google Scholar

Lloyd, J., and Taylor, J. A. (1994). On the temperature dependence of soil respiration. Funct. Ecol. 8, 315–323. doi: 10.2307/2389824

CrossRef Full Text | Google Scholar

Luo, X., and Keenan, T. F. (2020). Global evidence for the acclimation of ecosystem photosynthesis to light. Nat. Ecol. Evol. 4, 1351–1357. doi: 10.1038/s41559-020-1258-7

CrossRef Full Text | Google Scholar

Luo, Y., and Schuur, E. A. G. (2020). Model parameterization to represent processes at unresolved scales and changing properties of evolving systems. Glob. Chang. Biol. 26, 1109–1117. doi: 10.1111/gcb.14939

CrossRef Full Text | Google Scholar

Ma, S., Baldocchi, D. D., Xu, L., and Hehn, T. (2007). Inter-annual variability in carbon dioxide exchange of an oak/grass savanna and open grassland in California. Agric. For. Meteorol. 147, 157–171. doi: 10.1016/j.agrformet.2007.07.008

CrossRef Full Text | Google Scholar

Marcolla, B., Cescatti, A., Manca, G., Zorer, R., Cavagna, M., Fiora, A., et al. (2011). Climatic controls and ecosystem responses drive the inter-annual variability of the net ecosystem exchange of an alpine meadow. Agric. For. Meteorol. 151, 1233–1243. doi: 10.1016/j.agrformet.2011.04.015

CrossRef Full Text | Google Scholar

Medvigy, D., Jeong, S.-J., Clark, K. L., Skowronski, N. S., and Schäfer, K. V. R. (2013). Effects of seasonal variation of photosynthetic capacity on the carbon fluxes of a temperate deciduous forest. J. Geophysical Res. Biogeosci. 118, 1703–1714. doi: 10.1002/2013jg002421

CrossRef Full Text | Google Scholar

Moore, C. E., Brown, T., Keenan, T. F., Duursma, R. A., van Dijk, A. I. J. M., Beringer, J., et al. (2016). Reviews and syntheses: Australian vegetation phenology: new insights from satellite remote sensing and digital repeat photography. Biogeosciences 13, 5085–5102. doi: 10.5194/bg-13-5085-2016

CrossRef Full Text | Google Scholar

O’Mara, F. P. (2012). The role of grasslands in food security and climate change. Ann. Bot. 110, 1263–1270. doi: 10.1093/aob/mcs209

CrossRef Full Text | Google Scholar

Polley, H. W., Emmerich, W., Bradford, J. A., Sims, P. L., Johnson, D. A., Saliendra, N. Z., et al. (2010). Physiological and environmental regulation of interannual variability in CO₂ exchange on rangelands in the western United States. Glob. Chang. Biol. 16, 990–1002. doi: 10.1111/j.1365-2486.2009.01966.x

CrossRef Full Text | Google Scholar

Poulter, B., Frank, D., Ciais, P., Myneni, R. B., Andela, N., Bi, J., et al. (2014). Contribution of semi-arid ecosystems to interannual variability of the global carbon cycle. Nat. 509, 600–603. doi: 10.1038/nature13376

CrossRef Full Text | Google Scholar

Raz-Yaseef, N., Billesbach, D. P., Fischer, M. L., Biraud, S. C., Gunter, S. A., Bradford, J. A., et al. (2015). Vulnerability of crops and native grasses to summer drying in the U.S. southern Great Plains. Agric. Ecosyst. Environ. 213, 209–218. doi: 10.1016/j.agee.2015.07.021

CrossRef Full Text | Google Scholar

Reich, P. B., Sendall, K. M., Stefanski, A., Rich, R. L., Hobbie, S. E., and Montgomery, R. A. (2018). Effects of climate warming on photosynthesis in boreal tree species depend on soil moisture. Nat. 562, 263–267. doi: 10.1038/s41586-018-0582-4

CrossRef Full Text | Google Scholar

Reichstein, M., Bahn, M., Mahecha, M. D., Kattge, J., and Baldocchi, D. D. (2014). Linking plant and ecosystem functional biogeography. Proc. Natl. Acad. Sci. U. S. A. 111, 13697–13702. doi: 10.1073/pnas.1216065111

PubMed Abstract | CrossRef Full Text | Google Scholar

Renton, M., and Poorter, H. (2011). Using log-log scaling slope analysis for determining the contributions to variability in biological variables such as leaf mass per area: why it works, when it works and how it can be extended. New Phytol. 190, 5–8. doi: 10.1111/j.1469-8137.2010.03629.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Rogger, J., Hörtnagl, L., Buchmann, N., and Eugster, W. (2022). Carbon dioxide fluxes of a mountain grassland: drivers, anomalies and annual budgets. Agric. For. Meteorol. 314:108801. doi: 10.1016/j.agrformet.2021.108801

CrossRef Full Text | Google Scholar

Runkle, B. R. K., Rigby, J. R., Reba, M. L., Anapalli, S. S., Bhattacharjee, J., Krauss, K. W., et al. (2017). Delta-flux: an Eddy covariance network for a climate-smart lower Mississippi Basin. Agric. Environ. Lett. 2:ael2017.01.0003. doi: 10.2134/ael2017.01.0003

CrossRef Full Text | Google Scholar

Ryan, E. M., Ogle, K., Peltier, D., Walker, A. P., De Kauwe, M. G., Medlyn, B. E., et al. (2017). Gross primary production responses to warming, elevated CO₍₂₎, and irrigation: quantifying the drivers of ecosystem physiology in a semiarid grassland. Glob. Chang. Biol. 23, 3092–3106. doi: 10.1111/gcb.13602

CrossRef Full Text | Google Scholar

Scott, R. L., Biederman, J. A., Hamerlynck, E. P., and Barron-Gafford, G. A. (2015). The carbon balance pivot point of southwestern U.S. semiarid ecosystems: insights from the 21st century drought. J. Geophys. Res. Biogeosci. 120, 2612–2624. doi: 10.1002/2015jg003181

CrossRef Full Text | Google Scholar

Scott, R. L., Hamerlynck, E. P., Jenerette, G. D., Moran, M. S., and Barron-Gafford, G. A. (2010). Carbon dioxide exchange in a semidesert grassland through drought-induced vegetation change. J. Geophys. Res. 115:G03026. doi: 10.1029/2010JG001348

CrossRef Full Text | Google Scholar

Wang, N., Quesada, B., Xia, L., Butterbach-Bahl, K., Goodale, C. L., and Kiese, R. (2019). Effects of climate warming on carbon fluxes in grasslands-a global meta-analysis. Glob. Chang. Biol. 25, 1839–1851. doi: 10.1111/gcb.14603

PubMed Abstract | CrossRef Full Text | Google Scholar

Way, D. A., and Yamori, W. (2014). Thermal acclimation of photosynthesis: on the importance of adjusting our definitions and accounting for thermal acclimation of respiration. Photosynth. Res. 119, 89–100. doi: 10.1007/s11120-013-9873-7

CrossRef Full Text | Google Scholar

Wilson, K. B., Baldocchi, D. D., and Hanson, P. J. (2001). Leaf age affects the seasonal pattern of photosynthetic capacity and net ecosystem exchange of carbon in a deciduous forest. Plant Cell Environ. 24, 571–583. doi: 10.1046/j.0016-8025.2001.00706.x

CrossRef Full Text | Google Scholar

Wohlfahrt, G., Hammerle, A., Haslwanter, A., Bahn, M., Tappeiner, U., and Cernusca, A. (2008). Seasonal and inter-annual variability of the net ecosystem CO₍₂₎ exchange of a temperate mountain grassland: effects of climate and management. J. Geophys. Res. Atmos. 113:D08110. doi: 10.1029/2007jd009286

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Z., and Zhou, G. (2011). Responses of photosynthetic capacity to soil moisture gradient in perennial rhizome grass and perennial bunchgrass. BMC Plant Biol. 11:21. doi: 10.1186/1471-2229-11-21

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, L.-M., Yu, G.-R., Sun, X.-M., Wen, X.-F., Ren, C.-Y., Fu, Y.-L., et al. (2006). Seasonal variations of ecosystem apparent quantum yield (α) and maximum photosynthesis rate (Pmax) of different forest ecosystems in China. Agricul. Forest Meteorology 137, 176–187. doi: 10.1016/j.agrformet.2006.02.006

CrossRef Full Text | Google Scholar

Zeeman, M. J., Hiller, R., Gilgen, A. K., Michna, P., Plüss, P., Buchmann, N., et al. (2010). Management and climate impacts on net CO₂ fluxes and carbon budgets of three grasslands along an elevational gradient in Switzerland. Agric. For. Meteorol. 150, 519–530. doi: 10.1016/j.agrformet.2010.01.011

CrossRef Full Text | Google Scholar

Zhu, Z., Piao, S., Myneni, R. B., Huang, M., Zeng, Z., Canadell, J. G., et al. (2016). Greening of the earth and its drivers. Nat. Clim. Chang. 6, 791–795. doi: 10.1038/nclimate3004

CrossRef Full Text | Google Scholar