Wayne M. Getz1,2*- 1Department of Environment Sciences, Policy and Management, University of California, Berkeley, Berkeley, CA, United States
- 2School of Mathematics, Statistics & Computer Science, University of KwaZulu-Natal, Durban, South Africa
The methods used for predicting space use and geographic distribution adaptations of animals in response to global change have relied on fitting statistical and machine learning models to environmentally-contextualized movement and spatial distribution data. These predictions, however, are made at particular spatiotemporal scales (from home range to species distribution), but no comprehensive methods have been proposed for predicting how changes to subdiel segments of individual movement tracks may lead to emergent changes in the lifetime tracks of individuals, and hence in the redistribution of species under global change. In this article, we discuss in terms of a hierarchical movement track segmentation framework that, anchored by diel activity routines (DARs), how adaptions in the canonical activity modes (CAMs) of movement can be used to assess space use adaptations to landscape and climate change at scales ranging from subdiel movement segments to the lifetime tracks (LiTs) of individuals.
1. Introduction
Movement ecology has matured into an independent research field that supports its own eponymous meetings and journals, although it overlaps with several other distinct ecological fields. This overlap includes the following: (i) behavioral ecology's movement studies (Liedvogel et al., 2013; Hertel et al., 2020), (ii) resource ecology's search for resources dispersed over landscapes (Mueller and Fagan, 2008; Abrahms et al., 2021), and (iii) animal social ecology's coordinated movement studies (Couzin et al., 2005; Schweinfurth et al., 2022), as well as how movement is influenced by social networks (Jacoby and Freeman, 2016).
Movement ecology was created a decade-and-a-half earlier as the interplay of the why (motivational aspects), where (navigational aspects), when (external contexts), and how (modes of movement) of animal movements occurred (Nathan et al., 2008). This framing alone does not provide a road map for the construction of quantitative animal movement models, while the bulk of existing quantitative animal movement models, regardless of whether related to this framework or not, do not shed light upon how changes in daily movement patterns scale up when using models to forecast long-term space-use adaptations under global change.
The focus of forecasting models in movement ecology has been 2-fold. The first focus is on the resolution of fitting models to environmentally-contextualized sub-daily relocation time-series data (Dodge et al., 2013), a variety of statistical (Williams et al., 2020), state-space (Hooten et al., 2017; Patterson et al., 2017), and machine learning approaches (Wang, 2019; Torney et al., 2021) have been considered, including recurrent neural network learning incorporating step-selection kernel density constructions (Rew et al., 2019). The second focus is on the resolution of the seasonal location of populations over selected geographical regions, niches or species distribution models have been used to assess how the distribution of species shifts over time (Elith and Leathwick, 2009), with effects on dispersal in response to global change (Austin and Van Niel, 2011; Travis et al., 2013), which has particular relevance to movement ecology. Although the performance of these two types of models can be statistically assessed under certain assumptions, they are generally unable to forecast space-use adaptations that emerge because of locomotory changes in movement patterns at finer spatio-temporal scales of resolution.
2. Motivation for a hierarchical approach
Arguably, the best way to capture emergent space-use change at the locomotory data level is to model movement at hierarchical scales that parallel emergent patterns such as canonical activity modes (CAMs; i.e., track segments dominated by a distinguishing activity such as grazing, searching, or directed walking—e.g., see Getz and Saltz, 2008; Owen-Smith et al., 2010), diel activity routines (DARs; Owen-Smith and Goodall, 2014), and lifetime movement phases (LiMPs; Teitelbaum and Mueller, 2019), as well as lifetime tracks (LiTs) (Getz, 2022) (Table 1). For example, forecasting how seasonal use of spatial structures, such as home ranges, are likely to adapt to climate change may be best predicted by a model that relies on knowledge of how an individual's CAMs and DARs are affected by temperature and rainfall conditions, or the distribution of resources during the season under consideration. In this case, a hierarchical understanding of how the tracks of animals play out at different spatiotemporal scales (Torney et al., 2018) facilitates changes in the movement structure of animals tracks during their different LiMPs of dispersal (Travis et al., 2013), seasonal ranging (Burton-Roberts et al., 2022), and migration (Seebacher and Post, 2015) (Table 1).
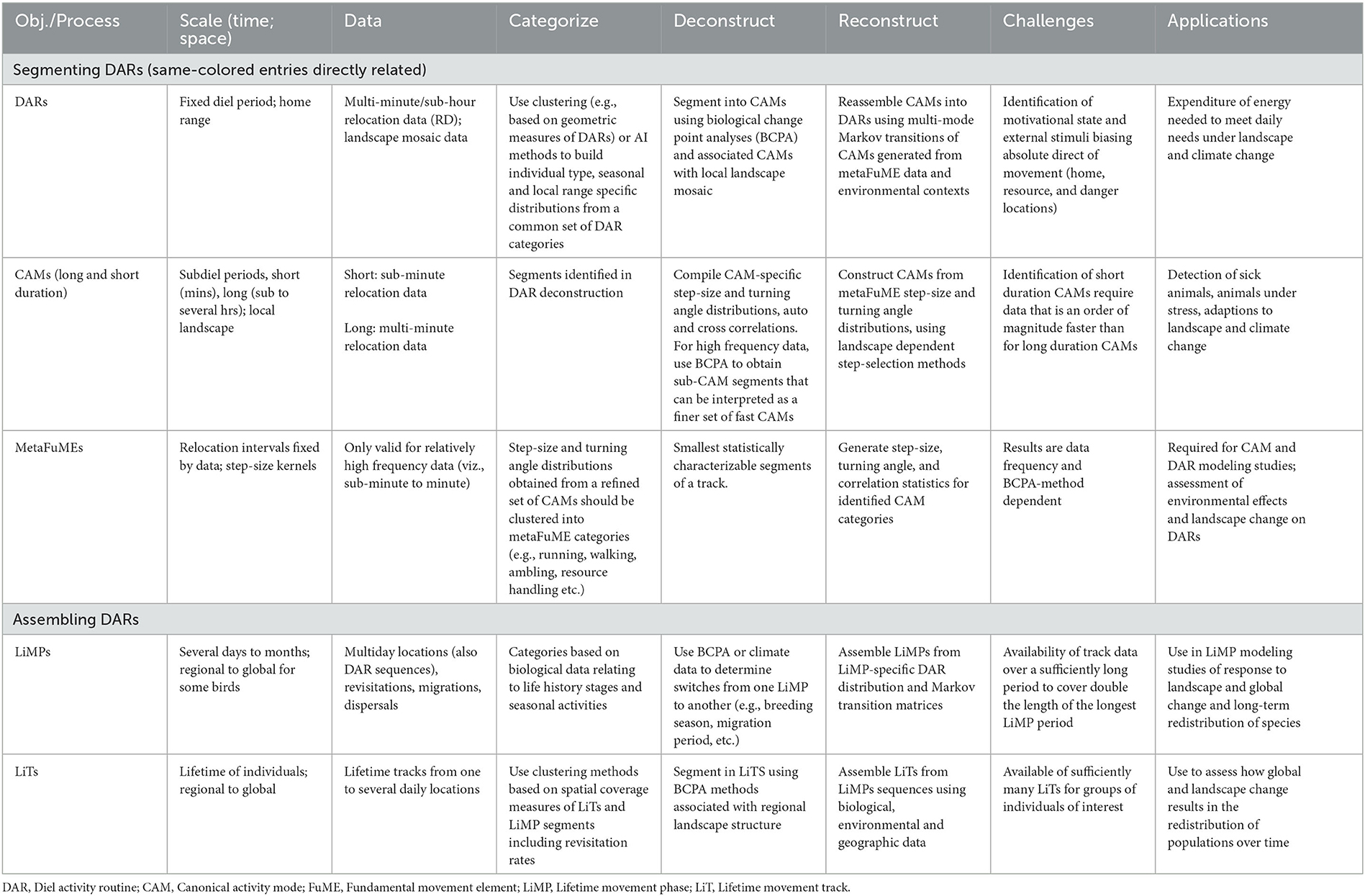
Table 1. Salient aspects of a hierarchical DAR-centered animal movement track segmentation, assembly, and simulation modeling scheme.
The changes in the structure of CAMs and DARs in response to changes in the landscape or climate may be statistically assessable if a sufficiently large sample of DARs is available for a range of landscape and climatic conditions corresponding to the anticipated changes. In the absence of suitable environmentally-contextualized DAR data, a more mechanistic approach is required. In order to develop such an approach, we must understand how the CAM segments of DARs may relate to various landscape and climatic conditions and how CAMs contribute to the emergent structure of DARs. CAMs themselves are built from finer scale movements that ultimately reduce to basic locomotory elements called fundamental movement elements (FuMEs) (Getz and Saltz, 2008; Getz et al., 2020; Getz, 2022).
Fundamental movement elements generally involve repeatable sequences of stereotypical body movements (e.g., walking, wing flapping, body undulating, trotting, galloping, and sprinting). These movements are generally executed at rates measured in seconds or fractions thereof in animals that weigh several kilograms or more. In smaller animals and birds, this rate could be measured in centiseconds (e.g., some hummingbirds flap their wings up to 60 times per second, Mahalingam and Welch, 2013). At longer time frames, various combinations of movements are strung together in repeatable ways that can be associated with different types of activities such as resting, walking toward a targeted location (i.e., directed walking), moving over a landscape to feed (e.g., grazing grass, or browsing trees), or collecting resources (e.g., searching for seeds) (Owen-Smith et al., 2010; Owen-Smith and Goodall, 2014). When these different activities are performed often in repeatable ways, they are called canonical activity modes (CAMs) (Getz and Saltz, 2008; Getz, 2022). Some CAMs may be short-lived and switched many times within an hour, such as a feeding or collecting resource CAM executed within a small landscape patch that is interspersed with a moving among patches CAM (Nams, 2005; Owen-Smith et al., 2010). Other CAMs may be long-lived and last several hours, such as a directed walking CAM executed when trekking to a distant location (e.g., a waterhole—Cain et al., 2012, or returning home after hunting many miles from a den where young have been sequestered—Hofer and East, 1993), preceded or followed by a search CAM (Bartumeus and Levin, 2008).
In addition to a time series of spatial location points (also known as relocation time series) collected at regular intervals of time, the amount of information needed to characterize a complete FuME sequence requires the simultaneous measurement of the relative motions of several different body parts (Miller et al., 2012). Thus, if the only information available is a relocation time series, the best information that can be generated are step sizes, turning angle distribution, and correlated measures (Getz, 2022). When relocation points are collected during the execution of a homogeneous movement activity (such as ambling, directed walking, or sprinting), the underlying elements can be statistically characterized in terms of average step size and turning angles with associated standard deviations and auto- and cross-correlations. These statistics can then be said to represent a metaFuME of that homogeneous activity. Obviously the values obtained depend on the frequency of location samples (i.e., the inverse of the sampling time interval). If the homogeneity of the movement behavior lasts an order of magnitude longer than the relocation sampling time frequency, then statistically reliable metaFuMEs can be constructed.
Finally, the underlying assumption of an animal track hierarchical segmentation framework is that each metaFuME basis will be general enough to apply to a class of individuals. If the class includes all individuals in the population, then it becomes so much better—but this is likely too much of an expectation. For example, the metaFuME that is the basis for a directed, uninterrupted walk between two points may have a characteristic (average with small standard deviations) “step size” or speed that depends on individual age or sex. Again, it is assumed that the classification of DARs, for example, may depend on particular traits, such as age or sex, have an environmental context, and may also reflect a particular syndromic personality type (Sih et al., 2004; Dingle, 2006; Abrahms et al., 2017; Spiegel et al., 2017). If inter-individual variation, though, is high beyond these specific groupings—i.e., variation becomes too idiosyncratic—then the generality of the hierarchical segmentation framework will be severally eroded and its ability to provide a basis for building forecasting models of populations' responses to global change is highly compromised.
3. Categorizing DARs
Within the metaFuME/CAM/DAR/LiMP/LiT segmentation hierarchy, metaFuMEs and DARs have fixed periods, whereas the CAMs, LiMPs, and LiTs have variable lengths (Getz, 2022). The metaFuME period is selected based on statistical criteria (primarily relocation data sample size) and the relocation sampling frequency (Getz et al., 2020). The DAR period, on the other hand, is fixed by the earth's rotation. The best choice of the start/end time, however, may vary among species. For the nocturnal barn owl, it is before the individual leaves for its nocturnal feeding bouts (Luisa Vissat et al., 2023), while for the black rhinoceros, a dawn start/end time is better than selecting midday, dusk, or midnight (Seidel et al., 2019).
Given that the DAR is the only segment of a LiT that has a natural fixed period, it is acceptable to use the DAR as the anchor for a hierarchical deconstruction (i.e., segmentation process) and reconstruction (i.e., assembling process) of animal tracks (Figure 1 and Table 1). Thus, one begins with a set of animal tracks with each track lasting at least one or more days long. These tracks are then organized into distinct diel segments once a particular start/end time has been selected. Each distinct diel segment is then regarded as one observation of a DAR. The result of this approach will be a set of DARs belonging to one or more individuals in a population. The ideal situation is to obtain sufficiently many segments to be able to conduct statistically relevant studies on the set of DARs obtained.
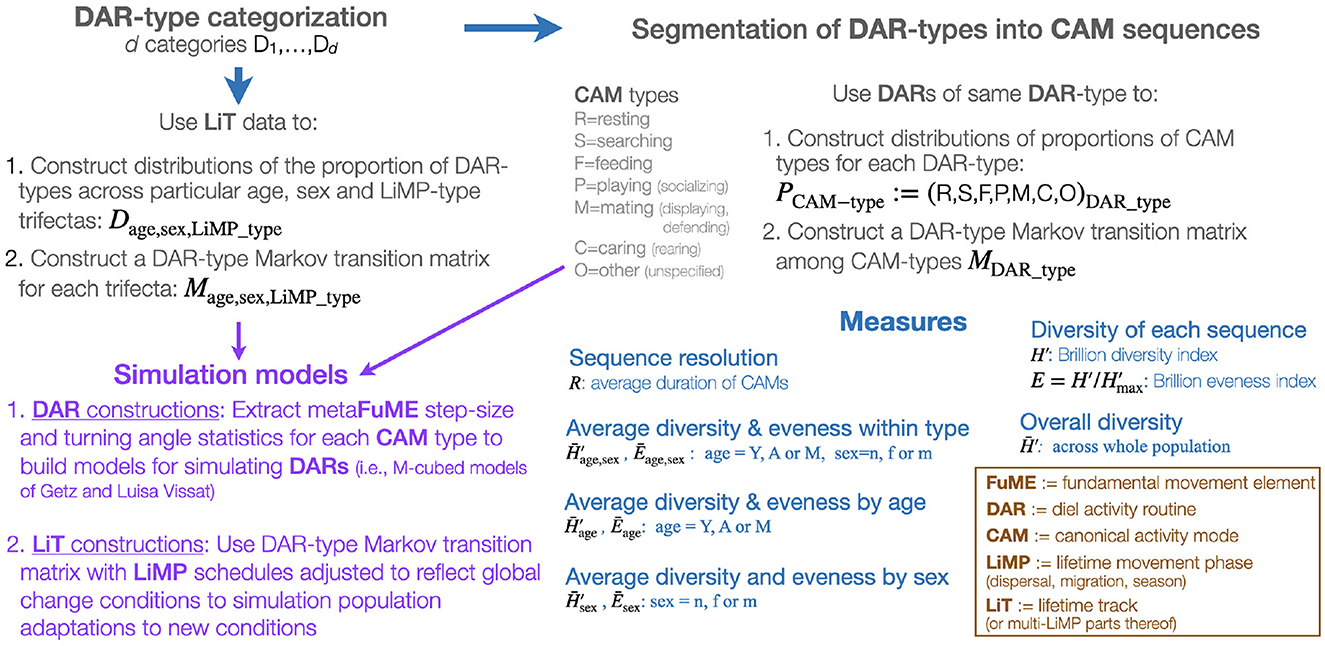
Figure 1. A graphical representation of a DAR-anchored animal movement track segmentation, assembly, and simulation modeling scheme.
At its crudest level, DARs can be plotted in terms of “activity” levels measure (e.g., energy expenditure rate, such as overall dynamic body acceleration (ODBA), although there are some issues with this latter concept, see Martin Lopez et al., 2022) or as has been done using camera trap data for 13 species of mammals on Barro Colorado Island, Panama (Rowcliffe et al., 2014). Such DAR plots can then be sorted in categories or types using a host of techniques, with the current best method being some kind of machine learning approach (Valletta et al., 2017; Wang, 2019; Torney et al., 2021). Obvious visual differences, though, include the timing of peak activity, the number of peaks, and the ratio of peak to trough periods.
Animal daily activity routines represent a combination of activities related to ensuring their survival, promoting their growth and development to reproductive maturity, and enhancing their reproductive fitness. As expressed by Papastamatiou et al. (2015) in a study of marine predators “Animal daily routines represent a compromise between maximizing foraging success and optimizing physiological performance, while minimizing the risk of predation.” Ectothermic marine predators, such as sharks, are expected to have DARs influenced by both prey abundance and thermal clines. In particular, if prey are relatively abundant, then predators may be expected to maximize their feeding rates by hunting in colder and resting in warmer than average waters (Papastamatiou et al., 2015). While, in a relatively depleted prey environment, Papastamatiou et al. (2015) posit that energy efficiency considerations may lead ectothermic marine predators to hunt in colder and rest in warmer than average waters.
In addition to categorizing DARs based on activity data and activity rate plots, various movement track generated measures may be used to sort DARs into categories using hierarchical clustering methods. As with many analytical methods in movement ecology (Codling and Hill, 2005; Codling and Plank, 2011), the method we propose in this study for categorizing DARs will exhibit some sensitivity to the relocation frequency of the data used. Thus, we recommend using data that has a sub-hourly or multi-minute frequency (e.g., 2–20 points an hour). In organizing the data for the DAR analysis, we need to determine where to break multi-day tracks into 24-h diel segments: the most appropriate start/end points will depend on the daily rhythms of the movement of individuals within a population (e.g., in the context of rhinos, see Seidel et al., 2019). After this, our method then employs a hierarchical clustering algorithm to identify a set of n cluster types (Murtagh and Contreras, 2012; Saxena et al., 2017). The number of clusters is determined using various heuristics (Saxena et al., 2017) that recognize that the optimal choice is actually a subjective trade-off among several criteria. These include capturing a desired level of the variation when the DARs are organized into descriptive spaces of lower dimension than the factor space itself; having sufficiently many categories to reveal novel phenomena that may be masked if particular categories are not separated out; and having few enough categories so that the number of DARs are sufficient to generate reliable average statistics in all categories. We emphasize, however, that any reliable cluster analysis suffices for our method, including various machine learning methods (Tarca et al., 2007; Valletta et al., 2017).
Luisa Vissat et al. (2023), for example, developed a method for categorizing DARs using the following four geometric measures: maximum displacement—from starting location, diameter—maximum distance between any two points on the DAR, width—maximum side-to-side extent perpendicular to the diameter, and net displacement—the distance between start and end locations. They then illustrated the approach using data from barn owls. Their analysis enabled them to distinguish how distributions of seven different types of DARs (five classes with little net displacement grouped by size and width/diameter characteristics, one class with moderate net displacement, and the remaining class with essentially one-way trips) varied as a function of age, gender, and location covariables. The question remained, though, how well these seven different types could be jointly segmented into distinct CAM segments, reflecting various behavioral models during the execution of DARS. Such segments likely include directed locomotion modes (at least one outbound and one inbound segment of this type for DARs with small net displacement), resource search, food item extraction, and handling modes, perhaps interspersed with periods of rest.
4. Segmenting DARs
Biological change point analyses (BCPA; Gurarie et al., 2009, 2016; Chen and Gupta, 2011; Matteson and James, 2014; Owen-Smith and Martin, 2015), including Hidden Markov Models (HMM; Langrock et al., 2012; Michelot et al., 2016; Zucchini et al., 2016; Pohle et al., 2017), can be used to segment DARs into sets of segments (Figure 1), where within set compared with across set movement statistics (step size, turning angle distributions, and auto and cross-correlated statistics–e.g., see Benhamou, 2004; Nams, 2014; Getz et al., 2020) are more homogeneous. The relatively homogeneous within set segments constitute distinct activity modes that can be regarded as canonical activity models (CAMs) when appropriate lengths of such different activity modes can be reassembled using simulation models (Figure 1) into different types of DARS. To some extent, some of these CAMs (e.g., directed locomotion) may be contextualized when their statistics depend on the age or gender of the individual, or even environmental attributes of the landscape including resistance to movement (Zeller et al., 2012).
The set of CAMs that have been identified may differ, depending on the resolution of the relocation data that are used to identify the points at which the “biological change” occurs. The number of types of CAMs identified is likely to be associated with an increasing function of the resolution of the data. Thus, relatively low resolution data may only support the division of DARs into high and low activity phases (Papastamatiou et al., 2015). On the other hand, relatively high resolution data may facilitate the segmentation of a mammalian, a herbivore foraging mode (i.e., a relatively long foraging CAM) into the actual handling of the resource (i.e., a short feeding CAM) interspersed with small movements among patches of resources (i.e., a short patch transfer CAM) (Owen-Smith, 2002). Another example is that animals involved in moving directly from one known location to another may stop from time to time to check for predators so that a relatively long period direct movement CAM may actually consist of shorter period segments of a persistent movement CAM interspersed with shorter periods of vigilance CAM (Kröschel et al., 2017). The vigilance CAM may also be evident during feeding activities (Robinson and Merrill, 2013).
Once a set of n different CAM types has been extracted from a set of DARs (where the best value of n that emerges from the cluster analysis will likely increase with the frequency of the relocation data), a set of underlying metaFuME statistics can then be extracted for each of these CAM types and used to formulate a simulation model (Figure 1) (Getz et al., 2020; Getz, 2022). Again, the metaFuME statistics may have some dependence on age, gender, or environmental covariates (attributes).
5. Assembling DARs and global change
The key to reassembling n identified categories of CAMs into DARs (the value of n will differ from one study to another) is to fit a set of n×n transition probability functions pij(ts, t) (i, j = 1, ⋯ , n, 0 ≤ ts ≤ t) to the DAR data from which the CAMs were extracted, where ts is the amount of time the individual has already been in CAM of type i, and t denotes the start time of the track in question. We note that the salient aspects of t will be its points in the 24-h diel cycle, the annual seasonal cycle, and possibly the lunar cycle (Polansky et al., 2010). If the functions pij(ts, t) were constants, then the n×n matrix P of elements (P)ij = pij would represent a Markov transition matrix, and the CAM construction would be a finite, discrete-time Markov process (Iosifescu, 2014). More likely, however, is that the transition probabilities are best fitted to switching functions of the form (Michalski et al., 2020), where σij(t) are CAM dependent switching “abruptness” and τij(t) are switching “location” parameters. In addition to the dependencies on residence and absolute times ts and t, the switching probabilities may also be influenced by individual type (e.g., sex or age) and are also almost certainly influenced by their “local” environmental context.
If we use the variables α to index an individual type, η to index its environmental context, and ξ to index its internal state (physiological/motivational), then for an individual of type α executing CAM i at time t for ts units of time with an internal state ξ and in environment η, the following applies. At time t+1, this individual will transition to CAM j with probability (where the parameters σ and τ in the switching functions may also be now α and η specific) and, hence, will remain in CAM i with probability . This implies that we always need to ensure that
We note that though time spent in a particular CAM has been explicitly identified, it may also be regarded as part of the internal state of an individual. It has been separated out because it may easier to measure than other internal state variables. These latter variables may be associated with salient geographic information that includes both learned landscape markers and remembered locations (Bracis and Mueller, 2017; Doherty and Driscoll, 2018) and sensory information obtained from magnetic and celestial cues. Such “global” cues will be implicated in the choice of CAMs initiated when heading absolute directions of motivate movement to distant locations, such as known resource areas, or return to home sites, or core areas of ranges. Once a simulation model that uses CAM-specific metaFuMEs to generate CAM segments that can then be strung together using the CAM transition matrix of switching functions to generate sets of DARs (Figure 1), we will then be in a position to string together the DARs themselves to reflect landscape use at the home range and seasonal spatiotemporal scales.
The scale at which environmental information is represented, for example, spectral data pertaining to a remotely sensed landscape pixel (Tsalyuk et al., 2017) containing the location of the individual, is important and is perhaps on the order of the distance that an individual can move under the current CAM in one metaFuME time step. Furthermore, for CAMs where turning angles are relatively ranged between [−π, π], fitted step-selection kernels (Thurfjell et al., 2014; Avgar et al., 2015; Tsalyuk et al., 2019) may prove useful in simulating a local movement track relocation sequence, particularly when barriers to movement are present on the landscape (Panzacchi et al., 2016).
6. Conclusion
From the above discussion, it is clear that the functions governing the transitions from one CAM to another can be complex. Thus an assumption that they remain constant is likely to only hold locally for short periods of time. The challenge then is to extract transition probabilities from empirical data that are sufficiently rich to allow dependencies on an individual type, internal state, and environmental context to be identified. This is a tall order, though one that is becoming more likely as our ability to collect environmentally contextualized relocation data increases (Nathan et al., 2022).
At this juncture, in terms of available data and methods of analysis, computing new sets of DARs from CAMs and transition probabilities that have little internal state information beyond time spent in the current CAM and some assessment of a modeled energy-expenditure/hunger variable (Malishev and Kramer-Schadt, 2021) should be attainable in the context of changing local landscape structures. The resulting DARs, when assembled using an empirically fitted set of DAR transitions functions, should permit forecasting home range adaptations, time of migrations, migration routes, and movement through corridors created to mitigate wildland habitat fragmentation (McClure et al., 2016; Panzacchi et al., 2016). In addition to such LiMPs, forecasting adapted LiTs should remain highly speculative until greater progress has been made and more experience obtained in modeling DAR and LiMP adaptations with some reliability. Furthermore, the inclusion of the motivational state of an individual to move to distant locations remains a challenge until we obtain a better understanding of how to detect such states within individuals and incorporate this information into simulation models, although heuristic inferred memory approaches may prove useful (Fagan et al., 2013; Abrahms et al., 2021).
A review of this article highlights that ideas presented herein are based largely on animal routine movements that are then used in a hierarchical framework to forecast animal movement responses, but the presentation fully ignores the literature on dispersal motivated by climate change. I agree that novel dispersal is a problem that also needs to be considered when forecasting the response of individuals to global change. In fact, the issue of individuals establishing a new home range when confronted with a novel environment (either due to natural dispersal or translocation) has been considered by me and others (Saltz and Getz, 2021). The question of then how to forecast when individuals make decisions to disperse in ways that are not part of their normal life cycle is a challenge that, as suggested by the title of this paper, is beyond the scope of this “Perspective” article. After all, many of the ideas presented in this article remain to be tested and can only be tested when sufficiently high resolution data become available on the movement responses of individuals to stressors resulting from the effects of global change.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This study was funded by the A. Starker Leopold Chair of Wildlife Ecology at the University of California, Berkeley.
Acknowledgments
The author thanks Norman Owen-Smith for motivating discussions.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abrahms, B., Aikens, E. O., Armstrong, J. B., Deacy, W. W., Kauffman, M. J., and Merkle, J. A. (2021). Emerging perspectives on resource tracking and animal movement ecology. Trends Ecol. Evol. 36, 308–320. doi: 10.1016/j.tree.2020.10.018
Abrahms, B., Seidel, D. P., Dougherty, E., Hazen, E. L., Bograd, S. J., Wilson, A. M., et al. (2017). Suite of simple metrics reveals common movement syndromes across vertebrate taxa. Movement Ecol. 5, 1–11. doi: 10.1186/s40462-017-0104-2
Austin, M. P., and Van Niel, K. P. (2011). Improving species distribution models for climate change studies: variable selection and scale. J. Biogeogr. 38, 1–8. doi: 10.1111/j.1365-2699.2010.02416.x
Avgar, T., Baker, J. A., Brown, G. S., Hagens, J. S., Kittle, A. M., Mallon, E. E., et al. (2015). Space-use behaviour of woodland caribou based on a cognitive movement model. J. Anim. Ecol. 84, 1059–1070. doi: 10.1111/1365-2656.12357
Bartumeus, F., and Levin, S. A. (2008). Fractal reorientation clocks: linking animal behavior to statistical patterns of search. Proc. Natl. Acad. Sci. U.S.A. 105, 19072–19077. doi: 10.1073/pnas.0801926105
Benhamou, S. (2004). How to reliably estimate the tortuosity of an animal's path:: straightness, sinuosity, or fractal dimension? J. Theoret. Biol. 229, 209–220. doi: 10.1016/j.jtbi.2004.03.016
Bracis, C., and Mueller, T. (2017). Memory, not just perception, plays an important role in terrestrial mammalian migration. Proc. R. Soc. B Biol. Sci. 284, 20170449. doi: 10.1098/rspb.2017.0449
Burton-Roberts, R., Cordes, L. S., Slotow, R., Vanak, A. T., Thaker, M., Govender, N., et al. (2022). Seasonal range fidelity of a megaherbivore in response to environmental change. Sci. Rep. 12, 22008. doi: 10.1038/s41598-022-25334-8
Cain, J. III., Owen-Smith, N., and Macandza, V. (2012). The costs of drinking: comparative water dependency of sable antelope and zebra. J. Zool. 286, 58–67. doi: 10.1111/j.1469-7998.2011.00848.x
Chen, J., and Gupta, A. K. (2011). Parametric Statistical Change Point Analysis: With Applications to Genetics, Medicine, and Finance. Springer Science & Business Media.
Codling, E., and Hill, N. (2005). Sampling rate effects on measurements of correlated and biased random walks. J. Theoret. Biol. 233, 573–588. doi: 10.1016/j.jtbi.2004.11.008
Codling, E. A., and Plank, M. J. (2011). Turn designation, sampling rate and the misidentification of power laws in movement path data using maximum likelihood estimates. Theoret. Ecol. 4, 397–406. doi: 10.1007/s12080-010-0086-9
Couzin, I. D., Krause, J., Franks, N. R., and Levin, S. A. (2005). Effective leadership and decision-making in animal groups on the move. Nature 433, 513. doi: 10.1038/nature03236
Dingle, H. (2006). Animal migration: is there a common migratory syndrome? J. Ornithol. 147, 212–220. doi: 10.1007/s10336-005-0052-2
Dodge, S., Bohrer, G., Weinzierl, R., Davidson, S. C., Kays, R., Douglas, D., et al. (2013). The environmental-data automated track annotation (ENV-data) system: linking animal tracks with environmental data. Movement Ecol. 1, 1–14. doi: 10.1186/2051-3933-1-3
Doherty, T. S., and Driscoll, D. A. (2018). Coupling movement and landscape ecology for animal conservation in production landscapes. Proc. R. Soc. B Biol. Sci. 285, 20172272. doi: 10.1098/rspb.2017.2272
Elith, J., and Leathwick, J. R. (2009). Species distribution models: ecological explanation and prediction across space and time. Annu. Rev. Ecol. Evol. Syst. 40, 677–697. doi: 10.1146/annurev.ecolsys.110308.120159
Fagan, W. F., Lewis, M. A., Auger-Méthé, M., Avgar, T., Benhamou, S., Breed, G., et al. (2013). Spatial memory and animal movement. Ecol. Lett. 16, 1316–1329. doi: 10.1111/ele.12165
Getz, W. M. (2022). A hierarchical path-segmentation movement ecology framework. Ecol. Process. 11, 1–15. doi: 10.1186/s13717-022-00399-5
Getz, W. M., and Saltz, D. (2008). A framework for generating and analyzing movement paths on ecological landscapes. Proc. Natl. Acad. Sci. U.S.A. 105, 19066–19071. doi: 10.1073/pnas.0801732105
Getz, W. M., Vissat, L. L., and Salter, R. (2020). “Simulation and analysis of animal movement paths using numerus model builder,” in 2020 Spring Simulation Conference (SpringSim) (IEEE), 1–12.
Gurarie, E., Andrews, R. D., and Laidre, K. L. (2009). A novel method for identifying behavioural changes in animal movement data. Ecol. Lett. 12, 395–408. doi: 10.1111/j.1461-0248.2009.01293.x
Gurarie, E., Bracis, C., Delgado, M., Meckley, T. D., Kojola, I., and Wagner, C. M. (2016). What is the animal doing? Tools for exploring behavioural structure in animal movements. J. Anim. Ecol. 85, 69–84. doi: 10.1111/1365-2656.12379
Hertel, A. G., Niemelä, P. T., Dingemanse, N. J., and Mueller, T. (2020). A guide for studying among-individual behavioral variation from movement data in the wild. Movement Ecol. 8, 1–18. doi: 10.1186/s40462-020-00216-8
Hofer, H., and East, M. L. (1993). The commuting system of serengeti spotted hyaenas: how a predator copes with migratory prey. I. social organization. Anim. Behav. 46, 547–557.
Hooten, M. B., Johnson, D. S., McClintock, B. T., and Morales, J. M. (2017). Animal Movement: Statistical Models for Telemetry Data. CRC Press.
Jacoby, D. M., and Freeman, R. (2016). Emerging network-based tools in movement ecology. Trends Ecol. Evol. 31, 301–314. doi: 10.1016/j.tree.2016.01.011
Kröschel, M., Reineking, B., Werwie, F., Wildi, F., and Storch, I. (2017). Remote monitoring of vigilance behavior in large herbivores using acceleration data. Anim. Biotelemetry 5, 1–15. doi: 10.1186/s40317-017-0125-z
Langrock, R., King, R., Matthiopoulos, J., Thomas, L., Fortin, D., and Morales, J. M. (2012). Flexible and practical modeling of animal telemetry data: hidden markov models and extensions. Ecology 93, 2336–2342. doi: 10.1890/11-2241.1
Liedvogel, M., Chapman, B. B., Muheim, R., and Åkesson, S. (2013). The behavioural ecology of animal movement: reflections upon potential synergies. Anim. Migrat. 1, 39–46. doi: 10.2478/ami-2013-0002
Luisa Vissat, L., Cain, S., Nathan, R., Toledo, S., Spiegel, O., and Getz, W. (2023). Categorizing animal diel movement patterns with examples from high-resolution barn owl tracking. Mov. Ecol. 11, 15. doi: 10.1186/s40462-023-00367-4
Mahalingam, S., and Welch, K. C. Jr. (2013). Neuromuscular control of hovering wingbeat kinematics in response to distinct flight challenges in the ruby-throated hummingbird, Archilochus colubris. J. Exp. Biol. 216, 4161–4171. doi: 10.1242/jeb.089383
Malishev, M., and Kramer-Schadt, S. (2021). Movement, models, and metabolism: individual-based energy budget models as next-generation extensions for predicting animal movement outcomes across scales. Ecol. Modell. 441, 109413. doi: 10.1016/j.ecolmodel.2020.109413
Martin Lopez, L. M., Aguilar de Soto, N., Madsen, P. T., and Johnson, M. (2022). Overall dynamic body acceleration measures activity differently on large vs. small aquatic animals. Methods Ecol. Evol. 13, 447–458. doi: 10.1111/2041-210X.13751
Matteson, D. S., and James, N. A. (2014). A nonparametric approach for multiple change point analysis of multivariate data. J. Am. Stat. Assoc. 109, 334–345. doi: 10.1080/01621459.2013.849605
McClure, M. L., Hansen, A. J., and Inman, R. M. (2016). Connecting models to movements: testing connectivity model predictions against empirical migration and dispersal data. Landscape Ecol. 31, 1419–1432. doi: 10.1007/s10980-016-0347-0
Michalski, J., Green, A. M., and Cisek, P. (2020). Reaching decisions during ongoing movements. J. Neurophysiol. 123, 1090–1102. doi: 10.1152/jn.00613.2019
Michelot, T., Langrock, R., and Patterson, T. A. (2016). moveHMM: an R package for the statistical modelling of animal movement data using hidden Markov models. Methods Ecol. Evol. 7, 1308–1315. doi: 10.1111/2041-210X.12578
Miller, L. A., Goldman, D. I., Hedrick, T. L., Tytell, E. D., Wang, Z. J., Yen, J., et al. (2012). Using computational and mechanical models to study animal locomotion. Integr. Comp. Biol. 52, 553–575. doi: 10.1093/icb/ics115
Mueller, T., and Fagan, W. F. (2008). Search and navigation in dynamic environments–from individual behaviors to population distributions. Oikos 117, 654–664. doi: 10.1111/j.0030-1299.2008.16291.x
Murtagh, F., and Contreras, P. (2012). Algorithms for hierarchical clustering: an overview. Wiley Interdiscipl. Rev. Data Mining Knowledge Discov. 2, 86–97. doi: 10.1002/widm.53
Nams, V. O. (2005). Using animal movement paths to measure response to spatial scale. Oecologia 143, 179–188. doi: 10.1007/s00442-004-1804-z
Nams, V. O. (2014). Combining animal movements and behavioural data to detect behavioural states. Ecol. Lett. 17, 1228–1237. doi: 10.1111/ele.12328
Nathan, R., Getz, W. M., Revilla, E., Holyoak, M., Kadmon, R., Saltz, D., et al. (2008). A movement ecology paradigm for unifying organismal movement research. Proc. Natl. Acad. Sci. U.S.A. 105, 19052–19059. doi: 10.1073/pnas.0800375105
Nathan, R., Monk, C. T., Arlinghaus, R., Adam, T., Alós, J., Assaf, M., et al. (2022). Big-data approaches lead to an increased understanding of the ecology of animal movement. Science 375, eabg1780. doi: 10.1126/science.abg1780
Owen-Smith, N., Fryxell, J., and Merrill, E. (2010). Foraging theory upscaled: the behavioural ecology of herbivore movement. Philos. Trans. R. Soc. B Biol. Sci. 365, 2267–2278. doi: 10.1098/rstb.2010.0095
Owen-Smith, N., and Goodall, V. (2014). Coping with savanna seasonality: comparative daily activity patterns of a frican ungulates as revealed by GPS telemetry. J. Zool. 293, 181–191. doi: 10.1111/jzo.12132
Owen-Smith, N., and Martin, J. (2015). Identifying space use at foraging arena scale within the home ranges of large herbivores. PLoS ONE 10, e0128821. doi: 10.1371/journal.pone.0128821
Owen-Smith, R. N. (2002). Adaptive Herbivore Ecology: From Resources to Populations in Variable Environments. Cambridge University Press.
Panzacchi, M., Van Moorter, B., Strand, O., Saerens, M., Kivimäki, I., St. Clair, C. C., et al. (2016). Predicting the continuum between corridors and barriers to animal movements using step selection functions and randomized shortest paths. J. Anim. Ecol. 85, 32–42. doi: 10.1111/1365-2656.12386
Papastamatiou, Y. P., Watanabe, Y. Y., Bradley, D., Dee, L. E., Weng, K., Lowe, C. G., et al. (2015). Drivers of daily routines in an ectothermic marine predator: hunt warm, rest warmer? PLoS ONE 10, e0127807. doi: 10.1371/journal.pone.0127807
Patterson, T. A., Parton, A., Langrock, R., Blackwell, P. G., Thomas, L., and King, R. (2017). Statistical modelling of individual animal movement: an overview of key methods and a discussion of practical challenges. AStA Adv. Stat. Anal. 101, 399–438. doi: 10.1007/s10182-017-0302-7
Pohle, J., Langrock, R., van Beest, F. M., and Schmidt, N. M. (2017). Selecting the number of states in hidden Markov models: pragmatic solutions illustrated using animal movement. J. Agric. Biol. Environ. Stat. 22, 270–293. doi: 10.1007/s13253-017-0283-8
Polansky, L., Wittemyer, G., Cross, P. C., Tambling, C. J., and Getz, W. M. (2010). From moonlight to movement and synchronized randomness: Fourier and wavelet analyses of animal location time series data. Ecology 91, 1506–1518. doi: 10.1890/08-2159.1
Rew, J., Park, S., Cho, Y., Jung, S., and Hwang, E. (2019). Animal movement prediction based on predictive recurrent neural network. Sensors 19, 4411. doi: 10.3390/s19204411
Robinson, B. G., and Merrill, E. H. (2013). Foraging–vigilance trade-offs in a partially migratory population: comparing migrants and residents on a sympatric range. Anim. Behav. 85, 849–856. doi: 10.1016/j.anbehav.2013.02.004
Rowcliffe, J. M., Kays, R., Kranstauber, B., Carbone, C., and Jansen, P. A. (2014). Quantifying levels of animal activity using camera trap data. Methods Ecol. Evol. 5, 1170–1179. doi: 10.1111/2041-210X.12278
Saltz, D., and Getz, W. M. (2021). Finding a home: stopping theory and its application to home range establishment in a novel environment. Front. Conserv. Sci. 2, 714580. doi: 10.3389/fcosc.2021.714580
Saxena, A., Prasad, M., Gupta, A., Bharill, N., Patel, O. P., Tiwari, A., et al. (2017). A review of clustering techniques and developments. Neurocomputing 267, 664–681. doi: 10.1016/j.neucom.2017.06.053
Schweinfurth, M. K., Baldridge, D. B., Finnerty, K., Call, J., and Knoblich, G. K. (2022). Inter-individual coordination in walking chimpanzees. Curr. Biol. 32, 5138–5143. doi: 10.1016/j.cub.2022.09.059
Seebacher, F., and Post, E. (2015). Climate change impacts on animal migration. Clim. Change Resp. 2, 5. doi: 10.1186/s40665-015-0013-9
Seidel, D. P., Linklater, W. L., Kilian, W., du Preez, P., and Getz, W. M. (2019). Mesoscale movement and recursion behaviors of namibian black rhinos. Movement Ecol. 7, 1–14. doi: 10.1186/s40462-019-0176-2
Sih, A., Bell, A., and Johnson, J. C. (2004). Behavioral syndromes: an ecological and evolutionary overview. Trends Ecol. Evol. 19, 372–378. doi: 10.1016/j.tree.2004.04.009
Spiegel, O., Leu, S. T., Bull, C. M., and Sih, A. (2017). What's your move? Movement as a link between personality and spatial dynamics in animal populations. Ecol. Lett. 20, 3–18. doi: 10.1111/ele.12708
Tarca, A. L., Carey, V. J., Chen, X.-w., Romero, R., and Drăghici, S. (2007). Machine learning and its applications to biology. PLoS Comput. Biol. 3, e116. doi: 10.1371/journal.pcbi.0030116
Teitelbaum, C. S., and Mueller, T. (2019). Beyond migration: causes and consequences of nomadic animal movements. Trends Ecol. Evol. 34, 569–581. doi: 10.1016/j.tree.2019.02.005
Thurfjell, H., Ciuti, S., and Boyce, M. S. (2014). Applications of step-selection functions in ecology and conservation. Mov. Ecol. 2, 4. doi: 10.1186/2051-3933-2-4
Torney, C. J., Hopcraft, J. G. C., Morrison, T. A., Couzin, I. D., and Levin, S. A. (2018). From single steps to mass migration: the problem of scale in the movement ecology of the serengeti wildebeest. Philos. Trans. R. Soc. B Biol. Sci. 373, 20170012. doi: 10.1098/rstb.2017.0012
Torney, C. J., Morales, J. M., and Husmeier, D. (2021). A hierarchical machine learning framework for the analysis of large scale animal movement data. Mov. Ecol. 9, 1–11. doi: 10.1186/s40462-021-00242-0
Travis, J. M., Delgado, M., Bocedi, G., Baguette, M., Bartoń, K., Bonte, D., et al. (2013). Dispersal and species' responses to climate change. Oikos 122, 1532–1540. doi: 10.1111/j.1600-0706.2013.00399.x
Tsalyuk, M., Kelly, M., and Getz, W. M. (2017). Improving the prediction of African Savanna vegetation variables using time series of modis products. ISPRS J. Photogram. Remote Sens. 131, 77–91. doi: 10.1016/j.isprsjprs.2017.07.012
Tsalyuk, M., Kilian, W., Reineking, B., and Getz, W. M. (2019). Temporal variation in resource selection of African elephants follows long-term variability in resource availability. Ecol. Monogr. 89, e01348. doi: 10.1002/ecm.1348
Valletta, J. J., Torney, C., Kings, M., Thornton, A., and Madden, J. (2017). Applications of machine learning in animal behaviour studies. Anim. Behav. 124, 203–220. doi: 10.1016/j.anbehav.2016.12.005
Wang, G. (2019). Machine learning for inferring animal behavior from location and movement data. Ecol. Inform. 49, 69–76. doi: 10.1016/j.ecoinf.2018.12.002
Williams, H. J., Taylor, L. A., Benhamou, S., Bijleveld, A. I., Clay, T. A., de Grissac, S., et al. (2020). Optimizing the use of biologgers for movement ecology research. J. Anim. Ecol. 89, 186–206. doi: 10.1111/1365-2656.13094
Zeller, K. A., McGarigal, K., and Whiteley, A. R. (2012). Estimating landscape resistance to movement: a review. Landscape Ecol. 27, 777–797. doi: 10.1007/s10980-012-9737-0
Keywords: diel activity routines (DARs), canonical activity modes (CAMs), lifetime movement phases (LiMPs), home-range adaptation, dispersal, migration, simulation
Citation: Getz WM (2023) An animal movement track segmentation framework for forecasting range adaptation under global change. Front. Ecol. Evol. 11:1171169. doi: 10.3389/fevo.2023.1171169
Received: 21 February 2023; Accepted: 25 May 2023;
Published: 29 June 2023.
Edited by:
Danish Ali Ahmed, Gulf University for Science and Technology, KuwaitReviewed by:
Jean Clobert, UMR5321 Station d'Ecologie Théorique et Expérimentale (SETE), FranceCopyright © 2023 Getz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wayne M. Getz, d2dldHomI3gwMDA0MDtiZXJrZWxleS5lZHU=