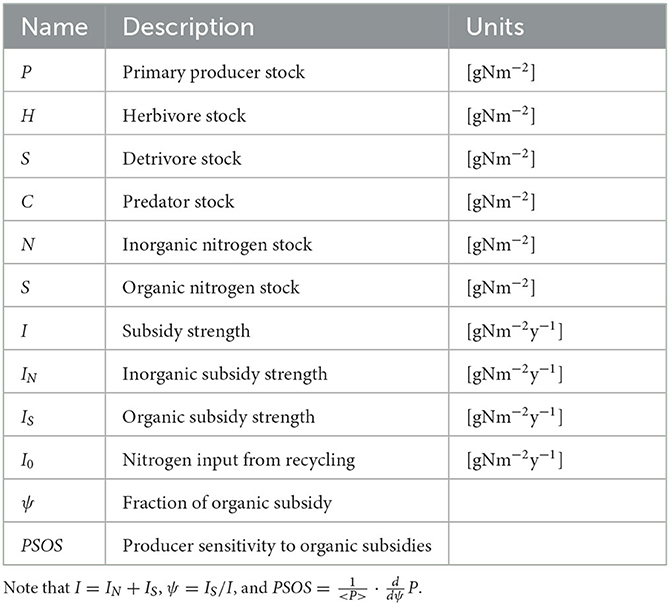
- 1Department of Ecology, Swedish University of Agricultural Sciences, Uppsala, Sweden
- 2Department of Physical Geography and Bolin Centre for Climate Research, Stockholm University, Stockholm, Sweden
Ecosystems worldwide receive large amounts of nutrients from both natural processes and human activities. While direct subsidy effects on primary production are relatively well-known (the green food web), the indirect effects of subsidies on producers as mediated by the brown food web and predators are poorly considered. With a dynamical green-brown food web model, parameterized using empirical estimates from the literature, we illustrate the effect of organic and inorganic nutrient subsidies on net primary production (NPP) (i.e., after removing loss to herbivory) in two idealized ecosystems—one terrestrial and one aquatic. We find that nutrient subsidies increase net primary production, an effect that saturates with increasing subsidies. Changing the quality of subsidies from inorganic to organic tends to increase net primary production in terrestrial ecosystems, but less often so in aquatic ecosystems. This occurs when organic nutrient inputs promote detritivores in the brown food web, and hence predators that in turn regulate herbivores, thereby promoting primary production. This previously largely overlooked effect is further enhanced by ecosystem properties such as fast decomposition and low rates of nutrient additions and demonstrates the importance of nutrient subsidy quality on ecosystem functioning.
1. Introduction
No ecosystem is an island, entirely cut off from external influences. On the contrary, the influx of materials and organisms into ecosystems, known as subsidies, significantly impact the state and functioning of ecosystems (Polis et al., 1997; Palumbi, 2003). The subsidies can take various forms, including mass transport of materials by water and air (Bobbink et al., 2010), animals that move across ecosystems for various activities such as foraging (Marczak et al., 2007; Buendía et al., 2018), and, an increasingly important phenomenon for ecosystems world-wide, input of resources such as nutrients through human activities (Raun and Johnson, 1999; Newsome et al., 2015). Subsidies can have diverse impacts. Adding nutrients in limited supply in the ecosystem often increases primary production (Polis et al., 1997; Montagano et al., 2018), but it can also reduce it when, for instance, adding one nutrient promotes plant–microbe competition for other nutrients (Čapek et al., 2018). The consequences of subsidies depend on the trophic interactions in the ecosystem. Introducing consumers changes ecosystem fluxes which affects biomass distributions across trophic levels (Allen and Wesner, 2016) and thereby how nutrients cycle in the ecosystem. Introduced species can change the behavior of the ecosystem entirely, as they create novel interactions and pathways (Baxter et al., 2004).
Subsidies can move both horizontally between food web compartments at a certain trophic level and vertically across trophic levels within a food web. Horizontal transfer occurs due to nutrient flows and interactions of organisms between food webs, and can occur through physical transfer of material between spatially separated webs in an ecosystem, or through species interactions in linked food webs (Nakano and Murakami, 2001; Baxter et al., 2004). For example, consumer species in green-brown food webs that rely on both primary producers in the green channel and detrital matter in the brown channel connect the two channels and their food webs (Moore et al., 2004; Allen and Wesner, 2016). Subsidies also lead to vertical exchanges between trophic levels within a food web. Subsidies provided from below, by influx of nutrients or direct provision to primary producers, propagates up to consumer species, increasing the overall biomass and altering the shape of biomass distribution in the food web (Hines et al., 2006). Predator subsidies lead to pressure on the herbivores they consume, and can lead to trophic cascades where primary producers are released from herbivory pressure due to predation (Leroux and Loreau, 2008; Newsome et al., 2015; Galiana et al., 2021). Hence, subsidies can cause positive albeit indirect effects on primary production via trophic interactions, but outcomes of such combined horizontal and vertical effects of subsidies in green-brown food webs are poorly explored.
Research on the impact of subsidies has centered on either the horizontal or the vertical flows, without bringing these two perspectives together (Rooney et al., 2006). Studies of landscape ecology and meta-ecosystem theory have focused on horizontal transfer between habitats (Darimont et al., 2009; Gravel et al., 2010), and how it interacts with spatial structure (Jacquet et al., 2022). In contrast, food web ecologists have focused on vertical flows that can change biomass distributions and can lead to trophic cascades (Leroux and Loreau, 2008). However, flow of energy and nutrients due to subsidies can be more nuanced due to the complexity of interactions within ecosystems, intertwining the horizontal and vertical flows. Moreover, research on subsidies has largely focused on green food webs (Nakano and Murakami, 2001; Loreau and Holt, 2004; Bobbink et al., 2010), with more recent interest in brown food webs (Allen and Wesner, 2016; McCary et al., 2020). Linking the two into integrated green-brown food webs has only just begun (Zou et al., 2016).
Nutrient subsidies into the brown channel of the food web has recently been shown to affect plant production (Riggi and Bommarco, 2019; Aguilera et al., 2021). The subsidies provide food for detritivores, which in turn increases predator populations, and lead to a trophic cascade where plants grow more as herbivory pressure is reduced by predators. However, a theoretical understanding of these processes and their relevance has lagged behind. While some theoretical investigations have been conducted on how organic matter subsidies affect primary producers and nutrient recycling (Leroux and Loreau, 2008; Gounand et al., 2014; Spiecker et al., 2016), we know of only two studies in which the full green-brown food web was considered in the context of subsidies (Attayde and Ripa, 2008; McCary et al., 2020). However, they did not consider how the input rate and quality of nutrient subsidies affect the food web.
Here, we develop and use a dynamical model to examine how nutrient subsidies affect primary production in coupled green-brown food webs in terrestrial and aquatic ecosystems. We focus on nitrogen as a key nutrient whose cycle has been widely disrupted by human activities, and measure net primary production (NPP) (i.e., the production remaining after herbivory), as a function of nutrient subsidy. The nutrient subsidy properties we consider are the amounts of inorganic and organic nitrogen in detrital matter (e.g., green or animal manure) and their relative proportions. Inorganic nitrogen is directly taken up by primary producers and fuels the green channel, while organic nitrogen is consumed by decomposers and fuels the brown channel. Combining the model with data from the literature on nitrogen fluxes and stocks we aim to assess, first, how the strength and quality of subsidies affect net primary production. Second, we investigate how food web properties, such as consumption, nitrogen conversion efficiencies, and metabolic rates for consumers, and ecosystem properties, such as nitrogen mineralization rate and primary producer mortality, modify the subsidy effect on primary producers. Our results focus on idealized aquatic and terrestrial ecosystems intended to be representative of widespread conditions on Earth.
2. Methods
We note that we use a similar methodology to another study (Zelnik et al., 2022), with the same model and some of the same sources for parameterizing the model. For clarity, we note a few main differences: (i) We base the parameterization of this model (see below) on fewer studies, as we focus less on the data synthesis aspect of the previous study and more on theoretical analysis. (ii) We use a more general parameter exploration, focusing on two generic ecosystem types rather than six specific types (e.g., forests) as in the previous model, and do not set any parameter to zero throughout, as we did for some parameters in the previous study. (iii) We focus here on net primary production, rather than on general trends of stocks and fluxes, as in the previous study.
2.1. Dynamical model
To model the dynamics of subsidized green-brown food webs, we write six mass balance equations describing the changes in nitrogen stock in units of [gN m−2] (see Table 1). Four compartments are functional groups of organisms: primary producers (P), herbivores (H), detritivores excluding microorganisms (D), and predators (C). The two other compartments are of organic nitrogen including microbial decomposers (S) and inorganic nitrogen (N).
While we focus on nitrogen as a key limiting nutrient in many ecosystems, we keep the model general, to open for the possibility to describe the dynamics of other nutrients as well. We follow Barbier and Loreau (2019) in defining the food web interactions, using a type I functional response for consumption terms, together with self-regulation (Barabás et al., 2017) of each species compartment. A conceptual diagram is given in Figure 1, and the model dynamics are detailed by the coupled ordinary differential equations, given in Equation (1).
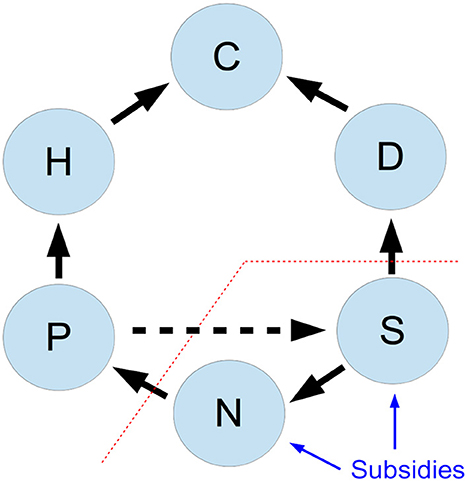
Figure 1. Interactions between the six compartments of an ecosystem model with nutrient subsidies. Compartments are: primary producers (P), herbivores (H), detritivores (D), predators (C), inorganic nutrients (N), active organic nitrogen (S). Black lines show nutrient fluxes between compartments; blue lines show the nutrient subsidies that are added to the ecosystem, the red line marks the separation between organism and substrate compartments, and the dashed arrow indicates nutrient recycling from dead primary producers to the organic nitrogen compartment.
For each of the first four compartments, with i designating the specific compartment, the parameter ri represents the consumption coefficient of the trophic level below (in units of [m2(gN)−1yr−1]), ϵi is the non-dimensional nutrient conversion efficiency associated with this consumption, ui is the natural mortality rate (units of (yr−1)), and qi is the self-regulation coefficient (e.g., light limitation for primary producers, or intra-guild predation for predators, in units of [m2(gN)−1yr−1]). In the two abiotic compartments, z is the rate of nitrogen mineralization, and ℓ is the loss rate of inorganic nitrogen due to mass transport and chemical transformations such as denitrification that remove nitrogen from the N pool, both in units of (yr−1). The latter is assumed independent of the subsidy amount and quality, even though nitrogen loss rates can depend on both amount and quality of the subsidy (e.g., N2O emissions, Shcherbak et al., 2014). IN and IS are the influx rates of nitrogen into the N and S compartments, respectively, which are interpreted as subsidy fluxes of inorganic and organic nitrogen. We define the nutrient subsidy strength as I = IN + IS. The fraction of organic subsidy, which we call subsidy quality or ψ, is calculated as IS/I. Thus, ψ = 0 for strictly inorganic subsidy and ψ = 1 for only organic inputs. I0 is the input of nutrients from recycled materials from primary producers, given as I0 = yuPP, with y the recycling rate (the quantitatively smaller recycling from other compartments is neglected for simplicity). The definitions of the different subsidy fluxes are also noted in Table 1.
A few modeling choices require some explanations. By having self-regulation terms (e.g., in the first equation) we can expect more well-behaved dynamics (Barabás et al., 2017), e.g., avoiding oscillatory dynamics observed in previous studies (Attayde and Ripa, 2008). We also make a neutral assumption on predator preference, in which predators are agnostic as to which prey they consume and can switch freely between herbivores and detritivores (i.e., generalist multichannel predators). We focus on a type-I functional response as it is simpler to analyze, and it is not a priori clear which type of functional response is the most relevant at the ecosystem level. Beyond type-I functional response, type-II functional response is often used in consumer–resource interactions (Attayde and Ripa, 2008; Wollrab et al., 2012), although its relevance has also been contested Jonsson (2017). Furthermore, it has been previously found that the choice of functional response type does not alter the qualitative outcomes of nutrient enrichment (Wollrab et al., 2012). To assert this also in our model, we test a model with a type-II functional response, and conclude that a type-I functional response is more relevant for our modeling approach, being less likely to lead to extinction of entire functional groups (e.g., no herbivores in the ecosystem) and temporal oscillations (Supplementary material).
Nutrient recycling (I0), represented by the dashed horizontal arrow in Figure 1, is a main nutrient source in many ecosystems, especially terrestrial and macrophyte-dominated aquatic ecosystems (Manzoni et al., 2018). As we show in the Supplementary material, including recycling has a similar effect as an increase in subsidy strength I and a decrease in ψ, compared to a scenario without recycling. This effect of recycling can be explained by noticing that even with only the inorganic nitrogen subsidy, the organic nitrogen compartment is fed by nitrogen recycling of primary producer biomass. Therefore, without loss of generality, we focus in the main text on ecosystem dynamics without nutrient recycling, i.e., setting y = 0. This assumption allows for a simplified analysis and presentation while retaining the qualitative behavior of the model. We also show that including detritus recycling gives qualitatively similar results (Supplementary material).
2.2. Model parameterization
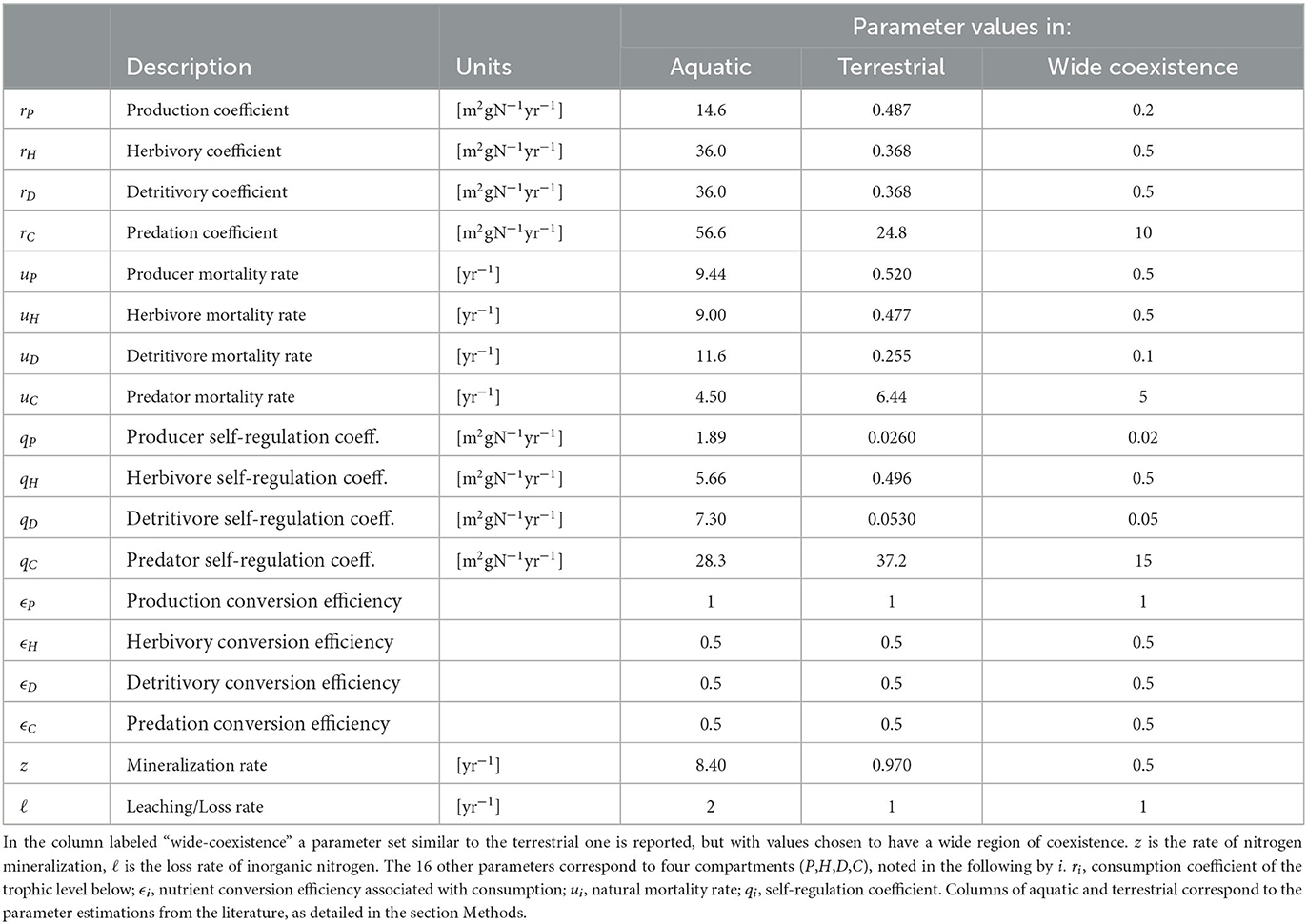
To analyze the effects of subsidies on primary production, we parameterize the model for two generic ecosystem types: a terrestrial and an aquatic ecosystem. These idealized ecosystems are used as baselines, and we test a wide range of parameters around these baseline values to ensure the generality of our results. We base the model parameterization on two data collections with estimates of nitrogen stocks and flow rates as defined in our model (Cebrian, 1999, 2004). We draw rough estimates of ecosystem properties such as nutrient conversion efficiencies from a dozen additional studies detailed in the Data collection subsection below. All values are converted to units of grams of nitrogen per square meter for stocks, and per year for rates. As explained below in the Parameter derivation subsection, we assume that Equation (1) are in equilibrium, and use the empirically-derived stock and rate estimates to back-calculate the model parameters for the terrestrial and aquatic ecosystem, respectively. We do this by estimating the production fluxes of the four compartments (P, H, D, C), and use these flux values together with values for fraction of production lost to processes such as predation, to estimate the various parameters. Finally, as explained in the Simulations and parameter exploration subsection 2.5, we use two methods to numerically explore the consequences on primary production of a wide range of possible parameter values representing different ecosystems.
2.3. Data collection
We combine the datasets from Cebrian (1999, 2004) according to idealized ecosystem type: terrestrial or aquatic. Terrestrial ecosystems include those labeled as forests, grasslands, savannas, drylands, and boreal ecosystems. Aquatic ecosystems include all marine and freshwater ecosystems, such as oceans, seagrass meadows, coral reefs, and lakes. We exclude data for marshes and swamps from either ecosystem type. With these definitions, we obtain 210 records for the terrestrial and 534 records for the aquatic idealized ecosystem from the datasets. The data types for each record and their associated units are: primary producer nitrogen content (νP [gN/gDW]; DW stands for dry weight), primary producer stocks (BP [gCm−2]), herbivore stocks (BH [gCm−2]), mineralization rate (z [yr−1]), decomposition flux (fD [gCyr−1m−2]), detrital production (fM [gCyr−1m−2]), primary production (fP [gCyr−1m−2]), herbivory fraction (ρPH). The geometric average of the available values is calculated for each data type and used in the subsequent estimation of the model parameters for each ecosystem type. The use of a geometric average is appropriate due to the wide range of values for various ecosystems (Bar-On et al., 2018). We use the primary producer average nitrogen content, together with a ratio of carbon to dry-weight ratio of 2.5 (Cebrian and Lartigue, 2004), to convert BP and all fluxes related to primary producers and detritus from carbon to nitrogen, for instance P = BP·(νP/2.5). We similarly use a carbon to nitrogen ratio for animals of 5 (Allgeier et al., 2020), to convert BH from carbon to nitrogen stocks. We estimate S using the ratio between the decomposition flux and mineralization, D = fD/z, where we take S as the effective stock of organic matter.
Beyond the data from Cebrian (1999, 2004), additional estimations of ratios of stocks and process rates are needed to parameterize our model. In absence of a cohesive empirical estimates for terrestrial and aquatic ecosystems, we use representative information from a variety of sources, striving to define plausible values for the model parameters so that nitrogen stocks and fluxes remain within reasonable observed ranges.
We begin by estimating the ratios between compartment stocks, i.e., of predators to herbivores σCH, detritivores to herbivores σDH, and of inorganic to organic nitrogen σNS. From a global estimation of biomass in the oceans (Bar-On et al., 2018), we see that the biomass of fish and large invertebrates is roughly similar to, or slightly smaller than, that of arthropods and protists. This similarity between vertebrates and invertebrates suggests that also the biomass of animals at different trophic levels could be similar because herbivores are mainly planktonic (e.g., protists), predators are mainly vertebrates (e.g., fish), and detritivores span both categories. We therefore assume that their stocks in the aquatic ecosystem to be the same, σCH = σDH = 1. Two reports of biomass of different trophic groups in forests (Brockie and Moeed, 1986) and grasslands (Perkins et al., 2018) show that detritivore biomass is an order of magnitude higher than (forest) and similar (grassland) to that of herbivores. Therefore, for terrestrial ecosystems we choose an intermediate value of detritivore biomass as five times the biomass of herbivores, i.e., σDH = 5. In the same studies they also find that predator biomass is substantially smaller than herbivore biomass. Hence, we assume for the terrestrial ecosystem that σCH = 0.2. These ratios for aquatic and terrestrial ecosystems are also roughly consistent with results for predators and prey across terrestrial and aquatic biomes (Hatton et al., 2015). A study of nitrogen cycling in aquatic ecosystems (Berman and Bronk, 2003) reported ratios between inorganic and organic nitrogen that were both higher and lower than 1. Conversely, Groffman and Rosi-Marshall (2013) found consistently lower inorganic nitrogen levels compared with organic nitrogen in terrestrial ecosystems, even when only considering the active proportion of soil organic material (around 5% of total organic matter; Paul, 2016). Based on this evidence, we assume σNS = 1 for the aquatic and σNS = 0.5 for the terrestrial ecosystems.
We also estimate fractions of production lost to predation and to self-regulation, which includes intra-guild predation. The fraction of secondary production lost to predation could be high, reaching 90% in forests (Hairston and Hairston, 1993). Because we deem this value to be extremely high, we choose a more moderate value, and assume that ρHC = ρHD = 0.5 for both the terrestrial and aquatic ecosystems. Estimations for how much production is lost to self-regulation are basically non-existent. It has been suggested that self-regulation and predation coefficients are roughly proportional for predators (Polis et al., 1989; Galiana et al., 2021). Assuming self-regulation and predation coefficients as equal (rC = qC), renders self-regulation fractions of ρCC = 1.0 for the aquatic and ρCC = 0.067 for the terrestrial ecosystem (see calculation in the Parameter derivation subsection). However, these values appear extreme and we therefore choose more moderate values, setting ρCC = 0.5 for the aquatic and ρCC = 0.1 for the terrestrial ecosystem. In doing so, we keep a large difference in self-regulation between ecosystem types, as suggested by the predation rates, but refrain from letting this difference be too large, potentially overshadowing other differences between ecosystem types. For other compartments there are no direct means to estimate self-regulation for a representative ecosystem. However, self-regulation for primary producers, e.g., via light limitation (Keddy, 2001), is likely more substantial than for herbivores and detritivores, which are probably more limited by predators and detrital matter, respectively (Hairston et al., 1960). We therefore choose, for both the terrestrial and aquatic ecosystems, small values for self-regulation fractions among herbivores and detritivores ρHH = ρDD = 0.05, but higher values for primary producers, ρPP = 0.2.
Finally, we estimate loss and leaching rates and nutrient conversion efficiencies. For the terrestrial ecosystem, the ratios between annual loss flux and stocks of inorganic nitrogen are between 0 and 2 (Groffman and Rosi-Marshall, 2013), so that we can assume an annual loss rate of nitrogen ℓ = 1 [yr−1]. For the aquatic ecosystem, estimates from multiple lakes (Hohener and Gachter, 1993) give a median value of ℓ = 2 [yr−1], assuming the relevant water column depth is 10 m (Middelboe and Markager, 1997). Next, we estimate nitrogen conversion efficiencies. These are generally higher than carbon conversion efficiencies, but by definition never higher than 1. Nutrient conversion efficiencies for animals have in previous models been assumed to be 0.8 (Zou et al., 2016), 0.5 and 0.25 (Attayde and Ripa, 2008). No loss for primary producer uptake of inorganic nitrogen was assumed. Following these assumptions, we set for primary producers ϵP = 1, and for animals an intermediate value of 0.5, i.e., ϵH = ϵD = ϵC = 0.5.
2.4. Parameter estimation
The values of all model parameters are estimated by inverting the model equations (Equation 1) for nitrogen fluxes, after setting nitrogen stocks, fluxes, and other ecosystem properties described in the previous subsection (Table 2). This approach is repeated for the terrestrial and aquatic ecosystems.
Since we need values for all six compartments to determine the parameter values, our estimations of stocks are complemented by the ratios between nitrogen stocks in different compartments, as described above: C = σCHH, D = σDHH, and N = σNSS. The values for stocks and fluxes are given in Table S3 in the Supplementary material.
The growth term in Equation (1a), fP = ϵPrPNP, is essentially the primary production in nitrogen units, so that we can find the consumption rate of nutrients by primary producers as:
Similarly, the loss term due to herbivory is rHPH, which can also be written as fPρPH (recall that ρPH is the fraction of primary production consumed by herbivores). It follows that the consumption rate by herbivores is:
We also assume the detritivory rate to be the same as for herbivores, i.e., rD = rH, as both herbivores and detritivores are typically mobile animals feeding on sessile material. Finally, the loss term of herbivore biomass due to predation is rCHC, which can also be written as fHρHC, where ρHC is the fraction of herbivore production consumed by predators, and fH is the flux herbivore gross production. We thus find that:
For primary producers, we use the detrital production flux fM, to find the natural mortality rate:
For the animal compartments we use the fraction left from predation from gross production of the compartment, to estimate the natural mortality:
We similarly use the fraction of production lost to self-regulation, normalized by the compartment's stock, to estimate the self-regulation coefficients:
The values of the other parameters, namely the nutrient conversion efficiencies and the parameters describing losses from the organic nitrogen compartment (z and ℓ), are taken directly from their empirical estimates (Table 2). These derivations yield two parameter sets of 18 parameters for each ecosystem (Table 2). Furthermore, we construct an additional parameter set, based on the terrestrial parameters noted as “wide coexistence” in Table 2. These parameter values are chosen with a wide range of ψ within the coexistence range when I = 10 [gN m−2yr−1] (i.e., with all compartments extant), while remaining closely similar to the terrestrial ecosystem parameter set. While the choice of the “wide coexistence” parameter values is arbitrary, it is done in order to visually demonstrate the effect of food web properties in Figure 1. We show in the Supplementary material that the specific parameter value choice does not effect the qualitative results, and thus emphasize that our choices of this “wide coexistence” parameter values are only for presentation purposes, and do not affect the conclusions.
2.5. Simulations and parameter exploration
In all simulations and calculations we focus on the equilibrium of the ecosystem model. We find this equilibrium by integrating in time, until the maximal change in stocks per year, calculated for all nutrient input options, is less than 10−5 [gN m−2], or until the simulation reached 1,000 years, whichever comes first. We note that most simulations reach equilibrium in less than 100 years, and very few reach the 1,000 years mark (Table S1).
To answer our questions on how (1) subsidy strength and quality affect net primary production (NPP) and (2) consumer rates and other ecosystem properties modify the subsidy effect on primary producers, we assess how NPP changes as the subsidy strength I and quality ψ are varied. The former is assumed to range between 1 and 100 [gN m−2yr−1], and the latter across all possible values, between 0 (only inorganic nitrogen) and 1 (only organic nitrogen).
Besides varying the external inputs, we also explore the effect of other parameters: (i) the effects of food web properties are assessed by changing several parameters in conjunction, and (ii) an uncorrelated random parameter exploration of all parameters is performed to confirm the generality of the results.
First, we test the effect on ecosystem dynamics of three over-arching properties of the food web: consumption, conversion efficiency, and metabolic rates. We vary the baseline values of the parameters by a factor γ, so that the parameters change together in a perfectly coordinated manner. For consumption, we change consumption coefficients for the animal compartment i as: . For conversion, we change nutrient conversion for the animal compartment i as , noting that the smaller range of nutrient conversion efficiencies is due to the constraint ϵi ≤ 1. For metabolic rates, we change the consumption coefficients, natural mortality and self-regulation coefficients in the three animal compartments as , where a stands for r, u, and q, and i identifies the animal compartment.
In these analyses, we vary the control parameter γ on a logarithmic scale between 0.1 and 10. Our focus on variations in the properties of the animal compartments is motivated by our interest in how primary production is altered in the food web. However, we also test if concurrently changing the parameters for the primary producers, P, changes the qualitative results (see Supplementary material). To present the dependence of NPP on ψ (Figure 3), we calculate the average value of NPP across the range of I-values for each ψ, and only show ψ-values where compartments coexist, i.e., where all compartments have non-zero values at equilibrium for at least some value of I. To present the NPP dependence on I, we do the same, but now averaging over the range of ψ values for each I.
Second, to robustly test the effect of changing each parameter, we perform a random parameter exploration. We take each of 18 model parameters: all parameters except I and ψ. We change their values relative to the baseline values of terrestrial or aquatic ecosystems (Table 2), without any correlation between parameters (in contrast to the first analysis). For each parameter, we assume a log-normal distribution, such that the base-10 logarithm values have a standard-deviation of 1, except for nutrient conversion efficiencies, for which we assume a standard-deviation of 0.25 and we cap the values at 1. We repeat the sampling to create 20,000 sets of randomly chosen parameters, and explore subsidy scenarios by considering a range of ψ values between 0 and 1, and seven values of I (1, 2, 5, 10, 20, 50, 100 [gN m−2yr−1]).
2.6. Ecosystem metrics for subsidy impact assessment
We focus on estimating NPP, and its dependence on nutrient subsidies. The effect of herbivory is included in our definition of NPP, motivated by our aim to describe variations in net biomass production increments, that is, primary production left after the herbivory fraction has been removed. This amounts to the term upP in Equation (1), which is also directly proportional to the producer biomass P (as opposed to the term rPϵPNP, which includes the production lost to herbivory). Since production is strongly dependent on input levels I, and we change I across two orders of magnitude, it is useful to normalize NPP by I. We thus use a measure of normalized production, given by uPP/I. We note that this normalized production term is dimensionless, representing an ecosystem-level nitrogen use efficiency if we assume that mortality is due to harvesting in analogy to agricultural ecosystems (Scaini et al., 2020). As we show in the results, it is also useful to examine how P changes when the subsidies are more organic, i.e., (uP and I are constant along the ψ axis, and we can therefore ignore them here). We normalize this term by the average primary producer biomass for a given level of subsidy strength I, and call this metric “Producer Sensitivity to Organic Subsidy” (PSOS): .
3. Results
3.1. General responses of primary production to changes in subsidy strength and quality
We begin by examining how subsidies, and in particular their strength I and their organic fraction ψ, affect NPP as given by the term uPP for our two representative ecosystems, terrestrial (Figure 2, left) and aquatic (Figure 2, right). In each ecosystem, all parameters are constant except the subsidy parameters I and ψ. In general, NPP increases with subsidy strength, as more nutrients are converted into biomass. To highlight the effect of subsidies on the efficiency of nutrient conversion to biomass, in Figure 2 and in the following we focus on the normalized production uPP/I. When nitrogen inputs are low (the lower region in subsidy parameter space), normalized production is also low (dark blue). At high inputs, normalized production levels saturate as more biomass is lost to top consumers in the aquatic ecosystem, or to inefficiencies related to primary producer self-regulation such as light limitation in the terrestrial ecosystem. Eventually, these effects will cause normalized production to decrease at very high subsidy strength, as seen on top of each panel in Figure 2.
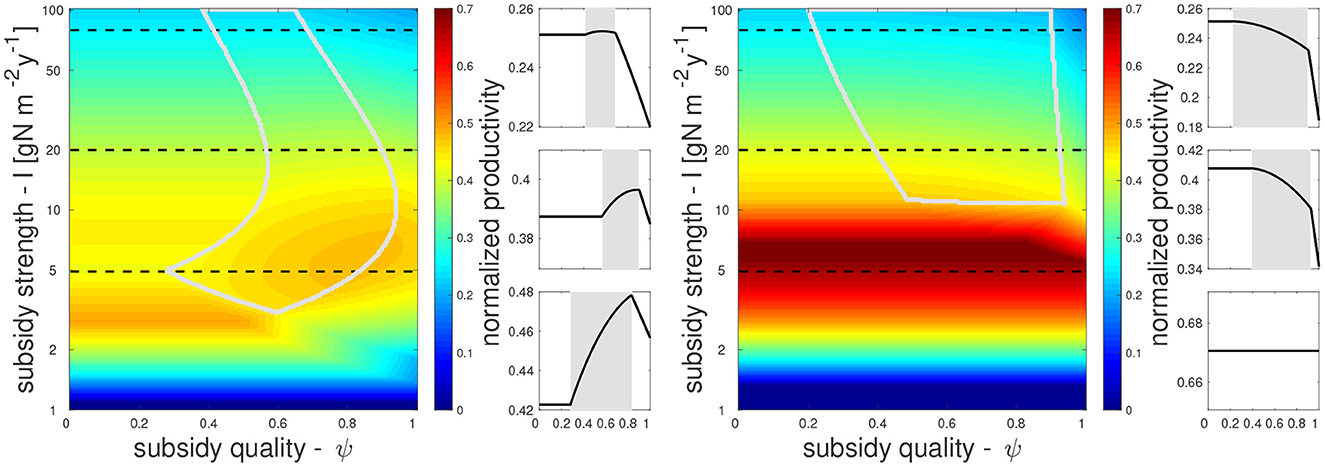
Figure 2. Normalized production uPP/I as a function of nitrogen subsidy strength (I) and quality (organic nitrogen fraction, ψ), in terrestrial (left) and aquatic (right) ecosystems. Besides I and ψ, other parameters are kept constant; gray lines enclose the coexistence region where all food web compartments (P,H,D,C) are extant. Small panels on the right of each parameter-space show normalized production at a constant value of I (gray background shows coexistence region), corresponding to the three horizontal dashed lines in each parameter-space.
As we increase the organic fraction of nitrogen inputs, i.e., moving left to right in the subsidy parameter space, NPP consistently decreases in the aquatic ecosystem. In contrast, NPP can also increase in the terrestrial ecosystem within certain ranges of organic fraction. This increase only occurs within the coexistence range where all compartments have non-zero values (marked by gray lines Figure 2). The positive trend in the terrestrial ecosystem occurs because organic nitrogen supports a large detritivore community, which feeds the predators that in turn reduce the herbivores, thereby allowing plants to grow more. At higher organic fractions outside the coexistence range, NPP decreases when larger amounts of nitrogen flow into the brown food web instead of being used by primary producers.
The behavior outside the coexistence region can be explained as follows. When D = 0 (due to low ψ), net nitrogen mineralization equals the input of organic nitrogen (zS = IS). Hence, all nitrogen inputs reach the N compartment at equilibrium, with ψ playing no further role. When H = 0 (due to high ψ) the only effect of detritivores on primary producers is competition over nitrogen, leading to a decrease of P with ψ. Here, the detritivores have opportunities to consume organic nitrogen before it is mineralized and consumed by the primary producers. Finally, when C = 0 (low I) no top-down control of the herbivores can occur, and hence D only exerts a negative effect via resource competition, similarly to the case where H = 0. Hereafter, we will focus on how nutrient subsidies determine NPP within the coexistence region, which changes depending on parameter selection because we expect the species groups represented in our model—primary producers, herbivores, predators, and detritivores—to all be extant in most ecosystems.
3.2. Effects of food web properties on production-subsidy relations
Focusing on the coexistence region, we can now assess how food web properties determine how NPP is affected by subsidy strength and quality. We consider three food web properties encoded in parameters describing the three animal compartments (H, D, C): consumption, conversion efficiency, and metabolic rates.
Net primary production, normalized by subsidy strength, is affected jointly by subsidy quality ψ (top of Figure 3) and strength I (bottom of Figure 3), and by food web properties (indicated by different colors). This is shown for a specific set of initial ecosystem parameters (denoted as “wide-coexistence” in Table 2), but we conduct a sensitivity analysis to test that the reported trends are consistent for a wide range of parameter sets, including parameters for aquatic ecosystems, as well as with internal recycling (see Supplementary material).
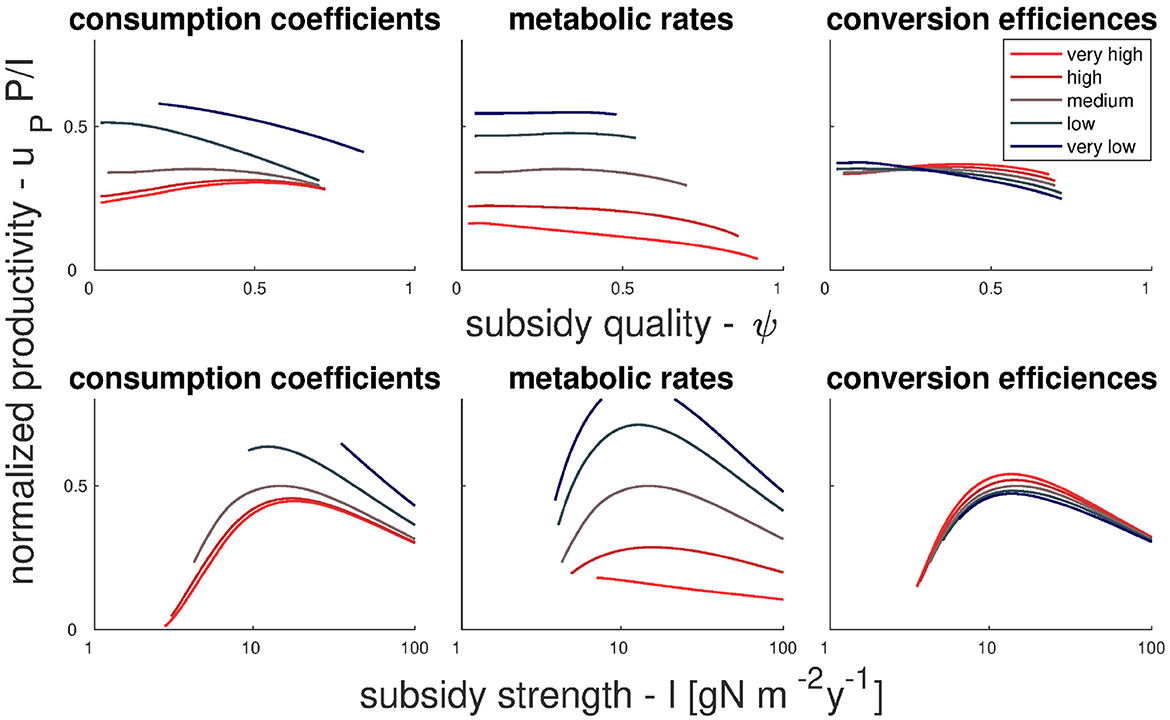
Figure 3. Effect of food web properties and subsidies on net primary production. Top and bottom panels show normalized production as a function of subsidy quality (top) and subsidy strength (bottom). Left, middle, and right panels show sensitivities to food web properties as described by the parameters characterizing the animal compartments H, D, and C [(left) consumption coefficients; (middle) consumption coefficients, mortality rates, and self-regulation coefficients; (right) nutrient conversion efficiencies]; shades from blue to red (light to dark) correspond to increasing values of model parameters. These changes are done relative to baseline parameters defined in Table 2 (column labeled “wide-coexistence”), corresponding to a terrestrial ecosystem with a large coexistence range. Results for other baseline parameter values are summarized in Figure S10.
Overall, the response of NPP is stronger when subsidy strength is varied than when varying subsidy quality, and it is often hump-shaped with a maximum at intermediate I. These responses vary in shape depending on the food web properties considered, indicating interactions between these properties and subsidies strength and quality. Net primary production decreases mildly with increasing consumption coefficients and strongly with increasing metabolic rates. In contrast, NPP varies less (and generally increases) with increasing nutrient conversion efficiency. Increasing metabolic rates causes a shift from mild positive dependency of NPP on subsidy quality to a mild negative dependency, whereas trends turn to positive when increasing consumption or conversion. The most notable interaction of food web properties with subsidy strength occurs when increasing metabolic rate, which causes a shift from hump-shaped to weakly negative relation between NPP and subsidy strength.
3.3. Analytical exploration of ecosystem processes driving production-subsidy relations
As we have seen in the results so far, a higher fraction of organic subsidies can increase NPP, in particular in terrestrial ecosystems and under scenarios of strong consumption and more efficient nutrient conversion by animals. Beside these food web properties, we now assess which model parameters and thus which associated ecosystem processes that play a role for the relationship between production and subsidy quality. We do this using both an analytical (this section) and a numerical approach (Section 3.4).
Starting from analytical arguments, it is useful to consider a simplified scenario where predator self-regulation is negligible (i.e., qCC ≈ 0). Not only is this approximation mathematically convenient, but this term is also indeed substantially smaller than other terms in terrestrial ecosystems: with our estimated C stock, we have qCC = 0.714≪6.44 = uC [yr−1]. Under this approximation, solving Equation (1d) at equilibrium yields
which means that increases in H are balanced by decreases in D and vice versa as ψ is increased, because their total is fixed. It is therefore natural to ask how P changes between the low ψ value where D = 0 and the high ψ value where H = 0. Note that D and H do not necessarily span this whole range for 0 < ψ < 1, but answering the question remains useful to clarify the role of model parameters. At low ψ and with D = 0, all nitrogen subsidies flow into N, and from Equation (1)a we have at equilibrium:
where PL = P(ψ ≈ 0). At high ψ and with H = 0, we have no herbivory term in Equation (1a), so that at equilibrium:
where PH = P(ψ ≈ 1) and we defined the parameter group , associated with nutrient uptake by detritivory. Equations (3) and (4) can be directly solved to find P, but it is more instructive to study the difference between their right hand sides, where state variables and parameters affecting stocks P, and hence also production, appear. Using these equations, we can estimate the sensitivity of production to changes in ψ because Equations (3) and (4) represent P at low and high ψ, respectively, and the derivative scales as PH−PL = P(ψ ≈ 1)−P(ψ ≈ 0). Subtracting the two equations, we find the difference between P stocks between ψ ≈ 1 and ψ ≈ 0,
We can largely disregard the first term in round brackets, because it only decreases the difference ΔP, but does not affect the direction of the ψ effect: if PH = PL this whole term vanishes, if PH > PL it is negative, and if PH < PL it is positive. The second term, , shows that herbivory increases ΔP. Similarly, the third and last term in the square brackets shows the effect of nutrient competition by detritivory, with a decrease in ΔP as ϕ decreases from its maximal value of 1.
The formulation of ΔP reveals how NPP is affected by larger fractions of organic inputs, seen by the changes in the second and third term of the equation. For instance, fast rates of organic nitrogen dynamics (large ℓ and z) lead to a more positive effect of ψ on P (positive ), since ℓ occurs in the denominator of the third term, and large z keeps ϕ closer to 1. For both ℓ and z, less nitrogen is lost due to resource competition with detritivores, and hence NPP gains due to lower herbivory become more important. Decreasing subsidy strength I or production coefficient rP has the same qualitative effect as increasing ℓ (i.e., decreasing the relative importance of the growth term), and hence also leads to a more positive .
Focusing on the second term that captures herbivory effects, a higher herbivory rate rH also leads to a more positive : if herbivory pressure is high, increase in ψ leads to larger P-values due to lower herbivore densities. Finally, higher rD decreases nutrient availability for producers by routing nutrients to decomposers (decreasing ϕ), thus also lowering . Effects of other parameters on production are harder to predict—for example, uC occurs in both the herbivory term and in ϕ, makings its effect less straight-forward.
3.4. Numerical exploration of ecosystem processes driving production-subsidy relations
We corroborate these analytical relationships with an extensive numerical exploration using randomly chosen parameter sets. In this exploration, we show how the metric PSOS, which represents the average sensitivity of producer biomass P on subsidy quality ψ, varies as a function of parameter values (Figure 4). We focus here on parameters characterizing the terrestrial ecosystem (see Table 2). A similar exploration of parameters for aquatic ecosystems shows overall comparable results (see Supplementary material), with a few exceptions, notably that in aquatic ecosystems organic additions have a more negative effect on NPP.
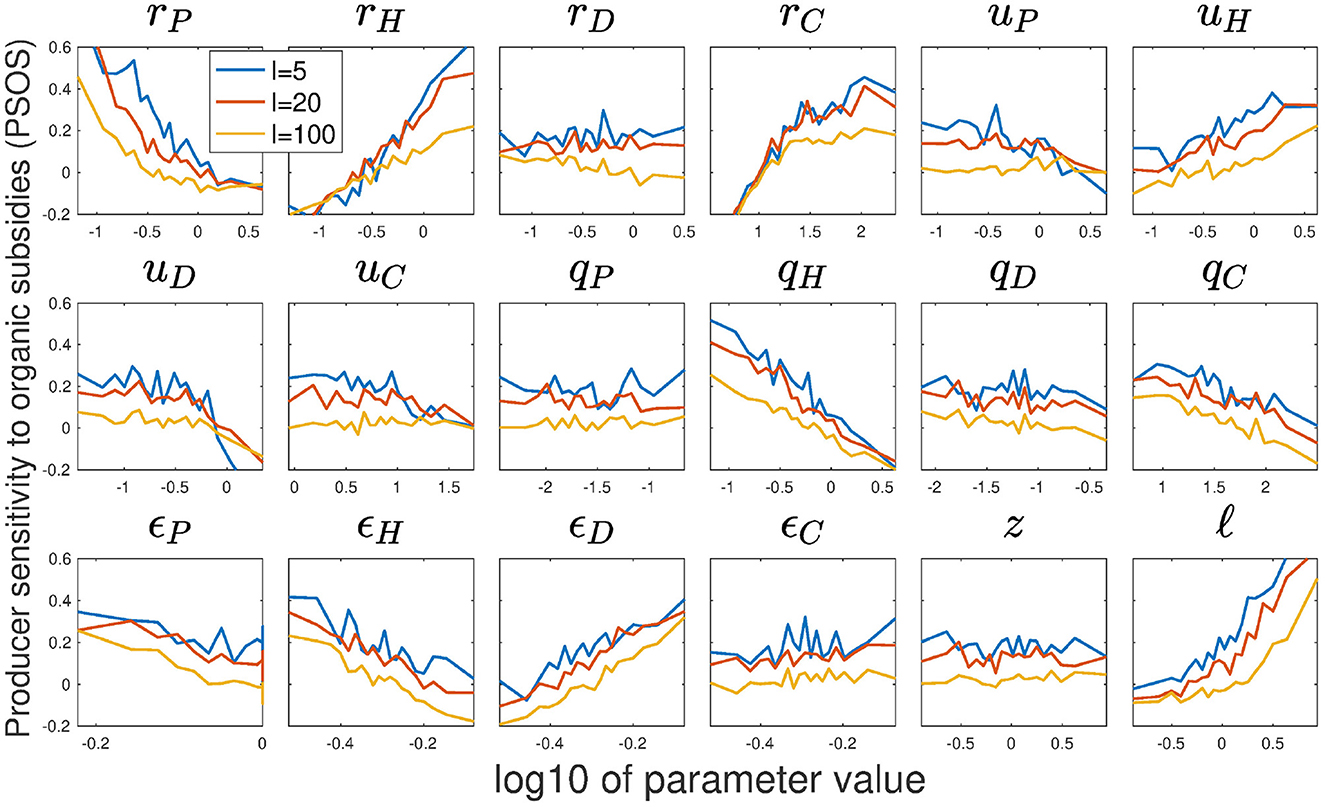
Figure 4. Producer sensitivity to organic subsidies (PSOS) as a function of variation in model parameters, averaged over 1,000 random parameter sets per point shown. Median parameter values for the terrestrial ecosystem are used to construct the random parameter space (see Table 2). Results are shown for varying subsidy strength I, as indicated by different colors: blue (I = 5), red (I = 20), and yellow (I = 100). PSOS is defined as: .
Producer sensitivity to organic subsidy increases with higher rH and ℓ, and decreases with I and rP, consistent with our analytical analysis (Figure 4). However, rD and z show the predicted trends only for parameters of aquatic ecosystems (and even then with weak trends, see Supplementary material). This suggests that herbivory (mediated by rH) and nutrient loss (ℓ, but also I and rP) play a significant role in determining the sensitivity of NPP on subsidy quality, while resource competition with detritivores (rD and z) does not. Moreover, PSOS increases with uH, ϵD, and rC, and decreases with ϵH and uD. Additionally, self-regulation of all animal compartments causes a weak negative trend, which virtually disappears in the aquatic ecosystems (see Supplementary material). The effect of rC and the animal self-regulation coefficients could not be seen using our analytical approach, since they are at odds with negligible predator self-regulation. rC is mainly relevant in relation to qC (Barbier and Loreau, 2019), and hence neglecting qC takes away our ability to see this effect. The other self-regulation coefficients can become important only when qC is large, as otherwise top-down control is too dominant—This is indeed evidenced by their minimal effect in the aquatic ecosystems where predator self-regulation is weak.
4. Discussion
4.1. Subsidy effects on net primary productivity
Our main results can be summarized along four main points. First, as expected, increasing (strengthening) nitrogen inputs leads to higher Net Primary Production (NPP), but this effect saturates as nutrients inputs increase, as can be seen by the decreasing normalized NPP values at higher subsidy strength (Figure 2). Second, we predict that increasing the fraction of nitrogen subsidies in organic form (higher ψ) will lead to higher NPP in many terrestrial ecosystems, but more often to lower NPP in aquatic ecosystems (Figure 2, Figure S6). Third, the slope of the production—subsidy quality relation increases with higher consumption coefficients, but decreases substantially with higher metabolic rates (Figure 3, Figure S10). Fourth, we find that several ecosystem properties mediate the effect of subsidy quality on NPP (Figure 4). For example, increasing the herbivory coefficient (rH), predation coefficient (rC), detritivory conversion efficiency (ϵD), and loss rate (ℓ), consistently and strongly increases the positive effect of an increasing fraction nitrogen in organic form (ψ) on NPP.
All these relationships between subsidy and NPP depend on the ecosystem in question, and we confirm that terrestrial and aquatic ecosystems respond differently to subsidies (Nakano and Murakami, 2001; Shurin et al., 2006; Leroux and Loreau, 2008). The finding that in terrestrial ecosystems NPP is more positively affected by organic additions than in aquatic ecosystems may seem surprising, given that this effect is driven by trophic cascades of predators suppressing herbivores—a process that is typically associated with aquatic ecosystems. One explanation could be that metabolic rates of herbivores are often higher in aquatic ecosystems (Cebrian and Lartigue, 2004), and, as we have seen (Figure 3), high metabolic rates lead to a more negative effect of organic inputs on NPP. We also find that increasing the mineralization rate (z), production coefficient (rP), herbivore mortality rate (uH), and herbivore self-regulation coefficient (qH) lead to a more positive relationship between ψ and NPP in aquatic ecosystems (Figure S5). This in turn implies that in aquatic systems primary producers are nutrient limited, so that increasing the mineralization rate (z) or production coefficient (rP) allows them to take up more nitrogen. In contrast, herbivores are already predator-controlled as increasing herbivore mortality rate (uH) or herbivore self-regulation coefficient (qH) decreases the predator control over herbivores. Hence, we predict that subsidizing aquatic ecosystems is less likely to increase NPP via the indirect effect of predator control, compared with terrestrial ecosystems. Finally, we note that aquatic ecosystems often receive substantial subsidies from nearby terrestrial ecosystems (Shurin et al., 2006; Leroux and Loreau, 2008), and high subsidy strength (I) weakens the importance of subsidy quality (ψ) (Figure 4). Therefore, aquatic ecosystems with high subsidy strength (I) are not likely to exhibit higher NPP due to higher fractions of organic subsidies.
From a theoretical perspective, the positive effect of organic subsidies on primary production can be understood as a particular case of apparent competition (Holt, 1977; Abrams et al., 1998), in which consumers are suppressed by predators that in turn benefit from the subsidies. In this light, the switch from positive to negative effects of subsidies on NPP, for instance when comparing terrestrial to aquatic systems (Figure S6), is conceptually similar to the switch between apparent competition and apparent mutualism (Montagano et al., 2018), since in both cases indirect effects on consumers due to predation pressure can have negative or positive effects, respectively. However, unlike the competition-mutualism switch that centers on predation alone, in our case it is the interplay between predation pressure and resource competition that determines the effect of subsidies. A similar situation may occur in meta-ecosystems where flows of abiotic resources and animals are often very different, highlighting the importance of incorporating high trophic levels into theoretical meta-ecosystem studies (Gounand et al., 2018).
Our numerical exploration (Figure 4) largely confirms our analytical results [using Equations (3) and (4)] where low subsidy strength (I) and high loss rate of inorganic nitrogen (ℓ) lead to a positive relationship between the fraction of organic subsidies and net primary production. However, our analytical analysis did not allow for identifying effects of other ecosystem parameters on the relationship between subsidy quality and NPP. The numerical analysis instead pointed to the negative impact of herbivory conversion efficiency (ϵH) and detritivore mortality rate (uD) and the positive impact of detritivory conversion efficiency (ϵD) and herbivore mortality rate (uH). Both high herbivore mortality rate (uH) and low herbivory conversion efficiency (ϵH) decrease herbivore biomass, whereas low detritivore mortality rate (uD) and high detritivory conversion efficiency (ϵD) increase detritivore biomass. All these changes lead to higher NPP when increasing organic subsidies. We thus find an asymmetry between the impacts on NPP of herbivores (which directly decrease NPP) and detritivores (which indirectly increase NPP by promoting predators).
4.2. Nitrogen recycling and other model assumptions
To ease the analysis and presentation, we chose not to include nitrogen recycling from producers and other compartments to the organic nitrogen compartment, which are often considered in theoretical analyses of ecosystem dynamics (De Mazancourt et al., 1998; Attayde and Ripa, 2008; Cherif and Loreau, 2009). However, as we show in the Supplementary material, the qualitative results are similar with and without nitrogen recycling, with three notable exceptions. Adding nitrogen recycling in the model results in higher production due to the increased efficiency of the system, leads to a slight shift left of coexistence boundaries on the ψ axis, as recycled material feeds the organic nutrient compartment and weakens the positive link between ψ and NPP. This last aspect implies that in ecosystems where nutrient recycling is minimal, such as in agricultural crop fields, switching from inorganic to organic nutrient inputs is more likely to increase NPP. It is also difficult to find a simple explanation to this last aspect, but it can be partially attributed to the increased effective inputs, which play the role of higher subsidy strength (I) (see, e.g., Figure 4).
Beyond nutrient recycling, we have made some other notable simplifying assumptions. We chose to use linear kinetics for the organic nitrogen compartment (as in most soil biogeochemical models, Manzoni and Porporato, 2009) and a type I functional response for species interactions. While converting literature data to the nitrogen stock units, constant carbon-to-nutrient ratios were assumed within each compartment. This assumption of stoichiometric homeostasis is supported by evidence for animals, but less so for primary producers (Elser et al., 2000). We also used a neutral assumption on predation choice, assuming that predators can predate on both herbivores and detritivores, and show no preference in the matter. This choice was used to highlight the distinct nature of green-brown food webs, where herbivores and detritivores compete for resources in an inherently non-equal way, leading to an interesting interplay between resource competition and apparent competition due to predation pressure. This is in contrast to previous research which has focused more on green food webs, and has considered both apparent competition and prey switching in detail (Abrams et al., 1998; Chase et al., 2002; Leroux and Loreau, 2012). While all these simplifications affect the results, we expect them to make second-order corrections, and they should affect the quantitative but not the qualitative outcomes. Since we focus here on the qualitative response of production to subsidies, we believe that, much like for nutrient recycling, these other simplifications will not impact our general conclusions.
Finally, the proposed model focuses on nitrogen flows and stocks, neglecting interactions of nitrogen and other elements that can modify the rates and efficiencies of nitrogen transfers among compartments, depending on the most limiting element (Sterner and Elser, 2002; Cherif and Loreau, 2013; Manzoni et al., 2017). This assumption has also implications for the interpretation of subsidy quality. Here, we have defined quality in terms of relative amounts of inorganic and organic N in the subsidy, but other measures of quality could be considered, including the elemental composition of the organic subsidy. For example, inputs of organic matter with high C:N ratio would cause C:N in the S compartment to increase, eventually resulting in inorganic nitrogen immobilization (Cherif and Loreau, 2013). In our framework, net immobilization is a nitrogen transfer from N to S, which we have not considered but that would reduce the amount of N available for primary producers. Thus, high C:N organic subsidies would be of “lower quality” compared to low C:N organic subsidies. In the long term, as carbon is removed from organic matter via respiration, nitrogen mineralization would be restored, but lower inorganic nitrogen and higher organic matter C:N ratio resulting from this low quality subsidies might lower the nitrogen content in primary producers, and increase the nitrogen assimilation efficiencies while decreasing the growth rates at higher trophic levels (due to lower efficiency of carbon conversion to biomass, Manzoni et al., 2017). However, a stoichiometric explicit model [building on Cherif and Loreau (2013) and Buchkowski et al. (2019)] would need to be used to assess these consequences on the food web as a whole.
By focusing on the nitrogen cycle only, our model did not include non-linear feedback mechanisms involving other variables partly controlled by nitrogen stocks. For example, subsidies can lead to nutrient accumulation in water bodies that promote NPP, but eventually can lead to eutrophication and a dramatic change in ecosystem function. This type of regime shifts (Scheffer and Carpenter, 2003) require a modeling approach that includes also state variables outside the nitrogen cycle, such as light and oxygen availability in the case of eutrophication.
4.3. Implications and future directions
An understanding of which parts of the parameter space that are relevant to real ecosystems will be useful for applied purposes. For instance, the model predicts that introducing organic fertilization in agriculture improves regulation of herbivores, which are potential pests on crop plants. Indeed, empirical work has shown that organic fertilization can suppress herbivores (Settle et al., 1996; Riggi and Bommarco, 2019), but does not always increase primary production (Halaj and Wise, 2002), emphasizing that benefits of organic subsidies to primary production are context dependent. Further, in conjunction with site-specific parameter estimates, the model we present with linked green and brown resource channels can be used to predict the effects of anthropogenic subsidies on specific natural ecosystems such as grasslands or forests. The model can indicate which ecosystems are more sensitive to nutrient enrichment. Furthermore, climate change affects various ecosystem properties such as metabolic rates and the kinetics of soil nutrient cycling, which in turn affect the impacts of nutrient subsidies on NPP.
It is difficult to extrapolate on the overall effect of climate change, given the range of positive and negative effects of different parameters (Figure 4, Figure S5), and the difficulty in estimating the effect of warming on model parameters (Bideault et al., 2021). However, if we assume that metabolic rates are more sensitive to warming than other ecosystem properties such as consumption coefficients, we can speculate from Figure 3 that warming will lead to a more negative impact of organic subsidies on NPP. This highlights the importance of exploring how ecosystems respond to compound climatic changes and perturbations in the subsidy strength and quality. These changes lead ecosystems toward conditions not previously experienced, which are therefore also harder to predict. Our approach of developing theory for subsidized ecosystems using dynamical models, parameterizing these models for a wide range of ecosystem and testing confounding effects of model parameters, is a step toward understanding how ecosystems respond to human influence. Importantly, it is clearly essential to consider the green and brown food webs in concert.
While useful for qualitative predictions, testing our theoretical predictions empirically in specific case studies is likely to be challenging. There are recent investigations of nutrient quality and quantity subsidy effects on primary producers in conjunction with food-web dynamics (Riggi and Bommarco, 2019; Aguilera et al., 2021), but it is difficult to directly connect their results to our theoretical findings. A particular problem is to normalize results by subsidy strength, i.e., empirically disentangling the effects of subsidy strength (I) and subsidy quality (ψ). This is of interest since the subsidy effect in the context of green-brown food webs should be most striking along the ψ axis, given that the effect of I on production is a more straightforward bottom-up one. Indeed, despite clear results showing that detritus additions increase primary producer stocks (Hagen et al., 2012), it is not possible to attribute subsidy effects to bottom-up vs. top-down mechanisms, because experiments typically manipulate both ψ and I, and increases in I may overshadow the top-down effects of higher ψ. A practical solution may be to compare ecosystems with and without herbivory and/or predation (e.g., due to pesticide use), where the effect of ψ for different parameter regimes should be most evident.
Here, we explored how two aspects of nutrient subsidies—strength and quality—impact primary production in green-brown food webs. Subsidy strength has a direct positive impact, mainly as a bottom-up direct effect on producers. The effect of subsidy quality truly connects the green and brown channels in food webs—organic subsidies can indirectly promote production via predator control on herbivores. This aspect of nutrient enrichment has been largely overlooked, and as we have seen here can play a major role in determining ecosystem functioning. These results show that the impact of nutrient enrichment depends on more than its strength, and that human overloading of ecosystems with inorganic nutrients is consequential not only because of its large amounts, but also due to higher proportions of inorganic nutrients, which promote production at the cost of losing the ecological function of the brown channel.
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found here: Cebrian (1999, 2004) and Cebrian and Lartigue (2004); model scripts are included as Supplementary material.
Author contributions
YZ, SM, and RB conceived the study and developed the model. YZ performed the data collection, analysis, and simulations. All authors interpreted the results. YZ led the writing, which SM and RB commented on and revised. All authors contributed to the article and approved the submitted version.
Funding
This research was funded by the Swedish University of Agricultural Sciences, the Swedish Research Council for Sustainable Development FORMAS (grant no. 2022-00928), and by the European Research Council (ERC) under the European Union Horizon 2020 Research and Innovation Programme (grant agreement no. 101001608). Open access publication fees were covered by Stockholm University.
Acknowledgments
A previous version of this manuscript was uploaded as a preprint to the bioRxiv repository (Zelnik et al., 2021).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2023.1106461/full#supplementary-material
References
Abrams, P. A., Holt, R. D., and Roth, J. D. (1998). Apparent competition or apparent mutualism? Shared predation when populations cycle. Ecology 79, 201–212. doi: 10.1890/0012-9658(1998)079[0201:ACOAMS]2.0.CO;2
Aguilera, G., Riggi, L., Miller, K., Roslin, T., and Bommarco, R. (2021). Organic fertilization suppresses aphid growth via carabids in the absence of specialist predators. J. Appl. Ecol. 58, 1455–1465. doi: 10.1111/1365-2664.13862
Allen D. C. and Wesner, J. S.. (2016). Synthesis: comparing effects of resource and consumer fluxes into recipient food webs using meta-analysis. Ecology 97, 594–604. doi: 10.1890/15-1109
Allgeier, J. E., Wenger, S., and Layman, C. A. (2020). Taxonomic identity best explains variation in body nutrient stoichiometry in a diverse marine animal community. Sci. Rep. 10, 13718. doi: 10.1038/s41598-020-67881-y
Attayde, J. L., and Ripa, J. (2008). The coupling between grazing and detritus food chains and the strength of trophic cascades across a gradient of nutrient enrichment. Ecosystems 11, 980–990. doi: 10.1007/s10021-008-9174-8
Barabás, G., Michalska-Smith, M. J., and Allesina, S. (2017). Self-regulation and the stability of large ecological networks. Nat. Ecol. Evol. 1, 1870–1875. doi: 10.1038/s41559-017-0357-6
Barbier, M., and Loreau, M. (2019). Pyramids and cascades: a synthesis of food chain functioning and stability. Ecol. Lett. 22, 405–419. doi: 10.1111/ele.13196
Bar-On, Y. M., Phillips, R., and Milo, R. (2018). The biomass distribution on earth. Proc. Natl. Acad. Sci. U.S.A. 115, 6506–6511. doi: 10.1073/pnas.1711842115
Baxter, C. V., Fausch, K. D., Murakami, M., and Chapman, P. L. (2004). Fish invasion restructures stream and forest food webs by interrupting reciprocal prey subsidies. Ecology 85, 2656–2663. doi: 10.1890/04-138
Berman, T., and Bronk, D. (2003). Dissolved organic nitrogen: a dynamic participant in aquatic ecosystems. Aquat. Microb. Ecol. 31, 279–305. doi: 10.3354/ame031279
Bideault, A., Galiana, N., Zelnik, Y. R., Gravel, D., Loreau, M., Barbier, M., et al. (2021). Thermal mismatches in biological rates determine trophic control and biomass distribution under warming. Glob. Change Biol. 27, 257–269. doi: 10.1111/gcb.15395
Bobbink, R., Hicks, K., Galloway, J., Spranger, T., Alkemade, R., Ashmore, M., et al. (2010). Global assessment of nitrogen deposition effects on terrestrial plant diversity: a synthesis. Ecol. Appl. 20, 30–59. doi: 10.1890/08-1140.1
Brockie, R. E., and Moeed, A. (1986). Animal biomass in a New Zealand forest compared with other parts of the world. Oecologia 70, 24–34. doi: 10.1007/BF00377108
Buchkowski, R. W., Leroux, S. J., and Schmitz, O. J. (2019). Microbial and animal nutrient limitation change the distribution of nitrogen within coupled green and brown food chains. Ecology 100, e02674. doi: 10.1002/ecy.2674
Buendía, C., Kleidon, A., Manzoni, S., Reu, B., and Porporato, A. (2018). Evaluating the effect of nutrient redistribution by animals on the phosphorus cycle of lowland Amazonia. Biogeosciences 15, 279–295. doi: 10.5194/bg-15-279-2018
Čapek, P., Manzoni, S., Kaštovská, E., Wild, B., Diáková, K., Bárta, J., et al. (2018). A plant–microbe interaction framework explaining nutrient effects on primary production. Nat. Ecol. Evol. 2, 1588–1596. doi: 10.1038/s41559-018-0662-8
Cebrian, J. (1999). Patterns in the fate of production in plant communities. Am. Nat. 154, 449–468. doi: 10.1086/303244
Cebrian, J. (2004). Role of first-order consumers in ecosystem carbon flow: carbon flow through first-order consumers. Ecol. Lett. 7, 232–240. doi: 10.1111/j.1461-0248.2004.00574.x
Cebrian, J., and Lartigue, J. (2004). Patterns of herbivory and decomposition in aquatic and terrestrial ecosystems. Ecol. Monogr. 74, 237–259. doi: 10.1890/03-4019
Chase, J. M., Abrams, P. A., Grover, J. P., Diehl, S., Chesson, P., Holt, R. D., et al. (2002). The interaction between predation and competition: a review and synthesis. Ecol. Lett. 5, 302–315. doi: 10.1046/j.1461-0248.2002.00315.x
Cherif, M., and Loreau, M. (2009). When microbes and consumers determine the limiting nutrient of autotrophs: a theoretical analysis. Proc. Roy. Soc. B Biol. Sci. 276, 487–497. doi: 10.1098/rspb.2008.0560
Cherif, M., and Loreau, M. (2013). Plant–herbivore–decomposer stoichiometric mismatches and nutrient cycling in ecosystems. Proc. Roy. Soc. B Biol. Sci. 280, 20122453. doi: 10.1098/rspb.2012.2453
Darimont, C. T., Paquet, P. C., and Reimchen, T. E. (2009). Landscape heterogeneity and marine subsidy generate extensive intrapopulation niche diversity in a large terrestrial vertebrate. J. Anim. Ecol. 78, 126–133. doi: 10.1111/j.1365-2656.2008.01473.x
De Mazancourt, C., Loreau, M., and Abbadie, L. (1998). Grazing optimization and nutrient cycling: when do herbivores enhance plant production? Ecology 79, 2242–2252. doi: 10.1890/0012-9658(1998)079[2242:GOANCW]2.0.CO;2
Elser, J. J., Fagan, W. F., Denno, R. F., Dobberfuhl, D. R., Folarin, A., Huberty, A., et al. (2000). Nutritional constraints in terrestrial and freshwater food webs. Nature 408, 578–580. doi: 10.1038/35046058
Galiana, N., Arnoldi, J.-F., Barbier, M., Acloque, A., Mazancourt, C., and Loreau, M. (2021). Can biomass distribution across trophic levels predict trophic cascades? Ecol. Lett. 24, 464–476. doi: 10.1111/ele.13658
Gounand, I., Harvey, E., Little, C. J., and Altermatt, F. (2018). Meta-ecosystems 2.0: rooting the theory into the field. Trends Ecol. Evol. 33, 36–46. doi: 10.1016/j.tree.2017.10.006
Gounand, I., Mouquet, N., Canard, E., Guichard, F., Hauzy, C., and Gravel, D. (2014). The paradox of enrichment in metaecosystems. Am. Nat. 184, 752–763. doi: 10.1086/678406
Gravel, D., Guichard, F., Loreau, M., and Mouquet, N. (2010). Source and sink dynamics in meta-ecosystems. Ecology 91, 2172–2184. doi: 10.1890/09-0843.1
Groffman, P. M., and Rosi-Marshall, E. J. (2013). “The nitrogen cycle,” in Fundamentals of Ecosystem Science, eds K. C. Weathers, D. L. Strayer, and G. E. Likens (New York, NY: Elsevier), 137–158. doi: 10.1016/B978-0-08-091680-4.00007-X
Hagen, E. M., McCluney, K. E., Wyant, K. A., Soykan, C. U., Keller, A. C., Luttermoser, K. C., et al. (2012). A meta-analysis of the effects of detritus on primary producers and consumers in marine, freshwater, and terrestrial ecosystems. Oikos 121, 1507–1515. doi: 10.1111/j.1600-0706.2011.19666.x
Hairston, N. G., and Hairston, N. G. (1993). Cause-effect relationships in energy flow, trophic structure, and interspecific interactions. Am. Nat. 142, 379–411. doi: 10.1086/285546
Hairston, N. G., Smith, F. E., and Slobodkin, L. B. (1960). Community structure, population control, and competition. Am. Nat. 94, 421–425. doi: 10.1086/282146
Halaj, J., and Wise, D. H. (2002). Impact of a detrital subsidy on trophic cascades in a terrestrial grazing food web. Ecology 83, 3141–3151. doi: 10.1890/0012-9658(2002)083[3141:IOADSO]2.0.CO;2
Hatton, I. A., McCann, K. S., Fryxell, J. M., Davies, T. J., Smerlak, M., Sinclair, A. R. E., et al. (2015). The predator-prey power law: biomass scaling across terrestrial and aquatic biomes. Science 349, aac6284. doi: 10.1126/science.aac6284
Hines, J., Megonigal, J. P., and Denno, R. F. (2006). Nutrient subsidies to belowground microbes impact aboveground food web interactions. Ecology 87, 1542–1555. doi: 10.1890/0012-9658(2006)87[1542:NSTBMI]2.0.CO;2
Hohener, P., and Gachter, R. (1993). Prediction of dissolved inorganic nitrogen (DIN) concentrations in deep, seasonally stratified lakes based on rates of DIN input and N removal processes. Aquat. Sci. 55, 112–131. doi: 10.1007/BF00877440
Holt, R. D. (1977). Predation, apparent competition, and the structure of prey communities. Theor. Popul. Biol. 12, 197–229. doi: 10.1016/0040-5809(77)90042-9
Jacquet, C., Carraro, L., and Altermatt, F. (2022). Meta-ecosystem dynamics drive the spatial distribution of functional groups in river networks. Oikos 2022, e09372. doi: 10.1111/oik.09372
Jonsson, T. (2017). Conditions for Eltonian pyramids in Lotka-Volterra food chains. Sci. Rep. 7, 10912. doi: 10.1038/s41598-017-11204-1
Keddy, P. (2001). Competition, 2nd Edn. Population and Community Biology Series 26. Louisiana, LA: Springer Science & Business Media.
Leroux, S. J., and Loreau, M. (2008). Subsidy hypothesis and strength of trophic cascades across ecosystems: subsidies and trophic cascades. Ecol. Lett. 11, 1147–1156. doi: 10.1111/j.1461-0248.2008.01235.x
Leroux, S. J., and Loreau, M. (2012). Dynamics of reciprocal pulsed subsidies in local and meta-ecosystems. Ecosystems 15, 48–59. doi: 10.1007/s10021-011-9492-0
Loreau, M., and Holt, R. D. (2004). Spatial flows and the regulation of ecosystems. Am. Nat. 163, 606–615. doi: 10.1086/382600
Manzoni, S., Čapek, P., Mooshammer, M., Lindahl, B. D., Richter, A., and Santruckova, H. (2017). Optimal metabolic regulation along resource stoichiometry gradients. Ecol. Lett. 20, 1182–1191. doi: 10.1111/ele.12815
Manzoni, S., Čapek, P., Porada, P., Thurner, M., Winterdahl, M., Beer, C., et al. (2018). Reviews and syntheses: carbon use efficiency from organisms to ecosystems–definitions, theories, and empirical evidence. Biogeosciences 15, 5929–5949. doi: 10.5194/bg-15-5929-2018
Manzoni, S., and Porporato, A. (2009). Soil carbon and nitrogen mineralization: theory and models across scales. Soil Biol. Biochem. 41, 1355–1379. doi: 10.1016/j.soilbio.2009.02.031
Marczak, L. B., Thompson, R. M., and Richardson, J. S. (2007). Meta-analysis: trophic level, habitat, and productivity shape the food web effects of resource subsidies. Ecology 88, 140–148. doi: 10.1890/0012-9658(2007)88[140:MTLHAP]2.0.CO;2
McCary, M. A., Phillips, J. S., Ramiadantsoa, T., Nell, L. A., McCormick, A. R., and Botsch, J. C. (2020). Transient top-down and bottom-up effects of resources pulsed to multiple trophic levels. Ecology 102, e03197. doi: 10.1002/ecy.3197
Middelboe, A. L., and Markager, S. (1997). Depth limits and minimum light requirements of freshwater macrophytes. Freshw. Biol. 37, 553–568. doi: 10.1046/j.1365-2427.1997.00183.x
Montagano, L., Leroux, S. J., Giroux, M.-A., and Lecomte, N. (2018). The strength of ecological subsidies across ecosystems: a latitudinal gradient of direct and indirect impacts on food webs. Ecol. Lett. 22, 265–274. doi: 10.1111/ele.13185
Moore, J. C., Berlow, E. L., Coleman, D. C., Ruiter, P. C., Dong, Q., Hastings, A., et al. (2004). Detritus, trophic dynamics and biodiversity: detritus, trophic dynamics and biodiversity. Ecol. Lett. 7, 584–600. doi: 10.1111/j.1461-0248.2004.00606.x
Nakano, S., and Murakami, M. (2001). Reciprocal subsidies: dynamic interdependence between terrestrial and aquatic food webs. Proc. Natl. Acad. Sci. U.S.A. 98, 166–170. doi: 10.1073/pnas.98.1.166
Newsome, T. M., Dellinger, J. A., Pavey, C. R., Ripple, W. J., Shores, C. R., Wirsing, A. J., et al. (2015). The ecological effects of providing resource subsidies to predators: resource subsidies and predators. Glob. Ecol. Biogeogr. 24, 1–11. doi: 10.1111/geb.12236
Palumbi, S. R. (2003). Ecological subsidies alter the structure of marine communities. Proc. Natl. Acad. Sci. U.S.A. 100, 11927–11928. doi: 10.1073/pnas.2335832100
Paul, E. A. (2016). The nature and dynamics of soil organic matter: plant inputs, microbial transformations, and organic matter stabilization. Soil Biol. Biochem. 98, 109–126. doi: 10.1016/j.soilbio.2016.04.001
Perkins, M. J., Inger, R., Bearhop, S., and Sanders, D. (2018). Multichannel feeding by spider functional groups is driven by feeding strategies and resource availability. Oikos 127, 23–33. doi: 10.1111/oik.04500
Polis, G. A., Anderson, W. B., and Holt, R. D. (1997). Toward an integration of landscape and food web ecology: the dynamics of spatially subsidized food webs. Annu. Rev. Ecol. Syst. 28, 289–316. doi: 10.1146/annurev.ecolsys.28.1.289
Polis, G. A., Myers, C. A., and Holt, R. D. (1989). The ecology and evolution of intraguild predation: potential competitors that eat each other. Annu. Rev. Ecol. Syst. 20, 297–330. doi: 10.1146/annurev.es.20.110189.001501
Raun, W. R., and Johnson, G. V. (1999). Improving nitrogen use efficiency for cereal production. Agron. J. 91, 357–363. doi: 10.2134/agronj1999.00021962009100030001x
Riggi, L. G., and Bommarco, R. (2019). Subsidy type and quality determine direction and strength of trophic cascades in arthropod food web in agro-ecosystems. J. Appl. Ecol. 56, 1982–1991. doi: 10.1111/1365-2664.13444
Rooney, N., McCann, K., Gellner, G., and Moore, J. C. (2006). Structural asymmetry and the stability of diverse food webs. Nature 442, 265–269. doi: 10.1038/nature04887
Scaini, A., Zamora, D., Livsey, J., Lyon, S. W., Bommarco, R., Weih, M., et al. (2020). Hydro-climatic controls explain variations in catchment-scale nitrogen use efficiency. Environ. Res. Lett. 15, 094006. doi: 10.1088/1748-9326/ab9691
Scheffer, M., and Carpenter, S. R. (2003). Catastrophic regime shifts in ecosystems: linking theory to observation. Trends Ecol. Evol. 18, 648–656. doi: 10.1016/j.tree.2003.09.002
Settle, W. H., Ariawan, H., Astuti, E. T., Cahyana, W., Hakim, A. L., Hindayana, D., et al. (1996). Managing tropical rice pests through conservation of generalist natural enemies and alternative prey. Ecology 77, 1975–1988. doi: 10.2307/2265694
Shcherbak, I., Millar, N., and Robertson, G. P. (2014). Global metaanalysis of the nonlinear response of soil nitrous oxide (N2O) emissions to fertilizer nitrogen. Proc. Natl. Acad. Sci. U.S.A. 111, 9199–9204. doi: 10.1073/pnas.1322434111
Shurin, J. B., Gruner, D. S., and Hillebrand, H. (2006). All wet or dried up? Real differences between aquatic and terrestrial food webs. Proc. Roy. Soc. B Biol. Sci. 273, 1–9. doi: 10.1098/rspb.2005.3377
Spiecker, B., Gouhier, T. C., and Guichard, F. (2016). Reciprocal feedbacks between spatial subsidies and reserve networks in coral reef meta-ecosystems. Ecol. Appl. 26, 264–278. doi: 10.1890/15-0478
Sterner, R. W., and Elser, J. J. (2002). Ecological Stoichiometry: The Biology of Elements from Molecules to the Biosphere. Princeton, NJ: Princeton University Press. doi: 10.1515/9781400885695
Wollrab, S., Diehl, S., and De Roos, A. M. (2012). Simple rules describe bottom-up and top-down control in food webs with alternative energy pathways. Ecol. Lett. 15, 935–946. doi: 10.1111/j.1461-0248.2012.01823.x
Zelnik, Y. R., Manzoni, S., and Bommarco, R. (2021). Primary productivity in subsidized green-brown food webs. bioRxiv. doi: 10.1101/2021.12.22.473860
Zelnik, Y. R., Manzoni, S., and Bommarco, R. (2022). The coordination of green–brown food webs and their disruption by anthropogenic nutrient inputs. Glob. Ecol. Biogeogr. 31, 2270–2280. doi: 10.1111/geb.13576
Keywords: nutrient subsidy, trophic cascade, primary production, ecosystem function, ecosystem modeling, organic fertilization, food web
Citation: Zelnik YR, Manzoni S and Bommarco R (2023) Primary production in subsidized green-brown food webs. Front. Ecol. Evol. 11:1106461. doi: 10.3389/fevo.2023.1106461
Received: 23 November 2022; Accepted: 09 February 2023;
Published: 20 March 2023.
Edited by:
Mehdi Cherif, INRA Centre Bordeaux-Aquitaine, FranceReviewed by:
Shawn James Leroux, Memorial University of Newfoundland, CanadaGina Marie Wimp, Georgetown University, United States
Copyright © 2023 Zelnik, Manzoni and Bommarco. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stefano Manzoni, c3RlZmFuby5tYW56b25pQG5hdGdlby5zdS5zZQ==
 Yuval R. Zelnik
Yuval R. Zelnik Stefano Manzoni
Stefano Manzoni Riccardo Bommarco
Riccardo Bommarco