Uncertainty propagation in a global biogeochemical model driven by leaf area data

Bian, Chenyu; Xia, Jianyang

doi:10.3389/fevo.2023.1105832

ORIGINAL RESEARCH article

Front. Ecol. Evol., 24 February 2023

Sec. Models in Ecology and Evolution

Volume 11 - 2023 | https://doi.org/10.3389/fevo.2023.1105832

This article is part of the Research Topic Models in Population, Community and Ecosystem Dynamics View all 11 articles

Uncertainty propagation in a global biogeochemical model driven by leaf area data

Chenyu Bian^1,2

Jianyang Xia^1,2^*

¹Zhejiang Tiantong Forest Ecosystem National Observation and Research Station, State Key Laboratory of Estuarine and Coastal Research, School of Ecological and Environmental Sciences, East China Normal University, Shanghai, China
²Research Center for Global Change and Complex Ecosystems, East China Normal University, Shanghai, China

Satellite-observed leaf area index (LAI) is often used to depict vegetation canopy structure and photosynthesis processes in terrestrial biogeochemical models. However, it remains unclear how the uncertainty of LAI among different satellite products propagates to the modeling of carbon (C), nitrogen (N), and phosphorus (P) cycles. Here, we separately drive a global biogeochemical model by three satellite-derived LAI products (i.e., GIMMS LAI3g, GLASS, and GLOBMAP) from 1982 to 2011. Using a traceability analysis, we explored the propagation of LAI-driven uncertainty to modeled C, N, and P storage among different biomes. The results showed that the data uncertainty of LAI was more considerable in the tropics than in non-tropical regions, whereas the modeling uncertainty of C, N, and P stocks showed a contrasting biogeographic pattern. The spread of simulated C, N, and P storage derived by different LAI datasets resulted from assimilation rates of elements in shrubland and C3 grassland but from the element residence time (τ) in deciduous needle leaf forest and tundra regions. Moreover, the assimilation rates of elements are the main contributing factor, with 67.6, 93.2, and 93% of vegetated grids for the modeled uncertainty of C, N, and P storage among the three simulations. We further traced the variations in τ to baseline residence times of different elements and the environmental scalars. These findings indicate that the data uncertainty of plant leaf traits can propagate to ecosystem processes in global biogeochemical models, especially in non-tropical forests.

1. Introduction

Over the past few decades, terrestrial ecosystems have absorbed nearly one-third of the CO₂ of anthropogenic emissions by vegetation canopy (Friedlingstein et al., 2022). However, the terrestrial carbon uptake by vegetation photosynthetic is widely limited by the availability of essential nutrients, especially nitrogen (N) and phosphorus (P) (Elser et al., 2007; LeBauer and Treseder, 2008; Xia and Wan, 2008; Allen et al., 2020; Hou et al., 2020). The availability of N and P affects vegetation productivity (Elser et al., 2007; Norby et al., 2010), carbon (C) allocation (Hofhansl et al., 2015), litter decomposition (Averill and Waring, 2018), and other processes (Sutton et al., 2008; Melillo et al., 2011). The availability of N and P also constrains soil carbon storage (Crowther et al., 2019), especially under the scenarios of climate change and increasing atmospheric CO₂ (Wang et al., 2020). Thus, global distributions of C, N, and P storages are crucial for modeling the global biogeochemical feedback to future climate change.

Many global biogeochemical models have coupled nutrients processes to provide more realistic simulations of terrestrial ecosystems (Thornton et al., 2007; Wang et al., 2007, 2010; Goll et al., 2012; Yang et al., 2014; Zhu et al., 2019; Sun et al., 2021). Several global models not only incorporated the N cycles (Manzoni and Porporato, 2009; Zaehle et al., 2014; Meyerholt and Zaehle, 2015) but also implemented the P processes, such as ORCHIDEE-CNP (Goll et al., 2017; Sun et al., 2021), QUINCY v1.0 (Thum et al., 2019), GOLUM-CNP (Wang et al., 2018), JSM (Yu et al., 2020), JULES-CNP (Nakhavali et al., 2022), and E3SM (Zhu et al., 2019). The coupled C-N-P cycle reduced the magnitude of disequilibrium in the terrestrial C cycle (Wei et al., 2022a), but how to accurately represent the nutrient cycles and the effects of N and P limitation in biogeochemical models are still challenges (Hungate et al., 2003; Thomas et al., 2015; Wieder et al., 2015; Sun et al., 2017).

Due to the difference in model structure and parameters (Zaehle and Dalmonech, 2011), the increased model complexity further hinders our understanding of the modeling uncertainty. However, most global biogeochemical models share a typical pool-flux structure and follow some fundamental properties of terrestrial element cycling (Xia et al., 2013; Luo et al., 2015). For example, C atoms enter the ecosystem through plant photosynthesis, while plants assimilate N and P mainly from mineral soil. The elements of C, N, and P are allocated among plant pools, then transferred to litter and soil pools, and eventually returned to the atmosphere via the decomposition of organic matter (Olson, 1963; Zhang et al., 2008). In biogeochemical models, there are a specific soil inorganic-N pool and a few soil inorganic P pools, which generally separate to distinct pools based on its chemical fractionation (Hedley et al., 1982; Cross and Schlesinger, 1995; Hou et al., 2018). Labile P usually comes from P mineralization, P weathering, and dust deposition (Wang et al., 2010). Some of the labile P can enter the sorbed P pool and subsequently become occluded, but this form is assumed to be unavailable by plants (Wang et al., 2018). Those specific processes of the coupled C-N-P biogeochemical cycles can be found in Figure 1.

FIGURE 1

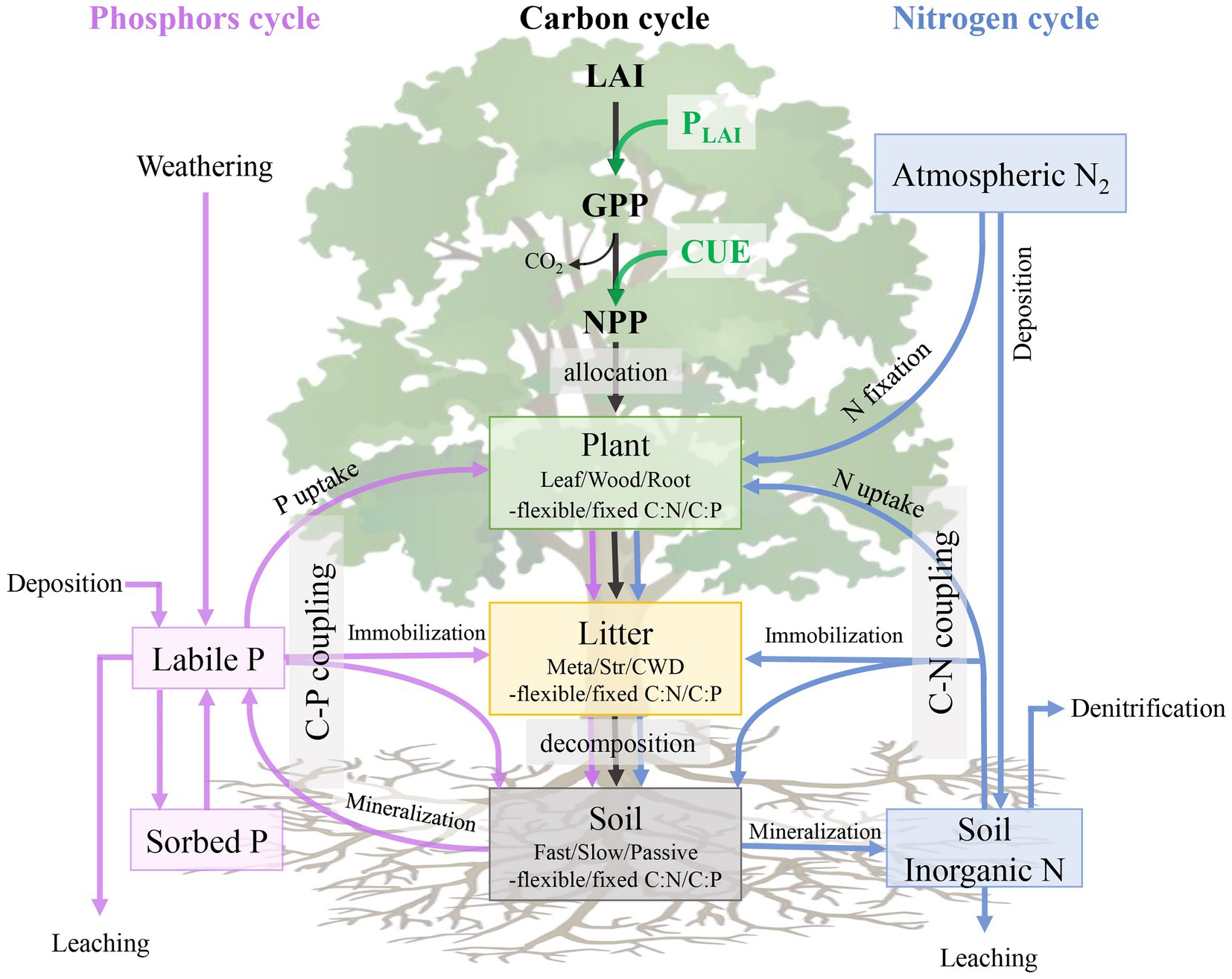
Figure 1. Schematic diagram of major carbon (C), nitrogen (N) and phosphorus (P) pools and fluxes in a terrestrial ecosystem. Black, blue and pink arrows indicate the C-cycle processes, N-cycle processes, and P-cycle processes, respectively. Green, yellow, and gray rectangles represent the vegetation, litter and soil pools of organic carbon, nitrogen, and phosphorus. LAI, leaf area index; P_LAI, LAI-leval photosynthesis, GPP, gross primary productivity, CUE, carbon use efficiency; NPP, net primady productivity; Meta, metabolic litter; Str, structural litter; CWD, coarse woody debris.

Leaf area index (LAI), as a significant uncertainty source of simulated photosynthetic carbon uptake (Li et al., 2018; Cui et al., 2019), is widely used as a critical parameter in the process-based biogeochemical models for depicting vegetation canopy structure (Forzieri et al., 2017; Zeng et al., 2017; Liu et al., 2018; Chen et al., 2019). Many inter-model comparisons on Earth system models (ESMs) have shown a large spread of LAI on a global scale (Zeng et al., 2016), partially leading to their persistent uncertainty in carbon storage projections (Wei et al., 2022b). Recently, many studies have used satellite-based LAI to directly force the models for a more realistic prediction of the global carbon (C) cycle (Zeng et al., 2017; Liu et al., 2018; Chen et al., 2019). However, there are significant discrepancies in different satellite-based LAI products on temporal and spatial scales (Jiang et al., 2017; Xiao et al., 2017; Liu et al., 2018). Therefore, understanding whether and how the data uncertainty in LAI observations propagates to global biogeochemical models helps provide a more accurate prediction of future terrestrial carbon sinks (Heinsch et al., 2006; Liu et al., 2018).

This study introduces a framework to decompose a complex biogeochemical model coupled with C-N-P processes into its traceable components. Considering that the N and P cycles are not a closed cyclic system, we only focused on the organic matter of C, N, and P in this study. Specifically, the framework traces the modeled ecosystem organic C, N, and P storage to the influx of C (i.e., net primary productivity, NPP), N, and P uptake and the corresponding ecosystem residence time [ $(i = C, N, P)$ ]. The $τ_{i}$ can be further traced to the baseline residence time [ $τ_{i}^{'} (i = C, N, P)]$ and environmental scalars ( $ξ$ ). The former $τ_{i}^{'}$ usually preset in models depends on the soil properties and vegetation characteristics, while the latter usually includes temperature and water scalars and is determined by climate forcings. Based on the framework, we further analyzed the difference among biomes (Supplementary Figure S1) in simulated C, N, and P storage caused by the disagreement of LAI estimates among three satellite-derived products (i.e., GIMMS LAI3g, GLASS, and GLOBMAP) with the Australian Community Atmosphere Biosphere Land Exchange (CABLE) model. The primary goal of this study is to explore the uncertainty propagation of LAI observations to global simulations of C, N, and P storage in the biogeochemical models.

2. Materials and methods

2.1. Satellite-derived leaf area index datasets

Leaf area index is an important parameter that consistently monitors vegetation structure dynamics over large spatial and temporal scales. This study uses three satellite-derived long-term global LAI products: GIMMS LAI3g, GLASS LAI, and GLOBMAP LAI. We re-sampled all three LAI datasets from their native resolution into 0.5° × 0.5° special resolution using the nearest neighbor algorithm and interpolated to the hourly temporal resolution to force the model. All three datasets have been validated and widely used to monitor terrestrial vegetation dynamics (Dardel et al., 2014; Piao et al., 2015; Zhu et al., 2016, 2017; Jiang et al., 2017).

2.1.1. GIMMS LAI3g product

The Global Inventory Modeling and Mapping Studies (GIMMS) LAI3g product (version 01) was generated by the Feed-Forward Neural Network (FFNN) algorithm based on the Advanced Very High Resolution Radiometer (AVHRR) GIMMS Normalized Difference Vegetation Index (NDVI) dataset and Moderate Resolution Imaging Spectroradiometer (MODIS) LAI (Zhu et al., 2013). It provides a global observation at 1/12-degree spatial resolution and 15-day temporal resolution from July 1981 to December 2011. The GIMMS LAI3g dataset was extensively evaluated by comparison with field LAI measurements, other satellite-derived data products, statistical climatic variables, and the simulation results from land models (Mao et al., 2013; Zhu et al., 2013).

2.1.2. GLASS LAI product

The Global LAnd Surface Satellite (GLASS version 03) long-time series LAI product was estimated from MODIS and AVHRR remote sensing data using the General Regression Neural Networks (GRNNs) approach (Xiao et al., 2014). The GRNNs were trained with the fused time-series LAI from MODIS and CYCLOPES products and the MODIS reflectance of the BELMANIP sites. The GLASS LAI product has a temporal resolution of 8 days and spans from 1981 to 2014. For the period of 1981–1999, the data product was generated from AVHRR reflectance data, providing a geographic projection at the spatial resolution of 0.05°. From 2000 to 2014, the LAI product was generated from MODIS surface reflectance data with a spatial resolution of 1 km (Xiao et al., 2014, 2016).

2.1.3. GLOBMAP LAI product

The consistent long-term GLOBMAP LAI product (version 01) was generated by a combination of AVHRR LAI (1981–2000) and MODIS LAI (2000–2011) (Liu et al., 2012). The MODIS LAI time series was generated from MODIS land surface reflectance data based on the GLOBCARBON LAI algorithm (Deng et al., 2006). By establishing a pixel by pixel relationships between AVHRR observations and MODIS LAI data series during the overlapped period (2000–2006), the AVHRR LAI could be retrieved back to 1981. The temporal resolution of this dataset is half a month and 8 days in 1981–2000 and 2001–2011, respectively. The spatial resolution of the AVHRR LAI dataset is 8 km.

2.2. Matrix representation of the carbon, nitrogen, and phosphorus cycle

We developed a theoretical framework for decomposing the terrestrial carbon, nitrogen, and phosphorus stock into some traceable components based on the biogeochemical principles of the terrestrial carbon cycle. For example, the terrestrial carbon cycle can be generally described as the following processes, which includes carbon enters the ecosystem via plant photosynthesis; photosynthetic carbon is then allocated among plant pools; part of this carbon is consumed by respiration, and the remainder is further transferred to litter and soil carbon pools; lastly, the carbon in the litter and soil pools is decomposed and back into the atmosphere (Luo and Weng, 2011; Luo et al., 2022). Plants assimilate the nitrogen and phosphorus from mineral soils and then transfer following the same flow with organic matter in terrestrial ecosystems. Therefore, following the approach developed by Xia et al. (2013), the biogeochemical cycle processes can be mathematically represented by three matrix equations:

{\begin{matrix} \frac{d X (t)}{d t} = B_{C} U_{C} (t) - A ξ (t) C X (t) \\ \frac{d N (t)}{d t} = B_{N} U_{N} (t) - A ξ (t) C N (t) \\ \frac{d P (t)}{d t} = B_{P} U_{P} (t) - A ξ (t) C P (t) \end{matrix} (1)

where X(t) = (X₁(t), X₂(t), …, X₉(t))^T , N(t) = (N₁(t), N₂(t), …, N₉(t))^T , and P(t) = (P₁(t), P₂(t), …, P₉(t))^T are 9 × 1 vector, which describes the C, N and P pool size of leaf, root, wood, metabolic litter, structural litter, coarse wood debris (CWD), fast soil, slow soil and passive soil pool at time t in CABLE model. $B_{i} = {(b_{1} b_{2} b_{3} 0 \dots 0)}^{T} (i = C, N, P)$ is a vector of allocation coefficients of C, N, and P among different plant pools. For the C allocation, the partitioning coefficients from NPP to root and wood carbon pools are equations of availably of light, nitrogen, and water, respectively. Then the rest of NPP goes to the leaf pool. For the N and P, the allocations of N and P uptake among different plant pools are calculated based on the proportion to each pool’s demand of N and P. The inputs of C, N, and P are represented by $U_{i} (t) (i = C, N, P)$ . $U_{C}$ is the fixed carbon by canopy photosynthesis, i.e., net primary production (NPP). $U_{N}$ and $U_{P}$ are the assimilated N and P via plant uptake from soil minerals. $ξ (t)$ is a diagonal matrix, the diagonal components representing the environmental scalars (such as temperature and soil moisture) effects on carbon decomposition rate at time t. C is a 9 × 9 diagonal matrix with diagonal entries by 9 × 1 vectors $c = {(c_{1} c_{2} \dots c_{3})}^{T}$ . The diagonal elements indicate the C decay rate for each pool. A is a transfer coefficients matrix, which can quantify how much carbon can be transferred among different pools. Therefore, the first term on the right side of Equation (1), $B_{i} U_{i}$ $(i = C, N, P)$ , describes the C, N, and P inputs and allocation among different plant pools, and the second term on the right represents the transfer and exit rates (Xia et al., 2013; Luo et al., 2017).

By letting Equation (1) equal zero, we obtained the C, N, and P pool size at steady-state as the product of ecosystem residence time and influx:

{\begin{matrix} X_{s s} = {(A ξ C)}^{- 1} B_{C} U_{C} \\ N_{s s} = {(A ξ C)}^{- 1} B_{N} U_{N} \\ P_{s s} = {(A ξ C)}^{- 1} B_{N} U_{P} \end{matrix} (2)

where $X_{s s}$ , $N_{s s}$ , and $P_{s s}$ are vectors that includes all the organic pools at steady state. $U_{C}$ , $U_{N}$ , and $U_{P}$ are the ecosystem C, N, and P influx at steady state. $U_{C}$ represents NPP in this study, which can be further decomposed to gross primary production (GPP) and carbon use efficiency (CUE) based on some previous studies (Bradford and Crowther, 2013; Xia et al., 2017). The term ${(A ξ C)}^{- 1} B_{i} (i = C, N, P)$ in Equation (2) are vectors of the residence time of individual pools as:

{\begin{matrix} τ_{C} = {(A ξ C)}^{- 1} B_{C} \\ τ_{N} = {(A ξ C)}^{- 1} B_{N} \\ τ_{P} = {(A ξ C)}^{- 1} B_{P} \end{matrix} (3)

The ecosystem-level residence time of C, N, or P was summed from all the individual pools. The ecosystem residence time can be determined by multiple ecological processes, such as allocation (i.e., the B vector), carbon transfer among different pools (i.e., the A matrix), decomposition rates (i.e., the C matrix), and the environmental scalars (i.e., $ξ$ ). The scalar $ξ$ usually consists of the temperature ( $ξ_{T}$ ) and water scalars ( $ξ_{W}$ ) as:

\begin{array}{l} ξ = ξ_{T} ξ_{W} & (4) \end{array}

Generally, the parameters of B, A, and C matrices are preset in a specific model according to model structure, soil properties, and vegetation characteristics (Zhou et al., 2018). By rearranging Equation (3), we can further decompose the residence time to the environment scalar and the corresponding preset parameters:

{\begin{matrix} τ_{C} = ξ^{- 1} \times {(AC)}^{- 1} B_{C} \\ τ_{N} = ξ^{- 1} \times {(AC)}^{- 1} B_{N} \\ τ_{P} = ξ^{- 1} \times {(AC)}^{- 1} B_{P} \end{matrix} (5)

The residence time can be further decomposed to environment scalars and baseline residence time vectors. The equation of baseline residence time can be expressed as:

{\begin{matrix} τ_{C}^{'} = {(AC)}^{- 1} B_{C} \\ τ_{N}^{'} = {(AC)}^{- 1} B_{N} \\ τ_{P}^{'} = {(AC)}^{- 1} B_{P} \end{matrix} (6)

2.3. The Community Atmosphere-Biosphere-Land Exchange (CABLE) model: overview and experiments

The Australian Community Atmosphere Biosphere Land Exchange (CABLE) model version 2 is a global land surface model that can simulate biophysical and biogeochemical processes (Wang et al., 2010, 2011). It includes five submodels: (1) radiation, (2) canopy micrometeorology, (3) surface flux, (4) soil and snow, and (5) ecosystem respiration, and it also incorporates carbon (C), nitrogen (N), and phosphorus (P) cycles. CABLE has been widely evaluated by other global observations (Piao et al., 2015), eddy-flux measurements (Best et al., 2015), and manipulated field experiments (De Kauwe et al., 2014). This model can be applied to attribution analysis (Zhang et al., 2016) or plant feedback effects (Lei et al., 2019) by doing a series of simulation experiments. The default settings of LAI are prognostic in the CABLE model, but a switch can control them. When the switch is turned on, the prognostic LAI can be calculated as the product between specific leaf area (SLA) and leaf biomass. SLA and the phenology phases (used to determine the leaf growth) are prescribed for each plant functional type.

In this study, we turned the switch off and replaced the modeled LAI with data from three satellite-observed products (GIMMS LAI3g, GLASS, and GLOBMAP). Based on the traceability analysis approach, we performed three simulations to diagnose the source of uncertainty in the biogeochemical cycle caused by LAI. The CABLE model was first spun up with the C-N-P coupled schemes to the steady state in 1,900 using a semi-analytical solution (Xia et al., 2012). The forcing data (Zhang et al., 2016) used to spin up the model concludes seven 6-hourly meteorological forcing variables (i.e., temperature, precipitation, downward shortwave radiation, downward longwave radiation, specific humidity, pressure, and wind speed) from the CRUNCEP version 5 (New et al., 1999, 2000, 2002). Using spin-up results as an initial value, we run the model from 1901 to 1981. After that, we performed three simulations by replacing the modeled LAI with three satellite-based LAI products (GIMMS LAI3g, GLASS, GLOBMAP), respectively. Lastly, we spun up CABLE to a steady state forced by the satellite-derived LAI datasets and time-variant CO₂ concentration from 1982 to 2011 (Supplementary Table S1).

3. Results

3.1. Spatial variations of terrestrial carbon, nitrogen, and phosphorus storage

The estimated global mean LAI was 1.24 ± 0.18 m² m⁻² (mean ± SD) across the three data products. The simulated global stocks of C, N, and P were 11.0 ± 1.4 C kg C m⁻², 504.3 ± 68.1 g N m⁻², and 97.7 ± 13.6 g P m⁻², respectively. All three simulations showed the highest mean LAI in tropical regions among the eight biomes (Figure 2A). Furthermore, the variability of LAI across three simulations was also higher in the tropics than in any other area (Figure 2B). However, the simulated element storage (i.e., C, N, and P) showed a divergent spatial pattern in magnitude and variability compared with LAI (Figures 2C–H). Specifically, northern high-latitude regions showed the highest annual mean element storage (12.0 kg C m⁻² for the C storage, 531.3 g N m⁻² for the N storage, and 93.1 g P m⁻² for the P storage) compared with other climate regions. In contrast, tropical regions showed a relatively high C storage (10.0 kg C m⁻²) but low storage of N (400. 2 g N m⁻²) and P (78.5 g P m⁻²) (Figures 2C,E,G). A similar distribution was also found in the spatial variability of elements (Figures 2D,F,H). In addition, it is noted that the high disagreement in P storage across three simulations is mainly located in the regions covered by herbaceous vegetation, such as eastern Australia, southeastern South America, and southern Africa (Figure 2H).

FIGURE 2

Figure 2. Spatial distributions of annual leaf area index (LAI, A), carbon (C), nitrogen (E) and phosphorus (G) storage and the corresponding standard deviation of LAI (B), C (D), N (F), and P (H) storage among three satellite-derived simulations. Note that we only consider the organic pools for nitrogen and phosphorus in this study.

3.2. Decomposing carbon, nitrogen, and phosphorus storage into ecosystem residence time and the corresponding influx

The ecosystem element storage can be decomposed into the corresponding element residence time ( $τ_{C}, τ_{N}, τ_{P}$ ) and the influx rate [U_C (NPP), U_N, and U_P] based on the traceability framework according to Equations (2, 3). Deciduous needle leaf forest (DNF) had the largest ensemble annual mean results of ecosystem C (86.0 kg C m⁻²), N (424.3 g N m⁻²), and P (24.4 g P m⁻²) storage among the eight biomes, resulting from its longest residence time ( $τ_{C}$ , 154.3 years; $τ_{N}$ , 78.4 years; $τ_{P}$ , 65.5 years) and mediated element input (NPP, 557.4 g C m⁻² yr.⁻¹; U_N, 5.4 g N m⁻² yr.⁻¹; U_P, 0.37 g P m⁻² yr.⁻¹). However, the order of the size in C, N, and P storage was inconsistent in the remaining seven biomes (Supplementary Table S2). Shrubland had the lowest C storage (10.7 kg C m⁻²) as a result of the smallest NPP (257.6 g C m⁻² yr.⁻¹) and a moderate $τ_{C}$ (41.4 years). Evergreen needle leaf forest (ENF) had a relatively long $τ_{N}$ (50.4 years) and low U_N (3.1 g N m⁻² yr.⁻¹). While evergreen broadleaf forest (EBF), deciduous broadleaf forest (DBF), and C3 grassland (C3G) had a short $τ_{N}$ (~25.0 years) and relatively high U_N (~9.0 g N m⁻² yr.⁻¹), leading to a moderate N storage. For P storage, EBF, DBF, and C3G had a relatively short $τ_{P}$ (~23.9 years) and relatively high U_P (~0.50 g P m⁻² yr.⁻¹), resulting in a moderate P storage. Although Tundra had a relatively long $τ_{N}$ (53.0 years) and $τ_{P}$ (50.9 years), it still has the lowest N (16.5 g N m⁻²) and P (1.4 g P m⁻²) storage as the result of the smallest U_N (0.31 g N m⁻² yr.⁻¹) and U_P (0.03 g P m⁻² yr.⁻¹). Additionally, the carbon influx via canopy photosynthesis (NPP) can be further decomposed into GPP and CUE (Xia et al., 2017). The results showed that EBF had the highest annual mean GPP (3312.2 g C m⁻² yr.⁻¹), followed by DBF (2103.1), C4 grassland (C4G, 1873.4), C3G (951.3), ENF (912.6), DNF (871.2), Shrubland (511.6) and Tundra (370.8) regions (Supplementary Figure S2 and Supplementary Table S2). The ranges of carbon use efficiency of all eight biomes from 0.37 to 0.71.

The ecosystem element storage derived from three satellite-based LAI differed among the eight biomes. For example, ENF, EBF, and DBF had similar C, N, and P storage for the three simulations (Figure 3). Although Shrubland and C3G had comparable values of element residence time ( $τ_{C}$ , $τ_{N}$ , and $τ_{P}$ ), their different element uptake rates (NPP, U_N, and U_P) led to variations in element storage across the three simulations. In addition, compared with the simulations derived from GIMMS LAI3g and GLASS, the simulation derived by GLOBMAP LAI had the smallest NPP, U_N, and U_P (Figure 3). Tundra and DNF had comparable C storage across three simulations. However, the N and P storage magnitude varied widely in these regions. The differences in N and P storage across the three simulations are mainly due to $τ_{N}$ and $τ_{P}$ (Supplementary Table S2).

FIGURE 3

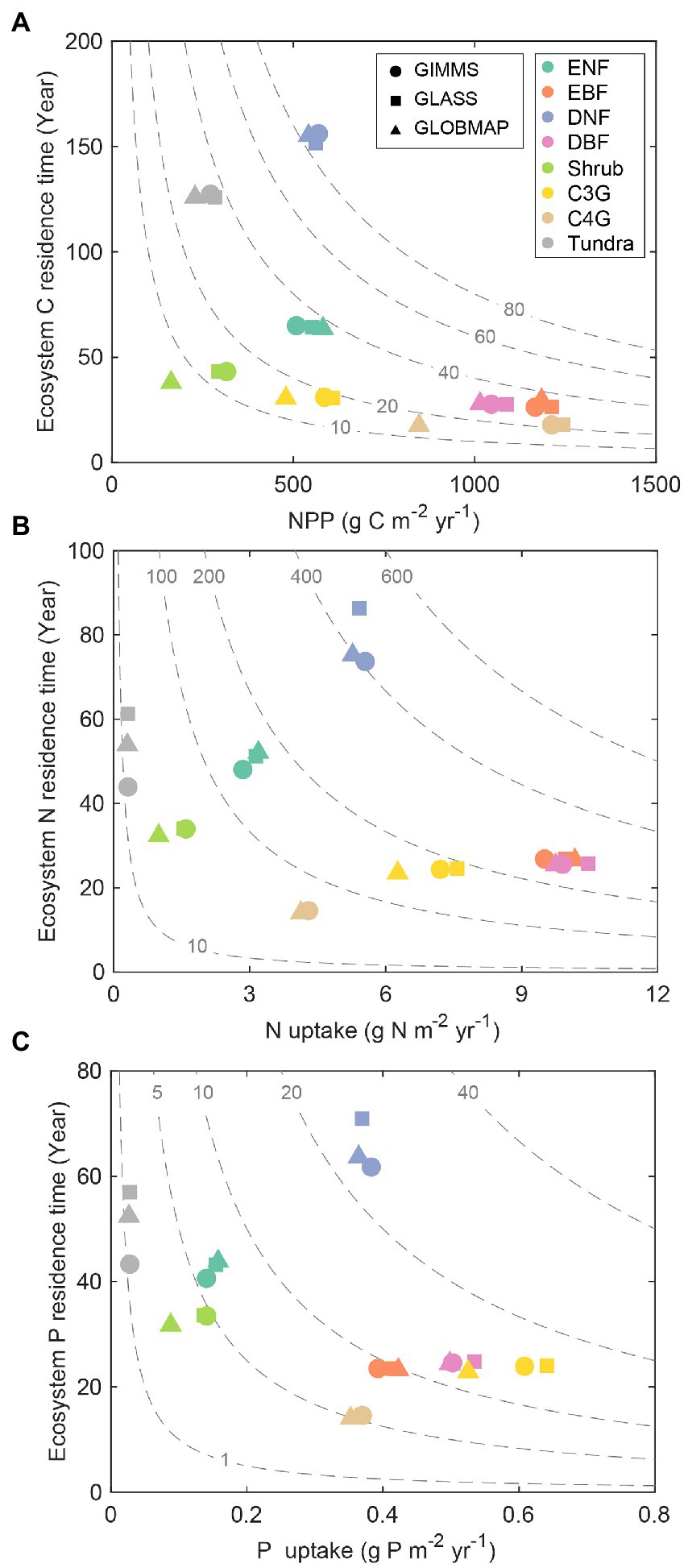
Figure 3. Decomposition of ecosystem carbon (A), nitrogen (B), and phosphorus (C) storage into its influx and ecosystem residence time in various biomes for each simulation. ENF, evergreen needleleaf forest; EBF, evergreen broadleaf forest; DNF, deciduous needleleaf forest; DBF, deciduous broadleaf forest; Shrub, shrub land; C3G, C₃ grassland; C4G, C₄ grassland.

3.3. Traceability analysis of ecosystem residence time

Ecosystem residence time can be decomposed into baseline residence time and environmental scalars. The baseline residence time is determined by the carbon transfer coefficients matrix (A matrix), decomposition rates (C matrix), and the allocation coefficients (B vector) among different plant element pools based on Equation 6. Considering that the element cycles (C, N, and P) share the same A and C matrix, the difference in baseline element residence time is mainly caused by the element allocation coefficients ( $B_{C}, B_{N}, B_{P}$ ). The baseline C residence time ( $τ_{C}^{'}$ ) is the longest compared with baseline N residence time ( $τ_{N}^{'}$ ) and baseline P residence time ( $τ_{P}^{'}$ ) (Supplementary Figure S3) in all the eight biomes. Deciduous needle leaf forest has a relatively long $τ_{C}^{'}$ (21.8 years), which is almost three times that of $τ_{N}^{'}$ (8.2 years) and $τ_{P}^{'}$ (6.8 years). Baseline element residence times were similar in C3 grassland ( $τ_{C}^{'}$ , 4.6 years; $τ_{N}^{'}$ , 3.7 years; $τ_{P}^{'}$ , 3.6 years), C4 grassland ( $τ_{C}^{'}$ , 5.6 years; $τ_{N}^{'}$ , 4.3 years; $τ_{P}^{'}$ , 4.3 years), and shrubland ( $τ_{C}^{'}$ , 8.7 years; $τ_{N}^{'}$ , 7.1 years; $τ_{P}^{'}$ , 7.1 years) regions. Additionally, $τ_{C}^{'}$ were similar to each other in three LAI-derived simulations. While $τ_{N}^{'}$ and $τ_{P}^{'}$ differed substantially across three simulations, especially in ENF, DNF, and tundra regions (Figure 4).

FIGURE 4

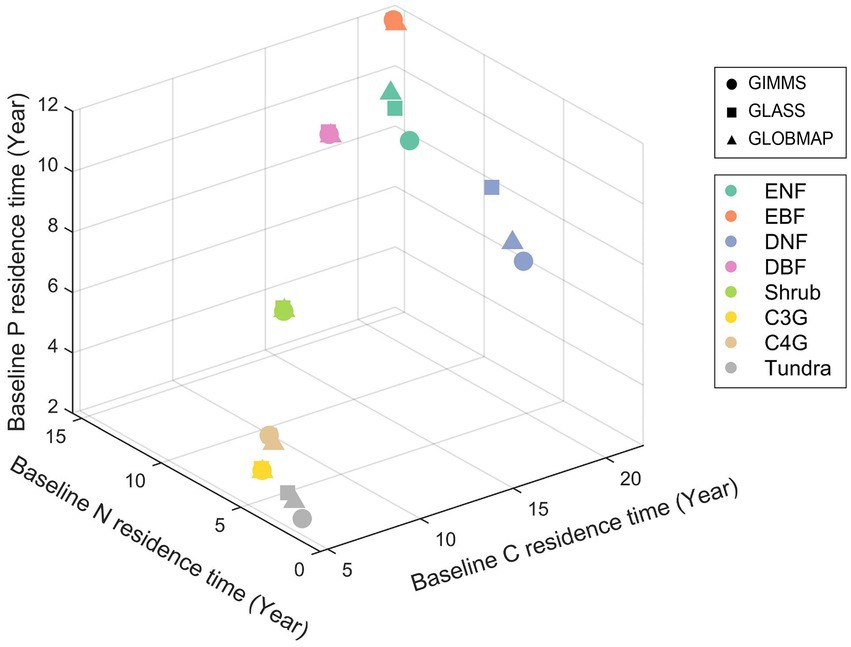
Figure 4. Comparison of baseline carbon, nitrogen and phosphorus residence time among different biomes with a three-dimensional scatter plot for each simulation. Abbreviations of biomes are given in Figure 3.

Environmental scalar ( $ξ$ ) can regulate ecosystem residence time by limiting the decomposition rates of litter and soil organic pools. By decomposing environmental scalar into temperature ( $ξ_{T}$ ) and water scalar ( $ξ_{W}$ ), we can found that the multi-year mean of $ξ_{T}$ ranges from 0.09 for deciduous needle leaf forest to 0.70 for C4 grassland, while $ξ_{W}$ ranges from 0.60 for tundra and 0.92 for C4 grassland (Figure 5). The global average of $ξ_{T}$ (0.38) is considerably lower than that of $ξ_{W}$ (0.82). In general, $ξ_{T}$ dominates the difference in $ξ$ among eight biomes compared with $ξ_{W}$ .

FIGURE 5

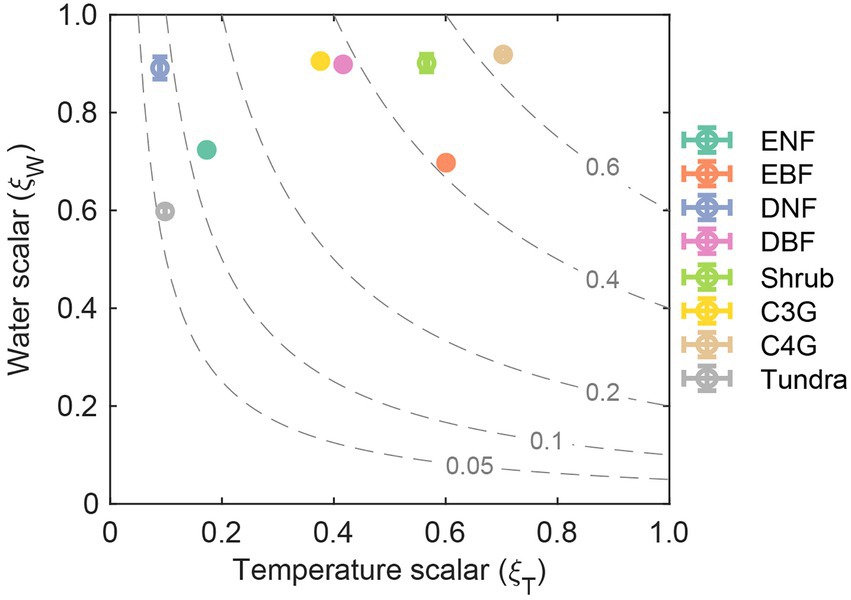
Figure 5. Determining of the environmental scalars ( $ξ$ ) by temperature scalars ( $ξ_{T}$ ) and water scalars ( $ξ_{W}$ ) among biomes. The dashed line show the constant value of environment scalars. Abbreviations of biomes are given in Figure 3.

3.4. Variation decomposition of the simulated carbon, nitrogen, and phosphorus storage

We decomposed the variations of element storage into several traceable components on each vegetated grid by a traceability analysis approach. Figure 6 shows the dominant traceable component for each grid which explains the greatest contrition to the element storage variation. The results showed that the element influx rates (i.e., NPP, U_N, and U_P) are the primary uncertainty source in 67.6, 93.2, and 93.0% of the vegetated grid cell for the C, N, and P storage, respectively. By further tracing the modeled variation of NPP into GPP and CUE, we found that GPP and CUE explained 91.6 and 8.4% of the variation across simulations, respectively. The baseline residence time has a larger uncertainty contribution than the environmental scalars (Figure 6). Specifically, the contributions of baseline element residence time (i.e., $τ_{C}^{'}$ , $τ_{N}^{'}$ , and $τ_{P}^{'}$ ) to the variation of ecosystem element residence time (i.e., $τ_{C}$ , $τ_{N}$ , and $τ_{P}$ ) is 75.3, 91.2, and 91.8%, respectively. While the contribution of $ξ$ is 24.7% for the variation of $τ_{C}$ , 8.8% for $τ_{N}$ , and 8.2% for $τ_{P}$ . In addition, the contributions of $ξ_{T}$ and $ξ_{W}$ to the variation of element storage are relatively small compared with other contributors, i.e., $ξ_{T}$ and $ξ_{W}$ only contribute 3.8 and 4.2% for C storage, 0.32 and 0.28% for N storage, and 0.28 and 0.29% for P storage variation, respectively.

FIGURE 6

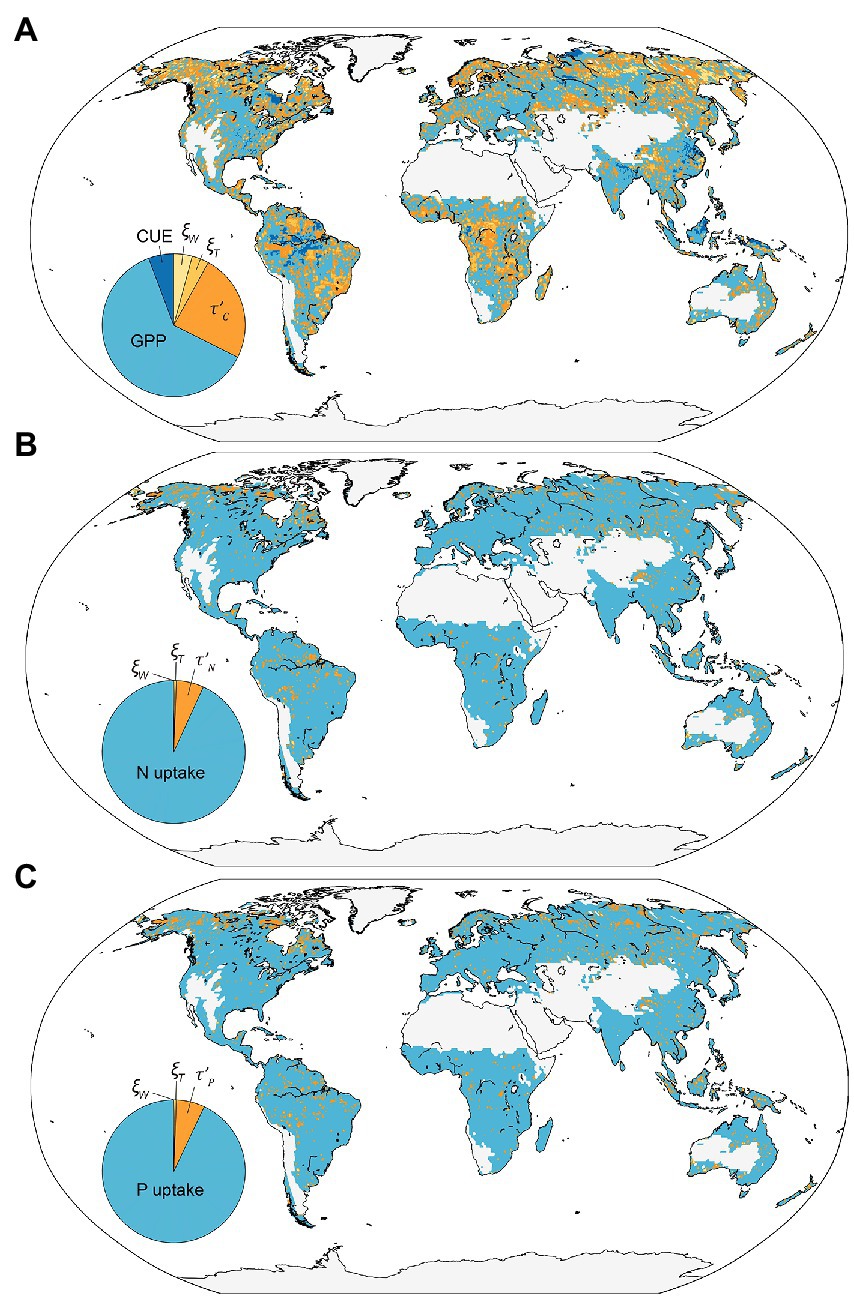
Figure 6. The global pattern of the dominant variable for the variation in simulated land carbon (A), nitrogen (B), and phosphorus (C) storage among three simulations. The insert panels indicate the proportion of each traceable components in global vegetated grids. GPP, gross primary productivity, CUE, carbon use efficiency; $ξ_{T}$ , temperature scalars; $ξ_{W}$ , water scalars; $τ_{C}^{'}$ , baseline C residence time; $τ_{N}^{'}$ , baseline N residence time; $τ_{P}^{'}$ , baseline P residence time.

4. Discussion

Several recent studies have compared the differences among the existing satellite-derived LAI products on regional and global scales (Jiang et al., 2017; Liu et al., 2018). However, few studies have explored the influences of data uncertainty on simulated element storage in biogeochemical models. Our study shows that the largest discrepancies in the magnitude and spatial variance among different LAI products are mainly located in the evergreen broadleaf forest (Figure 2B), which is consistent with some previous studies (Camacho et al., 2013; Fang et al., 2013; Xiao et al., 2017; Piao et al., 2020). The significant divergence in different satellite-based LAI observations is due to the saturation effects of LAI in dense vegetation (Goswami et al., 2015; Li et al., 2018), sensor degradation, changes in platforms and sensors, and contamination by clouds and aerosols (Jiang et al., 2017; Liu et al., 2018; Piao et al., 2020). However, the high northern latitudes rather than the tropical regions have the most considerable discrepancies in simulated element storage due to the uncertainty of permafrost processes and the difficulty of spinning the model to equilibrium (Thornton and Rosenbloom, 2005; Xia et al., 2012). The results of the uncertainty pattern in element storage are consistent with that emerged in the current generation of Earth System Models (Arora et al., 2013; Friedlingstein et al., 2014; Zhou et al., 2021; Wei et al., 2022b). The contrast spatial distribution of uncertainty between satellite-derived LAI data and the modeled C-N-P storages indicates a nonlinear propagation of leaf area uncertainty in the biogeochemical models.

Decomposing the modeled element storage to its traceable components can facilitate understanding of inter-biome distributions of terrestrial C, N, and P storage on the globe (Figure 2). For instance, due to the long residence times and the corresponding moderate uptake rate, the deciduous needle leaf forest has the highest C, N, and P storage among all the eight biomes (Figure 3). Although evergreen broadleaf forests have relatively large influxes of C and N, the corresponding short residence time results in intermediate C and N storages. The P storage in the evergreen broadleaf forest regions can be decomposed into the medium P uptake and residence time (Figure 3). The ecosystem element residence time can be further decomposed into the corresponding baseline residence time and environmental scalars. As shown in Figure 4, the evergreen broadleaf forest has almost the longest mean baseline residence times of C (21.9 years), N (15.5 years), and P (11.5 years). However, although deciduous needle leaf forest has a relatively long baseline C residence time (21.8 years), it has only moderate baseline N (8.2 years) and P (6.8 years) residence time (Figure 4). This is because more assimilated N and P than C are allocated to leaves (C: 0.08, N: 0.26, P: 0.38) with faster turnover (Supplementary Figure S4). Previous studies also reported a longer P residence time on soils with low P availability (Tsujii et al., 2020), which can contribute to more efficient P conservation to support plant productivity under nutrient-limited regions (Wang et al., 2018). In addition, environmental scalars can also influence ecosystem residence time by regulating the baseline residence time in the CABLE model. For example, the low temperature decreases the decomposition rates in north-high latitude regions, though the absolute magnitude of discrepancy is large (Figure 5; Koven et al., 2015). Our results indicate that compared with the water scalar, the temperature scaler is the main limiting factor in all eight biomes (Figure 5), which is also supported by the observational datasets in temperate forests on the site levels (Chen et al., 2022).

We diagnosed the uncertainty source of different simulations derived from three satellite-based LAI products based on the traceability framework. We further quantified the dominant traceable component for each grid on a global scale. The results indicate that the uncertainty of element storage across three LAI-derived simulations shows a large spatial variation. Specifically, our study demonstrates that GPP contributes most to the spatial uncertainty of C storage in 61.9% of vegetated grids, mainly located in subtropical and some tropical regions. By contrast, the baseline C residence time was the major contributing factor for northern high-latitude areas (Figure 6). The spatial pattern of the dominant uncertainty components of N and P storage was similar to C storage, with N and P uptake rates dominating >90% of the global vegetated grids.

Although our biogeochemical traceability framework helps trace the uncertainty propagation path, we also acknowledge that it still has some limitations. First, the steady-state assumptions developing the traceability framework in this study are widely used in decomposing the land surface models (Xia et al., 2013; Rafique et al., 2016; Wei et al., 2022b) and developing models (Wang et al., 2018). However, terrestrial ecosystems are not steady (Luo and Weng, 2011) due to increasing atmospheric CO₂, climate warming, nitrogen deposition, and other anthropogenic disturbances (Friedlingstein et al., 2006; Sitch et al., 2015). Second, the plant functional types in each land grid cell are prescribed in the CABLE model. Thus, the uncertainty of LAI data may propagate to different processes in dynamic vegetation models, such as the CLM-FATES (Fisher et al., 2015) and BiomeE (Weng et al., 2015, 2019). Third, we acknowledge that this approach mainly focuses on ecosystems’ emergent properties but ignores some understanding of internal ecological mechanisms such as competitive strategies and evolutionary systems. Furthermore, the traceability framework we applied in this study only considered organic pools and ignored soil inorganic N and P pools. The size of soil inorganic N and P pools may enhance or weaken the feedback between vegetation dynamics and climate change (Wei et al., 2019; Wang et al., 2022), calling for a further understanding of the interaction between vegetation and inorganic nutrient pools in biogeochemical models.

5. Conclusion

In summary, this study explored data uncertainty propagation to model uncertainty by decomposing the terrestrial organic element (i.e., C, N, and P) storage into its traceable components. Those components include the element uptake rates, ecosystem baseline residence time, temperature, and water scalars. Such a traceable analytical framework effectively reveals the mechanisms behind the simulation uncertainty and its propagation through ecosystem processes. By applying this framework, we can distinguish the reasons for the difference in simulated element storage caused by LAI among biomes and further diagnose the uncertainty source. It can be applied to other biogeochemical models to help characterize and quantify the uncertainty propagated in element cycles. The nonlinear uncertainty propagation of data to the model explored in this study can help improve biogeochemical models’ future prediction ability. The findings in this study also call for more research efforts on the causal links between leaf area and biogeochemical cycles in terrestrial ecosystems.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

CB performed simulations, analyzed the results, and wrote the first draft. JX designed the study and revised the manuscript. All authors approved the submitted version.

Funding

This work was financially supported by the National Natural Science Foundation of China (nos. 31722009 and 41630528).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2023.1105832/full#supplementary-material

References

Allen, K., Fisher, J. B., Phillips, R. P., Powers, J. S., and Brzostek, E. R. (2020). Modeling the carbon cost of plant nitrogen and phosphorus uptake across temperate and tropical forests. Front. For. Glob. Change 3:43. doi: 10.3389/ffgc.2020.00043