Temperature fluctuation alters optimal predator community composition for anticipated biological control

Laubmeier, Amanda N.; Tabassum, Nusrat; Tenhumberg, Brigitte

doi:10.3389/fevo.2022.998396

ORIGINAL RESEARCH article

Front. Ecol. Evol., 06 January 2023

Sec. Population, Community, and Ecosystem Dynamics

Volume 10 - 2022 | https://doi.org/10.3389/fevo.2022.998396

This article is part of the Research Topic Integrating Models into Practice: The Role of Modelling in Biocontrol and Integrated Pest Management View all 4 articles

Temperature fluctuation alters optimal predator community composition for anticipated biological control

$\nAmanda N. Laubmeier$ Amanda N. Laubmeier¹^*

Nusrat Tabassum¹

Brigitte Tenhumberg^2,3

¹Department of Mathematics and Statistics, Texas Tech University, Lubbock, TX, United States
²School of Biological Sciences, University of Nebraska–Lincoln, Lincoln, NE, United States
³Department of Mathematics, University of Nebraska–Lincoln, Lincoln, NE, United States

Alongside pesticides and specialist predators, natural communities of generalist beetle and spider predators play an important role in suppressing agricultural pests. However, the predation pressure of natural communities can be unpredictable. Overall predation pressure is influenced by a dense network of potential intraguild interactions, which are further shaped by species traits and environmental factors. Understanding how these different influences combine to impact pest control is especially important in the context of changing global temperatures. Recent empirical studies have demonstrated that the foraging behavior of arthropod predators is influenced by an interaction between temperature and predator body size. To explore the consequences of these findings for intraguild interactions and pest control, we expand a previously published model describing interactions between arthropod predators and a pest population. The model assumed that interaction strengths are influenced by body size and habitat preference. In our updated model, we incorporate the effect of temperature on predator foraging activity. We parameterize the model to match empirically observed predator community composition in 10 agricultural fields and use simulations to demonstrate how temperature-dependent behaviors change the expected efficiency of the natural predator community. Then, we use an optimization approach to identify the most efficient composition of natural predators for pest control. We then evaluate whether the most efficient predator compositions would change with increasing average daily temperature and its variability, as is expected under future temperature change. We find that optimal communities often include predators with complementary foraging activity and that in 2 fields, the optimal community changes drastically under future temperatures. We also note that at some temperatures, foraging activity reduces the negative effects of intraguild interference on pest consumption. This work allows us to assess the effect of climate change on the efficiency of natural predator communities to control pest populations and provide guidance for farmers to design pest management strategies tailored to different climate scenarios.

1. Introduction

An ongoing challenge for the use of biological control by natural enemies in agricultural fields is uncertainty around the efficiency of a given enemy community in controlling pest populations. Natural communities comprised of generalist arthropod predators, such as beetles and spiders, can be a valuable source of biological control alongside specialist predators (Snyder and Ives, 2003; Pekár et al., 2015; Athey et al., 2016). However, biological control by generalist predators is highly variable, because they not only consume insect pests but also other predators of these pests (intraguild predation). Intraguild predation may cause farmers to overestimate a predator community's potential for pest control, since intraguild interactions reduce the overall abundance of predators as well as the time surviving predators spend foraging for pests, because they are busy hunting other predators or avoiding predation risk (interference) (Schmidt-Entling and Siegenthaler, 2009; Culshaw-Maurer et al., 2020). However, understanding of biological control is further complicated by observations that intraguild interactions do not necessarily reduce pest consumption (Janssen et al., 2006). Additionally, temperature influences predator survival and behavior (attack rates and handling times) and pest growth (survival, fecundity, and development time). Such effects of temperature also change with body size (Lang et al., 2012). Accounting for the effects of temperature and intraguild predation is key for predicting how biological control might be affected by global climate change.

Predicting the effect of temperatures on pest control by the predator community is challenging. On the one hand, higher temperatures increase the metabolism of predators (Kooijman, 2010), and a higher metabolism may increase activity and attack rates of predators (Brown et al., 2004; Rall et al., 2012). This has the potential to improve biological control of pests, but increased activity might also increase prey escape rates. At the same time, it can increase the frequency of predator-predator interactions, potentially leading to increased intraguild predation or interference. Responses to temperature are characterized by a rapid decrease in performance (such as activity) beyond some optimal temperature threshold (Colinet et al., 2015). For active foragers, this decline in activity may correspond to seeking shelter to avoid overheating (behavioral thermoregulation; Sinclair et al., 2016). Since threshold temperatures may differ across predators, shelter-seeking by one predator may reduce intraguild interference for remaining active predators. Temperature also influences how long it takes a predator to consume its prey (handling times), which can increase or decrease with temperature or the relative size of a predator to its prey (Vucic-Pestic et al., 2010; Uiterwaal and DeLong, 2020). The body size of predators also affects their activity level, metabolism, and prey preferences (Brown et al., 2004; Gilljam et al., 2011). Large predators have high mobility, leading to high attack rates on insect pests as well as increased intraguild interactions. The outcome of these attacks and interactions depends on the relative size of a predator to its potential prey; a species generally will not eat prey larger than itself, but it also may not efficiently consume prey much smaller than itself. Additionally, high mobility of large predatrs corresponds to higher metabolisms and increased risk of starvation, especially at higher temperatures (Rall et al., 2010).

Mathematical models have been successfully used to predict the intricate effect of predator communities on pest populations. In particular, models build around predator body mass (termed allometric models) have shown great promise in integrating metabolic assumptions with trophic interactions (Martinez, 2020). Researchers have used allometric models to model complex ecosystems (Boit et al., 2012) and to determine how species interactions might be impacted by changes in community composition (Berlow et al., 2009). However, there is also evidence that allometric models are not sufficient to capture all species characteristics (Kalinoski and DeLong, 2016; Jonsson et al., 2018). In prior work, we investigated how predator foraging area influenced pest control outcomes using an allometric model (Laubmeier et al., 2020), which incorporated temperature and body size dependent metabolic rates accounting for larger predators having a higher chance of dying through starvation. In this manuscript we expand on that work by adding temperature-dependence in predator interaction rates. A recent study on dragonfly predators suggests that the change of attack rate and handling time with temperature depends on the body size of the predator, and that this has consequences for long-term ecosystem stability (Kratina et al., 2022). In many agricultural ecosystems with frequent human interference, predator-prey interactions are unlikely to stabilize. So, it is an open question how important these findings are for biological control in agroecosystems imposed by arthropod predator communities.

In this work, we address this question by constructing a mathematical model that incorporates intraguild predation and temperature-dependence, which also uses allometric scaling. The model explicitly describes how predator attack rates will depend on body size and change with temperature, which affects intraguild interactions and consumption of the pest population. The model can easily be parameterized with data from different systems. We apply the model to a specific agricultural ecosystem, using observed predator body size distributions and field temperatures. We then predict the seasonal levels of pest control at current temperatures and assuming temperatures were to increase by 2.5°C as a result of climate change. We consider pests which grow rapidly during a growing season and predators with much longer reproductive cycles, such that predator reproduction does not depend primarily on consumption of the pest within a season. The pest insect is a species of aphid, which is a widespread pest and frequently the focus of biological control research. We model how aphid populations are influenced by temperatures and the naturally-occurring community of groundbeetles and spiders observed in agricultural fields. For each predator, we specify temperature-dependent activity levels based on available empirical observations. Using an optimization approach, we determine which combinations of predators will best control the aphid pest. The model predictions are used to recommend management strategies, which foster the continued presence of the most optimal predator and augment the community with differently-sized predators that support pest control. In our model, we use temperatures observed at 10 different field sites, to predict how pest control efficiency varies between different fields. Then we simulate one possible future climate change scenario assuming that average temperature and its variability increases.

2. Materials and methods

2.1. Study system: Aphid control in barley fields by terrestrial arthropods

To parameterize our model, we consider the control of an aphid pest by a community of groundbeetles and spiders. We use data from Curtsdotter et al. (2019), who recorded the population dynamics of the aphid pest Rhopalosiphum padi and its natural predators across ten barley fields during the 2011 summer growing season in Uppland, Sweden. Data were collected over at least 34 days in each field, corresponding to a typical period of aphid colonization, followed by rapid population growth, and ending in a sharp decline in aphid abundance. We construct a mathematical model that mimics the agroecosystem reported by Curtsdotter et al. (2019) and use the temperature data from the ten fields and the observed predator community as a starting point for our simulations. We then determine which combination of the observed predator species would minimize aphid densities averaged over the 34 days, given the temperature series recorded in the ten fields. The ten fields were located at five sites within 2.2 km of each other and each site had two fields with different management styles (conventional or organic). Management styles may influence local predator communities, but prior work indicated this effect was minimal for the specific study system (Roubinet et al., 2017). The data includes air temperature measurements, collected every 15 min, from temperature loggers in each field. Despite proximity, the temperature series differed across the fields (Supplementary Figure S1).

Curtsdotter et al. (2019) recorded the average predator density and body size for nine categories of groundbeetles and spiders common to these fields. The groundbeetles included three larger species between 45 and 90 mg (Pterostichus, Harpalus, Poecilus) and two smaller groups below 6.5 mg (“Other Carabid,” Bembidion), all of which actively hunt on the ground or burrow under ground. The spiders included two larger categories around 12 mg (Lycosidae and “Other Spider,” which we combine into the same predator category due to similarity, for a total of eight categories) and two smaller species below 2mg (Tetragnathidae, Linyphiidae). We note that Lycosidae actively hunt on the ground or climb up plants, but web-weaving Tetragnathidae and Linyphiidae do not. For comparison, the body size of the aphid species Rhopalosiphum padi is 0.59 mg on average. The different species of groundbeetle and spider are generalist predators which engage in complex intraguild interactions, and Curtsdotter et al. (2019) observed feeding interactions between almost all groups. Alternate prey items, such as soil-dwelling detritivores, were also observed but interactions within the group were never parameterized; following the principle of parsimony, we omit these species in our modeling framework. Alternate prey species will reduce the overall attack rate of predators and improve their reproduction rates, but are unlikely to influence qualitative model predictions which are restricted to a single season and do not incorporate predator reproduction. Given the observed predator species and environmental conditions, we use our model to identify predator communities that would maximize natural biological control, which could aid the development of pest management strategies.

2.2. Mathematical model

To explore the effect of temperature and body size dependent foraging behavior of predators on controlling aphid populations, we constructed a mathematical model based on the Allometric Trophic Network model from Schneider et al. (2012). The Allometric Trophic Network model describes encounter rates, feeding preferences, handling times, and metabolic decline as functions of species body mass. In prior work, we expanded this model to also incorporate non-consumptive predator interference and how foraging ranges of different members of the predator community overlap with each other and with the aphid population (Laubmeier et al., 2020). Our model predicted that the amount of overlap was key in determining aphid control. This work builds on our prior work and incorporates temperature dependent foraging behavior of predators. Our model simulates predator-prey interactions and is given by

\begin{array}{l} \frac{d N}{d t} = r (T) N - \sum_{j = 2}^{9} \frac{a_{1 j} ν_{j} (T)}{F_{j} (T)} M_{j} N, \\ \frac{d M_{i}}{d t} = - \sum_{j = 2}^{9} \frac{a_{i j} ν_{i} (T) ν_{j} (T)}{F_{j} (T)} M_{j} M_{i} - x_{i} (T) M_{i}, \\ F_{j} (T) = 1 + a_{1 j} ν_{j} (T) h_{1 j} N + \sum_{l = 2}^{9} a_{l j} ν_{l} (T) ν_{j} (T) h_{l j} M_{l} \\ + \sum_{m = 2}^{9} b_{0} a_{j m} ν_{j} (T) ν_{m} (T) M_{m} . \end{array}

Aphid abundance is denoted by N and predator abundance is denoted by M_j, for j = 2, ..., 9 representing the eight different predator categories and the index j = 1 is used for interactions with aphids. Aphids experience an intrinsic population growth rate (r(T)), which changes with temperature T and accounts for population-level growth due to individual births and deaths over the season. Aphids experience decline due to consumption by predators at rate a_1jν_j(T), where a_1j is the potential attack rate of the predator on the aphid and ν_j(T) is the predator's temperature-dependent activity level. Consumption rates are adjusted according to the denominator of the functional response (F_j(T)) which depends on temperature. The functional response in this model is similar to a Beddington functional response (Beddington, 1975), which accounts for the rates at which potential prey (N or M_l) is attacked and the time spent consuming the prey h_ij (“handling time”), as well as the time a predator must spend avoiding intraguild predation. To account for interference from potential predators (M_m), we add an evasion time penalty (b₀). This assumes that interference levels are not influenced by temperatures. This assumption may not be correct, but we are unaware of studies estimating the effect of temperature on interference outcomes. As noted by Ruxton et al. (1992), a more complex functional response may alter long-term dynamics and be more appropriate for increasingly high levels of interference, especially in models which neglect other negative effects of intraguild predation. However, our data did not support parameterization of a more complex response, and in our model, predators also experience decline due to consumption, by other predator species (M_j) as well as members of their own species(M_i). Additionally predators may die from starvation, and the death rate (x_i(T)) depends on temperature and body size of the predator i. Within the 34 days we consider, predators do not reproduce because they have a much longer generation time.

We use the model by Asin and Pons (2001) to represent the intrinsic temperature-dependent aphid population growth rate.

\begin{array}{l} r (T) = {\begin{matrix} r_{max} e^{- \frac{1}{2} {(T - T_{u})}^{2} / C_{1}^{2}} & T < T_{u}, \\ r_{max} e^{- \frac{1}{2} {(T - T_{u})}^{2} / C_{2}^{2}} & T > T_{u}, \end{matrix} \end{array}

Where r_max is the maximum potential growth rate, T_u is a threshold temperature, and C₁ and C₂ are scaling constants. This function describes a growth rate that increases as temperatures increase up to a threshold temperature T_u. For temperatures greater than T_u, the growth rate rapidly decreases to zero. The resulting growth rate as a function of temperature is shown in Supplementary Figure S2. Following Schneider et al. (2012), we model the temperature-dependent metabolic death rate of predators as

\begin{array}{l} x_{j} (T) = x_{0} W_{j}^{3 / 4} e^{- E / k T}, \end{array}

Where x₀ is a scaling constant, E is activation energy, and k is the Boltzmann constant. This rate increases with temperature and with predator body size W_j, and serves as a penalty for the high metabolic demands of larger predators. The formulation of allometric parameters in our model assumes a 1/4 power scaling law as in Brown et al. (2004). However, there is debate on the value of this exponent (Kooijman, 2010), which may even be species-specific. Different exponential powers may change the magnitude of the body mass dependent terms, thereby changing both pest consumption and intraguild interference. Due to the complex interactions between these processes, it is difficult to know the overall effect of different exponential powers on pest control predictions.

Attack rates and handling times are also allometric parameters. The attack rate of species j on species i is given by

\begin{array}{l} a_{i j} = a_{0} W_{i}^{1 / 4} W_{j}^{1 / 4} {(\frac{W_{j} / W_{i}}{R_{opt}} e^{1 - \frac{W_{j} / W_{i}}{R_{opt}}})}^{ϕ}, \end{array}

Where a₀ is a scaling constant, R_opt is the predator's preferred predator-prey body mass ratio, and ϕ tunes the importance of prey preference in determining attack rates. Attack rates increase with either species body size (W_i or W_j), to account for the higher mobility of larger species. The term in parentheses describes the likelihood of a successful attack, determined by how similar the predator-prey body mass ratio is to the predator's feeding preference. The time required for predator j to catch and consume an individual of species i is given by

\begin{array}{l} h_{i j} = h_{0} W_{i}^{1 / 4} W_{j}^{- 1 / 4}, \end{array}

Where h₀ is a scaling constant. Handling times increase with prey body size (W_i) and decrease with predator body size (W_j). The handling time and likelihood of successful attack do not incorporate defensive or avoidance behaviors, which are not parameterized by the model but may reduce the predation risk of some species. For scaling constants, we use values from Wootton et al. (2022), which were estimated using mesocosm experiments (including between R. padi, a groundbeetle, and a spider). All model parameters are given in Supplementary Table S1. Note that the parameterizations give higher R_opt values for beetles than spiders, because beetle readily attack very small prey while spiders tend to attack prey closer to their own size.

Temperature-dependent predator activity is given by the function

\begin{array}{l} ν_{j} (T) = max (0, \frac{c_{1} - c_{1} e^{k_{1} (T - T_{a})}}{1 + c_{2} e^{- k_{2} (T - T_{b})}}), \end{array}

Which matches the assumption that predator activity gradually increases with temperature but quickly declines to zero at some threshold temperature. The values c₁, c₂, k₁, k₂, T_a, and T_b are phenomenological constants. We select these values so that predator activity matches temperature ranges observed in the literature, as reported in Table 1, and the resulting activity curves are plotted in Supplementary Figure S3. We additionally select the constant c₁ to account for web-weaving spiders (Tetragnathidae and Linyphiidae) having lower activity levels in the overlapping foraging areas. Importantly, attack rates between predators depend on the activity level of both predators at the same temperature (ν_i(T)ν_j(T)). For example, despite having wide respective temperature ranges, Pterostichus and Lycosidae have low attack rates on one another because they are mostly active during different temperatures.

TABLE 1

Table 1. Temperature range where the predators from our case study are active.

2.3. Optimal predator communities

To understand which combinations of predator body size and temperature threshold promote biological control, we identify predator communities that provide a high level of pest control. With this information, farmers can evaluate how close a natural predator community is to the optimal community. If the natural predator community is inefficient in controlling the pest population, farmers can choose practices which promote different predator groups or release predators of a certain size, to get closer to the optimal predator community. We implement an optimization algorithm that minimizes the average abundance of the aphid population over the 34-day simulation period. We obtain the abundance of the aphid population by solving our mathematical model, starting from some initial conditions. The initial aphid abundance is set to best-fit observed aphid abundance under the natural predator community (see Supplementary Figure S4). The initial aphid abundance usually has a minimal effect on the composition of an efficient predator community. The exception to this is when initial aphid abundance is extremely low or paired with inhospitable temperatures, such that aphids exhibit minimal growth; in this case, the aphid abundance is less sensitive to predator composition and may be eradicated quickly by most predators. However, this is not the case in our system, since aphids were observed to establish large populations. The modeled aphid abundance is therefore determined by changes to initial predator abundance. By optimizing with respect to initial predator abundance, we identify which predators are effective biological control agents.

For the set of initial predator abundances ${M_{j} (0)} = {M_{2}^{0}, M_{3}^{0}, . . ., M_{10}^{0}}$ , we denote the solution for aphid abundance at time t as N(t; {M_j(0)}). Then the average daily aphid abundance over 34 days is

\begin{array}{l} C = \frac{1}{34} (N (1; {M_{j} (0)}) + N (2; {M_{j} (0)}) + ... + N (34; {M_{j} (0)}))) . & (1) \end{array}

Minimizing this quantity is equivalent to minimizing the cumulative daily aphid count. We minimize this quantity over all possible initial predator abundances. However, without constraints on reasonable predator abundances, the minimization could result in arbitrarily large predator communities, which would be inconsistent with field conditions. We therefore minimized C subject to a constraint on initial predator abundances. We require that the biomass of the initial predator community match predator biomass observed in the field. That is, for $M_{j}^{0}$ the initial abundance of predator j and W_j the body mass of predator j, we require that

\begin{array}{l} \sum_{j = 2}^{9} W_{j} M_{j}^{0} = B, & (2) \end{array}

Where B is the average predator biomass from field observations.

We solve this problem using the MATLAB function fmincon, which numerically minimizes C subject to constraints (Equation 2). Due to sensitivity of numerical minimization routines to initial conditions, we implement the minimization using the multistart routine. This routine repeats the minimization from multiple starting points and helps to find the true solution to the minimization problem. The details of this implementation and MATLAB code are available in the Supplementary material. We repeat the optimization under the following conditions. First, we use temperature series observed in the field as model input and obtain optimal communities for the 10 field sites we considered. We also obtain an optimal community for all 10 fields simultaneously. Then, to approximate effects of climate change, we increase the average temperature recorded in each field by 2.5°C and increase daily variability by 10% (see Supplementary Section 1). We select the increase based on predictions of air temperatures for this region into the 2050s (Swedish Commission on Climate and Vulnerability, 2007), and the variability to create a maximum change of around 2°C for daily highs or lows, to maintain the same scale for temperature changes. For the 10 fields, we repeat the optimization problem using these future temperatures.

3. Results

3.1. Effect of temperature on attack rates

The attack rates of predators on aphids depends on the range of temperatures over which a species is active (through temperature-dependent ν_j(T)), as well as species body size and feeding preference (through a_ij). Figure 1 shows the attack rates predicted by our model (ν_j(T)a_1j). In general, larger groundbeetles are more active during cooler temperatures and consume higher quantities of prey. For instance, large groundbeetles, such as Pterostichus, have higher maximum attack rates at lower temperatures than small groundbeetles, such as Bembidion. Groundbeetles are generally larger and have higher attack rates compared to spiders. However, larger spiders, such as Lycosidae, can still have attack rates that are similar to beetles because they prefer consuming prey that is closer to their own size.

FIGURE 1

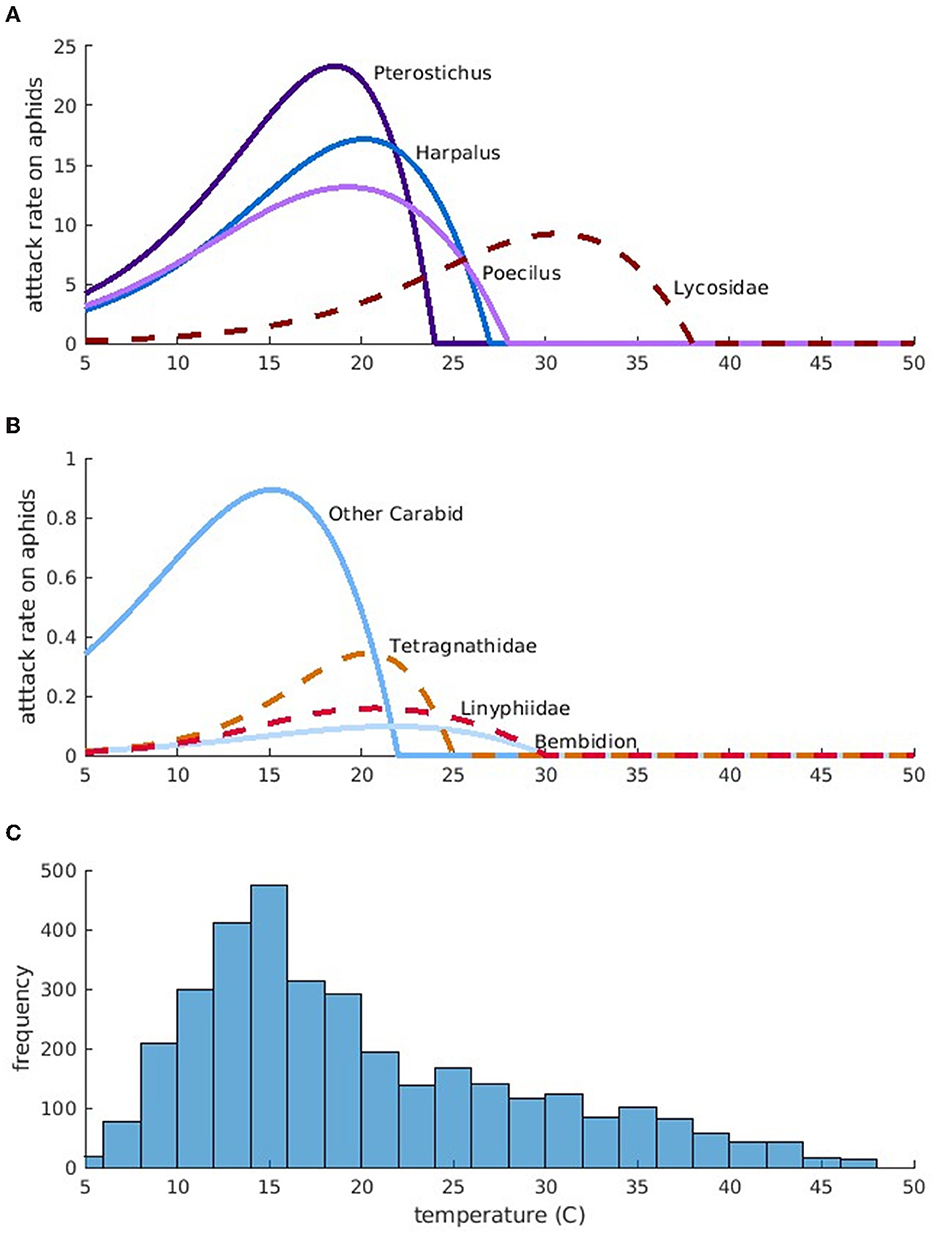
Figure 1. Simulated maximum potential aphid attack rates for each predator, per-capita as a function of temperature. Attack rates for larger predators are in (A) and attack rates for smaller predators are in (B). Blue-toned, solid lines indicate groundbeetles and red-toned, dashed lines indicate spiders. Darker colors indicate larger predators within either category. (C) Is a histogram of temperature observations across all field sites.

The predicted maximum potential attack rates on aphids vary greatly with temperature. Comparing the predicted temperature-dependent attack rates with the temperatures recorded in the field provides an indication of how efficient the predators are as biocontrol agents. In our study, field temperatures vary mostly between 10 and 20°C, and the most frequent temperature is around 15°C (Figure 1C). Groundbeetles, especially “Other Carabids” and Pterostichus have attack rates that peak during the most common temperatures, suggesting that groundbeetles are the most efficient predators. However, their attack rates drop to zero at temperatures between 22 and 27°C. When temperatures exceed 27°C, which can happen during hot afternoons, large spiders such as Lycosidae consume more aphids (peak attack rates around 30°C).

Next, we use predators with different peak activity ranges from each predator group (“Other Carabid” for groundbeetles and Lycosidae for spiders) to explore how their aphid attack rates on aphids (ν_j(T)a_1j) vary over the course of 2 days (Figure 2). We randomly choose one of our 10 temperature series and pick a 48 h window with sufficiently high temperature variation to demonstrate differences in predator attack rates on aphids. We first consider the potential attack rate on aphids in the absence of intraguild predation (Figure 2, solid lines). From t = 10 − 20 h and t = 32 − 44 h, the aphid attack rates of “Other Carabids” drop to zero because the temperatures become too high. However, spiders remain active during high temperatures and Lycosidae attack aphids during most of the period when “Other Carabids” are inactive. Only for very brief periods is the temperature too hot for Lycosidae to attack aphids (t = 35 − 37 and t = 37.5 − 40).

FIGURE 2

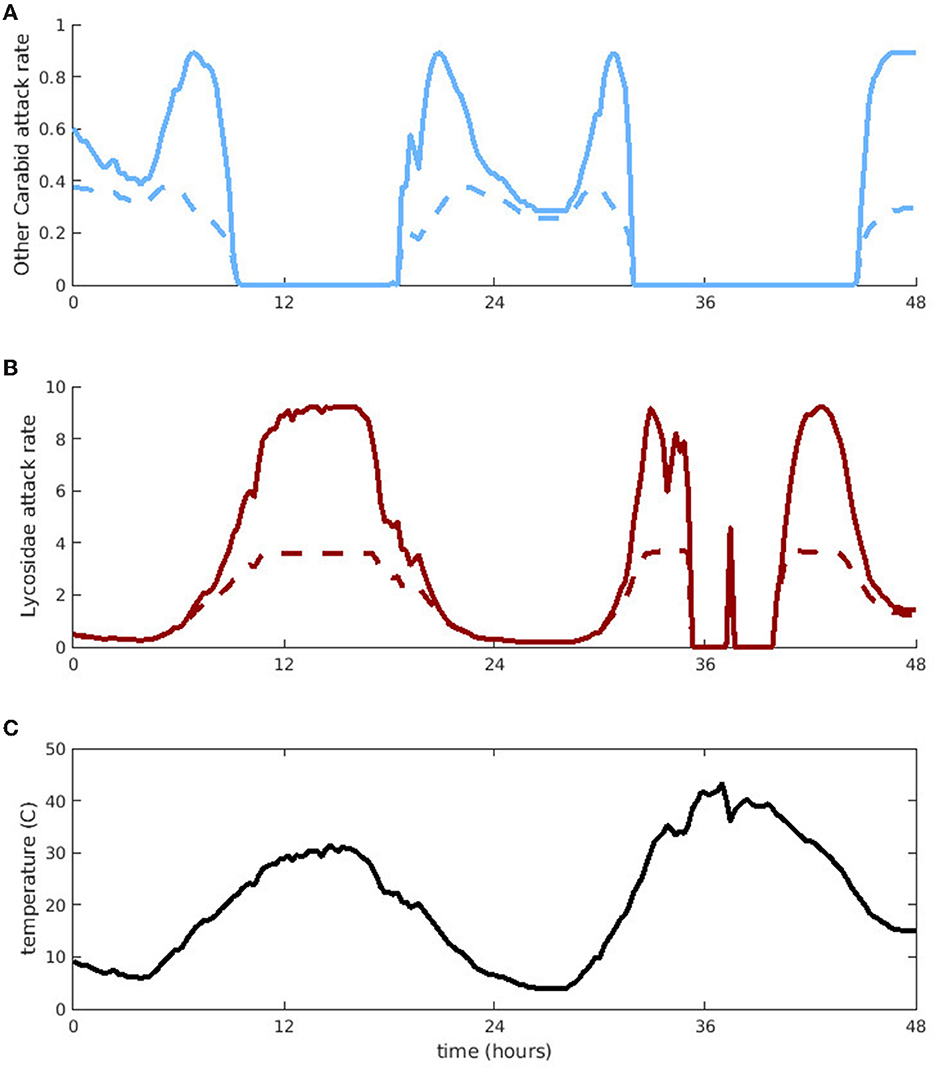
Figure 2. Per-capita aphid attack rates by “Other Carabid” and Lycosidae, as a function of time. (A) Is “Other Carabid” attack rate and (B) is Lycosidae attack rate. Solid lines denote the full potential attack rate and dashed lines denote the effective attack rate accounting for interference due to intraguild predation. (C) Indicates the corresponding temperatures for these attack rates, taken over 2 days in one of the fields.

To evaluate how much intraguild predation interferes with controlling aphid populations, we compare attack rates in the presence and absence of intraguild predation. We refer to aphid attack rates in the absence of intraguild predation as “potential attack rates” (solid lines in Figure 2) and aphid attack rates with intraguild predation as “effective attack rates” (dashed lines in Figure 2). The level of interference due to intraguild predation depends on predator abundance, which changes in time under our dynamic model. To facilitate comparison of the expected interference across temperatures, we use constant predator abundance. We assume predator abundance remains constant at the average observed abundance of predators in the field. For the same reason, we do not consider aphid handling time, because the total time predators spend handling aphids would depend on aphid density, which varies significantly over a season. Our simulations reveal that predator-predator interactions decrease aphid control the most at temperatures with high predator activity levels; although potential attack rates are highest at these temperatures, intraguild predation is also more common, causing effective attack rates to plateau. Additionally, Lycosidae experience more interference due to intraguild predation than “Other Carabids,” resulting in a larger difference between potential and effective attack rates (approximately a 1/4 maximum reduction for Lycosidae compared to a 1/2 maximum reduction for “Other Carabids”).

3.2. Optimal predator communities for pest control under varying temperature

We use the observed temperatures for the 10 fields to identify the predator community that produces the lowest average aphid population size over the 34 days of the growing season. Due to differences in temperature between fields, the composition of the optimal community is different for the 10 fields. Compared to the natural predator community, which did not control the pest under the model, optimal predator communities attain control of the pest in 8 of the 10 fields (Supplementary Figure S6). We summarize the variation in predator community across the different fields with a scatter plot (Figure 3, left), where each dot represents the optimal abundance of a predator in a single field. The horizontal lines in each predator category are the average optimal abundance across all fields. We also repeat the optimization across all ten fields simultaneously and denote this optimal abundance by a star. In observed predator communities (Supplementary Figure S7), Bembidion, Lycosidae, Linyphiidae, and “Other Carabid” had high biomass. In optimal communities, the most abundant predators are Lycosidae, which are active over the widest temperature range, followed by “Other Carabids,” which are active over the most common temperature range. There is moderate variability in the prevalence of Lycosidae between fields, with up to 20% of the community comprised of other predators for one field. However, the optimal community across all fields is more heavily skewed toward Lycosidae than the average between fields.

FIGURE 3

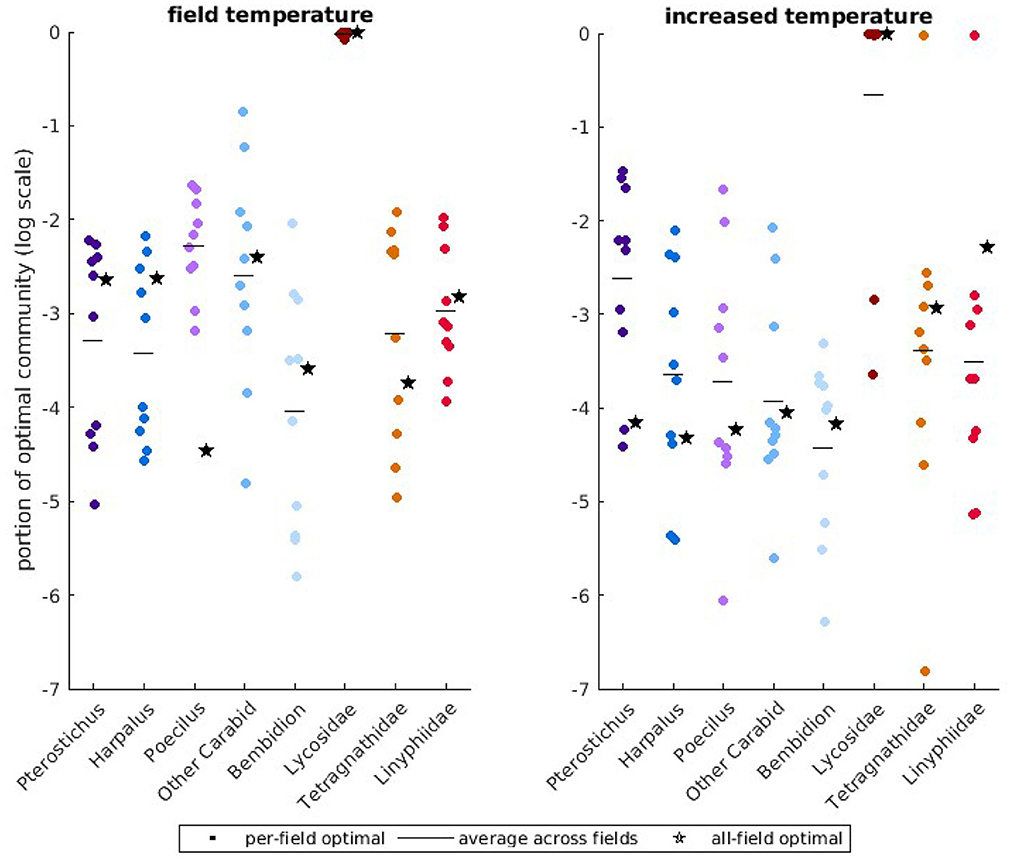
Figure 3. Portion of optimal predator communities plotted on a logarithmic scale for field temperatures and higher, more variable temperatures. In the (left), we show optimal predator communities at field temperatures and in the (right), we show the optimal predator communities at higher temperatures. Each dot denotes the optimal predator biomass for one field. The horizontal line for each predator indicates the average optimal biomass over all fields. The star marker indicates the optimal biomass over all fields simultaneously.

To assess performance of the optimal community at different temperatures (5–40°C), we compute the community-level attacks on aphids for the average optimal predator community. We keep the predator community constant and omit aphid handling times, to remove time-varying changes in density-dependent terms and facilitate comparison across different temperatures. We consider attack rates with and without temperature-dependent activity as well as with and without interference due to intraguild predation, to examine how these components of our model impact our understanding of community attack rates. Omitting temperature-dependent activity is equivalent to setting ν_j(T) = 1 for all temperatures T, and omitting intraguild predation is equivalent to assuming a linear functional response in our model. Including intraguild predation reduces attack rates on aphids, especially if attack rates are independent of temperature (Figure 4, difference between solid and dashed black line is much larger compared to solid and dashed blue lines). Including temperature-dependent attack rates reduces pest control over all temperatures in the absence of intraguild predation (Figure 4, black and blue solid lines). However, in the presence of intraguild predation, incorporating temperature-dependent attack rates increases pest control for temperatures between 17 and 37°C (Figure 4, black and blue dashed lines). This increase is not seen in attack rates by the observed community (Supplementary Figure S8), which peak at lower temperatures and are consistently reduced by intraguild predation.

FIGURE 4

Figure 4. Community-level attack rates on aphids by the average optimal predator community, plotted against temperature. Solid lines denote potential attack rates and dashed lines denote effective attack rates accounting for interference due to intraguild predation. Black lines do not incorporate temperature-dependent activity levels (with constant activity ν_j(T) = 1) and blue lines incorporate temperature-dependent activity levels (with varying activity ν_j(T)).

The model that includes temperature-dependent attack rates but no intraguild predation (Figure 4, solid blue line) predicts that the optimal predator community has the highest potential attack rates around 30°C, when Lycosidae are most active (Figure 1A), with a steep drop in attacks as temperatures approach the activity threshold for Lycosidae. Interestingly, this same temperature range corresponds to relatively low effective attack rates with intraguild predation (comparison between solid and dashed blue lines). The highest temperature-dependent attack rates with intraguild predation occur around 20°C, when predators other than Lycosidae are still active, or around 35°C, when Lycosidae activity begins to decrease. This is also the temperature range where temperature-dependent attack rates on aphids most exceeds temperature-independent attack rates (Figure 4), blue and black dashed lines). In Supplementary Figure S9, we show the same comparison between predator community attack rates for field temperatures over a 2 day period.

Since temperature-dependence in attack rate greatly changes the expected level of aphid control in our model (Figure 4), we explore the consequences of global climate change on the composition of the optimal predator community across the 10 field sites. Under these conditions, the optimal predator communities attain control of the pest in only 4 of the 10 fields (Supplementary Figure S10). In the right panels of Figure 3, we display how the optimal predator abundance would change if temperature increased by an average of 2.5°C and temperature variability increased by 10%. In several fields, and for the optimal community across all fields simultaneously, our model identifies increased clustering around an optimal community that is almost entirely comprised of Lycosidae. However, there is large variation in the optimal abundance of Lycosidae in the remaining fields, with some optimal communities comprised primarily of Tetragnathidae or Linyphiidae. The abundance of “Other Carabids” in the optimal communities decrease, with a shift toward larger groundbeetles Pterostichus and Poecilus that are active at slightly higher temperatures.

4. Discussion

Empirical work has demonstrated that predator activity changes with temperature (Kooijman, 2010) with varying effects on predator attack rates and handling times (Rall et al., 2012). By constructing a model that explicitly accounts for temperature dependent attack rates and applying it to the empirical system studied by Curtsdotter et al. (2019), we demonstrate that at observed field temperatures, there are long periods of reduced activity and attack rates by some predators due to high temperatures (such as “Other Carabids” in Figure 2). When such predators are abundant, this suggests that hot afternoons may provide temporal refuges for pest insects, where their populations are minimally impacted by the predator community. In a warmer climate, these temporal refuges are likely to increase and reduce the efficiency of the predator community to control pest populations. Increasing temporal refuges is an especially important consideration for rapidly growing pests. This paper uses aphids as an example, but temporal refuges likely exist for other pest insects. Our model suggests that the effect of temperature on predator attack rates is critically important for predicting the effect of predators on pest populations, because it reduces attack rates on aphids.

Temperature has a smaller effect on aphid control when the model includes intraguild predation (dashed lines in Figure 4). In this case, it is even possible that temperature-dependence in predator activity improves the expected level of natural pest control (17–37°C). Differences in ideal temperature ranges cause combined predator activity ν_i(T)ν_j(T) (and therefore the occurrence of intraguild predation) to decrease over key temperature ranges. We use our model to minimize simulated aphid abundances by identifying optimal predator communities. The optimal predator community consists primarily of Lycosidae, which are most active over a wide range of higher temperatures. The optimal predator community often includes “Other Carabids,” which are active at the most common field temperatures. By including both predator groups, biological control occurs over a wide temperature range. This finding is consistent with research indicating that functional differences between predators (such as “Other Carabids” and Lycosidae hunting at different times) improves overall pest control (Greenop et al., 2018). By including very few other species within each predator group, negative effects of predator-predator interference are minimized since groundbeetles and spiders are less likely to be simultaneously active. Similarly, empirical observations suggest that pest control is improved when predators avoid negative interactions by hunting in complementary ways, such as through habitat partitioning (Schmitz, 2009) or hunting strategies (Losey and Denno, 1998), and similar relationships have been studied using spatial models of predator interactions (Northfield et al., 2017).

Our modeling work reveals the importance of considering the complex community-level interactions to predict the efficiency of natural enemies controlling pest populations. Temperature has a smaller effect on aphid control when the model includes intraguild predation (dashed lines in Figure 4). In this case, it is even possible that temperature-dependence in predator activity improves the expected level of natural pest control (17–37°C). Differences in ideal temperature ranges cause combined predator activity ν_i(T)ν_j(T) (and therefore the occurrence of intraguild predation) to decrease over key temperature ranges. However, we also see that temperatures with increased predator activity correspond to decreased pest control due to intraguild predation (Figure 1), because predator-prey and predator-predator encounter rates increase simultaneously. This is especially important for Lycosidae, which engage in more intraspecific predation due to their preference for prey close to their own size (R_opt). At the temperature where these predators are most active, temperature-dependence in predator activity does not improve pest control in the presence of intraguild predation (Figure 4, 30°C).

Anticipating the outcome of community-level interactions based on empirical work alone would be extremely challenging, since complex interactions among members of insect communities are commonly characterized by non-additive effects. For example, Krey et al. (2021) observed that in fields with higher predator species richness, a generalist predator consumed more pests. Since the presence of multiple similar predators may reduce pest control, it is important to understand how pest control is affected by predator-predator interactions. Theoretical models incorporating such interactions therefore can serve as a powerful tool to inform farmers when designing pest control strategies that include biological control. In our study system, the observed predator community is primarily composed of Lycosidae and Bembidion. Based on our findings, we could recommend that managers do not disrupt the resident Lycosidae population but attempt to promote larger groundbeetles that are active at lower temperatures (for example via augmentative addition of groundbeetles alongside landscape management that promotes their retention, such as beetle banks or reduced tilling). Due to significant variability in optimal predator communities at higher temperatures, we could make field-specific recommendations for predator compositon; however, we note these results are specific to temperatures for a single season and may change with temperatures taken over longer periods. This mathematical model could also be applied to a range of other agroecosystems. We consider only predators that naturally occur in Swedish barley fields, but the model could be easily expanded to include novel predators as biological control agents or paramaterized to different systems. However, realistic predictions would require empirical data to estimate model parameters and specify predator responses to temperature.

Predicting the performance of insect predators under different climate change scenarios is an important issue in pest control, with significant challenges in preserving the complexity of natural predator communities (Facey et al., 2014). For example, Abbott et al. (2014) were able to empirically parameterize a model for the interaction between species responses to warming temperatures on pest control, but the model was restricted to only one predator. However, our results suggest that incorporating different predators' responses to temperature may be important for understanding many systems, including our own. Our model suggests that some predator species contributing to natural biological control under current climate conditions may not be important under warmer, more variable temperatures (“Other Carabid” in Figure 3). According to our model, the optimal community in many fields shifts to increase the importance of larger groundbeetles (Pterostichus and Poecilus). A diverse assemblage of differently-sized groundbeetles would be necessary to maintain biological control under current temperatures as well as warmer temperatures. In some fields, even the most important predator shifts entirely from Lycosidae to smaller spiders. This variability suggests that multiple, differently-sized spider predators are necessary to avoid a decline in pest control across different fields. These results suggest we should strive for high diversity in predator communities to ensure that there are efficient predator species even in a warmer world, which agrees with empirical observations of the benefit of diverse predator communities under warmer conditions (Drieu and Rusch, 2017). However, contrary to these observations, the overall optimal community under current and increased temperatures is primarily composed of a single species. For most fields at the individual level, there is minimal benefit to diversity in the predator community. In formulating pest control recommendations, it is important to consider whether individual fields require communities which are resilient to changes in temperature. Such work requires a close connection between empirical understanding and theoretical models which incorporate important biological details.

Future work in this area should utilize empirically-informed models which include additional behaviors and interactions that may affect the expected level of biological control. This model focuses on annual systems where insect pests and predators reproduce on different time scales (generation time of aphids is in the order of weeks, while that of the predator community is in the order of years), so that aphids have only a small influence on predator abundance within seasons. However, prey consumption and intraguild predation will affect predator abundance across multiple seasons. In order to study pest control across multiple seasons, such as in perennial crops where predators forage for the entire growing season, future models must include seasonal predator reproduction. One could also construct a model addressing how crop rotation shapes natural predator communities. Such a model would consider larger spatial scales and predator migration between different crop fields that are likely associated with different pest and predator communities. However, such work may be limited by the availability of data on predators' overwintering survival or long-term movement patterns. Additional details in a within-season model could also improve understanding of pest control. For example, defensive and avoidant behaviors of different species may reduce effective attack rates, as well as the abundance of alternative food sources in the field. As with our current model, we expect that predator behaviors change with temperature, and that, due to the combined effects of temperature and intraguild predation, consistent pest control requires a suite of predators that are active across a large range of temperatures. Our simulations also assume a consistent change in future temperatures, but a more detailed model for temperature change could highlight the existing environmental differences between different fields. Incorporating such factors would provide further insight into which predators are best-suited to varying conditions and the complex ways that pest control may change with temperature.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found at: https://doi.org/10.5061/dryad.41b5b06.

Author contributions

AL and BT collaborated on conception of the work. AL and NT collaborated on model development and numerical implementation. NT composed a preliminary summary of the work. AL drafted the first version of the article, which was significantly revised by BT. All authors agree to be accountable for the content of the work. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.998396/full#supplementary-material

References

Abbott, K. C., Harmon, J. P., and Fabina, N. S. (2014). The challenge of predicting temperature effects on short-term predator-prey dynamics. Popul. Ecol. 56, 375–392. doi: 10.1007/s10144-013-0426-x