Scaling of ant colony interaction networks

Toth, J. M.; Fewell, Jennifer H.; Waters, James S.

doi:10.3389/fevo.2022.993627

ORIGINAL RESEARCH article

Front. Ecol. Evol., 09 January 2023

Sec. Behavioral and Evolutionary Ecology

Volume 10 - 2022 | https://doi.org/10.3389/fevo.2022.993627

Scaling of ant colony interaction networks

J. M. Toth^1,2

Jennifer H. Fewell³^†

James S. Waters¹^*^†

¹Department of Biology, Providence College, Providence, RI, United States
²School of Medicine, University of Pittsburgh, Pittsburgh, PA, United States
³School of Life Sciences, Arizona State University, Tempe, AZ, United States

In social insect colonies, individuals are physically independent but functionally integrated by interaction networks which provide a foundation for communication and drive the emergence of collective behaviors, including nest architecture, division of labor, and potentially also the social regulation of metabolic rates. To investigate the relationship between interactions, metabolism, and colony size, we varied group size for harvester ant colonies (Pogonomyrmex californicus) and assessed their communication networks based on direct antennal contacts and compared these results with proximity networks and a random movement simulation. We found support for the hypothesis of social regulation; individuals did not interact with each other randomly but exhibited restraint. Connectivity scaled hypometrically with colony size, per-capita interaction rate was scale-invariant, and smaller colonies exhibited higher measures of closeness centrality and edge density, correlating with higher per-capita metabolic rates. Although the immediate energetic cost for two ants to interact is insignificant, the downstream effects of receiving and integrating social information can have metabolic consequences. Our results indicate that individuals in larger colonies are relatively more insulated from each other, a factor that may reduce or filter noisy stimuli and contribute to the hypometric scaling of their metabolic rates, and perhaps more generally, the evolution of larger colony sizes.

Introduction

Scaling laws are pervasive in biology, succinctly describing how numerous aspects of the nature of life depends on size. These scaling patterns are often represented in a form as simple as a power law with a coefficient and an exponent such as y = ax^b (LaBarbera, 1986; Bonner, 2006). That there is anything about the great diversity of life in all its splendor and forms which can be distilled into a relatively simple equation is remarkable, but nevertheless, support structures including tree trunks and vertebrate bones typically have diameters that scale with lengths^3/2, vertebrate lifespans typically scale with mass^1/4, and organismal metabolic rates from the smallest to the largest species typically scale with mass^3/4 (Spence, 2009). Although many models have been proposed, there is no consensus about why metabolic rates scale with mass^3/4 (Glazier, 2005; Del Rio, 2008). Though the precise value of the exponent can vary, it is generally hypometric (0 < b < 1) and is often robust to comparisons across development, among mature individuals of a single species, between species, and it has been demonstrated for collective animal groups including colonies of marine zooids (Nakaya et al., 2003, 2005) and social insects (Southwick, 1982; Southwick, 1985; Hou et al., 2010; Shik, 2010; Waters et al., 2010).

The striking commonality of this scaling across the diversity of life suggests that the underlying mechanisms driving metabolic use with size could be similarly universal. Increased size is necessarily associated with size-based scaling of the networks that sustain and maintain connectedness, whether for collections of cells within an organism or ants within a colony (Barabási and Oltvai, 2004; Moses et al., 2008). As with any organizational property, the communication networks used by organisms and complex social groups can be costly to construct and maintain; as such, the ways in which they are regulated with network size may provide important insights into allometric patterns of metabolic scaling with size.

Networks within organisms that can affect their metabolic rates include cardiovascular systems, cell signaling patterns, connections of the nervous system, endocrine feedback mechanisms, and gene regulatory networks. In social insect colonies, networks generally operate as non-hierarchical systems without direct leadership or central control (Wilson and Hölldobler, 1988; Bonabeau, 1998). Information transfer within a colony takes many forms, including antennation, dance, pheromonal communication, and other forms of indirect or direct contact (Gordon, 2007; Greene and Gordon, 2007). The spatial organization of individuals within colonies can influence the patterns of communication among workers (Boi et al., 1999; Mersch et al., 2013; Pinter-Wollman et al., 2013a; Baltiansky et al., 2021) and the resulting interaction networks provide the pathways thought to be responsible not only for the emergence and self-organization of complex patterns in foraging, nutritional regulation, house-hunting, and the division of labor, but potentially also how these patterns scale with colony size (Bonabeau et al., 1997; Beekman et al., 2001; Fewell, 2003; Dussutour and Simpson, 2009; Dornhaus et al., 2012; Donaldson-Matasci et al., 2013; Greenwald et al., 2018).

In a previous study using colonies of the California seed-harvester ant, Pogonomyrmex californicus, an experimental manipulation was designed to test whether the relationship between colony size and metabolic rate was simply a correlation (e.g., with another factor such as growth rate) or whether they were mechanistically linked (Waters et al., 2017). When the colonies were reduced to half their size, their mass-specific metabolic rates increased exactly as predicted by the power law of metabolic allometry, confirming that colony size was a causal driver of the effect, effectively and dynamically reducing the per-capita work expenditure of ants in larger colonies and increasing the same for ants in relatively smaller colonies (Supplementary Figure S1). An analysis of walking speeds among the ants in the colonies before and after the size-manipulation did not fully support the hypothesis that differences in metabolic rates were due to corresponding changes in movement, suggesting that other metabolically relevant aspects of social organization are involved. In this study we investigate the scaling of the interaction networks in these colonies, how they varied with total colony size, and how they changed following the experimental manipulation.

One of the most common and most easily measured forms of information transfer in an ant colony is antennal contact, where individuals place their antennae on other ants to receive chemical information. Previous studies have demonstrated that direct interactions such as antennation can drive changes in ant behavior, spatial fidelity, and disrupt homeostasis (Lenoir, 1982; Cabe et al., 2006; Pinter-Wollman et al., 2013a; Ulrich et al., 2018). Considering how these behaviors may change with colony size, we hypothesize that features of the ant colony social network that increase interactions at the individual scale and connectedness at the colony scale should be inversely correlated with metabolic rate and colony size. Furthermore, if aspects of the colony network are associated with the causal drivers of metabolic allometry, we expect them to scale in the same way. One caveat to this approach is that we would not necessarily know whether the scaling of network properties that we can quantify from our real-world observations was expected or not based simply on the increases or decreases in the group sizes and how network properties should theoretically scale with size.

Identifying novel functionality and investigating how network structures scale with size requires a relevant null model for comparison (Newman et al., 2002; Alon, 2007; Pinter-Wollman et al., 2013b; Davidson and Gordon, 2017). It should not be sufficient, for example, to say that anything is important about the result that a calculated metric such as average path length scales with a certain exponent unless that exponent is similar to or different from a predicted one. In many theoretical contexts, random graphs can offer a convenient and analytical baseline, but other network models such as hierarchical, small-world, or scale-free can be also generated (Newman, 2003). In our analysis of social insect interactions however, many of these theoretical or generative models are unrealistic because they do not consider the real constraints of the spatial dimension in which ants live (Barthélemy, 2011). If a model was not spatially based, it might predict that two ants on opposite sides of an arena would interact when this is not possible, at least not without accounting for their transit time. To test for the presence of any biologically unique or meaningful patterns in the scaling of real-world social insect interaction networks, we developed a spatially explicit random interaction simulation. The goal of this model was not to simulate in a detailed fashion the dynamic behavior of ants, but rather to generate first-order predictions for how spatially explicit random networks scale with size. By simulating random movements of virtual ants in groups of varying sizes, with parameters informed by our experimental design, we can generate hypothetical network data to offer a rigorous way to test for biological relevance by determining which, if any, of the features of our observed networks deviate from the predictions of randomly moving and interacting ants in the simulations.

Materials and methods

Ant colonies and experimental design

Whole colonies of California seed-harvester ants (P. californicus) were reared in the lab for this study (Supplementary Figure S1; Supplementary Table S1). This species has previously been shown to exhibit colony-level metabolic allometry (Waters et al., 2010) and has been studied for its division of labor (Smith et al., 2009; Holbrook et al., 2011, 2013) and communication network structure (Waters and Fewell, 2012). Recently mated P. californicus queens were collected in July 2011 from a location in Pine Valley, San Diego County, California (32°49′20″ N, 116°31′43″ W, 1136 m elevation) where the population is known to be pleometrotic, with multiple queens excavating new nests together. In the laboratory, where the room temperature was maintained at 30°C–32°C, queens were initially housed in groups of three within cotton-plugged water tubes and once workers were present, individuals were transferred into and housed within artificial nests constructed from a thin, square plastic enclosure (625 cm²) containing water reservoirs and area for foraging and construction of waste piles. All colonies consistently used nest spaces in this way and could be identified as relatively well acclimated based on observing clear brood piles, a retinue of workers tending to the queens, stationary workers, individuals foraging, and not many workers walking in circles around the outer edge of the enclosure. Colonies were fed with ad libitum Kentucky blue grass seeds, diluted honey water, and frozen adult Drosophila as protein sources. Colonies were reared in the lab for a year prior to the experiments, which were conducted from July to September in 2012. Additional information about the colonies used in this study and the original experimental design, including how metabolic rates were measured and the protocols for counting and weighing ants have been previously published (Waters et al., 2017).

To test for the effects of group size on the emergent patterns of connectivity within colonies, we studied two paired groups of ants: same-aged colonies that exhibited a natural range in their sizes after a year of growth and these colonies after they had experimentally reduced to half of their prior size. The size manipulation involved removing half of the prior number of workers, larvae, and pupae from across their enclosures. For all of these colonies, we assessed their interaction network structure by aggregating observed patterns of contact between individuals tracked using video recordings of the whole colonies in their artificial enclosures acquired while simultaneously measuring their metabolic rates using flow-through indirect calorimetry (Waters et al., 2017). Antennal contact networks were evaluated once at the colony’s original size (N = 5 colonies, ranging in size 86–324 ants), and a second time following a reduction to half of the colony’s size (N = 5 colonies; 43–164 ants) (Waters et al., 2017). Workers were removed and added back to colonies before the first analysis to control for disturbance effects.

For network analyses, video of the colony enclosures was recorded at 15 frames per second and at 1,224 × 1,224 pixel resolution, offering sufficient clarity to observe individual workers (305 +/− 14 pixels each, SE, N = 25), their antennae, and their interaction behavior. Recordings were made during the simultaneous measurement of their metabolic rates; the colonies were inside their artificial nest enclosures (the same ones they had continuously been reared within) and those nest enclosures were gently placed and secured within an aluminum metabolic respirometry chamber with a clear lid to allow filming of the colony. The recordings were able to capture the entire nest enclosures and one segment of video with 30-s duration was saved for each measurement, used in a previous study (Waters et al., 2017) to quantify walking speeds and in this study to assess interactions and connectivity.

To review video and quantify the social behavior of the ants, recorded movies were opened in ImageJ (Rasband, 1997), and all ants labeled across the sequential frames using the MTrackJ plugin (Meijering et al., 2012). The video was played backwards and forwards frame by frame to follow each ant and separately record the sequences of their contacts with each other as edge-list tab separated text files. Individual instances of antennal contacts were scored as interactions based on identifying which ant’s antennae were making contact with another ant and recording their identities. Both unidirectional and mutual interactions were observed. Observers were not blind to the size of colonies or their experimental state (whole-colony or size-reduced), but without specific a priori predictions about how the nature of interactions would change with colony size, we do not believe unconscious bias could have consistently influenced the scoring. Although automated tracking methods have potential utility, especially with respect to screening longer durations of behavior, since a prior study had demonstrated the heterogenous nature and highly skewed degree distribution of P. californicus interaction networks (Waters and Fewell, 2012), our goal was to capture a complete and accurate snapshot of the connectivity activity within these colonies, requiring the manual tracking of individuals and their behaviors across the N = 691,650 frames of video.

Simulating spatially explicit random interaction networks

The null model for this investigation consisted of a simulated grid-based enclosure in which ants, modeled as particles, move randomly through the space with the potential to interact with each other based on proximity. The simulations were run across a range of colony sizes to capture the range of worker numbers in the experimental colonies. The size of the simulation enclosure remained constant to match the experimental design with the real colonies; the overall density increased with colony size in both the experiments and the simulations.

At the start of the simulations, ants are placed randomly in the virtual space. We ran the model for a fixed amount of time (100 time steps) so that the number of interactions in a simulated colony was similar to the number of interactions of our average sized colony. Individual ants were identified with a number and occupied a grid cell within the colony space. For each time step of the simulation, each ant moved one grid cell in a random direction. If a movement would take an ant outside of the spatial bounds, a different direction was selected. An interaction was logged when an ant moved to a cell adjacent to another ant. Interactions did not influence the subsequent movement direction of the ant, with the exception that multiple ants are not able to occupy the same grid cell. Pairs of ants may log multiple interactions with each other, but only if both ants have interacted with other ants since their last interaction together. The simulation was written in R and produces output as two text files, one recording each ant’s trajectories (x, y, t) and a second recording the time-stamped edge list for the virtual interactions. The code is available in our online supplement and all code and data are also accessible on a Github repository.¹

Inferring interactions based on spatial proximity

To more precisely understand the role of spatial organization on interaction patterns, we used the individual tracking data from our colonies to generate a set of networks based on proximity. In contrast to the method previously described, relying on manually observing direct antennal contacts, these networks were based solely on individuals being within a set proximity of each other. The tracking data included individual labels and their coordinates.

In order to infer proximity based interactions, we replayed the trajectories recorded from real ants, and at each time step calculated the distances between each pair of ants. Interactions were logged whenever two ants entered a minimum interaction distance to each other. We recorded interactions when the tracked center points of individuals were separated by less than either 20 or 30 pixels. These values were based on the size of ants in our video and observing that antennal contacts were often made between ants one body length (30 pixels) away from each other. The closer value was selected to generate networks with a higher threshold for interactions and results closer in size to the ones based on antennal contacts. In both cases, we maintained the requirement from the Brownian motion simulations for non-sequential duplicate interactions.

Social network analysis and statistical comparisons

Social network analysis comparing the size-dependence of network properties between real-world and simulated networks was performed in R v4.0.4 (Team RC, 2021) with functions from the following packages: igraph (Csardi and Nepusz, 2006), tidyverse (Wickham et al., 2019), ggraph (Pedersen, 2021), tidygraph (Pedersen, 2020), and patchwork (Pedersen, 2019).

Since it is possible that an individual was present but did not interact with any other individuals, the number of inactive individuals was calculated as the difference between the number of ants in the colony and the number of nodes in the network. The per-capita interaction rate was calculated at the ratio of the number of edges to the total number of individuals present. We report centrality based on taking the mean of closeness centrality calculated using closeness() across all nodes within a network, and clustering coefficient was calculated using transitivity(). The largest connected component (LCC) was calculated by using clusters() to count connected components and record the size of the largest one. Modularity, an indicator of the degree to which interactions take place within subgraph communities rather than across the network, was calculated using Newman’s leading eigenvector method (Newman, 2006) as implemented by the cluster_leading_eigen() function.

The exponents of scaling equations were calculated by log₁₀ transforming the data, fitting a linear regression model, and testing for a slope that was significantly different than zero. To compare the network structure of observed networks before and after the size manipulation, and because the sample sizes were relatively small (only five data points for each of two groups), we used the nonparametric Wilcoxon rank sum exact test.

Results

We quantified patterns in the scaling of social insect interaction networks for five colonies in each of two states (whole colonies and colonies reduced to 50% of their numbers of workers, larvae, and pupae) and compared these results to the networks generated by our spatially-explicit random interaction simulation model and also to networks inferred from proximity in real ant spatial trajectory data (Supplementary Figures S2–S4; Supplementary Table S2). The numbers of workers in the colony groups ranged from 40 to 292, the number of nodes in their networks ranged from 18 to 168, and the number of interactions based on antennal contacts ranged from 23 to 562 (Figure 1A). The degree distributions were right-skewed (Figure 1B), with a minority of ants engaging in a disproportionately high number of interactions while the majority of ants interacted relatively less often.

FIGURE 1

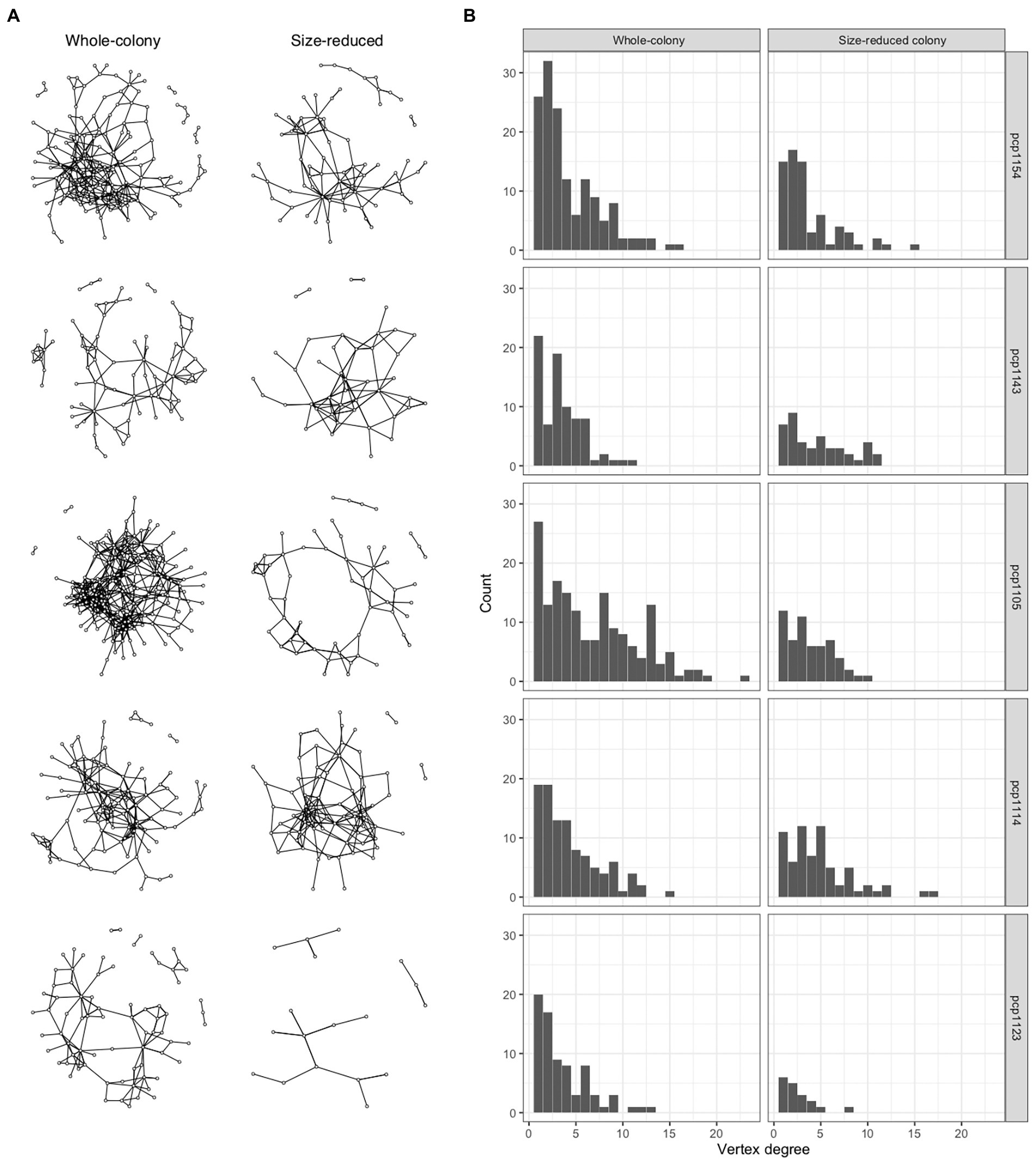
Figure 1. Social networks of P. californicus colonies. (A) These graphs show the 10 networks summarizing the interactions between workers in five colonies. The graphs in the column on the left were based on interactions in the whole-colonies prior to their manipulation, the graphs on the right are based on interactions in the same colonies, but after a manipulation in which 50% of the workers, brood, and pupae had been removed. (B) Degree distributions are plotted corresponding with the respective networks shown in (A) as determined by observing antennal contacts.

Following the experimental size reduction, the number of nodes and edges both decreased, but surprisingly, many aspects of the colony network structure remained unchanged (Supplementary Figure S5). Aspects that were not significantly (p > 0.05) affected by the manipulation included the average degree (4.17 +/− 0.34), average path length (3.78 +/− 0.21), clustering coefficient (0.18 +/− 0.03), diameter (9.7 +/− 0.7), the number of inactive individuals (71.3 +/− 17.4), modularity (0.58 +/− 0.03), and the average per-capita interactions (1.22 +/− 0.2, or expressed as a rate, 2.44 per minute). The largest connected component was significantly reduced following the manipulation (p = 0.01), as was the number of nodes and number of edges, but these were all likely direct results of there being fewer ants available to connect. Following the size-reduction, closeness centrality significantly increased from 0.0007 to 0.002 (p = 0.02) and graph density significantly increased from 0.02 to 0.05 (p = 0.007). The changes in centrality and density with decreasing colony size correlated significantly with the increases in mass-specific metabolic rates of these colonies (Figure 2).

FIGURE 2

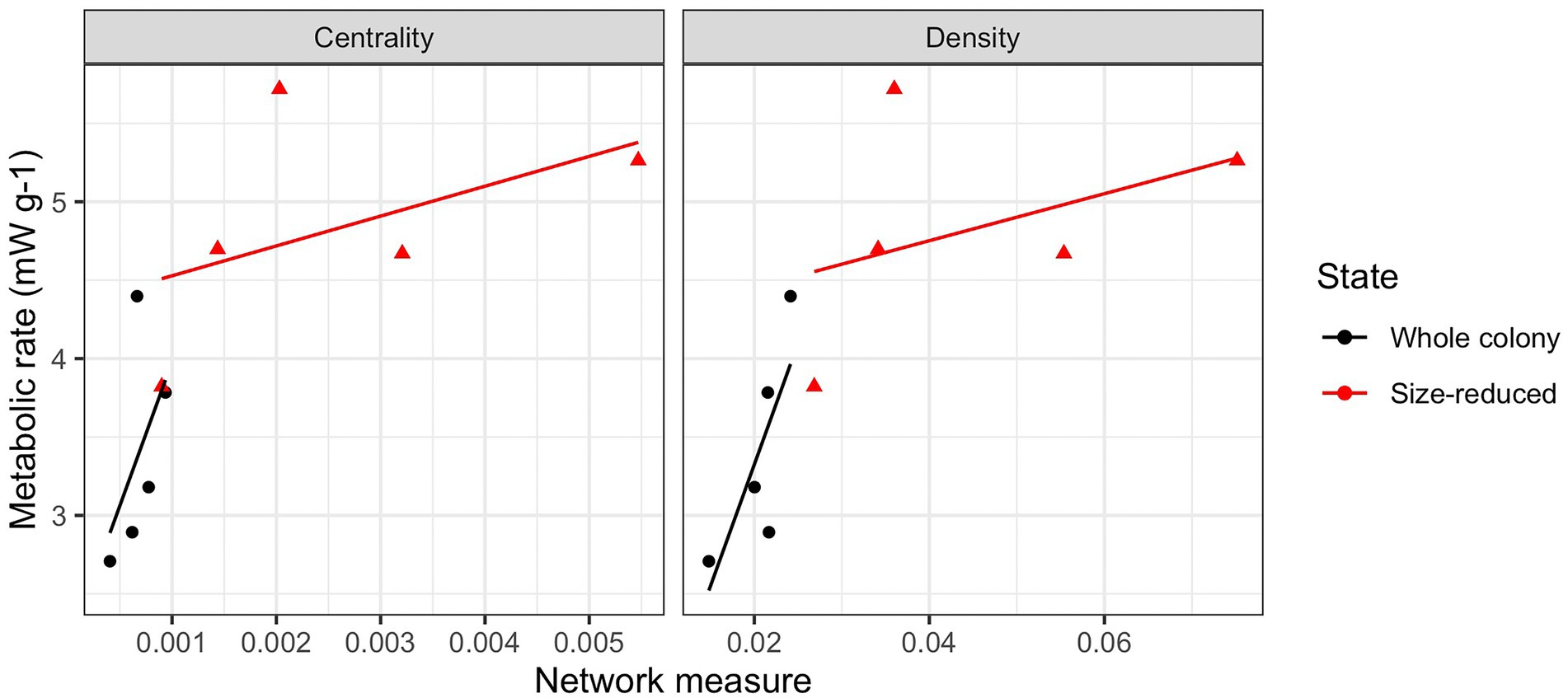
Figure 2. Correlations between network attributes and colony metabolic rates. Network centrality and density correlated with metabolic rates in a consistent manner both within treatment groups (whole colonies and size-reduced colonies) and between them. In both cases, increasing network centrality and density correlated positively with increases in the mass-specific metabolic rates of the colonies.

Four classes of scaling patterns were identified by pooling the available data on antennal-contact based P. californicus interaction networks and estimating the scaling exponents, b, for how these properties changed depending on colony size (Supplementary Figures S6, S7). We note that these results are based on measurements from a total of 10 networks with two each derived from five source colonies, one with the entire colony and another with half of the numbers of workers, larvae, and pupae removed. The different group sizes of the two measurements from each source colony motivates their consideration as independent points in a regression analysis, and this was further confirmed by testing for a significant effect of source colony. For all of the scaling analysis considered (Supplementary Table S3), including source colony as a co-variate did not significantly improve the quality of the fit (ANOVA p-values ranged from 0.11–0.93), and as such the data were pooled. The number of unconnected or socially inactive individuals exhibited a hypermetric allometry, increasing at a rate faster than proportionality (b = 1.41 +/− 0.39, F_1,8 = 12.6, R² = 0.61, p = 0.007). The number of edges and the size of the largest connected components both scaled proportionally with the number of workers. Two hypometric allometries, in which the network variable increases at a slower rate than increases in worker number included average path length (b = 0.21 +/− 0.08, F_1,8 = 7.3, R² = 0.48, p = 0.03) and the number of nodes in the networks (b = 0.85 +/− 0.2, F_1,8 = 17.5, R² = 0.69, p = 0.003). The hypometric scaling for the number of nodes is likely a complementary observation to the hypermetric scaling of unconnected individuals previously described. Inverse scaling relationships were found for centrality (b = −1.02 +/− 0.28, F_1,8 = 12.95, R² = 0.62, p = 007) and density (b = 0.-0.65 +/− 0.17, F_1,8 = 15.5, R² = 0.65, p = 0.004). The last class of scaling patterns we identified were aspects of colony network structure that appear to be scale-invariant, with no significant relationship with colony size (p > 0.05). These scale-invariant features included modularity, the average node degree, clustering coefficients, diameter, and the average per-capita interaction rate.

The spatially explicit random interaction simulation was used to generate networks ranging in size from 5 to over 300 virtual individuals and served as a null model against which to compare our colony network data (Figure 3). The most striking difference was that in the simulations, the number of edges and per-capita interaction rate increase exponentially with group size, but the ants held those features constant. There were relatively few unconnected (“inactive”) individuals in the simulations, and this number went down with increasing group size while it went up in the colonies. While the number of nodes scaled with a hypometric allometry in the colonies, it was a hypermetric allometry in the simulation data (b = 1.39 +/− 0.01, F_1,337 > 100, R² = 0.97, p < 0.001) and these two relationships were significantly different based on the 95% confidence intervals of the exponents. Modularity and clustering coefficients did not appear to scale with the size of the simulated groups, but both were on average higher than the values from our colonies, potentially indicating at the global and local scale respectively, that individuals in the simulation were more likely to interact with their nearest neighbors than ants in colonies. While centrality and density both decreased with increasing colony size in our antennal-contact based networks, these patterns were not predicted by the results of the simulation; although there are regions of overlap, the ant colony centrality in small colonies is especially high and the ant colony density in large colonies was relatively low.

FIGURE 3

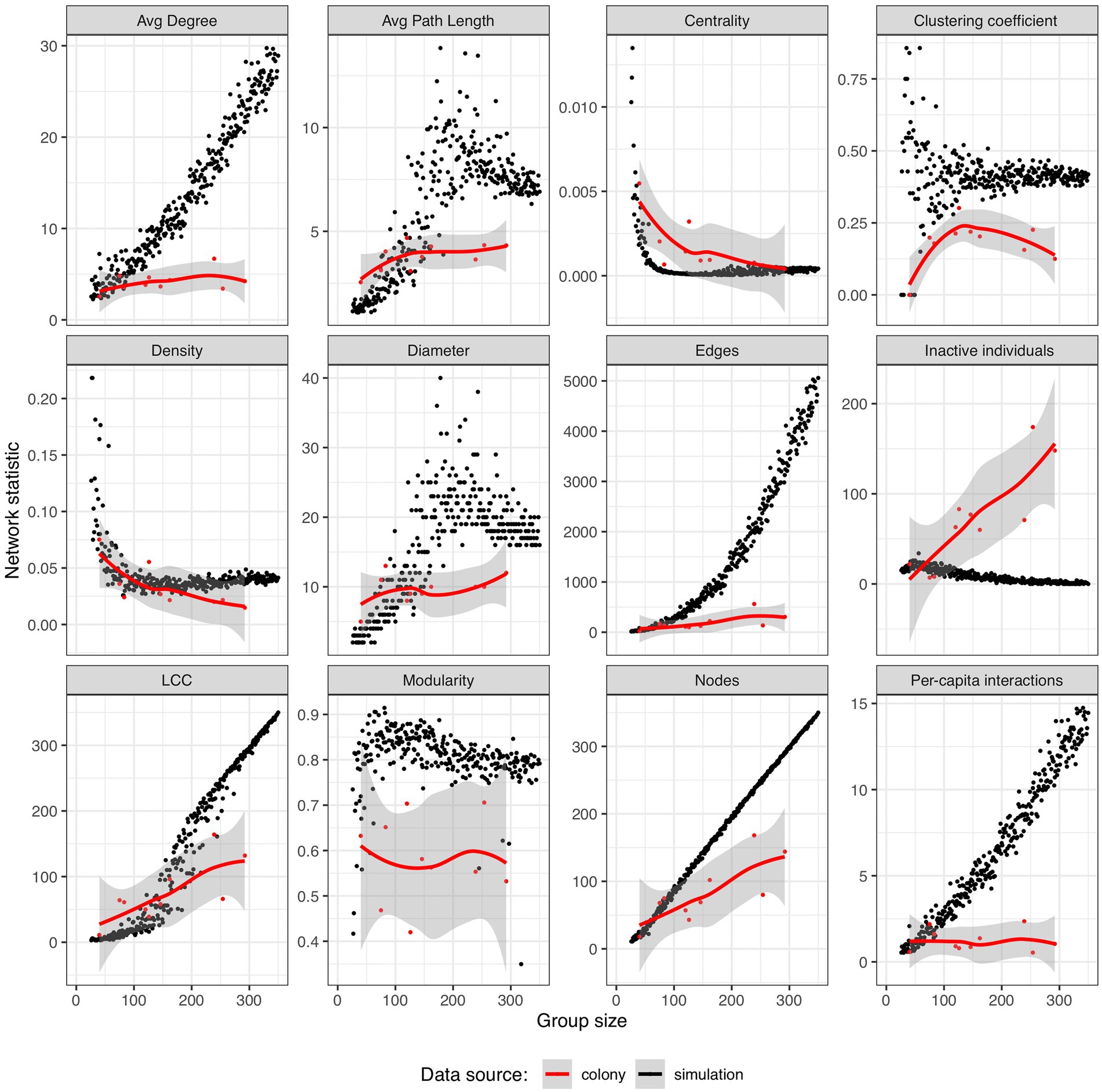
Figure 3. Comparing the scaling of antennation-based ant colony social network structure with the predictions of the spatially explicit random interaction simulation. Simulation results are plotted as black dots and P. californicus data are represented as red dots and additionally plotted with a loess smoothing curve in red and its associated error as a shaded region. Data are plotted for 324 simulated networks ranging in size from 25 to 357 individuals and in the number of nodes from 11 to 357.

We compared the scaling of social network characteristics with colony size for two different methods of determining interactions from our video recordings: (1) using observations of direct antennal contacts between individuals and (2) inferring interactions based on pairwise spatial and temporal proximity. The number of interactions measured by the proximity networks was sensitive to the distance threshold parameter. Although the 30-pixel distance was selected to match observed distances between ants making direct antennal contact, this threshold resulted in networks with an average of 7.7 interactions per-capita, more than six times the average number observed in direct antennal contact networks (1.22). Reducing the threshold for scoring interactions to 20-pixels still over-estimated the per-capita interaction rate (3.45), but the scaling of network properties of the proximity based networks was not significantly different than the scaling of network properties based on observing direct antennal contacts; the intercepts varied but the 95% confidence intervals for the fitted exponents overlapped in all cases (Supplementary Figure S8; Supplementary Table S3).

Discussion

The scaling of ant colony social networks exhibits some features consistent with the predictions of an intentionally simple agent-based model based on randomly moving and interacting individuals, but has other important features that are markedly different. In contrast to null expectations from the model and the results of proximity-based network detection, individual workers within our laboratory colonies often simply refrained from direct antennal contact. This included both individuals who were stationary and adjacent to each other and others who crossed paths while moving. Indeed, this is a common aspect of worker behavior across the numerous ant colonies we have observed and may indicate a greater selectivity in interactions, a mechanism for avoiding interactions, or greater spatial partitioning in larger colonies.

Another striking difference was that the per-capita interaction rate increased exponentially with group size in the simulation, but was scale-invariant and regulated in the observed networks, as previously shown for other ant species (Blonder and Dornhaus, 2011; Gordon et al., 2012). While the colony per-capita interaction rate was relatively constant, in comparison with the simulation predictions, it was substantially higher than expected in small colonies and lower than expected in large colonies.

While in the simulation, increasing density necessarily increased contact probabilities, ants in our laboratory colonies did not show the same effect. Ants in the simulation however, were distributed randomly and uniformly throughout the arena, but real ants do not similarly disperse, at least not when their colony’s social milieu is intact and they have had time to acclimate to a nest enclosure (Waters et al., 2010; Holbrook et al., 2011). In a similar way, groups of workers isolated from the rest of their colony, breaking the social context and organization, do not behave the same way or exhibit the same metabolic scaling patterns as when part of intact colonies; in these cases involving removed fragments, their metabolic demands increase proportional to their group size instead of exhibiting an allometry (Waters et al., 2010). As reported in other studies (Holbrook et al., 2011; Gordon et al., 2012), workers aggregate spatially around tasks and also cluster while resting, maintaining a roughly constant inter-individual spacing.

We compared the scaling of colony social network structure based on direct antennal contacts with networks based on inferring interaction due to the close proximity of individuals. Based on the common observation that adjacent ants may not directly interact with each other, we predicted that proximity would not be a faithful indicator of an interaction. This was partially confirmed by the proximity networks having vastly inflated numbers of interactions relative to the directly observed ones; ants in our colonies did not always make antennal contact when they were close to each other. However, and much to our surprise, the scaling of network properties with colony size was not significantly different when comparing between these two ways of determining the networks, the power-law scaling exponents for 12 metrics of social network structure were indistinguishable between these two different ways of assessing interactions. These findings support an idea that has long been reported in the cellular automata (Miramontes et al., 1993; Solé et al., 1993) and social insect literature (Boi et al., 1999; Sendova-Franks et al., 2010; Mersch et al., 2013; Razin et al., 2013; Quevillon et al., 2015; Richardsonv and Gorochowski, 2015; Davidson and Gordon, 2017; Crall et al., 2018; Gordon, 2020), that the function of complex systems like social insect colonies is strongly dependent on their spatial distributions. Although not yet studied in our model system, these changes could be driven either by active behavioral regulation or by indirect chemical communication potentially involving pheromones that structure the spatial organization within the nest enclosures and the resulting activity at the colony-level (Heyman et al., 2017).

As demonstrated in our antennal contact networks, restraint is a defining regulatory feature in the scaling of interaction networks in P. californicus colonies. Ultimately, there are ants that are crossing paths or standing adjacent to each other that could in theory interact, but do not. To the contrary, interacting ants often showed a form of distance attraction, traveling considerably farther between interactions than the average pairwise distance between all ants, a key finding in recent studies with honeybee colonies (Fard et al., 2020) and groups of raider ants (Ulrich et al., 2018), and a likely factor depressing the overall colony network modularity relative to the simulation results. Bernd Heinrich once proposed that “ultimately, the functional unity of a swarm is achieved not by physical configurations among the component bees, but by the communication among them” (Heinrich, 1981). Notably, highly social insect colonies also show lower modularity than other animal social networks, which are generally built around maintaining individual alliances with local neighbors rather than construction around coordination of work (Waters and Fewell, 2012; Nunn et al., 2015).

All behaviors have associated costs, whether the currency is time, energy, or risk. One of the differences between topological and spatial networks is that there can be costs associated with frequency or maintenance of long-distance connectivity in the latter (Barthélemy, 2011). In our experimental arenas, the metabolic costs of traveling from one side to the other are trivial, but the size and three-dimensional architecture of nest spaces in nature could impose measurable constraints (Perna and Theraulaz, 2017; Tschinkel and Hanley, 2017). In addition to the metabolic costs associated with movement, which even in the field may be minimal (Fewell, 1988), there are likely indirect costs associated with the effects of information exchanged during interactions. There is an abundance of support for the role of interactions in changing individual behaviors in social insect colonies (Pinter-Wollman et al., 2013a; Gordon, 2016; Gordon, 2020), and while the direct and immediate energetic cost for two ants to interact may be insignificant, the downstream effects of receiving and integrating social information can have short and long-term metabolic consequences.

Consistent with these ideas, the relatively lower graph densities and centrality metrics in larger colonies may promote energetic savings by optimally minimizing redundant or noisy information exchange. If there are metabolic costs associated with the downstream effects of interaction between individuals, these network characteristics could be among the factors either driving metabolic allometry or at least providing the means for regulating colony metabolic rates. With workers socially more distant from each other in the larger colonies, they may be less likely to frequently switch tasks, respond to ephemeral stimuli, or metabolically up-regulate than workers in smaller and more modular and densely connected colonies.

One of the major leaps associated with the evolution of complex insect societies was a transition away from the group as a means of strengthening social bonds and toward a functionally regulated collective (Fewell, 2003; Nandi et al., 2014). In many animal social networks, it is common to see features such as high clustering, feedback loops, and dense modularity; we even see these in our simulated random interaction data since they can result from spatial correlations. In contrast, the social networks of P. californicus have limited feedback and instead exhibit an abundance of regulatory elements such as the feed-forward loop subgraph motif (Waters and Fewell, 2012). Modularity has been proposed in a few recent contexts to help buffer the spread of disease in social groups (Nunn et al., 2015; Quevillon et al., 2015; Stroeymeyt et al., 2018), but this feature was not prominent in our P. californicus networks and may not be as common in contexts in which interactions are constrained to the individuals engaged in specific tasks. Especially when the downstream consequences of interactions can include energetically costly changes associated with task switching or fitness-reducing consequences associated with foraging in harsh conditions (Gordon, 2013), there may have been evolutionary pressure to inhibit the types of interaction that could trigger dangerous cascades and positive feedback loops within colonies. By regulating their interactions and exhibiting restraint, interacting only when necessary for updating information, the buffer of individuals not engaged in the social network of the colony can serve to filter noise and reduce the likelihood of an unintended contagion. If this homeostatic effect is associated with metabolic scaling more generally, it may also drive the evolution of large colony size and potentially larger functionally integrated collective groups in general.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JW and JF designed the experiment. JT wrote the simulation and proximity detection code. JW collected the data, and all authors edited and revised the manuscript. All authors contributed to the article and approved the submitted version.

Funding

JW acknowledges support from the James S. McDonnell Foundation and the National Science Foundation (IOS-1953451 and IOS-1110796); JF acknowledges support from NSF IOS-1558127.

Acknowledgments

The authors thank Alyssa Holmes and Ioulia Bespalova for their support and Dai Shizuka for an accessible tutorial on network analysis in R (https://dshizuka.github.io/networkanalysis/).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.993627/full#supplementary-material

SUPPLEMENTARY VIDEO 1 | Visualization illustrating the spatial trajectories and social network development over time in a real P. californicus colony with interactions determined based on observing instances of antennal contact between ants.

SUPPLEMENTARY VIDEO 2 | Visualization illustrating the spatial trajectories and social network development over time based on a simulated colony with interactions scored based on proximity.

SUPPLEMENTARY VIDEO 3 | Visualization illustrating the spatial trajectories and social network progression over time based on a real P. californicus colony with interactions inferred based on a proximity threshold between ants.

Footnotes

1. ^https://github.com/waterslab/ant-networks

References

Alon, U. (2007). Network motifs: theory and experimental approaches. Nat. Rev. Genet. 8, 450–461. doi: 10.1038/nrg2102