Metabolic responses of predators to prey density

The metabolic cost of foraging is the dark energy of ecological systems. It is much harder to observe and to measure than its beneficial counterpart, prey consumption, yet it is not inconsequential for the dynamics of prey and predator populations. Here I define the metabolic response as the change in energy expenditure of predators in response to changes in prey density. It is analogous and intrinsically linked to the functional response, which is the change in consumption rate with prey density, as they are both shaped by adjustments in foraging activity. These adjustments are adaptive, ubiquitous in nature, and are implicitly assumed by models of predator–prey dynamics that impose consumption saturation in functional responses. By ignoring the associated metabolic responses, these models violate the principle of energy conservation and likely underestimate the strength of predator–prey interactions. Using analytical and numerical approaches, I show that missing this component of interaction has broad consequences for dynamical stability and for the robustness of ecosystems to persistent environmental or anthropogenic stressors. Negative metabolic responses – those resulting from decreases in foraging activity when more prey is available, and arguably the most common – lead to lower local stability of food webs and a faster pace of change in population sizes, including higher excitability, higher frequency of oscillations, and quicker return times to equilibrium when stable. They can also buffer the effects of press perturbations, such as harvesting, on target populations and on their prey through top-down trophic cascades, but are expected to magnify bottom-up cascades, including the effects of nutrient enrichment or the effects of altering lower trophic levels that can be caused by environmental forcing and climate change. These results have implications for any resource management approach that relies on models of food web dynamics, which is the case of many applications of ecosystem-based fisheries management. Finally, besides having their own individual effects, metabolic responses have the potential to greatly alter, or even invert, functional response-stability relationships, and therefore can be critical to an integral understanding of predation and its influence on population dynamics and persistence.

Introduction

Predation is one of the most important ecological interactions, determining the flow of energy and matter in nature, and imposing selective pressures that shape the evolution of organism traits and their distribution in ecological communities (Elton, 1927; Lindeman, 1942; Paine, 1966; Sih et al., 1985; Vermeij, 1994; Abrams, 2000; Estes et al., 2011; Rossberg, 2013). Since its foundation from the Lotka-Volterra model in the early twentieth century, predator–prey theory has increasingly recognized the role of behavior and bioenergetics as drivers of trophic interactions and the dynamics of populations and ecosystems (Holling, 1966; Abrams, 1984, 2010; Yodzis and Innes, 1992; Lima, 1998; Kondoh, 2003; Schmitz et al., 2004; Rooney et al., 2006; Loeuille, 2010; Valdovinos et al., 2010). Relevant advancements include the adoption of a metabolic approach that imposes temperature and body size constraints to rates of predation from first principles of thermodynamics and allometry (Brown et al., 2004; Brose, 2010; Rall et al., 2012; Sibly et al., 2012; Gilbert et al., 2014). Such incorporation of more realistic features of foraging and metabolism into theory has been shown to greatly alter the dynamical stability, structure, and evolution of model populations (Yodzis and Innes, 1992; Kondoh, 2003; de Ruiter et al., 2005; Loeuille and Loreau, 2005; Brose et al., 2006; Otto et al., 2007; Petchey et al., 2008; Heckmann et al., 2012; Kalinkat et al., 2013; Fussmann et al., 2014; Pawar et al., 2015; Ho et al., 2021; Kratina et al., 2022), with implications for the management and conservation of natural resources.

When linking individual bioenergetics to the dynamics of populations and ecosystems, it is important to determine how both energy gains and losses of a predator organism, given by its rates of food consumption and metabolic expenditure, vary with prey density. This is because these two routes of energy flow entail different feedback mechanisms between predator and prey (Figure 1). As prey vary in density, so does the chance of finding and capturing them. The most assumed consequence is a change in the predator’s food consumption rate, which defines the functional response (Holling, 1959a). Another, usually overlooked consequence of prey density variation is a change in the predator’s metabolic expenditure, hereby referred to as metabolic response. The expenditure occurs in the form of respiration resulting from any type of activity that is responsive to the presence of prey, but often from that spent foraging. When prey become more abundant they will likely be easier to find, so one common predator behavior is to slow down the rate of foraging to save energy while attaining a certain level of consumption (Werner and Anholt, 1993; Giacomini et al., 2013), resulting in a negative metabolic response. If the chosen behavior is to increase effort, the result is a positive metabolic response. The functional response affects both populations directly through their exchange of energy. The metabolic response will affect the prey population only indirectly as a consequence of the predator’s adjustment in their own rate of energy loss. The two responses are nonetheless intrinsically linked as food consumption and metabolic expenditure are jointly determined by foraging effort.

FIGURE 1

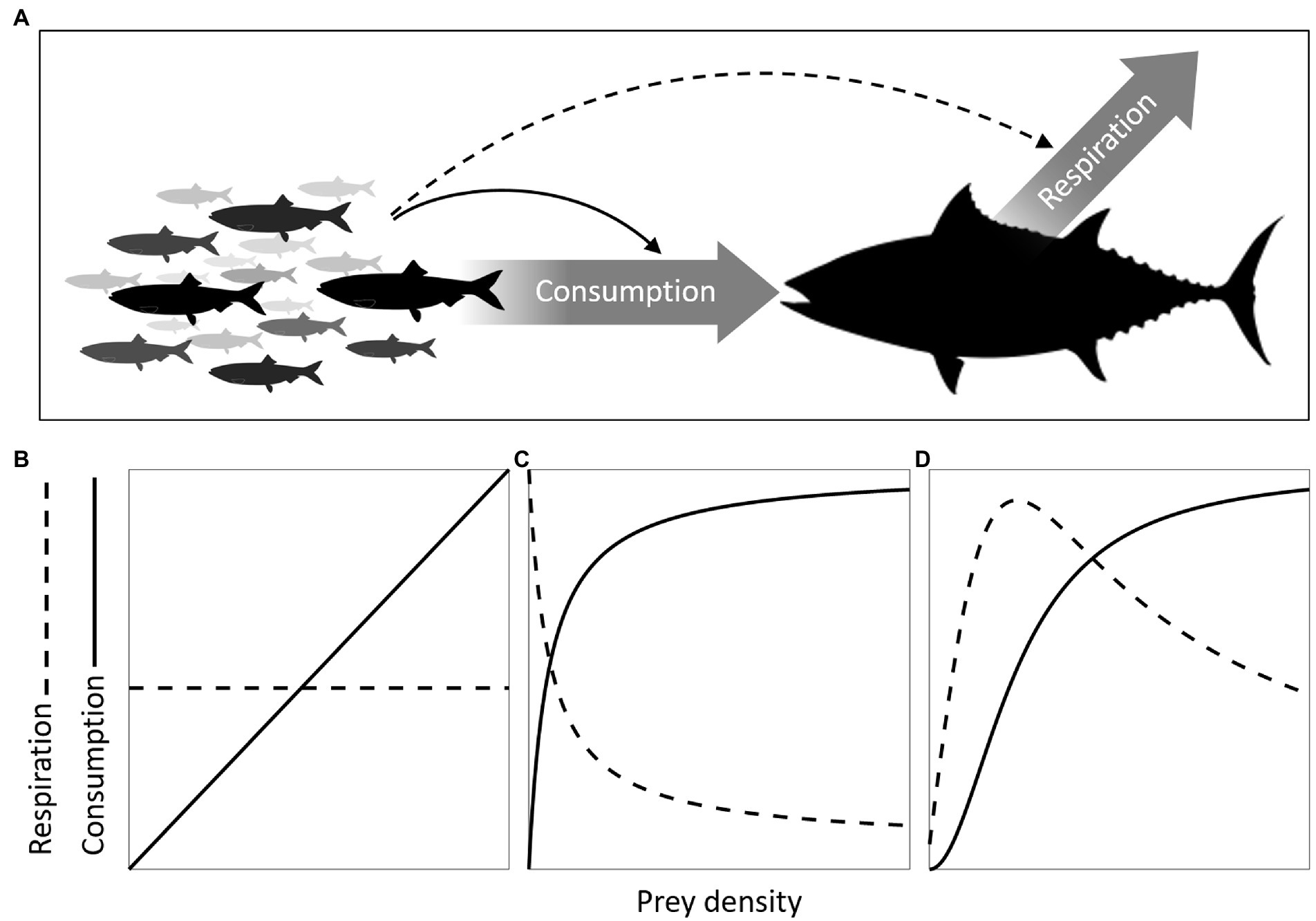
Figure 1. Functional and metabolic responses. (A) two major components of energy flow in predator organisms are food consumption and respiration rates (thick arrows). Prey density can influence predator dynamics through its influence on consumption (continuous arrow) and/or its influence on respiration (dashed arrow), configuring the functional and metabolic responses, respectively. As both responses can be mediated by changes in foraging effort, the three typical functional response curves (I, II, and III, Holling, 1959a) can be linked to their expected metabolic response counterparts (B–D). A type I functional response is the simplest and results from constant foraging effort leading to prey encounter rates that are proportional to prey density (B, continuous line), so the associated type I metabolic response is a constant (dashed horizontal line). A type II functional response is characterized by saturation of consumption rates at high prey densities (C). The associated type II metabolic response is a hyperbolic decline in metabolic expenditure (a negative response), reflecting a decline in the foraging effort required to reach a certain level of consumption as prey density increases. This same decline in foraging also explains the decelerating shape of the functional response (see the Supplementary material for mathematical derivation). In some cases, if prey density decreases to very low levels, it can be beneficial for the forager to slow down the rate of foraging and save energy. This results in a hump-shaped relationship between prey density and foraging effort and consequently a hump-shaped metabolic response (D), which is a type III metabolic response as the functional response emerging from the same foraging strategy has the characteristic sigmoidal shape. These associations between functional and metabolic response types are not supposed to be rigid though, they were chosen as archetypical expectations assuming both responses result solely from changes in foraging effort. Other associations may be possible in circumstances where functional responses are shaped by different factors.

Accounting for metabolic responses is especially relevant if a metabolic interpretation is given to consumption saturation. Maximum consumption rates can result from prey handling time limitation, as originally proposed for type II functional responses (Holling, 1959b). However, for a wide range of predators maximum consumption rates are determined by digestion limitation (Jeschke et al., 2002), which is assumed by many models to be set by metabolic rate, at least for broad comparisons between species and for time scales that are applicable to population dynamics (Peters, 1983; Yodzis and Innes, 1992; Jeschke et al., 2002; van Gils et al., 2005; Koen-Alonso, 2007; Otto et al., 2007; Brose, 2010; Hartvig et al., 2011; Rossberg, 2013; Papanikolaou et al., 2014, 2020). As argued by Jeschke et al. (2002), digestion is a background process, so foraging and capturing prey is still possible while digesting others. The most plausible mechanism for consumption saturation, which is also the assumed mechanism leading to a Holling type II response, is thus a decline in foraging effort as prey density goes up and hunger level goes down (Holling, 1966; Munk, 1995; Jeschke et al., 2002). The alternative, keeping foraging effort constant despite increases in prey density, would imply a nearly satiated predator spending unnecessary energy just to reject many useless prey encounters, and is therefore maladaptive and unrealistic. If we accept that changes in foraging effort form the mechanistic basis for saturating functional responses, we have also to accept that they should be accompanied by changes in metabolic costs if we abide to the Second Law of thermodynamics, or the principle by which energy transformations always incur losses through heat. Even if consumption rate is limited by prey handling, the mechanism for saturation would still involve adjustments in foraging: the longer the time spent handling prey, the less time there is available to search for them. The only scenario allowing for no variation of energetic expenditure in this case would be if the energetic cost per unit time were the same for handling and searching, which is too unlikely to be of general relevance. Therefore, models that impose consumption saturation in functional responses but ignore metabolic responses can be interpreted as making a difficult choice between two options: (i) to ignore the Second Law and assume that foraging effort and metabolic costs are not related, versus (ii) to follow the Second Law, but leave the changes in metabolic costs out of the model, in which case it cannot be claimed to fully account for mass balance in the system and thus violates the First Law of thermodynamics, or the principle of energy conservation.

Empirical evidence for metabolic responses comes from two main sources: (i) the widespread evidence that consumer organisms adjust foraging effort to varying prey density or quality, and (ii) the inevitable energetic costs associated with such an effort, as verified by a myriad of studies on bioenergetics. Adjustments in foraging have been observed both in the laboratory and in the field for a variety of taxa including birds (Cairns, 1987; Burger and Piatt, 1990; Bryant and Tatner, 1991; Tinbergen and Dietz, 1994; Thomas et al., 2001; Jodice et al., 2002, 2006; Tieleman and Williams, 2002; Fraser and Hofmann, 2003), mammals (Boyd, 1999; Hanya, 2004; Goldbogen et al., 2011; Shiratsuru et al., 2021), reptiles (Huey and Pianka, 1981; Formanowicz Jr et al., 1989), amphibians (Jaeger and Barnard, 1981; Anholt and Werner, 1995; Anholt et al., 2000), fish (Munk, 1995; Metcalfe et al., 1999; Pazzia et al., 2002; Sherwood et al., 2002; Biro et al., 2003; Iles and Rasmussen, 2005; Kaufman et al., 2006; Killen et al., 2007; Cruz-Font et al., 2019), and invertebrates (Formanowicz, 1982; Formanowicz Jr and Bradley, 1987; Kohler and McPeek, 1989; Johansson, 1991; Hirvonen, 1999; Kreiter and Wise, 2001; Scharf et al., 2011). In most of these examples, foraging effort decreases with increasing prey density, configuring a negative response. The energetic costs of activity, of which foraging is an important component, can in turn make up a large portion of total metabolic costs in the field. For example, Christian et al. (1997) estimated that the proportion of energy used for activity is >50% for most of their studied lizard species in the field, some reaching 80%, and sustained field metabolic rates were 1.1 to 5.1 times the resting metabolic rate. A similar picture emerged from a review of 37 vertebrate species by Peterson et al. (1990), including ecto-and endotherms, with most sustained metabolic rates being 1.5 to 5 times resting metabolic rates. Some are nearly 7 times the resting rate, which is close to maximum metabolism, as observed in breeding birds (Birt-Friesen et al., 1989; Peterson et al., 1990; Bryant and Tatner, 1991) and in Antarctic fur seals (Costa et al., 1989). Active metabolism is also an important part of the energy budget in fish, being responsible in some populations for most of the observed variation in growth (Boisclair and Leggett, 1989; Aubin-Horth et al., 1999; Sherwood et al., 2002; Rennie et al., 2005). These examples highlight that there is a large scope for variation in energy expenditure if adjustments in foraging are required. Such changes in metabolism may even be the predominant way by which the energy budget of many predators is affected by fluctuations in prey density. This conclusion is supported by examples in which prey encounter rate or consumption rate varies little in the wild despite broad ranges of prey density (Eby et al., 1995; Turesson and Brönmark, 2007), and more extensive evidence that consumers can be close to satiation despite experiencing low food availability (MacKenzie et al., 1990; Jeschke et al., 2002; Jeschke, 2007). The strategy of varying foraging effort to keep nearly constant consumption levels is also likely to be adaptive. For predators with size-structured diet, which is the case of fish and many other aquatic organisms, this constant satiation strategy is optimal under most of the biologically plausible range of life history parameters, prey community structure, and productivity in aquatic systems (Giacomini et al., 2013; Cruz-Font et al., 2019).

In this paper, I present an overview of the dynamical consequences of metabolic responses for predator–prey systems and food webs. The emphasis is on the implications for stability, including the frequency and amplitude of oscillations, and populations’ responses to direct and indirect press perturbations, such as harvesting and the resulting trophic cascades. Stability is one of the most important indicators of how an ecological system behaves in time and how it responds to perturbations, being defined in several ways but most commonly in ecological theory as the local stability of equilibrium points (Pimm, 1984; McCann, 2000); and because more stable systems are more likely to persist, understanding stability can also shed light into the structure of existing ecological communities (Borrelli et al., 2015). In the following, I start with a simple analytical model of predator–prey dynamics. The analysis is then extended numerically to complex food webs using a Generalized Modeling approach (Gross and Feudel, 2006; Gross et al., 2009), and finally to a modified Rosenzweig–MacArthur predator–prey model to illustrate the patterns predicted by the more general, analytical model. Along the way, I trace parallels with functional responses and show how the interpretation of their own effects on food web stability is contingent on the inclusion or not of metabolic responses. Even though the focus here is on predation, along the same line as the early approach to functional responses by Holling (1959a, 1966), the theory and results are applicable to other types of consumer-resource interactions, including herbivory and parasitism.

Implications for dynamics

A general predator–prey model

Here I use the terms biomass, energy, and density interchangeably, as is usually done for studies of food web or ecosystem dynamics. It is convenient to start with a simple and general model representing the rate of change in prey biomass ($B_1$) and predator biomass ($B_2$) as a system of differential equations:

$\begin{array}{ll}{G}_1=\frac{d{B}_1}{dt}=R{B}_1-F{B}_2& (1)\end{array}$

$\begin{array}{ll}{G}_2=\frac{d{B}_2}{dt}=\eta F{B}_2-M{B}_2& (1)\end{array}$

The rate of change in the prey population ($G_1$) depends firstly on its direct net biomass input ($R{B}_1$), which is the product of the prey biomass $B_1$ and a mass-specific input rate ($R$). $R$ could be divided into a birth and growth rate component and a non-predatory mortality component but is here represented as a single rate for simplicity. The second term determining the prey population change is the mortality caused by predation, whose rate is $F{B}_2$, the product of the predator mass-specific food consumption rate ($F$) and the predator biomass $B_2$. The predator rate of change ($G_2$) is the difference between the total energy assimilated ($\eta F{B}_2$, where $\eta$ is the food assimilation efficiency) and the total biomass losses ($M{B}_2$). $M$ is the mass-specific rate of biomass loss, which can be further divided into a metabolic expenditure (or respiration) component and a mortality component (biomass losses from deceased individuals). To further simplify analysis, I assume that $M$ is entirely determined by metabolic expenditure. This assumption should be a good enough approximation as respiration is a major component of energy losses, comparable if not greater than non-predatory mortality, especially for long-lived predator species. Most importantly, including a separate term for mortality would not alter the main conclusions, having the same influence as increasing the relative contribution of a prey-independent component of metabolic losses, such as standard or basal metabolism. Although it may weaken the relative strength of the metabolic response, it does not change the existence or direction of effects demonstrated in this and the next sections.

The dynamical behavior of the predator–prey system depends on how the mass-specific rates vary as a function of the biomasses of both prey and predator. The prey input rate $R$ can then be expressed as $R\left(B_1,B_2\right)$. The dependence of $R$ on $B_1$, whose direction and magnitude are measured by the partial derivative $\partial R/\partial B_1$, expresses the direct density dependence of prey growth, usually through population self-limitation ($\partial R/\partial B_1$< 0) which is most commonly represented by the logistic growth equation (Kingsland, 1995; Begon and Townsend, 2020). The dependence of $R$ on $B_2$, measured as $\partial R/\partial B_2$, incorporates non-consumptive effects of predators on prey (Lima, 1998; Peckarsky et al., 2008), and generally involves fear-driven behavioral adjustments of prey leading to decreased foraging and growth ($\partial R/\partial B_2$< 0). The function defining variation in consumption rate, $F\left(B_1,B_2\right)$, characterizes the functional response. Its prey dependence, $\partial F/\partial B_1$, has been described by many different functions (Jeschke et al., 2002) including the classical Holling type I, II, and III functional responses. Predator-dependence ($\partial F/\partial B_2$) has also received a great deal of attention (Abrams and Ginzburg, 2000; Skalski and Gilliam, 2001), and generally involve interference between competing predators negatively affecting consumption rates ($\partial F/\partial B_2<$ 0). Predator interference can also affect growth negatively through the energy loss term $M\left(B_1,B_2\right)$, for instance through increased stress or activity required to chase off competitors and defend territories (Heath et al., 2014), leading to a direct form of density-dependence ($\partial G_2/\partial B_2<$ 0 through $\partial M/\partial B_2>$ 0). Metabolic responses are manifested as prey-dependence of the energy loss term, i.e., $\partial M/\partial B_1$. To simplify notation, this derivative will be represented by $m$. Except for metabolic responses, all prey or predator-dependent terms described above have been studied for their effects on the dynamical stability and trophic cascades in food webs. It is also worth noting that, although the prey-dependences of both the functional and the metabolic response are mutually determined by foraging activity, this aspect will be omitted from the analysis of this simple predator–prey system as it does not affect either the results or the interpretation. It becomes relevant for the food web analysis and will be explicitly incorporated there.

In the following section I analyze the local stability of equilibrium states, which determines their response to small pulse perturbations, and later how the equilibrium state is affected by press perturbations in either the focal or interacting species. They can both be determined from the Jacobian matrix of the dynamical system at equilibrium, also known as the community matrix (May, 1973; Yodzis, 1988):

$\begin{array}{c}J={\left[\begin{array}{cc}\frac{\partial G_1}{\partial B_1}& \frac{\partial G_1}{\partial B_2}\\ \frac{\partial G_2}{\partial B_1}& \frac{\partial G_2}{\partial B_2}\end{array}\right]}_{\ast }\\ =\left[\begin{array}{cc}{B}_1^{\ast }{\frac{\partial R}{\partial B_1}|}_{\ast }+R^{\ast }-B_2^{\ast }{\frac{\partial F}{\partial B_1}|}_{\ast }& B_1^{\ast }{\frac{\partial R}{\partial B_2}|}_{\ast }-B_2^{\ast }{\frac{\partial F}{\partial B_2}|}_{\ast }-F^{\ast }\\ B_2^{\ast }\left(\eta {\frac{\partial F}{\partial B_1}|}_{\ast }-{\frac{\partial M}{\partial B_1}|}_{\ast }\right)& B_2^{\ast }\left(\eta {\frac{\partial F}{\partial B_2}|}_{\ast }-{\frac{\partial M}{\partial B_2}|}_{\ast }\right)+F^{\ast }-M^{\ast }\end{array}\right]\end{array}\text{ (2)}$

Each term $J_{ij}$ in the Jacobian gives the first degree or linear effect of species $j$ on the growth rate of species $i$ evaluated at the system equilibrium (indicated by *). The only term affected by the metabolic response is $J_{21}=\frac{\partial G_2}{\partial B_1}=B_2^{\ast }\left(\eta {\frac{\partial F}{\partial B_1}|}_{\ast }-{\frac{\partial M}{\partial B_1}|}_{\ast }\right)$, which gives the effect of prey density on predator’s growth and is in general positive. The contribution of the metabolic response $\left({m^{\ast }=\frac{\partial M}{\partial B_1}|}_{\ast }\right)$ to this interaction term will depend on whether the response is positive or negative. Hereby I will emphasize negative metabolic responses; the conclusions regarding the direction of effects will be exactly the opposite for positive responses. All other terms being equal, a negative metabolic response of increasing magnitude has the effect of increasing $J_{21}$, making it more positive, which implies a strengthening of the predator–prey interaction.

Local stability of the predator–prey system

To analyze the stability of a system’s equilibrium, we must assume the equilibrium is feasible in the first place: $B_1^{\ast }>0$ and $B_2^{\ast }>0$. By principle, the feasibility of equilibrium points is not be affected by metabolic responses because it is determined by the overall metabolic levels only, given by $M^{\ast }$. For any feasible equilibrium point ($B_1^{\ast }$,$B_2^{\ast }$) there exists a constant $M^{\ast }$ that could replace the metabolic function evaluated at that point, ${M\left(B_1,B_2\right)|}_{\ast }$, so the specific function or its derivative does not matter in this case. The same is valid for functional responses: what matters for feasibility is the overall consumption level at the equilibrium $F^{\ast }$, not its dependence on the prey or predator densities.

Local stability of the predator–prey system is indicated by the eigenvalues of J, given by ${\lambda }_{1,2}=\left(\tau \pm \sqrt{{\tau }^2-4\Delta }\right)/2$ (Strogatz, 2018), where $\tau =J_{11}+J_{22}$ is the trace of J (the sum across its main diagonal) and $\Delta =J_{11}{J}_{22}-J_{21}{J}_{12}$ is its determinant. The system has a locally stable equilibrium if both real parts of ${\lambda }_{1,2}$ are negative, which in this two-species case depends only on the trace, and if the determinant Δ is positive (Strogatz, 2018). The transition from negative to positive $\tau$ configures a Hopf bifurcation, changing the system from a stable equilibrium point to a limit cycle where both predator and prey populations fluctuate indefinitely. As $\tau$ does not contain the interaction term $J_{21}$, the metabolic response is not involved in Hopf bifurcations, therefore not contributing qualitatively to the occurrence of limit cycles in a simple predator–prey system. However, $J_{21}$ does affect the determinant Δ, which in turn can affect the quantitative behavior of cycles and other oscillations. Given that the product $J_{21}{J}_{12}$ is in general negative because the effect of prey on predator’s growth and the effect of predator on prey’s growth have opposite signs, the interaction term $J_{21}$ is expected to increase Δ, i.e., $\partial \Delta /\partial J_{21}>0$, and therefore $\partial \Delta /\partial m^{\ast }<0$.

For $\Delta >0$, increases in $J_{21}$ enhance the chance that the eigenvalues form a complex number conjugate (if ${\tau }^2-4\Delta <0$), with a common real part given by $\tau /2$ and imaginary parts given by $\pm i\sqrt{4\Delta -{\tau }^2}/2$. This transition from real to complex number marks the transition from non-excitable to excitable dynamics (McCann, 2011). A stable but excitable system oscillates in its trajectory toward the equilibrium state after a perturbation. Imaginary parts with greater magnitudes lead to faster oscillations. For unstable systems ($\tau <0$), these magnitudes are inversely proportional to the period of predator–prey cycles (Yodzis and Innes, 1992). Thus, by positively affecting $\Delta$, negative metabolic responses increase the chance that a stable system will oscillate before reaching equilibrium, besides increasing the frequency of cycles in unstable systems. A non-excitable system, in contrast, returns to equilibrium monotonically, without any fluctuation. This happens when both eigenvalues are real numbers. The largest of them, given by ${\lambda }_1=\left(\tau +\sqrt{{\tau }^2-4\Delta }\right)/2$, determines how quickly the system returns to equilibrium: its magnitude increases with Δ and is inversely proportional to return time (Pimm, 1982). This implies a quicker return to equilibrium, or greater resilience, in the presence of negative metabolic responses if the system is non-excitable.

Finally, for this simple predator–prey system, the determinant Δ can affect stability through a saddle-node bifurcation (McCann, 2011; Strogatz, 2018). The transition from a stable equilibrium point to a saddle occurs when Δ becomes negative ($J_{11}{J}_{22}-J_{21}{J}_{12}<0$). When the equilibrium point is a saddle, after a small perturbation the system will return to equilibrium along only one of the dimensions (e.g., the predator), but will depart away from that point in either direction along the other dimension (e.g., the prey), leading to an alternative equilibrium at a higher biomass or leading to extinction. This could happen, for example, if the prey is subjected to strong Alee effects (Stephens and Sutherland, 1999), meaning its population is under positive density dependence at or near the equilibrium (${J_{11}=\frac{\partial G_1}{\partial B_1}|}_{\ast }>0$). This in turn can make the first product of the determinant, $J_{11}{J}_{22}$, become negative if predators have the usual negative density dependence ($J_{22}<0$), and if the second product ($J_{21}{J}_{12}$, generally negative) has a small enough magnitude. The latter is plausible to occur if predators are efficient foragers with a functional response that saturates quickly, so that ${\frac{\partial F}{\partial B_1}|}_{\ast }\approx 0$. Negative metabolic responses can alleviate this effect by increasing the magnitude of $J_{21}$, preventing Δ from becoming negative. What this means is that the presence of a metabolic response enhances the feed-back between predator and prey populations, increasing the effect of the prey’s changing biomass on the predator’s growth when it would otherwise be negligible. This could also mean an enhanced global stability or permanence of the predator–prey system by preventing a prey’s runaway toward extinction when under the pressure of Alee effects and predators with saturated functional responses.

Local stability of a generalized food web model

For more realistic food webs containing three or more species, local stability depends in a more complicated manner on the community matrix J’s diagonal and non-diagonal terms (May, 1973; Allesina and Tang, 2012). In this case, metabolic responses can and do contribute to changes in qualitative stability, including the occurrence of Hopf bifurcations. To assess such contribution in large food webs, whose complexity prevents analytical solution of the community matrix eigenvalues, I used a Generalized Modeling (GM) approach (Gross and Feudel, 2006; see details in the Supplementary material). It is based on an even more general model version of Equation (1a and 1b) representing the growth of each species $i$ as:

$\begin{array}{l}\frac{d{B}_i}{dt}=B_i\left[S_i\left(B\right)+{\eta }_i{F}_i\left(B\right)-M_i\left(B\right)-{\displaystyle \sum }_{k=1}^N{L}_{k,i}\left(B\right)\right]\\ \mathrm{for}i=1,\dots ,N\end{array}\text{ (3)}$

where $S$ is the mass-specific rate of primary production (if the species is a primary producer); $F$ is the mass-specific rate of food consumption (if the species is a consumer); $\eta$ is food assimilation efficiency; $M$ is the mass-specific rate of energy loss from causes other than predation, which includes prey-dependent active metabolism; and $L_{k,i}$ is the mass-specific rate of energy loss through predation by species $k$ on $i$. Each one of these rates are functions of potentially every species in the community, whose biomasses are represented by the vector $B=\left\{B_1,\dots ,B_N\right\}$. The simple predator–prey model described by Equation (1) can be derived from Equation (3) through the relationships: $S_1\left(B\right)+{\eta }_1{F}_1\left(B\right)-M_1\left(B\right)=R$ and $B_1{\displaystyle \sum }_{k=1}^N{L}_{k,1}\left(B\right)=F{B}_2$ for prey growth; $S_2\left(B\right)=0$, ${\eta }_2{F}_2\left(B\right)=\eta F$, $M_2\left(B\right)=M$, and ${\displaystyle \sum }_{k=1}^N{L}_{k,2}\left(B\right)=0$ for predator growth.

GM allows the efficient computation of the community matrix numerically for a very large number of parameter combinations, without the need to explicitly determine equilibrium states. It does so by normalizing all state variables and rates of population change by their respective equilibrium values. The resulting parameters have clear biological interpretation and can be distinguished between (i) scale parameters, which include turnover rates and fractions (for instance, the fraction of total energy loss due to predation), and (ii) elasticity parameters. Elasticities give a normalized measure of the responsiveness of a given rate, such as consumption, to species densities or other state variables. For instance, the elasticity related to the functional response of species $i$ is given by ${\gamma }_i={\frac{\partial F_i}{\partial O_i}|}_{\ast }{\left(\frac{F_i^{\ast }}{O_i^{\ast }}\right)}^{-1}$, where $O_i$ is the total biomass of all prey available to $i$. This is equivalent to the slope of log-consumption with respect to log-prey biomass at equilibrium, ${\gamma }_i={\frac{\partial \log \left(F_i\right)}{\partial \log \left(O_i\right)}|}_{\ast }$, and for this reason elasticities are also called exponent parameters (Yeakel et al., 2011). If $\gamma =1$ the functional response is linear (type I response or type II at very low prey density), whereas $\gamma <1$ indicates a saturating functional response (type II or type III at high prey density, $\gamma =0$ implies complete saturation) and $\gamma >1$ indicates an accelerated functional response at equilibrium (type III at low prey density). Likewise, the elasticity of the metabolic response is derived as ${\frac{\partial M_i}{\partial O_i}|}_{\ast }{\left(\frac{M_i^{\ast }}{O_i^{\ast }}\right)}^{-1}$ or ${\frac{\partial \log \left(M_i\right)}{\partial \log \left(O_i\right)}|}_{\ast }$.

These two elasticities are connected through changes in foraging activity levels. It is therefore useful to represent consumption and metabolism as explicit functions of activity, which in turn is a function of prey biomass: $F=F\left(V\left(O\right),O\right)$ and $M=U\left(V\left(O\right)\right)+D$. Here $V\left(O\right)$ represents foraging activity rate, which is a combined result of the proportion of time active and the average speed while active. Total energy loss $M$ is split between a prey-dependent active metabolism component $U\left(V\left(O\right)\right)$ and a prey-independent component $D$ that represents basal metabolism, but which may also be used to represent death by causes other than predation. Consumption is a function of both activity and prey biomass alone because, in principle, it can vary with prey biomass through changes in encounter rates for any fixed activity. Using the chain rule, the full elasticity of the functional response is given by ${\gamma }_i={\delta }_i{\omega }_i+{\gamma }_i^{\ast }$ (Supplementary material), where ${\delta }_i$ is the elasticity of food consumption with respect to activity, ${\omega }_i$ is the elasticity of activity with respect to prey biomass, and ${\gamma }_i^{\ast }$ is the elasticity of consumption with respect to prey biomass independently of activity. The full elasticity of the metabolic response is given by ${\xi }_i={\epsilon }_i{\zeta }_i{\omega }_i$, where ${\epsilon }_i$ is the relative contribution of active metabolism to total energy loss (a scale parameter) and ${\zeta }_i$ is the elasticity of active metabolism with respect to activity rate. Here, I will focus on changes in elasticities caused by changes in activity, keeping ${\delta }_i$ and ${\gamma }_i^{\ast }$ constant, and investigate how stability is affected by the resulting functional and metabolic responses.

The Jacobian matrix resulting from the generalized model is defined by the following non-diagonal elements describing the effect of species $j$ on species $i$:

$J_{ij}={\alpha }_i\left\{\begin{array}{l}{\nu }_{i,j}{\chi }_{{}_{i,j}}\left[{\rho }_i\left({\delta }_i{\omega }_i+{\gamma }_i^{\ast }\right)-\left(1-{\sigma }_i\right){\epsilon }_i{\zeta }_i{\omega }_i\right]\\ -{\sigma }_i\left[{\beta }_{j,i}{\psi }_j+{\displaystyle {\sum }_{k=1}^N{\beta }_{k,i}{\nu }_{k,j}{\chi }_{{}_{k,j}}}\left({\delta }_k{\omega }_k+{\gamma }_k^{\ast }-1\right)\right]\end{array}\right\}\text{ (4a)}$

and the diagonal elements:

$\begin{array}{l}{J}_{ii}={\alpha }_i\left\{\left(1-{\rho }_i\right){\varphi }_i+{\nu }_{i,i}{\chi }_{{}_{i,i}}\left[{\rho }_i\left({\delta }_i{\omega }_i+{\gamma }_i^{\ast }\right)-\left(1-{\sigma }_i\right){\epsilon }_i{\zeta }_i{\omega }_i\right]\right.\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}+{\rho }_i{\psi }_i-\left(1-{\sigma }_i\right){\mu }_i\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\left.-{\sigma }_i\left[{\beta }_{i,i}{\psi }_i+{\displaystyle {\sum }_{k=1}^N{\beta }_{k,i}{\nu }_{k,i}}\left[{\chi }_{k,i}\left({\delta }_k{\omega }_k+{\gamma }_k^{\ast }-1\right)+1\right]\right]\right\}\end{array}\text{ (4b)}$

where ${\alpha }_i$ is the biomass turnover rate of species $i$; ${\rho }_i$, ${\sigma }_i$, ${\beta }_{k,i}$, and ${\chi }_{k,i}$ are scale parameters representing, respectively, the contribution of food consumption to biomass gain, the contribution of predation mortality to total biomass loss, the contribution predator species $k$ to total predation losses of species $i$, and the contribution of prey $i$ to the total amount of prey available to species $k$; ${\nu }_{k,i}$, ${\varphi }_i$, ${\mu }_i$, and ${\psi }_i$ are elasticity parameters representing, respectively, the nonlinearity of the contribution of prey $i$ to the diet of predator $k$ (a prey switching parameter), the sensitivity of primary production, the sensitivity of non-predatory energy loss, and the sensitivity of food consumption with respect to the species’ own biomass. A more detailed explanation of these parameters, the derivation of Equation (4a and 4b), and the description of procedures used for simulations can be found in the Supplementary material.

Before delving into the effects of functional and metabolic responses, it is worth honing in on a scale parameter that mediates these effects and is critical for understanding the consequences for stability: the relative contribution of predation mortality to the total energy loss in a population, defined as ${\sigma }_i={\displaystyle {\sum }_{k=1}^N{L}_{k,i}^{\ast }/}\left(M_i^{\ast }+{\displaystyle {\sum }_{k=1}^N{L}_{k,i}^{\ast }}\right)$. In the seminal work of Gross et al. (2009) that assessed the effects of GM parameters on food web stability, it was assumed that ${\sigma }_i=1$, except for top predators, which had ${\sigma }_i=0$, meaning all losses in basal species or intermediate consumers came from predation. However, when we include metabolic expenditure explicitly as a major component of the energy loss term $M$, the asumption of ${\sigma }_i=1$ does not hold as realistic anymore (Plitzko et al., 2012). It would imply that trophic transfer efficiency, defined as the biomass production ratio between consecutive trophic levels, is identical to food assimilation efficiency ${\eta }_i$ (Supplementary material), which for many predators including carnivores can be higher than 80% (Yodzis and Innes, 1992). But trophic transfer efficiency generally sits around 10% in natural ecosystems (Lindeman, 1942; Odum, 1971; Pauly and Christensen, 1995; Barnes et al., 2010), and varying ${\sigma }_i$ toward more realistic values can substantially change the conclusions regarding stability. Firstly, the generally accepted result that more saturated functional responses lead to less stable food webs is contingent on high values of ${\sigma }_i$. This is illustrated in Figure 2 for simulated food webs containing 20 species and 40 trophic links (10% connectance). Whereas increasing ${\gamma }_i$ increases the proportion of stable webs (PSW) when ${\sigma }_i=1$ (Figure 2A), the opposite is true for low ${\sigma }_i$ in the range 0.1–0.3 and for almost the entire range of ${\gamma }_i$ (Figure 2B). Under low ${\sigma }_i$, the positive relationship between stability and ${\gamma }_i$ is realized only when metabolic responses are accounted for, being more positive for stronger responses.

FIGURE 2

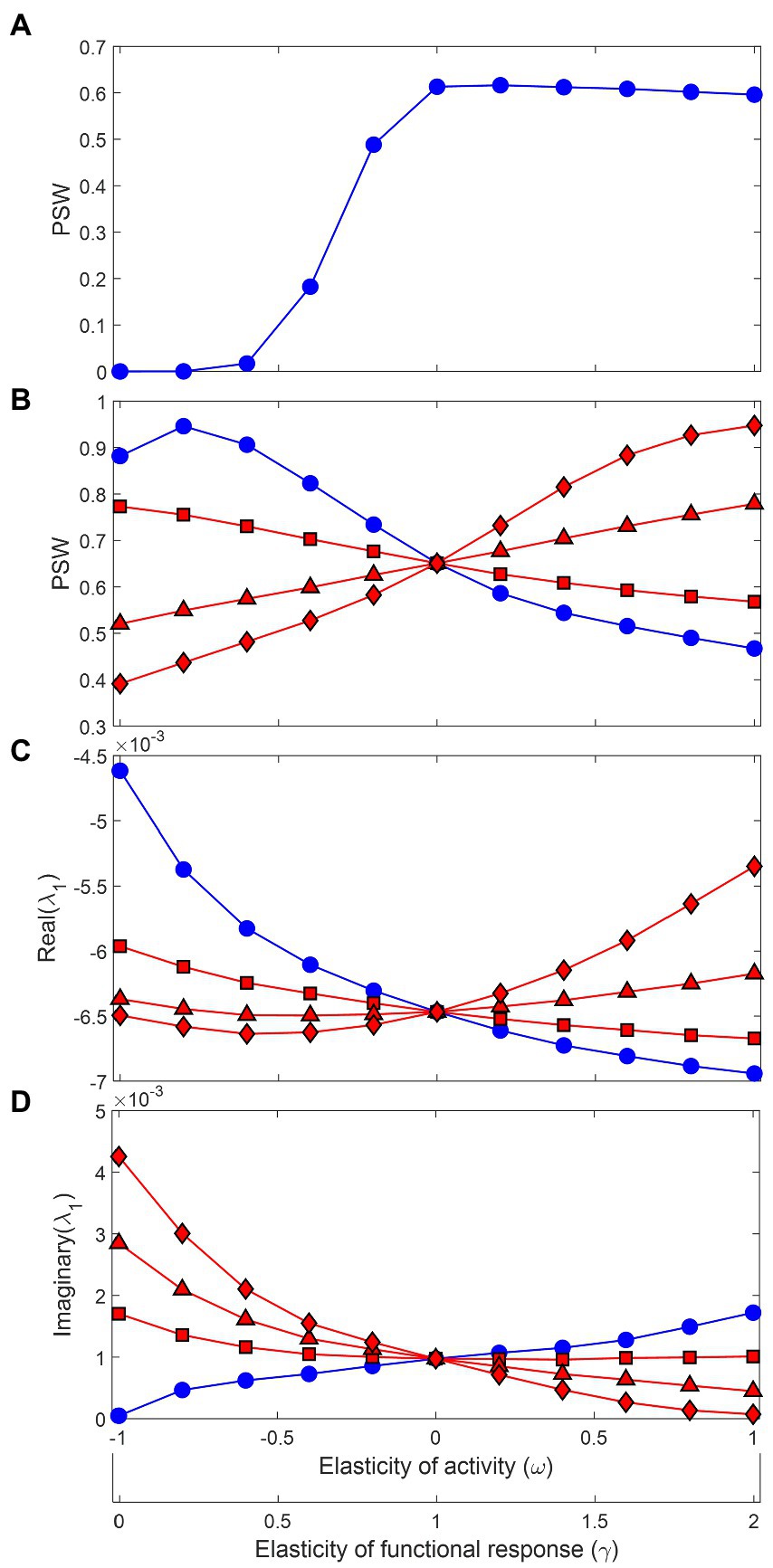
Figure 2. Stability from Generalized Modeling of community matrices generated by 10⁶ random parameter combinations. The x-axis represents changes in the elasticity of foraging activity with respect to prey density ($\omega$), from inversely proportional ($\omega =-1$) to proportional ($\omega =1$). It also shows the associated change in the elasticity of the functional response ($\gamma$), from a completely saturated functional response ($\gamma =0$, type II or type III at high prey densities), going through a locally linear response in the middle ($\gamma =1,$a type I response or type II at very low prey density), to a strongly accelerating functional response ($\gamma =2$, type III at low prey densities). In (A) and all other blue curves in B-D, the metabolic response is non-existent, which was done by setting the elasticity of active metabolism with respect to foraging activity to zero ($\zeta =0$). When the scale parameter $\sigma$ measuring the contribution of predation mortality to total energy loss is set to 1 (except for top predators), as in Gross et al. (2009), the proportion of stable webs (PSW) increases with the functional response elasticity, meaning accelerating responses are stabilizing. The relationship is reversed if $\sigma$ is set to a lower range of 0.1–0.3 (B, blue curve) and is reversed again if metabolic responses are included (red curves): $\zeta =1$ (squares), $\zeta =2$ (triangles), $\zeta =3$ (diamonds). The resulting mean real and imaginary parts of the dominant eigenvalues of the community matrices are presented in (C) and (D).

This contingency of food web stability on the relative level of predation mortality and the metabolic response can be understood by scrutinizing the elements of the community matrix J. Each element $J_{ij}$ in Equations (4a and 4b) can be simplified as the difference between two terms: $J_{ij}=A_{ij}-{\sigma }_i{\mathcal{B}}_{ij}$, each term being a function of several elasticity and scale parameters. I explicitly represented the multiplication ${\sigma }_i{\mathcal{B}}_{ij}$ in the second term to emphasize its dependence on the scale parameter ${\sigma }_i$. The first term ${\mathcal{A}}_{ij}$ describes mainly the positive effects of $j$ as a prey of $i$, including the possibility of cannibalism ($i=j$), whereas the second term ${\sigma }_i{\mathcal{B}}_{ij}$ describes the net effect of $j$ directly as a predator of $i$ or indirectly as a species contributing to predation mortality of $i$ by serving as prey of its predators. For diagonal elements $J_{ii}$, food webs are stabilized by increasing ${\sigma }_i{\mathcal{B}}_{ii}$ and decreasing ${\mathcal{A}}_{ii}$, promoting a negative feedback between population sizes and their own growth. The functional response contributes to changes in both ${\mathcal{A}}_{ij}$ and ${\mathcal{B}}_{ij}$ through its elasticity parameters: saturating responses are characterized by low ${\delta }_i{\omega }_i+{\gamma }_i^{\ast }$, thus having destabilizing effects by decreasing ${\mathcal{B}}_{ii}$ (Equation 4a and 4b) but also stabilizing effects by decreasing ${\mathcal{A}}_{ii}.$ For non-diagonal terms, the chance of a stable food web is enhanced by lower magnitudes $\left|J_{ij}\right|$ (Haydon, 1994). The effects can be more complicated in this case: they follow the opposite direction for negative $J_{ij}$ (e.g., $j$ is predator of $i$), but for positive $J_{ij}$ (e.g., $j$ is prey of $i$) they follow the same direction as predicted for diagonal elements, so it is plausible that the latter prevails overall. For low enough ${\sigma }_i$, the destabilizing effect of saturating functional responses on ${\sigma }_i{\mathcal{B}}_{ij}$ is diminished relative to the potential stabilizing effect on ${\mathcal{A}}_{ij}$. So, in the absence of a metabolic response and counter to prevailing theory, saturating functional responses can increase local stability, as shown in Figure 2B. However, a negative metabolic response has a destabilizing effect by increasing ${\mathcal{A}}_{ij}$ through the negative product ${\epsilon }_i{\zeta }_i{\omega }_i$. So, if changes in foraging leading to functional response saturation are accompanied by the appropriate negative metabolic response, the net effect on ${\mathcal{A}}_{ij}$ can be inverted, resulting in the commonly assumed negative relationship between functional response saturation and stability. This happens not because of the functional response’s own effects, but because the two responses covary through changes in the foraging component ${\omega }_i$.

Other relevant results include: (i) for stable food webs, negative metabolic responses lead to faster return times (more negative dominant eigenvalues, Figure 2C), and (ii) negative metabolic responses lead to more excitable dynamics and more frequent oscillations (higher imaginary part of dominant eigenvalues, Figure 2D). Both results are consistent with the analytical predictions from the simple predator–prey model.

Impacts of press perturbations and trophic cascades

Another important aspect of the system’s dynamical behavior is how its equilibrium or long-term state responds to a press perturbation. Examples of press perturbations include harvesting, the introduction of antagonistic invasive species, or the release of contaminants, which act as additional sources of mortality or energy losses; and nutrient enrichment or stocking, which act as additional sources of energy influx rates. The impact of a press perturbation can be measured as the rate of change in the equilibrium state with respect to the perturbation, given by $I_{ij}=\partial B_i^{\ast }/\partial K_j$ (Yodzis, 1988; Aufderheide et al., 2013), where $K_j$ gives the sign and magnitude of the perturbation, measured as a persistent change in the growth rate of species $j$. The impact can be direct, in which case $i=j$, or indirect, meaning the impacted species is not the target of perturbation ($i\ne j$). The later configures a trophic cascade, which can be bottom-up (a predator impacted by a perturbation on the prey) or top-down (a prey impacted by a perturbation on the predator) (Heath et al., 2014). A description of all impacts $I_{ij}$ in the predator–prey system (Equation 1) is given by the impact matrix I, whose computation depends on the inverse of the community matrix J (Yodzis, 1988) and a diagonal matrix K describing perturbations on either of the two target species (Aufderheide et al., 2013):

$\begin{array}{c}I=-J^{-1}K=-\frac{1}{\Delta }\left[\begin{array}{cc}{J}_{22}& -J_{12}\\ -J_{21}& J_{11}\end{array}\right]\left[\begin{array}{cc}{K}_1& 0\\ 0& K_2\end{array}\right]\\ =\left[\begin{array}{cc}\frac{-J_{22}{K}_1}{\Delta }& \frac{J_{12}{K}_2}{\Delta }\\ \frac{J_{21}{K}_1}{\Delta }& \frac{-J_{11}{K}_2}{\Delta }\end{array}\right]\end{array}\text{ (5)}$

The effect of the metabolic response $m^{\ast }$ on the individual impacts can be assessed by the derivative $\partial I_{ij}/\partial m^{\ast }$. For the direct impact of a perturbation on the prey, $I_{11}$, the derivative depends on the determinant Δ, which is a function of $J_{21}$, the interaction term that includes $m^{\ast }$ (Equation 2). Applying the chain rule, it results in $\frac{\partial I_{11}}{\partial m^{\ast }}=\frac{\partial I_{11}}{\partial \Delta }\frac{\partial \Delta }{\partial J_{21}}\frac{\partial J_{21}}{\partial m^{\ast }}=\frac{K_1{J}_{22}{J}_{12}{B}_2^{\ast }}{{\Delta }^2}$. Because $J_{22}$ and $J_{12}$ will most likely be both negative, and $B_2^{\ast }$ and ${\Delta }^2$ will always be positive, the derivative will have the same sign as the perturbation $K_1$. For example, if an additional harvest mortality is imposed on the prey population ($K_1<0$), increasing the metabolic response of the predator will decrease the impact on the prey $I_{11}$. Given that $I_{11}$ is likely negative in this case (Equation 5: $J_{22}<0,\Delta >0,K_1<0),$ having a more negative metabolic response implies a less negative, lower magnitude impact. This is illustrated in Figure 3, which shows the predicted effects of a negative metabolic response, as opposed to its absence, on all four types of impact $I_{ij}$ when the perturbation is negative. For the direct impact of a perturbation $K_2$ on the predator’s own population, $I_{22}$, the result is similar, as the derivative $\frac{\partial I_{22}}{\partial m^{\ast }}=\frac{K_2{J}_{11}{J}_{12}{B}_2^{\ast }}{{\Delta }^2}$ has the same sign as $K_2$.

FIGURE 3

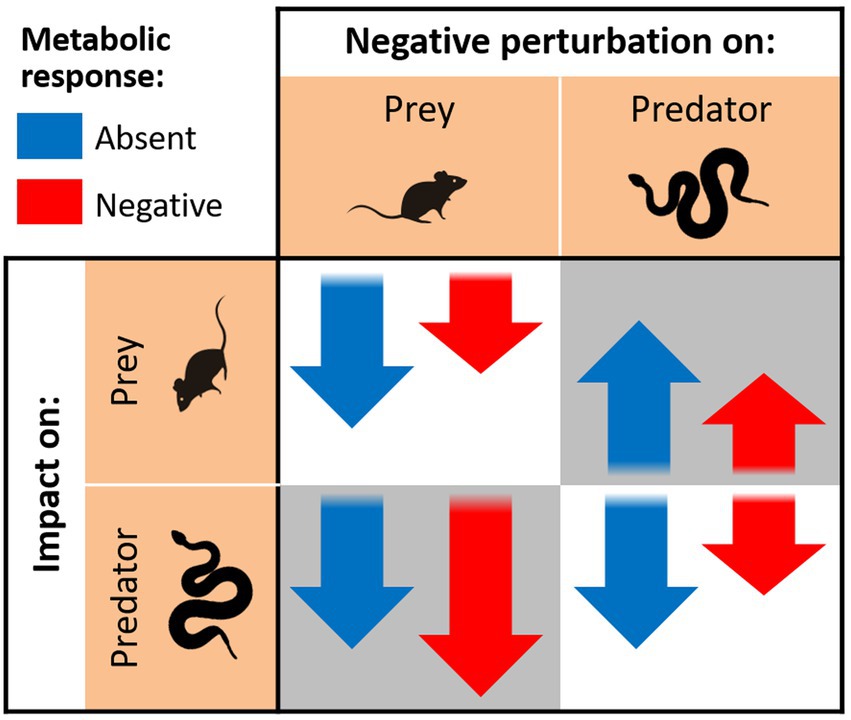
Figure 3. Schematic representation of impacts of negative press perturbations on the equilibrium population sizes of predator and prey. Downward pointing arrows represent negative impacts (declining population) and upward arrows represent positive impacts (increasing population). Arrow sizes represent relative magnitude of impacts, and arrow colors distinguish a scenario without a metabolic response (blue) versus a scenario with a negative metabolic response (red). The background identifies the type of impact, whether direct (white background) or a trophic cascade (gray).

The two types of trophic cascades are nevertheless affected differently. The top-down trophic cascade $I_{12}$ will generally have the opposite sign of the perturbation $K_2$, and the same is true for the derivative $\frac{\partial I_{12}}{\partial m^{\ast }}=-\frac{K_2{J}_{12}^2{B}_2^{\ast }}{{\Delta }^2}$, which means a negative perturbation on the predator will increase prey biomass, but less so in the presence of a negative metabolic response (Figure 3). In contrast, the bottom-up trophic cascade $I_{21}$has the same sign as the perturbation on the prey $K_1$, whereas the derivative $\frac{\partial I_{21}}{\partial m^{\ast }}=-\frac{K_1{J}_{11}{J}_{22}{B}_2^{\ast }}{{\Delta }^2}$ will most likely have the opposite sign, provided the direct density dependence of both prey ($J_{11}$) and predator ($J_{22}$) have the same sign (usually negative). In the presence of a negative metabolic response, the impact $I_{21}$ caused by a negative perturbation $K_1$ should therefore become even more negative, as illustrated in Figure 3.

For positive perturbations, the resulting impacts can be qualitatively derived from Figure 3 by simply inverting the direction of arrows. The main interpretation of results remains unchanged: negative metabolic responses have the effect of dampening the impact of direct perturbations and top-down trophic cascades, while magnifying bottom-up cascades.

To assess how generally these results apply to longer food chains, whose complexity prevents analytical solution of the impact matrix, I used the GM approach described in the previous section. The mean impacts of negative perturbations on a food chain with five trophic levels, resulting from 10⁶ parameter combinations, are shown in Figure 4. This choice of a relatively long food chain is to better illustrate how consistently the impacts and differences between scenarios propagate across trophic levels in both directions. The conclusions are essentially the same for shorter food chains, with three or four trophic levels (Supplementary material). All direct and bottom-up impacts have the same sign as the perturbation (negative), whereas top-down impacts show the characteristic alternation of signs (Oksanen et al., 1981; Heath et al., 2014), as the decline in a predator population releases the prey immediately below, which in turn increases predation and promote the decline of their own prey, and so on. The effects of metabolic responses are the same as those predicted from the analytical predator–prey model.

FIGURE 4

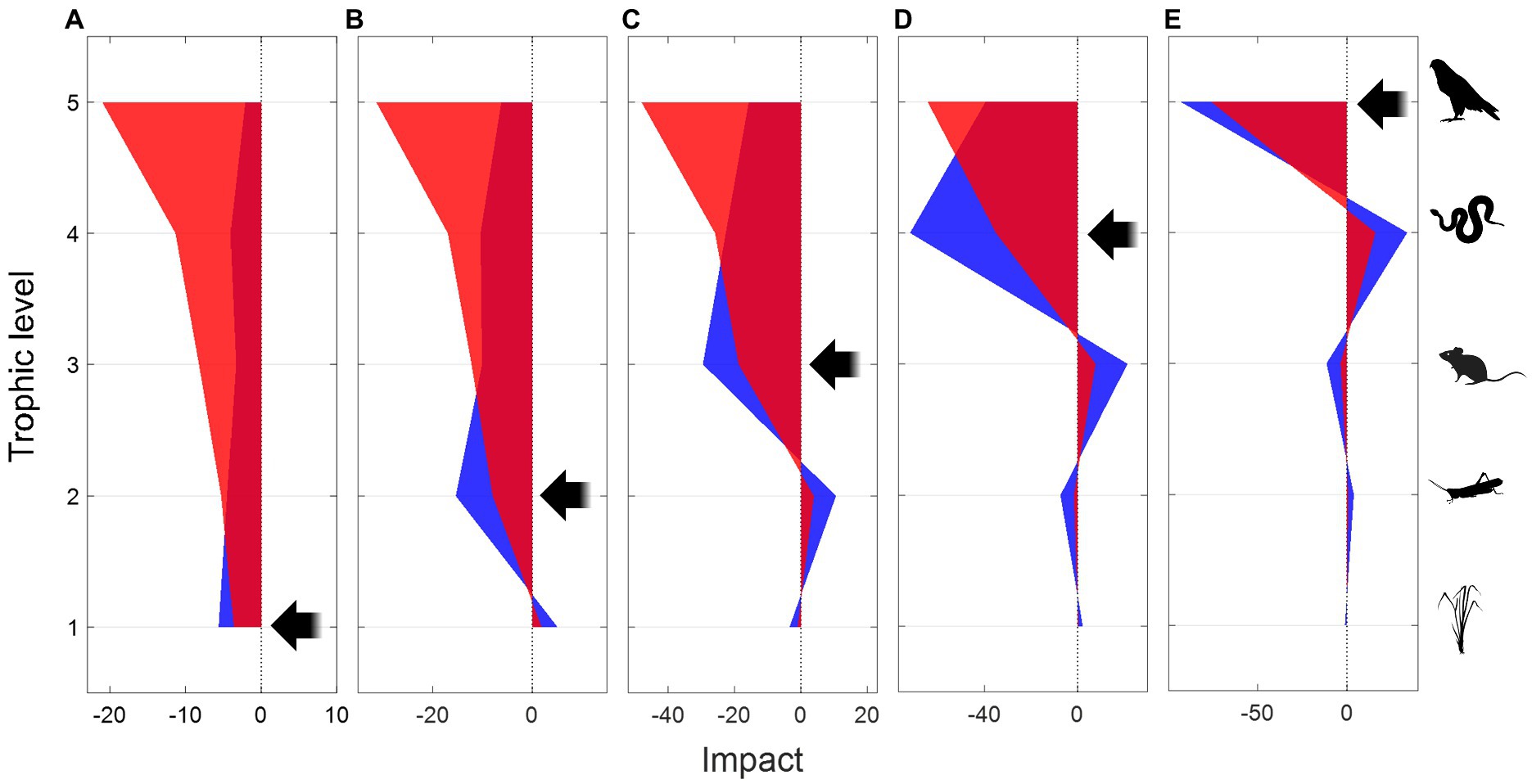
Figure 4. Trophic cascades resulting from negative press perturbations on a targeted trophic level, based on the mean values from 10⁶ random parameter combinations using Generalized Modeling of a five-species food chain. The impact (x-axis) measures the relative rate of change in equilibrium population sizes per unit change in the targeted species’ population growth rate. Negative (or positive) impacts indicate declining (or increasing) equilibrium population size. Black arrows indicate the direction of perturbation and the targeted trophic level (y-axis), from producers (A) to the top predator (E). Blue areas represent scenarios without metabolic responses, and the overlaid semi-transparent red areas represent scenarios with negative metabolic responses.

Dynamics of a modified Rosenzweig–MacArthur model

The Rosenzweig–MacArthur (RM) model is one of the most used to represent the dynamics of predator–prey or consumer-resource systems, serving as building blocks of more complex food web models (McCann, 2011). Compared to the foundational Lotka–Volterra model, the RM model incorporates two more realistic features of predator–prey interactions: (i) prey’s density dependence, in the form of a logistic function for the input rate (Equation 1a) $R\left(B_1\right)=r\left(1-\frac{B_1}{B_{\max }}\right)$, where $B_{\max }$ is the prey biomass’ carrying capacity and $r$ is the maximum intrinsic growth rate, (ii) a saturating functional response, in the form of a Holling type II disc equation $F\left(B_1\right)=\frac{F_{\max }A{B}_1}{F_{\max }+A{B}_1}$, where $F_{\max }$ is the maximum consumption rate, which can be interpreted as the inverse of digestion time, and $A$ is the attack rate while foraging. The implied mechanism leading to consumption saturation involves the existence of foraging adjustments to prey density that result in a type II metabolic response $M\left(B_1\right)$ (Figure 1C), whose derivation is presented in the Supplementary material. If we add this response, the model becomes:

$\begin{array}{ll}\frac{d{B}_1}{dt}=r\left(1-\frac{B_1}{B_{\max }}\right)B_1-\frac{F_{\max }A{B}_1}{F_{\max }+A{B}_1}{B}_2& (6)\end{array}$

$\begin{array}{ll}\frac{d{B}_2}{dt}=\eta \frac{F_{\max }A{B}_1}{F_{\max }+A{B}_1}{B}_2-\left(\frac{F_{\max }\phi A^{\theta }}{F_{\max }+A{B}_1}+b\right)B_2& (6)\end{array}$

The only difference between this version and the original RM model is the mass-specific energy loss term in Equation (6b), here given by a prey-dependent function $\frac{F_{\max }\phi A^{\theta }}{F_{\max }+A{B}_1}+b$ instead of a constant $M$. The term $\frac{F_{\max }}{F_{\max }+A{B}_1}$ gives the proportion of time foraging, and the power function $\phi A^{\theta }$ gives the scaling of active metabolic rate with the attack rate while foraging, following a general relationship between energy use and movement speed applicable to aquatic, terrestrial, and aerial locomotion (Taylor et al., 1982; Alexander, 2005; Papadopoulos, 2008; Bale et al., 2014). The constant $b$ represents basal metabolic rate, or more generally any source of prey-independent energy loss. To compare the two RM formulations, the model was parameterized following a simple set of assumptions and constraints. Firstly, $B_{\max }$ and $r$ were both set to 1 as they arbitrarily define the spatial and temporal scale. $F_{\max }$ was also set to 1, implying the predator’s maximum productivity is smaller than the prey’s. Based on an ecological scope of 4 (the ratio between $F_{\max }$ and field metabolic rate) and a factorial field metabolic scope of 4 (the ratio between field metabolic rate and basal metabolic rate), both good approximations at least for ectotherm vertebrates (Brose et al., 2006; Clarke and Pörtner, 2010; Barneche and Allen, 2018), the basal metabolic rate $b$ was assumed as 1/16^th of $F_{\max }$. The active metabolic rate exponent $\theta$ was set to 2, which is in the midrange of plausible values from 1, representing terrestrial animals, to 3, representing theoretical expectations for aquatic animals (Taylor et al., 1982; Videler and Nolet, 1990; Alexander, 2005). The coefficient $\phi$ was calculated so that maximum metabolism, given by $\phi A^{\theta }+b$, was equal to $F_{\max }$. This is consistent with a factorial maximum metabolic scope (ratio between maximum and basal metabolic rate) of 16, which is also within the plausible range for vertebrates (Clarke and Pörtner, 2010). The attack rate $A$ was constrained by a pre-defined consumption saturation index, given by the ratio between realized and maximum consumption at a reference prey biomass. I used, without loss of generality, the carrying capacity $B_{\max }$ as the reference biomass, so the corresponding saturation index was given by $F\left(B_{\max }\right)/F_{\max }$, and the attack rate calculated as $A=F\left(B_{\max }\right)/\left[B_{\max }\left(1-F\left(B_{\max }\right)/F_{\max }\right)\right]$. Given the importance of consumption saturation levels at equilibrium for stability (McCann, 2011), I varied $F\left(B_{\max }\right)/F_{\max }$ as an independent variable to show the effect of metabolic responses under different dynamical regimes. To represent the original RM model, the constant $M$ was set as equal to the total metabolic rate evaluated at the equilibrium, i.e., $M=M^{\ast }=M\left(B_1^{\ast }\right)$, so that the equilibrium was the same for both model versions.

For low consumption saturation, the system is characterized by a stable equilibrium and non-excitable dynamics: the dominant eigenvalue of the system’s Jacobian, ${\lambda }_1$, is negative and real (Figure 5A). As saturation increases, ${\lambda }_1$ initially decreases, which leads to faster return times. The presence of a metabolic response magnifies this effect, making the system even more resilient to perturbations. An example of system trajectory under this dynamical regime is shown in Figures 6A–C. After a critical saturation level, ${\lambda }_1$ acquires a non-zero imaginary part and the system becomes excitable. The parameter region associated with excitable dynamics is broader in the presence of a metabolic response, starting with $F\left(B_{\max }\right)/F_{\max }$ greater than $\approx$ 0.62, in contrast to $\approx$ 0.65 when the response is absent. The metabolic response also increases the magnitude of imaginary eigenvalues throughout the range and is therefore associated with faster predator–prey oscillations in their return to equilibrium. This is illustrated in Figures 6D–F. For $F\left(B_{\max }\right)/F_{\max }\approx$ 0.78, the real part of ${\lambda }_1$becomes positive and the system crosses a Hopf bifurcation threshold. The equilibrium becomes unstable and the system’s attractor becomes a limit cycle. Adding a metabolic response leads to shorter periods of cycles, which is associated with greater imaginary eigenvalues (Figure 5A). This is illustrated by the predator–prey trajectories in Figures 6G–I. The effect on the amplitude of cycles varies with the species: predators with a metabolic response tend to fluctuate more widely, the opposite occurring with the prey. This is more generally illustrated through bifurcations plots, shown in Figures 5B,C.

FIGURE 5

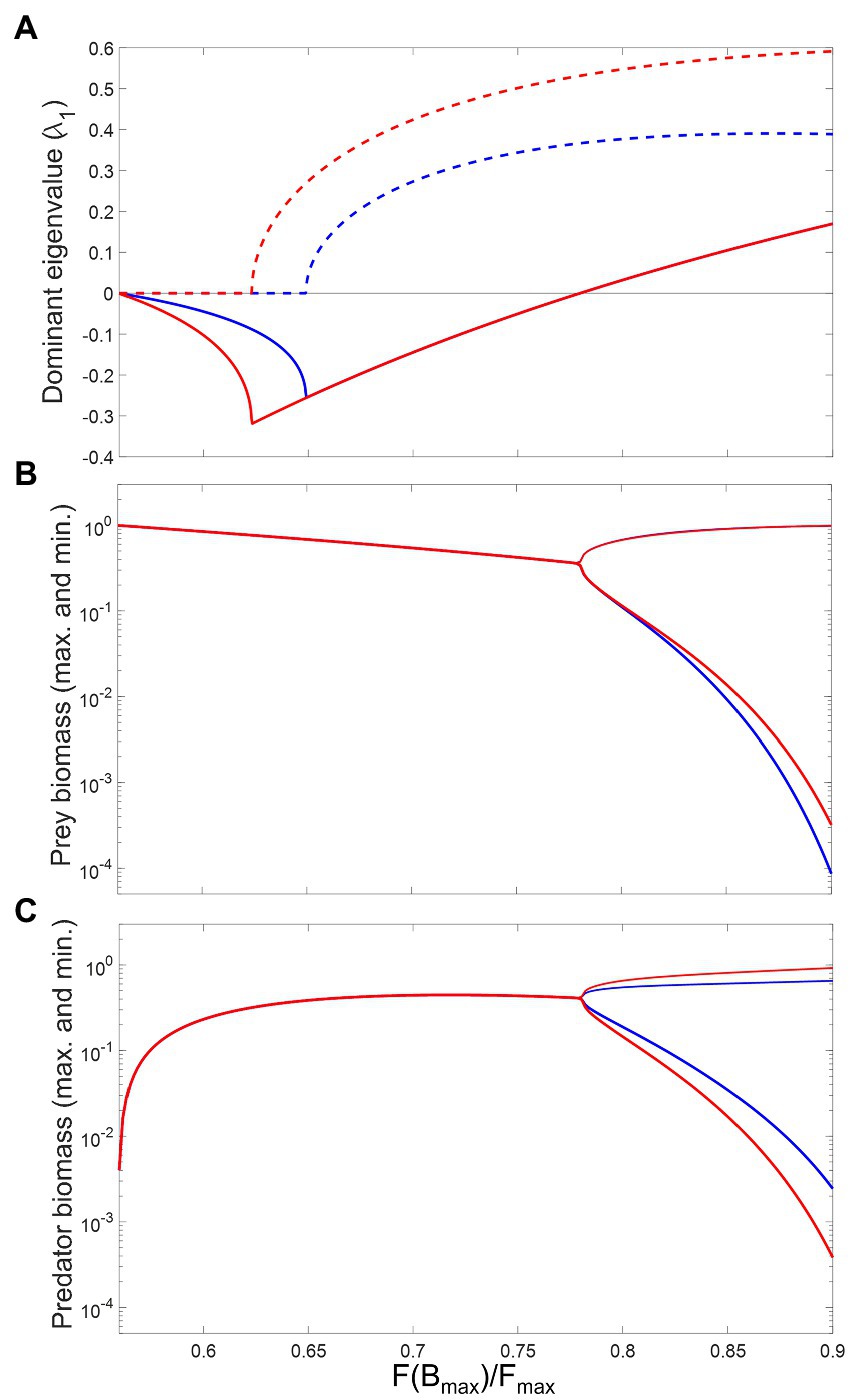
Figure 5. Effects of consumption saturation on the local stability and long-term biomass levels of prey and predator in the modified Rosenzweig–MacArthur model (Equation 6a and 6b). The x-axis measures consumption rate at a reference prey biomass ($B_{\max }$, their carrying capacity), relative to maximum consumption ($F_{\max }$). Blue versus red lines represent the absence versus the presence of a metabolic response, respectively. (A) plots the real (continuous lines) and imaginary (dashed lines) parts of the dominant eigenvalue of the Jacobian matrix. (B) and (C) are bifurcation plots showing long term maximum and minimum biomass of prey and predator, respectively. Other parameter values are: $r=B_{\max }=F_{\max }=1$, $b=1/16$, $\eta =0.85$, $\theta =2$, $A=F\left(B_{\max }\right)/\left[B_{\max }\left(1-F\left(B_{\max }\right)/F_{\max }\right)\right]$, $\phi =\left(F_{\max }-b\right)/A^{\theta }$.

FIGURE 6

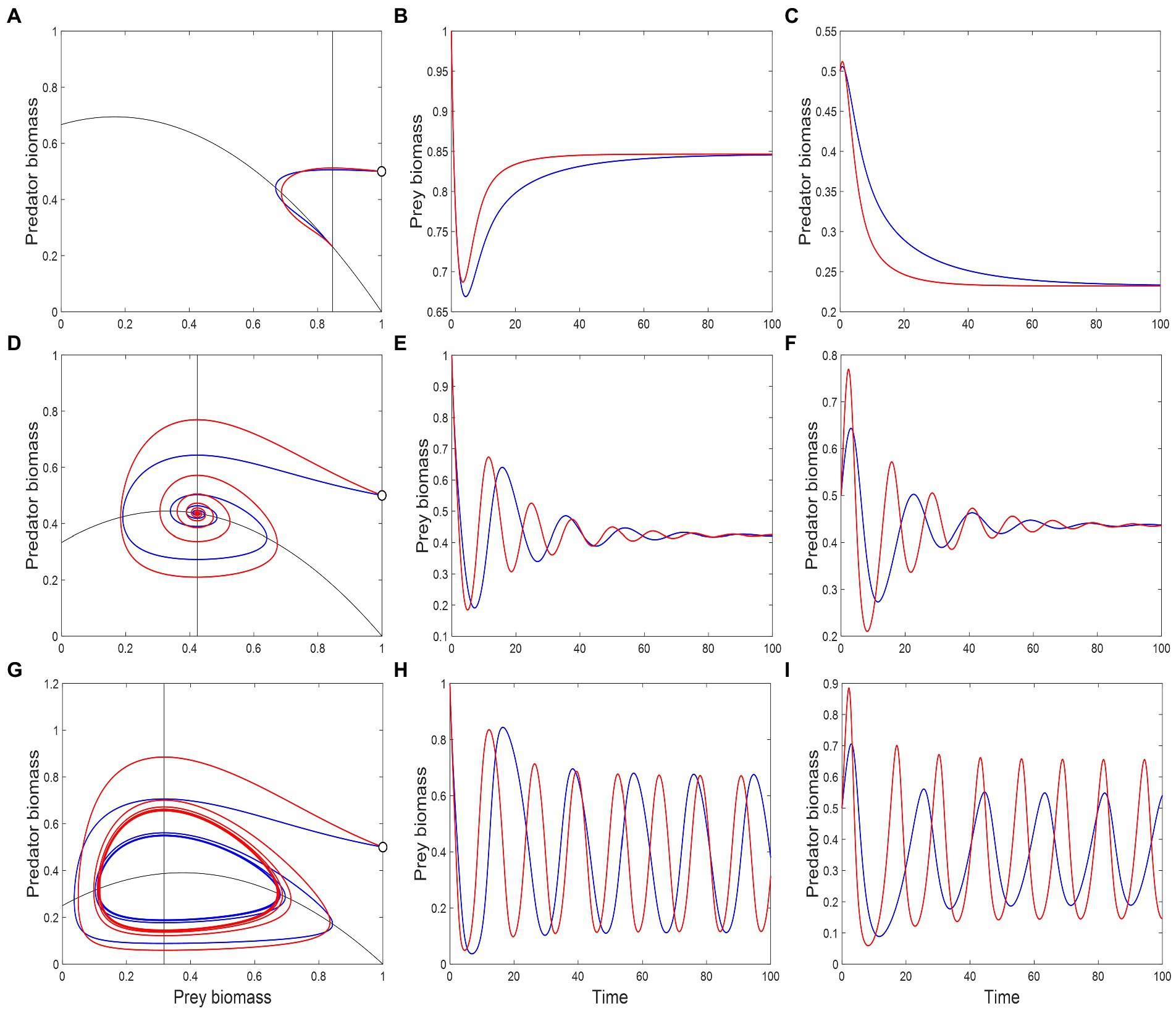
Figure 6. Phase-space plots and population trajectories from the modified Rosenzweig–MacArthur model (Equation 6a and 6b). Red and blue lines represent the system dynamics with and without a metabolic response, respectively. Black lines in the phase-space plots (A, D, G) are the predator and prey isoclines where $d{B}_i/dt=0$, and whose intersection determines the equilibrium state. In all three cases, the system starts at the white dot on the right-most edge of the phase-space plot where $B_1=1$ and $B_2=0.5$. The remaining plots show the trajectory of biomasses as a function of time. Consumption saturation values, given by $F\left(B_{\max }\right)/F_{\max }$, were chosen to characterize three different stability regimes: 0.6 (A–C), leading to a stable node equilibrium, 0.75 (D–F), leading to a stable spiral, and 0.8 (G–I), leading to a limit cycle. Other parameter values are: $r=B_{\max }=F_{\max }=1$, $b=1/16$, $\eta =0.85$, $\theta =2$, $A=F\left(B_{\max }\right)/\left[B_{\max }\left(1-F\left(B_{\max }\right)/F_{\max }\right)\right]$, $\phi =\left(F_{\max }-b\right)/A^{\theta }$.

When under a press perturbation such as harvesting, the predator population is expected to decline at a slower rate in the presence of a metabolic response, as predicted by the general model in “Impacts of press perturbations and trophic cascades”. The top-down cascade should also behave as expected, with an increase in the prey population, but at a slower pace if the predator has a negative metabolic response. However, the RM model has a particularity that makes it differ from the general model regarding the effects of harvesting the prey: because predators have no direct effect on their own growth ($J_{22}=\partial G_2/\partial B_2=0$), adding a mortality component to the prey has no effect on the prey’s equilibrium population size. This attribute of the RM model has been recognized as the cause of unusual or unrealistic predictions such as the paradox of enrichment (Rosenzweig, 1971) and ‘skipped-level’ bottom-up trophic cascades that do not match empirical patterns (McCann et al., 1998; Heath et al., 2014). As a consequence, the metabolic response does not affect the impact on either the prey or the predator population (remind that the derivatives $\partial I_{11}/\partial m^{\ast }$ and $\partial I_{21}/\partial m^{\ast }$ are both dependent on $J_{22}$).

To add another level of realism and better illustrate the general effects of harvesting on prey, I added a direct density-dependent mortality term for the predator (Heath et al., 2014), resulting in:

$\begin{array}{ll}\frac{d{B}_1}{dt}=r\left(1-\frac{B_1}{B_{\max }}\right)B_1-\frac{F_{\max }A{B}_1}{F_{\max }+A{B}_1}{B}_2-h_1{B}_1& (7)\end{array}$

$\begin{array}{l}\frac{d{B}_2}{dt}=\eta \frac{F_{\max }A{B}_1}{F_{\max }+A{B}_1}{B}_2-\left(\frac{F_{\max }\phi A^{\theta }}{F_{\max }+A{B}_1}+b\right)B_2-d{B}_2^2-h_2{B}_2\\ \end{array}\text{ (7b)}$

where $h_1$ and $h_2$ are the prey and predator harvest mortality rates, and $d$ is a coefficient determining the strength of predator’s direct density dependent mortality; all the other terms are identical to Equation (6a and 6b). Figure 7 shows the effects of increasing harvest of either the prey or the predator on their own equilibrium biomasses and the cascading impacts on one another. Without any predator’s direct density dependence ($d=0$) having a metabolic response can only make a difference when the predator is the target (Figures 7A–D). With $d>0$, the equilibrium prey population is allowed to change and all predictions match those from the general model: in the presence of a negative metabolic response, all populations change more slowly when under direct harvest or under a top-down cascading impact (Figures 7E,G,H), but the bottom-up impact of harvesting the prey on the predator’s population is magnified, leading to a faster decline (Figure 7F) and higher risk of extirpation.

FIGURE 7

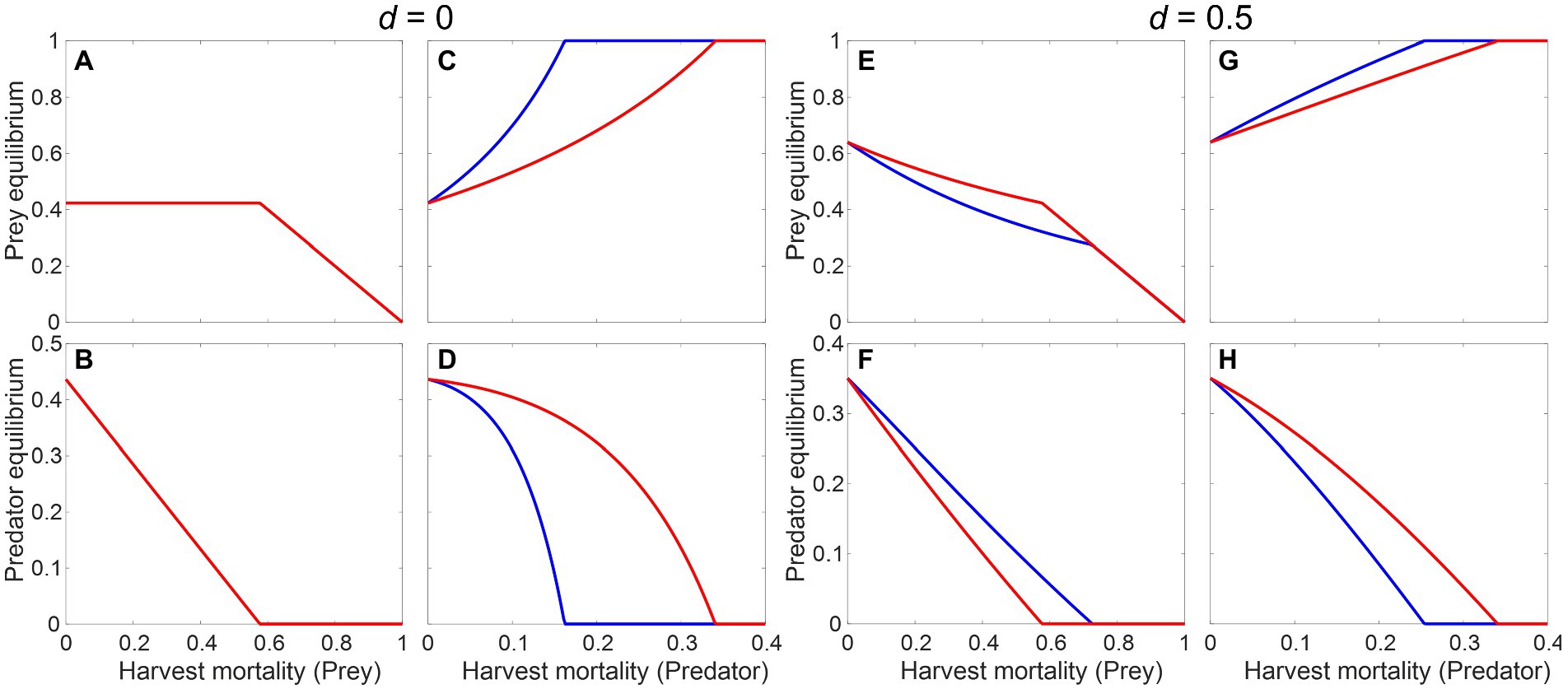
Figure 7. Effect of harvest on the equilibrium biomasses of predator and prey, based on the modified Rosenzweig–MacArthur model (Equation 7a and 7b) without (A–D) or with predator’s direct density dependence (E–H), measured by the parameter $d$. Red and blue lines represent the system dynamics with and without a metabolic response, respectively. Parameter values: $r=B_{\max }=F_{\max }=1$, $b=1/16$, $\eta =0.85$, $\theta =2$, $F(B_{\max })/F_{\max }=0.75$, $A=F\left(B_{\max }\right)/\left[B_{\max }\left(1-F\left(B_{\max }\right)/F_{\max }\right)\right]$, $\varphi =\left(F_{\max }-b\right)/A^{\theta }$.

Discussion

In this paper, I introduced the concept of metabolic response, in analogy to the functional response, and argued that the two responses are bound together through variation in foraging activity. Although the functional response is a fundamental piece defining the interaction between predator and prey, it is not sufficient to describe the mutual influence they exert on one another. By ignoring the associated changes in metabolism, ecological models may be missing an important part of the energy flow in ecosystems and underestimating the pace of change in populations. This configures a potential false exclusion, defined by Topping et al. (2015) as an error “where the model leaves out a process because it was assumed to not be essential when in fact it was” (see also Montagnes et al., 2019). The implications are multifold and involve both theoretical and applied areas in ecology.

For theory, the importance of metabolic responses can only become evident when the energetic cost of foraging is modeled explicitly as a variable in the equations governing dynamics. Following Jeschke et al. (2002), here I derived the metabolic response from underlying changes in hunger level and the proportion of time active in a manner consistent with a Holling type II functional response, given its widespread use. But changes in activity do not need to follow such simple function of hunger level or satiation, and many different shapes of functional and metabolic responses can emerge from organisms foraging adaptively (Abrams, 1982). Adaptive foraging models have been the main venue by which adjustments in activity are included as part of predator–prey dynamics (Abrams, 2010; Valdovinos et al., 2010). Historically, however, their emphasis has been on how effort should be allocated among alternative prey instead of how much effort should be spent on foraging overall (Fryxell and Lundberg, 1994; Křivan, 1996; Kondoh, 2003; Uchida et al., 2007; Valdovinos et al., 2010; Heckmann et al., 2012). For studies targeting changes in overall effort, the risk of mortality by predation has been a major hypothesized mechanism determining the cost of foraging (Ives and Dobson, 1987; Werner and Anholt, 1993; Lima, 1998; Brown et al., 1999; Valdovinos et al., 2010), whereas the metabolic cost has been rarely the focus in a predator–prey or food web context (Abrams, 1993; Gibert and Yeakel, 2019). Teasing apart these two costs is important because they involve different dynamical feedbacks and propagation of indirect effects within a community (Abrams, 1984). Predation risk changes with the density of predators and so should not be represented by a fixed function of foraging effort alone (Lima, 2002). This distinction was not recognized by some of the foundational models on optimal foraging effort (Abrams, 1982, 1991; Houston and McNamara, 1989; Werner and Anholt, 1993), or even more recent models (e.g., Kiørboe et al., 2018; Teckentrup et al., 2018). By not explicitly representing the dynamics of upper trophic levels, the interpretation of foraging costs in those models is more consistent with metabolic costs instead of increased risk of predation mortality as originally proposed.

The emphasis on predation risk also underscores the theory on the so-called trait-mediated interactions and non-consumptive effects in food webs, which usually takes a top-down perspective by focusing on non-lethal effects of predators on the prey’s growth rate (Schmitz et al., 1997, 2004; Brown et al., 1999; Werner and Peacor, 2003; Wirsing et al., 2021). Another kind of trait-mediated and non-consumptive effect, one that is bottom-up in nature and that has so far been ignored by theory, is when variation in prey density affects a predator’s growth rate without involving changes in consumption, and that is exactly what defines a metabolic response. Including metabolic responses explicitly in food web models can therefore expand the range of our understanding on trait-mediated and non-consumptive effects, bringing back into focus all those species whose metabolism is the major component of energy losses. This applies especially to large-sized and top-predator species, which in many cases have disproportionally large impacts on food webs and are valued economically and culturally (Estes et al., 2011).

There are of course practical challenges in the adoption of adaptive foraging models or any other model with prey-dependent energetic costs, and one of the main reasons is that they are more difficult to parameterize. The extension I have presented of the Rosenzweig–MacArthur consumer-resource model is an example: it requires two additional parameters to describe the scaling of active metabolic rate with the attack rate. Although some general knowledge on this relationship can be acquired from bioenergetic studies, parameter values may be species-specific and context-dependent, and laboratory studies may not be applicable to natural settings (although the same reasoning may apply to most functional response studies; Uiterwaal and DeLong, 2018; Griffen, 2021; Juliano et al., 2022). These difficulties notwithstanding, it is important firstly to recognize that metabolic responses do exist, and secondly to understand the consequences of not including them in ecological models. Besides having their own effects on dynamics and stability, metabolic responses determine how other components of interaction such as functional responses affect stability. For instance, the presumed destabilizing effect of saturating functional responses in complex food webs may not be as general as previously thought (Williams and Martinez, 2004; Gross et al., 2009; Vucic-Pestic et al., 2010), being contingent on high levels of predation mortality relative to metabolic expenditure. For levels that are more consistent with trophic transfer efficiencies in natural ecosystems the effect is reversed. This shift has been previously observed by Plitzko et al. (2012) for a limited range of functional response elasticities (~0.5–1) and high species richness (60). Nevertheless, the effect can be reversed once again toward the more familiar destabilizing influence if metabolic responses are accounted for.

The individual effect of metabolic responses on dynamical stability will depend on their own sign: all other things being equal, positive responses are stabilizing and negative responses are destabilizing. Although the sign may depend on many factors such as the time scale, the overall prey density, and the life history of the species (Norberg, 1977; Formanowicz Jr and Bradley, 1987; Abrams, 1991), it is likely it will be negative for most prey densities normally occurring in nature and capable of sustaining predator populations. The first evidence comes from an abundance of studies showing declines in foraging activity with increasing prey density or availability. In addition, a large compilation of foraging times by Rizzuto et al. (2018) also indicates that decreases in relative prey density and size can explain an increase in the proportion of time foraging by small carnivores (< 5 kg). This adds up to evidence that consumers commonly reach satiation in the field (Jeschke et al., 2002; Jeschke, 2007, but see Beardsell et al., 2022) and are expected to stay closer to satiation when foraging adaptively, which may explain positive complexity-stability relationships in food webs (Uchida and Drossel, 2007; Plitzko et al., 2012). If the shape of functional responses is any indication of changes in foraging activity (Abrams, 1982; Figure 1), positive metabolic responses and the associated accelerating (concave-up) portion of functional responses are expected to occur at low prey densities only, when predators are far from satiation. Such densities are unlikely to meet the energetic requirements of a viable predator population in the long term. Take for instance the classic Holling type III functional response, for which the prey-dependent term is a squared function of prey density, i.e., $F=f\left(B^2\right)$. Its inflection point, marking the transition from the accelerating to the saturating (concave-down) portion, occurs at a consumption level that is a quarter of the maximum ($F_{\max }/4$). This would be equal to the minimum required to just cover metabolic expenses of vertebrate ectotherms based on an ecological scope of 4 for this group (Yodzis and Innes, 1992; Brose et al., 2006), leaving no room for growth or reproduction. For endotherms, the value would be even lower than the minimum, implying prey densities for both groups should stay at or fluctuate around a value that is above the inflection point and therefore in the saturating portion if predators are to be viable. If a more general type III function is considered, so that $F=f\left(B^n\right)$ (Real, 1977), accelerating responses could be realized more often under higher values of the exponent $n$ (the Hill exponent), which pushes the inflection point to higher prey densities. However, estimated exponents seem to rarely exceed 2: it occurs in 18% of the 254 functional responses analyzed by Pawar et al. (2012), and in 5% of 939 type III functional responses analyzed by Uiterwaal and DeLong (2020) (the other 1,144 cases were best fitted by a type II response, for which $n$ is effectively equal to 1).

Food webs containing stronger negative metabolic responses are expected to exhibit smaller chances of local stability but faster return times when stable, higher excitability, and higher frequency of population oscillations. On the one hand, at the local community scale such higher than expected population variability would imply lower predictability and higher chances of population extinctions in the face of demographic and environmental stochasticity (Pimm, 1991). More excitable dynamics can also generate resonances with these stochastic components leading to persistent cycling even when internal dynamics is expected to follow a stable equilibrium in a deterministic sense (Pineda-Krch et al., 2007; McCann, 2011). On the other hand, it can also lower the correlation between population and environmental fluctuations, which can decrease temporal synchrony of abundances across the landscape and increase the adaptive capacity of food webs (McCann et al., 2016), both expected to increase their persistence at the larger, meta-community scales made of local communities spatially connected by mobile predators (Gouhier et al., 2010; McMeans et al., 2015; Hammond et al., 2020). Persistence can also be enhanced by negative metabolic responses in more extreme cases when predators are very efficient at low prey densities. A saturated consumption rate could drive the prey population to extinction by overexploitation, especially in the presence of Allee effects, as demonstrated for the general predator–prey model case. The main reason is that the predator population remains unresponsive to lowered prey density. This lack of feedback between predator and prey populations and the potential for prey extirpation are alleviated if one accounts for the negative metabolic response, which depletes predator’s growth and reproduction despite little or no change in consumption.

The present results have implications for any area of applied ecology that relies on models of ecosystem dynamics. One example is the ecosystem-based fisheries management approach (EBFM; Pikitch et al., 2004), which often represents the interactions between predators and prey through saturating (e.g., type II) functional responses. Models widely used as part of EBFM include Ecopath-with-Ecosim (Christensen and Walters, 2004), Atlantis (Audzijonyte et al., 2019), OSMOSE (Shin and Cury, 2001), and size spectrum models such as those in the R-package mizer (Scott et al., 2014), besides several other models included as part of the Fisheries and Marine Ecosystem Model Intercomparison Project (Tittensor et al., 2018). They quantify the effects of changing fishing regimes or climate on target and non-target species, both for the investigation of general theoretical questions or applied to the management of specific systems. By ignoring the associated negative metabolic responses, these models likely overestimate the effect of changing harvest rate on the long-term population size of the exploited species. With increased fishing mortality, its prey populations are partially released from predation, increasing in abundance. It in turn can benefit the predator’s growth through increases in consumption, but it can also make life easier by requiring less effort and energy expenditure for foraging. This added effect explains why in models with metabolic responses the exploited population declines less drastically with increases in mortality and is less prone to collapse and eventual extirpation. Such phenomenon configures a form of metabolic compensation or metabolic rescue, to make an analogy with the rescue effects in metapopulation ecology describing a decline in probability of local extinction in patches due to influx of immigrants (Van Schmidt and Beissinger, 2020), or evolutionary rescue, in which the risk of extinction is alleviated through adaptation by natural selection (Bell, 2017).

The same kind of buffering that characterizes the metabolic rescue affects the impacts on non-target species occupying lower trophic positions. The immediate prey of the exploited species will experience an increase in abundance, but a less pronounced one due to their metabolic response of increased energy expenditure for foraging on relatively fewer available organisms of their own prey, which in turn will experience enhanced availability of prey of their own, so their decline in abundance is alleviated by the energy saved from foraging, and so on. The situation changes if we consider non-target species occupying higher trophic positions: decreased abundance of the exploited population implies higher required effort for foraging by its immediate predators, having an additional detrimental effect on the predator population that is already expected to decline due to decreases in consumption rate. This magnifying effect should be felt all the way up along food chains, being stronger the more trophic links there are separating the impacted predator from the original source of perturbation. Current predictions from ecosystem models already show concerning declines of marine populations resulting from fishing on lower trophic level species which they feed on, such as krill and small forage fishes (Hill et al., 2006; Smith et al., 2011), a threat that extends outside the aquatic boundary and affects marine birds (Furness, 2007; Cury et al., 2011). These ecosystem modeling projections also indicate potential cascading effects from climate change, which can affect marine predators through declines in basal productivity (Klein et al., 2018; Bryndum-Buchholz et al., 2019; Lotze et al., 2019; Heneghan et al., 2021). The fact that none of these models account for metabolic responses, and are therefore expected to underestimate bottom-up trophic cascades, is one additional reason for concern.

As a first attempt to characterize the ecological consequences of metabolic responses, and to make things approachable enough, the present analyses had to rely on simplifying assumptions. One important simplification was that food web topologies were generated from the niche model (Williams and Martinez, 2000) for sake of consistency and for enabling direct comparisons with previous Generalized Modeling results (Gross et al., 2009; Plitzko et al., 2012; Aufderheide et al., 2013). It is possible that some of the stability properties investigated here will depend on the pattern of trophic connections among species, and that more realistic topological models could lead to different conclusions, as previously demonstrated for complexity-stability relationships (Kondoh, 2006). Another simplification was that the strength of metabolic responses, as measured by elasticities of foraging activity, was indiscriminately distributed across species. It is more probable that in natural systems the distribution of metabolic responses will be structured by species traits, such as body size and cognitive capacity, which in turn can correlate with relative positions within the food web (Woodward et al., 2005; Edmunds et al., 2016). The responses should be more pronounced in predators with higher behavioral flexibility and overall levels of activity, which in general have larger sizes and occupy higher trophic positions, at least in aquatic ecosystems (Shurin et al., 2006; Andersen et al., 2016; Potapov et al., 2019). These are the so-called demand organisms in the Dynamic Energy Budget (DEB) framework (Kooijman, 2010), as opposed to supply organisms, which have lower metabolic requirements, relatively simpler behavioral repertoire but a more plastic physiology, and tend to occupy lower trophic positions. It is also possible that metabolic responses, which occur at the same temporal scale as functional responses, interact with slower changes in overall metabolism determining maximum consumption and basal metabolic rates. These changes involve plastic physiological variation or adaptive evolution in response to long-term variation in resource availability (Mueller and Diamond, 2001), and are expected to occur more often or more rapidly in supply organisms. They can also explain negative or hump-shaped associations between metabolism and population density (DeLong et al., 2014; Einum, 2014). These so-called metabolic adjustments have been shown to enhance stability of model food webs in terms of species persistence and amplitude of biomass fluctuations (Quévreux and Brose, 2019). It is also worth noting that several other physiological or demographic attributes of predators can be dependent on prey density, including food assimilation efficiency, non-predatory death rates, and relative allocation to growth versus reproduction, all aspects not covered in this paper but which can greatly influence dynamics (Montagnes and Fenton, 2012; Montagnes et al., 2019). How the distribution of metabolic responses interacts with these adjustments and demographic attributes at different time scales (behavioral, physiological, and evolutive), either buffering, magnifying, or inverting their effects on dynamics and stability, and how these effects change with different criteria for stability (Pimm, 1984; Donohue et al., 2016), are still open questions and potential venues for further investigation.

The functional response has been the focus of much research on predator–prey interactions, and there are many proposed mechanisms to explain its shape. A non-exhaustive list includes handling time or digestion limitation (Holling, 1966; Jeschke et al., 2002), adaptive foraging (Abrams, 1982, 1990), learning (Holling, 1966), prey switching (Holling, 1966; Oaten and Murdoch, 1975), predator–prey mass ratios (Vucic-Pestic et al., 2010); temperature-dependence (Daugaard et al., 2019), spatial aggregation (Hossie and Murray, 2016), habitat dimensionality (Pawar et al., 2012; Giacomini et al., 2013), particulate versus filter feeding (Jeschke et al., 2004; Giacomini et al., 2013), and information limitation (Hein and Martin, 2020). Joining the list are ever more mechanistic models based on first principles of biomechanics and energetics (Portalier et al., 2019; Beardsell et al., 2022). However, we still lack more comprehensive studies or systematic reviews that can determine the extent to which variable foraging activity is responsible for changes in consumption rates, and the prevailing direction of foraging responses to prey density. The reasons for understanding why and how predators adjust their foraging do not end with defining the functional response shape: such adjustments are consequential for shaping the rate of energy losses through metabolism as well. The scarcity of studies characterizing metabolic responses is not necessarily an indication that they are irrelevant, it is more likely a consequence of practical difficulties in measuring respiration rates, in contrast to prey consumption which is a much more conspicuous component of the energy budget of animals. But techniques and instruments for measuring respiration in the laboratory and in the field do exist and can be designed to follow similar protocols of prey density variation as in functional response studies. They include respirometers (Clark et al., 2013; Byrnes et al., 2020), isotope-based methods such as doubly labeled water (Nagy et al., 1999; Butler et al., 2004), heart rates (Nolet et al., 1992; Butler et al., 2004), electromyograms (Cooke et al., 2004), accelerometers (Halsey et al., 2011; Brownscombe et al., 2014), and enzymatic approaches (Childress and Somero, 1990; Sherwood et al., 2002). Combining metabolic response measurements with the associated functional responses will bring important insights into how predators and prey interact and help improve the models that are so needed for understanding and managing ecosystems.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

The initial project giving rise to this paper was supported by a Québec-Brazil Postdoctoral fellowship scholarship from the Fonds de recherche du Québec – Nature et technologies (FRQNT), dossier 176474, in the period 2013–2014.

Acknowledgments

This paper was conceptualized during a postdoc at the Department of Biological Sciences of the Université du Québec à Montréal (UQÀM), supported by a Québec-Brazil Postdoctoral fellowship scholarship from the Fonds de recherche du Québec – Nature et technologies (FRQNT), dossier 176474. I thank Pedro Peres-Neto for the mentorship, support, and ideas that helped improve this manuscript, and two reviewers who also provided insightful comments.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.980812/full#supplementary-material

References

Abrams, P. A. (1982). Functional responses of optimal foragers. Am. Nat. 120, 382–390.

Google Scholar

Abrams, P. A. (1984). Foraging time optimization and interactions in food webs. Am. Nat. 124, 80–96.

Google Scholar

Abrams, P. A. (1990). The effects of adaptive behavior on the type-2 functional response. Ecology 71, 877–885.

Google Scholar

Abrams, P. A. (1991). Life history and the relationship between food availability and foraging effort. Ecology 72, 1242–1252.

Google Scholar

Abrams, P. A. (1993). Optimal traits when there are several costs: the interaction of mortality and energy costs in determining foraging behavior. Behav. Ecol. 4, 246–259.

Google Scholar

Abrams, P. A. (2000). The evolution of predator-prey interactions: theory and evidence. Annu. Rev. Ecol. Syst. 31, 79–105. doi: 10.1146/annurev.ecolsys.31.1.79

CrossRef Full Text | Google Scholar

Abrams, P. A. (2010). Implications of flexible foraging for interspecific interactions: lessons from simple models. Funct. Ecol. 24, 7–17. doi: 10.1111/j.1365-2435.2009.01621.x

CrossRef Full Text | Google Scholar

Abrams, P. A., and Ginzburg, L. R. (2000). The nature of predation: prey dependent, ratio dependent or neither? Trends Ecol. Evol. 15, 337–341.

Google Scholar

Alexander, R. M. (2005). Models and the scaling of energy costs for locomotion. J. Exp. Biol. 208, 1645–1652. doi: 10.1242/jeb.01484

CrossRef Full Text | Google Scholar

Allesina, S., and Tang, S. (2012). Stability criteria for complex ecosystems. Nature 483, 205–208. doi: 10.1038/nature10832

CrossRef Full Text | Google Scholar

Andersen, K. H., Jacobsen, N. S., and Farnsworth, K. D. (2016). The theoretical foundations for size spectrum models of fish communities. Can. J. Fish. Aquat. Sci. 73, 575–588. doi: 10.1139/cjfas-2015-0230

CrossRef Full Text | Google Scholar

Anholt, B. R., and Werner, E. E. (1995). Interaction between food availability and predation mortality mediated by adaptive behavior. Ecology 76, 2230–2234.

Google Scholar

Anholt, B. R., Werner, E., and Skelly, D. K. (2000). Effect of food and predators on the activity of four larval ranid frogs. Ecology 81, 3509–3521. doi: 10.1890/0012-9658(2000)081[3509:EOFAPO]2.0.CO;2

CrossRef Full Text | Google Scholar

Aubin-Horth, N., Gingras, J., and Boisclair, D. (1999). Comparison of activity rates of 1+ yellow perch (Perca flavescens) from populations of contrasting growth rates using underwater video observations. Can. J. Fish. Aquat. Sci. 56, 1122–1132.

Google Scholar

Audzijonyte, A., Pethybridge, H., Porobic, J., Gorton, R., Kaplan, I., and Fulton, E. A. (2019). AtlAntis: a spatially explicit end-to-end marine ecosystem model with dynamically integrated physics, ecology and socio-economic modules. Methods Ecol. Evol. 10, 1814–1819. doi: 10.1111/2041-210X.13272

CrossRef Full Text | Google Scholar

Aufderheide, H., Rudolf, L., Gross, T., and Lafferty, K. D. (2013). How to predict community responses to perturbations in the face of imperfect knowledge and network complexity. Proc. R. Soc. B Biol. Sci. 280:20132355. doi: 10.1098/rspb.2013.2355

CrossRef Full Text | Google Scholar

Bale, R., Hao, M., Bhalla, A. P. S., and Patankar, N. A. (2014). Energy efficiency and allometry of movement of swimming and flying animals. Proc. Natl. Acad. Sci. U. S. A. 111, 7517–7521. doi: 10.1073/pnas.131054411

CrossRef Full Text | Google Scholar

Barneche, D. R., and Allen, A. P. (2018). The energetics of fish growth and how it constrains food-web trophic structure. Ecol. Lett. 21, 836–844. doi: 10.1111/ele.12947

PubMed Abstract | CrossRef Full Text | Google Scholar

Barnes, C., Maxwell, D., Reuman, D. C., and Jennings, S. (2010). Global patterns in predator–prey size relationships reveal size dependency of trophic transfer efficiency. Ecology 91, 222–232. doi: 10.1890/08-2061.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Beardsell, A., Gravel, D., Berteaux, D., Gauthier, G., Clermont, J., Careau, V., et al. (2022). Derivation of predator functional responses using a mechanistic approach in a natural system. Front. Ecol. Evol. 9:630944. doi: 10.3389/fevo.2021.630944

CrossRef Full Text | Google Scholar

Begon, M., and Townsend, C. R. (2020). Ecology: From Individuals to Ecosystems. New York, NY: John Wiley & Sons.

Google Scholar

Bell, G. (2017). Evolutionary rescue. Annu. Rev. Ecol. Evol. Syst. 48, 605–627. doi: 10.1146/annurev-ecolsys-110316-023011

CrossRef Full Text | Google Scholar

Biro, P. A., Post, J. R., and Parkinson, E. A. (2003). From individuals to populations: prey fish risk-taking mediates mortality in whole-system experiments. Ecology 84, 2419–2431. doi: 10.1890/02-0416

CrossRef Full Text | Google Scholar

Birt-Friesen, V. L., Montevecchi, W. A., Cairns, D. K., and Macko, S. A. (1989). Activity-specific metabolic rates of free-living northern gannets and other seabirds. Ecology 70, 357–367. doi: 10.2307/1937540

CrossRef Full Text | Google Scholar

Boisclair, D., and Leggett, W. C. (1989). The importance of activity in bioenergetics models applied to actively foraging fishes. Can. J. Fish. Aquat. Sci. 46, 1859–1867. doi: 10.1139/f89-234

CrossRef Full Text | Google Scholar

Borrelli, J. J., Allesina, S., Amarasekare, P., Arditi, R., Chase, I., Damuth, J., et al. (2015). Selection on stability across ecological scales. Trends Ecol. Evol. 30, 417–425. doi: 10.1016/j.tree.2015.05.001

CrossRef Full Text | Google Scholar

Boyd, I. L. (1999). Foraging and provisioning in Antarctic fur seals: interannual variability in time-energy budgets. Behav. Ecol. 10, 198–208.

Google Scholar

Brose, U. (2010). Body-mass constraints on foraging behaviour determine population and food-web dynamics. Funct. Ecol. 24, 28–34. doi: 10.1111/j.1365-2435.2009.01618.x

CrossRef Full Text | Google Scholar

Brose, U., Williams, R. J., and Martinez, N. D. (2006). Allometric scaling enhances stability in complex food webs. Ecol. Lett. 9, 1228–1236. doi: 10.1111/j.1461-0248.2006.00978.x

CrossRef Full Text | Google Scholar

Brown, J. H., Gillooly, J. F., Allen, A. P., Savage, V. M., and West, G. B. (2004). Toward a metabolic theory of ecology. Ecology 85, 1771–1789. doi: 10.1890/03-9000

CrossRef Full Text | Google Scholar

Brown, J. S., Laundré, J. W., and Gurung, M. (1999). The ecology of fear: optimal foraging, game theory, and trophic interactions. J. Mammal. 80, 385–399.

Google Scholar

Brownscombe, J. W., Gutowsky, L. F., Danylchuk, A. J., and Cooke, S. J. (2014). Foraging behaviour and activity of a marine benthivorous fish estimated using tri-axial accelerometer biologgers. Mar. Ecol. Prog. Ser. 505, 241–251. doi: 10.3354/meps10786

CrossRef Full Text | Google Scholar

Bryant, D. M., and Tatner, P. (1991). Intraspecies variation in avian energy expenditure: correlates and constraints. Ibis 133, 236–245.

Google Scholar

Bryndum-Buchholz, A., Tittensor, D. P., Blanchard, J. L., Cheung, W. W., Coll, M., Galbraith, E. D., et al. (2019). Twenty-first-century climate change impacts on marine animal biomass and ecosystem structure across ocean basins. Glob. Chang. Biol. 25, 459–472. doi: 10.1111/gcb.14512

PubMed Abstract | CrossRef Full Text | Google Scholar

Burger, A. E., and Piatt, J. F. (1990). Flexible time budgets in breeding common Murres: buffers against variable prey availability. Stud. Avian Biol. 14, 71–83.

Google Scholar

Butler, P. J., Green, J. A., Boyd, I. L., and Speakman, J. R. (2004). Measuring metabolic rate in the field: the pros and cons of the doubly labelled water and heart rate methods. Funct. Ecol. 18, 168–183. doi: 10.1111/j.0269-8463.2004.00821.x

CrossRef Full Text | Google Scholar

Byrnes, E. E., Lear, K. O., Morgan, D. L., and Gleiss, A. C. (2020). Respirometer in a box: development and use of a portable field respirometer for estimating oxygen consumption of large-bodied fishes. J. Fish Biol. 96, 1045–1050. doi: 10.1111/jfb.14287

CrossRef Full Text | Google Scholar

Cairns, D. K. (1987). Seabirds as indicators of marine food supplies. Biol. Oceanogr. 5, 261–271.

Google Scholar

Childress, J. J., and Somero, G. N. (1990). Metabolic scaling: a new perspective based on scaling of glycolytic enzyme activities. Am. Zool. 30, 161–173.

Google Scholar

Christensen, V., and Walters, C. J. (2004). Ecopath with Ecosim: methods, capabilities and limitations. Ecol. Model. 172, 109–139. doi: 10.1016/j.ecolmodel.2003.09.003

CrossRef Full Text | Google Scholar

Christian, K. A., Baudinette, R. V., and Pamula, Y. (1997). Energetic costs of activity by lizards in the field. Funct. Ecol. 11, 392–397.

Google Scholar

Clark, T. D., Sandblom, E., and Jutfelt, F. (2013). Aerobic scope measurements of fishes in an era of climate change: respirometry, relevance and recommendations. J. Exp. Biol. 216, 2771–2782. doi: 10.1242/jeb.084251

CrossRef Full Text | Google Scholar

Clarke, A., and Pörtner, H. O. (2010). Temperature, metabolic power and the evolution of endothermy. Biol. Rev. 85, 703–727. doi: 10.1111/j.1469-185X.2010.00122.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Cooke, S. J., Thorstad, E. B., and Hinch, S. G. (2004). Activity and energetics of free-swimming fish: insights from electromyogram telemetry. Fish Fish. 5, 21–52. doi: 10.1111/j.1467-2960.2004.00136.x

CrossRef Full Text | Google Scholar

Costa, D. P., Croxall, J. P., and Duck, C. D. (1989). Foraging energetics of antartic fur seals in relation to changes in prey availability. Ecology 70, 596–606. doi: 10.2307/1940211

CrossRef Full Text | Google Scholar

Cruz-Font, L., Shuter, B. J., Blanchfield, P. J., Minns, C. K., and Rennie, M. D. (2019). Life at the top: Lake ecotype influences the foraging pattern, metabolic costs and life history of an apex fish predator. J. Anim. Ecol. 88, 702–716. doi: 10.1111/1365-2656.12956

CrossRef Full Text | Google Scholar

Cury, P. M., Boyd, I. L., Bonhommeau, S., Anker-Nilssen, T., Crawford, R. J., Furness, R. W., et al. (2011). Global seabird response to forage fish depletion—one-third for the birds. Science 334, 1703–1706. doi: 10.1126/science.1212928

CrossRef Full Text | Google Scholar

Daugaard, U., Petchey, O. L., and Pennekamp, F. (2019). Warming can destabilize predator–prey interactions by shifting the functional response from type III to type II. J. Anim. Ecol. 88, 1575–1586. doi: 10.1111/1365-2656.13053

PubMed Abstract | CrossRef Full Text | Google Scholar

De Ruiter, P. C., Wolters, V., and Moore, J. C. (2005). Dynamic Food Webs: Multispecies Assemblages, Ecosystem Development and Environmental Change. Boston, MA: Elsevier.

Google Scholar

DeLong, J. P., Hanley, T. C., and Vasseur, D. A. (2014). Competition and the density dependence of metabolic rates. J. Anim. Ecol. 83, 51–58. doi: 10.1111/1365-2656.12065

CrossRef Full Text | Google Scholar

Donohue, I., Hillebrand, H., Montoya, J. M., Petchey, O. L., Pimm, S. L., Fowler, M. S., et al. (2016). Navigating the complexity of ecological stability. Ecol. Lett. 19, 1172–1185. doi: 10.1111/ele.12648

PubMed Abstract | CrossRef Full Text | Google Scholar

Eby, L. A., Rudstam, L. G., and Kitchell, J. F. (1995). Predator responses to prey population dynamics: an empirical analysis based on lake trout growth rates. Can. J. Fish. Aquat. Sci. 52, 1564–1571. doi: 10.1139/f95-149

CrossRef Full Text | Google Scholar

Edmunds, N. B., Laberge, F., and McCann, K. S. (2016). A role for brain size and cognition in food webs. Ecol. Lett. 19, 948–955. doi: 10.1111/ele.12633

PubMed Abstract | CrossRef Full Text | Google Scholar

Einum, S. (2014). Ecological modeling of metabolic rates predicts diverging optima across food abundances. Am. Nat. 183, 410–417. doi: 10.1086/674951

PubMed Abstract | CrossRef Full Text | Google Scholar

Elton, C. S. (1927). Animal Ecology. Chicago, IL: University of Chicago Press.

Google Scholar

Estes, J. A., Terborgh, J., Brashares, J. S., Power, M. E., Berger, J., Bond, W. J., et al. (2011). Trophic downgrading of planet earth. Science. Science 333, 301–306. doi: 10.1126/science.1205106

PubMed Abstract | CrossRef Full Text | Google Scholar

Formanowicz, D. R. (1982). Foraging tactics of larvae of Dytiscus verticalis (Coleoptera: Dytiscidae): the assessment of prey density. J. Anim. Ecol. 51, 757–767. doi: 10.2307/4003

CrossRef Full Text | Google Scholar

Formanowicz, D. R. Jr., and Bradley, P. J. (1987). Fluctuations in prey density: effects on the foraging tactics of scolopendrid centipedes. Anim. Behav. 35, 453–461.

Google Scholar

Formanowicz, D. R. Jr., Brodie, E. D. Jr., and Wise, S. C. (1989). Foraging behavior of Matamata turtles: the effects of prey density and the presence of a conspecific. Herpetologica 45, 61–67.

Google Scholar

Fraser, W. R., and Hofmann, E. E. (2003). A predator¹s perspective on causal links between climate change, physical forcing and ecosystem response. Mar. Ecol. Prog. Ser. 265, 1–15. doi: 10.3354/meps265001

CrossRef Full Text | Google Scholar

Fryxell, J. M., and Lundberg, P. (1994). Diet choice and predator—prey dynamics. Evol. Ecol. 8, 407–421.

Google Scholar

Furness, R. W. (2007). Responses of seabirds to depletion of food fish stocks. J. Ornithol. 148, 247–252. doi: 10.1007/s10336-007-0152-2

CrossRef Full Text | Google Scholar

Fussmann, K. E., Schwarzmüller, F., Brose, U., Jousset, A., and Rall, B. C. (2014). Ecological stability in response to warming. Nat. Clim. Chang. 4, 206–210. doi: 10.1038/nclimate2134

CrossRef Full Text | Google Scholar

Giacomini, H. C., Shuter, B. J., and Lester, N. P. (2013). Predator bioenergetics and the prey size spectrum: do foraging costs determine fish production? J. Theor. Biol. 332, 249–260. doi: 10.1016/j.jtbi.2013.05.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibert, J. P., and Yeakel, J. D. (2019). Eco-evolutionary origins of diverse abundance, biomass, and trophic structures in food webs. Front. Ecol. Evol. 7:15. doi: 10.3389/fevo.2019.00015

CrossRef Full Text | Google Scholar

Gilbert, B., Tunney, T. D., McCann, K. S., DeLong, J. P., Vasseur, D. A., Savage, V., et al. (2014). A bioenergetic framework for the temperature dependence of trophic interactions. Ecol. Lett. 17, 902–914. doi: 10.1111/ele.12307

CrossRef Full Text | Google Scholar

Goldbogen, J. A., Calambokidis, J., Oleson, E., Potvin, J., Pyenson, N. D., Schorr, G., et al. (2011). Mechanics, hydrodynamics and energetics of blue whale lunge feeding: efficiency dependence on krill density. J. Exp. Biol. 214, 131–146. doi: 10.1242/jeb.048157

PubMed Abstract | CrossRef Full Text | Google Scholar

Gouhier, T. C., Guichard, F., and Gonzalez, A. (2010). Synchrony and stability of food webs in metacommunities. Am. Nat. 175, E16–E34. doi: 10.1086/649579

CrossRef Full Text | Google Scholar

Griffen, B. D. (2021). Considerations when applying the consumer functional response measured under artificial conditions. Front. Ecol. Evol. 461. doi: 10.3389/fevo.2021.713147

CrossRef Full Text | Google Scholar

Gross, T., and Feudel, U. (2006). Generalized models as a universal approach to the analysis of nonlinear dynamical systems. Phys. Rev. E 73:016205. doi: 10.1103/PhysRevE.73.016205

CrossRef Full Text | Google Scholar

Gross, T., Rudolf, L., Levin, S. A., and Dieckmann, U. (2009). Generalized models reveal stabilizing factors in food webs. Science 325, 747–750. doi: 10.1126/science.1173536

PubMed Abstract | CrossRef Full Text | Google Scholar

Halsey, L. G., Shepard, E. L., and Wilson, R. P. (2011). Assessing the development and application of the accelerometry technique for estimating energy expenditure. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 158, 305–314. doi: 10.1016/j.cbpa.2010.09.002

CrossRef Full Text | Google Scholar

Hammond, M., Loreau, M., De Mazancourt, C., and Kolasa, J. (2020). Disentangling local, metapopulation, and cross-community sources of stabilization and asynchrony in metacommunities. Ecosphere 11:e03078. doi: 10.1002/ecs2.3078

CrossRef Full Text | Google Scholar

Hanya, G. (2004). Seasonal variations in the activity budget of Japanese macaques in the coniferous forest of Yakushima: effects of food and temperature. Am. J. Primatol. 63, 165–177. doi: 10.1002/ajp.20049

PubMed Abstract | CrossRef Full Text | Google Scholar

Hartvig, M., Andersen, K. H., and Beyer, J. E. (2011). Food web framework for size-structured populations. J. Theor. Biol. 272, 113–120. doi: 10.1016/j.jtbi.2010.12.006

CrossRef Full Text | Google Scholar

Haydon, D. (1994). Pivotal assumptions determining the relationship between stability and complexity: an analytical synthesis of the stability-complexity debate. Am. Nat. 144, 14–29.

Google Scholar

Heath, M. R., Speirs, D. C., and Steele, J. H. (2014). Understanding patterns and processes in models of trophic cascades. Ecol. Lett. 17, 101–114. doi: 10.1111/ele.12200

CrossRef Full Text | Google Scholar

Heckmann, L., Drossel, B., Brose, U., and Guill, C. (2012). Interactive effects of body-size structure and adaptive foraging on food-web stability. Ecol. Lett. 15, 243–250. doi: 10.1111/j.1461-0248.2011.01733.x

CrossRef Full Text | Google Scholar

Hein, A. M., and Martin, B. T. (2020). Information limitation and the dynamics of coupled ecological systems. Nat. Ecol. Evol. 4, 82–90. doi: 10.1038/s41559-019-1008-x

CrossRef Full Text | Google Scholar

Heneghan, R. F., Galbraith, E., Blanchard, J. L., Harrison, C., Barrier, N., Bulman, C., et al. (2021). Disentangling diverse responses to climate change among global marine ecosystem models. Prog. Oceanogr. 198:102659. doi: 10.1016/j.pocean.2021.102659

CrossRef Full Text | Google Scholar

Hill, S. L., Murphy, E. J., Reid, K., Trathan, P. N., and Constable, A. J. (2006). Modeling Southern Ocean ecosystems: krill, the food-web, and the impacts of harvesting. Biol. Rev. 81, 581–608. doi: 10.1017/S1464793106007123

PubMed Abstract | CrossRef Full Text | Google Scholar

Hirvonen, H. (1999). Shifts in foraging tactics of larval damselflies: effects of prey density. Oikos 86, 443–452.

Google Scholar

Ho, H. C., Tylianakis, J. M., and Pawar, S. (2021). Behaviour moderates the impacts of food-web structure on species coexistence. Ecol. Lett. 24, 298–309. doi: 10.1111/ele.13643

PubMed Abstract | CrossRef Full Text | Google Scholar

Holling, C. S. (1959a). The components of predation as revealed by a study of small-mammal predation of the European pine sawfly. Can. Entomol. 91, 293–320.

Google Scholar

Holling, C. S. (1959b). Some characteristics of simple types of predation and parasitism. Can. Entomol. 91, 385–398.

Google Scholar

Holling, C. S. (1966). The functional response of invertebrate predators to prey density. Memoirs Entomol. Soc. Canada 98, 5–86.

Google Scholar

Hossie, T. J., and Murray, D. L. (2016). Spatial arrangement of prey affects the shape of ratio-dependent functional response in strongly antagonistic predators. Ecology 97, 834–841. doi: 10.1890/15-1535.1

CrossRef Full Text | Google Scholar

Houston, A. I., and McNamara, J. M. (1989). The value of food: effects of open and closed economies. Anim. Behav. 37, 546–562. doi: 10.1016/0003-3472(89)90034-1

CrossRef Full Text | Google Scholar

Huey, R. B., and Pianka, E. R. (1981). Ecological consequences of foraging mode. Ecology 62, 991–999.

Google Scholar

Iles, A. C., and Rasmussen, J. B. (2005). Indirect effects of metal contamination on energetics of yellow perch (Perca flavescens) resulting from food web simplification. Freshw. Biol. 50, 976–992. doi: 10.1111/j.1365-2427.2005.01380.x

CrossRef Full Text | Google Scholar

Ives, A. R., and Dobson, A. P. (1987). Antipredator behavior and the population dynamics of simple predator-prey systems. Am. Nat. 130, 431–447. doi: 10.1086/284719

CrossRef Full Text | Google Scholar

Jaeger, R. G., and Barnard, D. E. (1981). Foraging tactics of a terrestrial salamander: choice of diet in structurally simple environments. Am. Nat. 117, 639–664.

Google Scholar

Jeschke, J. M. (2007). When carnivores are “full and lazy”. Oecologia 152, 357–364. doi: 10.1007/s00442-006-0654-2

CrossRef Full Text | Google Scholar

Jeschke, J. M., Kopp, M., and Tollrian, R. (2002). Predator functional responses: discriminating between handling and digesting prey. Ecol. Monogr. 72, 95–112. doi: 10.1890/0012-9615(2002)072[0095:PFRDBH]2.0.CO;2

CrossRef Full Text | Google Scholar

Jeschke, J. M., Kopp, M., and Tollrian, R. (2004). Consumer-food systems: why type I functional responses are exclusive to filter feeders. Biol. Rev. 79, 337–349. doi: 10.1017/S1464793103006286

CrossRef Full Text | Google Scholar

Jodice, P. G., Roby, D. D., Hatch, S. A., Gill, V. A., Lanctot, R. B., and Visser, G. H. (2002). Does food availability affect energy expenditure rates of nesting seabirds? A supplemental-feeding experiment with black-legged kittiwakes (Rissa tridactyla). Can. J. Zool. 80, 214–222. doi: 10.1139/z01-221

CrossRef Full Text | Google Scholar

Jodice, P. G., Roby, D. D., Suryan, R. M., Irons, D. B., Turco, K. R., Brown, E. D., et al. (2006). Increased energy expenditure by a seabird in response to higher food abundance. Mar. Ecol. Prog. Ser. 306, 283–293. doi: 10.3354/meps306283

CrossRef Full Text | Google Scholar

Johansson, F. (1991). Foraging modes in an assemblage of odonate larvae—effects of prey and interference. Hydrobiologia 209, 79–87.

Google Scholar

Juliano, S. A., Goughnour, J. A., and Ower, G. D. (2022). Predation in many dimensions: spatial context is important for meaningful functional response experiments. Front. Ecol. Evol. 262. doi: 10.3389/fevo.2022.845560

CrossRef Full Text | Google Scholar

Kalinkat, G., Schneider, F. D., Digel, C., Guill, C., Rall, B. C., and Brose, U. (2013). Body masses, functional responses and predator–prey stability. Ecol. Lett. 16, 1126–1134. doi: 10.1111/ele.12147

CrossRef Full Text | Google Scholar

Kaufman, S. D., Gunn, J. M., Morgan, G. E., and Couture, P. (2006). Muscle enzymes reveal walleye (Sander vitreus) are less active when larger prey (cisco, Coregonus artedi) are present. Can. J. Fish. Aquat. Sci. 63, 970–979. doi: 10.1139/f06-004

CrossRef Full Text | Google Scholar

Killen, S. S., Brown, J. A., and Gamperl, A. K. (2007). The effect of prey density on foraging mode selection in juvenile lumpfish: balancing food intake with the metabolic cost of foraging. J. Anim. Ecol. 76, 814–825. doi: 10.1111/j.1365-2656.2007.01237.x

CrossRef Full Text | Google Scholar

Kingsland, S. E. (1995). Modeling Nature: Episodes in the History of Population Ecology, 2nd, Chicago, IL: Univ. of Chicago Press.

Google Scholar

Kiørboe, T., Saiz, E., Tiselius, P., and Andersen, K. H. (2018). Adaptive feeding behavior and functional responses in zooplankton. Limnol. Oceanogr. 63, 308–321. doi: 10.1002/lno.10632

CrossRef Full Text | Google Scholar

Klein, E. S., Hill, S. L., Hinke, J. T., Phillips, T., and Watters, G. M. (2018). Impacts of rising sea temperature on krill increase risks for predators in the Scotia Sea. PLoS One 13:e0191011. doi: 10.1371/journal.pone.0191011

PubMed Abstract | CrossRef Full Text | Google Scholar

Koen-Alonso, M. (2007). “A process-oriented approach to the multispecies functional response” in From Energetics to Ecosystems: The Dynamics and Structure of Ecological Systems (Dordrecht, Netherlands: Springer), 1–36.

Google Scholar

Kohler, S. L., and McPeek, M. A. (1989). Predation risk and the foraging behavior of competing stream insects. Ecology 70, 1811–1825.

Google Scholar

Kondoh, M. (2003). Foraging adaptation and the relationship between food-web complexity and stability. Science 299, 1388–1391. doi: 10.1126/science.1079154

CrossRef Full Text | Google Scholar

Kondoh, M. (2006). Does foraging adaptation create the positive complexity–stability relationship in realistic food-web structure? J. Theor. Biol. 238, 646–651. doi: 10.1016/j.jtbi.2005.06.028

CrossRef Full Text | Google Scholar

Kooijman, S. A. L. M. (2010). Dynamic Energy Budget Theory for Metabolic Organisation. Cambridge, United Kingdom: Cambridge University Press.

Google Scholar

Kratina, P., Rosenbaum, B., Gallo, B., Horas, E. L., and O’Gorman, E. J. (2022). The combined effects of warming and body size on the stability of predator-prey interactions. Front. Ecol. Evol. 9:772078. doi: 10.3389/fevo.2021.772078

CrossRef Full Text | Google Scholar

Kreiter, N. A., and Wise, D. H. (2001). Prey availability limits fecundity and influences the movement pattern of female fishing spiders. Oecologia 127, 417–424. doi: 10.1007/s004420000607

CrossRef Full Text | Google Scholar

Křivan, V. (1996). Optimal foraging and predator–prey dynamics. Theor. Popul. Biol. 49, 265–290.

Google Scholar

Lima, S. L. (1998). Nonlethal effects in the ecology of predator-prey interactions. Bioscience 48, 25–34.

Google Scholar

Lima, S. L. (2002). Putting predators back into behavioral predator–prey interactions. Trends Ecol. Evol. 17, 70–75. doi: 10.1016/S0169-5347(01)02393-X

CrossRef Full Text | Google Scholar

Lindeman, R. L. (1942). The trophic-dynamic aspect of ecology. Ecology 23, 399–417.

Google Scholar

Loeuille, N. (2010). Consequences of adaptive foraging in diverse communities. Funct. Ecol. 24, 18–27. doi: 10.1111/j.1365-2435.2009.01617.x

CrossRef Full Text | Google Scholar

Loeuille, N., and Loreau, M. (2005). Evolutionary emergence of size-structured food webs. Proc. Natl. Acad. Sci. 102, 5761–5766. doi: 10.1073/pnas.0408424102

PubMed Abstract | CrossRef Full Text | Google Scholar

Lotze, H. K., Tittensor, D. P., Bryndum-Buchholz, A., Eddy, T. D., Cheung, W. W., Galbraith, E. D., et al. (2019). Global ensemble projections reveal trophic amplification of ocean biomass declines with climate change. Proc. Natl. Acad. Sci. 116, 12907–12912. doi: 10.1073/pnas.1900194116

CrossRef Full Text | Google Scholar

MacKenzie, B. R., Leggett, W. C., and Peters, R. H. (1990). Estimating larval fish ingestion rates: can laboratory derived values be reliably extrapolated to the wild? Mar. Ecol. Prog. Series. 67, 209–225.

Google Scholar

May, R. M. (1973). Complexity and Stability in Model Ecosystems. Princeton, NJ: Princeton University Press.

Google Scholar

McCann, K. S. (2000). The diversity–stability debate. Nature 405, 228–233. doi: 10.1038/35012234

PubMed Abstract | CrossRef Full Text | Google Scholar

McCann, K. S. (2011). Food Webs. Monographs in Population Biology 50. Princeton, NJ: Princeton University Press.

Google Scholar

McCann, K. S., Gellner, G., McMeans, B. C., Deenik, T., Holtgrieve, G., Rooney, N., et al. (2016). Food webs and the sustainability of indiscriminate fisheries. Can. J. Fish. Aquat. Sci. 73, 656–665. doi: 10.1139/cjfas-2015-0044

CrossRef Full Text | Google Scholar

McCann, K. S., Hastings, A., and Strong, D. R. (1998). Trophic cascades and trophic trickles in pelagic food webs. Proc. R. Soc. Lond. Ser. B: Biol. Sci. 265, 205–209.

Google Scholar

McMeans, B. C., McCann, K. S., Humphries, M., Rooney, N., and Fisk, A. T. (2015). Food web structure in temporally-forced ecosystems. Trends Ecol. Evol. 30, 662–672. doi: 10.1016/j.tree.2015.09.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Metcalfe, N. B., Fraser, N. H., and Burns, M. D. (1999). Food availability and the nocturnal vs. diurnal foraging trade-off in juvenile salmon. J. Anim. Ecol. 68, 371–381.

Google Scholar

Montagnes, D. J. S., and Fenton, A. (2012). Prey-abundance affects zooplankton assimilation efficiency and the outcome of biogeochemical models. Ecol. Model. 243, 1–7. doi: 10.1016/j.ecolmodel.2012.05.006

CrossRef Full Text | Google Scholar

Montagnes, D. J., Zhu, X., Gu, L., Sun, Y., Wang, J., Horner, R., et al. (2019). False exclusion: a case to embed predator performance in classical population models. Am. Nat. 194, 654–670. doi: 10.5061/dryad.674p6n0

CrossRef Full Text | Google Scholar

Mueller, P., and Diamond, J. (2001). Metabolic rate and environmental productivity: well-provisioned animals evolved to run and idle fast. Proc. Natl. Acad. Sci. U. S. A. 98, 12550–12554. doi: 10.1073/pnas.221456698

CrossRef Full Text | Google Scholar

Munk, P. (1995). Foraging behaviour of larval cod (Gadus morhua) influenced by prey density and hunger. Mar. Biol. 122, 205–212. doi: 10.1007/BF00348933

CrossRef Full Text | Google Scholar

Nagy, K. A., Girard, I. A., and Brown, T. K. (1999). Energetics of free-ranging mammals, reptiles, and birds. Annu. Rev. Nutr. 19, 247–277.

Google Scholar

Nolet, B. A., Butler, P. J., Masman, D., and Woakes, A. J. (1992). Estimation of daily energy expenditure from heart rate and doubly labeled water in exercising geese. Physiol. Zool. 65, 1188–1216.

Google Scholar

Norberg, R. A. (1977). An ecological theory on foraging time and energetics and choice of optimal food-searching method. J. Anim. Ecol. 46, 511–529.

Google Scholar

Oaten, A., and Murdoch, W. W. (1975). Switching, functional response, and stability in predator-prey systems. Am. Nat. 109, 299–318.

Google Scholar

Odum, E. P. (1971) Fundamentals of Ecology, 3rd. WB Saunders, Philadelphia, PA

Google Scholar

Oksanen, L., Fretwell, S. D., Arruda, J., and Niemela, P. (1981). Exploitation ecosystems in gradients of primary productivity. Am. Nat. 118, 240–261.

Google Scholar

Otto, S. B., Rall, B. C., and Brose, U. (2007). Allometric degree distributions facilitate food-web stability. Nature 450, 1226–1229. doi: 10.1038/nature06359

CrossRef Full Text | Google Scholar

Paine, R. T. (1966). Food web complexity and species diversity. Am. Nat. 100, 65–75. doi: 10.1086/282400

CrossRef Full Text | Google Scholar

Papadopoulos, A. (2008). On the hydrodynamics-based power-law function and its application in fish swimming energetics. Trans. Am. Fish. Soc. 137, 997–1006. doi: 10.1577/T07-116.1

CrossRef Full Text | Google Scholar

Papanikolaou, N. E., Broufas, G. D., Papachristos, D. P., Pappas, M. L., Kyriakaki, C., Samaras, K., et al. (2020). On the mechanistic understanding of predator feeding behavior using the functional response concept. Ecosphere 11:e03147. doi: 10.1002/ecs2.3147

CrossRef Full Text | Google Scholar

Papanikolaou, N. E., Milonas, P. G., Demiris, N., Papachristos, D. P., and Matsinos, Y. G. (2014). Digestion limits the functional response of an aphidophagous coccinellid (Coleoptera: Coccinellidae). Ann. Entomol. Soc. Am. 107, 468–474. doi: 10.1603/AN13088

CrossRef Full Text | Google Scholar

Pauly, D., and Christensen, V. (1995). Primary production required to sustain global fisheries. Nature 374, 255–257. doi: 10.1038/374255a0

CrossRef Full Text | Google Scholar

Pawar, S., Dell, A. I., and Savage, V. M. (2012). Dimensionality of consumer search space drives trophic interaction strengths. Nature 486, 485–489. doi: 10.1038/nature11131

CrossRef Full Text | Google Scholar

Pawar, S., Dell, A. I., and Savage, V. M. (2015). “From metabolic constraints on individuals to the dynamics of ecosystems” in Aquatic Functional Biodiversity (Cambridge, MA: Academic Press), 3–36.

Google Scholar

Pazzia, I., Trudel, M., Ridgway, M., and Rasmussen, J. B. (2002). Influence of food web structure on the growth and bioenergetics of lake trout (Salvelinus namaycush). Can. J. Fish. Aquat. Sci. 59, 1593–1605. doi: 10.1139/f02-128

CrossRef Full Text | Google Scholar

Peckarsky, B. L., Abrams, P. A., Bolnick, D. I., Dill, L. M., Grabowski, J. H., Luttbeg, B., et al. (2008). Revisiting the classics: considering nonconsumptive effects in textbook examples of predator–prey interactions. Ecology 89, 2416–2425. doi: 10.1890/07-1131.1

CrossRef Full Text | Google Scholar

Petchey, O. L., Beckerman, A. P., Riede, J. O., and Warren, P. H. (2008). Size, foraging, and food web structure. Proc. Natl. Acad. Sci. 105, 4191–4196. doi: 10.1073/pnas.0710672105

CrossRef Full Text | Google Scholar

Peters, R. H. (1983). The Ecological Implications of Body Size. Cambridge, United Kingdom: Cambridge University Press.

Google Scholar

Peterson, C. C., Nagy, K. A., and Diamond, J. (1990). Sustained metabolic scope. Proc. Natl. Acad. Sci. U. S. A. 87, 2324–2328.

Google Scholar

Pikitch, E. K., Santora, C., Babcock, E. A., Bakun, A., Bonfil, R., Conover, D. O., et al. (2004). Ecosystem-based fishery management. Science 305, 346–347. doi: 10.1126/science.1098222

CrossRef Full Text | Google Scholar

Pimm, S. L. (1982). Food webs. Population and Community Biology Series. New York, NY: Chapman and Hall.

Google Scholar

Pimm, S. L. (1984). The complexity and stability of ecosystems. Nature 307, 321–326.

Google Scholar

Pimm, S. L. (1991). The Balance of Nature? Ecological Issues in the Conservation of Species and Communities. Chicago, IL: University of Chicago Press.

Google Scholar

Pineda-Krch, M., Blok, H. J., Dieckmann, U., and Doebeli, M. (2007). A tale of two cycles–distinguishing quasi-cycles and limit cycles in finite predator–prey populations. Oikos 116, 53–64. doi: 10.1111/j.2006.0030-1299.14940.x

CrossRef Full Text | Google Scholar

Plitzko, S. J., Drossel, B., and Guill, C. (2012). Complexity–stability relations in generalized food-web models with realistic parameters. J. Theor. Biol. 306, 7–14. doi: 10.1016/j.jtbi.2012.04.008

CrossRef Full Text | Google Scholar

Portalier, S. M., Fussmann, G. F., Loreau, M., and Cherif, M. (2019). The mechanics of predator–prey interactions: first principles of physics predict predator–prey size ratios. Funct. Ecol. 33, 323–334. doi: 10.1111/1365-2435.13254

CrossRef Full Text | Google Scholar

Potapov, A. M., Brose, U., Scheu, S., and Tiunov, A. V. (2019). Trophic position of consumers and size structure of food webs across aquatic and terrestrial ecosystems. Am. Nat. 194, 823–839. doi: 10.1086/705811

PubMed Abstract | CrossRef Full Text | Google Scholar

Quévreux, P., and Brose, U. (2019). Metabolic adjustment enhances food web stability. Oikos 128, 54–63. doi: 10.1111/oik.05422

CrossRef Full Text | Google Scholar

Rall, B. C., Brose, U., Hartvig, M., Kalinkat, G., Schwarzmüller, F., Vucic-Pestic, O., et al. (2012). Universal temperature and body-mass scaling of feeding rates. Philos. Transact. R. Soc. B Biol. Sci. 367, 2923–2934. doi: 10.1098/rstb.2012.0242

CrossRef Full Text | Google Scholar

Real, L. A. (1977). The kinetics of functional response. Am. Nat. 111, 289–300. doi: 10.1086/283161

CrossRef Full Text | Google Scholar

Rennie, M. D., Collins, N. C., Shuter, B. J., Rajotte, J. W., and Couture, P. (2005). A comparison of methods for estimating activity costs of wild fish populations: more active fish observed to grow slower. Can. J. Fish. Aquat. Sci. 62, 767–780. doi: 10.1139/f05-052

CrossRef Full Text | Google Scholar

Rizzuto, M., Carbone, C., and Pawar, S. (2018). Foraging constraints reverse the scaling of activity time in carnivores. Nat. Ecol. Evol. 2, 247–253. doi: 10.1038/s41559-017-0386-1

CrossRef Full Text | Google Scholar

Rooney, N., McCann, K. S., and Noakes, D. L. eds. (2006). From Energetics to Ecosystems: The Dynamics and Structure of Ecological Systems (Vol. 1). Berlin, Germany: Springer Science & Business Media.

Google Scholar

Rosenzweig, M. L. (1971). Paradox of enrichment: destabilization of exploitation ecosystems in ecological time. Science 171, 385–387.

Google Scholar

Rossberg, A. G. (2013). Food Webs and Biodiversity: Foundations, Models, Data. Hoboken, NJ: John Wiley & Sons.

Google Scholar

Scharf, I., Lubin, Y., and Ovadia, O. (2011). Foraging decisions and behavioural flexibility in trap-building predators: a review. Biol. Rev. 86, 626–639. doi: 10.1111/j.1469-185X.2010.00163.x

CrossRef Full Text | Google Scholar

Schmitz, O. J., Beckerman, A. P., and O’Brien, K. M. (1997). Behaviorally mediated trophic cascades: effects of predation risk on food web interactions. Ecology 78, 1388–1399.

Google Scholar

Schmitz, O. J., Krivan, V., and Ovadia, O. (2004). Trophic cascades: the primacy of trait-mediated indirect interactions. Ecol. Lett. 7, 153–163. doi: 10.1111/j.1461-0248.2003.00560.x

CrossRef Full Text | Google Scholar

Scott, F., Blanchard, J. L., and Andersen, K. H. (2014). Mizer: an R package for multispecies, trait-based and community size spectrum ecological modeling. Methods Ecol. Evol. 5, 1121–1125. doi: 10.1111/2041-210X.12256

CrossRef Full Text | Google Scholar

Sherwood, G. D., Pazzia, I., Moeser, A., Hontela, A., and Rasmussen, J. B. (2002). Shifting gears: enzymatic evidence for the energetic advantage of switching diet in wild-living fish. Can. J. Fish. Aquat. Sci. 59, 229–241. doi: 10.1139/f02-001

CrossRef Full Text | Google Scholar

Shin, Y. J., and Cury, P. (2001). Exploring fish community dynamics through size-dependent trophic interactions using a spatialized individual-based model. Aquat. Living Resour. 14, 65–80. doi: 10.1016/S0990-7440(01)01106-8

CrossRef Full Text | Google Scholar

Shiratsuru, S., Majchrzak, Y. N., Peers, M. J., Studd, E. K., Menzies, A. K., Derbyshire, R., et al. (2021). Food availability and long-term predation risk interactively affect antipredator response. Ecology 102:e03456. doi: 10.1002/ecy.3456

PubMed Abstract | CrossRef Full Text | Google Scholar

Shurin, J. B., Gruner, D. S., and Hillebrand, H. (2006). All wet or dried up? Real differences between aquatic and terrestrial food webs. Proc. R. Soc. B Biol. Sci. 273, 1–9. doi: 10.1098/rspb.2005.3377

CrossRef Full Text | Google Scholar

Sibly, R. M., Brown, J. H., and Kodric-Brown, A. eds. (2012). Metabolic Ecology: A Scaling Approach. Hoboken, NJ: John Wiley & Sons, doi: 10.1002/9781119968535.

CrossRef Full Text | Google Scholar

Sih, A., Crowley, P., McPeek, M., Petranka, J., and Strohmeier, K. (1985). Predation, competition, and prey communities: a review of field experiments. Annu. Rev. Ecol. Syst. 16, 269–311.

Google Scholar

Skalski, G. T., and Gilliam, J. F. (2001). Functional responses with predator interference: viable alternatives to the Holling type II model. Ecology 82, 3083–3092. doi: 10.1890/0012-9658(2001)082[3083:FRWPIV]2.0.CO;2

CrossRef Full Text | Google Scholar

Smith, A. D., Brown, C. J., Bulman, C. M., Fulton, E. A., Johnson, P., Kaplan, I. C., et al. (2011). Impacts of fishing low–trophic level species on marine ecosystems. Science 333, 1147–1150. doi: 10.1126/science.1209395

CrossRef Full Text | Google Scholar

Stephens, P. A., and Sutherland, W. J. (1999). Consequences of the Allee effect for behaviour, ecology and conservation. Trends Ecol. Evol. 14, 401–405. doi: 10.1016/S0169-5347(99)01684-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Strogatz, S. H. (2018). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Boca Raton, FL: CRC Press.

Google Scholar

Taylor, C. R., Heglund, N. C., and Maloiy, G. M. (1982). Energetics and mechanics of terrestrial locomotion. I. Metabolic energy consumption as a function of speed and body size in birds and mammals. J. Exp. Biol. 97, 1–21.

Google Scholar

Teckentrup, L., Grimm, V., Kramer-Schadt, S., and Jeltsch, F. (2018). Community consequences of foraging under fear. Ecol. Model. 383, 80–90. doi: 10.1016/j.ecolmodel.2018.05.015

CrossRef Full Text | Google Scholar

Thomas, D. W., Blondel, J., Perret, P., Lambrechts, M. M., and Speakman, J. R. (2001). Energetic and fitness costs of mismatching resource supply and demand in seasonally breeding birds. Science 291, 2598–2600. doi: 10.1126/science.1057487

CrossRef Full Text | Google Scholar

Tieleman, B. I., and Williams, J. B. (2002). Effects of food supplementation on behavioural decisions of hoopoe-larks in the Arabian Desert: balancing water, energy and thermoregulation. Anim. Behav. 63, 519–529. doi: 10.1006/anbe.2001.1927

CrossRef Full Text | Google Scholar

Tinbergen, J. M., and Dietz, M. W. (1994). Parental energy expenditure during brood rearing in the great tit (Parus major) in relation to body mass, temperature, food availability and clutch size. Funct. Ecol. 8, 563–572.

Google Scholar

Tittensor, D. P., Eddy, T. D., Lotze, H. K., Galbraith, E. D., Cheung, W., Barange, M., et al. (2018). A protocol for the intercomparison of marine fishery and ecosystem models: fish-MIP v1.0. Geosci. Model Dev. 11, 1421–1442. doi: 10.5194/gmd-11-1421-2018

CrossRef Full Text | Google Scholar

Topping, C. J., Alrøe, H. F., Farrell, K. N., and Grimm, V. (2015). Per aspera ad astra: through complex population modeling to predictive theory. Am. Nat. 186, 669–674. doi: 10.1086/683181

CrossRef Full Text | Google Scholar

Turesson, H., and Brönmark, C. (2007). Predator–prey encounter rates in freshwater piscivores: effects of prey density and water transparency. Oecologia 153, 281–290. doi: 10.1007/s00442-007-0728-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Uchida, S., and Drossel, B. (2007). Relation between complexity and stability in food webs with adaptive behavior. J. Theor. Biol. 247, 713–722. doi: 10.1016/j.jtbi.2007.04.019

CrossRef Full Text | Google Scholar

Uchida, S., Drossel, B., and Brose, U. (2007). The structure of food webs with adaptive behaviour. Ecol. Model. 206, 263–276. doi: 10.1016/j.ecolmodel.2007.03.035

CrossRef Full Text | Google Scholar

Uiterwaal, S. F., and DeLong, J. P. (2018). Multiple factors, including arena size, shape the functional responses of ladybird beetles. J. Appl. Ecol. 55, 2429–2438. doi: 10.1111/1365-2664.13159

CrossRef Full Text | Google Scholar

Uiterwaal, S. F., and DeLong, J. P. (2020). Functional responses are maximized at intermediate temperatures. Ecology 101:e02975. doi: 10.1002/ecy.2975

PubMed Abstract | CrossRef Full Text | Google Scholar

Valdovinos, F. S., Ramos-Jiliberto, R., Garay-Narváez, L., Urbani, P., and Dunne, J. A. (2010). Consequences of adaptive behaviour for the structure and dynamics of food webs. Ecol. Lett. 13, 1546–1559. doi: 10.1111/j.1461-0248.2010.01535.x

CrossRef Full Text | Google Scholar

Van Gils, J. A., De Rooij, S. R., Van Belle, J., Van Der Meer, J., Dekinga, A., Piersma, T., et al. (2005). Digestive bottleneck affects foraging decisions in red knots Calidris canutus. I. Prey choice. J. Anim. Ecol. 74, 105–119. doi: 10.1111/j.1365-2656.2004.00903.x

CrossRef Full Text | Google Scholar

Van Schmidt, N. D., and Beissinger, S. R. (2020). The rescue effect and inference from isolation–extinction relationships. Ecol. Lett. 23, 598–606. doi: 10.1111/ele.13460

CrossRef Full Text | Google Scholar

Vermeij, G. J. (1994). The evolutionary interaction among species: selection, escalation, and coevolution. Annu. Rev. Ecol. Syst. 25, 219–236.

Google Scholar

Videler, J. J., and Nolet, B. A. (1990). Costs of swimming measured at optimum speed: scale effects, differences between swimming styles, taxonomic groups and submerged and surface swimming. Comp. Biochem. Physiol. A Comp. Physiol. 97, 91–99. doi: 10.1016/0300-9629(90)90155-L

PubMed Abstract | CrossRef Full Text | Google Scholar

Vucic-Pestic, O., Rall, B. C., Kalinkat, G., and Brose, U. (2010). Allometric functional response model: body masses constrain interaction strengths. J. Anim. Ecol. 79, 249–256. doi: 10.1111/j.1365-2656.2009.01622.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Werner, E. E., and Anholt, B. R. (1993). Ecological consequences of the trade-off between growth and mortality rates mediated by foraging activity. Am. Nat. 142, 242–272.

Google Scholar

Werner, E. E., and Peacor, S. D. (2003). A review of trait-mediated indirect interactions in ecological communities. Ecology 84, 1083–1100. doi: 10.1890/0012-9658(2003)084[1083:AROTII]2.0.CO;2

CrossRef Full Text | Google Scholar

Williams, R. J., and Martinez, N. D. (2000). Simple rules yield complex food webs. Nature 404, 180–183.

Google Scholar

Williams, R. J., and Martinez, N. D. (2004). Stabilization of chaotic and non-permanent food-web dynamics. Eur. Phys. J. B 38, 297–303. doi: 10.1140/epjb/e2004-00122-1

CrossRef Full Text | Google Scholar

Wirsing, A. J., Heithaus, M. R., Brown, J. S., Kotler, B. P., and Schmitz, O. J. (2021). The context dependence of non-consumptive predator effects. Ecol. Lett. 24, 113–129. doi: 10.1111/ele.13614

CrossRef Full Text | Google Scholar

Woodward, G., Ebenman, B., Emmerson, M., Montoya, J. M., Olesen, J. M., Valido, A., et al. (2005). Body size in ecological networks. Trends Ecol. Evol. 20, 402–409. doi: 10.1016/j.tree.2005.04.005

CrossRef Full Text | Google Scholar

Yeakel, J. D., Stiefs, D., Novak, M., and Gross, T. (2011). Generalized modeling of ecological population dynamics. Theor. Ecol. 4, 179–194. doi: 10.1007/s12080-011-0112-6

CrossRef Full Text | Google Scholar

Yodzis, P. (1988). The indeterminacy of ecological interactions as perceived through perturbation experiments. Ecology 69, 508–515.

Google Scholar

Yodzis, P., and Innes, S. (1992). Body size and consumer-resource dynamics. Am. Nat. 139, 1151–1175.

Google Scholar