Mapping species diversification metrics in macroecology: Prospects and challenges

Velasco, Julián A.; Pinto-Ledezma, Jesús N.

doi:10.3389/fevo.2022.951271

REVIEW article

Front. Ecol. Evol., 28 September 2022

Sec. Biogeography and Macroecology

Volume 10 - 2022 | https://doi.org/10.3389/fevo.2022.951271

This article is part of the Research Topic Rising Stars in Biogeography and Macroecology 2021 View all 4 articles

Mapping species diversification metrics in macroecology: Prospects and challenges

$\r\nJulin A. Velasco*&#x;$ Julián A. Velasco^1*†

Jesús N. Pinto-Ledezma^2†

¹Instituto de Ciencias de la Atmósfera y Cambio Climático, Universidad Nacional Autónoma de México, Mexico City, Mexico
²Department of Ecology, Evolution, and Behavior, University of Minnesota, Saint Paul, MN, United States

The intersection of macroecology and macroevolution is one of today’s most active research in biology. In the last decade, we have witnessed a steady increment of macroecological studies that use metrics attempting to capture macroevolutionary processes to explain present-day biodiversity patterns. Evolutionary explanations of current species richness gradients are fundamental for understanding how diversity accumulates in a region. Although multiple hypotheses have been proposed to explain the patterns we observe in nature, it is well-known that the present-day diversity patterns result from speciation, extinction, colonization from nearby areas, or a combination of these macroevolutionary processes. Whether these metrics capture macroevolutionary processes across space is unknown. Some tip-rate metrics calculated directly from a phylogenetic tree (e.g., mean root distance -MRD-; mean diversification rate -mDR-) seem to return very similar geographical patterns regardless of how they are estimated (e.g., using branch lengths explicitly or not). Model-based tip-rate metrics —those estimated using macroevolutionary mixtures, e.g., the BAMM approach— seem to provide better net diversification estimates than only speciation rates. We argue that the lack of appropriate estimates of extinction and dispersal rates in phylogenetic trees may strongly limit our inferences about how species richness gradients have emerged at spatial and temporal scales. Here, we present a literature review about this topic and empirical comparisons between select taxa with several of these metrics. We implemented a simple null model approach to evaluate whether mapping of these metrics deviates from a random sampling process. We show that phylogenetic metrics by themselves are relatively poor at capturing speciation, extinction, and dispersal processes across geographical gradients. Furthermore, we provide evidence of how parametric biogeographic methods can improve our inference of past events and, therefore, our conclusions about the evolutionary processes driving biodiversity patterns. We recommend that further studies include several approaches simultaneously (e.g., spatial diversification modeling, parametric biogeographic methods, simulations) to disentangle the relative role of speciation, extinction, and dispersal in the generation and maintenance of species richness gradients at regional and global scales.

Introduction

The causes of geographical variation of biodiversity are among the most fundamental questions in ecology, biogeography, and macroecology (Brown, 1995, 2014; Hawkins et al., 2012; Fine, 2015; Jablonski et al., 2017). Recent studies have attempted to integrate different sets of ecological and evolutionary mechanisms driving species diversity at local and regional spatial scales into a single framework (Cutter and Gray, 2016; Pärtel et al., 2016; Cabral et al., 2017; Leidinger and Cabral, 2017; Pontarp et al., 2019; Machac, 2020; Hagen et al., 2021). However, it is well-established that three (macro)evolutionary processes ultimately modify the number of species in a given region: speciation, extinction, and dispersal (Wiens, 2011; Fine, 2015; Jablonski et al., 2017). These three processes may in turn be influenced by biotic factors [e.g., species’ trait variation within clades (Rabosky, 2006; Clavel and Morlon, 2017; Jezkova and Wiens, 2017; Moen and Wiens, 2017) competitive interactions (McPeek, 2008; Condamine et al., 2019)], abiotic factors [e.g., climatic and geological conditions (Condamine et al., 2013; Lewitus and Morlon, 2018)], and the ability to adapt to novel or harsh environments (Cutter and Gray, 2016). Further evidence has indicated that the time for speciation (Stephens and Wiens, 2003) and geographical area (Losos and Schluter, 2000) may also impact the rates of these macroevolutionary processes.

The integration of different disciplines within biology—e.g., phylogenetics, palaeontology, and historical biogeography—has improved our ability to discern between the different ecological and evolutionary processes acting across distinct spatial and temporal scales (Diniz-Filho et al., 2013; Fritz et al., 2013; Pontarp et al., 2019). For instance, it is well established that fossil data are crucial to accurately infer diversification dynamics (the balance between speciation and extinction) (Quental and Marshall, 2010; Rabosky, 2010). Recent advances in model-based approaches to reconstruct diversification dynamics have shown adequate progress (Morlon et al., 2010; Stadler, 2013; Morlon, 2014; Rabosky, 2014; Magee et al., 2020). New statistical approaches have been developed to analyze fossil occurrence datasets by explicitly incorporating sampling bias effects, thus improving estimates of speciation and extinction rates through time (Silvestro et al., 2014, 2016). These methodological advances have allowed us to gain new insights about the role of evolutionary dynamics on the accumulation of species within regions and the geographical gradients of biodiversity (Silvestro et al., 2014; Antonelli et al., 2015; Jablonski et al., 2017; Rabosky et al., 2018; Miller and Román-Palacios, 2021).

Macroecological studies mainly use two approaches to link species diversification rates with geographical gradients of biodiversity (Hawkins et al., 2003; Algar et al., 2009; Qian et al., 2015; Villalobos et al., 2020; García-Rodríguez et al., 2021a,b). The first approach relies on the use of phylogenetic metrics that seek to capture a geographical signature of species diversification dynamics (Diniz-Filho et al., 2013; Fritz et al., 2013; Table 1). These phylogenetic metrics, in general, are calculated as the average of metric values across all co-occurring species in a site or grid-cell (Table 1). These metrics can be classified as model-free rate metrics—mean root distance (MRD), residual phylogenetic diversity (rPD), mean diversification rate (mDR), phylogenetic species variability (PSV), mean ages (mAges); see also Table 1— and model-based metrics (e.g., species-specific diversification or tip rates from the BAMM approach; Rabosky, 2014, 2016). Although it is well-known that some of these metrics can only provide information about speciation events (see Title and Rabosky, 2019), many studies have used these metrics to test hypotheses about regional diversification or evolutionary time across geography (Sánchez-Ramírez et al., 2015; Machac et al., 2018; Machac, 2020; García-Rodríguez et al., 2021a,b; Miller and Román-Palacios, 2021). The second approach explicitly estimates diversification parameters across geography (Goldberg et al., 2005, 2011; Ramiadantsoa et al., 2017). For instance, the geographic state speciation and extinction model (GeoSSE sensu, Goldberg et al., 2011) and its extensions (Goldberg and Igić, 2012; Ramiadantsoa et al., 2017; Caetano et al., 2018) allow the estimation of speciation, extinction, and dispersal parameters across two regions (Table 1). Therefore, the GeoSSE approach disentangles the relative role of speciation, extinction, and dispersal on the origin and maintenance of geographical diversity gradients (Rolland et al., 2014; Pulido-Santacruz and Weir, 2016; Pinto-Ledezma et al., 2017). The main limitation of this approach is that only two regions may be tested for these effects, but see Ramiadantsoa et al. (2017) for an application to multiple regions. Despite methodological advances in both approaches, a challenge remains unsolved in macroecological research— the simultaneous modeling of evolutionary rates across spatial and temporal scales in macroecological research (Velasco et al., 2020; Villalobos et al., 2020).

TABLE 1

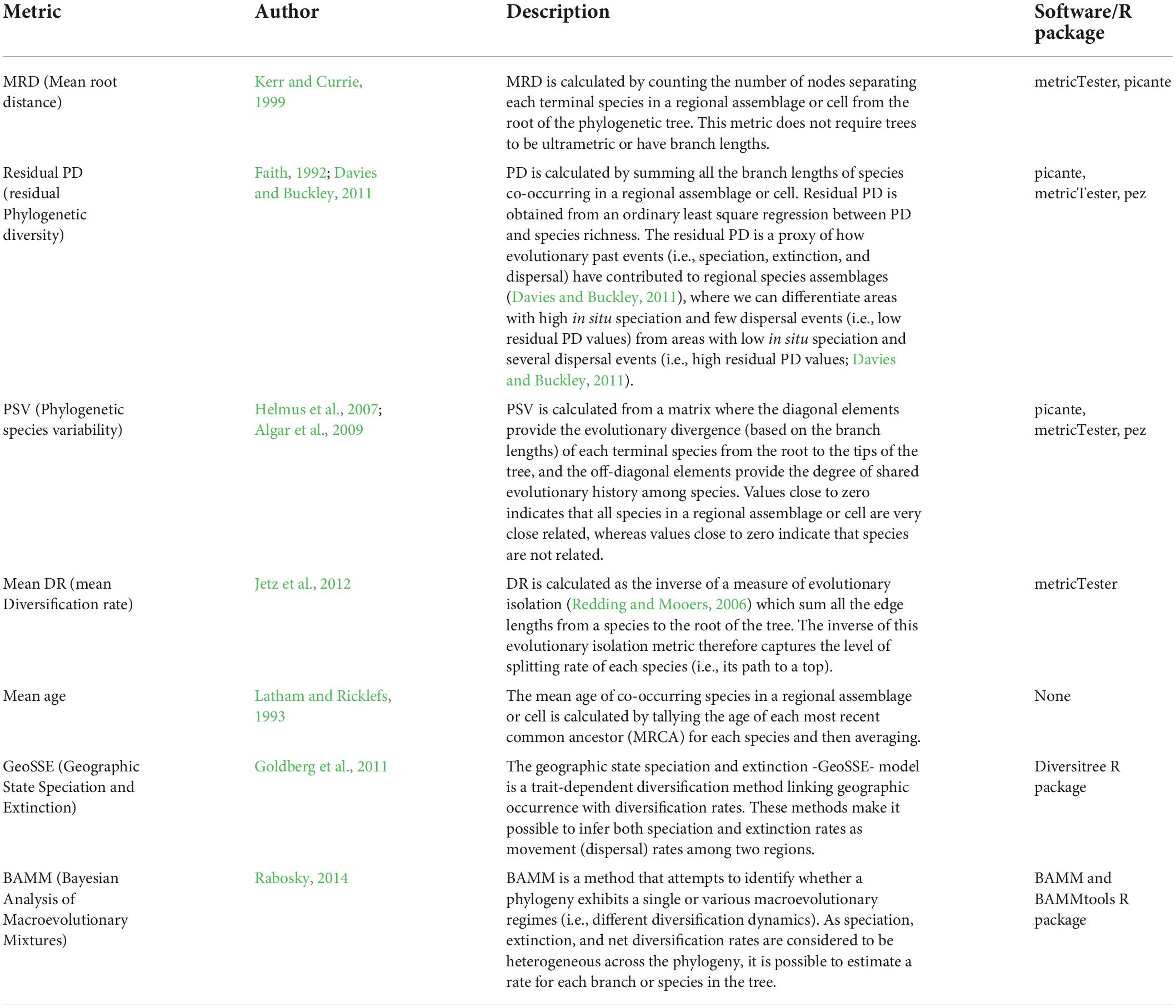
Table 1. Phylogenetic metrics and approaches used in macroecological studies to test the role of phylogenetic niche conservatism (PNC) and regional diversification (RD) shaping present-day species richness patterns across geography.

Here, we perform a literature review on the use of phylogenetic metrics to test different evolutionary hypotheses (Table 2). We aim to evaluate whether these metrics can capture species diversification and biogeographic processes that ultimately shape the geographical gradients of species diversity. Given the extensive literature on this topic, we only focused on a specific set of phylogenetic metrics that have been used extensively in the macroecological literature (Villalobos et al., 2020; Table 1). Additional phylogenetic metrics used in community ecology and conservation have been the focus of other reviews (e.g., Miller et al., 2017; Tucker et al., 2017), and are not reviewed here. For each of the included metrics, we discuss the main limitations focusing mainly on the extent to which these metrics can effectively capture spatial macroevolutionary dynamics. In addition, we explore how dispersal and extinction processes—usually explicitly neglected in macroecological studies—can limit our understanding of diversification dynamics across spatial gradients. To do so, we use three empirical examples from our own work and others (Algar et al., 2009; Pinto-Ledezma et al., 2017, 2019; Velasco et al., 2018) to illustrate these complex issues and highlight potential limitations (Figure 1). Finally, we call for a more integrative approach by implementing complementary approaches (e.g., null models, spatially explicit simulations, parametric biogeographical methods), which we believe will help improve inferences about spatial diversification dynamics in macroecological research.

TABLE 2

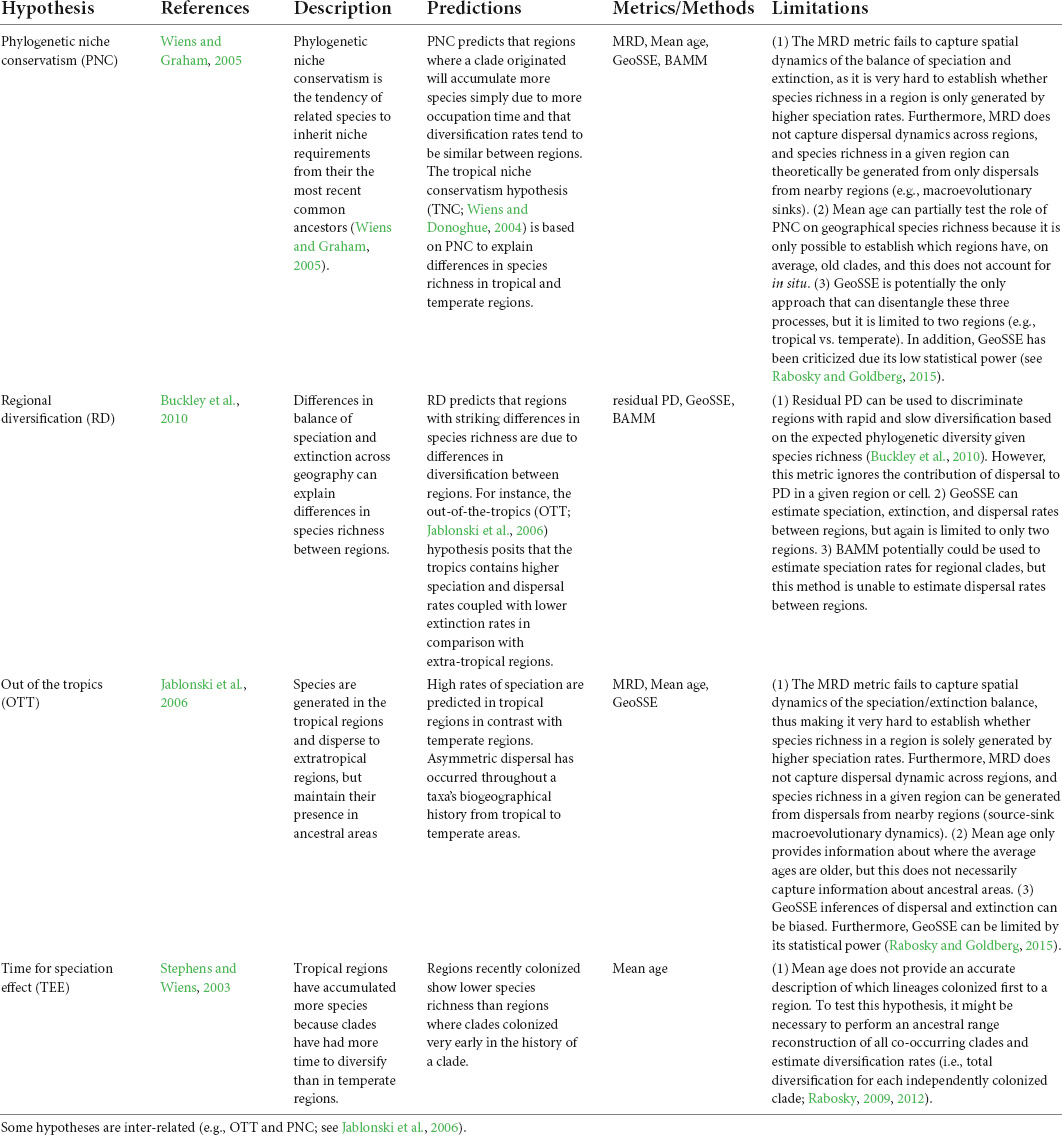
Table 2. Main evolutionary hypotheses tested in macroecological studies to explain and understand how present-day geographical diversity gradients emerged and are maintained.

FIGURE 1

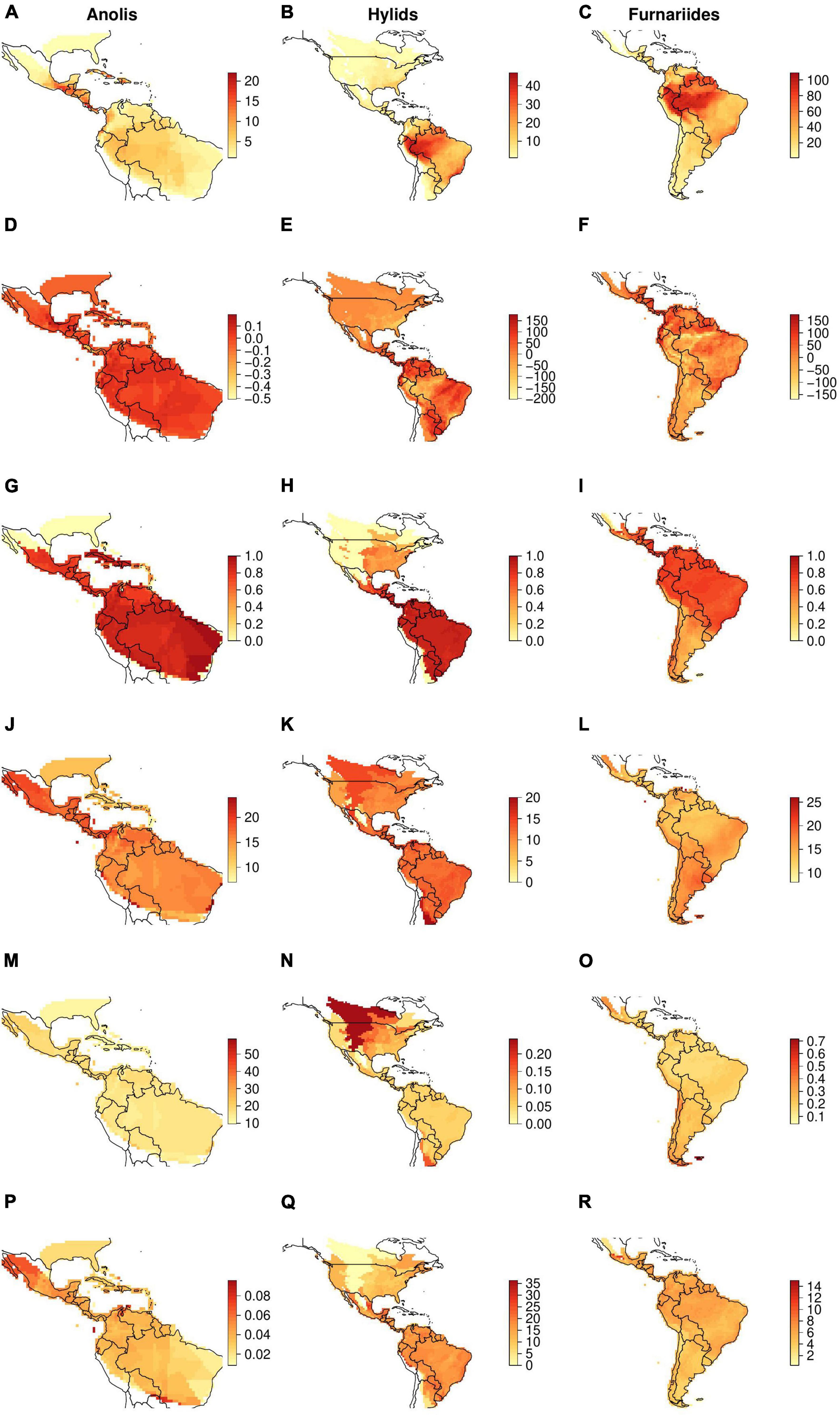
Figure 1. Geographical patterns of several phylogenetic metrics used in macroecological studies to explore evolutionary processes underlying geographical diversity gradients (also see Table 1 for a detailed explanation). Left column, Anolis lizards; middle column, hylid frogs; right column, Furnariides birds. (A–C) observed richness patterns; (D–F) rPD, residual phylogenetic diversity (i.e., after controlling for species richness); (G–I) PSV, phylogenetic species variability; (J–L) MRD, mean root distance; (M–O) mDR, mean diversification rate; (P–R) mAges, average ages of species.

Methods

We reviewed the literature to find studies focused on the role of diversification dynamics on the geographical biodiversity gradients published up until early-2021. We searched for articles in Web of Science using combinations of the following keywords: latitudinal diversity gradient*, macroecology*, diversification dynamics*, phylogenetic metrics*, species richness gradients*, phylogenetic diversity*, mean root distance*, phylogenetic species variability*, time for speciation effect*, evolutionary time*, diversification rates*, tip-rates*, GeoSSE*, BAMM*, BioGEOBEARS*, Biogeographical stochastic mapping*. We focused only on studies that used the following five phylogenetic metrics—mean root distance (MRD), residual phylogenetic diversity (rPD), phylogenetic species variability (PSV), mean diversification rate (mDR), mean Ages (mAges), and two model approaches as GeoSSE and BAMM (Table 1). The selected metrics have been extensively used as a proxy for diversification and/or evolutionary time. In addition, we selected studies adopting an explicit macroevolutionary or biogeographical approach (e.g., GeoSSE, BAMM, BioGEOBEARS). Although this is not meant to be an exhaustive review, we believe that the selected papers encompass a diverse set of authors and countries where macroecological research is being conducted. The majority of these papers also test the effect of historical processes/events as drivers of latitudinal diversity gradients (LDG) across several taxa.

We compared the geographical patterns of these metrics and their statistical performance by using a simple null model approach and comparing them against model-based methods (e.g., GeoSSE, BAMM, BioGEOBEARS). We explored whether the geographical patterns of these phylogenetic metrics in three empirical examples (see below) coincide with the macroevolutionary dynamics inferred using an explicit diversification modeling approach. The three empirical examples (Figure 1) were selected because, in previous work, they were used to test how evolutionary-based hypotheses affect the present-day species richness gradient (Algar et al., 2009; Pinto-Ledezma et al., 2017, 2019; Velasco et al., 2018) (see further details in each study and Supplementary Material). Here, as we are interested in evaluating whether the spatial gradients of each phylogenetic metric depart from a simple random sampling process, we randomly re-shuffled the presence-absence matrix (i.e., PAM) 1000 times, while maintaining the frequency of species occurrence and observed richness in the cells/assemblages (Gotelli, 2000). This kind of null model is standard in studies at the community/assemblage level that use phylogenetic information (Cavender-Bares et al., 2004; Pinto-Ledezma et al., 2020; Figure 2). The null model was implemented using customized scripts and core functions from the picante (Kembel et al., 2010) package in R. We also tested for differences in metric values between regions (e.g., forest habitats versus open habitats) using Bayesian-ANOVAs. Then we used Maximum A Posteriori (MAP) p-values to evaluate the evidence for those differences. Bayesian-ANOVAs were implemented in the probabilistic programming language Stan (Carpenter et al., 2017) through the R package brms (Bürkner, 2017), and the MAP p-values were estimated using the R package bayestestR (Makowski et al., 2019).

FIGURE 2

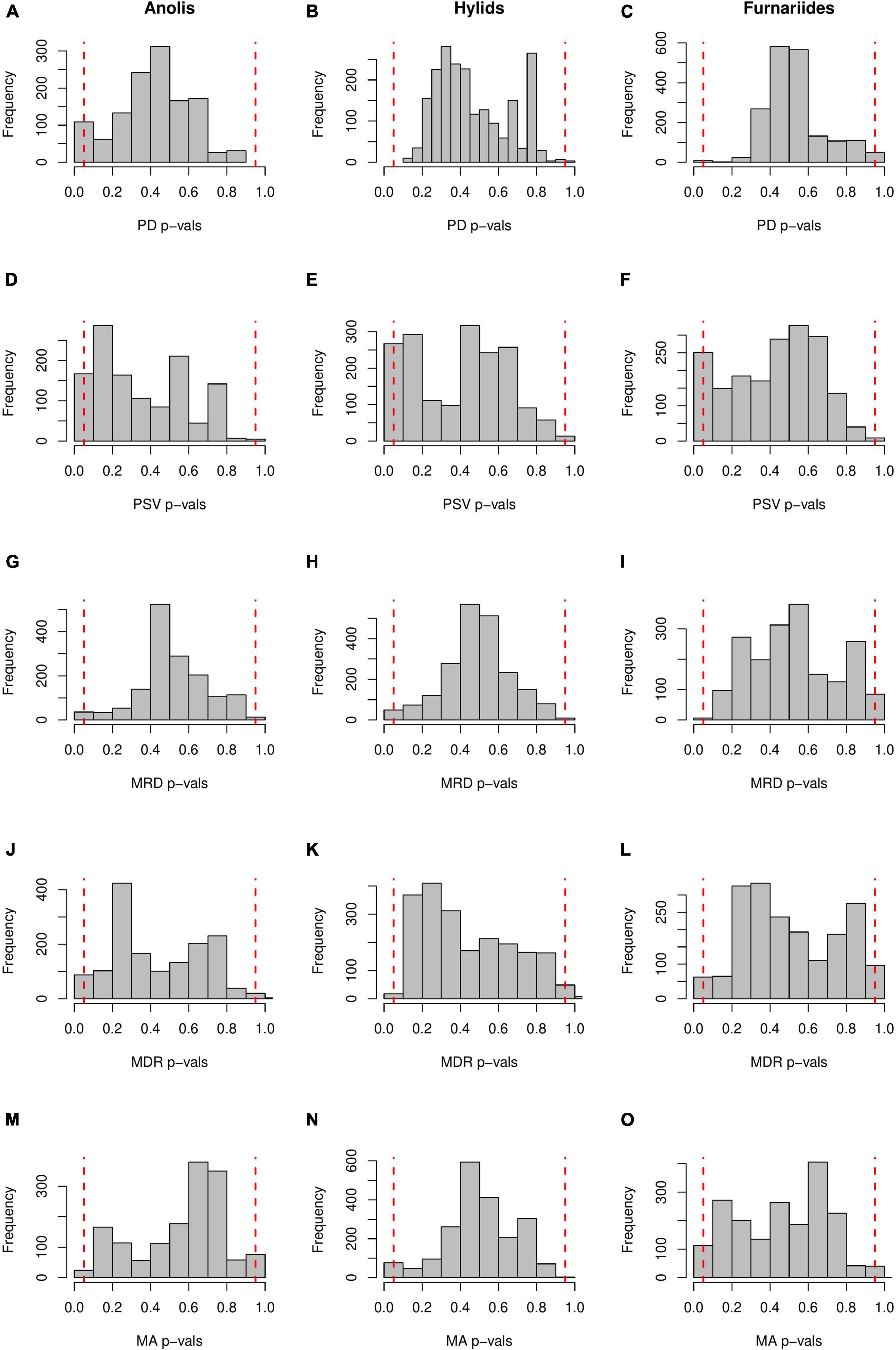
Figure 2. P-values for each phylogenetic metric obtained through null models. Histograms show the frequency distribution of p-values of Anolis lizards (left-panels A,D,G,J,M), hylid frogs (mid-panels B,E,H,K,N), and Furnariides birds (right-panels C,F,I,L,O). Vertical dashed red lines represent the low (metric value ≤ 0.05) and high (metric value ≥ 0.95) quantile values of the metrics expected under the null model. For example, high quantiles of phylogenetic diversity (PD p-vals ≥ 0.95) mean greater phylogenetic diversity among co-occurring species than expected by the null model, whereas low quantiles of phylogenetic diversity (PD p-vals ≤ 0.05) mean lower phylogenetic diversity among co-occurring species than expected under the null model. The null model used in this study was the ‘independentswap’ randomization algorithm that randomizes the observed presence-absence matrix while maintaining species occurrence frequency and species richness per grid-cell. See “Methods” section for more details.

We also implemented model-based approaches to evaluate how ignoring dispersal and extinction processes might affect our conclusions about the controls on geographical species richness gradients. We first used the GeoSSE model to estimate three macroevolutionary parameters (i.e., speciation, extinction, and dispersal) between two areas for each of the selected taxonomic groups (Tables 3, 4). We then implemented the biogeographical stochastic mapping (BSM) method (Dupin et al., 2017), which allows us to estimate more accurately the number of dispersal events between regions based on a better estimation of the clade’s ancestral area. Specifically, we tested how dispersal rates between regions can affect inferences drawn only from phylogenetic metrics in the three data sets. Finally, we used the Bayesian Analysis of Macroevolutionary Mixtures (BAMM) approach to obtain per-species level diversification rates (a tip-rate metric). The BAMM approach was implemented using the software BAMM 2.5.0 (Rabosky, 2014) (see Supplementary Material for further details).

TABLE 3

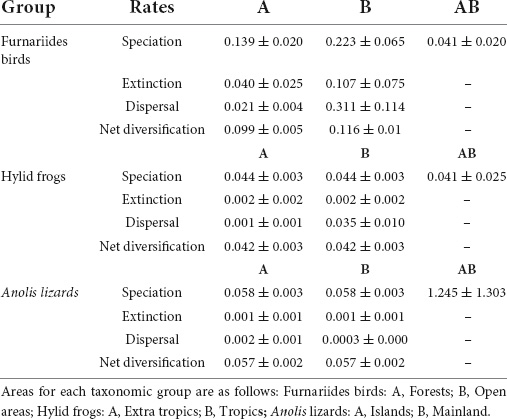
Table 3. Parameter estimates from the GeoSSE model for the three taxonomic groups examined in this study (Furnariides birds, hylid frogs, and Anolis lizards) across two regions.

TABLE 4

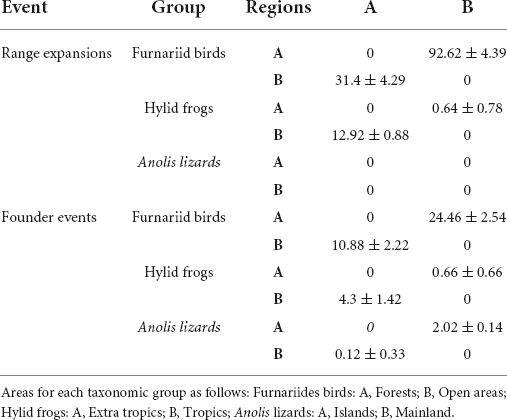
Table 4. Frequency of dispersal events inferred using biogeographical stochastic mapping (BSM) for the three taxonomic groups examined in this study (Furnariides birds, hylid frogs, and Anolis lizards) across two regions.

Results

A comparison of phylogenetic metrics to understand species diversification dynamics in macroecology

In the following section, we discuss each metric listed in Table 1. We compared the spatial patterns of these model-free phylogenetic metrics with estimates obtained from a model-based approach.

Mean root distance

Mean root distance, the number of nodes from the tips to the root, captures a total diversification value portraying the number of cladogenetic events co-occurring in a given region. In the case of furnariid birds, we found that MRD values tend to be higher in open areas than in forests (Figure 3). This metric suggests that more cladogenetic events occurred in open areas. The MRD metric for this bird clade is consistent with results from explicit diversification approaches (Table 3). For hylid frogs, although it seems that there are no differences in MRD values between extratropics and tropics areas (Figure 4), tropical areas have some cells with very high values. However, tropical areas have some cells with very high values. Again, MRD accurately describes the total diversification pattern in this clade across the latitudinal gradient. In Anolis lizards, we found that MRD values tend to be lower on islands than mainland areas (Figure 5). In this case, MRD did not accurately describe the evolutionary processes occurring between the mainland and insular anole assemblages. However, there is also a high probability that the high MRD values in the mainland reflect an idiosyncratic evolutionary trajectory of each of the two clades that radiated there (i.e., the Draconura and Dactyloa clades). In fact, a recent study found that these two clades exhibit differential diversification dynamics across geography (Patton et al., 2021).

FIGURE 3

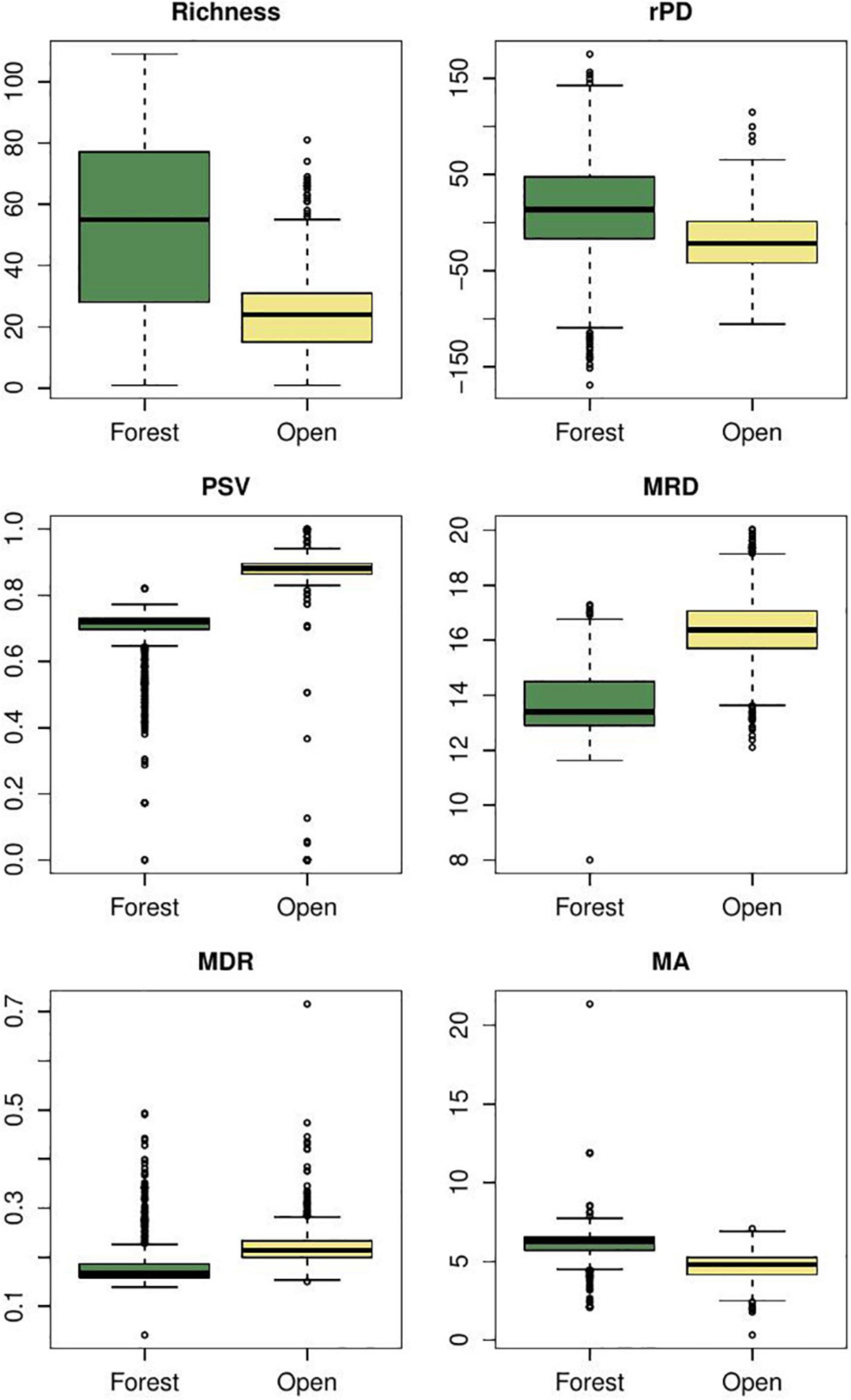
Figure 3. Variation of phylogenetic metric values in Furnariides birds for forested and open areas. rPD, residual phylogenetic diversity (i.e., after controlling for species richness); PSV, phylogenetic species variability; MRD, mean root distance; mDR, mean diversification rate; mAges, average ages of species. Y-labels correspond to the values of each metric. Comparisons of metrics between regions were evaluated using Bayesian ANOVAs and all differences were significant (Maximum A posteriori p-values < 0.001).

FIGURE 4

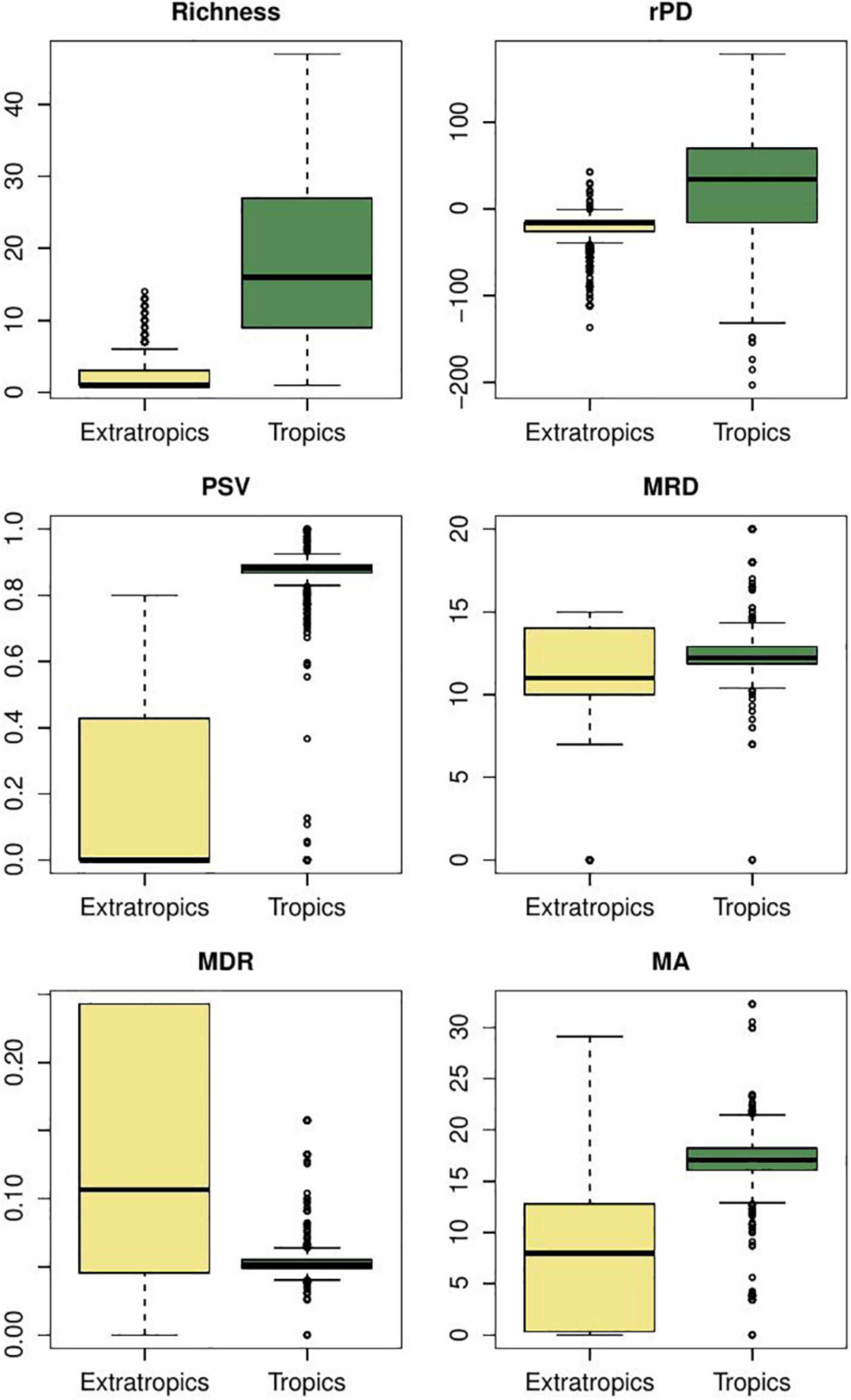
Figure 4. Variation of phylogenetic metric values in hylid frogs for the tropics and extra-tropical regions. rPD: residual phylogenetic diversity (i.e., after controlling for species richness); PSV, phylogenetic species variability; MRD, mean root distance; mDR, mean diversification rate; mAges, average ages of species. Y-labels correspond to the values of each metric. Comparisons of metrics between regions were evaluated using Bayesian ANOVAs and all were significant (Maximum A posteriori p-values < 0.001).

FIGURE 5

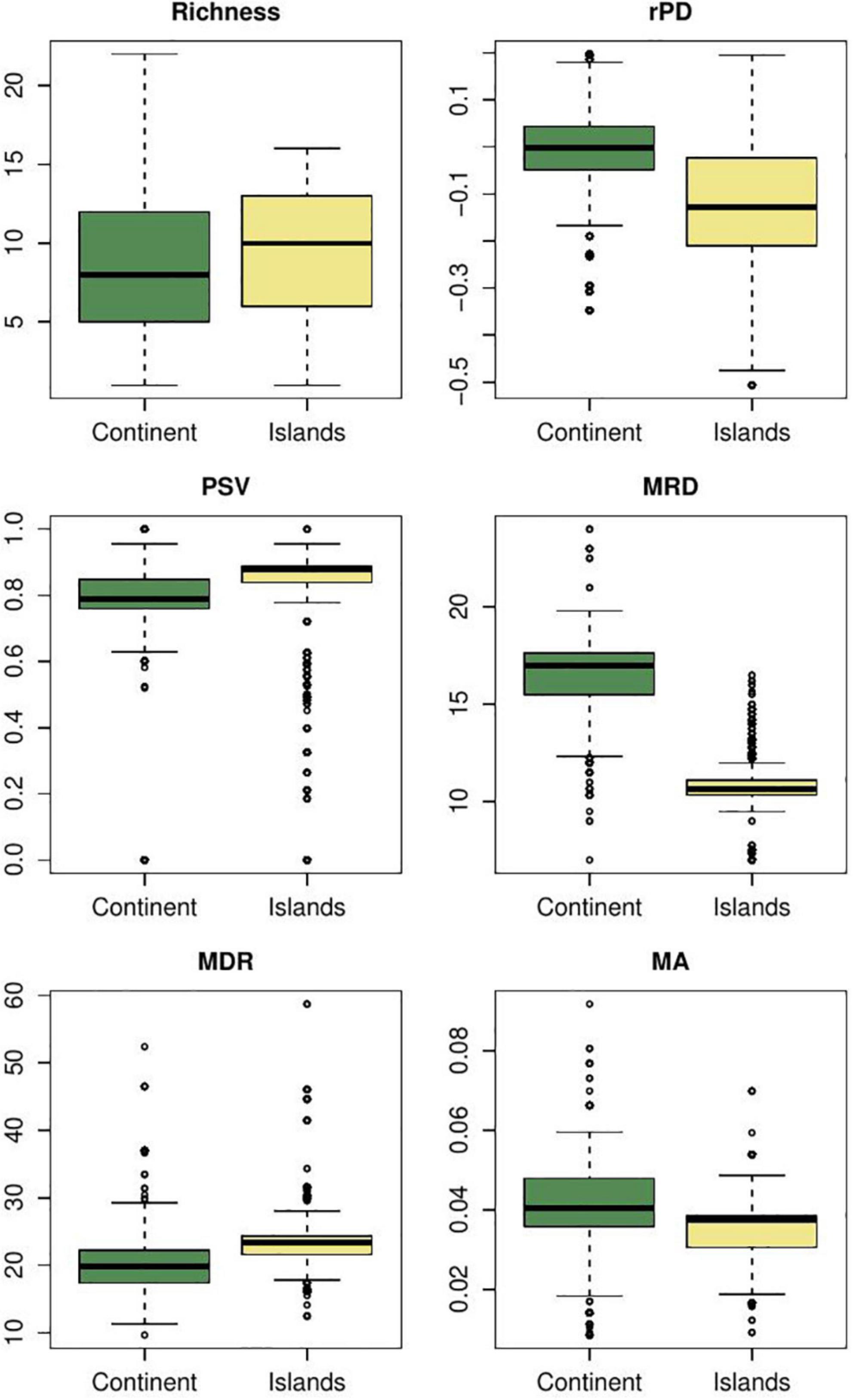
Figure 5. Variation of phylogenetic metric values in Anolis lizards for continental and insular areas. rPD, residual phylogenetic diversity (i.e., after controlling for species richness); PSV, phylogenetic species variability; MRD, mean root distance; mDR, mean diversification rate; mAges, average ages of species. Y-labels correspond to the values of each metric. Comparisons of metrics between regions were evaluated using Bayesian ANOVAs and all were significant (Maximum A posteriori p-values < 0.001) except for PSV (Maximum A posteriori p-values > 0.9).

Residual phylogenetic diversity

In the case of furnariid birds, we show that forested areas tend to exhibit slightly higher values of rPD than open areas (Figure 4; see also Figure 2). Under Davies and Buckley’s logic, these forest areas show slower diversification and frequent dispersal than open areas (similar to findings with MRD, see above). Using GeoSSE and BAMM approaches, Pinto-Ledezma et al. (2017) demonstrated that open areas exhibit higher net diversification rates than forested areas (Table 3). For hylid frogs, we found that tropical areas exhibit higher rPD values than extratropical regions (Figure 4); however, by adopting an explicit diversification approach (GeoSSE and BAMM), we found similar net diversification rates in both regions (Table 3). In the case of Anolis lizards, the rPD values were higher in the continent than in the island areas (Figure 5); however, using GeoSSE and BAMM, we found both rates to be similar (Table 3). Two additional studies support these results in finding species diversification rates similar between insular and mainland regions (Poe et al., 2018; Burress and Muñoz, 2022). Overall, these results suggest that rPD likely does not provide an accurate signature of the macroevolutionary dynamics at spatial scales. In fact, it seems that rPD tends to overestimate differences between regions when a stationary diversification process is occurring across geography. A potential solution might be to rethink the way in which we visualize rPD across geography, in contrast with the original meaning by Davies and Buckley (2011); see also Forest et al. (2007).

Phylogenetic species variability

The PSV metric provides information about how related species are in a given regional assemblage. In hylid frogs, we found that tropical assemblages tend to be composed of more related species than extratropical assemblages (Figure 4). Hylid assemblages in extratropical areas are composed of multiple lineages that dispersed from tropical areas and subsequently diversified. We found higher dispersal rates from tropical to extratropical regions than vice versa (Tables 3, 4). The same tendency is present in furnariid birds, where open areas exhibit higher PSV values than forest areas (Figure 3), and dispersal rates were higher from open to forest areas than the reverse pattern (Table 3). By contrast, we did not find any evidence for differences in PSV values between island and mainland Anolis assemblages (Figure 5). In addition, dispersal rates were very low between these two regions (Table 3; Poe et al., 2017). These results confirm that the PSV metric can provide insights about the role of dispersal in shaping regional assemblages. Moreover, we find evidence that multiple dispersal events and species-specific evolutionary history influence low PSV values (i.e., phylogenetically over-dispersed faunas).

Mean diversification rate

Jetz et al. (2012) proposed the DR metric as a species-level speciation rate metric based on the branch lengths along the path from the root of a tree to each individual species. Accordingly, the average DR (mean DR -mDR-) for all species co-occurring in a grid-cell or region may be calculated. We consider that both metrics (mDR versus per-species diversification rate from BAMM) leave the same geographic signature. In furnariid birds, we found that mDR was slightly higher in open versus forested areas, a pattern also recovered using the BAMM approach (Pinto-Ledezma et al., 2017; Figure 3 and Table 3). For hylid frogs, extratropical regions tended to exhibit higher values than tropical regions (Figure 4). In these taxa, mDR captured relatively well the differences in macroevolutionary diversification along the latitudinal diversity gradient. A similar pattern was recovered using the BAMM approach (Table 3). In Anolis, insular assemblages tended to exhibit higher mDR values than continental assemblages (Figure 5); however, no difference in the macroevolutionary dynamic between these two areas was recovered for these lizards (Poe et al., 2018; Burress and Muñoz, 2022).

Mean ages

The average ages of co-occurring lineages are used to test evolutionary hypotheses about whether a region maintains older lineages (i.e., a “museum”) or harbors a combination of both old and recent lineages (i.e., the “out of the tropics” -OTT- hypothesis, Table 1). Although this metric does not provide any inference of the ancestral area of the clade, explicit biogeographic approaches may be implemented to test this (see below). For example, in hylid frogs, we found that extratropical areas are composed of older lineages than tropical regions (Figure 4), and the biogeographic parametric approach inferred this same area as ancestral for the entire lineage (Supplementary Figure S7). In furnariid birds, the mean ages metric revealed that older lineages have accumulated more in forests than in open areas (Figure 3; Pinto-Ledezma et al., 2019). Similarly, a parametric biogeographic method inferred the ancestral area to be the forest (Supplementary Figure S8). In the case of anole lizards, we found that insular settings tend to be composed of older lineages than on continents (Figure 5); however, the ancestral area for the entire anole clade has been shown to be the mainland, particularly South America (Poe et al., 2017). The mainland Anolis radiation is composed of two clades, one that originated in South America (the Dactyloa clade; Poe et al., 2017) and subsequently colonized the Caribbean islands, and the other (the Norops clade; Poe et al., 2017) that originated in the Caribbean islands and then dispersed to the mainland in Middle America and dispersed to South America through Panama landbridge. The biogeographical history of the Anolis radiation has been complex and involves multiple dispersals between islands and mainland areas (Poe et al., 2017; Supplementary Figure S9). In general, mean ages do not provide enough information about the biogeographic origin and maintenance of a clade (García-Rodríguez et al., 2021a), as multiple dispersal events and subsequent in situ cladogenesis events may erase any simplistic pattern elucidated for this metric, as found in the case of Anolis lizards.

Testing evolutionary hypotheses using phylogenetic metrics and explicit diversification approaches

In this section, we discuss how different phylogenetic metrics have been used in macroecological studies to evaluate evolutionary factors related to the origin and maintenance of species richness gradients.

Several macroecological studies are still using the MRD metric to evaluate whether regional assemblages are composed of “basal” or “derivate” linages (Villalobos et al., 2020). We agree with other authors that this terminology should be avoided because it provides an incorrect interpretation of phylogenetic trees (Baum et al., 2005; Crisp and Cook, 2005; Omland et al., 2008). Although this metric does not incorporate information from branch lengths (Algar et al., 2009; Qian et al., 2015), it does provide the average number of nodes separating each species in a given region from the root of the phylogeny (Kerr and Currie, 1999). MRD, therefore, provides information about the number of cladogenetic events (splits) that have occurred through the history of co-occurring lineages in each region. Under this view, MRD may be interpreted as a metric of species diversification, where high MRD values indicate regional assemblages dominated by extensive cladogenesis, and low MRD values indicate assemblages with few cladogenetic events. However, a central concern with this metric is related to the fact that MRD does not provide any information about the macroevolutionary dynamics that shaped the regional diversity. For example, using this metric it is difficult to distinguish between diversity-dependent (Rabosky, 2009; Rabosky and Hurlbert, 2015) or time-dependent (Wiens, 2011; Harmon and Harrison, 2015) processes dominating regional diversity. Although the distinction between these two diversification dynamics, and their relationships with the origin and maintenance of regional diversity, is an intensely debated topic in the macroevolutionary literature (Rabosky, 2009; Wiens, 2011; Cornell, 2013; Harmon and Harrison, 2015; Rabosky and Hurlbert, 2015), more empirical and theoretical work may be necessary to establish what scenario plays a significant role in regional species richness assemblies (Etienne et al., 2012; Rabosky, 2012; Valente et al., 2015; Graham et al., 2018). In addition, it is unclear whether local ecological processes scaling up to regional scales or emergent effects (i.e., the existence of a strong equilibrium process) govern the build-up of regional diversity (Cornell, 2013; Harmon and Harrison, 2015; Rabosky and Hurlbert, 2015; Marshall and Quental, 2016).

The time-for-speciation effect, or evolutionary time hypothesis, states that the regional build-up of species richness is directly proportional to the colonization time of its constituent clades (Stephens and Wiens, 2003; Table 2). However, several phylogenetic metrics used as a proxy to test this hypothesis did not incorporate any age information of the regional assemblages (Qian et al., 2015; García-Rodríguez et al., 2021a). Although Qian et al. (2015) provided some predictions for the effect of time on the phylogenetic structure of regional assemblages, these predictions are not easy to deduce from the original time-for-speciation effect (Stephens and Wiens, 2003). In particular, Qian et al. (2015, p. 7) predicted that regions with low species richness (e.g., extra-tropical regions) should be composed of more closely related species than regions with high species richness (e.g., tropical regions). This statement, however, assumes that regions with low species richness were colonized recently, and therefore these lineages had little time for diversification. In addition, it is possible that high extinction rates may have occurred in species-poor regions due to marginal climatic conditions preventing adaptive diversification (Wellborn and Langerhans, 2015). By contrast, species-rich regions might also be influenced by multiple dispersals from nearby regions, thus becoming a macroevolutionary sink (Goldberg et al., 2005). In this case, species richness was not built-up by in situ speciation, but rather by continued dispersal through time. To evaluate which of these scenarios is more plausible, it is necessary to adopt an approach that explicitly infers the number of dispersal and cladogenetic events across regions (Roy and Goldberg, 2007; Dupin et al., 2017).

The diversification rate hypothesis is also considered among the main drivers of the geographical diversity gradients for many groups (Kennedy et al., 2014; Pinto-Ledezma et al., 2017, 2019). This hypothesis (Table 2) states that differences in net diversification rates between areas are the main driver of differences in regional species richness. Davies and Buckley (2011) used phylogenetic diversity controlled by species richness (i.e., residual PD –rPD–) to distinguish areas with different evolutionary processes. These authors predicted that regions with rapid speciation and low immigration events from other areas generally are dominated by large adaptive radiations (e.g., large islands; Losos and Schluter, 2000) and should have low values of rPD. By contrast, areas with slow speciation and that have been colonized by multiple lineages through time should have high values of rPD.

The “out of the tropics” (OTT) hypothesis (Jablonski et al., 2006; Table 2) states that the latitudinal diversity gradient is a product of the tropical origin of most lineages and posterior dispersal to extratropical regions. Under OTT, diversification rates are higher in tropical regions than in extratropical ones, and dispersal events are higher from tropics to extratropical regions than vice versa (Jablonski et al., 2006; Table 1). Rolland et al. (2014) tested this hypothesis to explain the latitudinal mammal diversity gradient using the GeoSSE model. They found that net diversification rates (i.e., the balance of speciation minus extinction) were higher in tropical than in extratropical regions, and dispersal rates were higher from the tropics to extratropical regions than the reverse. Similarly, Pinto-Ledezma et al. (2017) used the GeoSSE model to test an analog hypothesis to OTT, the Out of the Forest hypothesis (OTF), using furnariides birds as a model clade. Their findings favored a model where open areas have higher speciation, extinction, and dispersal rates than forested habitats. These results suggest that it is reasonable to use either phylogenetic metrics or explicit diversification approaches (e.g., the GeoSSE model) to evaluate hypotheses based on macroevolutionary processes as drivers of geographical diversity gradients. However, below we show that these approaches fail to capture the evolutionary and biogeographic processes at various spatial scales (Tables 3, 4).

Are phylogenetic metrics capturing the diversification processes appropriately across geography?

A deep understanding of the evolutionary processes that govern regional species assemblages comes from the integration of molecular phylogenies and the fossil record (Quental and Marshall, 2010; Marshall, 2017). From this integration of neontological and paleontological perspectives, it is clear that both approaches are necessary to test evolutionary-based hypotheses in macroecological research. Several hypotheses have been proposed to explain geographical diversity patterns, particularly the latitudinal diversity gradient (see Table 2 for a summary and compilation of the main hypotheses reported in the literature). Although the ideal approach is to generate robust conclusions from multiple lines of evidence (e.g., the fossil record, molecular phylogenies, biogeographical inference), this information is scarce for many taxonomic groups. Accordingly, many macroecological studies have adopted either phylogenetic metrics or explicit diversification approaches (e.g., the GeoSSE model) to evaluate the relative contributions of speciation, extinction, and dispersal as drivers of geographical diversity gradients (Supplementary Table S1).

Phylogenetic metrics used to test hypotheses about diversification and evolutionary time can be easily visualized in a geographical context. In some cases, phylogenetic metrics provide information about species-specific diversification rates (e.g., DR). These values can be associated with the corresponding species’ geographical range to obtain a mean value for cells or regions in a geographical domain (Table 1 and Figure 1). In other cases, they provide information about the regional assemblage in a given region or grid-cell (e.g., MRD, rPD, PSV, mAges). By contrast, model-based approaches (e.g., GeoSSE; BAMM) provide information about the diversification dynamics for an entire clade or regional assemblage (Rabosky, 2016). In the case of the BAMM approach, we can obtain a species-specific diversification rate and map these values across geography (Sánchez-Ramírez et al., 2015; Pérez-Escobar et al., 2017; Rabosky et al., 2018; García-Rodríguez et al., 2021a).

Different methods to estimate diversification rates may provide complementary evidence of how macroevolutionary dynamics have taken place across geography. For example, the number of species and the age of individual clades can be fit to a birth-death model to estimate a diversification rate (Magallón and Sanderson, 2001; Nee, 2006). With this model-fitting approach we also can discern whether diversity- or time-dependent diversification processes have taken place in a region (Etienne et al., 2012; Rabosky, 2014; Valente et al., 2015). In contrast, by mapping phylogenetic metrics we are not afforded this level of understanding about regional diversification processes [but see Machac (2020) for an alternative approach]. As these different approaches likely produce differential signatures across geography, it remains unclear which phylogenetic metrics can accurately describe the diversification dynamics across biodiversity gradients. In this sense, it is necessary to evaluate how different metrics generate redundant or contradictory information about spatial diversification dynamics (Figures 1, 2) and use null models to test whether these metrics reveal distinctive geographical patterns or if these patterns are simply an artifact of random sampling.

The geographical pattern of species richness and the five phylogenetic metrics applied to Anolis lizards, hylid frogs, and Furnariides birds are shown in Figure 1. Overall, we observe a higher species concentration near the Equator. Specifically, we found a high species concentrations for hylids and furnariides are found in the Amazon and the Atlantic forest, while Anolis lizards show higher richness in Central America and the Caribbean islands (Figures 1A–C; see also Algar et al., 2009; Pinto-Ledezma et al., 2017; Velasco et al., 2018 for a detailed description of the geographical species richness pattern for these clades, respectively). In terms of the geographical pattern of each phylogenetic metric (Figures 2D–R), cells with higher metric values are in most cases related to cells that contain high species richness and vice versa (Figures 2D–R and Supplementary Figure S4). However, the degree and direction of this relationship changes according to the phylogenetic metric used. For example, MRD, a metric of species derivedness, shows a negative correlation with species richness (Figures 1J–L and Supplementary Figure S4). Importantly, the spatial relationships between species richness and phylogenetic metrics found in our analyses could simply be the result of aggregated species-level attributes within cells or assemblages (Hawkins et al., 2017). Hence, any conclusion derived from these relationships needs to be considered carefully. Additionally, different levels of correlation are observed between phylogenetic metrics (Supplementary Figure S4). For example, mDR and mAges present a high but negative correlation, while the rPD–PSV and MRD–mDR relationships show a mid-high positive correlation (Supplementary Figure S4).

Although several studies have compared the performance of some of these metrics (Vellend et al., 2010; Fritz and Rahbek, 2012; Miller et al., 2017; Tucker et al., 2017), to our knowledge no previous study has evaluated the extent to which these metrics provide reliable and non-redundant information about spatial diversification dynamics and how they may be affected by dispersal and extinction processes. Furthermore, some of these metrics share mathematical assumptions, which may increase the likelihood of correlation between them. For example, metrics such as mDR could be approximated by considering the mean root distance (i.e., MRD metric) from the tips to the root (Freckleton et al., 2008); therefore further studies exploring the mathematical relationships between these phylogenetic metrics in the context of species diversification dynamics are necessary.

The null model approach implemented here allows us to explore the non-randomness in each of the phylogenetic metrics, i.e., how the likelihood of cells/assemblages are on average representations of a random sampling process from the species pool. We found that none of the five phylogenetic metrics deviate from the null expectation for the three clades (Figure 2). Also, very few cells/assemblages present p-values below the 0.05 threshold, thus indicating that most of them reflect random associations among species (Figure 2). These results may be further supported by repeating analyses in more clades at different spatial extents, but we reiterate that results obtained using these phylogenetic metrics should be interpreted carefully and complemented with additional biogeographical and model-based approaches (e.g., Böhm and Mayhew, 2005; Kennedy et al., 2017; Miller and Román-Palacios, 2021).

The dismissal of dispersal and extinction processes in macroecology

Dispersal is a key biogeographical process that determines regional species richness (Roy and Goldberg, 2007; Eiserhardt et al., 2013; Rolland et al., 2014; Chazot et al., 2016; Kennedy et al., 2017; Miller and Román-Palacios, 2021). Few studies have assessed how the direction of dispersal events between regions contributes to the generation of regional differences between areas (Chown and Gaston, 2000; Jablonski et al., 2006; Goldberg et al., 2011; Kennedy et al., 2017). In a seminal work, Roy and Goldberg (2007) used simulations to show that dispersal asymmetry between areas strongly impacted the regional species richness and the average lineage age. Phylogenetic metrics can be sensitive to dispersal between areas due to the difficulty of distinguishing if lineages originated by in situ speciation or simply due to dispersal from nearby areas. Goldberg et al. (2011) developed the GeoSSE model to evaluate how range evolution affects diversification rates in a phylogenetic comparative approach. However, the GeoSSE model only considers three states (A: endemic species to a region; B: endemic species to another region; and AB for widespread species) and makes a series of assumptions that may be problematic.

The first assumption is that a time-dependent process dominates the diversification dynamic in each region (Stephens and Wiens, 2003; Wiens, 2011). This conflicts with a diversity-dependent process assumption. Although this topic has been debated in the literature (Cornell, 2013; Harmon and Harrison, 2015; Rabosky and Hurlbert, 2015), both processes are not mutually exclusive (Pinto-Ledezma et al., 2017; Machac, 2020). The second problematic assumption stems from the fact that the GeoSSE model considers dispersal rates as stable across time and lineages. In other words, dispersal ability and therefore the frequency of transitions between areas are constant across the evolutionary history of a clade. There is plenty of empirical evidence showing that dispersal rates vary across time and space among lineages (McPeek and Holt, 1992; Sanmartín et al., 2008; Robledo-Arnuncio et al., 2014; Pinto-Ledezma et al., 2017). The GeoSSE model was used to evaluate the relative contributions of speciation, extinction, and dispersal in generating species richness gradients (e.g., Pyron, 2014; Rolland et al., 2014; Staggemeier et al., 2015; Looney et al., 2016; Morinière et al., 2016; Pulido-Santacruz and Weir, 2016; Alves et al., 2017; Hutter et al., 2017; Pinto-Ledezma et al., 2017). However, Rabosky and Goldberg (2015) found that state-dependent diversification models tend to excessively inflate false discovery rates (i.e., type I error rates). Specifically, they found that these models often recover false associations between trait shifts and shifts in macroevolutionary dynamics. Although this study was not based on the GeoSSE model, it is clear that transitions between areas (i.e., dispersal events) can be falsely associated with shifts in speciation and extinction rates across the phylogeny. In addition, Alves et al. (2017) found that geographical uncertainties in the assignment of species to a given area affect the parameter estimates (i.e., speciation, extinction, and dispersal rates) in the GeoSSE model. The same authors also showed the incorrect assignments of species to tropical or extra-tropical regions could lead to erroneous conclusions, which propagates to the inferences of the relative roles of speciation, extinction, and dispersal across a latitudinal diversity gradient. In response to these criticisms, Caetano et al. (2018) developed a Hidden State Model called GeoHiSSE to improve the elevated rates of “false positives” of the GeoSSE model.

Furthermore, Pulido-Santacruz and Weir (2016) used an extension of the GeoSSE model, called ClaSSE, to disentangle the relative effects of speciation, extinction, and dispersal on the latitudinal diversity gradient in birds. They found that extinction was prevalent across all bird clades and therefore suggested this process to be a main driver of the geographical bird diversity gradient. Similarly, Pyron (2014) using the GeoSSE model found that extratropical diversity in reptiles is due to higher extinction in these areas. However, these extinction estimates from the GeoSSE model should be treated with caution — for the few clades where the fossil record is abundant (e.g., marine bivalves; Jablonski et al., 2006), studies suggest that extinction differences between regions are due to a potential sampling bias (Jablonski et al., 2006, 2017). In addition, studies based on extensive simulations found that extinction inferences based only on molecular phylogenies are not reliable (Quental and Marshall, 2010; Rabosky, 2010, 2016), although extinction rates can be estimated relatively well using medium to large phylogenies (Beaulieu and O’Meara, 2015).

Detecting the extinction signature in molecular phylogenies may be possible using extensive simulations and lineage-through-time (LTT) plots (Antonelli and Sanmartın, 2011; Sanmartín and Meseguer, 2016). In particular, Sanmartín and Meseguer (2016) found that many birth-death models leave a similar phylogenetic imprint, which makes some scenarios indistinguishable. In addition, extinction events can substantially impact the ancestral range estimates and, therefore, the dispersal and extinction parameters in several parametric biogeographic methods [e.g., Dispersal-Vicariance (DIVA) and Dispersal-Extinction-Cladogenesis (DEC) models; Ronquist, 1997; Ree et al., 2005]. Some advances in historical biogeography approaches (e.g., Sanmartín and Meseguer, 2016) suggest that the adoption of a hierarchical Bayesian approach using continuous-time Markov Chain models returns a more accurate estimation of extinction rates using phylogenetic information across geography (Sanmartín et al., 2008, 2010). However, there remains a persistent problem in identifying the “true” diversification scenario from molecular phylogenies (Louca and Pennell, 2020; but see Morlon et al., 2022).

More recently, Rabosky and Goldberg (2017) developed a semi-parametric method (Fast, intuitive State-dependent Speciation-Extinction analysis -FiSSE-) to correct the statistical problems found in BiSSE-like models (Rabosky and Goldberg, 2015). However, FiSSE does not allow the estimation of dispersal rates, and thus prevents the evaluation of the contribution of dispersal on regional species richness. Despite the issues found in BiSSE-like models, the GeoSSE model remains as the best suitable framework to estimate relative contributions of speciation, extinction, and dispersal [as well as parametric biogeographic models (Matzke, 2014), see below]. We strongly recommend the adoption of simulation-based null scenarios to evaluate the power of BiSSE-like models (e.g., Alves et al., 2017; Pinto-Ledezma et al., 2017). For instance, by developing a parametric bootstrapping approach, Pinto-Ledezma et al. (2017) simulated traits to evaluate whether empirical inferences differed from those simulated. They simulated 100 datasets of neutral characters along with a set of empirical phylogenies and, using this new information, repeated the same procedure with empirical data [see Supplementary Appendix 1 in Pinto-Ledezma et al. (2017) for details of the bootstrapping approach]. This bootstrapping procedure assumes no direct effect of the geographic character states on the parameter estimations (Feldman et al., 2016; Pinto-Ledezma et al., 2017).

More research is necessary to establish how extinction affects estimation parameters in state-dependent diversification approaches (e.g., the GeoSSE model). For instance, the inclusion/exclusion of extinct species in simulated phylogenies using birth-death models could substantially affect the geographical inferences of speciation, extinction, and dispersal parameters in the GeoSEE model. This kind of approach might shed some light on the bias in the parameter estimates using only molecular phylogenies under the GeoSSE model or any other modeling approach. In addition, the effect of hidden-states (Beaulieu and O’Meara, 2016) has recently been recognized and incorporated into biogeographic models such as the GeoHiSSE model (Caetano et al., 2018).

The use of parametric biogeographic approaches represents an adequate alternative to estimate dispersal events across time and space (Matzke, 2014; Dupin et al., 2017). These approaches are promising in that they identify the relative roles of cladogenetic and anagenetic processes that shape regional species richness. Some advances such as biogeographical stochastic mapping (BSM) (e.g, Dupin et al., 2017) allow the inference of the number of dispersal and other biogeographical events within the evolutionary history of entire clades. BSM approaches allow inferences from multiple processes, including sympatric speciation, allopatric speciation, founder-event speciation, range expansion (i.e., dispersal without speciation), and local extinction (i.e., range contractions) based on a time-calibrated phylogenetic tree and the occurrence of species in geographical regions (see also Matzke, 2014 for a more detailed description of the method). These explicit biogeographical approaches are promising in macroecological studies since they allow simultaneously testing of a set evolutionary processes during the diversification of a clade in a region. In addition, with these new approaches it is possible to differentiate effectively between macroevolutionary source and sink areas (Goldberg et al., 2005; Castroviejo-Fisher et al., 2014; Poe et al., 2017). For instance, Poe et al. (2017) used a parametric biogeographical approach to estimate the number of events among regions and identify both areas where many cladogenetic events occurred (i.e., source areas) and areas where almost all diversity was built-up from extensive colonization from other regions (i.e., sink areas).

Biogeographical stochastic mapping (BSM; Dupin et al., 2017) is promising because it permits the estimation of the number of dispersal events between regions based on a more accurate estimation of the ancestral area for a clade (Dupin et al., 2017). In the three empirical datasets presented here, we evaluated how dispersal rates between regions can affect inferences drawn only from phylogenetic metrics. We implemented GeoSSE and BSM approaches for each data set (Tables 3, 4) to count the inferred number of dispersal events between tropical and extra-tropical regions in the Americas for hylid frogs, between open and forest areas for furnariid birds, and finally, between insular and mainland areas for anole lizards (Table 4).

The BSM approach allows for the disentanglement between dispersals that only resulted in range expansions and dispersals that generated a speciation event (i.e., founder-event speciation; Barton and Charlesworth, 1984; Templeton, 2008). In furnariid birds, we found that range expansions were three times higher from open habitats to forest habitats than vice versa, and founder events were twice as frequent from forest to open habitats than the opposite (Table 4 and Supplementary Figure S5). This result suggests that differences in species richness between forest and open areas are due to recurrent dispersal events along with the furnariid diversification history. Pinto-Ledezma et al. (2017) found a similar result using the GeoSSE approach, but they conducted a parametric simulation approach to evaluate whether there was a direct effect of geographic location on the parameter estimates. Their results show that the GeoSSE approach, in this case, had limited power to detect a signature of the geographic region on speciation, extinction, and dispersal rates. With our implementation of the BSM approach, we corroborate Pinto-Ledezma et al. (2017) findings with improved statistical power. For hylid frogs, we found more dispersal events from tropical to extra-tropical regions (Table 4 and Supplementary Figure S5). However, the number of founder events was relatively low in comparison with range expansions (Table 4 and Supplementary Figure S5). These results suggest that few dispersal events have occurred across the diversification of hylid frogs, corroborating that each region’s species richness largely originated from in situ speciation modulated by climatic factors (Wiens et al., 2006; Algar et al., 2009). Finally, for Anolis lizards, we found that dispersal events between insular and mainland regions were relatively low (Table 4 and Supplementary Figure S5). We did not find any evidence of range expansion events from the mainland to island or vice versa. This also corroborates previous findings that the evolutionary radiation of anoles in insular and mainland settings is due to extensive in situ diversification (Poe et al., 2018).

These results point out that the BSM approach (Dupin et al., 2017) may be an adequate complementary approach when testing the role of anagenetic and cladogenetic events in generating geographical species richness gradients. Although parametric biogeographic approaches are continually in development (Sanmartín, 2012; Matzke, 2014; Dupin et al., 2017), these methods allow us to evaluate macroevolutionary dynamics in an explicit geographical context. These methods are powerful in that they allow us to evaluate a series of models that explicitly account for the evolution of a lineages’ geographic range.

Integration of biogeographical and model-based diversification approaches in evolutionary macroecology

Although different parametric biogeographic methods have been developed over the last 25 years (Ronquist, 1997; Ree et al., 2005; Landis et al., 2013; Matzke, 2014; Dupin et al., 2017), their adoption to test evolutionary-based hypotheses underlying geographical diversity gradients has been slow (but see Böhm and Mayhew, 2005 for an early exemplar). Some recent studies have utilized them (Kennedy et al., 2017; Miller and Román-Palacios, 2021), but methodological limitations still remain. For instance, testing the effect of dispersal on the origin and generation of regional diversity in macroecological studies may need a spatially explicit approach at the grid-cell level. Recent progress in macroecological pattern-oriented modeling has expanded in that direction (Rangel et al., 2018; Hagen et al., 2021). Although progress in historical biogeography modeling calls for an evaluation of the relative frequency of cladogenetic and anagenetic processes (Matzke, 2014; Dupin et al., 2017), the inclusion of these parametric approaches in macroecological studies has been limited. These complementary approaches are necessary to improve our estimates of diversification and biogeographical parameters as causal factors in generating biodiversity gradients.

As we have shown, the resulting geographical pattern of several phylogenetic metrics failed to provide any robust evidence of a spatially explicit diversification dynamic. In fact, these resulting geographical patterns using phylogenetic metrics did not differ from those generated by a simple null model (Figure 2). It is hard to untangle causal mechanisms (i.e., speciation, extinction, and dispersal) from pure observed patterns of the geographical signature that these metrics attempt to capture. We recommend that phylogenetic metrics should only be used to visualize geographical patterns of total diversification (e.g., MRD, rPD; mDR), phylogenetic structure (e.g., PSV), or mean ages of co-distributed species (e.g., mAges) (Table 1). Furthermore, conclusions about the role of evolutionary processes in the generation and maintenance of diversity gradients based only on these metrics should be avoided, and additional approaches should always be used.

Some model-fitting phylogenetic approaches (Etienne et al., 2012; Rabosky, 2014; Valente et al., 2015) are useful for discerning the multiple macroevolutionary dynamics operating at regional scales. However, problems with their statistical power (e.g., high Type I errors) have been challenged by simulation and empirical studies (Rabosky and Goldberg, 2015; Alves et al., 2017). Parametric biogeographical approaches represent appropriate alternatives to test the role of evolutionary processes in driving the uneven diversity across regions. Notwithstanding, these approaches also contain computational and methodological limitations, specifically regarding the number of areas used to estimate dispersal events and other macroevolutionary processes. Still, parametric biogeographic approaches are promising and should be combined with standard macroecological approaches to better infer the relative frequency of cladogenetic and anagenetic processes shaping biodiversity gradients.

Author contributions

JV and JP-L conceived the idea and contributed to the conceptual design, analyzed the data, and wrote the manuscript. Both authors contributed to the article and approved the submitted version.

Funding

JV acknowledges funding from the Direction General de los Asuntos del Personal Académico (DGAPA) through the grant UNAM-PAPIIT IA201320 and a grant from the Programa de Investigación en Cambio Climático of UNAM (PINCC-UNAM). JP-L was supported by the US National Science Foundation (DEB 2017843 to JP-L).

Acknowledgments

JV thanks Oscar Flores Villela, Adrian García-Rodríguez, and Fabricio Villalobos for insightful discussions about historical biogeographical processes and evolutionary mechanisms underlying biodiversity gradients. JV and JP-L also thank Brett Butler for reviewing the English style and grammar.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.951271/full#supplementary-material

References

Algar, A. C., Kerr, J. T., and Currie, D. J. (2009). Evolutionary constraints on regional faunas: whom, but not how many. Ecol. Lett. 12, 57–65. doi: 10.1111/j.1461-0248.2008.01260.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Alves, D. M. C. C., Diniz-Filho, J. A. F., and Villalobos, F. (2017). Geographical diversification and the effect of model and data inadequacies: the bat diversity gradient as a case study. Biol. J. Linnean Soc. 121, 894–906.