Accounting for niche truncation to improve spatial and temporal predictions of species distributions

Species Distribution Models (SDMs) are essential tools for predicting climate change impact on species’ distributions and are commonly employed as an informative tool on which to base management and conservation actions. Focusing only on a part of the entire distribution of a species for fitting SDMs is a common approach. Yet, geographically restricting their range can result in considering only a subset of the species’ ecological niche (i.e., niche truncation) which could lead to biased spatial predictions of future climate change effects, particularly if future conditions belong to those parts of the species ecological niche that have been excluded for model fitting. The integration of large-scale distribution data encompassing the whole species range with more regional data can improve future predictions but comes along with challenges owing to the broader scale and/or lower quality usually associated with these data. Here, we compare future predictions obtained from a traditional SDM fitted on a regional dataset (Switzerland) to predictions obtained from data integration methods that combine regional and European datasets for several bird species breeding in Switzerland. Three models were fitted: a traditional SDM based only on regional data and thus not accounting for niche truncation, a data pooling model where the two datasets are merged without considering differences in extent or resolution, and a downscaling hierarchical approach that accounts for differences in extent and resolution. Results show that the traditional model leads to much larger predicted range changes (either positively or negatively) under climate change than both data integration methods. The traditional model also identified different variables as main drivers of species’ distribution compared to data-integration models. Differences between models regarding predicted range changes were larger for species where future conditions were outside the range of conditions existing in the regional dataset (i.e., when future conditions implied extrapolation). In conclusion, we showed that (i) models calibrated on a geographically restricted dataset provide markedly different predictions than data integration models and (ii) that these differences are at least partly explained by niche truncation. This suggests that using data integration methods could lead to more accurate predictions and more nuanced range changes than regional SDMs through a better characterization of species’ entire realized niches.

Introduction

Species distribution models (SDMs), also called ecological niche models (ENMs), have been widely used to study the environmental drivers of species occurrences (Guisan et al., 2017), to investigate the impact of various anthropogenic factors (e.g., climate change) on species distribution (Engler et al., 2011), or to predict the likelihood of establishment of invasive species in new areas (Mateo et al., 2015; Srivastava et al., 2019). SDMs represent powerful tools to manage and conserve species and their habitats and have already proved useful to inform measures and actions at regional and national scales (Jetz et al., 2012; Guisan et al., 2013; Knaus et al., 2018; Zurell et al., 2022). Climate change has strong implications for biodiversity with reported effects on species distributional ranges through poleward/altitudinal shifts (Tingley et al., 2012, 2009; Clement et al., 2016; Lenoir et al., 2020), but also on phenological events through the creation of mismatches between species and their necessary resources (Descombes et al., 2016; Iler et al., 2021). Additionally, climate change can interact with other threats (e.g., land use) to reinforce the pressure experienced by species in some locations (He et al., 2019; Vincent et al., 2019; Román-Palacios and Wiens, 2020). The current availability of different scenarios of future climate conditions makes it possible to predict how climate change could impact species distributions (Maggini et al., 2011). This knowledge can then be used to foster the development and application of measures to mitigate local extinction risk (Sinclair et al., 2010; Guisan et al., 2013) or to limit the propagation or the settlement of invasive species (Mateo et al., 2015; Srivastava et al., 2019).

Despite their increasing use and application for informing stakeholders and managers (Guisan et al., 2013; Tulloch et al., 2016; Sofaer et al., 2019), SDMs present several issues that may impact predictions (Thibaud et al., 2014; Warren et al., 2021), with potentially important consequences such as improper applications of conservation measures (Araújo et al., 2019; Santini et al., 2021). These issues could be related to different methodological and conceptual aspects including the accuracy/bias of the data (Bean et al., 2012; Tessarolo et al., 2014), the creation and use of pseudo-absences (Mateo et al., 2010; Barbet-Massin et al., 2012), or the extent and resolution of the data used for calibrating SDMs (Guisan et al., 2007; Barve et al., 2011; Suárez-Seoane et al., 2014; Niamir et al., 2016; Scherrer et al., 2021). Nowadays, many of these potential problems have been resolved and different roadmaps are available (Guisan et al., 2017; Araújo et al., 2019; Zurell et al., 2020). However, a crucial aspect remains unresolved: the fact that still many future climate change predictions are biased because they are based on regional SDMs only capturing a subset of species’ ecological niches (i.e., niche truncation; Thuiller et al., 2004; Petitpierre et al., 2016; Mateo et al., 2019a; Chevalier et al., 2021; Scherrer et al., 2021; Moran et al., 2022).

Niche truncation is common in ecological modeling exercises (Chevalier et al., 2021; Scherrer et al., 2021). For instance, as management is usually performed at regional or local scales, SDMs studies often rely on regional/national datasets collected by administrations or NGOs whose range of action is defined by restricted geographical or political borders (i.e., country or even provinces’ administrations). This implies that the entire niche of the species is usually not considered (i.e., the niche is truncated), and thus, that the model underestimates the environmental conditions that the species can withstand. This is not a problem if predictions are made in conditions that are similar to the ones used for model calibration (Webber et al., 2011; Chevalier et al., 2021). However, when this is not the case, misestimated response curves and inaccurate projections of species distributions can result in time (Thuiller et al., 2004) and space (Sánchez-Fernández et al., 2011), owing to extrapolation to conditions not used to fit the model. Currently, the fact that many SDM’s forecasts are based on spatially truncated datasets implies that the predicted effect of climate change on biodiversity may be inaccurate, precluding their use for management actions (Guisan et al., 2013; Santini et al., 2021).

Trying to cope with this issue comes with more considerations. The availability of global biodiversity information (e.g., from GBIF) has exploded over the last two decades, through the digitization of museum and herbarium specimens, initiatives of NGOs and administrations, and the development of citizen science (Anderson et al., 2016; Araújo et al., 2019; Heberling et al., 2021). However, these data usually come at a coarse resolution (e.g., IUCN range maps, atlases; Hurlbert and Jetz, 2007; Rocchini et al., 2011), can present spatial sampling bias (e.g., GBIF; Beck et al., 2014), and are not free of species identification errors which can lead to false absences/presences (Chevalier et al., 2021). Regional and local databases usually tend to present these issues to a lesser extent if the sampling strategy is adequate (Hirzel and Guisan, 2002; Knaus et al., 2018). However, they present the disadvantage that only a subset of the ecological conditions (ecological niche) experienced by species across their range is considered (i.e., niche truncation; Thuiller et al., 2004; Petitpierre et al., 2016; Mateo et al., 2019a; Chevalier et al., 2021). Modelers therefore face a trade-off: (1) either considering the full species niche to predict species distribution but only at a coarse resolution and with the potential that predictions are affected by various data issues, or (2) consider a subset of the species niche to derive fine-grain predictions but with extrapolation issues and potentially inaccurate forecasts.

Recently developed data integration methods, such as hierarchical niche models (HNMs; Mateo et al., 2019a,b), can be used to circumvent the problems associated with the sole use of these two datasets by harnessing the information contained in both through different options (see Mateo et al., 2019a), notably the joint likelihood approach (Dorazio, 2014; Koshkina et al., 2017; Pacifici et al., 2017; Miller et al., 2019). Data integration can thus be used to model both precise but environmentally truncated data (fine-grain regional data) together with coarse data that cover the full extent of species ranges (coarse-grain global data; Miller et al., 2019; Isaac et al., 2020). This philosophy is in line with some recent claims stating that the ideal hierarchical modeling framework should apply the concept of “hierarchical filters” in community ecology (de Bello et al., 2013; Hattab et al., 2014), and should incorporate the different scale dependent drivers of species distributions (Mateo et al., 2019a). The spatial distribution patterns of species are driven by different aspects at different scales (McGill, 2010) and thus, the spatial (ecological) scale is an important aspect to consider in order to properly categorize the ecological niche of species during SDMs calibration (Thuiller et al., 2004; Guisan et al., 2017). Therefore, SDMs calibrated at multiple scales should be able to better account for diverse scale-dependent drivers of species distributions (Vicente et al., 2014; Petitpierre et al., 2016; Mateo et al., 2019a).

Different methodological options can be used to perform data integration. Here, we will focus on two methods: the first one is a form of data-pooling that fits a similar model (e.g., generalized linear model (GLM) with quadratic effects) for each of the two datasets, whereas the second method implements a downscaling approach for the coarse-grain dataset where predictions are downscaled to the resolution of the regional dataset by making use of fine-grain environmental information (Keil et al., 2014). Both methods rely on a joint-likelihood approach, where some predictors (climate) and their associated coefficients are common between the two models, implying that their estimate is influenced by both datasets. While in the first method the two datasets are merged without considering differences in extent or resolution (a form of data-pooling though additional predictors are included in the regional model), the second method accounts for those differences between the two datasets (Fletcher et al., 2019).

In this study, our overarching objective is to highlight the importance of accounting for niche truncation in SDMs, especially regarding climate change or other temporal forecasts, and emphasize the potential of data integration methods to deal with this problem. We hypothesized that niche truncation would lead to differences in the extent of range changes predicted regarding the effect of climate change on species distribution. For this purpose, we used various measures to compare inferences obtained from a traditional SDM fitted on a regional dataset (Switzerland) to those obtained from data integration methods that combine the information contained in two datasets (Switzerland and European) for 79 bird species breeding in Switzerland. We expect differences between models to be related to some properties of the species and datasets, particularly, the extent to which the climatic conditions experienced by the species within the regional dataset covers the ones in the European dataset (i.e., how much the species niche is truncated).

Materials and methods

Datasets

Species data

Two bird datasets were considered: a regional (Switzerland) fine-grain (1 km²) atlas and a large (European) coarse-grain (50 km²) atlas.

The regional dataset was originally produced for the Swiss breeding bird atlas (Knaus et al., 2018). The aim of the atlas project was to provide a unique overview of the distribution and current state of population of birds breeding in Switzerland. During the period 2013–2016, 2,318 randomly distributed 1 km² sample quadrats were surveyed on 3 occasions (2 when the quadrats were above the treeline) during a single breeding season using the method of territory mapping (Bibby et al., 2020). The number of territories were counted for each species and then aggregated to presence-absence data for each quadrat. Altogether more than 1,000 volunteers were involved in this part of the atlas.

The larger-scale dataset consisted of the European Breeding Bird Atlas (EBBA2; Keller et al., 2020¹) project that was carried out by the EBCC (European Bird Census Council) over the whole of Europe. In total, around 120,000 fieldworkers contributed data to the atlas, the great majority of them on a voluntary basis, making EBBA2 one of the biggest citizen science projects on biodiversity ever. The main time frame for EBBA2 fieldwork was the period 2013–2017. Presence-absence data come in the form of a grid of 50 km resolution. The variety of methods used to collect the data required common standards and validations at the European level for a proper integration of the data. A detailed explanation can be found in the atlas itself and in Herrando et al. (2014).

To ensure robust parameter estimation at the two scales, only species with at least 5% occurrence in the two datasets were used for model fitting (i.e., 89 species).

Environmental data

We extracted environmental information for 19 bioclimatic variables (denoted Bio01 to Bio19) from CHELSA (Karger et al., 2017) at a 1-km resolution. To obtain coarse-environmental information, we upscaled the fine-grain information to the desired resolution (50 km²) by computing the average over all fine-grain cells contained within a coarse-grid cell. Future predictions for these 19 variables consisted of downscaled CMIP5 climatologies for 2,050 under the emission scenario RCP4.5 and the model ACCESS1-0. Because Switzerland is mainly composed of rugged landscapes (mountains), three additional covariates were considered to model fine-grain data: the topographic position index (Topo; describing the position of sites in a gradient from ridge to hollow), the slope (Slp), and the potential amount of annual solar radiation (Srad). These local scale variables are considered stable in the future.

Models

Three models were considered. The first model (traditional model) is a classical SDM based on a GLM calibrated on the regional dataset only ($Y_i^F$):

$Y_i^F\sim Bernoulli({\psi }_{\text{i}}^{\text{F}})(1)$

$logit\left({\psi }_{\text{i}}^{\text{F}}\right)=\mathrm{\alpha }+\sum _{z=1}^{22}{\beta }_z{X}_{iz}^F+{\mathrm{\gamma }}_z{X}_{iz}^{F^2}(2)$

where ${\psi }_{\text{i}}^{\text{F}}\psi i$ denotes the suitability values in fine-grain (denoted with the superscript F) cell i, α is the intercept representing average suitability, $X_{iz}^F$ represents the value of covariate z in fine-grain cell i (z includes the 19 bioclimatic variables plus the three local scale and thus varies from 1 to 22), β_z is the slope coefficient associated with covariate z and γ_z the associated quadratic coefficient. Note that we here use the term “suitability value” instead of “occurrence probability” because our models do not account for imperfect detection. Yet, since we are not using abundance but presence/absence data, the probability of completely missing a species in a 50 km square (or even in the 1 km for the Swiss data) after several visits is likely really low.

The two other models are making use of both datasets and rely on data integration performed through a joint likelihood approach to estimate model coefficients. In both models, fine-grain occurrence data are modeled in the same way as in the traditional model. They, however, differ regarding how coarse-grain data are modeled (denoted with the superscript C; $Y_j^C$). For the second model (data pooling model), a GLM, similar to the one used to model fine-grain data, is used to model coarse-grain data but this time using coarse-environmental values as predictors ($X_{iz}^C$). This GLM therefore includes the same bioclimatic variables as in the fine-grain GLM but excludes the three local scale variables (hence z varies from 1 to 19 for the coarse-grain model):

$Y_i^F\sim Bernoulli({\psi }_{\text{i}}^{\text{F}})(3)$

$logit\left({\psi }_{\text{i}}^{\text{F}}\right)=\mathrm{\alpha }+\sum _{z=1}^{22}{\beta }_z{X}_{iz}^F+{\mathrm{\gamma }}_z{X}_{iz}^{F^2}(4)$

$Y_j^C\sim Bernoulli({\psi }_j^C)(5)$

$logit\left({\psi }_j^C\right)=\mathrm{\alpha }+\sum _{z=1}^{19}{\beta }_z{X}_{jz}^{\text{C}}+{\mathrm{\gamma }}_z{X}_{iz}^{C^2}(6)$

where ${\psi }_j^C$ denotes the suitability values in coarse grain cell j. Since the coefficients are the same for the variables that are common between the two scales, the information is shared across the two models and coefficients are therefore influenced by both datasets (i.e., joint likelihood approach).

For the third model (downscaling model; see Keil and Jetz, 2014), coarse-grain data are modeled through a downscaling procedure where coarse-grain suitability values are downscaled to fine-grain suitability values using fine-grain environmental information:

$Y_i^F\sim Bernoulli({\psi }_{\text{i}}^{\text{F}})(7)$

$logit\left({\psi }_{\text{i}}^{\text{F}}\right)=\mathrm{\alpha }+\sum _{z=1}^{22}{\beta }_z{X}_{iz}^F+{\mathrm{\gamma }}_z{X}_{iz}^{F^2}(8)$

$Y_j^C\sim Bernoulli({\psi }_j^C)(9)$

$logit\left({\psi }_j^C\right)=\mathrm{\alpha }+\sum _{z=1}^{19}{\beta }_z{X}_{iz}^{\text{F}}+{\mathrm{\gamma }}_z{X}_{iz}^{F^2}(10)$

${\psi }_j^C=1-\prod _{i\in I_j}(1-{\psi }_{\text{i}}^{\text{C}})(11)$

where i ∈ I_j means that cell i lies within cell j and where ${\psi }_{\text{i}}^{\text{C}}$ represents the fine grain suitability values within the coarse grain cell C.

Parameter estimation

All models were fitted within a Bayesian framework using MCMC sampling with the software JAGS (Plummer, 2003) and the package R2jags (Su and Yajima, 2015). Three chains were run for each analysis with a burn-in of 5,000 iterations and an additional 55,000 iterations. Chains were thinned every 50 iterations, providing 1,000 samples for each chain. Because the large number of covariates included in the models may result in overfitting and collinearity issues, we used shrinkage priors (a form of penalized regression technique) to guard against overfitting and to select the most relevant variables to predict species distributions (van Erp et al., 2019). Specifically, we used an elastic net penalization (Zou and Hastie, 2005). The elastic net can be seen as a combination of the ridge and lasso and its prior is obtained with a scale mixture of normal distributions (see Li and Liny, 2010 for details). This prior was applied to all coefficients associated with predictors (i.e., the β’s). For the intercept, we used a normal distribution with a mean of zero and a standard deviation of 3. Convergence was assessed using the potential scale reduction factor with a threshold fixed to 1.1 (Gelman and Rubin, 1992). JAGS model codes are provided in Supplementary Figure 1.

Validation

We evaluated model performance using the maximization approach (Guisan et al., 2017) of the true skill statistic (TSS; Allouche et al., 2006), max.TSS, where the threshold used to binarize suitability values into presence and absence is selected to maximize both the sensitivity (the proportion of correctly predicted presences) and the specificity (the proportion of correctly predicted absences). Only species with a max.TSS above 0.4 were considered for model comparison (i.e., 79 species).

Model comparison

Differences between models regarding evaluation metrics and estimated range changes were assessed using Kruskal-Wallis non-parametric analysis of variance.

We evaluated the contribution of each predictor on the predicted suitability values. Variable importance was calculated in the same way as in the Biomod2 R package (Thuiller et al., 2009). Briefly, for a given predictor, the principle is to shuffle the values of the predictor and then to make predictions with this shuffled predictor. The variable importance is then assessed by computing one minus the Pearson’s correlation between reference predictions and shuffled predictions. The higher the value, the more influence the variable has on the model whereas a value of zero indicates no influence of the predictor on model predictions.

To assess how and to what extent models differed regarding their assessment of future changes in species distribution, we predicted presences and absences for all 1-km pixels over Switzerland using 100 random draws from a Bernoulli distribution based on the suitability values predicted by the model (median of the posterior distribution). These binarized predictions were obtained under both current and future environmental conditions. For each draw, we then computed the relative difference between the two binarized maps as follows:

$Range.change=\frac{Nfuture-Ncurrent}{Ncurrent}\times 100$

where _Ncurrent and _Nfuture are the number of predicted presences under current and future conditions, respectively. From the 100 predicted range changes, we extracted the average and the associated standard deviation.

To assess differences regarding the assessment of how species richness will evolve under climate change for each model, we summed the suitability values predicted by the models for each species over the study area. Summing suitability values of individual SDM predictions usually gives better estimates of species richness than stacked SDM based on binarized predictions (Dubuis et al., 2011; Calabrese et al., 2014). Predicted species richness were obtained both under current and future conditions and the difference between the two computed to reflect changes under climate change for the three models.

Determinants of differences between models

We considered different metrics to assess whether the differences observed between models regarding the predicted range changes can be explained by niche truncation. There is currently no existing framework to quantify niche truncation in ecological modeling resulting from the use of a geographically restricted dataset. Hence, we employed various measures to describe different aspects of niche truncation.

Niche overlap—we used the Schoener’s D coefficient (Broennimann et al., 2012) to measure the overlap between species ecological niches estimated from the regional and the European datasets. This was achieved using the function ecospat.niche.overlap in the ecospat R package (Di Cola et al., 2017).

Geographic range cover—we measured the proportion of the geographic species range captured by the regional dataset by dividing the area covered by presences in the regional dataset by the area covered by presences in the European dataset.

Niche size difference—we measured the difference between the sizes of ecological niches estimated from the two datasets. Specifically, for each dataset, we estimated environmental niches using a kernel density estimator (Blonder et al., 2014) applied to species occurrences projected within a two-dimensional space obtained from a principal component analysis performed on the 19 bioclimatic variables characterizing environmental conditions in the two datasets (note that niche overlap is also measured within this two-dimensional space). The area of each kernel was then used as an estimate of niche size.

Average difference in climatic coverage—we estimated the difference regarding the range of climatic conditions occupied by species between the two datasets, considering separately the two ends of the climatic gradient (i.e., differences regarding minimum and maximum values). Specifically, for each bioclimatic variable, we computed the minimum and maximum values across species occurrences for each dataset. We then computed the difference between the two minimums and the two maximums and averaged differences (in absolute values) across all variables. We also computed a global measure of differences by summing the two values. Overall, these three measures (global, minimum, and maximum) indicate how far (or more specifically “how nested within” given that we expect the regional dataset to be nested within the European dataset) the range of conditions occupied by species in the regional dataset is from the one occupied by the species in the European dataset.

Degree of extrapolation—we conducted a multivariate environmental similarity surface (MESS) analysis (Elith et al., 2010) to measure the similarity in the analyzed variables between the projection dataset (future environmental conditions in Switzerland) and the reference (calibration) dataset. For the traditional model, the calibration dataset is the regional dataset whereas for data integration models, the calibration dataset is a combination of both the regional and European datasets. This analysis returns a value for all localities (i.e., pixels) in the projection dataset with negative values indicating localities that are environmentally dissimilar (i.e., extrapolation) from the calibration dataset. We conducted this analysis separately for each calibration dataset using the ecospat.mess function from the ecospat R package (Di Cola et al., 2017). From this analysis, we extracted the sum of negative values corrected by the total number of predictors (i.e., the MESSw metric). From these values, we computed four different statistics. First, we computed the Spearman correlation between the future suitability values predicted by each model and the MESSw obtained from the regional dataset. Second, for each calibration dataset, we averaged MESSw in three ways: considering all pixels, considering only presence pixels and considering only absence pixels. From these averages, we computed the absolute difference between the two calibration datasets.

Difference in dataset’s global properties—besides niche truncation, the performance of SDMs can be affected by various properties of the data (Jiménez-Valverde et al., 2009). To investigate this, we extracted from each dataset the number of presences and absences along with the relative proportion of presences relative to absences (i.e., the prevalence). For each metric, we then computed the difference between the two datasets.

For all of the above-mentioned metrics (except the correlation between predicted future suitability and MESSw; see below), we expected larger differences between datasets to entail larger differences in model projection, except for the measure of niche overlap and for the proportion of geographic range covered where negative relationships are expected (a low overlap and a low proportion of geographic cover are assumed to entail a larger niche truncation). Differences between models were computed for each species as the absolute difference in average predictive range changes (similar results were obtained when considering the difference in suitability changes; see Supplementary Figures 5, 6). We tested the effect of each metric on model differences using Spearman correlations. Regarding the correlation between future suitability values and MESSw, we expect the correlation to be higher for models whose predictions are affected by extrapolation issues, as expected for the traditional model. We tested this effect between each model using Wilcoxon-paired tests. Owing to multiple testing, significance was assessed at an alpha level set to 0.01. Effects with p-values comprised between 0.01 and 0.05 were considered marginally significant.

Results

Model performance

Both traditional and data-integration methods showed good predictive performance according to the three metrics considered (max.TSS, max.Sensitivity and max.Specificity) and presented very similar results (Figure 1), showing no significant differences (Kruskall-Wallis; p > 0.05 in all cases). This suggests that (1) niche truncation is not a problem as long as predictions are made on the calibration area with current climatic conditions and (2) that we cannot rely only on validation metrics to distinguish if a particular model is better than another one to extrapolate to other climatic conditions, as, regarding the input data, they all perform similarly.

FIGURE 1

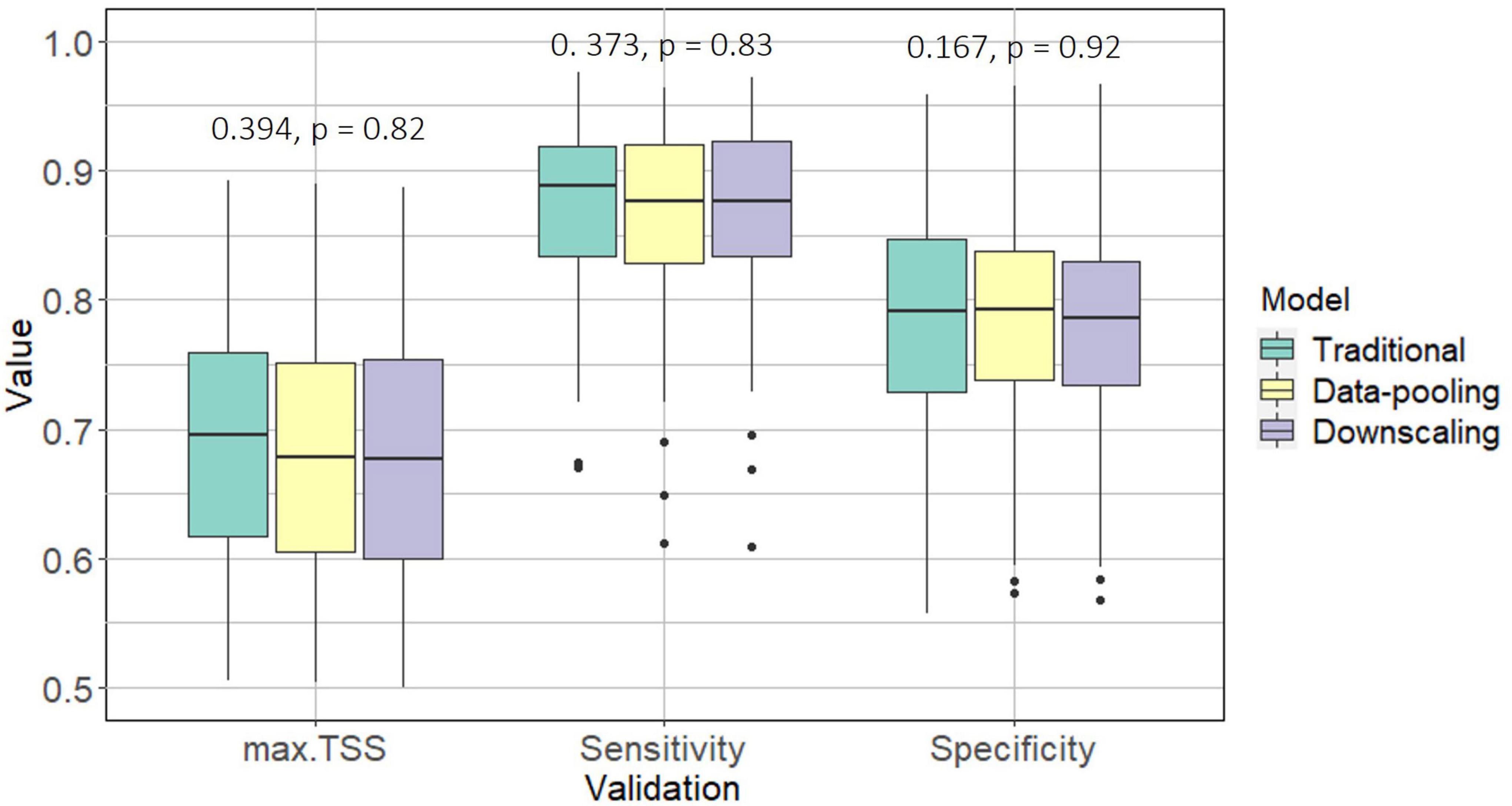
Figure 1. Boxplots representing the distribution of values obtained for max.TSS, max.Sensitivity, and max.Specificity for all bird species (those with a max.TSS > 0.4) and each of the considered models: traditional, data-pooling and downscaling. For each metric the Kruskall-Wallis statistic and its associated p-value are shown, with “*” marking significant differences between models.

Variable contribution and response curves

The two models accounting for niche truncation presented similar variable importance but gave different results than the traditional model (Figure 2 and Supplementary Figure 2). Specifically, the mean temperature of the warmest quarter (Bio10) appears clearly as the most important variable associated with bird distribution for the two data integration methods, whereas for the traditional model the contribution of this variable appears reduced and with values similar to those of Bio01 (the annual mean temperature) and Bio05 (the maximum temperature of the warmest month). Similarly, while the response curves representing species-environment relationships for the two data integration methods are almost identical, their shape was remarkably different for the traditional model, particularly regarding the variables that contributed little to the predictions obtained under data-integration methods (e.g., Bio02-Bio04; Supplementary Figure 3).

FIGURE 2

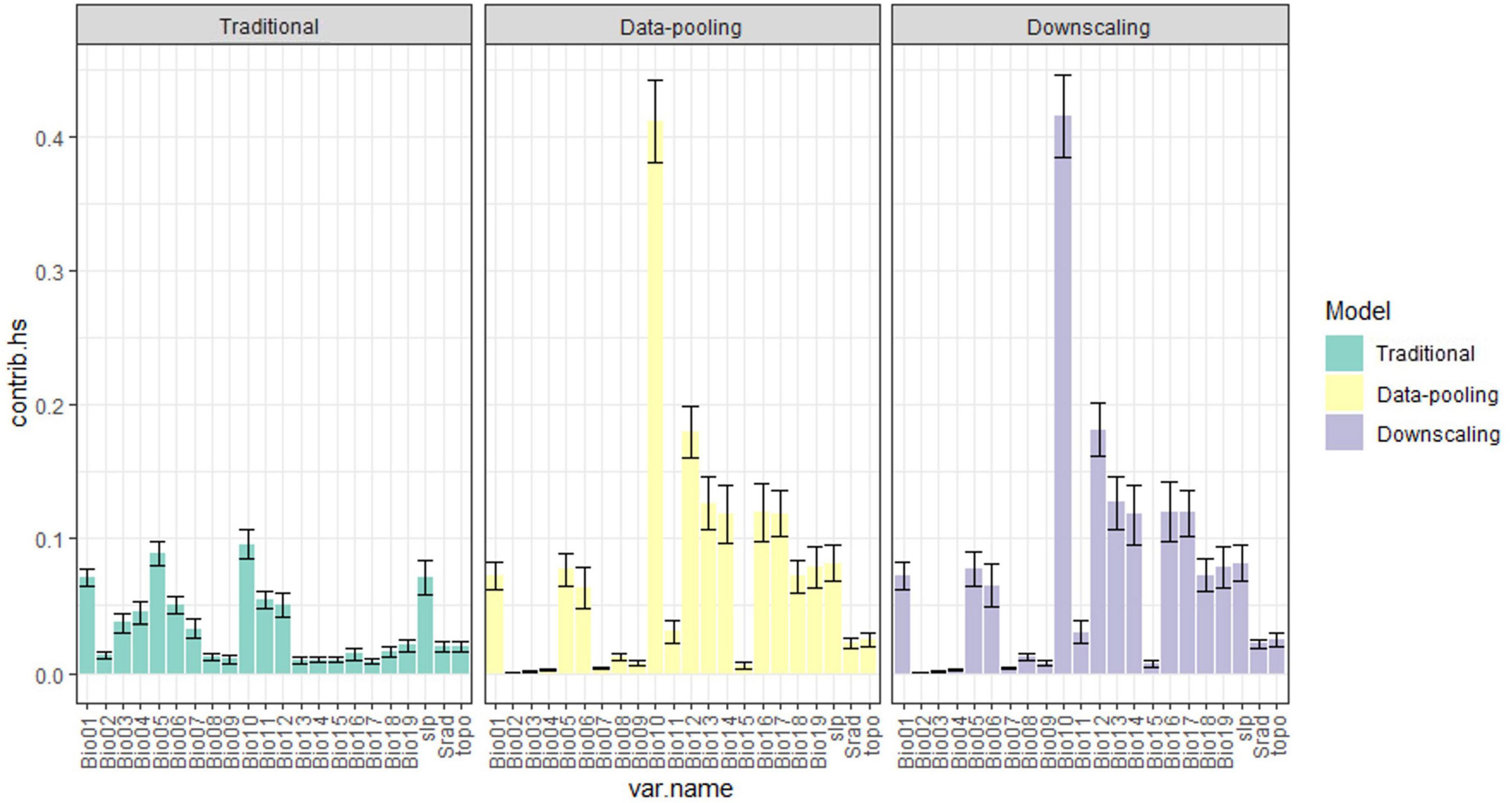
Figure 2. Barplot representing the estimated variable importance under the different models. The height of each bar represents the average importance across species while the vertical black bar represents the associated standard error.

Predicted range changes

The traditional model predicted significantly higher variations in range change (Kruskall-Wallis; p < 0.01 in both cases, Figure 3) than the two data-integration models, mostly inflating the effects of climate change on habitat suitability, either positively or negatively (Supplementary Table 1). Very similar results were obtained between the two data integration methods (Figure 3 and Supplementary Table 1). Overall, 42 species were predicted to have a range decrease under the traditional model with a percentage change equaling −67% on average (SD = 31) whereas 27 species were predicted to have a range increase (mean percentage change = +188%; SD = 223). In contrast, both data integration methods predicted that 34 species would decrease in range (mean percentage change = −1%; SD = 65) whereas 36 were predicted to have a range increase (mean percentage change = 15%; SD = 56).

FIGURE 3

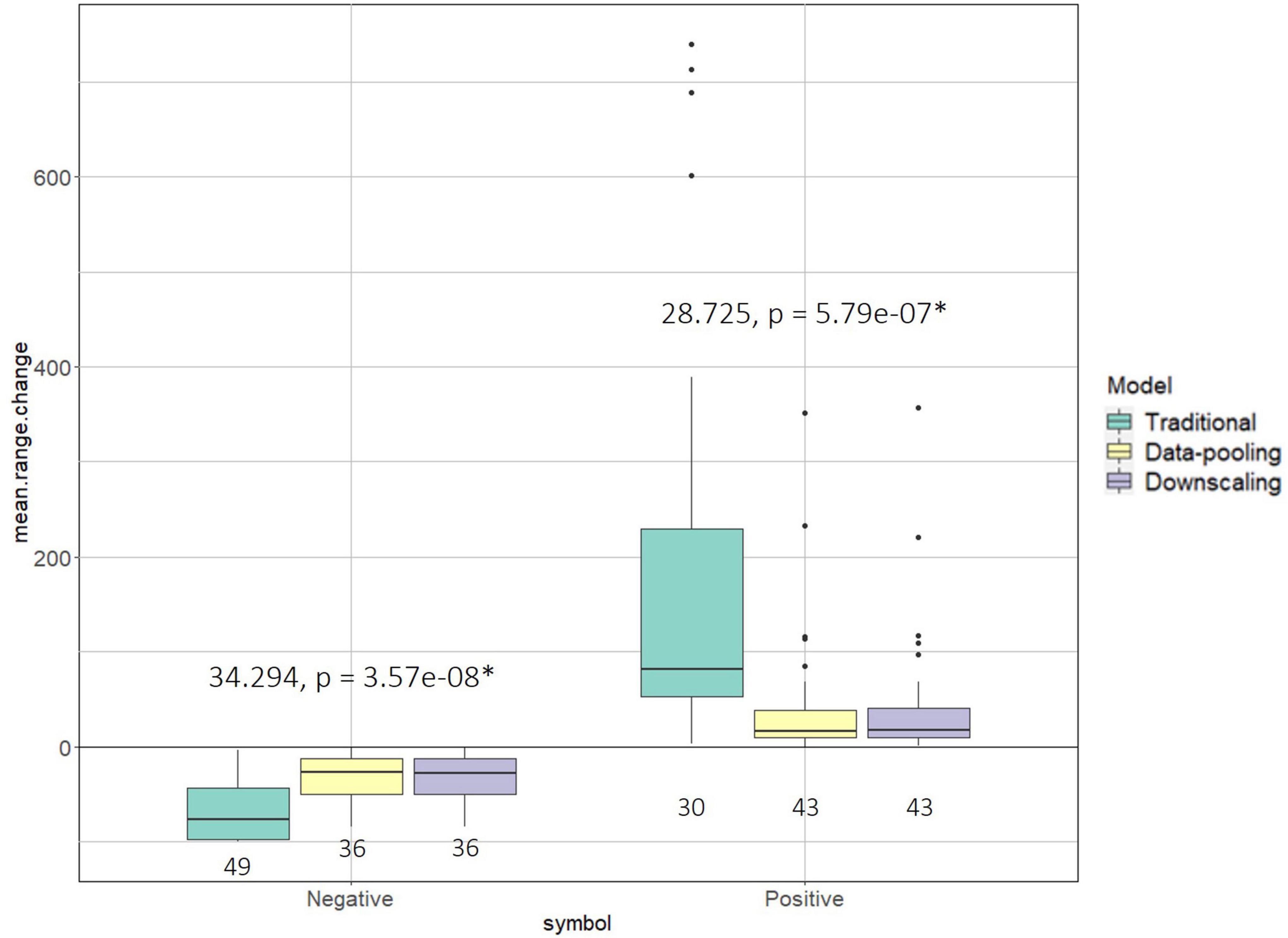
Figure 3. Boxplots representing the distribution of the predicted range changes (average over the 100 draws from the Bernouilli distribution) under climate change for all bird species under the three models (traditional, data-pooling, downscaling). To better reflect differences between models, we considered separately losses (negative values) and gains (positive values). For each group the Kruskall-Wallis statistic and its associated p-value are shown, with “*” marking significant differences between models. Below each box we also show the number of species (sample size) predicted to reduce (negative) or increase (positive) their range.

Spatial pattern in species richness

Under present environmental conditions all models predicted similar species richness (Figure 4), though with some differences with e.g., a tendency for the traditional model to predict lower species richness in the lowlands but higher species richness in the mountains relative to data integration methods (Supplementary Figure 4). In line with results obtained for each species, data integration methods predicted much lower changes in species richness in the future than the traditional model, with an estimated change in species richness ranging from −8 to +15 for the former and from −15 to +16 for the latter.

FIGURE 4

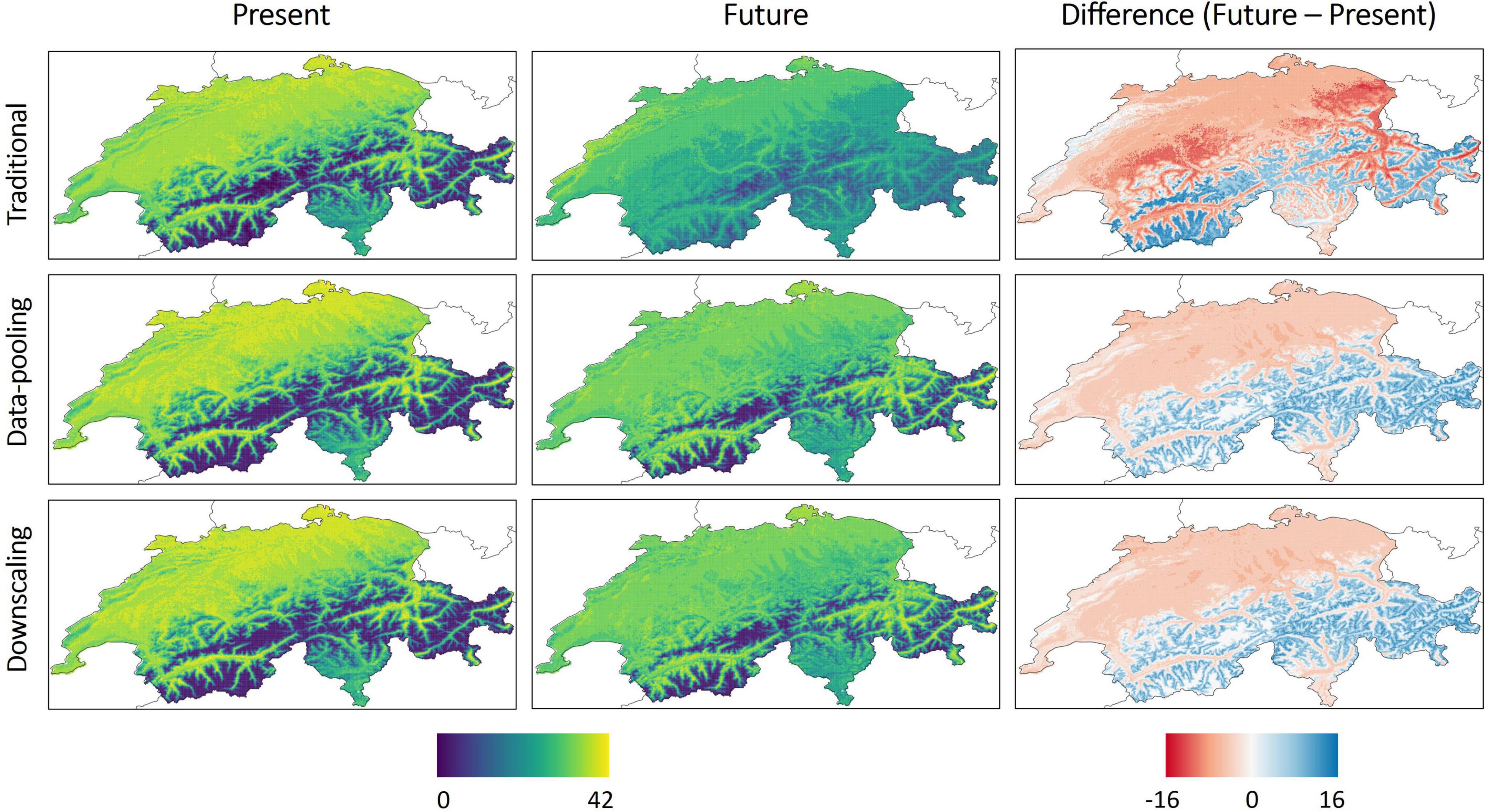
Figure 4. Spatial representation of species richness predicted under current and future environmental conditions for all 1-km pixels over Switzerland along with the difference between them for the three considered models. Species richness was computed by summing the predicted suitability values for all bird species.

Determinants of differences between models

Because the predictions obtained from the two data integration methods were highly similar, the results presented below are the same whether differences were computed between the traditional and the data-pooling model or between the traditional and the downscaling model.

Differences between models regarding average predicted range changes were not related to the degree of niche overlap (rho = −0.10; p > 0.34) or the difference in niche size (rho = 0.04; p = 0.69). Similarly, we found no effect of the difference in the range of conditions occupied by species between the two datasets either globally (rho = 0.07; p = 0.50) or regarding minimum (rho = 0.06; p = 0.87) and maximum (rho = 0.07; p = 0.61) environmental values. Differences between the number of presences (rho = 0.18; p = 0.09) and absences (rho = −0.01; p = 0.93) also had no effects on the difference between models. In contrast, the degree of global extrapolation showed a marginal significant and positive effect on model differences (rho = 0.25; p = 0.02). This positive effect turned negative (still marginally significant) when MESSw values were averaged over absences (rho = −0.23; p = 0.03), whereas no effect was detected when averaging over presences (rho = 0.18; p = 0.09). We further found a negative effect of the proportion of the species range covered by the regional dataset relative to the European dataset (rho = −0.38; p < 0.01) together with a positive effect of the difference in species prevalence (rho = 0.38; p < 0.01). Finally, we found a tendency (Wilcoxon-paired test: W = 3659.5; p = 0.06) for future suitability values to be more strongly correlated with MESSw (average rho = 0.51) for the traditional model than for data integration models (average rho = 0.4).

These effects slightly differed depending on whether the difference between models was negative (more pessimistic predictions of the traditional model) or positive (more optimistic predictions of the traditional model). Indeed, while the degree of global extrapolation (rho = 0.35; p = 0.04), the difference in species prevalence (rho = 0.46; p < 0.01) and the proportion of geographic range covered (rho = −0.44; p < 0.01) also had an effect when differences were positive, these effects were reduced and at best marginally significant when differences were negative [rho = (0.10, 0.27, −0.28); p = (0.48, 0.06, 0.04)].

Discussion

Owing to their popularity, SDMs are experiencing continuous and relentless analyses and review, exploring their shortfalls and developing new methodologies intended to improve their performance and usefulness (Moudrý and Šímová, 2012; Araújo et al., 2019; Zurell et al., 2020). There is an urgent need to produce robust and accurate predictions, especially given that these models are increasingly intended to be used to support specific decision-making processes for conservation and management of species and their habitats (Guisan et al., 2013; Guillera-Arroita et al., 2015). This study highlights the importance of considering the entire climatic niche of a species when predicting in conditions that belong to the species niche but that are not found in the calibration area (i.e., accounting for niche truncation caused by a too restricted geographic extent).

Due to uncertainty associated with future climate scenarios (Shiogama et al., 2016), we cannot determine which model provides the best forecasts. Yet, some factors such as the use of an inappropriate resolution have been shown to increase the uncertainty in future climate projections (Tang et al., 2018). Here, for the first time, we show that the traditional approach that consists in calibrating SDMs using a regional model based on an environmentally truncated dataset (fine-grain regional dataset) gives markedly different predictions relative to data integration methods that integrate other sources of information from larger scales (coarse-grain global dataset) to better characterize the entire species’ realized niche. Importantly, these differences occurred despite similar model performance, suggesting that we cannot rely only on validation metrics to distinguish if a model provides different and potentially better forecasts than another one. In the context of future changes, the truth is unknown, making it difficult to prove that one method (data integration) provides better predictions than another one (traditional SDM fitted on regional data). Hindcasting or simulation-based studies can be used for this purpose. For instance, Chevalier et al. (2021) used simulations to demonstrate the superiority of data integration methods over the traditional approach when extrapolating to novel climatic conditions in both space and or time. At the minimum, the results presented here indicate that niche truncation has important effects when predicting the extent to which species distributions would change under climate change, which can potentially lead to inappropriate recommendations for managers and stakeholders (Guisan et al., 2013). Yet, while we cannot determine which model provides the best forecasts, the magnitude of the changes obtained with the traditional model is rather extreme with regards to the climatic scenario considered (RCP 4.5). For instance, under the traditional model, 20 species are predicted to lose more than 90% of their range whereas the maximum predicted decline under data integration models was 83%. Similarly, 14 species are predicted to increase their range by more than 100% (with a maximum increase of 731%) for the traditional model compared to only four for data integration models (with a maximum increase of 360%). These extreme values suggest that, at least for some species, caution is advised when predicting using a model fitted on a spatially truncated dataset.

Our results indicate that the differences existing between the traditional model and data integration models depend on various factors describing differences between regional and global data. Yet, most of the factors supposed to describe niche truncation (e.g., niche overlap, niche differences, difference in the range of climatic conditions) did not explain model differences. Presumably, this absence of effect could either relate to the fact that these metrics were not appropriate to catch these model differences, or that niche truncation is not necessarily a problem if a large proportion of the conditions in the projection dataset do not belong to those parts of the niche that have not been considered for model fitting (i.e., that do not belong to the truncated part of the niche). Indeed, if the model omits the very cold conditions of the species niche, this may not be a problem given that temperatures are predicted to increase in the future. The fact that we found an effect of the degree of extrapolation on model differences tends to support this hypothesis and indicates that predictions obtained from data integration models are less affected by extrapolation. The predictor that had the most effect on model differences was the difference in species prevalence between the two datasets. Specifically, the positive effect recorded indicates larger differences between models when the prevalence is low in the regional dataset but high in the global dataset. This suggests that caution is advised when the species is rare in the regional dataset but common in other places. Such situations can occur for several reasons including spatial variation in sampling efficiency or if the regional dataset only captures the margins of the species geographical range or of the species environmental space. Interestingly, the effect of extrapolation and species prevalence on model differences appeared stronger when the traditional model predicted larger range increase compared to data integration models suggesting that the large increase reported for 14 species under the traditional model is questionable. While we detected a separate effect of several factors on model differences, it should be noted that these factors can possibly interact to reinforce differences between models. For instance, for species with large niche truncation and also showing a high degree of extrapolation, larger differences between models is expected with predictions from the traditional model likely inflated relative to data integration models. Overall, combined with the simulation study of Chevalier et al. (2021), our findings suggest that it is particularly urgent to consider the niche truncation issue in all climate change forecasts and related applications, especially when results are then incorporated in regional or global biodiversity assessments such as those by IPCC and IPBES (Araújo et al., 2019).

Currently, many predictions derived from SDM-based studies are likely to suffer from the niche truncation problem owing to the large tendency to only consider a subset of species ranges for model calibration (Scherrer et al., 2021). While this niche truncation problem had been raised for quite some time (Thuiller et al., 2004; Barbet-Massin et al., 2010; Mateo et al., 2019b), few studies attempted to deal with the problem and when they did, the approach considered was likely of limited value. For instance, some studies used data pooling to better reflect the species’ realized niche (Broennimann and Guisan, 2008; Nogués-Bravo et al., 2016), but data sources often presented various sampling designs, types of bias, and response variables with different attributes (e.g., spatial extent, resolution), such that it is unclear to which extent integrating these data helped improve predictions (Fletcher et al., 2019). It is only recently that methodological developments, notably data integration methods and the associated joint likelihood approaches (Fletcher et al., 2019; Miller et al., 2019; Isaac et al., 2020), provided a glimpse toward a resolution of the problem. This hierarchical niche approach (Mateo et al., 2019a,b) is particularly interesting because it can account for variation in spatial coverage and resolution and can allow for different predictors to be included for each data source (Miller et al., 2019).

Our results confirm that not accounting for niche truncation has large effects on model inference (see also Koshkina et al., 2017; Pacifici et al., 2017). Beyond differences regarding model forecasts, models differed regarding the most important variable driving species distributions, but also regarding how species respond along the different environmental gradients (Willis and Whittaker, 2002). These could have strong implications in conservation ecology given that inaccurate predictions and the mis-identification of the main drivers may imply spending resources into inefficient but costly restoration plans or missing populations of conservation concern (Guisan et al., 2013). Our study demonstrates that considering additional sources of information that cover a larger spatial extent (e.g., European scale), even if they come at a coarser resolution (e.g., 50 km²), leads to more nuanced changes, dampening the effect that climate change might have on species distributions reflecting the fact that many modeled species can indeed tolerate environmental conditions outside the area used to calibrate the models (Scherrer et al., 2021). This occurred regardless of the data integration method used to harness information from the two datasets. Thanks to the development of remote sensing techniques providing climatic data at high resolutions (Zellweger et al., 2019), along with the increasing availability of species range maps, atlases, and other citizen science data (Isaac et al., 2020), data integration and HNMs appear as promising tools to improve our ability to anticipate future changes and set-up pro-active management strategies. Nevertheless, it is important to note that species distribution can also be driven by non-climatic or biotic factors, and that their response to these factors may change over space and time, especially for migratory species such as birds (Fink et al., 2010).

Beyond their ability to harness information from different datasets that can potentially improve predictions (Koshkina et al., 2017), HNMs are flexible tools that can be used to model scale-dependent effects on species distributions (Pearson et al., 2004; Kéry and Royle, 2015; Fletcher et al., 2019). For instance, here, we used the European sub-model to improve the characterization of the species’ realized niche while accounting for the climatic and ecological drivers that are relevant at a regional scale with the Swiss sub-model. This likely resulted in a better description of the species’ realized niche than what would have been obtained from models fitted separately on each dataset (see also Koshkina et al., 2017). Furthermore, the regional sub-model accounted for the effect of landscape and topographic features that can have important regional effects (Randin et al., 2009). Using this approach resulted in less severe predicted effects of climate change on most bird species, presumably because the future climatic conditions predicted to occur in Switzerland were already found in other areas where species are currently breeding. For example, according to the traditional model the Eurasian wryneck (Jynx torquilla) is predicted to lose all good habitats in the country under future climatic conditions (Supplementary Table 1). Yet, this species currently inhabits warm areas from the Iberian to the Scandinavian Peninsula, covering most of Europe. Accordingly, and contrary to the traditional model, both data integration models predict a vast increase in the species range, likely because these models were able to identify that this species can sustain warmer climatic conditions.

Conclusion

Many SDM-based forecasts are likely affected by the niche truncation problem (Thuiller et al., 2004; Barbet-Massin et al., 2010). Using a large dataset on birds, we found that inferences based on a truncated overview of species’ realized niches usually inflates the predicted effect climate change can have on species ranges. Given the multiplicity of studies reporting common responses to climate change with e.g., poleward/altitudinal distribution shifts, it is clear that species distributions are affected by climate change. Yet, this study suggests that the magnitude of the reported responses could have been overestimated. In line with previous findings (e.g., Fletcher et al., 2019; Mateo et al., 2019a; Chevalier et al., 2021), our results suggest that data integration methods could be used to circumvent the problem of niche truncation. Combined with the increasing availability of large-scale datasets, these methods should be more routinely considered in SDM-based studies if we are to provide stakeholders and managers accurate predictions to mitigate the effect of future environmental changes on species (Araújo et al., 2019), or to prevent species invasion risks (Petitpierre et al., 2016).

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: EEBBA2 data on distribution and abundance are available for further use in research and conservation under some terms and conditions of use. The EBBA2 data policy was agreed among national partners and depending on type of the data the particular conditions differ. According to the principles agreed, some data are open access while some requests require the acceptance of the EBCC (https://ebba2.info/data-request/). Swiss bird data is available upon request (info@vogelwarte.ch). Requests to access these datasets should be directed to https://ebba2.info/data-request/ and info@vogelwarte.ch.

Ethics statement

Ethical review and approval was not required for the animal study because we used distribution data based on available collected locations from other sources.

Author contributions

MC and AG developed the idea and contributed to the conception and design of the study. JG organized the database and the sampling design of the Swiss data. MC performed the statistical analysis. AZ-A, RM, and MC wrote the first draft of the manuscript. All authors provided critical comments on the first draft, read, and approved the submitted version.

Funding

During this research, AG was financially supported by the ValPar.ch project funded by the Swiss Office of the Environment and AZ-A was financially supported by a Margarita Salas contract financed by the European Union-NextGenerationEU, Ministerio de Universidades y Plan de Recuperación, Transformación y Resiliencia, through the call of the Universidad de Oviedo (Asturias).

Acknowledgments

We are grateful to Thomas Sattler, Olivier Broennimann, Pierre-Louis Rey, and Antoine Adde for comments on a previous version of this manuscript. We are also thankful to the thousands of volunteers that contributed to collect the Swiss and European datasets, to all the national coordinators who coordinated the data collection, and to the EBCC who coordinated the whole EBBA2 project.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.944116/full#supplementary-material

Footnotes

1. ^ https://ebba2.info

References

Allouche, O., Tsoar, A., and Kadmon, R. (2006). Assessing the accuracy of species distribution models: Prevalence, kappa and the true skill statistic (TSS). J. Appl. Ecol. 43, 1223–1232. doi: 10.1111/j.1365-2664.2006.01214.x

CrossRef Full Text | Google Scholar

Anderson, R. P., Araújo, M., Guisan, A., Lobo, J. M., Martinez-Meyer, E., Peterson, A. T., et al. (2016). “Are species occurrence data in global online repositories fit for modeling species distributions? The case of the Global Biodiversity Information Facility (GBIF),” in Final Report of the Task Group on GBIF Data Fitness for Use in Distribution Modelling, (New York, NY: Global Biodiversity Information Facility).

Google Scholar

Araújo, M. B., Anderson, R. P., Barbosa, A. M., Beale, C. M., Dormann, C. F., Early, R., et al. (2019). Standards for distribution models in biodiversity assessments. Sci. Adv. 5, 1–12. doi: 10.1126/sciadv.aat4858

PubMed Abstract | CrossRef Full Text | Google Scholar

Barbet-Massin, M., Jiguet, F., Albert, C. H., and Thuiller, W. (2012). Selecting pseudo-absences for species distribution models: How, where and how many? Methods Ecol. Evol. 3, 327–338. doi: 10.1111/j.2041-210X.2011.00172.x

CrossRef Full Text | Google Scholar

Barbet-Massin, M., Thuiller, W., and Jiguet, F. (2010). How much do we overestimate future local extinction rates when restricting the range of occurrence data in climate suitability models? Ecography 33, 878–886. doi: 10.1111/j.1600-0587.2010.06181.x

CrossRef Full Text | Google Scholar

Barve, N., Barve, V., Jiménez-Valverde, A., Lira-Noriega, A., Maher, S. P., Peterson, A. T., et al. (2011). The crucial role of the accessible area in ecological niche modeling and species distribution modeling. Ecol. Modell. 222, 1810–1819. doi: 10.1016/j.ecolmodel.2011.02.011

CrossRef Full Text | Google Scholar

Bean, W. T., Stafford, R., and Brashares, J. S. (2012). The effects of small sample size and sample bias on threshold selection and accuracy assessment of species distribution models. Ecography 35, 250–258. doi: 10.1111/j.1600-0587.2011.06545.x

CrossRef Full Text | Google Scholar

Beck, J., Böller, M., Erhardt, A., and Schwanghart, W. (2014). Spatial bias in the GBIF database and its effect on modeling species’ geographic distributions. Ecol. Inform. 19, 10–15. doi: 10.1016/j.ecoinf.2013.11.002

CrossRef Full Text | Google Scholar

Bibby, C. J., Burgess, N. D., Hill, D. A., and Mustoe, S. H. (2020). Bird Census Techniques, 2nd Edn. Cambridge: Academic Press.

Google Scholar

Blonder, B., Lamanna, C., Violle, C., and Enquist, B. J. (2014). The n-dimensional hypervolume. Glob. Ecol. Biogeogr. 23, 595–609.

Google Scholar

Broennimann, O., and Guisan, A. (2008). Predicting current and future biological invasions: Both native and invaded ranges matter. Biol. Lett. 4, 585–589. doi: 10.1098/rsbl.2008.0254

PubMed Abstract | CrossRef Full Text | Google Scholar

Broennimann, O., Fitzpatrick, M. C., Pearman, P. B., Petitpierre, B., Pellissier, L., Yoccoz, N. G., et al. (2012). Measuring ecological niche overlap from occurrence and spatial environmental data. Glob. Ecol. Biogeogr. 21, 481–497. doi: 10.1111/j.1466-8238.2011.00698.x

CrossRef Full Text | Google Scholar

Calabrese, J. M., Certain, G., Kraan, C., and Dormann, C. F. (2014). Stacking species distribution models and adjusting bias by linking them to macroecological models. Glob. Ecol. Biogeogr. 23, 99–112. doi: 10.1111/geb.12102

CrossRef Full Text | Google Scholar

Chevalier, M., Broennimann, O., Cornuault, J., and Guisan, A. (2021). Data integration methods to account for spatial niche truncation effects in regional projections of species distribution. Ecol. Appl. 31:e02427.

Google Scholar

Clement, M. J., Hines, J. E., Nichols, J. D., Pardieck, K. L., and Ziolkowski, D. J. (2016). Estimating indices of range shifts in birds using dynamic models when detection is imperfect. Glob. Chang. Biol. 22, 3273–3285. doi: 10.1111/gcb.13283

PubMed Abstract | CrossRef Full Text | Google Scholar

de Bello, F., Lavorel, S., Lavergne, S., Albert, C. H., Boulangeat, I., Mazel, F., et al. (2013). Hierarchical effects of environmental filters on the functional structure of plant communities: A case study in the French Alps. Ecography 36, 393–402. doi: 10.1111/j.1600-0587.2012.07438.x

CrossRef Full Text | Google Scholar

Descombes, P., Pradervand, J. N., Golay, J., Guisan, A., and Pellissier, L. (2016). Simulated shifts in trophic niche breadth modulate range loss of alpine butterflies under climate change. Ecography 39, 796–804. doi: 10.1111/ecog.01557

CrossRef Full Text | Google Scholar

Di Cola, V., Broennimann, O., Petitpierre, B., Breiner, F. T., D’Amen, M., Randin, C., et al. (2017). ecospat: An R package to support spatial analyses and modeling of species niches and distributions. Ecography 40, 774–787. doi: 10.1111/ecog.02671

CrossRef Full Text | Google Scholar

Dorazio, R. M. (2014). Accounting for imperfect detection and survey bias in statistical analysis of presence-only data. Glob. Ecol. Biogeogr. 23, 1472–1484. doi: 10.1111/geb.12216

CrossRef Full Text | Google Scholar

Dubuis, A., Pottier, J., Rion, V., Pellissier, L., Theurillat, J. P., and Guisan, A. (2011). Predicting spatial patterns of plant species richness: A comparison of direct macroecological and species stacking modelling approaches. Divers. Distrib. 17, 1122–1131. doi: 10.1111/j.1472-4642.2011.00792.x

CrossRef Full Text | Google Scholar

Elith, J., Kearney, M., and Phillips, S. (2010). The art of modelling range-shifting species. Methods Ecol. Evol. 1, 330–342.

Google Scholar

Engler, R., Randin, C. F., Thuiller, W., Dullinger, S., Zimmermann, N. E., Araújo, M. B., et al. (2011). 21st century climate change threatens mountain flora unequally across Europe. Glob. Chang. Biol. 17, 2330–2341. doi: 10.1111/j.1365-2486.2010.02393.x

CrossRef Full Text | Google Scholar

Fink, D., Hochachka, W. M., Zuckerberg, B., Winkler, D. W., Shaby, B., Munson, M. A., et al. (2010). Spatiotemporal exploratory models for broad-scale survey data. Ecol. Appl. 20, 2131–2147.

Google Scholar

Fletcher, R. J., Hefley, T. J., Robertson, E. P., Zuckerberg, B., McCleery, R. A., and Dorazio, R. M. (2019). A practical guide for combining data to model species distributions. Ecology 100, 1–15. doi: 10.1002/ecy.2710

PubMed Abstract | CrossRef Full Text | Google Scholar

Gelman, A., and Rubin, D. B. (1992). Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 7, 457–511.

Google Scholar

Guillera-Arroita, G., Lahoz-Monfort, J. J., Elith, J., Gordon, A., Kujala, H., Lentini, P. E., et al. (2015). Is my species distribution model fit for purpose? Matching data and models to applications. Glob. Ecol. Biogeogr. 24, 276–292. doi: 10.1111/geb.12268

CrossRef Full Text | Google Scholar

Guisan, A., Graham, C. H., Elith, J., Huettmann, F., Dudik, M., Ferrier, S., et al. (2007). Sensitivity of predictive species distribution models to change in grain size. Divers. Distrib. 13, 332–340. doi: 10.1111/j.1472-4642.2007.00342.x

CrossRef Full Text | Google Scholar

Guisan, A., Thuiller, W., and Zimmermann, N. E. (2017). Habitat Suitability and Distribution models: with Applications in R. Cambridge: Cambridge University Press.

Google Scholar

Guisan, A., Tingley, R., Baumgartner, J. B., Naujokaitis-Lewis, I., Sutcliffe, P. R., Tulloch, A. I. T., et al. (2013). Predicting species distributions for conservation decisions. Ecol. Lett. 16, 1424–1435. doi: 10.1111/ele.12189

PubMed Abstract | CrossRef Full Text | Google Scholar

Hattab, T., Albouy, C., Lasram, F. B. R., Somot, S., Le Loc’h, F., and Leprieur, F. (2014). Towards a better understanding of potential impacts of climate change on marine species distribution: A multiscale modelling approach. Glob. Ecol. Biogeogr. 23, 1417–1429. doi: 10.1111/geb.12217

CrossRef Full Text | Google Scholar

He, X., Liang, J., Zeng, G., Yuan, Y., and Li, X. (2019). The Effects of Interaction between Climate Change and Land-Use/Cover Change on Biodiversity-Related Ecosystem Services. Glob. Challenges 3:1800095. doi: 10.1002/gch2.201800095

PubMed Abstract | CrossRef Full Text | Google Scholar

Heberling, J. M., Miller, J. T., Noesgaard, D., Weingart, S. B., and Schigel, D. (2021). Data integration enables global biodiversity synthesis. Proc. Natl. Acad. Sci. U.S.A. 118, 1–7. doi: 10.1073/pnas.2018093118

PubMed Abstract | CrossRef Full Text | Google Scholar

Herrando, S., Vorisek, P., and Keller, V. (2014). The methodology of the new European breeding bird atlas: Finding standards across diverse situations Promoted and organised by the European Bird Census Council. Bird Census News 26, 6–14.

Google Scholar

Hirzel, A., and Guisan, A. (2002). Which is the optimal sampling strategy for habitat suitability modelling. Ecol. Modell. 157, 331–341. doi: 10.1016/S0304-3800(02)00203-X

CrossRef Full Text | Google Scholar

Hurlbert, A. H., and Jetz, W. (2007). Species richness, hotspots, and the scale dependence of range maps in ecology and conservation. Proc. Natl. Acad. Sci. U.S.A. 104, 13384–13389. doi: 10.1073/pnas.0704469104

PubMed Abstract | CrossRef Full Text | Google Scholar

Iler, A. M., Caradonna, P. J., Forrest, J. R. K., and Post, E. (2021). Demographic Consequences of Phenological Shifts in Response to Climate Change. Annu. Rev. Ecol. Evol. Syst. 52, 221–245. doi: 10.1146/annurev-ecolsys-011921-032939

CrossRef Full Text | Google Scholar

Isaac, N. J. B., Jarzyna, M. A., Keil, P., Dambly, L. I., Boersch-Supan, P. H., Browning, E., et al. (2020). Data Integration for Large-Scale Models of Species Distributions. Trends Ecol. Evol. 35, 56–67. doi: 10.1016/j.tree.2019.08.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Jetz, W., McPherson, J. M., and Guralnick, R. P. (2012). Integrating biodiversity distribution knowledge: Toward a global map of life. Trends Ecol. Evol. 27, 151–159. doi: 10.1016/j.tree.2011.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiménez-Valverde, A., Lobo, J. M., and Hortal, J. (2009). The effect of prevalence and its interaction with sample size on the reliability of species distribution models. Community Ecol. 10, 196–205.

Google Scholar

Karger, D. N., Conrad, O., Böhner, J., Kawohl, T., Kreft, H., Soria-Auza, R. W., et al. (2017). Climatologies at high resolution for the earth’s land surface areas. Sci. Data 4, 1–20. doi: 10.1038/sdata.2017.122

PubMed Abstract | CrossRef Full Text | Google Scholar

Keil, P., and Jetz, W. (2014). Downscaling the environmental associations and spatial patterns of species richness. Ecol. Appl. 24, 823–831. doi: 10.1890/13-0805.1

CrossRef Full Text | Google Scholar

Keil, P., Wilson, A. M., and Jetz, W. (2014). Uncertainty, priors, autocorrelation and disparate data in downscaling of species distributions. Divers. Distrib. 20, 797–812. doi: 10.1111/ddi.12199

CrossRef Full Text | Google Scholar

Keller, V., Herrando, S., Vorísek, P., Franch, M., Kipson, M., Milanesi, P., et al. (2020). European Breeding Bird Atlas 2 – Distribution, Abundance and Change. Barcelona: Lynx Edicions.

Google Scholar

Kéry, M., and Royle, J. A. (2015). Applied Hierarchical Modeling in Ecology. Amsterdam: Elsevier, doi: 10.1016/c2013-0-19160-x

CrossRef Full Text | Google Scholar

Knaus, P., Antoniazza, S., Wechsler, S., Guélat, J., Kéry, M., Strebel, N., et al. (2018). Swiss Breeding Bird Atlas 2013–2016. Distribution and population trends of birds in Switzerland and Liechtenstein. Sempach: Swiss Ornithological Institute.

Google Scholar

Koshkina, V., Wang, Y., Gordon, A., Dorazio, R. M., White, M., and Stone, L. (2017). Integrated species distribution models: Combining presence-background data and site-occupany data with imperfect detection. Methods Ecol. Evol. 8, 420–430. doi: 10.1111/2041-210X.12738

CrossRef Full Text | Google Scholar

Lenoir, J., Bertrand, R., Comte, L., Bourgeaud, L., Hattab, T., Murienne, J., et al. (2020). Species better track climate warming in the oceans than on land. Nat. Ecol. Evol. 4, 1044–1059. doi: 10.1038/s41559-020-1198-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Q., and Liny, N. (2010). The Bayesian elastic net. Bayesian Anal. 5, 151–170. doi: 10.1214/10-BA506

CrossRef Full Text | Google Scholar

Maggini, R., Lehmann, A., Kéry, M., Schmid, H., Beniston, M., Jenni, L., et al. (2011). Are Swiss birds tracking climate change?. Detecting elevational shifts using response curve shapes. Ecol. Modell. 222, 21–32. doi: 10.1016/j.ecolmodel.2010.09.010

CrossRef Full Text | Google Scholar

Mateo, R. G., Aroca-Fernández, M. J., Gastón, A., Gomez-Rubio, V., Saura, S., and García-Viñas, J. I. (2019a). Looking for an optimal hierarchical approach for ecologically meaningful niche modelling. Ecol. Modell. 409:108735.

Google Scholar

Mateo, R. G., Gastón, A., Aroca-Fernández, M. J., Broennimann, O., Guisan, A., Saura, S., et al. (2019b). Hierarchical species distribution models in support of vegetation conservation at the landscape scale. J. Veg. Sci. 30, 386–396. doi: 10.1111/jvs.12726

CrossRef Full Text | Google Scholar

Mateo, R. G., Broennimann, O., Petitpierre, B., Muñoz, J., van Rooy, J., Laenen, B., et al. (2015). What is the potential of spread in invasive bryophytes? Ecography 38, 480–487. doi: 10.1111/ecog.01014

CrossRef Full Text | Google Scholar

Mateo, R. G., Croat, T. B., Felicísimo, ÁM., and Muñoz, J. (2010). Profile or group discriminative techniques? Generating reliable species distribution models using pseudo-absences and target-group absences from natural history collections. Divers. Distrib. 16, 84–94. doi: 10.1111/j.1472-4642.2009.00617.x

CrossRef Full Text | Google Scholar

McGill, B. J. (2010). Matters of scale. Science 328, 575–576. doi: 10.1126/science.1188528

PubMed Abstract | CrossRef Full Text | Google Scholar

Miller, D. A. W., Pacifici, K., Sanderlin, J. S., and Reich, B. J. (2019). The recent past and promising future for data integration methods to estimate species’ distributions. Methods Ecol. Evol. 10, 22–37. doi: 10.1111/2041-210X.13110

CrossRef Full Text | Google Scholar

Moran, E. V., Thuiller, W., Angert, A. L., and Benito Garzón, M. (2022). Editorial: Predicting and Managing Climate-Driven Range Shifts in Plants. Front. Ecol. Evol. 10:856213. doi: 10.3389/fevo.2022.856213

CrossRef Full Text | Google Scholar

Moudrý, V., and Šímová, P. (2012). Influence of positional accuracy, sample size and scale on modelling species distributions: A review. Int. J. Geogr. Inf. Sci. 26, 2083–2095. doi: 10.1080/13658816.2012.721553

CrossRef Full Text | Google Scholar

Niamir, A., Skidmore, A. K., Toxopeus, A. G., and Real, R. (2016). Use of taxonomy to delineate spatial extent of atlas data for species distribution models. Glob. Ecol. Biogeogr. 25, 227–237. doi: 10.1111/geb.12405

CrossRef Full Text | Google Scholar

Nogués-Bravo, D., Veloz, S., Holt, B. G., Singarayer, J., Valdes, P., Davis, B., et al. (2016). Amplified plant turnover in response to climate change forecast by Late Quaternary records. Nat. Clim. Chang. 6, 1115–1119. doi: 10.1038/nclimate3146

CrossRef Full Text | Google Scholar

Pacifici, K., Reich, B. J., Miller, D. A., Gardner, B., Stauffer, G., Singh, S., et al. (2017). Integrating multiple data sources in species distribution modeling: A framework for data fusion. Ecology 98, 840–850. doi: 10.1002/ecy.1710

PubMed Abstract | CrossRef Full Text | Google Scholar

Pearson, R. G., Dawson, T. P., and Liu, C. (2004). Modelling species distributions in Britain: A hierarchical integration of climate and land-cover data. Ecography 27, 285–298.

Google Scholar

Petitpierre, B., McDougall, K., Seipel, T., Broennimann, O., Guisan, A., and Kueffer, C. (2016). Will climate change increase the risk of plant invasions into mountains? Ecol. Appl. 26, 530–544. doi: 10.1890/14-1871

CrossRef Full Text | Google Scholar

Plummer, M. (2003). “JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling,” in Proceedings of the 3rd International Workshop on Distributed Statistical Computing (DSC 2003), eds K. Hornik, F. Leisch, and A. Zeileis (Vienna: Technische UniversitätWien).

Google Scholar

Randin, C. F., Engler, R., Normand, S., Zappa, M., Zimmermann, N. E., Pearman, P. B., et al. (2009). Climate change and plant distribution: Local models predict high-elevation persistence. Glob. Chang. Biol. 15, 1557–1569.

Google Scholar

Rocchini, D., Hortal, J., Lengyel, S., Lobo, J. M., Jiménez-Valverde, A., Ricotta, C., et al. (2011). Accounting for uncertainty when mapping species distributions: The need for maps of ignorance. Prog. Phys. Geogr. 35, 211–226. doi: 10.1177/0309133311399491

CrossRef Full Text | Google Scholar

Román-Palacios, C., and Wiens, J. J. (2020). Recent responses to climate change reveal the drivers of species extinction and survival. Proc. Natl. Acad. Sci. U.S.A. 117, 4211–4217. doi: 10.1073/pnas.1913007117

PubMed Abstract | CrossRef Full Text | Google Scholar

Sánchez-Fernández, D., Lobo, J. M., and Hernández-Manrique, O. L. (2011). Species distribution models that do not incorporate global data misrepresent potential distributions: A case study using Iberian diving beetles. Divers. Distrib. 17, 163–171. doi: 10.1111/j.1472-4642.2010.00716.x

CrossRef Full Text | Google Scholar

Santini, L., Benítez-López, A., Maiorano, L., Čengić, M., and Huijbregts, M. A. J. (2021). Assessing the reliability of species distribution projections in climate change research. Divers. Distrib. 27, 1035–1050. doi: 10.1111/ddi.13252

CrossRef Full Text | Google Scholar

Scherrer, D., Esperon-Rodriguez, M., Beaumont, L. J., Barradas, V. L., and Guisan, A. (2021). National assessments of species vulnerability to climate change strongly depend on selected data sources. Divers. Distrib. 27, 1367–1382. doi: 10.1111/ddi.13275

CrossRef Full Text | Google Scholar

Shiogama, H., Stone, D., Emori, S., Takahashi, K., Mori, S., Maeda, A., et al. (2016). Predicting future uncertainty constraints on global warming projections. Sci. Rep. 6, 1–7.

Google Scholar

Sinclair, S. J., White, M. D., and Newell, G. R. (2010). How useful are species distribution models for managing biodiversity under future climates? Ecol. Soc. 15, 299–305. doi: 10.5751/ES-03089-150108

PubMed Abstract | CrossRef Full Text | Google Scholar

Sofaer, H. R., Jarnevich, C. S., Pearse, I. S., Smyth, R. L., Auer, S., Cook, G. L., et al. (2019). Development and Delivery of Species Distribution Models to Inform Decision-Making. Bioscience 69, 544–557. doi: 10.1093/biosci/biz045

CrossRef Full Text | Google Scholar

Srivastava, V., Lafond, V., and Griess, V. C. (2019). Species distribution models (SDM): Applications, benefits and challenges in invasive species management. CAB Rev. Perspect. Agric. Vet. Sci. Nutr. Nat. Resour. 14, 1–13. doi: 10.1079/PAVSNNR201914020

CrossRef Full Text | Google Scholar

Su, Y. S., and Yajima, M. (2015). Package ‘R2jags.’ Cran-R.

Google Scholar

Suárez-Seoane, S., Virgós, E., Terroba, O., Pardavila, X., and Barea-Azcón, J. M. (2014). Scaling of species distribution models across spatial resolutions and extents along a biogeographic gradient. The case of the Iberian mole Talpa occidentalis. Ecography 37, 279–292.

Google Scholar

Tang, Y., Winkler, J. A., Viña, A., Liu, J., Zhang, Y., Zhang, X., et al. (2018). Uncertainty of future projections of species distributions in mountainous regions. PLoS One 13:e0189496. doi: 10.1371/journal.pone.0189496

PubMed Abstract | CrossRef Full Text | Google Scholar

Tessarolo, G., Rangel, T. F., Araújo, M. B., and Hortal, J. (2014). Uncertainty associated with survey design in species distribution models. Divers. Distrib. 20, 1258–1269. doi: 10.1111/ddi.12236

CrossRef Full Text | Google Scholar

Thibaud, E., Petitpierre, B., Broennimann, O., Davison, A. C., and Guisan, A. (2014). Measuring the relative effect of factors affecting species distribution model predictions. Methods Ecol. Evol. 5, 947–955. doi: 10.1111/2041-210x.12203

CrossRef Full Text | Google Scholar

Thuiller, W., Brotons, L., Araújo, M. B., and Lavorel, S. (2004). Effects of restricting environmental range of data to project current and future species distributions. Ecography 2, 165–172. doi: 10.1093/conphys/coaa090

PubMed Abstract | CrossRef Full Text | Google Scholar

Thuiller, W., Lafourcade, B., Engler, R., and Araújo, M. B. (2009). BIOMOD – A platform for ensemble forecasting of species distributions. Ecography 32, 369–373. doi: 10.1111/j.1600-0587.2008.05742.x

CrossRef Full Text | Google Scholar

Tingley, M. W., Koo, M. S., Moritz, C., Rush, A. C., and Beissinger, S. R. (2012). The push and pull of climate change causes heterogeneous shifts in avian elevational ranges. Glob. Chang. Biol. 18, 3279–3290. doi: 10.1111/j.1365-2486.2012.02784.x

CrossRef Full Text | Google Scholar

Tingley, M. W., Monahan, W. B., Beissinger, S. R., and Moritz, C. (2009). Birds track their Grinnellian niche through a century of climate change. Proc. Natl. Acad. Sci. U.S.A. 106, 19637–19643. doi: 10.1073/pnas.0901562106

PubMed Abstract | CrossRef Full Text | Google Scholar

Tulloch, A. I. T., Sutcliffe, P., Naujokaitis-Lewis, I., Tingley, R., Brotons, L., Ferraz, K. M. P. M. B., et al. (2016). Conservation planners tend to ignore improved accuracy of modelled species distributions to focus on multiple threats and ecological processes. Biol. Conserv. 199, 157–171. doi: 10.1016/j.biocon.2016.04.023

CrossRef Full Text | Google Scholar

van Erp, S., Oberski, D. L., and Mulder, J. (2019). Shrinkage priors for Bayesian penalized regression. J. Math. Psychol. 89, 31–50. doi: 10.1016/j.jmp.2018.12.004

CrossRef Full Text | Google Scholar

Vicente, J. R., Gonçalves, J., Honrado, J. P., Randin, C. F., Pottier, J., Broennimann, O., et al. (2014). A framework for assessing the scale of influence of environmental factors on ecological patterns. Ecol. Complex. 20, 151–156. doi: 10.1016/j.ecocom.2014.10.005

CrossRef Full Text | Google Scholar

Vincent, C., Fernandes, R. F., Cardoso, A. R., Broennimann, O., Di Cola, V., D’Amen, M., et al. (2019). Climate and land-use changes reshuffle politically-weighted priority areas of mountain biodiversity. Glob. Ecol. Conserv. 17:e00589. doi: 10.1016/j.gecco.2019.e00589

CrossRef Full Text | Google Scholar

Warren, D. L., Dornburg, A., Zapfe, K., and Iglesias, T. L. (2021). The effects of climate change on Australia’s only endemic Pokémon: Measuring bias in species distribution models. Methods Ecol. Evol. 12, 985–995. doi: 10.1111/2041-210X.13591

CrossRef Full Text | Google Scholar

Webber, B. L., Yates, C. J., Le Maitre, D. C., Scott, J. K., Kriticos, D. J., Ota, N., et al. (2011). Modelling horses for novel climate courses: Insights from projecting potential distributions of native and alien Australian acacias with correlative and mechanistic models. Divers. Distrib. 17, 978–1000. doi: 10.1111/j.1472-4642.2011.00811.x

CrossRef Full Text | Google Scholar

Willis, K. J., and Whittaker, R. J. (2002). Species diversity – Scale matters. Science 295, 1245–1248. doi: 10.1126/science.1067335

PubMed Abstract | CrossRef Full Text | Google Scholar

Zellweger, F., De Frenne, P., Lenoir, J., Rocchini, D., and Coomes, D. (2019). Advances in Microclimate Ecology Arising from Remote Sensing. Trends Ecol. Evol. 34, 327–341. doi: 10.1016/j.tree.2018.12.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Zou, H., and Hastie, T. (2005). Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 67, 301–320. doi: 10.1111/j.1467-9868.2005.00503.x

CrossRef Full Text | Google Scholar

Zurell, D., Franklin, J., König, C., Bouchet, P. J., Dormann, C. F., Elith, J., et al. (2020). A standard protocol for reporting species distribution models. Ecography 43, 1261–1277. doi: 10.1111/ecog.04960

CrossRef Full Text | Google Scholar

Zurell, D., König, C., Malchow, A. K., Kapitza, S., Bocedi, G., Travis, J., et al. (2022). Spatially explicit models for decision-making in animal conservation and restoration. Ecography 4. [Epub ahead of print]. doi: 10.1111/ecog.05787

CrossRef Full Text | Google Scholar