The Adaptive Significance of Flash Behavior: A Bayesian Model

Some cryptic animals have conspicuous color patches that are displayed when they move. This “flash behavior” may serve several functions, but perhaps the most widely invoked explanation is that the display makes it harder for the signaler to be found by predators once it has settled. There is now some experimental evidence that flash behavior while fleeing can enhance the survivorship of prey in the manner proposed. However, to date there has been no explicit mathematical model to help understand the way in which flash displays might interfere with the search process of predators. Here we apply Bayesian search theory to show that the higher the conspicuousness of a prey item, the sooner a predator should give up searching for it in an area where it appears to have settled, although the relationship is not always monotonically decreasing. Thus, fleeing prey that give the impression of being conspicuous will tend to survive at a higher rate than prey seen to flee in their cryptic state, since predators search for flashing prey for an inappropriately short period of time. The model is readily parameterized and makes several intuitive predictions including: (1) the more confident a predator is that a prey item has settled in a given area, the longer it will search there, (2) the more conspicuous the flash display, the greater its effect in reducing predation, (3) flash behavior will especially benefit those prey with an intermediate level of crypsis when at rest, and (4) the success of flash displays depends on the predator being uncertain of the prey’s resting appearance. We evaluate the empirical evidence for these predictions and discuss how the model might be further developed, including the incorporation of mimicry which would maintain the deception indefinitely.

Introduction

Some animals are cryptic at rest yet display conspicuous colors and/or sounds when they move, before resuming their cryptic state as they settle (Cott, 1940; Anonymous, 1945). Putative examples of this “flash behavior” include the conspicuous hindwing displays of many insect species [including Orthoptera (see Figure 1) and Lepidoptera], the prominent tail flagging of some Artiodactyla and Leporids, and the exposure of the gaudy tail feathers of many otherwise cryptic bird species (Edmunds, 1974, 2008). In each of these cases, the conspicuous traits remain hidden while the organism is at rest and yet they are suddenly revealed while fleeing. Since the hidden conspicuous traits of flashing species tend to be found in both males and females (Loeffler-Henry et al., 2019, 2021) and the flash display is invariably elicited by disturbance, the behavior likely serves as an anti-predator defense rather than as a sexual signal.

FIGURE 1

Figure 1. Examples of flash behavior in Orthoptera (grasshoppers and crickets). Many grasshoppers are cryptic at rest and have transparent wings when they fly. However, the blue-winged grasshopper Oedipoda caerulescens (Linnaeus) exposes bright blue wings when flying, before settling into a cryptic resting state (row 1). The Carolina locust Dissosteira carolina (Linnaeus) exposes dark brown wings in flight yet resumes crypsis when it settles (row 2). Similarly, the short-horned grasshopper Arphia conspersa (Scudd) flashes conspicuous yellow wings in flight (row 3). The images (except those provided by KL-H) were derived from Wikimedia Commons and are reproduced under the Creative Commons Licence. Photo credits (by row, left and right): (1) Charles Sharp, Didier Descouens; (2) anonymous, Karl Loeffler-Henry; (3) Even Dankowicz, Karl Loeffler-Henry.

Precisely how do conspicuous traits “which flash out during movement and vanish again, like a conjurer’s rabbit” (Cott, 1940, p. 376) serve as an anti-predator defense? It is possible that flash behavior may startle any would-be predator (Umbers et al., 2015) and/or make the signaler harder to catch while fleeing (Murali, 2018). However, the most widely discussed benefit is that would-be predators are misled into believing the prey item is always conspicuous in appearance, which hinders the predator’s subsequent search for it (Cott, 1940; Anonymous, 1945). Edmunds (1974, p. 146) made this case most explicitly, noting that a predator “may follow this color and be deceived by its sudden disappearance into assuming the prey has vanished whereas in reality the prey has come to rest in its normal cryptic posture with the colored structures hidden.” An implication of the hypothesis is that any predator coming to search for a conspicuous prey item would give up looking sooner if it did not see the prey item, since if the prey is not immediately found, it will likely be elsewhere (Figure 2).

FIGURE 2

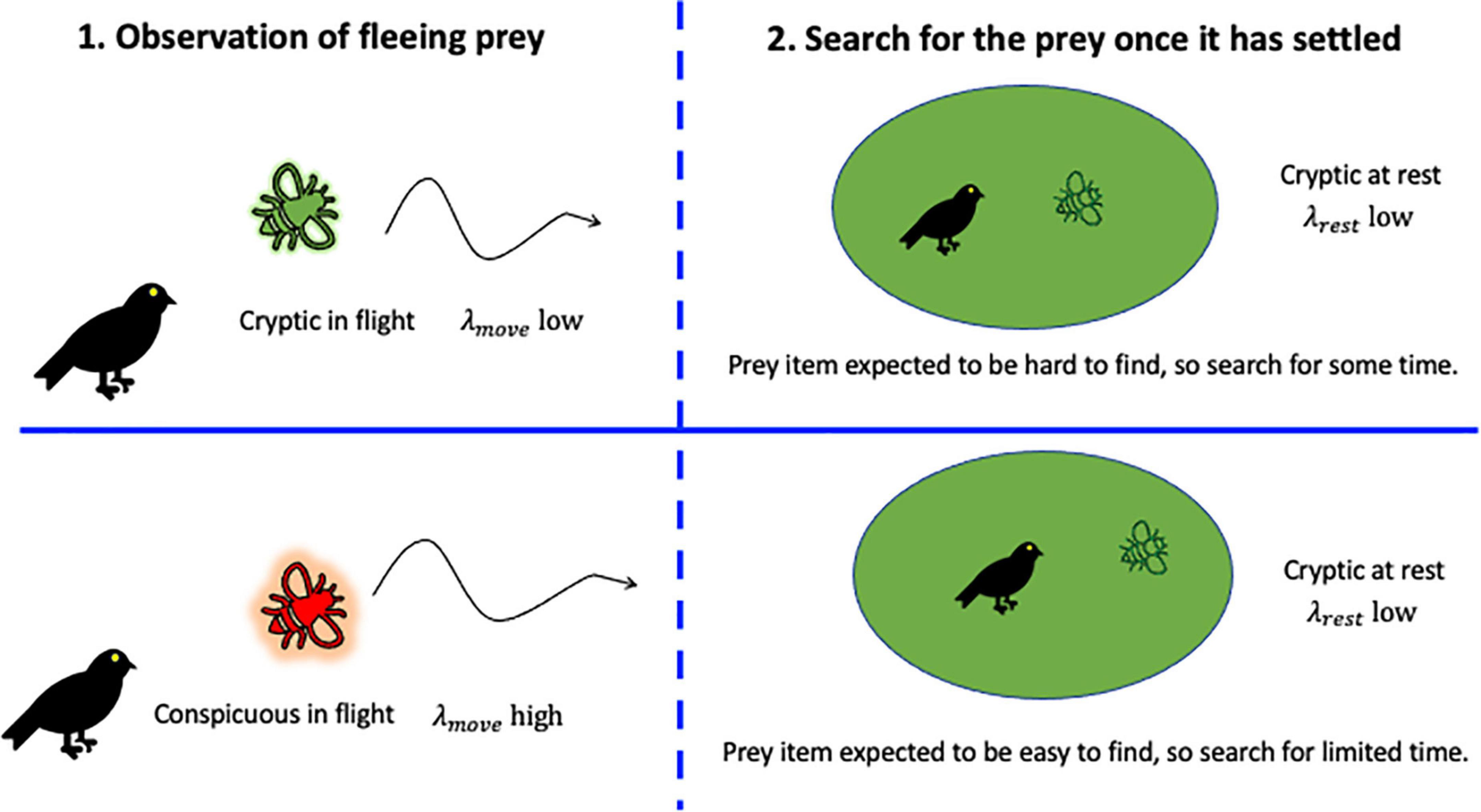
Figure 2. A visual depiction of how flash behavior when fleeing prey might interfere with the search process of predators. Predators that encounter a prey item that is perceived as conspicuous when it flees may expect to readily find the prey when they start to search for it. If the prey item is not quickly found, then the predator will soon cease searching, believing the prey to be elsewhere. Flash behavior may therefore work by deceit, causing predators to adopt an inappropriately short search time for the prey in any given location. The infographic uses stock images from Microsoft PowerPoint 16.6.

Despite their widespread taxonomic distribution, flash displays have only recently begun to be investigated. In a series of computer-based experiments using humans as visual predators, Loeffler-Henry et al. (2018) and Bae et al. (2019) found that participants were indeed more likely to give up looking for prey that had displayed conspicuous colors in motion but resumed crypsis when settled, compared to those prey that were cryptic in motion and at rest. Loeffler-Henry et al. (2021) ran similar experiments and found that flashing prey had a higher survival rate than non-flashing prey but only if predators were unaware of the true resting appearance of the prey, indicating that the benefit of the display was contingent on deception.

While we have an experimental “proof of concept” using computer-generated prey, to date no formal model has been proposed to help explain precisely how and when flash behavior would enhance survivorship. The development of such a model would be an advance for several reasons. First, it would help make the mechanism through which flash behavior hinders predator search more transparent. Second, it will help reveal implicit assumptions and render explicit predictions. Third, it would provide an extra level of rigor in establishing the plausibility of verbal arguments on a quantitative level. Fourth, a parameterizable model could provide a basis for experimental investigation. Here we present and explore just such a model, built on basic biological assumptions. As the model is based on a flashing species giving a misleading impression of its conspicuousness when settled, we first describe how predators should search for prey items of known conspicuousness. Most methods of efficient search use the logic of conditional probabilities and are therefore Bayesian in nature. We then describe how a fleeing prey can enhance its survivorship by giving the impression that it is more conspicuous at rest than it is.

Methods and Results

Imagine you have lost your wallet. You decide, quite rationally, to first look for your wallet in the place it is most likely to be, namely your bedroom. However, the longer you search your bedroom without finding it, the less likely it is to be there. After a while, there will reach a time at which it makes sense to check another room for your wallet, such as the kitchen. So, you move to the kitchen to look for it there, although this doesn’t preclude you coming back to continue to search your bedroom. As further time passes, with no sign of your wallet in all its plausible locations, you start to entertain the possibility the wallet has been stolen. Of course, you may never know for sure whether this is the case, but the prospect of finding your wallet in the house are becoming increasingly slim. After extensive fruitless search you simply give up because life is too short to waste more time looking.

The above scenario may sound all too familiar and the logic underlying the search intuitive. As we will see, with a formal model of the search process for a lost object, we can quantitatively identify the length of time one should spend searching in a given area before moving on. This model starts with a prior belief, expressed as a probability, that the object is in a certain location. As time passes and the object is not found there then this information can be combined with the prior belief to generate a posterior belief that the object is in the area being searched. The process of turning a prior belief into a posterior belief based on new data uses the algebra of conditional probabilities, namely Bayes’ rule (Courville et al., 2006; McNamara et al., 2006; McElreath, 2020). Bayesian search theory is a well-developed research field and involves the application of Bayesian inference to improve the efficiency of search for lost objects (Koopman, 1957, 1980; Stone, 1975). The approach has previously been used in a range of contexts from finding sunken treasure, to recovering flight recorders (McGrayne, 2012). Here we apply it in the context of a simple foraging problem in which a predator searches for prey. We then show how prey can exploit this optimal search strategy, and thereby improve their survivorship.

Optimal Search for a Hidden Object

We start by introducing the foraging problem. A predator (such as a bird) has disturbed a prey item (such as a grasshopper) and observed it flee. The predator believes that the prey item has settled in a certain area (a patch), but it is not entirely sure. The predator then attempts to pursue this prey item. Let us assume that a prey item has a fixed instantaneous rate λ (>0) of being detected by a predator if the predator is searching for the prey in the patch it has settled. Under these conditions, the probability density of the time taken of the predator to discover the prey will follow an exponential distribution, so the cumulative probability a predator will not have found the prey item by time t (i.e., the probability the prey remains undetected) will be:

$u\left(t\right)=e^{-\mathrm{\lambda }t}(1)$

We use λ parameter (otherwise known as the instantaneous hazard rate) as a measure of the prey item’s conspicuousness. Indeed, given the exponential distribution, the mean time taken to discover the prey item if it is present in the patch being searched is (1/λ) with variance (1/λ²), so a higher conspicuousness translates to shorter and less variable time to detection.

Of course, even if a predator observes a prey item with conspicuousness λ while fleeing, it may not be entirely confident where it has settled and so may consider several possibilities. We therefore assume that the predator has prior probabilities p₁,p₂,…,p_n that the fleeing prey item has settled in each of n (>1) alternative patches (sothat 0 < p_i <  1 and ${\sum }_1^n{p}_i=1).$ With no loss of generality we allow the subscripts to refer to the order of magnitude of prior probabilities such that p₁ > p₂ > … > p_n. Naturally, all else being equal, the predator should start its search in patch 1, where the prey item is most likely to be. However, the longer the predator searches in patch 1 without discovering the prey item, the less likely the prey item is in the patch. This lack of success provides information with which it can continually revise its beliefs that the prey item is in the patch (McNamara and Houston, 1985; Killeen et al., 1996).

Let A_i represent the event that the prey has settled in patch i and u(t) be the event that the prey has not been found in patch 1 after the predator spends time t searching there. For reasons that will become evident, we focus solely on decisions made on the first patch, so do not use a patch-specific subscript for either u or t. Expressed in mathematical terms we seek Pr(A₁ | u(t)), i.e., the posterior probability that patch 1 contains the prey item, given that the predator has been searching in that patch for the prey item for time t and it remains undetected. Invoking Bayes’ rule for conditional probabilities we know that:

$Pr\left(A_1\right|u\left(t\right))=\frac{Pr\left(u\left(t\right)\right|A_1)\text{Pr}(A_1)}{u\left(t\right)}(2)$

Here Pr (A₁) represents the prior probability that the prey item has settled in patch 1 (= p₁), while Pr⁡(u(t)|A₁) refers to probability that the prey item remains undiscovered by time t given that it has indeed settled in patch 1. The normalizing denominator u(t) refers to the overall likelihood of the prey item being undetected when the predator searches in patch 1, whether it has settled in patch 1 or not. There are two ways the prey item can remain undetected when the predator searches patch 1. It could be present in patch 1 but remain undiscovered which will arise with combined probability p₁e^−λt or it could be in one of the other patches, in which case it will certainly remain undetected. This outcome will arise with expected probability 1 − p₁. Substituting for the expressions in Eq. 2, we have:

$Pr\left(A_1\right|u\left(t\right))=\frac{e^{-\mathrm{\lambda }t}{p}_1}{p_1{e}^{-\mathrm{\lambda }t}+\left(1-p_1\right)}(3)$

Which simplifies to:

$Pr\left(A_1\right|u\left(t\right))=\frac{p_1}{p_1+\left(1-p_1\right)e^{\mathrm{\lambda }t}}(4)$

Note that Pr⁡(A₁|u(0)) = p₁ (with no information, a predator only uses its prior to estimate the probability that the prey item is in patch 1) and Pr(A₁|u(∞)) = 0 (the prey item is increasingly unlikely to be in patch 1 the longer the predator searches this patch without discovering it). If the candidate patches are close by one another, so that the travel time between them is negligible, then the predator should switch from patch 1 to patch 2 (the next likely area) when the estimated (posterior) probability of finding it in patch 1 falls to match the probability of finding it in the second patch. Naturally, however, the posteriors for the second patch are not unchanged – if the prey item is not found in the first patch in time t then this increases the probability that it is found in the other patches. Bayes’ theorem comes to the rescue again:

$\mathrm{Pr}\left(A_2|u\left(t\right)\right)=\frac{\mathrm{Pr}\left(u\left(t\right)|A_2\right)\text{Pr}(A_2)}{u\left(t\right)}(5)$

Here Pr⁡(u(t)|A₂) = 1 since it is certain that the prey item will not be found after searching time t in patch 1, given that the prey item is in patch 2.

Substituting, for Pr (A₂) (= p₂) and u(t) we have:

$\mathrm{Pr}\left(A_2|u\left(t\right)\right)=\frac{p_2}{p_1{e}^{-\mathrm{\lambda }t}+\left(1-p_1\right)}(6)$

Note that Pr⁡(A₂|u(0)) = p₂(with no time spent so far on patch 1, the predator will use its prior to estimate the probability that the prey item is present in patch 2) and $\mathrm{Pr}(A_2|u(\mathrm{\infty }))=\frac{p_2}{(1-p_1)}$ (since the prey item is highly unlikely to be in patch 1 after extensive search, the probability of the prey item being in patch 2 and all other patches commensurately increases).

We can identify the critical time ($t_1^{*}$) time a predator would spend searching fruitlessly for the prey item in patch 1 before the (posterior) probability of it occurring in patch 1 declines to equal the (increasing) posterior probability of the prey item being in patch 2. This is the critical time $t_1^{*}$ that satisfies:

$\mathrm{Pr}\left(A_1|u\left(t_1^{*}\right)\right)=\mathrm{Pr}(A_2|u(t_1^{*}))(7)$

Substituting Eqs 4, 6 in Eq. 7 and solving indicates:

$t_1^{*}=\frac{Log\left[\frac{p_1}{p_2}\right]}{\mathrm{\lambda }}(8)$

Note at the outset that this critical time is not the expected time a predator will spend searching in patch 1 but the predicted maximum time it should spend searching, because a proportion of times the prey item will have been present in the patch and it will have been found before the threshold is reached (McNamara and Houston, 1985). A direct consequence of Eq. 8 is that the more conspicuous a prey item is (i.e., the higher λ) the shorter the length of time a predator should look for it in patch 1 before moving on to the next most likely patch. Moreover, as might be expected, the more initially convinced a predator is that the prey item has settled in patch 1 (i.e., the higher p₁) the longer it will look there before moving on.

Abandoning Search: The Marginal Value Theorem

The above mathematics provides the optimal Bayesian search sequence of n patches, but all else being equal, if the predator moves to patch 2 and no prey item is immediately found then the predator should return to patch 1, moving back and forth until either it finds the prey item or the posterior (conditional) probabilities of being in either patch both become so low that patch 3 now becomes a plausible location where the prey item could be and is included in the search set (Killeen et al., 1996). Naturally, if the prey item is present in one of the n possible patches, and the predator has no incentive to stop, then the prey item will eventually be found. Even if the prey item is not present in any of the n patches (so that the prey item has settled in a patch outside the candidate set, despite the predator’s prior belief that this would arise with probability zero) then without a stopping rule the predator will continue to search the n patches forever.

There are many reasons why a searching predator might eventually give up searching the network of patches. One important reason is that time is valuable to the predator. Thus, rather than continuing to search without success, a time will come when it will be more profitable for the predator to stop searching for the lost prey and continue on its way. One could introduce a simple stopping rule in which a predator gives up searching a patch if the posterior probability of the prey item being present there falls below a certain threshold. However, this approach does not explicitly identify the search strategy that maximizes an appropriate fitness-related currency, such as the long-term rate of capture of prey. Charnov’s marginal value theorem (MVT) (Charnov, 1976) is an appropriate rule to invoke for this purpose and states a predator will maximize its long-term rate of reward if it leaves a given patch when its instantaneous rate of gain falls below that which could be gained from moving on and seeking an alternative patch. Here we apply this intuitive rule and explore its implications. For mathematical convenience, we focus on instances in which the predator starts out searching the most likely candidate patch, and if evidence accumulates that it is not present in the patch it abandons its search altogether rather than looking at the second most plausible patch. This strategy will be appropriate if there was only one area that could be profitably searched – for example, any prey item that had settled outside the patch being searched is able to conceal itself, or make its escape, while the predator is looking elsewhere. Note that this is not an overly restrictive assumption since the MVT would apply if the predator could search several patches before moving on, but it would complicate the model unnecessarily.

The original formulation of Charnov (1976) assumed a smooth deterministic gain function, and yet here any patch that is searched contains one prey item at most, which is found by chance. Models with stochastic encounters do not necessarily share the same optimal solutions as their deterministic counterparts (Oaten, 1977; Green, 1980; McNair, 1982). For example, if patch quality varies and the quality of the patch can be inferred from the predator’s accumulating experience, then a predator that uses patch-specific information will generally receive a higher payoff than a predator that uses some kind of average experience (Oaten, 1977). In our case, we have already allowed predators to use information on time spent searching to infer patch quality (i.e., the likelihood it contains a prey item). However, rather than use the actual rate of gain of an individual predator on a patch (which will be zero until it finds the prey item), we instead use the expected rate of gain of the predator in the immediate future as a measure of the predator’s short-term anticipated rate of success (McNamara, 1982; McNamara and Houston, 1985). We refer to the predator’s expected instantaneous rate of reward as r(t), noting that it will fall the longer the predator has been searching in a patch.

If the prey item is known to be present in the patch being searched, then the initial expected instantaneous rate at which the predator will detect the prey item [i.e., r(0)] will be λ. If the prey item is known to be absent from the patch being searched, then the instantaneous rate of detection of the prey item in this patch will always be 0. However, the searching predator will in general not know the prey item’s true location with certainty until it has found it. In this case, the instantaneous expected instantaneous rate of gain of the predator will be λ multiplied by the posterior probability of that the prey item is present in the patch given that it has not yet been found, namely:

$r\left(t\right)=\mathrm{\lambda }\mathrm{Pr}\left(A_1|u\left(t\right)\right)(9)$

Substituting Eq. 4 in Eq. 9 we have:

$r\left(t\right)=\frac{\mathrm{\lambda }{p}_1}{p_1+\left(1-p_1\right)e^{\mathrm{\lambda }t}}(10)$

Note that the expected instantaneous rate of gain of the predator starts at λp₁ at time 0 and moves toward zero as the time without finding the prey item increases, reflecting the fact that the prey item is increasingly less likely to be on the patch (see Supplementary Figure 1). We should now compare the expected instantaneous rate of gain of a searching predator with the rate of gain the predator could achieve by abandoning its current search and moving elsewhere. If all flush and search events of prey had the same characteristics, then we could calculate the expected long-term rate of gain of the predator by treating the current patch as a typical patch and incorporating a travel time between new prey items (τ) into the appropriate rate calculations (e.g., see McNamara and Houston, 1985). However, if there are a range of prey types that vary in energy content, conspicuousness, and ease at which they can be followed when fleeing, then the long-term rate of gain cannot be calculated from the characteristics of any single example of an encounter with prey. We therefore give the long-term rate of gain a fixed value of g.

The MVT dictates that a predator will abandon its search when the instantaneous expected rate of gain (which diminishes as search time continues) from searching for the prey item (see Eq. 10) falls below the long-term rate of gain from moving on, namely if:

$\frac{\mathrm{\lambda }{p}_1}{p_1+\left(1-p_1\right)e^{\mathrm{\lambda }t}}<g(11)$

Solving for the time at which the instantaneous gain matches the long-term gain from abandoning search, we have:

$t_s^{*}=\frac{Log\left[\frac{p_1\left(\mathrm{\lambda }-g\right)}{g\left(1-p_1\right)}\right]}{\mathrm{\lambda }}(12)$

which is greater than zero so long as λp₁ > g, i.e., the expected initial instantaneous rate of gain from searching exceeds the long-term rate of gain of the predator from moving on, otherwise the predator would not initiate searching.

Figure 3 shows the predicted relationship between the optimal time spent searching on patch 1 and the conspicuousness of the settled prey item. The optimal search time before moving on is typically shorter for prey items that are more conspicuous (indeed, $t_s^{*}\to 0$ as λ→∞). However, since $t_s^{*}\to$0 for λp₁→g from above and $t_s^{*}$ > 0 when λp₁ > g then the optimal maximum search time initially increases for low permissible λ and thereafter decreases. This maximum in optimal search time is readily explained by the fact that while the expected instantaneous rate of gain of a predator declines more rapidly for higher λ, the initial expected instantaneous rate of gain (i.e., the intercept λp₁) is lower for patches with more cryptic prey. So, if the threshold g happens to be close to λp₁ for cryptic prey, the optimal time spent searching for them may be less than that of a more conspicuous prey item (see Supplementary Figure 1). Put another way, for small λ then r(t) ≈ λ p1 (because a lack of success in finding cryptic prey does not have a strong effect on the posterior), so the contribution of λ to r(t) is positive. However, for large λ, the posterior probability is approximately proportional to e^−λt and since it dominates r(t) the contribution of λ to r(t) is negative.

FIGURE 3

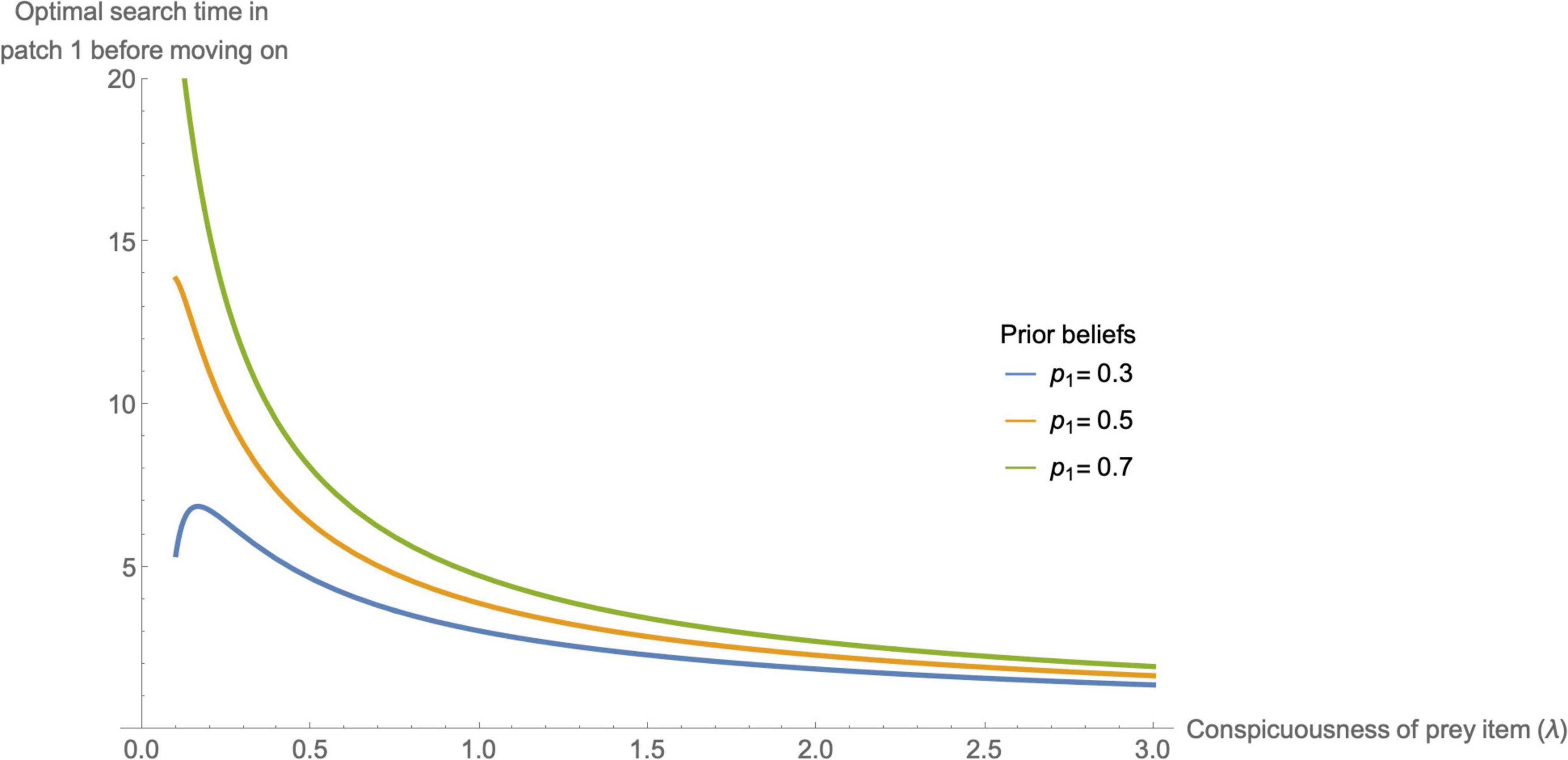
Figure 3. The optimal maximum search time of a predator looking for a prey item in patch 1 (the patch it believes the prey is most likely hiding) before abandoning its search and looking for prey elsewhere. Here we set the average long-term rate of gain from abandoning search (g) to be 0.02 and vary the conspicuousness of the fleeing prey item (λ) from 0.1 to 3 (so that it is always profitable to pursue the prey item so long as p₁ > 0.2). The predator’s prior probability that the most plausible patch 1 contains the prey item (p₁) is considered at three different levels (0.3, 0.5, and 0.7). In general, the higher the conspicuousness of the prey item, the shorter the maximal search time before abandonment (although it may pay a predator to search for cryptic prey items of borderline profitability for a relatively short period of time, hence a peak). The more confident the predator is that the prey have landed in the patch, the longer it should search.

Since the derivative of $t_s^{*}$ (Eq. 12) with respect to p₁ is {λp₁(1−p₁)}⁻¹, which is always positive the more initially convinced the predator is that the prey item is present in the patch the longer it will search the patch before giving up. Likewise, the derivative of $t_s^{*}$ with respect to g is {g(g−λ)}⁻¹ which is always negative for λp₁ > g, so the higher g, the less time a predator will spend searching on a patch before moving on.

The Survival Implications of Optimal Search for Prey

We now quantify the implications of the predator optimal search behavior for prey survivorship. Let us assume that the prey item does indeed land in patch 1 with probability p₁, as the predator initially believes. The probability of the prey item going undetected if the predator forages in the above optimal way is therefore given by:

$u\left(t_s^{*}\right)=p_1{e}^{-\mathrm{\lambda }{t}_s^{*}}+\left(1-p_1\right)(13)$

Substituting for $t_s^{*}$ from Eq. 12 in Eq. 13 we obtain a simple expression for prey survivorship following optimal search namely:

$u\left(t_s^{*}\right)=\mathit{\hspace{1em}}\frac{\mathrm{\lambda }\left(1-p_1\right)}{\left(\mathrm{\lambda }-g\right)}(14)$

Since the derivative of this function with respect to λ is negative for λ > g, then the survivorship of prey declines with their increasing conspicuousness, reaching an asymptote at (1−p₁): the only way an extremely conspicuous prey item can survive undetected by a predator is if it has settled in a patch that is not first explored.

Enhancing Prey Survival by Giving a False Idea of Conspicuousness

We can now formally quantify the survival benefits of a flash display. So far, we have assumed that a predator can infer the conspicuousness of a prey item at rest (λ_rest) from observing it in motion (λ_move). Naturally a predator’s estimation of the conspicuousness of a prey item will not be perfect, but probably sufficient for the predator to know whether it will be subsequently searching for something that is easy to find, or hard to find. Here we consider the implications of a fleeing prey giving a predator the false impression that it will be easy to find once it settles (i.e., conspicuous) when in fact it is hard to find (i.e., cryptic).

Let us assume that with non-flashing prey λ_move = λ_rest. In contrast, we assume that due to their colorful display flashing prey give a false impression of a higher conspicuousness at rest, such that λ_move > λ_rest. The probability of a prey item surviving undetected by a predator that is searching for it will therefore be dependent on its ease of detection when at rest (a function of λ_rest) and the maximum time the predator is prepared to search for it in the patch (a function of λ_move). Re-writing Eq. 13 and substituting for $t_s^{*}$ from Eq. 12 we have:

$u\left(t_s^{*}\right)=p_1{e}^{-{\mathrm{\lambda }}_{rest}\left(\frac{Log\left[\frac{p_1\left({\mathrm{\lambda }}_{move}-g\right)}{g\left(1-p_1\right)}\right]}{{\mathrm{\lambda }}_{move}}\right)}+\left(1-p_1\right)(15)$

Which simplifies to:

$u\left(t_s^{*}\right)=\left(1-p_1\right)+p_1{\left\{\frac{g\left(1-p_1\right)}{p_1\left({\mathrm{\lambda }}_{move}-g\right)}\right\}}^{\frac{{\mathrm{\lambda }}_{rest}}{{\mathrm{\lambda }}_{move}}}(16)$

When λ_move = λ_rest then Eq. 16 reduces to Eq. 14. Moreover, if λ_movep₁ > g (so that the prey item is sufficiently conspicuous, and sufficiently likely to be in a given patch, to be pursued) then 0 < $\frac{g\left(1-p_1\right)}{p_1\left({\mathrm{\lambda }}_{move}-g\right)}$ < 1. So, for a fixed λ_move the lower λ_rest the higher the overall survival. In other words, making a prey more cryptic when it settles will always enhance the prey item’s survivorship. However, since λ_move is also part of the denominator of Eq. 16, the reverse is not always true: a conspicuous flash does not unconditionally generate a higher survival rate in prey with a given fixed crypsis when settled, although this is often the case (Figure 4). As before, the counter intuitive results arise when g is slightly less than λ_movep₁ in which case predators will search for less time for a prey item they believe is cryptic than one they believe is slightly more conspicuous (see Supplementary Figure 2). Since r(t) declines more rapidly with increasing conspicuousness, then the slope will effectively overpower the intercept so that any solutions involving long $t_s^{*}$ (i.e., low g) will inevitably involve conspicuous prey items being searched for less time without success than cryptic prey items, and a corresponding increase in the survivorship of flashing prey. Indeed, as λ_move→∞ then $u\left(t_s^{*}\right)\to 1$, so a prey item that is extremely conspicuous when in flight for a given λ_rest will always enhance the survival of the item.

FIGURE 4

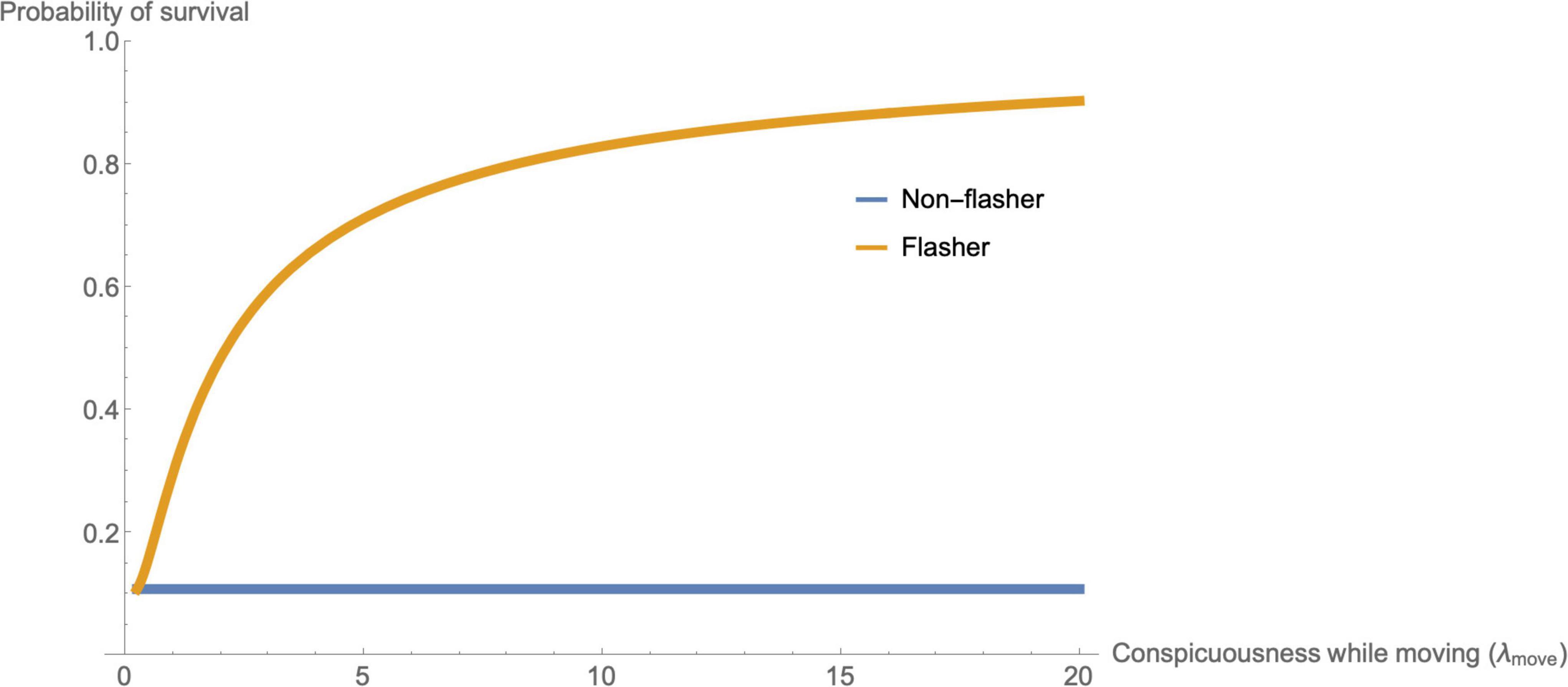
Figure 4. The survival rate of a non-flashing cryptic species (blue) that has the same appearance when moving as it does at rest (λ_move = λ_rest) compared with the survival rate of a flashing species that gives the false impression of being more conspicuous when it seen moving than it is once settled (λ_move > λ_rest). Here the apparent conspicuousness of the fleeing prey (λ_move) influences the time the predator spends searching for prey. In general, the higher the conspicuousness of the flashing prey while fleeing (x-axis) the greater its survivorship advantage over non-flashing prey because the lower the maximum amount of time predators are prepared to look for it. Here λ_rest = 0.25, p₁ = 0.9, g = 0.02, and λ_move is varied from 0.25 to 20. See Supplementary Figure 2 for a comparable plot when prey items are of borderline profitability to pursue, i.e., g = 0.2, so that λ_movep₁ ≈ g for low λ_move.

Some Predictions of the Model

To help draw the modeling threads together, here we take the opportunity to identify some basic predictions of our model. We consider the available evidence for and against these predictions in our Discussion.

Prediction 1: The More Confident a Predator Is That a Prey Is Present, the Longer the Search Time Before Giving up

The positive derivative of optimal prey search time (Eq. 12) with respect to p₁ suggests that the more initially convinced a predator is that the prey item is hiding in a patch, the longer it will spend searching there before giving up.

Prediction 2: The More Conspicuous the Flash Display, the Greater Its Effect in Reducing Predation

Figure 4 and Supplementary Figure 2 and the associated analysis (Eq. 16) indicate that, in general, the higher the conspicuousness of a flashing prey while moving, the shorter the subsequent optimal search time for the prey and the greater the flasher’s chances of surviving the search. This arises simply because if a prey item is believed to be conspicuous then it should be found quickly; so, if the prey fleeing item is not found quickly, it is unlikely to be present. Intriguingly, the relationship between optimal search time and perceived prey conspicuousness is not always monotonically increasing. However, a peak in search time only occurs when fleeing prey appear so hard to find and/or their location of settlement is so uncertain that they are of marginal profitability to pursue.

Prediction 3: Flash Behavior Will Especially Benefit Prey With an Intermediate Level of Crypsis

One might expect that prey items that are highly cryptic at rest would not benefit significantly from flash displays because the behavior would add little to their already high survivorship. Conversely, prey that are highly conspicuous at rest may be so easy to find that a flash display would also do little to protect them. The mathematical model supports this intuition. Figure 5 for example shows the relative survival benefits of a flash display (a species where λ_move > λ_rest) compared to a prey that lacks the flash (a species where λ_move = λ_rest) using Eq. 16 to determine the survivorship of the flasher and the survivorship of the non-flasher as we vary λ_rest. The ratio of survival of a flasher to a non-flasher is generally above 1, indicating a fitness benefit of a flash display. The higher the conspicuousness of the flash display used while in motion, the higher the relative benefit of the flash display (see also section “Prediction 2: The More Conspicuous the Flash Display, the Greater Its Effect in Reducing Predation”). However, prey that are extremely cryptic or extremely conspicuous at rest have little to gain from flash displays – indeed a flash display may harm a highly cryptic prey (survival ratio < 1) if the flash causes a predator to pursue the prey item it would not otherwise seek. For highly conspicuous prey the survival ratio approaches 1 as prey conspicuousness increases, indicating no benefit. The result is a nuanced relationship, in which the greatest relative benefit of a given flash display is for prey of intermediate conspicuousness (Figure 5).

FIGURE 5

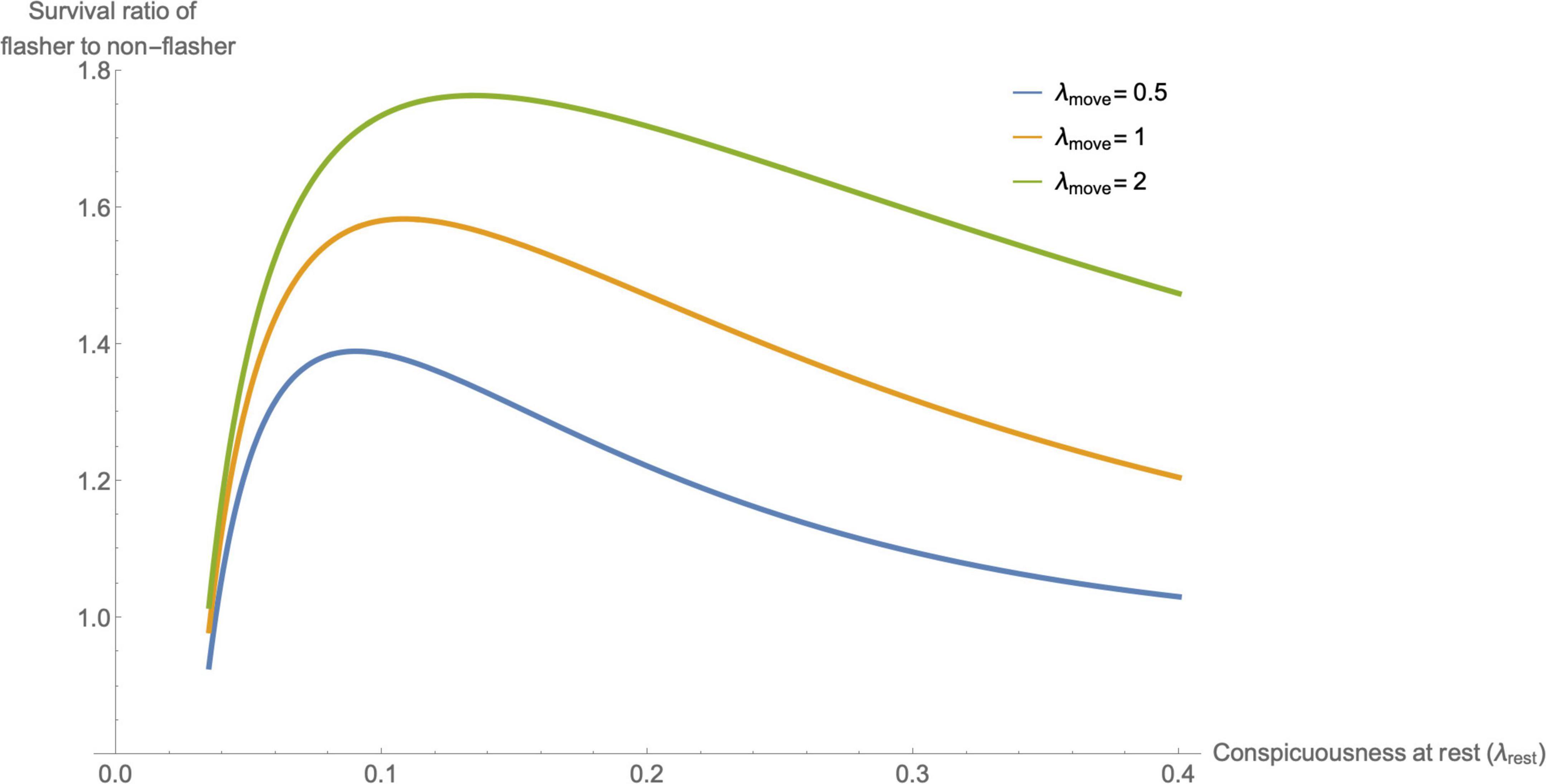
Figure 5. The ratio of survival for flashers compared to non-flashers as the level of prey conspicuousness when at rest (λ_rest) is varied (from 0.035 to 0.4). Here flashers exhibit fixed levels of the conspicuousness while moving, with λ_move = 0.5, 1 or 2 and we assume g = 0.02 and p₁ = 0.6. Prey that are highly cryptic at rest have little to gain from flashing (indeed they may be harmed by having a display). Prey that are highly conspicuous at rest will be readily seen whatever the nature of their flash display, so also have little to gain from flashing. For any flash display there is an intermediate level of resting crypsis (λ_rest) that maximizes the relative survival benefits of flashing.

Prediction 4: Species With Flash Displays Will Benefit More If the Predator Is Unaware of the Prey’s Resting Appearance

We have shown that when λ_move > λ_rest then the predator will frequently give up its search sooner because it expects to find a conspicuous prey item. However, if the predator learns that a prey type will be cryptic in appearance when settled, it should no longer apply an inappropriate search strategy and the benefits of the flash display will be removed entirely.

Discussion

If a predator is sufficiently confident of a prey item’s location, then it will search the patch where it believes the prey has landed so long as its immediate expected gain exceeds that of ignoring it and moving on to flush out another prey item. Assuming the predator decides to search the patch for the prey item that has fled, there will come a time when the predator gives up a fruitless search since it is increasingly likely that the prey is not present. We first show how Bayes’ rule can be used to update the predator’s belief that the fleeing prey item has settled in a patch that is being searched, given that it has not been found there yet. We then show that the optimal time spent looking in any given patch before moving on will in general be shorter for conspicuous items than cryptic prey items (which, by definition, tend to take time to find). Next, we show how the MVT of Charnov (1976) can be used to identify the time at which a predator should abandon a search that has so far been unsuccessful. Finally, we take the prey’s perspective and show how a cryptic prey item that gives the impression of being conspicuous while fleeing can exploit the predator’s optimal search strategy by causing the predator to move on sooner than it would otherwise do so. Since this simple form of deception will tend to enhance the survivorship of the prey, it readily explains how flash behavior evolves and is maintained.

Our model is relatively intuitive and can be readily parameterized. For example, λ can be estimated by fitting an exponential model to the distribution of discovery times for prey, whether the predator finds them or not (right censused). Likewise, g can be thought of as the reciprocal of the mean time taken between successful captures of prey (assuming the prey are of similar quality).

Evaluation of Model Predictions

While the primary purpose of our model was to show in a transparent way how flash displays can interfere with the search process and enhance prey survivorship, the model makes several testable predictions (see section “Some Predictions of the Model”) which evaluate below.

Prediction 1: The More Confident a Predator Is That a Prey Is Present, the Longer the Search Time Before Giving up

There is some evidence to support the intuitive prediction, although it is understandably indirect. In their experimental “proof of concept” paper, Loeffler-Henry et al. (2018) first trained human volunteers to follow moving prey of a given conspicuousness and search for them where they settled. They then introduced flashers and non-flashers and recorded whether each prey type was found, as well as the time taken to its discovery or abandonment of search. For the first 6 prey presented in the training phase, the authors introduced a 25% probability that the prey would not be present in the search phase. They incorporated these “duds” as a way of familiarizing volunteers with the possibility that there can sometimes be no prey present, so that they give up sooner. Indeed, if the human volunteers felt for certain there would always be a prey present, then with unlimited time to complete the experiment they might be motivated to persist a lot longer.

Clearly then, the number of duds experienced in the training phase will likely influence the perceived prior probability p₁ of the prey being present in the test phase, but precisely how? One way to quantify the relationship between the number of duds (d) experienced and p₁ is to assume that the volunteers begin with a Beta prior for the probability of the prey item being present in the search area. The Beta distribution provides a convenient prior not only because it is bounded by 0 and 1, but also because it is the conjugate for the binomial; that is, following new information the posteriors will also follow a Beta distribution, albeit with different parameters (DeGroot, 1970). The expectation of a Beta (α, β) is α/(α + β) with Beta (1, 1) representing a uniform distribution. Due to the conjugacy, if a volunteer starts with a Beta (α, β) prior and finds that no prey is present on d occasions from n trials, then the posterior probability distribution of the prey item being present in the search screen will follow Beta (α + n − d, β + d) with expectation (α + n − d)/(α + β + n). So, with n = 6 conspicuous training prey, and assuming that volunteers start with uniform priors, the maximum estimate of p₁ following training would be (7/8) when d = 0, and the minimum estimate of p₁ would be (1/8) when d = 6. Loeffler-Henry et al. (2018) reported that the number of duds significantly reduced the time taken before a search for prey was abandoned (Eq. 12), and consequently the probability that a prey was detected (Eq. 16), which are entirely consistent with the predictions of our model.

Prediction 2: The More Conspicuous the Flash Display, the Greater Its Effect in Reducing Predation

The model predicts that prey with conspicuous flash displays will tend to survive at a higher rate than prey with less conspicuous flash displays, since in the former case predators will give up their search sooner. Bae et al. (2019) presented a follow-up experiment to Loeffler-Henry et al. (2018) in which they manipulated the conspicuousness of the flash display to human volunteers. Intriguingly, they found that a flash display that was conspicuous (CONS) in motion had a greater effect in reducing predation than a flash display that simply involved a distinct cryptic color (CRY). Moreover, the mean giving-up time of the volunteer predators was significantly longer for the CRY prey than the CONS prey. As our model shows, if predators are searching for something that they believe to be cryptic (no matter how distinct it is) they should be prepared to spend longer looking for it. The results of Bae et al. (2019) therefore match what one would expect if the flash behavior enhanced survival by interfering with a search strategy of predators based on conspicuousness rather than novelty or distinctiveness.

Prediction 3: Flash Behavior Will Especially Benefit Prey With an Intermediate Level of Crypsis

In addition to varying conspicuousness, Bae et al. (2019) conducted a related experiment and found that flash coloration was more effective in reducing predation in large prey compared to small prey. They explained this finding on the basis that small prey items are intrinsically hard to find, so that flash displays would add little to already high survivorship. Naturally, however, as section “Prediction 3: Flash Behavior Will Especially Benefit Prey With an Intermediate Level of Crypsis” argues, there must be a sweet spot – prey that are highly conspicuous at rest (such as very large prey) may be so easy to detect that a flash display would do little to protect them. As such, Bae et al. (2019) provide some support for the model, although the possibility of an upper limit of resting conspicuousness beyond which there is no benefit has yet to be empirically established.

Prediction 4: Species With Flash Displays Will Benefit More If the Predator Is Unaware of the Prey’s Resting Appearance

Our model assumes that the benefits of the flash display are contingent on deception. So, if the true nature of the prey is revealed, then the predicted survival benefit should be diminished. This prediction was supported by a recent study by Loeffler-Henry et al. (2021) who showed that flash displays conferred a survivorship advantage but only in computer-generated prey that moved before the volunteer predator was able to observe their resting appearance.

Flash Display Mimicry?

The potential to recognize the nature of the trick being played (see section “Prediction 4: Species With Flash Displays Will Benefit More If the Predator Is Unaware of the Prey’s Resting Appearance”) is an obvious Achilles’ heel of the flashing strategy, just as startle (deimatic) displays can eventually be habituated to, see Ingalls (1993). If the flashing species is commonly encountered, then all else being equal, it is likely predators would learn to associate the conspicuous flash display with a prey item that is cryptic at rest. There is one important way, however, in which the effectiveness of the flash display may be maintained despite the ability of predators to catch on to the trick being played. Specifically, if the flash display were to resemble another organism or object familiar to the predator, which is conspicuous both when fleeing and when settled, then one might expect it would reduce the rate at which predators make the association. Indeed, the uncertainty generated by this form of mimicry could allow the flash behavior to persist indefinitely, just as Batesian mimics can co-exist with models (Ruxton et al., 2018). One prey species that is cryptic at rest but displays conspicuous color patterns in flight is the Carolina locust Dissosteira carolina (Linnaeus), seen in Figure 1 (middle row). Intriguingly, this species has long been speculated to resemble the sympatric mourning cloak butterfly Nymphalis antiopa (Linnaeus) both in appearance and flight behavior (Acorn, 2018); see Supplementary Figure 3 (top). Similarly, the otherwise cryptic speckle-winged rangeland grasshopper Arphia conspersa (Scudd.), seen in Figure 1 (bottom row), flashes conspicuous yellow wings in flight that resemble the alfalfa butterfly Colias eurytheme (Boisd.) (Balgooyen, 1997); see Supplementary Figure 3 (bottom). So, the conspicuous displays made by certain species when fleeing may not be arbitrary but instead selected to resemble other species or objects familiar to the predator that retain their conspicuous state throughout. We have not introduced the possibility of mimicry into the current model, although its effects could be thought of as the converse of “duds” (section “Prediction 1: The More Confident a Predator Is That a Prey Is Present, the Longer the Search Time Before Giving up”). If the conspicuous model was unprofitable to attack due to their unpalatability or evasiveness (which would account for their consistent conspicuousness), then the predator will be faced with an extra level of uncertainty that will influence whether the fleeing prey is pursued. If the prey item is pursued (because the models are profitable to capture and consume, or because the predator is sufficiently convinced it is a mimic) then the time a predator spends searching on a patch will not only affect the posterior probability that there is a prey present, but also whether it is one type of prey or another (since flashing species will be cryptic at rest, but the model will retain its conspicuousness).

Conclusion

The theory of optimal search is inherently Bayesian since it uses information gathered during the search (notably the lack of success) to revise beliefs as to where the hidden object might be (Stone, 1975; Koopman, 1980; Assaf and Zamir, 1985). At its core, it requires a consideration of all things that might have happened to a missing object, in terms of a prior probability distribution of it being in certain locations. It also requires an understanding of the probability of discovering the object within an area as a function of search time or effort applied there (since the ease and cost of detecting a lost object can potentially vary among locations). The theory has been applied in multiple real-life situations such as the search for missing aircraft and naval vessels (Richardson and Stone, 1971) and is even integrated into the United States coast-guard computer assisted search and rescue (Richardson and Discenza, 1980). Here we apply it in a somewhat unusual way to understand why some organisms are selected to give the illusion of being conspicuous, when they are cryptic at rest.

Data Availability Statement

Additional results and model explorations are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

TS and KL-H contributed to planning of approach and second drafting of the manuscript. TS contributed to development of and exploration of model and first drafting of the manuscript. Both authors contributed to the article and approved the submitted version.

Funding

TS and KL-H were funded by an NSERC Discovery Grant to TS.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer OP declared a past co-authorship with one of the authors TS to the handling editor.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Ian Dewan and our reviewers for insightful comments.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.903769/full#supplementary-material

References

Acorn, J. (2018). Cool Insects: The Mourning Cloak Butterfly [Online]. Available online at: https://esc-sec.ca/2018/05/29/cool-insectsthe-mourning-cloak-butterfly/. (Accessed date March 22 2022).

Google Scholar

Anonymous (1945). Animal concealment and flash coloration. Nature 155, 232–233.

Google Scholar

Assaf, D., and Zamir, S. (1985). Optimal sequential search: a Bayesian approach. Ann. Stat. 121:1219.

Google Scholar

Bae, S., Kim, D., Sherratt, T. N., Caro, T., and Kang, C. (2019). How size and conspicuousness affect the efficacy of flash coloration. Behav. Ecol. 30, 697–702. doi: 10.1093/beheco/arz006

CrossRef Full Text | Google Scholar

Balgooyen, T. G. (1997). Evasive mimicry involving a butterfly model and grasshopper mimic. Am. Midl. Natural. 137, 183–187. doi: 10.2307/2426768

CrossRef Full Text | Google Scholar

Charnov, E. L. (1976). Optimal foraging: the marginal value theorem. Theoret. Populat. Biol. 9, 129–136.

Google Scholar

Cott, H. B. (1940). Adaptive Coloration in Animals. London: Methuen & Co.

Google Scholar

Courville, A. C., Daw, N. D., and Touretzky, D. S. (2006). Bayesian theories of conditioning in a changing world. Trends Cogn. Sci. 10, 294–300. doi: 10.1016/j.tics.2006.05.004

PubMed Abstract | CrossRef Full Text | Google Scholar

DeGroot, M. H. (1970). Optimal Statistical Decisions. New Jersey, NJ: John Wiley & Sons.

Google Scholar

Edmunds, M. (1974). Defence in Animals: a Survey of Anti-predator Defences. Essex: Longman.

Google Scholar

Edmunds, M. (2008). “Flash colors,” in Encyclopedia of Entomology, ed. J. L. Capinera (Dordrecht (NL): Springer).

Google Scholar

Green, R. F. (1980). Bayesian birds: a simple example of Oaten’s stochastic model of optimal foraging. Theoret. Popul. Biol. 18, 244–256. doi: 10.1016/0040-5809(80)90051-9

CrossRef Full Text | Google Scholar

Ingalls, V. (1993). Startle and habituation responses of blue jays (Cyanocitta cristata) in a laboratory simulation of antipredator defenses of Catocala moths (Lepidoptera, Noctuidae). Behaviour 126, 77–96. doi: 10.1163/156853993x00353

CrossRef Full Text | Google Scholar

Killeen, P. R., Palombo, G.-M., Gottlob, L. R., and Beam, J. (1996). Bayesian analysis of foraging by pigeons (Columba livia). J. Exp. Psychol. Anim. Behav. Proc. 22, 480–496. doi: 10.1037//0097-7403.22.4.480

PubMed Abstract | CrossRef Full Text | Google Scholar

Koopman, B. O. (1957). The theory of search: III. The optimum distribution of searching effort. Operat. Res. 5, 613–626.

Google Scholar

Koopman, B. O. (1980). Search and Screening. New York, NY: Pergamon Press.

Google Scholar

Loeffler-Henry, K., Kang, C., and Sherratt, T. N. (2019). Consistent associations between body size and hidden contrasting color signals across a range of insect taxa. Am. Natural. 194, 28–37. doi: 10.1086/703535

PubMed Abstract | CrossRef Full Text | Google Scholar

Loeffler-Henry, K., Kang, C., and Sherratt, T. N. (2021). The anti-predation benefit of flash displays is related to the distance at which the prey initiates its escape. Proc. R. Soc. B 288:0210866. doi: 10.1098/rspb.2021.0866

PubMed Abstract | CrossRef Full Text | Google Scholar

Loeffler-Henry, K., Kang, C., Yip, Y., Caro, T., and Sherratt, T. N. (2018). Flash behavior increases prey survival. Behav. Ecol. 29, 528–533.

Google Scholar

McElreath, R. (2020). Statistical Rethinking. A Bayesian Course with Examples in R and Stan. Boca Raton: CRC Press.

Google Scholar

McGrayne, S. B. (2012). The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy. Yale: Yale University Press.

Google Scholar

McNair, J. N. (1982). Optimal giving-up times and the marginal value theorem. Am. Natural. 119, 511–529. doi: 10.1086/283929

CrossRef Full Text | Google Scholar

McNamara, J., and Houston, A. (1985). A simple model of information use in the exploitation of patchily distributed food. Anim. Behav. 33, 553–560. doi: 10.1016/s0003-3472(85)80078-6

CrossRef Full Text | Google Scholar

McNamara, J. M. (1982). Optimal patch use in a stochastic environment. Theoret. Populat. Biol. 21, 269–288. doi: 10.1016/0040-5809(82)90018-1

CrossRef Full Text | Google Scholar

McNamara, J. M., Green, R. F., and Olsson, O. (2006). Bayes’ theorem and its applications in animal behaviour. Oikos 112, 243–251. doi: 10.1111/j.0030-1299.2006.14228.x

CrossRef Full Text | Google Scholar

Murali, G. (2018). Now you see me, now you don’t: dynamic flash coloration as an antipredator strategy in motion. Anim. Behav. 142, 207–220. doi: 10.1016/j.anbehav.2018.06.017

CrossRef Full Text | Google Scholar

Oaten, A. (1977). Optimal foraging in patches: a case tbr stochasticity. Theoret. Populat. Biol. 12, 263–285. doi: 10.1016/0040-5809(77)90046-6

CrossRef Full Text | Google Scholar

Richardson, H. R., and Discenza, J. H. (1980). The United States Coast Guard computer-assisted search planning system (CASP). Nav. Res. Logist. Q. 27, 659–680. doi: 10.1002/nav.3800270413

CrossRef Full Text | Google Scholar

Richardson, H. R., and Stone, L. D. (1971). Operations analysis during the underwater search for Scorpion. Naval Res. Logist. Q. 18, 141–157.

Google Scholar

Ruxton, G. D., Allen, W. L., Sherratt, T. N., and Speed, M. P. (2018). Avoiding Attack: The Evolutionary Ecology of Crypsis, Aposematism and Mimicry. Oxford: Oxford University Press.

Google Scholar

Stone, L. D. (1975). Theory of Optimal Search. New York, NY: Academic Press.

Google Scholar

Umbers, K. D. L., Lehtonen, J., and Mappes, J. (2015). Deimatic displays. Curr. Biol. 25, R58–R59. doi: 10.1016/j.cub.2014.11.011

PubMed Abstract | CrossRef Full Text | Google Scholar