Comparing Methods of Defining Priority Areas for Greater Sage-Grouse

Parsons, Lindsey; Jenks, Jonathan; Runia, Travis; Gregory, Andrew

doi:10.3389/fevo.2022.896023

ORIGINAL RESEARCH article

Front. Ecol. Evol., 07 July 2022

Sec. Conservation and Restoration Ecology

Volume 10 - 2022 | https://doi.org/10.3389/fevo.2022.896023

This article is part of the Research Topic Connectivity and Conservation: Bridging Gaps between Research, Policy, and Practice View all 4 articles

Comparing Methods of Defining Priority Areas for Greater Sage-Grouse

$\r\nLindsey Parsons,*$ Lindsey Parsons^1,2*

Jonathan Jenks²

Travis Runia³

Andrew Gregory⁴

¹Montana Fish, Wildlife and Parks, Helena, MT, United States
²Department of Natural Resource Management, South Dakota State University, Brookings, SD, United States
³South Dakota Game, Fish and Parks, Huron, SD, United States
⁴Department of Biological Sciences, University of North Texas, Denton, TX, United States

Wildlife managers delineate priority areas for species to define critical habitat and to prioritize management efforts. Each method used to identify priority areas involves data that can be unavailable or expensive to obtain. Therefore, it is of interest to compare spatial efficiency between methods used for defining priority areas. We compared priority areas created using different methods and data types. We used resource selection function (RSF) models to predict areas of high use and generated a map depicting ≥ 90% predicted use in three seasons; it was 1,143 km², encompassed 91% of nests, 68% of summer locations, and 71% of winter locations. We compared the RSF priority area to priority areas developed using two alternative methods: (1) modified conservation buffer, and (2) utilization distribution (UD) models. The modified conservation buffer method was used by South Dakota Game, Fish and Parks in 2014 to delineate a priority area by buffering active lek sites by 6.4 km, including connectivity corridors defined via expert opinion, and known high use areas. The priority area generated by the modified conservation buffer method was 3,977 km², encompassed 95% of nest locations, 92% of spring/summer locations, and 99% of winter locations. Lastly, we developed a priority area using combined UDs from radio-tracking data gathered during spring/summer, and winter and included a lek buffer encompassing 90% of known nest-sites. This priority area was 3,498 km², encompassed 99% of nests, 98% of spring/summer locations, and 97% of winter locations. The priority area generated by RSF models was the smallest and encompassed the least number of nests and spring/summer and winter locations but was considered the most spatially efficient; it had the most nests, spring/summer locations, and winter locations per 100 km². The UD and modified conservation buffer methods created priority areas that were similar in size and spatial efficiency. The modified conservation buffer method encompassed >90% of known sage-grouse locations and nests, indicating that in the absence of detailed movement data and more sophisticated modeling, the method can be sufficient in developing an adequate priority area.

Introduction

Limited resources and an increasing need for conservation have created a push toward defining and prioritizing areas of high conservation value (Groves et al., 2002). For wildlife managers to make decisions about prioritizing conservation areas, they first must consider what important questions need answered, the data available to provide answers, the analysis methods necessary to evaluate the questions, and the conservation implications given the range of potential results. Not only do wildlife managers need to consider what they are trying to accomplish and how, they also need to consider time, budget, and expertise requirements and constraints. Each of these factors will ultimately lead the manager to select an approach, but often there are concerns about the tradeoffs of using one approach instead of another.

Multiple methods have been used to define priority areas, which vary depending on scale (Poiani et al., 2000). When taking a species-centric approach to conservation, areas where a species can persist long-term are typically identified and prioritized (Margules and Pressey, 2000). The Greater Sage-Grouse (Centrocercus urophasianus; hereafter sage-grouse) is a sagebrush (Artemisia spp.) obligate species (Wallestad and Eng, 1975), which has experienced population declines over the past several decades (Connelly et al., 2004; Western Association of Fish and Wildlife Agencies [WAFWA], 2015; Coates et al., 2021). Sage-grouse have warranted great efforts to define priority habitats, and these areas have been identified in all states where sage-grouse occur (United States Fish and Wildlife Service [USFWS], 2013). On a continent–wide scale, the Sage-Grouse Conservation Area was defined using the historical distribution of sage-grouse including a 50 km buffer; this area was used in a range-wide conservation assessment (Connelly et al., 2004; Schroeder et al., 2004). At smaller scales, when information is limited, using breeding season location data to generate priority areas has sufficed to encompass a high percentage of summer and winter locations as well as breeding season use (Fedy et al., 2012). Fedy et al. (2012) recommended seasonal habitat selection models within the sage-grouse distribution. There are multiple methods for identifying seasonal habitat selection. Occurrence models along with risk models have been used to identify highly selected sage-grouse habitats as well as source/sink habitats (Aldridge and Boyce, 2007; Dzialak et al., 2011). Landcover type within an Ecological Niche Factor Analysis has been used to identify and map suitable sage-grouse brood rearing habitat (Atamian et al., 2010), and lastly, modeling resource selection using resource selection functions (RSFs; Manly et al., 2002) has become a common method for identifying priority areas for sage-grouse (Doherty et al., 2008; Carpenter et al., 2010; Fedy et al., 2014).

Determining priority areas using RSFs has recently become popular (Johnson et al., 2004; Rachlow and Svancara, 2006; Fedy et al., 2014), and RSFs can be an advantageous approach to defining priority areas because they allow for predictions outside of areas directly evaluated, allow researchers and managers to estimate uncertainty in model predictions, and capture variability in the probability of use (Boyce et al., 2002; Manly et al., 2002). To generate an RSF, data requirements include locations of the species or individuals of interest, data associated with the used locations, as well as data from locations that were available to the species or individuals of interest (Manly et al., 2002).

Several assumptions must be met for RSF models and relative predicted probability of use maps to be used to delineate priority areas (Manly et al., 2002). First, uniquely identified individuals are random, and a representative sample of the population. Second, relocations of individuals are independent in time. Third, individuals and their selection of resources are independent of each other. Fourth, habitat availability is constant over the study area and is known. Fifth, accuracy of location data is within the range of model co-variates. Sixth, important variables to selection are selected and distribution of variables remains constant. Lastly, remotely sensed data accurately represent variables on the landscape.

Another common method for defining priority areas involves placing conservation buffers around known areas of importance (Burke and Gibbons, 1995; Jorgensen et al., 2000; Qiu, 2010; Manier et al., 2014). This method requires locations of important sites for the species of interest (leks, watering holes, nests, etc.), and a buffer around them. Several assumptions must be met for conservation buffers to create adequate priority areas. The first assumption is that a high proportion of the important sites have been mapped. Secondly, the distance needed to adequately buffer important sites is known and is stable, and third, encompassing important sites and the areas around them is sufficient for species conservation. The analysis required to generate conservation buffers is relatively simple in systems where spatial information about important sites already exists.

Using conservation buffers around leks is a common component for defining sage-grouse priority areas and has been used in several western states (South Dakota Department of Game, Fish and Parks, Division of Wildlife [SD GFP], 2014; Montana Fish, Wildlife and Parks [MT FWP], 2014; Robinson, 2014; State of Wyoming, 2015). However, adequate lek buffer distances are highly variable. In western Wyoming, Idaho, and South Dakota, >90% of nests were within 8.5, 3, and 6.4 km, respectively, of an active lek (Wakkinen et al., 1992a; Holloran and Anderson, 2005; Kaczor, 2008; South Dakota Department of Game, Fish and Parks, Division of Wildlife [SD GFP], 2014). Aldridge and Boyce (2007) suggested that >90% of source habitats occur within ∼10 km of lek sites and therefore, buffers that are <10 km may not be sufficient for encompassing brood rearing and nesting habitats.

To estimate the buffer distance that encompasses a majority of sage-grouse nests, a representative sample of nest locations must be documented (typically accomplished via radio-collaring and tracking females). Also, a high proportion of lek locations must be documented. Then, distances from each nest to the nearest active lek can be measured using a Geographic Information System.

Lastly, priority areas can also be estimated directly from location data via utilization distributions (UDs; Sawyer et al., 2009). Utilization distributions are commonly used for estimating home ranges, and were first defined by Van Winkle (1975) as the probability of re-locating an animal in a given place at any time. Utilization distributions can be developed by creating a bivariate normal fixed kernel estimate of a probability density around known animal locations (Worton, 1989). Kernel density functions have been used in defining priority areas for sage-grouse in Wyoming and Montana (Doherty et al., 2010a; Dzialak et al., 2011; State of Wyoming, 2015; Montana Fish, Wildlife and Parks [MT FWP], 2014). Kernel density estimates have been generated using different data types, such as lek sites, number of males at lek sites, or radio-collared individuals; each variation of this method has different data requirements and costs associated with data collection.

Two assumptions must be met if UDs are used to generate priority areas. The first is radio-collared individuals are a representative sample of the population’s space use. This is particularly important for sage-grouse that are highly associated with lek locations; to have space use around a lek represented, it must have individuals captured and radio-collared from it or have individuals that are already radio-collared move to it. Second, individuals should be located at relatively equal time intervals and in relatively equal frequencies to one another. Equal time intervals for tracking allow for an unbiased estimate of movement within a season. UDs are created on an individual basis; however, if certain individuals are not tracked as frequently as others due to; access, land cover, land use, or another factor, bias could be introduced when individual UDs are summed.

State and federal wildlife and land management agencies routinely collect data on lek locations and number of males observed at leks (Coates et al., 2021). Therefore, the lek location and lek-count data that are already being collected may cost less than radio-collaring individuals to obtain location data.

Ultimately, multiple factors affect the method that a wildlife manager uses to define a priority area. Although additional data may allow for creation of more accurate priority areas, it may be expensive or unfeasible to obtain. Also, time and skill level required for appropriate analysis may be a limiting factor. Therefore, we compared priority areas created using all possible data (data rich) as well as limited data (data poor) methods and compared the spatial efficiency of each. Here, we use the term spatial efficiency to mean encompassing a high percentage of known use in a small amount of space. This metric is especially relevant in cases where protecting or managing large areas of land is financially, logistically, or politically infeasible. We compared a landscape modeling approach, to two alternative methods of defining priority areas for sage-grouse conservation in South Dakota. Comparison metrics between methods included: total area, percent of known nests encompassed, percent of known spring/summer locations encompassed, percent of winter locations encompassed, nests/100 km², spring/summer locations/100 km² and winter locations/100 km².

Materials and Methods

Study Area

Our study was focused in Harding and Butte counties in northwest South Dakota (Figure 1). The total area of both counties is 12,805 km². Land use in the study area is dominated by pastureland (> 85%), followed by cropland (10–12%; United States Department of Agriculture [USDA], 2012). Over 84% of Butte and Harding counties has never been plowed (Bauman et al., 2018) and much of this land supports sagebrush. A majority of the land in the study area is privately owned (∼75–80%; United States Geological Survey [USGS], Gap Analysis Program [GAP], 2016). Annual average temperatures range from –1.7 to 0.6°C with an average of 39 cm of precipitation annually (National Oceanic and Atmospheric Administration [NOAA], and National Weather Service [NWS], 2019).

FIGURE 1

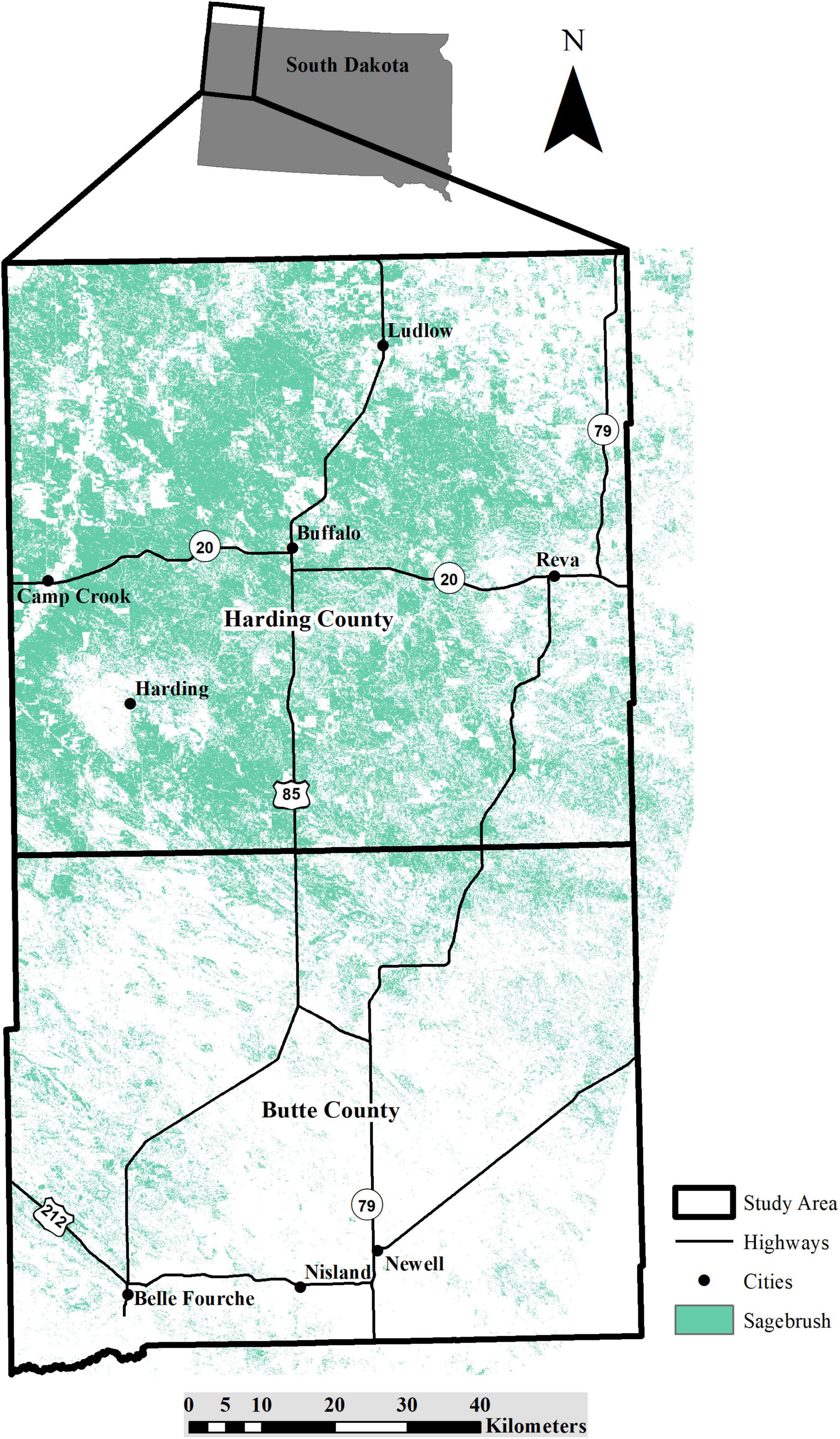
Figure 1. Study area in Butte and Harding counties, South Dakota with major highways and sagebrush landcover.

Our study area represents the eastern edge of the sagebrush distribution where an ecotone between the sagebrush steppe and grassland ecosystems occurs (Johnson, 1979; Kantrud and Kologiski, 1983; Cook and Irwin, 1992; Lewis, 2004; Smith et al., 2004; Johnson and Larson, 2007). Sagebrush found in South Dakota are shorter and have a lower percent canopy cover than those found elsewhere in the sagebrush steppe (Kantrud and Kologiski, 1983; Connelly et al., 2000; Kaczor et al., 2011). Common sagebrush species in the study area include silver sagebrush (Artemisia cana) and big sagebrush (Artemisia tridentata; Johnson and Larson, 2007).

Field Methods

We captured breeding-age female sage-grouse near active leks March-May, as well as at high sage-grouse use areas in August and September 2016–2017 using nocturnal spotlighting techniques (Giesen et al., 1982; Wakkinen et al., 1992b). We attempted to capture sage-grouse from all known active leks during 2016 and 2017. We opportunistically captured female sage-grouse; number of captured females was not equal among leks, nor stratified based on lek attendance. We aged and sexed captured sage-grouse based on morphological characteristics and plumage (Crunden, 1963; Beck et al., 1975; Bihrle, 1993). We fit each captured female sage-grouse with a 21.6 g necklace-type Very High Frequency (VHF) radio transmitter (model A4060, Advanced Telemetry Systems, Isanti, MN, United States) as well as a uniquely numbered aluminum butt-end leg band (National Band & Tag Company, Newport, KY, United States). We weighed all birds at the time of capture to ensure that radio-transmitters were less than 3% of body weight (Kenward, 2001). All animal handling procedures were approved by the Institutional Animal Care and Use Committee at South Dakota State University (IACUC approval # 15-074A).

Sage-grouse were located ≥ 1 time per week from 15 April to 15 September, and one time per week from 1 November to 28 February using the homing method (Samuel and Fuller, 1996; Fuller and Fuller, 2012) with a hand-held 3-element Yagi antenna or via fixed-wing aircraft equipped with a 2 element, “H” type, antenna on each wing. Additionally, we used sage-grouse location data from 2006 to 2007 collected using similar methods (Swanson, 2009; Kaczor et al., 2011), which included breeding age male and female locations as well as juvenile locations.

Modeling Landscape Use

We created RSF models for nest-site, spring/summer (1 April–15 September), and winter (1 November–28 February) selection. We sought to create RSF models that assessed 3^rd order selection; selection of points within the home range (Johnson, 1980). We implemented the use/available design, design II (nest-site selection), and design III (spring/summer and winter selection models) defined by Manly et al. (2002). In design II, resources used are assessed at an individual level, but availability of resources is quantified at a population level whereas in design III, both used and available resources are quantified at an individual level.

We developed landscape variables that were biologically relevant to sage-grouse habitat selection using the Spatial Analyst package in ArcGIS. Variables of interest included; lek locations, sagebrush, forest, water, roads, ruggedness, and undisturbed (unplowed) land (Table 1). Although leks are not specifically a habitat variable, we considered that sage-grouse may select resources based on the locations of leks, specifically during the breeding season and when selecting a nest-site. The hotspot hypothesis of lek evolution states that quality nesting habitat is located in closer proximity to leks than expected at random (Schroeder and White, 1993; Gibson, 1996; Aldridge and Boyce, 2007; Doherty et al., 2010b); also, leks seem to establish within or adjacent to nesting habitat (Connelly et al., 2000). Therefore, we used lek locations as a proxy for quality habitat.

TABLE 1

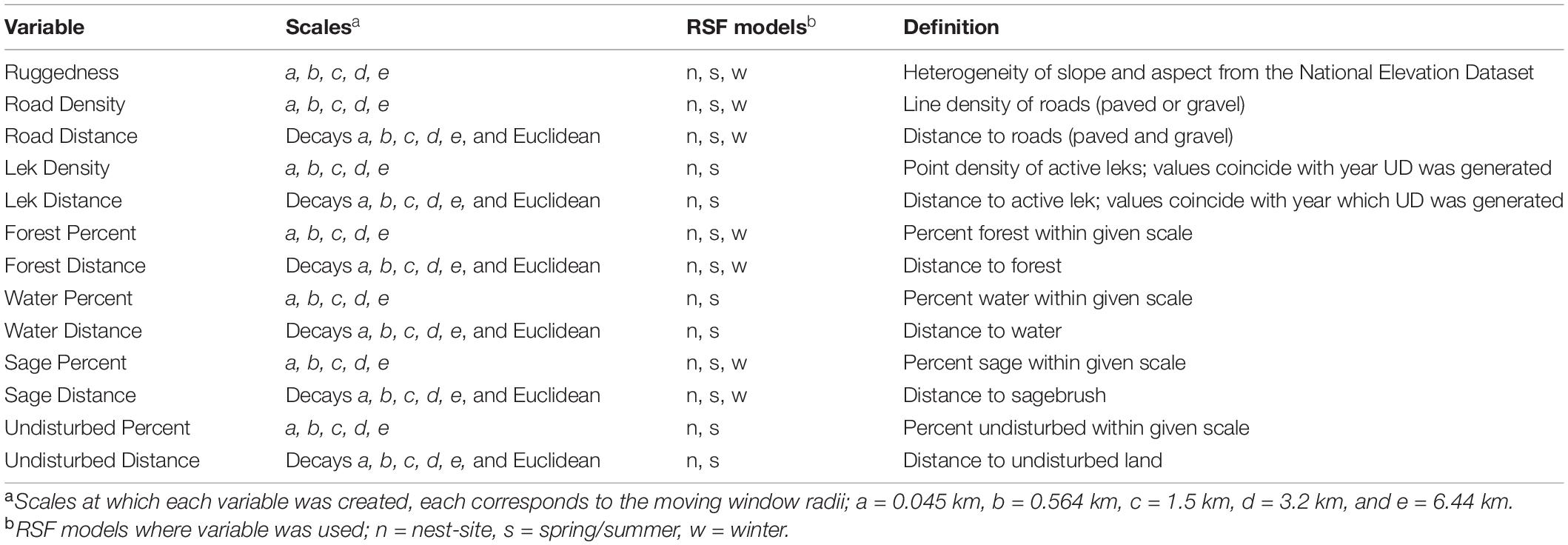
Table 1. Variables considered for use in all resource selection function (RSF) model types (nest-site, spring/summer, winter).

Lek count data were acquired from South Dakota Game, Fish and Parks. Active leks were defined for each of four years when data were collected (2006, 2007, 2016, and 2017). Leks were considered active if ≥ 1 male was observed displaying. We assigned lek data to each individual sage-grouse based on leks that were active in the year they were monitored. In final prediction maps, all leks that were considered active from 2006 to 2018 were used.

A data layer representing roads included primary to tertiary classes (South Dakota Department of Transportation [SD DOT], 2018; Montana State Library, 2019; Wyoming Department of Transportation GIS Group, 2019). Ruggedness of the landscape was quantified by using the Benthic Terrain Modeler Toolbox (Wright et al., 2005) in ArcGIS with the National Elevation Dataset (Gesch et al., 2002).

We used the Native Lands Data Layer (Bauman et al., 2018), which discriminates between land that has been plowed and land that has not. We considered unplowed land to be “undisturbed” and plowed land to be “disturbed.” This data layer alone does not distinguish between land that has been plowed and remains as non-sagebrush, and areas that were once plowed and contain regenerated sagebrush. However, a separate analysis revealed 74% of the “disturbed” land within the study area is currently grassland/pasture, other hay/non-alfalfa, or alfalfa (United States Department of Agriculture [USDA], 2019). Another consideration, is these data represent land that was plowed, and do not consider other methods of sagebrush removal that might have occurred (e.g., spraying, burning, chaining). Thus, to explore the response of sage-grouse to historically and currently plowed lands, we included the Native Lands Data Layer as a variable.

We included land cover attributes extracted from the 2011 National Land Cover Database (NLCD; Homer et al., 2015) including sagebrush (NLCD Shrubland Products; United States Geological Survey [USGS], 2017), water, and forest (NLCD; Homer et al., 2015). The NLCD Shrubland Products, percent sagebrush data layer (NLCD Shrubland Products; United States Geological Survey [USGS], 2017) has been shown to accurately represent the presence of sagebrush in South Dakota, but is inaccurate at predicting sagebrush canopy coverage in our study area (Parsons et al., 2019). Therefore, the percent sagebrush layer was re-classified in ArcGIS to reflect presence or absence of sagebrush in each 30 m pixel; presence included any canopy cover values >0. Water was identified by combining classes in the NLCD (“Open Water” + “Woody Wetlands” + “Emergent Herbaceous Wetlands”). Forest was identified by combining landcover classes from the NLCD (“Deciduous Forest” + “Evergreen Forest” + “Mixed Forest”).

Although we assumed that each variable included in this analysis was influential to sage-grouse resource selection, we were uncertain which form of the variable was most informative (i.e., distance to feature or density/percent of feature). Therefore, we created both distance metrics to each variable (with the exception of ruggedness) as well as mean values at multiple scales (Carpenter et al., 2010; Fedy et al., 2014). All layers were initially generated using a 30 m pixel size.

We followed the methods of Fedy et al. (2014) and generated variables of interest at five scales (0.006 km²;0.045 km radius, 1 km²;0.564 km radius, 7.07 km²;1.5 km radius, 32.17 km²;3.2 km radius, and 138.67 km²;6.44 km radius), which have been shown to be biologically relevant to sage-grouse (Holloran and Anderson, 2005; Aldridge and Boyce, 2007; Walker et al., 2007; Carpenter et al., 2010; Doherty et al., 2010b; Holloran et al., 2010; Fedy et al., 2012). We calculated mean values or percentages within each neighborhood using the Focal Statistics Tool in ArcGIS. Neighborhood was defined as a circular buffer with the search radius corresponding to each biologically relevant scale (Fedy et al., 2014). Values were extracted to each location after moving window analysis was complete. Because many of the winter locations were obtained from a fixed-wing aircraft, the location error was assumed to be greater than locations obtained from the ground during spring/summer and at nests. Therefore, the smallest scale was excluded in the winter models.

We calculated percentages within each radius for: forest, sagebrush, water, and undisturbed layers. We calculated mean values of ruggedness within each radius. Lek Density was calculated at each scale using the Point Density Tool in ArcGIS. Road density was calculated within each scale using the Line Density Tool in ArcGIS.

We calculated distance to features using the Euclidean Distance Tool in ArcGIS. We also created exponential decay as a function of Euclidean distance (Carpenter et al., 2010; Fedy et al., 2014). The decay function formula was as follows: e ^(–d/α ⁾ where d is the Euclidean distance to feature, and α is the value corresponding with each scale’s search radius. Decay distance functions allow a non-linear response to distance from features, and values range from 1 to 0. Areas near to features have higher values and as distance to feature increases, values reach 0. Distances at which values decrease more rapidly (thresholds) are dependent upon the scale’s search radius used in the decay equation. Euclidean distances represent linear responses of distances from features and values continue to increase until extent of the study area is reached. Distance decay values are closer to 1 when near to the feature, as distance increases, values reach 0. Euclidean distance values are low when near to the feature and increase as distance to features increase. Therefore, interpretation of distance decay coefficients is opposite Euclidean distance coefficients. Distance decay variables were generated using the Raster Calculator Tool in ArcGIS. Euclidean distance and decay function distances were calculated for the following variables: leks, water, forest, sagebrush, undisturbed, and roads (Table 1).

Prior to model development, we z-standardized all variables. We used univariate models to determine the form and scale that best represents sage-grouse resource selection. Each variable had a model set that included all forms and scales. We evaluated univariate models using Akaike’s Information Criterion corrected for small sample size bias (AIC_c; Burnham and Anderson, 2002). The selected form/scale combination with the lowest AIC_c score was used to represent that variable in the final model set (Gregory et al., 2011; Aldridge et al., 2012; Fedy et al., 2014). This approach allows for a multi-scale model that can contribute to better model performance compared to single-scale models (Graf et al., 2005). We ran all possible combinations of variables in final model sets.

We tested for correlations between all variables using a Pearson Product Moment correlation test. Variables were considered significantly correlated if r > | 0.7|. We tested for multicollinearity among variables in the final model set using variance inflation factors (VIF). We specified a null model to compare relative fit of subsequent models.

To model seasonal resource selection, we used generalized linear mixed-effect models (GLMMs) of the binomial family (Gillies et al., 2006; Koper and Manseau, 2009) within the R package, lme4 (Bates et al., 2018). Using this method, individual sage-grouse are treated as random effects (random intercepts), and our variables of interest as fixed effects. By treating each individual sage-grouse as a random intercept, individual responses to variables can vary in magnitude (Gillies et al., 2006).

For our spring/summer RSF models, we used data from breeding-age female sage-grouse. Sage-grouse form flocks during the winter (Eng and Schladweiler, 1972; Beck, 1977); although sexual segregation can occur, most large flocks consist of both sexes (Beck, 1977; Carpenter et al., 2010). During winter, female and male sage-grouse are consuming the same primary diet, which is sagebrush (Patterson, 1952; Dalke et al., 1963; Wallestad and Eng, 1975; Remington and Braun, 1985). Therefore, we used male sage-grouse locations in addition to our breeding-age female locations in our winter RSF models to increase our sample size. We also included juvenile sage-grouse locations because during fall/winter, juveniles become independent from mothers (Swanson, 2009), their diet shifts to primarily sagebrush (Klebenow and Gray, 1968; Peterson, 1970), and flocks are intermixed across age (Swanson, 2009).

We observed multiple sage-grouse migrating into Montana during the winter. Thus, we extended our area of assessment into Montana for winter models. We excluded the undisturbed layer for winter, because it was unavailable outside of South Dakota. We also excluded leks and water, as we did not see biological relevance for including these variables during winter.

We used individual UDs (described thoroughly in Quantifying Known Utilization section) to determine available resources for spring/summer and winter RSF models. We created a 95% isopleth for each UD and considered this a 95% seasonal home range. We considered the area within each 95% seasonal home range available to the individual for which it was created. We systematically generated available points at 250 m intervals within each individual’s 95% seasonal home range using the Create Fishnet Tool in ArcGIS. By systematically generating available locations, models may be approximated with fewer known locations compared to models with randomly generated availability (Warton and Shepherd, 2010; Aarts et al., 2012). Consequently, the number of available points was not directly related to number of used points, but rather was relative to the area of the 95% seasonal home range of each individual.

Models within the final model set were evaluated using Akaike’s Information Criterion corrected for small sample size (AIC_c; Burnham and Anderson, 2002). We considered models within 2 ΔAIC_c units from the top model as candidate models. We examined our candidate model set for nested models including ≥ 1 additional parameter and essentially the same log likelihood (Burnham and Anderson, 2002). Also, we tested for uninformative parameters by calculating 85% confidence intervals around parameter estimates; if 85% confidence intervals overlapped 0, the variable was deemed uninformative (Arnold, 2010). If model uncertainty existed, all models within 2 ΔAIC_c units from the top model were averaged to generate full model averaged coefficient estimates and standard errors (Burnham and Anderson, 2002).

We calculated and reported 95% confidence intervals around coefficient estimates using the profile likelihood method. To explore the amount of variation captured by our random effects (individual sage-grouse), we compared our top model to a simple logistic regression model that included the same data and variables but did not take into account individual effects. We did this by conducting a likelihood ratio test with an analysis of variance. We tested significance using a Chi-square test.

To model nest-site selection, we used binary regressions with the logit link in R. We pooled nests and available locations to avoid overfitting models resulting in a singular fit from comparing one nest-site to multiple random sites. We only used one nest per individual for the analysis even if there were multiple nests occupied by one individual within a single year or across years (Holloran and Anderson, 2005; Fedy et al., 2014). When multiple nests were documented for an individual, we randomly selected one nest to be used in analyses.

We calculated the maximum distance observed from nest to lek and buffered all leks by that amount; we used those buffered areas to determine availability for nest-site RSF models. The nest-nearest lek distance was calculated using active leks during the year in which the nest was active. We generated random points within the buffered area at a density of 1 point/km² with the minimum allowed distance between available points being 30 m following the methods of Fedy et al. (2014). Available data points were removed from analyses if they fell outside of the extent of spatial variable data. If model uncertainty existed, all models within 2 ΔAIC_c units from the top model were averaged to generate full model averaged coefficients and standard errors (Burnham and Anderson, 2002). We created seasonal GIS layers of relative selection by applying our parameter estimates to associated habitat layers using the logit link equation.

Additionally, we created categorical maps displaying areas in which 90% of seasonal use was predicted to occur. We identified this area using area adjusted frequencies; specifically, we categorized the map into two bins based on raster values using the Reclassify Tool in ArcGIS. The utilization value is a function of the probability of use and includes the area within each bin (Johnson et al., 2006). We adjusted the cutoff RSF value between the two bins until 90% of utilization was estimated within a single bin.

We summed the 90% predicted use layers for spring/summer, winter, and nest-site to determine which areas were predicted to be used in multiple seasons. We summed these layers using the Raster Calculator in ArcGIS. Because each of these layers were categorical (0,1), areas predicted to be used 90% of the time in all three seasons had a value of three, areas predicated to be used 90% of the time in two seasons had a value of two, areas predicted to be used 90% of the time during one season had a value of one, and areas predicted to be used <10% of the time in all seasons had a value of 0.

Common methods used for evaluating logistic regression models (e.g., ROC, Hosmer Lemeshow goodness of fit, Kappa) are inappropriate for evaluating presence/available data (Boyce et al., 2002; Johnson et al., 2006). To validate our spring/summer and winter RSF models, we used out-of-sample validation techniques, which are considered an option for validation of use/available data (Boyce et al., 2002). Individuals were assigned to the out-of-sample dataset if they did not have the minimum number of locations required to generate a seasonal UD (≥ 20 or ≥ 10 locations for spring/summer and winter, respectively). To meet independence assumptions, none of the individuals were included in both training and out-of-sample datasets and individuals used in the out-of-sample dataset were only included one year, even if multiple years of location data were available.

Because our modeling approach using GLMM is conditional (individual based), we could have withheld a certain percentage of each individual’s locations to validate our models (Koper and Manseau, 2009). However, we elected to use new individuals in our out-of-sample dataset. By using this method, we tested whether our model created using selection preferences of individuals could predict habitat selection of other individuals in the population. This approach indicates whether or not our model is robust in predicting habitat use at the population level using a conditional (individual based) approach. Although marginal (population level) estimates can be directly derived from conditional estimates, they can be biased (Agresti, 2002). For validating our GLMM nest-site models, we randomly withheld 29% of the nests from the training dataset for model validation (Huberty, 1994; Fielding and Bell, 1997).

We used model evaluation methods described by Johnson et al. (2006). We used the quantile classification in ArcGIS to generate 5 ranked bins, each encompassing approximately the same amount of area (Koper and Manseau, 2009). We calculated the utilization value for each bin as a function of the probability of use and the area within each bin. This value was multiplied by the number of locations in the out-of-sample dataset; this calculated value was number of observations expected per bin. Out-of-sample locations were overlaid on the predicted probability of use map and bin values were extracted for each location using the Extract Values Tool in ArcGIS.

To compare observed vs. expected numbers of observations in each bin, we used linear regression, regressing observed and expected observations across five bins. We also used a Chi-square test comparing observed and expected numbers of observations (Johnson et al., 2006). We considered a model valid if the following criteria were met: (1) slope of the regression line was significantly different than 0 and not significantly different from 1; (2) intercept was not significantly different from 0; (3) high r² value; and (4) non-significant Chi-square test. If these criteria were met, then the model was considered proportional to the probability of use (Johnson et al., 2006).

Modified Conservation Buffer Method

South Dakota Game, Fish and Parks primarily used a conservation buffer technique to delineate the South Dakota priority sage-grouse area in 2014. Specifically, they generated a 6.4 km buffer around all active leks in South Dakota and those within 6.4 km of the state border (South Dakota Department of Game, Fish and Parks, Division of Wildlife [SD GFP], 2014). State and BLM biologists collaborated by using all available data to manually delineate high use areas and connectivity corridors in an informal process. In areas where telemetry data was not available, biologists relied on expert opinion to similarly delineate likely connectivity corridors. Biologists also collaborated to remove areas of non-habitat that were initially within lek buffers such as forested areas. The final map was developed using a combination of lek buffers, high use areas and connectivity corridors. Active leks were considered those with ≥ two males in at least one of the previous five years (2010–2014). Additionally, in South Dakota, recent efforts to detect new or shifted leks using aerial surveys with and without forward looking infrared cameras suggest that lek detection is likely high (Travis Runia, SD GFP, personal communication).

Quantifying Known Utilization

We prioritized areas of known use by sage-grouse by calculating UDs for individuals during two seasons; spring/summer (1 April–15 September) and winter (1 November–28 February) and we also generated buffers around leks to encompass nests. We used the fixed-kernel method implemented via Home Range Tools 2.0 (Rodgers et al., 2015) for ArcGIS with sage-grouse tracking data to calculate probability density maps. UDs were calculated for each individual by creating a bivariate normal fixed kernel estimate of the probability density around each location.

Individuals were required to have ≥ 20 locations from 1 April to 15 September to be included in spring/summer analysis, and ≥ 10 locations from 1 November to 28 February to be included in winter analysis. If applicable, nest locations were only included once in the location data even if multiple locations were obtained while the female was incubating. Each individual was only included one year even if the individual was present during multiple years of data collection. In addition, each individual was limited to two locations per seven-day time interval.

To avoid over-smoothing, which would result in a positive bias in the probability density estimates, we used a rule based ad hoc smoothing parameter (h_{ad hoc}) by choosing the smallest increment of the reference bandwidth (h_ref) that resulted in a contiguous 95% kernel home range (Worton, 1989; Kie, 2013). The reference bandwidth (h_ref) was decreased by increments of 10% of (h_ref), until the most efficient smoothing parameter could be determined (i.e., h_{ad hoc} = 0.90 × h_ref, 0.80 × h_ref, 0.70 × h_ref etc.; Klaver et al., 2008; Grovenburg et al., 2012; Kie, 2013). However, since (h_{ad hoc}) is not allowed to be larger than (h_ref; Kie, 2013), if the 95% home range was fragmented at (h_ref), then (h_ref) was accepted as the smoothing parameter.

Each individual’s UD was generated at its full extent, which sometimes included areas of estimated utilization in Montana and North Dakota. Subsequently, each individual’s UD was clipped to the South Dakota boundary after creation. Individual UDs were merged across the study area using the Raster Calculator Tool in ArcGIS to generate a single layer representing cumulative utilization of the landscape during each season. We created isopleths including 90% of the estimated utilization using the Contour Tool within the Spatial Analyst package in ArcGIS for each season. We merged the spring/summer 90% isopleth polygon to the winter 90% isopleth polygon.

Summed UDs that are contoured at 90% could be biased due to individuals with dispersed UDs being excluded because only more extreme values are outlined. For example, an individual with a UD encompassed within a small area would have higher pixel values within that area; whereas an individual with a dispersed UD would have more pixels, but all would have lower values. The individual with a dispersed UD might not have any pixels included when only the top 90% of summed UD values are included in the contour.

We determined that a 6.0 km buffer around active leks encompassed ≥ 90% of nests. Leks were considered active for that year if ≥ 1 male was observed displaying. We calculated nest-lek distance using active leks in the year the nest was documented (2006, 2007, 2016, and 2017), but once calculated, applied the buffer to all active leks from 2006 to 2018. The lek buffer layer was clipped to South Dakota state boundaries. We combined the nest-lek buffer layer with the combined 90% UD isopleths to generate a priority area based on known utilization estimates.

Results

Modeling Landscape Use

Our spring/summer training dataset had 2,021 data points from 73 female sage-grouse. The top model was most parsimonious and included all variables except percent undisturbed at the 1.5 km scale (Table 2). Only the second ranked model was within 2 ΔAIC_c of the top model, but it was dismissed because it only differed by the addition of one uninformative variable (percent undisturbed at the 1.5 km scale).

TABLE 2

Table 2. Models for spring/summer resource selection function.

Coefficient estimates from the top model (Table 3) indicate the primary driver of this model was percent forest within a 1.5 km radius. Sage-grouse were avoiding forested areas, roads, and rugged terrain during spring/summer (Table 3). Sage-grouse were selecting for areas close to active leks, water, and sagebrush (Table 3); the top forms of these variables are all distance decay variables indicating a non-linear response to each feature, or the presence of a threshold. The distance at which responses decayed differed between variables; sagebrush and water have a relatively local effect on selection (0.564 km radius), whereas leks have a larger radius of impact on selection (3.2 km radius).

TABLE 3

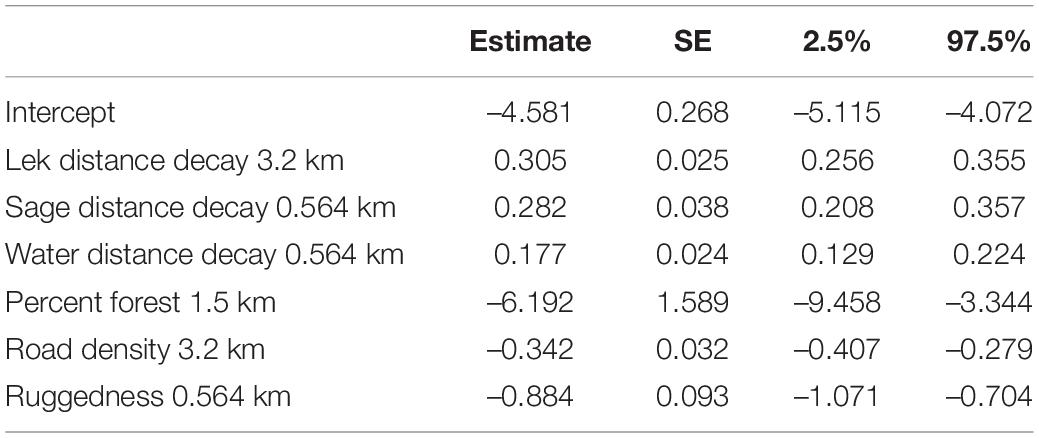
Table 3. Standardized coefficient estimates and profile likelihood 95% confidence intervals for top spring/summer resource selection function model.

Our model validation included 454 out-of-sample locations from 53 individuals. Our spring/summer RSF model met all the requirements to be considered a model that was proportional to the probability of use (Johnson et al., 2006). Additionally, we created a categorical map displaying areas predicted to be used 90% of the time during spring/summer (using area adjusted frequencies). The percent of out-of-sample locations (n = 454) that were within the 90% predicted use area was 86%.

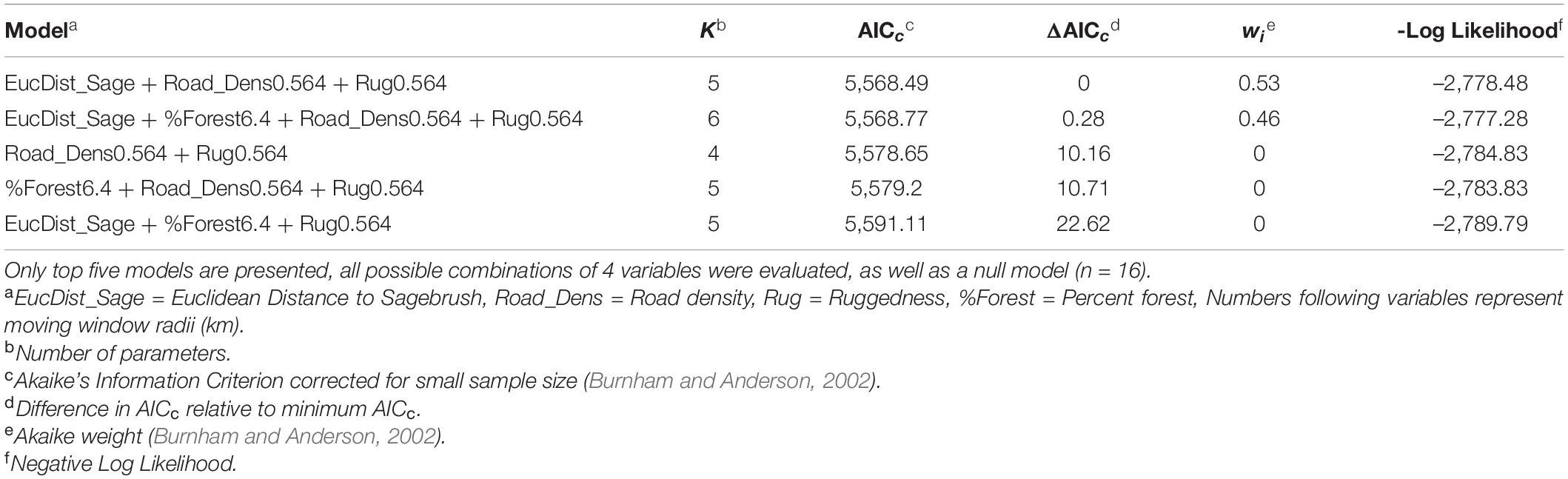
Our winter training dataset had 529 locations from 45 individuals. The top model was selected as most parsimonious and included the variables Euclidean distance to sagebrush, Road Density at the 0.564 km scale, and Ruggedness at the 0.564 km scale (Table 4). Only the second ranked model was within 2 ΔAIC_c of the top model, but it was dismissed because it only differed by the addition of one uninformative variable (percent forest at the 6.4 km scale).

TABLE 4

Table 4. Models for winter resource selection function.

During winter, sage-grouse selected for areas near sagebrush and avoided areas with high road density and rugged terrain (Table 5). The strongest predictor of selection during winter was mean ruggedness within a 0.564 km radius.

TABLE 5

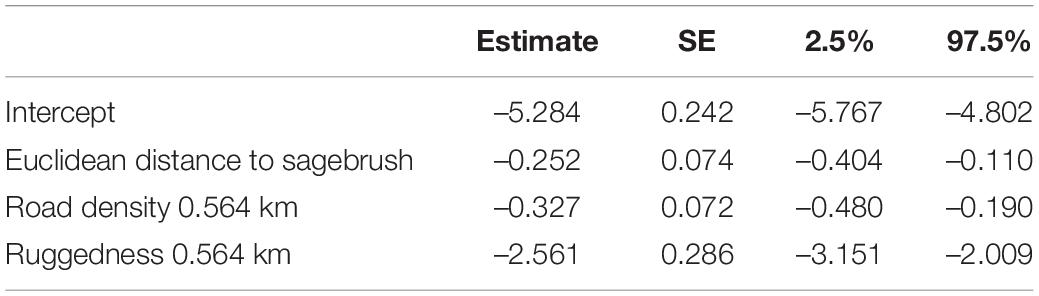
Table 5. Standardized coefficient estimates and profile likelihood 95% confidence intervals for top winter resource selection function model.

We used out-of-sample test data, which included 296 locations from 47 individuals to validate our model. Our winter RSF model met all requirements to be considered a model proportional to the probability of use (Johnson et al., 2006). Additionally, we created a categorical map displaying areas predicted to be used 90% of the time during winter (using area adjusted frequencies). The percent of out-of-sample locations (n = 296) that fell within the 90% predicted use area was 89%.

Results of the likelihood ratio tests using ANOVA for both spring/summer and winter models indicated there was significant model improvement (P < 0.05) by including individuals as random effects within the mixed effect model compared to the simple logistic regression model. This indicates that there is significant variation among individuals in terms of selection; this variation is better explained using mixed effect models.

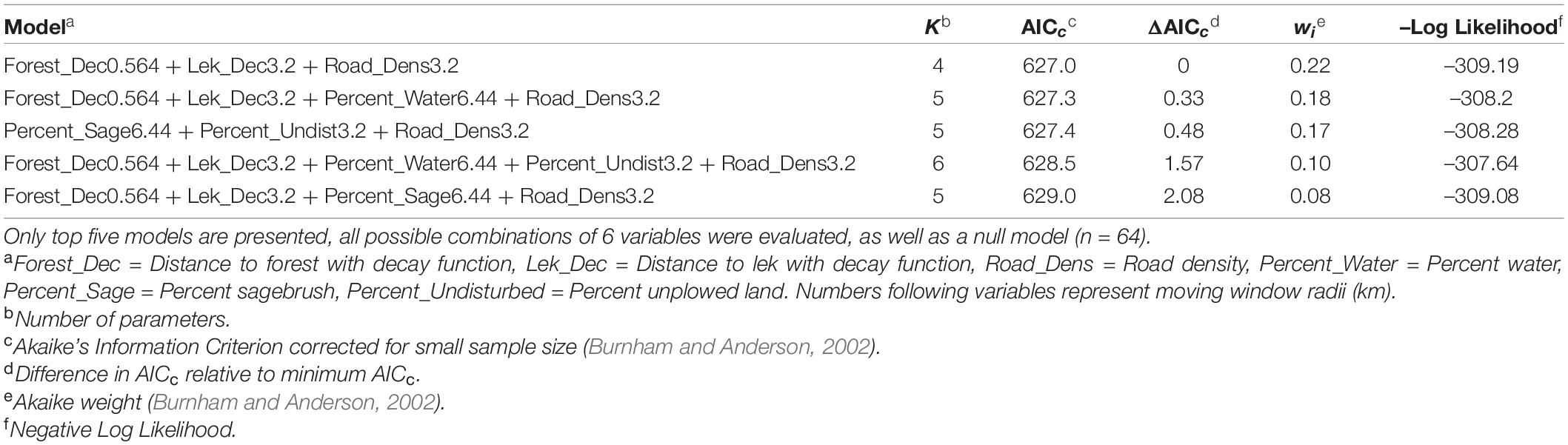
We had a total of 104 independent nests for modeling. We used 74 for training and 30 for validation. We observed two variables that exhibited perfect separation (ruggedness at 0.564 km scale, and percent forest within 1.5 km). To avoid using inflated coefficient estimates and possibly creating an overfitted model, we examined lower ΔAIC_c ranked forms and scales for each variable; however, these were still correlated (r ≥ 0.7 and VIF > 2) and therefore, we elected to use the variable with the lower ΔAIC_c score (decay distance from forest at the 0.564 km scale).

There were four nest-site models within 2 ΔAIC_c units from the top model indicating high model uncertainty (Table 6). Consequently, we model averaged the top four models, which had a combined model weight w_i = 0.67. Our model averaged coefficient estimates indicated a positive selection near leks and percent undisturbed lands within a 3.2 km radius and avoided forest, high road density, and high percent water when selecting nest-sites (Table 7).

TABLE 6

Table 6. Models for nest-site resource selection function.

TABLE 7

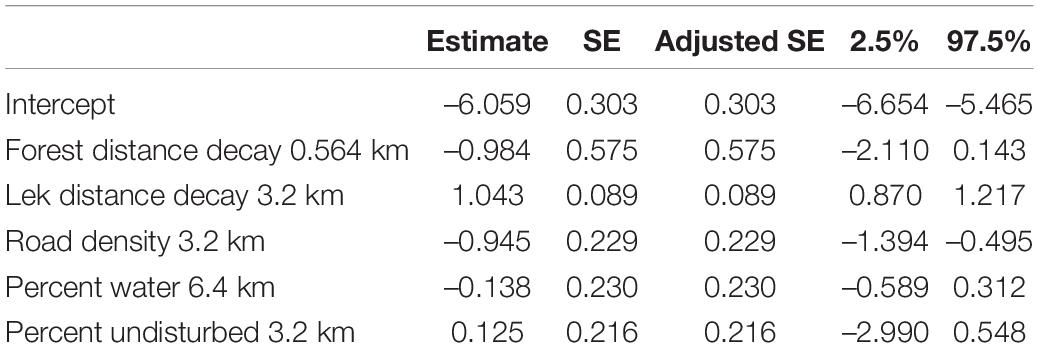
Table 7. Full model averaged standardized coefficient estimates and profile likelihood 95% confidence intervals for nest-site resource selection function models.

We used 30 out-of-sample nests to validate our model. The nest-site selection model met all criteria for describing proportional probability of use (Johnson et al., 2006). Because our out-of-sample size was small, we tested the nest RSF model on all observed nests (n = 150) as a secondary measure of validation. This included nests that were used in model building, initial testing, and some that were not included in either analysis due to lack of independence (re-nest attempts, nests from same individual in different years). The second validation again indicated the nest-site selection model met all criteria to be considered a valid model capable of describing proportion probability of use (Johnson et al., 2006).

Additionally, we created a categorical map displaying areas in which 90% of nest-sites were predicted to fall (using area adjusted frequencies). The percent of out-of-sample nests (n = 30) that fell within the 90% predicted use area was 90%. The percent of total known nests (n = 150) that were within the 90% predicted use area was 91%.

Our multi-season predicted use map (Figure 2) summarized areas predicted to be used 90% of the time in; one season, two seasons, all three seasons, or <10% of the time in all three seasons. When we combined all known spring/summer and winter locations from sage-grouse of both sexes and all ages, and compared them to the multi-season predicted use area, 70% were within areas predicted to be used 90% of the time in all three seasons, followed by 22% predicted to be used 90% of the time in two of the three seasons evaluated; 5 and 2% of locations were within the areas predicted to be used 90% of the time in one season, and none of the seasons, respectively (n = 3,943).

FIGURE 2

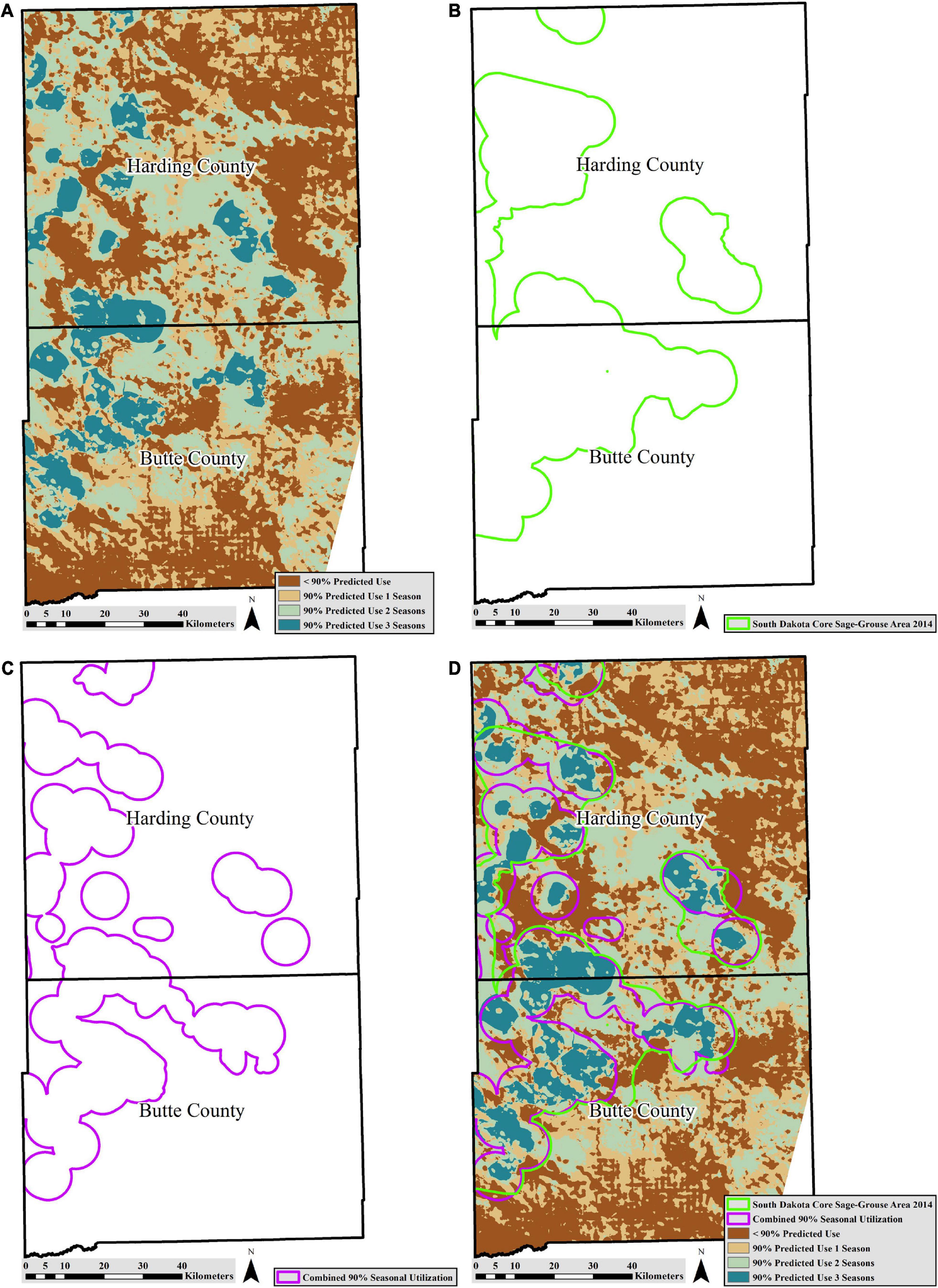
Figure 2. Study area in Butte and Harding counties, South Dakota with: (A) predicted multi-season use generated from resource selection function (RSF) models, (B) 2014 South Dakota sage-grouse priority area generated using 6.4 km lek buffers, high use areas, and connectivity corridors, (C) combined 90% isopleths from spring/summer utilization distribution, winter utilization distribution, and a 6 km lek buffer, and (D) all three methods of defining a priority area overlaid on one another for comparison.

Modified Conservation Buffer Method

The priority sage-grouse area defined by South Dakota Game, Fish and Parks encompassed 3,977 km² (Figure 2; South Dakota Department of Game, Fish and Parks, Division of Wildlife [SD GFP], 2014).

Quantifying Known Utilization

We created spring/summer UDs for 73 female sage-grouse (2,021 locations). The isopleth containing 90% of known utilization during spring/summer encompassed 1,347 km². Similarly, we created winter UDs for 45 individuals (529 locations). The isopleth encompassing 90% of estimated winter utilization encompassed 825 km². To characterize areas of known nest-sites, we buffered active leks by a distance of 6 km; this buffer distance encompassed 90% of known nests (n = 150) and encompassed 3,084 km².

Comparing Spatial Efficiencies

The priority area generated from a combination of seasonal RSF models, was 1,143 km² (Figure 2) and encompassed 91% of known nests (n = 150), 68% of female spring/summer locations (n = 2,475), and 71% of winter locations (n = 740). Of the methods compared, it was considered the most spatially efficient because it encompassed the highest number of nests, spring/summer, and winter locations per 100 km² (Table 8).

TABLE 8

Table 8. Comparison of priority areas generated via different methods.

The priority sage-grouse area defined using a modified conservation buffer approach encompassed 3,977 km² (Figure 2). It encompassed 95% of known sage-grouse nests (n = 150), 93% of breeding-age female locations during spring/summer (n = 2,475), and 99% of winter sage-grouse locations in South Dakota (n = 740). Of the three methods compared, this was the least spatially efficient, as it was the largest area with the least number of nests, spring/summer and winter locations per 100 km² (Table 8).

The combined 90% isopleths from the spring/summer and winter UDs, along with the 6.0 km lek buffer area (Figure 2) was 3,498 km² and encompassed 99% of known nests (n = 150), 98% of known breeding-age female spring/summer locations (n = 2,475), and 97% of known winter locations (n = 740). This priority area was considered moderately spatially efficient, as it had fewer nests, spring/summer and winter locations per 100 km² than the RSF generated priority area, but more nests, spring/summer and winter locations per 100 km² than the modified conservation buffer method priority area (Table 8). However, the size and spatial efficiencies of the UD generated priority area and the modified conservation buffer method priority area were similar (Table 8).

Discussion

All three methods used to define priority habitat for sage-grouse in South Dakota contained a high amount of the documented sage-grouse locations. The RSF analysis resulted in a spatially efficient priority area that contained the highest density of nests, spring/summer and winter locations within it. Additionally, an RSF modeling approach can provide managers with a better understanding of space use at multiple scales, can predict areas of use outside of “known use” areas, and can assess variation in selection probabilities. However, even when seasonal RSF maps were categorized into two categories (≥90% use and <10% use) and combined for all three seasons, the predicted high use areas were disjunct. Making a contiguous priority area using these data is not possible without including some predicted low use areas, which would need to be determined by expert opinion or by additional analysis.

The South Dakota priority sage-grouse area, defined using the modified conservation buffer method, suffices to meet the goals set forth in the South Dakota Sage-Grouse Management Plan (South Dakota Department of Game, Fish and Parks, Division of Wildlife [SD GFP], 2014), which is that the area is targeted at productive landscapes in a fraction of the sage-grouse distribution (South Dakota Department of Game, Fish and Parks, Division of Wildlife [SD GFP], 2014). Over 90% of seasonal use was included in South Dakota’s current priority sage-grouse area. However, some areas that were predicted to have high multi-season use (from the RSF method) were not included in South Dakota’s 2014 priority sage-grouse area, suggesting that the 2014 South Dakota priority sage-grouse area may not have been adequate (Figure 2). If the South Dakota priority area were to be updated to include a buffer around recently discovered leks, a majority of crucial areas would be encompassed. However, this limitation is a reality of generating priority areas with limited information; a reality that could be overcome by using a modeling approach to predict high use areas. Regardless, the modified conservation buffer method appears to be sound, valid, and an adequate approach to define management areas when more detailed location, movement, and landscape data are out of date and/or not available.

The priority area developed by combining seasonal utilization estimates is the most inclusive in terms of encompassing nests and spring/summer locations (Figure 2 and Table 8). The priority area defined using combined seasonal UDs was mostly contiguous.

Although the RSF method did not create a contiguous area, there are other benefits of using this method. One major benefit is allowing managers to predict areas of high use in areas where there is no known use. For example, our predicted 90% use maps for spring/summer and winter generated from RSFs both suggest the eastern side of the study area should be selected/used by sage-grouse. However, this area does not currently encompass any known sage-grouse use (leks or documented sage-grouse locations). There are numerous non-mutually exclusive explanations for this finding. First, it is possible that the habitat and resources in those identified areas are suitable and not occupied; historic lek count data shows sage-grouse were present in some of those areas historically. Because South Dakota’s sage-grouse are a fringe population that has experienced range and population constriction through time, the identified areas might have become extirpated and have not re-populated (Hanski, 1998), which is plausible based on research by Coates et al. (2021) finding that peripheral populations were declining faster than other areas within the sage-grouse distribution. Second, it is possible that sage-grouse select habitats that are near critical habitat used in other seasons. This could explain why most of our known sage-grouse locations (∼92%) are near or within habitat identified to be used in all three seasons or at minimum two seasons (Figure 2). Third, the sagebrush data we used was re-classified to represent presence; then represented as percent sagebrush pixels or distance to sagebrush pixel. It is possible that although there is sagebrush in the area, it does not meet the height or canopy cover requirements for sage-grouse.

Management Implications

Wildlife managers should first define the criteria necessary to consider their priority area adequate, then consider the data necessary to create and assess a priority area that would meet those criteria, and lastly, consider any constraints of using the data currently available to them, or the need to obtain additional data.

In the case of sage-grouse, we found that using lek buffers, expert opinion, and connectivity corridors was sufficient to encompass most known sage-grouse locations and nests. However, by incorporating movement data into utilization distributions and modeled resource selection we were able to identify smaller areas that captured a greater proportion of the important sites. Thus, the investment in these more data intensive and computationally intensive approaches may be warranted when there are logistical or political constraints on the amount of land that can be conserved.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The animal study was reviewed and approved by South Dakota State University (IACUC approval # 15-074A).

Author Contributions

LP collected and analyzed data, drafted the manuscript, and edited. JJ collected data, contributed ideas, and edited. TR collected data, contributed ideas, provided data, and edited. AG collected data, contributed ideas, and edited. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the South Dakota Game, Fish and Parks, State Wildlife Grant T-70-R-1 #2481.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank the private landowners who granted us access to their land to conduct this research. We thank C. Berdan, E. Mitchell, and numerous volunteers for assisting with sage-grouse capture. We also sincerely thank J. Gehrt, C. Sink, K. Norton, S. Arent, S. Hone, and D. Pecenka for collecting sage-grouse locations.

References

Aarts, G., Fieberg, J., and Matthiopoulos, J. (2012). Comparative interpretation of count, presence–absence and point methods for species distribution models. Methods Ecol. Evol. 3, 177–187. doi: 10.1111/j.2041-210X.2011.00141.x