Synchrony and Stability in Trophic Metacommunities: When Top Predators Navigate in a Heterogeneous World

Ecosystem stability strongly depends on spatial aspects since localized perturbations spread across an entire region through species dispersal. Assessing the synchrony of the response of connected populations is fundamental to understand stability at different scales because if populations fluctuate asynchronously, the risk of their simultaneous extinction is low, thus reducing the species' regional extinction risk. Here, we consider a metacommunity model consisting of two food chains connected by dispersal and we review the various mechanisms governing the transmission of small perturbations affecting populations in the vicinity of equilibrium. First, we describe how perturbations propagate vertically (i.e., within food chains through trophic interactions) and horizontally (i.e., between food chains through dispersal) in metacommunities. Then, we discuss the mechanisms susceptible to alter synchrony patterns such as density-depend dispersal or spatial heterogeneity. Density-dependent dispersal, which is the influence of prey or predator abundance on dispersal, has a major impact because the species with the highest coefficient of variation of biomass governs the dispersal rate of the dispersing species and determines the synchrony of its populations, thus bypassing the classic vertical transmission of perturbations. Spatial heterogeneity, which is a disparity between patches of the attack rate of predators on prey in our model, alters the vertical transmission of perturbations in each patch, thus making synchrony dependent on which patch is perturbed. Finally, by combining our understanding of the impact of each of these mechanisms on synchrony, we are able to full explain the response of realistic metacommunities such as the model developed by Rooney et al. (2006). By disentangling the main mechanisms governing synchrony, our metacommunity model provides a broad insight into the consequences of spacial aspects on food web stability.

Introduction

Biodiversity is facing major threats because of ever growing anthropogenic perturbations as reported by the IPBES assessment published in 2019 (Díaz et al., 2019). Human activities fragment and alter species habitat, thus changing the connectivity between different populations and the local conditions governing ecosystem functioning (Haddad et al., 2015). These distant populations experience their own dynamics whose synchrony is key for species persistence and stability. Indeed, asynchronous dynamics limit the risk of simultaneous local extinctions leading to regional extinction (Blasius et al., 1999) and reduces the temporal variability of species biomass at regional scale (Wang et al., 2015). The metacommunity framework is particularly interesting to address this spatial aspect of community dynamics (Loreau et al., 2003; Leibold et al., 2004; Amarasekare, 2008; Leibold and Chase, 2017; Gross et al., 2020), because it represents space as a collection of patches hosting communities whose populations are linked between patches by dispersal. Thus, in a landscape altered by human activities, individuals navigate in a heterogeneous metacommunity where the parameters governing community dynamics vary among patches.

Rooney et al. (2006) set a milestone as they showed that top predators can couple distinct energy channels that differ in both productivity and turnover rate. They translated this statement into a mathematical model with two asymmetric energy channels, i.e., two parallel food chains with different interaction strengths, and showed that this asymmetry promotes both local and non-local stability in food webs. In their model, top predators derive their energy from two distinct food chains characterized by different interaction strengths and they preferentially feed on the food chain where prey are most abundant (Figure 1). Their work opened research perspectives on some mechanisms governing food web stability in metacommunities, in particular spatial heterogeneity and habitat selection.

FIGURE 1

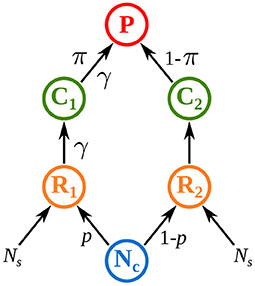
Figure 1. Model of Rooney et al. (2006) where top predators P couple two food chains consisting of a resource R and a consumer C. Both resources feed on a common nutrient pool N_c. Interaction strength between R₁ and C₁ and between C₁ and P is γ times higher than in food chain 2. A fraction p of nutrients from the common pool N_c is absorbed by R₁. Top predators preferentially prey on the consumer that has the highest biomass density (π = C₁/(C₁ + C₂) defines the preference for C₁). See Equation (11) and Supplementary Table S1-2 in the Supplementary Material for a detailed description of the model and its parameters.

Spatial heterogeneity is a major factor in ecology and the metacommunity framework is particularly adapted to study its impact on food web dynamics. Organisms couple various habitats by migration (Furey et al., 2018) and large mobile predators couple different energetic pathways by feeding on several prey (Vadeboncoeur et al., 2005; Rooney et al., 2006; Olff et al., 2009). Spatial heterogeneity leads to different dynamics in each patch, which is supposed to promote asynchrony. However, dispersal couples distant patches and links their dynamics. Goldwyn and Hastings (2009) demonstrated that low heterogeneity is enough to generate strong asynchrony in metacommunities. Rooney et al. (2006) showed that spatial heterogeneity (named structural asymmetry in their study), stabilizes food webs by increasing its asymptotic resilience and decreasing the synchrony of prey dynamics when predators are perturbed. Unfortunately, Rooney et al. (2006) only considered perturbations affecting top predators and prey preference depending on prey abundance (Figure 1), thus confounding the effects of spatial heterogeneity and prey preference. Pierre et al. (In prep.) proposed an extensive description of the response of heterogeneous metacommunities to stochastic perturbations. They showed that spatial heterogeneity is not a fundamentally stabilizing factor in metacommunities because it promotes either synchrony or asynchrony of the populations of a species depending on which population is perturbed (i.e., if the perturbed population is in the patch where interaction strength is the highest).

Metacommunity models usually represent dispersal as a passive flow of individuals from high-density to low-density patches. However, organisms select their habitat depending on many factors, such as resource availability, predator avoidance and climatic requirements (Fronhofer et al., 2015; Jacob et al., 2015). Thus, dispersal is triggered by the abundance of other prey and predators, as shown experimentally across many taxa (Hauzy et al., 2007; Fronhofer et al., 2018; Harman et al., 2020), thus generalizing density-dependent dispersal. Density-dependent dispersal is closely related to the prey preference implemented by Rooney et al. (2006) when predators have a high dispersal rate and strongly couple prey population dynamics because, in both cases, predation selectively increases in the food chain with the highest biomass density of prey. This mechanism increases asymptotic resilience and dampens the oscillations of biomass dynamics (Post et al., 2000; McCann et al., 2005; Rooney et al., 2006). Density-dependent dispersal also promotes asynchrony in metacommunity models (Li et al., 2005; Hauzy et al., 2010; Liu et al., 2016). Only Quévreux et al. (2021c), however, considered stochastic perturbations. They found that the predictions of models with density-dependent dispersal are opposite to those of models with passive dispersal because density-dependent dispersal alters the transmission of perturbations between patches.

All these studies were focused on food web stability. However, the notion of stability is the subject of intense debate in ecology (McCann, 2000), and its various definitions do not measure the same features of ecosystem dynamics (Arnoldi et al., 2016). Many studies, including Rooney et al. (2006), considered asymptotic resilience, which is the rate at which a system returns to equilibrium after a perturbation in a very long run, as measured by the dominant eigenvalue of the Jacobian matrix of the system. Asymptotic resilience has often been used to describe the stability of the entire system but Haegeman et al. (2016), Arnoldi et al. (2018) demonstrated that it is actually driven by rare species and ignores abundant species, which contribute most to total biomass. Therefore, the temporal variability of biomass, measured by coefficient of variation (CV), is a much better metric because it can be easily measured experimentally and gives access to synchrony (Vasseur and Fox, 2009; Fox et al., 2013). In addition, the CV of biomass in response to stochastic perturbations is a powerful theoretical tool used by Quévreux et al. (2021a) to disentangle the different mechanisms governing synchrony as perturbations can affect particular species and are then transmitted across the metacommunity.

Recently, several mechanisms governing synchrony in metacommunities have been extensively described. The effects of spatial heterogeneity and density-dependent dispersal on synchrony in metacommunities have received particular attention but these mechanisms were studies in isolation. Here, we propose to go back to Rooney et al. (2006) and to reinterpret their results in the light of the recent studies cites above. We first describe the general framework of our model and how stability can be assessed. We then summarize the results of our recent studies on density-dependent dispersal (Quévreux et al., 2021c) and spatial heterogeneity (Quévreux et al., in prep.). Finally, we explain how these two mechanisms interact and shape synchrony in a model similar to that developed by Rooney et al. (2006).

Measuring Stability

Stochastic Perturbations

As mentioned above, stability can be measured by the temporal variability of biomass generated by stochastic perturbations (Arnoldi et al., 2016, 2019). Stochastic perturbations are applied to one or several populations to measure the variance of the biomass of each population following the transmission of perturbations in the entire metacommunity. Mathematically, stochastic perturbations are modeled as follows:

$\begin{array}{ll}d{B}_i={\displaystyle \underset{\text{deterministic}}{{\displaystyle \underbrace{f_i(B_1,...,B_S)dt}}}}+{\displaystyle \underset{\text{perturbation}}{{\displaystyle \underbrace{{\sigma }_i{B}_i^{z}d{W}_i}}}}& (1)\end{array}$

f_i(B₁, ..., B_S) is the deterministic part of the dynamics of the biomass of the species i, which depends on the biomass of the S species present in the metacommunity (see Equations 8a, 8b bellow). Stochastic perturbations are defined by their standard deviation σ_i and a white noise term dW_i with mean 0 and variance 1. In addition, perturbations scale with each species' biomass with an exponent z depending on the type of perturbation considered (Haegeman and Loreau, 2011; Arnoldi et al., 2019): exogenous stochasticity (from harvesting for instance) corresponds to z = 0, demographic stochasticity (from birth-death processes) to z = 0.5, and environmental factors to z = 1 (see demonstration in Lande et al., 2003 and in the Supplementary Material of Quévreux et al., 2021a). Arnoldi et al. (2019) showed that when a species is perturbed, the ratio of its biomass variance to perturbation variance increases with the species' biomass in the case of environmental perturbations, while it is independent of its biomass in the case of demographic perturbations. Therefore, Quévreux et al. (2021a) and Quévreux et al. (2021c) chose demographic perturbations in their analysis as these enabled them to perturb different species with the same relative intensity regardless of their abundance.

Response to Perturbations

Synchrony in the metacommunity can be evaluated from the covariance between the temporal variations of the various species and patches, which are encoded in the variance-covariance matrix C^*. If the metacommunity is at equilibrium and perturbations are small enough, we can linearise the system in the vicinity of the equilibrium to get Equation (2) where $X_i=B_i-B_i^{*}$ is the deviation from equilibrium [see the Supplementary Material of Quévreux et al. (2021a) for more mathematical details].

$\begin{array}{ll}\frac{d\vec{X}}{dt}=J\vec{X}+T\vec{E}& (2)\end{array}$

J is the Jacobian matrix and T defines how the perturbations E_j = σ_jdW_j affect the dynamics. For instance, T_ij tells us how perturbation j affects species i. In the case of independent demographic perturbations, T is a diagonal matrix whose elements are $T_{ii}=B_i^{*0.5}$.

Then, we get the variance-covariance matrix C^* of species biomasses (variance-covariance matrix of $\vec{X}$) from the variance-covariance matrix of perturbations V_E (variance-covariance matrix of $\vec{E}$) by solving the Lyapunov (Equation 3) (Arnold, 1974; Wang et al., 2015; Arnoldi et al., 2016; Shanafelt and Loreau, 2018, and see the Supplementary Material of Quévreux et al., 2021a for a detailed description of the solution of Equation 3).

$\begin{array}{ll}J{C}^{*}+C^{*}{J}^{\top }+T{V}_E{T}^{\top }=0& (3)\end{array}$

From the variance-covariance matrix C^*, whose elements are w_ij, we can compute the correlation matrix R^* of the system whose elements ρ_ij are defined by:

$\begin{array}{ll}{\rho }_{ij}=\frac{w_{ij}}{\sqrt{w_{ii}{w}_{jj}}}& (4)\end{array}$

Correlation coefficients represent the pairwise synchrony of species i and j: if ρ_ij > 0 (correlation), species i and j are synchronous and if ρ_ij < 0 (anti-correlation), species i and j are asynchronous. Note that this metric is different from the community-wide synchrony defined by Loreau and de Mazancourt (2008), which measures the overall synchrony of many species.

Trophic Metacommunity Model

The metacommunity model used by Quévreux et al. (2021a) and Quévreux et al. (2021c) is based on the food chain model developed by Barbier and Loreau (2019), which corresponds to the “intra-patch dynamics” part of Equations (5a) and (5b), and integrates a dispersal term to consider a metacommunity with two patches (Figure 2A).

$\begin{array}{ll}\frac{d{B}_1^{(1)}}{dt}=B_1^{(1)}(g_1-D_1{B}_1^{(1)}-{\alpha }_{2,1}{B}_2^{(1)})+{\delta }_1(B_1^{(2)}-B_1^{(1)})& (\mathrm{5a})\end{array}$

$\begin{array}{l}\frac{d{B}_i^{(1)}}{dt}={\displaystyle \underset{\text{intra-patch dynamics}}{{\displaystyle \underbrace{B_i^{(1)}(-r_i-D_i{B}_i^{(1)}+\epsilon {\alpha }_{i,i-1}{B}_{i-1}^{(1)}-{\alpha }_{i+1,i}{B}_{i+1}^{(1)})}}}}\\ +{\displaystyle \underset{\text{dispersal}}{{\displaystyle \underbrace{{\delta }_i(B_i^{(2)}-B_i^{(1)})}}}}\text{for\hspace{1em}}i>1& (\mathrm{5b})\end{array}$

$B_i^{(1)}$ is the biomass of trophic level i in patch #1, $B_i^{(2)}$ its biomass in patch #2, ε is the biomass conversion efficiency and α_i,j is the interaction strength between consumer i and prey j. Species i disperses between the two patches at rate δ_i. The density independent net growth rate of primary producers g₁ in Equation (5a), the mortality rate of consumers r_i in Equation (5b) and the density dependent mortality rate D_i scale with species metabolic rates m_i as biological rates are linked to energy expenditure.

$\begin{array}{ll}{g}_1=m_{1}g{r}_i=m_{i}r{D}_i=m_{i}D& (6)\end{array}$

In order to get a broad range of possible responses, we assume the predator-prey metabolic rate ratio m and the interaction strength to self-regulation ratio a to be constant. These ratios capture the relations between parameters and trophic levels. This enables us to consider contrasting situations while keeping the model as simple as possible.

$\begin{array}{ll}m=\frac{m_{i+1}}{m_i}a=\frac{{\alpha }_{i,i-1}}{D_i}{d}_i=\frac{{\delta }_i}{D_i}& (7)\end{array}$

Varying m leads to food chains where predators have either faster or slower biomass dynamics than their prey and varying a leads to food chains where interspecific interactions do or do not prevail over intraspecific interactions. As all biological rates are rescaled by D_i, we also define d_i, the dispersal rate relative to self-regulation (referred as scaled dispersal rate in the rest of the study), in order to keep the values of the dispersal rate relative to the other biological rates consistent across trophic levels. Finally, the time scale of the system is defined by setting the metabolic rate of primary producers m₁ to unity. Equations (5a) and (5b) then become:

$\begin{array}{ll}\frac{1}{D}\frac{d{B}_1^{(1)}}{dt}=B_1^{(1)}(\frac{g}{D}-B_1^{(1)}-ma{B}_2^{(1)})+d_1(B_1^{(2)}-B_1^{(1)})& (\mathrm{8a})\end{array}$

$\begin{array}{l}\frac{1}{m^{i-1}D}\frac{d{B}_i^{(1)}}{dt}={\displaystyle \underset{\text{intra-patch dynamics}}{{\displaystyle \underbrace{B_i^{(1)}(-\frac{r}{D}-B_i^{(1)}+\epsilon a{B}_{i-1}^{(1)}-ma{B}_{i+1}^{(1)})}}}}\\ +{\displaystyle \underset{\text{dispersal}}{{\displaystyle \underbrace{d_i(B_i^{(2)}-B_i^{(1)})}}}}\text{for\hspace{1em}}i>1& (\mathrm{8b})\end{array}$

Thus, εa and ma define the positive effect of the prey on its predator and the negative effect of the predator on its prey, respectively (Figure 2B). These two synthetic parameters define the overall behavior of the food chain and are varied over the interval [0.1, 10] to consider a broad range of possible responses (see Supplementary Table S1-1 for the values of the other parameters). Indeed, over this range of parameters, biomass distribution varies from bottom-heavy (i.e., prey are more abundant than their predators) to top-heavy (i.e., predators are more abundant than their prey), or display a trophic cascade pattern with an alternation of abundant and rare species, top predators always being abundant (Figure 2C). By covering this range of possible responses, the robustness of the results to various ecological contexts can be assessed to demonstrate the generality of the involved mechanisms. However, for the sake of simplicity, we will only show results for one combination of εa and ma in the following [εa = 10 and ma = 10 because they are close to the values used by Rooney et al. (2006)].

FIGURE 2

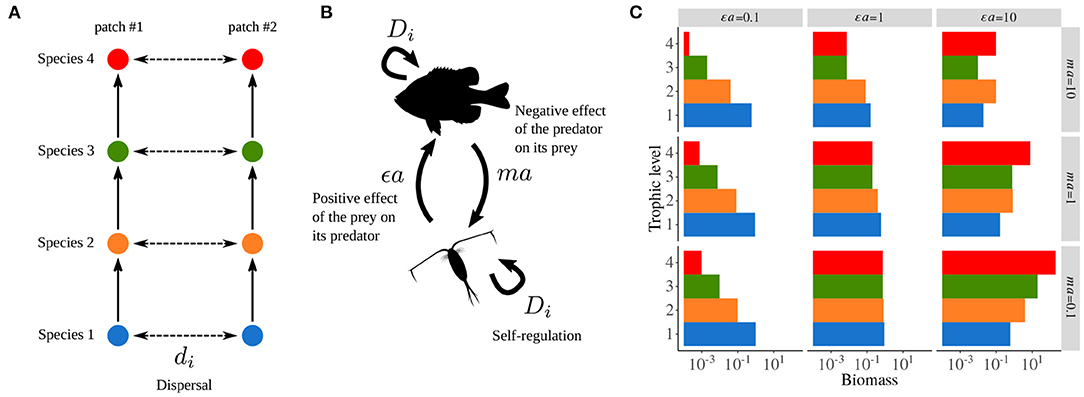
Figure 2. General description of the metacommunity model. (A) Metacommunity model with two patches, each sustaining a food chain with the same species whose populations are linked by dispersal. (B) Food web model: εa the positive effect of the prey on its predator and ma the negative effect of the predator on its prey. D_i is self-regulation, which represents negative intra-specific interactions (e.g., disease and territoriality). (C) Biomass distribution in an isolated food chain depending on εa and ma (g = 1, r = 0, ε = 0.65, D = 1, d_i = 0). Adapted from Quévreux et al. (2021a).

Fundamental Rules of Perturbation Transmission and Spatial Correlation

The fundamental rules of perturbation transmission in trophic metacommunities in the vicinity of equilibrium have been described by Quévreux et al. (2021a). To summarize their results, we consider a two patch predator-prey metacommunity with passive dispersal of predators exclusively and perturbation of prey in patch #1 (Figure 3A). Perturbations propagate vertically in patch #1 through trophic interactions and correlate the dynamics of prey and predators in patch #1 by a bottom-up effect (Figure 3B ①). Indeed, if perturbations increase prey biomass, predator biomass also increases because of the vertical transfer of biomass. Then, the passive dispersal of predators transmits the perturbations horizontally and correlates their populations spatially (Figure 3B ②). Finally, predators in patch #2 transmit perturbations vertically to the rest of the food chain in patch #2 by a top-down effect. This leads to the temporal anti-correlation of the dynamics of predators and prey (Figure 3B ③), because if a perturbation increases predator biomass, prey biomass decreases due to the negative effect of predators on prey. The final result of all these effects is the spatial anti-correlation of prey biomass dynamics (Figure 3B ④). It is possible to explain the entire correlation matrix of the metacommunity in the same way (Figure 3C).

FIGURE 3

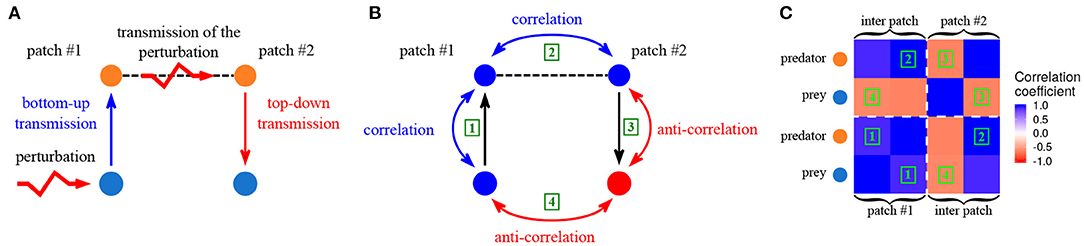
Figure 3. Synchrony in a two-patches predator prey metacommunity. Only predators are able to disperse and prey receive stochastic perturbations in patch #1. (A) Propagation of perturbations from patch #1 to patch #2. (B) Correlation between the various populations in response to perturbations. (C) Correlation matrix of the metacommunity. Each colored square represents the correlation coefficient between two populations. The green numbers correspond to the correlations showed in (B), for instance, squares labeled with 1 are the correlation between prey and predators in patch #1. The diagonal blocks (delimited by white dashed lines) represent the correlation of populations within the same patch, while the off-diagonal blocks represent the correlation of populations belonging to different patches. (εa = 0.1, ma = 10 and $d_2=10^3$, from Quévreux et al., 2021c).

This simple mechanism can be easily applied to more complex setups. When several species are able to disperse, Quévreux et al. (2021a) showed that the species with the highest dispersal relative to the other local demographic processes (e.g., predation and self-regulation) transmits perturbations to the other patch. In addition, the effects of independent perturbations on the variance and correlation of species are additive (see Quévreux et al., 2021a; Supplementary Material). Thus, a metacommunity of many species receiving multiple independent perturbations can be simplified into a sum of tractable sub-metacommunities to explain the synchrony of its different populations.

Breaking the Rules

Several mechanisms may alter these fundamental rules governing perturbation transmission in metacommunities. In the following, we describe two mechanisms that can reverse the synchrony predicted by the simple model described previously: density-dependent dispersal and spatial heterogeneity.

Density-Dependent Dispersal

Most metacommunity models consider passive dispersal for the sake of simplicity. However, many species emigrate to find food or avoid predators (Fronhofer et al., 2015; Jacob et al., 2015). Quévreux et al. (2021c) included the density-dependent dispersal function of Hauzy et al. (2010) in the metacommunity model developed by Quévreux et al. (2021a) (see Equation 10 in the Supplementary Material).

Thus, the dispersal of species i can be modulated by its own density, prey density and/or predator density. In the following, we only consider the prey density-dependent dispersal of predators (f_prey,i detailed in Equation 9a), but the two other dependencies are thoroughly described in Quévreux et al. (2021c).

$\begin{array}{ll}{f}_{prey,i}(B_{i-1})=\frac{B_{i-1}^{-1}}{B_{i-1}^{-1}+S_{i,i-1}^{-1}}& (\mathrm{9a})\end{array}$

$\begin{array}{ll}{S}_{i,j}=S_{0,i}{B}_j^{*}& (\mathrm{9b})\end{array}$

S_i,j is the sensitivity of the dispersal of species i to species j biomass density, with S_0,i a constant and $B_j^{*}$ the biomass of species j at equilibrium. f_prey,i(B_i−1) is a decreasing function of B_i−1, which means that a higher biomass density of prey in patch #1 decreases the emigration of predators to patch #2 (negative density-dependent dispersal). In addition, varying S_0,i enables us to tune the sensitivity of dispersal to biomass density. For instance, for prey density-dependent dispersal f_prey,i, a small value of S_0,i leads to a strong response to prey biomass while a high value leads to a weak response. In the latter case, dispersal is similar to passive dispersal.

Quévreux et al. (2021c) showed that taking density-dependent dispersal into account can lead to synchrony patterns in total contradiction to those predicted by models considering passive dispersal. As an example, we consider a metacommunity with two trophic levels where only predators are able to disperse depending on prey density (see Equation 10 in the Supplementary Material), and prey in patch #1 receive stochastic perturbations. If predator dispersal is not sensitive to prey density ($S_{0,i}=10^3$), the dynamics of prey populations are anti-correlated (Figure 4), according to the results of Quévreux et al. (2021a) presented in Figure 3. If predator dispersal is sensitive to prey density ($S_{0,i}=10^{-3}$), the dynamics of prey populations become correlated and predator populations tend to be anti-correlated (Figure 4).

FIGURE 4

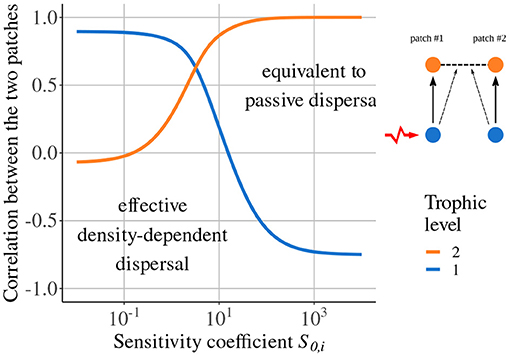
Figure 4. Correlation between populations in the two patches depending on the sensitivity coefficient S_0,i. Prey in patch #1 receive stochastic perturbations and predator dispersal depends on prey biomass density. Prey do not disperse (εa = 10, ma = 10 and $d_2=10^3$). Adapted from Quévreux et al. (2021c).

To explain these correlation patterns, Quévreux et al. (2021c) proposed two mechanisms, which we detail in the case of a perturbation that increases the biomass of prey in patch #1. First, when dispersal depends on the density of several species, the species with the highest biomass CV drives dispersal, i.e., prey in the case we consider (Supplementary Figure S1-1A). Note this mechanisms is acting for prey and predator density-dependent dispersal (Figure 5A). This makes predators immigrate in patch #1 because prey are abundant there, and leads the opposite variations of predator biomass between the two patches (Supplementary Figure S1-1B). Thus, perturbations are directly transmitted from prey in patch #1 (Figure 5B ①) to patch #2 and bypass the classic vertical transmission through trophic interactions (Figure 5B ②). Finally, perturbations are transmitted vertically in patch #2 (Figure 5B ③), and the release of predator pressure in patch #2 increases prey biomass in patch #2.

FIGURE 5

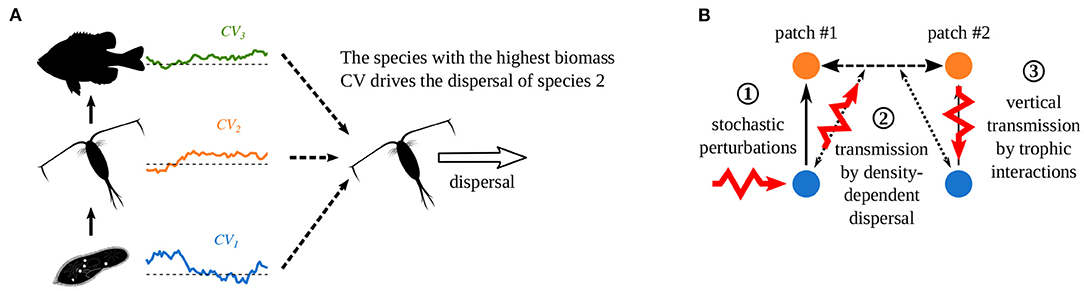
Figure 5. Effect of density-dependent dispersal on perturbation propagation in metacommunities. (A) If dispersal depends on the density of several species, the species with the highest biomass CV drives dispersal. (B) Propagation of stochastic perturbations when predators have prey density-dependent dispersal. ① Direct stochastic perturbation of prey in patch #1. ② Horizontal transmission to the predators in patch #2 by density-dependent dispersal that bypasses vertical transmission in patch #1. ③ Vertical transmission in patch #2 through trophic interactions. (Adapted from Quévreux et al., 2021c).

Spatial Heterogeneity

Representing spatial heterogeneity is one of the major purposes of the metacommunity framework. Quévreux et al. (in prep.) represented spatial heterogeneity in the same way as Rooney et al. (2006) by increasing interaction strength by a factor γ in patch #1 (Figure 6). They also increased biomass production by primary producers by a factor ω, which is set equal to γ in the following. They showed that varying ω does not change synchrony qualitatively but strongly affects species persistence.

FIGURE 6

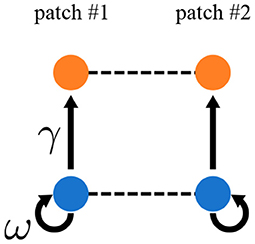
Figure 6. Metacommunity model with spatial asymmetry in interaction strength. Interaction strength and biomass production by primary producers are γ and ω times higher, respectively, in patch #1 than in patch #2.

Quévreux et al. (in prep.) mainly showed that, in heterogeneous metacommunities, synchrony depends on which patch is perturbed, i.e., perturbing the population of a species in patch #1 or #2 does not lead to the same correlation pattern between patches. Here, we consider a metacommunity where interaction strength is higher in patch #1 and only predators are able to disperse. Increasing asymmetry of interaction strength γ increases the correlation of prey populations when prey are perturbed in patch #1 while it decreases it when prey are perturbed in patch #2 (Figure 7). This discrepancy is due to the source-sink dynamics of predators (predator biomass produced in excess in patch #1 spills over patch #2), which increases apparent competition for prey and leads to a lower prey biomass in patch #2 than in patch #1 (Figure 8 ① and Supplementary Figures S1-2A,B). This alters predator-prey dynamics: when prey are perturbed in patch #1, high prey biomass and high interaction strength generate strong responses of prey and predator biomasses (Figure 8A ② and Supplementary Figures S1-2C) that are transmitted to prey in patch #2, which are completely under predator control (Figure 8A ③). This increases synchrony because predators drive the dynamics in the two patches. When prey are perturbed in patch #2, predator-prey dynamics are weak because of low prey biomass and weak interaction strength (Figure 8B ②). Thus, perturbations are weakly transmitted to patch #2 (Figure 8B ③) and prey populations slowly return to equilibrium, which leads to asynchrony (Supplementary Figure S1-2C).

FIGURE 7

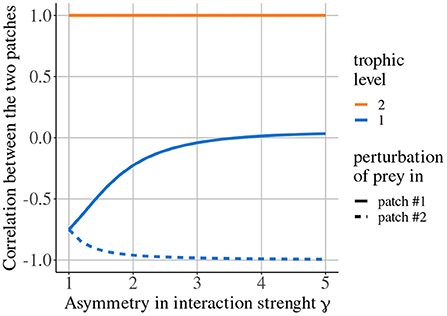
Figure 7. Correlation between the two populations of prey and predators depending on asymmetry of interaction strength γ when prey are perturbed in either patch #1 or patch #2. Only predators are able to disperse (εa = 10, ma = 10, $d_2=10^3$ and ω = γ). Adapted from Quévreux et al. (in prep.).

FIGURE 8

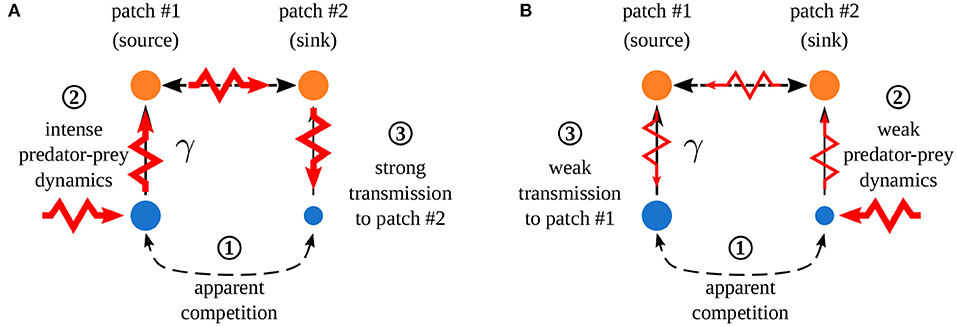
Figure 8. Effect of spatial heterogeneity on synchrony. Asymmetry of interaction strength γ leads to a strong apparent competition ①, creating biomass difference between the two patches (disk size). (A) Perturbation of prey in patch #1 which ② leads to strong responses of prey and predator biomasses due to abundant prey biomasses and high interaction strength. ③ Strong transmission in patch #2 increasing the correlation of prey populations (control of prey populations by predators). (B) Perturbation of prey in patch #2 which ② leads to weak predator-prey dynamics due to low prey biomass and low interaction strength. ③ Weak transmission in patch #2 leading to almost independent recovery in each patch, which decreases correlation. Adapted from Quévreux et al. (in prep.).

When Density-Dependent Dispersal and Spatial Heterogeneity Collide

We now build a model similar to Rooney et al.'s (2006) food web model (Figure 9A). We consider four trophic levels and we set dispersal to mimic the coupling of the two food chains in Rooney et al.'s (2006) model (Figure 9B). Primary producers have a high passive dispersal, which correlates its two populations, in order to mimic the common nutrient pool of Rooney et al.'s (2006) model (see Equation 11 and Supplementary Table S1-2 in the Supplementary Material for a detailed description of the model). Top predators have a prey density-dependent dispersal that is equivalent to the prey preference governing foraging effort in Rooney et al.'s (2006) model (see Equations 12, 13 and Supplementary Figures S1-3–S1-6 in the Supplementary Material). We set the scaled dispersal rates of primary producers and top predator equal to 10³ to strongly couple the two populations and make them equivalent to a unique population. Finally, Rooney et al. (2006) did not consider self-regulation and biomass was distributed in a trophic cascade pattern in their model (see Supplementary Figure S1-3C), thus we study our model for εa = 10 and ma = 10 to have similar characteristics.

FIGURE 9

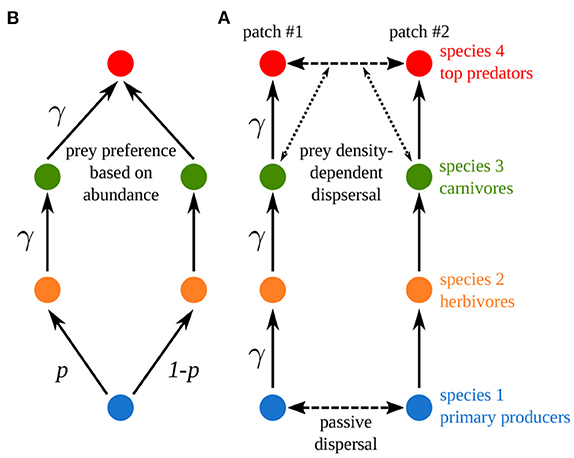
Figure 9. Comparison between (A) Rooney et al.'s and (B) our metacommunity model. γ is the asymmetry of interaction strength and p the fraction of nutrients taken up by resource species in food chain #1 (p = 0.5). Four species are considered: primary producers (species 1), herbivores (species 2), carnivores (species 3) and top predators (species 4).

Rooney et al. (2006) only considered perturbations of top predators but here, we also consider perturbations affecting their prey to understand how the coupling described in Rooney et al. (2006) transmits perturbations across space. When top predators (species 4) are perturbed, their population dynamics are strongly correlated (Figure 10A) because the passive component of dispersal (i.e., imbalance in top predator biomass distribution among patches) prevails due to rapid dispersal ($d_4=10^3$) while the transmission to carnivores (species 3) through trophic interactions is slower (ma = 10). This correlation of top predators leads to the correlation of carnivore because of the synchronous top-down transmission of perturbations in both patches. The observed decrease in synchrony with asymmetry of interaction strength γ is due to the slight difference in the dynamics of the two patches.

FIGURE 10

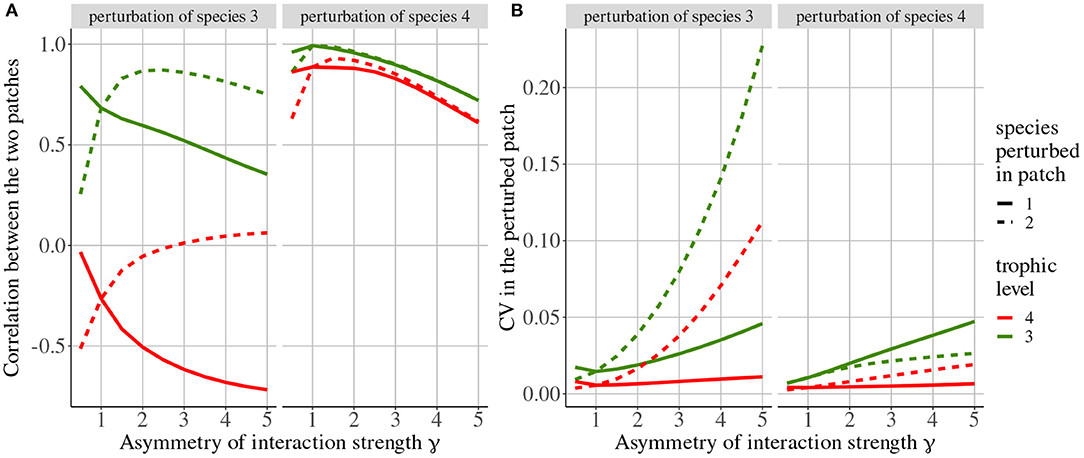
Figure 10. Response of the metacommunity to stochastic perturbations depending on asymmetry of interaction strength γ and the perturbed species (top label). Line types represent the patch where species are perturbed. (A) Correlation between populations of top predators (species 4 in red) and carnivores (species 3 in green). (B) Coefficient of variation of biomass of top predators and carnivores in the patch where perturbations occur (i.e., if top predators are perturbed in patch #1, we only display the biomass CV of species in patch #1).

When carnivores (species 3) are perturbed, their population dynamics are correlated while the dynamics of the top predator (species 4) are anti-correlated (Figure 10A), in accordance with the results of the model with density-dependent dispersal alone (Figure 4). Indeed, when carnivores are perturbed, their biomass CV is higher than that of top predators (Figure 10B), and the dispersal of top predators is governed by their prey density-dependent component.

Increasing the asymmetry of interaction strength γ affects several aspects of the metacommunity. First, it alters the biomass distribution in the metacommunity. Because of increased interaction strength in patch #1, primary producers (species 1) are heavily predated in patch #1, which acts as a sink, while patch #2 is a source. Thus, the biomass of all consumers is higher in patch #1 than in patch #2 (Figure 11A). The biomass of all species is higher than in the same food chain without dispersal in patch #1, while it is lower in patch #2 (Figure 11B). Second, increasing γ decreases the correlation of carnivore dynamics (species 3) when they are perturbed in patch #1, while it mostly increases this correlation when carnivores are perturbed in patch #2 (Figure 10A). This result is in contradiction with the results of the model with asymmetry alone that predicts the opposite (Figure 4). This discrepancy is explained by the interaction between the effects of density-dependent dispersal and spatial heterogeneity. For instance, when carnivores are perturbed in patch #1 (Figure 12A ①), perturbations are directly transmitted in patch #2 by density-dependent dispersal (vertical trophic transmission is bypassed, see Figures 5, 12A ②). Then, weak trophic interactions in patch #2, because of low interaction strength and low biomass (Figure 11), poorly transmit perturbations and decrease the correlation between the two populations of carnivores (Figure 12A ③). Conversely, strong trophic interactions in patch #1 permit a good transmission of perturbations and lead to the strong correlation of the two populations of carnivores when they are perturbed in patch #2 (Figure 11B ③). To sum up, because of density-dependent dispersal, perturbations bypass the vertical transmission in the patch where they occur and directly affect the other patch where vertical transmission matters. This is different from Pierre et al. (In prep.), who found that the vertical transmission of perturbations in the perturbed patch was central to determine correlation patterns. Therefore, the swap of the patch where vertical transmission of perturbations matters due to density-dependent dispersal explains the discrepancies between Figures 7, 10A.

FIGURE 11

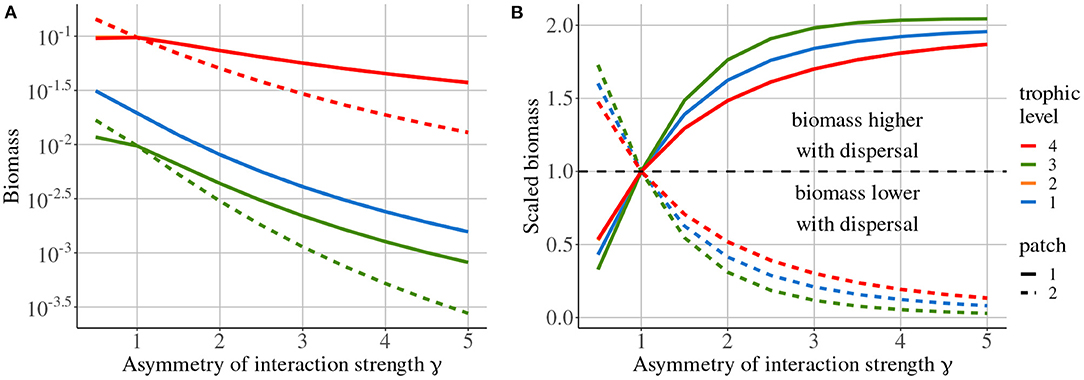
Figure 11. Biomass distribution depending on asymmetry of interaction strength γ. (A) Absolute biomass of each species in each patch. (B) Biomass scaled to the biomass measured in a metacommunity without dispersal. Note that the curves of species 2 are not missing but simply overlap with the curves of species 4.

FIGURE 12

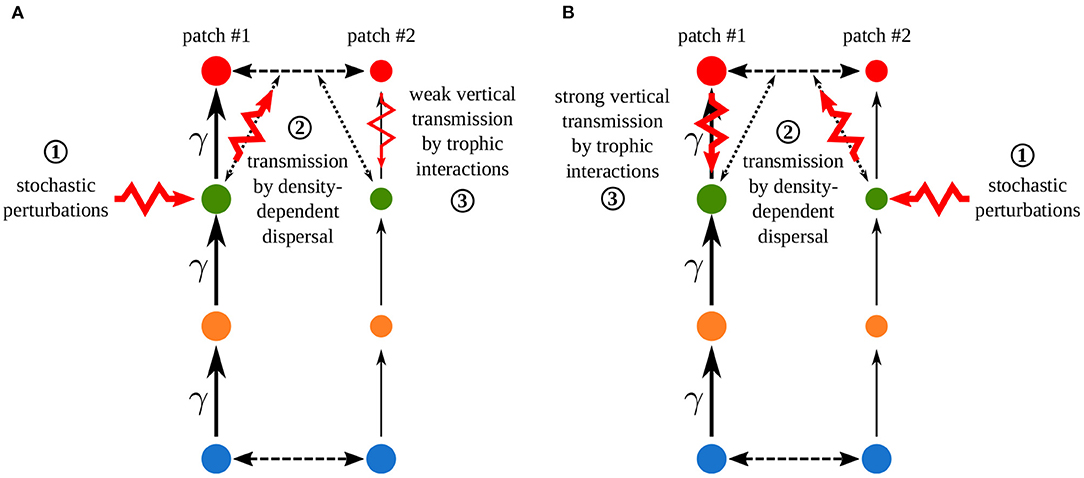
Figure 12. Crossed effects of density-dependent dispersal and asymmetry of interaction strength γ when carnivores are perturbed (A) in patch #1 or (B) in patch #2. Synchrony is explained by the successive steps of perturbation propagation across the metacommunity. ① Direct stochastic perturbation of carnivores in one patch. ② Horizontal transmission to the other patch by density-dependent dispersal that bypasses vertical transmission in the perturbed patch. ③ Vertical transmission in the other patch through trophic interactions. This vertical transmission is stronger in patch #1 than in patch #2 because of the high biomasses (disc size) and the interaction strength, which is γ times higher in patch #1 than in patch #2, which leads to strong trophic interactions (arrow size).

Discussion

In this paper, we have presented a broad overview of the mechanisms that govern synchrony in metacommunities affected by perturbations in the vicinity of equilibrium. Fundamentally, in a homogeneous metacommunity with passive dispersal, which is our null model of metacommunity, passive dispersal correlates the dynamics of the dispersing species and transmits perturbations between patches. Thus, perturbations have a bottom-up transmission in one patch and a top-down transmission in the other patch (Figures 3B, 13A), which leads to different correlation patterns in each patch. Then, comparing these intra-patch correlation patterns is enough to predict the inter-patch correlation patterns (i.e., the correlation of the dynamics of population belonging to different patches). We have detailed two mechanisms that alter these fundamental rules: density-dependent dispersal and spatial heterogeneity. First, if dispersal depends on the biomass density of other species, perturbations can affect the dispersing species directly and bypass the classic vertical transmission through trophic interactions (Figures 5B, 13B). In this case, correlation patterns can be opposite to those predicted by the null model, which only consider passive dispersal (Figure 4). Second, if space is heterogeneous, with different interaction strengths in the two patches in our case, perturbations are either transmitted strongly in the patch where interaction strength is high or weakly transmitted in the patch where interaction strength is low (Figures 8, 13C). The correlation of the dynamics of the two populations of the perturbed species depends on which patch is perturbed: perturbing the patch with low interaction strength decreases the correlation while perturbing the patch with high interaction strength increases the correlation compared with that predicted by a model with an homogeneous space (Figure 7). Finally, combining density-dependent dispersal and spatial heterogeneity leads to the reversal of the effect of heterogeneity on synchrony. In fact, density-dependent dispersal bypasses the vertical transmission of perturbations in the perturbed patch and transmits perturbations to the other patch directly, where vertical transmission matters (Figure 12).

FIGURE 13

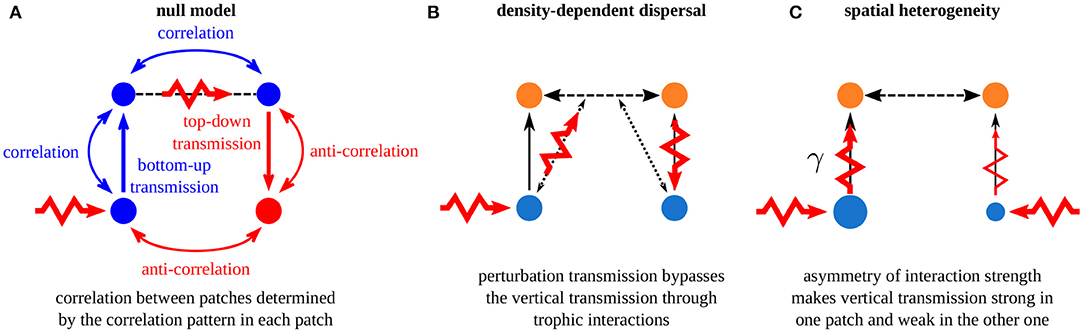
Figure 13. Summary of the mechanisms governing synchrony in metacommunities. (A) Fundamental rules of perturbation transmission in a homogeneous metacommunity with passive dispersal. (B) Density-dependent dispersal alters the horizontal transmission of perturbations. (C) Spatial asymmetry alters the biomass densities and the vertical transmission of perturbations in each patch.

Contribution of Models to Explain Synchrony

Dispersal is a complex process that has received much attention in the last two decades in order to understand the dynamics of metacommunities. Many mechanisms have been identified (Amarasekare, 2008; Gross et al., 2020), but most of them have been studied with different models (metacommunity or coupled food webs) displaying different dynamical regimes (equilibrium or limit cycles) and with different measures of stability (asymptotic resilience, occurrence of Hopf bifurcation, or temporal variability). Here, we propose a general framework based on a food web model that covers a broad range of ecological contexts, which enables us to derive robust conclusions. In addition, the flexibility of the model, which can be easily modified, and the use stochastic perturbations, which can target specific trophic levels in a particular patch, enable us to have a deep understanding of the mechanisms acting in the metacommity. Most previous studies described the factors governing synchrony and stability without explaining the mechanisms underlying the observed effects. For instance, Hauzy et al. (2010) and Rooney et al. (2006) did not explain how density-dependent dispersal and asymmetry affect synchrony.

Our model fills this gap: it is easy to handle because it is linearised and most of the mechanisms have additive effects. For instance, the effects of density-dependent dispersal and spatial heterogeneity can be disentangled properly. It appears that spatial heterogeneity has a weaker effect on predator (species 3) synchrony than density-dependent dispersal since the overall correlation of their populations is qualitatively similar to that obtained in a model with density-dependent dispersal only. Thus, in Rooney et al. (2006) model, prey preference is the major driver of synchrony and structural asymmetry, which is how they defined spatial heterogeneity, has minor effects. The comparison with Rooney et al.'s (2006) model stresses the continuum between coupled food chains and metacommunities. Many studies consider a unique population of mobile top predators feeding on two distinct energetic channels (Post et al., 2000; McCann et al., 2005; Rooney et al., 2006; Vasseur and Fox, 2007; Attayde and Ripa, 2008), but these models are actually a limiting case of a metacommunity in which top predators have a density-dependent dispersal and a high dispersal rate.

Our results based on a two-patch metacommunity may well explains what would happen in a larger landscape with many patches since the overall response to perturbations would be the additive effect of pairwise connections between patches. Synchrony in multi-patch metacommunities has been addressed by models with limit cycles (Marleau et al., 2014; Hayes and Anderson, 2018), but the response of such large metacommunities to perturbations remains to be explored.

Trophic Context of Dispersal

Synchrony in metacommunities is tightly linked to trophic interactions and biomass distribution. Barbier and Loreau (2019) and Quévreux et al. (2021a) showed that perturbations tend to have a bottom-up (top-down) transmission when biomass pyramid is bottom (top) heavy. This is mostly due to the distribution of metabolic rates among species: when m is high, high trophic levels have a faster metabolic rate than lower trophic levels, which accelerates their biomass dynamics (Equation 8b). Thus, these fast top predators will quickly dampen perturbations while perturbed lower trophic levels with a slower pace of life will have a stronger impact on the rest of the food chain. In addition, some types of perturbations can affect species depending on their abundance. Arnoldi et al. (2019) showed that immigration perturbations strongly affect rare species while environmental perturbations strongly affect abundant species. Demographic perturbations are generally used because they affect species with the same intensity regardless of their biomass but environmental perturbations are more relevant from an ecological point of view. Thus, synchrony in metacommunities under environmental stressors affecting every species may be more easily understood by tracking the transmission of perturbations affecting the most abundant species.

The effect of dispersal is conditioned indirectly by trophic dynamics. Quévreux et al. (2021a) showed that perturbation transmission depends on the relative importance of dispersal compared with the other local demographic processes. Thus, in a metacommunity, dispersal will have the biggest impact not on the species with the highest dispersal rate but on the species for whom dispersal has the highest relative contribution to biomass dynamics. This distinction is critical because many studies reported that the dispersal of particular trophic levels is stabilizing (Koelle and Vandermeer, 2005; Pedersen et al., 2016).

The trophic context of dispersal is even more important for density-dependent dispersal. Quévreux et al. (2021c) showed that vertical transmission through trophic interactions is bypassed only if the species interacting with the dispersing species have a higher biomass CV than the dispersing species (Figure 5A). Species biomass CV depends on perturbation intensity but also on its transmission across the food chain. Shanafelt and Loreau (2018) demonstrated that in food chains displaying a trophic cascade, species experiencing a strong top-town control have a high biomass CV because they have a low biomass. Thus, trophic cascades also translate into stability cascades with species being more or less stable depending on their trophic position. In the case of density-dependent dispersal, these rare species should have a major impact on dispersal in many situations.

Finally, we were able to draw general conclusions from the wide range of responses displayed by the model. A key factor of Barbier and Loreau (2019) model is self-regulation, which encapsulates various negative intra-specific interactions such as territoriality, cannibalism and disease transmission that lead to a density-dependent mortality rate. Self-regulation remains neglected in many food web models, although it has been identified in natural marine phytoplankton communities (Picoche and Barraquand, 2020), where it promotes species coexistence (Picoche and Barraquand, 2019) and food web stability (Barabás et al., 2017) by dampening interspecific interactions relative to intraspecific interactions. Thus, self-regulation definitively interferes with dispersal and must be taken into account in future metacommunity models.

Equilibrium and Nonequilibrium Dynamics

As we explained above, our model is easy to handle because it is linearised and thus most of its responses to perturbations have additive effects. However, this may not hold with systems that are not at equilibrium or subject to perturbations pushing them to far from equilibrium. For instance, Post et al. (2000), McCann et al. (2005), Hauzy et al. (2010), and Marleau et al. (2014) did not consider self-regulation and their food web models were characterized by strong inter-specific interactions leading to limit cycles.

In systems with limit cycles, phase-locking, which is a constant phase difference between patches through time, can occur and lead to emergent metacommunity properties (Jansen, 1999; Lloyd and May, 1999). For instance, Goldwyn and Hastings (2009) showed that even a 0.1% variation in species parameters among patches (small spatial heterogeneity) is enough to generate substantial asynchrony. Two components of the structure of the metacommunity are critical for its stability. First, the dispersal of particular trophic levels determines the occurrence of limit cycles and the synchrony of their phase (Koelle and Vandermeer, 2005; Hauzy et al., 2010; Pedersen et al., 2016). Second, in spatially explicit metacommunities, connectivity between patches (Guichard et al., 2019) and their spatial organization (Marleau et al., 2014; Hayes and Anderson, 2018) drive phase synchrony. For instance, in riverine metacommunities, patch linked to multiple upstream and downstream patches have communities with less temporal variability (Anderson and Hayes, 2018).

These responses of oscillating systems are not disconnected from responses to stochastic perturbations. Vasseur and Fox (2007) demonstrated that small synchronous stochastic perturbations can continuously deviate the system from its regular oscillations and dampen predator dynamics. Thus, stochastic perturbations and limit cycles can strongly interact to drive food web stability. Finally, in systems at equilibrium but with strong predator-prey interactions (high values of εa and ma), perturbations lead to dampened oscillations (see Rooney et al., 2006 and Supplementary Figure S1-2). Large perturbations affecting this kind of system could then lead to responses at the interface between stochastic perturbations and limit cycles. Thus, the theoretical framework used to understand synchrony in systems with limit cycles may be used in future studies to understand the response to perturbations of systems close to the Hopf bifurcation.

Empirical Testing

Theoretical models help us to understand the response of ecosystems to perturbations, but empirical tests are required to confirm the effects of the described mechanisms in real systems. Fortunately, empiricists have already developed methods and equipments for manipulating metacommunities. Microcosms offer immense possibilities because of their high level of control, as extensively described by Altermatt et al. (2015). Bacteria and protists represent huge populations with predator-prey dynamics that can be quantified efficiently by flow cytometry and image analysis to record fine scale times series (Vasseur and Fox, 2009; Fox et al., 2013). For instance, Vasseur and Fox (2009) manually drove dispersal by pipetting medium from one microcosm to another and applied stochastic perturbations by randomly changing temperature. Harvey et al. (2016) and Harvey et al. (2020) coupled microcosms by exchanging subsidies (microwaved aliquots of medium) and oriented dispersal by asymmetric transfer of medium between microcosms.

Larger facilities are required to perform experiments with populations of large mobile organisms such as flying insects and vertebrates. The terrestrial metatron consists of 48 interconnected caged patches (10 × 10 × 2 m) where temperature, humidity and illuminance can be controlled (Legrand et al., 2012). There, Fronhofer et al. (2018) measured density-dependent dispersal of butterflies and damselflies in the presence of predators such as toads and frogs. Its aquatic equivalent consists of 144 basins of 2 m³ each that can be connected by aquatic or aerial corridors and in which temperature can be controlled. The PLANAQUA experimental facility includes an aquatic macrocosm platform consisting of 16 artificial lakes with an individual volume of 700 m³, connected to each other by dispersal corridors, and equipped with an automated instrumentation (Mougin et al., 2015). With such a platform, long-term experiments with large fish populations can be performed in a controlled environment, which is close to a natural shallow pond integrating littoral, benthic, and pelagic zones. However, a strong sampling effort is required to get the time series of predator-prey dynamics and assess their temporal stability (Rakowski et al., 2019).

Adding the Ecosystem Perspective

We summarized a few mechanisms that govern synchrony in metacommunities but these mechanisms are population centered and do not account for the rest of the ecosystem. Ecosystems are linked by flows of matter and energy (Gruber and Galloway, 2008; Gounand et al., 2018b), turning metacommunities into metaecosystems (Loreau et al., 2003; Massol et al., 2011; Guichard, 2017; Gounand et al., 2018a). Nutrient cycling strongly affects ecosystem dynamics (DeAngelis, 1992; Loreau, 1994, 2010; Quévreux et al., 2021b) and the response of local ecosystems to perturbations (Theis et al., 2022). Nutrient flows between ecosystems create subsidies that alter local dynamics and can be destabilizing by increasing the amplitude of biomass oscillations (Marleau et al., 2010), while the dispersal of particular trophic levels in such metaecosystems can dampen these negative effect (Leroux and Loreau, 2012; Gounand et al., 2014). However, the general response of metaecosystems to stochastic perturbations is yet to be studied.

Conclusion

In the context of global changes, in a world where habitat is fragmented and subject to anthropogenic perturbations, understanding the drivers of species dispersal and how spatial structure shapes the dynamics at landscape scale are crucial for conservation policies. The metacommunity framework is a powerful tool to achieve this goal because it enables us to disentangle the various mechanisms governing the synchrony of species dynamics at local and regional scales. This paper has summarized some aspects of metacomminities such as density-dependent dispersal and spatial heterogeneity, which are key to predict the response of metacommunities to perturbations. These mechanisms can be studied in isolation and their individual effects can be added up to have an insight in the response of realistic metacommunity to perturbations. Ultimately, our results help us to identify the species and the patches for which perturbations must be mitigated to improve stability at local and regional scales.

Author Contributions

PQ and ML conceptualized the study. ML acquired the funding and revised and edited the manuscript. PQ performed the analysis and wrote the manuscript. Both authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the TULIP Laboratory of Excellence (ANR-10-LABX-41) and by the BIOSTASES Advanced Grant, funded by the European Research Council under the European Union's Horizon 2020 research and innovation programme (666971).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Neil Rooney and Kevin McCann for their help in reproducing their results and Bart Haegeman for his wise remarks and advice.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.865398/full#supplementary-material

References

Altermatt, F., Fronhofer, E. A., Garnier, A., Giometto, A., Hammes, F., Klecka, J., et al. (2015). Big answers from small worlds: a user's guide for protist microcosms as a model system in ecology and evolution. Methods Ecol. Evolut. 6, 218–231. doi: 10.1111/2041-210X.12312

CrossRef Full Text | Google Scholar

Amarasekare, P. (2008). Spatial dynamics of keystone predation. J. Anim. Ecol. 77, 1306–1315. doi: 10.1111/j.1365-2656.2008.01439.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, K. E., and Hayes, S. M. (2018). The effects of dispersal and river spatial structure on asynchrony in consumer-resource metacommunities. Freshw Biol. 63, 100–113. doi: 10.1111/fwb.12998

CrossRef Full Text | Google Scholar

Arnold, L. (1974). Stochastic Differential Equations: Theory and Applications. New York, NY: Wiley.

Google Scholar

Arnoldi, J., Bideault, A., Loreau, M., and Haegeman, B. (2018). How ecosystems recover from pulse perturbations: a theory of short- to long-term responses. J. Theor. Biol. 436, 79–92. doi: 10.1016/j.jtbi.2017.10.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Arnoldi, J., Loreau, M., and Haegeman, B. (2016). Resilience, reactivity and variability: a mathematical comparison of ecological stability measures. J. Theor. Biol. 389, 47–59. doi: 10.1016/j.jtbi.2015.10.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Arnoldi, J., Loreau, M., and Haegeman, B. (2019). The inherent multidimensionality of temporal variability: how common and rare species shape stability patterns. Ecol. Lett. 22, 1557–1567. doi: 10.1111/ele.13345

PubMed Abstract | CrossRef Full Text | Google Scholar

Attayde, J. L., and Ripa, J. (2008). The coupling between grazing and detritus food chains and the strength of trophic cascades across a gradient of nutrient enrichment. Ecosystems 11, 980–990. doi: 10.1007/s10021-008-9174-8

CrossRef Full Text | Google Scholar

Barabás, G., Michalska-Smith, M. J., and Allesina, S. (2017). Self-regulation and the stability of large ecological networks. Nat. Ecol. Evolut. 1, 1870–1875. doi: 10.1038/s41559-017-0357-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Barbier, M., and Loreau, M. (2019). Pyramids and cascades: a synthesis of food chain functioning and stability. Ecol. Lett. 22, 405–419. doi: 10.1111/ele.13196

PubMed Abstract | CrossRef Full Text | Google Scholar

Blasius, B., Huppert, A., and Stone, L. (1999). Complex dynamics and phase synchronization in spatially extended ecological systems. Nature 399, 354–359. doi: 10.1038/20676

PubMed Abstract | CrossRef Full Text | Google Scholar

DeAngelis, D. L. (1992). Dynamics of Nutrient Cycling and Food Webs. Number 9 in Population and Community Biology Series, 1st Edn. London: Chapman & Hall.

Google Scholar

Díaz, S., Settele, J., Brondizio, E., Ngo, H. T., Guèze, M., Agard, J., et al. (2019). Summary for Policymakers of the Global Assessment Report on BIodiversity and Ecosystem Services of the Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services. Bonn: IPBES.

Google Scholar

Fox, J. W., Legault, G., Vasseur, D. A., and Einarson, J. A. (2013). Nonlinear effect of dispersal rate on spatial synchrony of predator-prey cycles. PLoS ONE 8, e79527. doi: 10.1371/journal.pone.0079527

PubMed Abstract | CrossRef Full Text | Google Scholar

Fronhofer, E. A., Klecka, J., Melián, C. J., and Altermatt, F. (2015). Condition-dependent movement and dispersal in experimental metacommunities. Ecol. Lett. 18, 954–963. doi: 10.1111/ele.12475

PubMed Abstract | CrossRef Full Text | Google Scholar

Fronhofer, E. A., Legrand, D., Altermatt, F., Ansart, A., Blanchet, S., Bonte, D., et al. (2018). Bottom-up and top-down control of dispersal across major organismal groups. Nat. Ecol. Evolut. 2, 1859–1863. doi: 10.1038/s41559-018-0686-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Furey, N. B., Armstrong, J. B., Beauchamp, D. A., and Hinch, S. G. (2018). Migratory coupling between predators and prey. Nat. Ecol. Evolut. 2, 1846–1853. doi: 10.1038/s41559-018-0711-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldwyn, E. E., and Hastings, A. (2009). Small heterogeneity has large effects on synchronization of ecological oscillators. Bull. Math. Biol. 71, 130–144. doi: 10.1007/s11538-008-9355-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Gounand, I., Harvey, E., Little, C. J., and Altermatt, F. (2018a). Meta-Ecosystems 2.0: rooting the theory into the field. Trends Ecol. Evolut. 33, 36–46. doi: 10.1016/j.tree.2017.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Gounand, I., Little, C. J., Harvey, E., and Altermatt, F. (2018b). Cross-ecosystem carbon flows connecting ecosystems worldwide. Nat. Commun. 9, 4825. doi: 10.1038/s41467-018-07238-2

PubMed Abstract | CrossRef Full Text

Gounand, I., Mouquet, N., Canard, E., Guichard, F., Hauzy, C., and Gravel, D. (2014). The paradox of enrichment in metaecosystems. Am. Nat. 184, 752–763. doi: 10.1086/678406

PubMed Abstract | CrossRef Full Text | Google Scholar

Gross, T., Allhoff, K. T., Blasius, B., Brose, U., Drossel, B., Fahimipour, A. K., et al. (2020). Modern models of trophic meta-communities. Philos. Trans. R. Soc. B Biol. Sci. 375, 20190455. doi: 10.1098/rstb.2019.0455

PubMed Abstract | CrossRef Full Text | Google Scholar

Gruber, N., and Galloway, J. N. (2008). An Earth-system perspective of the global nitrogen cycle. Nature 451, 293–296. doi: 10.1038/nature06592

PubMed Abstract | CrossRef Full Text | Google Scholar

Guichard, F. (2017). Recent advances in metacommunities and meta-ecosystem theories. F1000Research 6, 610. doi: 10.12688/f1000research.10758.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Guichard, F., Zhang, Y., and Lutscher, F. (2019). The emergence of phase asynchrony and frequency modulation in metacommunities. Theor. Ecol. 12, 329–343. doi: 10.1007/s12080-018-0398-8

CrossRef Full Text | Google Scholar

Haddad, N. M., Brudvig, L. A., Clobert, J., Davies, K. F., Gonzalez, A., Holt, R. D., et al. (2015). Habitat fragmentation and its lasting impact on Earth's ecosystems. Sci. Adv. 1, e1500052. doi: 10.1126/sciadv.1500052

PubMed Abstract | CrossRef Full Text | Google Scholar

Haegeman, B., Arnoldi, J.-F., Wang, S., de Mazancourt, C., Montoya, J. M., and Loreau, M. (2016). Resilience, invariability, and ecological stability across levels of organization. bioRxiv. doi: 10.1101/085852

CrossRef Full Text | Google Scholar

Haegeman, B., and Loreau, M. (2011). A mathematical synthesis of niche and neutral theories in community ecology. J. Theor. Biol. 269, 150–165. doi: 10.1016/j.jtbi.2010.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Harman, R. R., Goddard, J., Shivaji, R., and Cronin, J. T. (2020). Frequency of occurrence and population-dynamic consequences of different forms of density-dependent emigration. Am. Nat. 195, 851–867. doi: 10.1086/708156

PubMed Abstract | CrossRef Full Text | Google Scholar

Harvey, E., Gounand, I., Fronhofer, E. A., and Altermatt, F. (2020). Metaecosystem dynamics drive community composition in experimental, multi-layered spatial networks. Oikos 129, 402–412. doi: 10.1111/oik.07037

CrossRef Full Text | Google Scholar

Harvey, E., Gounand, I., Ganesanandamoorthy, P., and Altermatt, F. (2016). Spatially cascading effect of perturbations in experimental meta-ecosystems. Proc. R. Soc. B Biol. Sci. 283, 20161496. doi: 10.1098/rspb.2016.1496

PubMed Abstract | CrossRef Full Text | Google Scholar

Hauzy, C., Gauduchon, M., Hulot, F. D., and Loreau, M. (2010). Density-dependent dispersal and relative dispersal affect the stability of predator-prey metacommunities. J. Theor. Biol. 266, 458–469. doi: 10.1016/j.jtbi.2010.07.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Hauzy, C., Hulot, F. D., Gins, A., and Loreau, M. (2007). Intra-and interspecific density-dependent dispersal in an aquatic prey-predator system. J. Anim. Ecol. 76, 552–558. doi: 10.1111/j.1365-2656.2007.01227.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hayes, S. M., and Anderson, K. E. (2018). Beyond connectivity: how the structure of dispersal influences metacommunity dynamics. Theor. Ecol. 11, 151–159. doi: 10.1007/s12080-017-0355-y

CrossRef Full Text | Google Scholar

Jacob, S., Bestion, E., Legrand, D., Clobert, J., and Cote, J. (2015). Habitat matching and spatial heterogeneity of phenotypes: implications for metapopulation and metacommunity functioning. Evol. Ecol. 29, 851–871. doi: 10.1007/s10682-015-9776-5

CrossRef Full Text | Google Scholar

Jansen, V. A. A. (1999). Phase locking: another cause of synchronicity in predator-prey systems. Trends Ecol. Evolut. 14, 278–279. doi: 10.1016/S0169-5347(99)01654-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Koelle, K., and Vandermeer, J. (2005). Dispersal-induced desynchronization: from metapopulations to metacommunities. Ecol. Lett. 8, 167–175. doi: 10.1111/j.1461-0248.2004.00703.x

CrossRef Full Text | Google Scholar

Lande, R., Engen, S., and Saether, B.-E. (2003). Stochastic Population Dynamics in Ecology and Conservation. Oxford: Oxford University Press.

Google Scholar

Legrand, D., Guillaume, O., Baguette, M., Cote, J., Trochet, A., Calvez, O., et al. (2012). The Metatron: an experimental system to study dispersal and metaecosystems for terrestrial organisms. Nat. Methods 9, 828–833. doi: 10.1038/nmeth.2104

PubMed Abstract | CrossRef Full Text | Google Scholar

Leibold, M. A., and Chase, J. M. (2017). Metacommunity Ecology, volume 59 of Monographs in Population Biology. Princeton, NJ: Princeton University Press.

Google Scholar

Leibold, M. A., Holyoak, M., Mouquet, N., Amarasekare, P., Chase, J. M., Hoopes, M. F., et al. (2004). The metacommunity concept: a framework for multi-scale community ecology. Ecol. Lett. 7, 601–613. doi: 10.1111/j.1461-0248.2004.00608.x

CrossRef Full Text | Google Scholar

Leroux, S. J., and Loreau, M. (2012). Dynamics of reciprocal pulsed subsidies in local and meta-ecosystems. Ecosystems 15, 48–59. doi: 10.1007/s10021-011-9492-0

CrossRef Full Text | Google Scholar

Li, Z.-Z., Gao, M., Hui, C., Han, X.-Z., and Shi, H. (2005). Impact of predator pursuit and prey evasion on synchrony and spatial patterns in metapopulation. Ecol. Modell. 185, 245–254. doi: 10.1016/j.ecolmodel.2004.12.008

CrossRef Full Text | Google Scholar

Liu, Z., Zhang, F., and Hui, C. (2016). Density-dependent dispersal complicates spatial synchrony in tri-trophic food chains. Popul. Ecol. 58, 223–230. doi: 10.1007/s10144-015-0515-0

CrossRef Full Text | Google Scholar

Lloyd, A. L., and May, R. M. (1999). Synchronicity, chaos and population cycles: spatial coherence in an uncertain world. Trends Ecol. Evolut. 14, 417–418. doi: 10.1016/S0169-5347(99)01717-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Loreau, M. (1994). Material cycling and the stability of ecosystems. Am. Nat. 143, 508–513. doi: 10.1086/285616

CrossRef Full Text | Google Scholar

Loreau, M. (2010). “Material cycling and the overall functioning of ecosystems,” in From Populations to Ecosystems: Theoretical Foundations for a New Ecological Synthesis, Volume 46 of Monographs in Population Biology (Princeton, NJ: Princeton University Press), 164–195.

PubMed Abstract

Loreau, M., and de Mazancourt, C. (2008). Species synchrony and its drivers: neutral and nonneutral community dynamics in fluctuating environments. Am. Nat. 172, E48-E66. doi: 10.1086/589746

PubMed Abstract | CrossRef Full Text | Google Scholar

Loreau, M., Mouquet, N., and Holt, R. D. (2003). Meta-ecosystems: a theoretical framework for a spatial ecosystem ecology. Ecol. Lett. 6, 673–679. doi: 10.1046/j.1461-0248.2003.00483.x

CrossRef Full Text | Google Scholar

Marleau, J., Guichard, F., and Loreau, M. (2014). Meta-ecosystem dynamics and functioning on finite spatial networks. Proc. R. Soc. B Biol. Sci. 281, 20132094. doi: 10.1098/rspb.2013.2094

PubMed Abstract | CrossRef Full Text | Google Scholar

Marleau, J. N., Guichard, F., Mallard, F., and Loreau, M. (2010). Nutrient flows between ecosystems can destabilize simple food chains. J. Theor. Biol. 266, 162–174. doi: 10.1016/j.jtbi.2010.06.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Massol, F., Gravel, D., Mouquet, N., Cadotte, M. W., Fukami, T., and Leibold, M. A. (2011). Linking community and ecosystem dynamics through spatial ecology. Ecol. Lett. 14, 313–323. doi: 10.1111/j.1461-0248.2011.01588.x

PubMed Abstract | CrossRef Full Text | Google Scholar

McCann, K. S. (2000). The diversity-stability debate. Nature 405, 228–233. doi: 10.1038/35012234

PubMed Abstract | CrossRef Full Text | Google Scholar

McCann, K. S., Rasmussen, J. B., and Umbanhowar, J. (2005). The dynamics of spatially coupled food webs. Ecol. Lett. 8, 513–523. doi: 10.1111/j.1461-0248.2005.00742.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Mougin, C., Azam, D., Caquet, T., Cheviron, N., Dequiedt, S., Le Galliard, J.-F., et al. (2015). A coordinated set of ecosystem research platforms open to international research in ecotoxicology, AnaEE-France. Environ. Sci. Pollut. Res. 22, 16215–16228. doi: 10.1007/s11356-015-5233-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Olff, H., Alonso, D., Berg, M. P., Eriksson, B. K., Loreau, M., Piersma, T., et al. (2009). Parallel ecological networks in ecosystems. Philos. Trans. R. Soc. B Biol. Sci. 364, 1755–1779. doi: 10.1098/rstb.2008.0222

PubMed Abstract | CrossRef Full Text | Google Scholar

Pedersen, E. J., Marleau, J. N., Granados, M., Moeller, H. V., and Guichard, F. (2016). Nonhierarchical dispersal promotes stability and resilience in a tritrophic metacommunity. Am. Nat. 187, E116-E128. doi: 10.1086/685773

PubMed Abstract | CrossRef Full Text | Google Scholar

Picoche, C., and Barraquand, F. (2019). How self-regulation, the storage effect, and their interaction contribute to coexistence in stochastic and seasonal environments. Theor. Ecol. 12, 489–500. doi: 10.1007/s12080-019-0420-9

CrossRef Full Text | Google Scholar

Picoche, C., and Barraquand, F. (2020). Strong self-regulation and widespread facilitative interactions in phytoplankton communities. J. Ecol. 108, 2232–2242. doi: 10.1111/1365-2745.13410

CrossRef Full Text | Google Scholar

Pierre, Q., Bart, H., and Michel, L. Spatial heterogeneity of interaction strength has constrasting effects on synchrony and stability in trophic metacommunities.

Post, D. M., Conners, M. E., and Goldberg, D. S. (2000). Prey preference by a top-predator and the stability of linked food chains. Ecology 81, 8–14. doi: 10.1890/0012-9658(2000)081[0008:PPBATP]2.0.CO;2

CrossRef Full Text | Google Scholar

Quévreux, P., Barbier, M., and Loreau, M. (2021a). Synchrony and perturbation transmission in trophic metacommunities. Am. Naturalist 197, 714131. doi: 10.1101/2020.01.21.914093

PubMed Abstract | CrossRef Full Text | Google Scholar

Quévreux, P., Barot, S., and Thébault, L. (2021b). Interplay between the paradox of enrichment and nutrient cycling in food webs. Oikos 130, 95–109. doi: 10.1111/oik.07937

CrossRef Full Text | Google Scholar

Quévreux, P., Pigeault, R., and Loreau, M. (2021c). Predator avoidance and foraging for food shape synchrony and response to perturbations in trophic metacommunities. J. Theor. Biol. 528, 110836. doi: 10.1016/j.jtbi.2021.110836

PubMed Abstract | CrossRef Full Text | Google Scholar

Rakowski, C. J., Farrior, C. E., Manning, S. R., and Leibold, M. A. (2019). Predator complementarity dampens variability of phytoplankton biomass in a diversity-stability trophic cascade. bioRxiv. doi: 10.1101/851642

PubMed Abstract | CrossRef Full Text | Google Scholar

Rooney, N., McCann, K. S., Gellner, G., and Moore, J. C. (2006). Structural asymmetry and the stability of diverse food webs. Nature 442, 265–269. doi: 10.1038/nature04887

PubMed Abstract | CrossRef Full Text | Google Scholar

Shanafelt, D. W., and Loreau, M. (2018). Stability trophic cascades in food chains. R. Soc. Open Sci. 5, 180995. doi: 10.1098/rsos.180995

PubMed Abstract | CrossRef Full Text | Google Scholar

Theis, K., Quévreux, P., and Loreau, M. (2022). Nutrient cycling and self-regulation determine food web stability. Funct. Ecol. 36, 202–213. doi: 10.1111/1365-2435.13961

CrossRef Full Text | Google Scholar

Vadeboncoeur, Y., McCann, K. S., Zanden, M. J. V., and Rasmussen, J. B. (2005). Effects of multi-chain omnivory on the strength of trophic control in lakes. Ecosystems 8, 682–693. doi: 10.1007/s10021-003-0149-5

CrossRef Full Text | Google Scholar

Vasseur, D. A., and Fox, J. W. (2007). Environmental fluctuations can stabilize food web dynamics by increasing synchrony. Ecol. Lett. 10, 1066–1074. doi: 10.1111/j.1461-0248.2007.01099.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Vasseur, D. A., and Fox, J. W. (2009). Phase-locking and environmental fluctuations generate synchrony in a predator-prey community. Nature 460, 1007–1010. doi: 10.1038/nature08208

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, S., Haegeman, B., and Loreau, M. (2015). Dispersal and metapopulation stability. PeerJ 3, e1295. doi: 10.7717/peerj.1295

PubMed Abstract | CrossRef Full Text | Google Scholar