Associational Effects and Indirect Interactions-The Dynamical Effects of Consumer and Resource Traits on Generalist-Resource Interactions

Trophic interaction modifications occur in food webs when the direct or indirect interaction between two species is affected by a third species. These behavioral modification effects are often referred to as associational effects. Changes in focal resource availability and consumption by a generalist herbivore can affect a range of outcomes from resource exclusion to multiple resources coexisting with the focal plant species. Here, we investigate the indirect interaction between a focal and alternative resource mediated by a generalist consumer. Using theoretical approaches we analyse the conceptual link between associational effects (both resistance and susceptibility) and the theory of apparent competition and resource switching. We find that changes in focal resource traits have the potential to affect the long-term outcome of indirect interactions. Inclusion of density-dependence expands generalist life-histories and broadens the range where, through associational effects, the availability of alternative resources positively influence a focal resource. We conclude that different forms of associational effects could, in the long-term, lead to a range of indirect interaction dynamics, including apparent competition and apparent mutualism. Our work aims to connects the theoretical body of work on indirect interactions to the concepts of associational effects. The indirect interactions between multiple resources need more thorough investigation to appreciate the range of associational effects that could result from the dynamical interaction between a generalist consumers and its focal and alternative resources.

1. Introduction

Species exist in complex webs of interactions (Joern and Laws, 2013) and foraging choices by generalist consumers are often found to have a range of indirect effects on the patterns of coexistence of their multiple food resources (Ohgushi, 2005). Indirect effects occur when the effect of one species influences the strength of interaction between other species within interaction webs (Werner and Peacor, 2003) leading to alternative dynamical outcomes (Golubski and Abrams, 2011; Terry et al., 2017). Many ecological processes are affected by within-species behavioral syndromes (Sih et al., 2012) and it is known that these sets of behavioral syndromes could operate in trophic interactions such as indirect interactions. As such, these behaviors (e.g., changes in survival strategies, foraging decisions and/or the occurrence of associational defenses), mediated through functional responses, are mechanisms of trophic interaction modifications (Bolker et al., 2003; Terry et al., 2017).

Modifications of trophic interactions involve behavioral responses of consumers to the availability of alternative resources—the outcome of these interactions are often identified as associational effects (Barbosa et al., 2009; Underwood et al., 2014). The concept of associational effects is used to describe indirect interactions (similar to apparent competition) where the risk of herbivory to a focal plant species depends on the composition of the neighboring plant community (Sato, 2018). Associational effects can be divided into associational resistance and associational susceptibility. Associational resistance refers to the situation where the focal plant receives less damage, whereas associational susceptibility occurs when the focal plant receives more damage, depending on the plant species in the neighborhood (Sato, 2018). Based on a review of the literature, Sato (2018) concludes that the outcomes of these associational effects depends on herbivore behavior and plant trait changes. Furthermore, studies have investigated how neighborhood effects through resource traits, ie. density and frequency of focal resource and neighboring resources, affect consumer load (Hamback et al., 2014; Underwood et al., 2014; Kim, 2017). More recently the effect of resource neighborhood on consumer traits has come under scrutiny, the focus has shifted to consumer foraging behavior as a key-driver of associational effects (Hahn and Orrock, 2016; Verschut et al., 2016). The spatial scale of resource selection (Hamback et al., 2014; Verschut et al., 2018), responses to resource cues (Verschut et al., 2017b) and the physiological state of the consumer (Verschut et al., 2017a) all contribute to the likelihood of the occurrence of associational effects. Hence, mechanisms of associational effects are thought to act through neighborhood effects on resource traits and consumer traits as well as predator load, microclimate and relevant feedbacks (Kim, 2017).

In the context of long-term dynamics, the occurrence of these mechanisms will give rise to indirect interactions between the focal and the alternative resource. The outcome of the indirect interaction is then dependent on the conditions for the establishment of associational effects together with the state and behavior of the consumer and focal resource (Figure 1; Underwood et al., 2014). An anticipated long-term outcome could be either positive or negative apparent competitive interactions; the presence of one resource species could affect the consumer traits altering the interaction of the consumer with the other (alternative) resource (Werner and Peacor, 2003).

FIGURE 1

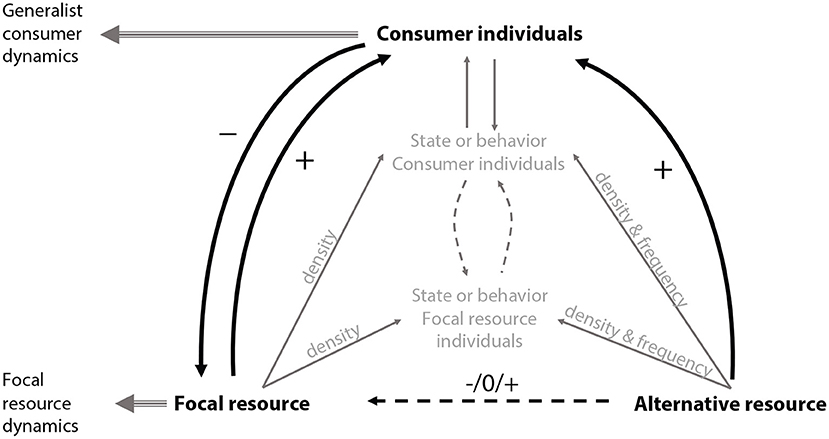
Figure 1. Conceptual figure of the theory of apparent competition (Holt, 1977) and associational effects (Underwood et al., 2014). The black arrows indicate the indirect apparent interactions (+/0/– symbols indicate the direction of direct or indirect effects) and the gray arrows indicate the associational effects of resource neighborhood on indirect interactions between the resources and the effects on the consumers and feedback between the separate factors in the system. The figure does not include feedbacks from the focal resource and the consumer on the alternative resource, as in the case of a generalist consumer, as the alternative resource can be represented by multiple resources.

Underpinning the outcomes of positive and negative apparent interactions are foraging and resource switching decisions by the consumer. These behavioral decisions are also critically important for the occurrence of associational effects (Hahn and Orrock, 2016; Verschut et al., 2017a). Switching resource preferences, where the proportion of resource consumed varies from less to greater than expected, can influence the dynamics of competing (or non-competing) resources (e.g., Oaten and Murdoch, 1975; Hassell, 2000). Although switching might not be an unequivocal mechanism promoting the stability of resource-consumer systems (May, 1977), Holt (1977) suggested that strong switching behavior by generalists may relax apparent competition between resources. van Baalen et al. (2001) explore the conditions for stability and population persistence and conclude that the presence of an alternative resource is not necessarily a determinant for population stability but will, under broader conditions, enable population persistence. Resource switching that relaxes apparent competition will thus influence the associational effect of alternative resource on the focal resource. Within this paradigm, the aim of our work is to link the concept of associational effects to the theory of resource switching by generalist consumers and investigate how this modifies the indirect interactions between the resources (Figure 1).

The scale of generalist foraging (Hassell and Southwood, 1978) related to resource density (Krivan and Eisner, 2003) and quality (Eubanks and Denno, 2000), and their variability (van Baalen et al., 2001), is a key condition for the appearance of associational effects (Figure 1; Hamback et al., 2014; Underwood et al., 2014). For instance, when the consumer has no strict preference for a particular resource the attack rate is mostly determined by the abundance of the alternative resource (Chesson, 1989) and the generalist consumer growth rates are equally influenced by each resource (Holt, 1977). In systems where a consumer interacts with multiple potential resources, resource preference might be determined by other factors than resource abundance. The effect of encounter rate on switching and subsequent coexistence has been investigated under optimal foraging and/or functional response of the generalist (van Baalen et al., 2001; Krivan and Eisner, 2003, 2006; Abrams and Matsuda, 2004). Deviations in handling time and resource quality between focal and alternative resource will lead to persistence of the focal resource given that the quality of the alternative resource is not too low (ie. not eaten) or too high (i.e., deregulate the consumer dynamics; van Baalen et al., 2001). Under optimal foraging decisions by generalist consumers, Krivan and Eisner (2006) showed how top-down population regulation or the combination of both bottom-up and top-down population regulation affects patterns of resource coexistence. If resources are top-down regulated and consumers have inflexible foraging strategies this can result in competitive exclusion of one of the resources. However, if the consumers forage so that they optimize their per capita growth rate, coexistence of both resources is promoted, suggesting that underlying resource dynamics can be important for the outcome of consumer-mediated indirect interactions between resources. Furthermore, the scale of the interaction between alternative resources and foraging generalists has complex consequences for resource-consumer interactions. Specifically, generalist foraging can be modified by neighborhoods and the density of alternative resources (Hahn and Orrock, 2016). The presence of an alternative resource thus has profound implications for the outcomes of coexistence and indirect interactions, and can therefore effect the long-term outcome of dynamics related to associational effects (Kim et al., 2013). When a generalist consumer feeds on multiple resources, apparent competition between resources might arise (Holt, 1977). Empirically, apparent competition is a potent force in the structuring of multi-species assemblages (Holt, 1977; Holt and Lawton, 1993; Chaneton and Bonsall, 2000; Holt and Bonsall, 2017) and has been shown to occur in many systems including host-parasitoid interactions (e.g., Bonsall and Hassell, 1997), marine intertidal ecosystems (e.g., Menge, 1995), host-parasite interactions (Zhang and Buckling, 2016) and plant-herbivore systems (e.g., Hamback and Ekerholm, 1997).

In our study, we approach apparent competition and associational effects as two sides of the same phenomenon. We analyse consumer switching behavior and density dependence, as these are known to affect the outcome of apparent interactions between two resources and a shared consumer, using drivers of associational effects as the mechanism giving rise to apparent interactions. We explore the following drivers of associational effects: the relative density of focal and alternative resource, effects of generalist density on the quality of focal and alternative resource and the effect of the alternative resource density on the quality of the focal resource. We start with the introduction of the model, and proceed to analyse the stability conditions and how these relate to the relative densities of the focal and alternative resource. Then we use the model to explore the effects of consumer switching and consumer density dependence as underlying mechanisms of apparent competition. In the discussion, we combine the mechanisms and drivers arguing that short-term consumer choices can have long-term on outcomes of trophic interactions.

2. Consumer-Resource Dynamics

To explore the indirect effects of associations between resources, we adapted a basic consumer—resource dynamics model (Rosenzweig and Macarthur, 1963),

$\begin{array}{ll}\frac{dG}{dt}=G(t)(\alpha R(t)+\alpha U-{\mu }_G).& (1)\end{array}$

This model framework is used to investigate the effect of resource switching on the indirect interaction between a focal and alternative resource. The generalist (consumer) dynamics are described by:

$\begin{array}{ll}\frac{dG}{dt}=G(t)\left[\left(\frac{R{(t)}^m}{R{(t)}^m+U^m}\right)\alpha R(t)+\left(1-\frac{R{(t)}^m}{R{(t)}^m+U^m}\right)\alpha U-{\mu }_G\right]& (2)\end{array}$

where $\frac{dG}{dt}$ describes the change in density of the generalist (G) with respect to time (t), R(t) is the abundance of the focal resource at time t, U is the abundance of alternative resource at time t and m is a parameter describing the shape of the switching effect within the functional response. α is the resource consumption rate and μ_G the density-independent mortality rate (see below). The focal resource dynamics are described by:

$\begin{array}{ll}\frac{dR}{dt}={\lambda }_R-\left(\frac{R{(t)}^m}{R{(t)}^m+U^m}\right)\alpha R(t)G(t)-{\mu }_{R}R(t)& (3)\end{array}$

where λ_R is the constant (allochthonous) rate of resource supply, μ_R is the density-independent resource loss rate &the combination of α and the resource preference response $\frac{R{(t)}^m}{R{(t)}^m+U^m}$ can be seen as scaled foraging rate ($\alpha \left(\frac{R{(t)}^m}{R{(t)}^m+U^m}\right)$) of the generalist on the focal resource (functional response). The formulation of the switching response has been applied previously by Hutson (1984) and Teramoto et al. (1979) in studies of predator-prey interactions.

2.1. Model Assumptions

The underlying assumptions of the model are that (i) the generalist-focal resource dynamics are coupled, with the generalist only imposing mortality on the focal resource, and this resource contributes to the population dynamics of the generalist; and, (ii) the alternative resource (U) contributes to generalist population-level growth but is not affected by the generalist. The model framework links ideas of associational effects (Figure 1) through the relationship between the density/frequency of the focal resource in relation to the alternative resource and its effect on consumer behavior (m). An illustrative example where these assumptions apply to associational effect is Choristoneura fumiferana, the Eastern spruce budworm, an outbreak species known to attack a wide range of tree species. Balsam fir (Abies balsamea) is the preferred host. After after several years of repeated defoliation, the tree will die. A secondary host, an alternative resource for the Eastern spruce budworm, is white spruce (Picea glauca) which is considerably less sensitive to spruce budworm defoliation; while these trees might be attacked, they rarely suffer mortality from defoliation (MacLean, 1984). While the long-term fate of spruce-fir forests to budworm attack might be complex, recent work has shown that spruce budworm can drive differential tree mortality, in these mixed species stands, Corona et al. (2022) due to both the short-term (e.g., presence of shared herbivory affecting quality of resource) (Nealis and Régnière, 2018) and long-term (e.g., shifts in bud-burst phenology) (Deslauriers et al., 2019) ecological effects.

2.1.1. Resource Preference and Consumer Behavior

By including $\left(\frac{R{(t)}^m}{R{(t)}^m+U^m}\right)$, the functional response of the consumer becomes dependent on the density-ratio of the focal resource to the alternative resource (Box 1.1). The constant m represents the strength of the link (interaction) between the focal resource and the generalist. The shape of the preference can change from a linear (m = 1) to sigmoid (m = 3) relationship as the value of m increases. If the densities of the focal and the alternative resource are equal then the preference for either the focal or alternative resource is equal. When m>0 the preference of the generalist depends on the density of the resources. Similarly, under a condition of equal preference (m = 0), foraging is independent of resource density (Box 1.1). If the density of the focal resource is higher than the density of the alternative resource, the generalist will always prefer the focal resource but when the density of the alternative resource is higher than the focal resource the alternative resource will be preferred. The strength of the preference depends on the ratio between the focal and the alternative resource ($\left(\frac{R{(t)}^m}{R{(t)}^m+U^m}\right)$) and on the magnitude of the switching functional response (i.e., the value of m).

Box 1. The model parameters that are manipulated to simulate scenarios of associational effects. Each section of the box discusses one of the parameters and their role in describing the effects within the framework as presented in Figure 1.

2.1.2. Resource Preference and Consumer Behavior; Density-Dependent Consumer Dynamics

The model for the generalist dynamics can be extended to explore the effects of density-dependence by introducing feedbacks acting on mortality through density-dependence (Box 1.2). Different forms of density-dependence capture different types of consumers; density-dependence acting at lower density regimes are used to describe organisms with a long life span and low yearly offspring production (e.g., mammalian consumers). While regulatory processes acting close to carrying capacity are used to describe short lived organisms with high yearly offspring production and capacity to over exploit resource systems (e.g., arthropod consumers; Fowler, 1981). In order to include density-dependence acting on the generalist population we replace the constant for density-independent mortality (μ_G) with a density-dependent function. Bellows (1981) provides a comprehensive investigation into these sorts of density-dependent models (for describing insect population dynamics). Two simple density-dependence functions that we use in this study are Bellows' model f(G) = ηG^ν and Maynard Smith & Slatkin's model f(G) = ln(1 + (ηG)^ν) where 1/η is a threshold density when the effects of density-dependence occur and ν is the magnitude of the density-dependent effect. These two forms of density-dependence capture different ways in which the relationship between numbers of survivors and initial density is described (Bellows, 1981). These two functions can express different forms of intraspecific competitive density-dependence by varying ν. Contest competition can be imposed on the dynamics of the generalist consumer by including ν ≤ 1 and scramble competition by ν > 1. In combination with the effects of resource preference, these density-dependent effects allow the analysis of different types of consumer life history and their effect on apparent competitive or mutualistic interactions (Nicholson, 1954).

2.1.3. Resource Preference and Consumer Behavior; Consumer Foraging Rate

In the basic model, the resource foraging rate is represented $\alpha \left(\frac{R{(t)}^m}{R{(t)}^m+U^m}\right)$. Increasing the conversion rate (α) will lead to an increased foraging rate. Initially, we consider that the conversion rate is equal for consumption of either resource. To investigate the dynamical consequences of associational effects, the foraging rate is dependent on either the generalist density (G(t)), the focal resource density (R(t)) and the alternative resource density (U) by including a contact rate, q. This parameter defines the strength of the indirect effect on the scaled foraging rate $\left(\frac{R{(t)}^m}{R{(t)}^m+U^m}\right)\alpha Q$, where Q is defined as $\alpha \frac{c}{1+a{e}^{qP}}$ and P is either G(t), R(t) or U (Box 1.3), a and c are scaling variables (a = 1 and c = 1). When the conversion rate (α) is negatively dependent on generalist consumer densities (G(t)), this describes the biological relationship between consumption and host resource quality, where high levels of consumption are linked with lower resource quality (Agrawal et al., 2006, Box 1.3). When the conversion of the focal resource, by the generalist, is negatively related to focal resource density, this is a resource quality effect that has potential consequences for the strength of intraspecific competition on the focal resource. If the conversion rate of the focal resource, by the generalist, is dependent on alternative resource density this can also affect the population-level growth of the focal resource. For instance, a potential negative effect of alternative resource on the conversion rate of the focal resource by the generalist can reduce the number of offspring produced by the focal resource. This scenario could arise through interspecific competitive processes for nutrients or if damage on the alternative resource primes the focal resource to produce defense compounds (Kessler et al., 2006).

3. Model Analysis

We start with the analysis of the density-independent consumer—resource model (Equation 1) to understand the behavior of the model when the focal and alternative resource are equally preferred. The density of the focal and alternative resource will determine the outcome of the interaction. It has been proposed that this interaction will lead to apparent competition (Holt and Bonsall, 2017), analyzing the model will guide understanding whether this is the case for the dynamics described by the our model. In addition, the same approach will be used to analyze the model under different forms of density-dependence and provide a basis for the initial conditions for further numerical analyses.

3.1. Stability Conditions-Mathematical Analysis

3.1.1. Stability Conditions of the Density-Independent Consumer-Resource Dynamics

By taking a simple limiting case of the focal resource—generalist dynamics, we can derive general conditions for the stability of this interaction. We begin by assuming that alternative resource is absent (U = 0) and the generalist dynamics are then:

$\begin{array}{ll}\frac{dG}{dt}=G\left[\alpha R-{\mu }_G\right]& (4)\end{array}$

and the resource dynamics are (if U = 0):

$\begin{array}{ll}\frac{dR}{dt}={\lambda }_R-\alpha RG-{\mu }_{R}R(t)& (5)\end{array}$

This interaction has the following equilibria:

$\begin{array}{ll}{R}^{*}=\frac{{\mu }_G}{\alpha }& (6)\end{array}$

$\begin{array}{ll}{G}^{*}=\frac{{\lambda }_R}{{\mu }_G}-\frac{{\mu }_R}{\alpha }& (7)\end{array}$

which are always stable as $-\frac{\alpha {\lambda }_R}{{\mu }_G}<0$.

3.1.2. Resource-Mediated Density-Dependence

To investigate the ecological mechanism of stability, a second limiting case can be derived by assuming that (i) the resource dynamics act on a faster time scale (and are therefore essentially constant through time) than the generalist dynamics and, (ii) that resource consumption exceeds resource loss rates then:

$\begin{array}{ll}\frac{dR}{dt}={\lambda }_R-\alpha RG& (8)\end{array}$

Setting $\frac{dR}{dt}=0$ (constant resource dynamics) yields:

$\begin{array}{ll}R=\frac{{\lambda }_R}{\alpha G}& (9)\end{array}$

Substituting this into the simplified equation for generalist dynamics (Equation 4) gives:

$\begin{array}{ll}\frac{dG}{dt}={\lambda }_R-{\mu }_{G}G& (10)\end{array}$

which, at time T, has solution:

$\begin{array}{ll}G(T)=\frac{{\lambda }_R}{{\mu }_G}(1-exp(-{\mu }_{G}T))& (11)\end{array}$

The resource dynamics introduce a donor-mediated mechanism of density-dependence into the generalist dynamics and this form of density-dependence can influence the stability and the dynamics of population-level interactions.

3.1.3. Effects of Alternative Resources

The effects of the alternative resource on the focal resource dynamics can be investigated by determining the focal resource equilibrium in the presence of the alternative resource ($R_U^{*}$). This can be found from the solution to:

$\begin{array}{ll}\alpha R_U\left(\frac{R_U^m}{U^m+R_U^m}\right)+\alpha U\left(1-\frac{R_U^m}{R_U^m+U^m}\right)-{\mu }_G=0.& (12)\end{array}$

For equal resource preference (m = 0), this is a linear relationship and the focal resource equilibrium is $R_U^{*}=\frac{2{\mu }_G}{\alpha }-U$. So $R_U^{*}>R^{*}$ holds only if the density of the alternative resource U is greater than the density of the focal resource (R^*) ($U>\frac{{\mu }_G}{\alpha }$). When there is linear resource preference (m = 1), the solution(s) to Equation (12) is a quadratic relationship in R_U:

$\begin{array}{ll}{R}_U^{*}=\frac{{\mu }_G}{2\alpha }\pm \sqrt{{\left(\frac{{\mu }_G}{\alpha }\right)}^2+\frac{4U}{\alpha }({\mu }_G-\alpha U)}.& (13)\end{array}$

Under this linear preference for either resource the equilibrium density of the focal resource in the presence of the alternative resource ($R_U^{*}$) is greater than the equilibrium density of this resource in the absence of the alternative resource (R^*) if $U\ge \frac{2{\mu }_G+\sqrt{7{\mu }_G}}{4\alpha }$. Under combinations of generalist life-history traits associated resource conversion rate α and generalist mortality rate μ_G, the availability of additional resources can increase the abundance of a focal resource ($R_U^{*}>R^{*}$) as the generalist facilitates apparent mutualisms. It is expected that given this threshold condition for the effects of the availability of alternative resource on focal resource density, the outcome of apparent competition (when $R_U^{*}<R^{*}$) is more likely to occur for long-lived generalist (Figure 2).

FIGURE 2

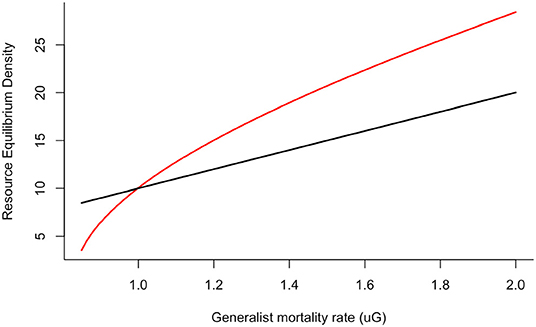
Figure 2. Equilibrium density of the focal resource in the absence (black line) and presence (red line) of the alternative resource (U). When generalists are long-lived (low mortality), the abundance of the focal resource is lower in the presence of the alternative resource due to the effects of apparent competition. By contrast, when generalists are short-lived, the abundance of the focal resources increases beyond the level found in the absence of the alternative resource due to apparent mutualism. Other parameters were α = 0.1 and U = 10.

3.2. Indirect Interactions-Numerical Analysis

To investigate these effects further and assess the role of the population dynamics under density independent and density dependent conditions in the presence of the alternative resource, numerical analysis was used. Numerical analyses were undertaken using a 4th order Runge-Kutta numerical integration scheme (implemented in R; R Core Team, 2014). For each simulation 5,000 iterations were used and the replacement rate of the alternative resource density was varied. The last 20% of the observations were selected and plotted to represent the asymptotic dynamics at each density of the alternative resource, using bifurcation analysis. We ran bifurcation analysis for the consumer-resource model at m = 0 for α, μ_G, μ_R and λ_R and for m at α = 0.05, μ_G = 2, λ_R = 10, μ_R = 0.001 the results are presented in the online appendix (Figure 1A in Appendix A). Observations of resource and generalist density with respect to the density (replacement rate) of the alternative resource can be used to infer the generalist—mediated relationship between the two resources. By using similar simulations for different values of the switching parameter (m = {0, 1, 2, 3}), the effect of resource preference can be assessed in a similar way and compared between the different models. Also, the density-dependent models allow for different strengths of non-linear density-dependence (under-compensatory, complete compensatory and over-compensatory) to be investigated by using different values of the form of the density-dependence (ν).

3.2.1. Resource Preference and Consumer Behavior; Density-Independent Consumer Dynamics

We find that the equilibrium density of the focal resource is always less when both resources are present, and equally preferred, compared to the equilibrium density of the focal resource in absence of the alternative resource (Figure 2 black line and Figure 3A; m = 0). If the resource preference is linearly related to resource density (m = 1), the equilibrium density of the focal resource increases. When resource preference describes an asymptotic or sigmoid relationship (m > 1), the stability equilibria of the focal resource increase less but over a larger range of alternative resource densities. However, the equilibrium densities decline more steeply after the maximum is reached. This maximum is lower than the maximum found for the scenario under the linear preference. Our results indicate that, independent of resource limitation (i.e., the alternative resource is renewed at the same rate each generation), the indirect interaction can result in coexistence and that this is facilitated when the consumer has a stronger preference for the focal resource over a wider range of alternative resource density (i.e., low m; Figure 3A). Gradual switching in resource preference (Figure 3, Box 1.1, and Figure B1) is more likely to facilitate coexistence between both resources (Abrams and Matsuda, 2004) and facilitates apparent mutualistic effects for the focal resource.

FIGURE 3

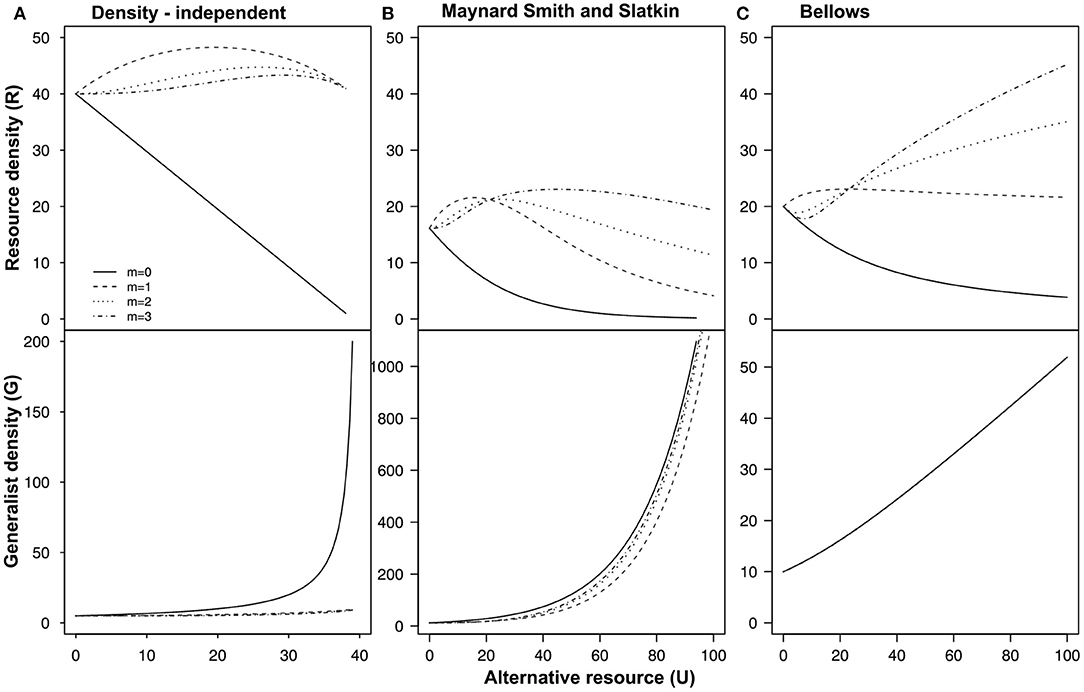
Figure 3. Graphical representation of the population equilibria at different values of U and m under: (A) density-independent conditions; (B) Maynard Smith & Slatkin density-dependence; (C) Bellows density-dependence. Resource consumer preference is determined by $\frac{R{(t)}^m}{R{(t)}^m+U^m}$ (from Equation 1). The values for U range from 0 to 45. The different lines represent: Solid m = 0; Dashed m = 1; Dotted m = 2; Dash-Dot m = 3 [Other parameters values are: α = 0.05, μ_G = 2, λ_R = 10, and μ_R = 0.001 under density-independent conditions and under density-independent conditions α = 0.05, η = 0.1, ν = 1, λ_R = 10, and μ_R = 0.001]. The lines in the figure are obtained using bifurcation analysis.

3.2.2. Resource Preference and Consumer Behavior; Density-Dependent Consumer Dynamics

When we included density-dependent mortality in the generalist population dynamics, the equilibrium density of the focal resource at U = 0 is lower (Figures 3B,C) compared to the equilibrium under the density-independent scenario (Figure 3A). Including density-dependent generalist mortality results in an apparent mutualistic interaction for the focal resource over a large range of alternative resource density. Equal resource preference leads to either a small decrease in equilibrium density compared to the equilibrium density at U = 0 (Figures 3B,C). When the generalist population dynamics experience Bellow's density-dependence, the focal resource density increases above the equilibrium densities for density-independent scenarios (Figure 3). Under Bellows density-dependence, stronger, more abrupt, switching behavior results in higher equilibrium densities of the focal resource (i.e., m > 1), i.e., apparent mutualism. Hence, slow acting density dependence (Bellows density-dependence) facilitates apparent mutualism at certain switching responses whereas faster acting density-dependence (Maynard Smith and Slatkin density dependence) is more likely to result in apparent competition at higher densities of the alternative resource.

Contest competition (Figures 4A,B) creates fewer opportunities for apparent mutualisms compared to scramble competition (Figures 4C,D). For both the Bellows and Maynard Smith & Smith forms of density dependence, contest competition leads to stronger apparent competition compared to the complete compensation scenario (compare with Figures 3B,C). Equal preference (m = 0) will lead to unstable dynamics and extinction under contest competition for both Bellows and MMS density-dependence. Hence, life history of the mediating consumer influence the direction of the apparent interaction between the shared resources.

FIGURE 4

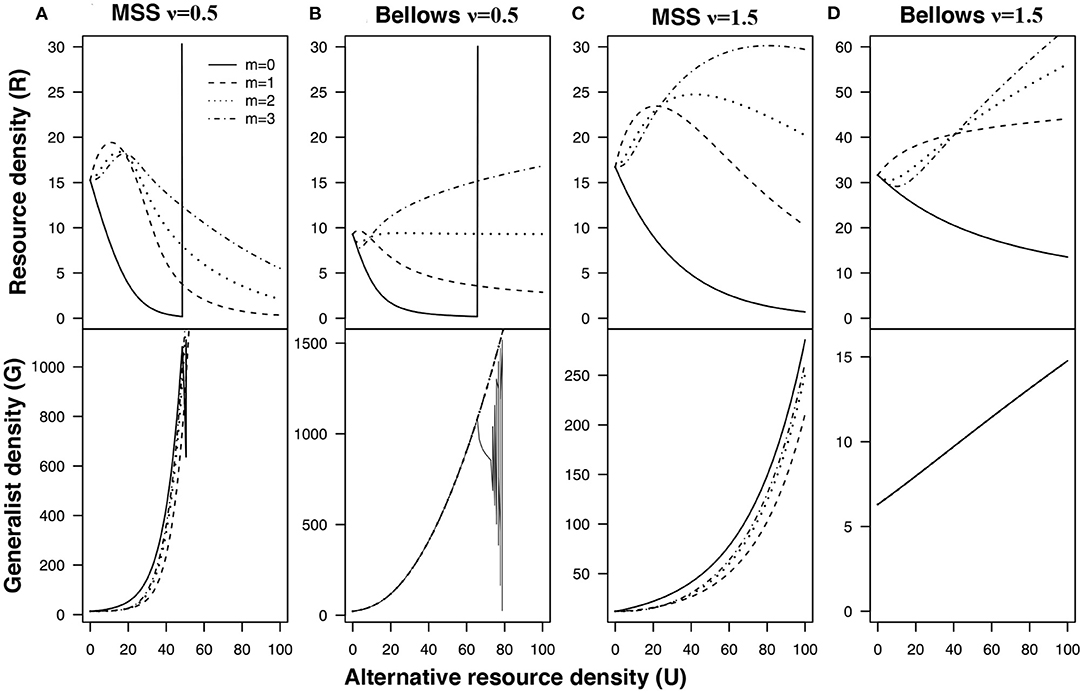
Figure 4. Generalist abundance with under compensatory density dependence (contest competition) under: (A) Maynard Smith and Slatkin f(G) = ln(1 + (ηG)^ν): and (B) Bellows f(G) = ηG^ν: and generalist abundance with over compensatory density dependence (scramble competition) under (C) Maynard Smith and Slatkin; and (D) Bellows. Intraspecific-competition parameter ν is either ν = 0.5 and ν = 1.5. The different lines represent different values of m; Solid m = 0; Dashed m = 1; Dotted m = 2; Dash-Dot m = 3 [other parameters α = 0.05, μ_G = 2, λ_R = 10, and μ_R = 0.001]. The lines in the figure are obtained using bifurcation analysis.

3.2.3. Resource Preference and Consumer Behavior; Consumer Foraging Rate

Changing conversion rates does not affect consumer density or the shape of the relationship between the focal and alternative resource (compare Figure 3A with Figure 5). However, making the conversion rates dependent or either generalist, focal or alternative density increases the equilibrium at U = 0. When conversion rates are dependent on the density of the focal resource and resource preference is equal (m = 0), the equilibrium densities show fluctuating dynamics. Negative feedback on the conversion rate of the focal resource in response to either the density of the focal resource (Figure 5–black line) or the density of the alternative resource (Figure 5–blue line) results in a stronger apparently mutualistic interaction between the focal and the alternative resource compared to the scenario of equal constant conversion rates (Merwin et al., 2017). Our results show that, also under this scenario, the long-term outcome of the interaction is very much dependent on the switching response of the consumer (Krivan and Eisner, 2003).

FIGURE 5

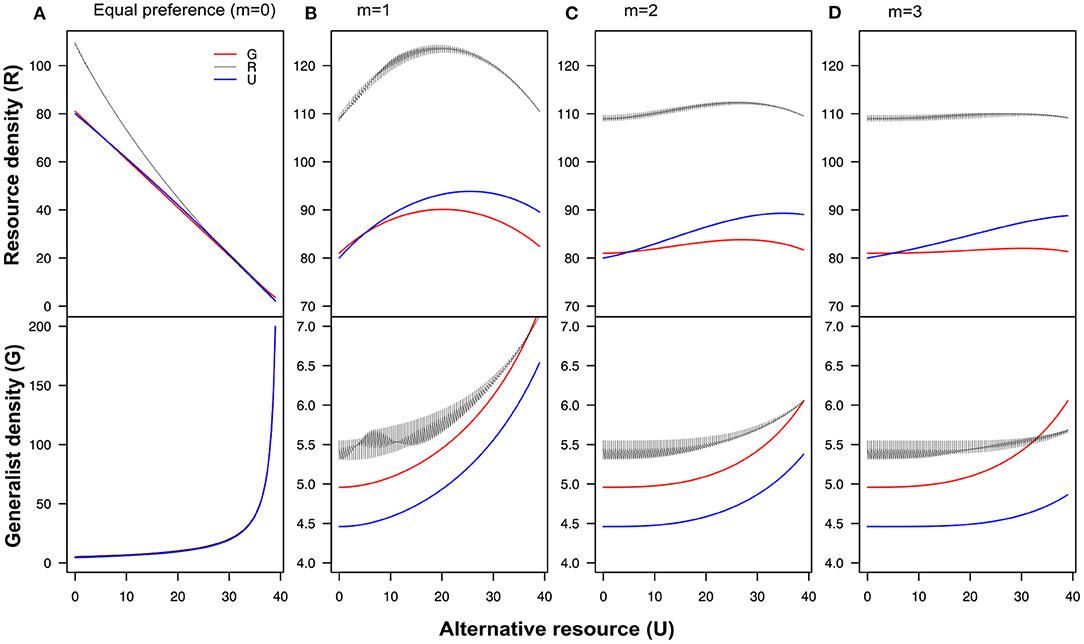
Figure 5. The equilibrium densities of the focal resource and the generalist plotted against the density of the alternative resource. (A) When the resources are equally preferred over the whole range of relative densities (m = 0). (B) When m = 1 (C) m = 2, (D) m = 3. In each panel, the red line represents the equilibrium densities of the focal resource (upper panel) and the generalist (lower panel) when α depends on the densities of the generalist consumer $\alpha \frac{c}{1+a{e}^{qG(t)}}$, the black line represents α dependent on the focal resource density $\alpha \frac{c}{1+a{e}^{qR(t)}}$, and the blue line represents the equilibrium densities when α depends on the densities of the alternative resource $\alpha \frac{c}{1+a{e}^{qU}}$, and q = 0.005 [Other parameters values are: alpha = 0.05, μ_G = 2, λ_R = 10, and μ_R = 0.001]. The lines in the figure are obtained using bifurcation analysis.

4. Discussion

Here, we have investigated the behavioral effects associated with resource preference (associational effects) and our results show that these effects can lead to either apparent competition or mutualism between resources. The direction and strength of the apparent interaction between resources depends on switching behavior and life history of the shared consumer. We show that short time-scale choices by the consumer can have long-term implications for resource coexistence patterns. Our results indicate that consumer traits, like switching behavior, density-dependent mortality and intraspecific competition, can have a strong effect on the outcome of long-term consumer mediated interactions between resources, leading to facilitation of coexistence. Negative feedbacks on conversion rates (α) change equilibrium densities but not the apparent interactions (Figure 5) and could therefore be of less importance for resource dynamics.

Our approach to modeling the effect of resource switching on the stability of consumer-resource interactions differs from that in previous studies in the way that our model aims to capture different life histories of the consumer. Previous approaches have focused on the effects of consumer density, resource quality, handling time and/or consumer foraging behavior (van Baalen et al., 2001; Krivan and Eisner, 2003, 2006). As associational effects are often hypothesized to result from focal resource neighborhood (Underwood et al., 2014), our model describes the interactions between two resources and a shared consumer. In our model the switching parameter is determined by the relative density of the focal resource and the alternative resource instead of either a threshold consumer density (van Baalen et al., 2001) or a more profitable resource (Krivan and Eisner, 2003). Using this approach, the mathematical analysis of the model shows the resource-consumer dynamics exhibit donor-controlled stability under equal preference and density independent conditions, which is analogous to findings of van Baalen et al. (2001). Moreover, we find apparent and mutualistic effects on the focal resource within the stability range of the consumer-resource interaction, which provides a different perspective to the effects of consumer switching and allows us to connect these interaction to the long-term impacts of associational effects.

By including density-dependence in the dynamics of the generalist the model reflects, amongst other things, either intraspecific competition leading to density-dependent mortality (Royama, 1992, p. 40–41). Further, when the generalist responds to herbivore density in a (spatially) density-dependent manner, i.e., an aggregative response (Turchin, 2003, p. 78), any increases in the mortality of the consumer can result in an increase in the equilibrium level of coexisting plants. The strength of the density-dependence, form of intraspecific competition and/or predation pressure, will determine the coexistence equilibrium for the focal resource (Figures 3B,C; Long et al., 2012). Predators are known to respond also to resource neighborhood (Guyot et al., 2015). Hence, making the number of offspring negatively related to the density of the alternative resource could reflect either the dilution effect for consumers (Civitello et al., 2015) or increased availability of resources for the predator as predicted by the natural enemy hypothesis (Stiling et al., 2003). Both of these mechanisms have been observed empirically to lead to associational resistance (Castagneyrol et al., 2013; Guyot et al., 2015) and will, as our model confirms, lead to long-term apparent mutualistic effects (Figure 5).

We investigated some of the mechanisms proposed to underlie associational effects and some of the expected feedbacks (Figure 1; Underwood et al., 2014; Kim, 2017). Our results suggest that the outcome of generalist consumer—multiple resource interactions are important to understand from the perspective of associational effects (Underwood et al., 2014) and on a wider scale, trophic interaction modifications (Terry et al., 2017). From an applied perspective, increased herbivore pest mortality as a result of apparent competition does not necessarily reduce inflicted damage on individual plants in agricultural crop systems (Jaworski et al., 2015) as positive ecological effects might not always mean positive economical effects. Using generalist natural enemies for biological control might have negative effects on non-target organisms (Elkinton and Boettner, 2012), potentially without reducing the population density of the target organism. Our results become especially relevant when the theory of associational resistance is applied to managed ecosystems, such as agricultural or forestry systems. We highlight that increasing diversity, either at the resource or consumer level, could benefit the target organism if mechanisms acting at the population level of generalist consumers allow for mutualistic interactions rather than apparent competitive outcomes. However, enriching ecosystems is well known to lead to paradoxical outcomes (e.g., Gilpin and Rosenzweig, 1972) and extending this to the breadth of indirect ecological interactions requires more attention (Bonsall and Holt, 2003). Hence, caution and further study is needed in developing these ecological concepts for production systems.

Further empirical work is needed to tease apart the effects of frequency and density on the dynamics resulting from associational effects (Kim and Underwood, 2015). Within season experiments on consumer choice might not be informative about the outcome of long-term interactions as well as the outcome of interactions at larger spatial scales (van Nouhuys and Kraft, 2012; Hamback et al., 2014). At the food web level, sharing consumers will support the occurrence of indirect (positive or negative) effects when the resources exhibit different, individual population dynamics (Tack et al., 2011). By including density-dependence in the generalist consumer dynamics, we show that the effect of alternative resource(s) on the likelihood of mutualistic interactions increases, this is further enhanced if the focal resource is a nutritionally better resource. As all natural populations are subjected to some form of density-dependence, any kind of indirect interaction should be considered in this context.

In addition, empirical research has shown that behavior as well as spatial scale are important determinants of associational resistance or associational susceptibility (Hahn and Orrock, 2016; Verschut et al., 2016). Sensory responses to plant traits will determine occurrence of associational effects at different spatial scales of foraging (Verschut et al., 2017a,b). Our work has investigated the effect of decisions made by the consumer at patch level, and it has been shown that patch level diversity will determine the consumer load on the focal resource, lower numbers of consumers at higher levels of diversity (Hamback et al., 2014). Further theoretical work is necessary to increase the understanding of the importance of spatial scale in the context of the population dynamical outcomes of associational effects at the patch scale.

In conclusion, our work connects the theoretical body of work on indirect interactions to the concepts of associational effects. Adapting the associational effects framework (Figure 1 and Box 1) together with the results presented here suggests that the indirect interactions between multiple resources need more thorough investigation to appreciate the range of associational effects that could result from the dynamical interaction between a generalist consumers and its focal and alternative resources.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://osf.io/w7atk/

Author Contributions

MB: conceptualization, formal analysis, validation, writing–original draft, and writing–review and editing. MK: conceptualization, numerical analysis, writing–original draft, and writing–review and editing. Both authors contributed to the article and approved the submitted version.

Funding

MK was funded by the Mistra-financed project Future Forests and by the FORMAS research grant reg no. 2015-55.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.854222/full#supplementary-material

References

Abrams, P. A., and Matsuda, H. (2004). Consequences of behavioral dynamics for the population dynamics of predator-prey systems with switching. Populat. Ecol. 46, 13–25. doi: 10.1007/s10144-003-0168-2

CrossRef Full Text | Google Scholar

Agrawal, A. A., Lau, J. A., and Hamback, P. A. (2006). Community heterogeneity and the evolution of interactions between plants and insect herbivores. Q. Rev. Biol. 81, 349–376. doi: 10.1086/511529

PubMed Abstract | CrossRef Full Text | Google Scholar

Barbosa, P., Hines, J., Kaplan, I., Martinson, H., Szczepaniec, A., and Szendrei, Z. (2009). Associational resistance and associational susceptibility: having right or wrong neighbors. Ann. Rev. Ecol. Evolut. Syst. 40, 1–20. doi: 10.1146/annurev.ecolsys.110308.120242

CrossRef Full Text | Google Scholar

Bellows, T. S. (1981). The descriptive properties of some models for density dependence. J. Anim. Ecol. 50, 139–156. doi: 10.2307/4037

CrossRef Full Text | Google Scholar

Bolker, B., Holyoak, M., Krivan, V., Rowe, L., and Schmitz, O. (2003). Connecting theoretical and empirical studies of trait-mediated interactions. Ecology 84, 1101–1114. doi: 10.1890/0012-9658(2003)084(1101:CTAESO)2.0.CO;2

CrossRef Full Text | Google Scholar

Bonsall, M., and Hassell, M. (1997). Apparent competition structures ecological assemblages. Nature 388, 371. doi: 10.1038/41084

CrossRef Full Text | Google Scholar

Bonsall, M. B., and Holt, R. D. (2003). The effects of enrichment on the dynamics of apparent competitive interactions in stage-structured systems. Am. Nat. 162, 780–795. doi: 10.1086/379203

PubMed Abstract | CrossRef Full Text | Google Scholar

Castagneyrol, B., Giffard, B., Pere, C., and Jactel, H. (2013). Plant apparency, an overlooked driver of associational resistance to insect herbivory. J. Ecol. 101, 418–429. doi: 10.1111/1365-2745.12055

CrossRef Full Text | Google Scholar

Chaneton, E. J., and Bonsall, M. B. (2000). Enemy-mediated apparent competition: empirical patterns and the evidence. Oikos 88, 380–394. doi: 10.1034/j.1600-0706.2000.880217.x

CrossRef Full Text | Google Scholar

Chesson, J. (1989). The effect of alternative prey on the functional-response of Notonecta-hoffmani. Ecology 70, 1227–1235. doi: 10.2307/1938180

CrossRef Full Text | Google Scholar

Civitello, D. J., Cohen, J., Fatima, H., Halstead, N. T., Liriano, J., McMahon, T. A., et al. (2015). Biodiversity inhibits parasites: broad evidence for the dilution effect. Proc. Natl. Acad. Sci. U.S.A. 112, 8667–8671. doi: 10.1073/pnas.1506279112

PubMed Abstract | CrossRef Full Text | Google Scholar

Corona, C., Leeper, A., and LaMontagne, J. (2022). Differential defoliation and mortality of white spruce and balsam fir by eastern spruce budworm. For. Ecol. Manag. 508, 120042. doi: 10.1016/j.foreco.2022.120042

CrossRef Full Text | Google Scholar

Deslauriers, A., Fournier, M.-P., Carteni, F., and Mackay, J. (2019). Phenological shifts in conifer species stressed by spruce budworm defoliation. Tree Physiol. 39, 590–605. doi: 10.1093/treephys/tpy135

PubMed Abstract | CrossRef Full Text | Google Scholar

Elkinton, J. S., and Boettner, G. H. (2012). Benefits and harm caused by the introduced generalist tachinid, Compsilura concinnata, in North America. Biocontrol 57, 277–288. doi: 10.1007/s10526-011-9437-8

CrossRef Full Text | Google Scholar

Eubanks, M. D., and Denno, R. F. (2000). Health food versus fast food: the effects of prey quality and mobility on prey selection by a generalist predator and indirect interactions among prey species. Ecol. Entomol. 25, 140–146. doi: 10.1046/j.1365-2311.2000.00243.x

CrossRef Full Text | Google Scholar

Fowler, C. W. (1981). Density dependence as related to life history strategy. Ecology 62, 602–610. doi: 10.2307/1937727

CrossRef Full Text | Google Scholar

Gilpin, M. E., and Rosenzweig, M. L. (1972). Enriched predator-prey systems: theoretical stability. Science 177, 902–904. doi: 10.1126/science.177.4052.902

PubMed Abstract | CrossRef Full Text | Google Scholar

Golubski, A. J., and Abrams, P. A. (2011). Modifying modifiers: what happens when interspecific interactions interact? J. Anim. Ecol. 80, 1097–1108. doi: 10.1111/j.1365-2656.2011.01852.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Guyot, V., Castagneyrol, B., Vialatte, A., Deconchat, M., Selvi, F., Bussotti, F., et al. (2015). Tree diversity limits the impact of an invasive forest pest. PLoS ONE 10, e0136469. doi: 10.1371/journal.pone.0136469

PubMed Abstract | CrossRef Full Text | Google Scholar

Hahn, P. G., and Orrock, J. L. (2016). Neighbor palatability generates associational effects by altering herbivore foraging behavior. Ecology 97, 2103–2111. doi: 10.1002/ecy.1430

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamback, P. A., and Ekerholm, P. (1997). Mechanisms of apparent competition in seasonal environments: an example with vole herbivory. Oikos 80, 276–288. doi: 10.2307/3546596

CrossRef Full Text | Google Scholar

Hamback, P. A., Inouye, B. D., Andersson, P., and Underwood, N. (2014). Effects of plant neighborhoods on plant-herbivore interactions: resource dilution and associational effects. Ecology 95, 1370–1383. doi: 10.1890/13-0793.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Hassell, M. P. (2000). The Spatial and Temporal Dynamics of Host-Parasitoid Interactions. Oxford Series in Ecology and Evolution. Oxford: Oxford University Press.

Google Scholar

Hassell, M. P., and Southwood, T. R. E. (1978). Foraging strategies of insects. Annu. Rev. Ecol. Syst. 9, 75–98. doi: 10.1146/annurev.es.09.110178.000451

CrossRef Full Text | Google Scholar

Holt, R. D. (1977). Predation, apparent competition, and structure of prey communities. Theor. Popul. Biol. 12, 197–229. doi: 10.1016/0040-5809(77)90042-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Holt, R. D., and Bonsall, M. B. (2017). Apparent competition. Ann. Rev. Ecol. Evolut. Syst. 48, 447–471. doi: 10.1146/annurev-ecolsys-110316-022628

CrossRef Full Text | Google Scholar

Holt, R. D., and Lawton, J. H. (1993). Apparent competition and enemy-free space in insect host-parasitoid communities. Am. Nat. 142, 623–645. doi: 10.1086/285561

PubMed Abstract | CrossRef Full Text | Google Scholar

Hutson, V. (1984). Predator mediated coexistence with a switching predator. Math. Biosci. 68, 233–246. doi: 10.1016/0025-5564(84)90033-6

CrossRef Full Text | Google Scholar

Jaworski, C. C., Chailleux, A., Bearez, P., and Desneux, N. (2015). Apparent competition between major pests reduces pest population densities on tomato crop, but not yield loss. J. Pest. Sci. 88, 793–803. doi: 10.1007/s10340-015-0698-3

CrossRef Full Text | Google Scholar

Joern, A., and Laws, A. N. (2013). Ecological mechanisms underlying arthropod species diversity in grasslands. Ann. Rev. Entomol. 58, 19–36. doi: 10.1146/annurev-ento-120811-153540

PubMed Abstract | CrossRef Full Text | Google Scholar

Kessler, A., Halitschke, R., Diezel, C., and Baldwin, I. T. (2006). Priming of plant defense responses in nature by airborne signaling between Artemisia tridentata and Nicotiana attenuata. Oecologia 148, 280–292. doi: 10.1007/s00442-006-0365-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, T. N. (2017). How plant neighborhood composition influences herbivory: Testing four mechanisms of associational resistance and susceptibility. PLoS ONE 12, e0176499. doi: 10.1371/journal.pone.0176499

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, T. N., and Underwood, N. (2015). Plant neighborhood effects on herbivory: damage is both density and frequency dependent. Ecology 96, 1431–1437. doi: 10.1890/14-1097.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, T. N., Underwood, N., and Inouye, B. D. (2013). Insect herbivores change the outcome of plant competition through both inter and intraspecific processes. Ecology 94, 1753–1763. doi: 10.1890/12-1261.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Krivan, V., and Eisner, J. (2003). Optimal foraging and predator-prey dynamics III. Theor. Popul. Biol. 63, 269–279. doi: 10.1016/S0040-5809(03)00012-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Krivan, V., and Eisner, J. (2006). The effect of the holling type II functional response on apparent competition. Theor. Popul. Biol. 70, 421–430. doi: 10.1016/j.tpb.2006.07.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Long, W. C., Gamelin, E. F., Johnson, E. G., and Hines, A. H. (2012). Density-dependent indirect effects: apparent mutualism and apparent competition coexist in a two-prey system. Mar. Ecol. Prog. Ser. 456, 139–148. doi: 10.3354/meps09702

CrossRef Full Text | Google Scholar

MacLean, D. A. (1984). Effects of spruce budworm outbreaks on the productivity and stability of balsam fir forests. For. Chronicle 60, 273–279. doi: 10.5558/tfc60273-5

CrossRef Full Text | Google Scholar

May, R. M. (1977). Predators that switch. Nature 269, 103–104. doi: 10.1038/269103a0

CrossRef Full Text | Google Scholar

Menge, B. A. (1995). Indirect effects in marine rocky intertidal interaction webs - patterns and importance. Ecol. Monogr. 65, 21–74. doi: 10.2307/2937158

CrossRef Full Text | Google Scholar

Merwin, A. C., Underwood, N., and Inouye, B. D. (2017). Increased consumer density reduces the strength of neighborhood effects in a model system. Ecology 98, 2904–2913. doi: 10.1002/ecy.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Nealis, V., and Régniére, J. (2018). Insect-host relationships influencing disturbance by the spruce budworm in a boreal mixedwood forest. Can. J. For. Res. 34, 1870–1882. doi: 10.1139/x04-061

CrossRef Full Text | Google Scholar

Nicholson, A. J. (1954). An outline of the dynamics of animal populations. Aust. J. Zool. 2, 9–65. doi: 10.1071/ZO9540009

CrossRef Full Text | Google Scholar

Oaten, A., and Murdoch, W. W. (1975). Switching, functional response, and stability in predator-prey systems. Am. Nat. 109, 299–318. doi: 10.1086/282999

CrossRef Full Text | Google Scholar

Ohgushi, T. (2005). Indirect interaction webs: Herbivore-induced effects through trait change in plants. Ann. Rev. Ecol. Evolut. Syst. 36, 81–105. doi: 10.1146/annurev.ecolsys.36.091704.175523

CrossRef Full Text | Google Scholar

R Core Team (2014). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.

Google Scholar

Rosenzweig, M. L., and Macarthur, R. H. (1963). Graphical representation and stability conditions of predator-prey interactions. Am. Nat. 97, 209–223. doi: 10.1086/282272

CrossRef Full Text | Google Scholar

Royama, T. (1992). Analytical Population Dynamics, Volume 10 of Population and Community Biology Series. London: Chapman & Hall.

Google Scholar

Sato, Y. (2018). Associational effects and the maintenance of polymorphism in plant defense against herbivores: review and evidence. Plant Species Biol. 33, 91–108. doi: 10.1111/1442-1984.12201

CrossRef Full Text | Google Scholar

Sih, A., Cote, J., Evans, M., Fogarty, S., and Pruitt, J. (2012). Ecological implications of behavioural syndromes. Ecol. Lett. 15, 278–289. doi: 10.1111/j.1461-0248.2011.01731.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Stiling, P., Rossi, A. M., and Cattell, M. V. (2003). Associational resistance mediated by natural enemies. Ecol. Entomol. 28, 587–592. doi: 10.1046/j.1365-2311.2003.00546.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Tack, A. J. M., Gripenberg, S., and Roslin, T. (2011). Can we predict indirect interactions from quantitative food webs?-an experimental approach. J. Anim. Ecol. 80, 108–118. doi: 10.1111/j.1365-2656.2010.01744.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Teramoto, E., Kawasaki, K., and Shigesada, N. (1979). Switching effect of predation on competitive prey species. J. Theor. Biol. 79, 303–315. doi: 10.1016/0022-5193(79)90348-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Terry, J. C. D., Morris, R. J., and Bonsall, M. B. (2017). Trophic interaction modifications: an empirical and theoretical framework. Ecol. Lett. 20, 1219–1230. doi: 10.1111/ele.12824

PubMed Abstract | CrossRef Full Text | Google Scholar

Turchin, P. (2003). Complex Population Dynamics: A Theoretical/Emperical Synthesis. Princeton, NJ: Princeton University Press.

Google Scholar

Underwood, N., Inouye, B. D., and Hamback, P. A. (2014). A conceptual framework for associational effects: when do neighbours matter and how would we know? Q. Rev. Biol. 89, 1–19. doi: 10.1086/674991

PubMed Abstract | CrossRef Full Text | Google Scholar

van Baalen, M., Krivan, V., van Rijn, P. C., and Sabelis, M. W. (2001). Alternative food, switching predators, and the persistence of predator-prey systems. Am. Nat. 157, 512–524. doi: 10.1086/319933

PubMed Abstract | CrossRef Full Text | Google Scholar

van Nouhuys, S., and Kraft, T. S. (2012). Indirect interaction between butterfly species mediated by a shared pupal parasitoid. Popul. Ecol. 54, 251–260. doi: 10.1007/s10144-011-0302-5

CrossRef Full Text | Google Scholar

Verschut, T. A., Becher, P. G., Anderson, P., and Hambäck, P. A. (2016). Disentangling associational effects: both resource density and resource frequency affect search behaviour in complex environments. Funct. Ecol. 30, 1826–1833. doi: 10.1111/1365-2435.12670

CrossRef Full Text | Google Scholar

Verschut, T. A., Carlsson, M. A., Anderson, P., and Hambäck, P. A. (2017a). Sensory mutations in Drosophila melanogaster influence associational effects between resources during oviposition. Scientific Rep. 7, 9352. doi: 10.1038/s41598-017-09728-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Verschut, T. A., Hambäck, P. A., and Anderson, P. (2017b). Mating affects resource selection and modulates associational effects between neighbouring resources. Oikos 126, 1708–1716. doi: 10.1111/oik.04315

CrossRef Full Text | Google Scholar

Verschut, T. A., Inouye, B. D., and Hamback, P. A. (2018). Sensory deficiencies affect resource selection and associational effects at two spatial scales. Ecol. Evol. 8, 10569–10577. doi: 10.1002/ece3.4534

PubMed Abstract | CrossRef Full Text | Google Scholar

Werner, E. E., and Peacor, S. D. (2003). A review of trait–mediated indirect interactions in ecological communities. Ecology 84, 1083–1100. doi: 10.1890/0012-9658(2003)084(1083:AROTII)2.0.CO;2

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Q. G., and Buckling, A. (2016). Migration highways and migration barriers created by host-parasite interactions. Ecol. Lett. 19, 1479–1485. doi: 10.1111/ele.12700

PubMed Abstract | CrossRef Full Text | Google Scholar