- Institute of Agricultural and Life Sciences, Academic Assembly, Shimane University, Matsue, Japan
In recent years, phenology – the seasonal timing of biological life cycles – has received increasing attention as climate change threatens to shift phenology. Phenology is crucial to the life cycle of organisms and their interactions with intimate partner species; hence, phenology has important fitness consequences suggesting that phenology can change through adaptive processes caused by species interaction. However, to date, there is limited understanding of how phenological adaptation occurs among interacting species and consequently affects ecological population dynamics. In this study, a phenological predator–prey co-adaptation model was evaluated to determine how adaptive phenological changes occur in prey and predator and how phenological coadaptation affects their coexistence. Population fluctuations tend to decrease and become stabilized when adaptation occurs rapidly. Furthermore, when adaptation is slow, predator–prey dynamics can be stabilized or destabilized depending on the initial difference in phenological timing between species. These results suggest that phenology shaped by slow coevolution can shift with changes in activity timing caused by environmental changes and simultaneously alter the stability of predator–prey dynamics. In contrast, phenology caused by rapid adaptation, such as phenotypic plasticity, may be robust to environmental change and maintain the stability of predator–prey dynamics. Understanding the types of adaptative processes that shape species phenologies may be crucial for predicting the ecological effects of climate change.
Introduction
Phenology is defined as the seasonal timing of biological life cycles, including all activities and events that take place within a season, such as reproduction, migration, and hibernation. The study of phenology has recently garnered attention in response to the observation that climate change can disrupt existing – and trigger new – phenological shifts (Visser and Both, 2005; Parmesan, 2006; Kharouba et al., 2018; Renner and Zohner, 2018; Visser and Gienapp, 2019). Because such shifts can affect interactions between species (Johansson et al., 2015; Visser and Gienapp, 2019), phenology is expected to have coadapted through species interactions and plays a key role in maintaining species interactions. However, to date, there is limited understanding about the relationship between phenological coadaptation and ecological population dynamics.
Most ecological systems and their species interactions are highly structured based on seasons (White and Hastings, 2018; Rudolf, 2019). Such complex systems require the emergence of consumers and/or pollinators to be precisely timed with that of essential resources. Several predators are ecologically specialized to predate certain prey species, implying that a small phenological shift in timing could result in starvation (Damien and Tougeron, 2019). These limitations infer that slight shifts in physiological pressures in abiotic environments – such as temperature – will force predator and prey to evolve their phenological requirements synchronously and asynchronously, respectively (Johansson et al., 2015; Lindén, 2018; Visser and Gienapp, 2019). Because seasonal rhythms of biological activities and life history events are controlled by genetic factors (Bradshaw and Holzapfel, 2001; Réale et al., 2003; Tauber et al., 2007; van Asch et al., 2007; Liedvogel et al., 2009; Wilczek et al., 2010), phenology can change through the occurrence of microevolution and/or phenotypic plasticity (Merilä and Hendry, 2014; Johansson et al., 2015; Radchuk et al., 2019).
The alignment and/or mismatch of phenological adaptation among interacting species indeed affect population dynamics (Hunter et al., 1997; McLaughlin et al., 2002; Hellmann et al., 2003; Deacy et al., 2017; Simmonds et al., 2020). Because of the species-specific phenological response to environmental changes, the interspecific variation in phenological shifts may disrupt species interactions, particularly when these interactions strongly depend on each other (Visser and Both, 2005; Donnelly et al., 2011; Forrest, 2015). Phenological mismatch causes changes in survival/reproduction and, thus, changes in demographics, and may result in species extinction (Both et al., 2006; Burkle et al., 2013; Budroni et al., 2018). However, seasonality adapts in response to fitness consequences just as well as it does in response to phenological mismatching among interacting species. This highlights the need to examine both ecological and evolutionary perspectives of phenological interactions among interacting species to gain a deeper understanding of the effects of phenological shifts on species interactions and community responses (Forrest and Miller-Rushing, 2010; Johansson et al., 2015; Visser and Gienapp, 2019).
Short-term evolutionary adaptation driven by rapid evolution or phenotypic plasticity can largely influence ecological population dynamics (Hairston et al., 2005; Miner et al., 2005). Such eco-evolutionary dynamics plays a key role in understanding the intricate population dynamics of interacting species (Fussmann et al., 2007). However, in previous theoretical studies, ecological and evolutionary dynamics of phenological interactions have often been examined independently (Williams et al., 2017). Considering each approach, a broader understanding of how phenological adaptation among interacting species and their population dynamics affect each other is limited, if not entirely lacking (Miller and Klausmeier, 2017; Sun et al., 2020). In particular, there are few theories on the coevolution of phenology among multiple interacting species (Miller and Klausmeier, 2017); this is despite the historically large development of the coevolutionary theory (Fussmann et al., 2007; Thompson, 2014). In this study, using an eco-evolutionary model, the coevolutionary dynamics of phenology in prey and predator species was examined to determine its effects on population dynamics. A single specialist predator that preys on a single species was targeted; this is because specialists are predicted to suffer most from phenological mismatching (Damien and Tougeron, 2019).
Model
Population Dynamics
Consider the simplest “one predator–one prey” system defined by the following ordinary differential equations:
where X, Y, and Z is the abundance of prey species, predator species, and resource species, respectively. For simplicity, it is assumed that resources affect prey dynamics, while prey does not affect resource dynamics (donor control). ε is the self-regulation of prey; aX is the consumption rate, i.e., the rate at which the prey consumes its resource; aY is the capture rate, i.e., the rate at which the predator captures its prey; gi is the conversion efficiency, which relates the prey or predator’s birth rate to resource or prey consumption, respectively; di is the death rate of each species; and ci is the cost of changing phenological traits from an optimal trait value perspective for each species. This is a physiological cost coming from being active at non-optimal temperatures (John-Alder et al., 1988; Rebaudo and Rabhi, 2018).
Here, aX = a0XpX[t] and aY = a0YpX[t]pY[t], where a0X is the basal consumption rate of a resource and a0Y is the basal capture rate of prey. Z = Z0pZ[t], where Z0 represents a constant that controls the absolute resource size, and pZ[t] is a time-varying function, which represents the resource seasonal cycle: pZ[t] = 1 + sin(2πt/T). The values pX[t] and pY[t] are time-varying functions, which represent the activity cycles of prey and predator species, respectively. Each basal biological cycle is described by the following sinusoidal function (Abrams, 2004; Nakazawa and Doi, 2012; Mougi, 2020):
where γi, T, and ui are the amplitude, cycle period, and timing of activity peaks, respectively, for prey and predator species. The consumption rate dependent on the activity rates of both predator and prey is closely related to the idea of the ecology of fear, in which frightened prey naturally forages less, while it can pass the risk of predation due to the inactivity (Clinchy et al., 2013). The timing of activity peaks is the evolving trait (see below). With activity cycles, γi = 1 is assumed, because activity levels need to be approximately zero when they take rest or hibernate during the inactive season. In this study, T = 365.
The cost functions are described by the following inverse bell-shaped function:
where c0i is the minimum cost at an optimal trait value, , in each species, and θi (>0) is the shape parameter of the function. As θi increases, the steepness of the function increases, implying that the trait change is very costly.
Dynamics of Phenological Trait
Dynamics of the mean trait value, ui, are modeled by a quantitative trait evolution model:
where Gi (i ∈ X, Y) represents the speed of adaptation (Abrams et al., 1993). The value Wi is the fitness of the mutant trait , defined as the per capita growth rate of the mutants: WX = and WY = . Equation 4 indicates that the rate of adaptive change in traits should be proportional to the selection gradient. If the selection gradient is positive (negative), the trait value increases (decrease). The direction of adaptive change is determined by the difference in the strength of the cost constraint (-c’i) and the increasing rate of benefit of developing the trait gXZ∂ aX /∂uX and -Y∂aY/∂uX in prey and gYX∂aY/∂uY in predator. Hence, the prey activity peak will change not only to increase its growth rate but also to adapt to predator activity and abundance. The predator will also adapt in response to prey activity and abundance. In this model, the trait values never converge to an trait equilibrium state because the system is always fluctuating on a long time scale. Hence, the trait cycle is the only final state.
For convenience, it is assumed that the trait value is normalized by the season period Ui = ui/T. Then, the trait dynamics are described as:
Note that Ui = ui/T is also substituted in Eq. 1. The r.h.s of Eq. 5 is transformed as: Giωi. Here ωX = CcX - B(gXaXZ -aYY) for prey, and CcY - BgYaYX for predator, where ci is the cost function, C = 2Tθi , B = 2πqi[t], = and qi(t) = cos{2π(t - TUi)/T} = sin{2π(t - TUi)/T + π/2}.
Here, consider the orders of a parameter ωi. I find that the order of a parameter, ωi, is similar to that of population dynamics. More specifically, the orders for C are 10–2 to 10–1, and that for B is 100 = 1. Thus, given that parameters except for B and C are those of population dynamics, the speed of ωi is determined by a term with B. Since B does not affect the order of the parameters that determine the speed of population dynamics, the relative speeds of population dynamics and trait dynamics are determined by Gi. When Gi < 1, trait dynamics are slower than population dynamics. When Gi > 1, trait dynamics are faster than population dynamics. In evolutionary adaptation, Gi would be small (Gi < 1) (DeLong et al., 2016) because trait change often occurs across generations, while with phenotypic plasticity, Gi would be large (Gi > 1) because trait change usually occurs within a generation.
The differential equations of coupled population and trait dynamics were calculated (Eq. 1 with Ui = ui/T and Eq. 5) using a computer simulation, and the effects of trait dynamics on the population dynamics of predator and prey were examined. With a sufficiently long simulation run (t = 5 × 105) to evaluate system stability in the non-equilibrium state, asymptotic behavior was obtained (4.8 × 105 < t < 5 × 105). I judged that if the value of stability index mentioned below is saturated after a long time period, the system converges to an attractor. Following this logic, changes were calculated numerically for the coefficient of variation of population size (CV), which is a stability index (the first part of the time series was excluded to avoid transient dynamics). As CV decreases, stability increases. This measure is one of the various indices of stability but may apply to empirical studies (McCann, 2000). Parameter values in the text are used for a middle range between organisms with shorter (e.g., plankton) and longer (e.g., mammal) generation time (see the Supplementary Table 1 for the parameter ranges examined). Alternatively, in the supplemental analysis (see section “Discussion”), I used real two extreme parameter settings in Daphnia (predator)-Chlamydomonas (prey) system (shorter generation times), and Weasel (predator)-Vole (prey) system (longer generation times) (Sherratt, 2001).
In the absence of adaptive dynamics (Gi = 0), predator and prey always show population oscillations with large amplitudes driven by seasonal activity cycles. In this study, I examined the coevolution of phenology (Gi > 0) caused by the timing of activity peaks (ui), and how phenological adaptation affects predator–prey population dynamics.
Results
When species cannot evolve (Gi = 0), activity cycles forcibly oscillate the otherwise globally stable prey–predator system (Figures 1A,B).

Figure 1. The speed of adaptation changes predator–prey dynamics. Dynamics of population sizes (A) and activity cycles (B) without adaptation. (C–F) Dynamics of population sizes in relation to the speed of adaptation. GX = GY = G is assumed. Faster adaptation (increasing G) tends to decrease the amplitudes of population cycles. (A,B) G = 0; (C) G = 0.001; (D) G = 0.05; (E) G = 1; and (F) G = 20. I–IV represent the patterns shown in different phases (see Figures 2, 3). Initial values X(0), Y(0), UX(0), and UY(0) are 0.1, 0.1, 10/365, and 20/365, respectively. Parameters are Z0 = 2, a0i = 0.5, ε = 0.1, gi = 0.2, di = 0.01, c0i = 0.01, θi = 0.001, = 10/365, and = 20/365. The time range shown on the horizontal axis is from 5 × 105–2T to 5 × 105 (for convenience, the initial time is notated as 0).
Once each species can shift its activity timing, however, this instability can be mitigated. To show how adaptation speed influences the behavior of the system, tests first focused on a case in which the adaptation speed of both species is equal (GX = GY = G). As the speed of adaptation increases, the amplitude of population cycles changes non-monotonically (Figures 1C–F). A key pattern is that the stability of both predator and prey dynamics, as measured by the CV, is higher when adaptation rates are high (G > > 1) (Figure 2D), and this does not change under various parameter conditions (Supplementary Figures 1, 2). Stabilization owing to faster adaptation is also observed even when the adaptation speeds of the species are unequal (GX≠GY) (Supplementary Figure 3). Another shape of the activity cycle does not change this pattern (Supplementary Figure 4). The strong stabilization effect as a result of faster adaptation (G > > 1) is maintained (Figures 2D–F) irrespective of the initial activity peak timings for the two species Ui(0).
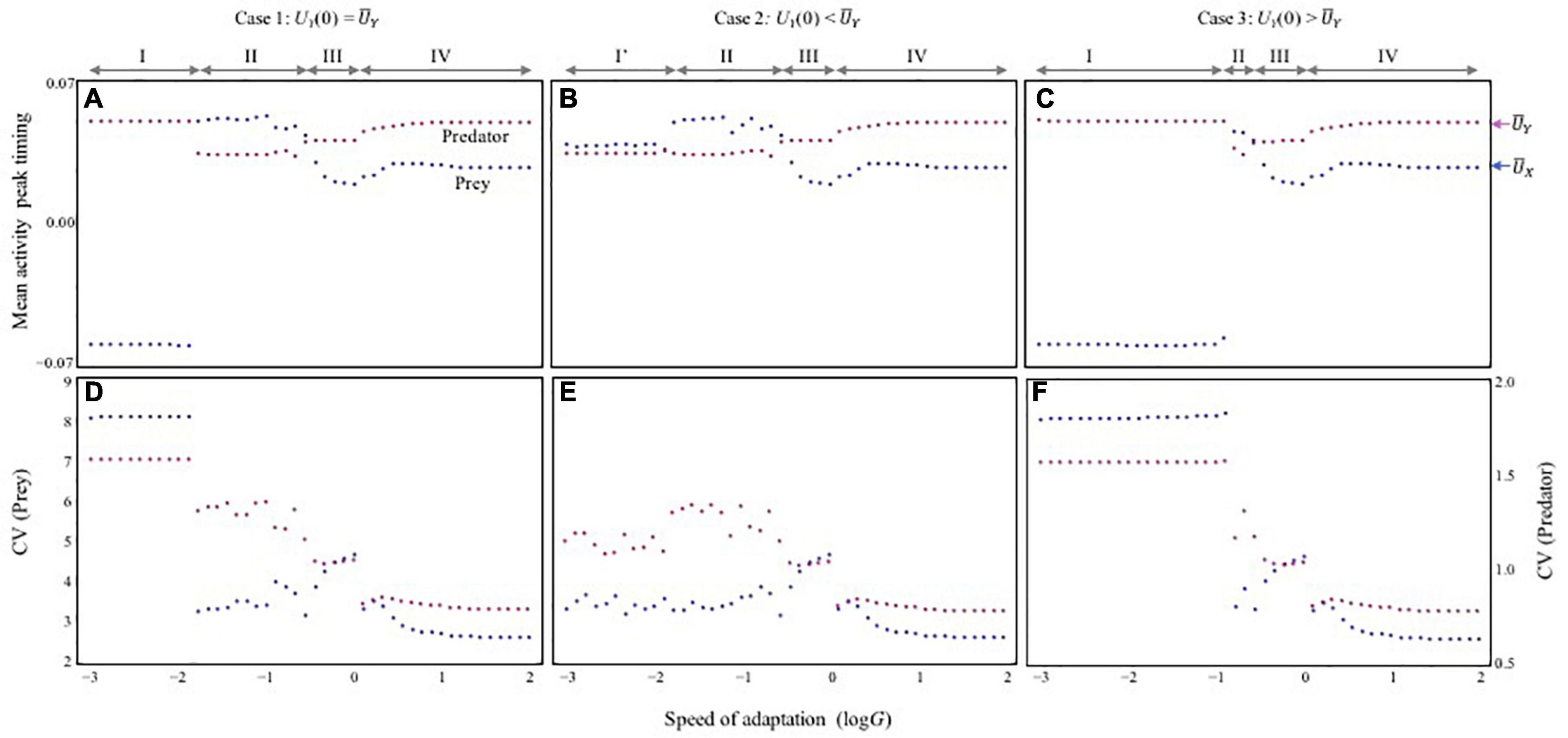
Figure 2. The relationship between adaptation speed and stability of population dynamics. (A–C) Mean activity peak timing (mean trait values) (A–C) and stability of population dynamics (D–F) with varying speed of adaptation. The stability is evaluated by the coefficient of variation (CV) of population sizes during a certain period after sufficient time (t), which corresponds with the time taken for the dynamics to reach an asymptote (see section “Model” for details). Mean trait values are also calculated in the same period. Red and blue arrows shown in (C) represent values of physiological optimal activity peak timing, and , respectively. In (d–f), red and blue represent the CV of predator (left vertical axis) and prey (right vertical axis), respectively. Parameters are the same as those of Figure 1. Under different initial variable conditions, three cases are observed. I checked whether bi-stability occurs by systematically changing initial values of traits (within a range –0.1 < Ui(0) < 0.1 with 0.01 increments). The three cases are based on the difference in the initial trait value of UY(0). (A,D) UY(0) = . (B,E) UY(0) < . (C,F) UY(0) > . It is assumed that UX(0) = = 10/365 and UY(0) = = 20/365 in (A,D), UY(0) = -0.01 in (B,E), and UY(0) = + 0.04 in (C,F).
In contrast, the ecological consequences of slow adaptation (G < < 1) can be altered by the initial activity peak timing Ui(0). The system can have alternative attractors (Supplementary Figure 5). Three qualitatively different patterns were observed (Figure 2) by changing UY(0) from the optimal , given UX(0) = . First, consider that both species have optimal timings, Ui(0) = . In this case, very slow adaptation has a strong destabilizing effect (phase I in Figures 2A,D). When UY(0) > , this pattern is maintained, but the instability occurs over a broader range of adaptation speeds (phase I in Figures 2C,F). These results indicate that if predator activity timing is later than that of its prey, the difference is not likely to be compensated for Figure 3A. Later predator activity delays the regulation of prey growth by the predator, resulting in destabilization. In contrast, when UY(0) < , the observed destabilization with slow adaptation is mitigated (phase I’ in Figures 2B,E). This result indicates that if predator activity timing is closer to that of its prey, the predator can evolve to match the prey activity timing or precede it (Figure 3E). Earlier predator activity can facilitate the regulation of prey growth by the predator, resulting in stabilization. When UY(0) ≦ , this type of stabilization is also observed with faster adaptation (phase II in Figures 2A–E, 3B). The multiple attractors disappear when adaptation speed is faster (phase III, IV in Figure 2). With rapid adaptation, predator and prey can maintain averagely physiologically optimal activity timing (phase IV in Figures 2A–C, 3D). When adaptation speed is at an intermediate level or similar to the speed of population dynamics, both species have greater costs compared with those for the faster adaptation case (phase III in Figures 2A–C, 3C). This difference in cost based on the adaptation speed can cause differences in stability because population reduction from costs and slow adaptation to environmental change can trigger fluctuations in abundance. The sudden jumps in the outcomes with increasing G are related to whether bi-stability occurs. In slow adaptation, bi-stability is likely to occur. Thus, if the initial setting is close to one attractor, trait value cannot reach to another attractor because the trait cannot change largely. Then, if the speed of adaptation becomes faster, it is possible that the trait can reach to another attractor particularly when the initial trait value is close to another attractor.
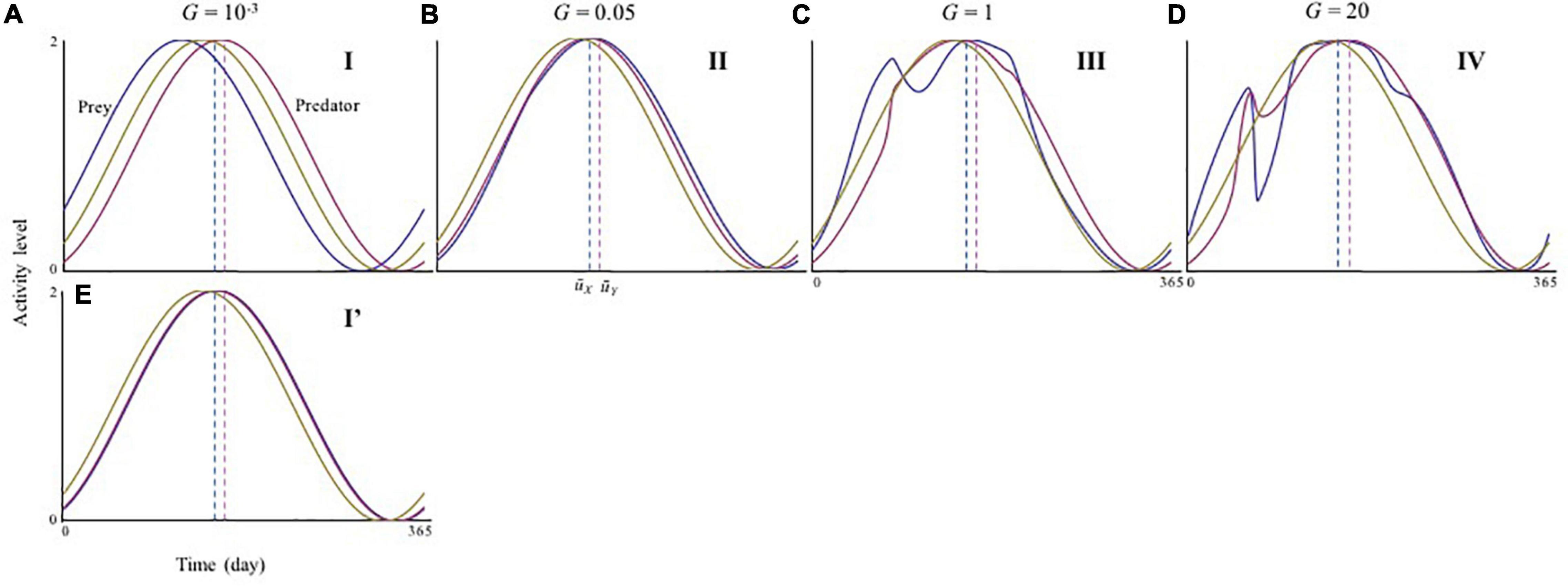
Figure 3. Activity cycles with varying adaptation speeds. (A–E) is seasonal activity cycle in different speed of adaptation, which corresponds to distinct phases shown in Figure 2. (A) G = 0.001 (phase I); (B) G = 0.05 (phase II); (C) G = 1 (phase III); (D) G = 20 (phase IV); and (E) G = 0.001 (phase I’). Yellow lines are the resource cycle. The blue and red dashed lines represent the physiological optimal activity peak timing and T and T, respectively. The time range shown in the horizontal axes is from 5 × 105–T to 5 × 105 (for convenience, the initial time is noted as 0). Parameters are the same as those of Figure 2.
Discussion
The present theory is based on the assumption that rapid phenological coadaptation can stabilize otherwise strongly oscillating predator–prey population dynamics. The speed of adaptation is a key element for the stabilization of these dynamics. When rapid adaptive changes in phenology can occur, population dynamics can stabilize. However, very slow phenological changes can have remarkably different ecological consequences, including destabilization or stabilization, depending on the initial timing of activity peaks. Fluctuations in phenology caused by climate changes can change the phenologies of predator and prey and alter the stability of predator–prey dynamics.
A coevolution of predator–prey relationships can occur in phenology. This observation was previously predicted based on a classic coevolutionary theory and is often used to explain a mismatch of phenological traits for predator and prey in nature (Singer and Parmesan, 2010; Lindén, 2018). The evolution of mismatching is expected only because prey–predator interaction is asymmetrical (Van Valen, 1973; Dawkins and Krebs, 1979). This is because, in theory, the exploiter should benefit from better synchrony, and the resource should benefit from less synchrony. However, this simple prediction was based on coevolutionary models of morphological, physiological, or behavioral traits related to their offense or defense. Trait interaction named as matching traits or bidirectional axes of victim vulnerability is most closely related to the present model (Abrams, 2000; Nuismer et al., 2005; Mougi, 2012). In such models, as with the present model, prey can increase their ability to escape from predators by becoming either significantly larger or significantly smaller in trait value. Although it is a reasonable model for morphological trait coevolution in some systems – e.g., predator gape size vs. prey size – it cannot be directly applied to phenological coevolution. This is because phenology itself, which drives population dynamics, is not considered. Additionally, in this model, prey does not evolve in response to the predator, contrary to the predator. In this contest, an intuitive prediction is not mismatching of phenology among species because the predator can benefit from better synchrony but prey cannot depart from the predator phenology. Interestingly, this study showed that mismatching can occur even in this situation. Phenology mismatching can be adaptive for a predator depending on the evolutionary speed. This suggests that phenological mismatching can occur only by species phenological adaptations even without external climate shifts.
Phenological adaptation has a similar stabilization mechanism to adaptive habitat choice behavior. In a habitat choice model, prey moves to a habitat where predators are scarce, while predators move to prey-rich areas. This spatial cycling can stabilize predator–prey population dynamics (Abrams, 2007). This type of adaptation can be a key stabilizing mechanism when each species has a high migration ability and can survive across a broad spatial range, which is in contrast to phenological adaptation. In addition, spatial adaptation can be complementary to phenological adaptation. If so, the activity patterns in a season shaped by phenological and spatial adaptations may compensate for insufficient temporal adaptation. In addition to spatial adaptation, adaptation to multiple biological rhythms or complexity of activity cycles (Mougi, 2020, 2021) may compensate for phenological adaptation. Activities are influenced not only by annual cycles but also daily and monthly cycles. The complexity of spatial and temporal adaptation and its influence on predator–prey dynamics should be the focus of future studies.
The type of predator–prey interaction may also affect model results. Analysis of two predator–prey systems with faster or slower population dynamics than the present model would be useful to address this question. I tested two systems with parameter settings for Daphnia (predator) and Chlamydomonas (prey), and in weasel (predator) and vole (prey) (Sherratt, 2001). The former (plankton) and latter (mammalian) systems have faster and slower population dynamics than the present model system (Supplementary Table 2). In a mammalian system, a qualitatively similar effect of adaptation speed to stability is observed and can show high destabilization at an intermediate speed of adaptation (Supplementary Figure 6). In the plankton system, no effects of initial conditions were detected (Supplementary Figure 7) but population dynamics were destabilized at an intermediate adaptation speed. In both systems, strong stabilization as a result of faster adaptation was commonly observed. These results suggest that stabilization effects owing to faster phenological adaptation, such as phenotypic plasticity, are a general consequence. Instability at intermediate speeds of adaptation is the second key consequence. Whether multiple attractors appear with slow adaptation or evolution depends on the system. Systems with faster population dynamics are not likely to stay in a particular state, and the multiple attractors in slow adaptation may be unlikely to occur in predators/prey with shorter generation times. To test this theory, and examine whether the adaptation occurs through evolution or plasticity, we need to examine the speed of adaptation itself. For a deeper understanding of phenological coadaptation, particularly when knowledge is not limited by the view of adaptation speed, there needs to be a more realistic model with microevolution and phenotypic plasticity. This model would need to be driven by both evolution and phenotypic plasticity in phenology. If both can occur, plasticity may relax the effect evolution slowdown and may cause increased stabilization of population dynamics. In addition, other rich complexities, such as a stage structure, functional response, and behavior (Khajanchi, 2014; Khajanchi and Banerjee, 2017; Sarkar et al., 2020; Sarkar and Khajanchi, 2020), will need to be considered to confirm the robustness of the theory.
Our results may potentially answer an important qualitative suggestion on how climate change can affect ecological consequences of consumer-resource dynamics. Climate change may destabilize population dynamics through fluctuations in the timing of activity of interacting species and/or slowing down evolutionary speed. Predator–prey phenology and population dynamics can both be changed evolutionarily if the activity timings are altered by factors such as climate change. Furthermore, climate change may destabilize consumer-resource dynamics by decreasing genotypes vulnerable to environmental change. Genetic variance of evolving traits is related to the speed of evolution (Abrams et al., 1993); therefore, the loss of particular genotypes in response to climate change can decrease evolution speed. If the existing genetic variance is so extensive that current populations can rapidly evolve, such a slowdown in evolutionary speed cold amplify population fluctuations of both consumer and resource.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
AM performed all parts of this research and wrote the manuscript.
Funding
This study was supported by a Grant-in-Aid for Scientific Research (C) (#20K06826) from the Japan Society for the Promotion of Science. The author appreciates the support from the Faculty of Life and Environmental Science at Shimane University for providing financial aid to publish this article.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.817339/full#supplementary-material
References
Abrams, P. A. (2000). The evolution of predator-prey interactions: theory and evidence. Annu. Rev. Ecol. Syst. 31, 79–105. doi: 10.1146/annurev.ecolsys.31.1.79
Abrams, P. A. (2004). When does periodic variation in resource growth allow robust coexistence of competing consumer species? Ecology 85, 372–382. doi: 10.1890/02-0684
Abrams, P. A. (2007). Habitat choice in predator–prey systems: spatial instability due to interacting adaptive movements. Am. Nat. 169, 581–594. doi: 10.1086/512688
Abrams, P. A., Matsuda, H., and Harada, Y. (1993). Evolutionarily unstable fitness maxima and stable fitness minima of continuous traits. Evol. Ecol. 7, 465–487. doi: 10.1007/bf01237642
Both, C., Bouwhuis, S., Lessells, C. M., and Visser, M. E. (2006). Climate change and population declines in a long-distance migratory bird. Nature 441, 81–83. doi: 10.1038/nature04539
Bradshaw, W. E., and Holzapfel, C. M. (2001). Genetic shift in photoperiodic response correlated with global warming. Proc. Natl. Acad. Sci. U S A. 98, 14509–14511. doi: 10.1073/pnas.241391498
Budroni, M. A., Loru, L., Pantaleoni, R. A., and Rustici, M. (2018). Effects of an asynchronous alien host on a native host-parasitoid system. Ecol. Complex. 33, 84–92. doi: 10.1016/j.ecocom.2018.01.001
Burkle, L. A., Marlin, J. C., and Knight, T. M. (2013). Plant-pollinator interactions over 120 years: loss of species, co-occurrence, and function. Science 339, 1611–1615. doi: 10.1126/science.1232728
Clinchy, M., Sheriff, M. J., and Zanette, L. Y. (2013). Predator-induced stree ans the ecology of fear. Func. Ecol. 27, 56–65. doi: 10.1111/1365-2435.12007
Damien, M., and Tougeron, K. (2019). Prey-predator phenological mismatch under climate change. Curr. Opin. Insect Sci. 35, 60–68. doi: 10.1016/j.cois.2019.07.002
Dawkins, R., and Krebs, J. R. (1979). Arms races between and within species. Proc. R. Soc. London. Ser. B. Biol. Sci. 205, 489–511. doi: 10.1098/rspb.1979.0081
Deacy, W. W., Armstrong, J. B., Leacock, W. B., Robbins, C. T., Gustine, D. D., Ward, E. J., et al. (2017). Phenological synchronization disrupts trophic interactions between Kodiak brown bears and salmon. Proc. Natl. Acad. Sci. U S A. 114, 10432–10437. doi: 10.1073/pnas.1705248114
DeLong, J. P., Forbes, V. E., Galic, N., Gibert, J. P., Laport, R. G., Phillips, J. S., et al. (2016). How fast is fast? eco-evolutionary dynamics and rates of change in populations and phenotypes. Ecol. Evol. 6, 573–581. doi: 10.1002/ece3.1899
Donnelly, A., Caffarra, A., and O’Neill, B. F. (2011). A review of climate-driven mismatches between interdependent phenophases in terrestrial and aquatic ecosystems. Int. J. Biometeorol. 55, 805–817. doi: 10.1007/s00484-011-0426-5
Forrest, J. R. K. (2015). Plant–pollinator interactions and phenological change: what can we learn about climate impacts from experiments and observations? Oikos 124, 4–13. doi: 10.1111/oik.01386
Forrest, J., and Miller-Rushing, A. J. (2010). Toward a synthetic understanding of the role of phenology in ecology and evolution. Philos. Trans. R. Soc. B Biol Sci. 365, 3101–3112. doi: 10.1098/rstb.2010.0145
Fussmann, G. F., Loreau, M., and Abrams, P. (2007). A. eco-evolutionary dynamics of communities and ecosystems. Funct. Ecol. 21, 465–477. doi: 10.1111/j.1365-2435.2007.01275.x
Hairston, N. G. Jr., Ellner, S. P., Geber, M. A., Yoshida, T., and Fox, J. A. (2005). Rapid evolution and the convergence of ecological and evolutionary time. Ecol. Lett. 8, 1114–1127. doi: 10.1111/j.1461-0248.2005.00812.x
Hellmann, J. J., Weiss, S., Mclaughlin, J. F., Boggs, C. L., Ehrlich, P. R., Launer, A., et al. (2003). Do hypotheses from short-term studies hold in the long-term? an empirical test. Ecol. Entomol. 28, 74–84. doi: 10.1046/j.1365-2311.2003.00484.x
Hunter, M. D., Varley, G. C., and Gradwell, G. R. (1997). Estimating the relative roles of top-down and bottom-up forces on insect herbivore populations: a classic study revisited. Proc. Natl. Acad. Sci. U S A. 94, 9176–9181. doi: 10.1073/pnas.94.17.9176
Johansson, J., Kristensen, N. P., Nilsson, J. Å, and Jonzén, N. (2015). The eco-evolutionary consequences of interspecific phenological asynchrony - a theoretical perspective. Oikos 124, 102–112. doi: 10.1111/oik.01909
John-Alder, H. B., Morin, P. J., and Lawler, S. (1988). Thermal physiology, phenology, and distribution of tree frogs. Am. Nat. 132, 506–520. doi: 10.1086/284868
Khajanchi, S. (2014). Dynamic behavior of a Beddington-DeAngelis type stage structured predator-prey model. Appl. Math. Comp. 244, 344–360. doi: 10.1016/j.amc.2014.06.109
Khajanchi, S., and Banerjee, S. (2017). Role of constant prey refuge on stage structure predator-prey model with ratio dependent functional response. Appl. Math. Comp. 314, 193–198. doi: 10.1016/j.amc.2017.07.017
Kharouba, H. M., Ehrlén, J., Gelman, A., Bolmgren, K., Allen, J. M., Travers, S. E., et al. (2018). Global shifts in the phenological synchrony of species interactions over recent decades. Proc. Natl. Acad. Sci. U S A. 115, 5211–5216. doi: 10.1073/pnas.1714511115
Liedvogel, M., Szulkin, M., Knowles, S. C. L., Wood, M. J., and Sheldon, B. C. (2009). Phenotypic correlates of Clock gene variation in a wild blue tit population: evidence for a role in seasonal timing of reproduction. Mol. Ecol. 18, 2444–2456. doi: 10.1111/j.1365-294X.2009.04204.x
Lindén, A. (2018). Adaptive and nonadaptive changes in phenological synchrony. Proc. Natl. Acad. Sci. U S A. 115, 5057–5059. doi: 10.1073/pnas.1805698115
McLaughlin, J. F., Hellmann, J. J., Boggs, C. L., and Ehrlich, P. R. (2002). The route to extinction: population dynamics of a threatened butterfly. Oecologia 132, 538–548. doi: 10.1007/s00442-002-0997-2
Merilä, J., and Hendry, A. P. (2014). Climate change, adaptation, and phenotypic plasticity: thee problem and the evidence. Evol. Appl. 7, 1–14. doi: 10.1111/eva.12137
Miller, E. T., and Klausmeier, C. A. (2017). Evolutionary stability of coexistence due to the storage effect in a two-season model. Theor. Ecol. 10, 91–103. doi: 10.1007/s12080-016-0314-z
Miner, B. G., Sultan, S. E., Morgan, S. G., Padilla, D. K., and Relyea, R. (2005). A. ecological consequences of phenotypic plasticity. Trends Ecol. Evol. 20, 685–692.
Mougi, A. (2012). Predator-prey coevolution driven by size selective predation can cause anti-synchronized and cryptic population dynamics. Theor. Popul. Biol. 81, 113–118. doi: 10.1016/j.tpb.2011.12.005
Mougi, A. (2020). Polyrhythmic foraging and competitive coexistence. Sci. Rep. 10:20282. doi: 10.1038/s41598-020-77483-3
Mougi, A. (2021). Diversity of biological rhythm and food web stability. Biol. Lett. 17:20200673. doi: 10.1098/rsbl.2020.0673
Nakazawa, T., and Doi, H. (2012). A perspective on match/mismatch of phenology in community contexts. Oikos 121, 489–495. doi: 10.1111/j.1600-0706.2011.20171.x
Nuismer, S. L., Doebeli, M., and Browning, D. (2005). The coevolutionary dynamics of antagonistic interactions mediated by quantitative traits with evolving variances. Evolution 59, 2073–2082. doi: 10.1554/05-141.1
Parmesan, C. (2006). Ecological and evolutionary responses to recent climate change. Annu. Rev. Ecol. Evol. Syst. 37, 637–669. doi: 10.1146/annurev.ecolsys.37.091305.110100
Radchuk, V., Reed, T., Teplitsky, C., van de Pol, M., Charmantier, A., Hassall, C., et al. (2019). Adaptive responses of animals to climate change are most likely insufficient. Nat. Commun. 10:3109. doi: 10.1038/s41467-019-10924-4
Réale, D., McAdam, A. G., Boutin, S., and Berteaux, D. (2003). Genetic and plastic responses of a northern mammal to climate change. Proc. R. Soc. London. Ser. B Biol. Sci. 270, 591–596. doi: 10.1098/rspb.2002.2224
Rebaudo, F., and Rabhi, V.-B. (2018). Modeling temperature-dependent development rate and phenology in insects: review of major developments, challenges, and future directions. Entomol. Exp. Appl. 166, 607–617. doi: 10.1111/eea.12693
Renner, S. S., and Zohner, C. M. (2018). Climate change and phenological mismatch in trophic interactions among plants, insects, and vertebrates. Annu. Rev. Ecol. Evol. Syst. 49, 165–182. doi: 10.1146/annurev-ecolsys-110617-062535
Rudolf, V. H. W. (2019). The role of seasonal timing and phenological shifts for species coexistence. Ecol. Lett. 22, 1324–1338. doi: 10.1111/ele.13277
Sarkar, K., and Khajanchi, S. (2020). Impact of fear effect on the growth of prey in a predator-prey interaction model. Ecol. Complex. 42:100826. doi: 10.1016/j.ecocom.2020.100826
Sarkar, K., Khajanchi, S., Chandra Mali, P., and Nieto, J. J. (2020). Rich dynamics of a predator-prey system with different kinds of functional responses. Complexity 2020:4285294.
Sherratt, J. A. (2001). Periodic traveling waves in cyclic predator-prey systems. Ecol. Lett. 4, 30–37. doi: 10.1046/j.1461-0248.2001.00193.x
Simmonds, E. G., Cole, E. F., Sheldon, B. C., and Coulson, T. (2020). Phenological asynchrony: a ticking time-bomb for seemingly stable populations? Ecol. Lett. 23, 1766–1775. doi: 10.1111/ele.13603
Singer, M. C., and Parmesan, C. (2010). Phenological asynchrony between herbivorous insects and their hosts: signal of climate change or pre-existing adaptive strategy? Philos. Trans. R. Soc. B Biol. Sci. 365, 3161–3176. doi: 10.1098/rstb.2010.0144
Sun, Z., Parvinen, K., Heino, M., Metz, J., Marc de Roos, A., et al. (2020). Evolution of reproduction periods in seasonal environments. Am. Nat. 196, E88–E109. doi: 10.1086/708274
Tauber, E., Zordan, M., Sandrelli, F., Pegoraro, M., Osterwalder, N., Breda, C., et al. (2007). Natural selection favors a newly derived timeless allele in Drosophila melanogaster. Science 316, 1895–1898. doi: 10.1126/science.1138412
van Asch, M., van Tienderen, P. H., Holleman, L. J. M., and Visser, M. E. (2007). Predicting adaptation of phenology in response to climate change, an insect herbivore example. Glob. Chang. Biol. 13, 1596–1604. doi: 10.1111/j.1365-2486.2007.01400.x
Visser, M. E., and Both, C. (2005). Shifts in phenology due to global climate change: the need for a yardstick. Proc. R. Soc. B Biol. Sci. 272, 2561–2569. doi: 10.1098/rspb.2005.3356
Visser, M. E., and Gienapp, P. (2019). Evolutionary and demographic consequences of phenological mismatches. Nat. Ecol. Evol. 3, 879–885. doi: 10.1038/s41559-019-0880-8
White, E. R., and Hastings, A. (2018). Seasonality in ecology: progress and prospects in theory. PeerJ [Preprint]. doi: 10.7287/peerj.preprints.27235v1
Wilczek, A. M., Burghardt, L. T., Cobb, A. R., Cooper, M. D., Welch, S. M., and Schmitt, J. (2010). Genetic and physiological bases for phenological responses to current and predicted climates. Philos. Trans. Biol. Sci. 365, 3129–3147. doi: 10.1098/rstb.2010.0128
Keywords: phenology, coevolution, predation, population dynamics, stability
Citation: Mougi A (2022) Phenological Coadaptation Can Stabilize Predator–Prey Dynamics. Front. Ecol. Evol. 10:817339. doi: 10.3389/fevo.2022.817339
Received: 17 November 2021; Accepted: 04 May 2022;
Published: 18 May 2022.
Edited by:
Michael Sears, Clemson University, United StatesReviewed by:
Eric Jason Pedersen, Concordia University, CanadaSubhas Khajanchi, Presidency University, India
Hao Wang, University of Alberta, Canada
Mohd Hafiz Mohd, Universiti Sains Malaysia, Malaysia
Copyright © 2022 Mougi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Akihiko Mougi, YW1vdWdpQGdtYWlsLmNvbQ==
 Akihiko Mougi
Akihiko Mougi