- 1Anhui Province Key Laboratory of Wetland Ecosystem Protection and Restoration, School of Resources and Environmental Engineering, Anhui University, Hefei, China
- 2School of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming, China
- 3School of Ecology and Environment, Northwestern Polytechnical University, Xi’an, China
Due to density-dependent selection, the ecological factors impacting population dynamics can play an important role in promoting cooperation, and accordingly, benefit a population from the eco-evolutionary feedback. This implies that cooperation between individuals could help resist the attack of infectious diseases. Yet, little is known about how cooperation evolves in response to infections. We here examined theoretically the impact of disease infections with various transmission types on cooperation evolution and its feedback to population dynamics. Results show that infected populations can evolve to be more cooperative, and the level of cooperation increases with the transmission rate, which can protect the population against decline due to infection and prevent population extinction driven by defection. A high transmission rate can stabilize population fluctuation, while a relatively low transmission rate could destabilize population dynamics. We argue that the mechanism underlying such stress-induced cooperation is analogous to the cascade effect of trophic interactions in food webs: reduction in selfishness from environmental stress indirectly relaxes the exploitation of cooperators by defectors. These findings emphasize the role of eco-evolutionary feedback in evolving cooperation and the ecological significance of cooperation evolution for populations withstanding disease infection.
Introduction
Cooperative behaviors are often observed in organisms ranging from microorganisms to animals and humans, and have become a fascinating problem attracting much attention in evolutionary ecology and social biology (Dugatkin, 1997; Wilson, 2000; West et al., 2006; Kurzban et al., 2015). Because cooperative individuals benefit others at cost to themselves, an evolving population is often dominated by defectors who receive the benefit from cooperators without cost (Doebeli and Hauert, 2005). This raises the question of how cooperative behaviors survive in such a selfish population or by what mechanisms cooperation can emerge (Nowak, 2006b).
The Prisoner’s Dilemma game has been developed as a general paradigm for studying the evolution of cooperation, which captures the fundamental nature of cooperation in a simple form (May, 1987; Doebeli and Hauert, 2005). So far, based on the paradigm, three theories on cooperation evolution have been developed, which are kin selection (Hamilton, 1963, 1964), reciprocal altruism (Trivers, 1971; Axelrod and Hamilton, 1981), and group selection (Wilson, 2000; Traulsen and Nowak, 2006). These theories all reveal that non-random assortative interactions play a key role for the evolution of cooperation; that is, cooperative individuals have a higher probability to interact (play game) with other cooperators compared to the probability of random interactions. Mechanisms that can give rise to such assortment are diverse and, for instance, involve kinships, complex interplays, and population structures, suggesting multiple routes to cooperative phenomena in nature (Nowak, 2006b).
It is worth noting that the classic evolutionary games are often modeled under the assumption of infinite population [e.g., replicator equations derived from exponential population growth (Hofbauer and Sigmund, 1998; Zheng et al., 2018)] or constant population size [e.g., spatial game (Nowak and May, 1992), network game (Lieberman et al., 2005), and finite population game (Nowak et al., 2004)], ignoring population dynamics. With this assumption, evolutionary dynamics have to only describe the change of various strategies in relative frequency even when game-environment feedback involved (Weitz et al., 2016; Tilman et al., 2020). This treatment typically presumes that population dynamics are considered operating at a much faster pace relative to evolutionary processes—populations normally first reach ecological equilibria when evolutionary changes occur (Pásztor et al., 2016), or that individuals imitate more successful ones in social learning, implying population size remains unchanged when the frequency of strategies vary over time (Hofbauer and Sigmund, 1998). In recent years, however, empirical evidence has emerged to support that ecological and evolutionary dynamics could occur on the same time scale and impose strong effects on each other in the form of eco-evolutionary feedback loops (Hairston et al., 1999, Hairston<suffix>Jr.</suffix>, Ellner et al., 2005; Schoener, 2011; Hendry, 2017). In particular, some theoretical and experimental studies suggest that, when facing the challenge of harsh external environment, cooperative individuals can be selected to mitigate the negative environmental stress (Zhang et al., 2005; Zhang and Hui, 2011; Datta et al., 2013; Sanchez and Gore, 2013). Consequently, within the ecological context, the interaction between individuals has to be based on instantaneous population density rather than just the frequency of different strategies, resulting in density-dependent selection instead of frequency-dependent selection. Evidently, environmental stress that reduces population density can potentially release the cooperative individuals from defectors’ exploitation (Hui et al., 2005; Zhang et al., 2010; Zhang and Hui, 2011). This implies that any factors in relation to population density could have profound influences on the evolution of cooperation.
Infectious diseases can seriously threaten ecosystem and human health, especially attributable to the accelerating biodiversity loss (Morens et al., 2004; Pimm et al., 2014). Infectious diseases necessarily impact the dynamics of host population, and accordingly could have significant influence on the evolution of cooperation; and, in turn, the cooperation between individuals plays a potential role to suppress the infectious spread. However, to the best of our knowledge, there is little research on the evolution of cooperation in infected populations. In this study, based on the classic epidemiological models (SI, SIS, and SIR models), we developed the eco-evolutionary feedback models for cooperation evolution in populations infected under different transmission types, and analyzed how the population responds to disease infections in the aspect of cooperation evolution.
Models
We consider a population, of which individuals have either a cooperative or defective behavioral strategy (respectively denoted by C and D). A cooperator yields benefit b to its opponent at cost c, whereas a defector doesn’t generate any benefit due to paying nothing (i.e., the Prisoner’s Dilemma game with b > c > 0). The population inhabits a habitat consisting of a large number of suitable sites, each of which is either occupied by a cooperator or a defector, or being empty. Each individual plays the game with an individual of the same strategy at probability m and with an individual in a randomly chosen site at probability 1-m; no action is taken if the site is empty. The mean payoff of a cooperative individual can be calculated by fC = (b−c)(m + (1−m)pC)−c(1−m)pD and that of a defective individual by fD = b(1−m)pC, where pC and pD are the density of cooperators and defectors, i.e., the proportion of sites respectively occupied by cooperators and defectors (Zhang and Hui, 2011). This assumption is similar to the definition to assortment by Eshel and Cavalli-Sforza (1982). The parameter m indicates the strength of assortment. Assuming that the reproduction success of each individual is associated with its payoff from playing games and depends on the density of available empty sites, the dynamics of the population can be described by the differential equations:
Here, ξC and ξD are respectively the per capita reproduction rate of cooperators and defectors, which are baseline reproduction rate ξ plus the mean payoff of them, i.e., ξC = ξ + fC and ξD = ξ + fD, and δ is mortality. The term 1−pC−pD indicates the proportion of empty sites, suggesting density-dependent reproduction. The dynamics of the population is similar to the colonization-extinction process of Levins’ metapopulation, but each site can be occupied by only one individual instead of a subpopulation (Levins, 1969). Note that both the baseline reproduction rate and the mortality are independent of individual’s behavioral strategy. This implies that all individuals within the population, either cooperators or defectors, are under the same ecological context except for gaming interactions between them. This model is typically different from the classical replicator equation in two aspects: (1) the game payoff depends on the absolute density of a strategy in population rather than its relative frequency as described in the replicator equation; (2) the dynamical change of population size (i.e., population demography) is considered explicitly, leading to the dimensionality of the system to be one more than the corresponding replicator equation (noting that the dimensionality of replicator equation is one less than the number of strategies). Therefore, this model not only describes ecological dynamics (i.e., the dynamical change of population size) but also incorporates the biological evolutionary dynamics (i.e., the change of the frequency of both strategies in the Prisoner’s Dilemma game under density-dependent selection) into the ecological context; consequently, it allows us to study the impact of the eco-evolutionary feedback and various ecological factors on the evolution of cooperation.
In this study, we specifically pay attention to the impact of infectious diseases as an ecological factor on the evolution of cooperation. There are three kinds of classic models for studying the transmission dynamics of infectious diseases (Keeling and Rohani, 2008): SI, SIS, and SIR models (S, I, and R represent, respectively, the susceptible, the infected, and the recovered with acquired immunity). The SI model is designed for the cases that susceptible individuals may be infected but they cannot recover once infected (thus succumb to infection), i.e., a unidirectional transmission from the susceptible to the infected. In the SIS models, the infected can recover but are unable to acquire immunity (still susceptible after recovery), representing a bidirectional transformation between the susceptible and the infected. The SIR models consider the cases that the recovered can acquire immunity, resulting in a unidirectional transformation from the susceptible to the infected and eventually to the recovered. Despite the diversity and complexity of pathogenic diseases, these models largely capture fundamental epidemiological process of infectious diseases: transmission, recovery, and lethality, and provide basic frameworks for almost all extended epidemiological models (Keeling and Rohani, 2008). Therefore, these models are capable for exploring the effect of infectious diseases on the evolution of cooperation.
In what follows, we present how to couple the three kinds of epidemiological models with the ecological Prisoner’s Dilemma game (Equation 1) to develop the mathematical models of cooperation evolution in infected populations. In the SI case, we can identify four categories of individuals in an infected population of cooperation evolution: susceptible cooperators, susceptible defectors, infected cooperators, and infected defectors. Assuming that both the interactions between individuals and non-interactive random contacts can incur disease transmission, the change of the density of the four categories of individuals (denoted by pCS,pDS,pCI, and pDI ) over time can be formulated by the differential equations
Here β1 = β + κ(1−m) is the transmission rate due to random interactions (κ(1−m)) as well as non-interactive random contacts (β), and β2 = κm the transmission rate due to assortative interaction, where κ indicates the transmission rate when individuals interact. The parameter μ is death rate caused by infection (due to lethality of infectious disease); and pC = pCS + pCI and pD = pDS + pDI. All the other parameters are the same as in Equation 1. In particular, when β = 0 and κ = 0 (i.e., no infection), the model turns back into Equation 1. If we consider the non-immune recovery of infected individuals, i.e., the SIS case, Equation 2 can be modified as
where γ is recovery rate (assuming cooperators and defectors have the same recovery rate). If the recovered individuals have acquired immunity, i.e., the SIR case, we need to consider the density of cooperators and defectors recovered from infection (denoted by pCR and pDR) besides the density of abovementioned four categories. The dynamics of the infected population can then be expressed as
Here, parameter γ, the same as in Equation 3, refers to the recovery rate, but the recovered individuals have acquired immunity instead of still being susceptible as expressed in Equation 3. In addition, pC = pCS + pCI + pCR and pD = pDS + pDI + pDR, slightly different from that in Equations 2, 3.
Now, we have developed four sets of models for the evolution of cooperation in the populations either not infected (Equation 1) or infected by pathogens with various transmission types (Equation 2–4). The infectious diseases are characterized by transmission rate, recovery rate, and lethality, as well as whether infected individuals can recover and whether recovered individuals can acquire immunity. Therefore, the models allow us to study the effect of diseases that spread in the different ways on the evolution of cooperation. Through comparing the evolutionary dynamics of infected populations (Equations 2–4) with their uninfected counterparts (Equation 1), we study how individuals with different game strategies (cooperation versus defection) fare in a population in response to disease infections.
Results
The dynamics of the uninfected population (i.e., Equation 1) was first analyzed. In doing so, we made a distinction between weak assortment, defined as , and strong assortment, defined as . For the case of weak assortment, the system manifests diverse dynamical behaviors. When δ < ξ, both cooperative and defective individuals can persist alone in the absence of the other (illustrated in white and light gray on the left-hand side of Figures 1A,B). But the cooperative individuals can be invaded and excluded by defectors when (note that the right side is always smaller than ξ (see Supplementary Materials); illustrated in white on the left-hand side of Figures 1C,D). This means the occurrence of cooperation requires mortality sufficient high (i.e., , as shown by light gray in Figures 1C,D). When δ > ξ, cooperative individuals can exist in the form of either global stability or bi-stability (strong Allee effect) in the absence of defectors, but defective individuals fail to survive alone without cooperators (as shown by gray, dark gray, and purple in Figures 1A,B). However, in this case, defectors can invade the cooperative population by exploiting cooperators when extinction rate is below a threshold, i.e., δ < δ* (illustrated in gray in Figures 1C,D), where the threshold is when (note that the right side is always smaller than c/b, which means this condition still retains weak assortment) and when (see Supplementary Materials). Consequently, defectors possibly coexist with cooperators in the form of asymptotic stability, damping oscillation, or periodic fluctuation (illustrated in gray in Figures 1C,D). Interestingly, the invasion of defectors into a cooperative population does not always result in coexistence; the whole population may go extinct due to the invasion of defectors when mortality is relatively high (illustrated in dark gray in Figures 1A,C, 5A). For the case of strong assortment defined as above, cooperative individuals are absolutely immune to defectors: cooperators always successfully expel defectors completely even if they can persist alone without cooperators (see Supplementary Materials).
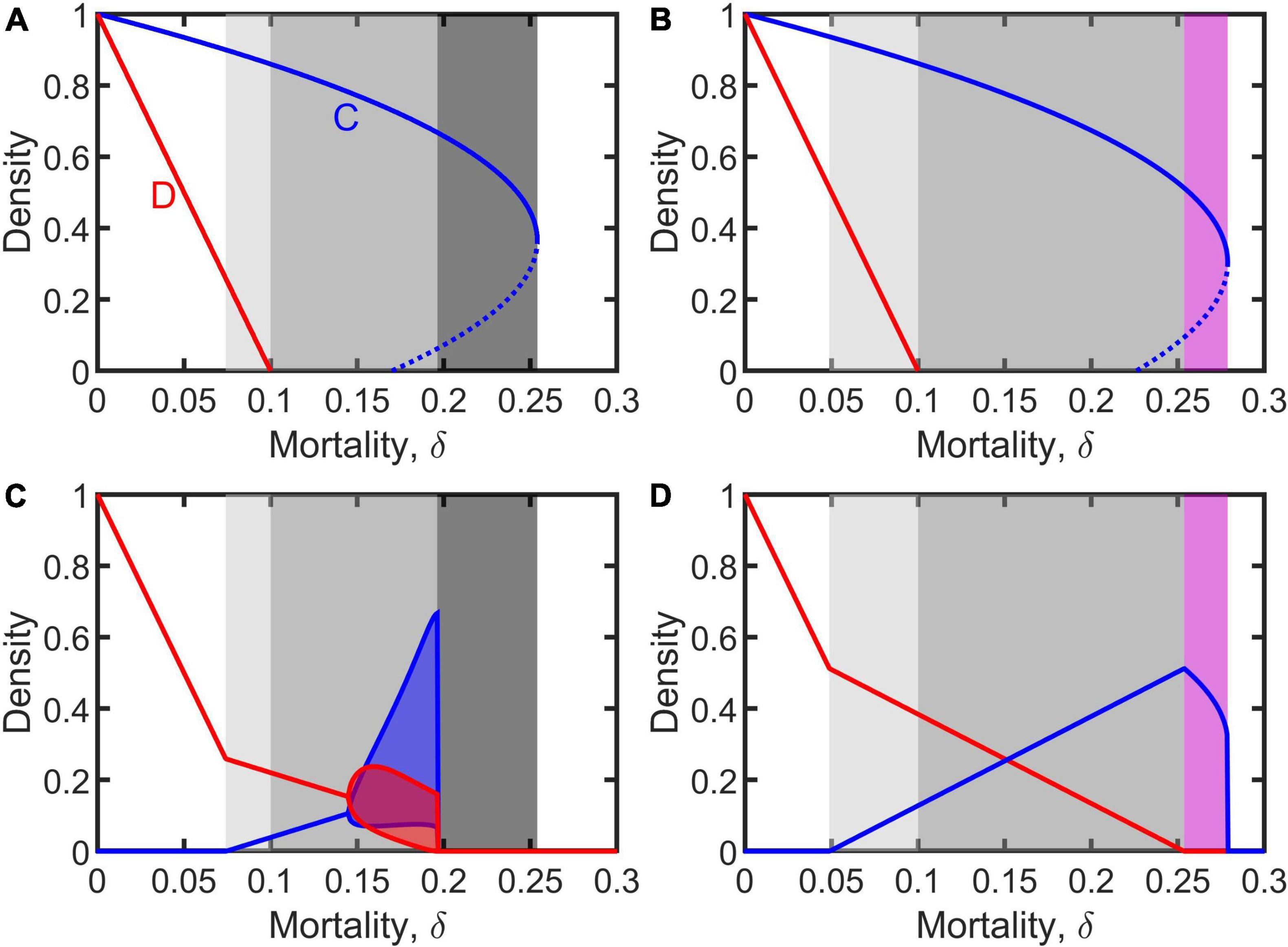
Figure 1. Equilibrium density of cooperators and defectors (denoted by blue and red), as a function of mortality, when living alone (A,B) or coevolving together (C,D). Light gray indicates that cooperators and defectors can persist separately and also coexist; gray represents that they can coexist but defectors cannot survive alone; dark gray represents that defectors can invade cooperative population but leading to the entire population to go extinct; and purple represents that defectors cannot invade cooperative population. Dashed lines on panels (A,B) indicates unstable equilibrium. Blue and red shadows on panel (C) represent the fluctuant range of densities in periodic solutions. Parameters: b = 1, c = 0.3, ξ = 0.1, and m = 0.1 for panels (A,C) representing the case of and m = 0.18 for panels (B,D) representing the case of (see first paragraph in Results). Supplementary Figure 1 in Supplementary Materials shows the similar results with different parameter values.
Based on the SI, SIS, and SIR model of cooperation evolution (Equations 2–4), we analyzed the condition that an infectious disease can successfully invade a population when a small number of infections occur initially. The results show that the infectious disease can invade the population (i.e., per-capita infection rate is greater than zero) if the following inequality holds
Here, piS = pCS if the initial infected individuals are cooperators and piS = pDS if they are defectors (note that initial infections are either all cooperators or defectors due to their rarity); pS = pCS + pDS represents the density of susceptible individuals; and α = δ + μ for the SI model and α = δ + μ + γ for the SIS and SIR models, which indicates the rate at which the infected are removed. The inequality (5) shows that the invasion condition of a pathogen into the population is when the mean number of susceptible individuals infected by an infectious individual in one unit time (β1pS + β2piS) exceeds the mean number removed from the group of infectious individuals (α); in other words, the mean time that an infected individual needs to infect another individual () shorter than the mean duration of the infection (). Note that is the basic reproduction number of disease transmission, referring to as the number of infections caused by a single infected individual per unit time (β1pS + β2piS) multiplied by the mean duration of the infection (). The inequality (5) hence gives the basic condition of epidemic outbreak, i.e., R0 > 1.
If the population is situated at a coexisting equilibrium when getting infected, i.e., , , and (see Supplementary Materials), then Equation 5 can be rewritten as
when the individuals infected initially are all cooperators, and
when the individuals infected initially are all defectors. The first term in Equations 6, 7 describes the number of individuals infected by an infectious individual in one unit time through non-interactive contacts, while the second term is due to playing games between individuals. It is worth noting that the former is independent of baseline reproduction rate ξ and mortality δ but the later depends on them. The effective contact rate in playing games (the term in brackets) decreases with the baseline reproduction rate when infections start with cooperative individuals, but it increases with mortality. This result is reversed for the invasion of infectious disease starting with defective individuals. Notably, an infectious disease invades the population more easily from initially infecting cooperative individuals than defective ones when the term in brackets of Equation 6 is greater than that of Equation 7, i.e., the following inequality holds
Otherwise, it is easier to invade the population from initially infecting defective individuals. The inequality (8) shows that, although a population with high mortality is able to evolve to be more cooperative (Figures 1C,D), it is also at a higher risk of infection through cooperators. In particular, if κ = 0 (i.e., no transmission by interactions), both Equations 6, 7 become
where is the transmission rate divided by the removal rate, and refers to the reward rate of cooperation per paying unit cost. The inequality (9) directly connects the relative transmission rate of diseases (left side) with the parameters related to the evolution of cooperation (right side), and defines an invasion threshold for pathogenic diseases (Figure 2). The greater the two cooperation parameters (i.e., and m) are, the easier the population is getting infected, while a high removal rate can resist infection due to its reduction of the relative transmission rate. Note that the invasion condition is independent of population’s baseline reproduction rate (ξ) and mortality (δ), while they affect the coexistence of cooperators and defectors (Figure 1).
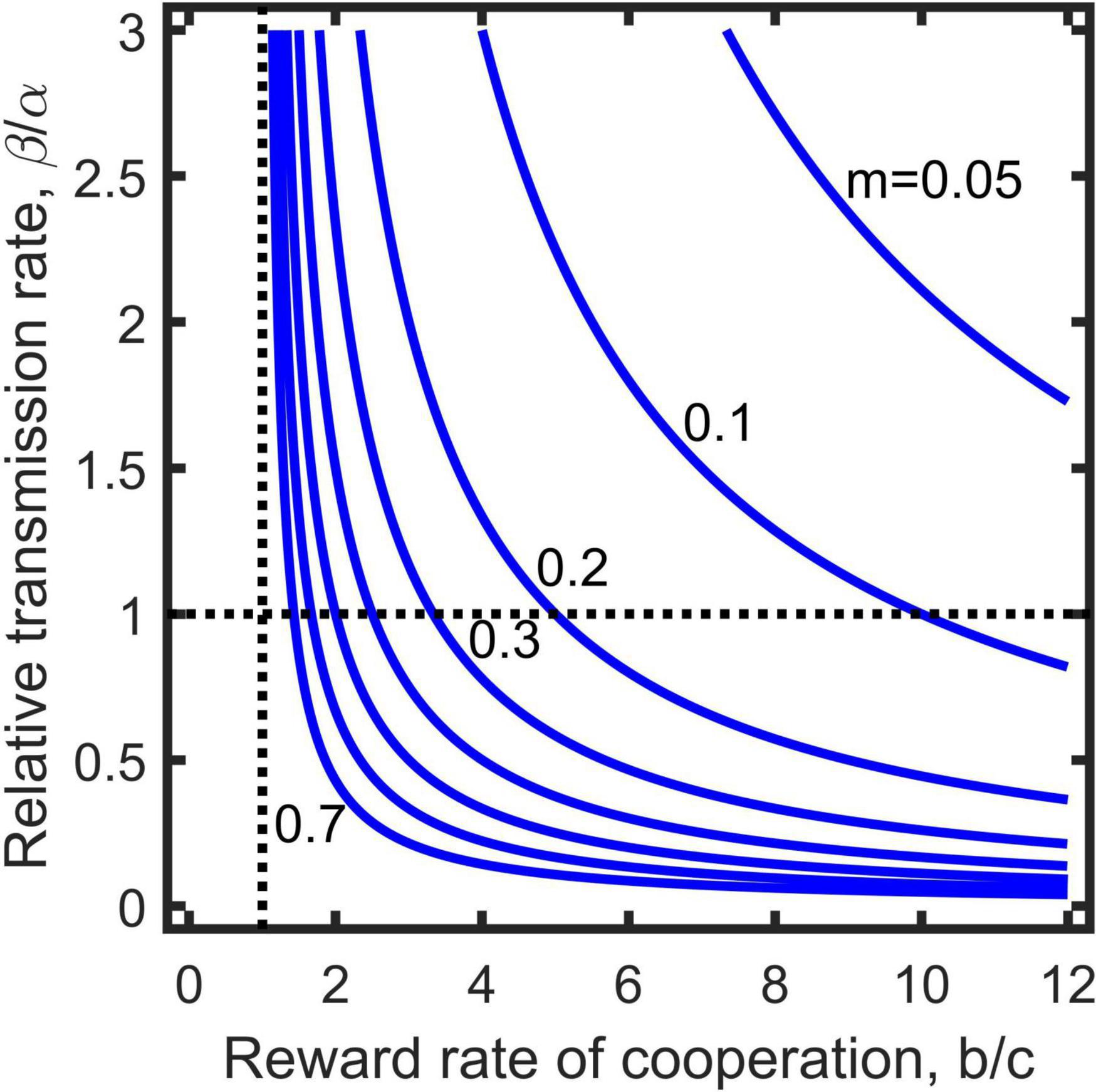
Figure 2. Invasion threshold of pathogenic diseases to the population of cooperation evolution when transmission by interaction is absent (Equation 9). The parameter values taken above the curves assures invasion successful, otherwise, below which invasion fails. Vertical dashed line indicates cooperation benefit is equal to cost (i.e., ), and horizontal dashed line separates weak assortment (above the line, ) from strong assortment (below the line, ).
The dynamical behaviors of the epidemiological models (Equations 2–4) after invaded by infectious diseases were investigated by numerical simulations. Our simulations show that, in general, regardless whether the population is at a stable equilibrium status or periodically fluctuating before infected, and regardless of disease transmission type (e.g., SI, SIS, or SIR), the spreading of infectious diseases can make the population evolve toward becoming more cooperative (Figure 3). The density of cooperators increases with increasing transmission rate (non-interactive β and interactive κ) while the density of defectors declines (Figure 4 and Supplementary Figures 2–4). Moreover, the epidemic spreading with a high transmission rate can eliminate the periodic fluctuation of populations caused by the feedback between evolutionary games and ecological dynamics (see Figures 3B,D,F, and the bottom panels in Figure 4 and Supplementary Figures 2–4), while a relative low transmission rate could trigger new periodic fluctuations or intensify existing fluctuations (see the bottom two rows of panels in Figure 4 and Supplementary Figures 2–4). In addition, we found that, although the invasion of defective strategy into a cooperative population might trigger the extinction of the entire population under the eco-evolutionary feedback especially when mortality is high (Figures 1A,C, 5A), pathogenic infections with a high transmission rate, regardless of transmission type, could prevent such an extinction and lead to the coexistence of cooperators and defectors (Figure 5B).
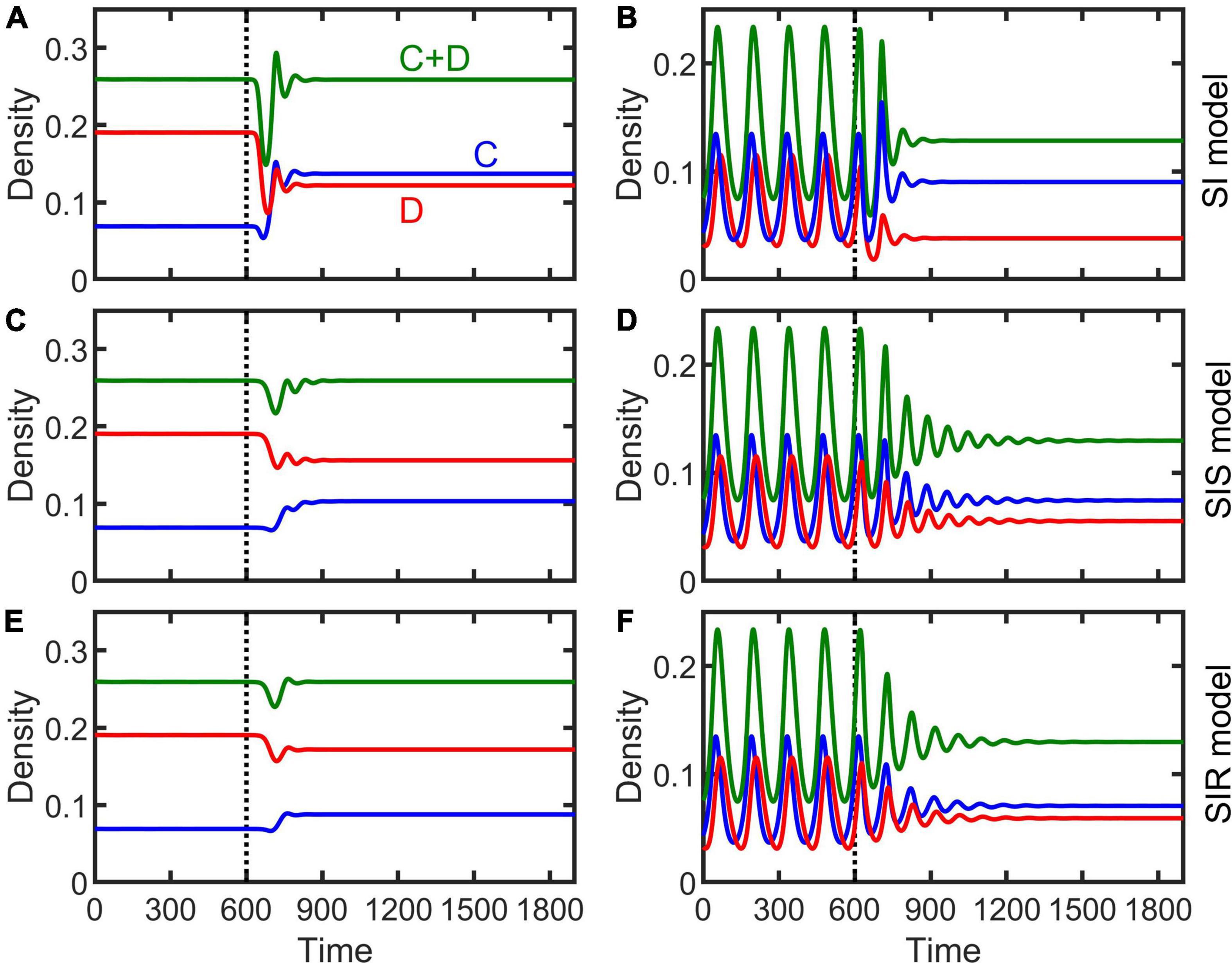
Figure 3. Effect of infectious diseases on the evolution of cooperation in stable (left column) or periodically fluctuating (right column) populations in the SI (A,B), SIS (C,D), and SIR (E,F) models. Vertical dashed lines indicate the time when infectious disease occurs in the population. Parameters are β = 0.8, κ = 0.8, ξ = 0.1, γ = 0.1, δ = 0.12 for left column and δ = 0.16 for right column, and the other parameters the same as Figures 1A,C.
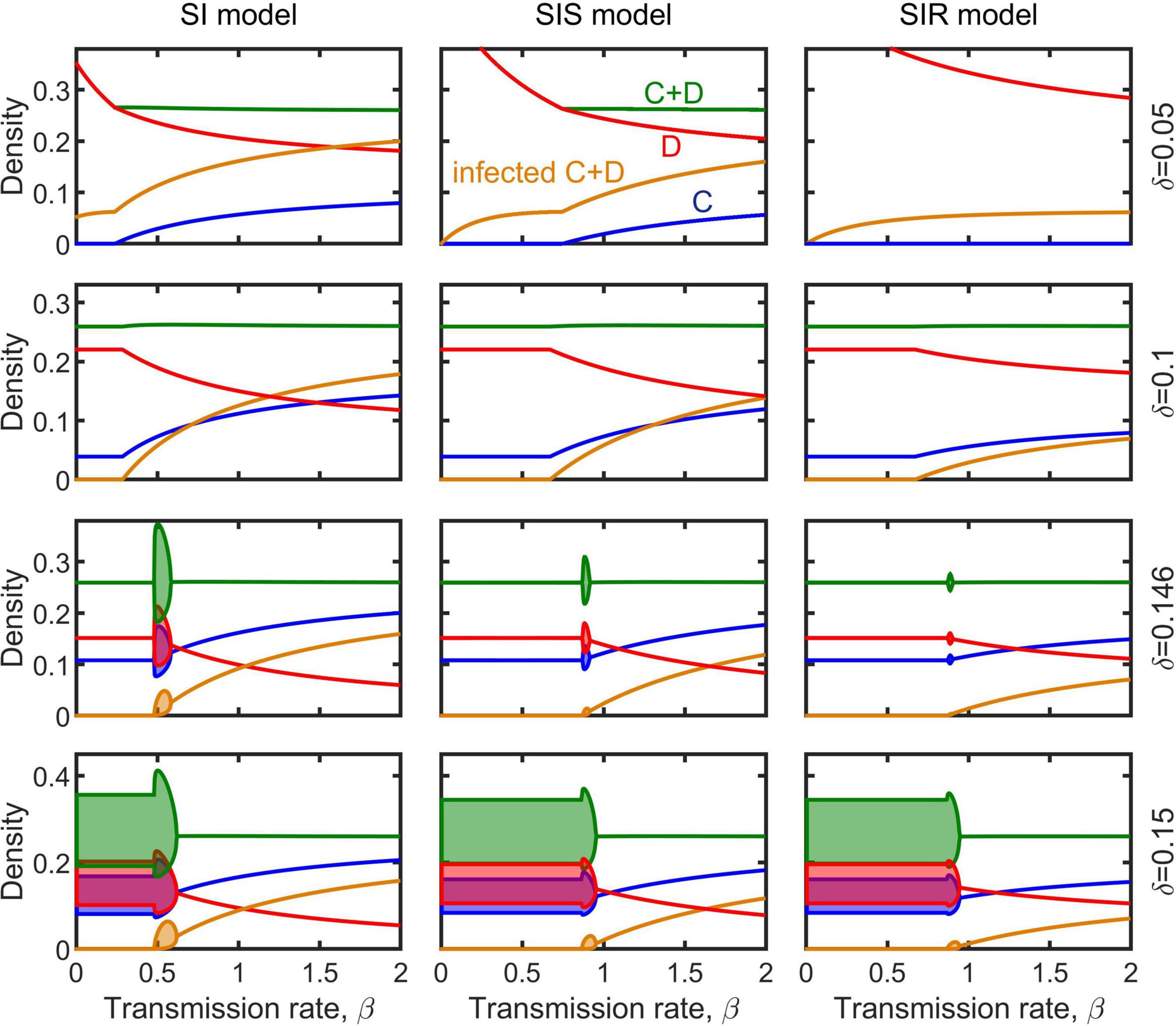
Figure 4. Effect of transmission rate β on the evolution of cooperation in the model of SI (left column), SIS (middle column), and SIR (right column). Blue, red, brown, and green shadows represent the density range of cooperators, defectors, infectious individuals, and the whole population in periodic solution, respectively. Parameters are b = 1, c = 0.3, m = 0.1, ξ = 0.1, γ = 0.1, and κ = 0.5.
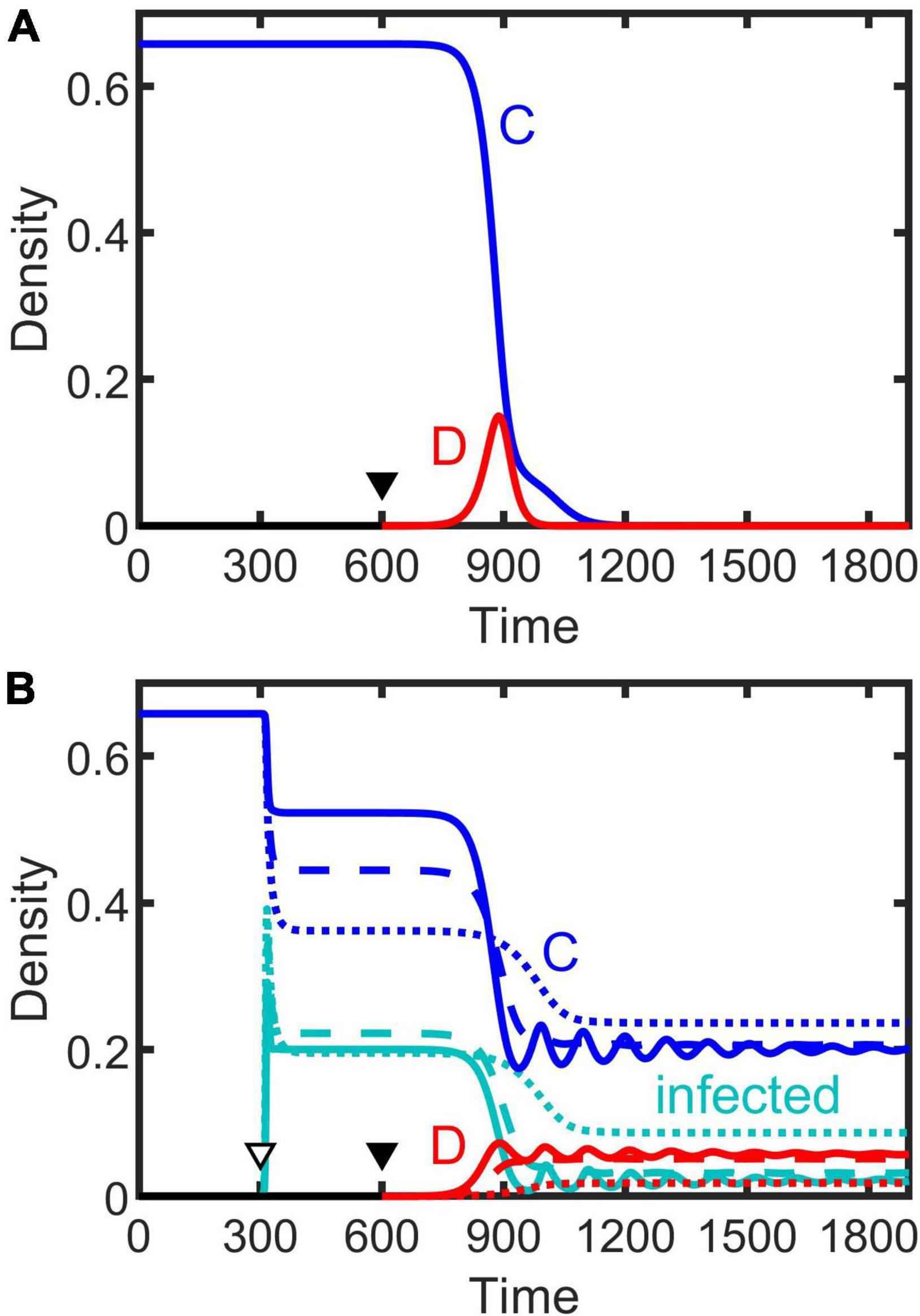
Figure 5. Population extinction driven by invasion of defection (A), as shown by dark gray in Figures 1A,C, which can be prevented by infection with a high transmission rate (B). Solid triangles indicate when defectors invade a cooperative population, and the hollow triangle denotes when it is infected. Solid, dashed, and dotted lines result from the SI, SIS, and SIR model, respectively. Parameters: β = 0.9, κ = 0.9, γ = 0.1, δ = 0.2, and the others are the same as Figures 1A,C.
The transmission type of disease also has some effect on cooperation evolution. The minimum transmission rate that the disease can invade the population is smaller in the SI case than in the SIS and SIR case (Figure 4 and Supplementary Figures 2–4). The equilibrium density of cooperation is highest in the SI case, while lowest in the SIR case, at the same conditions (Figures 3–5). Interestingly, although disease infections potentially lead to cooperators and defectors to change relatively in their densities, the whole population was not affected in the long term, with its total density (or average density for the periodic cases) almost unchanged by infections and even increased slightly (Figures 3, 4 and Supplementary Figures 2–4).
Discussion
The traditional methods to describe evolutionary games consider only the change of different strategies (also genotypes or phenotypes) in relative frequency under natural selection, ignoring the ecological dynamics of populations (Nowak and Sigmund, 2004). This treatment actually assumes an infinite large population (e.g., replicator equation) (Hofbauer and Sigmund, 1998); even if spatial and stochastic effects are involved, population size is always assumed to be constant (Nowak and May, 1992; Nowak et al., 2004; Lieberman et al., 2005). Undoubtedly, such evolutionary game models have captured the fundamental property of natural selection in a simple way and provided great insights into better comprehension of the dynamic consequences from frequency-dependent selection (Maynard Smith, 1982; Hofbauer and Sigmund, 1998; Nowak, 2006a). However, the evolutionary games often represent the selection dynamics of a pre-defined strategy set from generation to generation. This implies this kind of evolution is at the time scale of ecological dynamics. Therefore, when the impacts of ecological and evolutionary process on each other are evident, the ecological dynamics must be considered at the same time scale of evolutionary dynamics (Hauert et al., 2006; Ross Gillespie et al., 2009; Zhang and Hui, 2011). In such a case, the game payoff (fitness) should also depend on the absolute density of each strategy rather than the relative frequency of them. In that way, natural selection and ecological processes can tangle together to shape into the so-called eco-evolutionary feedback dynamics.
In our models, the population density varies over time; this fluctuation depends not only on ecological interactions such as the birth-death process and pathogenic infection, but also on the selection process of cooperation evolution. The change of population density can also affect the evolution of cooperation through density-dependent selection because the fitness of cooperators and defectors (i.e., reproduction rate ξC and ξD) depends on the densities of them (i.e., density-dependent fitness). Therefore, such eco-evolutionary feedback is easily mediated by the ecological factors that have significant influences on population density, which could profoundly change the selection process and evolutionary outcomes (Doebeli et al., 1997; Hauert et al., 2006, 2008; Alizon and Taylor, 2008; Zhang and Hui, 2011). As our results suggested, the increase of mortality drives a population to be more cooperative but possibly causes it to fluctuate periodically (i.e., population instability, Figure 1C), which may further be affected by other ecological factors such as disease infection (Figures 3, 4), predation (Krams et al., 2010), and habitat degradation (Hui et al., 2005; Zhang et al., 2005). Recent experimental studies have demonstrated the feedback loop between ecological and evolutionary dynamics in social microbial populations (Sanchez and Gore, 2013), which can promote cooperation when the population expands its spatial range in response to changes in the environment (Datta et al., 2013) or undergoes intermediate disturbances (Brockhurst et al., 2007).
The reason that a population becomes more cooperative in harsh environments could be that its instantaneous density first declines from the environmental stress, which then potentially releases cooperative individuals from exploitations by defective individuals. This mechanism is similar to the cascade effect of trophic interactions (Carpenter et al., 1985). In food webs, although the top predator reduces both the intermediate predator and the prey, the reduction in the intermediate predator indirectly relaxes the consumption of the prey species by them. The asymmetric impact of the top predator on the intermediate predator and the prey may give rise benefit to the prey essentially. Similarly, in the ecological game, environmental stress reduces the density of both defectors and cooperators, but the reduction of defectors indirectly relaxes their exploitation of cooperators, which possibly leads to the increase of cooperators (Figure 6). The increase of cooperators could, in turn, foster defectors, which then suppress cooperators again; such feedback between cooperators and defectors in the ecological context could result in the periodic fluctuation of their densities (Figures 1C, 3B,D).
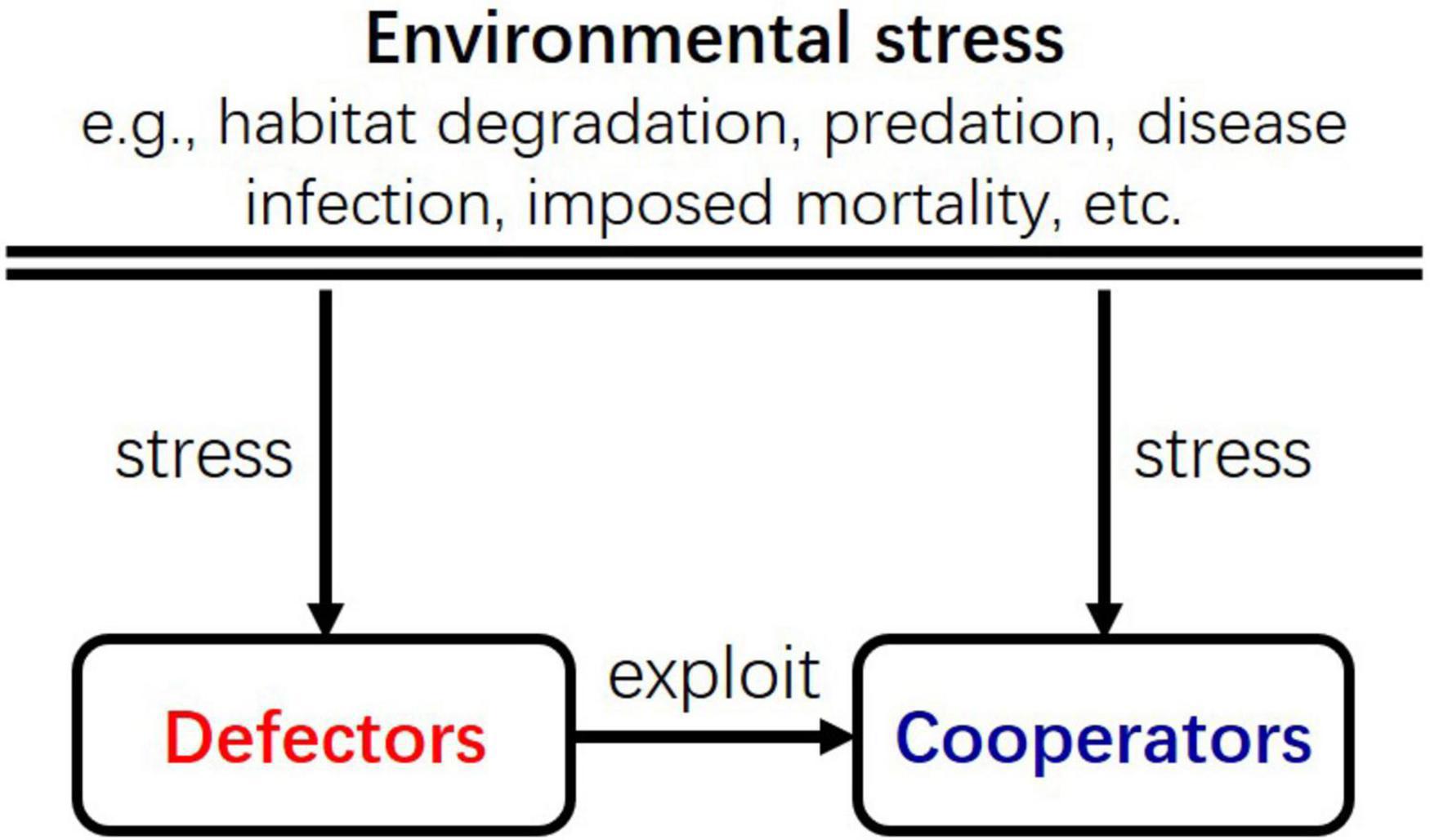
Figure 6. A schematic diagram illustrating the interactions among cooperators, defectors, and the environment. The effect of environmental stress to defectors and cooperators is similar to the cascade effect of trophic interactions in food webs. Environmental stress on defectors indirectly relaxes their exploitation of cooperators, just as the predation on intermediate predators indirectly relaxes the preys at the lower trophic level.
When a population experiences high mortality, cooperators can survive via mutual support to overcome a harsh environment, whereas, in such a case, the population could be extremely fragile, easily goes extinct due to the invasion of defectors, namely the defection-driven extinction (Figures 1C, 5A). This is because the exploitation from defectors makes cooperators no longer be able to overcome the high mortality. Disease infections can prevent this kind of extinction because the decline in population density due to the infections could slow down the takeover by defectors (Figure 5). In addition, intensifying the interaction between cooperators (i.e., stronger assortment) can largely promote cooperation, extending the range of parameters that cooperation can occur, stabilizing the dynamics of the population, enhancing the ability of cooperators to resist defectors’ exploitation, and consequently increasing population density (comparing Figures 1C,D).
In conclusion, the eco-evolutionary feedback can trigger complex evolutionary dynamics due to the involvement of density-dependent selection in population dynamics. High mortality imposed by environmental stress such as habitat degradation, predation, and infectious diseases, can release the cooperators from defectors’ suppression because of the cascade effect of cooperation evolution, consequently making the population more cooperative and stable from the eco-evolutionary feedback. The variation of behavioral strategies is thus an important mechanism for a population to withstand disease infections without the necessity to decline.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
FZ, LS, and RW conceived the idea. FZ and MC ran the analyses. FZ wrote the manuscript. All authors contributed to further editing on the final version.
Funding
This work was supported by the Key Program of the National Natural Science Foundation of China (11931015), the NSFC-Yunnan United Fund (U2102221), the Natural Science Foundation of Anhui Province (2008085MC62), and Anhui University (S020118002/101).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.758659/full#supplementary-material
References
Alizon, S., and Taylor, P. (2008). Empty sites can promote altruistic behavior. Evolution 62, 1335–1344. doi: 10.1111/j.1558-5646.2008.00369.x
Brockhurst, M. A., Buckling, A., and Gardner, A. (2007). Cooperation peaks at intermediate disturbance. Curr. Biol. 17, 761–765. doi: 10.1016/j.cub.2007.02.057
Carpenter, S. R., Kitchell, J. F., and Hodgson, J. R. (1985). Cascading trophic interactions and lake productivity. BioScience 35, 634–639. doi: 10.2307/1309989
Datta, M. S., Korolev, K. S., Cvijovic, I., Dudley, C., and Gore, J. (2013). Range expansion promotes cooperation in an experimental microbial metapopulation. Proc. Natl. Acad. Sci. 110, 7354–7359. doi: 10.1073/pnas.1217517110
Doebeli, M., Blarer, A., and Ackermann, M. (1997). Population dynamics, demographic stochasticity, and the evolution of cooperation. Proc. Natl. Acad. Sci. 94, 5167–5171. doi: 10.1073/pnas.94.10.5167
Doebeli, M., and Hauert, C. (2005). Models of cooperation based on the Prisoner’s Dilemma and the Snowdrift game. Ecol. Lett. 8, 748–766. doi: 10.1111/j.1461-0248.2005.00773.x
Dugatkin, L. A. (1997). Cooperation Among Animals: an Evolutionary Perspective. New York: Oxford University Press.
Eshel, I., and Cavalli-Sforza, L. L. (1982). Assortment of encounters and evolution of cooperativeness. Proc. Natl. Acad. Sci. 79, 1331–1335. doi: 10.1073/pnas.79.4.1331
Hairston, N. G. Jr., Ellner, S. P., Geber, M. A., Yoshida, T., and Fox, J. A. (2005). Rapid evolution and the convergence of ecological and evolutionary time. Ecol. Lett. 8, 1114–1127. doi: 10.1111/j.1461-0248.2005.00812.x
Hairston, N. G., Lampert, W., Cáceres, C. E., Holtmeier, C. L., Weider, L. J., Gaedke, U., et al. (1999). Rapid evolution revealed by dormant eggs. Nature 401, 446–446. doi: 10.1038/46731
Hamilton, W. (1964). The genetical evolution of social behaviour I and II. J. Theo. Biol. 7, 1–52. doi: 10.1016/0022-5193(64)90038-4
Hauert, C., Holmes, M., and Doebeli, M. (2006). Evolutionary games and population dynamics: maintenance of cooperation in public goods games. Proc. R. Soc. B Biol. Sci. 273, 3131–3132. doi: 10.1098/rspb.2006.3717
Hauert, C., Wakano, J. Y., and Doebeli, M. (2008). Ecological public goods games: cooperation and bifurcation. Theor. Popul. Biol. 73, 257–263. doi: 10.1016/j.tpb.2007.11.007
Hofbauer, J., and Sigmund, K. (1998). Evolutionary games and population dynamics. Cambridge: Cambridge University Press.
Hui, C., Zhang, F., Han, X., and Li, Z. (2005). Cooperation evolution and self-regulation dynamics in metapopulation: stage-equilibrium hypothesis. Ecol. Model. 184, 397–412. doi: 10.1016/j.ecolmodel.2004.11.004
Keeling, M. J., and Rohani, P. (2008). Modeling Infectious Diseases in Humans and Animals. Princeton: Princeton University Press.
Krams, I., Berzins, A., Krama, T., Wheatcroft, D., Igaune, K., and Rantala, M. J. (2010). The increased risk of predation enhances cooperation. Proc. R. Soc. B Biol. Sci. 277, 513–518. doi: 10.1098/rspb.2009.1614
Kurzban, R., Burton-Chellew, M. N., and West, S. A. (2015). The evolution of altruism in humans. Ann. Rev. Psychol. 66, 575–599. doi: 10.1146/annurev-psych-010814-015355
Levins, R. (1969). Some demographic and genetic consequences of environmental heterogeneity for biological control. Bull. Entomol. Soc. Am. 15, 237–240. doi: 10.1093/besa/15.3.237
Lieberman, E., Hauert, C., and Nowak, M. A. (2005). Evolutionary dynamics on graphs. Nature 433, 312–316. doi: 10.1038/nature03204
Morens, D. M., Folkers, G. K., and Fauci, A. S. (2004). The challenge of emerging and re-emerging infectious diseases. Nature 430, 242–249.
Nowak, M. A. (2006a). Evolutionary Dynamics: Exploring the Equations of Life. Cambridge: Harvard University Press.
Nowak, M. A. (2006b). Five rules for the evolution of cooperation. Science 314, 1560–1563. doi: 10.1126/science.1133755
Nowak, M. A., and May, R. M. (1992). Evolutionary games and spatial chaos. Nature 359, 826–829. doi: 10.1038/359826a0
Nowak, M. A., Sasaki, A., Taylor, C., and Fudenberg, D. (2004). Emergence of cooperation and evolutionary stability in finite populations. Nature 428, 646–650. doi: 10.1038/nature02414
Nowak, M. A., and Sigmund, K. (2004). Evolutionary dynamics of biological games. Science 303, 793–799. doi: 10.1126/science.1093411
Pásztor, L., Dukát, Z. B., Magyar, G., Czárán, T., and Meszéna, G. (2016). Theory Based Ecology: A Darwinian Approach. Oxford: Oxford University Press.
Pimm, S. L., Jenkins, C. N., Abell, R., Brooks, T. M., Gittleman, J. L., Joppa, L. N., et al. (2014). The biodiversity of species and their rates of extinction, distribution, and protection. Science 344:1246752 doi: 10.1126/science.1246752
Ross Gillespie, A., Gardner, A., Buckling, A., West, S. A., and Griffin, A. S. (2009). Density dependence and cooperation: theory and a test with bacteria. Evolution 63, 2315–2325. doi: 10.1111/j.1558-5646.2009.00nbreak723.x
Sanchez, A., and Gore, J. (2013). Feedback between population and evolutionary dynamics determines the fate of social microbial populations. PLos Biol. 11:e1001547. doi: 10.1371/journal.pbio.1001547
Schoener, T. W. (2011). The newest synthesis: understanding the interplay of evolutionary and ecological dynamics. Science 331, 426–429. doi: 10.1126/science.1193954
Tilman, A. R., Plotkin, J. B., and Akcay, E. (2020). Evolutionary games with environmental feedbacks. Nat. Commun. 11:915. doi: 10.1038/s41467-020-14531-6
Traulsen, A., and Nowak, M. A. (2006). Evolution of cooperation by multilevel selection. Proc. Nat. Acad. Sci. 103, 10952–10955.
Trivers, R. L. (1971). The Evolution of Reciprocal Altruism. Q. Rev. Biol. 46, 35–57. doi: 10.1086/406755
Weitz, J. S., Eksin, C., Paarporn, K., Brown, S. P., and Ratcliff, W. C. (2016). An oscillating tragedy of the commons in replicator dynamics with game-environment feedback. Proc. Natl. Acad. Sci. U.S.A. 113, E7518–E7525. doi: 10.1073/pnas.1604096113
West, S. A., Griffin, A. S., Gardner, A., and Diggle, S. P. (2006). Social evolution theory for microbes. Nat. Rev. Microbiol. 4, 597–607. doi: 10.1038/nrmicro1461
Zhang, F., and Hui, C. (2011). Eco-evolutionary feedback and the invasion of cooperation in Prisoner’s Dilemma Games. PLos One 6:e27523. doi: 10.1371/journal.pone.0027523
Zhang, F., Hui, C., Han, X., and Li, Z. (2005). Evolution of cooperation in patchy habitat under patch decay and isolation. Ecol. Res. 20, 461–469. doi: 10.1007/s11284-005-0072-7
Zhang, F., Tao, Y., Li, Z., and Hui, C. (2010). The evolution of cooperation on fragmented landscapes: the spatial Hamilton rule. Evol. Ecol. Res. 12, 23–33.
Keywords: altruistic behavior, mutualistic interaction, eco-evolutionary feedback, bi-stability, defection-driven extinction, assortment, cascading trophic interaction, epidemiological model
Citation: Zhang F, Cao M, Shi L and Wang R (2022) Disease-Induced Cooperation Mitigates Populations Against Decline: The Cascade Effect of Cooperation Evolution. Front. Ecol. Evol. 10:758659. doi: 10.3389/fevo.2022.758659
Received: 14 August 2021; Accepted: 08 March 2022;
Published: 30 March 2022.
Edited by:
Åke Brännström, Umeå University, SwedenReviewed by:
Lingzi Wang, Lund University, SwedenLinh Phuong Nguyen, Université Pierre et Marie Curie, France
Copyright © 2022 Zhang, Cao, Shi and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lei Shi, c2hpX2xlaTY1QGhvdG1haWwuY29t; Ruiwu Wang, d2FuZ3J3QG53cHUuZWR1LmNu
 Feng Zhang
Feng Zhang Menglan Cao
Menglan Cao Lei Shi
Lei Shi Ruiwu Wang
Ruiwu Wang