Heterogeneous individual motility biases group composition in a model of aggregating cells

Aggregative life cycles are characterized by alternating phases of unicellular growth and multicellular development. Their multiple, independent evolutionary emergence suggests that they may have coopted pervasive properties of single-celled ancestors. Primitive multicellular aggregates, where coordination mechanisms were less efficient than in extant aggregative microbes, must have faced high levels of conflict between different co-aggregating populations. Such conflicts within a multicellular body manifest in the differential reproductive output of cells of different types. Here, we study how heterogeneity in cell motility affects the aggregation process and creates a mismatch between the composition of the population and that of self-organized groups of active adhesive particles. We model cells as self-propelled particles and describe aggregation in a plane starting from a dispersed configuration. Inspired by the life cycle of aggregative model organisms such as Dictyostelium discoideum or Myxococcus xanthus, whose cells interact for a fixed duration before the onset of chimeric multicellular development, we study finite-time configurations for identical particles and in binary mixes. We show that co-aggregation results in three different types of frequency-dependent biases, one of which is associated to evolutionarily stable coexistence of particles with different motility. We propose a heuristic explanation of such observations, based on the competition between delayed aggregation of slower particles and detachment of faster particles. Unexpectedly, despite the complexity and non-linearity of the system, biases can be largely predicted from the behavior of the two corresponding homogenous populations. This model points to differential motility as a possibly important factor in driving the evolutionary emergence of facultatively multicellular life-cycles.

1. Introduction

Aggregative life cycles are set to the boundary between unicellular and multicellular organization. In aggregative life-cycles, initially sparse cells come together and form multicellular groups. Multicellular development following aggregation is essential for the formation and successive dispersal of stress-resistant dormant cells. Such cysts or spores seed subsequent generations, where cells undergo unicellular, vegetative growth (Raper, 1940). Both in prokaryotes, e.g., Myxobacteria, and in eukaryotes, e.g., Dictyostelids, multicellular development is associated with cell differentiation and division of labor, analogous to organisms whose body derives from clonal growth. Those two orders, and in particular the model species Myxococcus xantus and Dyctiostelium discoideum, have thus been extensively regarded as highly informative on the transition from unicellular to multicellular organization (Vos and Velicer, 2009; Kraemer and Velicer, 2011; Strassmann and Queller, 2011; Forget et al., 2021).

A key feature of aggregative multicellular species is their motility, that allows cells to actively pursue their bacterial preys during the solitary phase of the life-cycle, and to engage in a series of collective behaviors, such as swarming (Shi et al., 1993) and collective taxis (Bonner et al., 1950). Individual cell movement moreover allows cells to rapidly coalesce into multicellular aggregates as a response to stressful environmental conditions, typically nutrient exhaustion. Attaining collective functions without delay has been argued to constitute an important adaptive advantage to aggregative vs. clonal multicellularity (Marquez-Zacarias et al., 2021).

As a side effect, it is almost inevitable that motility leads to mixing of heterogenous cells to a much larger extent than in colonies of sessile microbes or clonally growing multicellular organisms. Indeed, genetic chimerism occurs naturally in aggregative multicellular species (Strassmann et al., 2000; Fortunato et al., 2003b; Gilbert et al., 2007; Vos and Velicer, 2009; Kraemer and Velicer, 2011; Sathe et al., 2014). Within chimeric aggregates, genotypes reaping group benefits—i.e., “cheaters”—are expected to bear a selective advantage relative to more “cooperative” types. In the absence of positive assortment, selection favors cheaters over cooperators, as reproductive gains are amplified across cycles of multicellular aggregation. Such “tragedy of the commons” scenario (Hardin, 1968; Rankin et al., 2007) is commonly invoked as a threat to the evolutionary stability of multicellularity, and of particular relevance close to the transition from single cells to higher levels of integration (Clarke, 2014; Rainey and De Monte, 2014).

In the absence of mechanisms that efficiently purge invading cheaters—such as single-cell bottlenecks in clonally growing organisms—aggregative life cycles are particularly fragile to conflicts (Strassmann et al., 2000; Vos and Velicer, 2009). Theory indeed predicts that a sufficient degree of positive assortment, or high relatedness, is necessary for cooperation to be evolutionarily stable (Queller, 1994; Fletcher and Doebeli, 2009). If cooperators recognize cooperators, for instance through mechanisms of kin recognition or green beard effects (Hamilton, 1964), then cooperative groups can be advantaged over excluded cheaters. Even though recognition mechanisms have been identified in Dictyostelium, high segregation efficiency is only attained among distant species (Sathe et al., 2014). Moreover, it is unlikely that highly sophisticated recognition systems were present before multicellular organization was stabilized, leaving the question open of how positive assortment was first established in primitive multicellular life cycles (Clarke, 2014). More relevant to understanding the independent repeated evolution of aggregative life cycles (Grosberg and Strathmann, 2007) seem thus to be passive mechanisms of assortment. Ancestral heterogeneity in individual cell properties, indeed, can be the source of positive assortment also in the absence of cell-cell signaling and recognition. Theoretical explorations have for instance shown that costly adhesive traits are selected if they enhance group cohesion, even when cells reshuffling at every generation brakes identity of descent in multicellular groups (Garcia and De Monte, 2013; Garcia et al., 2014, 2015; van Gestel and Nowak, 2016).

Here, we focus on heterogeneity in motility as a possible source of assortment when multicellular aggregates are generated by self-organization of moving cells, represented as self-propelled disks that can stick to one another upon encounter (Szabó et al., 2006). Heterogeneity in cell motility is observed both in M. xantus (Vos and Velicer, 2008) and D. discoideum, where it has been associated to diverse developmental fates (Azhar et al., 2001) and to efficient foraging (Rossine et al., 2022). Differences in motility, moreover, have been proposed to drive the emergence of life cycles with temporally compartmentalized phases of aggregation and disaggregation (Miele and De Monte, 2021). A feature of such cycles, as well as of aggregative life cycles, is the collective timescale that cells have at their disposal to aggregate. After a specific time span, multicellular aggregates proceed to further developmental steps, or are dispersed. Evolution thus proceeds across a succession of aggregation-dispersal cycles, whereby a subset of aggregated cells founds the successive generation. Whenever the aggregated state enhances survival of the constituent cells, cell types that are over-represented in aggregates at the final time will in the long run dominate the population.

In aggregative microbes, reproductive fitness of different co-aggregating types is defined in terms of the fraction of spores (or cysts) they have produced at the moment of dispersal, as these are the only cells that resist long-term starvation. In Dictyostelium, “spore bias” of a given strain, i.e., the deviation in the proportion of spores of that strain from its proportion in the initial mix, is thus commonly used as a metric for pair-wise comparison of the social behavior of different cellular populations (Strassmann et al., 2000; Fortunato et al., 2003a; Gilbert et al., 2007; Buttery et al., 2010; Kuzdzal-Fick et al., 2010, 2011). If aggregates all had a similar composition (no segregation), and cells of different types behaved identically during development, spore bias would be essentially set by the proportion of cells that did not join the aggregates, the so-called “loners” in D. discoideum (Tarnita et al., 2013; Dubravcic et al., 2014; Martínez-García and Tarnita, 2016) or “peripheral rods” in Myxococcus xanthus (O'Connor and Zusman, 1991). The propensity of aggregative species to give rise to non-aggregated cells has been proposed to be key to survival in unpredictably fluctuating environments, and to the maintenance of diversity in natural settings (O'Connor and Zusman, 1991; Dubravcic et al., 2014; Tarnita et al., 2015). If it is known that the propensity of cells to aggregate depends on context (both on the abiotic and biotic environmental conditions; O'Connor and Zusman, 1991; Rossine et al., 2020), the mechanisms determining how many and what cells are more likely to aggregate are still unknown.

We leverage numerical methods developed in active matter physics to explore how heterogeneity in motility affects aggregation biases. Previous studies on Brownian particles with different activity have focused on dense mixtures, where Motility-Induced Phase Separation (MIPS) gives rise to the coexistence of a gas of isolated particles with aggregates, even in the absence of adhesive forces between particles (Stenhammar et al., 2015; Kolb and Klotsa, 2020; Rogel Rodriguez et al., 2020). Within aggregates, moreover, motility differences result in sorting (Jones et al., 1989; Beatrici and Brunnet, 2011) and they may contribute, along with cell adhesion and signaling, to the establishment of dynamics morphological patterns that structured the evolution of multicellular development (Newman and Bhat, 2009).

We characterize finite-time aggregation patterns in low-density binary mixes of adhesive particles that only differ for their intrinsic motility. Given the potential implications of such motility differences in the evolutionary origin of aggregative multicellular life cycles, we propose a criterion to infer aggregation bias in binary mixes from the properties of homogeneous populations. Moreover, we address the dependence of aggregation biases on the frequency of cells of different motility, showing that non-trivial outcomes are possible, though not all that could be expected to occur. A particularly interesting case is the establishment of frequency-dependent selection associated to the evolutionarily stable coexistence of different motility types.

2. Methods

2.1. Source code

Simulations were performed using the Python language. The Pytorch library (Paszke et al., 2019) for tensor computation allowed us to reduce the computational time while working with a large number of particles (N = 10⁴). The source code for the simulation can be found online (https://github.com/MathieuForget/HeteroSpeed_Aggregation.git).

2.1.1. Identification of aggregates

Aggregates are defined as groups of at least 5 aggregated particles. To be considered as aggregated, a particle has to be connected to at least 4 others particles in the final state of the simulation. Two particles are considered connected if their pairwise distance is lower than R₀, the parameter that defined their interaction range (see Figure 1B and lines 267–281 of the code).

FIGURE 1

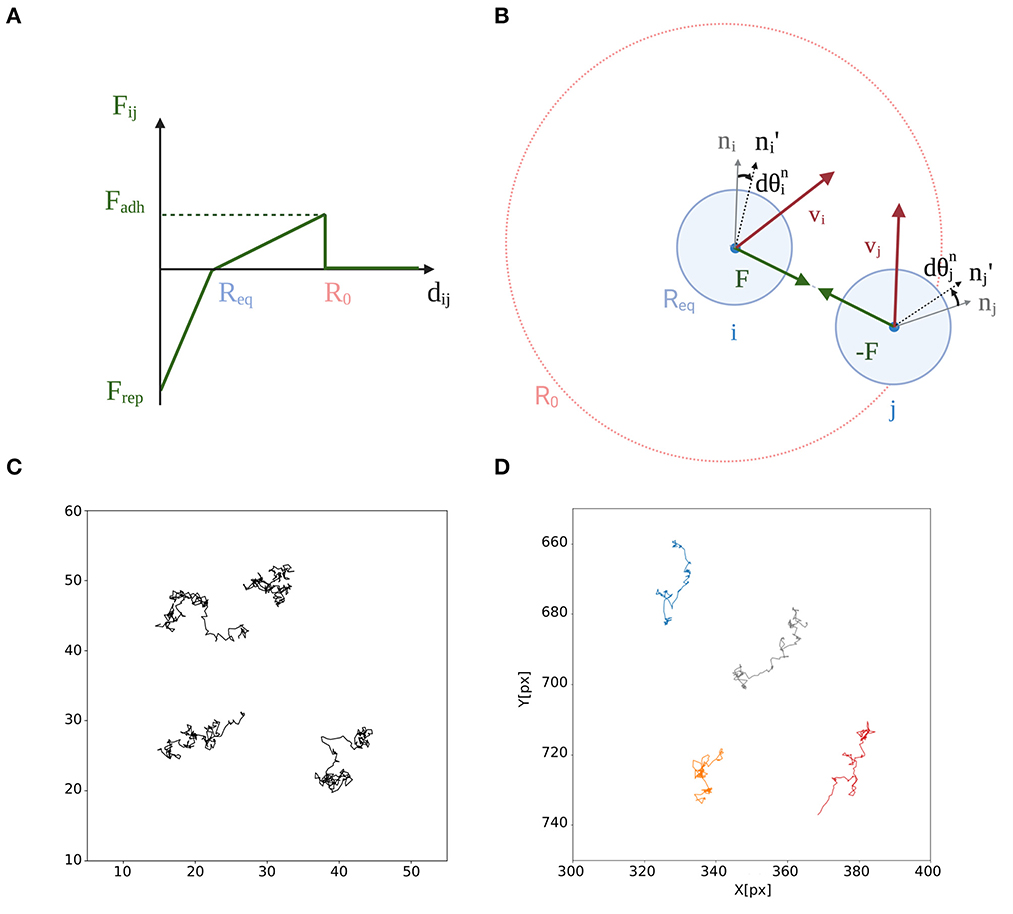
Figure 1. Self-propelled particle model for migrating and interacting cells. (A) Finite-range interaction forces F(d_ij) between two particles of positions r_i and r_j and velocities v_i and v_j (accounting for both auto-propulsion and interaction forces, according to Equation 1) contribute to align ${\text{n}}_i^{\prime }$ and ${\text{n}}_j^{\prime }$ (n′ = n(t + dt)), the direction of particles' auto-propelled velocities. These forces only act when the Euclidean distance d_ij = |r_i − r_j| ≤ R₀. See text for the definition of the other variables. (B) Radial component of the force between the two particles. When d_ij < R_eq, particle i exerts a strong repulsive force on particle j. Otherwise, within the range of interaction R₀, the latter attracts particle j with a weaker elastic force, representing adhesion between different cells. (C) Typical trajectories of isolated particles during a simulation (t_f = 100) using parameters values in Table 1 that, in the absence of interactions, follow a persistent random walk resembling that of Dictyostelium's single cells. (D) Trajectories of starved Dictyostelium cells recorded every 30 s during 1 h.

2.1.2. Bias in aggregates composition

At the end of each simulation, the mean proportion of each population in the aggregates is estimated. The bias in aggregate composition of the focal population is measured as the deviation between its mean proportion in the aggregates and its proportion in the mix (line 325 of the code).

2.1.3. Particles connectivity

The number of particles that are closer than R₀ to a focal particle is used as a proxy for its connectivity. We estimated populations mean connectivity by averaging the connectivity of aggregated particles of a given type. In binary mixes, the relative connectivity of this type was estimated as the deviation between its mean connectivity and that of the other type of particles (lines 332–344 of the code).

3. Results

3.1. A self-propelled particles model for the aggregation of motile cells

In order for aggregation to bring together cells of different populations, cells need to be motile. Different aggregative organisms have different types of motility and different shapes. Here, we consider a simple representation of moving cells as persistent Brownian walkers. This representation corresponds to observations of single-cell motility in Dictyostelium discoideum (Golé et al., 2011; Li et al., 2011), and was used to model collective behavior of keratocytes populations (Szabó et al., 2006). Single cells are represented as self-propelled disks of equilibrium radius R_eq/2 (R_eq being the equilibrium distance between two interacting particles). Interaction forces only act within a finite range R₀ and determine, together with stochastic fluctuations, the position of each disk and the orientation of each particle's velocity. In order to avoid to define their behavior at the boundaries, particles are let move in a square of side L with periodic boundary conditions. In the following, we will study the aggregation of particles that are initially distributed uniformly and randomly in this square.

The equation of motion of a particle i with position r_i ∈[L, L] is:

$\begin{array}{ll}\frac{d{r}_i}{dt}=v_0{n}_i+\mu {\displaystyle \sum _{j=1}^{N}F}(d_{ij}).& (1)\end{array}$

where v₀ is the self-propelled speed of particle i (whose direction is given by a polarization unitary vector n_i) N is the population size, and F is the interaction force between particles i and j, that only depends on their Euclidean distance d_ij = ∥r_j − r_i∥. The mobility parameter μ ensures dimensional consistence, and is set to 1. Equation (1) is adimensional, as the reference unit of length and time are not specified. If it were to be applied to a real system, where speed and force are directly measured, one would have to choose correspondingly the mobility parameter and to scale appropriately position and time.

Cell-cell adhesion acts only on cells that are not too far apart. The model considers a radial, finite-range interaction force F that is piecewise-linear in the distance d_ij (Figure 1A). If d_ij ≤ R_eq, the two particles i and j repulse each other strongly, in order to account for cell volume exclusion. If R_eq < d_ij ≤ R₀, the two particles attract each other with an elastic force of intensity F_adh that quantifies adhesion strength. This choice reflects the possibility that cell shape deformation allows cells to be more distant than twice their equilibrium radius. The radial force is thus defined as:

$\begin{array}{ll}F(d_{ij})=e_{ij}F(d_{ij})& (2)\end{array}$

where $e_{ij}=\frac{r_i-r_j}{\Vert r_i-r_j\Vert }$ is the unitary vector connecting the centers of the two particles and

$\begin{array}{ll}F(d)=\{\begin{array}{cc}{F}_{rep}\frac{d-R_{eq}}{R_{eq}}& d<R_{eq}\\ F_{adh}\frac{d-R_{eq}}{R_0-R_{eq}}& R_{eq}\le d\le R_0\\ 0& R_0\le d\end{array}& (3)\end{array}$

The force F and its action on particles' self-velocity are represented in Figures 1A,B. In the simulations, time is discretized in steps of (short) duration dt. Between two successive time steps, interaction forces induce a small incremental change in the angle ${\theta }_i^n(t)=arcsin(n_i(t))$ of particle self-propelling velocity. Even though there is no direct velocity alignment in this model, the action of the force is to reduce the deviation of the particle velocity from the scattering direction $v_i=\frac{d{r}_i}{dt}$ defined by Equation (1). Such a relaxation happens on the timescale τ. The equation of motion for the angle is therefore:

$\begin{array}{ll}\frac{d{\theta }_i^n}{dt}=\frac{1}{\tau }\arcsin \left[\left(n_i\times \frac{v_i}{\left|v_i\right|}\right)·e_z\right]+\eta {\xi }_i& (4)\end{array}$

where e_z is a unit vector orthogonal to the plane of motion. The cross product is null when the velocity and the force are aligned, case in which the direction of motion will not be altered by particles interaction.

In isolation (i.e., in the absence of interaction forces F = 0), particles move as persistent random walkers. Typical trajectories, shown in Figure 1C, are consistent with previous (Golé et al., 2011; Li et al., 2011) and our own (Figure 1D) experimental observation of individual Dictyostelium discoideum cells trajectories. The orientation ${\theta }_i^n$ of the self-propelled velocity v_i = v₀ n_i (Equation 1) is described by a Wiener process (Huang and Cambanis, 1978), where a white angular noise term ηξ_i is added between successive time steps. ξ_i(t) is a random variable chosen with a uniform probability on the interval [−2π, 2π], uncorrelated across successive time steps. The noise intensity η defines the characteristic timescale ${\tau }_r=1/{\eta }^2$ of persistence of the random motion. The larger the angular noise, the less persistent is the motion of the particle.

When particles are closer than the radius of interaction R₀ (see Figure 1), the radial force causes the velocity vectors to align on a characteristic relaxation time scale τ. The smaller this is, the higher the tendency of particles to move collectively in dynamic, highly polarized, flocks (Grégoire et al., 2003; Casiulis et al., 2020). In the following, we will consider situations where τ_r is small (large η) compared to τ, so that aggregates do not display collective motility, where groups can merge and fragment. We focus instead on regimes where particles form long-lived, quasi-stationary aggregates, as occurs in the early stages of aggregation of Dictyostelids. These aggregates remain separated even later, when they form distinct slugs. The time scale corresponding to the formation of separate aggregates, rather than the asymptotic behavior of the system, is thus what we are concerned with.

The self-propelled particles model was implemented through a custom Python program (https://github.com/MathieuForget/HeteroSpeed_Aggregation.git). Model's parameters (collected in Table 1) were set as described in the Supplementary material to reproduce the aggregation of a fraction of particles in multiple non-motile aggregates, with some particles remaining isolated, similar to what is observed for aggregative multicellular species (O'Connor and Zusman, 1991; Dubravcic et al., 2014).

TABLE 1

Table 1. Model parameters Values.

3.2. Finite-time states of homogeneous populations

We first explored how the system's parameters affect the patterns of aggregation of particles with identical velocities. Characterizing how particles self-organize in aggregates is an important first step for understanding how they create emergent biases in group composition, that are the relevant quantities to evaluate what cell type would have an advantage in dispersal, and thus increase its frequency in successive generations—in the absence of additional biases incurred during multicellular development.

Particular attention was given to two parameters that can be controlled or at least measured in experiments, and that are known to influence encounter rates among particles: the packing fraction ρ and the particles' self-propulsion speed v₀.

The packing fraction is the ratio between the areas covered by the particles relative to the total area of the simulation space. It is thus proportional to population density, which is straightforward to tune in experimental settings, and is known to critically affect collective behavior in aggregative species (Hashimoto et al., 1975). As motivated in the introduction, the speed of particle displacement v₀ is interesting because heterogeneity in cell motility was revealed by single-cell observations (Vos and Velicer, 2008; Goury-Sistla et al., 2012), and it can be altered by changing growth conditions in the lab (Varnum et al., 1986; Forget et al., 2022). Particle encounters become more likely when both packing fraction and velocity are increased. However, increasing one or the other is not equivalent, as we will see.

The self-organized patterns reached after a finite time by a population of identical particles were examined for different values of speed v₀ and packing fraction ρ (Figure 2 and Supplementary Figure 1). Simulations were run for a fixed duration t_f. This choice reflects the fact that cells do not have an infinite time at their disposal to complete aggregation. In biological populations, such a timescale is set by the duration of different phases of the life cycle or, for ancestral unicellular types, by environmental variation. In the final state—analyzed whether the system had converged to its asymptotic configuration or not—aggregates were defined as groups of at least 5 particles as described in Section 2. The setting of a size threshold reflects the observation that in Dictyostelium aggregate speed is positively correlated to size (Bonner, 1995; Rieu et al., 2005), so that small slugs have impaired collective motility, and possibly development. Therefore, their contribution to successive generations is akin to that of solitary cells. More generally, size-dependence is a shared feature of many collective functions, which require a quorum of composing cells for selection to start acting on them (Cornforth et al., 2012).

FIGURE 2

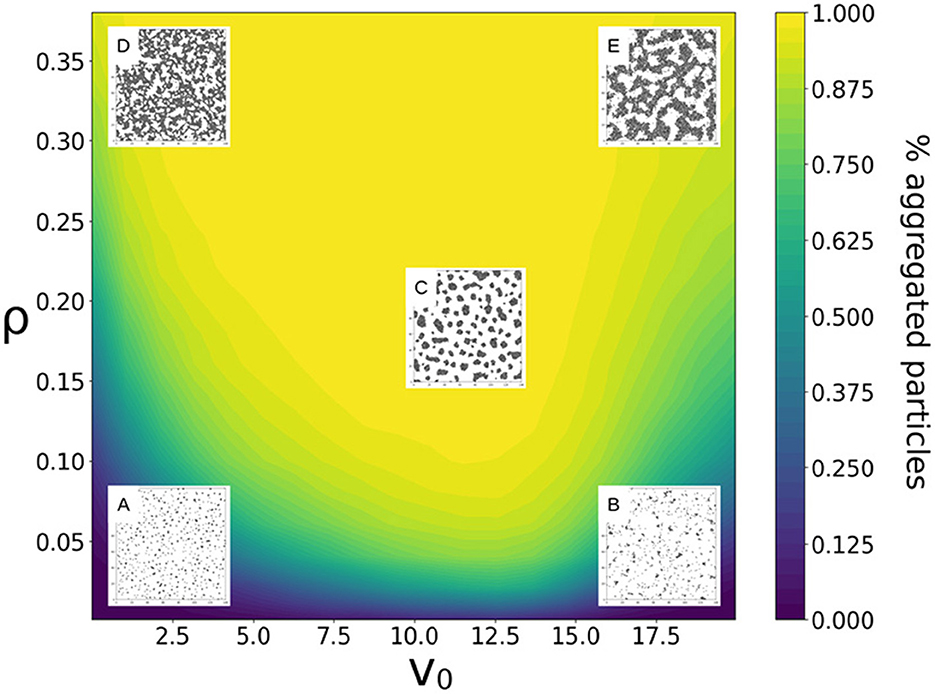
Figure 2. Finite-time state diagram for a population of identical particles of speed v₀ and packing fraction ρ. The fraction of aggregated particles at the end of the simulation (t_f = 100) is illustrated as a heatmap, indicating that the highest fraction of aggregated particles is reached for intermediate particle speeds. Overlaid, snapshots illustrate the final particle distribution for five cases (A: v₀ = 2.5, ρ = 0.05, B: v₀ = 17.5, ρ = 0.05, C: v₀ = 12, ρ = 0.2, D: v₀ = 2.5, ρ = 0.35 and E: v₀ = 17.5, ρ = 0.35), whose aggregation dynamics is discussed in more detail in Supplementary Figure 1. Fixed parameters values are those indicated in Table 1. The packing fraction was varied by changing L, keeping N constant.

At very low packing fractions, the system does not display any sizeable aggregate, consistently with experimental observations of Dictyostelium aggregation (Hashimoto et al., 1975). Indeed, particles do not have the time to overcome the average distance that initially separates them, or they do not stay together if they happen to encounter. The same is true for denser populations when either particles are very slow, or they are very fast. In both cases, the final state is gas-like, meaning that particles are mostly found isolated from one another. For intermediate velocities and larger densities, particles form aggregates of different geometry, including well-separated groups of similar size corresponding to the aggregation behavior of Dictyostelium under standard conditions.

Figure 2 and Supplementary Figure 1 represent, overlaid to the heatmap of the fraction of aggregated particles, the final snapshot of simulations and the variation in time of different population-level statistics. Different possible qualitative outcomes of the aggregation process illustrated there are discussed below.

At low packing fraction ρ and low velocity v₀, particles self-organize into a large number of relatively small aggregates (Figure 2, case A). Within clusters, particle distribution is isotropic, i.e., it is similar in all directions, reflecting the homogeneity of the initial particle distribution. At the end of the simulations, a sizeable fraction of particles are found outside the aggregates. As indicated by the monotonous increase in the fraction of aggregated particles over time (Supplementary Figure 1A), this is a finite-time effect and every particle would eventually aggregate for higher t_f-values (Supplementary Figure 2). Under these conditions, the fate of each particle therefore depends on its local environment at the beginning of the simulation. This parallels the hypothesis by Rossine et al. that local fluctuations in the concentration of a quorum signal explains why some Dictyostelium cells end up as loners at the end of aggregation (Rossine et al., 2020).

At high particle speed and low packing fraction (Figure 2, case B), the number of aggregates quickly reaches a plateau and then slowly decreases, whereas aggregate mean size constantly increases over time (Supplementary Figure 2B). Similarly to an Ostwald ripening process (Ostwald, 1896), where smaller droplets in an emulsion progressively merge with larger, more energetically favorable droplets, particles evaporate (i.e., detach) from small groups to join bigger and more stable aggregates (Supplementary Figure 2). Aggregate accretion is essentially limited by particles evaporation, causing a fraction of particles to be always found outside the aggregates.

By continuously increasing particle speed at low packing fraction, the system transitions between the two previously described states where particle clusters coexist with non-aggregated particles. The latter have however different origin depending on particle speed. At low particle speed, aggregation leaves out “latecomer” particles that did not reach any aggregate within the finite time of the simulation; at high speed, the “gas-like phase” is composed by particles that have evaporated from aggregates. Increasing particle speed, the transition between these two scenarios occurs through a phase where aggregation is very efficient. The fraction of aggregated particles, indeed, first increases and then decreases, and reaches a maximum at the optimal speed v_opt, which depends weakly on the packing fraction ρ.

At such intermediate velocity and packing fractions (illustrated in Figure 2, case C), self-organization leads to the formation of multiple rounded aggregates, that contain almost every particle. For much longer simulation times, aggregates would coarsen and progressively merge into one single aggregate of size N, as indicated by the combined decrease in aggregate number and increase in mean size (Supplementary Figure 1C). Such coarsening process however is largely irrelevant for aggregation over finite times.

Finally, at higher packing fraction, particles rapidly self-organize into labyrinthine structures (Figure 2, cases D and E). Similarly to what can be observed at lower packing fractions, the few non-aggregated particles at low speed are “latecomers”, whereas at high particle speed, non-aggregated particles are “gas-like particles”, where—as for MIPS (Fily and Marchetti, 2012)—steric interactions limit the coexistence of multiple independent aggregates. The measure of aggregate size is not meaningful under these conditions, the packing fraction being so high that every particle is connected to a large number of other particles virtually from the start.

3.3. Differences in motility bias the outcome of aggregation

Variation in particle speed gives rise to different finite-time aggregation patterns in homogeneous populations, leading to the production of non-aggregated cells through two qualitatively distinct routes: delayed aggregation (DA) and evaporation (E). It is thus natural to expect that mixing particles of different speed would reflect into differential rates of aggregation. It is however not obvious how the emergent aggregation patterns, which result from individual interactions, are related to the collective behavior of each particle types in homogeneous populations. In order to explore this question, we run simulations of binary mixes of particles with two different constant speeds v₁ and v₂.

Let us first consider two 1:1 binary mixes where particles have self-propelled velocities that are either both to the left (v₁ = 3 and v₂ = 6), or both to the right (v₁ = 15 and v₂ = 18) of v_opt, so that non-aggregated particles stem from the same of the two previously discussed mechanisms (Figure 3A). We refer to those as “delayed aggregation” (DA) mix and “evaporation” (E) mix, respectively, to signify the different origin of non-aggregated particles.

FIGURE 3

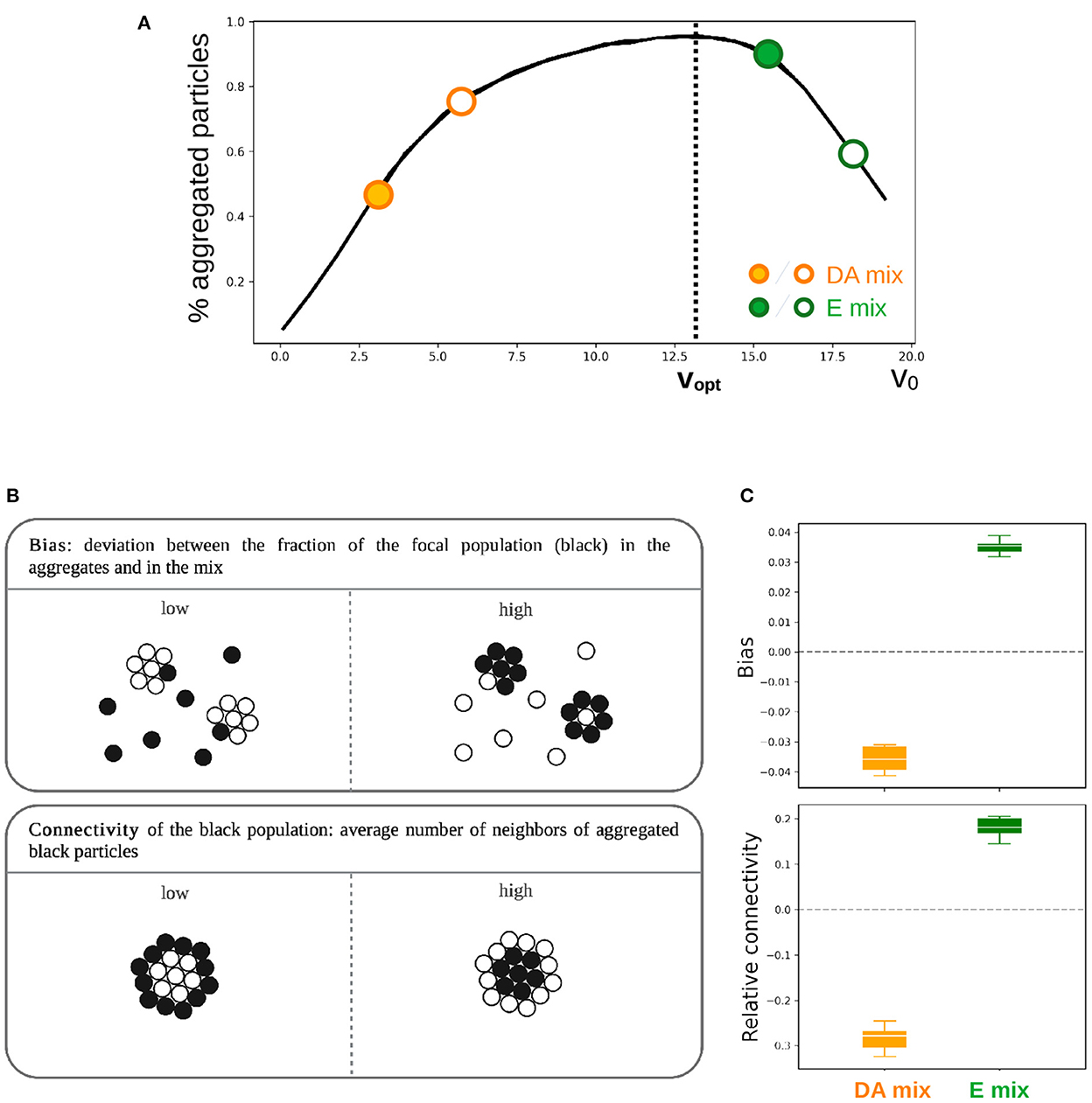
Figure 3. Effect of heterogeneity in cell motility on the outcome of aggregation in two different types of binary mix. (A) Two populations of particles with different motility (DA mix: v₁=3 and v₂=6, E mix: v₁=13 and v₂=16) where mixed in equal proportion (N = 10⁴, ρ = 0.07 for the total population). The focal population is indicated by a full circle. (B) Order parameters allowing to capture the effect of heterogeneity in particles motility on the outcome of aggregation. (C) Aggregation bias and mean connectivity of the focal population within the aggregates estimated at the end of 6 independent simulations as described in (B).

Aggregation biases can manifest as differential fractions of particles that aggregate, in aggregate composition, or in the topology of interactions within aggregates.

We first assessed whether particles of different types segregated during aggregation. Indeed, if particles assorted preferentially with those of the same type, aggregate composition would be bimodally distributed, and the overall behavior would be close to the superposition of the patterns of each composing population in isolation. This scenario may for instance be expected in biological chimeras where cells are able to discriminate and preferentially aggregate with kins (Gruenheit et al., 2017). In our case, we did not find evidence of segregation, and group composition was unimodally distributed for both mixes around a “typical” value, as displayed in Supplementary Figure 3.

We further quantified two statistical properties or order parameters that provide indications on the partition of particles among the aggregated and free component, and on the internal structure of groups (illustrated in Figure 3B): aggregation bias and connectivity. These metrics are easy enough to be measured in real populations, as long as there is a way to visually distinguish two co-aggregating populations.

Aggregation bias was estimated as the deviation between the mean aggregate composition and the proportion of each type of particles in the initial mix. This metric indicates to what extent differences in particle speed skew their ability to aggregate. In aggregative microbes only cells that manage to partake multicellular development have a chance to survive prolonged starvation. The aggregation bias measured in chimeras can thus be used as a proxy to connect the outcome of one cycle of aggregation with the long term success of a population, in the absence of further developmentally-induced divergence in cell fate (Tarnita et al., 2013; Dubravcic et al., 2014).

Finally, we quantified particles mean within-aggregate connectivity. For each type of aggregated particles, connectivity is measured as the number of particles (of any type) to which a focal particle is connected within an aggregate. Two particles are considered connected at a given time if they are closer than the maximal distance of interaction R₀ (see Section 2). High connectivity is associated to a central position within an aggregate, whereas particles with a lower connectivity are located closer to aggregates periphery. Connectivity thus reflects different spatial arrangements within clusters. In extant aggregative microbes, a more central or peripheral positioning can be associated to differential exposition to stress (Smukalla et al., 2008) or to differentiation cues (Julien et al., 2000).

Figure 3C displays these order parameters for two binary mixes of particles with different speed, as per Figure 3A. In both cases, the focal population is the slower one.

By analyzing biases in mean aggregates composition relative to the 1:1 composition of the mix (Figure 3C), we found that the slower type was under-represented in the aggregates (i.e., with a negative bias) in the DA mix, whereas the opposite results was found in E mix. Heterogeneity in particle speed thus biases the representation of the two co-aggregating populations in the aggregates, so that particles that aggregate more efficiently in isolation are over-represented in the aggregates. These are the type whose fraction of aggregated particles at t = t_f is higher (Figure 3A), i.e., the faster type in the DA mix and the slower type in the E mix.

Mean particle connectivity of the two particle types indicates that, moreover, particles that aggregate more efficiently in isolation are enriched in the core of the aggregates (Figure 3C). On the other hand, particles that in isolation are less efficient aggregators have, within the aggregates, a smaller number of neighbors, thus are preferentially located at the periphery. The type whose speed is closer to v_opt seems to nucleate the aggregation of the other type and ends up being over-represented in the aggregates at the end of the simulation.

3.4. Differences in motility result into three types of frequency-dependent aggregation biases

The process of self-organization responsible for the aggregation biases discussed above results from interactions between particles with different speed. It is hence expected to be sensitive to the proportion of each type of particles in the mix, which underpins the probability that particles of the same or different type encounter. Frequency-dependent biases have been moreover observed in aggregative multicellular species: the intensity of spore bias in Dictyostelium, and sometimes even its sign (Madgwick et al., 2018; Sathe and Nanjundiah, 2018), depend on the proportion of cells in the binary mix. Such frequency-dependent social interactions can lead, on the evolutionary timescale, to regimes where contrasting social strategies coexist, as we will discuss later. In order to identify the possible paths open to the evolution of aggregation in populations with heterogeneous cell motility, we investigated the effect of binary mix composition on aggregation bias.

Let f₁ be the proportion of particles with speed v₁ in the binary mix (then f₂ = 1 − f₁ is the proportion of particles with speed v₂). As indicated in Figure 4, there are only four qualitative types of biases that are continuous in the frequency f₁ and change sign at most once in the interval [0, 1]. These scenarios can be classified by looking at the variation of the bias for extreme values of f₁: when the slope of the bias has the same sign at low and high frequency, the type associated with negative bias gets excluded over evolutionary times (Figures 4A,B); when there is positive (negative) frequency-dependence at low (high) frequency, coexistence of the two types is evolutionary stable (Figure 4C); when there is negative (positive) frequency-dependence at low (high) frequency, the monomorphic populations are two alternative evolutionary stable solutions (Figure 4D). Assuming that every aggregated particle has the same probability of being transmitted to the next generation, which is reasonable for primitive aggregative life-cycles, the shape of the bias in aggregate composition predicts the outcome of evolution over repeated cycles of aggregation and dispersal, as exemplified in Figure 4A.

FIGURE 4

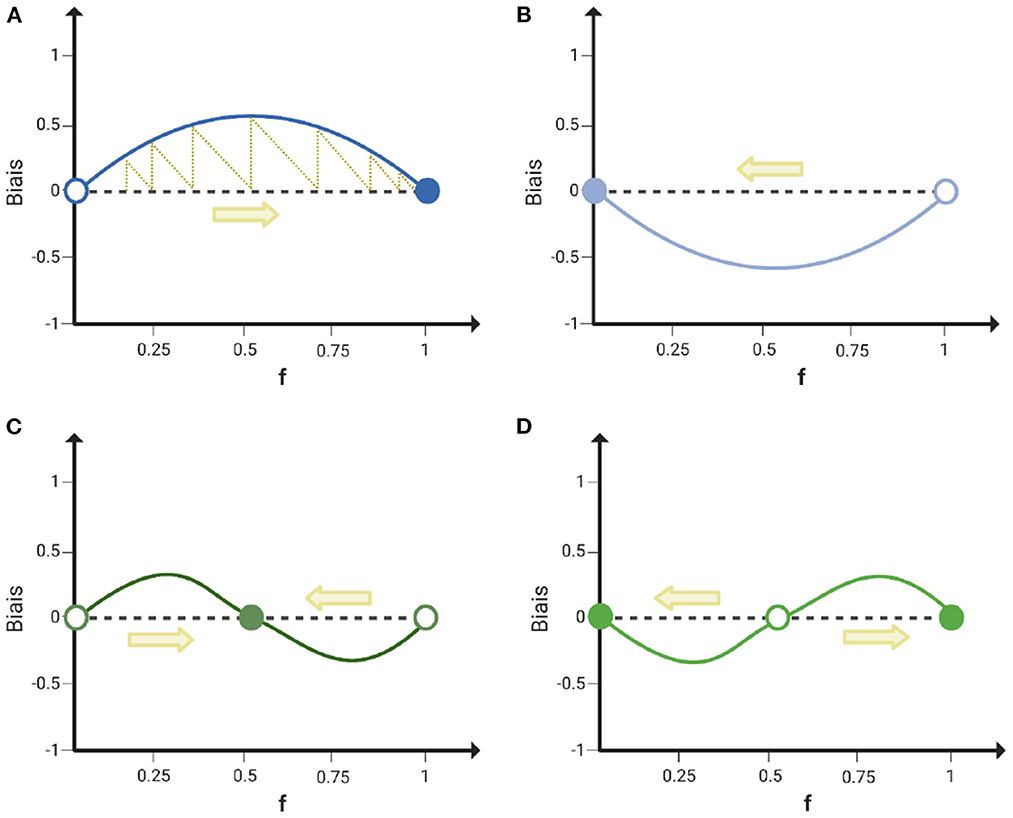
Figure 4. Four qualitatively different frequency-dependent aggregation biases correspond to distinct evolutionary stable states. Schematic representation of the four simplest classes of bias that can be obtained in a binary mix. The evolutionary dynamics of a binary mix composition (f) over many rounds of co-aggregation is represented by the yellow arrows. Stable equilibria are represented as filled circles and unstable ones as empty circles. The yellow dotted line in (A) illustrates the construction of the evolutionary trajectory: Each round starts with a mix composition equal to the aggregates composition at the end of the previous round, that is obtained by adding to the initial composition the aggregation bias. The four classes of bias give rise to different evolutionary stable solutions: fixation of the focal type (A) exclusion of the focal type (B), coexistence of both types (C) and bistability (D).

We examined what types of bias could be observed in binary mixtures of particles of different speed, and tried to establish a link to the properties of homogeneous populations of each type on its own. Aggregate composition was analyzed in binary mixes of different composition, keeping the packing fraction equal to 0.07. In order to reduce simulation time, we considered only extreme f₁-values (0 < f₁ < 0.05 and 0.95 < f₁ < 1).

We expect the aggregation process to be influenced both by the absolute and by the relative value of the velocities of the two types of particles. We have thus explored separately two scenarios: first, the speed of the first type was fixed and that of the second type was changed; second, both speeds were changed, but their difference was kept constant.

In the first analysis, the speed of particles of the focal population (v₁-particles) was set to the “optimal” value (v₁ = v_opt = 13) and the speed differential Δv = v₁−v₂ between the two particles types was gradually changed from negative to positive. This scan (Supplementary Figure 4) confirms the intuition that the better aggregator is always over-represented in the aggregates when mixed with particles with a different speed, whatever the mix composition f₁. Indeed, the bias in aggregate composition of the better-aggregator (i.e., the v₁-population) is systematically positive at both low and high f₁-values. Moreover, the slope of the bias for low and high f₁ increases with |Δv|, indicating that the bias intensity is positively correlated with the level of heterogeneity between the two particles types.

In the second type of binary mix, where the speed differential Δv is kept constant while particle speeds are simultaneously increased, the slopes at extreme frequencies instead change sign (Supplementary Figure 5). Besides the two cases where one particle type dominates for any frequency (Figures 4A,B), we observed also the frequency-dependent profile that predicts long-term coexistence of particles with different motility over repeated cycles of aggregation and dispersal (Figure 4C). The latter occurs when binary mixes are composed of particles whose speed is on opposite sides of v_opt (Supplementary Figure 5, third and fourth row). The bias is in favor of the slower particles when they are at low frequency in the mix, whereas at high frequencies they are under-represented in the aggregates.

Biases in aggregates composition however appear rather weak and noisy (as indicated by the large confidence intervals in some of the scans illustrated in Supplementary Figures 4, 5). We thus ran 20 independent simulations for f₁-values ranging from 0 to 1 and using a larger speed differential (Δv = 6, as illustrated in Figure 5A) to confirm that binary mixes composed of particles whose speed falls on different sides of v_opt sustain a bias profile that is compatible with evolutionarily stable heterogeneity in particles motility. As expected, this combination yielded a more conspicuous and less variable bias (Figure 5B).

FIGURE 5

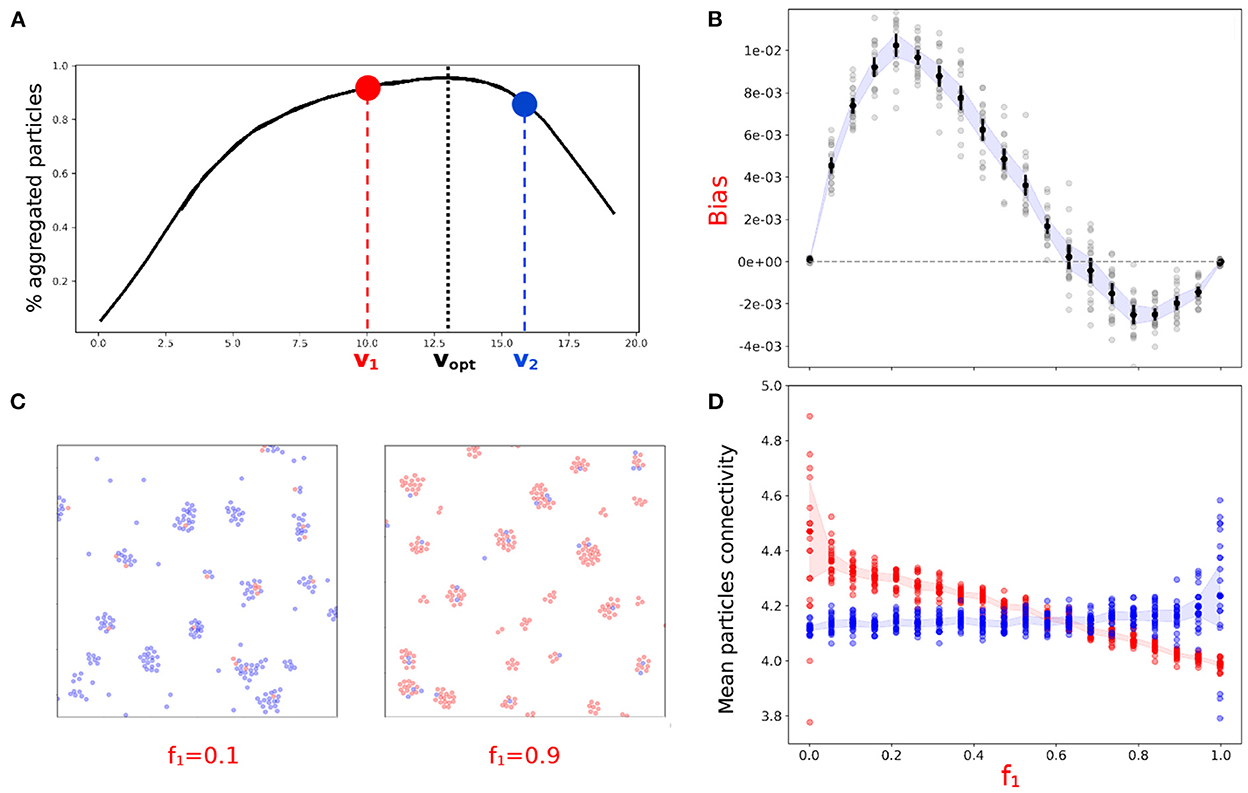
Figure 5. Heterogeneity in particle speed induces biases whose sign depends on composition of the binary mix. (A) Binary mix of particles with speed on both sides of v_opt. (B) Aggregation bias of the slower population when mixed in different proportion (f₁) with the faster population. (C) Zoom on snapshots of the final state of the system for f₁ = 0.1 and f₁ = 0.9. (D) Mean connectivity of the two types of aggregated particles as a function of f₁. (B,D) Twenty independent simulations were run were for each f₁-value. The shaded area represents the 95% confidence interval.

Mean connectivity of aggregated particles for the two particles types provides mechanistic information on the underpinning of such frequency-dependent bias. Figure 5D shows that particles with higher connectivity—i.e., more central in the aggregates—are over-represented in the aggregated fraction, irrespective of their speed, consistent with previous observations (Figure 3C). When slow particles are in low proportion in the mix, aggregates are essentially composed of fast particles. In such aggregates, fast particles have lower connectivity (Figures 5C,D), i.e., a peripheral location, so that they can be pushed out of the aggregate by stochastic fluctuations and detach, joining the population of isolated cells. Slow particles, on the other hand, have a high chance of being integrated in an aggregate quickly formed by fast particles, hence the positive bias in aggregates composition is in their favor. When slow particles are in high proportion in the binary mix, they prevail in the aggregates. Due to their higher speed, fast particles join aggregates earlier and are thus located closer to the aggregates center than slow particles (Figure 5C). The central location of fast particles prevents their evaporation, and delayed aggregation simultaneously causes slow particles to be under-represented in the aggregates. On longer timescales, however, all slow particles join an aggregate, and fast particles are expected to sort to the periphery of aggregates (Jones et al., 1989). The bias against particles that are too slow to aggregate is therefore expected to progressively vanish as the time t_f available to aggregate increases.

Numerical simulations of the binary mix of Figure 5 were run for twice and five times longer time spans (t_f = 200 and t_f = 500). As predicted, the range of f₁-values for which the slower particles are under-represented in the aggregated fraction decreases accordingly, and vanishes for the longest period (Figure 6).

FIGURE 6

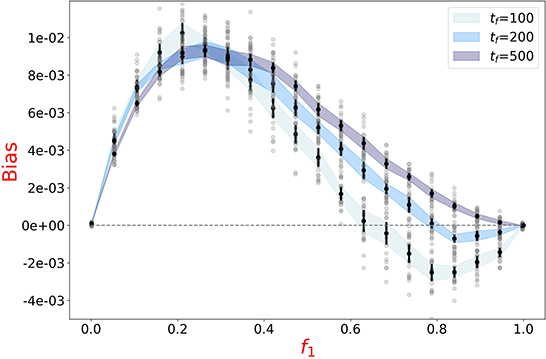
Figure 6. Prolonged aggregation mitigates the frequency-dependent inversion of bias. Aggregation bias of the v₁-population as a function of its frequency f₁ in a binary mix of particles (v₁ = 10 and v₂ = 16), estimated after different simulation time (t_f). Twenty replicates were performed for each f₁-value. The shaded area represents the 95% confidence interval.

When aggregation lasts long enough, so that all particles end up aggregating, evaporation of fast particles is thus the only source of aggregation biases. Hence, only the bias in favor of slower particles (Figure 4) is asymptotically observed. As a consequence, the existence of life cycles that bound the duration of the aggregation phase could support the evolutionary maintenance of highly motile cells, being otherwise counter-selected, and simultaneously the establishment of a polymorphic equilibrium.

Alongside particle speed, adhesion strength is certainly a parameter that plays a key role in determining the outcome of an aggregation process. Moreover, it is likely to be heterogeneous in cellular populations. The complete examination of the interplay of speed and adhesion heterogeneity is beyond the scope of this work, however it is important to consider the extent to which the conclusions drawn so far keep holding when adhesion strength is varied.

3.5. Biases induced by heterogeneity in particles motility depend predictably on particles adhesion strength

In addition to particle speed and packing fraction (Figure 2), particle adhesion strength is also expected to affect aggregation efficiency. This parameter indeed determines the probability that two particles stick together when they encounter. Increasing particles adhesion strength can thus be expected to reduce the rate at which particles detach from aggregates, hence affect the balance between evaporation and delayed aggregation.

The fraction of aggregated particles at the end of the simulation was estimated for a range of particle speeds and adhesion strengths in a population with homogeneous speed in order to obtain a quantitative understanding of how particle adhesive strength influences the outcome of aggregation. Supplementary Figure 6 displays the proportion of aggregated particles for packing fraction ρ = 0.07.

Variation in F_adh does not affect the outcome of aggregation for small particle speeds. In this regime, aggregation over a finite time is indeed limited by the low encounter rate of isolated slow particles. As soon as particles are fast enough to interact, almost any adhesion strength except the weakest leads to aggregation. The fraction of aggregated particles increases with their speed to the point where evaporation starts being important. The higher v₀, the higher the force intensity required to counterbalance the effect of evaporation. In the Supplementary material, we present a model for the interaction between two particles that predicts the quadratic relation between F_adh and particle speed observed in the simulations (Figure 7A).

FIGURE 7

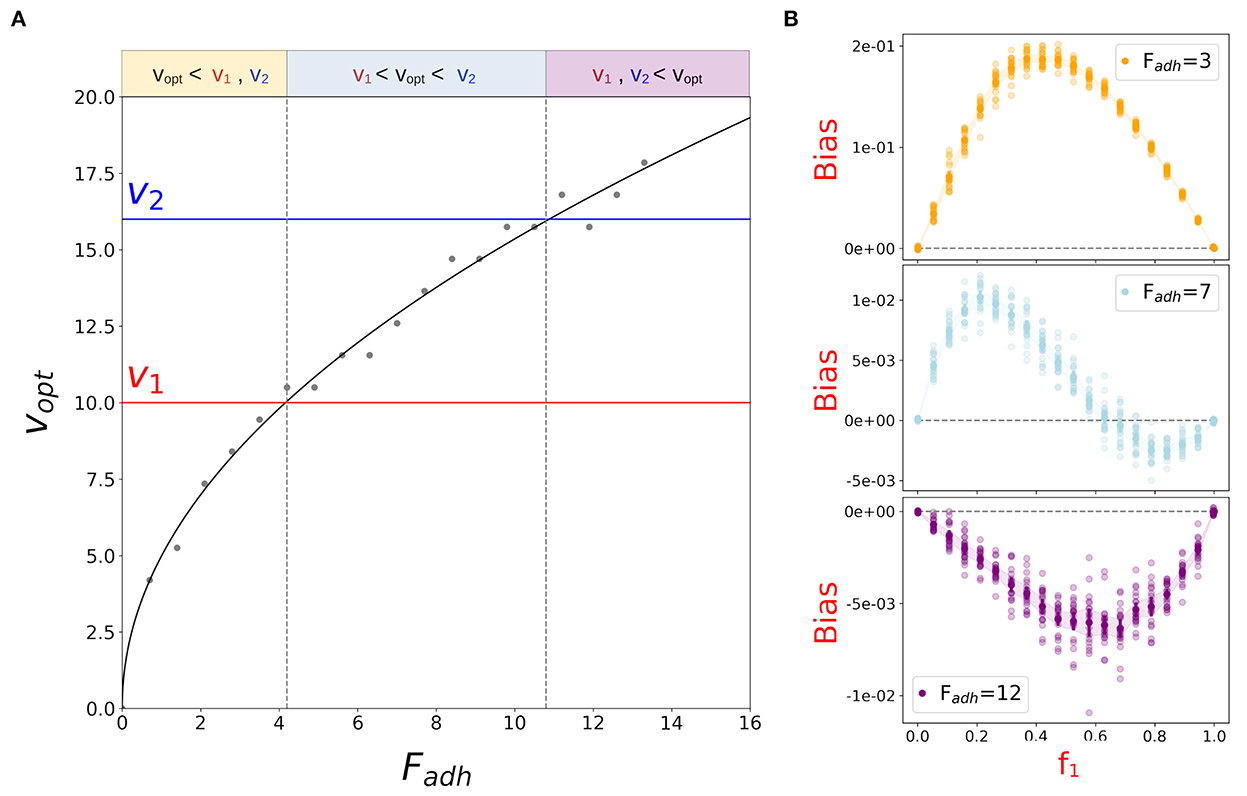
Figure 7. Particle adhesion affects the outcome of aggregation in binary mixes of particles with heterogeneous speed. (A) Particle speed v_opt for which the proportion of aggregated particles at t = t_f is highest increases with the intensity of adhesive forces F_adh (see Supplementary Figure 6). The curve $v_{opt}~\sqrt{F_{adh}}$ (see Supplementary material for a derivation from microscopic principles) was fitted to the optimal speed obtained from simulations (gray dots). Three F_adh ranges can be defined depending on the relative position of v₁, v₂, and v_opt (indicated by different colors), as previously discussed for varying v₀. (B) Aggregation bias of the slower population measured at the end of simulations of the binary mix described in Figure 5, for adhesive strength within the ranges indicated in the left panel (F_adh = 3, F_adh = 7 and F_adh = 12).

Let us now consider a binary mix of particles with different speed, where adhesion strength varies uniformly for both particle types, while other parameters are the same as for Figure 5 (v₁ = 10, v₂ = 16, ρ = 0.07). We previously proposed that the type of bias in aggregate composition depends on the position of v₁ and v₂ relative to v_opt. We can now check that this assumption correctly predicts the change of the bias when v_opt changes as a function of F_adh. For any fixed couple of velocities v₁ and v₂, there are three possible ranges of F_adh where v_opt is located to the left, to the right, or in between their values, as illustrated in Figure 7. By choosing adhesion strengths that belong to such intervals, we can retrieve the same qualitative form of bias as predicted: for low adhesion strengths, where both velocities are larger than v_opt, slower particles are positively biased (Figure 7B, orange); for high adhesion strengths, the opposite occurs because of delayed aggregation (Figure 7B, purple); for intermediate adhesion strengths, positive frequency-dependence is observed (Figure 7B, blue).

Overall, when the two co-aggregating populations are on both side of v_opt, aggregates composition is biased because of the interplay of two counteracting processes: evaporation of fast particles and delayed aggregation of slow particles. The relative contribution of these two factors determines the sign of the bias and depends on the proportion of the types in the binary mix. When the speed of both particle types is smaller than v_opt, the slower is under-represented in the aggregates due to delayed aggregation. When both speeds are larger than v_opt, the slower type is over-represented in the aggregates due to the higher evaporation of faster particles. Finally, when v₁ < v_opt < v₂, the competition between delayed aggregation of the slower particles and evaporation of the faster particles provides different results if one or the other particle is at low frequency, giving rise to a bias that changes sign at intermediate frequencies. As long as the duration of the aggregation phase is finite, then, the evolutionary dynamics is predicted to stabilize the coexistence of different types of particles. Interestingly, the frequency-dependent bias associated to bistability (Figure 4D) was not observed. This scenario would require particles faster than v_opt to be over-represented in the aggregates when abundant (low f₁-values), which can only be achieved if differential evaporation in favor of fast-particles can be compensated. Theoretically, this may occur if fast particles were surrounded by a “shell” of slow particles, which, for initially uniformly assorted particles, would require additional mechanisms of spatial sorting. It may, for instance, be achievable if slower particles were also less adhesive (Garcia et al., 2014).

These results show that, somehow unexpectedly given the complexity of the self-organized dynamics and the transient nature of aggregation patterns, biases in binary mixes can be predicted once the behavior of the two populations in isolation is characterized.

4. Discussion

When multicellularity emerged from unicellular ancestors, a transition occurred from populations under selection for individual properties to a higher level of biological organization, where collective adaptation became possible. Aggregative multicellularity, one of the two routes followed in this transition, involves the integration of cell aggregation into a life-cycle that also encompasses free living. Cell aggregation offers a mechanism of fast and transient grouping, that may be adaptive for coping with rapidly and unpredictably changing environments (Marquez-Zacarias et al., 2021). As a side-effect of fast grouping, multicellular aggregates are however generally composed of a mosaic of cells in different phenotypic states. Also observed in extant aggregative species (Fortunato et al., 2003b; Gilbert et al., 2007; Sathe et al., 2010), single-cell heterogeneity between co-aggregating cells may have been particularly important for the early steps of the transition to aggregative multicellularity, as it can promote the recruitment of ancestral functions toward incipient division of labor. On the other hand, before mechanisms of assortment evolved to reduce it, intra-group heterogeneity might have caused widespread genetic conflicts that threatened multicellular organization.

Differences in cell properties between co-aggregating cells is known to bias their probability to differentiate into dormant phenotypes at the end of multicellular development (Forget et al., 2021). However, understanding the evolutionary implications of such single-cell heterogeneity on the outcome of aggregation is currently limited by a lack of mechanistic explanations, in particular of how initial diversity translates into biases in the composition of multicellular aggregates. Among the many features that display cell-to-cell variation, cell motility can be expected to directly impact the probability that a cell joins a multicellular aggregate, and therefore to affect spore bias. Indeed, as already pointed out for D. discoideum loners (Dubravcic et al., 2014; Tarnita et al., 2015) only aggregated cells can differentiate into spores and survive the dispersal phase of the life cycle.

We used individual-based simulations to confirm the intuition that heterogeneity in cell motility affects the outcome of aggregation. Heterogeneity in single-cell properties is known to act within multicellular aggregates, where cell sorting can be a source of bias in the developmental fate of cells (Houle et al., 1989; Jones et al., 1989; Umeda and Inouye, 2004; Strandkvist et al., 2014). We showed that biases can also emerge during aggregation, before cells experience proper “social” interactions. In primitive aggregative life-cycles, before the evolution of cell coordination mechanisms susceptible of reshuffling or canceling out aggregation biases, cell motility properties inherited from a unicellular ancestor may therefore have been recruited for their effects on group adaptation.

Numerical exploration of different binary mixes highlighted three types of aggregation biases resulting from heterogeneity in particles motility. Notably, when particles that are too slow to join a group before the end of aggregation are mixed with particles that are fast enough to leave an aggregate, the sign of the bias in the aggregated fraction changes with frequency. Slow particles are over-represented in the aggregates when they are rare in the population, but the opposite is true when they are in high proportion. This type of frequency-dependent bias allows to stabilize polymorphism in populations of interacting genotypes (Hudson et al., 2002; Brännström and Dieckmann, 2005). Frequency-dependent spore bias has been invoked (Parkinson et al., 2011; Madgwick et al., 2018) as a possible mechanisms for the maintenance of the diversity of strains observed in natural populations of aggregative species, such as Dictyostelium (Francis and Eisenberg, 1993; Fortunato et al., 2003b) or M. xanthus (Vos and Velicer, 2009; Kraemer and Velicer, 2011). However, it is typically associated to developmental biases that emerge in the course of the multicellular stage of the life cycle (Parkinson et al., 2011; Madgwick et al., 2018). We have shown that such biases can also emerge passively from heterogeneity in single-cell properties during aggregation. As such, they may have stabilized genetic chimerism early in the transition to aggregative multicellularity, even before development became highly regulated and contributed to limit genetic conflicts in primitive aggregative life-cycle.

Beyond its constructive role on fostering polymorphism during aggregation, heterogeneity in cell speed can also play an active role in later developmental stages. Motility-induced cell sorting within multicellular aggregates (Jones et al., 1989; Beatrici and Brunnet, 2011) indeed paves the way toward the exploitation of morphogen gradients for establishing differential cell fates. Hence, heterogeneity in cell speed during aggregation could have concomitantly fueled the evolution of division of labor, and played a role in establishing dynamical patterning modules during multicellular development (Newman and Bhat, 2009). In extant aggregative species such as D. discoideum and M. xanthus, position within an aggregate is known to determine cell probability to form a spore (Araki et al., 1997; Huang et al., 1997; Julien et al., 2000). In a model describing cell arrangement within Dictyostelium slugs, slower cells sort to the back during migration (Umeda and Inouye, 2004), thus populating preferentially the region that will eventually turn into the spore mass. Developmental sorting can act in the same or opposite direction relative to aggregation biases. In the evaporation-limited region, faster particles are doubly disadvantaged, as they would be both over-represented in the loners and in the stalk. Motility differences instead act in opposite directions, and could even cancel out, when non-aggregated particles are mostly slow particles delaying their aggregation. In this region, slow particles are indeed under-represented in the aggregates, but once they have joined an aggregate, they are expected to sort to the back of the slug hence to differentiate into spores. Combining aggregation and multicellular development delineates an evolutionary trade-off between being sufficiently fast to join an aggregate during aggregation on the one hand, and sufficiently slow to sort to the back of the slugs on the other hand.

When cell motility is a heritable trait, aggregation biases induced by heterogeneity in single-cell properties underpin its evolutionary trajectory over multiple cycles of aggregation and dispersal. We can imagine that cell motility evolves by the appearance of mutant cells whose speed is a small variation of the resident population. The bias in aggregate formation then determines the likelihood that the mutant trait substitutes the resident, as illustrated in Figure 4. Our results indicate that, as long as both the mutant and the resident traits are on the same side of v_opt, selection will push particles to approach the optimal, intermediate velocity for which aggregation is maximally efficient. Indeed, the better aggregator in isolation is always over-represented in the aggregates, so that evolution would climb the gradient of the proportion of aggregated particles, that is concave and has a unique maximum (Figure 3A). However, if the resident and the mutant fall on the opposite sides of v_opt—which is increasingly likely, as the optimal value is approached—polymorphic solutions become available, where particles with different motility can coexist. Evolutionary branching is possible in such a situation, as predicted in models for the adaptive dynamics of social strategies (Doebeli, 2004). As discussed above, and argued elsewhere (Miele and De Monte, 2021), coexistence of slow and fast cells may be integral to the establishment of aggregative life cycles, perhaps even before the two phenotypes were unified as plastic manifestations of one single genotype.

During the last decades, emergent patterns of populations of self-propelled particles have been at the core of research in active matter physics (Marchetti et al., 2013). In particular, motility-induced phase separation has been evidenced as a state where steric interactions generate, in sufficiently dense populations, the coexistence of gas and aggregated phases (Fily and Marchetti, 2012). We focused instead on lower densities, where we could observe the emergence of multiple particle aggregates, similar to a field of aggregation of slime molds. At these packing fractions, adhesion plays a fundamental role in determining the aggregation pattern. The probability that cells remain together upon encounter indeed derives from a balance between adhesive forces and self-velocity, modulated by fluctuations. Several qualitatively different particle arrangements have been identified as steady-states of populations whose particles are both adhesive and align their motion (Grégoire et al., 2003). Before stabilizing their distribution on asymptotic patterns, active particles also display transient clustering (Ostwald, 1896; van der Linden et al., 2019). Such long-lasting regimes can be relevant for biological populations, where aggregation occurs over a finite timescale. Including non-stationary patterns led us to identify two possible regimes where clusters coexist with isolated particles. At low speed, non-aggregated particles are “latecomers” that did not have the chance to interact with other particles by the end of the simulation. Their proportion in the aggregated fraction depends on the duration of aggregation, other than on particle density, and is expected to converge to one as the system reaches its stationary state. A consequence of time-constrained aggregation is that, when they are rare, slow particles are overrepresented in aggregates relative to particles fast enough to evaporate, but have a negative bias when common. Such a frequency-dependent bias is not found in simple models where diversity among interacting agents is depicted in terms of fixed social strategies. Game theoretical representations of interactions within multicellular bodies indeed typically predict that “cheater” types, that have by definition a positive bias, would be evolutionary stable in the absence of mechanisms favoring interactions among kins (Strassmann et al., 2000; Strassmann and Queller, 2011). Complementing explanations based on strategic decision-making of cells during multicellular development (Madgwick et al., 2018), we propose here that frequency-dependent biases can also be established by passive mechanisms, based on individual heterogeneity. It will be the subject of future studies whether such dependence is robust to heterogeneity in other parameters. In particular, adhesion on top of velocity could be chosen as a heterogeneous trait, possibly correlated with speed.

These extensions can be informed by experimental observations of aggregative multicellular microbes, where parameters—at least those controlling single-cell motility—may be estimated for specific populations. The possibility that frequency-dependent biases are induced during the aggregation phase could be tested in extant aggregative microbes. The aggregation dynamics of populations with different motility could be assessed when they aggregate separately, and in chimeras with different proportions of two types. We are not aware of non-invasive methods to modulate Dictyostelium motility. One possible strategy to generate populations with differential motility is to apply contrasting selective pressures in a directed evolution experiment, as realized for cell adhesion in Adiba et al. (2022).

More generally, a better understanding of the mechanical properties of unicellular organisms may prove essential to capture the diversity of paths leading to current forms of multicellular organization.

5. Conclusion

In aggregative life cycles, multicellular aggregates encompass a much higher degree of heterogeneity than clonally growing bodies, and therefore face a degree of conflict that can be deleterious to the evolutionary stability of multicellular functions. The maintenance of such functions is commonly explained by the existence of mechanisms that allow cells to recognize kin, so as to direct the benefits of cooperation toward them. Such recognition mechanisms may however not have been present in primitive forms of aggregative life cycles, where former unicellular organisms were not yet adapted to group living.

Here, we have explored the possibility that evolutionarily relevant biases in aggregate composition may follow from heterogeneity in a physical property of cells that involves no coordination with other cells. Cell speed may have varied among unicellular ancestors well before multicellular organization emerged. We therefore asked how cells of different motility would be represented inside and outside aggregates that formed by adhesion after cell encounter.

Simulations of an individual-based self-propelled particles model indicates that as long as aggregation occurs on a finite time scale—as it does in extant aggregative microbes—velocity differences reflect in compositional biases of the self-organized groups. Such biases suggest that particle-level selection may act as to keep cell motility bounded, and simultaneously lead to an optimal aggregation efficiency that can be attained at an intermediate particle speed. Moreover, in binary mixes of particles whose speed is below and above the optimal value, frequency-dependent biases can give rise to the evolutionary convergence toward a polymorphic state, where coexistence of different velocities may be exploited during successive developmental stages.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author/s.

Author contributions

MF, SA, LB, and SD: conceptualization. MF, LB, and SD: methodology and formal analysis. MF and LB: investigation. MF and SD: writing—original draft and revised manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work has received support under the program Investissements d'Avenir launched by the French Government and implemented by ANR with the references ANR–10–LABX–54 MEMOLIFE and ANR–10–IDEX–0001–02 PSL* Université Paris, Q-life ANR-17-CONV-6150005, and the project ANR-19-CE45-0002 ADHeC PSL research University. LB thanks the Brazilian agencies CNPq and Capes for their support.

Acknowledgments

The authors are grateful to Gabriel Peyré for his help in optimizing the Python program. The authors also thank Thibaut Arnoulx de Pirey Saint Alby for helpful discussions on the link between the adhesion strength and the rate of evaporation and Nirbhay Patil for discussions on active matter physics.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.1052309/full#supplementary-material

References

Adiba, S., Forget, M., and Monte, S. D. (2022). Evolving social behavior through selection of single-cell adhesion in Dictyostelium discoideum. iScience 25, 105006. doi: 10.1016/j.isci.2022.105006

PubMed Abstract | CrossRef Full Text | Google Scholar

Araki, T., Abe, T., Williams, J. G., and Maeda, Y. (1997). Symmetry breaking in Dictyostelium morphogenesis: evidence that a combination of cell cycle stage and positional information dictates cell fate. Dev. Biol. 192, 645–648. doi: 10.1006/dbio.1997.8784

PubMed Abstract | CrossRef Full Text | Google Scholar

Azhar, M., Kennady, P. K., Pande, G., Espiritu, M., Holloman, W., Brazill, D., et al. (2001). Cell cycle phase, cellular Ca2+ and development in Dictyostelium discoideum. Int. J. Dev. Biol. 45, 405–414.

Google Scholar

Beatrici, C. P., and Brunnet, L. G. (2011). Cell sorting based on motility differences. Phys. Rev. E 84, 031927. doi: 10.1103/PhysRevE.84.031927

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonner, J. T. (1995). Why does slug length correlate with speed during migration in Dictyostelium discoideum? J. Biosci. 20, 1–6. doi: 10.1007/BF02711575

CrossRef Full Text | Google Scholar

Bonner, J. T., Clarke, W. W., Neely, C. L., and Slifkin, M. K. (1950). The orientation to light and the extermely sensitive orientation to temperature gradients in the slime mold Dictyostelium discoideum. J. Cell. Comp. Physiol. 36, 149–158. doi: 10.1002/jcp.1030360203

PubMed Abstract | CrossRef Full Text | Google Scholar

Brännström, Å., and Dieckmann, U. (2005). Evolutionary dynamics of altruism and cheating among social amoebas. Proc. R. Soc. B Biol. Sci. 272, 1609–1616. doi: 10.1098/rspb.2005.3116

PubMed Abstract | CrossRef Full Text | Google Scholar

Buttery, N. J., Thompson, C. R. L., and Wolf, J. B. (2010). Complex genotype interactions influence social fitness during the developmental phase of the social amoeba Dictyostelium discoideum. J. Evol. Biol. 23, 1664–1671. doi: 10.1111/j.1420-9101.2010.02032.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Casiulis, M., Tarzia, M., Cugliandolo, L. F., and Dauchot, O. (2020). Velocity and speed correlations in Hamiltonian flocks. Phys. Rev. Lett. 124, 198001. doi: 10.1103/PhysRevLett.124.198001

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, E. (2014). Origins of evolutionary transitions. J. Biosci. 39, 303–317. doi: 10.1007/s12038-013-9375-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Cornforth, D. M., Sumpter, D. J. T., Brown, S. P., and Brännström, Å. (2012). Synergy and group size in microbial cooperation. Am. Nat. 180, 296–305. doi: 10.1086/667193

PubMed Abstract | CrossRef Full Text | Google Scholar

Doebeli, M. (2004). The evolutionary origin of cooperators and defectors. Science 306, 859–862. doi: 10.1126/science.1101456

PubMed Abstract | CrossRef Full Text | Google Scholar

Dubravcic, D., van Baalen, M., and Nizak, C. (2014). An evolutionarily significant unicellular strategy in response to starvation in Dictyostelium social amoebae. F1000Res. 3, 133. doi: 10.12688/f1000research.4218.2

PubMed Abstract | CrossRef Full Text | Google Scholar

Fily, Y., and Marchetti, M. C. (2012). Athermal phase separation of self-propelled particles with no alignment. Phys. Rev. Lett. 108, 235702. doi: 10.1103/PhysRevLett.108.235702

PubMed Abstract | CrossRef Full Text | Google Scholar

Fletcher, J. A., and Doebeli, M. (2009). A simple and general explanation for the evolution of altruism. Proc. R. Soc. B Biol. Sci. 276, 13–19. doi: 10.1098/rspb.2008.0829

PubMed Abstract | CrossRef Full Text | Google Scholar

Forget, M., Adiba, S., and De Monte, S. (2021). Social conflicts in Dictyostelium discoideum: a matter of scales. Peer Commun. J. 1, e58. doi: 10.24072/pcjournal.39

CrossRef Full Text | Google Scholar

Forhet, M., Adiba, S., and de Monte, S. (2022). Single-Cell Phenotypic Plasticity Modulates Social Behaviour in Dictyostelium Discoideum. Cold Spring Harbor Laboratory. doi: 10.1101/2022.10.10.511564

CrossRef Full Text | Google Scholar

Fortunato, A., Queller, D. C., and Strassmann, J. E. (2003a). A linear dominance hierarchy among clones in chimeras of the social amoeba Dictyostelium discoideum: Hierarchies of clones in social amoebae. J. Evol. Biol. 16, 438–445. doi: 10.1046/j.1420-9101.2003.00545.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortunato, A., Strassmann, J. E., Santorelli, L., and Queller, D. C. (2003b). Co-occurrence in nature of different clones of the social amoeba, Dictyostelium discoideum. Mol. Ecol. 12, 1031–1038. doi: 10.1046/j.1365-294X.2003.01792.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Francis, D., and Eisenberg, R. (1993). Genetic structure of a natural population of Dictyostelium discoideum, a cellular slime mould. Mol. Ecol. 2, 385–391. doi: 10.1111/j.1365-294X.1993.tb00031.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Garcia, T., Brunnet, L. G., and De Monte, S. (2014). Differential adhesion between moving particles as a mechanism for the evolution of social groups. PLoS Comput. Biol. 10, e1003482. doi: 10.1371/journal.pcbi.1003482

PubMed Abstract | CrossRef Full Text | Google Scholar

Garcia, T., and De Monte, S. (2013). Group formation and the evolution of sociality. Evolution 67, 131–141. doi: 10.1111/j.1558-5646.2012.01739.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Garcia, T., Doulcier, G., and De Monte, S. (2015). The evolution of adhesiveness as a social adaptation. eLife 4, e08595. doi: 10.7554/eLife.08595

PubMed Abstract | CrossRef Full Text | Google Scholar

Gilbert, O. M., Foster, K. R., Mehdiabadi, N. J., Strassmann, J. E., and Queller, D. C. (2007). High relatedness maintains multicellular cooperation in a social amoeba by controlling cheater mutants. Proc. Natl. Acad. Sci. U.S.A. 104, 8913–8917. doi: 10.1073/pnas.0702723104

PubMed Abstract | CrossRef Full Text | Google Scholar

Golé, L., Rivière, C., Hayakawa, Y., and Rieu, J.-P. (2011). A quorum-sensing factor in vegetative Dictyostelium discoideum cells revealed by quantitative migration analysis. PLoS ONE 6, e26901. doi: 10.1371/journal.pone.0026901

PubMed Abstract | CrossRef Full Text | Google Scholar

Goury-Sistla, P., Nanjundiah, V., and Pande, G. (2012). Bimodal distribution of motility and cell fate in Dictyostelium discoideum. Int. J. Dev. Biol. 56, 263–272. doi: 10.1387/ijdb.113384ps

PubMed Abstract | CrossRef Full Text | Google Scholar

Grégoire, G., Chaté, H., and Tu, Y. (2003). Moving and staying together without a leader. Phys. D Nonlinear Phenomena 181, 157–170. doi: 10.1016/S0167-2789(03)00102-7

CrossRef Full Text | Google Scholar

Grosberg, R. K., and Strathmann, R. R. (2007). The evolution of multicellularity: a minor major transition? Annu. Rev. Ecol. Evol. Syst. 38, 621–654. doi: 10.1146/annurev.ecolsys.36.102403.114735

CrossRef Full Text | Google Scholar

Gruenheit, N., Parkinson, K., Stewart, B., Howie, J. A., Wolf, J. B., and Thompson, C. R. L. (2017). A polychromatic “greenbeard” locus determines patterns of cooperation in a social amoeba. Nat. Commun. 8, 1–9. doi: 10.1038/ncomms14171

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamilton, W. D. (1964). The genetical evolution of social behaviour. I. J. Theoret. Biol. 7, 1–16. doi: 10.1016/0022-5193(64)90038-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardin, G. (1968). The tragedy of the commons. Science 162, 1243–1248. doi: 10.1126/science.162.3859.1243

PubMed Abstract | CrossRef Full Text | Google Scholar

Hashimoto, Y., Cohen, M., and Robertson, A. (1975). Cell density dependence of the aggregation characteristics of the cellular slime mould Dictyostelium discoideum. J. Cell Sci. 19, 215–229. doi: 10.1242/jcs.19.1.215

PubMed Abstract | CrossRef Full Text | Google Scholar

Houle, J., Balthazar, J., and West, C. M. (1989). A glycosylation mutation affects cell fate in chimeras of Dictyostelium discoideum. Proc. Natl. Acad. Sci. U.S.A. 86, 3679–3683. doi: 10.1073/pnas.86.10.3679

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, H.-J., Takagawa, D., Weeks, G., and Pears, C. (1997). Cells at the center of Dictyostelium aggregates become spores. Dev. Biol. 192, 564–571. doi: 10.1006/dbio.1997.8769

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, S. T., and Cambanis, S. (1978). Stochastic and multiple wiener integrals for Gaussian processes. Ann. Probabil. 6, 585–614. doi: 10.1214/aop/1176995480

CrossRef Full Text | Google Scholar

Hudson, R. E., Aukema, J. E., Rispe, C., and Roze, D. (2002). Altruism, cheating, and anticheater adaptations in cellular slime molds. Am. Nat. 160, 31–43. doi: 10.1086/340613

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones, B. M., Evans, P. M., and Lee, D. A. (1989). Relation between the rate of cell movement under agarose and the positioning of cells in heterotypic aggregates. Exp. Cell Res. 180, 287–296. doi: 10.1016/0014-4827(89)90233-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Julien, B., Kaiser, A. D., and Garza, A. (2000). Spatial control of cell differentiation in Myxococcus xanthus. Proc. Natl. Acad. Sci. U.S.A. 97, 9098–9103. doi: 10.1073/pnas.97.16.9098

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolb, T., and Klotsa, D. (2020). Active binary mixtures of fast and slow hard spheres. Soft Matter 16, 1967–1978. doi: 10.1039/C9SM01799B

PubMed Abstract | CrossRef Full Text | Google Scholar

Kraemer, S. A., and Velicer, G. J. (2011). Endemic social diversity within natural kin groups of a cooperative bacterium. Proc. Natl. Acad. Sci. U.S.A. 108(Suppl. _2), 10823–10830. doi: 10.1073/pnas.1100307108

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuzdzal-Fick, J. J., Fox, S. A., Strassmann, J. E., and Queller, D. C. (2011). High relatedness is necessary and sufficient to maintain multicellularity in Dictyostelium. Science 334, 1548–1551. doi: 10.1126/science.1213272

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuzdzal-Fick, J. J., Queller, D. C., and Strassmann, J. E. (2010). An invitation to die: initiators of sociality in a social amoeba become selfish spores. Biol. Lett. 6, 800–802. doi: 10.1098/rsbl.2010.0257

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, L., Cox, E. C., and Flyvbjerg, H. (2011). “Dicty dynamics”: Dictyostelium motility as persistent random motion. Phys. Biol. 8, 046006. doi: 10.1088/1478-3975/8/4/046006

PubMed Abstract | CrossRef Full Text | Google Scholar

Madgwick, P. G., Stewart, B., Belcher, L. J., Thompson, C. R. L., and Wolf, J. B. (2018). Strategic investment explains patterns of cooperation and cheating in a microbe. Proc. Natl. Acad. Sci. U.S.A. 115, E4823–E4832. doi: 10.1073/pnas.1716087115

PubMed Abstract | CrossRef Full Text | Google Scholar

Marchetti, M. C., Joanny, J. F., Ramaswamy, S., Liverpool, T. B., Prost, J., Rao, M., et al. (2013). Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1189. doi: 10.1103/RevModPhys.85.1143

CrossRef Full Text | Google Scholar

Marquez-Zacarias, P., Conlin, P. L., Tong, K., Pentz, J. T., and Ratcliff, W. C. (2021). Why have aggregative multicellular organisms stayed simple? Curr. Genet. 67, 871–876. doi: 10.1007/s00294-021-01193-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Martínez-García, R., and Tarnita, C. E. (2016). Lack of ecological and life history context can create the illusion of social interactions in Dictyostelium discoideum. PLoS Comput. Biol. 12, e1005246. doi: 10.1371/journal.pcbi.1005246

PubMed Abstract | CrossRef Full Text | Google Scholar

Miele, L., and De Monte, S. (2021). Aggregative cycles evolve as a solution to conflicts in social investment. PLoS Comput. Biol. 17, e1008617. doi: 10.1371/journal.pcbi.1008617

PubMed Abstract | CrossRef Full Text | Google Scholar

Newman, S. A., and Bhat, R. (2009). Dynamical patterning modules: a “pattern language” for development and evolution of multicellular form. Int. J. Dev. Biol. 53, 693–705. doi: 10.1387/ijdb.072481sn

PubMed Abstract | CrossRef Full Text | Google Scholar

O'Connor, K. A., and Zusman, D. R. (1991). Behavior of peripheral rods and their role in the life cycle of Myxococcus xanthus. J. Bacteriol. 173, 3342–3355. doi: 10.1128/jb.173.11.3342-3355.1991

PubMed Abstract | CrossRef Full Text | Google Scholar

Ostwald, W. (1896). Lehrbuch der Allgemeinen Chemie, Vol. 2, Part 1. Leipzig: Engelmann.

Google Scholar

Parkinson, K., Buttery, N. J., Wolf, J. B., and Thompson, C. R. L. (2011). A simple mechanism for complex social behavior. PLoS Biol. 9, e1001039. doi: 10.1371/journal.pbio.1001039

PubMed Abstract | CrossRef Full Text | Google Scholar

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., et al. (2019). “PyTorch: an imperative style, high-performance deep learning library,” in Advances in Neural Information Processing Systems 32, eds H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett (Curran Associates, Inc.), 8024–8035. Available online at: https://github.com/pytorch/pytorch/blob/master/CITATION.cff

Google Scholar

Queller, D. C. (1994). Genetic relatedness in viscous populations. Evol. Ecol. 8, 70–73. doi: 10.1007/BF01237667

CrossRef Full Text | Google Scholar

Rainey, P. B., and De Monte, S. (2014). Resolving conflicts during the evolutionary transition to multicellular life. Annu. Rev. Ecol. Evol. Syst. 45, 599–620. doi: 10.1146/annurev-ecolsys-120213-091740

CrossRef Full Text | Google Scholar

Rankin, D. J., Bargum, K., and Kokko, H. (2007). The tragedy of the commons in evolutionary biology. Trends Ecol. Evol. 22, 643–651. doi: 10.1016/j.tree.2007.07.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Raper, K. B. (1940). Pseudoplasmodium formation and organization in Dictyostelium discoideum. J. Elisha Mitchell Sci. Soc. 56, 241–282.

Google Scholar

Rieu, J.-P., Barentin, C., Maeda, Y., and Sawada, Y. (2005). Direct mechanical force measurements during the migration of Dictyostelium slugs using flexible substrata. Biophys. J. 89, 3563–3576. doi: 10.1529/biophysj.104.056333

PubMed Abstract | CrossRef Full Text | Google Scholar

Rogel Rodriguez, D., Alarcon, F., Martinez, R., Ramirez, J., and Valeriani, C. (2020). Phase behaviour and dynamical features of a two-dimensional binary mixture of active/passive spherical particles. Soft Matter 16, 1162–1169. doi: 10.1039/C9SM01803D

PubMed Abstract | CrossRef Full Text | Google Scholar

Rossine, F. W., Martinez-Garcia, R., Sgro, A. E., Gregor, T., and Tarnita, C. E. (2020). Eco-evolutionary significance of “loners”. PLoS Biol. 18, e3000642. doi: 10.1371/journal.pbio.3000642

PubMed Abstract | CrossRef Full Text | Google Scholar

Rossine, F. W., Vercelli, G., Tarnita, C. E., and Gregor, T. (2022). Structured foraging of soil predators unveils functional responses to bacterial defenses. arXiv preprint arXiv:2205.12341. doi: 10.48550/arXiv.2205.12341

CrossRef Full Text | Google Scholar

Sathe, S., Kaushik, S., Lalremruata, A., Aggarwal, R. K., Cavender, J. C., and Nanjundiah, V. (2010). Genetic heterogeneity in wild isolates of cellular slime mold social groups. Microb. Ecol. 60, 137–148. doi: 10.1007/s00248-010-9635-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Sathe, S., Khetan, N., and Nanjundiah, V. (2014). Interspecies and intraspecies interactions in social amoebae. J. Evol. Biol. 27, 349–362. doi: 10.1111/jeb.12298

PubMed Abstract | CrossRef Full Text | Google Scholar

Sathe, S., and Nanjundiah, V. (2018). Complex interactions underpin social behaviour in Dictyostelium giganteum. Behav. Ecol. Sociobiol. 72, 167. doi: 10.1007/s00265-018-2572-9

CrossRef Full Text | Google Scholar

Shi, W., Köhler, T., and Zusman, D. R. (1993). Chemotaxis plays a role in the social behaviour of Myxococcus xanthus. Mol. Microbiol. 9, 601–611. doi: 10.1111/j.1365-2958.1993.tb01720.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Smukalla, S., Caldara, M., Pochet, N., Beauvais, A., Guadagnini, S., Yan, C., et al. (2008). FLO1 is a variable green beard gene that drives biofilm-like cooperation in budding yeast. Cell 135, 726–737. doi: 10.1016/j.cell.2008.09.037

PubMed Abstract | CrossRef Full Text | Google Scholar

Stenhammar, J., Wittkowski, R., Marenduzzo, D., and Cates, M. E. (2015). Activity-induced phase separation and self-assembly in mixtures of active and passive particles. Phys. Rev. Lett. 114, 018301. doi: 10.1103/PhysRevLett.114.018301

PubMed Abstract | CrossRef Full Text | Google Scholar

Strandkvist, C., Juul, J., Baum, B., Kabla, A. J., and Duke, T. (2014). A kinetic mechanism for cell sorting based on local variations in cell motility. Interface Focus 4, 20140013. doi: 10.1098/rsfs.2014.0013

PubMed Abstract | CrossRef Full Text | Google Scholar

Strassmann, J. E., and Queller, D. C. (2011). Evolution of cooperation and control of cheating in a social microbe. Proc. Natl. Acad. Sci. U.S.A. 108(Suppl. _2), 10855–10862. doi: 10.1073/pnas.1102451108

PubMed Abstract | CrossRef Full Text | Google Scholar

Strassmann, J. E., Zhu, Y., and Queller, D. C. (2000). Altruism and social cheating in the social amoeba Dictyostelium discoideum. Nature 408, 965–967. doi: 10.1038/35050087

PubMed Abstract | CrossRef Full Text | Google Scholar

Szabó, B., Szöllösi, G. J., Gönci, B., Jurányi, Z., Selmeczi, D., and Vicsek, T. (2006). Phase transition in the collective migration of tissue cells: experiment and model. Phys. Rev. E 74, 061908. doi: 10.1103/PhysRevE.74.061908

PubMed Abstract | CrossRef Full Text | Google Scholar

Tarnita, C. E., Taubes, C. H., and Nowak, M. A. (2013). Evolutionary construction by staying together and coming together. J. Theoret. Biol. 320, 10–22. doi: 10.1016/j.jtbi.2012.11.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Tarnita, C. E., Washburne, A., Martinez-Garcia, R., Sgro, A. E., and Levin, S. A. (2015). Fitness tradeoffs between spores and nonaggregating cells can explain the coexistence of diverse genotypes in cellular slime molds. Proc. Natl. Acad. Sci. U.S.A. 112, 2776–2781. doi: 10.1073/pnas.1424242112

PubMed Abstract | CrossRef Full Text | Google Scholar

Umeda, T., and Inouye, K. (2004). Cell sorting by differential cell motility: a model for pattern formation in Dictyostelium. J. Theoret. Biol. 226, 215–224. doi: 10.1016/j.jtbi.2003.08.016

PubMed Abstract | CrossRef Full Text | Google Scholar

van der Linden, M. N., Alexander, L. C., Aarts, D. G., and Dauchot, O. (2019). Interrupted motility induced phase separation in aligning active colloids. Phys. Rev. Lett. 123, 098001. doi: 10.1103/PhysRevLett.123.098001

PubMed Abstract | CrossRef Full Text | Google Scholar

van Gestel, J., and Nowak, M. A. (2016). Phenotypic heterogeneity and the evolution of bacterial life cycles. PLoS Comput. Biol. 12, e1004764. doi: 10.1371/journal.pcbi.1004764

PubMed Abstract | CrossRef Full Text | Google Scholar

Varnum, B., Edwards, K. B., and Soll, D. R. (1986). The developmental regulation of single-cell motility in Dictyostelium discoideum. Dev. Biol. 113, 218–227. doi: 10.1016/0012-1606(86)90124-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Vos, M., and Velicer, G. J. (2008). Natural variation of gliding motility in a centimetre-scale population of Myxococcus xanthus: gliding motility in Myxococcus xanthus isolates. FEMS Microbiol. Ecol. 64, 343–350. doi: 10.1111/j.1574-6941.2008.00484.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Vos, M., and Velicer, G. J. (2009). Social conflict in centimeter-and global-scale populations of the bacterium Myxococcus xanthus. Curr. Biol. 19, 1763–1767. doi: 10.1016/j.cub.2009.08.061

PubMed Abstract | CrossRef Full Text | Google Scholar