Biased Learning as a Simple Adaptive Foraging Mechanism

Adaptive cognitive biases, such as “optimism,” may have evolved as heuristic rules for computationally efficient decision-making, or as error-management tools when error payoff is asymmetrical. Ecologists typically use the term “optimism” to describe unrealistically positive expectations from the future that are driven by positively biased initial belief. Cognitive psychologists on the other hand, focus on valence-dependent optimism bias, an asymmetric learning process where information about undesirable outcomes is discounted (sometimes also termed “positivity biased learning”). These two perspectives are not mutually exclusive, and both may lead to similar emerging space-use patterns, such as increased exploration. The distinction between these two biases may becomes important, however, when considering the adaptive value of balancing the exploitation of known resources with the exploration of an ever-changing environment. Deepening our theoretical understanding of the adaptive value of valence-dependent learning, as well as its emerging space-use and foraging patterns, may be crucial for understanding whether, when and where might species withstand rapid environmental change. We present the results of an optimal-foraging model implemented as an individual-based simulation in continuous time and discrete space. Our forager, equipped with partial knowledge of average patch quality and inter-patch travel time, iteratively decides whether to stay in the current patch, return to previously exploited patches, or explore new ones. Every time the forager explores a new patch, it updates its prior belief using a simple single-parameter model of valence-dependent learning. We find that valence-dependent optimism results in the maintenance of positively biased expectations (prior-based optimism), which, depending on the spatiotemporal variability of the environment, often leads to greater fitness gains. These results provide insights into the potential ecological and evolutionary significance of valence-dependent optimism and its interplay with prior-based optimism.

Introduction

Cognitive biases are “consistent deviations from an accurate perception or judgment of the world” (Fawcett et al., 2014). Such biases, as well as their associated costs and benefits, are increasingly studied by biologists, psychologists and neuroscientists (Marshall et al., 2013). The general consensus is that some cognitive biases may be beneficial under ecologically relevant conditions and incomplete information, suggesting they are an adaptive product of natural selection. Adaptive cognitive biases may have evolved as either heuristic rules for computationally efficient decision making, i.e., as computational “shortcuts” to avoid information-processing limitations (Haselton et al., 2015; Trimmer, 2016), or as error-management tools when error payoff is asymmetrical (Tversky and Kahneman, 1974; Haselton et al., 2015; Bateson, 2016; Trimmer, 2016; Jefferson, 2017; Trimmer et al., 2017).

The disposition to expect a favorable outcome when faced with uncertainty is a well-studied cognitive bias, often termed “optimism”. A behavioral decision can be defined as optimistic if it is consistent with having a positively biased expectation of reward, or a negatively biased expectation of punishment (Bateson, 2016). Ecologists typically use the term “optimism” to describe a positively biased innate or initial belief (McNamara et al., 2011; Berger-Tal and Avgar, 2012; Houston et al., 2012; Marshall et al., 2015; Krakenberg et al., 2019), which we will refer to hereafter as “prior-based” optimism. Consequently, ecological research on optimism mostly focuses on the role of prior knowledge in creating cognitive biases, leading to circumstances in which animals treat resources that are seemingly identical as strikingly different, depending on their past experiences (Stroeymeyt et al., 2011; Berger-Tal et al., 2014a). Notably, the acquisition of this prior knowledge may range from the immediate time scale (Bateson et al., 2011; Hui and Williams, 2017), to experiences acquired through the individual’s life, development or maternal effects, or even evolutionary history (Murphy et al., 2014; Bateson et al., 2015).

Unlike ecologists, human cognitive psychologists often focus on valence-dependent learning as the basis for optimism (sometimes also termed “positivity bias”). Healthy human subjects are known to display unrealistically positive expectations about the future that are driven by an asymmetric learning process, where information about undesirable outcomes is discounted while information about desirable outcomes in amplified (Weinstein, 1980; Sharot, 2011; Kuzmanovic et al., 2015; Gesiarz et al., 2019; Garrett and Daw, 2020). Interestingly, subjects suffering from depression display valence-dependent pessimism – due to an overemphasis on information about undesirable outcomes, their expectations about what the future holds are typically grimmer than what they should be based on the information they have (Strunk et al., 2006; Sharot et al., 2007). The proximate mechanisms underlying this phenomenon have been extensively studied in humans, as well as its consequences (Sharot et al., 2007, 2012; Sharot, 2011; Lefebvre et al., 2017; Dundon et al., 2019). These consequences may range from positive effects of mild optimism on various aspects of human wellbeing, to negative effects of extreme optimism that may extend as far as global financial collapse (Johnson and Fowler, 2011; Sharot, 2011; Jefferson, 2017). Optimism bias is thus considered the only form of misbelief in humans that may have evolved as an adaptive trait (McKay and Dennett, 2009; Johnson and Fowler, 2011; Marshall et al., 2015). To sum, whereas the ecological perspective on optimism translates into a biased belief that erodes toward the truth with the accumulation of experience (a rigid learning process; Berger-Tal and Avgar, 2012), the psychological perspective translates into a dynamic learning process, where biased beliefs do not erode but instead continuously update at a rate that is proportional to the magnitude of environmental changes (Stankevicius et al., 2014; Kuzmanovic et al., 2015; Bateson, 2016). Importantly, valence-dependent optimism (or pessimism) is a plausible mechanism for the emergence of temporally dynamic prior-based optimism (or pessimism), even in the absence of environmental change.

The study of optimism may be particularly relevant to the well-known trade-off between exploration and exploitation (Berger-Tal et al., 2014b; Mehlhorn et al., 2015; Addicott et al., 2017). Consumers, whether they are foraging animals, capital investment firms, or fishing vessels, are constantly balancing known resource exploitation with the time and energy devoted to exploring new resources in order to reduce uncertainty and broaden their portfolio (Cohen et al., 2007; Berger-Tal et al., 2014b; Bartumeus et al., 2016; Votier et al., 2017; Kembro et al., 2019; O’Farrell et al., 2019). The trade-off stems from the fact that gathering information and exploiting it are, to a large degree, two mutually exclusive activities (March, 1991). Exploratory behavior is, however, typically viewed under one of two contrasting perspectives (Warren et al., 2017). One assuming that exploration tendencies have evolved as an adaptive trait in itself, treating information as independently sought-after currency (Dall et al., 2005; McNamara and Dall, 2010; Marvin and Shohamy, 2016). The contrasting, and arguably more mechanistically parsimonious perspective, views exploration as an emerging pattern rather than an adaptive process. Under this view, exploratory behavior emerges from the interactions between simple foraging heuristics, the informational state of the animal, and the environment (Berger-Tal and Avgar, 2012; Avgar et al., 2013; Riotte-Lambert et al., 2017; Davidson and El Hady, 2019). For example, a consumer’s decision to exploit a known resource or explore a new one would depend on the perceived likelihood that exploration would lead to improved long-term payoff (i.e., over multiple consumptive events), which in turn depends of the consumer’s belief about the availability and quality of yet unexplored resources. Thus, an optimistic consumer will tend to “favor” exploration over exploitation (Berger-Tal and Avgar, 2012), although the adaptive value of this strategy will depend on the dynamics of the environment across space and time.

Optimal Foraging Theory, perhaps more than any other branch of ecology, emphasizes the importance of prior knowledge in determining animal decision-making in the context of the exploration-exploitation tradeoff. Optimal foragers are expected to maximize their long-term intake rate by exploring new patches when their current exploitation rate falls to a rate that is equal to the average intake rate in the surrounding environment (Charnov, 1976; Brown, 1988). However, real-world environments are constantly changing, and foragers do not possess perfect information about them. Bayesian Foraging Theory addresses this reality by assuming that the forager’s decisions are based on a prior belief about the expected value of the environment, and about the variability around this expectation, a belief that is constantly being updated as the forager acquires new knowledge (Green, 2006; McNamara et al., 2006; Biernaskie et al., 2009; Berger-Tal and Avgar, 2012). A positively biased prior belief about the quality of other patches thus corresponds to “optimism” as it is typically used by ecologists (prior-based), whereas a positively biased updating of this belief (learning more from positive compared to negative reinforcements) corresponds to “optimism” as it is typically used by psychologists (valence-dependent). If the environment does not change across space and time, and in the absence of valence dependence, prior-based optimists would converge to the optimal exploration rate after learning the true expected value of the environment.

We have previously shown that, in the absence of valence dependence, prior-based optimists are expected to outperform prior-based pessimists (foragers with a negatively biased initial belief about the expected quality of the environment), and, when capable of revisiting patches following a resource renewal process, prior-based optimists should outperform unbiased foragers (Berger-Tal and Avgar, 2012). As far as we are aware, the temporal dynamics and foraging performance of valence-dependent optimists (or pessimists) has not yet been explored in an ecological context, nor have the emerging space-use patterns and consequences of such biased learners when faced with a rapidly changing environment. Our goal here is thus twofold; first, we aim to map the (theoretical) fitness response to various degrees of valence-dependencies under different ecological scenarios, and second, we aim to derive expectations about the relationship between the two types of optimism bias, environmental characteristics, and animal space-use patterns.

Materials and Methods

Model Description

The model used here is an individual-based, fitness-maximizing simulation, in continuous time and discrete (albeit implicit) space. This model builds and expends on a model we developed a decade ago to explore the role of prior-based optimism in optimal foraging under uncertainty (Berger-Tal and Avgar, 2012). Simulations start with the forager arriving in a new patch equipped with some initial energy reserves, E(t = 0), and prior beliefs about the average quality of patches on the landscape, Q(t = 0), and the average travel time between patches, T(t = 0). Energy is gained by consuming discrete “food units” (a mouthful, a bite, or a single resource item), and the duration of each such consumption event, Δt, is calculated based on current food availability in the occupied patch, k, following a Type II functional response with search rate a and handling time h (Holling, 1959):

$\mathrm{\Delta }t={\left(a\cdot k\right)}^{-1}+h$

Energy is lost via a constant field metabolic rate, FMR, or via reproduction, with a per-offspring reproductive cost, E_r. The forager reproduces whenever energy reserves exceeded the sum of its initial energy reserves and its reproductive cost (E(t) > E(t = 0) + E_r), at which point its energy reserves are adjusted accordingly (E(t)←E(t)−E_r). If at any time, the forager’s net energy reserve is insufficient (E(t)≤0), the forager dies of “starvation”. The forager may also die due to “predation” with per-unit-time probabilities p_travel (when traveling between food patches) and p_forage (when foraging within a patch). Simulations end with the forager either dying, or reaching a predefined longevity threshold, t_max. The forager’s fitness is its lifetime reproductive success – the total number of offspring it produced. Fitness is thus a product of two aspects of the forager’s resource-consumption rate: its long-term mean (which directly translates into reproductive rate), and its temporal variability (which enhances the risk of starvation and predation). The longer a forager lives, and the more it was able to consume during its lifetime, the greater would be its fitness.

After each consumption event, the forager “decides” (sensu Leavell and Bernal, 2019) whether to stay in the current patch, travel to a previously visited (memorized) patch, or travel in search of a new patch. The decision to leave the current patch is based on the forager’s expectation regarding the optimal Giving-Up Density (GUD; the amount of resources left in a departed patch; Brown, 1988) and associated time and predation costs:

(1) First, assume it is best to leave the current patch; the current food availability in this patch is the optimal GUD and so assume that the next patch will be utilized until it reaches this GUD.

(2) Based on this assumption, calculate expected consumption rates in each of the alternative patches: n memorized patches + one yet-unvisited patch. Note that n does not remain constant through the simulation but rather increases as the forager visits more and more patches. The expected consumption rate is calculated by dividing the expected cumulative food intake in each of these patches (the patch’s expected quality minus the GUD) by the expected time it will take to reduce each to the GUD, τ_i,GUD (i = 1:n + 1) (Olsson and Brown, 2006). τ_i,GUD = τ_i,travel + τ_i,forage, where τ_i,travel is the expect time it will take to travel from the current patch to patch i, whereas τ_i,forage is the expected time it will take to deplete patch i to the GUD (the sum of all Δt’s starting from k = expected patch quality, and ending at k = GUD + 1).

(3) For each of these alternative patches, also calculate the expected survival based on the expected time in each of two movement states (travel and forage), τ_i,travel and τ_i,forage(τ_i,GUD = τ_i,travel + τ_i,forage). The average per-unit-time probability of surviving predation (until GUD is reached) is then given by:

$s_i=\sqrt[{\mathrm{\tau }}_{i,GUD}]{{\left[1-p_{travel}\right]}^{{\mathrm{\tau }}_{i,travel}}\cdot {\left[1-p_{forage}\right]}^{{\mathrm{\tau }}_{i,forage}}}$

(4) Next, assume instead that it is best to stay in the current patch for (at least) the duration of the next consumption event, and hence the optimal GUD is the current food availability in this patch, minus one. Under this assumption, it is best to forage in the current patch (i = 0) for the duration of the next consumption event (τ_{i = 0,GUD} = τ_{i = 0,forage} = Δt), with an associated consumption rate of ${\mathrm{\tau }}_{i=0,GUD}^{-1}$, and average per-unit-time probability of surviving predation, s_{i = 0} = p_forage.

(5) “Decide” whether to stay in the current patch or leave to either of the n+1 alternative patches, by choosing the option that maximizes the product of the expected consumption rate and the average per-unit-time probability of surviving predation (s_i).

Once a decision is made, a “starvation mortality” terminates the simulation if the forager’s energetic reserve (E(t)) is lower than the product of its FMR and the time elapsed since its previous bite. The simulation may also end due to a “predation mortality”, with probability 1−([1−p_travel]^τ_travel(t) ⋅ [1−p_forage]^τ_forage(t)), where τ_travel(t) is the realized duration of traveling (τ_travel(t) = 0 if the forager did not leave the patch), and τ_forage(t) is the time to consume the next bite. If the forager survived, the focal patch’s quality is updated by subtracting one bite, and E(t) is updated by adding one bite and subtracting FMR expenditure (and, if E(t) > E(t = 0) + E_r, reproductive cost). If the forager moved to a previously unvisited patch, then n is updated accordingly (n←n + 1). The qualities of the n previously visited patches are updated after each consumption event based on a stochastic logistic regrowth model.

The forager is assumed to “know” the concurrent qualities of all patches it has visited before, as well as the times it takes to travel between any particular pair of patches, as long as that particular journey was undertaken at least once before. What the forager does not know with certainty is the quality (food abundance) of yet unexplored patches, and the travel time between pairs of patches it did not visit sequentially before. Instead, the forager relies on its current (at time t) beliefs about average patch quality, Q(t) and travel time, T(t). Once a new inter-patch journey is decided on or a new patch is visited, the true duration of that journey, τ_travel(t), or the true quality of that patch, k(t), are sampled from two respective Gamma distributions, each with its own characteristic mean and variance. The foraging environmental is characterized by the values of these means and coefficients of variation $\left(CV=\sqrt{variance}/mean\right)$. The forager’s beliefs about the expected values of these quantities is then updated using a simple yet powerful linear approximation to Bayesian learning (McNamara and Houston, 1987; Lange and Dukas, 2009; Berger-Tal and Avgar, 2012):

$\{\begin{array}{c}\hfill T\left(t+\mathrm{\tau }\right)={\mathrm{\theta }}_T\left(t\right)\cdot {\mathrm{\tau }}_{travel}\left(t\right)+\left[1-{\mathrm{\theta }}_T\left(t\right)\right]\cdot T\left(t\right)\hfill \\ \hfill Q\left(t+\mathrm{\tau }\right)={\mathrm{\theta }}_Q\left(t\right)\cdot k\left(t\right)+\left[1-{\mathrm{\theta }}_Q\left(t\right)\right]\cdot Q\left(t\right)\hfill \end{array}$

where θ_T(t) and θ_Q(t) are (temporally dynamic) normalized weights [0,1].

The novelty of our approach lies in introducing valence-dependent learning by allowing the θ_T(t) and θ_Q(t) to vary with the difference between the current beliefs, T(t) and Q(t), and newly acquired information, τ_travel(t) and k(t):

$\{\begin{array}{c}\hfill {\mathrm{\theta }}_T\left(t\right)=\frac{{\mathrm{\eta }}_T}{{\mathrm{\eta }}_T+\left(1-{\mathrm{\eta }}_T\right)\cdot \text{exp}\left({\mathrm{\alpha }}_T\cdot \left[{\mathrm{\tau }}_{travel}\left(t\right)-T\left(t\right)\right]\right)}\hfill \\ \hfill {\mathrm{\theta }}_Q\left(t\right)=\frac{{\mathrm{\eta }}_Q}{{\mathrm{\eta }}_Q+\left(1-{\mathrm{\eta }}_Q\right)\cdot \text{exp}\left({\mathrm{\alpha }}_Q\cdot \left[Q\left(t\right)-k\left(t\right)\right]\right)}\hfill \end{array}$

Here, η_T and η_Q[0,1] are the basal normalized weights (learning rates in the absence of a valence effect; unitless), whereas α_T and α_Q are valence-dependent learning parameters (with units of time^–1 and quality^–1, respectively). Positive values of α_T and α_Q correspond to an increase in the respective normalized weights whenever τ_travel(t) < T(t) or Q(t) < k(t), emphasizing new information when this information exceeds expectations. Negative values of α_T and α_Q correspond to an increase in their respective normalized weights whenever τ_travel(t) > T(t) or Q(t) > k(t), emphasizing new information when this information is disappointing compared to expectations. Consequently, for each of the two environmental variables (patch quality and inter-patch travel time), our model has two “cognitive traits”. The basal normalized weight, η, is inversely related to the effect of prior-based judgment bias; in the absence of valence-dependent learning (α = 0), new information has little effect on the forager’s initial beliefs [i.e., Q(t = 0) and T(t = 0)] if it is low (close to 0), whereas new information is heavily weighted and hence prior beliefs are quickly eroded if it is high (close to 1). The valence-dependent learning parameter, α, is our mathematical depiction of valence-dependent judgment bias; if it is positive, the forager’s beliefs are affected more by new information if that information is positive (“optimism”), and vice versa.

Through their effects on the forager’s space-use decisions (when and where to go), α_T and α_Q affect the forager’s resource acquisition rate, risk of starvation, and exposure to predation. Everything else being equal, those values of α_T and α_Q that result in the greatest lifetime reproductive success (a product of longevity and consumption rate), are expected to be evolutionary adaptive.

Numerical Experiments

Our numerical experiments consisted of running 1,000 stochastic realizations of the simulation across a full factorial design of parameter and variable values, as detailed in Table 1. While there are many axes along which our model could be investigated, our focus here is on optimal valence-dependent learning bias and its dependence on environmental variability and prior-based bias. Environmental variability is manifested in our “experiments” along two orthogonal axes. First, we varied the coefficients of variation of patch qualities and inter-patch travel times [CV(Q) and CV(T)] while keeping the mean values constant (variability across space). High CV(Q) means patches are more heterogeneous in their quality across space, and an exploring forager is more likely to encounter either an exceptionally rich patch, or an exceptionally poor one. High CV(T) means patches are more aggregated in space, and an exploring forager is more likely to travel either for an exceptionally short time, or for exceptionally long time, before encountering a new patch. Second, we varied the prior belief the forager held with regards to each of these two landscape attributes at the beginning of the simulation [Q(t = 0) and T(t = 0)], reflecting a mismatch between the forager’s expectations and the true environmental characteristics (e.g., due to abrupt change in mean environmental qualities; variability across time). By varying Q(t = 0) and T(t = 0), rather than $\widehat{Q}$ and $\widehat{T}$, we are able to compare foraging performance, and the resulting fitness, across different scenarios while keeping the mean characteristics of the environment constant. We envision a shift into a relatively enriched [$\widehat{Q}>Q(t=0)$ or $\widehat{T}<T(t=0)$] or degraded [$\widehat{Q}<Q(t=0)$ or $\widehat{T}>T(t=0)$] environment as one possible cause of prior-based pessimism or optimism, respectively.

TABLE 1

Table 1. the various parameters and state variables used in our numerical experiments.

To reduce dimensionality (and hence make our results as general as possible), we expressed several non-focal parameters and variables as functions of others (Table 1). That said, we acknowledge that the robustness of our results depends on a comprehensive factorial sensitivity analysis, an analysis that we view as the next step along this line of investigation. To summarize our results, the outputs of each scenario (1,000 vectors of the various state variables) were bootstrapped 1,000 times, each time recording the average starvation rate, longevity, consumption rate, and lifetime reproductive output, as well as other attributes of the simulated realizations, such as the average GUD or home range size (number of unique patches utilized over the forager’s lifetime).

Results

First, we examine the relationship between our valence-dependent learning parameters and the resulting beliefs held by the foragers at the end of the simulation (Figure 1 and Supplementary Figure 1). The terminal belief (held at the end of the simulation) about the mean patch quality, Q(end), is always biased low (pessimism) at large negative values of the valence-dependent Q-learning parameter (α_Q ≪ 0; valence-dependent pessimism), and high (optimism) at large positive values of α_Q (valence-dependent optimism). The α_Q value at which an unbiased terminal belief is obtained $\left(Q\left(end\right)=\widehat{Q}\right)$ decreases with the initial prior belief (Q(t = 0)), and the strength of the effect increases with spatial variability in patch quality (CV(Q)). These results are mirrored in the relationship between α_T and T(end) (Supplementary Figure 1). Note that, high spatial variability in either patch quality or inter-patch travel time translates into skewed distributions of these attributes (for the Gamma distribution, skewness = 2⋅CV). As a result, the magnitude of terminal optimism at α_Q ≫ 0 is much larger than the magnitude of terminal pessimism at α_Q ≪ 0 (Figure 1, lower panels), and the magnitude of terminal optimism at α_T ≫ 0 is much smaller than the magnitude of terminal pessimism at α_T ≫ 0 (Supplementary Figure 1, lower panels).

FIGURE 1

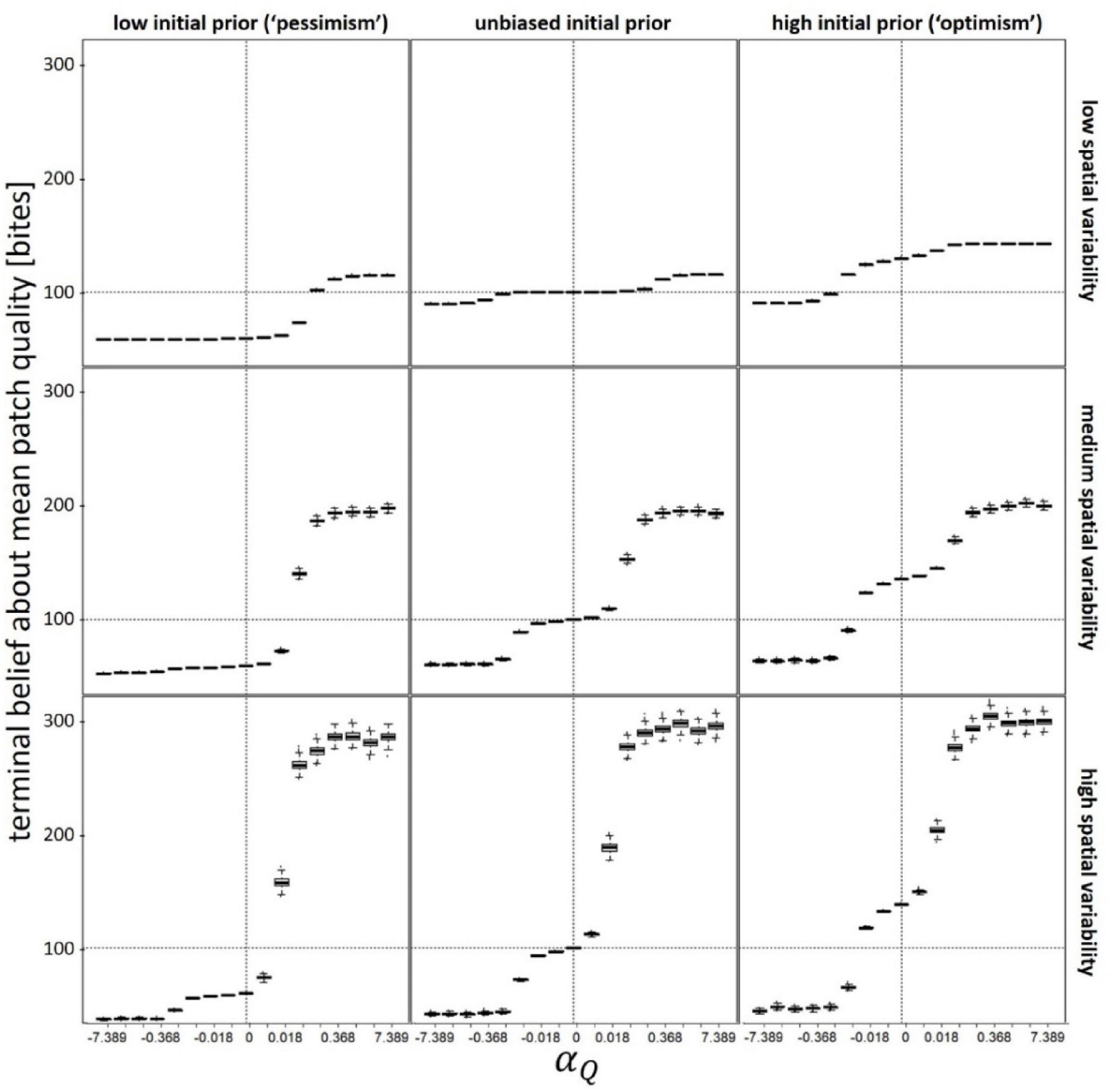
Figure 1. Terminal belief (at the end of the simulation) about the mean patch quality as function of valence-dependence for patch quality (positive values of α_Q correspond to valence-dependent optimism whereas negative values correspond to valence-dependent pessimism). Vertical dashed lines denote unbiased learning (α_Q = 0), whereas horizontal dashed lines denote an unbiased terminal belief$\left(Q\left(end\right)=\widehat{Q}\right)$. Different panels refer to different scenarios: low (Q(t = 0) = 50), unbiased (Q(t = 0) = 100), and high (Q(t = 0) = 150) initial prior belief (columns), and low (CV(Q) = 0.1), medium (CV(Q) = 0.5), and high (CV(Q) = 1) spatial variability (rows). In each scenario, α_T was kept constant at its optimal (fitness maximizing) value. T(t = 0) = $\widehat{T}$ = 10; CV(T) = 0.5; P_travel = t_max^–1 other parameters and variables were as detailed in Table 1.

The fitness-maximizing value of the valence-dependent Q-learning parameter (α_Q), varies with environmental variability across space and time (Figure 2). Moderate valence-dependent optimism (α_Q > 0) is adaptive (i.e., it results in greater lifetime reproductive output) in six out of the nine scenarios depicted in Figure 2. Valence-dependent optimism is associated with greatest (relative) fitness gain when the forager is also a “prior-based pessimist” (which may be interpreted as a shift into an enriched environment), and when spatial variability in patch quality is high. Valence-dependent pessimism (α_Q < 0) is adaptive in only two out of the nine scenarios, when the forager is “prior-based optimist” (which may be interpreted as a shift into a degraded environment), and the spatial variability of patch quality is medium or low. It should be noted that the shape and magnitude of these response curves vary with values of T(t = 0), CV(T), and all other variables and parameters (e.g., p_travel; Supplementary Figure 2). Overall, however, across all scenarios, moderate valence-dependent optimism with regards to patch quality is the most common fitness-maximizing strategy (146 out of 243 scenarios).

FIGURE 2

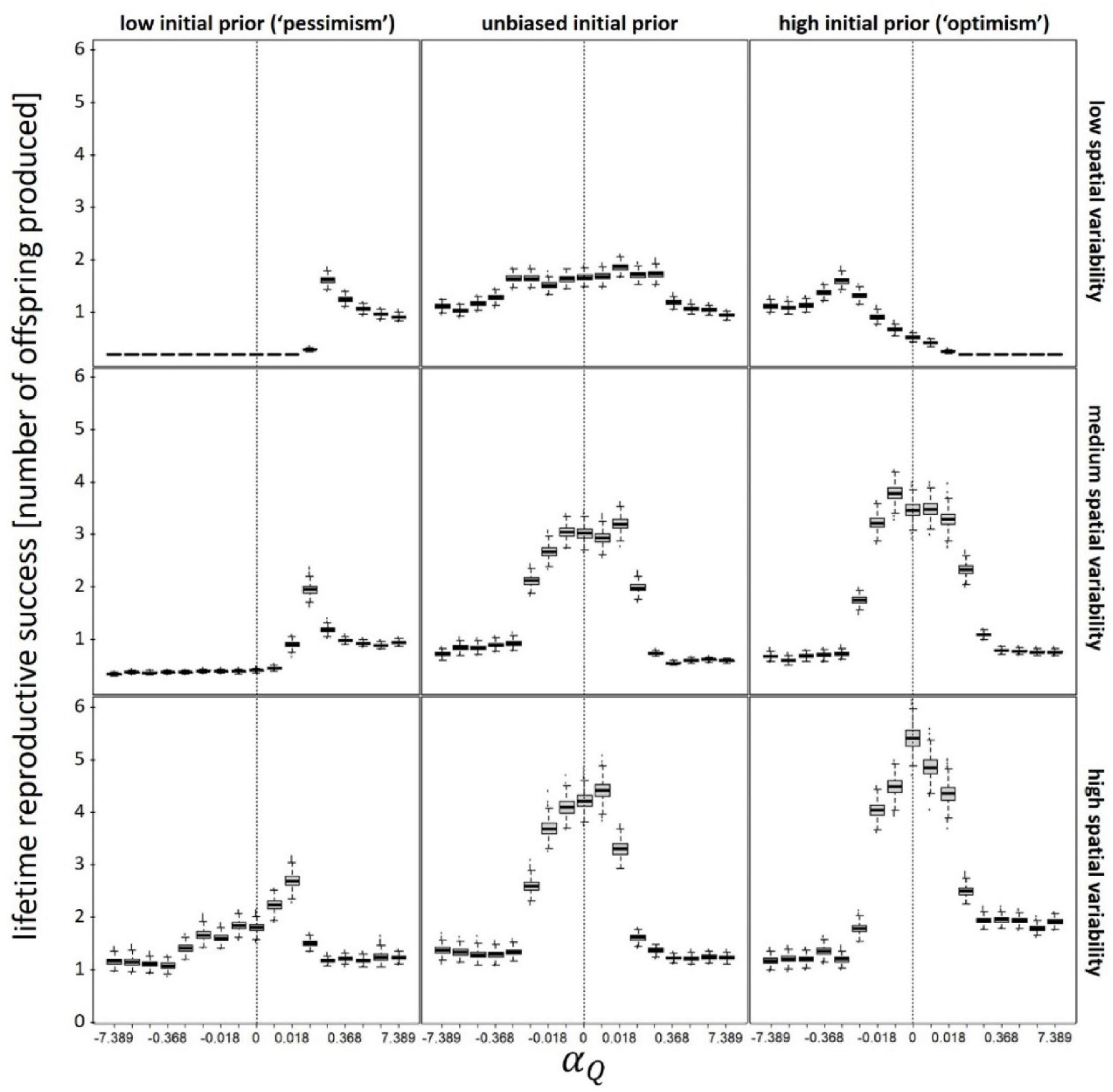
Figure 2. Lifetime reproductive output as function of valence-dependence for patch quality (positive values of α_Q correspond to valence-dependent optimism whereas negative values correspond to valence-dependent pessimism). Vertical dashed lines denote unbiased learning (α_Q = 0). Different panels refer to different scenarios: low (Q(t = 0) = 50), unbiased (Q(t = 0) = 100), and high (Q(t = 0) = 150) initial prior belief (columns), and low (CV(Q) = 0.1), medium (CV(Q) = 0.5), and high (CV(Q) = 1) spatial variability (rows). In each scenario, α_T was kept constant at its optimal (fitness maximizing) value. T(t = 0) = $\widehat{T}$ = 10; CV(T) = 0.5; P_travel = t_max^–1; other parameters and variables were as detailed in Table 1.

The fitness effect of the valence-dependent T-learning parameter (α_T) follows similar trends but is less pronounced than the effect of α_Q (Supplementary Figure 3), which is to be expected considering the range of T is an order of magnitude smaller than that of Q. For the same reason, in those scenarios where valence-dependent optimism is adaptive, it is typically extreme (α_T ≫ 0; Supplementary Figure 3). Valence-dependent optimism is adaptive in unchanged or newly enriched environments (i.e., for unbiased or pessimistic priors), but only when CV(T) is moderate or high (patches are aggregated in space). When CV(T) is low, α_T has no significant effect on lifetime reproductive success. When the environment is newly degraded (i.e., for prior-based optimists) and CV(T) is high, lifetime reproductive success is maximized when α_T = 0 (i.e., unbiased learning; Supplementary Figure 3). Overall, across all scenarios, valence-dependent optimism with regards to travel time is the most common fitness-maximizing strategy (121 out of 243 scenarios).

As for the adaptive value of prior-based biases, optimism is, most often, the fitness maximizing strategy. For both medium and high spatial variability in patch quality, absolute fitness is highest for prior-based optimists, and lowest for prior-based pessimists, across all levels of valance-dependent learning (lower panels of Figure 2 and Supplementary Figure 2). This is also true, albeit to a lesser degree, for prior-based optimism with regards to travel time; for a given value of α_T, the absolute fitness value is highest when the forager is a prior-based optimist, and lowest when the forager is a prior-based pessimist (Supplementary Figure 3).

To gain better understanding of these results, we examine the effects of our valence-dependent learning parameters on the components of fitness, namely consumption rate and longevity (lifetime reproductive success is the product of these two variables; Figures 3, 4). The effects of the valence-dependent Q-learning parameter (α_Q) on consumption rates follow similar trends to those described above for lifetime reproductive output (Figure 3). Mild valance-dependent optimism is advantageous in newly enriched environments (i.e., for prior-based pessimists), whereas valance-dependent pessimism is only advantageous in relatively homogenous [low CV(Q)] and newly degraded environments (i.e., for prior-based optimists). Prior-based optimism about patch quality is associated with a marked increase in absolute consumption rates across all α_Q values, under both moderate and high values (Figure 3). As for the effect of our valence-dependent T-learning parameter (α_T) on consumption rates (Supplementary Figure 4), valence-dependent optimism is advantageous in unchanged or newly enriched environments (i.e., for unbiased or pessimistic priors), but only when CV(T) is moderate or high (patches are aggregated in space). When CV(T) is low, α_T has no significant effect on consumption rate. When the environment is newly degraded (i.e., for prior-based optimists) and CV(T) is moderate or high, consumption rates are maximized when α_T = 0 (i.e., unbiased learning; Supplementary Figure 4). Finally, prior-based optimism about inter-patch travel times is associated with small but significant increase in absolute consumption rates across all α_T values, under both moderate and high CV(T) values (Supplementary Figure 4).

FIGURE 3

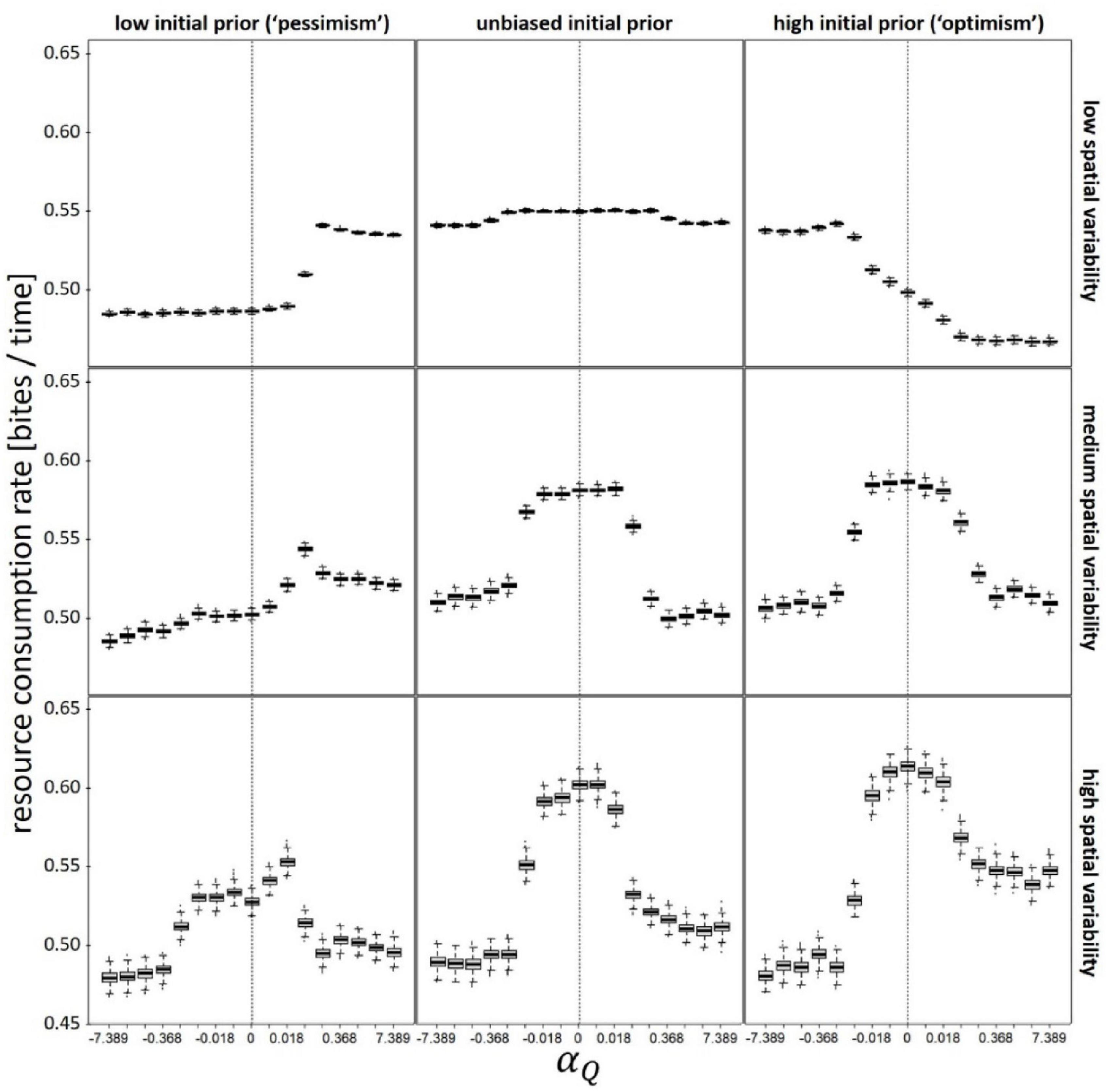
Figure 3. Consumption (feeding) rate as function of valence-dependence for patch quality (positive values of α_Q correspond to valence-dependent optimism whereas negative values correspond to valence-dependent pessimism). Vertical dashed lines denote unbiased learning (α_Q = 0). Different panels refer to different scenarios: low (Q(t = 0) = 50), unbiased (Q(t = 0) = 100), and high (Q(t = 0) = 150) initial prior belief (columns), and low (CV(Q) = 0.1), medium (CV(Q) = 0.5), and high (CV(Q) = 1) spatial variability (rows). In each scenario, α_T was kept constant at its optimal (fitness maximizing) value. T(t = 0) = $\widehat{T}$ = 10; CV(T) = 0.5; P_travel = t_max^–1; other parameters and variables were as detailed in Table 1.

FIGURE 4

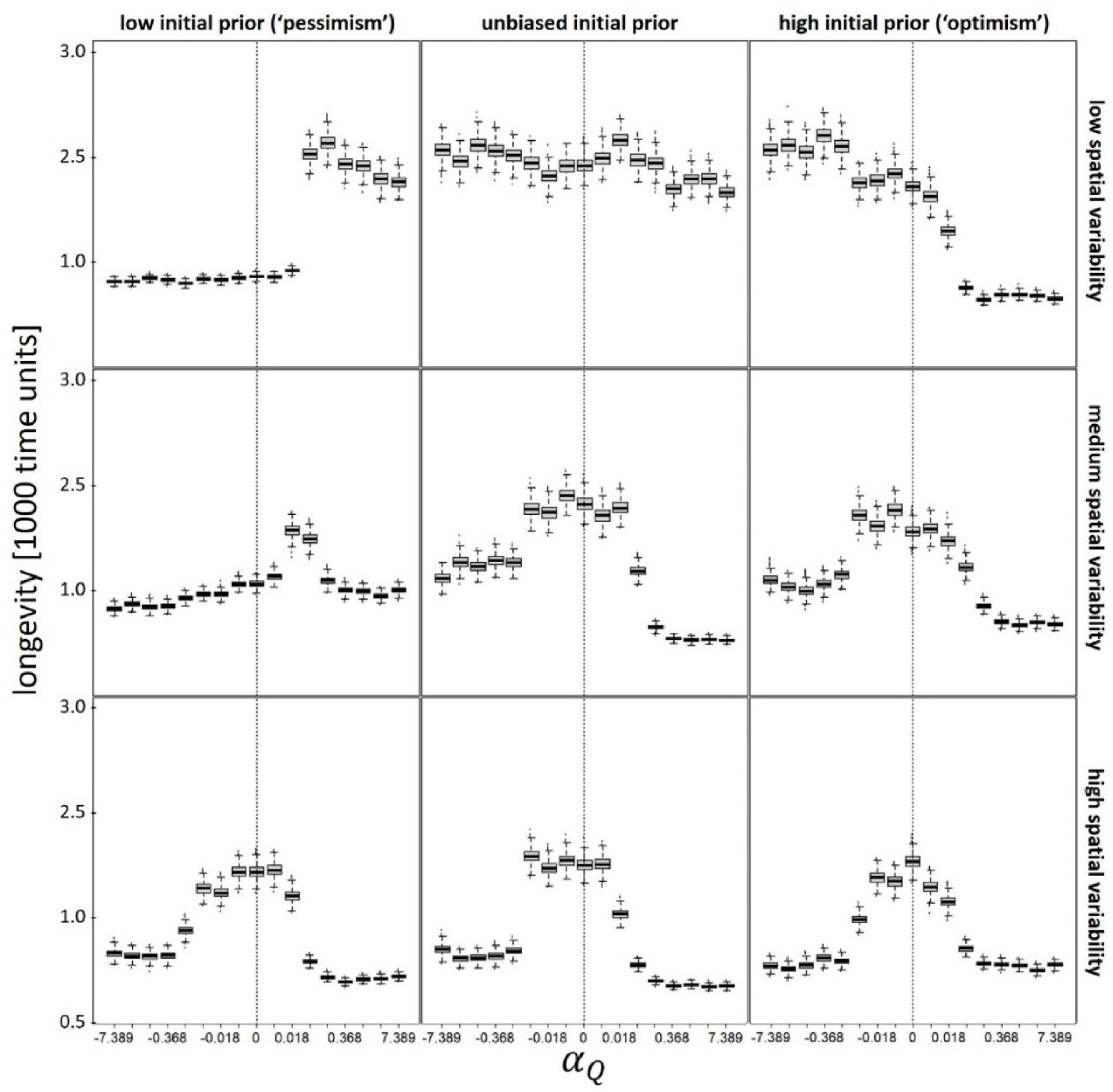
Figure 4. Longevity (life expectancy) as function of valence-dependence for patch quality (positive values of α_Q correspond to valence-dependent optimism whereas negative values correspond to valence-dependent pessimism). Vertical dashed lines denote unbiased learning (α_Q = 0). Different panels refer to different scenarios: low (Q(t = 0) = 50), unbiased (Q(t = 0) = 100), and high (Q(t = 0) = 150) initial prior belief (columns), and low (CV(Q) = 0.1), medium (CV(Q) = 0.5), and high (CV(Q) = 1) spatial variability (rows). In each scenario, α_T was kept constant at its optimal (fitness maximizing) value. T(t = 0) = $\widehat{T}$ = 10; CV(T) = 0.5; P_travel = t_max^–1; other parameters and variables were as detailed in Table 1.

Across all scenarios and parameters values, our simulated foragers typically “died” of “natural causes” (either predation or starvation), with less than 0.01% of simulations reaching t_max (our maximum longevity cutoff). Variability in longevity (Figure 4) is driven primarily by variability in starvation mortality (Supplementary Figure 6); individuals that die young typically die from starvation, whereas those that live long, eventually die of predation (Figure 4 and Supplementary Figures 5, 6). When spatial variability in patch quality is low (CV(Q) = 0.1), valence-dependent optimism is associated with longer life span (higher probability of survival) in newly enriched environments (compared to the forager’s initial expectation, i.e., for prior-based pessimists), whereas valence-dependent pessimism is associated with longer life span in newly degraded environments (compared to the forager’s initial expectation, i.e., for prior-based optimists; Figure 4). In contrast, when spatial variability in patch quality is moderate or high (CV(Q)≥0.5), longevity is typically maximized in the absence of valence-dependent learning (although slight deviations from α_Q = 0 have little effect), with the exception of prior-based pessimists under intermediate environmental variability, where mild optimism is associated with distinctly longer life span (Figure 4). Longevity is otherwise insensitive to the prior-based bias, and is also unaffected by the value of the valence-dependent T-learning parameter (Supplementary Figure 7).

Lastly, we examine the relationship between our valence-dependent learning parameters and emerging space-use patterns (Figure 5). Movement rate (% time spent travelling; Figure 5A) remain mostly unaffected by the valence-dependent Q-learning parameter, until the latter reaches large positive values (extreme valence-dependent optimism), where movement rate doubles and then plateaus. Exploration rate (% patch departures to new patches; Figure 5B) show a double sigmoidal increase pattern with α_Q, with an intermediate plateau at moderate α_Q values (mild pessimism or optimism), followed by full saturation (all patch departures are explorations) at large positive α_Q values. Home-range size (number of unique patches used by a forager over its lifetime; Figure 5C), and patch giving-up densities (GUD; Figure 5D) follow a similar pattern as that or exploration rate. As with other results, these patterns were similar for the effect of α_T, although exploration rate was mostly insensitive to α_T. These patterns also showed slight sensitivities to the values of other variable and parameters, but were otherwise qualitatively similar across all scenarios. Overall, valence-dependent optimists explore more and consequently occupy larger home ranges, and have higher giving-up densities (exploit less), then unbiased or pessimistic learners.

FIGURE 5

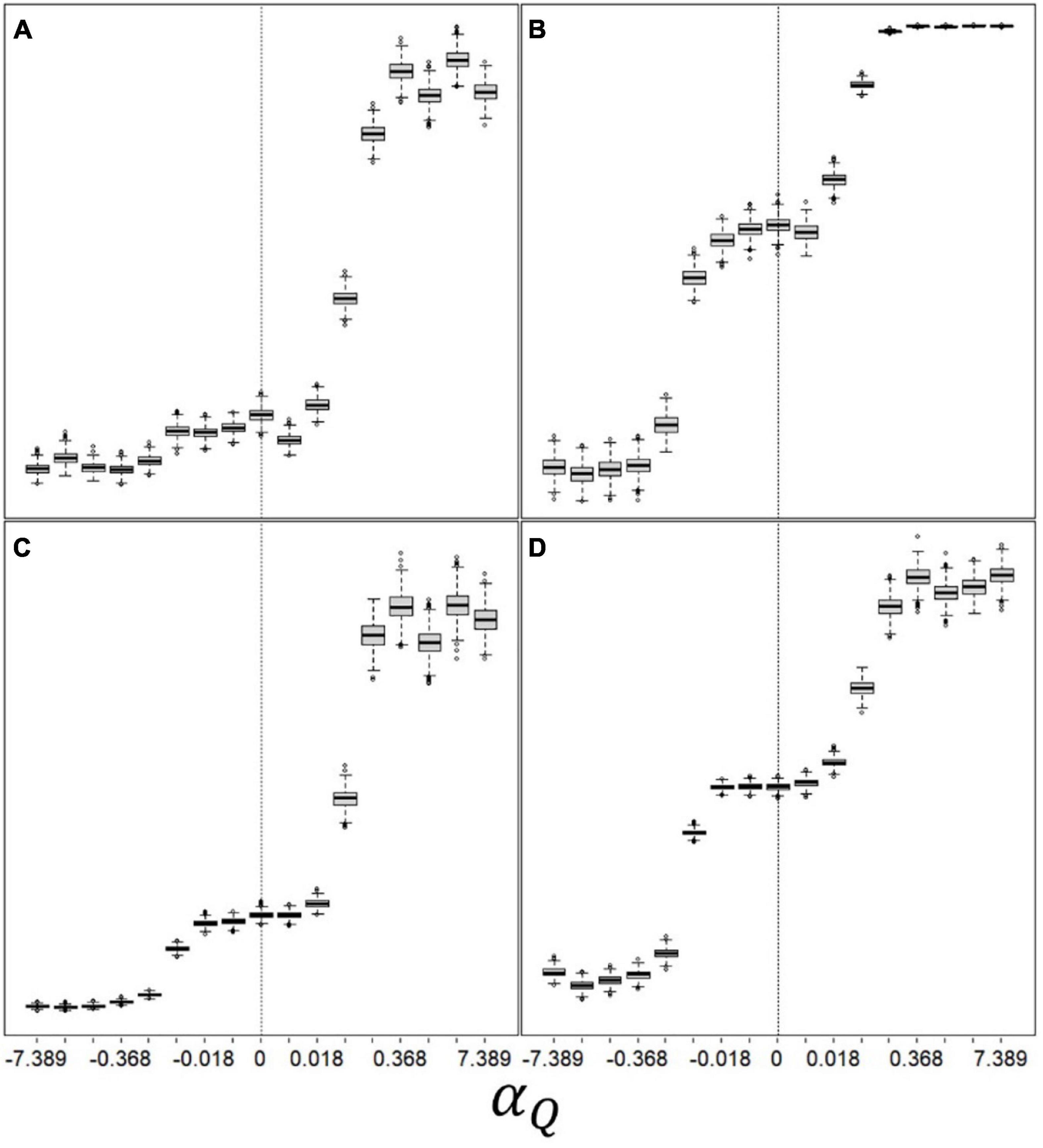
Figure 5. Emerging space-use patterns as function of valence-dependence for patch quality: (A) “movement rate” (% time spent travelling; 9–23), (B) “exploration rate” (% patch departures to new patches; 55–100), (C) home-range size (number of unique patches used during the simulation; 5–24), and (D) mean giving-up density (average number of bites remaining in a patch once departed; 36–80) Q(t = 0) = $\widehat{Q}$ = 100; T(t = 0) = $\widehat{T}$ = 10; CV(Q) = CV(T) = 0.5; p_travel = 2 t_max^–1; other parameters and variables were as detailed in Table 1. α_T was kept constant at its optimal value (which is 0 in this specific scenario).

Discussion

Throughout their evolutionary history, animals faced novel environments and situations primarily following dispersal into new territories (Ronce, 2007; Dingle, 2014). However, human-induced rapid environmental changes (HIREC; Sih et al., 2016) makes encountering novel stimuli the rule rather than the exception under many natural situations. Moreover, conservation translocations (in which humans deliberately release animals into novel environments) are increasingly used for the conservation of species or the restoration of ecosystems (Berger-Tal and Saltz, 2014; Berger-Tal et al., 2020). Successful conservation therefore depends on understanding how animals might cope with novel environments and stimuli (Dunlap et al., 2017; Crowley et al., 2019), and how they balance their exploration and exploitation needs in an unknown environment. Optimism is likely to play an important role in decision-making under novel situations, since it is thought to encourage exploration and increase movement rates and home range sizes. This seems to be the case regardless of the suggested mechanism for this cognitive bias – either a positively biased initial belief (“prior-based” optimism; Berger-Tal and Avgar, 2012), or an asymmetric learning process where information about undesirable outcomes is discounted (“valence-dependent” optimism; Figure 5).

In this manuscript, we examined the adaptive value of valence-dependent optimism (positivity biased learning). Valence dependence is the main mechanism used by cognitive psychologists to explain the emergence of optimism bias (Weinstein, 1980; Sharot, 2011; Kuzmanovic et al., 2015; Garrett and Daw, 2020; Gesiarz et al., 2019), but has rarely been tested in an ecological framework. More specifically, whereas several studies demonstrated the existence of “valence-dependent” optimism in non-human animals, its explicit evolutionary adaptive value has, to our knowledge, never been evaluated. We found that moderate valence-dependent optimism is the most common fitness-maximizing strategy across a wide range of ecological scenarios. Further, valence-dependent optimism results in the maintenance of prior-based optimism (Figure 1), and consequently to enhanced fitness in spatially variable environments. Lastly, optimism promotes exploration and consequently always leads to enhanced learning. The resulting rapid acquisition of information may be advantageous even when it results in slightly suboptimal short-term foraging patterns. Taken together, these theoretical explorations suggest we should expect behavioral responses consistent with having positively biased expectations to be the rule in many natural systems.

Optimism, whether valence-dependent or prior-based, promotes exploration. Consistently expecting to find better resources or condition “out there” leads to spending less time in familiar places (exploitation) and more time searching, and consequently learning. We thus expect optimism, which is generally adaptive even in the absence of HIREC, should play an important role in species adjusting their behavioral patterns to new conditions brought about by HIREC. Optimism will not help a species persist in an environment that is degraded to the point it cannot support it, but it should accelerate information-based shifts in behavioral strategies, promoting post-HIREC population viability. It is worth noting that we have found a clear fitness advantage of mild valence-dependent pessimism in scenarios where foragers are (initially) prior-based optimists, and spatial environmental variability is low (e.g., top-right panel of Figure 2). This leads to the prediction that species with recent evolutionary history dominated by spatially homogenous yet temporally degrading environments, should be valence-dependent pessimists. Consequently, such species are expected to explore less, be slower to learn, and hence be more vulnerable to HIREC.

In our simulations, mortality was driven primarily by starvation. Extreme valence-dependent optimists or pessimists tend to die of starvation early in life due to low resource consumption rates (except when they are also prior-based pessimists or optimists, respectively, and living in homogenous environment). Fitness, however, is a product of life expectancy and reproductive rate, with the latter being tightly linked to resource consumption rate, which is generally highest for mild optimists. Hence, we get scenarios (particularly when environmental spatial heterogeneity is high; e.g., the bottom mid and left panels in Figures 2–4) where strategies that lead to longer lives are not necessarily those with the highest fitness. A useful perspective on this tradeoff may be based on the notion of “pace of life” (Careau et al., 2011; Nakayama et al., 2017; Campos-Candela et al., 2018; Mathot and Frankenhuis, 2018; Betini et al., 2019) – a “fast” (optimistic) forager may not live for a longer period of time, but it accomplishes more in the time it has, presumably due to higher exploration rate which allows it to encounter and utilize high quality patches.

Prior-based (“innate”) expectations about the environment are an emerging product of the learning process, the prior belief held at its onset, and the characteristics of the environment. Consequently, these beliefs should be viewed as a dynamic state variable (rather than a rigid trait), which continually change through time, even if the characteristics of the environment do not (Figure 1 here and Figure 1B in Berger-Tal and Avgar, 2012). The rate and direction of this change depend on initial beliefs, environmental heterogeneity, and valence-dependent learning (Figure 1). There are at least three processes that may give rise to a prior-based optimism at a certain point in time: an innate disposition that is unaffected by learning (e.g., due to genetic effects or early-life imprinting), a history of learning in a better environment (where expectations would be set high compared to the current environment), and positively biased learning (valence-dependent optimism). We have shown here that the latter is advantageous on its own accord, and is a plausible mechanism for the emergence of temporally dynamics prior-based biases.

The initial value of innate expectations (prior-based bias) has a large effect on both the shape and magnitude of the relationship between valance-dependent learning bias and fitness (Figure 2). These interactions deserve an explicitly dynamic investigation, one that will track the trajectories of innate expectations not only within, but also across generations. Such an analysis is beyond the scope of the current work but we would nevertheless like to speculate here about the nature of these dynamics. Assuming first that innate beliefs are passed on from parent to offspring, so that offspring start their life with the same innate beliefs their parents held at the end of theirs, and that the environment does not change across generations. Under these assumptions, the fitness advantage of mild valence-dependent optimism we have observed here should lead to the next generation consisting mostly of prior-based and valence-dependent optimists. These optimists will then suffer reduced fitness compared to either prior-based or valence-dependent pessimists (Figure 2). Consequently, we might then expect an emerging pattern of fluctuating selection across generations (despite a constant environment); selection pressure will alternate back and forth between valence-dependent optimism and pessimism. If, on the other hand, the initial beliefs held by offspring are independent of the terminal beliefs of their parents, valence-dependent optimism should maintain (on average) its adaptive advantage. Lastly, let us assume the environment itself fluctuates from one generation to the next (either in terms of its mean quality, or its spatial heterogeneity), and offspring initial beliefs are affected by their parents’ environment and/or terminal belief. Under these assumptions, the long-term fitness value of valence-dependent optimism (or pessimism) should depend on the direction (trend) and temporal autocorrelation of this environmental change, with long-term degradation leading to a selection for optimism, and vice versa. Either way, we believe these dynamics should be further studied in the context of evolutionary traps (Robertson et al., 2013; Robertson and Blumstein, 2019), and whether optimism is in fact such a trap, or rather a way out of it.

Other important aspects of foraging dynamics that were not addressed here, for the sake of simplicity, are the effects of competitive interactions, density dependence, and memory decay. Even in the absence of territoriality or other social interactions, an optimal forager operating in a shared space must also consider the effect competitors may have on current patch qualities (via exploitation), and possibly even predation risk (due to a dilution effect; Avgar et al., 2020). It is possible that the effect of resource exploitations by competitors could be boiled down to increased uncertainty in patch quality across space and/or time (Riotte-Lambert and Matthiopoulos, 2020). However, we must consider the possibility that, in the absence of spatiotemporal-specific information about the foraging activity of others, the utility of learning and revisiting a set of patches (known as “traplining”) is critically diminished (but see Riotte-Lambert et al., 2015, 2017). In that case, memory decay me be not only more realistic, but also adaptive. Competition may moreover have qualitative effects on the relationship between environmental heterogeneity and fitness (Trevail et al., 2019). At the same time, social information, gained by following or monitoring competitors, plays a major role in the cognitive movement ecology of many species (Kashetsky et al., 2021), and may have non-trivial interactions with the effects of cognitive biases. Lastly, the presence of other individuals with different cognitive strategies (e.g., different levels of optimism) could potentially play an important role in the evolution of an optimal cognitive strategy, and hence the formation of a cognitive niches, via either density- or frequency-dependent selection (Beecham, 2001). The consideration of explicit exploitative interactions among individual foragers, cognitive limitations such as memory decay, and the availability and use of social information are thus important future avenues for research.

Whereas our model focuses on a theoretical exploration of the roles of prior-based and valence-dependent optimism in shaping animal behavior and determining population viability (through their effects on fitness), our model can also serve as the basis for a slew of predictions that can be empirically tested in the field. Supplementary Figure 8 details some of these predictions regarding the space-use patterns of individuals maintaining an optimal valence-dependent cognitive bias. For example, an increase in predation risk is expected to lead to a decrease in home range size, patch giving-up density, and lifetime reproductive output, but also an increase in both movement and exploration rates. Reproductive output is expected to increase with environmental variability, movement rate is expected to be substantially lower when variability in patch quality is low, but giving-up density is expected to be highest at an intermediate degree of patch quality variability. Lastly, exploration rate is expected to be substantially lower when variability in patch travel time is high (i.e., when patches are more aggregated in space). Whereas some of these predictions are consistent with previous theory (Calcagno et al., 2014; Riotte-Lambert and Matthiopoulos, 2020), some others are counterintuitive and novel, and warrant further theoretical and empirical investigations.

To summarize, we have shown how cognitive biases can serve as an adaptive foraging strategy. The question remains on whether these biases can help individual cope with a rapidly changing environment, or whether changing environments can turn such cognitive biases into dangerous evolutionary traps. As any other model, ours suffers from simplifications, intentional omissions, and operational assumptions that might or might not be important. That said, we believe our carful treatment of “fitness” [considering the effects of predation, starvation, and reproductive investment; (Houston et al., 1993)], and our broad consideration of various ecological scenarios, provide solid foundation for our findings. We are thus optimistic about future extensions of our investigation.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

TA coded and analyzed the model. TA and OB-T designed the study, wrote the manuscript, and approved the submitted version.

Funding

TA was partially supported by the Utah Agricultural Experiment Station and the Ecology Center at Utah State University.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to thank Tali Sharot for insightful conversations that motivated this work. Two reviewers provided detailed feedback that helped substentially improve the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.759133/full#supplementary-material

References

Addicott, M. A., Pearson, J. M., Sweitzer, M. M., Barack, D. L., and Platt, M. L. (2017). A primer on foraging and the explore/exploit trade-off for psychiatry research. Neuropsychopharmacology 42, 1931–1939. doi: 10.1038/npp.2017.108

PubMed Abstract | CrossRef Full Text | Google Scholar

Avgar, T., Betini, G. S., and Fryxell, J. M. (2020). Habitat selection patterns are density dependent under the ideal free distribution. J. Anim. Ecol. 89, 2777–2787. doi: 10.1111/1365-2656.13352

PubMed Abstract | CrossRef Full Text | Google Scholar

Avgar, T., Deardon, R., and Fryxell, J. M. (2013). An empirically parameterized individual-based model of animal movement, perception and memory. Ecol. Modell. 251, 158–172. doi: 10.1016/j.ecolmodel.2012.12.002

CrossRef Full Text | Google Scholar

Bartumeus, F., Campos, D., Ryu, W. S., Lloret-Cabot, R., Méndez, V., and Catalan, J. (2016). Foraging success under uncertainty: search tradeoffs and optimal space use. Ecol. Lett. 19, 1299–1313. doi: 10.1111/ele.12660

PubMed Abstract | CrossRef Full Text | Google Scholar

Bateson, M. (2016). Optimistic and pessimistic biases: a primer for behavioural ecologists. Curr. Opin. Behav. Sci. 12, 115–121. doi: 10.1016/j.cobeha.2016.09.013

CrossRef Full Text | Google Scholar

Bateson, M., Desire, S., Gartside, S. E., and Wright, G. A. (2011). Agitated honeybees exhibit pessimistic cognitive biases. Curr. Biol. 21, 1070–1073. doi: 10.1016/j.cub.2011.05.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Bateson, M., Emmerson, M., Ergün, G., Monaghan, P., and Nettle, D. (2015). Opposite effects of early-life competition and developmental telomere attrition on cognitive biases in juvenile european starlings. PLoS One 10:e0132602. doi: 10.1371/journal.pone.0132602

PubMed Abstract | CrossRef Full Text | Google Scholar

Beecham, J. A. (2001). Towards a cognitive niche: divergent foraging strategies resulting from limited cognitive ability of foraging herbivores in a spatially complex environment. Biosystems 61, 55–68. doi: 10.1016/s0303-2647(01)00129-0

CrossRef Full Text | Google Scholar

Berger-Tal, O., and Avgar, T. (2012). The glass is half-full: overestimating the quality of a novel environment is advantageous. PLoS One 7:e34578. doi: 10.1371/journal.pone.0034578

PubMed Abstract | CrossRef Full Text | Google Scholar

Berger-Tal, O., Blumstein, D. T., and Swaisgood, R. R. (2020). Conservation translocations: a review of common difficulties and promising directions. Anim Conserv. 23, 121–131. doi: 10.1111/acv.12534

CrossRef Full Text | Google Scholar

Berger-Tal, O., Embar, K., Kotler, B. P., and Saltz, D. (2014a). Past experiences and future expectations generate context-dependent costs of foraging. Behav. Ecol. Sociobiol. 68, 1769–1776. doi: 10.1007/s00265-014-1785-9

CrossRef Full Text | Google Scholar

Berger-Tal, O., Nathan, J., Meron, E., and Saltz, D. (2014b). The exploration-exploitation dilemma: a multidisciplinary framework. PLoS One 9:e95693. doi: 10.1371/journal.pone.0095693

PubMed Abstract | CrossRef Full Text | Google Scholar

Berger-Tal, O., and Saltz, D. (2014). Using the movement patterns of reintroduced animals to improve reintroduction success. Curr. Zool. 60, 515–526. doi: 10.1002/zoo.21054

PubMed Abstract | CrossRef Full Text | Google Scholar

Betini, G. S., Wang, X., Avgar, T., Guzzo, M. M., and Fryxell, J. M. (2019). Food availability modulates temperature-dependent effects on growth, reproduction, and survival in daphnia magna. Ecol. Evol. 10, 756–762. doi: 10.1002/ece3.5925

PubMed Abstract | CrossRef Full Text | Google Scholar

Biernaskie, J. M., Walker, S. C., and Gegear, R. J. (2009). Bumblebees learn to forage like bayesians. Am. Nat. 174, 413–423. doi: 10.1086/603629

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, J. S. (1988). Patch use as an indicator of habitat preference, predation risk, and competition. Behav. Ecol. Sociobiol. 22, 37–47. doi: 10.1007/BF00395696

CrossRef Full Text | Google Scholar

Calcagno, V., Grognard, F., Hamelin, F. M., Wajnberg, É, and Mailleret, L. (2014). The functional response predicts the effect of resource distribution on the optimal movement rate of consumers. Edited by David Hosken. Ecol. Lett. 17, 1570–1579. doi: 10.1111/ele.12379

PubMed Abstract | CrossRef Full Text | Google Scholar

Campos-Candela, A., Palmer, M., Balle, S., Álvarez, A., and Alós, J. (2018). A mechanistic theory of personality-dependent movement behaviour based on dynamic energy budgets. Ecol. Lett. 22, 213–232. doi: 10.1111/ele.13187

PubMed Abstract | CrossRef Full Text | Google Scholar

Careau, V., Thomas, D., Pelletier, F., Turki, L., Landry, F., Garant, D., et al. (2011). Genetic correlation between resting metabolic rate and exploratory behaviour in deer mice (Peromyscus maniculatus). J. Evol. Biol. 24, 2153–2163. doi: 10.1111/j.1420-9101.2011.02344.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Charnov, E. L. (1976). Optimal foraging, the marginal value theorem. Theor. Popul. Biol. 9, 129–136. doi: 10.1016/0040-5809(76)90040-X

CrossRef Full Text | Google Scholar

Cohen, J. D., McClure, S. M., and Yu, A. J. (2007). Should i stay or should i go? How the human brain manages the trade-off between exploitation and exploration. Philos. Trans. R. Soc. Lond. B Biol Sci. 362, 933–942. doi: 10.1098/rstb.2007.2098

PubMed Abstract | CrossRef Full Text | Google Scholar

Crowley, P. H., Trimmer, P. C., Spiegel, O., Ehlman, S. M., Cuello, W. S., and Sih, A. (2019). Predicting habitat choice after rapid environmental change. Am. Nat. 193, 619–632. doi: 10.1086/702590

PubMed Abstract | CrossRef Full Text | Google Scholar

Dall, S. R. X., Giraldeau, L. A., Olsson, O., McNamara, J. M., and Stephens, D. W. (2005). Information and its use by animals in evolutionary ecology. Trends Ecol. Evol. 20, 187–193. doi: 10.1016/j.tree.2005.01.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Davidson, J. D., and El Hady, A. (2019). Foraging as an evidence accumulation process. PLoS Comput. Biol. 15:e1007060. doi: 10.1371/journal.pcbi.1007060

PubMed Abstract | CrossRef Full Text | Google Scholar

Dingle, H. (2014). Migration: The Biology of Life on the Move. Oxford: Oxford University Press.

Google Scholar

Dundon, N. M., Garrett, N., Babenko, V., Cieslak, M., Daw, N. D., and Grafton, S. T. (2019). Sympathetic and parasympathetic involvement in time constrained sequential foraging. bioRxiv [Preprint] bioRxiv752493. doi: 10.3758/s13415-020-00799-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunlap, A. S., Papaj, D. R., and Dornhaus, A. (2017). Sampling and tracking a changing environment: persistence and reward in the foraging decisions of bumblebees. Interface Focus 7:20160149. doi: 10.1098/rsfs.2016.0149

PubMed Abstract | CrossRef Full Text | Google Scholar

Fawcett, T. W., Fallenstein, B., Higginson, A. D., Houston, A. I., Mallpress, D. E., Trimmer, P. C., et al. (2014). The evolution of decision rules in complex environments. Trends Cogn. Sci. 18, 153–161. doi: 10.1016/j.tics.2013.12.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Garrett, N., and Daw, N. D. (2020). Biased belief updating and suboptimal choice in foraging decisions. Na. Commun. 11, 1–12. doi: 10.1038/s41467-020-16964-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Gesiarz, F., Cahill, D., and Sharot, T. (2019). Evidence accumulation is biased by motivation: a computational account. PLoS Comput. Biol. 15:e1007089. doi: 10.1371/journal.pcbi.1007089

PubMed Abstract | CrossRef Full Text | Google Scholar

Green, R. F. (2006). A simpler, more general method of finding the optimal foraging strategy for bayesian birds. Oikos 112, 274–284. doi: 10.1111/j.0030-1299.2006.13462.x

CrossRef Full Text | Google Scholar

Haselton, M. G., Nettle, D., and Andrews, P. W. (2015). “The evolution of cognitive bias,” in The Handbook of Evolutionary Psychology, ed. D. M. Buss (Hoboken, NJ: John Wiley & Sons, Inc), doi: 10.1002/9780470939376.ch25

CrossRef Full Text | Google Scholar

Holling, C. S. (1959). Some characteristics of simple types of predation and parasitism. Can. Entomol. 91, 385–398. doi: 10.4039/ent91385-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Houston, A. I., Trimmer, P. C., Fawcett, T. W., Higginson, A. D., Marshall, J. A., and McNamara, J. M. (2012). Is optimism optimal? Functional causes of apparent behavioural biases. Behav. Processes 89, 172–178. doi: 10.1016/j.beproc.2011.10.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Houston, A. I., McNamara, J. M., and Hutchinson, J. M. C. (1993). General results concerning the trade-off between gaining energy and avoiding predation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 341, 375–397. doi: 10.1098/rstb.1993.0123

CrossRef Full Text | Google Scholar

Hui, T. Y., and Williams, G. A. (2017). Experience matters: context-dependent decisions explain spatial foraging patterns in the deposit-feeding crab Scopimera intermedia. Proc. R. Soc. Lond. B Biol. Sci. 284:20171442. doi: 10.1098/rspb.2017.1442

PubMed Abstract | CrossRef Full Text | Google Scholar

Jefferson, A. (2017). Born to be biased? Unrealistic optimism and error management theory. Philos. Psychol. 30, 1159–1175. doi: 10.1080/09515089.2017.1370085

CrossRef Full Text | Google Scholar

Johnson, D. D. P., and Fowler, J. H. (2011). The evolution of overconfidence. Nature 477, 317–320. doi: 10.1038/nature10384

PubMed Abstract | CrossRef Full Text | Google Scholar

Kashetsky, T., Avgar, T., and Dukas, R. (2021). The cognitive ecology of animal movement: evidence from birds and mammals. Front. Ecol. Evol. 9:724887. doi: 10.3389/fevo.2021.724887

CrossRef Full Text | Google Scholar

Kembro, J. M., Lihoreau, M., Garriga, J., Raposo, E. P., and Bartumeus, F. (2019). Bumblebees learn foraging routes through exploitation–exploration cycles. J. R. Soc. Interface 16:20190103. doi: 10.1098/rsif.2019.0103

PubMed Abstract | CrossRef Full Text | Google Scholar

Krakenberg, V., Wewer, M., Palme, R., Kaiser, S., Sachser, N., and Richter, S. H. (2019). Technology or ecology? New tools to assess cognitive judgement bias in mice. Behav. Brain Res. 362, 279–287. doi: 10.1016/j.bbr.2019.01.021

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuzmanovic, B., Jefferson, A., and Vogeley, K. (2015). Self-specific optimism bias in belief updating is associated with high trait optimism. J. Behavi. Decis. Making 28, 281–293. doi: 10.1002/bdm.1849

CrossRef Full Text | Google Scholar

Lange, A., and Dukas, R. (2009). Bayesian approximations and extensions: optimal decisions for small brains and possibly big ones too. J. Theor. Biol. 259, 503–516. doi: 10.1016/j.jtbi.2009.03.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Leavell, B. C., and Bernal, X. E. (2019). The cognitive ecology of stimulus ambiguity: a predator–prey perspective. Trends Ecol. Evol. 34, 1048–1060. doi: 10.1016/j.tree.2019.07.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Lefebvre, G., Lebreton, M., Meyniel, F., Bourgeois-Gironde, S., and Palminteri, S. (2017). Behavioural and neural characterization of optimistic reinforcement learning. Nat. Hum. Behav. 1, 1–9. doi: 10.1038/s41562-017-0067

CrossRef Full Text | Google Scholar

March, J. G. (1991). Exploration and exploitation in organizational learning. Organ. Sci. 2, 71–87. doi: 10.1287/orsc.2.1.71

PubMed Abstract | CrossRef Full Text | Google Scholar

Marshall, J. A. R., Favreau-Peigné, A., Fromhage, L., McNamara, J. M., Meah, L. F. S., and Houston, A. I. (2015). Cross inhibition improves activity selection when switching incurs time costs. Curr. Zool. 61, 242–250. doi: 10.1093/czoolo/61.2.242

CrossRef Full Text | Google Scholar

Marshall, J. A. R., Trimmer, P. C., Houston, A. I., and McNamara, J. M. (2013). On evolutionary explanations of cognitive biases. Trends Ecol. Evol. 28, 469–473. doi: 10.1016/j.tree.2013.05.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Marvin, C. B., and Shohamy, D. (2016). Curiosity and reward: valence predicts choice and information prediction errors enhance learning. J. Exp. Psychol. 145, 266–272. doi: 10.1037/xge0000140

PubMed Abstract | CrossRef Full Text | Google Scholar

Mathot, K. J., and Frankenhuis, W. E. (2018). Models of pace-of-life syndromes (POLS): a systematic review. Behav. Ecol. Sociobiol. 72:41. doi: 10.1007/s00265-018-2459-9

CrossRef Full Text | Google Scholar

McKay, R. T., and Dennett, D. C. (2009). The evolution of misbelief. Behav. Brain Sci. 32, 493–510. doi: 10.1017/S0140525X09990975

PubMed Abstract | CrossRef Full Text | Google Scholar

McNamara, J. M., and Dall, S. R. X. (2010). Information is a fitness enhancing resource. Oikos 119, 231–236. doi: 10.1111/j.1600-0706.2009.17509.x

CrossRef Full Text | Google Scholar

McNamara, J. M., Green, R. F., and Olsson, O. (2006). Bayes’ theorem and its applications in animal behaviour. Oikos 112, 243–251.

Google Scholar

McNamara, J. M., and Houston, A. I. (1987). Memory and the Efficient Use of Information. J. Theor. Biol. 125, 385–395. doi: 10.1016/S0022-5193(87)80209-6

CrossRef Full Text | Google Scholar

McNamara, J. M., Trimmer, P. C., Eriksson, A., Marshall, J. A., and Houston, A. I. (2011). Environmental variability can select for optimism or pessimism. Ecol. Lett. 14, 58–62. doi: 10.1111/j.1461-0248.2010.01556.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Mehlhorn, K., Newell, B. R., Todd, P. M., Lee, M. D., Morgan, K., Braithwaite, V. A., et al. (2015). Unpacking the exploration-exploitation tradeoff: a synthesis of human and animal literatures. Decision 2, 191–215. doi: 10.1037/dec0000033

CrossRef Full Text | Google Scholar

Murphy, E., Kraak, L., van den Broek, J., Nordquist, R. E., and van der Staay, F. J. (2014). Decision-making under risk and ambiguity in low-birth-weight pigs. Anim. Cogn. 18, 561–572. doi: 10.1007/s10071-014-0825-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakayama, S., Rapp, T., and Arlinghaus, R. (2017). Fast–slow life history is correlated with individual differences in movements and prey selection in an aquatic predator in the wild. J. Anim. Ecol. 86, 192–201. doi: 10.1111/1365-2656.12603

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Farrell, S., Sanchirico, J. N., Spiegel, O., Dépalle, M., Haynie, A. C., Murawski, S., et al. (2019). Disturbance modifies payoffs in the explore-exploit trade-off. Nat. Commun. 10, 1–9. doi: 10.1038/s41467-019-11106-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Olsson, O., and Brown, J. S. (2006). The foraging benefits of information and the penalty of ignoranc. Oikos 112, 260–273. doi: 10.1016/j.tpb.2006.04.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Riotte-Lambert, L., Benhamou, S., and Chamaillé-Jammes, S. (2015). How memory-based movement leads to nonterritorial spatial segregation. Am. Nat. 185, E103–E116. doi: 10.1086/680009

PubMed Abstract | CrossRef Full Text | Google Scholar

Riotte-Lambert, L., Benhamou, S., and Chamaillé-Jammes, S. (2017). From randomness to traplining: a framework for the study of routine movement behavior. Behav. Ecol. 28, 280–287. doi: 10.1093/beheco/arw154

CrossRef Full Text | Google Scholar

Riotte-Lambert, L., and Matthiopoulos, J. (2020). Environmental predictability as a cause and consequence of animal movement. Trends Ecol. Evol. 35, 163–174. doi: 10.1016/j.tree.2019.09.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Robertson, B. A., and Blumstein, D. T. (2019). How to disarm an evolutionary trap. Conserv. Scie. Pract. 1:e116. doi: 10.1111/csp2.116

CrossRef Full Text | Google Scholar

Robertson, B. A., Rehage, J. S., and Sih, A. (2013). Ecological novelty and the emergence of evolutionary traps. Trends Ecol. Evol. 28, 552–560. doi: 10.1016/j.tree.2013.04.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Ronce, O. (2007). How does it feel to be like a rolling stone? Ten questions about dispersal evolution. Annu. Rev. Ecol. Evol. Syst. 38, 231–253. doi: 10.1146/annurev.ecolsys.38.091206.095611

CrossRef Full Text | Google Scholar

Sharot, T. (2011). The optimism bias. Curr. Biol. 21, R941–R945. doi: 10.1016/j.cub.2011.10.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharot, T., Guitart-Masip, M., Korn, C. W., Chowdhury, R., and Dolan, R. J. (2012). How dopamine enhances an optimism bias in humans. Curr. Biol. 22, 1477–1481. doi: 10.1016/j.cub.2012.05.053

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharot, T., Riccardi, A., Raio, C., and Phelps, E. A. (2007). Neural mechanisms mediating optimism bias. Nature 450, 102–105. doi: 10.1038/nature06280

PubMed Abstract | CrossRef Full Text | Google Scholar

Sih, A., Trimmer, P. C., and Ehlman, S. M. (2016). A conceptual framework for understanding behavioral responses to HIREC. Curr. Opin. Behav. Sci. 12, 109–114. doi: 10.1016/j.cobeha.2016.09.014

CrossRef Full Text | Google Scholar

Stankevicius, A., Huys, Q. J., Kalra, A., and Seriès, P. (2014). Optimism as a prior belief about the probability of future reward. PLoS Comput. Biol. 10:e1003605. doi: 10.1371/journal.pcbi.1003605

PubMed Abstract | CrossRef Full Text | Google Scholar

Stroeymeyt, N., Robinson, E. J., Hogan, P. M., Marshall, J. A., Giurfa, M., and Franks, N. R. (2011). Experience-dependent flexibility in collective decision making by house-hunting ants. Behav. Ecol. 22, 535–542. doi: 10.1093/beheco/arr007

CrossRef Full Text | Google Scholar

Strunk, D. R., Lopez, H., and DeRubeis, R. J. (2006). Depressive symptoms are associated with unrealistic negative predictions of future life events. Behav. Res. Ther. 44, 861–882. doi: 10.1016/j.brat.2005.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Trevail, A. M., Green, J. A., Sharples, J., Polton, J. A., Miller, P. I., Daunt, F., et al. (2019). Environmental heterogeneity decreases reproductive success via effects on foraging behaviour. Proc. R. Soc. B 286:20190795. doi: 10.1098/rspb.2019.0795

PubMed Abstract | CrossRef Full Text | Google Scholar

Trimmer, P. C. (2016). Optimistic and Realistic Perspectives on Cognitive Biases. Curr. Opin. Behav. Sci. 12, 37–43. doi: 10.1016/j.cobeha.2016.09.004

CrossRef Full Text | Google Scholar

Trimmer, P. C., Ehlman, S. M., and Sih, A. (2017). Predicting behavioural responses to novel organisms: state-dependent detection theory. Proc. R. Soc. B 284:20162108. doi: 10.1098/rspb.2016.2108

PubMed Abstract | CrossRef Full Text | Google Scholar

Tversky, A., and Kahneman, D. (1974). Judgment under uncertainty: heuristics and biases. Science 185, 1124–1131. doi: 10.1126/science.185.4157.1124

PubMed Abstract | CrossRef Full Text | Google Scholar

Votier, S. C., Fayet, A. L., Bearhop, S., Bodey, T. W., Clark, B. L., Grecian, J., et al. (2017). Effects of age and reproductive status on individual foraging site fidelity in a long-lived marine predator. Proc. R. Soc. Lond. B 284:20171068. doi: 10.1098/rspb.2017.1068

PubMed Abstract | CrossRef Full Text | Google Scholar

Warren, C. M., Wilson, R. C., van der Wee, N. J., Giltay, E. J., van Noorden, M. S., Cohen, J. D., et al. (2017). The effect of atomoxetine on random and directed exploration in humans. PLoS One 12:e0176034. doi: 10.1371/journal.pone.0176034

PubMed Abstract | CrossRef Full Text | Google Scholar

Weinstein, N. D. (1980). Unrealistic optimism about future life events. J. Pers. Soc. Psychol. 39, 806–820. doi: 10.1037/0022-3514.39.5.806

CrossRef Full Text | Google Scholar