Hierarchical Functional Response of a Forager on a Wetland Landscape

We show that for some foragers the form that a functional response takes depends on the temporal and spatial scales considered. In representing the consumption rate of an organism, it may be necessary to use a hierarchy of functional responses. Consider, for example, a wading bird foraging in wetland landscape characterized by a spatial distribution of potential foraging sites, such as ponds. At the smallest time scale of minutes or hours, during which a wading bird is foraging within a single site, the functional response will reflect the local density of prey, as well as features of the site that affect the feeding rate, such as water depth. At this short time scale, which is determined by the giving up time of the wading bird in a particular site, prey density may be relatively constant. The food intake from a particular pond is then the product of the time spent before giving-up time and moving to another site and the rate of prey consumption at that site. A prey-centered functional response is most appropriate for describing the prey consumption rate. We propose that over the longer time scale of a day, during which a wading bird may visit several foraging sites, the type of functional response can be considered to be patch centered. That is, it is influenced by the spatial configuration of sites with available prey and the wading bird’s strategy of choosing among different sites and decisions on how long to stay in any given sites. Over the time scale of a day, if the prey densities stay relatively constant, the patch-centered functional response for a constant environment is adequate. However, on the longer time scale of a breeding season, in which changing water levels result in temporal changes in the availability of prey in sites, a third hierarchical level may be relevant. At that scale, the way in which the landscape pattern changes through time, and how the wading bird responds, influences the functional response. This hierarchical concept applies to a colony of breeding wading birds foraging in wetlands such as the Everglades.

Introduction

The introduction of mathematical modeling into ecology is close to 100 years old. The first attempts at modeling the interactions between populations of predators and prey were made in the 1920s, independently in America by Alfred J. Lotka and in Italy by Vito Volterra (Lotka, 1925; Volterra, 1937). Because the simple linear functions for the interaction between the species used in these early models were critiqued as being not realistic, Holling (1959) attempted to find a comprehensive functional response that could apply in a wide range of situations, and yet still be relatively simple. He was able to study predation by small mammals on pine sawflies in the cocoon stage which lay distributed randomly in pine needles in a Scots and jack pine stand. This led to empirical functional responses termed Holling types 2 and 3, which had the important non-linear feature of saturating for high prey densities.

The functional response found empirically by Holling can be derived mathematically by making some simple assumptions. Imagine that a predator is searching in a region in which there are prey items scattered randomly, with a uniform spatial density, N, across the spatial area being searched. The question is, how many prey items will the predator capture and consume per unit time, if it spends all its time either searching for prey or handling and consuming them? That question can be answered if the searching rate (i.e., movement rate) and visual range of the consumer, the detectability of prey, probability of the consumer capturing prey items, and the time it takes the predator to capture and consume an individual prey item (i.e., the handling time) can be quantified.

This conceptual scheme of Holling (1959) is centered around the predator’s search for, capture, and consumption of individual prey items within a relatively homogenous foraging space. Another conceptual scheme was proposed by MacArthur and Pianka (1966), in which the foraging space is composed of heterogeneous patches with varying energetic quality, and ideally the forager selects an itinerary of patches that at least comes close to maximizing intake. Both this scheme and the Holling-type scheme include decisions made by the forager, but at different scales. In Holling’s prey-centered model, the decision scale is an individual prey item. By choosing to pursue or not to pursue a given potential prey item, the consumer makes an implicit decision on how to split time between searching for and consuming prey, where handling of a prey item subtracts from the time available to search for others. In this case, the spatial scale represents an area with relatively uniform prey composition. In the patch-centered model, the decision scale is at the level of the prey patch rather than individual prey. The consumer makes a decision on whether to visit a particular patch and how long to remain in the patch of prey before moving to another patch, with the duration in a particular patch subtracting from search time for other patches (Stephens and Krebs, 1986). This spatial scale represents an area that can encompass spatial variability in prey availability across sites but that is small enough that the consumer can access these sites within some period of interest. Although both these concepts involve searching, the mode of searching has different consequences for the form of the functional response.

For many consumers, it is not an “either or” situation between prey-centered and patch-centered foraging; rather, both conceptual models may apply, considering that a forager may need first to use patch-centered search for locations (patches) in which prey are likely to occur, and then use prey-centered search for individual prey within those patches. In this sense, the functional response is hierarchical, both temporally and spatially. An example of a forager with such a hierarchically structured functional response are wading birds of the orders Ciconiiformes and Pelicaniformes. The main prey of many wading birds are small fish and crayfish, which tend to be concentrated in shallow aquatic depressions such as sloughs, ponds, and creeks, where fish concentrations can change through time (Coulter and Bryan, 1993; Botson et al., 2016). Over the period of a day, the wading bird may search for such sites in which it can forage (Kushlan, 1973; Gawlik, 2002). The foraging process at that scale may involve finding a site, sampling it for a period of time and then, depending on foraging success there, moving to another site after some period of time. This process could continue throughout the day in the manner of patch-centered search. Once the bird has arrived at a site, feeding within the site would then be prey-centered, and therefore likely be described by a classical functional response of the type introduced by Holling.

In addition to these two temporal and spatial hierarchical levels of functional response, a third hierarchical level might need to be considered, in which the landscape itself is changing due to seasonality in water levels, which impact the availability of prey. At the landscape scale, heterogeneity in geomorphology, patterns of vegetation, connectivity of habitats and dispersal corridors, and dispersal vectors such as hydrology, winds, and tides all become influential. Decisions made by foragers at this scale include the need to move to new areas of prey availability on the landscape as current ones become exhausted or dry up. In the case of wading birds, large aggregations of birds have been observed that coincide with regional-scale drying of wetlands, which results in rapid concentration of fish and invertebrate prey in high densities at sufficiently shallow and accessible water depths (e.g., Bancroft et al., 2002; Beerens et al., 2015). Wading birds may also change their foraging strategies as prey availability changes from year to year (Kushlan, 1986; Pierce and Gawlik, 2010; Beerens et al., 2011). Therefore, the functional response at the temporal scale of a breeding season is determined predominantly by physical landscape processes of hydrology, including seasonal inundation and drying, and alternating patterns of connectivity and isolation of wetland depressions and aquatic corridors (Yurek et al., 2016), such that wading birds are responding to larger spatial scale over this time period than over the period of a day.

The hierarchical structuring of the functional response of a forager to prey is typical of wading birds in the Florida Everglades (United States), which is a flat subtropical wetland well known for its large wading bird breeding colonies. Rainfall is seasonal, with most rainfall occurring between May and November. During that period the area of the Everglades that is flooded expands and the abundance of the small fish community and crayfish, which are the primary food source of most wading bird species, grows. During the subsequent dry season, water levels fall, so that small fishes are entrained and concentrated into areas such as ponds, sloughs, and depressions that have not dried out. Crayfish are included in this concentration process (e.g., Cook et al., 2014; Dorn and Cook, 2015), and we will use “prey” to refer to both fish and crayfish. During this period prey concentrations may become large enough and the local water level decreases to depths favorable to foraging (e.g., < 30 cm), such that wading birds can accumulate enough food each day to raise offspring. The quality of foraging varies among sites, so wading birds may sample different sites during a day (Gawlik, 2002), staying for longer periods in sites with high prey density. These high concentrations of prey are transient in any given site, as the prey are lost through exploitation or the site completely dries out. Given this patchy distribution, Everglades wading birds form colonial nests from which they forage, consistent with Horn’s (1968) model for conditions in which central place foraging, rather than territoriality, occur. However, because the landscape has a slight elevational gradient, new sites of high fish density and appropriate depths for foraging continue to appear as others disappear over the dry season with falling water levels. This regional-scale spatial pattern of drying differs from year to year because of varying climate and weather patterns, and water management.

Therefore, we will describe the functional response relevant to each of three hierarchical scales. (1) On the scale of a day the wading bird may use patch-centered foraging on a number of accessible foraging sites (i.e., the mesoscale) in order to capture enough prey. (2) Within a given foraging site, that is, at the microscale, the functional response may resemble a variation on the Holling type prey-centered functional response. (3) At the scale of the breeding season, a colony of wading birds need to bring in enough prey to sustain its nestlings for several weeks, so the wading bird uses a large area, the macroscale, in which to forage over the course of a season. The separation of these scales into three hierarchical levels helps keep the task of understanding wading bird foraging conceptually simple. We will start with the time scale of a day at which the forager searches for ponds and then proceed to the shorter within-pond scale, and finally the foraging strategy over a longer time period in which the landscape is changing dynamically.

Daily Search for Foraging Sites

Within a day a wading bird must spend time finding a foraging site (we will use “pond” as a general descriptor) in the right depth range and prey density and then exploiting the prey in that pond until it consumes enough to feed itself and any offspring (Figure 1). A basic question is how much time should it spend trying to find a pond that has adequate conditions? Which pond to settle in may depend on various factors that give a clue to its likely prey density, such as the number of other wading birds already present, or perhaps memory from feeding in that pond in a previous time. However, the prey availability is not precisely predictable in advance, so the wading bird may make a second type of decision once it has spent some time in the pond and gained information on current conditions. It may decide to leave the pond and search for another if its food intake is not sufficiently high after a period of sampling. Thus, these real-time decisions made during the time spent at the patch can occur independently of the earlier decisions made when searching and settling.

FIGURE 1

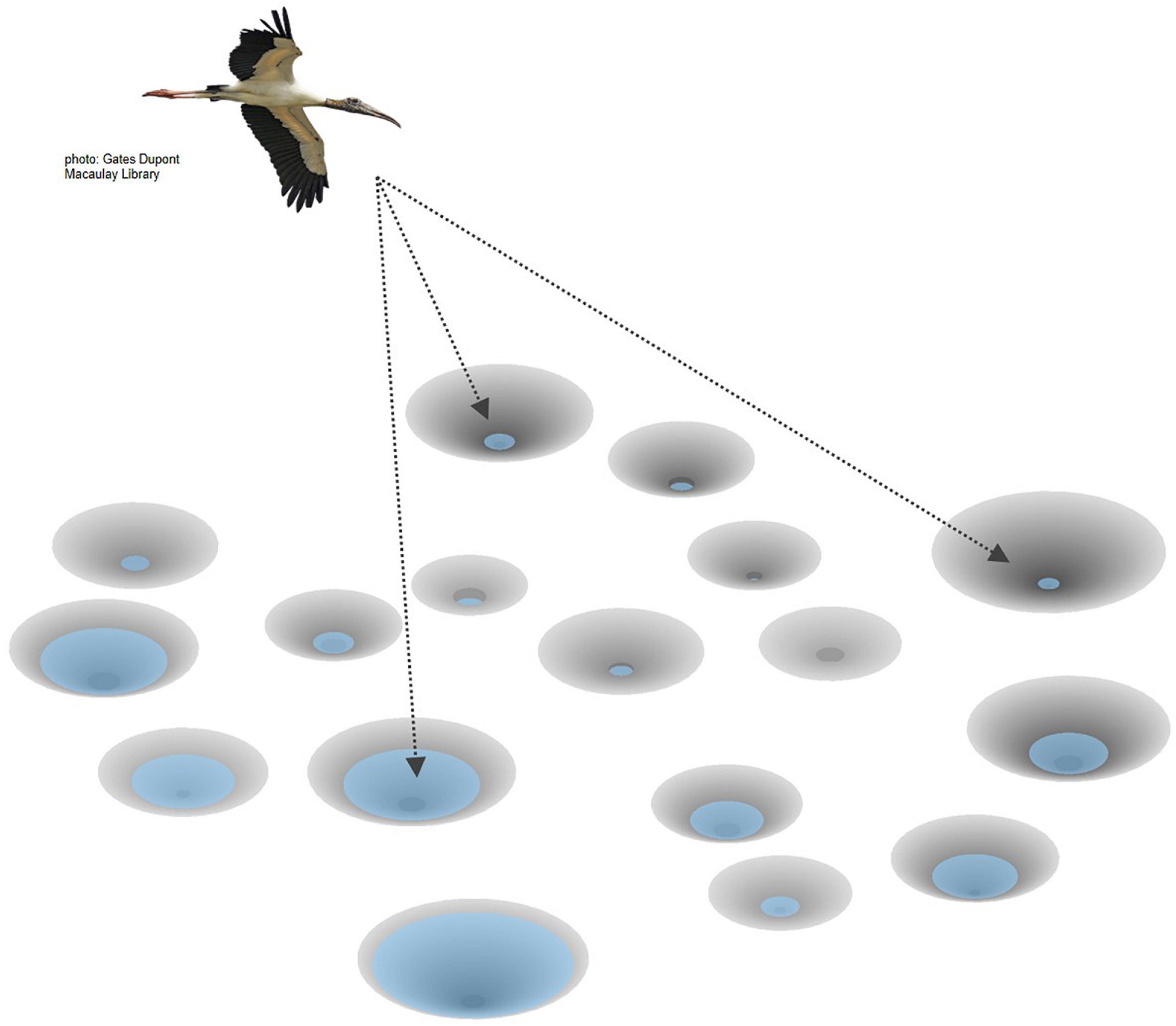
Figure 1. Wading bird selecting among a conceptual array of foraging ponds with varying local hydrology. Photo: Gates Dupont, Macaulay Library.

Kushlan (1981) noted, “For species such as the White Ibis, choice of foraging patch may in some cases be a primary factor in foraging optimization (Kushlan, 1979). The energy penalty for wrong choices may be rather severe, because of the relatively high costs incurred by large birds moving from place to place. Thus, there is probably considerable pressure for wading birds to sample foraging patches efficiently.” Wolff (1994) noted: “After arriving at a site, a bird will stay at least long enough to assess the density of prey. If the density is so low that none or only a few catches could be made in a 15-min time span, then the bird will give up and fly to another cell…” Similarly, Toquenaga et al. (1994) stated, “poorer patches should be refused quickly.” These observations suggest that a giving-up time rule (Krebs et al., 1974; Stephens and Krebs, 1986) is appropriate when a bird lands at a site where food availability is low. It is worth noting that a giving-up time rule is deemed to be most useful when patches vary highly in quality and cannot be recognized beforehand (Iwasa et al., 1989).

Consider the daily scale of foraging that largely involves searching for and feeding within ponds with prey (fish and crayfish) availability and water depth conditions that are adequate for foraging. We follow the more general model of Stephens and Krebs (1986), who assume that a rate of intake of prey biomass from feeding within a time period (in this case the time scale of a day) can be written as their Equation (2.14);

$$\mathit{\text{R}}=\frac{{\sum }_{\mathit{i}=\mathit{1}}^{\mathit{n}}{\mathrm{\lambda }}_{\mathit{i}}{\mathit{\text{g}}}_{\mathit{i}}\left({\mathit{\text{t}}}_{\mathit{i}}\right)-\mathit{\text{s}}}{\mathit{1}+{\sum }_{\mathit{i}=\mathit{1}}^{\mathit{n}}{\mathrm{\lambda }}_{\mathit{i}}{\mathit{\text{t}}}_{\mathit{i}}}(1)$$

where λ_i is the rate of encounter of patchesof type i, s is the loss of energy in search, t_i is the time spent in a patch of type i, and g_i(t_i) is the gain function for energy intake for time t_i spent in the patch. The time t_i spent in a patch is at the discretion of the forager, and could be selected to maximize consumption rate, R. Stephens and Krebs (1986) suggest several hypothetical curves for g_i(t_i), which can differ in shape, depending on the nature of the prey availability.

The approach we take here for wading birds and ponds differs slightly from that leading to equation (1). In Equation 1, searching times during the foraging period (such as a day) are canceled out in the numerator and denominator. In our approach, we assume that search time is independent of travel time between ponds and can be independently quantified. We propose the general functional response for prey intake per day, expressed as energy values, as follows:

$$\begin{array}{c}\mathit{E}\mathit{n}\mathit{e}\mathit{r}\mathit{g}\mathit{y }\mathit{\text{Intake Rate over a Day}}\mathit{\equiv }{\mathit{F}}_{\mathit{i}\mathit{n}\mathit{\text{take,day}}}\hfill \\ \mathit{=}\frac{{\mathit{\Sigma }}_{\mathit{i}\mathit{=}\mathit{1}}^{{\mathit{N}}_{\mathit{p}\mathit{o}\mathit{n}\mathit{d}\mathit{s}}}{\mathit{\text{Energy intake from pond}}}_{\mathit{i}}\mathit{ - }\mathit{C}\mathit{o}\mathit{s}\mathit{t} \mathit{\text{of Travel}}}{{\mathit{\Sigma }}_{\mathit{i}\mathit{=}\mathit{1}}^{{\mathit{N}}_{\mathit{p}\mathit{o}\mathit{n}\mathit{d}\mathit{s}}}{\mathit{\text{Time Spends in pond}}}_{\mathit{i}}\mathit{ + }\mathit{\text{Travel}} \mathit{\text{Time}}}\hfill \\ \mathit{=}\frac{{\mathit{\Sigma }}_{\mathit{i}\mathit{=}\mathit{1}}^{{\mathit{N}}_{\mathit{p}\mathit{o}\mathit{n}\mathit{d}\mathit{s}}}{\mathit{F}}_{\mathit{int}\mathit{a}\mathit{k}\mathit{e}\mathit{,}\mathit{p}\mathit{o}\mathit{n}\mathit{d}\mathit{,}\mathit{i}}\mathit{ - }{\mathit{C}}_{\mathit{t}\mathit{r}\mathit{a}\mathit{v}\mathit{e}\mathit{l}}}{{\mathit{\Sigma }}_{\mathit{i}\mathit{=}\mathit{1}}^{{\mathit{N}}_{\mathit{p}\mathit{o}\mathit{n}\mathit{d}\mathit{s}}}{\mathit{T}}_{\mathit{p}\mathit{o}\mathit{n}\mathit{d}\mathit{,}\mathit{i}}\mathit{ + }{\mathit{\text{T}}}_{\mathit{t}\mathit{r}\mathit{a}\mathit{v}\mathit{e}\mathit{l}}}\hfill \end{array}(2)$$

where, N_ponds = number of ponds visited per day, where i refers to a pond, and where the total time is restricted to daylight hours available for foraging in a single day. Energy Intake from Pond_i (F_{intake,pond,i}) refers to the net intake of energy, which is a function of number and sizes of prey captured, along with the assimilation rate, minus respiration cost while in the pond. Time Spent in Pond_i (T_pond,i) is the time spent in pond i, during which the wading bird is assumed to be feeding. Travel Time (T_travel) includes the time taken to and from the nesting site and between the ponds. This can vary depending on the routes taken between ponds. Cost of Travel (C_travel) is the metabolism associated with flying between the nesting sites and ponds and between ponds.

Wading bird researchers have experimentally identified density levels below which wading birds will give up foraging in a pond and move to another site. This is called the “giving up density” or GUD. For our model we translate GUD to “giving up time” GUT. As noted by Wolff (1994), wading birds require some time in a pond to estimate prey density, for example, tactile foragers such as wood storks and roseate spoonbills which probe areas with their bills, waiting for a prey encounter. Therefore, we assume there is a “giving up time” (GUT) that is positively related to the prey availability in the pond; that is, the higher the prey density and, by extension, the rate of encounters, the longer the wading bird will stay before deciding to try to do better elsewhere.

Giving-Up Time

If the net energy intake rate is low in the pond in which it is currently foraging, the forager is likely to leave and search for a new pond. The higher the rate of intake of prey, the longer the forager is likely to stay. Thus, we can say

$$\begin{array}{ccc}\mathit{T}\mathit{i}\mathit{m}\mathit{e }{\mathit{Spent\; in\; Pond}}_{\mathit{i}}& =& \mathit{G}\mathit{U}\mathit{T}\mathit{\left(}\mathit{E}\mathit{n}\mathit{e}\mathit{r}\mathit{g}\mathit{y }{\mathit{\text{Intake Rate in Pond}}}_{\mathit{i}}\mathit{\right)}\hfill \\ & =& \mathit{G}\mathit{U}\mathit{T}\mathit{\left(}{\mathit{F}}_{\mathit{\text{intake rate, pond i}}}\mathit{\right)}\hfill \end{array}(3)$$

where GUT (F_{intake rate,i}) is the functional relationship between the amount of time the forager spends in a pond and its rate of prey ingestion. Note that we are assuming that the decision to leave a pond is made based on the perceived rates of energy intake and that decisions take place on a short time scale within a day, during which prey density can be assumed constant. It has been noted that different wading bird species have different giving-up prey densities (Beerens et al., 2011) and so will be likely to have different values of GUT, due to their varying behavioral foraging strategies. We will assume a generic function here, but one that is most appropriate for wading birds that feed in large flocks, such as the White Ibis (Eudocimus albus) or the Wood Stork (Mycteria americana).

The rate of prey intake within a pond will be given by a within-pond functional response, f_R, at the lower hierarchical level of the individual pond, which depends on prey availability in the pond and other characteristics of the pond;

$${\mathit{\text{F}}}_{\mathit{intake}\mathit{rate},\mathit{pond}\mathit{i}}=\mathrm{\gamma }{\mathit{\text{f}}}_{\mathit{R}}\left(\mathit{Prey}\mathit{availability}\mathit{in}{\mathit{\text{Pond}}}_{\mathit{i}}\right)=\mathrm{\gamma }{\mathit{\text{f}}}_{\mathit{R}}({\mathit{\text{P}}}_{\mathit{available},\mathit{i}}),(4)$$

where γ is the assimilation rate, or energy assimilated per unit prey biomass, and where f_R(P_available) depends on prey, largely fish density, in addition to other characteristics such as water depths, vegetation coverage, etc., that affect intake rate of prey. This within-pond functional response is a prey-centered functional response of the type introduced by Holling and will be considered in the next section.

Spatial Distribution of Prey Availability

The prey availability will differ across ponds, which motivates a wading bird to move when it might expect to find higher prey availability elsewhere than in its current location. We can define a spatial probability density distribution Prey Availability Across Ponds over the subset of the landscape that could be potential foraging sites; D(P_available,i). This can be a relatively small or large portion of the total landscape, depending on hydrologic conditions, and the wading bird will be restricted to ponds within this area. The pond that the forager happens to be in will also depend on the forager’s method of search. If the method of search includes strategies like use of memory or use of cues, then the wading bird will be more likely be in one of the ponds with higher prey availability than the mean of D(P_available,i).

Cost of Travel

The Cost of Travel, C_travel in Equation (2) is a function of the Travel Time,T_travel,and the cost per unit distance C_{per time}. Here we will assume a mean travel time between ponds, T_travel,mean, and a travel time between the nest and ponds

$${\mathit{\text{C}}}_{\mathit{travel}}=({\mathit{\text{N}}}_{\mathit{ponds}}-\mathit{1}){\mathit{\text{C}}}_{\mathit{per}\mathit{time}}{\mathit{\text{T}}}_{\mathit{travel},\mathit{mean}}+\mathit{2}{\mathit{\text{C}}}_{\mathit{per}\mathit{time}}{\mathit{\text{T}}}_{\mathit{between}\mathit{nests}\mathit{and}\mathit{ponds}}(5)$$

that is, the cost per unit distance times the mean travel time between two ponds times the number of trips between ponds, N_ponds - 1, which represents landscape heterogeneity and the spatial configuration of ponds with respect to each other. Specific values for each pair-wise distance between ponds can also be used, which represent the explicit pond orientations and cost-paths for birds. Separate times for travel between nests and ponds are assumed, as these may be different from times between ponds.

Energy Intake

The Energy Intake from a Pond_i, or F_{intake,pond,i}, from a particular pond i, will be a product of the giving-up time and the rate of prey intake in the pond; that is, the functional response of the pond;

$${\mathit{\text{F}}}_{\mathit{intake},\mathit{pond},\mathit{i}}=\mathit{\text{GUT}}\left({\mathit{\text{F}}}_{\mathit{intake}\mathit{rate},\mathit{pond}\mathit{i}}\right)*{\mathit{\text{F}}}_{\mathit{intake}\mathit{rate},\mathit{pond}\mathit{i}}(6)$$

This is analogous to the gain function of Equation 1 but includes dynamic decisions by birds. From the above, it can be concluded that to define the functional response, three relationships are needed, which have to be specified from empirical data on the system.

Giving-up time as a function of food intake rate = GUT(F_{intake rate,pond i}); Rate of Prey Intake in Pond = F_{intake rate,pond i} = f_R(P_available,i); Probability Density Function for Pond Quality = D(P_available,i); In addition, estimates are needed of mean travel time between ponds,T_travel,mean, and energy cost per time, C_{per time}.

Functional Response at the Daily Scale

After the above general overview, we can examine in more detail the functional response that emerges over the period of a day. A factor in the success of the wading bird forager is the distribution of prey densities in the ponds; the Prey Availability Across Ponds, D(P_available,i). A probability density distribution exists for the maximum fish densities that can be found in the ponds that are accessible to the wading bird during the course of the day; for example, the hypothetical distribution in Figure 2. In the absence of a priori information on the prey availability in any of the ponds, and ignoring the proximity of a given pond to other pond, the wading bird will select from that distribution, With more information on prey availability, and taking into account which ponds are closer to the pond the wading bird currently occupies, a for efficient choice of where to move to next can be made. If P_available,i is the prey availability within a given pond, i, then we can assume that the consumption rate of the wading bird on the fish can be described by a functional response such as the Holling type 2 (see the following section),

$${\mathit{\text{F}}}_{\mathit{intake}\mathit{rate},\mathit{pond}\mathit{i}}=\mathrm{\gamma }{\mathit{\text{f}}}_{\mathit{R}}\left({\mathit{\text{P}}}_{\mathit{available},\mathit{i}}\right)=\frac{\mathrm{\gamma }{\mathit{\text{aP}}}_{\mathit{available},\mathit{i}}}{\mathit{1}+{\mathit{\text{ahP}}}_{\mathit{available},}}(7)$$

where the parameters a, the maximum intake rate, and h, the handling time, depend on characteristics of the wading bird. Different ponds will also have features, such as vegetation density, that affect the feeding rate that can be attained in each pond but we assume here that, if there are water depths in the suitable range, difference in fish density are all that is important at the pond scale.

FIGURE 2

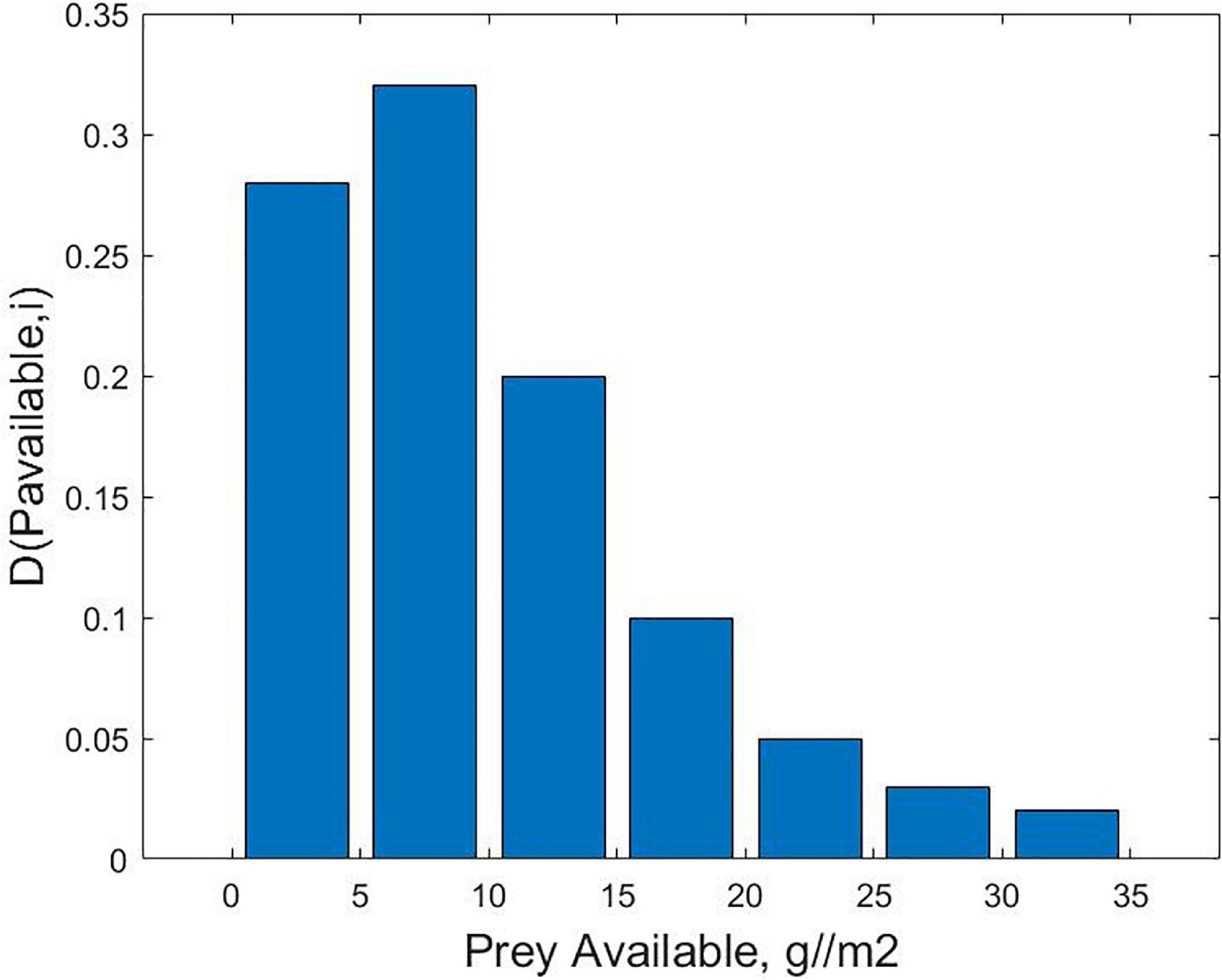
Figure 2. Hypothetical probability density distribution for maximum available prey density,D(P_available,i)(grams fish biomass per square meter).

It is assumed that a foraging bout can involve visits to one or more ponds before the bird ceases foraging for the day and returns to its nest. In each pond the wading bird will have a giving-up time, GUT, that depends on its rate of prey ingestion. One possible assumption on GUT is, following McNair (1982), that it will be an increasing function of F_{intake rate, pond i}, which in the case of a Holling type 2 functional response within the pond, is

$$\mathit{\text{GUT}}\left({\mathit{\text{F}}}_{\mathit{intake}\mathit{rate},\mathit{pond}\mathit{i}}\right)=\mathrm{\alpha }{\left({\mathit{\text{F}}}_{\mathit{intake}\mathit{rate},\mathit{pond}\mathit{i}}\right)}^{\beta }=\alpha {\left(\frac{\mathrm{\gamma }{\mathit{\text{aP}}}_{\mathit{available},\mathit{i}}}{\mathit{1}+{\mathit{\text{ahP}}}_{\mathit{available},\mathit{i},}}\right)}^{\beta }(8)$$

where α and β are constants (β > 0). Other assumptions will be proposed in Supplementary Appendix 1. Also, it would be necessary for the foraging wading bird to spend at least some minimum time in the pond to assess its quality in terms of food intake rate. Therefore, we add a minimum time, T_minimum, to obtain

$$\mathit{\text{GUT}}\left({\mathit{\text{F}}}_{\mathit{intake}\mathit{rate},\mathit{pond}\mathit{i}}\right)=\mathrm{\alpha }{\left(\frac{\mathrm{\gamma }{\mathit{\text{aP}}}_{\mathit{available},\mathit{i}}}{\mathit{1}+{\mathit{\text{ahP}}}_{\mathit{available},}}\right)}^{\beta }+{\mathit{\text{T}}}_{\mathit{minimum}}(9)$$

Therefore, assuming fish density remains the same during the time the wading bird spends in the pond, the amount of prey consumed in a particular pond i is

$${\mathit{\text{F}}}_{\mathit{intake}\mathit{pond},\mathit{i}}={\mathit{\text{F}}}_{\mathit{intake}\mathit{rate},\mathit{pond}\mathit{i}}*\mathit{\text{GUT}}\mathbf{\left(}{\mathit{\text{F}}}_{\mathit{intake}\mathit{rate},\mathit{pond}\mathit{i}}\mathbf{\right)}\mathrm{}=\frac{\mathrm{\gamma }{\mathit{\text{aP}}}_{\mathit{available},\mathit{i}}}{\mathit{1}+{\mathit{\text{ahP}}}_{\mathit{available},}}{}^{}*\mathbf{(}\mathrm{\alpha }{\mathbf{\left(}\frac{\mathrm{\gamma }{\mathit{\text{aP}}}_{\mathit{available},\mathit{i}}}{\mathit{1}+{\mathit{\text{ahP}}}_{\mathit{available}},}\mathbf{\right)}}^{\mathrm{\beta }}+{\mathit{\text{T}}}_{\mathit{minimum}}\mathbf{)}(10)$$

Then, using Equations (5, 9, 10), along with T_travel,mean, Equation (2) can be specified in terms of the basic quantities related to ponds and prey densities.

The general form of a functional response in Equation (2) is a starting point onto which specific circumstances related to foraging in a multi-patch system during the course of a day can be built. There are two types of complications to this starting point that need to be added. First, Equation (2) refers to a single bout of foraging among number of ponds, N_ponds. If the foraging wading bird makes only one such bout in a day, then all that is needed is the cost of flying time back and forth once between the wading bird’s nesting site and the ponds. However, it is possible that the wading bird returns to its nesting site more than once during the day, so there may be more than one such bout. For example, Bryan et al. (1995) recorded wood storks having a mean foraging trip of 4.0 +/− 1.4 h. A second aspect of the foraging that is built into Equation (2) is that the forager stay the amount of time T_pond,i in each pond predicted by Equation (9) and ingests the amount of prey F_{intake pond,i} by Equation (10). However, it is possible that, because the wading bird has obtained as much food as it can carry before using the amount of time predicted by (9), the time actually spent in the pond may be less. Another possibility is that conditions for foraging may decline, such that the wading bird must return to its nest before obtaining as much food as predicted from that pond. These variations will not be described further here.

A second type of specialization of Equation (2) is that it does not explicitly incorporate the way that the wading bird moves among different ponds. The wading bird’s pond-choosing strategy is important and must be added for a realistic estimate of the bird’s food intake. A simple baseline assumption is that the wading bird merely moves at random among pond, not having any prior knowledge of the prey availability in any pond. However, it is more likely that the wading bird can either use cues about which ponds are better, such as observing the number of other wading birds already present (e.g., Toquenaga et al., 1994). Also, memory of previously sampled ponds can help it make a decision to return to those that have had high prey abundances. As noted by Kushlan (1981, p. 153) “Other tactics used to decrease the frequency of wrong sampling choices include trial and error, learning, return to previously used patches, territoriality and sequential sampling.” As Toquenaga et al. (1994) point out, an uneven distribution of prey densities in potential foraging sites will not likely lead to territoriality but should lead to a wading bird using densities of wading birds already at a site for cues. These different tactics are discussed in Supplementary Appendix 1.

Within-Pond Dynamics and Functional Response

To understand when a given pond becomes a profitable site for a wading bird to forage for fish, it is necessary to understand the annual dynamics of water and fish within that pond. As noted earlier, the Everglades is a pulsed wetland whose average water level rises during the rainy season and falls during the dry season, so that its flooded area expands and contracts annually. The resultant concentration effect on prey during the dry season can be easily conceptualized and modeled by considering a simple circular geometric representation of the type of ponds that occur in Big Cypress National Preserve (BCNP) in the Greater Everglades in southern Florida (25° 44′ 50″ N 80° 56′ 50″ W). As shown in Supplementary Figure 1, this shape is idealized, but aerial views of the ponds in BCNP shows them to be remarkably circular (e.g., Quintero and Cohen, 2019). The pond has an inner area that is deep enough to be virtually permanent. Outside of the permanent pond is a much larger drainage area with very gradual constant slope. During the wet season this greater pond area can become flooded, greatly expanding the inundated area from that of just the permanent pond. During the dry season, this greater pond area can rapidly contract to the permanent pond footprint. The geometric representation of the pond makes it easy to calculate the rate at which the pond area shrinks as water levels decrease through evaporation (Figure 3). A simulation of the flooded area of the geometric pond (Supplementary Figure 1) shows the magnitude of change over a year (Supplementary Figure 2).

FIGURE 3

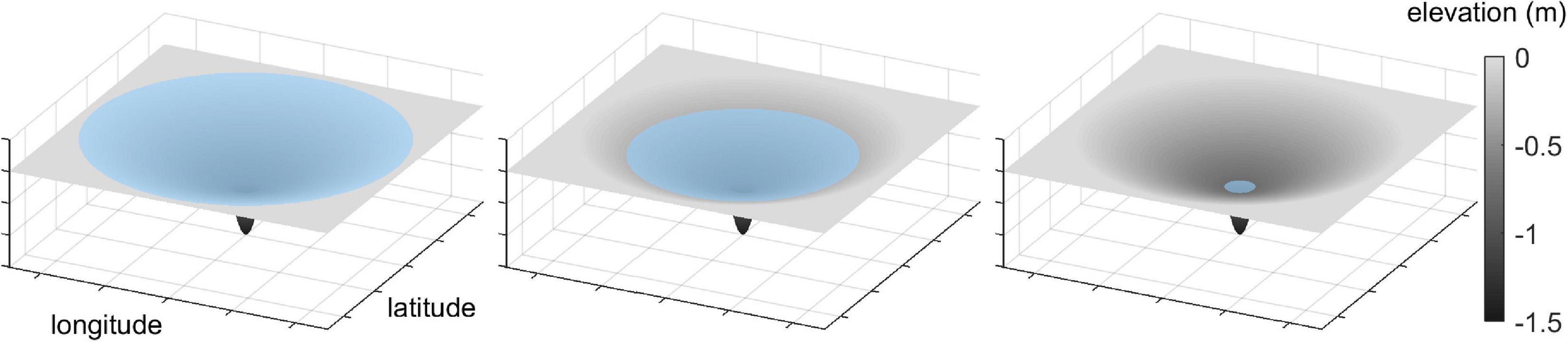
Figure 3. Dynamic water depths within pond basin through time from largely flooded to drying down such that only the permanent pond has water.

This pond area shrinkage leads to dynamically increasing prey (fish) concentrations, as the fish, which have built up in population size during the wet season, move in response to the receding water to avoid desiccation, dispersing to stay within the flooded area. It is likely that the fish are not spread out uniformly in the flooded area at any given time, but that they tend to aggregate around preferred depths. A calculation of such aggregation is done in Supplementary Appendix 2. The combination of water depth change through the year and fish aggregation leads to change in the maximum fish density. It can be assumed that sufficiently high fish concentrations in a certain area are high enough to attract wading birds. These local within-patch concentrations can greatly increase the overall foraging value of the patch for the forager, and thus if present, are important to represent. Stephens and Krebs (1986, 2019 as ebook) note that if a forager searches patches systematically, and the prey items within a patch are more or less randomly distributed, the gain function would look like a Holling type functional response.

A simulation using the idealized pond in Supplementary Figure 1 shows that high fish densities that are sufficient for successful foraging by wading birds can accumulate rapidly over a few days and be maintained for 1 or 2 weeks. At the scale of a single day, these densities may be constant enough to use the within-pond functional response described in Equation 7. For this simulation, we assumed that both the greater pond area and the total fish biomass for the greater pond area had reached a maximum size by the end of the wet season and that the pond was then beginning to shrink at peak water levels. The prey concentration changed with pond areal shrinkage. When wading birds began to forage, the prey were further depleted. For the wading birds, we assumed that more birds would be attracted by higher densities of fish; in particular, the daily average number of wading birds recruiting to the pond would be proportional to fish biomass density. Specifically, we assumed that wading birds would be present only if the density of fish biomass was greater than a threshold of 2.0 g m^–2 wet weight. Above that density, the number of wading birds would increase by 10 individuals for every increase of fish biomass density by 1 g m^–2 wet weight. Foraging occurs when any part of the greater pond area has water depths suitable for foraging (less than about 30 cm). Further details are described in Yurek and DeAngelis (2019), as well as in Supplementary Appendix 3. It is shown that the fish biomass density spikes as water levels fall to the point that only the permanent pond is still flooded (Supplementary Figure 3), even though wading bird removal of fish biomass is sustained at high levels. The spike in fish density can last for several days so that a particular pond may be suitable for foraging over that period. The wading bird numbers in the pond also spike at the same time (Supplementary Figure 4). Fish density rapidly decreases due to foraging, but a remnant population survives in the permanent pond, which is too deep for efficient foraging by most wading birds. Note that the scale of prey depletion (days to weeks) is greater than the scale at which the wading birds sample and abandon ponds (hours). The specific quantitative assumptions here are simply guestimates that must be improved with further information, but they produce a qualitative pattern that appears reasonable.

Seasonal Landscape-Scale Functional Response

Thus far we have discussed the local foraging at the time scale of a day, at which the foraging wading bird makes decisions on selecting among accessible foraging patches to obtain sufficient levels of energy intake. This domain is limited to patches that are available for visiting by the forager within a day and that have appropriate water depths and sufficiently high prey densities. We have also discussed the finer scale of the patches themselves, where the forager is simply extracting prey according to prey densities and making choices on how long to remain at the patch. We now move on to the larger regional scale, at which seasonal landscape processes determine how foraging patches become available and unavailable to a wading bird over the breeding season, as landscape conditions change throughout the year. Importantly, at this scale, the decision making of the forager is primarily focused on survival and reproduction; that is, how to obtain enough energy to rear a clutch of nestlings (Frederick and Ogden, 2001; Lantz et al., 2011; Boyle et al., 2012), and not on the finer scale decision making of selecting among foraging patches. According to the “prey availability hypothesis,” this involves timing the breeding season with periods of maximum prey availability on the landscape (Kushlan, 1986; Bancroft et al., 1994; Gawlik, 2002; Trexler and Goss, 2009; Herring et al., 2010). Anticipating shifting patterns of prey availability over the season, and in response to recent intake, the forager engages a mode of higher intake to accommodate increased demands for supporting its offspring (Wolff, 1994). This may also involve increased search effort to locate areas of the landscape where hotspots are emerging. At this scale, the forager is entirely dependent on the spatial pattern of physical landscape processes that determine prey availability and must follow the moving fronts of prey hotspots, as they propagate across the landscape (Silliman et al., 2013). A critical aspect of Everglades conservation is understanding how wading bird ecology tracks these landscape processes of spatially dynamic hydrology and prey concentrations at the regional scale of the Greater Everglades watershed (Trexler et al., 2002; Trexler and Goss, 2009; Pierce and Gawlik, 2010; Klassen et al., 2016).

In the case of the Everglades, landscape processes are driven primarily by seasonal inundation and drying over roughly 10,000 km² of wetlands, oriented along a regional elevation gradient that descends southward from Lake Okeechobee to Florida Bay at approximately 2.8 cm km^–1 (Gunderson and Loftus, 1993). The central and southern areas of the Everglades landscape have longer annual hydroperiods than those along the eastern, western, and northern fringe. Thus, as water levels recede during the drying phase, these peripheral areas dry out first, and when conditions are appropriate, are the first to produce large spikes in prey density. This drying front then moves southward and inward to deeper, centralized sloughs, and along with it, fish prey can move where there is connectivity. In particular, the Big Cypress National Preserve adjacent to the northern edge of Everglades National Park, has a pattern of permanent ponds whose areas greatly increase into in the rainy season to include extensive shallow flooded areas that become good foraging sites for wading birds as water levels recede in the dry season. We will use this region to illustrate the largest hierarchical scale of wading bird functional response, with simulations over several years and a landscape area of several km². Note that this uses elements from previous sections, but we consider it a separate layer in the functional response hierarchy.

We focus on a portion of Everglades “fringe” landscape located in Big Cypress National Preserve, which comprises approximately 3,000 km² of seasonal, short-hydroperiod wetlands on primarily rocky marl geology. Here, wetland depressions form as solution holes, ponds, shallow creeks, or strands that interact with groundwater (Duever, 2005; Bernhardt and Willard, 2006). Ponds in this region are oriented more or less regularly with respect to each other (Watts et al., 2014). Connectivity of ponds in this region changes as water levels flood and then dry out the landscape. Ponds are pan-connected when the landscape is fully inundated but become isolated and dry out as water levels fall. The timing of drying of each pond varies according its location along the elevation gradient.

We developed generalized model landscapes to represent how this spatially varying hydrology mediates and produces rapid spikes in high densities of prey, which emerge differentially as ponds dry out in succession across the landscape. As described earlier, each permanent pond is surrounded by a local basin. The elevations of each basin are varied by orienting them on a modeled regional elevation gradient. The parameters determining the relative geometry of each pond and basin are also varied, though preserving the parabolic shape of the pond and funnel shape of the basin (see Supplementary Appendix 3 for details of each pond). The combination of variable elevations and dimensions of each local basin and pond produces local variation in the interaction of hydrology and local basin topography, and in turn, the temporal dynamics of fish concentration within each basin. The overall result is a dynamic set of foraging patches, which ephemerally become available and then unavailable to wading bird foragers. Water levels were applied to this landscape following the water stage function described in Supplementary Appendix 3. Figure 4 shows the resulting spatiotemporal variation in hydrology at each pond basin across the landscape, for four different hydrologic stages.

FIGURE 4

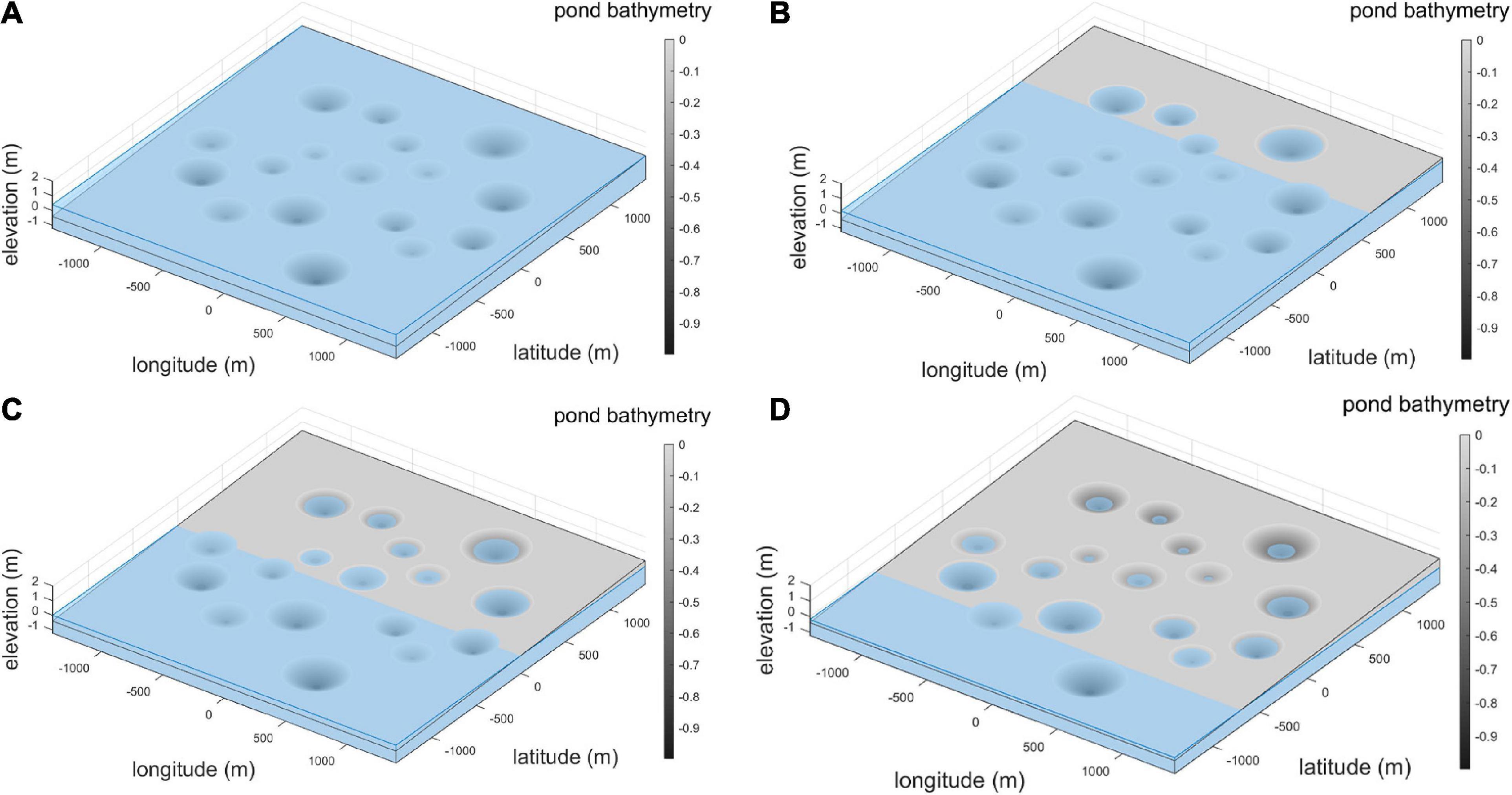
Figure 4. Change in local pond dynamics with regional scale drying pattern. (A) Wet season, (B) early dry season, (C) middle dry season, (D) late dry season.

To represent temporal dynamics of fish prey concentration, fish populations were tracked separately within each pond basin. When water levels fall low enough to isolate a basin from the greater landscape, the volume of water within the basin gradually diminishes, increasing the concentration of fish per unit volume. Here the fish are assumed to disperse toward the pond centers along with the drying front, so that their densities spatially accumulate as the local water volume contracts. Some emigration from pond basins to the greater landscape is assumed when basins become fully flooded and hydrologically reconnected with the marsh platform.

In this section, wading bird feeding on fish prey represents a population of birds distributed across the landscape, which gives a sense of the “background” population of conspecifics or similar foraging types that a single wading bird may interact with. We also specifically consider the role of landscape connectivity and geomorphology in mediating heterogeneity in the availability of foraging patches. Simulations of fish prey concentration and the wading birds feeding on fish follow the same rules as Section “Within-Pond Dynamics and Functional Response,” including the wading bird within-pond functional response (Equation 7) and the number of birds per prey density. Figure 5 shows these dynamics modeled concurrently over 5 years on time steps of 1 h. Each colored line represents dynamics at each pond basin. Rapid spikes in fish density are delayed through time among basins, resulting in high prey densities being available across the landscape over approximately 8 months. Another important effect is that local fish concentrations (third row) are not necessarily correlated with total fish population size (second row), which implies that the predator-prey system is somewhat buffered against large swings in fish population size.

FIGURE 5

Figure 5. Predator-prey-landscape system modeled through time.

Importantly, the physical landscape processes mediate predator-prey interactions across the landscape. Within each pond basin, wading bird foragers rapidly deplete prey pulses as they emerge through concentration. Yet, if water levels recede at a sufficiently slow rate to allow basins to dry somewhat out of phase of each other, the concentration dynamics at each basin will be staggered through time, allowing new foraging patches to emerge while others are nearing depletion. The central “prey availability hypothesis” shared among many Everglades wading bird ecologists is that such a spatially- and temporally staggered progression of prey availability is a critical landscape dynamic for sustaining high density prey patches over long breeding seasons of the wading birds. Therefore, it can be said that prey availability among foraging patches is determined by three key factors: (1) hydrology interacting with local basin geomorphology, (2) local amount of wet season fish and invertebrate biomass available to be rapidly concentrated, and (3) the ongoing, rapid depletion of prey by wading birds. This offers a new twist on the concept of resource depression by Charnov (1976), which here occurs at a greater time scale that that of patch selection, and on the spatial variability in patch quality outlined by MacArthur and Pianka (1966) and Stephens and Krebs.

Discussion

It is essential to take into consideration spatial and temporal scales of any ecological system under study (Gonzalez et al., 2020). Likewise, it is important to consider multiple scales of functional responses. We have shown that, in describing the behavior of a forager such as a wading bird, it may be appropriate to formulate multiple, separate functional responses depending on the temporal scale at which foraging is being considered. At the scale of a single foraging site, such as a pond, in which the wading bird’s presence is transient, a prey-centered response, such as that of Holling’s type 1, 2, or 3 may be appropriate. At the time scale of a day, in which the forager is searching for and choosing among different locations of various quality, foraging is patch-centered and involves moving among a number of foraging sites and staying longer at those sites that are more profitable. At the still larger scale of a season, in which water levels and prey densities are changing across the landscape, foraging will involve following the changing prey availability conditions across the landscape.

The history of functional response modeling for birds that forage in shallow aquatic habitats (e.g., wading birds, shorebirds, waterfowl) tends to focus on the local spatial scale of within-patch feeding, using classic Holling-type responses. These include both hypothesized relationships and those tested with field monitoring. Holling type 2 functional responses were proposed for knots (Calidris canutus) feeding on mussels (Piersma et al., 1995), Bewick’s swans (Cynus columbianus bewicki) feeding on belowground tubers (Nolet and Klaassen, 2009), and oystercatchers (Haematopus ostralegus) feeding on cockles (Norris and Johnstone, 1998). However, two variations on the Holling type 2 response, in which predator interference effects are taken into account, e.g., the Crowley and Martin and Beddington and DeAngelis functional responses, were shown to give better fits to feeding rate of a mixed-species flock of Great Egrets, Tricolored Herons, and Snowy Egrets (Collazo et al., 2010). However, species vary in their sensitivity to the density of conspecifics (Kushlan, 1976), with wood storks, large herons and egrets, and ibises being less sensitive and perhaps deriving an advantage from other foragers stirring up prey; that is, as “beaters” and “followers” (Erwin, 1983). In any case, functional responses that are at least similar to the Holling type 2 response seem to predominate for describing wading birds or similar species feeding in water. Marginal value theorem (MVT) has been widely used to estimate GUT (Nonacs, 2001). Based on MVT, there are a few models developed to estimate the GUT in the uncertain environments (Nishimura, 1992; Morgan et al., 1997). However, MVT assumes that the quality of resource patches are significantly decreased during the foraging. This assumption may not proper to large size resource patch like ponds.

There seem to be fewer studies that use mathematical modeling to examine the foraging and decision making of wading birds or other waterbirds at the patch scale than at the smaller, transient scale. Toquenaga et al. (1994), however, simulate the choices made by egrets foraging over a group of foraging sites. Also, many empirical studies examine foraging behaviors at the scale of patches and the larger landscape scale, through analyses of prey diets and switching (Dorn et al., 2011; Boyle et al., 2012; Klassen et al., 2016), and through studies on theoretical foraging behaviors, for example, “searcher” vs. “exploiter” examined by Beerens et al. (2011). These studies could be complemented with numerical modeling to examine how the hypothesized strategies unfold across the landscape through time.

The idea that functional responses can be scale-dependent is not new. The ratio-dependent, or Arditi-Ginzburg functional response (Arditi and Ginzburg, 2012), focuses on accurately capturing dynamics that emerge at the coarse landscape-scale, and is not derivable in following the assumptions of the Holling type responses. Instead, Arditi and Ginzburg assumed that foragers affect each other’s food intake, and these interactions are implicitly averaged over space and time in their model such that the foraging rate depends on the ratio of consumers to available resources. This differs from our approach, in which an emergent functional response is an aggregate of submodels that address different temporal scales. In particular, we represent the intermediate patch scale in which consumers attempt to forage optimally based on less than perfect knowledge (Pyke, 1984). In this sense, our approach could function as a bridge to scale up from local to landscape scales.

The hierarchical model presented here is limited at present in that it is only in conceptual form. Although it is motivated by interest in wading bird colonies in the Everglades, we have not yet quantified the parameters, in particular, how to characterize and quantify energetic costs. Detailed quantitative models of wading bird foraging exist, however. Wolff (1994) developed an individual-based model of a wood stork breeding colony in the Everglades. Data from that study could be used to help parameterize the present model. The conceptual simplicity of the hierarchical model may make it easier to put into practice. Moving forward, it will be important to work directly with wading bird ecologists to develop appropriate scenarios for decision making, for example, how birds modulate their foraging behavior when confronted with overall poor availability years and considerably suboptimal prey resources (Dorn et al., 2011).

There is strong motivation to develop and use models of wading bird foraging on the Everglades landscape, as numbers of nesting wading birds have declined precipitously from historic levels (Frederick et al., 2009). Reasons for the decline include loss of habitat that can be used for foraging, especially early in the breeding season, and decrease in the amount of water flow into the Everglades (Fleming et al., 1994). The decrease on water flow causes a decrease in hydroperiod and thus less time for fish populations to increase in number. Deviation in the rate of decrease in water levels during the dry season from a steady, predictable decline may also disrupt the success of a breeding colony, as it may interfere with the process of concentration of fish densities (Kushlan, 1986). All of these problems make breeding success more problematic. But simulation modeling can help by allowing managers to explore ways in which water flow into the Everglades can be regulated in a way that allows wading bird foraging at all three hierarchical scales to be optimized as far as possible. Future work with the modeling described here will be directed toward that application.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

DD was the main contributor to sections “Introduction” and “Daily Search for Foraging Sites”. SY was the main contributor to sections “Seasonal Landscape-Scale Functional Response” and “Discussion”. HL and ST contributed to sections “Daily Search for Foraging Sites” and “Within-Pond Dynamics and Functional Response” and Supplementary Material. All authors contributed to the article and approved the submitted version.

Funding

DD and SY were supported in part by the U.S. Geological Survey’s Greater Everglades Priority Ecosystem Science Program (GX.21.MR00.CTFAT.00).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We greatly appreciate the very useful review by Mark Cook of the South Florida Water Management District and of two reviewers. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.729236/full#supplementary-material

References

Arditi, R., and Ginzburg, L. R. (2012). How Species Interact: Altering the Standard View on Trophic Ecology. Oxford: Oxford University Press.

Google Scholar

Bancroft, G. T., Gawlik, D. E., and Rutchey, K. (2002). Distribution of wading birds relative to vegetation and water depths in the northern Everglades of Florida, USA. Waterbirds 25, 265–277. doi: 10.1675/1524-46952002025%0265:DOWBRT%2.0.CO;2

CrossRef Full Text | Google Scholar

Bancroft, G. T., Strong, A. M., Sawicki, R. J., Hoffman, W., and Jewell, S. D. (1994). “Relationship among wading bird foraging patterns, colony locations, and hydrology in the Everglades,” in Everglades, the Ecosystem and its Restoration, eds S. M. Davis and J. C. Ogden (Delray Beach, FL: St. Lucie Press), 615–657.

Google Scholar

Beerens, J. M., Gawlik, D. E., Herring, G., and Cook, M. I. (2011). Dynamic habitat selection by two wading bird species with divergent foraging strategies in a seasonally fluctuating wetland. Auk 128, 651–662. doi: 10.1525/auk.2011.10165

CrossRef Full Text | Google Scholar

Beerens, J. M., Noonburg, E. G., and Gawlik, D. E. (2015). Linking dynamic habitat selection with wading bird foraging distributions across resource gradients. PLoS One 10:e0128182. doi: 10.1371/journal.pone.0128182

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernhardt, C. E., and Willard, D. A. (2006). Marl Prairie Vegetation Response to 20th Century Hydrologic Change. Open File Report, 1355. Reston, VA: US Geological Survey, 1–9.

Google Scholar

Botson, B. A., Gawlik, D. E., and Trexler, J. C. (2016). Mechanisms that generate resource pulses in a fluctuating wetland. PLoS One 11:e0158864. doi: 10.1371/journal.pone.0158864

PubMed Abstract | CrossRef Full Text | Google Scholar

Boyle, R. A., Dorn, N. J., and Cook, M. I. (2012). Nestling diet of three sympatrically nesting wading bird species in the Florida Everglades. Waterbirds 35, 154–159.

Google Scholar

Bryan, A. L. Jr., Coulter, M. C., and Pennycuick, C. J. (1995). Foraging strategies and energetic costs of foraging flights by breeding wood storks. Condor 97, 133–140. doi: 10.2307/1368991

CrossRef Full Text | Google Scholar

Charnov, E. L. (1976). Optimal foraging: attack strategy of a mantid. Am. Nat. 110, 141–151. doi: 10.1086/283054

CrossRef Full Text | Google Scholar

Collazo, J. A., Gilliam, J. F., and Miranda-Castro, L. (2010). Functional response models to estimate feeding rates of wading birds. Waterbirds 33, 33–40. doi: 10.1675/063.033.0104

CrossRef Full Text | Google Scholar

Cook, M. I., Call, E. M., Kobza, R. M., Hill, S. D., and Saunders, C. J. (2014). Seasonal movements of crayfish in a fluctuating wetland: implications for restoring wading bird populations. Freshw. Biol. 59, 1608–1621. doi: 10.1111/fwb.12367

CrossRef Full Text | Google Scholar

Coulter, M. C., and Bryan, A. L. Jr. (1993). Foraging ecology of wood storks (Mycteria Americana) in East-central Georgia I. Characteristics of foraging sites. Coln. Waterbirds 16, 59–70. doi: 10.2307/1521557

CrossRef Full Text | Google Scholar

Dorn, N. J., and Cook, M. I. (2015). Hydrological disturbance diminishes predator control in wetlands. Ecology 96, 2984–2993. doi: 10.1890/14-1505.1

CrossRef Full Text | Google Scholar

Dorn, N. J., Cook, M. I., Herring, G., Boyle, R. A., Nelson, J., and Gawlik, D. E. (2011). Aquatic prey switching and urban foraging by the White Ibis Eudocimus albus are determined by wetland hydrological conditions. Ibis 153, 323–335.

Google Scholar

Duever, M. J. (2005). Big Cypress regional ecosystem conceptual ecological model. Wetlands 25, 843–853.

Google Scholar

Erwin, R. M. (1983). Feeding habitats of nesting wading birds: spatial use and social influences. Auk 100, 960–970. doi: 10.1093/auk/100.4.960

CrossRef Full Text | Google Scholar

Fleming, D. M., Wolff, W. F., and DeAngelis, D. L. (1994). Importance of landscape heterogeneity to wood storks in Florida Everglades. Environ. Manag. 18, 743–757. doi: 10.1007/BF02394637

CrossRef Full Text | Google Scholar

Frederick, P., Gawlik, D. E., Ogden, J. C., Cook, M. I., and Lusk, M. (2009). The White Ibis and WoodStork as indicators for restoration of the Everglades ecosystem. Ecol. Indic. 9, S83–S95. doi: 10.1016/j.ecolind.2008.10.012

CrossRef Full Text | Google Scholar

Frederick, P. C., and Ogden, J. C. (2001). Pulsed breeding of long-legged wading birds and the importance of infrequent severe drought conditions in the Florida Everglades. Wetlands 21, 484–491. doi: 10.1672/0277-52122001021[0484:PBOLLW]2.0.CO;2

CrossRef Full Text | Google Scholar

Gawlik, D. E. (2002). The effects of prey availability on the numerical response of wading birds. Ecol. Monogr. 72, 329–346. doi: 10.1890/0012-96152002072[0329:TEOPAO]2.0.CO;2

CrossRef Full Text | Google Scholar

Gonzalez, A., Germain, R. M., Srivastava, D. S., Filotas, E., Dee, L. E., Gravel, D., et al. (2020). Scaling-up biodiversity-ecosystem functioning research. Ecol. Lett. 23, 757–776. doi: 10.1111/ele.13456

PubMed Abstract | CrossRef Full Text | Google Scholar

Gunderson, L. H., and Loftus, W. F. (1993). “The Everglades,” in Biodiversity of the Southeastern United States, Vol. 2, eds W. H. Martin, S. C. Boyce, and A. T. Echternacht (New York, NY: John Wiley and Sons), 199–255.

Google Scholar

Herring, G., Gawlik, D. E., Cook, M. I., and Beerens, J. M. (2010). Sensitivity of nesting Great Egrets (Ardea alba) and White Ibises (Eudocimus albus) to reduced prey availability. Auk 127, 660–670.

Google Scholar

Holling, C. S. (1959). A model of the functional response of predator to prey density involving the hunger effect. Can. Entomol. 91, 385–398. doi: 10.4039/Ent91385-7

CrossRef Full Text | Google Scholar

Horn, H. S. (1968). The adaptive significance of colonial nesting in the Brewer’s blackbird (Euphagus cyanocephalus). Ecology 49, 682–694. doi: 10.2307/1935532

CrossRef Full Text | Google Scholar

Iwasa, Y., Levin, S. A., and Andreasen, V. (1989). Aggregation in model ecosystems II. Approximate aggregation. Math. Med. Biol. A J. IMA 6, 1–23. doi: 10.1093/imammb/6.1.1-a

CrossRef Full Text | Google Scholar

Klassen, J. A., Gawlik, D. E., and Frederick, P. C. (2016). Linking wading bird prey selection to number of nests. J. Wildl. Manag. 80, 1450–1460.

Google Scholar

Krebs, J. R., Ryan, J. C., and Charnov, E. L. (1974). Hunting by expectation or optimal foraging? A study of patch use by chickadees. Anim. Behav. 22, 953–IN3.

Google Scholar

Kushlan, J. A. (1973). An ecological Study of An Alligator Pond in the Big Cypress Swamp of Southern Florida. M.S. thesis. Coral Gables, FL: University of Miami.

Google Scholar

Kushlan, J. A. (1976). Wading bird predation in a seasonally fluctuating pond. Auk 93, 464–476.

Google Scholar

Kushlan, J. A. (1979). Feeding ecology and prey selection in the white ibis. Condor 81, 376–389.

Google Scholar

Kushlan, J. A. (1981). Resource use strategies of wading birds. Wilson Bull. 93, 145–163.

Google Scholar

Kushlan, J. A. (1986). Responses of wading birds to seasonally fluctuating water levels: strategies and their limits. Col. Waterbirds 9, 155–162. doi: 10.2307/1521208

CrossRef Full Text | Google Scholar

Lantz, S. M., Gawlik, D. E., and Cook, M. I. (2011). The effects of water depth and emergent vegetation on foraging success and habitat selection of wading birds in the Everglades. Waterbirds 34, 439–447. doi: 10.1675/063.034.0406

CrossRef Full Text | Google Scholar

Lotka, A. J. (1925). Elements of Physical Biology. Philadelphia, PA: Williams & Wilkins.

Google Scholar

MacArthur, R. H., and Pianka, E. R. (1966). On optimal use of a patchy environment. Am. Nat. 100, 603–609. doi: 10.1086/282454

CrossRef Full Text | Google Scholar

McNair, J. N. (1982). Optimal giving-up times and the marginal value theorem. Am. Nat. 119, 511–529. doi: 10.1086/283929

CrossRef Full Text | Google Scholar

Morgan, R. A., Brown, J. S., and Thorson, J. M. (1997). The effect of spatial scale on the functional response of fox squirrels. Ecology 78, 1087–1097.

Google Scholar

Nishimura, K. (1992). Foraging in an uncertain environment: patch exploitation. J. Theor. Biol. 156, 91–111. doi: 10.1016/s0022-5193(05)80658-7

CrossRef Full Text | Google Scholar

Nolet, B. A., and Klaassen, M. (2009). Retrodicting patch use by foraging swans in a heterogeneous environment using a set of functional responses. Oikos 118, 431–439. doi: 10.1111/j.1600-0706.2008.16857.x

CrossRef Full Text | Google Scholar

Nonacs, P. (2001). State dependent behavior and the marginal value theorem. Behav. Ecol. 12, 71–83. doi: 10.1093/oxfordjournals.beheco.a000381

CrossRef Full Text | Google Scholar

Norris, K. E. N., and Johnstone, I. A. N. (1998). The functional response of oystercatchers (Haematopus ostralegus) searching for cockles (Cerastoderma edule) by touch. J. Anim. Ecol. 67, 329–346. doi: 10.1046/j.1365-2656.1998.00196.x

CrossRef Full Text | Google Scholar

Pierce, R. L., and Gawlik, D. E. (2010). Wading bird foraging habitat selection in the Florida Everglades. Waterbirds 33, 494–503. doi: 10.1675/063.033.0408

CrossRef Full Text | Google Scholar

Piersma, T., Van Gils, J., De Goeij, P., and Van Der Meer, J. (1995). Holling’s functional response model as a tool to link the food-finding mechanism of a probing shorebird with its spatial distribution. J. Anim. Ecol. 64, 493–504. doi: 10.2307/5652

CrossRef Full Text | Google Scholar

Pyke, G. H. (1984). Optimal foraging theory: a critical review. Annu. Rev. Ecol. Syst. 15, 523–575.

Google Scholar

Quintero, C. J., and Cohen, M. J. (2019). Scale-dependent patterning of wetland depressions in a low-relief karst landscape. J. Geophys. Res. Earth Surf. 124, 2101–2117.

Google Scholar

Silliman, B. R., McCoy, M. W., Angelini, C., Holt, R. D., Griffin, J. N., and van de Koppel, J. (2013). Consumer fronts, global change, and runaway collapse in ecosystems. Annu. Rev. Ecol. Evol. Syst. 44, 503–538. doi: 10.1146/annurev-ecolsys-110512-135753

CrossRef Full Text | Google Scholar

Stephens, D. W., and Krebs, J. R. (1986). Foraging Theory. (and as an ebook in 2019). Princeton, NJ: Princeton University Press.

Google Scholar

Toquenaga, Y., Kajitani, I., and Hoshino, T. (1994). Egrets of a feather flock together. Artif. Life 1, 391–411. doi: 10.1162/artl.1994.1.4.391

CrossRef Full Text | Google Scholar

Trexler, J. C., and Goss, C. W. (2009). Aquatic fauna as indicators for Everglades restoration: applying dynamic targets in assessments. Ecol. Indic. 9(Suppl. 1), S108–S119.

Google Scholar

Trexler, J. C., Loftus, W. F., Jordan, F., Chick, J. H., Kandl, K. L., McElroy, T. C., et al. (2002). “Ecological scale and its implications for freshwater fishes in the Florida Everglades,” in The Everglades, Florida Bay, and Coral Reefs of the Florida Keys: An Ecosystem Sourcebook, eds J. W. Porter, and K. G. Porter (Boca Raton, FL: CRC Press), 153–181.

Google Scholar

Volterra, V. (1937). Principes de biologie mathématique. Acta Biotheor. 3, 1–36. doi: 10.1007/BF01556501

CrossRef Full Text | Google Scholar

Watts, A. C., Watts, D. L., Cohen, M. J., Heffernan, J. B., McLaughlin, D. L., Martin, J. B., et al. (2014). Evidence of biogeomorphic patterning in a low-relief karst landscape. Earth Surf. Process. Landf. 39, 2027–2037. doi: 10.1002/esp.3597

CrossRef Full Text | Google Scholar

Wolff, W. F. (1994). An individual-oriented model of a wading bird nesting colony. Ecol. Modell. 72, 75–114. doi: 10.1016/0304-3800(94)90146-5

CrossRef Full Text | Google Scholar

Yurek, S., and DeAngelis, D. L. (2019). Resource concentration mechanisms facilitate foraging success in simulations of a pulsed oligotrophic wetland. Landsc. Ecol. 34, 583–601. doi: 10.1007/s10980-019-00784-0

CrossRef Full Text | Google Scholar

Yurek, S., DeAngelis, D. L., Trexler, J. C., Klassen, J. A., and Larsen, L. G. (2016). Persistence and diversity of directional landscape connectivity improves pulsed energy transfers in dynamic oligotrophic wetlands. Ecol. Complex. 28, 1–11.

Google Scholar