Yuri V. Tyutyunov
Lyudmila I. Titova- 1Southern Scientific Center of the Russian Academy of Sciences, Rostov-on-Don, Russia
- 2Independent Researcher, Rostov-on-Don, Russia
The functional response (trophic function or individual ration) quantifies the average amount of prey consumed per unit of time by a single predator. Since the seminal Lotka-Volterra model, it is a key element of the predation theory. Holling has enhanced the theory by classifying prey-dependent functional responses into three types that long remained a generally accepted basis of modeling predator-prey interactions. However, contradictions between the observed dynamics of natural ecosystems and the properties of predator-prey models with Holling-type trophic functions, such as the paradox of enrichment, the paradox of biological control, and the paradoxical enrichment response mediated by trophic cascades, required further improvement of the theory. This led to the idea of the inclusion of predator interference into the trophic function. Various functional responses depending on both prey and predator densities have been suggested and compared in their performance to fit observed data. At the end of the 1980s, Arditi and Ginzburg stimulated a lively debate having a strong impact on predation theory. They proposed the concept of a spectrum of predator-dependent trophic functions, with two opposite edges being the prey-dependent and the ratio-dependent cases, and they suggested revising the theory by using the ratio-dependent edge of the spectrum as a null model of predator interference. Ratio-dependence offers the simplest way of accounting for mutual interference in predator-prey models, resolving the abovementioned contradictions between theory and natural observations. Depending on the practical needs and the availability of observations, the more detailed models can be built on this theoretical basis.
Introduction
Since the first predator-prey model (Lotka, 1925; Volterra, 1926), classical trophic functions ignored interactions (i.e., interference) among predators, depending only on prey density, g(N) (refer to the examples in Table 1). Due to this, the Lotka-Volterra (LV)-type models demonstrate either structural instability (Svirezhev and Logofet, 1983; Bazykin, 1989) or large-amplitude oscillations with periodic drops of population abundances to extremely low levels in scenarios when the coexistence of more stable species is expected (Rosenzweig, 1971; Arditi and Ginzburg, 1989; Luck, 1990; Arditi and Berryman, 1991; Berryman, 1999; Sapoukhina et al., 2003). In a stochastic environment, such large fluctuations should cause the extinction of the consumer (Arditi et al., 2004; Jensen and Ginzburg, 2005; Hastings et al., 2018). The use of predator-dependent trophic functions (Table 1) corrects the models, enabling them to reproduce stable dynamic patterns that more closely approximate nature.
Table 1. Examples of trophic functions without and with mutual interference of predators.
Arditi and Ginzburg (1989) proposed the idea of a spectrum of every possible predator-dependent trophic functions, with two opposite edges being the prey-dependent and ratio-dependentcases:
Spectrum (1) ranks trophic functions from one extreme case of non-sharing to the other extreme case of perfect sharing of food among predators. Having highlighted the contradictions between the observed dynamics of natural ecosystems and the qualitative properties of predator-prey models with prey-dependent trophic functions, Arditi and Ginzburg (1989) suggested revising theoretical models by means of ratio-dependent functions providing the most parsimonious way of accounting for predator interference (Arditi et al., 1992). Their ideas inspired a lively debate stimulating great interest in justifying criteria for realistic functional response. The study by Arditi and Ginzburg (2012) summarizes their view on the current results of the long-lasting debate.
Some theoretical models with variable interference allow a much stronger (overcompensating) level of mutual interference than ratio-dependence. The analysis of these models (Arditi et al., 2004) showed that only moderate interference has the stabilizing effect on large oscillations, i.e., both low and strong interference levels increase the risk of predator extinction in a stochastic environment. Thus, the overcompensating interference should be rare in natural trophic systems subjected to non-adaptive selection (Borrelli et al., 2015), although observations reveal the cases of predator interference beyond ratio-dependence (Arditi and Akçakaya, 1990; Arditi and Ginzburg, 2012; Hossie and Murray, 2016; Novak and Stouffer, 2021a). Notably, both low and overcompensating interferences imply imperfect sharing of prey, thus falling inside the domain of spectrum (1). Unfortunately, opponents of the ratio-dependent theory misinterpret the meaning of the spectrum, alleging that it includes only functional responses reducible to ratio-dependence, excluding cases with interference stronger than ratio-dependence (Abrams, 1994, 2015).
The fundamental question of the ratio-dependent theory is which of the two ends of the spectrum (1) better describes predator-prey systems. Seeking for the simplest model providing qualitatively realistic predator-prey dynamics, Arditi and Ginzburg (1989, 2012, 2014) suggested using the ratio-dependent trophic function as a null model of predator interference. The concept of a minimal model that can be a starting point for building a more detailed description of a studied system is highly important. Such basic model is a compact mathematical formulation of theory providing general predictions over a set of different models for specific situations (Ginzburg and Colyvan, 2004; Ginzburg and Jensen, 2008; Batterman and Collin, 2014). Solving particular problems may require more detailed descriptions of a trophic system and elaborating the basic ratio-dependent model into a more general predator-dependent model if necessary.
Transferring the Basis of Predation Theory From Prey- to Ratio-Dependence
Historical Primacy of Prey-Dependent Models
The LV model, ignoring the intraspecies competition of prey, implies unlimited Malthusian growth of prey in the absence of predator. Being sensitive to initial conditions, the model is structurally unstable (Kostitzin, 1937; Kolmogorov, 1972; Svirezhev and Logofet, 1983; Begon et al., 1986; Bazykin, 1989). Replacing Malthusian prey growth with logistic law stabilizes the model. However, this does not solve the problem of unlimited consumption rates by an individual predator. Such consumption is an unrealistic hypothesis because a predator does not consume all encountered prey (Nicholson, 1933). The fate of prey depends on the satiety of the predator. Making the same assumptions, Gause (1934) has proposed and experimentally validated an exponential trophic function saturating with prey density. This dependence [Ivlev-Gause (IG), Table 1] well describes the individual food ration of fish (Ivlev, 1961) and crustaceans (Sushchenya, 1975).
Holling (1959a,b, 1965) has identified three types of functional responses accounting for two kinds of predator activity, namely, searching for and handling prey. All types of the functional responses of Holling (1959a) are bounded monotonically increasing prey-dependent functions. The Holling type I function increases linearly for small N and is limited from above for large N. Although in his illustration, Holling (1959a) smoothly connected the linear growth phase with a horizontal line of the saturation phase, the piecewise-linear function (H-I, Table 1) provides a convenient approximation (Svirezhev and Logofet, 1983; Bazykin, 1989; Jeschke et al., 2004). Type I trophic functions are typical for non-selective filter feeders (Jeschke et al., 2004) and for some parasitoids (Kaçar et al., 2017).
The type II functional response is a concave saturating function. Thus, the Ivlev trophic function IG belongs to type II (Holling, 1965). The most popular parameterization of the Holling type II trophic function is the famous “disk-equation” of Holling (1959b) accounting for the handling time h (H-II, Table 1). It coincides with a microbial population growth model by Monod (1949) and with the Michaelis–Menten model of enzyme kinetics (Michaelis and Menten, 1913). Its modification gives the sigmoid Holling type III (H-III, Table 1) functional response (Real, 1977).
Contrary to the constant searching efficiency a in H-II, the searching efficiency in H-III depends on the prey density: . The most practical value of n used in empirical and theoretical studies is n=2 (Bazykin, 1989; Sarnelle and Wilson, 2008; Svirezhev, 2008; Prokopenko et al., 2017). Sigmoid trophic functions are suitable for predators that increase their searching efficiency with prey density and for polyphagous predators that switch to more abundant alternative prey (Holling, 1959a; Murdoch, 1969; Jeschke et al., 2004). Sarnelle and Wilson (2008) demonstrated evidence of a type III response for Daphnia.
The Fallacies of Conventional Models and Their Correction With Predator-Dependence
With logistic prey growth and constant predator mortality, the considered predator-prey model is a system of differential equations as follows:
where g(⋅) denotes a trophic function with the appropriate argument(s).
The classical predation theory assumes that predators encounter prey at random and the trophic function depends on prey density only, g(⋅) = g(N). This leads to paradoxical contradiction noted by Arditi and Ginzburg (1989). On the one hand, classical trophic functions fit data collected from the laboratory trophic systems (Gause, 1934; Holling, 1959a,b, 1965; Ivlev, 1961; Veilleux, 1979; Arditi and Saïah, 1992; Bohannan and Lenski, 1997; Jeschke et al., 2004; Tully et al., 2005). On the other hand, attempts to apply the prey-dependent model (2) to describe the dynamics of large-scale ecosystems often fail. The unrealistic dynamic patterns of conventional models include the paradox of enrichment demonstrated by the Rosenzweig-MacArthur predator-prey model [system (2) with trophic function H-II] (Rosenzweig and MacArthur, 1963; Rosenzweig, 1971) and the closely related paradox of biological control (Luck, 1990; Arditi and Berryman, 1991; Berryman, 1999; Sapoukhina et al., 2003), as well as the absurd divergently directed reaction of “trophic cascade” levels to bottom-up biomanipulation, called enrichment response (Jensen and Ginzburg, 2005; Arditi and Ginzburg, 2012). Jensen and Ginzburg (2005) opine that all known attempts to find natural observations of such dynamics involve either inaccurate processing or erroneous interpretation of the data (Akçakaya et al., 1995). The fundamental cause of the abovementioned contradictions is the verticality of zero-isocline of the predator equation IsoP in models with prey-dependent trophic function g(N) (Arditi and Ginzburg, 1989). The verticality of IsoP in Figure 1A implies that it is enough to have a constant number of prey to maintain any abundance of a predator population. A hypothesis of mutual interference among the predators is more realistic (Begon et al., 1986): “individual consumption rates decline with predator abundance, and additional prey are required to maintain a predator population of any given size.” In this case, the slanting line of predator zero-isocline stabilizes the system dynamics (Figure 1B). Nowadays, most researchers admit that for resolving the contradictions at a large spatiotemporal scale, the functional response should take into account the mutual interference of predator, being a function of both prey and predator densities (DeAngelis et al., 1975, 2021; Berdnikov et al., 1999; Cosner et al., 1999; Abrams and Ginzburg, 2000; Arditi and Ginzburg, 2012). Experiments with appropriate variation in predator densities also show evidence of predator dependence (Skalski and Gilliam, 2001; DeLong and Vasseur, 2011; Novak and Stouffer, 2021a). However, choosing a particular form of the predator-dependence remains a point of controversy (Abrams and Ginzburg, 2000).
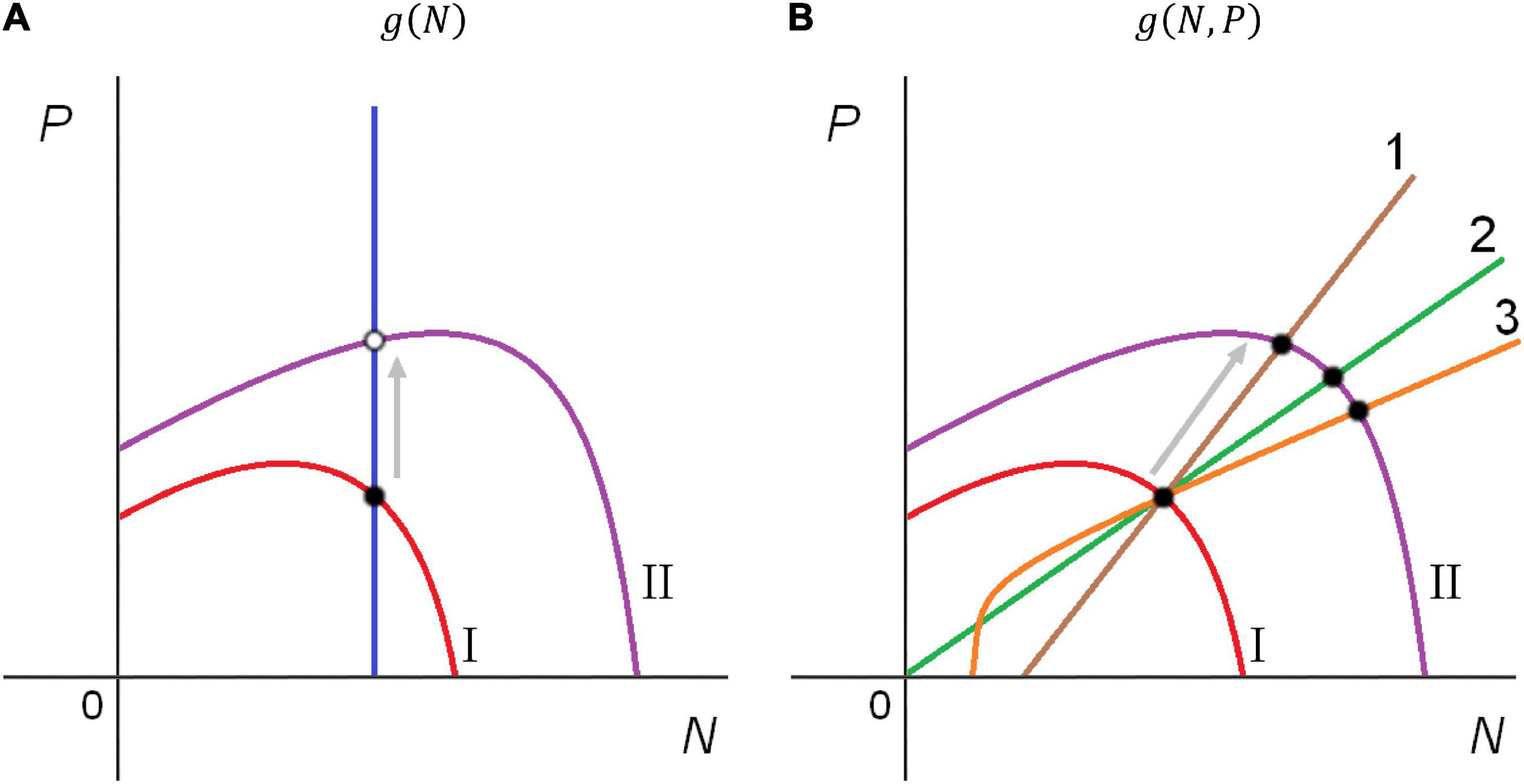
Figure 1. Responding to prey enrichment, the prey zero-isocline in the predator-prey model changes its shape and position from I to II. Due to the verticality of the predator isocline in the prey-dependent models (A), enrichment increases the predator equilibrium abundance but not the prey equilibrium; the initially stable equilibrium can become unstable. Slanted predator isoclines preserve the stability of the initially stable equilibrium in various predator-dependent models (B). Lines 1, 2, and 3 show the predator zero-isoclines for the Beddington-DeAngelis, ratio-dependent, and gradual interference trophic functions, respectively. Solid and hollow points mark stable and unstable equilibria, respectively. Refer to the text for further details.
Having suggested transferring the basis of the predation theory from the prey-dependent to the ratio-dependent edge of the spectrum (1), Arditi and Ginzburg (1989) proposed the simplest ratio-dependent modification of the H-II trophic function that assumes that predator interference diminishes the predator searching efficiency: a = a(P) = α/P. The Arditi–Ginzburg trophic function (AGC, Table 1) coincides with the Contois (1959) model describing the per capita growth rate of bacteria. The joint article of Arditi and Ginzburg (1989) followed the studies of the two authors on the ratio-dependence (Ginzburg et al., 1971, 1974; Ginzburg, 1975, 1986; Arditi et al., 1978; Arditi, 1983) and the results of other authors on predator interference. Table 1 represents examples and references from the review (Tyutyunov and Titova, 2020).
Underlying Mechanisms and Minimal Model of Predator Interference
Some predator-dependent trophic functions in either particular or asymptotic case approach the ratio-dependence. Moreover, the identification of the Hassel-Varley-Holling (HVH) function (Table 1) from the experimental data (Arditi and Akçakaya, 1990) has established that parameter m was often close to 1 (i.e., to ratio-dependence). Later, Novak and Stouffer (2021a) revealed that the estimates of interference strength in HVH model could be statistically biased upward by low sample sizes. In general, observations suggest that predator-dependence is widespread, more frequent than prey-dependence, and the most common values of m in HVH function are slightly less than 1 (DeLong and Vasseur, 2011, 2013). This agrees with the analytical results of Arditi et al. (2004) who provided evolutionary arguments in favor of a ratio-dependent pattern of consumption: both small and extremely large values of parameters characterizing mutual interference in the Hassel-Varley (HV), HVH, and Beddington-DeAngelis (BDA; Table 1) trophic functions destabilize the model, increasing the chances of predator extinction due to the accidental drop of population abundances. Some authors interpret the deviation of m from 1 as an argument against ratio-dependence, asserting that having a variety of predator-dependent trophic functions is more practical than a simple ratio-dependent model (Barraquand, 2014; Abrams, 2015). Replying to this criticism, Arditi and Ginzburg (2014) emphasized that their model is not an alternative to other existing models but rather a reasonable null model, i.e., a starting theoretical point for building a description of a predator-prey system. The AGC function is a minimal extension of the H-II dependence, which greatly widens the dynamical spectrum of model (2) and eliminates the shortcomings of the classical theory without adding extra parameters (Arditi and Berryman, 1991; Arditi et al., 1991; Ginzburg and Akçakaya, 1992; Akçakaya et al., 1995; Berezovskaya et al., 2001, 2007, 2021; Ginzburg and Colyvan, 2004; Arditi and Ginzburg, 2012). Zero-isocline IsoP for model (2) with the ratio-dependent AGC function is a straight line starting at the origin (line 2, Figure 1B). Thus, formally, similar to other predator-dependent trophic functions, the AGC relationship stabilizes the model due to the slant of IsoP. Problems with the behavior of ratio-dependent systems near the origin (Oksanen et al., 1992; Freedman and Mathsen, 1993; Abrams, 1994, 2015; Barraquand, 2014) can be overcome by applying the blow-up technics in the analysis (Berezovskaya et al., 2001, 2007, 2021) or by adding the Allee effect to make the models more realistic by introducing the deterministic extinction of species at low density (Sen et al., 2012).
Plots of IsoP in the predator-dependent models can have different forms or layouts, e.g., line 1 in Figure 1 corresponds to the BDA model. However, the HV, HVH, BDA, Bazykin-Crowley-Martin (BCM), and Bazykin-Harrison (BH) functions have common shortcomings: there is a special parameter regulating the strength of predator interference (m, w, or β, respectively). The gradual interference hypothesis (Arditi and Ginzburg, 2012) consists in the use of some universal trophic function g(N,P) exhibiting density-dependence for the high population abundances but weakening interference for the low population densities (zero-isocline 3, Figure 1). This conception allows synthesizing prey-dependent and predator-dependent models (Abrams and Ginzburg, 2000; Ginzburg and Jensen, 2008). Table 1 represents the examples of such hybrid trophic functions, allowing transition between prey- and ratio-dependence: non-saturating (Trân hybrid model of prey sharing and Trân hybrid model of prey depletion) and saturating [General RD model 1 (GRD-1) and General RD model 1 (GRD-2)] models of individual ration. Such universal functions can explain why Monod (1949) and Contois (1959), studying bacteria growth, came to different models coinciding with the dependences H-II and AGC, respectively. Monod was working with low concentrations of bacteria, while Contois experimented with high concentrations (Arditi and Ginzburg, 2012). Nevertheless, compared to AGC, HVH, and BDA trophic functions, universal GRD functions do not demonstrate far superior performance and flexibility in fitting the observed data (Tyutyunov et al., 2010; Prokopenko et al., 2017; Novak and Stouffer, 2021b). Accordingly, simpler models provide just as good approximations to reality.
Finally, the functional response depends on the spatiotemporal scale. DeAngelis et al. (2021) stressed that the ratio-dependent functional response focuses on accurately capturing dynamics emerging at the coarse landscape scale and is not derivable in following the assumptions of the Holling-type responses. DeAngelis et al. (2021) suggested a conceptual approach of hierarchical patch-centered functional response models functioning as a bridge to scale up from local to landscape scale. This conception agrees with the idea that while prey-dependent trophic functions g(N) are suitable to model small microcosms with low consumer density, choosing an appropriate tool for studying large-scale heterogeneous ecosystems, one should select some predator-dependent function. Within the frameworks of non-spatial (point) predator-prey systems, taking the AGC function as a null model of mutual interference can be a good decision (Ginzburg and Colyvan, 2004). This function provides a modeler with the simplest possibility to implicitly include the various effects of the environmental heterogeneity and the spatial behavior of consumers into a non-spatial model. Recent studies emphasize the importance of spatial effects in predator-prey systems, in particular, the mechanisms of pattern formation and dynamic properties emerging at a large spatiotemporal scale (Tyutyunov et al., 2020; Frank et al., 2021; Sun et al., 2021; Xue et al., 2021; Wang et al., 2022). Modeling gives a mechanistic explanation for the emergence of mutual interference. With a model that considers prey refuges, Poggiale et al. (1998) explained the emergence of donor control, i.e., a special case of ratio-dependence. Spatially explicit continuous (Arditi et al., 2001; Tyutyunov et al., 2002) and individual-based (Tyutyunov et al., 2008, 2013) models revealed that the motility of predator and its ability to move directionally in response to the heterogeneity of prey distribution (prey-taxis) is a key factor causing the emergence of the predator- and ratio-dependence at the population level. These results agree with feeding patterns observed in the laboratory cascade of reservoirs, demonstrating the emergence of consumer interference caused by the spatial clustering of cladocerans (Arditi and Saïah, 1992). They confirm also the theoretical conjectures by Cosner et al. (1999) and Arditi and Ginzburg (1989, 2012) about different behaviors corresponding to different functional responses: passive consumption leads to prey-dependence, and active predation leads to predator- and ratio-dependence (see also Ginzburg and Jensen, 2008). Unfortunately, opponents of the ratio-dependent theory did not acknowledge justification for ratio-dependence obtained with the prey-taxis models. Arguing against the spatial heterogeneity justification, they refer to a simple two-patch model (Abrams, 1994) and to spatial models (Barraquand, 2014; Abrams, 2015) that ignore directed movements of predators, and thus cannot demonstrate the emergence of predator- or ratio-dependence at the population level. Predator-prey models with prey-taxis show that the active movements of predators generate spatially heterogeneous dynamics, stabilizing trophic systems at both local and landscape scales (Sapoukhina et al., 2003; Tyutyunov et al., 2019). Emerging population clustering induces predator interference at the population level. Besides, the movements of the predator density patches create temporal refuges for the prey, providing an advantage for both predator (increasing consumption) and prey (increasing abundance) (Arditi et al., 2001; Sapoukhina et al., 2003; Tyutyunov et al., 2017, 2020).
Conclusion
Interestingly, the first trophic function taking into account the mutual interference of predators was ratio-dependent. Ivlev (1947, 1961) suggested this function (IRD, Table 1) to describe the phenomenon of “complicated competition” of fed individuals, which he discovered empirically in experiments with fish. Later, Park (1954) termed this phenomenon as “mutual interference.” Designing his experiments, Ivlev devoted much attention to the spatial distribution of food and jointly foraging consumers, reproducing natural conditions in detail. Since then, models assuming the dependence of predator ration on ratio N/P were based on the natural and laboratory observations, which provided evidence for ratio-dependence (Arditi and Saïah, 1992; Vucetich et al., 2002; Jost et al., 2005; Tyutyunov et al., 2010; DeLong and Vasseur, 2011; Arditi and Ginzburg, 2012; Spataro et al., 2012; Hebblewhite, 2013; Médoc et al., 2013, 2015; Hossie and Murray, 2016; Prokopenko et al., 2017; De Troyer et al., 2021). While predator interference can be overestimated due to systematic bias arising at a low sample size (Novak and Stouffer, 2021a), the parsimonious ratio-dependent model could satisfactorily describe the predation process, providing a reasonable trade-off between complexity and performance, particularly in such cases of scarce data (Ginzburg and Colyvan, 2004; Weijs and Ruddell, 2020).
The “alternative” approach to the mathematical description of the trophic relationship between species, proposed by Arditi and Ginzburg, gradually supersedes the traditional Lotka-Volerra model, taking deserved place in monographs and textbooks. Since its 7th edition, the popular textbook on ecology (Molles, 2016) presents both LV and AGC models as the fundamental predator-prey systems. The theory of ratio-dependent predation had already given an impetus to the development of the modern trophic theory. However, many challenging multidisciplinary problems remain unsolved. As such, future studies will benefit from collaboration between empiricists, field biologists, and theoreticians (Arditi and Ginzburg, 2014; Hossie and Murray, 2016).
Author Contributions
YuT designed the scope of the manuscript. YuT and LT reviewed the literature and prepared the manuscript. Both authors have equally contributed to this study.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors thank Inna N. Senina, Roger Arditi, Lev R. Ginzburg, and John Damuth for stimulating discussions and valuable comments on the manuscript draft. YuT acknowledges the State Allocation No. 01201363188 to SSC RAS.
References
Abrams, P. A. (1994). The fallacies of “ratio-dependent” predation. Ecology 75, 1842–1850. doi: 10.2307/1939644
Abrams, P. A. (2015). Why ratio dependence is (still) a bad model of predation. Biol. Rev. 90, 794–814. doi: 10.1111/brv.12134
Abrams, P. A., and Ginzburg, L. R. (2000). The nature of predation: prey dependent, ratio dependent or neither? Trends Ecol. Evol. 15, 337–341. doi: 10.1016/S0169-5347(00)01908-X
Akçakaya, H. R., Arditi, R., and Ginzburg, L. R. (1995). Ratio-dependent predation: an abstraction that works. Ecology 76, 995–1004. doi: 10.2307/1939362
Arditi, R. (1983). A unified model of the functional response of predators and parasitoids. J. Anim. Ecol. 52, 293–303. doi: 10.2307/4601
Arditi, R., Abillon, J. M., and Vieira da Silva, J. (1978). A predator-prey model with satiation and intraspecific competition. Ecol. Model 5, 173–191. doi: 10.1016/0304-3800(78)90019-4
Arditi, R., and Akçakaya, H. R. (1990). Underestimation of mutual interference of predators. Oecologia 83, 358–361. doi: 10.1007/BF00317560
Arditi, R., and Berryman, A. A. (1991). The biological control paradox. Trends Ecol. Evol. 6:32. doi: 10.1016/0169-5347(91)90148-Q
Arditi, R., and Ginzburg, L. (2014). Improving communications between theoretical ecologists, mathematical ecologists, and ecological modelers: response to the critique of our book How species interact. Theor. Ecol. 7, 21–22. doi: 10.1007/s12080-013-0203-7
Arditi, R., and Ginzburg, L. R. (1989). Coupling in predator-prey dynamics: ratio-dependence. J. Theor. Biol. 139, 311–326. doi: 10.1016/S0022-5193(89)80211-5
Arditi, R., and Ginzburg, L. R. (2012). How Species Interact: Altering the Standard View on Trophic Ecology. New York, NY: Oxford University Press.
Arditi, R., and Saïah, H. (1992). Empirical evidence of the role of heterogeneity in ratio-dependent consumption. Ecology 73, 1544–1551. doi: 10.2307/1940007
Arditi, R., Callois, J.-M., Tyutyunov, Yu., and Jost, C. (2004). Does mutual interference always stabilize predator–prey dynamics? A comparison of models. C. R. Biol. 327, 1037–1057. doi: 10.1016/j.crvi.2004.06.007
Arditi, R., Ginzburg, L. R., and Akcakaya, H. R. (1991). Variation in plankton densities among lakes: a case for ratio-dependent predation models. Am. Nat. 138, 1287–1296. doi: 10.1086/285286
Arditi, R., Ginzburg, L. R., and Perrin, N. (1992). Scale invariance is a reasonable approximation in predation models: reply to Ruxton and Gurney. Oikos 65, 336–337. doi: 10.2307/3545028
Arditi, R., Tyutyunov, Yu., Morgulis, A., Govorukhin, V., and Senina, I. (2001). Directed movement of predators and the emergence of density dependence in predator-prey models. Theor. Popul. Biol. 59, 207–221. doi: 10.1006/tpbi.2001.1513
Barraquand, F. (2014). Functional responses and predator-prey models: a critique of ratio dependence. Theor. Ecol. 7, 3–20. doi: 10.1007/s12080-013-0201-9
Batterman, R. W., and Collin, C. R. (2014). Minimal model explanations. Philos. Sci. 81, 349–376. doi: 10.1086/676677
Bazykin, A. D. (1985). Mathematical Biophysics of Interacting Populations [in Russian]. Moscow: Nauka, 182.
Bazykin, A. D. (1989). Nonlinear Dynamics of Interacting Populations. World Scientific Series on Nonlinear Science Series A. Singapore: World Scientific, 11. doi: 10.1142/2284
Bazykin, A. D., Berezovskaya, F. S., Denisov, G. A., and Kuznetzov, Yu. A. (1981). The influence of predator saturation effect and competition among predators on predator–prey system dynamics. Ecol. Model 14, 39–57. doi: 10.1016/0304-3800(81)90013-2
Beddington, J. R. (1975). Mutual interference between parasites or predators and its effect on searching efficiency. J. Anim. Ecol. 44, 331–340. doi: 10.2307/3866
Begon, M., Harper, J. L., and Townsend, C. R. (1986). Ecology: Individuals, Populations and Communities. Oxford: Blackwell Scientific Publications.
Berdnikov, S. V., Selyutin, V. V., Vasilchenko, V. V., and Caddy, J. F. (1999). Trophodynamic model of the Black and Azov seas pelagic ecosystem: consequences of the comb jelly, Mnemiopsis leydei, invasion. Fish. Res. 42, 261–289. doi: 10.1016/S0165-7836(99)00049-1
Berezovskaya, F. S., Novozhilov, A. S., and Karev, G. P. (2007). Population models with singular equilibrium. Math. Biosci. 208, 270–299. doi: 10.1016/j.mbs.2006.10.006
Berezovskaya, F., Karev, G., and Arditi, R. (2001). Parametric analysis of the ratio-dependent predator–prey model. J. Math. Biol. 43, 221–246. doi: 10.1007/s002850000078
Berezovskaya, F., Karev, G., and Koonin, E. V. (2021). A ratio-dependent model of replicator-genetic parasite coevolution demonstrates instability of the parasite-free state. bioRxiv [Preprint] doi: 10.1101/2021.02.20.432109
Berryman, A. A. (1999). “The theoretical foundations of biological control,” in Theoretical Approaches to Biological Control, eds B. A. Hawkins and H. V. Cornell (Cambridge: Cambridge University Press), 3–21.
Bohannan, B. J., and Lenski, R. E. (1997). Effect of resource enrichment on a chemostat community of bacteria and bacteriophage. Ecology 78, 2303–2315.
Borrelli, J. J., Allesina, S., Amarasekare, P., Arditi, R., Chase, I., Damuth, J., et al. (2015). Selection on stability across ecological scales. Trends Ecol. Evol. 30, 417–425. doi: 10.1016/j.tree.2015.05.001
Contois, D. E. (1959). Kinetic of bacterial growth relationship between population density and specific growth rate of continuous culture. J. Gen. Microbiol. 21, 40–50. doi: 10.1099/00221287-21-1-40
Cosner, C., DeAngelis, D. L., Ault, J. S., and Olson, D. B. (1999). Effect of spatial grouping on the functional response of predators. Theor. Pop. Biol. 56, 65–75. doi: 10.1006/tpbi.1999.1414
Crowley, P. H., and Martin, E. K. (1989). Functional responses and interference within and between year classes of a dragonfly population. J. North Am. Benthol. Soc. 8, 211–221. doi: 10.2307/1467324
De Troyer, N., Bruneel, S., Lock, K., Greener, M. S., Facq, E., Deknock, A., et al. (2021). Ratio-dependent functional response of two common Cladocera present in farmland ponds to Batrachochytrium dendrobatidis. Fungal Ecol. 53:101089. doi: 10.1016/j.funeco.2021.101089
DeAngelis, D. L., Goldstein, R. A., and O’Neill, R. V. (1975). A model for trophic interaction. Ecology 56, 881–892. doi: 10.2307/1936298
DeAngelis, D. L., Yurek, S., Tennenbaum, S., and Lee, H. W. (2021). Hierarchical functional response of a forager on a wetland landscape. Front. Ecol. Evol. 9:729236. doi: 10.3389/fevo.2021.729236
DeLong, J. P., and Vasseur, D. A. (2011). Mutual interference is common and mostly intermediate in magnitude. BMC Ecol. 11:1. doi: 10.1186/1472-6785-11-1
DeLong, J. P., and Vasseur, D. A. (2013). Linked exploitation and interference competition drives the variable behavior of a classic predator-prey system. Oikos 122, 1393–1400. doi: 10.1111/j.1600-0706.2013.00418.x
Frank, A., Subbey, S., Kobras, M., and Gjøsæter, H. (2021). Population dynamic regulators in an empirical predator-prey system. J. Theor. Biol. 527:110814. doi: 10.1016/j.jtbi.2021.110814
Freedman, H. I., and Mathsen, R. M. (1993). Persistence in predator-prey systems with ratio-dependent predator influence. Bull. Math. Biol. 55, 817–827. doi: 10.1016/S0092-8240(05)80190-9
Ginzburg, L. R. (1975). “Equations of the theory of biological communities,” in Mathematical Models in Biology [in Russian], ed. A. M. Molchanov (Moscow: Nauka), 53–91.
Ginzburg, L. R. (1986). The theory of population dynamics: I. Back to first principles. J. Theor. Biol. 122, 385–399. doi: 10.1016/s0022-5193(86)80180-1
Ginzburg, L. R., and Akçakaya, H. R. (1992). Consequences of ratio-dependent predation for steady-state properties of ecosystems. Ecology 73, 1536–1543. doi: 10.2307/1940006
Ginzburg, L. R., and Colyvan, M. (2004). Ecological Orbits: How Planets Move and Populations Grow. New York, NY: Oxford University Press.
Ginzburg, L. R., and Jensen, C. X. (2008). From controversy to consensus: the indirect interference functional response. Verh. Int. Ver. Theor. Angew. Limnol. 30, 297–301.
Ginzburg, L. R., Goldman Yu, I., and Railkin, A. I. (1971). A mathematical model of interaction between two populations – “predator-prey” [in Russian]. Zh. Obshch. Biol. 32, 724–730.
Ginzburg, L. R., Konovalov, N. Y., and Epelman, G. S. (1974). A mathematical model of interaction between two populations. IV. Theoretical and experimental data [in Russian]. Zh. Obshch. Biol. 35, 613–619.
Harrison, G. W. (1995). Comparing predator–prey models to Luckinbill’s experiment with Didinium and Paramecium. Ecology 76, 357–374. doi: 10.2307/1941195
Hassell, M. P., and Varley, G. C. (1969). New inductive population model for insect parasites and its bearing on biological control. Nature 223, 1133–1137. doi: 10.1038/2231133a0
Hastings, A., Abbott, K. C., Cuddington, K., Francis, T., Gellner, G., Lai, Y. C., et al. (2018). Transient phenomena in ecology. Science 361:eaat6412. doi: 10.1126/science.aat6412
Hebblewhite, M. (2013). Consequences of ratio-dependent predation by wolves for elk population dynamics. Popul. Ecol. 55, 511–522. doi: 10.1007/s10144-013-0384-3
Holling, C. S. (1959a). The components of predation as revealed by a study of small-mammal predation of the European sawfly. Can. Entomol. 91, 293–320. doi: 10.4039/Ent91293-5
Holling, C. S. (1959b). Some characteristics of simple types of predation and parasitism. Can. Entomol. 91, 385–398. doi: 10.4039/Ent91385-7
Holling, C. S. (1965). The functional response of predators to prey density and its role in mimicry and population regulation. Mem. Ent. Soc. Can. 97, 5–60. doi: 10.4039/entm9745fv
Hossie, T. J., and Murray, D. L. (2016). Spatial arrangement of prey affects the shape of ratio-dependent functional response in strongly antagonistic predators. Ecology 97, 834–841. doi: 10.1890/15-1535.1
Ivlev, V. S. (1947). Some questions of fed animals’ competitions. Usp. Sovremennoy Biol. 24, 417–432.
Ivlev, V. S. (1955). Experimental Ecology of the Feeding of Fishes [in Russian]. Мoscow: Pishchepromizdat, 272.
Ivlev, V. S. (1961). Experimental Ecology of the Feeding of Fishes. New Haven, CT: Yale University Press.
Jensen, C. X. J., and Ginzburg, L. R. (2005). Paradoxes or theoretical failures? The jury is still out. Ecol. Model 188, 3–14. doi: 10.1016/j.ecolmodel.2005.05.001
Jeschke, J. M., Kopp, M., and Tollrian, R. (2004). Consumer-food systems: why type I functional responses are exclusive to filter feeders. Biol. Rev. Camb. Philos. Soc. 79, 337–349. doi: 10.1017/s1464793103006286
Jost, C., Devulder, G., Vucetich, J. A., Peterson, R. O., and Arditi, R. (2005). The wolves of isle royale display scale-invariant satiation and ratio-dependent predation on moose. J. Anim. Ecol. 74, 809–816. doi: 10.1111/j.1365-2656.2005.00977.x
Kaçar, G., Wang, X. G., Biondi, A., and Daane, K. M. (2017). Linear functional response by two pupal Drosophila parasitoids foraging within single or multiple patch environments. PLoS One 12:e0183525. doi: 10.1371/journal.pone.0183525
Kolmogorov, A. N. (1972). “Qualitative analysis of mathematical models of populations,” in Problems of Cybernetics [in Russian], ed. A. A. Lyapunov (Moscow: Nauka), 25, 100–106.
Luck, R. F. (1990). Evaluation of natural enemies for biological control: a behavioral approach. Trends Ecol. Evol. 5, 196–199. doi: 10.1016/0169-5347(90)90210-5
Médoc, V., Albert, H., and Spataro, T. (2015). Functional response comparisons among freshwater amphipods: ratio-dependence and higher predation for Gammarus pulex compared to the non-natives Dikerogammarus villosus and Echinogammarus berilloni. Biol. Invasions 17, 3625–3637. doi: 10.1111/j.1365-2656.2009.01622.x
Médoc, V., Spataro, T., and Arditi, R. (2013). Prey: predator ratio dependence in the functional response of a freshwater amphipod. Freshw. Biol. 58, 858–865. doi: 10.1111/fwb.12091
Monod, J. (1949). The growth of bacterial cultures. Annu. Rev. Microbiol. 3, 371–394. doi: 10.1146/annurev.mi.03.100149.002103
Murdoch, W. W. (1969). Switching in general predators: experiments on predator specificity and stability of prey populations. Ecol. Monogr. 39, 335–354. doi: 10.2307/1942352
Novak, M., and Stouffer, D. B. (2021a). Systematic bias in studies of consumer functional responses. Ecol. Lett. 24, 580–593. doi: 10.1111/ele.13660
Novak, M., and Stouffer, D. B. (2021b). Geometric complexity and the information-theoretic comparison of functional-response models. Front. Ecol. Evol. 9:740362. doi: 10.3389/fevo.2021.740362
Oksanen, L., Moen, J., and Lundberg, P. A. (1992). The time-scale problem in exploiter-victim models: does the solution lie in ratio-dependent exploitation? Am. Nat. 140, 938–960. doi: 10.1086/285449
Park, T. (1954). Experimental studies of interspecific competition. II. Temperature, humidity and competition in two species of Tribolium. Physiol. Zool. 27, 177–238. doi: 10.1086/physzool.27.3.30152164
Poggiale, J. C., Michalski, J., and Arditi, R. (1998). Emergence of donor control in patchy predator-prey systems. Bull. Math. Biol. 60, 1149–1166. doi: 10.1006/S0092-8240(98)90006-4
Prokopenko, C. M., Turgeon, K., and Fryxell, J. M. (2017). Evaluation of alternative prey-, predator-, and ratio-dependent functional response models in a zooplankton microcosm. Can. J. Zool. 95, 177–182. doi: 10.1139/cjz-2016-0106
Real, L. A. (1977). The kinetics of the functional response. Am. Nat. 111, 289–300. doi: 10.1086/283161
Rosenzweig, M. L. (1971). Paradox of enrichment: destabilization of exploitation ecosystem in ecological time. Science 171, 385–387. doi: 10.1126/science.171.3969.385
Rosenzweig, M. L., and MacArthur, R. H. (1963). Graphical representation and stability conditions of predator-prey interactions. Am. Nat. 97, 217–223. doi: 10.1086/282272
Sapoukhina, N., Tyutyunov, Yu., and Arditi, R. (2003). The role of prey taxis in biological control: a spatial theoretical model. Am. Nat. 162, 61–76. doi: 10.1086/375297
Sarnelle, O., and Wilson, A. E. (2008). Type III functional response in Daphnia. Ecology 89, 1723–1732. doi: 10.1890/07-0935.1
Sen, D., Banerjee, M., and Morozov, A. (2012). Bifurcation analysis of a ratio-dependent prey-predator model with the Allee effect. Ecol. Complex 11, 12–27. doi: 10.1016/j.ecocom.2012.01.002
Skalski, G. T., and Gilliam, J. F. (2001). Functional responses with predator interference: viable alternatives to the Holling type II model. Ecology 82, 3083–3092.
Spataro, T., Bacher, S., Bersier, L.-F., and Arditi, R. (2012). Ratio-dependent predation in a field experiment with wasps. Ecosphere 3:124. doi: 10.1890/ES12-00133.1
Sun, G. Q., Zhang, H. T., Wang, J. S., Li, J., Wang, Y., Li, L., et al. (2021). Mathematical modeling and mechanisms of pattern formation in ecological systems: a review. Nonlinear Dyn. 104, 1–20. doi: 10.1007/s11071-021-06314-5
Sutherland, W. J. (1983). Aggregation and the ‘ideal free’ distribution. J. Anim. Ecol. 52, 821–828.
Svirezhev, Yu. M. (2008). Nonlinearities in mathematical ecology: phenomena and models. Would we live in Volterra’s world? Ecol. Model. 216, 89–101. doi: 10.1016/j.ecolmodel.2008.03.028
Svirezhev, Y. M., and Logofet, D. O. (1983). Stability of Biological Communities. Moscow: MIR Publishers.
Trân, J. K. (2008). A predator-prey functional response incorporating indirect interference and depletion. Verh. Int. Ver. Theor. Angew. Limnol. 30, 302–305.
Tully, T., Cassey, P., and Ferrière, R. (2005). Functional response: rigorous estimation and sensitivity to genetic variation in prey. Oikos 111, 479–487. doi: 10.1111/j.1600-0706.2005.14062.x
Tyutyunov, Yu. V., Sapoukhina, N. Yu., Senina, I. N., and Arditi, R. (2002). Explicit model for searching behavior of predator [in Russian]. Zhurn. Obshch. Biol. 63, 137–148.
Tyutyunov, Yu. V., and Titova, L. I. (2020). From Lotka-Volterra to Arditi-Ginzburg: 90 years of evolving trophic functions. Biol. Bull. Rev. 10, 167–185. doi: 10.1134/S207908642003007X
Tyutyunov, Yu. V., Sen, D., Titova, L. I., and Banerjee, M. (2019). Predator overcomes the Allee effect due to indirect prey-taxis. Ecol. Complex 39, 100772. doi: 10.1016/j.ecocom.2019.100772
Tyutyunov, Yu. V., Titova, L. I., and Berdnikov, S. V. (2013). A mechanistic model for interference and Allee effect in the predator population. Biophysics 58, 258–264. doi: 10.1134/S000635091302022X
Tyutyunov, Yu. V., Titova, L. I., and Senina, I. N. (2017). Prey-taxis destabilizes homogeneous stationary state in spatial Gause-Kolmogorov-type model for predator-prey system. Ecol. Complex 31, 170–180. doi: 10.1016/j.ecocom.2017.07.001
Tyutyunov, Yu. V., Titova, L. I., Surkov, F. A., and Bakaeva, E. N. (2010). Trophic function of phytophagous rotifers (Rotatoria) [in Russian]. Experiment and modelling. Zhurn. Obshch. Biol. 71, 52–62.
Tyutyunov, Yu. V., Zagrebneva, A. D., and Azovsky, A. I. (2020). Spatiotemporal pattern formation in a prey-predator system: the case study of short-term interactions between diatom microalgae and microcrustaceans. Mathematics 8:1065. doi: 10.3390/math8071065
Tyutyunov, Yu., Titova, L., and Arditi, R. (2008). Predator interference emerging from trophotaxis in predator-prey systems: an individual-based approach. Ecol. Complex 5, 48–58. doi: 10.1016/j.ecocom.2007.09.001
Veilleux, B. G. (1979). An analysis of the predatory interaction between Paramecium and Didinium. J. Anim. Ecol. 48, 787–803. doi: 10.2307/4195
Volterra, V. (1926). Fluctuations in the abundance of a species considered mathematically. Nature 188, 558–560. doi: 10.1038/118558a0
Vucetich, J. A., Peterson, R. O., and Schaefer, C. L. (2002). The effect of prey and predator densities on wolf predation. Ecology 83, 3003–3013.
Wang, L., Qiu, Z., Feng, T., and Kang, Y. (2022). An eco-epidemiological model with social predation subject to a component Allee effect. Appl. Math. Model. 101, 111–131. doi: 10.1016/j.apm.2021.07.037
Weijs, S. V., and Ruddell, B. L. (2020). Debates: does information theory provide a new paradigm for earth science? Sharper predictions using Occam’s digital razor. Water Resour. Res. 56:e2019WR026471. doi: 10.1029/2019wr026471
Keywords: functional response, trophic function, non-adaptive selection, predator interference, ratio-dependence, predator-dependence, Arditi–Ginzburg functional response
Citation: Tyutyunov YuV and Titova LI (2021) Ratio-Dependence in Predator-Prey Systems as an Edge and Basic Minimal Model of Predator Interference. Front. Ecol. Evol. 9:725041. doi: 10.3389/fevo.2021.725041
Received: 14 June 2021; Accepted: 10 November 2021;
Published: 07 December 2021.
Edited by:
Thomas John Hossie, Trent University, CanadaReviewed by:
John Paul DeLong, University of Nebraska-Lincoln, United StatesGui-Quan Sun, North University of China, China
Copyright © 2021 Tyutyunov and Titova. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuri V. Tyutyunov, yuri.tyutyunov@yandex.ru