Directional Selection on Tree Seedling Traits Driven by Experimental Drought Differs Between Mesic and Dry Populations

We evaluated population differences and drought-induced phenotypic selection on four seedling traits of the Australian forest tree Eucalyptus pauciflora using a glasshouse dry-down experiment. We compared dry and mesic populations and tested for directional selection on lamina length (reflecting leaf size), leaf shape, the node of ontogenetic transition to the petiolate leaf (reflecting the loss of vegetative juvenility), and lignotuber size (reflecting a recovery trait). On average, the dry population had smaller and broader leaves, greater retention of the juvenile leaf state and larger lignotubers than the mesic population, but the populations did not differ in seedling survival. While there was statistical support for directional selection acting on the focal traits in one or other population, and for differences between populations in selection gradient estimates for two traits, only one trait—lamina length—exhibited a pattern of directional selection consistent with the observed population differences being a result of past adaptation to reduce seedling susceptibility to acute drought. The observed directional selection for lamina length in the mesic population suggests that future increases in drought risk in the wild will shift the mean of the mesic population toward that of the dry population. Further, we provide evidence suggesting an early age trade-off between drought damage and recovery traits, with phenotypes which develop larger lignotubers early being more susceptible to drought death. Such trade-offs could have contributed to the absence of population mean differences in survival, despite marked differentiation in seedling traits.

Introduction

Global warming is leading to major shifts in the distribution of plant and animal species globally (Chen et al., 2011). Sessile species, such as forest trees, are among the most vulnerable owing to their often poor dispersal abilities and long life histories (Petit and Hampe, 2006). Already, extreme climate events causing heat and drought stress have been linked directly (Allen et al., 2010; Matusick et al., 2013) and indirectly (Buotte et al., 2016) to forest dieback in many parts of the world. Ongoing climate change is expected to exacerbate such stresses (Allen et al., 2010; Schwalm et al., 2017), and it has long been argued that the rate of climate change may exceed the adaptive capacity of tree populations (Davis and Shaw, 2001; Jump and Peñuelas, 2005; Aitken et al., 2008).

Tree adaptation to major environmental gradients such as aridity is polygenic and genome-wide (Kramer et al., 2015; Jordan et al., 2017; Steane et al., 2017), involves diverse functional traits (Alberto et al., 2013; Kremer et al., 2014), and potentially also genetic constraints (Bourne et al., 2017; Costa e Silva et al., 2020). Detecting adaptive changes in local populations of long-lived organisms, such as forest trees, is difficult due to numerous factors (Alberto et al., 2013), including long-life cycles (Petit and Hampe, 2006), ontogenetic (Brunner et al., 2016) and plastic (Nicotra et al., 2010; McLean et al., 2014) changes in phenotype, superimposed on the normal selective filtering of mal-adapted inbred progeny during stand development (Koelewijn et al., 1999; Costa e Silva et al., 2011; Griffin et al., 2019). Molecular markers are often used to detect signatures of adaptive genetic variation in tree species (Keller et al., 2012; Alberto et al., 2013; Dillon et al., 2014; Pluess et al., 2016; Frachon et al., 2018) and, as the effects of putative adaptive markers/SNPs become validated, there will be increasing opportunity for their use to monitor adaptive changes in forest tree populations following selection. However, traditional analysis of phenotypic selection and quantitative genetic studies of functional traits continue to provide valuable insights into the effects of natural selection, and have been applied in many animal and plant species (Kingsolver et al., 2001, 2012; Shaw and Etterson, 2012; Merilä and Hendry, 2014). Despite this, there is a paucity of empirical studies in forest tree populations that address the adaptive value of functional traits through their impact on fitness components (Gómez, 2004; Alberto et al., 2013; Ramírez-Valiente et al., 2014, 2015; Costa e Silva et al., 2018; Warwell and Shaw, 2018, 2019), as is the case for most long-lived species (Monica and Lauren, 2003).

Lande and Arnold (1983) developed a least-squares multiple regression framework for the analysis of phenotypic selection based on the relationship between relative fitness (i.e., the fitness of an individual divided by the mean fitness of the population) and phenotypic measures for a set of traits. This approach assumes a causal fitness-trait relationship, such that a trait (or a trait combination) is expected to be under selection when significantly influencing fitness. The partial regression coefficients thus represent selection gradients that quantify the direct effects of trait variables on relative fitness, and the complete model with linear, quadratic and cross-product terms provides a quadratic approximation to the individual fitness surface (Phillips and Arnold, 1989). In particular, by characterizing directional selection, the linear selection gradient has a direct application in the prediction of evolutionary change between generations, under the assumption of multivariate normal distribution of breeding values (Lande, 1979). Fitness components used to evaluate selection commonly involve discrete variables (e.g., viability and fecundity measured by survival and the number of offspring), and generalized linear models have been described for the estimation of selection gradients with non-normal distributions of fitness responses (Janzen and Stern, 1998; Morrissey and Sakrejda, 2013).

Numerous studies have shown significant directional selection in wild populations (Kingsolver and Diamond, 2011; Kingsolver et al., 2012; Siepielski et al., 2013). Such selection can vary with time/seasons (Siepielski et al., 2009; Steele et al., 2011; Ramírez-Valiente et al., 2014, 2015; Warwell and Shaw, 2018, 2019) and environment (Dudley, 1996; Etterson, 2004; Heschel and Riginos, 2005; Donovan et al., 2009; Lau et al., 2014; Warwell and Shaw, 2018), and this variation drives population divergence and local adaptation within a species (Siepielski et al., 2013; Hendry, 2017). However, there are often multiple phenotypic solutions to the same adaptive requirement (e.g., drought survival—McDowell et al., 2011; Choat et al., 2018; Klein et al., 2018) and increasing evidence from common-garden trials that the focal traits under selection can be population specific (Dudley, 1996; Etterson, 2004; Heschel and Riginos, 2005; Donovan et al., 2009). Understanding population differences in the focal traits under selection following the same selection event can allow insights into functional traits that may be underlying local adaptation (Dudley, 1996; Monica and Lauren, 2003) and how these vary within a species. Such understanding is a key step toward evaluating the effects of selection due to, for example, climate change (Hoffmann and Sgro, 2011; Alberto et al., 2013; Merilä and Hendry, 2014), including outcomes for different populations or parts of the species distribution.

The present study focuses on the Australian tree species Eucalyptus pauciflora Sieber ex Spreng.. Eucalyptus pauciflora has one of the broadest altitudinal ranges of any eucalypt species (i.e., growing from sea-level to near the alpine tree line on both continental Australia and the island of Tasmania), and is one of the main tree species used for ecological restoration in the dry midlands of Tasmania (Prober et al., 2016; Bailey et al., 2021). Climate change is predicted to result in most Tasmanian E. pauciflora populations being outside the contemporary climate envelope of the species and at risk of maladaptation by 2080 (Harrison, 2017). This risk of maladaptation mainly reflects the predicted increasing temperatures and evapotranspiration across Tasmania (Corney et al., 2010; Harrison et al., 2017), and thus increased risk of drought stress. Both water deficit and high temperatures contribute to drought stress (Park Williams et al., 2013; Duan et al., 2014; Mitchell et al., 2014) and could, independently or combined, drive selection on plant traits (Costa e Silva et al., 2019). The challenge in understanding adaptation is to unravel these multiple effects. Here we focus on just a single factor—water deficit, which has both plastic (Cano et al., 2014; Duan et al., 2014; McKiernan et al., 2016) and genetic-based (Ammitzboll et al., 2020) selective impacts on eucalypt seedlings.

As with other forest tree studies on drought-induced selection (e.g., Warwell and Shaw, 2019), we focused on the seedling life stage as: (i) there is usually significant seedling mortality in wild and planted eucalypt populations, with water deficit being the most common cause (Battaglia and Reid, 1993; Stoneman, 1994; Tozer and Bradstock, 1998); (ii) the phenotypic and genetic variation in morphological traits at this life stage has been well-characterized in E. pauciflora (Gauli et al., 2015); and (iii) there are signals that variation in some seedling morphological traits of E. pauciflora is adaptive (Gauli et al., 2015; Costa e Silva et al., 2019). We specifically aimed to: (1) assess the difference between dry and mesic populations in four seedling traits that potentially may influence the plant’s response to acute drought; (2) evaluate the consequences of the variation in the focal seedling traits on fitness in each population; and (3) estimate whether the relationship between fitness and the focal traits differs between populations. We hypothesized that, if selection acting on the studied traits via seedling survival was driven by acute drought stress in wild populations, then an imposed artificial drought would elicit a shift in character states of the mesic population toward those of the dry population.

Materials and Methods

Populations Studied

The current study used seedlings from two populations of E. pauciflora, which were grown in a common-garden glasshouse trial subject to an artificial drought. These two lowland Tasmanian populations were from Brushy Lagoon and Ross, and were from mesic and dry parts of the climatic range of E. pauciflora on the island, respectively. These populations were selected to accentuate rainfall differences and minimize the differences in other environmental factors. The mean annual precipitation at Ross is nearly 50% lower than at Brushy Lagoon, but Ross also has a slightly higher mean maximum temperature of the warmest period than Brushy Lagoon (Table 1). These populations are located over 90 km apart, well-exceeding the distance of significant genetic spatial autocorrelation in the species (i.e., 27 km—Gauli et al., 2013). The populations have similar high outcrossing rates (Gauli et al., 2013) and inbreeding levels in their open-pollinated progeny (Gauli et al., 2014), but differ markedly in numerous seedling traits (Gauli et al., 2015).

TABLE 1

Table 1. Population information for the mesic (Brushy Lagoon) and dry (Ross) populations of Eucalyptus pauciflora used in the dry-down experiment.

Drought Experiment

Each population was represented by 12 families corresponding to 12 mother-trees randomly selected within native stands and situated by more than two canopy heights apart. The seedlings of each family were obtained from open-pollinated seeds collected randomly from near the middle of the canopy of the mother-tree. Seedlings from these families were grown in soil-filled pots (9 cm × 9 cm × 18 cm) and, when the plants were 14-week-old, the pots were arranged into an experimental design for imposing drought stress under glasshouse conditions. The experiment was conducted in two glasshouses, though a large portion of window panels were removed so that seedlings were exposed to ambient air conditions. Temperature and relative humidity were similar between the two glasshouses, and temperature reflected external ambient air temperature over the duration of the experiment (Supplementary Figure 1). Over the course of the dry-down period, the average daily maximum temperature inside the glasshouses was 16.9 and 16.0°C, and the average daily minimum temperatures were 6.5 and 6.8°C. Daily maxima did not exceed 27°C and daily minima did not go below −1°C. Humidity ranged from an average daily maximum of 88.5 and 90.9% to an average daily minimum of 51.6 and 58.5% in the two glasshouses, respectively. The experimental layout was effectively a split-plot design comprising four replicates (blocks), two in each glasshouse. Each replicate included two main plots (hereafter denoted as population plots), one of the Brushy Lagoon families and one of the Ross families, and families were randomized as single-tree plots within these population plots. Overall, there were 387 and 386 seedlings in the Brushy Lagoon and Ross populations, respectively, available for analysis. Across the experiment, the sizes of the population plots varied between 92 and 101 seedlings in Brushy Lagoon, and between 93 and 100 seedlings in Ross. The family sizes across all four replicates ranged from 22 to 38 seedlings in Brushy Lagoon, and from 19 to 38 seedlings in Ross, with an average of 32 seedlings per family in both populations. The degree of unbalance in family sizes was moderate: the variation of family sizes as measured by the coefficient of variation was 16% in both populations.

The water deficit treatment was applied using floral foam, in a manner adapted from Fernández and Reynolds (2000) and Marchin et al. (2020). Each population plot consisted of a water basin containing a layer of floral foam (Oasis Ideal Standard Super 60; Apack Pty Ltd., Dandenong South, Australia). Potted seedlings were placed on the foam, with a small amount of fine washed sand in drainage holes to ensure effective contact with foam. Water basins were topped up twice daily to within approximately 10 cm from the top of the foam, enabling self-watering by wicking, though with reduced water availability for plants (see Marchin et al., 2020). Exposed foam, above the top of the water basins, was wrapped in plastic to minimize water loss through evaporation.

After placing seedlings in the experimental design, they were left to acclimate for 10 days, over which time morphometric measurements were taken from the seedlings (see below). After 10 days, no further water was added to the water basins, initiating the drought component of the experiment. At the end of the experiment 67 days later, seedling survival was scored as a binary outcome, based on the following assessments: a seedling was classified as dead (scored as 0) when all leaves, including laterals, and the apical meristem had dried out; otherwise it was classified as alive (scored as 1). As scored, seedling survival refers to observable “canopy” mortality immediately following termination of the dry-down experiment, and does not account for the possibility of differential recovery if rewatering had occurred. This measure of seedling survival was used as a fitness component for individuals in the analysis of phenotypic selection.

Trait Measurements

Phenotypic trait measurements were taken from the seedlings during the 10-day acclimation period. At this time, a single leaf was sampled from the third pair of leaves up the main stem (cotyledonary node = 0), and individually digitally photographed with a constant size scale for the measurement of leaf dimensions (see below). Following the removal of the third-node leaf, these seedlings were also measured for the lignotuber diameter—i.e., the diameter (mm) across the lignotubers developed in the axils of the cotyledons—and for the stem diameter (mm) perpendicular to the axis of maximum lignotuber diameter. The seedling height (cm) and the node number of the first petiolate leaf (counted from the cotyledonary node) were also recorded. The node number of the first petiolate leaf is a trait that reflects the ontogenetic transition from sessile (juvenile) to petiolate (mature) leaves in Eucalyptus spp., and is hereafter referred to as “vegetative juvenility” (i.e., the higher the node number, the later the petiole development is in nodes, and thus the more the seedling is vegetatively juvenile). Leaf dimensions were manually measured from the digital images of the seedling leaves, and included the lamina length (mm) and lamina width (mm). In the present study, seedling leaf morphology, lignotuber size and vegetative juvenility were represented by four functional traits—lamina length, leaf shape index, adjusted lignotuber size and vegetative juvenility (see below). Photos of lignotubers and vegetative juvenility in seedlings of E. pauciflora are provided in Figure 3 of Costa e Silva et al. (2019).

Data Analyses

The data analyses entailed two main components. Firstly, population mean differentiation and variance estimation were addressed for the focal functional traits and seedling survival. Then, phenotypic selection analysis was pursued within populations to measure directional selection acting on the focal traits through seedling survival, and differences between populations in estimated selection gradients for a trait were subsequently evaluated. To account for the inherent positive allometric relationship between lamina length and lamina width, the lamina width measurements were adjusted for seedling differences in lamina length in the data analyses. The adjusted lamina width thus provides a measure that reflects leaf shape, and is hereafter denoted as “leaf shape index” (with increasing values meaning broader leaves). The lignotuber diameter measurement is also inherently dependent on stem diameter and, following Costa e Silva et al. (2019), was also adjusted in the data analyses to provide a measure independent of stem diameter, hereafter referred to as “adjusted lignotuber size.” Finally, in addition to the focal traits, seedling height and stem diameter were modeled as “nuisance variables” in the phenotypic selection analysis. This was done to account for the effects of initial plant size on drought-induced mortality, as the seedlings were growing in pots with a defined soil volume, and bigger plants are expected to inherently use more water (Ammitzboll et al., 2020).

The SAS 9.4 software (SAS, 2017) was used in the data analyses. In particular, linear mixed models were estimated with the procedure MIXED, and generalized linear mixed models were estimated with the procedures GLIMMIX and NLMIXED.

Linear Mixed Model for the Continuous Variables (Lamina Length, Leaf Shape Index and Adjusted Lignotuber Size)

The following linear mixed model (LMM) was fitted for the continuous variables:

$\mathbf{\text{y}}=\mathbf{\text{X}}\mathit{\beta }\text{+}{\mathbf{\text{Z}}}_1{\mathbf{\text{b}}}_1\text{+}{\mathbf{\text{Z}}}_2{\mathbf{\text{b}}}_2\text{+}\mathbf{\text{e}}(1)$

where y is a n x 1 vector of observations (n = total number of seedlings in the experiment); β is a p × 1 vector of fixed-effect parameters; b₁ and b₂ are q × 1 vectors of random-effect parameters for families within the Brushy Lagoon and Ross populations, respectively; X is a design matrix relating y to the parameters in β; Z₁ and Z₂ are design matrices relating y to the random effects in b₁ and b₂, respectively; e is a n × 1 vector of residuals of the observations. The vector β included the intercept, and effects for population, block and population-by-block interaction for all traits. The analyses of leaf shape index and adjusted lignotuber size involved the adjustment of the lamina width and lignotuber diameter measurements using lamina length and stem diameter as covariates, respectively. In these cases, β included also the corresponding coefficients for the regression parameter and its interaction with population. The family effects and residuals were modeled by considering a heterogeneous variance structure at the population level. In this sense, it was assumed that $\left(\begin{array}{c}{\mathbf{b}}_1\\ {\mathbf{b}}_2\end{array}\right)$ ∼ MVN(0, G), with G = $\left[\begin{array}{cc}\hfill {\mathbf{\text{I}}}_{q_1}{\mathrm{\sigma }}_{b_1}^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathbf{\text{I}}}_{q_2}{\mathrm{\sigma }}_{b_2}^2\hfill \end{array}\right]$, where ${\mathrm{\sigma }}_{b_1}^2$ and ${\mathrm{\sigma }}_{b_2}^2$ are family variances in Brushy Lagoon and Ross, respectively; I_q1 and I_q2 are identity matrices of dimension equal to the number of families in Brushy Lagoon (q₁) and Ross (q₂). Conditional on the family random effects, the residuals were assumed $\left(\begin{array}{c}{\mathbf{e}}_1\\ {\mathbf{e}}_2\end{array}\right)$ ∼ MVN(0, R), with R = $\left[\begin{array}{cc}\hfill {\mathbf{\text{I}}}_{n_1}{\mathrm{\sigma }}_{e_1}^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathbf{\text{I}}}_{n_2}{\mathrm{\sigma }}_{e_2}^2\hfill \end{array}\right]$, where ${\mathrm{\sigma }}_{e_1}^2$ and ${\mathrm{\sigma }}_{e_2}^2$ are residual variances in Brushy Lagoon and Ross, respectively; I_n1 and I_n2 are identity matrices of dimension equal to the number of seedlings in Brushy Lagoon (n₁) and Ross (n₂); it was further assumed that the residuals and random effects were independent. Visual inspection of histograms and quantile-quantile plots of conditional studentized residuals showed residual distributions conforming reasonably well to a normal distribution for all traits. In addition, the residuals did not appear to co-vary with random effects, as generally indicated by small and statistically non-significant correlations estimated within either population. The (co)variance structure of y was defined by V = ZGZ′ + R, where $\mathbf{Z}=\left[\begin{array}{cc}{\mathbf{Z}}_1& 0\\ 0& {\mathbf{Z}}_2\end{array}\right]$; through G, the V-matrix captures the covariance of the observations within families, which will be reflected in the estimation of the fixed-effect parameters and their standard errors (Raudenbush and Bryk, 2002; see next paragraph).

The variances in G and R were estimated by restricted maximum likelihood (REML; Patterson and Thompson, 1971). Following the estimation of variance components, fixed-effect parameters were estimated by generalized least-squares, i.e. $\widehat{\mathit{\beta }}={(\mathbf{\text{X}}{}^{\prime }\widehat{\mathbf{\text{V}}}^{-\mathbf{1}}\mathbf{\text{X}})}^{-\mathbf{1}}{\mathbf{\text{X}}}^{\prime }{\widehat{\mathbf{\text{V}}}}^{-\mathbf{1}}\mathbf{\text{y}}$, with the associated model-based sampling (co)variance matrix being given by $\mathit{Var}(\widehat{\mathit{\beta }})={(\mathbf{\text{X}}{}^{\prime }\widehat{\mathbf{\text{V}}}^{-\mathbf{1}}\mathbf{\text{X}})}^{-\mathbf{1}}$. This matrix was corrected by using the Kenward-Roger (KR) adjustment, to provide estimates of standard errors of $\widehat{\mathit{\beta }}$ that account for potential finite-sample bias and the uncertainty in the estimation of G and R (Kenward and Roger, 2009). Based on a corrected $\mathit{Var}(\widehat{\mathit{\beta }})$ matrix, the Kenward and Roger (1997, 2009) approximation to compute denominator degrees of freedom was applied to improve statistical inference about the fixed effects. For sample sizes comparable to the number of families and the within-family sizes in our study, simulation work with LMMs using REML indicated that applying the KR method to fixed-effect parameters produced accurate estimates of standard errors, and maintained Type-I error rates and confidence interval coverage close to the specified (α = 0.05) nominal level (Ferron et al., 2009; Baldwin and Fellingham, 2013; McNeish and Stapleton, 2016a; see also Supplementary Methods 1).

Statistical inference about the fixed-effect model terms was based on F-tests, which indicated that the interactions of population with blocks, and with either lamina length or stem diameter used as covariates (in the LMM for leaf shape index or adjusted lignotuber size, respectively), were not statistically significant (p > 0.05). Thus, a final LMM without the interaction terms was then fitted for all traits. One-sided likelihood ratio tests (Self and Liang, 1987) were applied to assess whether estimated family variances were significantly greater than zero. In preliminary analyses, a one-sided likelihood ratio test was also used to test the variance estimate associated with a random term modeling a block-by-family interaction: as no significant effects were detected (suggesting an efficient randomization of seedlings within blocks), the interaction term was excluded in the LMM defined in Equation (1). The population least-squares mean (LS-Mean) for a trait was calculated with a linear function of $\widehat{\mathit{\beta }}$ estimates, i.e. $\mathbf{\text{L}}\widehat{\mathit{\beta }}$, where L is the coefficient matrix pertaining to the LS-Mean. The standard error of a LS-Mean estimate was approximated by the square-root of $\mathbf{\text{L}}\mathit{Var}(\widehat{\mathit{\beta }}){\mathbf{\text{L}}}^{\prime }$. The KR approximation for computation of degrees of freedom was also applied to obtain the critical values for the student’s t-distribution used for estimating the 95% confidence interval of a LS-Mean.

Generalized Linear Mixed Model for the Discrete Variables (Seedling Survival and Vegetative Juvenility)

The following generalized linear mixed model (GLMM) was fitted for the discrete variables:

$g(E(\mathbf{y}|\mathbf{X},{\mathbf{\text{b}}}_1,{\mathbf{\text{b}}}_2))=g(\mathit{\mu })=\mathbf{\text{X}}\mathit{\beta }+{\mathbf{\text{Z}}}_1{\mathbf{\text{b}}}_1+{\mathbf{\text{Z}}}_2{\mathbf{\text{b}}}_2(2)$

where g(.) is a link function relating the conditional expectation [i.e. E(y|X, b₁, b₂) = μ, where μ is the mean vector] of the response variable to the linear predictor η = Xβ +Z₁b₁ +Z₂b₂; the vectors and matrices in η were defined as in Equation (1) (except that η does not contain a definite error term, nor continuous covariates in X as in the LMMs for leaf shape index and adjusted lignotuber size); for b₁ and b₂, the model specification with heterogeneous variances and the distributional assumptions were the same as in the LMM. Conditional on the random effects, the observations were assumed to be independently distributed, with Bernoulli and Poisson distributions for the binary (seedling survival) and count (vegetative juvenility) variables, respectively. For the binary variable, E(y|X, b₁, b₂) is also the conditional probability of seedling survival [i.e. P(y =  1|X, b₁, b₂)]. The probit link function was used to model survival, such that P(y =  1|X, b₁, b₂) = g⁻¹(η) = Φ(Xβ+Z₁b₁ +Z₂b₂), where g⁻¹(.) is the inverse of g(.) and Φ(.) is the standard normal cumulative distribution function. For vegetative juvenility, g(.) was the logarithmic link function, and thus E(y|X, b₁, b₂) = g⁻¹(η) = exp(Xβ+Z₁b₁ +Z₂b₂), where exp denotes the exponential function. The choice of the probit link function for seedling survival was based on the conclusions obtained by Hahn and Soyer (2005) with a random-intercept GLMM [i.e., akin to the model described in Equation (2)]. Previous GLMM analyses conducted separately in each population showed that the variance of the Pearson residuals was close to one for seedling survival, but was clearly smaller than one for vegetative juvenility, thus indicating that the GLMM for the latter trait was under-dispersed relative to the Poisson distribution. Consequently, as an alternative to the standard Poisson model, we used a quasi-Poisson GLMM for vegetative juvenility, under which the equi-dispersion assumption can be relaxed (Wedderburn, 1974; Gardner et al., 1995). The quasi-Poisson GLMM considered heterogeneity of dispersion effects at the population level, and further details are provided in Supplementary Methods 2.

Parameter estimation under the GLMMs fitted for the discrete variables was based on the residual pseudo-likelihood (RSPL) method, which enables extension of the concept of REML variance component estimation to the non-normal case (Wolfinger and O’Connell, 1993). Estimates of β were obtained by generalized least-squares, and the KR approximations described above were used to improve the model-based standard errors of $\widehat{\mathit{\beta }}$ and the statistical inference concerning fixed-effect model terms. For conditions covering those in the current study (i.e., sample sizes, survival prevalence, and mean vegetative juvenility), simulation work with cross-sectional clustered data indicated that RSPL together with the KR adjustments performed better than maximum likelihood (ML) methods, regarding the accuracy of estimates of the random-intercept variance (e.g., family variance) and the coverage of fixed-effect confidence intervals for binary and count variables (McNeish, 2016, 2019; see also Supplementary Methods 1).

Results from F-tests indicated that the fixed-effect term for the population-by-block interaction was significant (p < 0.05) for seedling survival, but not for vegetative juvenility; thus, the interaction term was excluded in a final GLMM for the latter trait only. The population LS-Mean for a variable was estimated on the linked scale by $\mathbf{\text{L}}\widehat{\mathit{\beta }}$ and then converted to the original scale via the inverse link transformation. The standard error of a LS-Mean on the original scale was approximated by $\varphi (\mathbf{\text{L}}\widehat{\mathit{\beta }}).\mathrm{stde}(\mathbf{\text{L}}\widehat{\mathit{\beta }})$ and $\mathit{exp}(\mathbf{\text{L}}\widehat{\mathit{\beta }}).\mathrm{stde}(\mathbf{\text{L}}\widehat{\mathit{\beta }})$ for seedling survival and vegetative juvenility, respectively, where: $\varphi (\mathbf{\text{L}}\widehat{\mathit{\beta }})$ is the probability density function of the standard normal distribution evaluated at $\mathbf{\text{L}}\widehat{\mathit{\beta }}$; and $\mathrm{stde}(\mathbf{\text{L}}\widehat{\mathit{\beta }})$ is the estimated standard error of the LS-Mean on the linked scale. The 95% confidence interval of a LS-Mean on the original scale was obtained by applying the inverse link transformation to the confidence limits on the linked scale.

Under the RSPL method, the absence of a true log-likelihood function for the overall optimization process precludes the comparison of nested models using likelihood ratio tests (e.g., Hedeker and Gibbons, 2006; McNeish, 2016). Nevertheless, for comparison with RSPL estimates, family variances were also estimated for seedling survival and vegetative juvenility using ML, which enabled their statistical significance to be assessed by one-sided likelihood ratio tests. In this context, the Conway-Maxwell Poisson (CMP) distribution was assumed in the GLMM fitted for vegetative juvenility, since the estimation of a R-side multiplicative dispersion parameter as in the quasi-Poisson model (see Supplementary Methods 2) is not permitted with ML methods (e.g., Capanu et al., 2013). The CMP distribution is a two-parameter generalized form of the Poisson distribution that allows the modeling of empirical distributions of count variables that are over- or under-dispersed relative to the Poisson distribution (Shmueli et al., 2005; Guikema and Goffelt, 2008). Details on the parameterization of the CMP distribution, and on the GLMM for joint modeling the mean response and dispersion of vegetative juvenility, are given in Supplementary Methods 3. The GLMM fitted for seedling survival was defined as in Equation (2). ML estimation of the model parameters was based on an adaptive Gaussian quadrature, which entails a numerical integration method to approximate the marginal log-likelihood of the data (Pinheiro and Bates, 1995); 10 quadrature points were used to integrate the likelihood function over the random-effects distribution.

For both the LMMs and GLMMs, the intra-class correlation (ICC) coefficient was calculated as the proportion of the total variance attributable to the family variance, and thus was used to measure the relative importance of the family variance for each variable. In particular, for vegetative juvenility and seedling survival, the ICCs were estimated as described by Nakagawa et al. (2017) (see Supplementary Methods 4).

Analysis of Phenotypic Selection

In the present study, we focused on the estimation of linear selection gradients to measure the direction and strength of directional selection acting on traits in each population, and then we evaluated the difference between populations in selection gradient estimates for a given trait. The analysis of phenotypic selection assessed the fitness consequences of variation in four traits—lamina length, leaf shape index, adjusted lignotuber size and vegetative juvenility—using seedling survival as a fitness component. In addition to the target traits, seedling height and stem diameter were modeled as “nuisance variables.” Prior to analyses, the data were pre-processed as follows: (i) linear least-squares regression was used to pre-adjust lamina width and lignotuber diameter in a population for seedling differences in lamina length and stem diameter, respectively, and the adjusted observations (obtained from the regression residuals) were then mean standardized—these data thus refer to leaf shape index and adjusted lignotuber size; and (ii) the remaining variables were centered at their means and then mean-standardized in a population. Mean standardization has been suggested for comparing the strengths of selection estimates on a similar scale (Hereford et al., 2004), and scaling in relation to the mean is both permissible and meaningful for the independent variables used in the current analysis (Houle et al., 2011).

The analysis of phenotypic selection was undertaken separately in each population, with the GLMM fitted for seedling survival including: a vector β with the intercept, block effects, and the linear regression coefficients for the focal and nuisance variables; and a vector b of random effects for families within the population, assuming b ∼ MVN(0, G), with G = ${\mathbf{\text{I}}}_q{\mathrm{\sigma }}_b^2$. Akin to the GLMM described in Equation (2), g(.) was the probit link function, and the model parameters were estimated by the RSPL algorithm.

As opposed to least-squares multiple regression, the marginal effect of a predictor variable (i.e., the partial effect of a unit change in the predictor on the probability of seedling survival) cannot be directly obtained from the estimates of β in the GLMM. In this context, for a focal variable, the directional selection gradient can be obtained from the average gradient of the estimated fitness surface, which can be approximated by averaging the slope of the fitness surface over the distribution of the phenotypic observations (Janzen and Stern, 1998; Morrissey and Sakrejda, 2013). This procedure was undertaken as follows: (i) the marginal effect at each observation point in the data was estimated for a given focal variable; (ii) the estimated marginal effects were averaged over all observations in a population; and (iii) the average of the marginal effects was standardized to the relative fitness scale (i.e., division by the population mean of seedling survival), yielding a measure that can be quantitatively interpretable as a selection gradient. Following these sequential steps, Supplementary Methods 5 provides the methodological details used to obtain directional selection gradients, based on the model parameters estimated from the random-intercept GLMM fitted to the data of a given population. The resulting selection gradient estimates have a population-averaged interpretation (see Supplementary Methods 5), although this does not apply to the estimates of β from the GLMM, which have a conditional interpretation (e.g., Molenberghs et al., 2002; Gardiner et al., 2009; McNeish, 2016; see also Supplementary Methods 7).

Non-parametric bootstrap was used to obtain standard errors and 95% confidence intervals for the directional selection gradient estimates in a population, and for their differences between populations for a trait. Bootstrap samples were generated while preserving the conditional independence of seedlings within families. Further details on this procedure, and on the estimation of standard errors and 95% confidence intervals, are given in Supplementary Methods 6. Statistical support against a null hypothesis being true (i.e., against the absence of an effect for either a selection gradient in a population or its difference between populations) was provided by a 95% confidence interval not overlapping with zero. Although directional selection was the main focus of the current study, we also computed 95% confidence intervals from bootstrapping for quadratic and correlational selection gradients (with their estimation based on second derivatives approximated at each observation by second-order central finite differences; e.g., see Supplemental File, point 8.4, in Franklin and Morrissey, 2017). As these confidence intervals overlapped with zero, the effects of non-linear selection were judged to be unimportant, and they will not be further considered here.

Results

A diagrammatic summary of the overall results is provided in Figure 1. Table 2 presents the estimates of LS-Means, and related results from statistical tests of the population effect, for four functional traits and the fitness component, measured in the mesic (Brushy Lagoon) and dry (Ross) populations. Results from statistical inference about all the fixed-effect model terms included in the final LMMs and GLMMs fitted to the continuous and discrete variables are shown in Supplementary Tables 1, 2, respectively. When compared to the mesic population, the LS-Means in the dry population were lower for lamina length, and higher for leaf shape index, adjusted lignotuber size and vegetative juvenility. Population-mean differences were statistically significant at the 0.1% (lamina length, adjusted lignotuber size, and vegetative juvenility) and 1% (leaf shape index) significance levels for the functional traits. The LS-Means for the probability of seedling survival were similar in the mesic and dry populations, and not statistically different (p > 0.05). For discrete variables (vegetative juvenility and seedling survival), LS-Means based on the conditional fixed-effect coefficients from the GLMM (as presented in Table 2) were similar to corresponding estimates calculated from fixed-effect coefficients with a marginal (i.e., population-averaged) interpretation (see Supplementary Methods 7).

FIGURE 1

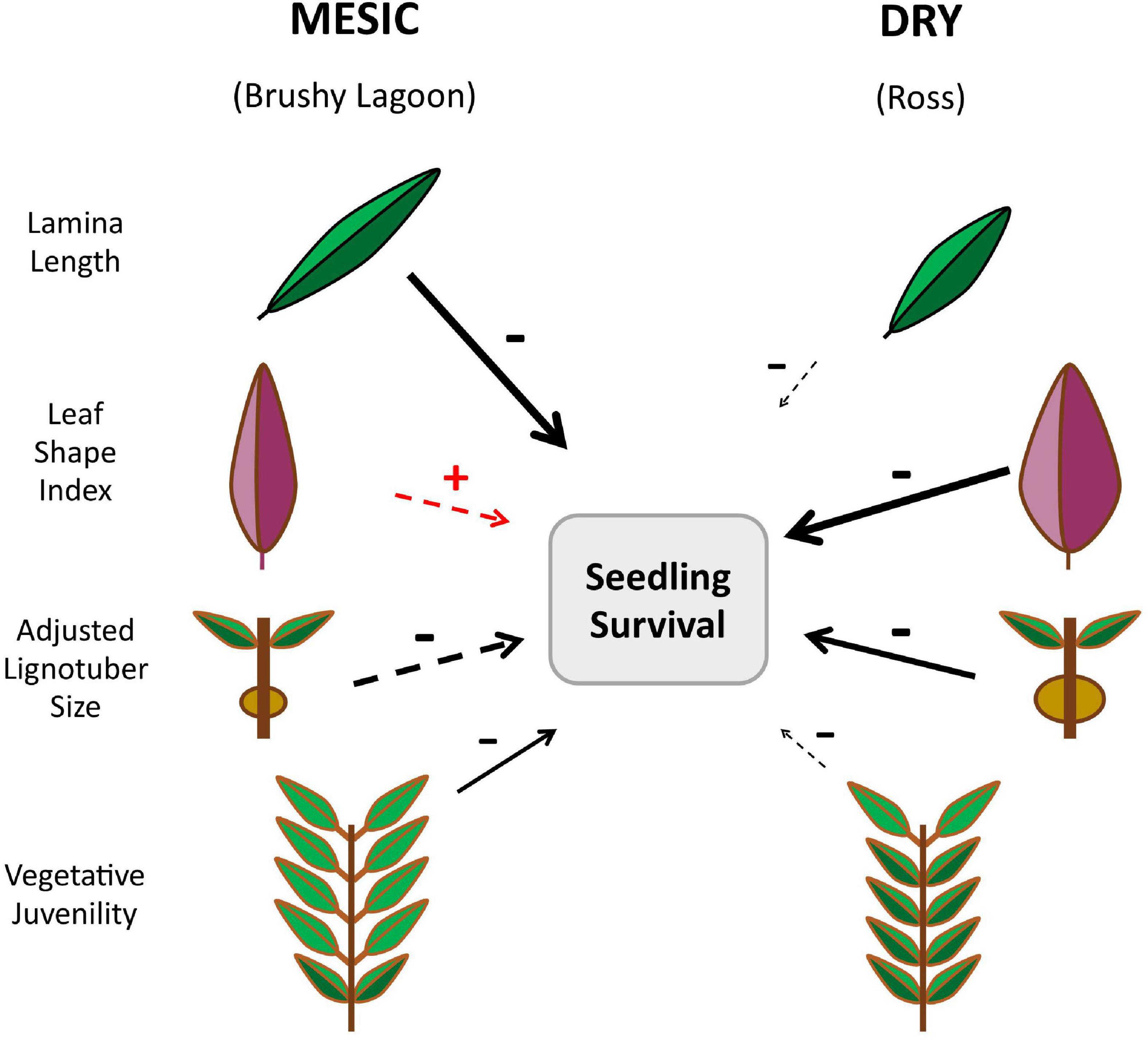
Figure 1. Infographic summarizing the differences between the mesic (Brushy Lagoon) and dry (Ross) populations of Eucalyptus pauciflora for the least-squares means and directional selection gradients estimated for four seedling functional traits. Population-mean differences were statistically significantly (p < 0.01) for all focal traits assessed (Table 2). The directional selection gradient estimates for each population are symbolized by the arrows, which refer to the partial linear effect of a focal trait on seedling canopy (relative) survival evaluated after 67 days of dry-down. The increasing length and width of the arrows is indicative of increasing strength of the directional selection gradient estimates, and their directionality is shown by the +/− signs. In addition, a solid arrow indicates that the bootstrapped 95% confidence interval (CI) for the selection gradient estimate did not overlap with zero, providing statistical support against the null hypothesis of no effect on relative seedling survival (Table 5). A dashed arrow signifies that the bootstrapped 95% CI for the selection gradient estimate overlapped with zero, being indicative of no statistical support for the existence of fitness consequences of variation in the trait. The strong negative selection gradient estimated for lamina length in the mesic population suggests that a future occurrence of severe drought in the wild will shift the mean of the trait in the mesic population toward that of the dry population. The negative selection gradient estimated for adjusted lignotuber size in both populations suggests an early age trade-off between drought damage and recovery traits, with the canopies of phenotypes which develop larger lignotubers at the seedling stage being more susceptible to drought death.

TABLE 2

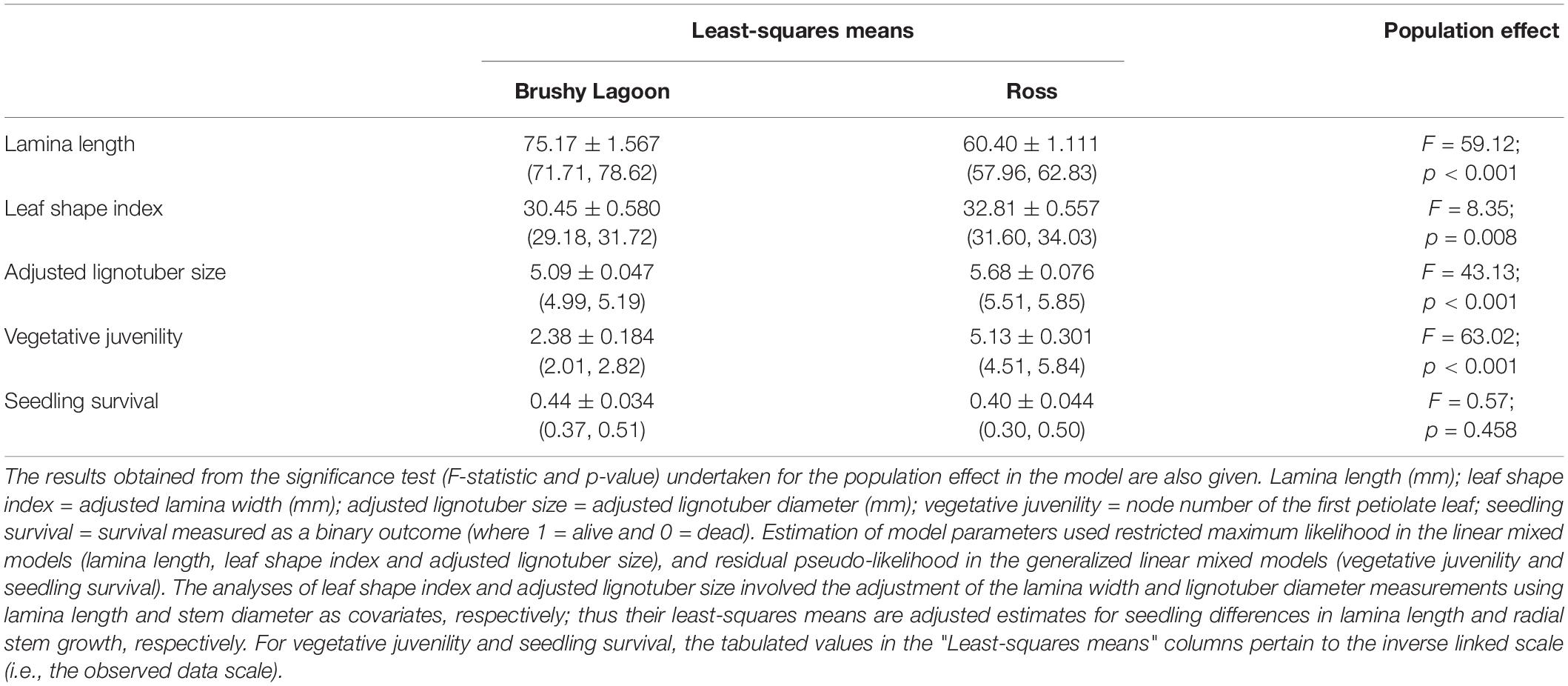
Table 2. Estimates of least-squares means and their standard errors (with 95% confidence intervals within parentheses) for four functional traits (lamina length, leaf shape index, adjusted lignotuber size and vegetative juvenility) and a fitness component (seedling survival) measured in the mesic (Brushy Lagoon) and dry (Ross) populations of E. pauciflora.

REML estimates of family and residual variances are shown in Table 3 for the continuous variables. Based on one-sided likelihood ratio tests, statistically significant (p < 0.05) family variance estimates were found for lamina length, leaf shape index and adjusted lignotuber size in both populations, suggesting significant genetic variation within each population for these traits. The proportion of the total variation explained by the family variance (i.e., ICC) was ≈ 0.2 for lamina length and leaf shape index, but lower for adjusted lignotuber size (i.e., 0.03 and 0.07 in Brushy Lagoon and Ross, respectively; Table 3). Two-sided likelihood ratio tests undertaken to evaluate whether residual variances differed between populations indicated significant variance heterogeneity for lamina length and adjusted lignotuber size (p < 0.001), but not for leaf shape index (p > 0.05). In addition, for the difference between populations in family variances, two-sided likelihood ratio tests did not indicate significant variance heterogeneity at the 5% significance level for any of the traits. However, the latter results may reflect the lack of statistical power to detect variance heterogeneity (see also below) for some traits, given that family variance estimates differed between populations by a factor of two for lamina length and three for adjusted lignotuber size (Table 3).

TABLE 3

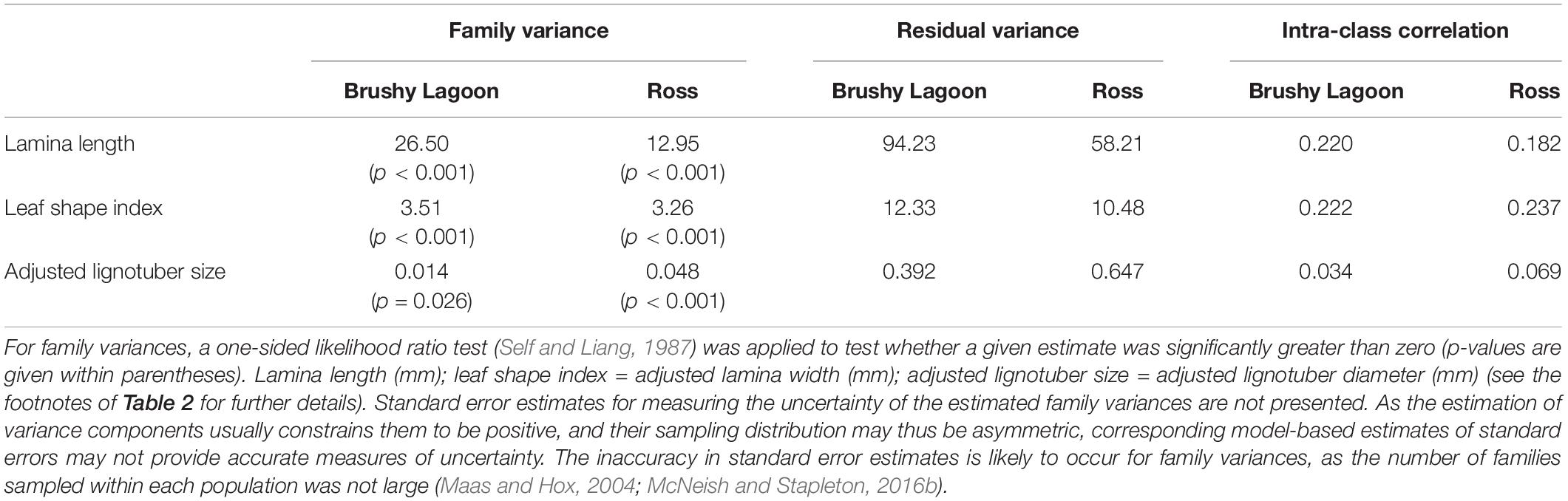
Table 3. Family and residual variances estimated by restricted maximum likelihood (REML), and estimates of intra-class correlation (ICC) coefficients, for continuous variables (lamina length, leaf shape index and adjusted lignotuber size) measured in the mesic (Brushy Lagoon) and dry (Ross) populations of E. pauciflora.

Table 4 provides the family variances estimated by RSPL and ML for the discrete variables. The ML estimates of family variances were noticeably smaller than their counterparts estimated by RSPL: for Brushy Lagoon and Ross, the differences of the ML estimates relative to the RSPL estimates were 33 and 18% for vegetative juvenility, and 16 and 11% for seedling survival (Table 4). Although the true parameter values are not known, these results are consistent with the downward finite-sample bias that may emerge for ML estimates of variance components in GLMMs with discrete variables when the number of clustering units is not large (see references in Supplementary Methods 1). RSPL estimates of family variances were thus considered to be more accurate than their ML counterparts, given that simulation studies (e.g., McNeish, 2016, 2019) using sample sizes comparable to the number of families and their sizes in the current study indicated substantial downward bias in ML estimates of variances for the random-intercept term, and no evidence of noticeable bias for corresponding RSPL estimates. Underestimation of variances will also lead to underestimation of standard errors for fixed-effect parameters, which may result in less conservative hypothesis tests for fixed-effect model terms. Nevertheless, for the examined vegetative juvenility and seedling survival data, the method to estimate model parameters was inconsequential regarding conclusions on the statistical significance of the population effect (although the F-value increased under ML estimation, particularly for vegetative juvenility; Supplementary Table 2).

TABLE 4

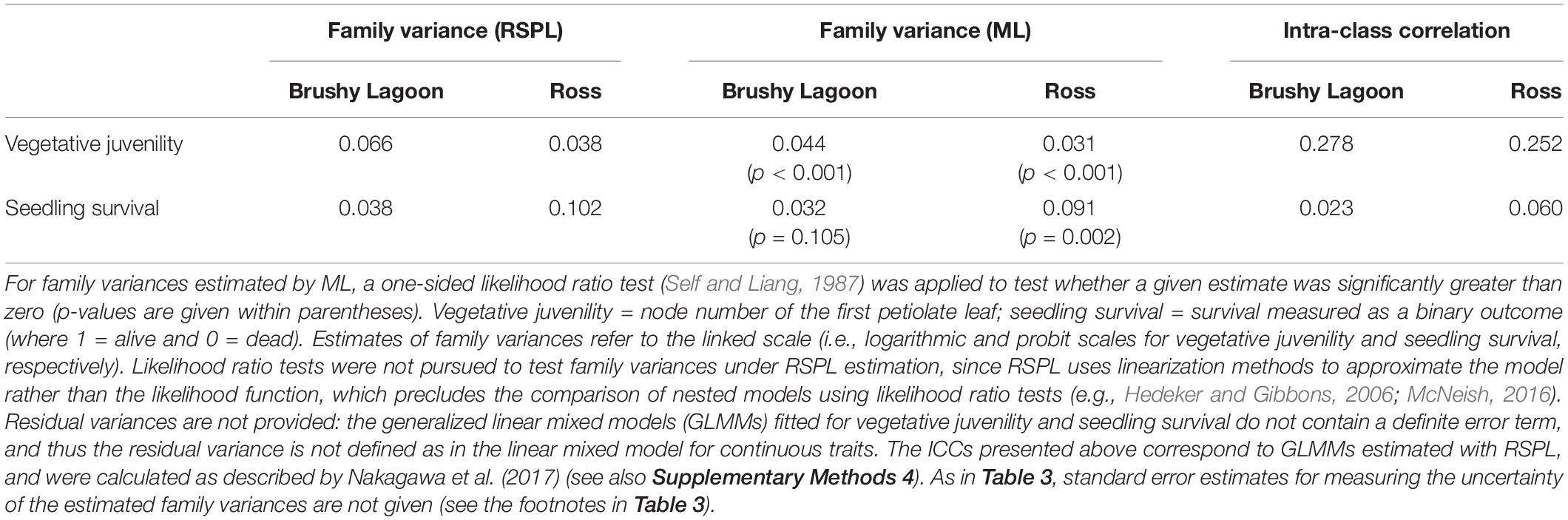
Table 4. Family variances estimated by residual-pseudo likelihood (RSPL) and maximum likelihood (ML), and estimates of intra-class correlation (ICC) coefficients, for discrete variables (vegetative juvenility and seedling survival) measured in the mesic (Brushy Lagoon) and dry (Ross) populations of E. pauciflora.

Based on RSPL estimates of family variances, the ICC ranged from 0.25 to 0.28 for vegetative juvenility, and from 0.02 to 0.06 for seedling survival (Table 4). As RSPL applies linearization methods to approximate the model rather than the likelihood function, ML estimates were used to conduct one-sided likelihood ratio tests for family variances of vegetative juvenility and seedling survival. These tests detected statistically significant (p < 0.05) family variance estimates (and thus genetic variation) for vegetative juvenility in both populations, but only in Ross for seedling survival (Table 4). However, for seedling survival in Brushy Lagoon, the likelihood ratio test is likely to have a low statistical power: with our family sizes, the number of families would need to be larger for detecting a non-null family variance, as suggested by simulation work with binary variables and weak ICCs (Austin and Leckie, 2018). Lack of statistical power may also have affected two-sided likelihood ratio tests pursued to evaluate whether family variances differed between populations, as variance heterogeneity was not found to be statistically significant (p > 0.05), despite the ≈ three times difference between populations in family variances for seedling survival (Table 4). Conversely, under a GLMM using a CMP distribution for vegetative juvenility, two-sided likelihood ratio tests indicated statistically significant (p < 0.001) heterogeneity between populations in dispersion of the observations (see footnotes of Supplementary Table 2).

Table 5 shows the estimates of directional selection gradients and their population differences for the focal functional traits. For Brushy Lagoon, statistical support against the null hypothesis of no effect on relative fitness (i.e., as indicated by a 95% confidence interval not overlapping with zero) was found for the selection gradients of lamina length and vegetative juvenility, with directional selection favoring seedlings exhibiting lower values in these traits (i.e., a decrease of 1% from the mean of lamina length and vegetative juvenility was expected to increase relative fitness by 1.5 and 0.3%, respectively). For Ross, statistical support for the existence of fitness consequences of variation in the traits was provided for the selection gradients of leaf shape index and adjusted lignotuber size, indicating directional selection favoring phenotypes with lower values in these traits (i.e., an increase in 1.2 and 0.9% in relative fitness was expected from decreasing leaf shape index and adjusted lignotuber size by 1% from their means, respectively). Statistical support for the difference between populations in directional selection was observed in the selection gradient estimates for lamina length and leaf shape index, but not for adjusted lignotuber size and vegetative juvenility. Similar conclusions regarding the potential importance of directional selection acting on the traits within populations, and its difference between populations for a trait, were indicated from formal statistical inference about parameter estimates (on the probit scale) obtained from a GLMM fitted for data of the two populations combined (Supplementary Table 3).

TABLE 5

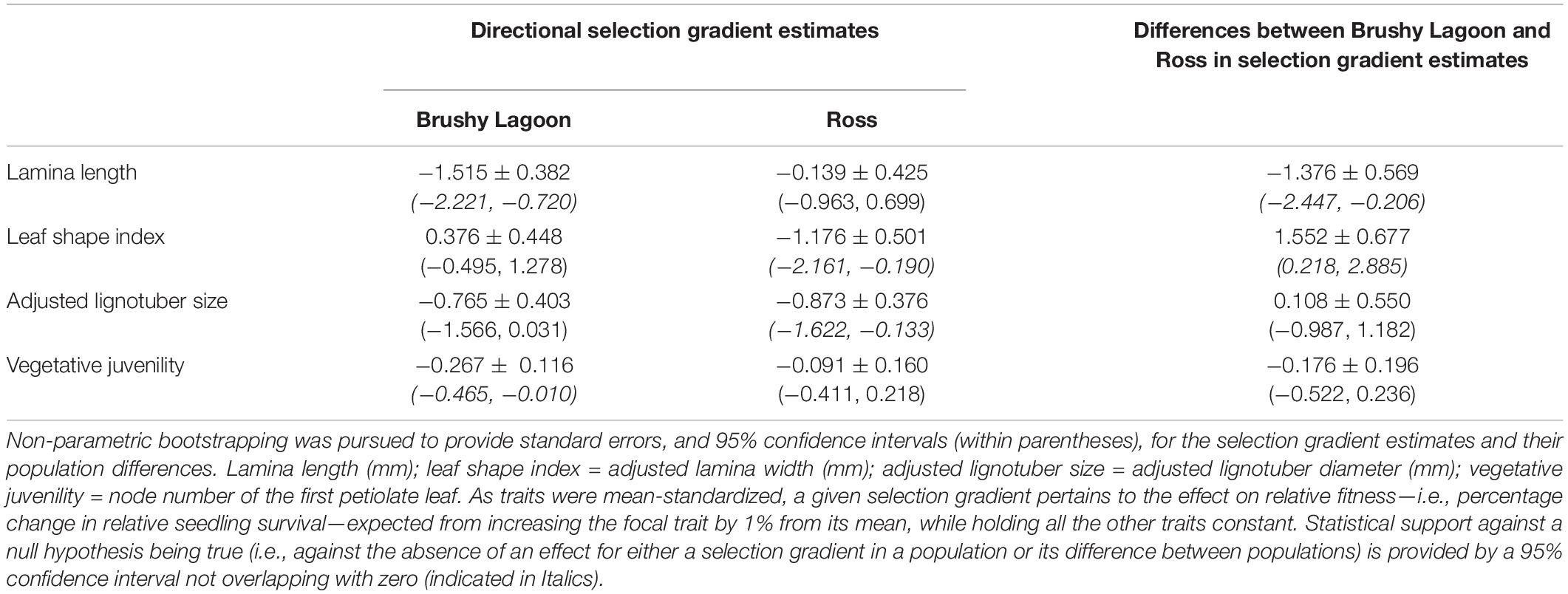
Table 5. Estimates of directional selection gradients, and their population differences, for four functional traits (lamina length, leaf shape index, adjusted lignotuber size and vegetative juvenility) measured in the mesic (Brushy Lagoon) and dry (Ross) populations of E. pauciflora.

Discussion

This study identified significant functional trait differences and differing acute drought-induced phenotypic selection gradients between two populations from contrasting environments of the forest tree E. pauciflora (summarized in Figure 1). Significant genetic variation within populations, and significant mean differences between populations in all four focal traits studied suggest adaptive differences between the mesic and dry populations. While seedling survival did not differ between the two populations, when subject to acute drought stress, the traits under phenotypic selection varied between populations, suggesting different response strategies. Statistical support for the presence of fitness consequences of variation in the focal traits was detected for all traits in one or other population, but only one trait—lamina length—exhibited a pattern of directional selection consistent with a shift in the mean of the mesic population toward that of the dry population following acute drought stress. Further, we provide evidence suggesting an early age trade-off between drought susceptibility and a recovery trait, with seedlings which develop larger lignotubers being more susceptible to drought death. Such trade-offs may have contributed to the observed similar population survival, despite the marked population differentiation in seedling traits.

Genetic variation within, and marked mean differences between, the mesic and dry populations for all four focal traits suggest adaptive differences between these populations, with seedlings of the dry population having on average smaller and broader leaves, longer vegetative juvenility, and larger lignotuber size than the mesic population. The mesic and dry populations compared were selected to accentuate rainfall differences and minimize the differences in other environmental factors. Accordingly, we expect that the observed population differences in the four functional traits reflect historic natural selection and adaptation to differences in water availability. Lamina length was strongly positively related to leaf area (r = 0.88, n = 380; unpublished data) and, as a surrogate of leaf size, its observed reduction in the dry population, for example, accords with the trait-environment associations reported in other Eucalyptus species (McLean et al., 2014). It is also consistent with species-level trends in south-eastern Australia, where species occurring in low rainfall areas tend to have smaller leaves through various changes in leaf length and width (McDonald et al., 2003). The longer vegetative juvenility observed in seedlings from the dry population also accords with the broader trends observed in a previous glasshouse trial with 37 E. pauciflora populations, where seedling vegetative juvenility was retained longer in populations from drier home-sites (Gauli et al., 2015; Costa e Silva et al., 2019). In this range-wide trial, the trait assessed was the percentage of nodes with petiolate leaves, which is negatively related to our measure of juvenility used in the present study. The difference between the dry and mesic populations is also consistent with trends in the E. risdonii/tenuiramis complex, where the retention of sessile juvenile leaves is extreme (into the reproductive stage) in populations from hot and dry environments (Costa e Silva et al., 2018). Populations of eucalypt species from hot/dry environments also have larger lignotubers than populations from mesic environments (Ladiges, 1974; Walters et al., 2005; Costa e Silva et al., 2019), as evident in our comparison.

Despite mean differences between the mesic and dry populations in putatively adaptive traits, the two populations did not differ significantly in survival following acute drought stress as induced in our dry-down experiment (Table 2). However, the two populations varied in the traits detected to be under directional selection, indicating that differences between the populations reside in the manner they selectively respond rather than in overall fitness under acute drought stress. Significant genetic-based family variance in survival was detected within the dry population, together with directional selection toward narrower leaves (smaller leaf shape index) and smaller lignotubers under acute drought stress. In contrast, no statistically significant family variance in survival was detected in the mesic population, and acute drought stress favored smaller leaf area (through shorter leaves) and earlier vegetative maturation (earlier development of petiolate leaves). However, statistical support for an important difference between the dry and mesic populations in directional selection gradients was provided for lamina length and leaf shape index only. For a given trait, the population difference in the directional selection gradients could in part be due to a difference between populations in the phenotypic variance (Steele et al., 2011; De Lisle and Svensson, 2017). This would particularly apply to lamina length, where the statistical support for a difference between populations in directional selection (Table 5) could, to some extent, reflect a stronger selection in the more variable population (i.e., Brushy Lagoon; Table 3). Alternatively, the strength and direction of directional selection can be a function of the deviation of the population mean phenotype from the optimal phenotype for the environment (Steele et al., 2011; Hendry, 2017, p. 88). Regardless of the cause, given the significant genetic variation detected for all functional traits within each population (family variances in Tables 3, 4), evolutionary change would be expected in these traits following the observed directional selection acting on them (Lande, 1979; Lande and Arnold, 1983).

The directional selection observed in lamina length, reflecting leaf area, is consistent with the hypothesis that the initial trait difference between the two populations could reflect, at least in part, the effects of past natural selection on the trait to reduce seedling susceptibility to events of acute drought stress. However, with drought risk likely to increase in the wild with climate change (and thus with more frequent episodes of severe drought), the direction and strength of the selection gradient estimates in the dry-down experiment suggest that, in the future, directional selection would shift the mean lamina length of the mesic population toward that of the dry population. A reduction in leaf area may also underlie directional selection favoring narrower leaves within the dry population (i.e., smaller leaf shape index) in the dry-down experiment. As noted above, reducing leaf area is well-recognized as an adaptation to drier conditions. In dry environments, selection has been shown to favor smaller leaves (Dudley, 1996; Ramírez-Valiente and Cavender-Bares, 2017). Smaller leaves may facilitate adaptation to drier conditions via greater main vein density reducing hydraulic vulnerability (Scoffoni et al., 2011) or through having a thinner boundary layer of still air allowing better heat shedding than larger leaves, and thus reducing the need for transpiration and associated water loss to shed heat (McDonald et al., 2003). As also mentioned above, the difference between the two populations in directional selection for a trait could reflect adaptation to different trait optima. For example, selection for narrower leaves, but not shorter leaves, in the dry population may be due to the already shorter leaves of this population being close to a phenotypic optimum, and thus only the variation in leaf shape index would determine selection mediated by seedling survival. In Quercus, narrow leaves were favored in a dry year but not in a wet year, although a statistically significant year-by-trait interaction could not be detected (Ramírez-Valiente et al., 2015). However, there was evidence in the current study for an important difference between the mesic and dry populations in directional selection gradient estimates for leaf shape index. In a species-level study in south-eastern Australia, combinations of reductions in leaf width in addition to leaf length were responsible for a reduction in leaf area in low rainfall areas (McDonald et al., 2003).

The selection gradient estimates for lignotuber size showed an opposite trend to what would be expected if the differences between the mesic and dry population means were the result of differences in adaptation arising from past natural selection to reduce susceptibility to acute drought stress. The dry population had larger lignotubers than the mesic population, but experienced directional selection in favor of seedlings with smaller lignotubers, shifting its mean toward the more mesic population. The same trend in directional selection, toward smaller lignotubers, was evident in the mesic population, but without statistical support for an important effect on seedling survival (as evaluated based on seedling canopy mortality). Susceptibility to drought damage and recovery can be considered as genetically different “traits” in eucalypts (Ammitzboll et al., 2020). While our unexpected finding is consistent with lignotubers having a key role in drought recovery, it signals a cost to their development. Such cost suggests a resistance vs. tolerance trade-off, common in the evolution of adaptations to periodic strong selection events arising from biotic (Best et al., 2008; Moreira et al., 2014) and abiotic (Vesk and Westoby, 2003; Agrawal et al., 2004; Ramírez-Valiente and Cavender-Bares, 2017) stress. In the present case, the observed cost may be transient and only evident at this early seedling stage (Orians et al., 2010; Hoque and Avila-Sakar, 2015), or persist through the life-cycle but out-weighed by the benefits of the better development of a recovery organ and gains in tolerance.

Lignotubers are generally considered a store of non-structural carbohydrates and dormant buds to enable basal re-sprouting following the death of the main stem (Walters et al., 2005; Borzak et al., 2016; Ammitzboll et al., 2020). If the main stem is not severely damaged, it is also possible that re-allocation of non-structural carbohydrates, such as starch, may help recover hydraulic function or photosynthetic activity (as suggested in Costa e Silva et al., 2019). However, the lignotuber does not appear to be an organ particularly specialized for the storage of non-structural carbohydrates such as starch, and likely serves primarily as a bud bank (Carrodus and Blake, 1970; Smith et al., 2018). The fact that selection favored smaller lignotuber sizes in the arid population under acute drought stress suggests that there is a cost associated with the early allocation of seedling resources to the development of this recovery organ. Non-structural carbohydrates support respiration and growth when photosynthesis is reduced during periods of water stress to avoid transpiration (McDowell et al., 2011; Mitchell et al., 2013). If the ready availability of non-structural carbohydrates is reduced due to resources being allocated to the lignotuber, or their storage within the lignotuber, then seedlings with larger lignotubers may be more susceptible to “carbon starvation” during prolonged water stress, and thus death of the seedling canopy. Lignotubers themselves have also been reported to have smaller and contorted vessels compared to those in the stems, and their resistance to water flow may be twice that of the stem (Myers, 1995). An alternative cause of drought-induced selection favoring small lignotubers may thus relate to their offering less resistance to water flow between the roots and the stem. Regardless of the cause, with the arid population having significantly larger lignotubers than the mesic population, a trade-off between avoiding susceptibility to drought damage at the seedling stage vs. future seedling recovery could contribute to the absence of population differences in survival following the acute drought stress imposed. Indeed, with the evaluation of survival based on seedling canopy mortality at the termination of the experiment, re-watering and evaluation of recovery (Lu et al., 2010; Zhang et al., 2017; Ruehr et al., 2019) may well have provided the conditions under which population differences become manifest.

Drought-induced directional selection was found to favor early loss of vegetative juvenility in the mesic population, but had no effect on this trait in the dry population. There was thus no evidence from our phenotypic selection analysis that adaptation to acute drought stress would delay the development of the petiolate leaf in seedlings of the mesic population, and thus would shift the mean vegetative juvenility of the mesic population toward that of the dry population. Using growth performance as a fitness proxy, Costa e Silva et al. (2019) found no association between family-level variation in seedling juvenility and the fitness proxy in a E. pauciflora common-garden field trial established on a dry site, which is consistent with the results currently obtained in the dry population. In contrast, a common-garden trial of populations from the E. risdonii/tenuiramis complex established on a wet site showed that directional selection favored phenotypes with early ontogenetic transition to the petiolate “adult” leaf (Costa e Silva et al., 2018). This finding is consistent with the selection gradient estimate for vegetative juvenility in the mesic population. However, environmental context is important to the interpretation of trait-fitness relationships (MacColl, 2011), and this result from a wet site does not explain why such selection should also occur under acute drought stress.

Translating results of phenotypic selection analysis into mechanistic responses can be challenging (Wade and Kalisz, 1990; MacColl, 2011; Kingsolver et al., 2012). Whilst all four focal traits showed evidence of directional selection associated with acute drought stress in one or other of the tested populations, it is possible that selection on a measured trait may occur via indirect selection acting on unmeasured traits, correlated with the measured focal trait (Lande and Arnold, 1983; Mitchell-Olds and Shaw, 1987). Indeed, of the four traits studied, vegetative juvenility would be the one most likely to reflect indirect selection involving unmeasured (“hidden”) traits that could also influence seedling survival. While we assessed vegetative juvenility of the seedlings based on the node at which the first petiolate leaf was produced, this is potentially a surrogate for a wide range of physical, chemical and physiological changes that can occur, as documented in other eucalypt species (James and Bell, 2001; Borzak et al., 2015; Vlasveld et al., 2018; Lucani et al., 2019). It is therefore possible that the directional selection detected against vegetative juvenility in the mesic population could reflect indirect selection on a “hidden” (unmeasured) trait with a negative phenotypic correlation with vegetative juvenility. Nevertheless, it is also possible that there is direct phenotypic selection on the early development of the petiole, which is only manifest in the early maturing mesic population and could be specific to the timing of the onset of acute drought stress with respect to the seedling ontogeny. Such direct selection could, for example, relate to the enhanced potential for changing leaf orientation, a key trait affecting light interception and heat avoidance in eucalypts and facilitated by the petiole (Cameron, 1970; King, 1997; James and Bell, 2000).

Our selection analysis focused on survival of acute drought stress as evaluated based on seedling canopy mortality. However, historic adaptation to long-term dry environments may be expected to involve a complexity of different selection forces driving a suite of adaptive differences associated with water availability more generally, not only acute drought stress. From an evolutionary perspective, growth in water limited environments may require different adaptations to those involved in surviving periodic acute drought stress. Xylem embolism is believed to be a key cause of tree mortality under severe water stress (Urli et al., 2013; Brodribb, 2017; Choat et al., 2018), including eucalypts (Li et al., 2018), although long periods of water stress and a prolonged reduction in photosynthetic activity can also contribute to mortality through “carbon starvation” and susceptibility to biotic attack (Galiano et al., 2011; McDowell et al., 2011; Mitchell et al., 2013). These selective mechanisms are part of a broader suite of traits which control water uptake and loss (Li et al., 2018), the potential coordination of leaf and stem traits (Bourne et al., 2017) and the important role of recovery mechanisms in drought adaptation (Zeppel et al., 2015; Ruehr et al., 2019). The different roles of such factors in adaptation to acute vs. chronic water stress may have contributed to the absence of our population difference in the studied fitness component, despite differences in focal trait mean values. In particular, historic adaptation in the dry population may potentially involve selection favoring seedling traits, as well as adult traits, that enhance survival in water limited environments more so than survival during periodic acute drought stress.

Nevertheless, it is possible that population differences in fitness following acute drought stress do exist, but depend upon their pattern of acclimation (also referred to as pre-conditioning and priming—McDowell et al., 2008; Wang et al., 2017). Non-lethal water stress has been shown to result in marked metabolic changes in E. pauciflora seedlings with, for example, leaf carbohydrate concentrations increasing and contributing to osmotic adjustment (Warren et al., 2012). In other eucalypts, differential plastic pre-adjustments to water stress have already been described for functional traits at the species (Warren et al., 2011, 2012), provenance (Li et al., 2000; McLean et al., 2014) and genotype (Pita and Pardos, 2001) levels in Eucalyptus. Further, it is possible that population differences in susceptibility to drought may only be expressed following a specific type of drought, such as one which includes water limitation combined with high temperature stress (Groom et al., 2004; Mitchell et al., 2014). This is particularly relevant as our dry-down experiment was conducted over autumn, and the maximum daily temperature the seedlings experienced averaged only 16–17°C, and did not exceed 27°C on any one day. The capacity to adapt to acute drought stress is likely to become more important into the future, with predictions of increasing extreme climate events. The results of this study suggest that: firstly, there may be genetic variation available in the focal traits (i.e., depending on the extent of genetic constraints in determining adaptive evolution; e.g., Costa e Silva et al., 2020) upon which they can respond to selection; and secondly, that the traits under phenotypic selection may vary between populations, reflecting in part differing historic selection pressures and adaptations, but also indicating potential different acute drought response strategies that may occur under future changes in the climate.

Conclusion

In conclusion, our dry-down experiment revealed different traits under directional selection between the studied dry and mesic populations, despite no difference in overall seedling survival. These results highlight the complexity of drought adaptation and the potential role of different traits and strategies in responses to acute drought stress. Further work on more populations from a wider range of environments, as well as replicated populations within the same environment, would help elucidate the various response strategies of E. pauciflora to drought stress, including key traits and mechanisms in different environments. Similarly, a better understanding of interacting factors, such as heat and drought pre-conditioning, in determining the dry-down tolerance of plants is required. Ultimately, a greater understanding of the variation in traits under selection and potential mechanisms across environments will contribute to predictions of resilience, or vulnerability, of populations to future climate stress.

Data Availability Statement

The data upon which this research work is based is currently being used in another study, but can be requested from the corresponding author for consideration.

Author Contributions

JCS conceived and conceptualized the research question and analytical design, performed the data analyses, and prepared the associated document provided in Supplementary Material. Data for this study was collected from a dry-down experiment designed and undertaken by RJ, EP, and SMP. BMP and RJ were responsible for data scoring of the experiment and compiling the datasets used in the analyses. JCS, RJ, and BMP wrote the manuscript. All authors contributed to the manuscript revision, read, and approved the submitted version.

Funding

The contribution of JCS to this research work was supported by Fundação para a Ciência e a Tecnologia I.P. (FCT), Portugal, through the Norma Transitória DL 57/2016/CP1382/CT0008 and UID/AGR/00239/2019. This research was also funded by the Centro de Estudos Florestais, Portugal, a research unit that is funded by FCT (Unit Project Reference: UIDB/00239/2020). BMP acknowledges support of the Australian Research Discovery (ARC) grant DP190102053.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank and acknowledge Dorothy Steane’s contribution to the design and implementation of the dry-down experiment, and Tim Brodribb for helpful discussion. We also thank Paul Tilyard, Fiona Walsh, and Dale Worledge for assistance with running and scoring the dry-down experiment. We are grateful to all institutions mentioned for their financial support, which provided the opportunity to complete this study.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.722964/full#supplementary-material

References

Agrawal, A. A., Conner, J. K., and Stinchcombe, J. R. (2004). Evolution of plant resistance and tolerance to frost damage. Ecol. Lett. 7, 1199–1208. doi: 10.1111/j.1461-0248.2004.00680.x

CrossRef Full Text | Google Scholar

Aitken, S. N., Yeaman, S., Holliday, J. A., Wang, T., and Curtis-McLane, S. (2008). Adaptation, migration or extirpation: climate change outcomes for tree populations. Evol. Appl. 1, 95–111. doi: 10.1111/j.1752-4571.2007.00013.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Alberto, F. J., Aitken, S. N., Alía, R., González-Martínez, S. C., Hänninen, H., Kremer, A., et al. (2013). Potential for evolutionary responses to climate change–evidence from tree populations. Glob. Chang. Biol. 19, 1645–1661. doi: 10.1111/gcb.12181

PubMed Abstract | CrossRef Full Text | Google Scholar

Allen, C. D., Macalady, A. K., Chenchouni, H., Bachelet, D., McDowell, N., Vennetier, M., et al. (2010). A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manage. 259, 660–684. doi: 10.1016/j.foreco.2009.09.001

CrossRef Full Text | Google Scholar

Ammitzboll, H., Vaillancourt, R. E., Potts, B. M., Harrison, P. A., Brodribb, T., Sussmilch, F. C., et al. (2020). Independent genetic control of drought resistance, recovery, and growth of Eucalyptus globulus seedlings. Plant Cell Environ. 43, 103–115. doi: 10.1111/pce.13649

PubMed Abstract | CrossRef Full Text | Google Scholar

Austin, P. C., and Leckie, G. (2018). The effect of number of clusters and cluster size on statistical power and type I error rates when testing random effects variance components in multilevel linear and logistic regression models. J. Stat. Comput. Simul. 88, 3151–3163. doi: 10.1080/00949655.2018.1504945

CrossRef Full Text | Google Scholar

Bailey, T., Harrison, P., Davidson, N., Weller-Wong, A., Tilyard, P., Steane, D., et al. (2021). Embedding genetics experiments in restoration to guide plant choice for a degraded landscape with a changing climate. Ecol. Manage. Restor. (in press).

Google Scholar

Baldwin, S. A., and Fellingham, G. W. (2013). Bayesian methods for the analysis of small sample multilevel data with a complex variance structure. Psychol. Methods 18, 151–164. doi: 10.1037/a0030642

PubMed Abstract | CrossRef Full Text | Google Scholar

Battaglia, M., and Reid, J. (1993). The effect of microsite variation on seed-germination and seedling survival of Eucalyptus delegatensis. Aust. J. Bot. 41, 169–181. doi: 10.1071/BT9930169

CrossRef Full Text | Google Scholar

Best, A., White, A., and Boots, M. (2008). Maintenance of host variation in tolerance to pathogens and parasites. Proc. Natl. Acad. Sci. U.S.A. 105, 20786–20791. doi: 10.1073/pnas.0809558105

PubMed Abstract | CrossRef Full Text | Google Scholar

Borzak, C. L., Potts, B. M., Davies, N. W., and O’Reilly-Wapstra, J. M. (2015). Population divergence in the ontogenetic trajectories of foliar terpenes of a Eucalyptus species. Ann. Bot. 115, 159–170. doi: 10.1093/aob/mcu222

PubMed Abstract | CrossRef Full Text | Google Scholar

Borzak, C. L., Potts, B. M., and O’Reilly-Wapstra, J. M. (2016). Survival and recovery of Eucalyptus globulus seedlings from severe defoliation. For. Ecol. Manage. 379, 243–251. doi: 10.1016/j.foreco.2016.08.025

CrossRef Full Text | Google Scholar

Bourne, A. E., Creek, D., Peters, J. M. R., Ellsworth, D. S., and Choat, B. (2017). Species climate range influences hydraulic and stomatal traits in Eucalyptus species. Ann. Bot. 120, 123–133. doi: 10.1093/aob/mcx020

PubMed Abstract | CrossRef Full Text | Google Scholar

Brodribb, T. J. (2017). Progressing from ‘functional’ to mechanistic traits. New Phytol. 215, 9–11. doi: 10.1111/nph.14620

PubMed Abstract | CrossRef Full Text | Google Scholar

Brunner, A. M., Varkonyi-Gasic, E., and Jones, R. C. (2016). “Phase change and phenology in trees,” in Plant Genetics and Genomics: Crops and Models, Vol. 21, eds A. Groover and Q. Cronk (Cham: Springer), 227–274.

Google Scholar

Buotte, P. C., Hicke, J. A., Preisler, H. K., Abatzoglou, J. T., Raffa, K. F., and Logan, J. A. (2016). Climate influences on whitebark pine mortality from mountain pine beetle in the greater yellowstone ecosystem. Ecol. Appl. 26, 2507–2524. doi: 10.1002/eap.1396

PubMed Abstract | CrossRef Full Text | Google Scholar

Cameron, R. (1970). Light intensity and the growth of Eucalyptus seedlings. I. Ontogenetic variation in E. fastigata. Aust. J. Bot. 18, 29–43.

Google Scholar

Cano, F. J., López, R., and Warren, C. R. (2014). Implications of the mesophyll conductance to CO2 for photosynthesis and water-use efficiency during long-term water stress and recovery in two contrasting Eucalyptus species. Plant Cell Environ. 37, 2470–2490. doi: 10.1111/pce.12325

PubMed Abstract | CrossRef Full Text | Google Scholar

Capanu, M., Gönen, M., and Begg, C. B. (2013). An assessment of estimation methods for generalized linear mixed models with binary outcomes. Stat. Med. 32, 4550–4566. doi: 10.1002/sim.5866

PubMed Abstract | CrossRef Full Text | Google Scholar

Carrodus, B. B., and Blake, T. J. (1970). Studies on the lignotubers of Eucalyptus obliqua L’Heri. New Phytol. 69, 1069–1072.

Google Scholar

Chen, I.-C., Hill, J. K., Ohlemüller, R., Roy, D. B., and Thomas, C. D. (2011). Rapid range shifts of species associated with high levels of climate warming. Science 333, 1024–1026. doi: 10.1126/science.1206432

PubMed Abstract | CrossRef Full Text | Google Scholar

Choat, B., Brodribb, T. J., Brodersen, C. R., Duursma, R. A., López, R., and Medlyn, B. E. (2018). Triggers of tree mortality under drought. Nature 558, 531–539. doi: 10.1038/s41586-018-0240-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Corney, S., Katzfey, J., McGregor, J., Grose, M., Bennett, J., White, C., et al. (2010). Climate Futures for Tasmania: Climate Modelling Technical Report. Hobart, TAS: Antartic Climate & Ecosystem CRC.

Google Scholar

Costa e Silva, J., Hardner, C., Tilyard, P., and Potts, B. M. (2011). The effects of age and environment on the expression of inbreeding depression in Eucalyptus globulus. Heredity 107, 50–60. doi: 10.1038/hdy.2010.154

PubMed Abstract | CrossRef Full Text | Google Scholar

Costa e Silva, J., Harrison, P. A., Wiltshire, R., and Potts, B. M. (2018). Evidence that divergent selection shapes a developmental cline in a forest tree species complex. Ann. Bot. 122, 181–194. doi: 10.1093/aob/mcy064

PubMed Abstract | CrossRef Full Text | Google Scholar

Costa e Silva, J., Potts, B., Harrison, P. A., and Bailey, T. (2019). Temperature and rainfall are separate agents of selection shaping population differentiation in a forest tree. Forests 10:1145. doi: 10.3390/f10121145

CrossRef Full Text | Google Scholar

Costa e Silva, J., Potts, B. M., and Harrison, P. A. (2020). Population divergence along a genetic line of least resistance in the tree species Eucalyptus globulus. Genes 11:1095.

Google Scholar

Davis, M. B., and Shaw, R. G. (2001). Range shifts and adaptive responses to quaternary climate change. Science 292, 673–679.

Google Scholar

De Lisle, S. P., and Svensson, E. I. (2017). On the standardization of fitness and traits in comparative studies of phenotypic selection. Evolution 71, 2313–2326. doi: 10.1111/evo.13325

PubMed Abstract | CrossRef Full Text | Google Scholar

Dillon, S., McEvoy, R., Baldwin, D. S., Rees, G. N., Parsons, Y., and Southerton, S. (2014). Characterisation of adaptive genetic diversity in environmentally contrasted populations of Eucalyptus camaldulensis Dehnh. (river red gum). PLoS One 9:e103515. doi: 10.1371/journal.pone.0103515

PubMed Abstract | CrossRef Full Text | Google Scholar

Donovan, L. A., Ludwig, F., Rosenthal, D. M., Rieseberg, L. H., and Dudley, S. A. (2009). Phenotypic selection on leaf ecophysiological traits in Helianthus. New Phytol. 183, 868–879. doi: 10.1111/j.1469-8137.2009.02916.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, H., Duursma, R. A., Huang, G., Smith, R. A., Choat, B., O’Grady, A. P., et al. (2014). Elevated [CO2] does not ameliorate the negative effects of elevated temperature on drought-induced mortality in Eucalyptus radiata seedlings. Plant Cell Environ. 37, 1598–1613. doi: 10.1111/pce.12260

PubMed Abstract | CrossRef Full Text | Google Scholar

Dudley, S. A. (1996). Differing selection on plant physiological traits in response to environmental water availability: a test of adaptive hypotheses. Evolution 50, 92–102. doi: 10.1111/j.1558-5646.1996.tb04475.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Etterson, J. R. (2004). Evolutionary potential of Chamaecrista fasciculata in relation to climate change. I. Clinal patterns of selection along an environmental gradient in the Great Plains. Evolution 58, 1446–1458. doi: 10.1554/04-053

CrossRef Full Text | Google Scholar

Fernández, R. J., and Reynolds, J. F. (2000). Potential growth and drought tolerance of eight desert grasses: lack of a trade-off? Oecologia 123, 90–98. doi: 10.1007/s004420050993

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferron, J. M., Bell, B. A., Hess, M. R., Rendina-Gobioff, G., and Hibbard, S. T. (2009). Making treatment effect inferences from multiple-baseline data: the utility of multilevel modeling approaches. Behav. Res. Methods 41, 372–384. doi: 10.3758/BRM.41.2.372

PubMed Abstract | CrossRef Full Text | Google Scholar

Frachon, L., Bartoli, C., Carrère, S., Bouchez, O., Chaubet, A., Gautier, M., et al. (2018). A genomic map of climate adaptation in Arabidopsis thaliana at a micro-geographic scale. Front. Plant Sci. 9:967. doi: 10.3389/fpls.2018.00967

PubMed Abstract | CrossRef Full Text | Google Scholar

Franklin, O. D., and Morrissey, M. B. (2017). Inference of selection gradients using performance measures as fitness proxies. Methods Ecol. Evol. 8, 663–677. doi: 10.1111/2041-210X.12737

CrossRef Full Text | Google Scholar

Galiano, L., Martínez-Vilalta, J., and Lloret, F. (2011). Carbon reserves and canopy defoliation determine the recovery of scots pine 4 yr after a drought episode. New Phytol. 190, 750–759. doi: 10.1111/j.1469-8137.2010.03628.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Gardiner, J. C., Luo, Z., and Roman, L. A. (2009). Fixed effects, random effects and GEE: what are the differences? Stat. Med. 28, 221–239. doi: 10.1002/sim.3478

PubMed Abstract | CrossRef Full Text | Google Scholar

Gardner, W., Mulvey, E. P., and Shaw, E. C. (1995). Regression analyses of counts and rates: poisson, overdispersed poisson, and negative binomial models. Psychol. Bull. 118, 392–404. doi: 10.1037/0033-2909.118.3.392

PubMed Abstract | CrossRef Full Text | Google Scholar

Gauli, A., Steane, D. A., Vaillancourt, R. E., and Potts, B. M. (2014). Molecular genetic diversity and population structure in Eucalyptus pauciflora subsp pauciflora (Myrtaceae) on the island of Tasmania. Aust. J. Bot. 62, 175–188. doi: 10.1071/bt14036

CrossRef Full Text | Google Scholar

Gauli, A., Vaillancourt, R. E., Bailey, T. G., Steane, D. A., and Potts, B. M. (2015). Evidence for local climate adaptation in early-life traits of Tasmanian populations of Eucalyptus pauciflora. Tree Genet. Genomes 11:104. doi: 10.1007/s11295-015-0930-6

CrossRef Full Text | Google Scholar

Gauli, A., Vaillancourt, R. E., Steane, D. A., Bailey, T. G., and Potts, B. M. (2013). Effect of forest fragmentation and altitude on the mating system of Eucalyptus pauciflora (Myrtaceae). Aust. J. Bot. 61, 622–632.

Google Scholar

Gómez, J. M. (2004). Bigger is not always better: conflicting selective pressures on seed size in Quercus ilex. Evolution 58, 71–80. doi: 10.1111/j.0014-3820.2004.tb01574.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Griffin, A. R., Potts, B. M., Vaillancourt, R. E., and Bell, J. C. (2019). Life cycle expression of inbreeding depression in Eucalyptus regnans and inter-generational stability of its mixed mating system. Ann. Bot. 124, 179–187. doi: 10.1093/aob/mcz059

PubMed Abstract | CrossRef Full Text | Google Scholar

Groom, P. K., Lamont, B. B., Leighton, S., Leighton, P., and Burrows, C. (2004). Heat damage in sclerophylls is influenced by their leaf properties and plant environment. Ecoscience 11, 94–101. doi: 10.1080/11956860.2004.11682813

CrossRef Full Text | Google Scholar

Guikema, S. D., and Goffelt, J. P. (2008). A flexible count data regression model for risk analysis. Risk Anal. 28, 213–223. doi: 10.1111/j.1539-6924.2008.01014.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hahn, E. D., and Soyer, R. (2005). Probit and Logit Models: Differences in the Multivariate Realm. Available online at: http://home.gwu.edu/~soyer/mv1h.pdf (accessed December 29, 2020).

Google Scholar

Harrison, P. (2017). Integrating Climate Change into Conservation and Restoration Strategies : The Case of the Tasmanian Eucalypts. Ph.D. thesis. Hobart, TAS: University of Tasmania.

Google Scholar

Harrison, P. A., Vaillancourt, R. E., Harris, R. M. B., and Potts, B. M. (2017). Integrating climate change and habitat fragmentation to identify candidate seed sources for ecological restoration. Restor. Ecol. 25, 524–531. doi: 10.1111/rec.12488

CrossRef Full Text | Google Scholar

Hedeker, D., and Gibbons, R. D. (2006). Longitudinal Data Analysis. Hoboken, NJ: Wiley.

Google Scholar

Hendry, A. P. (2017). Eco-Evolutionary Dynamics. Oxford: Princeton University Press.

Google Scholar

Hereford, J., Hansen, T. F., and Houle, D. (2004). Comparing strengths of directional selection: how strong is strong? Evolution 58, 2133–2143. doi: 10.1111/j.0014-3820.2004.tb01592.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Heschel, M. S., and Riginos, C. (2005). Mechanisms of selection for drought stress tolerance and avoidance in Impatiens capensis (Balsaminaceae). Am. J. Bot. 92, 37–44. doi: 10.3732/ajb.92.1.37

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoffmann, A. A., and Sgro, C. M. (2011). Climate change and evolutionary adaptation. Nature 470, 479–485. doi: 10.1038/nature09670

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoque, S., and Avila-Sakar, G. (2015). Trade-offs and ontogenetic changes in resistance and tolerance to insect herbivory in Arabidopsis. Int. J. Plant Sci. 176, 150–158. doi: 10.1086/679478

CrossRef Full Text | Google Scholar

Houle, D., Pélabon, C., Wagner, G. P., and Hansen, T. F. (2011). Measurement and meaning in biology. Q. Rev. Biol. 86, 3–34. doi: 10.1086/658408

PubMed Abstract | CrossRef Full Text | Google Scholar

James, S. A., and Bell, D. T. (2000). Leaf orientation, light interception and stomatal conductance of Eucalyptus globulus ssp. globulus leaves. Tree Physiol. 20, 815–823. doi: 10.1093/treephys/20.12.815

PubMed Abstract | CrossRef Full Text | Google Scholar

James, S. A., and Bell, D. T. (2001). Leaf morphological and anatomical characteristics of heteroblastic Eucalyptus globulus ssp globulus (Myrtaceae). Aust. J. Bot. 49, 259–269.

Google Scholar

Janzen, F. J., and Stern, H. S. (1998). Logistic regression for empirical studies of multivariate selection. Evolution 52, 1564–1571. doi: 10.1111/j.1558-5646.1998.tb02237.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Jordan, R., Hoffmann, A. A., Dillon, S. K., and Prober, S. M. (2017). Evidence of genomic adaptation to climate in Eucalyptus microcarpa: implications for adaptive potential to projected climate change. Mol. Ecol. 26, 6002–6020. doi: 10.1111/mec.14341

PubMed Abstract | CrossRef Full Text | Google Scholar

Jump, A. S., and Peñuelas, J. (2005). Running to stand still: adaptation and the response of plants to rapid climate change. Ecol. Lett. 8, 1010–1020. doi: 10.1111/j.1461-0248.2005.00796.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Keller, S. R., Levsen, N., Olson, M. S., and Tiffin, P. (2012). Local adaptation in the flowering-time gene network of balsam poplar, Populus balsamifera L. Mol. Biol. Evol. 29, 3143–3152. doi: 10.1093/molbev/mss121

PubMed Abstract | CrossRef Full Text | Google Scholar

Kenward, M. G., and Roger, J. H. (1997). Small sample inference for fixed effects from restricted maximum likelihood. Biometrics 53, 983–997.

Google Scholar

Kenward, M. G., and Roger, J. H. (2009). An improved approximation to the precision of fixed effects from restricted maximum likelihood. Comput. Stat. Data Anal. 53, 2583–2595. doi: 10.1016/j.csda.2008.12.013

CrossRef Full Text | Google Scholar

King, D. A. (1997). The functional significance of leaf angle in Eucalyptus. Aust. J. Bot. 45, 619–639. doi: 10.1071/BT96063

CrossRef Full Text | Google Scholar

Kingsolver, J. G., and Diamond, S. E. (2011). Phenotypic selection in natural populations: what limits directional selection? Am. Nat. 177, 346–357. doi: 10.1086/658341

PubMed Abstract | CrossRef Full Text | Google Scholar

Kingsolver, J. G., Diamond, S. E., Siepielski, A. M., and Carlson, S. M. (2012). Synthetic analyses of phenotypic selection in natural populations: lessons, limitations and future directions. Evol. Ecol. 26, 1101–1118. doi: 10.1007/s10682-012-9563-5

CrossRef Full Text | Google Scholar

Kingsolver, J. G., Hoekstra, H. E., Hoekstra, J. M., Berrigan, D., Vignieri, S. N., Hill, C. E., et al. (2001). The strength of phenotypic selection in natural populations. Am. Nat. 157, 245–261. doi: 10.1086/319193

PubMed Abstract | CrossRef Full Text | Google Scholar

Klein, T., Zeppel, M. J. B., Anderegg, W. R. L., Bloemen, J., De Kauwe, M. G., Hudson, P., et al. (2018). Xylem embolism refilling and resilience against drought-induced mortality in woody plants: processes and trade-offs. Ecol. Res. 33, 839–855. doi: 10.1007/s11284-018-1588-y

CrossRef Full Text | Google Scholar

Koelewijn, H. P., Koski, V., and Savolainen, O. (1999). Magnitude and timing of inbreeding depression in scots pine (Pinus sylvestris L.). Evolution 53, 758–768.

Google Scholar

Kramer, K., van der Werf, B., and Schelhaas, M.-J. (2015). Bring in the genes: genetic-ecophysiological modeling of the adaptive response of trees to environmental change. With application to the annual cycle. Front. Plant Sci. 5:742. doi: 10.3389/fpls.2014.00742

PubMed Abstract | CrossRef Full Text | Google Scholar

Kremer, A., Potts, B. M., and Delzon, S. (2014). Genetic divergence in forest trees: understanding the consequences of climate change. Funct. Ecol. 28, 22–36. doi: 10.1111/1365-2435.12169

CrossRef Full Text | Google Scholar

Ladiges, P. Y. (1974). Differentiation in some populations of Eucalyptus viminalis Labill. in relation to factors affecting seedling establishment. Aust. J. Bot. 22, 471–487. doi: 10.1071/bt9740471

CrossRef Full Text | Google Scholar

Lande, R. (1979). Quantitative genetic analysis of multivariate evolution, applied to brain:body size allometry. Evolution 33, 402–416.

Google Scholar

Lande, R., and Arnold, S. J. (1983). The measurement of selection on correlated characters. Evolution 37, 1210–1226. doi: 10.2307/2408842

CrossRef Full Text | Google Scholar

Lau, J. A., Shaw, R. G., Reich, P. B., and Tiffin, P. (2014). Indirect effects drive evolutionary responses to global change. New Phytol. 201, 335–343. doi: 10.1111/nph.12490

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, C. Y., Berninger, F., Koskela, J., and Sonninen, E. (2000). Drought responses of Eucalyptus microtheca provenances depend on seasonality of rainfall in their place of origin. Aust. J. Plant Physiol. 27, 231–238.

Google Scholar

Li, X., Blackman, C. J., Choat, B., Duursma, R. A., Rymer, P. D., Medlyn, B. E., et al. (2018). Tree hydraulic traits are coordinated and strongly linked to climate-of-origin across a rainfall gradient. Plant Cell Environ. 41, 646–660. doi: 10.1111/pce.13129

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, Y., Equiza, M. A., Deng, X., and Tyree, M. T. (2010). Recovery of Populus tremuloides seedlings following severe drought causing total leaf mortality and extreme stem embolism. Physiol. Plant. 140, 246–257.

Google Scholar

Lucani, C. J., Brodribb, T. J., Jordan, G. J., and Mitchell, P. J. (2019). Juvenile and adult leaves of heteroblastic Eucalyptus globulus vary in xylem vulnerability. Trees Struct. Funct. 33, 1167–1178. doi: 10.1007/s00468-019-01851-4

CrossRef Full Text | Google Scholar

Maas, C. J. M., and Hox, J. J. (2004). Robustness issues in multilevel regression analysis. Stat. Neerl. 58, 127–137. doi: 10.1046/j.0039-0402.2003.00252.x

CrossRef Full Text | Google Scholar

MacColl, A. D. (2011). The ecological causes of evolution. Trends Ecol. Evol. 26, 514–522. doi: 10.1016/j.tree.2011.06.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Marchin, R. M., Ossola, A., Leishman, M. R., and Ellsworth, D. S. (2020). A simple method for simulating drought effects on plants. Front. Plant Sci. 10:1715. doi: 10.3389/fpls.2019.01715

PubMed Abstract | CrossRef Full Text | Google Scholar

Matusick, G., Ruthrof, K. X., Brouwers, N. C., Dell, B., and Hardy, G. S. J. (2013). Sudden forest canopy collapse corresponding with extreme drought and heat in a mediterranean-type eucalypt forest in southwestern Australia. Eur. J. For. Res. 132, 497–510. doi: 10.1007/s10342-013-0690-5

CrossRef Full Text | Google Scholar

McDonald, P. G., Fonseca, C. R., Overton, J. M., and Westoby, M. (2003). Leaf-size divergence along rainfall and soil-nutrient gradients: is the method of size reduction common among clades? Funct. Ecol. 17, 50–57. doi: 10.1046/j.1365-2435.2003.00698.x

CrossRef Full Text | Google Scholar

McDowell, N., Pockman, W. T., Allen, C. D., Breshears, D. D., Cobb, N., Kolb, T., et al. (2008). Mechanisms of plant survival and mortality during drought: why do some plants survive while others succumb to drought? New Phytol. 178, 719–739.

Google Scholar

McDowell, N. G., Beerling, D. J., Breshears, D. D., Fisher, R. A., Raffa, K. F., and Stitt, M. (2011). The interdependence of mechanisms underlying climate-driven vegetation mortality. Trends Ecol. Evol. 26, 523–532. doi: 10.1016/j.tree.2011.06.003

PubMed Abstract | CrossRef Full Text | Google Scholar

McKiernan, A. B., Potts, B. M., Brodribb, T. J., Hovenden, M. J., Davies, N. W., McAdam, S. A. M., et al. (2016). Responses to mild water deficit and rewatering differ among secondary metabolites but are similar among provenances within Eucalyptus species. Tree Physiol. 36, 133–147. doi: 10.1093/treephys/tpv106

PubMed Abstract | CrossRef Full Text | Google Scholar

McLean, E. H., Prober, S. M., Stock, W. D., Steane, D. A., Potts, B. M., Vaillancourt, R. E., et al. (2014). Plasticity of functional traits varies clinally along a rainfall gradient in Eucalyptus tricarpa. Plant Cell Environ. 37, 1440–1451. doi: 10.1111/pce.12251

PubMed Abstract | CrossRef Full Text | Google Scholar

McNeish, D. (2016). Estimation methods for mixed logistic models with few clusters. Multivariate Behav. Res. 51, 790–804. doi: 10.1080/00273171.2016.1236237

PubMed Abstract | CrossRef Full Text | Google Scholar

McNeish, D. (2019). Poisson multilevel models with small samples. Multivariate Behav. Res. 54, 444–455. doi: 10.1080/00273171.2018.1545630

PubMed Abstract | CrossRef Full Text | Google Scholar

McNeish, D. M., and Stapleton, L. M. (2016a). Modeling clustered data with very few clusters. Multivariate Behav. Res. 51, 495–518. doi: 10.1080/00273171.2016.1167008

PubMed Abstract | CrossRef Full Text | Google Scholar

McNeish, D. M., and Stapleton, L. M. (2016b). The effect of small sample size on two-level model estimates: a review and illustration. Educ. Psychol. Rev. 28, 295–314. doi: 10.1007/s10648-014-9287-x

CrossRef Full Text | Google Scholar

Merilä, J., and Hendry, A. P. (2014). Climate change, adaptation, and phenotypic plasticity: the problem and the evidence. Evol. Appl. 7, 1–14. doi: 10.1111/eva.12137

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchell, P. J., O’Grady, A. P., Hayes, K. R., and Pinkard, E. A. (2014). Exposure of trees to drought- induced die- off is defined by a common climatic threshold across different vegetation types. Ecol. Evol. 4, 1088–1101. doi: 10.1002/ece3.1008

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchell, P. J., O’Grady, A. P., Tissue, D. T., White, D. A., Ottenschlaeger, M. L., and Pinkard, E. A. (2013). Drought response strategies define the relative contributions of hydraulic dysfunction and carbohydrate depletion during tree mortality. New Phytol. 197, 862–872. doi: 10.1111/nph.12064

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchell-Olds, T., and Shaw, R. G. (1987). Regression analysis of natural selection: statistical inference and biological interpretation. Evolution 41, 1149–1161. doi: 10.2307/2409084

CrossRef Full Text | Google Scholar

Molenberghs, G., Didier, R., and Verbeke, G. (2002). A review of generalized linear mixed models. J. Soc. Fr. Statistique 143, 53–57.

Google Scholar

Monica, A. G., and Lauren, R. G. (2003). Inheritance and natural selection on functional traits. Int. J. Plant Sci. 164, S21–S42. doi: 10.1086/368233

CrossRef Full Text | Google Scholar

Moreira, X., Mooney, K. A., Rasmann, S., Petry, W. K., Carrillo-Gavilan, A., Zas, R., et al. (2014). Trade-offs between constitutive and induced defences drive geographical and climatic clines in pine chemical defences. Ecol. Lett. 17, 537–546. doi: 10.1111/ele.12253

PubMed Abstract | CrossRef Full Text | Google Scholar

Morrissey, M. B., and Sakrejda, K. (2013). Unification of regression-based methods for the analysis of natural selection. Evolution 67, 2094–2100. doi: 10.1111/evo.12077

PubMed Abstract | CrossRef Full Text | Google Scholar

Myers, B. (1995). The Influence of the lignotuber on hydraulic conductance and leaf conductance in Eucalyptus behriana seedlings. Funct. Plant Biol. 22, 857–863. doi: 10.1071/PP9950857

CrossRef Full Text | Google Scholar

Nakagawa, S., Johnson, P. C. D., and Schielzeth, H. (2017). The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. J. R. Soc. Interface 14:20170213. doi: 10.1098/rsif.2017.0213

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicotra, A. B., Atkin, O. K., Bonser, S. P., Davidson, A. M., Finnegan, E. J., Mathesius, U., et al. (2010). Plant phenotypic plasticity in a changing climate. Trends Plant Sci. 15, 684–692.

Google Scholar

Orians, C. M., Hochwender, C. G., Fritz, R. S., and Snall, T. (2010). Growth and chemical defense in willow seedlings: trade-offs are transient. Oecologia 163, 283–290. doi: 10.1007/s00442-009-1521-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Park Williams, A., Allen, C. D., Macalady, A. K., Griffin, D., Woodhouse, C. A., Meko, D. M., et al. (2013). Temperature as a potent driver of regional forest drought stress and tree mortality. Nat. Clim. Chang. 3, 292–297. doi: 10.1038/nclimate1693

CrossRef Full Text | Google Scholar

Patterson, H. D., and Thompson, R. (1971). Recovery of inter-block information when block sizes are unequal. Biometrika 58, 545–554.

Google Scholar

Petit, R. J., and Hampe, A. (2006). Some evolutionary consequences of being a tree. Annu. Rev. Ecol. Evol. Syst. 37, 187–214. doi: 10.1146/annurev.ecolsys.37.091305.110215

CrossRef Full Text | Google Scholar

Phillips, P. C., and Arnold, S. J. (1989). Visualizing multivariate selection. Evolution 43, 1209–1222. doi: 10.1111/j.1558-5646.1989.tb02569.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinheiro, J. C., and Bates, D. M. (1995). Approximations to the log-likelihood function in the nonlinear mixed-effects model. J. Comput. Graph. Stat. 4, 12–35. doi: 10.1080/10618600.1995.10474663

CrossRef Full Text | Google Scholar

Pita, P., and Pardos, J. A. (2001). Growth, leaf morphology, water use and tissue water relations of Eucalyptus globulus clones in response to water deficit. Tree Physiol. 21, 599–607.

Google Scholar

Pluess, A. R., Frank, A., Heiri, C., Lalagüe, H., Vendramin, G. G., and Oddou-Muratorio, S. (2016). Genome–environment association study suggests local adaptation to climate at the regional scale in Fagus sylvatica. New Phytol. 210, 589–601. doi: 10.1111/nph.13809

PubMed Abstract | CrossRef Full Text | Google Scholar

Prober, S. M., Potts, B. M., Bailey, T., Byrne, M., Dillon, S., Harrison, P. A., et al. (2016). Climate adaptation and ecological restoration in eucalypts. Proc. R. Soc. Vic. 128, 40–53.

Google Scholar

Ramírez-Valiente, J. A., and Cavender-Bares, J. (2017). Evolutionary trade-offs between drought resistance mechanisms across a precipitation gradient in a seasonally dry tropical oak (Quercus oleoides). Tree Physiol. 37, 889–901. doi: 10.1093/treephys/tpx040

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramírez-Valiente, J. A., Valladares, F., Delgado, A., Nicotra, A. B., and Aranda, I. (2015). Understanding the importance of intrapopulation functional variability and phenotypic plasticity in Quercus suber. Tree Genet. Genomes 11:35. doi: 10.1007/s11295-015-0856-z

CrossRef Full Text | Google Scholar

Ramírez-Valiente, J. A., Valladares, F., Sanchez-Gomez, D., Delgado, A., and Aranda, I. (2014). Population variation and natural selection on leaf traits in cork oak throughout its distribution range. Acta Oecol. Int. J. Ecol. 58, 49–56. doi: 10.1016/j.actao.2014.04.004

CrossRef Full Text | Google Scholar

Raudenbush, S. W., and Bryk, A. S. (2002). Hierarchical Linear Models: Applications and Data Analysis Methods. Thousand Oaks, CA: Sage Publications.

Google Scholar

Ruehr, N. K., Grote, R., Mayr, S., and Arneth, A. (2019). Beyond the extreme: recovery of carbon and water relations in woody plants following heat and drought stress. Tree Physiol. 39, 1285–1299.

Google Scholar

SAS (2017). SAS/STAT§14.3 User’s Guide. Cary, NC: SAS Institute Inc.

Google Scholar

Schwalm, C. R., Anderegg, W. R. L., Michalak, A. M., Fisher, J. B., Biondi, F., Koch, G., et al. (2017). Global patterns of drought recovery. Nature 548, 202–205. doi: 10.1038/nature23021

PubMed Abstract | CrossRef Full Text | Google Scholar

Scoffoni, C., Rawls, M., McKown, A., Cochard, H., and Sack, L. (2011). Decline of leaf hydraulic conductance with dehydration: relationship to leaf size and venation architecture. Plant Physiol. 156, 832–843. doi: 10.1104/pp.111.173856

PubMed Abstract | CrossRef Full Text | Google Scholar

Self, S. G., and Liang, K.-Y. (1987). Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under nonstandard conditions. J. Am. Stat. Assoc. 82, 605–610. doi: 10.1080/01621459.1987.10478472

CrossRef Full Text | Google Scholar

Shaw, R. G., and Etterson, J. R. (2012). Rapid climate change and the rate of adaptation: insight from experimental quantitative genetics. New Phytol. 195, 752–765. doi: 10.1111/j.1469-8137.2012.04230.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Shmueli, G., Minka, T. P., Kadane, J. B., Borle, S., and Boatwright, P. (2005). A useful distribution for fitting discrete data: revival of the Conway–Maxwell–Poisson distribution. J. Roy. Stat. Soc. Ser. C. (Appl. Stat.) 54, 127–142. doi: 10.1111/j.1467-9876.2005.00474.x

CrossRef Full Text | Google Scholar

Siepielski, A. M., DiBattista, J. D., and Carlson, S. M. (2009). It’s about time: the temporal dynamics of phenotypic selection in the wild. Ecol. Lett. 12, 1261–1276. doi: 10.1111/j.1461-0248.2009.01381.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Siepielski, A. M., Gotanda, K. M., Morrissey, M. B., Diamond, S. E., DiBattista, J. D., and Carlson, S. M. (2013). The spatial patterns of directional phenotypic selection. Ecol. Lett. 16, 1382–1392. doi: 10.1111/ele.12174

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, M. G., Arndt, S. K., Miller, R. E., Kasel, S., and Bennett, L. T. (2018). Trees use more non-structural carbohydrate reserves during epicormic than basal resprouting. Tree Physiol. 38, 1779–1791.

Google Scholar

Steane, D. A., Potts, B. M., McLean, E. H., Collins, L., Holland, B. R., Prober, S. M., et al. (2017). Genomic scans across three eucalypts suggest that adaptation to aridity is a genome-wide phenomenon. Genome Biol. Evol. 9, 253–265. doi: 10.1093/gbe/evw290

PubMed Abstract | CrossRef Full Text | Google Scholar

Steele, D. B., Siepielski, A. M., and McPeek, M. A. (2011). Sexual selection and temporal phenotypic variation in a damselfly population. J. Evol. Biol. 24, 1517–1532. doi: 10.1111/j.1420-9101.2011.02284.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Stoneman, G. L. (1994). Ecology and physiology of establishment of eucalypt seedlings from seed: a review. Aust. For. 57, 11–29. doi: 10.1080/00049158.1994.10676109

CrossRef Full Text | Google Scholar

Tozer, M. G., and Bradstock, R. A. (1998). Factors influencing the establishment of seedlings of the mallee, Eucalyptus luehmanniana (Myrtaceae). Aust. J. Bot. 45, 997–1008. doi: 10.1071/BT96111

CrossRef Full Text | Google Scholar

Urli, M., Porté, A. J., Cochard, H., Guengant, Y., Burlett, R., and Delzon, S. (2013). Xylem embolism threshold for catastrophic hydraulic failure in angiosperm trees. Tree Physiol. 33, 672–683. doi: 10.1093/treephys/tpt030

PubMed Abstract | CrossRef Full Text | Google Scholar

Vesk, P. A., and Westoby, M. (2003). Drought damage and recovery–a conceptual model [2]. New Phytol. 160, 7–14.

Google Scholar

Vlasveld, C., O’Leary, B., Udovicic, F., and Burd, M. (2018). Leaf heteroblasty in eucalypts: biogeographic evidence of ecological function. Aust. J. Bot. 66, 191–201. doi: 10.1071/BT17134

CrossRef Full Text | Google Scholar

Wade, M. J., and Kalisz, S. (1990). The causes of natural selection. Evolution 44, 1947–1955. doi: 10.2307/2409605

CrossRef Full Text | Google Scholar

Walters, J. R., Bell, T. L., and Read, S. (2005). Intra-specific variation in carbohydrate reserves and sprouting ability in Eucalyptus obliqua seedlings. Aust. J. Bot. 53, 195–203.

Google Scholar

Wang, X., Liu, F.l., and Jiang, D. (2017). Priming: a promising strategy for crop production in response to future climate. J. Integr. Agric. 16, 2709–2716. doi: 10.1016/S2095-3119(17)61786-6

CrossRef Full Text | Google Scholar

Warren, C. R., Aranda, I., and Cano, F. J. (2011). Responses to water stress of gas exchange and metabolites in Eucalyptus and Acacia spp. Plant Cell Environ. 34, 1609–1629. doi: 10.1111/j.1365-3040.2011.02357.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Warren, C. R., Aranda, I., and Cano, F. J. (2012). Metabolomics demonstrates divergent responses of two Eucalyptus species to water stress. Metabolomics 8, 186–200. doi: 10.1007/s11306-011-0299-y

CrossRef Full Text | Google Scholar

Warwell, M. V., and Shaw, R. G. (2018). Phenotypic selection on growth rhythm in whitebark pine under climatic conditions warmer than seed origins. J. Evol. Biol. 31, 1284–1299. doi: 10.1111/jeb.13301

PubMed Abstract | CrossRef Full Text | Google Scholar

Warwell, M. V., and Shaw, R. G. (2019). Phenotypic selection on ponderosa pine seed and seedling traits in the field under three experimentally manipulated drought treatments. Evol. Appl. 12, 159–174. doi: 10.1111/eva.12685

PubMed Abstract | CrossRef Full Text | Google Scholar

Wedderburn, R. W. M. (1974). Quasi-likelihood functions, generalized linear models, and the Gauss-Newton method. Biometrika 61, 439–447. doi: 10.1093/biomet/61.3.439

CrossRef Full Text | Google Scholar

Wolfinger, R., and O’Connell, M. (1993). Generalized linear mixed models a pseudo-likelihood approach. J. Stat. Comput. Simul. 48, 233–243. doi: 10.1080/00949659308811554

CrossRef Full Text | Google Scholar

Zeppel, M. J. B., Harrison, S. P., Adams, H. D., Kelley, D. I., Li, G., Tissue, D. T., et al. (2015). Drought and resprouting plants. New Phytol. 206, 583–589. doi: 10.1111/nph.13205

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Xie, J.-B., and Li, Y. (2017). Effects of increasing root carbon investment on the mortality and resprouting of Haloxylon ammodendron seedlings under drought. Plant Biol. 19, 191–200.

Google Scholar