
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Ecol. Evol., 18 November 2021
Sec. Models in Ecology and Evolution
Volume 9 - 2021 | https://doi.org/10.3389/fevo.2021.658713
Information about the distribution of a study object (e.g., species or habitat) is essential in face of increasing pressure from land or sea use, and climate change. Distribution models are instrumental for acquiring such information, but also encumbered by uncertainties caused by different sources of error, bias and inaccuracy that need to be dealt with. In this paper we identify the most common sources of uncertainties and link them to different phases in the modeling process. Our aim is to outline the implications of these uncertainties for the reliability of distribution models and to summarize the precautions needed to be taken. We performed a step-by-step assessment of errors, biases and inaccuracies related to the five main steps in a standard distribution modeling process: (1) ecological understanding, assumptions and problem formulation; (2) data collection and preparation; (3) choice of modeling method, model tuning and parameterization; (4) evaluation of models; and, finally, (5) implementation and use. Our synthesis highlights the need to consider the entire distribution modeling process when the reliability and applicability of the models are assessed. A key recommendation is to evaluate the model properly by use of a dataset that is collected independently of the training data. We support initiatives to establish international protocols and open geodatabases for distribution models.
Distribution modeling is a process which aims to understand and visualize, in a spatial context, the past, present or future distribution of a study object by relating it to predictor (explanatory) variables (Guisan and Zimmermann, 2000). The predictors can be stand-alone variables, interactions between variables, or even abstract complex-gradients (Simensen et al., 2020). This places distribution modeling among gradient analysis techniques (Halvorsen, 2012) as a correlative procedure for modeling the realized distribution of the study object (Wiens et al., 2009). Distribution modeling methodology has proliferated strongly over the last two decades (Franklin, 2010; Yates et al., 2018), and is now used to predict the distribution of single species, species assemblages, species richness, communities, and habitats (e.g., Drew et al., 2011; Moriondo et al., 2013; Horvath et al., 2019).
The diversity of research disciplines in ecology, questions asked, data collected and methods used for distribution modeling, has led to the development of several parallel distribution modeling practices (Araújo et al., 2019). These practices compete with and/or encompass a variety of terms, such as ecological niche modeling, habitat suitability modeling, species distribution modeling and occupancy modeling (see e.g., Gogol-Prokurat, 2011; Sales et al., 2021, and references therein). The practices differ in many respects, but they build on a common theoretical basis that focus on correlative predictions of distributions in general (e.g., Guisan and Zimmermann, 2000; Austin, 2007; Halvorsen, 2012). Although there are many ways of presenting distribution modeling (see Brown and Yoder, 2015; Mazzoni et al., 2015; Rodríguez-Rey et al., 2019; Zurell et al., 2020), for the purpose of this synthesis we have generalized the process into a five-step conceptual framework illustrated in Figure 1: (step 1) ecological understanding, assumptions and problem formulation; (step 2) data collection and preparation; (step 3) modeling method: choice, tuning (determining options and settings) and parameterization; (step 4) model evaluation; and (step 5) implementation and use, e.g., presentation of modeling results in the form of maps of an object’s predicted distribution, in a given area (space) and/or at a given time.
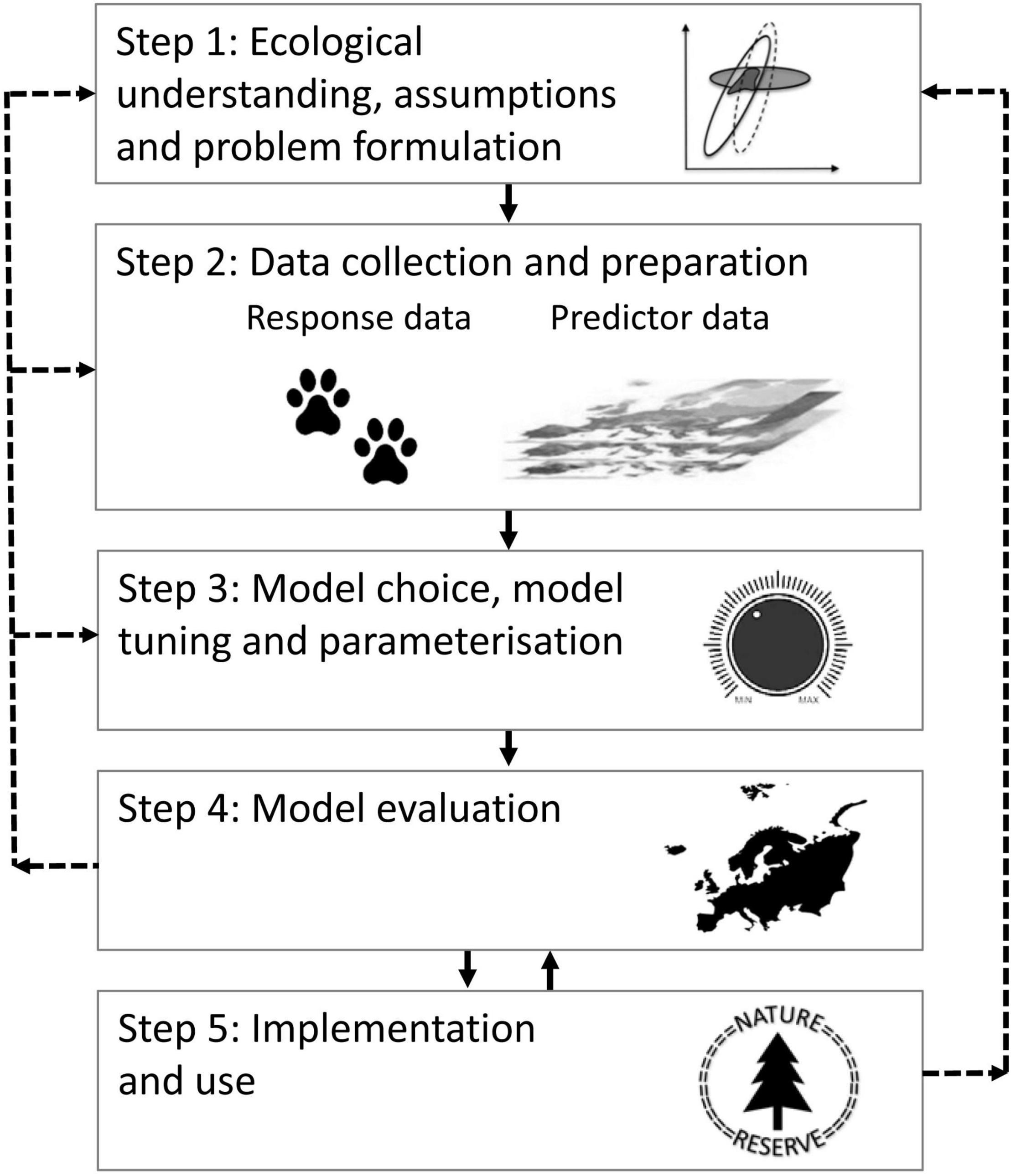
Figure 1. A conceptual framework for the distribution modeling process described in this synthesis. The broken arrows from Step 4 to Step 1–3 illustrate the recommended path after evaluating the model, i.e., formulating new problems, collecting new data and/or making new model choices and tunings. The broken arrow between Step 5 and Step 1 illustrates feedbacks from end users that may trigger new problem formulations, collection of new training data and/or improvements to other parts of the modeling process. The reciprocal arrows between Step 4 and 5 opens for feedback from model use to model evaluation, i.e., by facilitating collection of new evaluation data, which again can lead to improved model implementation and use.
A series of important decisions are made throughout the distribution modeling process. The reliability, or uncertainty, of the output will be determined by the errors, biases and inaccuracies that have accumulated throughout the process, from problem formulation to model evaluation and use (Lindner et al., 2014). Identification of potential uncertainties at each step (Figure 1) challenges the modeler’s knowledge of the study object, the dataset and of modeling methodology in general. While the modeler is responsible for providing end users with information about the reliability of the model, the responsibility for appropriate use of the modeling outcome (which typically is a map) lies with the end user. Although the attention given to reliability in distribution modeling is increasing (e.g., Beale and Lennon, 2012; Mouquet et al., 2015; Yates et al., 2018), most studies addressing this have focused on specific parts of the distribution modeling process, such as the implication of missing environmental variables or low spatial resolution (Suárez-Seoane et al., 2014), lack of map layers that represent biotic interactions (Svenning et al., 2014; Kass et al., 2021), quality of input data (Aubry et al., 2017), the relative performance of statistical methods (Elith et al., 2006; Lobo et al., 2008), sampling bias (Varela et al., 2014; Støa et al., 2018), transferability (Yates et al., 2018) or model evaluation (Halvorsen et al., 2016; Fernandes et al., 2018). The many sources of uncertainties in distribution models strongly call for a systematic approach to avoid, reduce, or at least understand, the major sources of uncertainty at each step in the modeling process. In order to improve the quality of distribution models and facilitate model interpretation, such a systematic approach should inspect the effects of uncertainties accumulated throughout the process. The purpose of this synthesis is therefore to identify the main sources and main implications of accumulated errors, biases, and inaccuracies for the reliability of distribution models, to describe how uncertainties may be reduced, and to come up with recommendations, in the form of step-by-step guidelines, for dealing with these uncertainties. We accomplish this aim by presenting and discussing each of the five steps in the distribution modeling process (Figure 1). Our ambition is that this synthesis will be useful for both modelers and end users of distribution modeling results, such as planning authorities, nature managers and industry stakeholders. The focus of this synthesis is limited to correlative distribution models and will neither address dynamic (e.g., Horvath et al., 2021) nor mechanistic (e.g., Dormann et al., 2012), i.e., process-based, models.
A major challenge for distribution modeling has been, and to some extent still is, the lack of a unified theoretical basis and consensus on best-practice standards (but see Halvorsen, 2012; Araújo et al., 2019; Zurell et al., 2020). Incomplete knowledge of the natural variation of the study object and its environment, and lack of understanding of the ecological processes responsible for the study object’s relationship with its surroundings, may result in suboptimal decisions at some point in the distribution modeling process. Species’ distributions are controlled by four main structuring processes: (1) the inherent biological adaptations of the species, which set limits for their ecophysiological tolerance; (2) biotic interactions with other organisms, such as competition, amensalism, mutualism, and predation (e.g., Svenning et al., 2014); (3) demographic processes such as dispersal, establishment, survival and space limitation (e.g., van Groenendael et al., 2000); and (4) feedback mechanisms with the abiotic surroundings (e.g., Bonan, 2008) or engineering of the ecosystem by the species themselves (Linder et al., 2012). Lack of knowledge about causality and the object’s abiotic or biotic constraints may lead to misleading or even meaningless models.
A fundamental assumption of distribution models is the existence of an equilibrium between the study object and the surrounding environment, i.e., that the object occurs in all or a predictable fraction of suitable sites and is absent from all unsuitable ones (Guisan and Zimmermann, 2000). This is, however, not necessarily true, even for species typical of relatively stable habitats. Species may, for instance, maintain sink populations in some areas for some time or moderate the ecosystem to their specific needs (Linder et al., 2012). Moreover, environmental change causes lack of equilibrium in species abundances and time-lagged responses, in the forms of extinction debts or immigration credits (Jackson and Sax, 2010). The time-lags involved in community dynamics may vary from species to species and from area to area, depending on properties such as generation time, the mode and capacity of dispersal and the rates of environmental change (Svenning and Skov, 2005). The more extensive the environmental change, the larger extinction debt and immigration credit can be expected. This is particularly relevant for distribution models developed for evaluation of range shifts, such as altitudinal or latitudinal responses to climate change (e.g., tree lines, Bryn et al., 2013). Invasive species that have not yet reached all suitable habitats also violate the assumption of equilibrium with the environment (Barbet-Massin et al., 2018; Dimson et al., 2019).
Distribution modeling methods can be applied for a variety of reasons. The most basic purpose of distribution modeling is to produce a model that fits a study object’s distribution within an area at a specific time-point (or time interval) in the best possible way (Franklin, 2010). Distribution modeling methodology can also be used to transfer model predictions to another spatial and/or temporal setting than the one represented by the available data (Yates et al., 2018). Examples are efforts to predict effects of future climate change, for cost-efficient search for rare species, to identify areas suitable for habitat restoration, or in search for optimal locations for an activity, such as aquaculture.
Most purposes of distribution modeling can be placed along one single gradient of distribution modeling purposes. In accordance with Halvorsen (2012), we use the terms spatial prediction modeling (SPM) and ecological response modeling (ERM) for the end-points of this gradient. In SPM, the fit between model predictions and the true distribution of the study object in a specific geographical space is optimized, while in ERM the object’s response to major environmental variables, i.e., a relationship in a general ecological space is modeled. While SPM represents a purely descriptive purpose, ERM comes with an intention of understanding the study object’s distribution. The extremes along the gradient of distribution modeling purposes call for different sampling designs and methods for data collection (step 2), as well as different choices at the subsequent steps in the modeling process (steps 3–5). Because lack of a clearly formulated modeling purpose at step 1 may severely impair the reliability and applicability of distribution modeling end products, the specific problem formulation and the position of the modeling purpose along the SPM-ERM gradient could guide the choices made during all steps in the modeling process.
The lack of a unified theoretical basis and consensus on best-practice standards poses both advantages and challenges. Advantages have been creative proliferation, leading to rapid mobilization of data, development of new methods and operationalization of these methods in user-friendly software. Challenges are a large diversity of distribution modeling concepts built on different assumptions, with different demands on data quality and methods. The reliability of the resulting plethora of methods and models obviously varies, but lack of a unified theoretical basis makes them hard to compare. A statement of model assumptions and a clear formulation of the problem are necessary for transparency in the communication of modeling results.
To be able to formulate a modeling purpose precisely, a certain degree of ecological understanding of the relationship between the study object, environmental predictors and other important structuring factors (such as biotic interactions) is needed. Furthermore, it should be noted that the purpose of projecting modeling results to a different area or future climate scenarios, requires models that addresses the general relationship of the study object with the environment, i.e., an ERM model. Furthermore, knowledge of relationships in the new area or assumptions about processes that drive future development is crucial. A complete understanding of causality is, however, difficult, even often impossible, to achieve; distribution modeling basically addresses correlative relationships (see Shipley, 2016). Biotic interactions, time-lags (e.g., dispersal processes) and historical constraints (e.g., isolation due to ice age barriers) are particularly difficult to take into account in distribution modeling, as these mechanisms are difficult to represent by predictor variables. Acknowledging the lack of information on, for example, biotic interactions, as a source of reduced model performance are therefore important (Dormann et al., 2018a). We therefore recommend a conscious selection of a scale (both spatial and temporal) for the study that accord with its purpose. Of relevance in this context is that although biotic interactions are basically neighbor (local) phenomena that affect coexistence of species at finer scales, biotic interactions may occur so regularly or over so large areas that they add up to patterns that are recognizable on regional scales (Giannini et al., 2013). Moreover, when genetically and ecologically different sub-populations are to be modeled, knowledge on the ecological response at sub-population level is needed.
Violation of the assumption of equilibrium between the distribution of the modeled object and its environment reduces the reliability of the model (Chen and Leites, 2020). Violating this assumption will likely lead to under- or overpredictions by the model, depending on whether the object is a “leading edge” or a “rear end” species (e.g., Rumpf et al., 2018) and on the environment’s direction of change. Accordingly, a complex pattern of environmentally conditioned under- and overpredicted sites may result for one and the same study area. In such cases, the distribution model provides a map of the potential distribution of the study object given a specific set of assumptions (see Wiens et al., 2009). Even then, the map may be useful for specific purposes, but it should be specified that the model is predicting suitable habitats rather than a map of the realized distribution (see e.g., Gogol-Prokurat, 2011).
The properties of the modeled object and the size of the study area relative to the extent of the study object’s occurrence influence the expected level of uncertainty in distribution models (Stokland et al., 2011): weak relationships with the environment result in distribution models with lower predictability, as expected for instance for short-lived compared to longer-lived species (Hanspach et al., 2010) and for fast growing and early successional tree species compared to slow-growing species with high competitive abilities (Guisan et al., 2007). Furthermore, dispersal constraints are expected to be rare when the size of the study area is small, or if the study object is widely distributed (Soberón and Peterson, 2005).
In theory, although not yet tested in practice, compensating for violation of the assumption of equilibrium between the object’s distribution and its environment should be possible, given that the following conditions are satisfied: First, the main reason for lack of equilibrium must be recognized, for example that climate warming causes upward treeline shifts. Second, an idea about the response time or distributional time-lag of the study object is needed. For example, the time needed for treeline trees to disperse and grow tall at higher elevations. Third, historic and up-to-date climate data as well as the response of the study object must be available at the resolution relevant for distribution modeling, for example high-resolution data layers on temperature and monitoring data of treeline dynamics. If these assumptions hold true, time-lag corrected predictions can be obtained by parameterizing a model using response data that represent the present distribution and appropriate historical climate data, and project to the present climate. An example of how the response- or predictor data can be used to compensate for non-equilibrium situations is given in Figure 2. For species with rapidly advancing ranges, such as invasive species, the equilibrium assumption may be tested by building retrospective models (Barbet-Massin et al., 2018; Dimson et al., 2019).
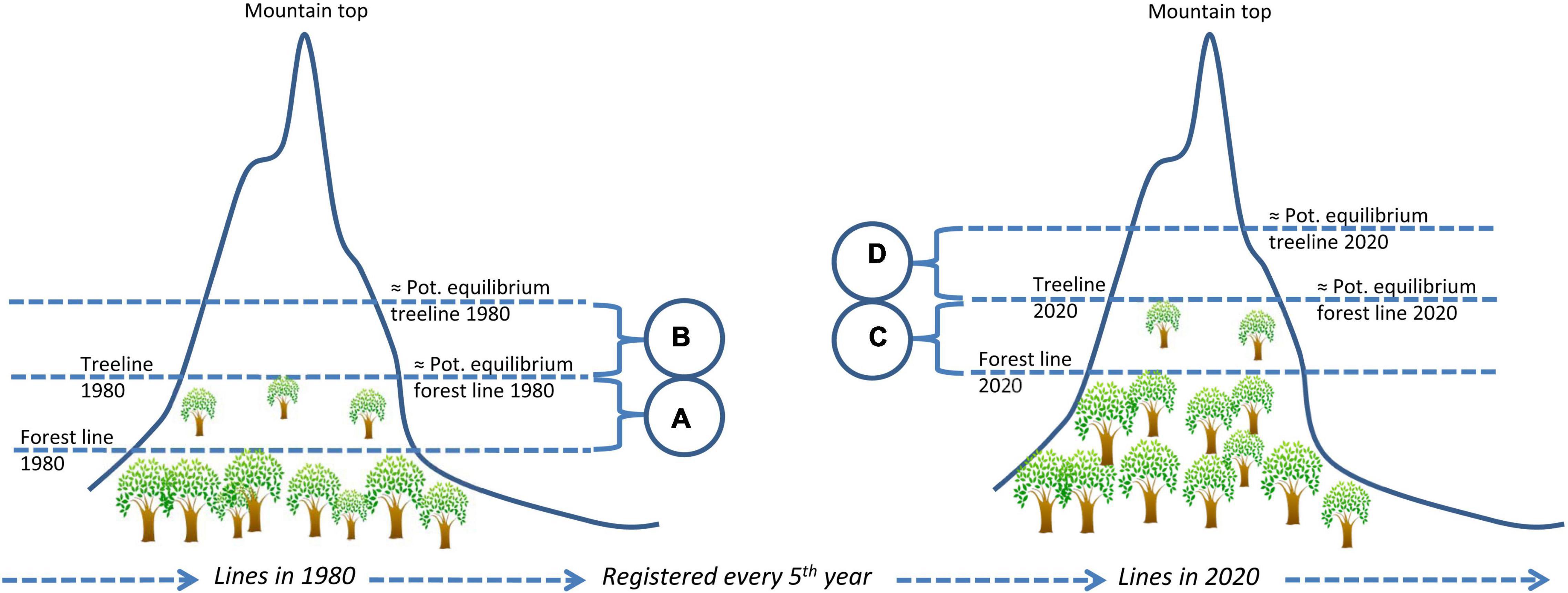
Figure 2. An example of how time-lags can be dealt with in distribution modeling by compensating for violation of the assumption of equilibrium between the object’s distribution and its environment. In the example, a time-lag of 40 years is expected to take place for trees and forests lines to expand to a specific, higher, elevation following a period of climate warming. To compensate for this lack of equilibrium, the empirical treeline in 2020 can be used as response variable in a model of the equilibrium forest line in 1980. The illustration shows the forest and tree lines in 1980 and 2020, illustrating a time-lagged process. Altitudinal intervals (A,C) indicate forest lines elevations whereas (B,D) indicate treelines elevations. Pot, Potential.
According to Osborne and Leitão (2009), sampling bias is the biggest potential source of error in response variable data for a study object. Other errors are related to imprecise or wrong georeferencing and direct errors such as misidentification of species and typing (punching) errors. All of these shortcomings introduce uncertainties into distribution models. While the accumulated impact of direct errors on the modeling result is simply proportional to the number of such errors, georeferencing errors/inaccuracies and sampling bias have more complex effects.
Georeferencing inaccuracies. We often assume that the study object is recorded without georeferencing errors (Osborne and Leitão, 2009). However, positioning inaccuracies are, to some degree, present in all georeferenced data, e.g., due to imprecision in the equipment used for recording positions. This is the case for museum records (Bloom et al., 2017), but in particular for data from citizen science projects, where considerable variation in the quality of the equipment (GPS) used for georeferencing must be expected. When mapping objects at sea, weather conditions, such as strong winds, waves and currents, will impact the precision of the recordings (Figure 3). Overall, positioning accuracy and reliability of georeferenced data has improved considerably over the last decades, after GPS equipment came into common usage. This will introduce differences in georeferencing accuracy among old and new observations. Also, the effect of positioning inaccuracies may vary in space, e.g., be higher in areas with large variation in environmental conditions over short distances, such as in steep terrain, or within the narrow tidal zone along the coast.
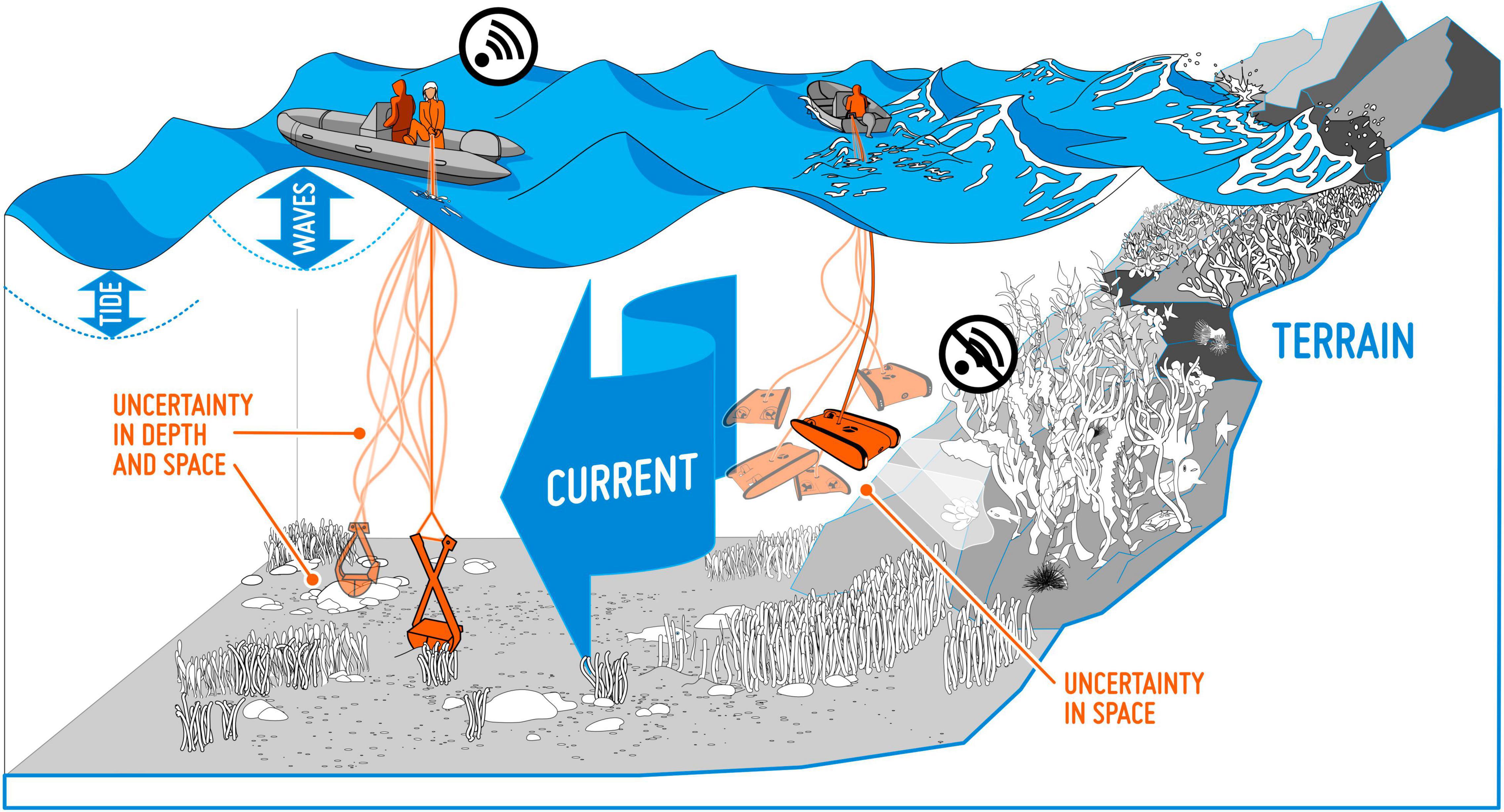
Figure 3. Collecting data from a boat at sea is associated with many potential uncertainties. Wind, waves and currents may, for instance, give rise to geopositioning inaccuracy in seabed samples.
Spatial autocorrelation is the systematic spatial variation in a variable, i.e., the tendency of observations from closely situated sites to be more similar (positive spatial autocorrelation) or less similar (negative spatial autocorrelation) than observations made further apart. Positive spatial autocorrelation is most common in data representing ecological phenomena. Spatial autocorrelation in data used for training as well as evaluation of distribution models poses challenges, and has been shown to impact both coefficients and inference in statistical analyses (e.g., Dormann et al., 2007 and references therein). This is exemplified by Tognelli and Kelt (2004) who found that the relative importance of explanatory variables may depend on the presence or absence of spatial autocorrelation in the data. Halvorsen et al. (2016) argue that challenges with spatial autocorrelation in the context of distribution modeling arise from autocorrelated residuals in the response variable and point to the importance of accounting for the spatial autocorrelation by predictor variables in the model.
Sampling bias is a broad term that encompasses many types of biases. We find it useful to distinguish between spatial, temporal and study-object bias; see discussions in Robertson et al. (2010) and Støa et al. (2018). Spatial bias is very common and occurs when some parts of the geographical and environmental space are sampled more intensively than others or when object detections are imperfect (see e.g., Lahoz-Monfort et al., 2013; Tobler et al., 2019 and references therein). That is, where the sampled frequency distribution deviates from the objects’ true distribution in the geographical and environmental space (Støa et al., 2018). This typically applies to deep oceans, high mountains, extremely strongly wave-exposed sites, war zones or other sites that are difficult to access. Spatial bias in the form of oversampling is likely to occur in particularly easily accessible locations (e.g., Wollan et al., 2008), for example as a result of sampling by citizen science (Hughes et al., 2021). Temporal bias occurs if an object is more intensively sampled during some periods (e.g., summer or daytime) than others or if, e.g., new museum material is digitized and made available before older material. Study-object bias results from specific properties of the study object (e.g., species or habitat). Thus, rare and/or inconspicuous species may be represented by too few observations to give an appropriate picture of their distribution (e.g., Varela et al., 2011) while more charismatic, “iconic” or commercially interesting ones are more prone to oversampling. Study-object bias influences the reliability of model comparison studies.
Contrary to the response data, which are sampled as point data, wall-to-wall data layers of the whole study area is needed for wall-to-wall predictive maps (Franklin, 2010). This is an important constraint which typically precludes many relevant predictors from being available for distribution modeling. Also, a predictor layer may itself be the output of a modeling process, e.g., climate data interpolated from observations at weather stations or composite layers (Simensen et al., 2020; Tessarolo et al., 2021). Depending on their origin, explanatory (predictor) data used for distribution modeling are subject to many sources of inaccuracies and errors, such as imprecise or erroneous variable values and inappropriate resolution (in space or time). Too often, the predictor variables used in distribution models come with unknown degrees of uncertainty. Typical examples are WorldClim data for terrestrial modeling (Fick and Hijmans, 2017), Bio-ORACLE for marine modeling (Assis et al., 2018) and variables derived from digital elevation models (DEM), as well as land-cover and land-use maps. When many such variables are used to build distribution models, uncertainties accumulate to an unknown magnitude.
Lack of explanatory data needed to predict an object’s distribution accurately may give rise to negative results (models with no or low predictability). This is a type of “omission error” that is likely to be underreported because of the tendency for a positive publication bias, i.e., that negative results fail to get published (Kicinski, 2013). Factors known to be important for the distribution of a species cannot be included as a predictor in the analysis unless available as wall-to-wall maps.
Lack of ecological relevance of the explanatory variables included in a distribution model is common, attributed to the fact that when variables that adequately represent the factors likely to govern the distribution of the study object are not available, we use proxies or substitutes instead. Examples of predictors that are hard or impossible to obtain wall-to-wall coverage for, are nutrient availability, oxygen level or substrate type in marine systems (Bekkby et al., 2008; Rinde et al., 2014) and water deficiency in terrestrial systems (Slette et al., 2019). Lack of relevant predictors will inevitably reduce the explanatory power of a model. Although use of proxies or substitutes that are correlated with the causal factors may improve the predictive ability of spatial prediction models, they are inappropriate for ERMs unless their relationship to the putatively causal factors is well known. Moreover, inclusion of redundant predictors may lead to errors in parameter estimates (because of collinearity), reduce precision in parameter estimation and lead to overfitting of SPM models (see e.g., Beale and Lennon, 2012; Dormann et al., 2013; Cade, 2015) and make ERMs inapplicable for their purpose.
Imprecise or erroneous predictor variable values may, for instance, be introduced by spatial interpolation of environmental models (Peters et al., 2009) based on a limited number of observations, of which each comes with its own uncertainties. The quality and relevance of modeled predictor variables used in distribution modeling studies are rarely discussed, and deserve more attention.
Inappropriate spatial resolution of important explanatory variables may impact the final model. Contrary to the response data, which are typically registered at a fine resolution in a restricted study area, predictor layers are often generated from DEM, remote sensing products or interpolated from climate data, and therefore usually available as broad-scale, low-resolution maps. Mismatch between the spatial resolutions of predictor and the response variable(s) often results in a modeling of fine-scale distributions by use of coarse-scale explanatory variables.
Inappropriate temporary resolution is exemplified by predictor variable data that do not represent the environmental conditions at the time when the distribution of the modeled object was shaped. Averaged or composite climate variables have low explanatory power when the object’s distribution is restricted by past weather extremes (e.g., Wernberg et al., 2012). The same may be the case when historic distributional data are modeled as a response to predictors that describe present environmental conditions.
Georeferencing inaccuracies should always be reduced to a minimum. This can be accomplished by using high-quality, state-of-the-art GPS equipment. However, an off-the-shelf GPS with an accuracy of 2–10 m will be sufficient for most distribution modeling purposes. If historic data (with low georeferencing quality) or data sampled under suboptimal conditions (e.g., bad weather or turbulent sea) have to be used, reliable estimates of the uncertainty should be taken into account when the distribution map is interpreted. This applies both to the model builder and the model user. The impact of georeferencing uncertainty on distribution modeling results can be estimated by simulating random location errors (see Graham et al., 2008). A general recommendation is to choose a pixel resolution that is large enough to reduce the impact of georeferencing uncertainty while at the same time accord with the modeling purpose (see e.g., Gábor et al., 2020). Finally, standardized protocols for correction of inaccurate geographic coordinates may be used, for example the SAGA protocol proposed by Bloom et al. (2017) for museum data. Such protocols are useful for correction of already sampled data, but a more provident solution is to develop rigorous protocols for sampling of new data so that the problem itself diminishes with time.
Although recent studies have indicated that spatially autocorrelated response data for the study object influences modeling results less than previously assumed (Halvorsen et al., 2016), spatial autocorrelation may still represent a challenge. Several measures can be taken to reduce the effects of this phenomenon. For instance, a number of studies enforce minimum distances between presence observations (e.g., Bryn et al., 2013) or buffering methods to avoid spatial autocorrelation (e.g., Simensen et al., 2020), whereas other studies apply systematically sampled (area-representative) training data (e.g., Horvath et al., 2019). An alternative approach, which is based on the assumption that spatial autocorrelation is less problematic than previously assumed, is “background thickening” (Vollering et al., 2019a). By this method, the density of randomized uninformed background observations to be used in presence-only distribution modeling is increased or decreased locally to match the density of presence points.
In order to reduce sampling bias, knowledge about the study object’s autecology is crucial. A basic requirement for good distribution models is that the sampling design provides accurate information about the frequency of presence (FoP) of the modeled object along all important environmental gradients (Merow et al., 2013; Halvorsen et al., 2015; Støa et al., 2018) and that the sampling matches the detectability of the study object. Irregularities in the sampling, i.e., parts of important environmental gradients that are under- or overrepresented in the sample, may be detected by comparison between observed and theoretical FoP curves (Støa et al., 2018). Identifying areas or contexts where the model is not valid, i.e., parts of gradients not adequately represented by data, will help to identify the problem. When already sampled data, for instance from museum collections or public databases (e.g., GBIF), are used for distribution modeling, all available information about sampling design and other methodological aspects related to the sampling should be used to assess potential sampling bias inherent in the dataset. Ideally, only external data that are described properly should be used. Fortunately, the number of peer reviewed data papers are increasing rapidly, e.g., in GBIF from 1 in 2011 via 13 in 2014 to 27 in 2018 (GBIF, 2019).
Small datasets come with more stochasticity, which normally entails higher difficulties in obtaining significant and interpretable patterns by modeling. Ideally, data should be collected specifically for each modeling study, based on a tailor-made sampling design that matches the specific modeling purpose. The spatial pattern of objects with “clumped distributions” and specific environmental demands can generally be modeled with greater precision than patterns of widely distributed objects (Carrascal et al., 2006; Hernandez et al., 2006; Stokland et al., 2011). In order to model “ubiquitous” objects, the spatial resolution of the predictor variables should be high enough to capture variation along relevant local environmental variables (Halvorsen, 2012). MacKenzie et al. (2002) and Tyre et al. (2003) provide methods for taking imperfect detection of small, rare and inconspicuous organisms into account when building models.
Lack of access to explanatory variables that may directly represent factors known to be important for an object’s distribution can be dealt with by using available proxies. This could be ocean depth as a proxy for solar irradiance at the sea floor, or altitude as a proxy for terrestrial temperature. However, the use of proxies reduces the interpretability of the studied object’s relationship with the environment, as many proxies are strongly correlated with several predictor variables. Global environmental models, such as those provided by WorldClim (Fick and Hijmans, 2017) and Bio-ORACLE (Assis et al., 2018) for terrestrial and marine environments, respectively, have rapidly become very popular, and are used in many bioclimatic studies. Still, they should be used with caution, for several reasons. First, such models are often developed from data with unknown levels of inaccuracy. Second, generic data may not match the appropriate scale for a specific study and hence be more or less irrelevant, or even direct the study toward a suboptimal choice of spatial resolution. Advantages of using easily accessible, modeled predictor data are that they have typically been described, tested and analyzed with respect to uncertainty in many studies, and that much experience has been gained by their use for practical distribution modeling (e.g., Bedia et al., 2013). Furthermore, in general we think that the use of remote sensing based explanatory variables could be exploited more in ecological distribution models (see e.g., Tang et al., 2020).
One way to deal with imprecise predictor variables, or biased response data, is to create a confidence map, which provides the user with information about where a distribution model is judged or estimated to be reliable and where it is less so (e.g., Hemsing and Bryn, 2012). A confidence map may, for instance, contain information about the number of data points that back up each pixel value, areas with poor coverage of satellite data, areas where comparable datasets produced by others deviate, or areas where predictions from models obtained by different methods deviate.
The use of correlative (i.e., not causative) predictors in space or time can be justified if the aim is to obtain the model that best predicts patterns of presence in a certain area in a specific time interval, i.e., SPM. In these cases, the correlative predictors may serve as useful proxies for missing relevant variables. However, if the aim is ERM, in order to understand ecological relationships or to transfer (extrapolate) predictions to another spatial and/or temporal setting than those represented by the data, great caution should be taken when using non-causative variables in the modeling.
A vast number of different distribution modeling methods, as well as a variety of software and interfaces, have been developed and applied for distribution modeling over the last decades. This has made distribution modeling more accessible as a tool, and easier to adapt for different types of data and purposes. Early distribution modeling packages and procedures, such as BIOCLIM (Busby, 1991) and HABITAT (Walker and Cocks, 1991) were developed for envelope modeling. Other models were based on dissimilarity or ecological distance, such as DOMAIN (Carpenter et al., 1993) and ENFA (Hirzel et al., 2002), respectively. The different methods come with different assumptions and tuning options and are vulnerable to errors, biases and inaccuracies in different ways and to different degrees. The momentum of distribution modeling has later turned toward more flexible methods, such as boosted regression trees (BRT; Elith et al., 2008), maximum entropy (MaxEnt; Phillips et al., 2006) and random forest (RF; Breiman, 2001). This change of focus is most likely related to the easy access of presence-only data available through open access geodatabases such as GBIF. Modeling methods which use presence-absence data, such as generalized linear models (GLM; Guisan et al., 2002) and generalized additive models (GAM; Guisan et al., 2002) are also frequently used in distribution modeling studies. Presence-only (PO) and presence-absence (PA) data differ fundamentally with respect to size and type of uncertainties. PA data contain concrete information about presence and absence localities for the study object, if assuming perfect detection and identification. PO data, on the other hand, only contains a sample of localities with known presence. Most distribution modeling methods adapted for use with PO data, such as MaxEnt, makes use of uninformed background observations. The uninformed background may contain presence as well as absence observations.
The modeling methods are constantly developed, improved, and adapted to specific purposes, data processes and input data formats (Barry and Elith, 2006; Beale and Lennon, 2012; Fernandes et al., 2018). A strong, recent trend is to make the methods available as code-packages in R (e.g., Phillips et al., 2017; Vollering et al., 2019b). Both regression-based and machine learning methods can potentially fit models well to the response data. With regression-based methods the user can define the form of the relationship and any interaction a priori, whereas machine learning methods have the advantage of modeling non-linear relationships and interactions among variables based on the data. Both may sometimes produce highly overfitted or underfitted models (Figure 4), depending on how the model is tuned under options and settings. Different methods are suited for different kinds of data, allow for different kinds of tuning and are affected differently by errors, biases and inaccuracies. For example, Fernandes et al. (2018) showed that models with high fit (e.g., using Random Forest) were more negatively influenced by errors and biases (lower predictive success) compared with models with lower fit (e.g., GLMs), whereas models assuming a linear relationship (e.g., GLMs/GLMMs) are more affected by collinearity and multicollinearity. Schank et al. (2019) showed that integrated distribution models can improve the handling of sampling bias whereas Tobler et al. (2019) discuss the impact of measurement errors and correlation between objects in joint distribution models.
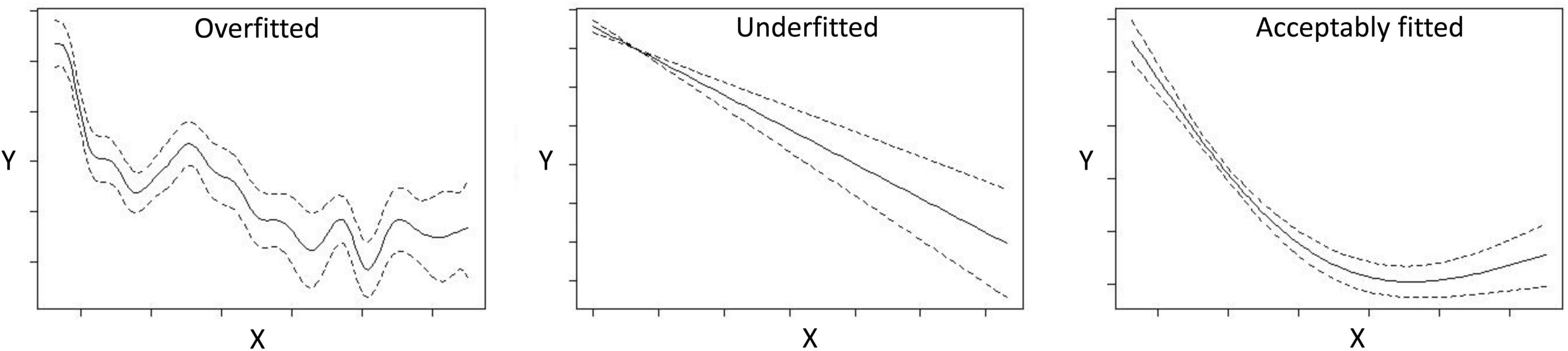
Figure 4. Examples of response (Y) plots from GAM analyses showing an overfitted, underfitted and acceptably fitted curve against the predictor variable (X).
To avoid biologically unrealistic or otherwise unreliable modeling results and interpretations, a deep ecological understanding of the study object is needed (Figure 5). Thus, the choice of modeling method and the tuning of different parameters to optimize predictive accuracy should be guided by the modeling purpose and the properties of the study object and the types of response and predictor data used. The type of response data, such as PO, PA, ordered factor, or continuous, call for different choices of method. Methods for PO data call for particular attention to the sampling design for uninformed background or pseudo-absence observation, which may heavily impact modeling results (Stokland et al., 2011; Støa et al., 2018). Several alternative sampling strategies have been proposed, for example “target-group background,” “presence thinning,” and “background thickening” (Phillips and Dudík, 2008; Støa et al., 2018; Vollering et al., 2019a). In general, model performance is more affected by false positives than false negatives (Fernandes et al., 2018).
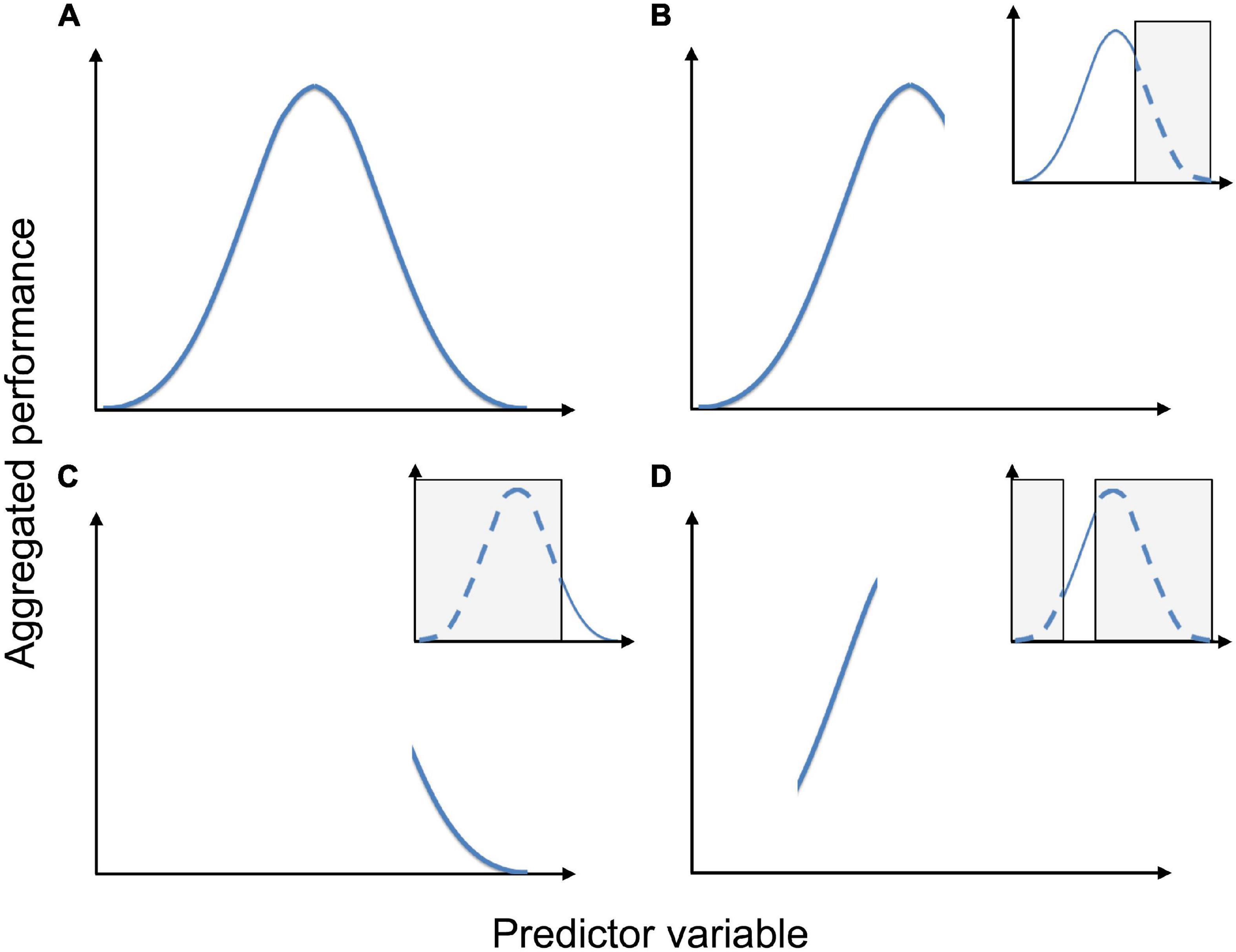
Figure 5. The effect of sampling pattern on the shape of a species’ response to a predictor variable. Aggregated performance is a collective term for the species’ performance (e.g., probability of occurrence, average cover etc.), aggregated for observations units in each segment of an environmental gradient (the predictor variable). (A) Unimodal response in a sample that spans the entire tolerance of the species. (B) Truncated unimodal response in a sample that includes the species’ optimum and one of its tolerance limits. (C) Hinge-shaped response in a sample that only includes a smaller portion of the environmental gradient close to one of the species’ tolerance limits. (D) Apparently linear response in a sample that neither includes the optimum nor any tolerance limit. Inserts show which part(s) of the species’ tolerance that is not sampled (gray). Figure reproduced from Halvorsen (2012).
Different distribution modeling approaches rely on different assumptions and have different advantages and disadvantages (see discussion in Shabani et al., 2016). For instance, some methods lean on a priori assumptions about the residual distribution (e.g., normal, binomial or poisson) or response curve shapes (e.g., linear or non-linear); some methods are suitable for capturing non-additive behaviors and complex interactions; some produce complex and often overfitted models that open for spurious interpretations while others may tend to produce too simple models. Some methods are robust to noise, some require large datasets, whereas others may perform well also with small samples (see Heikkinen et al., 2006). Furthermore, although many modeling methods are flexible with respect to data properties, available data and data formats will reduce the number of appropriate modeling methods. For instance, some methods handle presence-only data well (e.g., MaxEnt), others are developed for analyzing presence-absence data (e.g., GAM), whereas others again handle ordinal response variables (e.g., CLM). Explorative statistical analyses of data, such as calculation of descriptive statistics and analysis of frequency-of-presence (FoP) curves, should be standard elements in all distribution modeling studies, conducted before any definite decisions about modeling setup is made.
Many distribution modeling methods come with considerable flexibility with respect to tuning for complexity. In general, the choice between simpler or more complex models should be guided by modeling purpose; a complex SPM model is not overfit if its predictive ability is better than any simpler model, while ERM models are overfit if they include predictors that are not generally important for the distribution of the study object (Halvorsen, 2012). The tuning options of, for example, the regularization multiplier (Warren and Seifert, 2011) or the significance level of the F-ratio test in MaxEnt (Halvorsen, 2013) or the smoothing function in GAM (Guisan et al., 2002) are examples that control the fit of the model to data and modeling purpose. Empirically based advices on how to make these choices are, among others, given by Merow et al. (2013) and Halvorsen et al. (2015). Building models with an appropriate degree of complexity (fit) is critical for robust inference (Merow et al., 2014). Complexity indicators such as number of parameters and shapes of predicted relative FoP curves (Støa et al., 2018) are important tools for assessment of model reliability.
Model averaging or ensemble modeling, with the purpose of generating a unified (and agreed-on) model are increasingly used in distribution modeling studies (Buisson et al., 2010; Dormann et al., 2018b). Ensemble modeling may reduce the effect of biases, inaccuracies and errors in each component model. However, the merging of results from different approaches does not resolve fundamental challenges such as modeling with biased training data, missing explanatory variables, model misspecification or under- and overfitted models. Merging the outputs from many models may make detection of such pitfalls more difficult, among others by signaling degrees of precision and quality that are not supported by the models. A general advice is therefore to run distribution models with different methods, not with the purpose of obtaining and presenting one unified model, but as a means for comparing results and testing model robustness. For averaging and ensemble modeling, it would be beneficial to establish protocols for how to present the material, methods and outputs. An example of this is the World Climate Research Programme (WCRP), where the Coupled Model Intercomparison Project (CMIP) was established to standardize multi-model output formats of Earth System Models, as well as other goals (Eyring et al., 2016).
Distribution models can be built with biased data, without a relevant spatial raster resolution, without important explanatory variables, and with inappropriate choice of methods or options or inappropriate tuning of these options. Ecologically nonsense models may result if the pitfalls, shortcomings and uncertainties discussed above at each step in the modeling process are not taken into account. This is why all distribution models, in fact all models, should be evaluated (e.g., Oreskes et al., 1994; Araújo and Guisan, 2006). Several approaches to evaluation of distribution models are available (Araújo et al., 2005); e.g., re-substitution, cross-validation and data partitioning. However, these methods share the basic shortcoming that the training and evaluation datasets are subsets of the same sample, collected by the same sampling design and under the same “knowledge regime.” The data used for modeling and evaluation then contain the same errors, biases, and inaccuracies (Roberts et al., 2017). A fully independent evaluation implies collecting evaluation data independently of the data collected for parameterization of the model, i.e., at a different place, at a different time, and/or by using a different sampling design (Araújo et al., 2005; Halvorsen, 2012).
Modeling methods developed for handling presence-absence (PA) data, such as GLM and GAM, are frequently used for distribution modeling. When used with PA data, these methods provide estimates of predicted probabilities of presence (PPP) in the terminology of Halvorsen (2012), i.e., occurrence probability values on the 0–1 probability scale. In contrast, the use of presence-only (PO) data with these or other methods provides relative probabilities of presence (RPPP; Halvorsen, 2012) or relative occurrence rates (Merow et al., 2013), i.e., a ranking of the sites by occurrence probability. Despite the fundamental difference between these two types of output, Yackulic et al. (2013) found that approximately 50% of the reviewed MaxEnt studies, in which the default logistic output format was applied, contained erroneous interpretations of model predictions as PPP.
Distribution models used for predictions in time, for example to predict future range shifts under varying climate scenarios or the potential spread of invasive species (Gallien et al., 2012), cannot be evaluated in the strict sense of the term. When the predicted events have not yet taken place, no “true” distributions exist that can be described by sampling of evaluation data (Buisson et al., 2010). This is also the case for hindcasts, when historical evaluation data is not available. For forecast and hindcast, the evolutionary plasticity and potential for adaptions of the target, often termed niche conservatism (see e.g., Wiens and Graham, 2005), should be considered when modeling decades or centuries in time (depending on the study object).
Evaluation by use of fully independent data is the only way to completely circumvent pitfalls related to sampling bias in a dataset (Austin, 2007; Veloz, 2009). Most likely, an independently collected evaluation dataset will not include the same errors, biases and inaccuracies as the training dataset, but it may come with its own shortcomings. The ideal dataset for evaluation of distribution models is collected by a sampling strategy that avoids sampling bias of any kind. Many uncertainties of models that are based upon PO data can only be circumvented by access to independent PA data for model calibration (Merow et al., 2013; Halvorsen et al., 2015); i.e., assessment of the numerical accuracy of model predictions. According to Harrell et al. (1996), independent presence-absence data are required for any kind of model calibration, i.e., the conversion of model predictions from a relative (RPPP) to a predicted probability scale (PPP).
Independent P-A evaluation data can be obtained by a wide spectrum of different approaches, e.g.: (1) Stratified random sampling, using modeled RPPP values as a criterion for stratification (Halvorsen et al., 2015). (2) Environmentally stratified sampling, by which all levels along all environmental gradients important for the study object is deliberately captured. (3) Spatially systematic sampling involves the selection of observations according to a pre-designed spatial sampling. This method avoids over- or underrepresentation (spatial clustering or the converse) of data points (Horvath et al., 2019). These three sampling procedures have different advantages and disadvantages. While approach (1) may be optimal for testing one particular model, it is less useful for testing other models. Also, it implies a two-phase sampling procedure. Environmentally stratified sampling (2) may be theoretically optimal because it provides balanced data for calculation of frequency-of-presence (FoP) curves (e.g., Halvorsen et al., 2015), but difficult to carry out in practice when models are complex with many predictor variables. Both of approaches (2) and (3) may fail to provide enough data for valid evaluation of models for study objects with low prevalence due to spatially aggregated and/or restricted occurrences. Furthermore, these approaches will be practically unmanageable for study areas with large extent and/or contains a large fraction of remote or otherwise inaccessible areas.
When the modeling purpose is predictions in time, and evaluation by independent data is not possible, comparing models trained with different data and parallel use of several modeling methods is pivotal (e.g., Elith et al., 2006).
Since many of the choices made during this process are determined by the modeling purpose, use of models outside their intended purpose is not recommended and should, in any case, be done with great care. However, once a distribution model is published and available “out there,” it will be picked up by other scientists, managers, planners, NGOs, politicians, industrialists or others. Typically, knowledge of errors, biases and uncertainties tend to be lost during transfer of a distribution model from developer to multiple potential users. An example of this is when results of a local study is extrapolated to a larger area or to other areas, for instance as part of spatial planning. Models based on fine-resolution data are often used for prediction in other areas, using input data with coarser resolution, without ensuring that the model is robust to this change of scale (Yates et al., 2018). Such use may, e.g., lead to misinterpretation of areas as suitable for an object or of marginal areas for a threatened study object as its core area.
Pearson (2010) points out that end users of distribution models may get an impression of reliability simply by being impressed by the apparent complexity of the technology. Whether this is common or not is hard to assess, but as mentioned above (Step 4), even model builders themselves often misinterpret the output of their modeling (Yackulic et al., 2013). Thus, although not yet supported by research, the risk that non-scientific users misinterpret modeling results is expected to be even greater. Incorrectly interpreted models, errors and biases that are overlooked, and unfounded faith can all lead to wrong decisions, such as the initiation of inappropriate actions or putting required management on hold.
To make a distribution model and model-derived results useful for other purposes and other users than originally intended, these auxiliary users should be provided the basic information needed to make well-informed judgments of the appropriateness of the product for their intended use. Models should therefore be accompanied by a fact sheet that includes understandable information on the original modeling purpose, the data and the methods used, and, if relevant, specific restrictions to the generality of the model. Confidence maps and other documentation or judgments of biases, errors and uncertainties should be standard elements in the fact sheet. The ODMAP protocol suggested by Zurell et al. (2020), or the INSPIRE data infrastructure for mapping and modeling in EU, which also includes standards for metadata1, may be relevant.
The users of distribution models need to be reminded that a distribution model is not a true map of the object’s distribution or abundance, but rather mapped predictions of the (relative) potential for a given object to be present in each grid cell based on the available explanatory variables and response data. The study object may well be absent from a grid cell with high predicted probability of presence, or present in a cell with low predicted value. This uncertainty calls for special care when models are used for prioritization for conservation purposes (Schuetz et al., 2015). Information about the predictive performance of the model (e.g., Mouton et al., 2010), preferably obtained by evaluation on independent data, is therefore essential.
Maps resulting from distribution modeling can be tailored to different purposes by, for instance, selecting different cut-off values, i.e., threshold values used to transform predictions from a continuous scale to binary predictions (presences and absences, Figure 6; Scherrer et al., 2020). It is often assumed that binary predictions makes prediction maps easier for managers and planners to understand and use than continuous maps. Binary maps based upon a high threshold value may be useful for users who want to identify areas of high probability of finding the study object (Figure 6). However, for users who want to identify areas that maximize the chance of covering the range of a study object, a low cut-off value is more appropriate (see Freeman and Moisen, 2008). It should be noted, however, that conversion from continuous to binary predictions inevitably implies loss of information. Another possibility is to refine or post-process the distributions models afterward (e.g., Kass et al., 2021), so that the models are improved according to the specific needs.
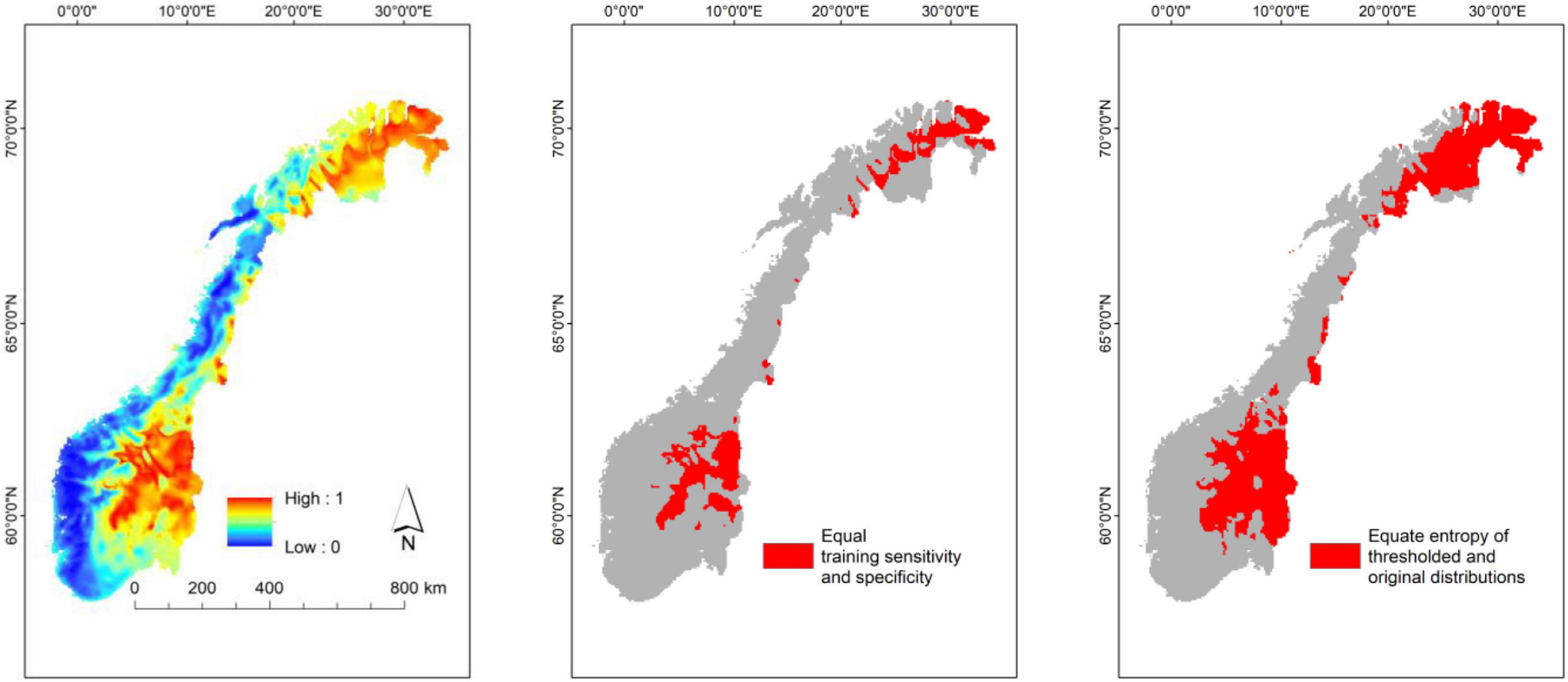
Figure 6. Example of distribution model with continuous prediction values (left) converted into two binary maps for practical management purposes, using high (mid; Equal training sensitivity and specificity) and low thresholds (right; Equate entropy of thresholded and original distributions).
In this synthesis, we have described the uncertainties associated with each step of the distribution modeling process (Figure 1). We have explained how biases, errors and inaccuracies influence model reliability and tried to provide some general guidelines on how to deal with them. Although quoted many times, we think it is appropriate to repeat the famous words of Box (1979, p. 202): “All models are wrong, but some are useful.” Although distribution models vary with respect to assumptions, data material, methods and evaluation schemes, the complexity of ecological relationships and the modeling process itself (Figure 1) inevitably implies accumulation of biases, errors and inaccuracies, some of which may be recognized, while others will remain hidden. At some level of detail, all distribution models are bound to be wrong, but for the specific purposes they may yet be useful.
Different errors, biases and inaccuracies have different implications for end users. Most of these implications are, however, hard or impossible to recognize, of unknown magnitude, with effects that will remain unexplored. Their impact may vary in space (e.g., be more influential in steeper than in flat terrain), in time (e.g., being more serious for old than for new data), and/or between species (e.g., mobile species being more difficult to model than sedentary ones) or other objects. Since distribution models, like other results of statistical analyses, are simplifications of the real world, removing all uncertainty is not possible. But we can aim for minimizing the uncertainties and understand their sources and their implications on the reliability of the end product. Table 1 sum up our recommendations on how to deal with the uncertainties at the different steps of the distribution modeling process.

Table 1. Summary of considerations regarding biases, errors and inaccuracies at each step in the process of distribution modeling, and recommendations on how to deal with them.
A major focus in distribution modeling is to identify spatial patterns in datasets and to use these patterns to predict the potential distribution of study objects. Practical experience with distribution models suggests that these models are often reasonably good in spite of the uncertainties that accumulate throughout the modeling process. We believe that a major reason for this is the strong structuring of geographical patterns by fundamental ecological complex gradients (Halvorsen, 2012) such as temperature, precipitation, seawater salinity, soil cation concentrations and soil moisture. Together these predictors explain a large fraction of the variation in the distribution of species and habitats at local and regional scales (see Bekkby et al., 2008; Horvath et al., 2019).
All in all, we recommend a standard for distribution modeling to ensure that the model and the data on which it is based are clearly communicated. This could be done in fact sheets that may include confidence maps, metadata and model evaluation results, e.g., following the ODMAP protocol (Zurell et al., 2020). Furthermore, despite the costs, evaluation of distribution models by truly independent data should become the norm rather than a rare exception. We also want to stress the difference between deductive implementation of distribution models, by which data are sampled with the aim of testing a hypothesis, and inductive approaches, by which hypotheses are generated from analysis of observations. Inductive studies, which prevail today, are useful for creating hypotheses about poorly known study objects. They may serve SPM as well as ERM purposes. When specific ecological hypotheses are to be tested, deductive studies are recommended. Linking the correlative approach of distribution modeling to mechanistic and dynamic modeling (Dormann et al., 2012), may improve both methods and increases the credibility if they support the same ecological story (Horvath et al., 2021).
Finally, the accumulated uncertainty throughout the distribution modeling process is hardly possible to coerce into simple indices. The potential influence of each error, bias and inaccuracy that enters the final model at each step of the distribution modeling process is too diverse to be expressed by simple estimators. Instead, each step should be dealt with successively and confronted with the goals of the study, so that measures to increase the reliability can be taken during all parts of the modeling process.
AB and TB conceived the idea and drafted the manuscript. All authors contributed equally on the manuscript thereafter.
This work has been funded by the University of Oslo, Norwegian Institute for Water Research and Norwegian Institute of Bioeconomy Research.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We thank Anders K. Wollan, Bente Støa, Dag Endresen, Lars Erikstad, Peter Horvath, Thijs C. van Son, Trond Simensen, and Vegar Bakkestuen for comments on the manuscript. Thanks to Jan Heuschele for making Figure 3.
Araújo, M. B., and Guisan, A. (2006). Five (or so) challenges for distribution modelling. J. Biogeogr. 33, 1677–1688. doi: 10.1111/j.1365-2699.2006.01584.x
Araújo, M. B., Anderson, R. P., Barbosa, A. M., Beale, C. M., Dormann, C. F., Early, R., et al. (2019). Standards for distribution models in biodiversity assessments. Sci. Adv. 5:eaat4858. doi: 10.1126/sciadv.aat4858
Araújo, M. B., Pearson, R. G., Thuiller, W., and Erhard, M. (2005). Validation of species–climate impact models under climate change. Glob. Change Biol. 11, 1504–1513. doi: 10.1111/j.1365-2486.2005.01000.x
Assis, J., Tyberghein, L., Bosch, S., Verbruggen, H., Serrão, E. A., and De Clerck, O. (2018). Bio-ORACLE v2.0: extending marine data layers for bioclimatic modelling. Glob. Ecol. Biogeogr. 27, 277–284. doi: 10.1111/geb.12693
Aubry, K. B., Raley, C. M., and McKelvey, K. S. (2017). The importance of data quality for generating reliable distribution models for rare, elusive, and cryptic species. PLoS One 12:e0179152. doi: 10.1371/journal.pone.0179152
Austin, M. (2007). Species distribution models and ecological theory: a critical assessment and some possible new approaches. Ecol. Modelling 200, 1–19. doi: 10.1016/j.ecolmodel.2006.07.005
Barbet-Massin, M., Rome, Q., Villemant, C., and Courchamp, F. (2018). Can species distribution models really predict the expansion of invasive species? PLoS One 13:e0193085. doi: 10.1371/journal.pone.0193085
Barry, S., and Elith, J. (2006). Error and uncertainty in habitat models. J. Appl. Ecol. 43, 413–423. doi: 10.1111/j.1365-2664.2006.01136.x
Beale, C. M., and Lennon, J. J. (2012). Incorporating uncertainty in predictive species distribution modelling. Philos. Trans. R. Soc. B 367, 247–258. doi: 10.1098/rstb.2011.0178
Bedia, J., Herrera, S., and Gutierrez, J. M. (2013). Dangers of using global bioclimatic datasets for ecological niche modeling. Limitations for future climate projections. Glob. Planet. Change 107, 1–12. doi: 10.1016/j.gloplacha.2013.04.005
Bekkby, T., Rinde, E., Erikstad, L., Bakkestuen, V., Longva, O., Christensen, O., et al. (2008). Spatial probability modelling of eelgrass Zostera marina L. distribution on the West coast of Norway. ICES J. Mar. Sci. 65, 1093–1101. doi: 10.1093/icesjms/fsn095
Bloom, T. D., Flower, A., and DeChaine, E. G. (2017). Why georeferencing matters: Introducing a practical protocol to prepare species occurrence records for spatial analysis. Ecol. Evol. 8, 765–777. doi: 10.1002/ece3.3516
Bonan, G. (2008). Forests and climate change: forcings, feedbacks, and the climate benefits of forests. Science 320, 1444–1449. doi: 10.1126/science.1155121
Box, G. E. P. (1979). “Robustness in the strategy of scientific model building,” in Robustness in Statistics, eds R. L. Launer and G. N. Wilkinson (Cambridge, MA: Academic Press), 201–236.
Brown, J. L., and Yoder, A. D. (2015). Shifting ranges and conservation challenges for lemurs in the face of climate change. Ecol. Evol. 5, 1131–1142. doi: 10.1002/ece3.1418
Bryn, A., Dourojeanni, P., Hemsing, L. Ø, and O’Donnel, S. (2013). A high-resolution GIS null model of potential forest expansion following land use changes in Norway. Scand. J. For. Res. 28, 81–98. doi: 10.1080/02827581.2012.689005
Buisson, L., Thuiller, W., Casajus, N., Lek, S., and Grenouillet, G. (2010). Uncertainty in ensemble forecasting of species distribution. Glob. Change Biol. 16, 1145–1157. doi: 10.1111/j.1365-2486.2009.02000.x
Busby, J. R. (1991). “BIOCLIM – a bioclimate analysis and prediction system,” in Nature Conservation: Cost Effective Biological Surveys And Data Analysis, eds C. R. Margules and M. P. Austin (Melbourne, VIC: CSIRO), 64–68.
Cade, B. S. (2015). Model averaging and muddled multimodel inferences. Ecology 96, 2370–2382. doi: 10.1890/14-1639.1
Carpenter, G., Gillison, A. N., and Winter, J. (1993). DOMAIN: a flexible modelling procedure for mapping potential distributions of animals and plants. Biodivers. Conserv. 2, 667–680. doi: 10.1007/bf00051966
Carrascal, L. M., Seoane, J., Palomino, D., Alonso, C. L., and Lobo, J. M. (2006). Species-specific features affect the ability of census-derived models to map winter avian distribution. Ecol. Res. 21, 681–691. doi: 10.1007/s11284-006-0173-y
Chen, X., and Leites, L. (2020). The importance of land-use legacies for modeling present-day species distributions. Landsc. Ecol. 35, 2759–2775. doi: 10.1007/s10980-020-01119-0
Dimson, M., Lynch, S. C., and Gillespie, T. W. (2019). Using biased sampling data to model the distribution of invasive shot-hole borers in California. Biol. Invasions 21, 2693–2712. doi: 10.1007/s10530-019-02010-z
Dormann, C. F., Bobrowski, M., Dehling, D. M., Harris, D. J., Hartig, F., Lischke, H., et al. (2018a). Biotic interactions in species distribution modelling: 10 questions to guide interpretation and avoid false conclusions. Glob. Ecol. Biogeogr. 27, 1004–1016. doi: 10.1111/geb.12759
Dormann, C. F., Calabrese, J. M., Guillera-Arroita, G., Matechou, E., Bahn, V., Bartoń, K., et al. (2018b). Model averaging in ecology: a review of Bayesian, information-theoretic, and tactical approaches for predictive inference. Ecol. Monogr. 88, 485–504. doi: 10.1002/ecm.1309
Dormann, C. F., Elith, J., Bacher, S., Buchmann, C., Carl, G., Carré, G., et al. (2013). Collinearity: a review of methods to deal with it and a simulation study evaluating their performance. Ecography 36, 27–46. doi: 10.1111/j.1600-0587.2012.07348.x
Dormann, C. F., McPherson, J. M., Araújo, M. B., Bivand, R., Bolliger, J., Carl, G., et al. (2007). Methods to account for spatial autocorrelation in the analysis of species distributional data: a review. Ecography 30, 609–628. doi: 10.1111/j.2007.0906-7590.05171.x
Dormann, C. F., Schymanski, S. J., Cabral, J., Chuine, I., Graham, C., Hartig, F., et al. (2012). Correlation and process in species distribution models: bridging a dichotomy. J. Biogeogr. 39, 2119–2131. doi: 10.1111/j.1365-2699.2011.02659.x
Drew, C. A., Wiersma, Y. F., and Huettmann, F. (2011). Predictive Species And Habitat Modelling In Landscape Ecology: Concepts And Applications. Berlin: Springer Verlag.
Elith, J., Graham, C. H., Anderson, R. P., Dudík, M., Ferrier, S., Guisan, A., et al. (2006). Novel methods improve prediction of species’ distributions from occurrence data. Ecography 29, 129–151. doi: 10.1111/j.2006.0906-7590.04596.x
Elith, J., Leathwick, J. R., and Hastie, T. (2008). A working guide to boosted regression trees. J. Anim. Ecol. 77, 802–813. doi: 10.1111/j.1365-2656.2008.01390.x
Eyring, V., Bony, S., Meehl, G. A., Senior, C. A., Stevens, B., Stouffer, R. J., et al. (2016). Overview of the coupled model intercomparison project phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 9, 1937–1958. doi: 10.5194/gmd-9-1937-2016
Fernandes, R. F., Scherrer, D., and Guisan, A. (2018). Effects of simulated observation errors on the performance of species distribution models. Divers. Distrib. 25, 400–413. doi: 10.1111/ddi.12868
Fick, S. E., and Hijmans, R. J. (2017). Worldclim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 37, 4302–4315. doi: 10.1002/joc.5086
Franklin, J. (2010). Mapping Species Distributions: Spatial Inference And Prediction. Cambridge: Cambridge University Press.
Freeman, E. A., and Moisen, G. G. (2008). A comparison of the performance of threshold criteria for binary classification in terms of predicted prevalence and kappa. Ecol. Modelling 217, 48–58. doi: 10.1016/j.ecolmodel.2008.05.015
Gábor, L., Moudrý, V., Lecours, V., Malavasi, M., Barták, V., Fogl, M., et al. (2020). The effect of positional error on fine scale species distribution models increases for specialist species. Ecography 43, 256–269. doi: 10.1111/ecog.04687
Gallien, L., Douzet, R., Pratte, S., Zimmermann, N. E., and Thuiller, W. (2012). Invasive species distribution models – how violating the equilibrium assumption can create new insight. Glob. Ecol. Biogeogr. 21, 1126–1136. doi: 10.1111/j.1466-8238.2012.00768.x
GBIF (2019). Available online at: https://www.gbif.org/data-papers (accessed January 22, 2019).
Giannini, T. C., Chapman, D. S., Saraiva, A. M., Alves-dos-Santos, I., and Biesmeijer, J. C. (2013). Improving species distribution models using biotic interactions: a case study of parasites, pollinators and plants. Ecography 36, 649–656. doi: 10.1111/j.1600-0587.2012.07191.x
Gogol-Prokurat, M. (2011). Predicting habitat suitability for rare plants at local spatial scales using a species distribution model. Ecol. Appl. 21, 33–47. doi: 10.1890/09-1190.1
Graham, C. H., Elith, J., Hijmans, R. J., Guisan, A., Townsend Peterson, A., and Loiselle, B. A. (2008). The influence of spatial errors in species occurrence data used in distribution models. J. Appl. Ecol. 45, 239–247. doi: 10.1111/j.1365-2664.2007.01408.x
Guisan, A., and Zimmermann, N. E. (2000). Predictive habitat distribution models in ecology. Ecol. Modelling 135, 147–186. doi: 10.1016/s0304-3800(00)00354-9
Guisan, A., Edwards, T. C., and Hastie, T. (2002). Generalized linear and generalized additive models in studies of species distributions: setting the scene. Ecol. Modelling 157, 89–100. doi: 10.1016/s0304-3800(02)00204-1
Guisan, A., Zimmermann, N. E., Elith, J., Graham, C. H., Phillips, S., and Peterson, A. T. (2007). What matters for predicting the occurrences of trees: techniques, data or species characteristics? Ecol. Monogr. 77, 615–630. doi: 10.1890/06-1060.1
Halvorsen, R. (2012). A gradient analytic perspective on distribution modelling. Sommerfeltia 35, 1–165. doi: 10.2478/v10208-011-0015-3
Halvorsen, R. (2013). A strict maximum likelihood explanation of MaxEnt, and some implications for distribution modelling. Sommerfeltia 36, 1–132. doi: 10.2478/v10208-011-0016-2
Halvorsen, R., Mazzoni, S., Bryn, A., and Bakkestuen, V. (2015). Opportunities for improved distribution modelling practice via a strict maximum likelihood interpretation of MaxEnt. Ecography 38, 172–183. doi: 10.1111/ecog.00565
Halvorsen, R., Mazzoni, S., Dirksen, J. W., Næsset, E., Gobakken, T., and Ohlson, M. (2016). How important are choice of model selection method and spatial autocorrelation of presence data for distribution modelling by MaxEnt? Ecol. Modelling 328, 108–118. doi: 10.1016/j.ecolmodel.2016.02.021
Hanspach, J., Kühn, I., Pompe, S., and Klotz, S. (2010). Predictive performance of plant species distribution models depends on species traits. Perspect. Plant Ecol. Evol. Syst. 12, 219–225. doi: 10.1016/j.ppees.2010.04.002
Harrell, F. E., Lee, K. L., and Mark, D. B. (1996). Multivariate prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat. Med. 15, 361–387.
Heikkinen, R. K., Luoto, M., Araújo, M. B., Virkkala, R., Thuiller, W., and Sykes, M. T. (2006). Methods and uncertainties in bioclimatic envelope modelling under climate change. Prog. Phys. Geography 30, 751–777. doi: 10.1177/0309133306071957
Hemsing, L. Ø, and Bryn, A. (2012). Three methods for modelling potential natural vegetation (PNV) compared: a methodological case study from south-central Norway. Norwegian J. Geogr. 66, 11–29. doi: 10.1080/00291951.2011.644321
Hernandez, P. A., Graham, C. H., Master, L. L., and Albert, D. L. (2006). The effect of sample size and species characteristics on performance of different species distribution modeling methods. Ecography 29, 773–785. doi: 10.1111/j.0906-7590.2006.04700.x
Hirzel, A. H., Hausser, J., Chessel, D., and Perrin, N. (2002). Ecological-niche factor analysis: how to compute habitat-suitability maps without absence data? Ecology 83, 2027–2036.
Horvath, P., Halvorsen, R., Stordal, F., Tallaksen, L. M., Tang, H., and Bryn, A. (2019). Distribution modelling of vegetation types based on an area frame survey. Appl. Veg. Sci. 22, 547–560. doi: 10.1111/avsc.12451
Horvath, P., Tang, H., Halvorsen, R., Stordal, F., Tallaksen, L. M., Berntsen, T. K., et al. (2021). Improving the representation of high-latitude vegetation distribution in dynamic global vegetation models. Biogeosciences 18, 95–112. doi: 10.5194/bg-18-95-2021
Hughes, A. C., Orr, M. C., Ma, K., Costello, M. J., Waller, J., Provoost, P., et al. (2021). Sampling bias shape our view of the world. Ecography 44, 1259–1269. doi: 10.1111/ecog.05926
Jackson, S. T., and Sax, D. F. (2010). Balancing biodiversity in a changing environment: extinction debt, immigration credit and species turnover. Trends Ecol. Evol. 25, 153–160. doi: 10.1016/j.tree.2009.10.001
Kass, J. M., Meenan, S. I., Tinoco, N., Burneo, S. F., and Anderson, R. P. (2021). Improving area of occupancy estimates for parapatric species using distribution models and support vector machines. Ecol. Appl. 31:e02229. doi: 10.1002/eap.2228
Kicinski, M. (2013). Publication bias in recent meta-analyses. PLoS One 8:e81823. doi: 10.1371/journal.pone.0081823
Lahoz-Monfort, J. J., Guillera-Arroita, G., and Wintle, B. A. (2013). Imperfect detection impacts the performance of species distribution models. Glob. Ecol. Biogeogr. 23, 504–515. doi: 10.1111/geb.12138
Linder, H. P., Bykova, O., Dyke, J., Etienne, R. S., Hickler, T., Kühn, I., et al. (2012). Biotic modifiers, environmental modulation and species distribution models. J. Biogeogr. 39, 2179–2190. doi: 10.1111/j.1365-2699.2012.02705.x
Lindner, M., Fitzgerald, J. B., Zimmermann, N. E., Reyer, C., Delzon, S., van der Maaten, E., et al. (2014). Climate change and European forests: what do we know, what are the uncertainties, and what are the implications for forest management? J. Environ. Manag. 146, 69–83. doi: 10.1016/j.jenvman.2014.07.030
Lobo, J. M., Jiménez-Valverde, A., and Real, R. (2008). AUC: a misleading measure of the performance of predictive distribution models. Glob. Ecol. Biogeogr. 17, 145–151. doi: 10.1111/j.1466-8238.2007.00358.x
MacKenzie, D. I., Nichols, J. D., Lachman, G. B., Droege, S., Royle, J. A., and Langtimm, C. A. (2002). Estimating site occupancy rates when detection probabilities are less than one. Ecology 83, 2248–2255.
Mazzoni, S., Halvorsen, R., and Bakkestuen, V. (2015). MIAT: modular R-wrappers for flexible implementation of MaxEnt distribution modelling. Ecol. Inform. 30, 215–221. doi: 10.1016/j.ecoinf.2015.07.001
Merow, C., Smith, M. J., and Silander, J. A. (2013). A practical guide to MaxEnt for modeling species’ distributions: what it does, and why inputs and settings matter. Ecography 36, 1058–1069. doi: 10.1111/j.1600-0587.2013.07872.x
Merow, C., Smith, M. J., Edwards, T. C., Guisan, A., McMahon, S. M., Norman, S., et al. (2014). What do we gain from simplicity versus complexity in species distribution models? Ecography 37, 1267–1281. doi: 10.1111/ecog.00845
Moriondo, M., Jones, G. V., Bois, B., Dibari, C., Ferrise, R., Trombi, G., et al. (2013). Projected shifts of wine regions in response to climate change. Clim. Change 119, 825–839. doi: 10.1007/s10584-013-0739-y
Mouquet, N., Lagadeuc, Y., Devictor, V., Doyen, L., Duputie, A., Eveillard, D., et al. (2015). Predictive ecology in a changing world. J. Appl. Ecol. 52, 1293–1310. doi: 10.1111/1365-2664.12482
Mouton, A. M., de Baets, B., and Goethals, P. L. M. (2010). Ecological relevance of performance criteria for species distribution models. Ecol. Modelling 221, 1995–2002. doi: 10.1016/j.ecolmodel.2010.04.017
Oreskes, N., Schrader-Frechette, K., and Belitz, K. (1994). Verification, validation, and confirmation of numerical models in the earth sciences. Science 263, 641–646. doi: 10.1126/science.263.5147.641
Osborne, P. E., and Leitão, P. J. (2009). Effects of species and habitat positional errors on the performance and interpretation of species distribution models. Divers. Distrib. 15, 671–681. doi: 10.1111/j.1472-4642.2009.00572.x
Pearson, R. G. (2010). Species’ distribution modeling for conservation educators and practitioners. Lessons Conserv. 3, 54–89.
Peters, J., Verhoest, N. E. C., Samson, R., van Meirvenne, M., Cockx, L., and de Baets, B. (2009). Uncertainty propagation in vegetation distribution models based on ensemble classifiers. Ecol. Modelling 220, 791–804. doi: 10.1016/j.ecolmodel.2008.12.022
Phillips, S. J., and Dudík, M. (2008). Modeling of species distributions with Maxent: new extensions and a comprehensive evaluation. Ecography 31, 161–175. doi: 10.1111/j.0906-7590.2008.5203.x
Phillips, S. J., Anderson, R. P., and Schapire, R. E. (2006). Maximum entropy modeling of species geographic distributions. Ecol. Modelling 190, 231–259. doi: 10.1016/j.ecolmodel.2005.03.026
Phillips, S. J., Anderson, R. P., Dudík, M., Schapire, R. E., and Blair, M. E. (2017). Opening the black box: an open-source release of Maxent. Ecography 40, 887–893. doi: 10.1111/ecog.03049
Rinde, E., Christie, H., Fagerli, C. W., Bekkby, T., Gundersen, H., Norderhaug, K. M., et al. (2014). The influence of physical factors on kelp and sea urchin distribution in previously and still grazed areas in the NE Atlantic. PLoS One 9:e0100222. doi: 10.1371/journal.pone.0100222
Roberts, D. R., Bahn, V., Ciuti, S., Boyce, M. S., Elith, J., Guillera-Arroita, G., et al. (2017). Cross-validation strategies for data with temporal, spatial, hierarchical, or phylogenetic structure. Ecography 40, 913–929. doi: 10.1111/ecog.02881
Robertson, M. P., Cumming, G. S., and Erasmus, B. F. N. (2010). Getting the most out of atlas data. Divers. Distrib. 16, 363–375. doi: 10.1111/j.1472-4642.2010.00639.x
Rodríguez-Rey, M., Consuegra, S., Börger, L., and Garcia de Leaniz, C. (2019). Improving species distribution modelling of freshwater invasive species for management applications. PLoS One 14:e0217896. doi: 10.1371/journal.pone.0217896
Rumpf, S. B., Hulber, K., Klonner, G., Moser, D., Schutz, M., Wessely, J., et al. (2018). Range dynamics of mountain plants decrease with elevation. Proc. Natl. Acad. Sci. U.S.A. 115, 1848–1853. doi: 10.1073/pnas.1713936115
Sales, L. P., Hayward, M. W., and Loyloa, R. (2021). What do you mean by “niche”? Modern ecological theories are not coherent on rhetoric about the niche concept. Acta Oecol. 110:103701. doi: 10.1016/j.actao.2020.103701
Schank, C. J., Cove, M. V., Kelly, M. J., Nielsen, C. K., O’Farrill, G., Meyer, N., et al. (2019). A sensitivity analysis of the application of integrated species distribution models to mobile species: a case study with the endangered Baird’s Tapir. Environ. Conserv. 46, 184–192. doi: 10.1016/10.1017/S0376892919000055
Scherrer, D., Mod, H. K., and Guisan, A. (2020). How to evaluate community predictions without thresholding? Methods Ecol. Evol. 11, 51–63. doi: 10.1111/2041-210x.13312
Schuetz, J. G., Langham, G. M., Soykan, C. U., Wilsey, C. B., Auer, T., and Sanchez, C. C. (2015). Making spatial prioritizations robust to climate change uncertainties: a case study with North American birds. Ecol. Appl. 25, 1819–1831. doi: 10.1890/14-1903.1
Shabani, F., Kumar, L., and Ahmadi, M. (2016). A comparison of absolute performance of different correlative and mechanistic species distribution models in an independent area. Ecol. Evol. 6, 5973–5986. doi: 10.1002/ece3.2332
Simensen, T., Horvath, P., Vollering, J., Erikstad, L., Halvorsen, R., and Bryn, A. (2020). Composite landscape predictors improve distribution models of ecosystem types. Divers. Distrib. 26, 928–943. doi: 10.1111/ddi.13060
Slette, I. J., Post, A. K., Awad, M., Even, T., Punzalan, A., Williams, S., et al. (2019). How ecologists define drought, and why we should do better. Glob. Change Biol. 25, 3193–3200. doi: 10.1111/gcb.14747
Soberón, J., and Peterson, A. T. (2005). Interpretation of models of fundamental ecological niches and species’ distributional areas. Biodivers. Informatics 2, 1–10. doi: 10.17161/bi.v2i0.4
Støa, B., Halvorsen, R., Mazzoni, S., and Gusarov, V. I. (2018). Sampling bias in presence-only data used for species distribution modelling: theory and methods for detecting sample bias and its effects on models. Sommerfeltia 38, 1–53. doi: 10.2478/som-2018-0001
Stokland, J. N., Halvorsen, R., and Støa, B. (2011). Species distribution modelling – effect of design and sample size of pseudo-absence observations. Ecol. Modelling 222, 1800–1809. doi: 10.1016/j.ecolmodel.2011.02.025
Suárez-Seoane, S., Virgós, E., Terroba, O., Pardavila, X., and Barea-Azcón, J. M. (2014). Scaling of species distribution models across spatial resolutions and extents along a biogeographic gradient. The case of the Iberian mole Talpa occidentalis. Ecography 37, 279–292. doi: 10.1111/j.1600-0587.2013.00077.x
Svenning, J.-C., and Skov, F. (2005). The relative roles of environment and history as controls of tree species composition and richness in Europe. J. Biogeogr. 32, 1019–1033. doi: 10.1111/j.1365-2699.2005.01219.x
Svenning, J.-C., Gravel, D., Holt, R. D., Schurr, F. M., Thuiller, W., Münkemüller, T., et al. (2014). The influence of interspecific interactions on species range expansion rates. Ecography 37, 1198–1209. doi: 10.1111/j.1600-0587.2013.00574.x
Tang, Y., Winkler, J. A., Vina, A., Wang, F., Zhang, J. D., Zhao, Z. Q., et al. (2020). Expanding ensembles of species present-day and future climatic suitability to consider the limitations of species occurrence data. Ecol. Indic. 110:105891. doi: 10.1016/j.ecolind.2019.105891
Tessarolo, G., Lobo, J. M., Rangel, T. F., and Hortal, J. (2021). High uncertainty in the effects of data characteristics on the performance of species distribution models. Ecol. Indic. 121:107147. doi: 10.1016/j.ecolind.2020.107147
Tobler, M. W., Kéry, M., Hui, F. K., Guillera-Arriota, G., Knaus, P., and Sattler, T. (2019). Joint species distribution models with species correlations and imperfect detection. Ecology 100:e02754. doi: 10.1002/ecy.2754
Tognelli, M. F., and Kelt, D. A. (2004). Analysis of determinants of mammalian species richness in South America using spatial autoregressive models. Ecography 27, 427–436. doi: 10.1111/j.0906-7590.2004.03732.x
Tyre, A. J., Tenhumberg, B., Field, S. A., Niejalke, D., Parris, K., and Possingham, H. P. (2003). Improving precision and reducing bias in biological surveys: estimating false-negative error rates. Ecol. Appl. 13, 1790–1801. doi: 10.1890/02-5078
van Groenendael, J., Ehrlén, J., and Svensson, B. M. (2000). Dispersal and persistence: population processes and community dynamics. Folia Geobot. 35, 107–114. doi: 10.1007/bf02803090
Varela, S., Anderson, R. P., García-Valdés, R., and Fernández-González, F. (2014). Environmental filters reduce the effects of sampling bias and improve predictions of ecological niche models. Ecography 37, 1084–1091. doi: 10.1111/j.1600-0587.2013.00441.x
Varela, S., Lobo, J. M., and Hortal, J. (2011). Using species distribution models in paleobiogeography: a matter of data, predictors and concepts. Palaeogeogr. Palaeoclimatol. Palaeoecol. 310, 451–463. doi: 10.1016/j.palaeo.2011.07.021
Veloz, S. D. (2009). Spatially autocorrelated sampling falsely inflates measures of accuracy for presence-only niche models. J. Biogeogr. 36, 2290–2299. doi: 10.1111/j.1365-2699.2009.02174.x
Vollering, J., Halvorsen, R., Austad, I., and Rydgren, K. (2019a). Bunching up the background betters bias in species distribution models. Ecography 42, 1717–1727. doi: 10.1111/ecog.04503
Vollering, J., Halvorsen, R., and Mazzoni, S. (2019b). The MIAmaxent R package: variable transformation and model selection for species distribution models. Ecol. Evol. 9, 12051–12068. doi: 10.1002/ece3.5654
Walker, P. A., and Cocks, K. D. (1991). HABITAT: a procedure for modelling a disjoint environmental envelope for a plant or animal species. Glob. Ecol. Biogeogr. Lett. 1, 108–118. doi: 10.2307/2997706
Warren, D. L., and Seifert, S. N. (2011). Ecological niche modeling in Maxent: the importance of model complexity and the performance of model selection criteria. Ecol. Appl. 21, 335–342. doi: 10.1890/10-1171.1
Wernberg, T., Smale, D. A., Tuya, F., Thomsen, M. S., Langlois, T. J., de Bettignies, T., et al. (2012). An extreme climatic event alters marine ecosystem structure in a global biodiversity hotspot. Nat. Clim. Change 3, 78–82. doi: 10.1038/nclimate1627
Wiens, J. A., Stralberg, D., Jongsomjit, D., Howell, C. A., and Snyder, M. A. (2009). Niches, models, and climate change: assessing the assumptions and uncertainties. Proc. Natl. Acad. Sci. U.S.A. 106, 19729–19736. doi: 10.1073/pnas.0901639106
Wiens, J. J., and Graham, C. H. (2005). Niche conservatism: integrating evolution, ecology, and conservation biology. Annu. Rev. Ecol. Evol. Syst. 36, 519–539.
Wollan, A. K., Bakkestuen, V., Kauserud, H., Gulden, G., and Halvorsen, R. (2008). Modelling and predicting fungal distribution pattern using herbarium data. J. Biogeogr. 35, 2298–2310. doi: 10.1111/j.1365-2699.2008.01965.x
Yackulic, C. B., Chandler, R., Zipkin, E. F., Royle, J. A., Nichols, J. D., Grant, E. H. C., et al. (2013). Presence-only modelling using MAXENT: when can we trust the inferences? Methods Ecol. Evol. 4, 236–243. doi: 10.1111/2041-210x.12004
Yates, K. L., Bouchet, P. J., Caley, M. J., Mengersen, K., Randin, C. F., Parnell, S., et al. (2018). Outstanding challenges in the transferability of ecological models. Trends Ecol. Evol. 33, 790–802. doi: 10.1016/j.tree.2018.08.001
Keywords: assumptions, bias, distribution modeling, equilibrium, errors, inaccuracies, spatial prediction, uncertainties
Citation: Bryn A, Bekkby T, Rinde E, Gundersen H and Halvorsen R (2021) Reliability in Distribution Modeling—A Synthesis and Step-by-Step Guidelines for Improved Practice. Front. Ecol. Evol. 9:658713. doi: 10.3389/fevo.2021.658713
Received: 26 January 2021; Accepted: 28 October 2021;
Published: 18 November 2021.
Edited by:
Michael Sears, Clemson University, United StatesReviewed by:
Peter Goethals, Ghent University, BelgiumCopyright © 2021 Bryn, Bekkby, Rinde, Gundersen and Halvorsen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anders Bryn, YW5kZXJzLmJyeW5AbmhtLnVpby5ubw==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.