Biogeographic Drivers of Evolutionary Radiations

Some lineages radiate spectacularly when colonizing a region, but others do not. Large radiations are often attributed to species’ adaptation into niches, or to other drivers, such as biogeography including dispersal ability and spatial structure of the landscape. Here we aim to disentangle the factors determining radiation size, by modeling simplified scenarios without the complexity of explicit niches. We build a spatially structured neutral model free from niches and incorporating a form of protracted speciation that accounts for gene flow between populations. We find that a wide range of radiation sizes are possible in this model depending on the combination of geographic isolation and species’ dispersal ability. At extremely low rates of dispersal between patches, each patch maintains its own endemic species. Intermediate dispersal rates foster larger radiations as they allow occasional movement between patches whilst sufficiently restricting gene flow to support further speciation in allopatry. As dispersal rates increase further, a critical point is reached at which demographically identical lineages may vary greatly in radiation size due to rare and stochastic dispersal events. At the critical point in dispersal frequency, some lineages remain a single species for a comparatively long time, whilst others with identical characteristics produce the largest radiations of all via a new mechanism for rapid radiation that we term a ‘radiation cascade’. Given a single species covering many patches connected with gene flow, a radiation cascade is triggered when stochastic dispersal is unusually low for a period, leading to an initial speciation event. This speciation means there are fewer individuals per species and thus further reduced gene flow between conspecifics. Reduced gene flow in turn makes it easier for further speciation to occur. During a radiation cascade, dispersal of individuals between patches continues at the same rate as before, but due to the increasing diversity it primarily introduces novel species that will later speciate, rather than adding to gene flow of existing species. Once a radiation cascade begins, it continues rapidly until it is arrested by a new equilibrium between speciation and extinction. We speculate that such radiation cascades may occur more generally and are not only present in neutral models. This process may help to explain rapid radiation, and the extreme radiation sizes of certain lineages with dispersing ancestors. Whilst niches no doubt play a role in community assembly, our findings lead us to question whether diversification and adaptation into niches is sometimes an effect of speciation and rapid radiation, rather than its cause.

Introduction

Radiations are an evolutionary phenomenon in which one species proliferates into many (Erwin, 1992; Stroud and Losos, 2016). Radiations are often studied on island and archipelago settings as their spatial structure provides prominent opportunities for allopatric speciation, with celebrated examples including Darwin’s finches of the Galapagos (Grant and Grant, 2011, 2014), anolis lizards of the Caribbean (Losos, 2011), lobeliads and silverswords of Hawaii (Robichaux et al., 1990; Givnish et al., 2009) and others (Lovette et al., 2002; Kocher, 2004). Since Darwin’s early work, the mechanism behind radiation has captured the interest of a wide range of ecologists and evolutionary biologists. Most studies have focused on adaptive radiations (Harvey and Rambaut, 2000; Yoder et al., 2010; Wellborn and Langerhans, 2015), in which the radiation was accompanied by diversification of phenotypes enabling the species to fill different niches (Schluter, 2000). Geographic radiations, in which spatially structured landscapes are the main driver of species proliferation, have been relatively overlooked (Ibanez et al., 2018). A combination of adaptation and geography may explain the overall pattern of species proliferation in most cases (Rundell and Price, 2009; Simões et al., 2016).

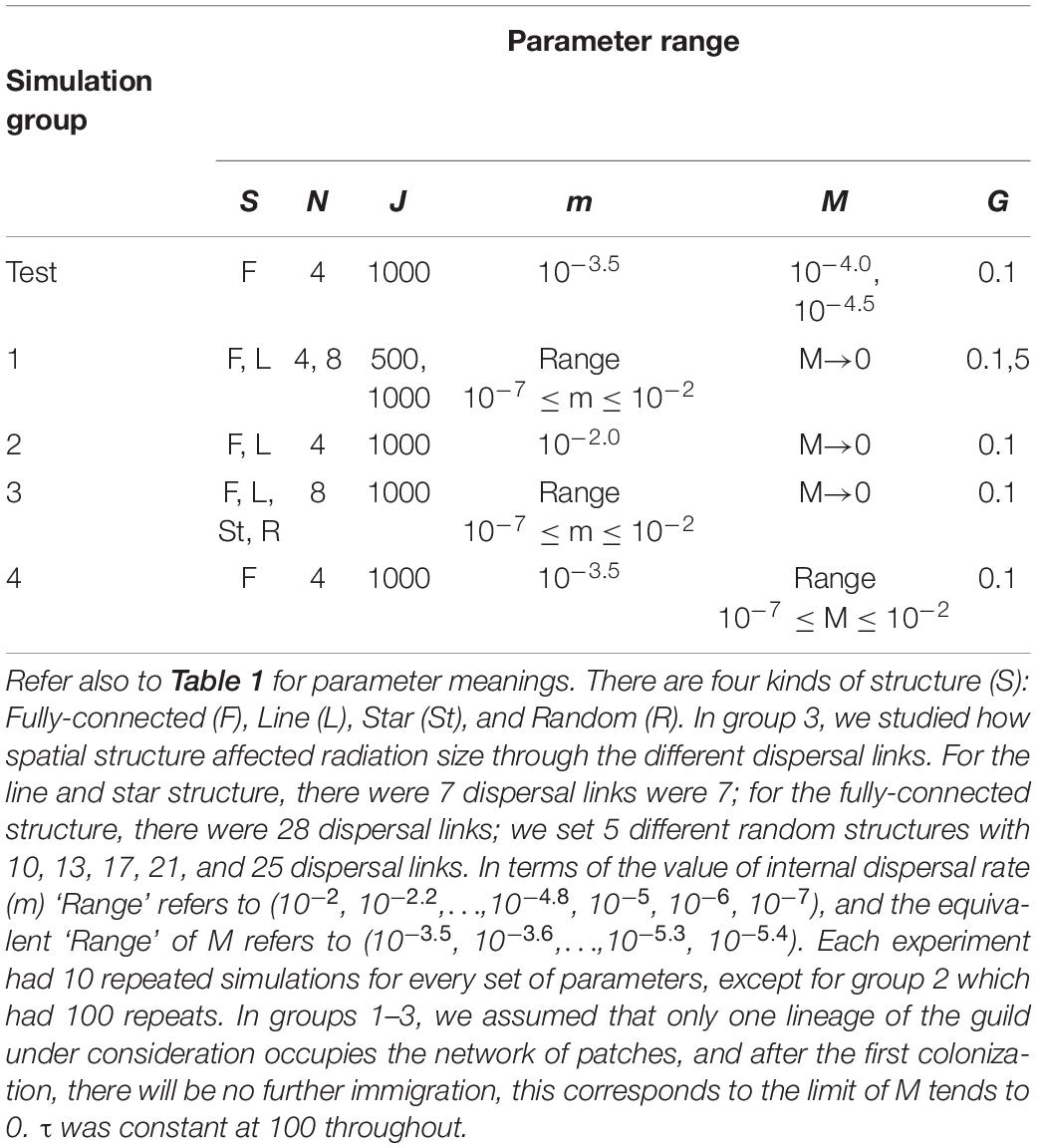
Adaptive radiation is explained by ecological opportunity (Simpson, 1953; Losos, 2010; Losos et al., 2010), but some phenomena cannot be explained in this way. For example, in the Galapagos, Darwin’s finches proliferated into fourteen species (Lamichhaney et al., 2015; Grant, 2017), while mockingbirds only four species (Arbogast et al., 2006) and most other bird lineages remained as single taxa. For the Hawaiian flora, a few lineages have large species richness, while many colonist lineages did not radiate at all (Figure 1). What explains such disparity in radiation size? If ecological opportunity is the important factor, what prevented such opportunities from being filled more evenly by the various immigrating lineages? The answer might be partly to do with the order or timing of immigration (Fukami, 2015; De Meester et al., 2016) and/or the influences of geography and stochasticity on dispersal. Indeed, propagule size, dispersal mechanism and breeding system can interact with geography and the extent of natural barriers between islands and habitat patches to influence radiation size in plants (Price and Wagner, 2018).

FIGURE 1

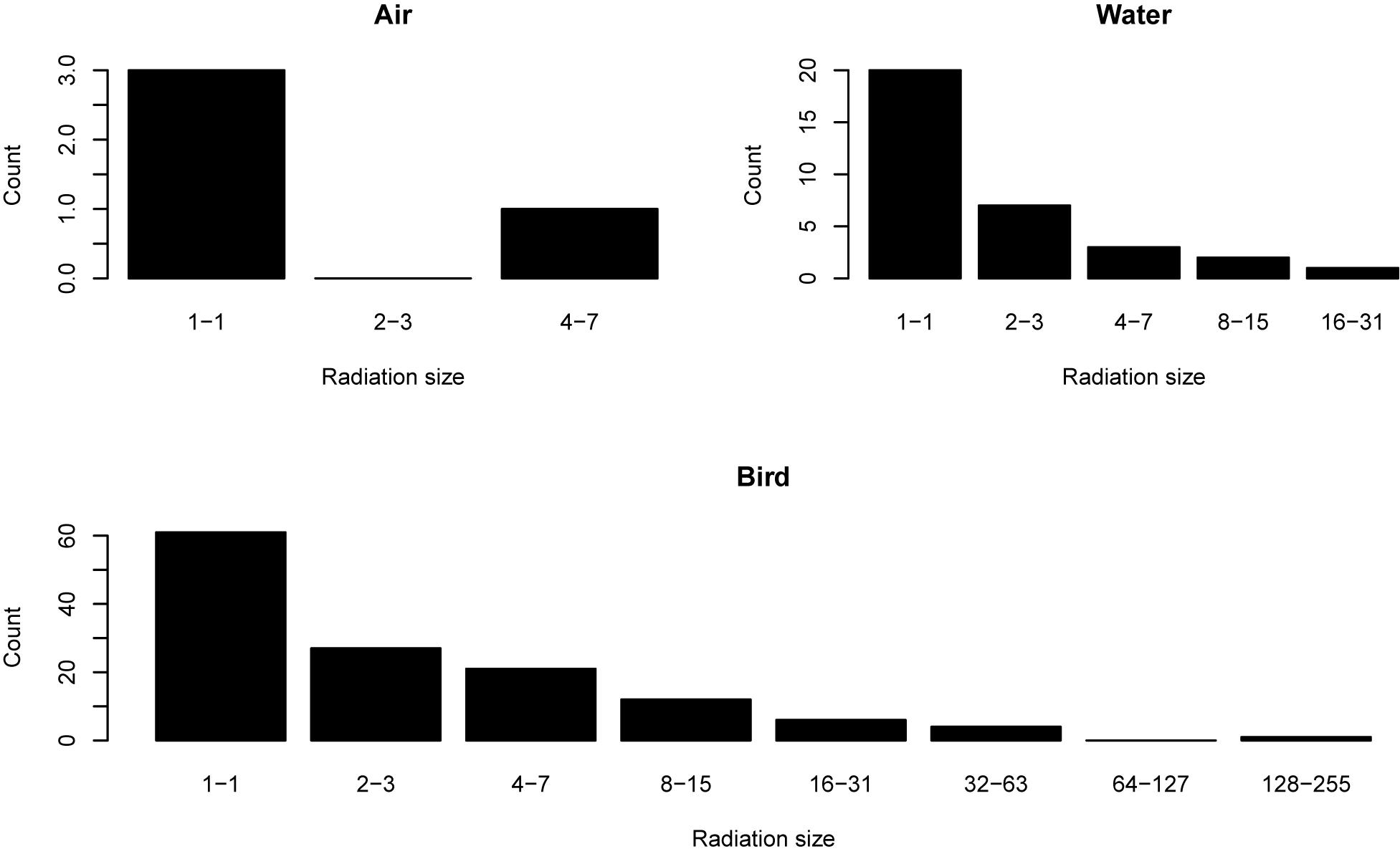
Figure 1. Radiation sizes of Hawaiian angiosperm lineages, separated by dispersal vector. The data are from Price and Wagner (2018). Lineages dispersed by air never reached radiation sizes beyond the 4–7 category. Those dispersing over water were able to reach radiation sizes in the 16–32 category. All the lineages with the greatest radiation sizes of 32 or more were dispersed by birds.

Recent research has revealed that, in many cases, geographic and ecological factors both influence radiation size (Bennett and O’Grady, 2013; Yu et al., 2014; Simões et al., 2016; Schenk and Steppan, 2018). Some have proposed that a diverse radiated lineage might undergo both adaptive and geographic radiation (Simões et al., 2016). However, such hypotheses are hard to test. We suggest that stochasticity and geography should not simply be a ‘backup’ explanation invoked only if an adaptive story cannot be found, as they are likely to work alongside adaptation in a much greater proportion of cases. One approach to disentangle the role of adaptation is by modeling radiation in the absence of niches or adaptation, to explore the effects of stochasticity, dispersal and geography on radiation size. Neutral theory (Hubbell, 2001) provides a natural direction for building such a model because it does not include specific niches and instead emphasizes biogeographic factors such as dispersal and landscape spatial structure (Rosindell et al., 2011).

We investigated the quantitative influence of biogeographic drivers on radiation size with a mechanistic model based on neutral theory (Hubbell, 2001). Our model integrates both spatial structure and a protracted speciation process that explicitly accounts for gene flow between multiple habitat patches (Rosindell et al., 2010; Rosindell and Phillimore, 2011; Gascuel et al., 2016). We found that biogeography alone can drive a very large variation in radiation size. We also find a potential new mechanism for rapid radiation: a ‘radiation cascade’ in which initial speciation of a widespread species reduces gene flow between conspecifics and as a result leads to yet more speciation in a reinforcing cycle.

Materials and Methods

We built a neutral model with spatial structure to explicitly simulate the proliferation of one or more radiating lineages within a network of connected habitat patches, which could represent islands. We conducted experiments simulating different sets of parameters to identify the relationship between radiation size and biogeographic factors.

Model Description

Our neutral model is based on birth-death cycles, where the total number of individuals is constant (zero-sum). Unlike the classic neutral model of Hubbell (2001), which contains one local community and a single metacommunity, our model uses a spatially structured community network containing multiple patches linked together (Economo and Keitt, 2008; Gascuel et al., 2016) as well as a remote metacommunity (Hubbell, 2001). The community network can receive external immigrants from the metacommunity. Within the network, local patches represent local communities that may be connected to a greater or lesser extent. There are internal dispersal events between local patches. An isolated archipelago of islands is one example of a system that can naturally be represented in this way. The assumption of neutral theory, and our model, is that an individual’s chances of birth, death and movement are independent of its species identity. This neutrality assumption aids understanding of the ecological processes other than niches and selection, with the constraint that species are from a single trophic level and guild (Hubbell, 2001).

In our simulation, one individual dies at each time step, leaving a gap that is filled by the new-born offspring of either a local parent, or an immigrant from another local patch or an external immigrant from the metacommunity (Figure 2). The network of dispersal opportunities between every pair of local patches is represented by a probability-matrix P. In this matrix, P_i,j gives the probability for the gap in patch i to be filled by an individual from patch j. P_i,i gives the probability of a deceased individual in patch i being replaced by the offspring of a local individual. In practice we simulated a simplified scenario in which all local patches were of the same size J, in terms of total number of individuals, and, where present, any links between patches were of the same strength given by m. As a result P_i,j, where i≠j, is either 0 or m and P_i,i is set so that ${\sum }_{\mathrm{j}=1}^{\text{N}}{P}_{\mathrm{i}.\mathrm{j}}=1-m$. Here, N is the total number of local patches in the system and M is the probability of dispersal from the external metacommunity. To simplify the simulation further and improve tractability, species abundances within the metacommunity resource pool were not modeled explicitly; any individual arriving from the metacommunity was considered a different species, which would be reasonable for a large, diverse, and distant metacommunity.

FIGURE 2

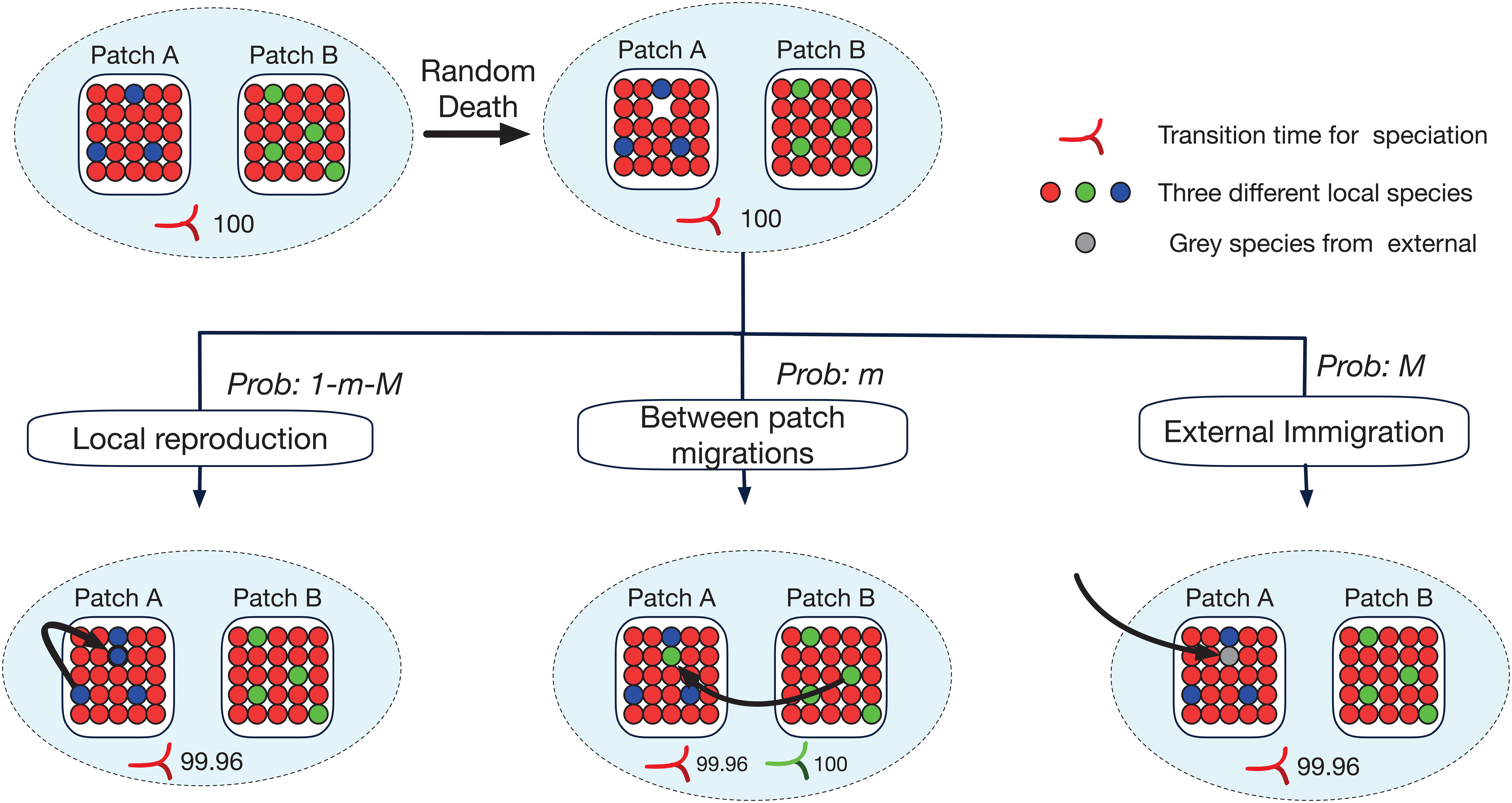
Figure 2. Schematic representation of the network structure used in our study. In this example, we show three initial species (red, blue, and green) in the community network of two patches (A and B). There are 50 individuals in total. The time step shown represents a birth-death cycle: that is 2/50 = 0.04 of a generation. The minimum duration of speciation (τ) is set at 100 generations meaning that in the absence of gene flow speciation will complete in 100 generations. The gene flow effect (G) is 5 in this example meaning that every individual gene flow event causes a 5-generation delay to the conclusion of the speciation process. The numbers at the bottom of each panel are the speciation ‘clocks’ for each species showing how many generations without gene flow are required to completely sever that species into two. Only when a species has conspecific populations in different patches is a speciation ‘clock’ required. Any ‘clock’ is initialized with τ generations (here 100), and will then count down over time but increase by G whenever a dispersal event of a conspecific occurs (gene flow).

Speciation Process

We modeled speciation as a protracted process (Rosindell et al., 2010) that takes time to complete. Each possible new species has a countdown ‘clock’ (measured in generations) until its speciation process has completed. Given that generations are overlapping in our model, we defined one generation as the amount of time required for half of the individuals in the community to have died and been replaced with offspring of other individuals (Rosindell et al., 2010). Following the protracted speciation model with gene flow of Rosindell and Phillimore (2011), any new colonization of a local patch will start the countdown to a potential speciation event that would result in the newly colonized local patch becoming a new species (Figure 2). The shortest possible duration of speciation is given by a parameter (τ), the number of generations taken for allopatric speciation in the absence of any gene flow between local patches. Any immigration event of conspecific individuals between different local patches increases the amount of time until speciation will complete for that species by a predefined parameter G giving the gene flow effect. This increases the amount of time until the populations within the local patches concerned can be considered as two different species (Figure 2). Here, we expand the two-community (island mainland) model of Rosindell and Phillimore (2011) to allow arbitrary networks of local patches. In cases where there are more than two patches, every possible pair of patches has its own independent speciation clock for each species, keeping track of gene flow events between those two patches. Individuals in a local patch (or collection of local patches) speciate in allopatry from their former conspecifics in other local patches when they can be split into two groups so that the speciation clock for every local patch in one group has counted down to zero (or less) in terms of connection to every local patch in the other group (Figure 3). If the speciation clock for two local patches has counted down to zero but they are still linked through other local patches with speciation clocks that have not yet counted down to zero, speciation does not yet complete and gene flow between disconnected links may resume if new dispersal events take place. We simulated our model forwards in time rather than using a backward in time coalescence approach (Rosindell et al., 2008; Thompson et al., 2020). This is because a model with multiple habitat patches and protracted speciation with gene flow can only be approximated with coalescence (Rosindell and Phillimore, 2011; Gascuel et al., 2016).

FIGURE 3

Figure 3. A schematic diagram showing how allopatric speciation (cladogenesis) happens in a community network of patches. Assume there are 3 patches (A, B, and C) fully connected to each other. In this example, the red species has spread to all 3 patches, so gene flow occurs between all these patches and links them as a gene flow network. The gene flow strength is shown by the width of the red line. The ‘clock’ for speciation is initially equal to τ = 100. When the conspecific link between red species population in patch A and C has been eroded by lack of gene flow, these populations remain conspecific because they are connected via patch B: red individuals in patch A and B are conspecific and the same is true for red individuals in patch C and B - so patch A and C must also remain conspecific. Irreversible speciation finally occurs when the conspecific link between patch C and B is cut, and the conspecific link between patch A and C remains unconnected so that the red population in patch C can now speciate from its relatives in patches A and B to from a new yellow species by allopatric speciation. In the scenario where gene flow resumes, the conspecific link between patch A and C has been revived, so the red species in all three local patches is back to being a complete gene flow network.

Analytical and Scaling Results

We expect that a critical point in the system will be reached when m, the rate of dispersal between any pair of local patches, passes $m_{\text{crit}}=\frac{1}{G\times J}$. Here, m_crit represents the dispersal rate where, in a community with only one species on all islands, gene flow events add to the speciation clock at precisely the same rate that time erodes it. G is the gene flow effect and J represents the population size of each local patch. Gene flow between a pair of patches can come from dispersal in either direction, so there is a pool of 2 × J individuals who could disperse with probability m_crit per reproduction event. However, given the way a generation is defined above, only half of those of 2 × J individuals will reproduce per generation. The total effect of gene flow per generation will therefore be given by m_crit×G×J and setting this to one gives our solution for m_crit. We will compare the critical point m_crit against our simulated results for radiation size across a wide range of values for dispersal rate m.

We also wish to test the idea that increasing the number of links in a network of local patches has a similar effect on radiation size as increasing the strength (amount of immigration) of each link. To do this we plot of graph against the compound parameter (immigration rate × number of links) for a range of different spatial network structures to observe if the structure itself has any effect beyond its raw number of links.

Experimental Design

We designed a series of experiments to investigate different biogeographic drivers of radiation patterns in a network of local patches. We investigated three main spatial structures for the network of dispersal between local patches: ‘line’ structure, ‘fully-connected’ structure, and ‘random’ structure. The ‘Line’ structure represents a chain of local patches connected only to their direct neighbors. The ‘Fully-connected’ structure represents a network where every local patch is connected to every other local patch with equal strength. The ‘Random’ structure is a network of local patches with random connections between them starting with a line structure (the minimum number of links to connect the network) and choosing a given number of additional links to add at random, up to a maximum corresponding to a fully connected network. See Table 1 for a complete list of all model parameters.

TABLE 1

Table 1. A list of all parameters used in our simulations and their meaning.

To identify the relationship between habitat size and radiation, we varied the number of local patches as well as the number of individuals in each local patch. We tested a wide range of internal dispersal rates and rates of dispersal from the metacommunity. Our simulations were conducted in groups, each with a distinct purpose (Table 2). After test simulations, the first groups (1–3) used a single immigration event from the metacommunity, a simplification to focus on the effects of dispersal between patches, network structure and gene flow effect. This is equivalent to assuming M→0 where M represents the rate of immigration from the metacommunity and not to be confused with m representing the rate of immigration between connected local community patches. Simulation group 1 investigated how radiation size varied with changes of all simulation parameters except for M. Simulation group 2 then focused on parameters values where the radiation cascade was observed and replicated simulations of those one hundred times with different random seeds in order to obtain a more complete picture of the radiation cascades. Simulation group 3 varied the number of links within the network as well as the internal dispersal strength to capture their co-effect on radiation size. Finally, group 4 simulations incorporated external immigration from the metacommunity (M > 0) to observe the radiation patterns resulting from multiple immigration events.

TABLE 2

Table 2. Parameters used for all groups of simulations.

To ensure simulation groups 1–3 reached equilibrium, we discarded the first half of all simulated data as a burn in. To show this was sufficient we also produced a second set of results that retained only the last quarter of the simulation. The simulations in group 4, where M > 0 detected equilibrium as the time when the island was populated entirely with lineages that immigrated onto the island during the simulation. Thus, at equilibrium, the individuals that formed the initial state on the island had all died out leaving no descendants and no meaningful way to influence the outcome (Rosindell and Harmon, 2013).

Results

In the test simulations, the radiation size produced by our model fluctuated over time and included a mixture of both single patch endemics and multi-patch species (Figure 4). It is normal in this model to observe extinction of entire lineages and recovery of nearly extinct lineages to radiate again (Figure 4). For the simulations in groups 1–3 with only one immigrating lineage, high immigration between local patches resulted in only one species across all simulations. In contrast, if immigration between local patches was extremely low each local patch would hold its own locally endemic species, so radiation size equals the number of local patches. The largest radiation size occurred when between-patch dispersal was intermediate (Figures 5, 6). These results were broadly robust to the length of burn in period (see Supplementary Material). The only exception was at the critical point where a limited number of additional lineages underwent radiation cascades after the longer burn in (see Supplementary Material).

FIGURE 4

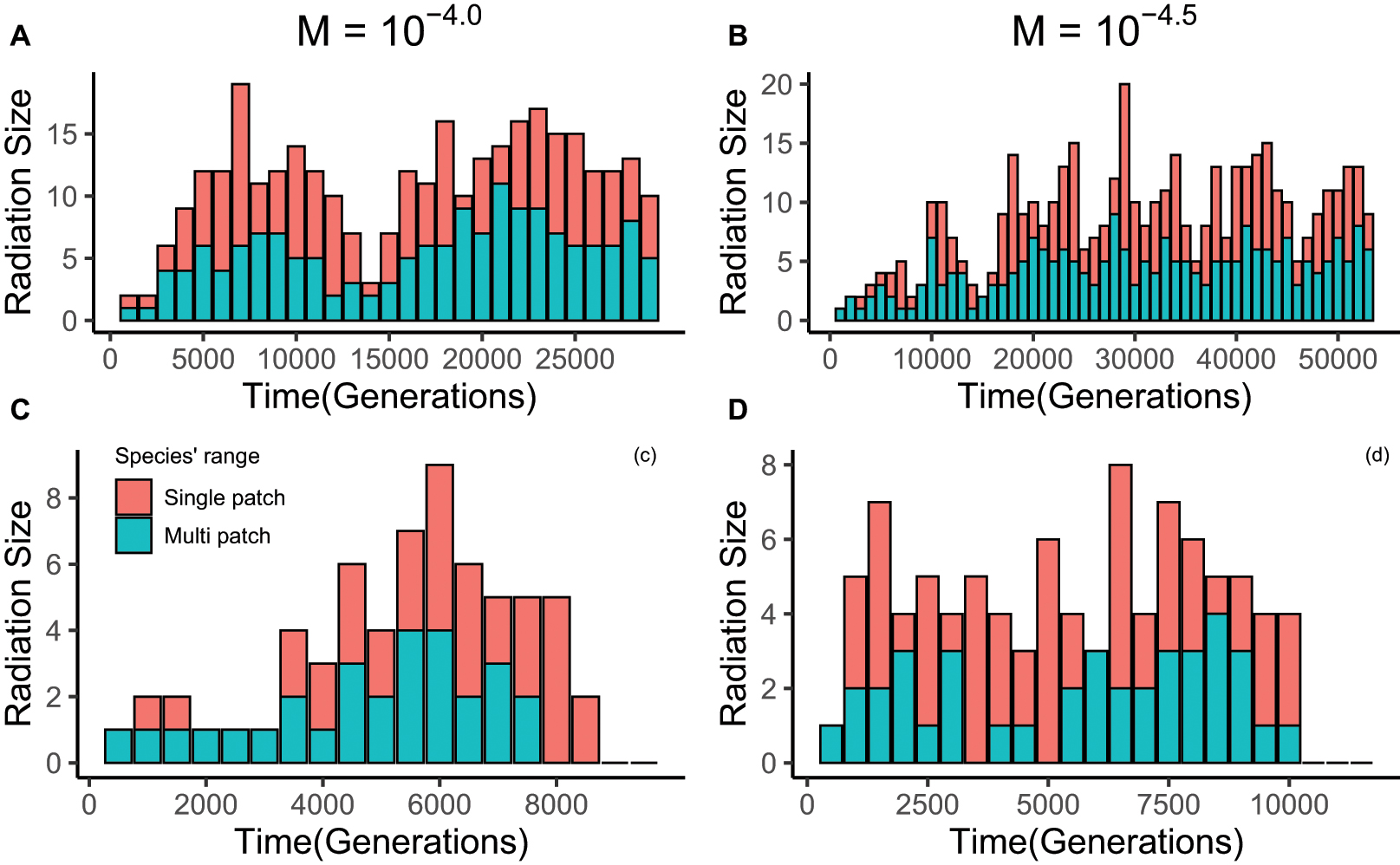
Figure 4. Examples of lineage radiation size through time for 4 well-radiated lineages from two simulations. From each simulation, we chose one lineage that still exists at the end of the simulation and one lineage that has gone extinct. The lineages in panels (A,C) are from one simulation, the lineages in panels (B,D) from another simulation. Data in panels (A,B) were collected every 1000 generations, while the interval in panels (C,D) was 500 generations. The external immigration rate in panels (A,C) is 10^{– 4}, and in panels (B,D) is 10^{– 4.5}. The features of the community simulated were: 4 local patches, each with 1000 individuals; fully-connected spatial structure; internal dispersal rate is 10^{– 3.5}; gene flow effect (G) is 0.1. The red portion of the stacked bar represents the species that are only endemic to a single local patch; the portion represents endemic species that have spread onto multiple patches. This figure illustrates that, for our model, fluctuations in radiation size are normal, as is extinction of entire lineages and recovery of nearly extinct lineages to radiate again.

FIGURE 5

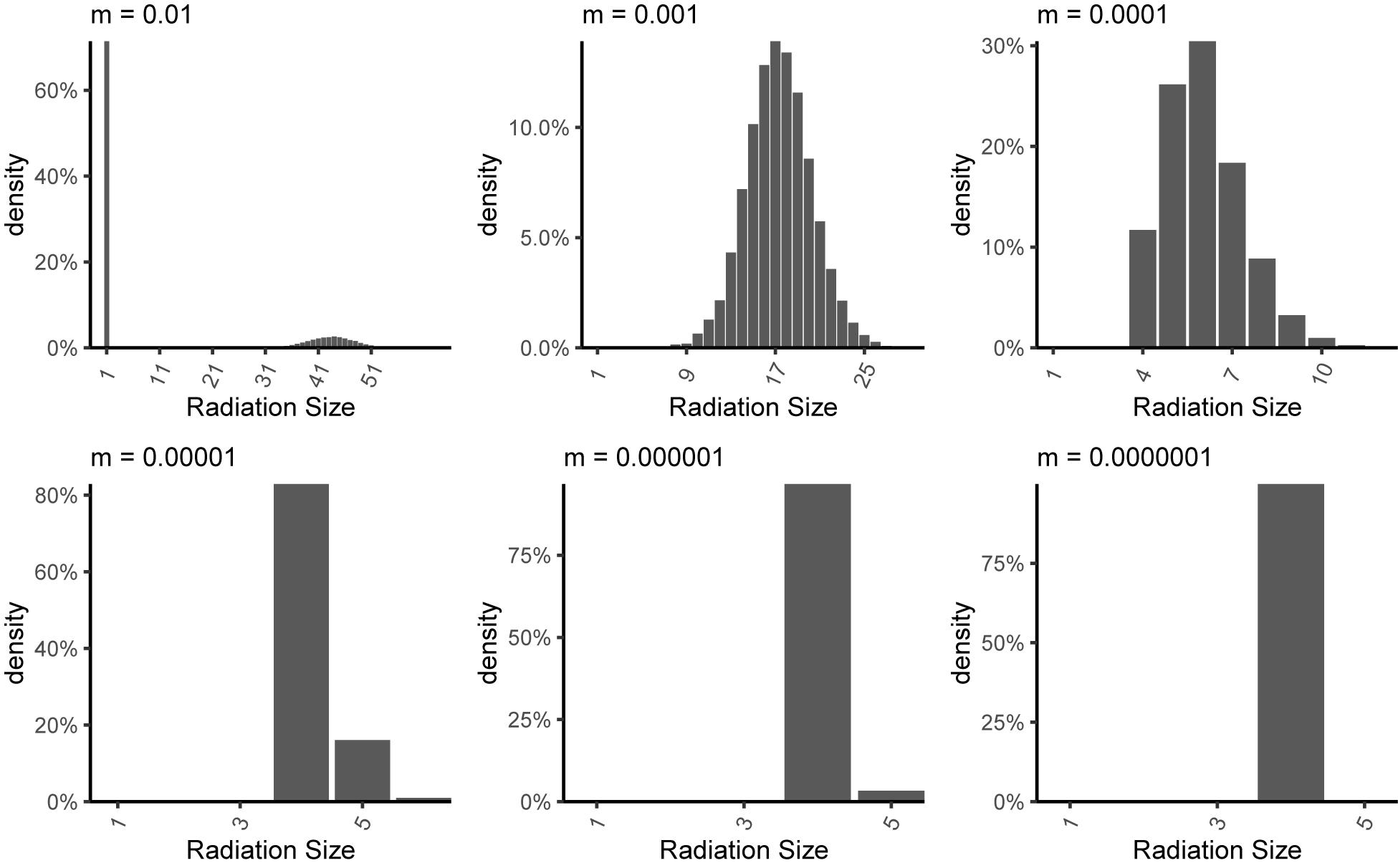
Figure 5. Radiation size distributions across repeat simulations for a single immigrating lineage under different rates of internal dispersal (m). The numbers given above each panel indicate the internal dispersal rate (m). The habitat network simulated was a line structure with 4 patches, each having 1000 individuals. Gene flow effect (G) was 0.1.

FIGURE 6

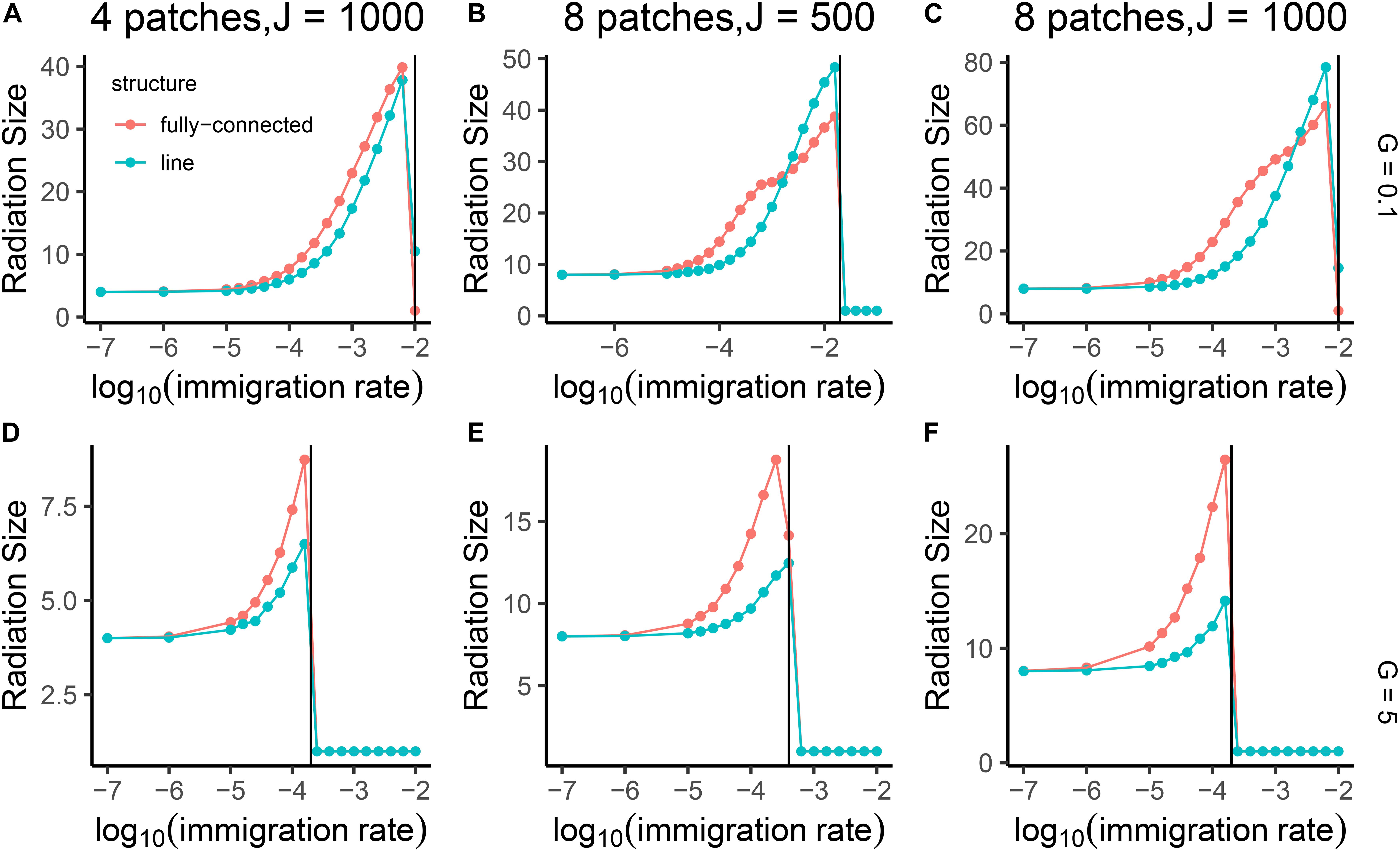
Figure 6. Mean radiation size of the single lineage in the community network, shown as a function of internal dispersal rate (m) on log 10 scale. The three columns of panels correspond to three different sizes of community network: 4 patches each with 1000 individuals (A,D), 8 patches each with 500 individuals (B,E), and 8 patches each with 1000 individuals (C,F). The gene flow effect (G) was set to 5 and 0.1 shown as two rows of panels. Blue lines represent results from a line-structured network of local patches, and red lines represent results from a fully-connected structure. The vertical black lines give the predicted value of the critical point m_crit for each panel based on the formula m_crit = $\frac{1}{G\times J}$ that was described in the Material and Methods section.

At a critical point where the immigration between local patches was high, but not yet high enough to homogenize the patches and result in a single species, the radiation size was either 1 or very high (e.g., over 40, Figure 5). At this critical point in immigration between patches, lineages could radiate dramatically at any time, but after this would be stable in a species rich configuration (Figure 7). The critical point was comparable to the one predicted from our proposed formula of $m=\frac{1}{G\times J}$ (Figure 6).

FIGURE 7

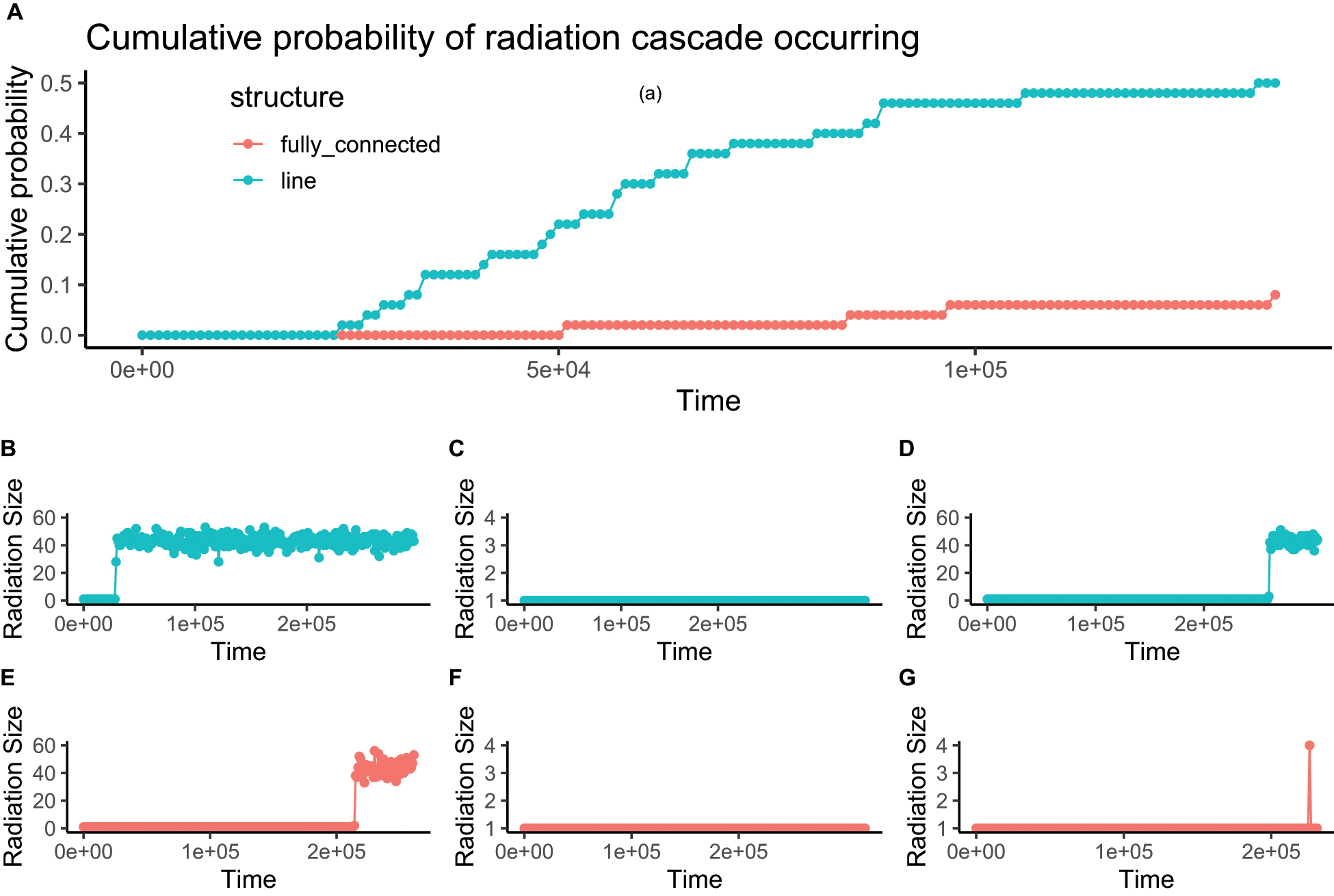
Figure 7. Example time series of radiation size (panels B–G) showing radiation cascades occurring in some simulation runs, but not in others with the same parameters. Two extreme scenarios are possible: the radiation can be very large or non-existent. After a radiation cascade has occurred, it cannot easily be reversed. The cumulative probability for a lineage to undergo a radiation cascade increases but shows that in some cases the cascade may not occur for a long time (panel A). Blue lines represent results from a line-structured network of local patches and red lines represent results from a fully connected structure of local patches. The figure was produced with gene flow effect (G) equal to 0.1 and community network containing 4 patches each with 1000 individuals, within the network, the internal dispersal rate (m) was 0.01.

We found that fragmentation and community size had positive effects on radiation size. A network with eight patches showed approximately twice the radiation size of a network with four patches. The Radiation size also increased in response to larger local patches without changing the number of patches. When gene flow effect was high (5), the fully-connected network showed a larger radiation than the line-structured one. When the gene flow effect was low (0.1) and immigration rate between local patches was high, the line-structured network had the larger radiations (Figure 6). We found that when gene flow effect was low (0.1) and internal immigration rate was also relatively low (how low depends on the number of links), the radiation size was not regulated by internal dispersal independently but rather by the combined effect of internal dispersal rate multiplied by number of dispersal links between local patches (Figure 8). These results were robust to the length of burn in period (see Supplementary Material).

FIGURE 8

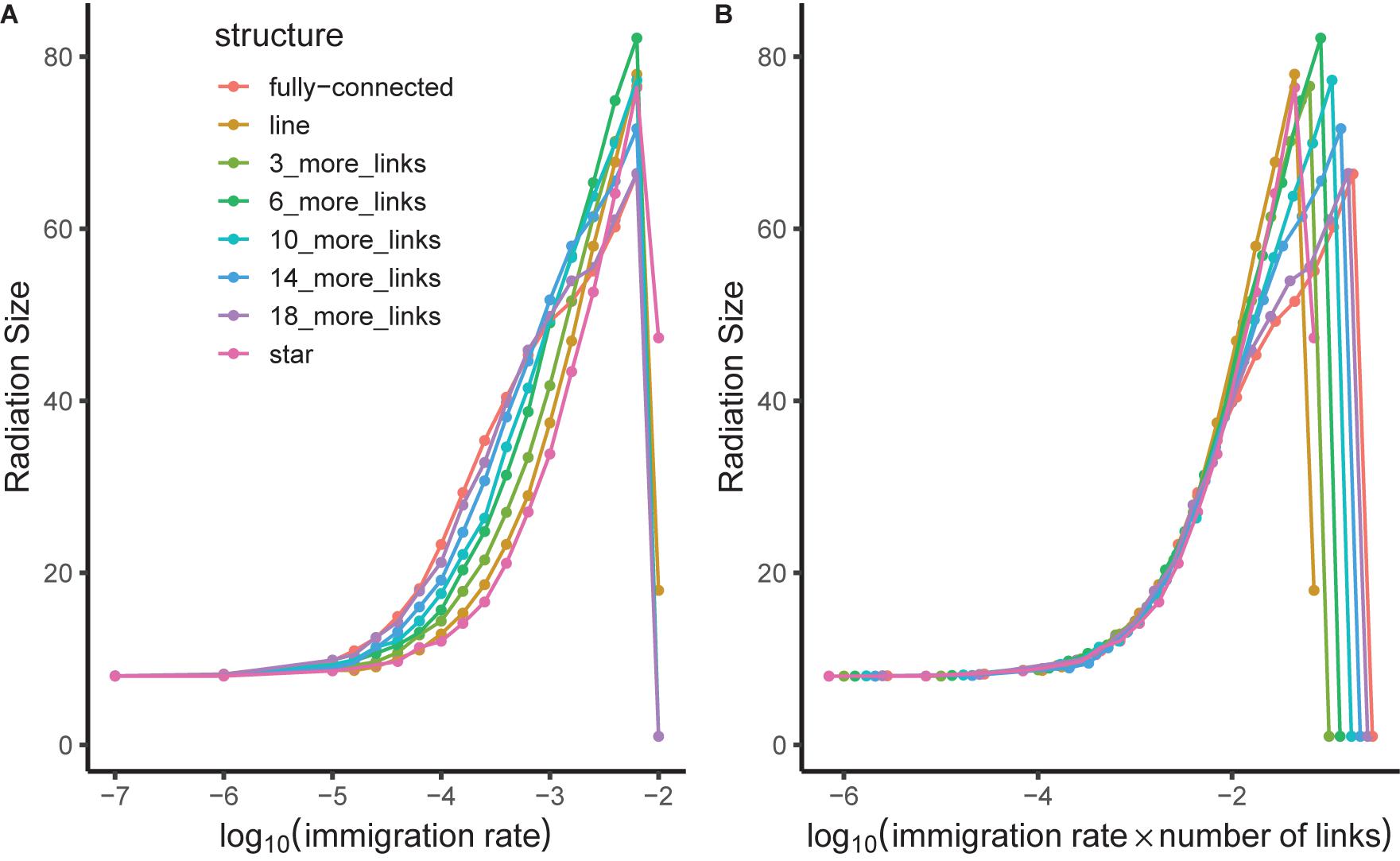
Figure 8. Mean radiation size of a single lineage in a community network as a function of internal immigration rate (m) on log 10 scale. Results show a broad range of connection networks with different numbers of links in different colors. Panel (A) shows the raw data. Panel (B) shows a scaling collapse based on the same data; here, the horizontal axis shows immigration rate multiplied by number of links in the network. The leftmost part of the graph for relatively low immigration rates thus has a radiation size predicted by immigration rate × number of links rather than depending independently on those two parameters. The figure was produced with gene flow effect (G) equal to 0.1 and community network containing 8 patches each with 1000 individuals.

For the simulations with a metacommunity, the radiation size for multiple immigrants varied from no radiation to a radiation of size 24 with our parameters. There was a relatively narrow range between lower quartile and upper quartile, but a much larger range of extremes was possible, especially at lower rates of external immigration (Figure 9).

FIGURE 9

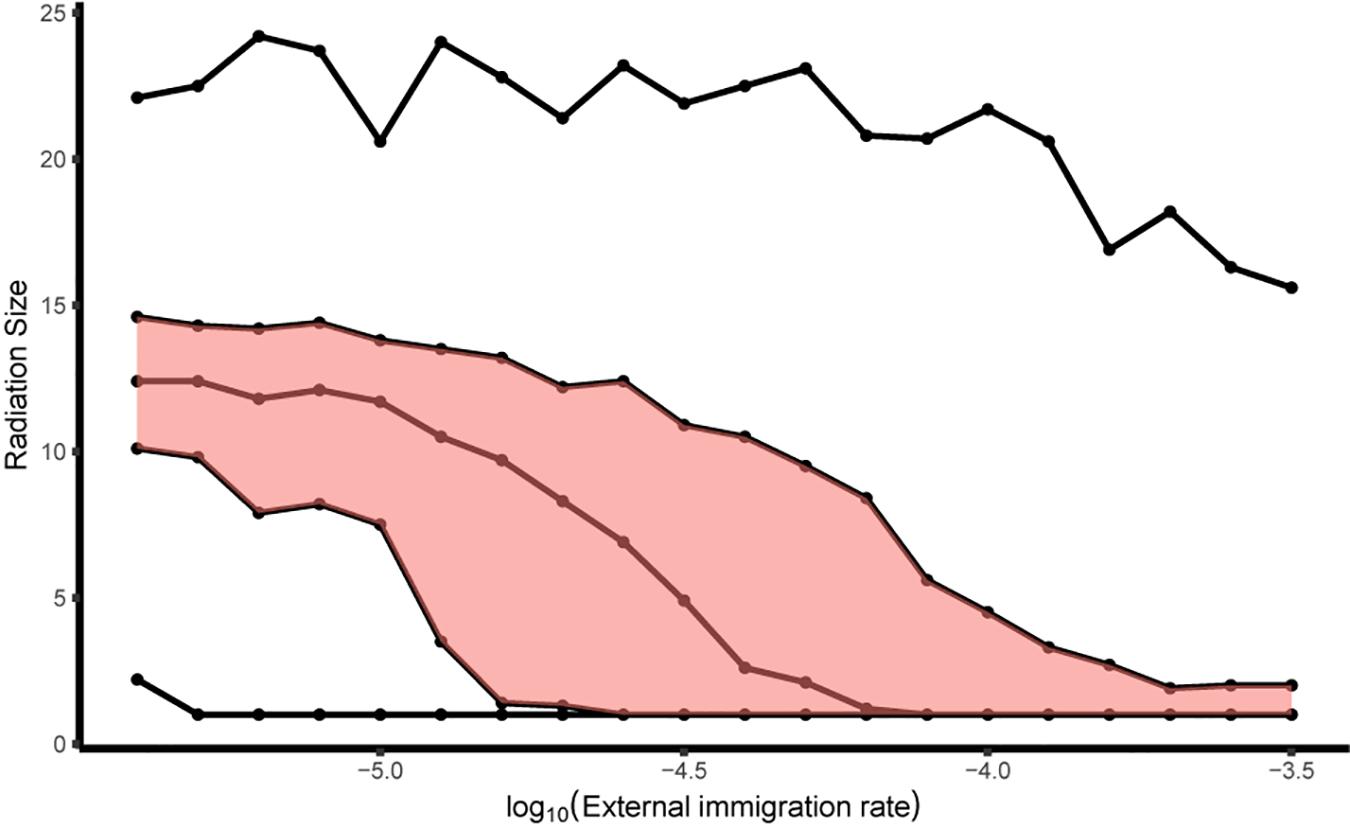
Figure 9. The range of radiation sizes for all lineages in a community network as a function of the external immigration rate (M) on log 10 scale. The five lines correspond to: minimum, lower quartile, median, upper quartile, and maximum, of the distribution of radiation sizes. The range between upper quartile and lower quartile is shaded in red. The gene flow effect (G) was 0.1. Internal dispersal rate (m) was 10^{– 3.5} and the community network was simulated with 4 patches, each having 1000 individuals.

Discussion

In our model, dispersal within the community of patches was a key determinant of radiation size. Internal dispersal could impede radiation by maintaining gene flow or promote radiation by providing opportunities for small populations to jump across barriers and later go on to speciate. An intermediate rate of internal dispersal therefore led to the largest radiations, consistent with the earlier findings from a simpler neutral model (Rosindell and Phillimore, 2011) as well as the intermediate dispersal model (Claramunt et al., 2012; Agnarsson et al., 2014), which predicts that taxa with intermediate dispersal ability diversify more readily. Our analyses extended these previous results with a fully mechanistic model that explicitly allows for multiple islands or patches in the community. We found that under these conditions the largest radiations occur at intermediate levels of dispersal. We also found, however, that the largest radiations arise due to conditions at singular critical points, at which lineages may radiate dramatically, or remain as one species for a relatively long period of time. The radiation size of a single lineage naturally fluctuates over time and may either go extinct or recover from a nearly extinct state to radiate again (Figure 4). These fluctuations appear reminiscent of the taxon cycle (Ricklefs and Bermingham, 2002), though they are driven by different mechanisms.

In larger and more complex communities the connectivity between any two local communities becomes a complex property determined by multiple factors, including both direct dispersal between the communities and indirect dispersal between them using other communities as stepping-stones. The largest radiations occurred when internal dispersal rates were at a critical point. In systems at this critical point, a period of slightly fewer than normal stochastic dispersal events to a patch can result in a very large radiation, but otherwise the same system may simply remain stable for a long while with no radiation at all. When radiation does occur in such cases, it is very rapid and forms a feedback loop that we call a ‘radiation cascade’. The mechanism behind a radiation cascade is that once the first allopatric speciation has occurred, population sizes of the resulting daughter species are smaller. Gene flow between conspecific populations on different patches is the product of number of individuals and per individual dispersal rate. Consequently, whilst dispersal rate has not changed, the reduction in number of individuals leads to less gene flow for each species. A decrease in gene flow in turn promotes further speciation and a positive feedback cycle is formed (Figure 10). The feedback is finally broken when species decline to abundances low enough to promote extinction and thus speciation is balanced by extinction with a new dynamic equilibrium (MacArthur and Wilson, 1967; Hubbell, 2001).

FIGURE 10

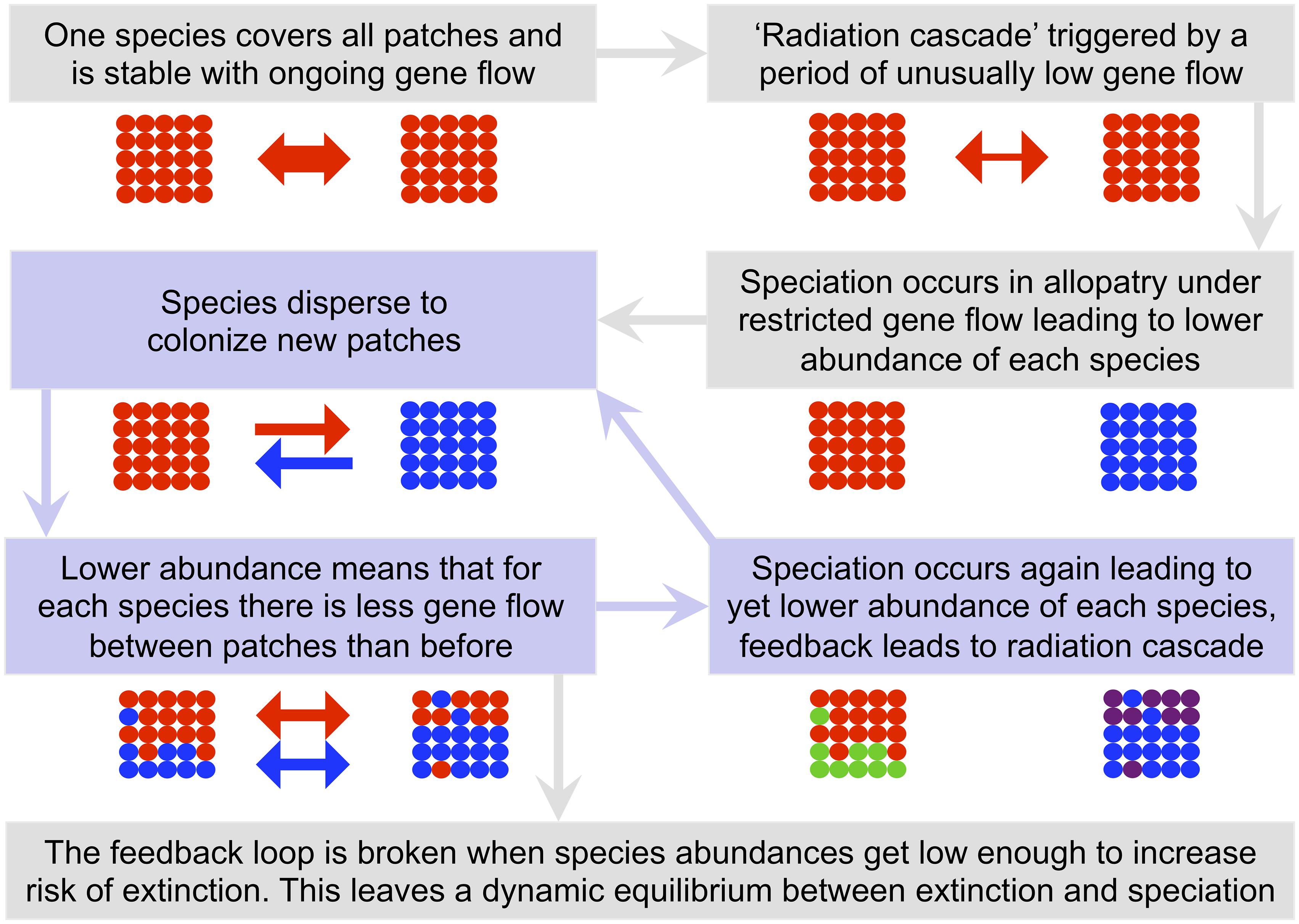
Figure 10. A cartoon explaining the radiation cascade mechanism. In this example the community consists of two local habitat patches each with 25 individuals. Colored circles represent individual organisms with color representing species. The arrow(s) between the two local habitat patches indicate the strength and direction of dispersal (and thus gene flow) for each species individually. The gene flow arrows are colored to match the color of the species to which they refer. Shaded boxes and lightly shaded arrows between them indicate the stages of a radiation cascade, with the focal feedback loop that leads to the cascade being shown in a light blue.

We propose that radiation cascades might explain the paradox of how speciation can be sustained at a rapid rate in early bursts of speciation (Martin and Richards, 2019). Radiation cascades may only happen when inter patch dispersal is close to a critical point and also depend on stochastic outcomes; this might explain why ‘early bursts’ are relatively rare in nature (Harmon et al., 2010).

Our work suggests that radiation cascades may be added to the list of many previously proposed mechanisms for rapid radiation, including diversity begets diversity, sexual signal complexity, the transporter hypothesis, ecological opportunity, fitness landscape connectivity, and plasticity first (Martin and Richards, 2019). These previously described mechanisms may not fully describe radiation processes in nature. According to the diversity begets diversity hypothesis, speciation opportunities arise directly from the number of species themselves, such that the speciation process becomes positive feedback cycle. However, this mechanism would not explain how initial diversity originated in the first place, or why diversification would ultimately cease rather than expanding indefinitely at ever increasing rates. The sexual signal complexity mechanism, in which sexual signaling promotes speciation, may also explain the ease of rapid radiation, but not the extent to which a lineage will ultimately radiate before speciation slows. The remaining mechanisms provide different ways in which a lineage may be prone to future radiation due to its genes (transporter hypothesis), accessible niches (ecological opportunity and fitness landscape connectivity) or phenotypes (plasticity first). While none of these factors were added in our model, we propose that the radiation cascade mechanism is another likely candidate for the mechanism behind some rapid bursts of radiation that is independent of species numbers or biological features invoked by the previously-proposed mechanisms. What is perhaps unique to the radiation cascade mechanism is that in some cases, with the right dispersal and gene flow effect parameters, a single species and a large radiation form quasi-stable states. In this case intermediate radiation sizes are inherently unstable and thus very quickly result in further rapid speciation, or occasionally in extinction and return to the single species state.

The role of the connectivity among communities in enabling radiations is clarified by a scaling collapse (Figure 8) identified in our study, that is a relationship between model parameters and results that simplifies the model and increases our understanding of the system in particular cases. Specifically, a local community network with more links can be equivalent to one with stronger links, provided that the overall connectivity between local communities is still relatively weak. The intuitive rationale for this invariance to the precise network structure is that when dispersal is rare, every dispersal event results in a new species if it survives (ongoing gene flow is negligible). Consequently, the total number of dispersal events is all that matters for model dynamics as this gives the potential number of new species later on. The total number of dispersal events is given by the product of number of connections and rate of movement along each connection; this can be increased by having more connections, or by strengthening existing connections.

Our models show that more isolated community networks with fewer external immigrants will naturally have larger radiation sizes. The reason is likely that external immigrants compete neutrally with pre-existing lineages and thus restrict the extent to which the pre-existing lineages can increase their range and abundance. This in turn reduces the amount of diversification taking place in pre-existing lineages. Colonizers that do arrive on more isolated communities, with fewer immigrating competitors, have more resources to proliferate and can therefore attain larger radiation sizes.

We have framed our work in terms of local community networks and a metacommunity. Yet, the concepts would also apply an archipelago of isolated islands and a very distant mainland source pool. These processes would also occur for patches where speciation occurs in allopatry at a sub-island scale. For example, many islands are volcanic, providing isolated topographical patches throughout, e.g., at different altitudes or cut off by topographic complexity. Indeed, Losos and Parent (2009) proposed that larger areas hold larger habitat diversity leading to more radiation. Our model would be consistent with this view if the larger habitats and increased habitat diversity manifest as a more complex network of local communities. However, our model also shows that habitat diversity in itself is not a prerequisite for large radiation sizes, which could also be attributed to dispersal and isolation across a single habitat type as has been observed in diversification of micro-snail species complexes (Hendriks et al., 2019).

The radiation cascades we report here are shown only under idealized simulated conditions. It could be that in the real world, natural amounts of gene flow between pairs of patches are so variable that not many connections are at a critical point at the same time, preventing such an extreme cascade from occurring. It could be that natural variation over time of factors that affect gene flow will more likely drive the radiation forward once it has started. In real world island systems, the dispersal ability of immigrating lineages may be reduced through evolutionary processes to avoid loss of dispersers (or propagules) into the ocean (Gillespie and Baldwin, 2010). Whilst this was not explicit in our model, an evolutionary reduction in dispersal could provide another way in which a radiation cascade could suddenly be triggered: as a deterministic outcome of evolutionary change reducing dispersal rate, rather than as a rarely seen paucity of stochastic dispersal events over a sufficiently long period of time. Despite the caveats that apply to our precise model formulation, we suggest that the primary mechanisms we describe as driving radiation cascades may apply in many real systems. The fundamental conditions for a radiation cascade are simply that (i) reduced gene flow promotes speciation and (ii) speciation reduces abundance and thus reduces gene flow between conspecific populations within each new species. Together these conditions create a feedback mechanism and explain part of the reason why radiations in geographically isolated structures (such as archipelagos) are so rapid for some species and non-existent for other species.

It seems logical, as we observe radiations with myriad functional forms adapted to different niches, to assume that the niches and adaptive processes were the only, or at least the primary driving force behind the radiation. However, our results suggest the possibility that, in some cases, the intertwined factors of stochastic dispersal events and spatial structure are the primary drivers for speciation and radiation. The resulting species that survive of course become adapted to their local niches, but as an effect of their isolation and speciation, rather than the cause of their isolation and speciation. In a radiation of Saxifragales, a major clade of temperate angiosperms, the rates of niche and phenotype evolution indeed lagged behind speciation (diversification in macroevolutionary terms) (Folk et al., 2019).

There is further support for the idea of niche adaptation as an effect rather than a cause in the case of generalist species. Suppose that a founding lineage displaying rapid radiation into niches had a high dispersal ability, and/or arrived in conditions enabling easy dispersal between the different habitat types. Gene flow may thereby continue between the different habitats, preventing radiation into locally endemic species in different niches, and instead creating the conditions for a single more generalist and widespread species to evolve that can tolerate a wide range of environmental conditions. This idea is consistent with recent observations among oceanic island plants that lineages undergoing spectacular radiations yield species that are rare and with narrow niches: “evolutionary winners are ecological losers” (Fernández-Palacios et al., 2021). Thus, we propose that radiation—or lack thereof—may arise more from dispersal limitation or genetic factors rather than the existence of the niches themselves.

Of course, in practice both perspectives will likely have elements of truth, with niches being both a cause and an effect of speciation and radiation to some extent. Ecologically distinct environments will hasten the speciation process, but with the process still requiring some degree of dispersal limitation and thus still being also subject to stochastic factors that determine radiations – including, possibly, radiation cascades.

There is much of scope for further work in this field. For example, one could experiment with different implementations of the speciation clock, which may be sensitive to population size or restrict the maximum time the speciation clock can reach, even given unlimited gene flow. More complex network structures, including structures with unequal connections between pairs of patches, would enable a more realistic view closer to real networks of local community patches (or islands). This is important as it might soften the sharp binary edge of a radiation cascade either occurring or not occurring. A more detailed study of radiation size, as a time series under different conditions, may shed further light on the new radiation cascade mechanism and when it arises. There is potential to add explicit niches, selection and adaptation into the model. It has been pointed out before that species commonness and rarity (that is, species abundance, measured in terms of numbers of individuals) could provide additional insight into community processes on islands (Rosindell and Phillimore, 2011). Indeed, neutral models of the kind we study here have often been both criticized (Enquist et al., 2002) and praised based on their predictions of commonness and rarity (Hubbell, 2001). In the context of determining radiation size, the combination of phylogenetic information and species abundances could prove to be a powerful approach to diagnosing the true underlying processes (Overcast et al., 2020).

Our study provided a mechanistic model to help understand the effects of biogeography and stochasticity on radiation size in the idealized scenario where there are no effects of adaptation. Our main finding suggests possible new drivers of radiation size in connected groups of isolated communities, including radiation cascades. This leads us to tentatively suggest that niche differentiation can be an effect rather than a cause of rapid radiations. We hope that our work will promote development of further mechanistic models of radiations and further thinking about the possible causes for rapid radiation, toward resolving why some lineages radiate so spectacularly when others do not.

Data Availability Statement

Publicly available datasets were analyzed in this study and are available here: https://onlinelibrary.wiley.com/doi/full/10.1111/jse.12465.

Author Contributions

JR proposed the model and study after early discussion with LS. RT wrote the code, did all the analyses, and produced all the graphs, with regular supervisory input from JR throughout. RT and JR produced the conceptual figures and wrote the manuscript. LS provided comments on manuscript drafts. All authors contributed to the article and approved the submitted version.

Funding

JR was funded by fellowships from the Natural Environment Research Council (NERC) (NE/I021179/1 and NE/L011611/1). This study is an output of the Georgina Mace centre for the Living Planet at Imperial College London. All simulations were run on high-throughput computing systems run by research computing services at Imperial College London.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Tim Barraclough, Rampal Etienne, Luke Harmon, and Ally Phillimore for insightful conversations about the topic, some of which occurred a long time in the past but were not forgotten. We thank Ryan Chisholm for valuable discussions and for his comments on a draft manuscript. We also thank two referees and the editors for their comments and suggestions. RT thanks Hongye Wang for her support as well as for valuable suggestions about the figure presentation from a reader’s perspective.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.644328/full#supplementary-material

References

Agnarsson, I., Cheng, R.-C., and Kuntner, M. (2014). A multi-clade test supports the intermediate dispersal model of biogeography. PLoS One 9:e86780. doi: 10.1371/journal.pone.0086780

PubMed Abstract | CrossRef Full Text | Google Scholar

Arbogast, B. S., Drovetski, S. V., Curry, R. L., Boag, P. T., Seutin, G., Grant, P. R., et al. (2006). The origin and diversification of Galapagos mockingbirds. Evolut. Int. J. Organic Evolut. 60, 370–382. doi: 10.1554/03-749.1

CrossRef Full Text | Google Scholar

Bennett, G. M., and O’Grady, P. M. (2013). Historical biogeography and ecological opportunity in the adaptive radiation of native Hawaiian leafhoppers (Cicadellidae: Nesophrosyne). J. Biogeogr. 40, 1512–1523. doi: 10.1111/jbi.12099

CrossRef Full Text | Google Scholar

Claramunt, S., Derryberry, E. P., Remsen, J. V. Jr., and Brumfield, R. T. (2012). High dispersal ability inhibits speciation in a continental radiation of passerine birds. Proc. Biol. Sci. R. Soc. 279, 1567–1574. doi: 10.1098/rspb.2011.1922

PubMed Abstract | CrossRef Full Text | Google Scholar

De Meester, L., Vanoverbeke, J., Kilsdonk, L. J., and Urban, M. C. (2016). Evolving perspectives on monopolization and priority effects. Trends Ecol. Evolut. 31, 136–146. doi: 10.1016/j.tree.2015.12.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Economo, E. P., and Keitt, T. H. (2008). Species diversity in neutral metacommunities: a network approach. Ecol. Lett. 11, 52–62.

Google Scholar

Enquist, B. J., Sanderson, J., and Weiser, M. D. (2002). Modeling macroscopic patterns in ecology. Science 295, 1835–1838.

Google Scholar

Erwin, D. H. (1992). A preliminary classification of evolutionary radiations. Hist. Biol. 6, 133–147. doi: 10.1080/10292389209380423

CrossRef Full Text | Google Scholar

Fernández-Palacios, J. M., Otto, R., Borregaard, M. K., Kreft, H., Price, J. P., Steinbauer, M. J., et al. (2021). Evolutionary winners are ecological losers among oceanic island plants. J. Biogeogr. doi: 10.1111/jbi.14143 [Epub ahead of print].

CrossRef Full Text | Google Scholar

Folk, R. A., Stubbs, R. L., Mort, M. E., Cellinese, N., Allen, J. M., Soltis, P. S., et al. (2019). Rates of niche and phenotype evolution lag behind diversification in a temperate radiation. Proc. Natl. Acad. Sci. U S A. 116, 10874–10882. doi: 10.1073/pnas.1817999116

PubMed Abstract | CrossRef Full Text | Google Scholar

Fukami, T. (2015). Historical contingency in community assembly: integrating niches, species pools, and priority effects. Annu. Rev. Ecol. Evolut. Systemat. 46, 1–23. doi: 10.1146/annurev-ecolsys-110411-160340

CrossRef Full Text | Google Scholar

Gascuel, F., Laroche, F., Bonnet-Lebrun, A.-S., and Rodrigues, A. S. L. (2016). The effects of archipelago spatial structure on island diversity and endemism: predictions from a spatially-structured neutral model. Evol. Int. J. Organic Evolut. 70, 2657–2666. doi: 10.1111/evo.13067

PubMed Abstract | CrossRef Full Text | Google Scholar

Gillespie, R. G., and Baldwin, B. G. (2010). “Island biogeography of remote archipelagoes: interplay between ecological and evolutionary processes,” in The theory of island biogeography at 40: impacts and prospects, eds J. B. Losos and R. E. Ricklefs (Princeton, NJ: Princeton University Press), 358–378. doi: 10.1515/9781400831920.358

CrossRef Full Text | Google Scholar

Givnish, T. J., Millam, K. C., Mast, A. R., Paterson, T. B., Theim, T. J., Hipp, A. L., et al. (2009). Origin, adaptive radiation and diversification of the Hawaiian lobeliads (Asterales: Campanulaceae). Proc. R. Soc. B Biol. Sci. 276, 407–416. doi: 10.1098/rspb.2008.1204

PubMed Abstract | CrossRef Full Text | Google Scholar

Grant, P. R. (2017). Ecology and Evolution of Darwin’s Finches (Princeton Science Library Edition): Princeton Science Library Edition. Princeton, NJ: Princeton University Press.

Google Scholar

Grant, P. R., and Grant, B. R. (2011). How and Why Species Multiply: The Radiation of Darwin’s Finches. Princeton, NJ: Princeton University Press.

Google Scholar

Grant, P. R., and Grant, B. R. (2014). 40 Years of Evolution: Darwin’s Finches on Daphne Major Island. Princeton, NJ: Princeton University Press.

Google Scholar

Harmon, L. J., Losos, J. B., Jonathan Davies, T., Gillespie, R. G., Gittleman, J. L., Bryan Jennings, W., et al. (2010). Early bursts of body size and shape evolution are rare in comparative data. Evolut. Int. J. Organic Evolut. 64, 2385–2396.

Google Scholar

Harvey, P. H., and Rambaut, A. (2000). Comparative analyses for adaptive radiations. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 355, 1599–1605. doi: 10.1098/rstb.2000.0721

PubMed Abstract | CrossRef Full Text | Google Scholar

Hendriks, K. P., Alciatore, G., Schilthuizen, M., and Etienne, R. S. (2019). Phylogeography of Bornean land snails suggests long-distance dispersal as a cause of endemism. J. Biogeogr. 46, 932–944. doi: 10.1111/jbi.13546

CrossRef Full Text | Google Scholar

Hubbell, S. P. (2001). The Unified Neutral Theory of Biodiversity and Biogeography (MPB-32). Princeton, NJ: Princeton University Press.

Google Scholar

Ibanez, T., Keppel, G., Baider, C., Birkinshaw, C., Culmsee, H., Cordell, S., et al. (2018). Regional forcing explains local species diversity and turnover on tropical islands. Glob. Ecol. Biogeogr. 27, 474–486. doi: 10.1111/geb.12712

CrossRef Full Text | Google Scholar

Kocher, T. D. (2004). Adaptive evolution and explosive speciation: the cichlid fish model. Nat. Rev. Genet. 5, 288–298. doi: 10.1038/nrg1316

PubMed Abstract | CrossRef Full Text | Google Scholar

Lamichhaney, S., Berglund, J., Almén, M. S., Maqbool, K., Grabherr, M., Martinez-Barrio, A., et al. (2015). Evolution of Darwin’s finches and their beaks revealed by genome sequencing. Nature 518, 371–375. doi: 10.1038/nature14181

PubMed Abstract | CrossRef Full Text | Google Scholar

Losos, J. B. (2010). Adaptive radiation, ecological opportunity, and evolutionary determinism. American Society of Naturalists E. O. Wilson award address. Am. Natural. 175, 623–639. doi: 10.1086/652433

PubMed Abstract | CrossRef Full Text | Google Scholar

Losos, J. B. (2011). Lizards in an evolutionary tree: ecology and adaptive radiation of anoles, Vol. 10. California: Univ of California Press.

Google Scholar

Losos, J. B., and Parent, C. E. (2009). The speciation-area relationship. The Theory of Island Biogeography Revisited. Princeton, NJ: Princeton University Press, 415–438.

Google Scholar

Losos, J. B., Mahler, D. L., and Others. (2010). Adaptive radiation: the interaction of ecological opportunity, adaptation, and speciation. Evolut. Darwin First 150, 381–420.

Google Scholar

Lovette, I. J., Bermingham, E., and Ricklefs, R. E. (2002). Clade-specific morphological diversification and adaptive radiation in Hawaiian songbirds. Proc. Biol. Sci. R. Soc. 269, 37–42. doi: 10.1098/rspb.2001.1789

PubMed Abstract | CrossRef Full Text | Google Scholar

MacArthur, R. H., and Wilson, E. O. (1967). The Theory of Island Biogeography. Princeton, NJ: Princeton University Press.

Google Scholar

Martin, C. H., and Richards, E. J. (2019). The paradox behind the pattern of rapid adaptive radiation: how can the speciation process sustain itself through an early burst? Annu. Rev. Ecol. Evolut. Systemat. 50, 569–593. doi: 10.1146/annurev-ecolsys-110617-062443

CrossRef Full Text | Google Scholar

Overcast, I., Ruffley, M., Rosindell, J., Harmon, L., Borges, P. A., Emerson, B. C., et al. (2020). A unified model of species abundance, genetic diversity, and functional diversity reveals the mechanisms structuring ecological communities. BioRxiv. [Preprint].

Google Scholar

Price, J. P., and Wagner, W. L. (2018). Origins of the Hawaiian flora: Phylogenies and biogeography reveal patterns of long−distance dispersal. J. Systemat. Evolut. 56, 600–620. doi: 10.1111/jse.12465

CrossRef Full Text | Google Scholar

Ricklefs, R. E., and Bermingham, E. (2002). The concept of the taxon cycle in biogeography. Glob. Ecol. Biogeogr. J. Macroecol. 11, 353–361. doi: 10.1046/j.1466-822x.2002.00300.x

CrossRef Full Text | Google Scholar

Robichaux, R. H., Carr, G. D., Liebman, M., and Pearcy, R. W. (1990). Adaptive Radiation of the Hawaiian Silversword Alliance (Compositae- Madiinae): Ecological, Morphological, and Physiological Diversity. Ann. Missouri Botanic. Garden. 77, 64–72. doi: 10.2307/2399626

CrossRef Full Text | Google Scholar

Rosindell, J., and Harmon, L. J. (2013). A unified model of species immigration, extinction and abundance on islands. J. Biogeogr. 40, 1107–1118. doi: 10.1111/jbi.12064

CrossRef Full Text | Google Scholar

Rosindell, J., and Phillimore, A. B. (2011). A unified model of island biogeography sheds light on the zone of radiation. Ecol. Lett. 14, 552–560. doi: 10.1111/j.1461-0248.2011.01617.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosindell, J., Cornell, S. J., Hubbell, S. P., and Etienne, R. S. (2010). Protracted speciation revitalizes the neutral theory of biodiversity. Ecol. Lett. 13, 716–727. doi: 10.1111/j.1461-0248.2010.01463.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosindell, J., Hubbell, S. P., and Etienne, R. S. (2011). The unified neutral theory of biodiversity and biogeography at age ten. Trends Ecol. Evol. 26, 340–348. doi: 10.1016/j.tree.2011.03.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosindell, J., Wong, Y., and Etienne, R. S. (2008). A coalescence approach to spatial neutral ecology. Ecol. Inform. 3, 259–271. doi: 10.1016/j.ecoinf.2008.05.001

CrossRef Full Text | Google Scholar

Rundell, R. J., and Price, T. D. (2009). Adaptive radiation, nonadaptive radiation, ecological speciation and nonecological speciation. Trends Ecol. Evolut. 24, 394–399. doi: 10.1016/j.tree.2009.02.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Schenk, J. J., and Steppan, S. J. (2018). The Role of Geography in Adaptive Radiation. Am. Natural. 192, 415–431. doi: 10.1086/699221

PubMed Abstract | CrossRef Full Text | Google Scholar

Schluter, D. (2000). The ecology of adaptive radiation. Oxford: OUP Oxford.

Google Scholar

Simões, M., Breitkreuz, L., Alvarado, M., Baca, S., Cooper, J. C., Heins, L., et al. (2016). The Evolving Theory of Evolutionary Radiations. Trends Ecol. Evolut. 31, 27–34. doi: 10.1016/j.tree.2015.10.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Simpson, G. G. (1953). The Major Features of Evolution. Columbia: Columbia University Press.

Google Scholar

Stroud, J. T., and Losos, J. B. (2016). Ecological opportunity and adaptive radiation. Annu. Rev. Ecol. Evolut. Systemat. 47, 507–532. doi: 10.1146/annurev-ecolsys-121415-032254

CrossRef Full Text | Google Scholar

Thompson, S. E., Chisholm, R. A., and Rosindell, J. (2020). pycoalescence and rcoalescence: packages for simulating spatially explicit neutral models of biodiversity. Methods Ecol. Evol. 11, 1237–1246. doi: 10.1111/2041-210X.13451

CrossRef Full Text | Google Scholar

Wellborn, G. A., and Langerhans, R. B. (2015). Ecological opportunity and the adaptive diversification of lineages. Ecol. Evolut. 5, 176–195. doi: 10.1002/ece3.1347

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoder, J. B., Clancey, E., Des Roches, S., Eastman, J. M., Gentry, L., Godsoe, W., et al. (2010). Ecological opportunity and the origin of adaptive radiations. J. Evolut. Biol. 23, 1581–1596. doi: 10.1111/j.1420-9101.2010.02029.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, X. Q., Maki, M., Drew, B. T., Paton, A. J., Li, H. W., Zhao, J. L., et al. (2014). Phylogeny and historical biogeography of Isodon (Lamiaceae): rapid radiation in south-west China and Miocene overland dispersal into Africa. Mol. Phylogenet. Evolut. 77, 183–194. doi: 10.1016/j.ympev.2014.04.017

PubMed Abstract | CrossRef Full Text | Google Scholar