
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Ecol. Evol. , 06 April 2021
Sec. Behavioral and Evolutionary Ecology
Volume 9 - 2021 | https://doi.org/10.3389/fevo.2021.636039
This article is part of the Research Topic Recent Advances in the Evolution of Euarchontoglires View all 15 articles
Differences between arboreal and terrestrial supports likely pose less contrasting functional demands on the locomotor system at a small body size. For arboreal mammals of small body size, asymmetrical gaits have been demonstrated to be advantageous to increase dynamic stability. Many of the extant arboreal squirrel-related rodents display a small body size, claws on all digits, and limited prehensility, a combination that was proposed to have characterized the earliest Euarchontoglires. Thus, motion analysis of such a modern analog could shed light onto the early locomotor evolution of eurarchontoglirans. In this study, we investigated how Swinhoe’s striped squirrels (Tamiops swinhoei; Scuiromorpha) adjust their locomotion when faced with different orientations on broad supports and simulated small branches. We simultaneously recorded high-Hz videos (501 trials) and support reaction forces (451 trials) of squirrels running on two types of instrumented trackways installed at either a 45° incline (we recorded locomotion on inclines and declines) or with a horizontal orientation. The striped squirrels almost exclusively used asymmetrical gaits with a preference for full bounds. Locomotion on simulated branches did not differ substantially from locomotion on the flat trackway. We interpreted several of the quantified adjustments on declines and inclines (in comparison to horizontal supports) as mechanisms to increase stability (e.g., by minimizing toppling moments) and as adjustments to the differential loading of fore- and hind limbs on inclined supports. Our data, in addition to published comparative data and similarities to the locomotion of other small arboreal rodents, tree shrews, and primates as well as a likely small body size at the crown-group node of Euarchontoglires, render a preference for asymmetrical gaits in early members of the clade plausible. This contributes to our understanding of the ancestral lifestyle of this mammalian ‘superclade’.
Evidence from the fossil record suggests stem placentals (i.e., eutherian mammals) to have been small scansorial animals. For example, Juramaia sinensis from the Jurassic of China (ca. 160 million years ago, mya) was a small, approx. mouse-sized animal which featured wrist bones that are similar to those of modern arboreal mammals (Luo et al., 2011). Eomaia scansoria (ca. 125 mya) from China was characterized by very similar body proportions and overall small size (Ji et al., 2002). Within placentals, the ‘superclades’ or ‘grandorders’ Laurasiatheria and Euarchontoglires form well-accepted monophyletic sister taxa (Murphy et al., 2001; Asher et al., 2009; Zhou et al., 2015). Euarchontoglires include the Lagomorpha (rabbits and pikas) and Rodentia (rodents), which together constitute the Glires (Simpson, 1945; Novacek, 1992; Murphy et al., 2001; Meredith et al., 2011). Also part of the Euarchontoglires are the taxa that together form the Euarchonta (Adkins and Honeycutt, 1991; Springer et al., 2004; Bininda-Emonds et al., 2007). The Euarchonta include the Dermoptera (colugos), the Scandentia (treeshrews), and the Primates (monkeys, apes and humans). Similarly to stem placentals, body size of early euarchontans (e.g., plesiadapiforms) was likely small, too (Silcox and López-Torres, 2017). A consensus regarding the phylogenetic affinities of the taxa forming the Euarchontoglires has not been reached despite considerable effort over recent years (reviewed in Nyakatura, 2019).
To help conceptualize the evolution of the Euarchontoglires (and specifically early primates), Sargis et al. (2007) proposed a small, clawed, and non-grasping mammal to represent the Euarchontoglires node. For the Euarchonta node, a clawed arboreal mammal with pedal grasping was suggested (Sargis et al., 2007). It can thus be expected that these small scansorial animals were not dissimilar to even earlier stem eutherians such as J. sinensis or E. scansoria. Since functional demands acting on the locomotor-system of small scansorial mammals and small arboreal mammals have been proposed to be highly similar (Jenkins, 1974), we here hypothesize that a small (∼100 g), clawed, scansorial or arboreal mammal could be regarded as a modern analog to early Euarchontoglires (or even stem placentals). Motion analysis to assess kinematic and dynamic adjustments could help to gain an improved understanding of the functional demands acting on the locomotor system of such an animal when confronted with simulated arboreal supports.
Small representatives of the squirrel-related clade (Sciuromorpha) combine many of the characteristics that Sargis et al. (2007) proposed for the Euarchontoglires and Euarchonta nodes. Sciuromorpha is the sister clade to all other rodents (Fabre et al., 2012) and it is likely that its most recent common ancestor was characterized by an arboreal lifestyle (Wölfer et al., 2019). Swinhoe’s striped squirrels (Tamiops swinhoei) live in forests consisting of evergreen broadleaf trees or conifers that spread from central China to northern Vietnam/Laos (Smith and Xie, 2013). They are characterized by an arboreal lifestyle including feeding on young shoots, fruits, and insects, and long jumps between trees, but are also found on the ground (Smith and Xie, 2013). Swinhoe’s striped squirrels are of relatively small size, with non-grasping (i.e., non-divergent) hallux and pollex, and with a crown-rump length of ca. 10 cm and a total mass of approx. 100 g. T. swinhoei also has claws on all digits. Moreover, striped squirrels almost entirely employ asymmetrical gaits, i.e., the species relies on full bounds, half-bounds, and gallops (Mielke et al., 2018).
Chadwell and Young (2015) proposed the existence of an evolutionary trade-off between the benefits and drawbacks of asymmetrical gaits which is related to body mass and support diameter. Asymmetrical gaits offer the advantages of generally higher locomotor speeds, the possibility to bridge gaps in the discontinuous arboreal habitat during the aerial phases of leaps, and the possibility to ‘grasp’ a thin support (e.g., a terminal branch) between the left and right appendage of each girdle without the necessity of grasping autopodia with opposable fingers or toes (cf. Lammers and Zurcher, 2011). However, high speeds and substantial aerial phases will incur large support reaction forces and could result in breaking thin arboreal supports (terminal branches) or in oscillations that complicate locomotor control. Thus, the authors proposed that arboreal species using asymmetrical locomotion in the terminal branch habitat should be restricted to small body size (Chadwell and Young, 2015).
We here employ motion analysis (kinematics and dynamics) on simulated arboreal supports of Swinhoe’s striped squirrels (Tamiops swinhoei, Sciuromorpha, Rodentia), a viable modern analog for the Euarchonta and Euarchontoglires nodes, to inform the reconstruction of functional demands that might have acted on early representatives of this mammalian ‘superclade’. Specifically, we tested whether the following expectations regarding the adjustments of spatio-temporal and dynamic parameters of locomotion, when confronted with simulated arboreal supports (narrow and/or inclined) were met (Table 1).
1. When comparing locomotion on thin simulated branches with locomotion on flat supports, we expected running speed, jumping distance, jumping height (normal to the support), and peak support reaction force (SRF) in the normal and fore-aft direction to be reduced and duty factor (DF) to be increased for both, fore- and hind limbs. This would facilitate better control over the oscillations of the center of mass as previously proposed based on analyses of larger arboreal species (different primates and Eastern gray squirrels Schmitt, 1999; Dunham et al., 2019). These previously observed adjustments are usually interpreted to increase aspects of static stability. Since it has been pointed out that the difference between terrestrial and arboreal supports is less consequential for smaller animals (Jenkins, 1974), we expected to find less emphasized differences between the flat trackway and the simulated branch in the small species we analyzed.
2. When comparing downhill and uphill to horizontal locomotion on both, simulated branches and flat trackways, we expected the avoidance of whole-body suspensions, increases in limb contact duration, and increases in the time interval between the landing of trailing and leading limbs as observed for the asymmetrical locomotion of mouse lemurs on similarly challenging supports (Shapiro et al., 2016). Again, similar trends have also been documented in the spatio-temporal parameters of Eastern gray squirrels and were proposed to promote stability (Dunham et al., 2019).
3. We further expected that the striped squirrels of our study would grasp further around the simulated branch with their feet than with their hands when running down a decline to allow a secure grip of the support between both feet and to avoid toppling forwards. We expected the opposite kinematic adjustment during incline locomotion to avoid toppling backwards as shown for considerably larger European red squirrels by Schmidt and Fischer (2011). These expectations are based on Siberian chipmunks (Tamias sibiricus) on a horizontal pole, which used the autopodia of both limbs of a girdle to grasp a simulated branch on opposite sides (Lammers and Zurcher, 2011). By this, the subjects controlled rolling torques of the body’s center of mass (CoM) to stay within a range even though net-rolling torque was usually non-zero over just one stride (Lammers and Zurcher, 2011). Grasping further around the pole can thus be expected to emphasize this control strategy on more demanding supports. On a declined flat trackway, we expected the squirrels to abduct their hind limbs more than their forelimbs based on a similar consideration. This ‘leaning backward’ adjustment would shift the center of mass posteriorly and toward the support, and would reduce the chance of toppling over forwards. Accordingly, we expected the squirrels to abduct their forelimbs more than their hindlimbs during inclined locomotion on the flat trackway. This ‘leaning forward’ adjustment would shift the CoM forwards and closer to the support, and would reduce the chance of toppling over backwards.
4. Regarding SRFs, we expected that the peak normal components of the SRF are slightly larger in the forelimbs than in the hind limbs during steady speed on a horizontal support as is usual in non-primate quadrupedal mammals, in contrast to the opposite pattern regularly observed in primates (cf. Schmidt, 2005; Lammers and Gauntner, 2008; Hesse et al., 2015). Further, we expected generally smaller peak normal and fore-aft SRF components to occur on the narrow, simulated branch when compared to the flat trackway to minimize dangerous impacts on potentially flexible and easily breaking narrow terminal branches (Schmitt, 1999). When confronted with declines, we expected to observe a shift toward larger peak normal SRFs and a larger peak braking force during forelimb support to facilitate deceleration as has been observed in symmetrical gaits of tamarins on declined simulated branches (Hesse et al., 2015) and in asymmetrical gaits of short-tailed opossums on a declined flat trackway (Lammers et al., 2006). We expected larger peak normal SRFs and a larger peak accelerating force during hind limb support when running up an incline to facilitate acceleration against gravity.
Four adult male individuals of Tamiops swinhoei, aged between 2 and 4 years, were filmed. They were born in captivity and kept in a cage (300 cm × 200 cm × 120 cm) with numerous hiding places and branches imitating an arboreal habitat. The animals were provided with food and water ad libitum. It was ensured that each animal was well rested before each recording session. Recording occurred 3 days a week at maximum with at least 1 day of rest in between from November 2017 until March 2018. The weights of the animals were documented before each session. The four individuals with the IDs a1-a4 had an average body mass ± standard deviation of 98.6 ± 2.4 g, 107 ± 4 g, 101 ± 4.7 g, and 106 ± 2.5 g, respectively. Two hours of filming in the morning were followed by 2 h in the afternoon after at least a 1-h break, in which the animals were kept in their transport cages. All procedures involving live animals were approved by the Humboldt-Universität zu Berlin and in correspondence with the regulations of animal welfare in Berlin, Germany, and approved by the relevant authority (LAGeSo reg. no.: 0098/16).
We recorded the locomotion on two different setups, which were additionally installed at different slopes (Figure 1). The first support was a trackway of approximately 2 m which was covered with a thin layer of cork to facilitate enough friction during fast locomotion. We assumed the cork to be thin enough to not dampen the impact during the support phase. A force plate was implemented into the center of the trackway with a small gap around it in order to minimize the transfer of oscillations. The second support covered with the same type of cork was a raised dowel to simulate a branch (diameter = 13.3 mm). It had a similar length of approximately 2 m and was mounted on the trackway. The central part of this pole with a length of 14.6 cm was mounted separately on the force plate underneath leaving a small gap to the adjoining dowels, thus also minimizing the transfer of oscillations. The trackway was covered by an acrylic glass enclosure high enough to not restrain the maximum jumping height of the animals [we previously studied the influence of the enclosure size on locomotor parameters (Mielke et al., 2018)].

Figure 1. Camera views used for kinematic analysis of the experimental setups. Overview on (A) the flat trackway (here oriented horizontally) and (B) on the branch-like pole (here inclined by 45°, the squirrel is heading downwards). (C,D) Close-up views on the trackway to measure the distance (d1) between the claws of the phalanges III of the hands and the distance (d2) between the metatarsophalangeal joints III, respectively. (E) Close-up view on the pole to measure the distance (d3) between the metacarpo- and metatarsophalangeal joint III, respectively, and the lower margin of the pole.
Both supports were then either fixed on a table or inclined to form a slope of 45°. The subjects were filmed using three high speed CamPhF 2000 cameras (Photonfocus AG, Lachen, Switzerland). Recording was accomplished using the software Contemplas Templo (Contemplas GmbH, Kempten, Germany). One camera was positioned at the side of the setup in a right angle for an overview of the entire trackway. It recorded with a framerate of initially 200 and later 300 frames per second (fps), which was finally increased to 350 fps (used for the vast majority of the trials). This camera was used to analyze running speed, jumping distance, jumping height, and DF.
For the flat trackway set up, the other two cameras were positioned to facilitate a close-up view on the force plate. They were used to measure limb abduction (Figure 1). Regarding the pole setup, the other two cameras were placed closer on both sides of the central pole to measure the positioning of the hand and feet during touchdown. These two cameras always recorded with a framerate of 600 fps. They were additionally used to determine if the animals put all four limbs ‘cleanly’ on the force plate (or the pole mounted on top of it) or if they stepped over a margin, resulting in incomplete force measurements. This facilitated a selection of appropriate trials for the analysis of SRFs. For the experiments, two individuals were placed inside the setup at a time as we noticed that subjects were more motivated to move around when not alone, resulting in more recorded trials. However, only trials were used during which a single individual was contacting the force plate. Normal, fore-aft, and mediolateral (not used in this study) SRFs were recorded for all limbs combined using a single AMTI HE6X6-1 force plate (Advanced Mechanical Technology, Inc., Watertown, MA, United States) at a rate of 1800 Hz (Figure 1). A completely separate recording of single limb forces was not possible as ipsilateral fore- and hind limbs overlapped in their stem phases and were additionally placed closely adjacent to each other. Camera- and force plate recordings allowed for a visual matching of touchdown/lift-off events and SRF changes since both devices were not perfectly synchronized electronically.
We aimed at only including trials approximating a steady running speed. Swinhoe’s striped squirrels are non-cursorial animals characterized by fast acceleration and deceleration within a few stride cycles (Mielke et al., 2018). We only analyzed the two cycles ending and beginning with contacting the force plate, respectively. A stride cycle was defined as starting with a touchdown of the first forelimb and ending with the last frame before the subsequent touchdown of the first forelimb. The videos from the overview camera were imported, calibrated, and the kinematics were analyzed in Vicon Motus 3D (Contemplas GmbH, Kempten, Germany). The tip of the nose of the respective subject was digitized with a landmark in each frame of interest. To obtain a measure of running speed, the x-coordinate of each landmark was subtracted from the x-coordinate of the landmark of the previous frame and then multiplied by the frame rate to obtain the speed (the x-axis was defined as being parallel to the support). The speed values of a stride cycle were then averaged, labeled just speed in the following. According to our criterion, all trials with a speed difference of more than 25% between the two analyzed stride cycles were discarded, with 501 trials remaining for analysis (Supplementary Table 1). In case a sequence adhered to our steady speed criterion, the landmarks of the second cycle (starting with the first forelimb touchdown on the force plate) were used for analysis. The absolute difference between the x-coordinates of the last and first landmarks placed during the second stride cycle was used as the jumping distance. Jumping height was obtained by selecting the landmark with the largest y-coordinate value. Note that in the inclined setup, the camera was also tilted by 45° to the side. Thus, this variable refers to the maximum distance of the tip of the animal’s nose from the support and not to the height in line with gravitational acceleration.
Frames associated with the touchdowns (including the ones of the consecutive cycle) and lift-offs of all limbs were recorded for the computation of DFs and lead duration. The DFs of the limbs of a girdle were averaged to obtain the mean DFs of the fore- and hind limbs (DF-FL and DF-HL, respectively). The ratio between DF-FL and DF-HL was also computed (DF-R). The leads of the fore- and hind limbs were computed to evaluate the gait type.
The close-up camera videos were imported to ImageJ2 (Rueden et al., 2017). Regarding the trackway, the force plate’s width was used for calibration to measure limb abduction. Forelimb abduction was quantified by measuring the distance between the claws of left and right phalanx III and hind limb abduction was measured as the distance between the centers of the metatarsophalangeal joints (as the phalanges were not visible; Figure 1). The ratio between the former and the latter was computed, but the raw measures were also analyzed to determine the contribution of forelimb and hind limb adjustments to changes in the ratio. On the pole, the distance between the metacarpophalangeal or metatarsophalangeal joints III (MCPJ III or MTPJ III) and the lower margin of the pole was measured to quantify hand and foot positioning, respectively (Figure 1). Only the camera on one side was used to obtain these data. The distance was normalized by the diameter of the pole. Values above 100% were possible when the hand/foot was placed close to the top or on top of the pole. A ratio between MCPJ III and MTPJ III positioning was computed. Hence, we also analyzed the ratio as well as the two distances themselves.
The SRF data were directly exported from Templo. The normal force (normal to the support), as well as accelerating and decelerating forces (fore-aft forces, in line with the running direction) were analyzed, as well as their relative timings within the duration from the first forelimb touchdown to the last hind limb lift-off. 451 of 501 trials contained appropriate force data, which were trimmed to match this duration. Forces were then smoothed using a simple moving average filter including three consecutive time points and standardized by the body weight of the animal. The support phase duration (from forelimb touchdown to hind limb lift-off) was standardized to 100%. SRFs of all limbs combined were evaluated just graphically in terms of their trajectory. We did not calculate peak forces or impulses and thus, we did not include inferential statistics, as fore- and hind limbs generally overlapped in their contacts with the force plate (see above).
All statistical analyses were conducted with the software R (R Core Team, 2020). The following additional packages were used for data preparation, visualization, and analysis: readxl (Wickham and Bryan, 2019), tidyverse (Wickham et al., 2019), psych (Lenth, 2020), nlme (Pinheiro et al., 2020), and emmeans (Lenth, 2020).
The gaits were classified using forelimb and hind limb lead duration, respectively, in percent of the stride cycle duration of the left hindlimb. Cut-off lead percentages were defined according to Hildebrand (1977). Linear regression modeling was used to investigate the influence of support orientation, support type, and speed on the respective parameters. We followed the guidelines provided by Zuur et al. (2009) to obtain regression models with significant explanatory variables that also sufficiently fulfill the necessary modeling assumptions. The following procedure was applied to each dependent variable (Table 1).
Firstly, a simple linear regression including all fixed effects and possible interaction effects among them was conducted. Residual outliers were assessed via boxplots and removed if considered too extreme, i.e., they were distinctly separated from all other data points in the residual distribution.
Secondly, the animal ID was included as a random effect using the lme function. To avoid overfitting, differences among animals regarding the effects of support type, support orientation, and speed on the dependent variable were assessed graphically while disregarding interactions. The most complex combination of random effects that seemed meaningful was included. The random term was then simplified via backwards elimination, using likelihood ratio tests to compare the more complex model to the simpler model at each step. If the p-value was above 0.05, the simpler model was selected; otherwise the complex model was retained. If two different simpler models were both considered more appropriate than the more complex parent model, they were compared using the Akaike information criterion (AIC; Burnham and Anderson, 2002) and the model with the lower value was retained. In case the random effect did not significantly contribute to model likelihood, it was removed completely.
Thirdly, the homoscedasticity of the residuals was assessed graphically. Again, the most complex model adjustments that appeared to be necessary were included using the weights argument in the lme function (or the gls function in case a random effect was not retained). The model was simplified using backwards elimination as outlined above until the most parsimonious adjustment for heteroscedasticity was achieved.
Finally, the fixed effects and their interaction were removed via backwards elimination as outlined above, always removing interaction effects before the associated main effects. The final model was checked in regard of normality and homoscedasticity of within-subject residuals. If extreme outliers were present again, they were removed. All in all, outliers were removed for three dependent variables, with five outliers being the maximum. Estimated marginal means of support orientations and support types were compared post hoc using the contrast function of the emmeans package and the Tukey method for adjusting p-values. In case interactions with speed were significant, post hoc tests for support type and support orientation were conducted at three speed values (low, moderate, and high, see Results). A significance level of 0.05 was chosen for all analyses. See Supplementary Data Sheets 1, 2 for the R script and data, respectively, to reproduce all regression results.
Regression results are presented in the following way: (1) descriptive statistics of the dependent variables (see also Supplementary Table 2), (2) specifications of the final regression models (see also Supplementary Table 3), (3) comparisons between pole and trackway for all support orientations, (4) comparisons between downhill and horizontal locomotion on both support types, and (5) comparisons between uphill and horizontal locomotion on both support types. An overview of the regression results including the coefficient table, the variance function estimates, the estimated marginal means, and all pairwise post hoc comparisons is provided in Supplementary Tables 4–15.
Out of 501 stride cycles used for kinematic analysis, 500 showed asymmetrical gaits; One stride cycle was characterized by an asymmetrical forelimb pattern and a symmetrical hind limb pattern (hind limb lead > 40%; Figure 2). The asymmetrical gaits could be distinguished into full bound (456 times, common for all setups), half bound (31 times, observed during downhill locomotion irrespective of the support type), crutch walk (6 times) and gallop (7 times), both modes mostly being used during declined locomotion on the trackway.
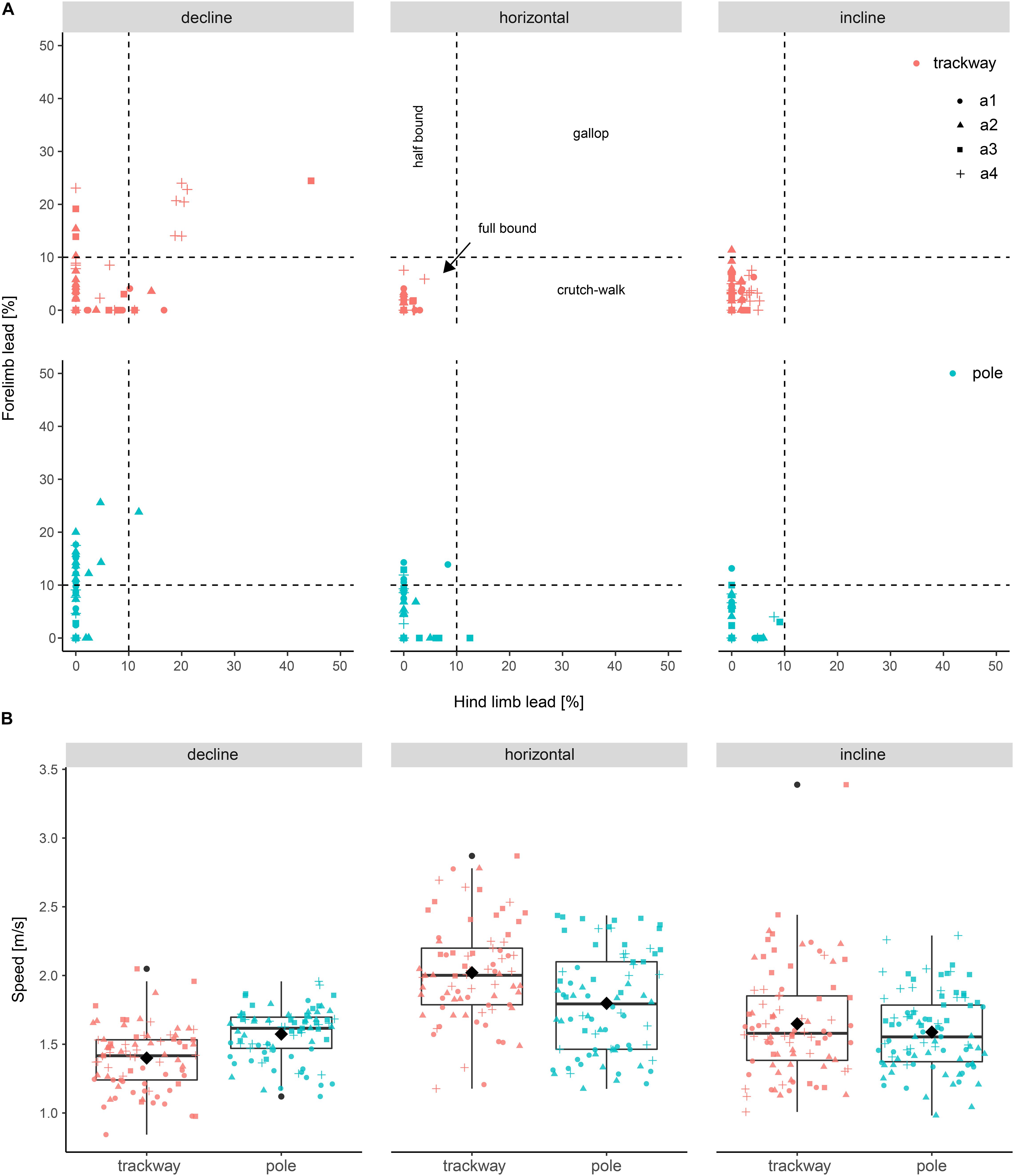
Figure 2. Forelimb lead versus hind limb lead and speed differences among setups. (A) Lead used to quantify asymmetrical gaits. Cut-off values according to Hildebrandt (1977). Trials with a forelimb and hind limb lead < 10% are categorized as full bounds, trials with forelimb lead > 10% and hind limb lead < 10% are categorized as half bounds, trials with forelimb lead < 10% and hind limb lead > 10% are categorized as crutch walks, and trials with forelimb and hind limb lead > 10% are categorized as gallops. (B) Speed distributions shown as boxplots. a1–a4 refer to the studied individuals.
The average speed across all observations was 1.7 ± 0.4 ms–1. The minimum speed was 0.8 ms–1 and the maximum speed was 3.4 ms–1. However, the latter value was an extreme value and speeds above 2.5 ms–1 were generally rare (Figure 2). The following three values were chosen for all other locomotion parameters (i.e., the dependent variables except for speed) to compare support types and support orientation levels post hoc in case of significant interactions with speed: 1.2 m/s – low, 1.8 m/s – medium, 2.4 m/s – high. This was considered a meaningful range with a doubling in speed from smallest to largest value. Furthermore, all three speed values lay within the range of four of the six combinations of support types and support orientations. A speed of 2.4 ms–1 was not observed during downhill locomotion on the trackway and the pole (Figure 2). Hence, comparisons involving downhill locomotion at this speed were not interpreted.
The final regression model included support type and support orientation and their interaction as fixed effects and animal specific effects of support orientation as a random effect. The variance function accounted for heterogeneity by including different variances for all combinations of support orientation and support type.
The speed was significantly lower on average on the pole compared to the trackway when running horizontally (p < 0.001; Figure 2 and Table 2). Running down the decline, the opposite case was observed with a significantly higher speed being observed on the pole (p < 0.001). There was no significant difference between the two support types during uphill locomotion (p = 0.783). The speed was significantly lower on average on the trackway when the squirrels ran downhill compared to horizontally (p < 0.001), but this was not the case on the pole (p = 0.138). Comparing uphill to horizontal locomotion, the speed was significantly lower during uphill locomotion on both support types (p ≤ 0.002).
The DF-FL was 41.8 ± 10.5% on average, with a minimum of 18.8% and a maximum of 71.2%. The DF-HL was 42 ± 9.9% on average, with a minimum of 19.4% and a maximum of 70.2%. The DF-R was 1 ± 0.2 on average, with a minimum of 0.5 and a maximum of 1.9.
All three final models included support type and support orientation as fixed effects and speed as a covariate. The regression models with DF-FL and DF-HL as a dependent variable, respectively, included all possible interactions and different effects of speed and support orientation on the DF per animal as a random effect. The variance function for the model with DF-HL accounted for heterogeneity by including a dependence of the variance of the DF-HL on speed that differed between all combinations of support orientations and support types. The regression model with DF-R as a dependent variable included two two-way-interactions (support type x speed and support orientation x speed) and different effects of support orientation on the DF-R per animal as a random effect. The variance function accounted for heterogeneity by including a different variance of the DF-R for each support orientation.
The DF-FL as well as the DF-HL were significantly larger on the pole compared to the trackway at all three speeds when the squirrels ran horizontally (p-always < 0.001; Figure 3 and Table 3). During downhill locomotion, the DF-FL was only significantly larger on the pole at a low speed (p < 0.001), but not at a medium speed (p = 0.114), whereas the DF-HL was never significantly different (p ≥ 0.290). Regarding uphill locomotion, the DF-FL was significantly larger on the pole at medium and high speeds (p-always < 0.001), but not at a low speed (p = 0.615).
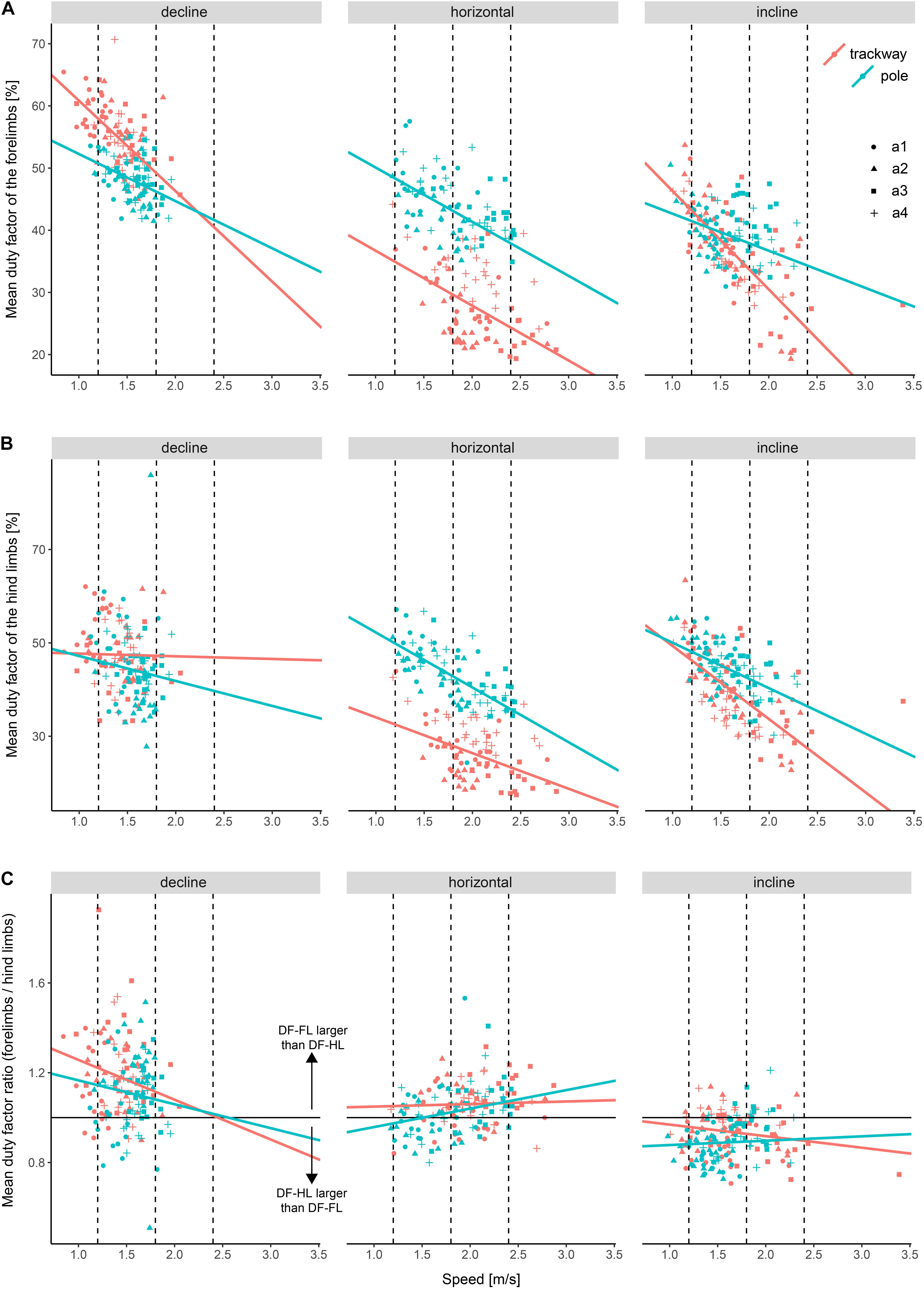
Figure 3. Duty factor differences among experimental setups. (A) Mean duty factor of the forelimbs (DF-FL), (B) mean duty factor of the hind limbs (DF-HL), and (C) Ratio between the two mean duty factors. Dashed lines indicate the speed values at which setups were compared statistically post hoc. a1–a4 refer to the studied individuals.
On the trackway, the DF-FL and the DF-HL were significantly increased during downhill compared to horizontal locomotion at both, low and medium speeds (p-always < 0.001). On the pole, no significant differences were observed for both between declined and horizontal locomotion at these speeds (p ≥ 0.527). The DF-R was only significantly larger during downhill compared to horizontal locomotion at a low speed irrespective of support type (p < 0.001), but not at a medium speed (p = 0.257).
Comparing uphill to horizontal locomotion on the trackway, the DF-FL was significantly larger at a low speed (p = 0.007) but not at medium and high speeds (p ≥ 0.431), whereas the DF-HL was significantly larger at low and medium speeds (p-always < 0.001) but not at a high speed (p = 0.731). On the pole, the animals displayed a similar DF-FL pattern, with it being significantly larger at a low speed (p = 0.034) but not at medium and high speeds (p ≥ 0.122). However, the DF-HL did not differ significantly between uphill and horizontal locomotion at all three speeds (p ≥ 0.994). The DF-R was significantly smaller during uphill locomotion irrespective of the support type (p-always < 0.001).
The average jumping distance was 20.8 ± 7 cm, with a minimum of 10.8 cm and a maximum of 51.3 cm. The final model included support type, support orientation, speed and all possible interactions as fixed effects/covariate and different effects of support orientation and speed on jumping distance per animal as a random effect. The variance function accounted for heterogeneity by including a dependence of variance in jumping distance on speed that differed between support types.
The jumping distance was always significantly lower on average on the pole compared to the trackway (p ≤ 0.001; Figure 4 and Table 4). Comparing downhill to horizontal locomotion, the squirrels jumped a significantly shorter distance on average on the trackway (p ≤ 0.001), but not on the pole (p ≥ 0.988). When comparing uphill to horizontal locomotion at all three speeds, the squirrels jumped a significantly shorter distance on average only at a medium running speed while on the trackway (p = 0.001, else p ≥ 0.140), whereas jumping distance was significantly shorter for both, low and medium speeds on the pole (p ≥ 0.002, else 0.309).
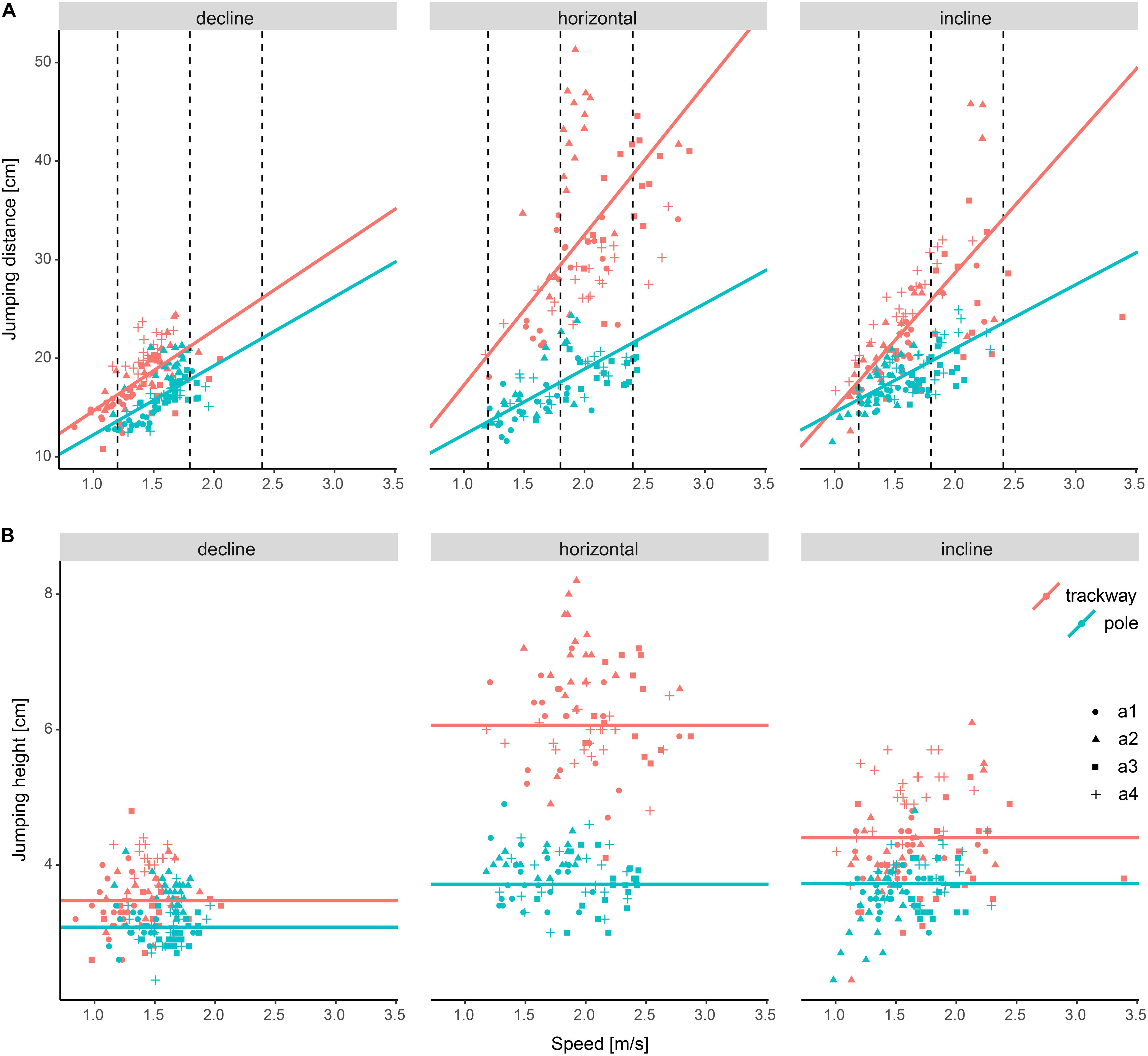
Figure 4. Differences in jumping distance and jumping height among experimental setups. (A) Jumping distance and (B) Jumping height. Dashed lines indicate the speed values at which setups were compared statistically post hoc (not relevant for jumping height as speed had no significant effect and hence was removed from the final regression model). a1–a4 refer to the studied individuals.
The jumping height was 4.1 ± 1.1 cm on average, with a minimum of 2.3 cm and a maximum of 8.2 cm. The final model included support type and support orientation as well as their interaction as fixed effects and different effects of support orientation and speed on jumping height per animal as a random effect. The variance function accounted for heterogeneity by including a dependence of the variance of jumping height on speed that differed between all combinations of support orientations and support types.
The jumping height was significantly lower on average on the pole compared to the trackway for all three support orientations (p-always < 0.001). It was also significantly lower when comparing downhill to horizontal locomotion on both support types (p-always < 0.001). When running uphill, jumping height was significantly lower compared to the horizontal support orientation on the trackway (p < 0.001), but not on the pole (p > 0.999).
The distance between the hands was 44.4 ± 11.3 mm on average, with a minimum of 23.2 mm and a maximum of 75 mm. The distance between the feet was 49.2 ± 7.3 mm on average, with a minimum of 33.9 mm and a maximum of 70 mm. The ratio of hand to foot distance was 0.9 ± 0.3 on average, with a minimum of 0.4 and a maximum of 1.9.
All three final models included support orientation as a fixed effect. The models with forelimb distance and the ratio of forelimb to hind limb distance, respectively, additionally included speed as a covariate and its interaction with support orientation as a fixed effect. All three models accounted for different effects of support orientation on forelimb distance per animal as a random effect and included a variance function accounting for heterogeneity by including different variances for all support orientations.
There was no significant difference in the average distance between hands (p ≥ 0.567 at low and medium speeds) or between feet (p = 0.082) when comparing declined to horizontal trackway, although the distance between feet appeared to be larger when running downhill (Supplementary Image 1 and Supplementary Tables 10, 11). Contrary to our expectation, the ratio was not significantly smaller when comparing locomotion on the declined trackway to that on the horizontal trackway at low and medium speeds (p ≥ 0.053), although a trend in this direction was observable at a low speed (Figure 5 and Table 5). There was a significant difference in the average distance between hands (p-always < 0.001, larger distance on the incline) as well as between feet (p < 0.001, smaller distance on the incline) when comparing uphill to horizontal locomotion. As expected, the ratio was significantly larger on the incline at all three speeds (p-always < 0.001).
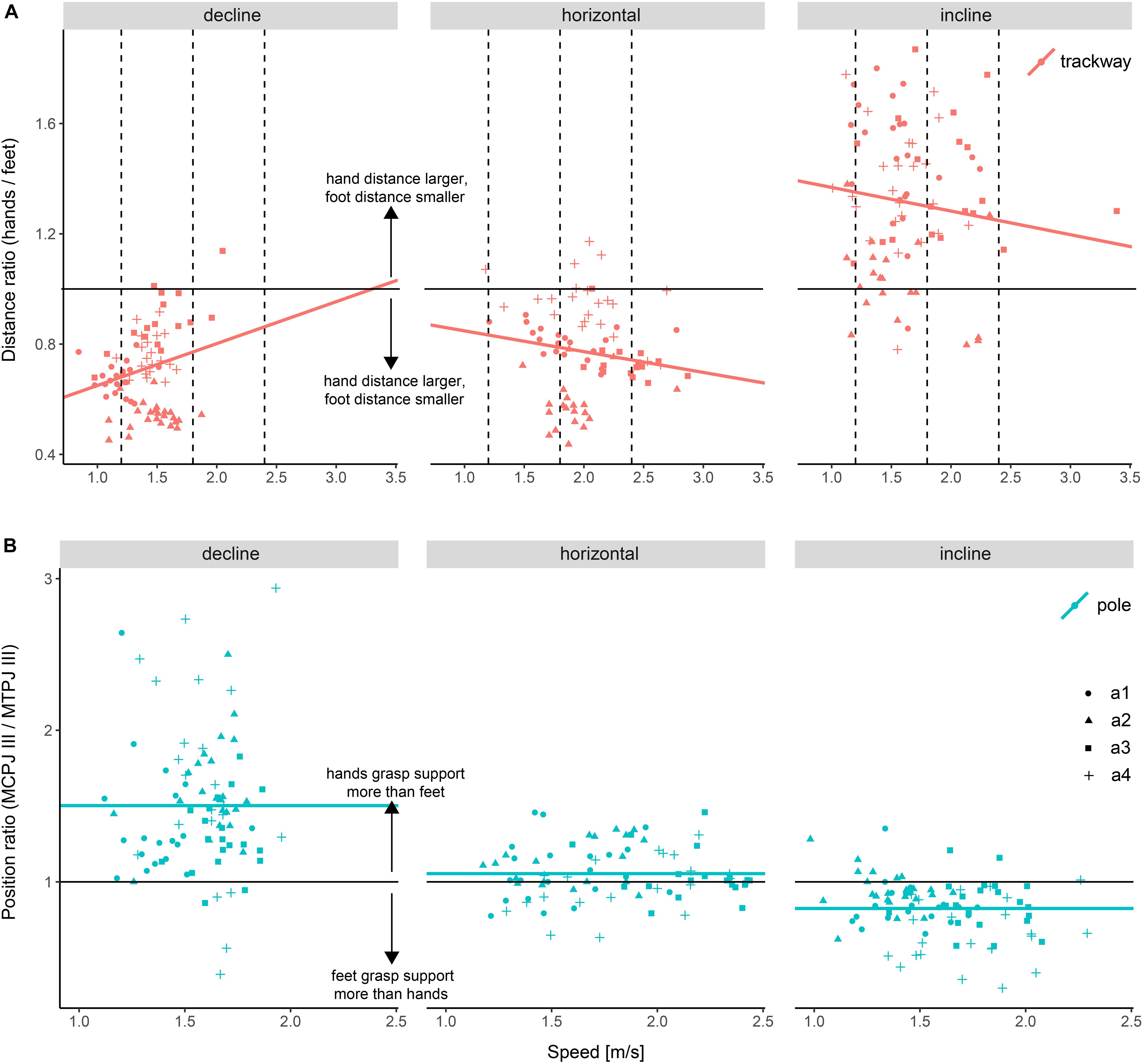
Figure 5. Differences in autopodial placement depending on support orientation. (A) Ratio of the distance between hands to the distance between feet on the flat trackway. (B) Ratio between the position of the metacarpophalangeal joint III (MCPJ III) and metatarsophalangeal joint III (MTPJ III) on the pole. Position was measured as the distance from the lower margin of the pole. Dashed lines indicate the speed values at which setups were compared statistically post hoc (not relevant for (B) as speed had no significant effect and hence was removed from the final regression model). a1–a4 refer to the studied individuals.
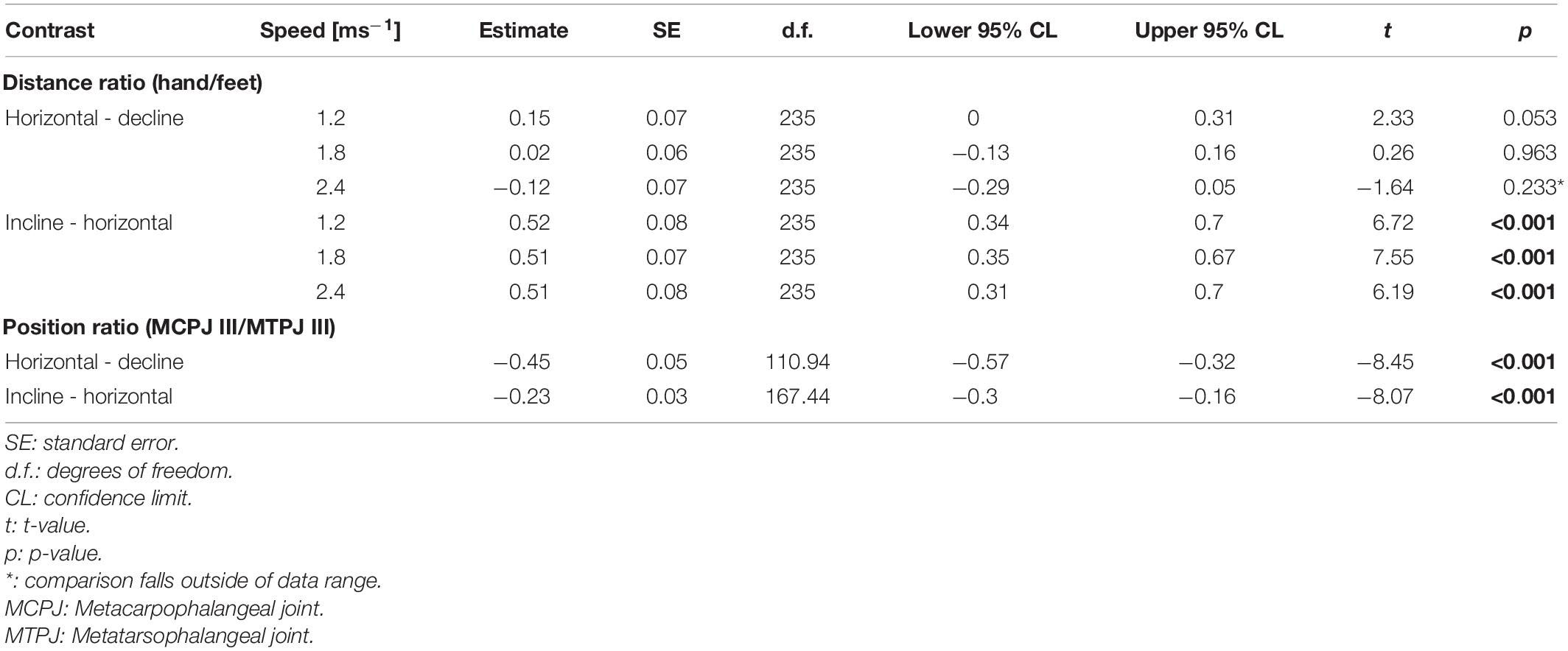
Table 5. Post hoc contrasts for the regressions of the ratio of hand/foot distance on the trackway and the ratio of the positions of the MCPJ III and MTPJ III on the pole.
The relative position of the MCPJ III from the lower margin of the pole was 99.7 ± 19.2% on average, with a minimum of 32.7% and a maximum of 131.3%. The relative position of the MTPJ III on the pole was 95.3 ± 21.9% on average, with a minimum of 33.9% and a maximum of 138.3%. The ratio between hand and foot positioning was 1.1 ± 0.4 on average, with a minimum of 0.3 and a maximum of 2.9.
The three final models included support orientation as a fixed effect. Except for the ratio regression model, speed was considered a significant covariate. The regression model for MCPJ III included different intercepts per animal as a random effect, whereas the other two regression models included a variance formula that accounted for heterogeneity by including a different variance for each support orientation.
There was no significant difference in the average hand positioning on the pole between running down a decline and horizontal locomotion (p = 0.993), but the foot was positioned significantly closer to the lower margin of the pole when running on a decline compared to horizontal locomotion (p < 0.001; Supplementary Image 2 and Supplementary Tables 13, 14). The ratio was significantly larger when comparing downhill to horizontal locomotion (p < 0.001; Figure 5 and Table 5), supporting the previous finding. Running on an incline, the hand was positioned significantly lower on average compared to horizontal locomotion (p < 0.001), whereas the foot was positioned significantly higher on average (p = 0.02), although the estimated difference was a lot smaller for the latter (∼6% compared to ∼18%). Using the ratio to compare foot to hand placement, the ratio was significantly smaller when comparing inclined to horizontal locomotion (p < 0.001), supporting these findings.
Overall, the average SRF patterns were very similar between pole and trackway. On both supports, the normal force on a horizontal support is characterized on average by two large peaks (Figure 6). Each is representing the support phase of a limb girdle of which the forelimbs exert a higher maximum force on average. When running down a decline, the peak of the forelimbs is larger compared to that of hind limbs, whereas the opposite is the case for running up an incline. On a horizontal support, fore-aft forces of each girdle are characterized by an initial deceleration which is later followed by an acceleration. It appears from Figure 6 that the forelimbs are net decelerating and the hind limbs are net accelerating.
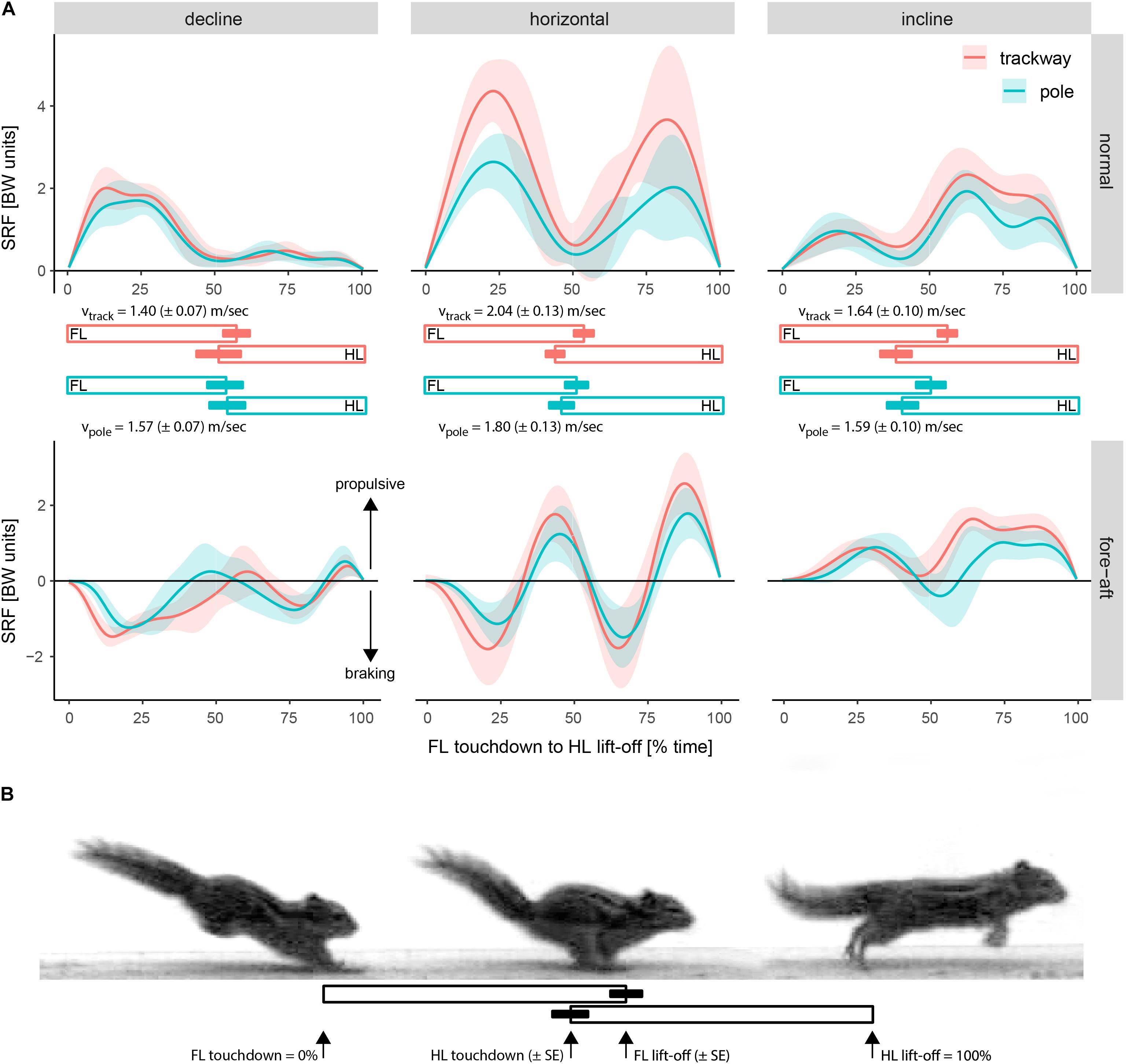
Figure 6. Differences in the average support reaction force trajectories over time among setups. (A) Support reaction force (SRF) of all limbs combined in percentage of body weight (BW units) depending on time from forelimb (FL) touchdown to hind limb (HL) lift-off [%]. Shaded areas represent values within a range of ± one standard deviation from the mean SRF. Bars indicate the average support duration [%] ± one standard deviation from the mean for the forelimbs and hind limbs on each setup. The average running speed (v) ± one standard error is reported for each setup to facilitate the comparison of SRFs (see Results). (B) Illustration of typical touchdown and lift-off events.
When comparing the average SRFs among setups, it is important to take into account the average running speeds. The average peak normal and fore-aft forces during locomotion on a decline appear to be similar between trackway and pole according to Figure 6. As the speed was significantly higher on average on the pole (see Table 2), this suggests that peak normal forces tended to be decreased on the pole. A similar reasoning can be applied to the inclined locomotion. The average peak normal and fore-aft forces during inclined locomotion tended to be higher on the trackway than on the pole according to Figure 6, but the speed did not differ significantly between support types (see Table 2), indicating that this difference is not an effect of speed.
When running down the decline, the animals instantly exerted a braking force at touchdown, followed by a short and, on average, much smaller acceleration phase by the forelimbs (Figure 6). The hind limbs also exerted a braking force, followed by a weak acceleration phase. In contrast, when running up the incline, the animals on average immediately exerted an accelerating force with the forelimbs after touchdown, sometimes followed by a relatively short and small deceleration phase. This was followed by an emphasized acceleration phase by the hind limbs.
In order to gain insight into the locomotion of the ancestor of Euarchontoglires, one strategy is to analyze the locomotion of extant species that share the morphological features assumed to have been characteristic of the crown-group node, i.e., conducting an analysis of identified modern analogs. Here, we analyzed the locomotion of Tamiops swinhoei, a small arboreal squirrel species displaying many of the postcranial features proposed for the last common ancestor of Euarchontoglires (Sargis et al., 2007). We studied how the squirrels adjust their locomotion when faced with a flat trackway and a narrow branch-like support and when confronted with different orientations.
We found our expectations to be supported by the data in most of the cases. However, when our hypotheses were not supported, it was due to a more complex relationship between the independent and dependent variables, including interaction effects among support type, support orientation, and running speed. Our findings for a relatively small squirrel species sometimes contrast and thus expand on the findings of Schmidt and Fischer (2011) and Dunham et al. (2019), who studied adjustments of the locomotor kinematics in the larger squirrel species Sciurus vulgaris (∼350 g) and Sciurus carolinensis (∼500 g), respectively, on poles of varying support orientations and diameters.
We found that Tamiops swinhoei more often increases leads (except when running on the declined support), and reduces speed, jumping distance and jumping height as well as peak SRFs when running along a pole compared to the trackway. Moreover, the squirrels increase DF on the branch-like support. This indicates the need for more grounded gaits that reduce the oscillations of the CoM (Schmitt et al., 2006; Young, 2009). Many of these kinematic and dynamic adjustments, however, were relatively subtle on inclines and declines and generally locomotion did not differ dramatically between the flat trackway and the simulated branch. This corroborates the notion of Jenkins (1974) that functional demands posed on the locomotor system by these support types become more similar with decreasing body size. However, on the horizontal support, mechanical adjustments were comparably more pronounced (Figures 2–4, 6), though T. swinhoei still rarely departed from using full bounds on this support orientation, too (Figure 1).
The retention of asymmetrical gaits on the pole is also likely to be determined by the relation between body size and substrate size as found in other rodents (e.g., Karantanis et al., 2017a, b). A narrower pole diameter somewhere below 13 mm might have forced the squirrels in our study to switch to symmetrical gaits as observed for species used in these two studies by Karantanis et al. (2017c). Nevertheless, narrower substrates come with increased compliance, a confounding factor when comparing pole to trackway that was not of interest in this study. The relevance of substrate compliance for T. swinhoei during foraging in the fine-branch niche and when jumping between trees is not known by now. Dedicated behavioral and performance studies could give insight into how this non-grasping species adapts its biomechanics to such conditions.
Many of the final regression models included animal ID as a random effect, suggesting that the extent of biomechanical adjustments to speed, support type, and support orientation can differ among individuals. This becomes also evident from the more or less separated point clouds of the individuals in Figures 2–5. Larger interindividual differences appear to occur during locomotion on the trackway, indicating that a flat surface poses less constraints on the biomechanics compared to the branch-like substrate.
A comparison of locomotion on inclines and declines with horizontal locomotion revealed more pronounced gait differences, too, suggesting the need for more complex adjustments. During locomotion on declines, it appeared that on the pole, the lead of both girdles was less variable. The squirrel might have been more comfortable controlling the descent by the means of establishing a firm grip via grasping the branch-like support between the autopodia of a girdle than using their pronated autopodia to brake on a flat support. When running up an inclined support, leads and average speed were fairly similar on the pole and on the trackway. Similar adjustments were also observed in mouse lemurs and gray squirrels when confronted with different inclines and declines (Shapiro et al., 2016; Dunham et al., 2019).
More specifically, when faced with a decline, the squirrels’ gaits exhibited a suite of ‘security promoting’ adjustments in overall slower trials with reduced jumping height (trackway and pole) and distance (trackway only), and larger DFs with an emphasis of the forelimbs (reflected in the DF-R). By and large, similar combinations of kinematic adjustments to declines have been documented for several small euarchontogliran species including primates (Hesse et al., 2015; Shapiro et al., 2016) and rodents (Karantanis et al., 2017a, c, 2018). Moreover, similar adjustments have been observed in small arboreal marsupials (Shapiro et al., 2014). SRFs reflect the increased net-braking role of the forelimbs and the decreased net-propulsive role of the forelimbs which has similarly been observed in opossums (Lammers et al., 2006) and cotton-top tamarins (Hesse et al., 2015). In accordance with our expectation, also the posture was adjusted to mitigate large forward toppling moments. For example, hindlimb abduction tended to be increased on the declined trackway, bringing the posterior body closer to the support, most likely to avoid toppling over forwards. Similarly, the feet played a larger role in grasping further around the pole on the decline. Generally, hand and foot postures are adjusted to accommodate differences of supports in all arboreal species analyzed in detail so far (e.g., Toussaint et al., 2020), but the specific functional significance of these often-overlooked kinematic adjustments requires more dedicated research, for example with use of new spatially-resolved force sensors (Llamosi and Toussaint, 2019).
When confronted with inclines, the striped squirrels displayed a few similar adjustments, but also a few notable kinematic and dynamic differences. Comparable to declines, the subjects reduced their jumping distance (trackway and pole) and height (only on trackway) when comparing similar speeds. These adjustments, in combination with an overall decrease of speed and peak SRFs, suggest a reduction of whole-body suspensions and a stronger emphasis on locomotor control. Also, as in the opossum (Lammers et al., 2006), the forelimb DF of striped squirrels was larger, similar to the adjustment to the decline. Nevertheless, the DF-R on inclines reflects the more pronounced hind limb contact phase as has been observed in several species previously (Vilensky et al., 1994; Nyakatura et al., 2008; Shapiro et al., 2016). This pronounced contact relates to the increased need for acceleration to overcome the additional gravitational pull on a decline (Preuschoft, 2002; Birn-Jeffery and Higham, 2014) and was also observed in opossums (Lammers et al., 2006) and cotton-top tamarins (Hesse et al., 2015). Autopodial positioning displayed a contrary pattern compared to the adjustments to the declined support. For example, increased forelimb abduction and decreased hind limb abduction were observed on the inclined trackway, both contributing to shifting the CoM to the forelimbs, perhaps reducing the chance of toppling over backwards. On the pole, the hands grasped further around the pole while the feet were placed more on top of it. Thus, despite its general significance, it appears that autopodial repositioning plays a more extensive role for T. swinhoei when shifting from a horizontal to an inclined support than from a horizontal to a declined support.
According to Jenkins (1974) and due to their small body size, ancestral mammals were likely well-suited to exploit both, terrestrial and arboreal supports. For small, non-cursorial, and relatively generalized mammals in a forest habitat, the distinction between arboreal and terrestrial locomotion is rather artificial, because the uneven and disordered supports for locomotion (relative to the size of the animals) require an identical locomotor repertoire (Jenkins, 1974; reviewed in Nyakatura, 2019). Thus, the small early Euarchontoglires likely were not yet specialized climbers and probably lacked salient morphological adaptations to arboreal locomotion. In accordance with this view, Sargis et al. (2007) proposed a non-grasping mode of arboreal locomotion to be representative for the ancestor of Euarchontoglires. Hence, small, arboreal squirrels appear to be a well-suited model system for the understanding of the locomotor mechanics of the earliest Euarchontoglires and perhaps even stem placentals, as they are found in the fine branch niche (Orkin and Pontzer, 2011; Youlatos and Samaras, 2011; Dunham et al., 2019), but also display different degrees of terrestriality when it comes, for example, to foraging (Thorington et al., 2012). This might have constrained them to relatively minor modifications compared to, e.g., primates (Orkin and Pontzer, 2011; Dunham et al., 2019).
Studies of locomotor kinetics and kinematics in arboreal squirrels are relatively rare (e.g., Orkin and Pontzer, 2011; Schmidt, 2011; Schmidt and Fischer, 2011; Lammers and Sufka, 2013; Dunham et al., 2019), but these studies, albeit analyzing larger species than the small Tamiops swinhoei studied here, together with our results suggest that these clawed animals without grasping abilities are able to adjust biomechanically to the challenges of different support types and orientations while maintaining fast asymmetrical gaits. In accordance with Jenkins’ considerations, Tamiops swinhoei showed rare deviations from a full bound, displayed similar speeds on the flat trackway and the branch-like support during inclined locomotion and even higher speeds on the latter when running on declines. This supports the idea that squirrels, similar to relatively small clawed callitrichids and even smaller mouse lemurs, exploit dynamic stability during asymmetrical gaits (Young, 2009; Schmidt and Fischer, 2011; Chadwell and Young, 2015; Shapiro et al., 2016). For example, synchronous use of both limbs of a girdle during asymmetrical gaits allows them to pinch the branch simultaneously between left and right autopodia, which has been proposed to mitigate large roll torques around the CoM, with small disturbances canceled out over several rapid subsequent stride cycles (Lammers and Zurcher, 2011; Schmidt and Biknevicius, 2014).
Considering the likely small body size as suggested by stem placental fossils (Ji et al., 2002; Luo et al., 2011; Youlatos et al., 2015) and early members of the Euarchontoglires (e.g., plesiadapiforms, Silcox and López-Torres, 2017), small body size should be one of the main considerations when identifying potential modern analogs for early primates and further early Euarchontoglires (Nyakatura, 2019). This is especially important considering the size threshold for effective asymmetrical locomotion proposed by Chadwell and Young (2015). The authors described an evolutionary trade-off between the benefits and drawbacks of asymmetrical locomotion which is related to both body mass and support diameter (Chadwell and Young, 2015). While asymmetrical gaits offer benefits such as locomotion with relatively high speeds combined with aerial phases that can be used to bridge gaps between supports in a discontinuous habitat, this locomotor type also involves relatively high forces that are exerted onto the supports (peak forces of several times the body mass documented in our study). Asymmetrical gaits are therefore either limited to larger, more robust branches, or the animals must be lightweight to be able to use asymmetrical gaits on fine branches.
Still, little comparative kinematic and dynamic data for small (below ∼100 g), arboreal members of the Euarchontoglires on simulated arboreal supports are available. But strikingly, all available data for such potential modern analogs documents ubiquitous occurrence of asymmetrical gaits. This includes the small scandentian Dendrogale murina (Youlatos et al., 2017), the small primate Microcebus murinus (Shapiro et al., 2016; Herbin et al., 2018), and small arboreal rodents such as Apodemus flavicollis (Karantanis et al., 2017c) and Tamiops swinhoei (our study). The lagomorphs are usually larger and only non-arboreal pikas can be smaller than 100 g. Similarly, members of the Dermoptera are larger. While more comparative data is necessary to consolidate the database for the development of evolutionary scenarios, this points to asymmetrical gaits being present at the origin of Euarchontoglires. Further, our results on a viable modern analog suggests that small-bodied, early crown group members of the Euarchontoglires have already been capable of exploiting the arboreal habitats including the fine, terminal branches and other challenging supports using asymmetrical gaits.
Fossil evidence points to a small body size in stem placentals and early Euarchontoglires. Small, arboreal squirrels arguably represent viable modern analogs for early Euarchontoglires and help to conceptualize the locomotor characteristics at the crown-group node. When confronted with narrow, branch-like supports, striped squirrels studied here do not dramatically alter their kinematics and especially dynamics when compared to a flat trackway, albeit some minor adjustments of spatio-temporal parameters in accordance to other published accounts of small arboreal mammal locomotion. This underscores the notion of Jenkins (1974) that the difference between terrestrial and arboreal supports is largely inconsequential for small mammals. Adjustments to different orientations involved kinematic changes that increased security, while changes in the dynamic data reflected an emphasis on hind limb acceleration on inclines and forelimb braking on declines. In line with a proposed size-related threshold up to which the benefits of asymmetrical locomotion outweigh the drawbacks of it (Chadwell and Young, 2015), limited available comparative kinematic and dynamic data for locomotion on simulated arboreal supports suggests a strong preference of asymmetrical locomotion in small (less than 100 g), arboreal Euarchontoglires. This apparent preference of asymmetrical gaits in small arboreal and scansorial eurarchontoglirans lets us assume that asymmetrical locomotion has been an important part of the locomotor repertoire of the animals at the crown-group node of this mammalian ‘superclade’.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
The animal study was reviewed and approved by Landesamt für Gesundheit und Soziales, Berlin.
JW and JN conceived of the study. TA, JM, and JW conducted the experiments and acquired and analyzed the data. JW conducted the statistical analysis. JW and JN drafted the manuscript and all authors contributed to the final version of the manuscript.
We are grateful for funding by the German Research Council (DFG EXC 1027 to JW and JN and DFG NY 63/2-1 to JN).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We thank N. Erickson, S. Thiel and S. Grübel for their help with keeping the animals at the animal facility of the Humboldt University. Finally, we thank all members of the Comparative Zoology lab at HU for critical comments and inspiring discussions.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.636039/full#supplementary-material
Adkins, R. M., and Honeycutt, R. L. (1991). Molecular phylogeny of the superorder archonta. Proc. Natl. Acad. Sci. 88, 10317–10321. doi: 10.1073/pnas.88.22.10317
Asher, R. J., Bennett, N., and Lehmann, T. (2009). The new framework for understanding placental mammal evolution. Bioessays 31, 853–864. doi: 10.1002/bies.200900053
Bininda-Emonds, O. R., Cardillo, M., Jones, K. E., MacPhee, R. D., Beck, R. M., Grenyer, R., et al. (2007). The delayed rise of present-day mammals. Nature 446, 507–512. doi: 10.1038/nature05634
Birn-Jeffery, A. V., and Higham, T. E. (2014). The scaling of uphill and downhill locomotion in legged animals. Integ. Comp. Biol. 54, 1159–1172. doi: 10.1093/icb/icu015
Burnham, K. P., and Anderson, D. R. (2002). Model selection and multimodel inference: a practical information-theoretic approach, 2 Edn. New York, NY: Springer Science & Business Media.
Chadwell, B. A., and Young, J. W. (2015). Angular momentum and arboreal stability in common marmosets (Callithrix jacchus). Am. J. Phys. Anthropol. 156, 565–576. doi: 10.1002/ajpa.22683
Dunham, N. T., McNamara, A., Shapiro, L., Phelps, T., Wolfe, A. N., and Young, J. W. (2019). Locomotor kinematics of tree squirrels (Sciurus carolinensis) in free-ranging and laboratory environments: Implications for primate locomotion and evolution. J. Exp. Zool. Part A Ecol.Integ. Physiol. 331, 103–119. doi: 10.1002/jez.2242
Fabre, P. H., Hautier, L., Dimitrov, D., and Douzery, E. J. (2012). A glimpse on the pattern of rodent diversification: a phylogenetic approach. BMC Evol. Biol. 12:88. doi: 10.1186/1471-2148-12-88
Herbin, M., Hommet, E., Hanotin-Dossot, V., Perret, M., and Hackert, R. (2018). Treadmill locomotion of the mouse lemur (Microcebus murinus); kinematic parameters during symmetrical and asymmetrical gaits. J. Comp. Physiol. A 204, 537–547. doi: 10.1007/s00359-018-1256-2
Hesse, B., Nyakatura, J. A., Fischer, M. S., and Schmidt, M. (2015). Adjustments of limb mechanics in cotton-top tamarins to moderate and steep support orientations: significance for the understanding of early primate evolution. J. Mammal. Evol. 22, 435–450. doi: 10.1007/s10914-014-9283-4
Jenkins, F. A. (1974). “Tree shrew locomotion and the origins of primate arborealism,” in Primate locomotion, ed. F. A. Jenkins (New York: Academic Press), 85–115. doi: 10.1016/B978-0-12-384050-9.50008-8
Ji, Q., Luo, Z. X., Yuan, C. X., Wible, J. R., Zhang, J. P., and Georgi, J. A. (2002). The earliest known eutherian mammal. Nature 416, 816–822. doi: 10.1038/416816a
Karantanis, N.-E., Rychlik, L., Herrel, A., and Youlatos, D. (2017a). Arboreality in acacia rats (Thallomys paedulcus; Rodentia, Muridae): gaits and gait metrics. J. Zool. 303, 107–119. doi: 10.1111/jzo.12473
Karantanis, N.-E., Rychlik, L., Herrel, A., and Youlatos, D. (2017b). Comparing the arboreal gaits of Muscardinus avellanarius and Glis glis (gliridae, rodentia): a first quantitative analysis. Mammal Study 42, 161–172. doi: 10.3106/041.042.0306
Karantanis, N. E., Rychlik, L., Herrel, A., and Youlatos, D. (2017c). Arboreal gaits in three sympatric rodents Apodemus agrarius, Apodemus flavicollis (rodentia, muridae) and Myodes glareolus (rodentia, cricetidae). Mammalian Biol. 83, 51–63. doi: 10.1016/j.mambio.2016.12.004
Karantanis, N. E., Rychlik, L., Herrel, A., and Youlatos, D. (2018). Vertical locomotion in Micromys minutus (Rodentia: Muridae): insights into the evolution of eutherian climbing. J. Mammalian Evol. 25, 277–289. doi: 10.1007/s10914-016-9374-5
Lammers, A. R., Earls, K. D., and Biknevicius, A. R. (2006). Locomotor kinetics and kinematics on inclines and declines in the gray short-tailed opossum Monodelphis domestica. J. Exp. Biol. 209, 4154–4166. doi: 10.1242/jeb.02493
Lammers, A. R., and Gauntner, T. (2008). Mechanics of torque generation during quadrupedal arboreal locomotion. J. Biomech. 41, 2388–2395. doi: 10.1016/j.jbiomech.2008.05.038
Lammers, A. R., and Sufka, K. M. (2013). Turning the corner in quadrupedal arboreal locomotion: kinetics of changing direction while running in the siberian chipmunk (Tamias sibiricus). J. Exp. Zool. Part A Ecol. Genet. Physiol. 319, 99–112. doi: 10.1002/jez.1775
Lammers, A. R., and Zurcher, U. (2011). Torque around the center of mass: dynamic stability during quadrupedal arboreal locomotion in the siberian chipmunk (Tamias sibiricus). Zoology 114, 95–103. doi: 10.1016/j.zool.2010.11.004
Llamosi, A., and Toussaint, S. (2019). Measuring force intensity and direction with a spatially resolved soft sensor for biomechanics and robotic haptic capability. Soft Robotics 6, 346–355. doi: 10.1089/soro.2018.0044
Luo, Z. X., Yuan, C. X., Meng, Q. J., and Ji, Q. (2011). A Jurassic eutherian mammal and divergence of marsupials and placentals. Nature 476, 442–445. doi: 10.1038/nature10291
Meredith, R. W., Janečka, J. E., Gatesy, J., Ryder, O. A., Fisher, C. A., Teeling, E. C., et al. (2011). Impacts of the cretaceous terrestrial revolution and KPg extinction on mammal diversification. Science 334, 521–524. doi: 10.1126/science.1211028
Mielke, F., Schunke, V., Wölfer, J., and Nyakatura, J. A. (2018). Motion analysis of non-model organisms using a hierarchical model: influence of setup enclosure dimensions on gait parameters of Swinhoe’s striped squirrels as a test case. Zoology 129, 35–44. doi: 10.1016/j.zool.2018.05.009
Murphy, W. J., Eizirik, E., Johnson, W. E., Zhang, Y. P., Ryder, O. A., and O’Brien, S. J. (2001). Molecular phylogenetics and the origins of placental mammals. Nature 409, 614–618. doi: 10.1038/35054550
Novacek, M. J. (1992). Mammalian phylogeny: shaking the tree. Nature 356, 121–125. doi: 10.1038/356121a0
Nyakatura, J. A. (2019). Early primate evolution: insights into the functional significance of grasping from motion analyses of extant mammals. Biol. J. Linnean Soc. 127, 611–631. doi: 10.1093/biolinnean/blz057
Nyakatura, J. A., Fischer, M. S., and Schmidt, M. (2008). Gait parameter adjustments of cotton-top tamarins (Saguinus oedipus, callitrichidae) to locomotion on inclined arboreal substrates. Am. J. Phys. Anthropol. 135, 13–26. doi: 10.1002/ajpa.20699
Orkin, J. D., and Pontzer, H. (2011). The narrow niche hypothesis: gray squirrels shed new light on primate origins. Am. J. Phys. Anthropol. 144, 617–624. doi: 10.1002/ajpa.21450
Pinheiro, J., Bates, D., DebRoy, S., Sarkar, D., and R Core Team. (2020). nlme: Linear and Nonlinear Mixed Effects Models_. R package version 3.1-149.
Preuschoft, H. (2002). What does “arboreal locomotion” mean exactly and what are the relationships between “climbing”, environment and morphology? Zeitschrift für Morphologie und Anthropologie 83, 171–188.
R Core Team. (2020). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. Revelle, W. (2020) psych: Procedures for Personality and Psychological Research. Illinois, USA: Northwestern University, Evanston.
Rueden, C. T., Schindelin, J., Hiner, M. C., DeZonia, B. E., Walter, A. E., Arena, E. T., et al. (2017). ImageJ2: imagej for the next generation of scientific image data. BMC Bioinform. 18:529. doi: 10.1186/s12859-017-1934-z
Sargis, E. J., Boyer, D. M., Bloch, J. I., and Silcox, M. T. (2007). Evolution of pedal grasping in Primates. J. Hum. Evol. 53, 103–107. doi: 10.1016/j.jhevol.2007.01.008
Schmidt, A. (2011). Functional differentiation of trailing and leading forelimbs during locomotion on the ground and on a horizontal branch in the european red squirrel (Sciurus vulgaris, rodentia). Zoology 114, 155–164. doi: 10.1016/j.zool.2011.01.001
Schmidt, A., and Biknevicius, A. R. (2014). Structured variability of steady-speed locomotion in rats. J. Exp. Biol. 217, 1402–1406. doi: 10.1242/jeb.092668
Schmidt, A., and Fischer, M. S. (2011). The kinematic consequences of locomotion on sloped arboreal substrates in a generalized (Rattus norvegicus) and a specialized (Sciurus vulgaris) rodent. J. Exp. Biol. 214, 2544–2559. doi: 10.1242/jeb.051086
Schmidt, M. (2005). Quadrupedal locomotion in squirrel monkeys (Cebidae Saimiri sciureus): a cineradiographic study of limb kinematics and related substrate reaction forces. Am. J. Phys. Anthropol. 128, 359–370. doi: 10.1002/ajpa.20089
Schmitt, D. (1999). Compliant walking in primates. J. Zool. 248, 149–160. doi: 10.1111/j.1469-7998.1999.tb01191.x
Schmitt, D., Cartmill, M., Griffin, T. M., Hanna, J. B., and Lemelin, P. (2006). Adaptive value of ambling gaits in primates and other mammals. J. Exp. Biol. 209, 2042–2049. doi: 10.1242/jeb.02235
Shapiro, L. J., Kemp, A. D., and Young, J. W. (2016). Effects of substrate size and orientation on quadrupedal gait kinematics in mouse lemurs (Microcebus murinus). J. Exp. Zool. 325, 329–343. doi: 10.1002/jez.2020
Shapiro, L. J., Young, J. W., and VandeBerg, J. L. (2014). Body size and the small branch niche: using marsupial ontogeny to model primate locomotor evolution. J. Hum. Evol. 68, 14–31. doi: 10.1016/j.jhevol.2013.12.006
Silcox, M. T., and López-Torres, S. (2017). Major questions in the study of primate origins. Ann. Rev. Earth Planetary Sci. 45, 113–137. doi: 10.1146/annurev-earth-063016-015637
Simpson, G. G. (1945). The principles of classification and a classification of mammals. Bull. Amer. Mus. Nat. Hist. 85:350.
Springer, M. S., Stanhope, M. J., Madsen, O., and de Jong, W. W. (2004). Molecules consolidate the placental mammal tree. Trends Ecol. Evol. 19, 430–438. doi: 10.1016/j.tree.2004.05.006
Thorington, R. W. Jr., Koprowski, J. L., Steele, M. A., and Whatton, J. F. (2012). Squirrels of the world. Baltimore, MD: John Hopkins University Press.
Toussaint, S., Llamosi, A., Morino, L., and Youlatos, D. (2020). The central role of small vertical substrates for the origin of grasping in early primates. Curr. Biol. 30, 1600–1613. doi: 10.1016/j.cub.2020.02.012
Vilensky, J. A., Moore, A. M., and Libii, J. N. (1994). Squirrel monkey locomotion on an inclined treadmill: implications for the evolution of gaits. J. Hum. Evol. 26, 375–386. doi: 10.1006/jhev.1994.1024
Wickham, H., Averick, M., Bryan, J., Chang, W., McGowan, L., François, R., et al. (2019). Welcome to the tidyverse. J. Open Source Software 4:1686. doi: 10.21105/joss.01686
Wölfer, J., Amson, E., Arnold, P., Botton-Divet, L., Fabre, A. C., van Heteren, A. H., et al. (2019). Femoral morphology of sciuromorph rodents in light of scaling and locomotor ecology. J. Anat. 234, 731–747. doi: 10.1111/joa.12980
Youlatos, D., Karantanis, N. E., Byron, C. D., and Panyutina, A. (2015). Pedal grasping in an arboreal rodent relates to above-branch behavior on slender substrates. J. Zool. 296, 239–248. doi: 10.1111/jzo.12237
Youlatos, D., Karantanis, N. E., and Panyutina, A. (2017). Pedal grasping in the northern smooth-tailed treeshrew Dendrogale murina (tupaiidae, scandentia): insights for euarchontan pedal evolution. Mammalia 81, 61–70. doi: 10.1515/mammalia-2015-0113
Youlatos, D., and Samaras, A. (2011). Arboreal locomotor and postural behaviour of European red squirrels (Sciurus vulgaris L.) in northern Greece. J. Ethol. 29, 235–242. doi: 10.1007/s10164-010-0248-7
Young, J. W. (2009). Substrate determines asymmetrical gait dynamics in marmosets (Callithrix jacchus) and squirrel monkeys (Saimiri boliviensis). Am. J. Phys. Anthropol. 138, 403–420. doi: 10.1002/ajpa.20953
Zhou, X., Sun, F., Xu, S., Yang, G., and Li, M. (2015). The position of tree shrews in the mammalian tree: comparing multi-gene analyses with phylogenomic results leaves monophyly of Euarchonta doubtful. Integrative Zool. 10, 186–198. doi: 10.1111/1749-4877.12116
Keywords: Tamiops, locomotion, support reaction forces, gait, asymmetrical locomotion
Citation: Wölfer J, Aschenbach T, Michel J and Nyakatura JA (2021) Mechanics of Arboreal Locomotion in Swinhoe’s Striped Squirrels: A Potential Model for Early Euarchontoglires. Front. Ecol. Evol. 9:636039. doi: 10.3389/fevo.2021.636039
Received: 30 November 2020; Accepted: 25 February 2021;
Published: 06 April 2021.
Edited by:
Irina Ruf, Senckenberg Research Institute and Natural History Museum Frankfurt, GermanyReviewed by:
Michael Granatosky, New York Institute of Technology, United StatesCopyright © 2021 Wölfer, Aschenbach, Michel and Nyakatura. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: John A. Nyakatura, am9obi5ueWFrYXR1cmFAaHUtYmVybGluLmRl
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.