Easton R. White
Christie A. Bahlai- 1Department of Biology, University of Vermont, Burlington, VT, United States
- 2Gund Institute for Environment, University of Vermont, Burlington, VT, United States
- 3Department of Biological Sciences, Kent State University, Kent, OH, United States
Long-term monitoring programs are a fundamental part of both understanding ecological systems and informing management decisions. However, there are many constraints which might prevent monitoring programs from being designed to consider statistical power, site selection, or the full costs and benefits of monitoring. Key considerations can be incorporated into the optimal design of a management program with simulations and experiments. Here, we advocate for the expanded use of a third approach: non-random resampling of previously-collected data. This approach conducts experiments with available data to understand the consequences of different monitoring approaches. We first illustrate non-random resampling in determining the optimal length and frequency of monitoring programs to assess species trends. We then apply the approach to a pair of additional case studies, from fisheries and agriculture. Non-random resampling of previously-collected data is underutilized, but has the potential to improve monitoring programs.
1. Long-Term Environmental Monitoring
Long-term monitoring programs are an essential piece of modern ecological research and conservation science (Hughes et al., 2017). Numerous studies have demonstrated that long-term monitoring can have disproportionately large contributions in terms of advancing scientific understanding and policy (Giron-Nava et al., 2017). Environmental monitoring programs, like the USA-based Long Term Ecological Research (LTER) Network, as well as compilations of time series, like the Living Planet Index, show the scope of long-term datasets now available (Maguran et al., 2010; Foundation, 2016). Furthermore, with the advent of infrastructure that connects and stores data collected by a wide variety of professional and amateur naturalists, monitoring should continue to become more feasible and cost-effective. For example, large-scale citizen science programs, like iNaturalist (https://www.inaturalist.org/) and eBird (https://ebird.org/home), allow for increased collection of data documenting species occurrence, extent and relative population size, as well as providing platforms to support data use and reuse across a variety of applications (Sullivan et al., 2009; Joppa, 2017). Similarly, numerous new technologies, including eDNA and drones, will bring down the cost of monitoring through automation and increasing the sheer taxonomic, temporal, and spatial resolution of observations (Bohmann et al., 2014; Hodgson et al., 2018). All of these efforts will lead to increases in the number of species monitored as well as the quantity and quality of the data collected, to previously unimaginable levels.
2. Challenges of Monitoring Programs
Despite the recognized importance of long-term monitoring programs, key questions remain. Several authors have pointed out that long-term monitoring programs are not necessarily designed in a way to best address key questions of interest (Legg and Nagy, 2006; Nichols and Williams, 2006; Field et al., 2007; McDonald-Madden et al., 2010; Lindenmayer et al., 2012, 2020). For instance, suppose that a monitoring site was selected to monitor dynamics in a bird population near a university. A long-term study could certainly reveal the population trend for that specific location. However, the site may have been chosen specifically because it was at high abundance at the beginning of the study—this causes a site-selection bias (Fournier et al., 2019). Populations naturally vary, both in time and in space, so the very act of initially selecting a site to monitor with particular population attributes can potentially confound the very patterns they seek to monitor. Birds in this hypothetical population may undergo a cyclic dynamic related to resource exploitation, or rotate between different patches for nesting from year to year. Thus, when we ask new questions of long-term monitoring data, we have to think carefully about how the monitoring program was originally designed and whether or not we have adequate statistical power (Lindenmayer and Likens, 2010; White, 2019) as well as the risks of making type I vs. type II errors (Mapstone, 1995). These considerations, amongst others, are especially relevant when data from different sources are combined for comparisons—which is increasingly performed (Maguran et al., 2010; Keith et al., 2015; Giron-Nava et al., 2017; White, 2019). Lastly, the tradeoff between information gained from monitoring and the cost of monitoring has to be considered (Bennett et al., 2018).
3. Designing Monitoring Programs
Principles from experimental design, including randomization and replication, are key components in designing any monitoring program (Seavy and Reynolds, 2007). However, many tools from experimental design are inadequate for monitoring programs. For example, by their very nature, data from monitoring programs require handling spatial and temporal auto-correlation between sampling points. In order to manage these issues, a lot of work on optimizing monitoring programs has its roots in decision science (McDonald-Madden et al., 2010). Decision theory allows one to build a structured process to decide between alternative solutions while accounting for costs and benefits (Raiffa, 1968; McDonald-Madden et al., 2010; Conroy and Peterson, 2012). In addition, decision theory allows for the incorporation of uncertainties (McCarthy, 2014). In the context of environmental monitoring, decision theory can help formalize the process of selecting sites and the specific survey design (Gerber et al., 2005; Chades et al., 2011; Tulloch et al., 2013). As an example, Hauser et al. (2006) explored how frequently a managed population of red kangaroo (Macropus rufus) in Australia should be monitored. They used a simulation approach to determine how frequently monitoring should occur given tradeoffs between the costs of monitoring and the potential insights for management. They found that an adaptive monitoring program outperformed the standard fixed-interval monitoring.
This leads to one of the most important contributions of decision theory to environmental monitoring—the value of information (Canessa et al., 2015; Maxwell et al., 2015; Bennett et al., 2018). Value of information theory explicitly accounts for the information gained from performing some action, and the costs associated with doing so, when designing a management plan. For example, Bennett et al. (2018) used information theory in the context of threatened plant management in Southern Ontario. They simulate a situation where a conservation agency is willing to pay landowners to protect part of their land. However, species occurrence is uncertain on each plot of land. Thus, it is necessary assess the value of the information gained from monitoring versus its costs. They were able to demonstrate how the information gained from monitoring increased with high levels of species detectability and low costs of monitoring.
4. Tools for Designing Monitoring Programs
4.1. Simulations
To address the challenges associated with designing monitoring programs, there are three classes of tools available to design and evaluate monitoring programs. First, the most commonly used approach are simulation models (Gerrodette, 1987; Rhodes and Jonzen, 2011). Using prior knowledge about the system under question, a virtual ecologist (Zurell et al., 2010) approach would use simulation models constructed to incorporate key factors that affect species dynamics. With an appropriate model, simulations can then be run for a variety of scenarios, including changing the number of samples taken per year, altering the number of sites sampled, and sampling for different lengths of time (Rhodes and Jonzen, 2011; Barry et al., 2017; Christie et al., 2019; Weiser et al., 2019; White, 2019). Simulations can also be useful in deciding which streams of data to use (Weiser et al., 2020) or the effect of changing sampling methodology during the course of a study (Southwell et al., 2019). A lot of prior work has also used simulations to better understand optimal sampling schemes for invasive species (Chades et al., 2011; Holden and Ellner, 2016). Although powerful, this approach is limited to systems in which many aspects of the biology are already known, or can be reasonably estimated.
4.2. Experimental and Comparative
Second, experiments can also be used to test the effect of different sampling protocols. As in the case of simulation models, experiments with different levels of monitoring, or different monitoring approaches, can be used. Experiments provide replication, which is important to understand the probability that monitoring is likely to achieve the desired goals given inherent variability in the system (White et al., 2019). A related approach would simply be to compare different sampling regimes across systems to evaluate which are the most successful at realizing monitoring goals. Indeed, integrated population modeling was developed as an analytical approach to identify and address data discrepancies between data taken by differing methodologies or at differing times in a species's life history (Saunders et al., 2019). This method has been applied with great success to advance understanding of the trajectories of populations of well-monitored taxa such as waterfowl (Arnold et al., 2018). However, the key disadvantage of this approach is, like simulation models, integrative modeling approaches are reliant on the availability of large amounts of data, documenting multiple facets of a species' biology. Of course, these types of experiments providing multi-faceted data are often infeasible or impossible for many systems.
4.3. Non-random Resampling
Here, we advocate for the expanded use of a third approach: non-random resampling of previously-collected monitoring data. Non-random sampling involves artificially “degrading” a complete data set into smaller data samples for comparison. This concept leverages existing information by starting with long-term monitoring data already collected for a system. The data is then subsampled, or divided, in non-random ways depending on the question of interest (Figure 1A). Then a metric (for example, a mean or a slope) is calculated for each subsample. Each subsample metric is then compared to the metric for complete data (all the data combined). The complete data acts as a “true value” for comparison. This is analogous to simulation studies where the true parameters are known (Bolker, 2008). Thus, the assumption that the complete data set can serve as a “true” comparison is critical. Non-random sampling differs from random sampling approaches (e.g., jackknifing, bootstrapping) where random subsamples are taken, allowing estimation of various statistics. With non-random sampling, we learn about the elements of a good monitoring program by examining which subsamples of the data are most influential and the number of subsamples needed to have a high probability of detecting the true value of the metric. Bahlai et al. (2020) describes this technique from a computational viewpoint specifically for time series. Although this approach has been used previously (Grantham et al., 2008; Bennett et al., 2016; Wauchope et al., 2019; White, 2019; Bahlai et al., 2020; Cusser et al., 2020), its adoption has been largely informal and not specifically stated.
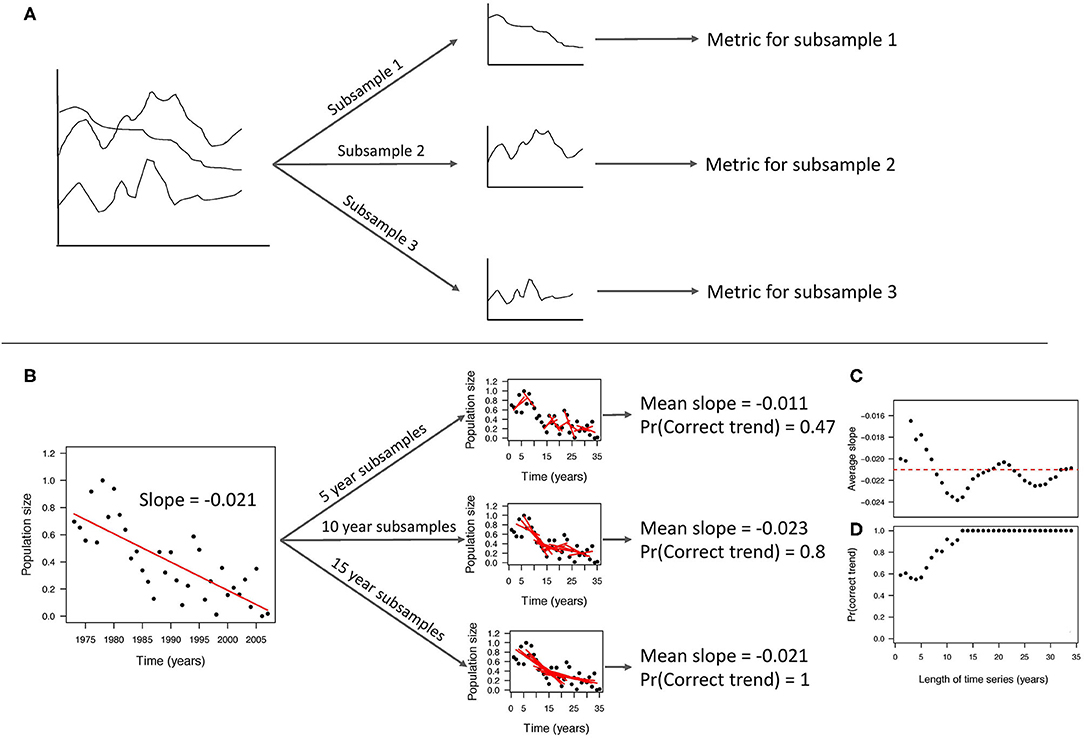
Figure 1. (A) The general process of non-random resampling of past data from left to right (i.e., sequentially, starting with data from farthest into the past) includes: dividing data into non-random subsamples (based on the question of interest), calculating metrics on those subsamples, and comparing the subsample metrics to the combined (i.e. “true metric”) dataset, (B) same process as Table (a), but for specific example of examining the minimum number of years required to detect long-term population trends (White, 2019). The pair of figures on the bottom right show how the (C) average slope and the (D) probability of correcting identifying a trend change with the number of years monitored.
This approach is best described with a simple example (Figure 1B). White (2019) studied how many years of monitoring were required to detect population trends. For a given time series, White (2019) examined all possible subsamples of different lengths of time. For instance, a 10-year time series consists of two 9-year subsamples, three 8-year subsamples, and so forth. This is different than taking random subsamples of data as the subsamples are chosen to maintain the temporal autocorrelation. White (2019) then calculated the population trend (i.e., the slope from linear regression) for each subsample (Figure 1B). The fraction of subsamples of a particular length, that had the same overall trend as the complete time series (i.e., the “true trend”), is the statistical power. Thus, the minimum time series required was the time series length that met a high enough threshold of statistical power. White (2019) applied this approach to 822 population time series, allowing for comparison across species and systems. Using resampling of the breeding bird survey, Wauchope et al. (2019) found that sampling for a short period, or infrequently, was adequate to determine the species trend direction, i.e., positive or negative. However, more frequent and longer monitoring was required to estimate the percent changes over time.
Monitoring programs need to be designed to both adequately address a question of interest and to be cost effective (Grantham et al., 2008; Rout et al., 2014; Maxwell et al., 2015; Bennett et al., 2018). In this context, it is essential to study the trade-off between the information gained from monitoring and the cost. For example, Bennett et al. (2016) used resampling approaches to study monitoring requirements for diatoms in lake samples. They found that in several cases much lower levels of sampling, in terms of the number of lakes sampled and observer effort, were required to ensure accuracy. This translated into potentially millions of dollars in savings (Bennett et al., 2016). Bruel and White (2020) used a similar approach to show how lake soil core sampling could be optimized to ensure accuracy in detecting ecosystem shifts while also reducing costs.
Non-random resampling of past data also helps address some common issues with other approaches to designing monitoring programs. For instance, mechanistic simulation models require at least some knowledge of the basic species biology in order to construct the model (Zurell et al., 2010). In addition, although possible with simulations, resampling approaches already explicitly account for the inherent temporal and spatial autocorrelation of monitoring data. Resampling approaches are also particularly useful in situations where experiments are expensive or impractical. Lastly, resampling approaches are also quick and easy to implement. Along with these advantages, resampling of past data has two major limitations. First, monitoring data already has to be available for the system of interest or a related one. And second, the previously-collected data needs to be a good representation of the system dynamics. This is due to the full data acting as the “true representation” of this system. Similarly, if resampling approaches are used for one system to learn about another, the original system has to be a good representation of the latter in terms of the general system dynamics. Nonetheless, long-term monitoring programs are always under pressure from logistical and financial constraints. These resampling methods can be a useful tool for researchers and managers to refine and update programs as funding changes and still achieve their research goals.
5. Non-random Resampling in Other Contexts
5.1. Fisheries Management
Non-random resampling of past data can be applied to a variety of contexts beyond estimating long-term population trends. For example, to study data-poor fisheries (Dowling et al., 2015, Table 1 of Chrysafi and Kuparinen, 2015), past work has primarily used simulation models. To study data-poor fisheries using random and non-random resampling, one should instead study data-rich fisheries. The goal would be to artificially degrade the data-rich examples until the point that the fishery would be considered data-poor (Figure 2). We can then see how various methods of data-poor fisheries perform given that we have the full data set to act as a “true” comparison. As an example, we took data on darkblotched rockfish (Sebastes crameri) from the U.S. West Coast Groundfish Bottom Trawl Survey data (Keller et al., 2017; Stock et al., 2019). We then conducted two “experiments” with the data.
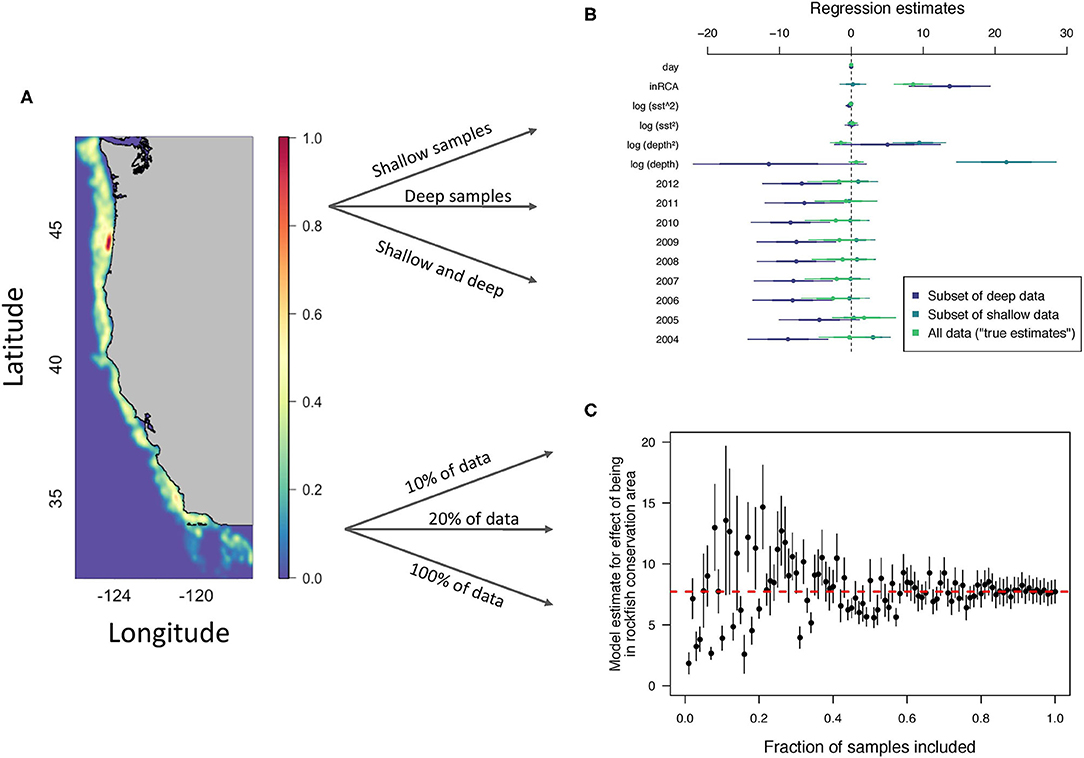
Figure 2. Subsampling process for darkblotched rockfish (Sebastes crameri) catch in kg in U.S. West Coast Groundfish Bottom Trawl Survey data from 2003 to 2012. (A) Bivariate kernel density estimate showing smoothed density of fishing effort (7,161 haul locations) (Keller et al., 2017; Stock et al., 2019). (B) Parameter estimations for linear regression of three subsamples of data: deep trawls, shallow trawls, and all combined data (Note: the number of records was kept consistent for the three groups). (C) Estimate for the effect of being in a rockfish conservation area (inRCA) on catch for different amounts of data included. The horizontal, dashed line is the “true” estimate which is the estimate when 100% of the data is included.
First, suppose we only had access to shallow or deep data because of technology limitations. We can test the effect of these data limitations by non-randomly resampling the data depending on whether the samples came from deep or shallow trawls. We show that regression estimates of parameters differs based on which depths were included in Figure 2B. This contrasts with random resampling of the data. Suppose instead, we examine the effect of degrading the data to only a fraction of the totals records we have available. This is actually random resampling as we are taking actual random samples from the time series. We see that model estimates for the effect of being within a rockfish conservation area are not accurate until a large fraction of the original data is included (Figure 2C).
5.2. Agricultural Practices
Agricultural management recommendations are often based on conclusions from short to medium-term field trials (ca. 1–5 years), and it is common to observe contradictory findings between trials. When multiple factors are considered, such as crop water use, greenhouse gas emissions and relative profitability of practices, responses may vary dramatically and unequally to short-term environmental variation. Cusser et al. (2020) applied a non-random sequential resampling algorithm (Bahlai, 2019) to long-term data examining the effects of tillage practices on productivity, sustainability attributes, and return-on investment. They found that, because of high natural variability in the system, 15 years of data of data were required to observe the “true” pattern of difference between treatments in soil water availability and crop yield, and that more than a third of the sampled sequences shorter than 10 years led to outright misleading results. Furthermore, they were unable to detect consistent treatment differences in nitrus oxide emissions, although non-random resampling indicated that spurious trends could be observed in observation periods as long as 9 years. Finally, although profitability of adopting a new tillage practice was highly variable in initial years after adoption, by 10 years after, 86% of resampled windows indicated a net financial gain associated with the change. Whereas, it is unlikely that practitioners making management decisions can consistently rely on a decade of data to guide them, the results of the non-random sequential resampling of long-term data provide guidance on reconciling apparently differing trends between trials. Furthermore, non-random resampling gives land managers insight into the likelihood and duration of a particular management outcome in a variable environment.
6. Conclusions
Data from long-term monitoring programs are used in assessing trends in environmental observations, understanding system dynamics, and making management decisions. It is critical that these monitoring programs be designed in order to address our questions of interest (Field et al., 2007; McDonald-Madden et al., 2010; Lindenmayer et al., 2020). This is particularly relevant when new questions are asked of monitoring data or data from disparate monitoring programs are combined. We show that non-random resampling of past monitoring programs can be used to understand sampling requirements and the consequences of bias (Figures 1, 2). This approach can be applied to a variety of systems and questions (Table 1) beyond environmental monitoring. In addition to simulations and experimental approaches, we argue that non-random resampling of past data should be used more widely to study questions related to sampling design. Combined with information on the cost of monitoring, this approach also helps identify when ecological monitoring is a good investment or when it may be a waste of effort that does not answer to a program's aims and objectives. Further, resampling approaches can be used as part of adaptive management to refine monitoring programs. Continued research in this area will allow scientists and managers to better evaluate past efforts and to design new monitoring programs using evidence-based approaches.
Table 1. Example questions that could be addressed using non-random resampling.
Author Contributions
EW and CB conceived the ideas, designed the methodology, and analyzed the data. Both authors contributed critically to the drafts and gave final approval for publication.
Funding
CB was supported by data from the Kellogg Biological Station Long Term Ecological Research site (https://lter.kbs.msu.edu/ National Science Foundation grants 1027253, 1637653), and a grant from the National Science Foundation (grant OAC-1838807; https://www.nsf.gov/) during the development of this work.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Arnold, T. W., Clark, R. G., Koons, D. N., and Schaub, M. (2018). Integrated population models facilitate ecological understanding and improved management decisions. J. Wildl. Manage. 82, 266–274. doi: 10.1002/jwmg.21404
Bahlai, C. A., White, E. R., Perrone, J. D., Cusser, S., and Whitney, K. S. (2020). An algorithm for quantifying and characterizing misleading trajectories in ecological processes. bioRxiv [Preprint]. doi: 10.1101/2020.07.07.192211
Barry, J., Maxwell, D., Jennings, S., Walker, D., and Murray, J. (2017). Emon: An R-package to support the design of marine ecological and environmental studies, surveys and monitoring programmes. Methods Ecol. Evol. 8, 1342–1346. doi: 10.1111/2041-210X.12748
Bennett, J. R., Maxwell, S. L., Martin, A. E., Chadés, I., Fahrig, L., and Gilbert, B. (2018). When to monitor and when to act: Value of information theory for multiple management units and limited budgets. J. Appl. Ecol. 55, 2102–2113. doi: 10.1111/1365-2664.13132
Bennett, J. R., Rühland, K. M., and Smol, J. P. (2016). No magic number: determining cost-effective sample size and enumeration effort for diatom-based environmental assessment analyses. Can. J. Fisher. Aquat. Sci. 74, 208–215. doi: 10.1139/cjfas-2016-0066
Bohmann, K., Evans, A., Gilbert, M. T. P., Carvalho, G. R., Creer, S., Knapp, M., et al. (2014). Environmental DNA for wildlife biology and biodiversity monitoring. Trends Ecol. Evol. 29, 358–367. doi: 10.1016/j.tree.2014.04.003
Bolker, B. M. (2008). Ecological Models and Data in R, 1st Edn. Princeton, NJ: Princeton University Press.
Bruel, R., and White, E. R. (2020). Sampling requirements and approaches to detect ecosystem shifts. Ecol. Indic. 121:107096. doi: 10.1016/j.ecolind.2020.107096
Canessa, S., Guillera-Arroita, G., Lahoz-Monfort, J. J., Southwell, D. M., Armstrong, D. P., Chadés, I., et al. (2015). When do we need more data? A primer on calculating the value of information for applied ecologists. Methods Ecol. Evol. 6, 1219–1228. doi: 10.1111/2041-210X.12423
Chades, I., Martin, T. G., Nicol, S., Burgman, M. A., Possingham, H. P., and Buckley, Y. M. (2011). General rules for managing and surveying networks of pests, diseases, and endangered species. Proc. Natl. Acad. Sci. U.S.A. 108, 8323–8328. doi: 10.1073/pnas.1016846108
Christie, A. P., Amano, T., Martin, P. A., Shackelford, G. E., Simmons, B. I., and Sutherland, W. J. (2019). Simple study designs in ecology produce inaccurate estimates of biodiversity responses. J. Appl. Ecol. 56, 2742–2754. doi: 10.1111/1365-2664.13499
Chrysafi, A., and Kuparinen, A. (2015). Assessing abundance of populations with limited data: Lessons learned from data-poor fisheries stock assessment. Environ. Rev. 24, 25–38. doi: 10.1139/er-2015-0044
Conroy, M. J., and Peterson, J. T. (2012). Decision Making in Natural Resource Management: A Structured, Adaptive Approach. West Sussex: John Wiley and Sons. doi: 10.1002/9781118506196
Cusser, S., Bahlai, C., Swinton, S. M., Robertson, G. P., and Haddad, N. M. (2020). Long-term research avoids spurious and misleading trends in sustainability attributes of no-till. Glob. Change Biol. 26, 3715–3725. doi: 10.1111/gcb.15080
Dowling, N. A., Dichmont, C. M., Haddon, M., Smith, D. C., Smith, A. D., and Sainsbury, K. (2015). Empirical harvest strategies for data-poor fisheries: a review of the literature. Fisher. Res. 171, 141–153. doi: 10.1016/j.fishres.2014.11.005
Field, S. A., Connor, P. J. O., Tyre, A. J., and Possingham, H. P. (2007). Making monitoring meaningful. Aust. Ecol. 32, 485–491. doi: 10.1111/j.1442-9993.2007.01715.x
Foundation, W. W. (2016). Living Planet Report 2016 - Risk and Resilience in a New Era. Technical Report 9782940529407, World Wildlife Foundation.
Fournier, A. M., White, E. R., and Heard, S. B. (2019). Site-selection bias and apparent population declines in long-term studies. Conserv. Biol. 33, 1–10. doi: 10.1111/cobi.13371
Gerber, L. R., Beger, M., McCarthy, M. A., and Possingham, H. P. (2005). A theory for optimal monitoring of marine reserves. Ecol. Lett. 8, 829–837. doi: 10.1111/j.1461-0248.2005.00784.x
Gerrodette, T. (1987). A power analysis for detecting trends. Ecology 68, 1364–1372. doi: 10.2307/1939220
Giron-Nava, A., James, C. C., Johnson, A. F., Dannecker, D., Kolody, B., Lee, A., et al. (2017). Quantitative argument for long-term ecological monitoring. Mar. Ecol. Prog. Ser. 572, 269–274. doi: 10.3354/meps12149
Grantham, H. S., Moilanen, A., Wilson, K. A., Pressey, R. L., Rebelo, T. G., and Possingham, H. P. (2008). Diminishing return on investment for biodiversity data in conservation planning. Conserv. Lett. 1, 190–198. doi: 10.1111/j.1755-263X.2008.00029.x
Hauser, C. E., Pople, A. R., and Possingham, H. P. (2006). Should managed populations be monitored every year? Ecol. Appl. 16, 807–819. doi: 10.1890/1051-0761(2006)016[0807:SMPBME]2.0.CO;2
Hodgson, J. C., Mott, R., Baylis, S. M., Pham, T. T., Wotherspoon, S., Kilpatrick, A. D., et al. (2018). Drones count wildlife more accurately and precisely than humans. Methods Ecol. Evol. 9, 1160–1167. doi: 10.1111/2041-210X.12974
Holden, M. H., and Ellner, S. P. (2016). Human judgment vs. quantitative models for the management of ecological resources. Ecol. Appl. 26, 1553–1565. doi: 10.1890/15-1295
Hughes, B. B., Beas-luna, R., Barner, A. K., Brewitt, K., Brumbaugh, D. R., Cerny-Chipman, E. B., et al. (2017). Long-term studies contribute disproportionately to ecology and policy. BioScience 67, 271–281. doi: 10.1093/biosci/biw185
Joppa, L. N. (2017). The case for technology investments in the environment. Nature 552, 325–328. doi: 10.1038/d41586-017-08675-7
Keith, D., Akçakaya, H. R., Butchart, S. H., Collen, B., Dulvy, N. K., Holmes, E. E., et al. (2015). Temporal correlations in population trends: Conservation implications from time-series analysis of diverse animal taxa. Biol. Conserv. 192, 247–257. doi: 10.1016/j.biocon.2015.09.021
Keller, A. A., Wallace, J. R., and Methot, R. D. (2017). The Northwest Fisheries Science Center's West Coast Groundfish Bottom Trawl Survey: History, Design, and Description. Technical Report, National Oceanic and Atmospheric Administration.
Legg, C. J., and Nagy, L. (2006). Why most conservation monitoring is, but need not be, a waste of time. J. Environ. Manage. 78, 194–199. doi: 10.1016/j.jenvman.2005.04.016
Lindenmayer, D., Woinarski, J., Legge, S., Southwell, D., Lavery, T., Robinson, N., et al. (2020). A checklist of attributes for effective monitoring of threatened species and threatened ecosystems. J. Environ. Manage. 262:110312. doi: 10.1016/j.jenvman.2020.110312
Lindenmayer, D. B., Gibbons, P., Bourke, M., Burgman, M., Dickman, C. R., Ferrier, S., et al. (2012). Improving biodiversity monitoring. Aust. Ecol. 37, 285–294. doi: 10.1111/j.1442-9993.2011.02314.x
Lindenmayer, D. B., and Likens, G. E. (2010). The science and application of ecological monitoring. Biol. Conserv. 143, 1317–1328. doi: 10.1016/j.biocon.2010.02.013
Maguran, A. E., Baillie, S. R., Buckland, S. T., Dick, J. M., Elston, D. A., Scott, E. M., et al. (2010). Long-term datasets in biodiversity research and monitoring: assessing change in ecological communities through time. Trends Ecol. Evol. 25, 574–582. doi: 10.1016/j.tree.2010.06.016
Mapstone, B. D. (1995). Scalable decision rules for environmental impact studies: effect Size, type I, and type II errors. Ecol. Appl. 5, 401–410. doi: 10.2307/1942031
Maxwell, S. L., Rhodes, J. R., Runge, M. C., Possingham, H. P., Ng, C. F., and McDonald-Madden, E. (2015). How much is new information worth? Evaluating the financial benefit of resolving management uncertainty. J. Appl. Ecol. 52, 12–20. doi: 10.1111/1365-2664.12373
McCarthy, M. A. (2014). Contending with uncertainty in conservation management decisions. Ann. N.Y. Acad. Sci. 1322, 77–91. doi: 10.1111/nyas.12507
McDonald-Madden, E., Baxter, P. W. J., Fuller, R. A., Martin, T. G., Game, E. T., Montambault, J., et al. (2010). Monitoring does not always count. Trends Ecol. Evol. 25, 547–550. doi: 10.1016/j.tree.2010.07.002
Nichols, J. D., and Williams, B. K. (2006). Monitoring for conservation. Trends Ecol. Evol. 21, 668–673. doi: 10.1016/j.tree.2006.08.007
Raiffa, H. (1968). Decision Analysis: Introductory Lectures on Choices Under Uncertainty. Reading, MA: Addison-Wesley. doi: 10.2307/2987280
Rhodes, J. R., and Jonzen, N. (2011). Monitoring temporal trends in spatially structured populations: how should sampling effort be allocated between space and time? Ecography 34, 1040–1048. doi: 10.1111/j.1600-0587.2011.06370.x
Rout, T. M., Moore, J. L., and Mccarthy, M. A. (2014). Prevent, search or destroy? A partially observable model for invasive species management. J. Appl. Ecol. 51, 804–813. doi: 10.1111/1365-2664.12234
Saunders, S. P., Farr, M. T., Wright, A. D., Bahlai, C. A., Ribeiro, J. W., Rossman, S., et al. (2019). Disentangling data discrepancies with integrated population models. Ecology 100, 1–14. doi: 10.1002/ecy.2714
Seavy, N. E., and Reynolds, M. H. (2007). Is statistical power to detect trends a good assessment of population monitoring? Biol. Conserv. 140, 187–191. doi: 10.1016/j.biocon.2007.08.007
Southwell, D. M., Einoder, L. D., Lahoz-Monfort, J. J., Fisher, A., Gillespie, G. R., and Wintle, B. A. (2019). Spatially explicit power analysis for detecting occupancy trends for multiple species. Ecol. Appl. 29:e01950. doi: 10.1002/eap.1950
Stock, B. C., Ward, E. J., Eguchi, T., Jannot, J. E., Thorson, J. T., Feist, B. E., et al. (2019). Comparing predictions of fisheries by catch using multiple spatiotemporal species distribution model framework. Can. J. Fisher. Aquat. Sci. 77, 1–66. doi: 10.1139/cjfas-2018-0281
Sullivan, B. L., Wood, C. L., Iliff, M. J., Bonney, R. E., Fink, D., and Kelling, S. (2009). eBird: A citizen-based bird observation network in the biological sciences. Biol. Conserv. 142, 2282–2292. doi: 10.1016/j.biocon.2009.05.006
Tulloch, A. I. T., Chadés, I., and Possingham, H. P. (2013). Accounting for complementarity to maximize monitoring power for species management: complementary monitoring indicators. Conserv. Biol. 27, 988–999. doi: 10.1111/cobi.12092
Wauchope, H. S., Johnston, A., Amano, T., and Sutherland, W. J. (2019). When can we trust population trends? A method for quantifying the effects of sampling interval and duration. Methods Ecol. Evol. 10, 498170–498170. doi: 10.1111/2041-210X.13302
Weiser, E. L., Diffendorfer, J. E., Grundel, R., López-Hoffman, L., Pecoraro, S., Semmens, D., et al. (2019). Balancing sampling intensity against spatial coverage for a community science monitoring programme. J. Appl. Ecol. 56, 2252–2263. doi: 10.1111/1365-2664.13491
Weiser, E. L., Diffendorfer, J. E., Lopez-Hoffman, L., Semmens, D., and Thogmartin, W. E. (2020). Challenges for leveraging citizen science to support statistically robust monitoring programs. Biol. Conserv. 242:108411. doi: 10.1016/j.biocon.2020.108411
White, E. R. (2019). Minimum time required to detect population trends: the need for long-term monitoring programs. BioScience 69, 40–46. doi: 10.1093/biosci/biy144
White, E. R., Cox, K., Melbourne, B. A., and Hastings, A. (2019). Success and failure of ecological management is highly variable in an experimental test. Proc. Natl. Acad. Sci. U.S.A. 116, 23169–23173. doi: 10.1073/pnas.1911440116
Keywords: statistical power, population trends, data-poor fisheries, species monitoring, resampling
Citation: White ER and Bahlai CA (2021) Experimenting With the Past to Improve Environmental Monitoring. Front. Ecol. Evol. 8:572979. doi: 10.3389/fevo.2020.572979
Received: 15 June 2020; Accepted: 15 October 2020;
Published: 20 January 2021.
Edited by:
Su Wang, Beijing Academy of Agricultural and Forestry Sciences, ChinaReviewed by:
Aaron Greenville, The University of Sydney, AustraliaAndrea Sciarretta, University of Molise, Italy
Copyright © 2021 White and Bahlai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Easton R. White, ZWFzdG9ucndoaXRlJiN4MDAwNDA7Z21haWwuY29t