
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Ecol. Evol. , 22 October 2020
Sec. Biogeography and Macroecology
Volume 8 - 2020 | https://doi.org/10.3389/fevo.2020.561838
This article is part of the Research Topic Metacommunity Spatio-Temporal Dynamics: Conservation and Management Implications View all 11 articles
The development of metacommunity theory has boosted the implementation of numerous empirical tests with field data, mostly focused on the role of spatial and environmental gradients on metacommunity organization. These studies showed an important dependence of the results on the observational scale considered, i.e., spatial grain, sampling spacing, and extent. However, few works deal with time per se as a component explaining metacommunity structure, even when data from periodic sampling are available. We suggest adding time explicitly to metacommunity analysis, but taking into account that the temporal scale of observation could affect the estimation of the relative influence of environment, space, and time, as previously recorded for spatial scale variation. Here, we analyze temporal scale dependence using simulated and empirical metacommunities of aquatic invertebrates. The effects of the study duration (i.e., temporal extent) were stronger when most metacommunity variation occurred along the temporal axis, so that local communities were spatially homogenized under high dispersal rates. Contrarily, dispersal limitation and niche differentiation (depending on the spatio-temporal structure of the environment) kept constant the spatial heterogeneity of the metacommunity, reducing the temporal variation and the importance of the temporal scale of observation. Our results highlight the importance of the temporal scale chosen for the analysis of metacommunity dynamics and emphasizes the temporal perspective of metacommunities, suggesting novel and interesting avenues in this research program.
Ecological communities are assembled by a complex interaction of processes, such as niche-related selection, dispersal, and ecological drift (Vellend, 2010; Leibold and Chase, 2017). Our perception of these processes strongly depends on the observational scale considered (Soininen et al., 2011; Heino et al., 2015; Viana and Chase, 2019), but most studies have treated this issue from a spatial point of view, suggesting a similar behavior for temporal scales. Nevertheless, the effects of variable temporal scales remain largely unknown (Korhonen et al., 2010; Tomašových and Kidwell, 2010; Dornelas et al., 2014).
The relative importance of selection, dispersal and drift vary with the spatial extent of the study following a generalized conceptual model (Leibold et al., 2004; Leibold and Chase, 2017). At a small spatial extent, environmental conditions can be mostly homogeneous. Then, all the species in the metacommunity may have similar environmental niches and only stochastic dynamics (i.e., ecological drift) foster metacommunity variation (Neutral Theory archetype, NT; Hubbell, 2001). However, despite the small spatial extent, localities could be environmentally heterogeneous, sorting species with different niches. Then, high dispersal (facilitated by short distances among sites) could maintain populations at suboptimal environmental conditions, hindering the deterministic responses of the species to the environment (Mass Effects archetype, ME; Mouquet and Loreau, 2003). At an intermediate spatial scale, environmental heterogeneity can increase, and niche filtering then originates spatial differences in community composition, while dispersal rates still allow the movement of species to reach (without surplus) their potentially suitable localities (Species Sorting archetype, SS; Chase and Leibold, 2003). At a larger spatial extent, dispersal limitation may spatially restrict the distribution of species, creating spatial dissimilarities independently of the environmental conditions and species' niches (Patch Dynamics archetype, PD; Leibold et al., 2004), and biogeographic effects.
Under a temporal focus, local temporal turnover can increase with the study duration (i.e., temporal extent; Wu and Li, 2006) just because of stochastic fluctuations, as NT and PD (even ME) assume (Leibold and Chase, 2017). However, environmental changes can also determine the temporal turnover due to species sorting, potentially reaching rates higher than those predicted by stochastic dynamics (Dornelas et al., 2014). At the metacommunity level, long-term studies have shown either stable (e.g., Azeria and Kolasa, 2008; Huttunen et al., 2018; Lindholm et al., 2020) or changing metacommunities through time, due to environmental fluctuations or disturbances observed (e.g., Datry et al., 2016; Sarremejane et al., 2017; Cañedo-Argüelles et al., 2020). Nevertheless, the spatio-temporal scale of observation in each study could explain these differences, depending on whether or not the study duration covered those relevant environmental fluctuations (Korhonen et al., 2010).
Previous studies estimated the relative relevance of different ecological processes by means of partitioning the metacommunity variation in species composition between the effects of environmental and spatial variables (e.g., Cottenie, 2005). With this approach, we assume that the fraction of the species variation explained by environmental variables is associated with selection (SS) and the rest of the variation (included pure space and unexplained fractions) is due to neutral dispersal and drift (NT and PD, even ME). Spatial variables can capture any spatial variation in the metacommunity, although we usually choose those spatial variables that are associated with broad-scale patterns (Dray et al., 2006). These spatial patterns may be generated by dispersal limitation (i.e., poor connected localities follow different stochastic dynamics; pure spatial fraction) and/or be associated with spatial patterns of the environment (the shared fraction between environment and space). Some studies have also considered introducing temporal variables in variation partitioning analyses (e.g., Anderson and Cribble, 1998; Muylaert et al., 2000; Padial et al., 2014). As with spatial variables, the temporal variables can explain either community changes related to (stochastic) fluctuations and biological cycles or those affected by a temporally-structured environment (the shared fraction between environment and time). Considering the relevance of spatio-temporal variables in these analytical methods is crucial, since metacommunities are to be considered as dynamic structures, with both spatial and temporal variation.
Here, we used simulated metacommunities to analyze the effects of study duration on the relative importance of environmental, spatial, and temporal variables. We expected that (1) the effects of the variation in study duration should be relevant when the metacommunity varies along the temporal axis (high temporal variation; Figures 1A,B). This could be a consequence of high dispersal rates, diluting the spatial variation through time. In this context, local communities may experience a process of mixing by the high number of colonizers, temporally synchronizing the metacommunity (Loreau et al., 2003). On the other hand, we envisage that (2) the study duration should be less relevant when the spatial structure of the metacommunity is maintained through time (low temporal variation; Figures 1C,D). Dispersal limitation can create permanent differences among localities and therefore spatial patterns would acquire more relevance (with high spatial variation; Figure 1D). Similarly, environmental conditions could also create spatial or temporal patterns in those metacommunities depending on the environmental variation, increasing the importance of the temporal scale when the environmental conditions vary through time. These two predictions can be considered two extremes of a continuum between unique temporal or spatial variation. Additionally, we analyze empirical data sets of aquatic invertebrates from a temperate setting to compare our expectations as resulting from the simulations with the field data.
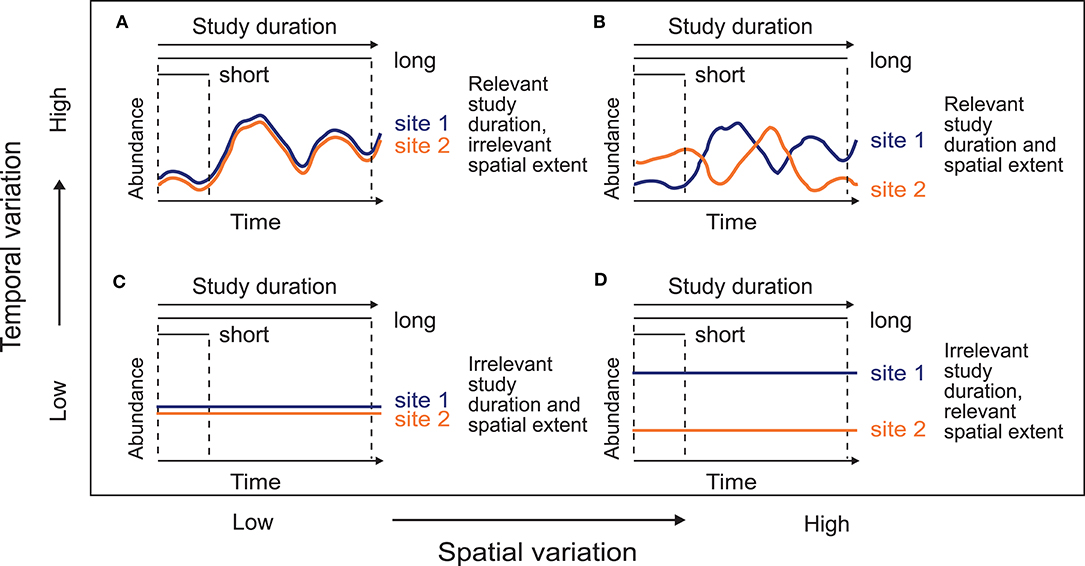
Figure 1. Conceptual model of the variation distribution between the spatial and the temporal axes. Lines represent the abundance dynamics of an hypothetical species in two sites through time. When abundances temporally vary (A,B), increasing the study duration is relevant because it allows encompassing more metacommunity variation. On the other hand, when abundances do not vary over time (C,D), extending the temporal extent of observation (i.e., study duration) should not be relevant, because short and long-term studies show the same temporal variability. Similarly, spatial extent is important in the sampling design, depending on the spatial variation.
The objective of our simulations was to emulate the temporal dynamics of metacommunities constrained by different conditions of selection and dispersal (Figure 2A). To this aim, we obtained species matrices (i.e., locality × species) at several points in time for each simulated metacommunity. Then, we sampled the species matrices changing the study duration but keeping constant the number of temporal sampling points. Consequently, we increased the time lag between sampling events as we extended the study duration (Figures 2B,C).
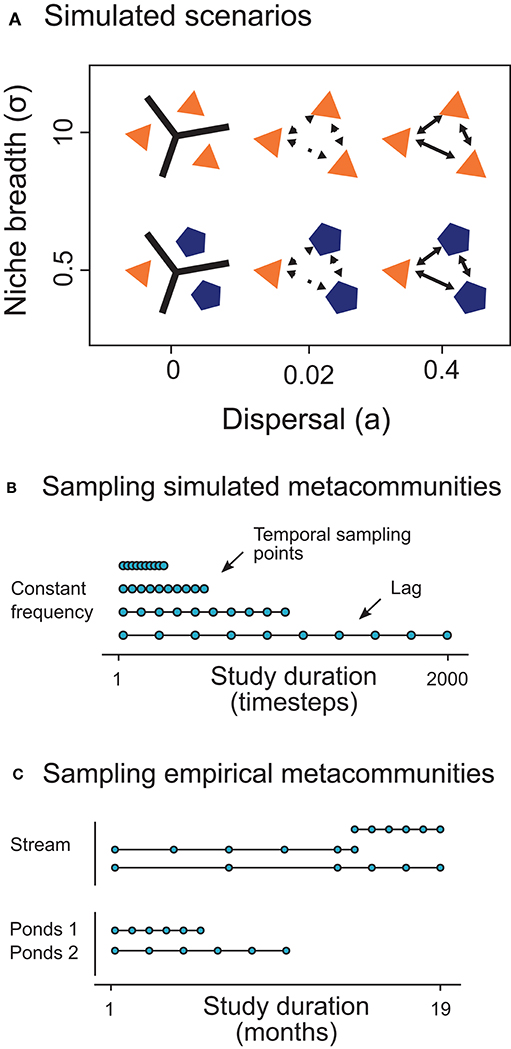
Figure 2. Summary of the simulated scenarios across niche breadth (i.e., selection; σ) and dispersal rate (a) gradients (A) and a summary of the temporal sampling procedure in simulated (B) and empirical (C) metacommunities. In the conceptual models, polygons, and colors represent localities with different suitable conditions for an hypothetical species depending on its niche. The lines and arrows between the polygons show the connectivity among them.
We used a model based on previous metacommunity simulations (Gravel et al., 2006; Sokol et al., 2017; Thompson et al., 2020). These models allow the observation of simulated metacommunity dynamics along different gradients of selection and dispersal. The model used had two parts differentiated in the simulation routine. First (Equation 1), species disperse among localities and then (Equation 2), the species compete at each locality depending on their relative abundances and the environmental conditions, determining the species composition for the next round. In the Equations 1 and 2, Nij(t) is the abundance of individuals of the species i in the site j at time t, Nij(t + 1)d is this abundance after dispersal (i.e., after Equation 1), and Nij(t + 1)c after environmental filtering and competition (i.e., after Equation 2). M is the total number of localities (being k any other than j) and S the regional species richness (where g are different species than i).
In step 1, dispersal rates were determined by the proportion of potential emigrants (a; Loreau et al., 2003). We randomized the number of emigrants (aNij(t)) following a Poisson distribution (Thompson et al., 2020). Following Equation 1, all the localities received the same number of immigrants of each species. Additionally, we also considered an unequal distribution of emigrants relying on the distance among localities (Gravel et al., 2006; Sokol et al., 2017; Viana and Chase, 2019), increasing dispersal resistance with the distances among sites (see Supplementary Material). For simplicity, we only show here the results in a scenario where emigrants could reach all the localities with the same probabilities (i.e., very low distance limitation).
In step 2 (Equation 2), local dynamics were influenced by the abundance of each species after dispersal (Nij(t + 1)d), the intrinsic growth rate (ri) and competition (α). The intrinsic growth rate (ri) relied on the performance of each species (λi) to the environmental conditions (E), which characterized the strength of the niche differentiation (Tilman, 2004; Gravel et al., 2006). The performance was defined by a Gaussian distribution, where μi is the optimal environmental value and σi is the niche breadth (Equation 3). We randomly modified the resulting riλi(E)Nij(t + 1)d following a Poisson distribution in each step, adding stochasticity to the model (Hubbell, 2001; Adler et al., 2007). We also considered intra- (αintra) and interspecific (αinter) competition in each locality (equation 2; Chesson, 2000; Adler et al., 2007).
The model ran in simulated landscapes of 10 localities with 10 species during 3,000 timesteps. Localities were randomly distributed in a square of 100 units of side. We simulated one environmental variable ranging from 0 to 1 for each landscape, which was spatially and temporally autocorrelated based on an exponential covariance model (Thompson et al., 2020). We set a spatial and temporal scale of autocorrelation of 50 and 500 units, respectively (see Supplementary Material). We generated different landscapes for each simulation.
The initial species matrix composition was randomly configured with a mean of 1 individual of each species per locality in a Poisson distribution. During the first 200 timesteps the environmental variable was kept constant in each locality (maintaining the spatial variability). In this period, we added each 10 steps more individuals following the same procedure as in the starting species matrix. After that, the environmental variable varied spatially and temporally and we did not add more individuals. We later removed the first 1,000 timesteps (200 + 800 steps) for further analyses to avoid the effect of the initial conditions on the results (Thompson et al., 2020).
We considered two levels of niche differentiation in the simulations (Figure 2A). In both scenarios, we set the same intrinsic growth rate for all the species (r = 10). The niche differentiation was determined by the niche breadth (σi) and it was the same for all the species in each metacommunity (Gravel et al., 2006; Sokol et al., 2017; Viana and Chase, 2019). In the neutral conditions (σ = 10), niche breadths were so wide to overlap species niches and cover the whole environmental gradient with the highest fitness (consequently all species have the same fitness at all the environmental values; Hubbell, 2001). Otherwise, with niche differentiation (σ = 0.5), niches were not totally overlapped and fitness was different for each species relying on their optimal environmental value (μi) and the environmental conditions at each site and time. We also assumed stable local coexistence in both scenarios. For this purpose, in the neutral scenario with equivalent fitness among species, stabilizing processes were weak (αintra = 0.050; αinter = 0.048). But we reinforced stabilization in the niche scenario due to established differences in fitness (αintra = 0.050; αinter = 0.028; Adler et al., 2007).
For each scenario, we explored 3 dispersal levels changing the proportion of emigrants (low: a = 0; intermediate: a = 0.02; high: a = 0.4; Loreau et al., 2003). Therefore, we studied 6 scenarios (2 niche × 3 dispersal levels; Figure 2A). We replicated 10 times the simulations of each scenario (6 × 10 = 60 simulations).
We used three databases of aquatic invertebrates from previous works, which were here reanalyzed with other purposes. The first database had 10 localities in a stream sampled on 11 occasions for 19 months (the first months were sampled seasonally and the last ones monthly; Mezquita et al., 1999; Rueda et al., 2002). The other two databases correspond to two groups of interdunal ponds, with 9 and 13 localities, respectively, sampled monthly during 12 months (Valls et al., 2013; Rueda, 2015). All the data originate from the eastern Iberian Peninsula, with an intra-annual fluctuation of temperatures and precipitations typical of Mediterranean regions (i.e., mild winters, hot and dry summers, and rainfalls concentrated in autumn months).
We selected four groups of arthropods (Ostracoda, Odonata, Coleoptera, and Diptera), each one corresponding to a taxonomic group with similar trophic features for the encompassed species, which potentially compete in a region for similar resources (Hubbell, 2001). Ostracods are benthic microcrustaceans which are predominantly omnivorous and they spread passively among ponds (Mesquita-Joanes et al., 2012). The other three groups have active dispersal with winged adults, although they have different dispersal capabilities and body sizes (Schmidt-Kloiber and Hering, 2015). Dragonflies and damselflies (Odonata) are predators, as well as the coleopterans (here, only family Dytiscidae). However, these two groups have different prey preference, attack strategies and life histories. Finally, dipterans (only families Stratiomyidae, Psychodidae, Ephydridae, and Dixidae) present aquatic larvae mostly consuming detritus. The criteria for selecting these groups were based on their abundance and species richness in the datasets. Overall, we analyzed nine datasets, separating the invertebrate groups in each landscape setting (3 in each landscape). More information of the empirical data is available in the Supplementary Material.
We sampled the simulated and the empirical metacommunities across a gradient of study durations (i.e., temporal extents), maintaining the number of temporal sampling points or frequency (therefore varying the lag between samples; Figures 2B,C). In the simulated data, we sampled the metacommunities varying the temporal extent from 20 to 2,000 timesteps (Figure 2B), fixing the frequency at 10 times. In a similar way, empirical metacommunities were sampled at different study durations maintaining the number of temporal points at a frequency of 6 times (Figure 2C). After being sampled, the simulated and the empirical data have the same arrangement in matrices, and we applied the same analytical routine for both types of datasets, as follows.
The empirical and the simulated data (after sampling) were analyzed by means of variation partitioning between environmental, spatial and temporal variables (Borcard et al., 1992; Anderson and Cribble, 1998; Peres-Neto et al., 2006). Environmental variables in the empirical dataset were previously log-transformed, and later we carried out a PCA to use the principal components as orthogonal environmental variables with all the environmental variability measured. In the simulated data, we used directly the simulated environmental variable (E).
We used Moran Eigenvector Maps (MEMs; Dray et al., 2006) to model spatio-temporal variables (see Supplementary Material). For this purpose, we created a three-dimensional network with the sampling points and the links among them, distributing them across space (x and y axes) and time (z axes). The links among samples were decided in two ways. In the spatial axes, the samples of each temporal point were connected following a Gabriel graph criterion, but never across time (Legendre and Legendre, 2012). In the temporal axis, we linked independently all the temporal points of each site separately, uniquely connecting each sample with the previous and the next one in the same site (Legendre and Gauthier, 2014). Therefore, we did not establish temporal connections between different sites. All the links were row standardized depending on the number of links of each point (e.g., 1 link = 1, 2 links = 0.5, and 0.5, 3 links = 0.3, 0.3, and 0.3, and so on), obtaining the weights of each link and calculating the MEMs (Dray et al., 2006).
With this method, the resulting MEMs modeled spatio-temporal patterns. We separated them in pure spatial and pure temporal MEMs by means of a two-way ANOVA, using each MEM as a response variable and spatial sites (space) and temporal points (time) as categorical explanatory variables (based on Legendre et al., 2010; Legendre and Gauthier, 2014). We considered spatial MEMs those with significant space, and temporal MEMs with significant time. Some of them could be significant for both space and time or for any of them. These MEMs were added into the two groups (spatial and temporal), and eventually, variation partitioning can attribute the explanation associated to these MEMs as the shared fractions among space and time (spatio-temporal fraction).
The variation partitioning procedure was based on RDA to calculate the fraction of variation of the species matrix explained by environmental, spatial, and temporal variables as R2 (Peres-Neto et al., 2006; Legendre and Legendre, 2012). RDA presents some important limitations which could affect the explained fractions (Viana et al., 2019), although it is one of the most used in metacommunity analysis. For example, RDA uses linear regressions to obtain the R2, although the species response to an environmental gradient could be non-linear (niches are usually Gaussian as in our simulation). In order to minimize this issue, we added a quadratic term for the environmental variables. In RDA, species matrices were transformed with the Hellinger method (i.e., the square-root-transformation of the relative abundance; Legendre and Gallagher, 2001). Additionally, we performed the same analyses by means of RDA without the quadratic term, so as with CCA and dbRDA (see Supplementary Material).
Variation partitioning has further limitations. Spurious correlations between environmental and spatio-temporal variables can occur due to spatio-temporal autocorrelation of the environment (Smith and Lundholm, 2010). This artificially increases the fractions (as R2) shared between the environment and the spatio-temporal variables, whereas this spurious correlation is not associated with the environment. We corrected R2 using a method based on MSR (Wagner and Dray, 2015), creating replicates of an environmental matrix with the same autocorrelation properties but removing their relationship with the species matrix (as a null model; Clappe et al., 2018). Previously to the variation partitioning, we selected subsets of each set of explanatory variables (environmental and all the MEMs with significant positive Moran's indices, before separating them in spatial and temporal) by means of forward selection, with a double stopping criterion (Blanchet et al., 2008a). We applied a Bonferroni correction for multiple testing to the p-values of the selected variables, i.e., those with adjusted p-values lower than 0.05.
All the simulations and metacommunity analyses were performed in R 3.6.3 (R Core Team, 2020), using the packages vegan (Oksanen et al., 2019), adespatial (Dray et al., 2020), spdep (Bivand and Wong, 2018), and RandomFields (Schlather et al., 2015). All the codes are available in https://github.com/andreucastillo/TemporalScalesMetacommunities.
In the simulated metacommunities, the explained fractions (adjusted R2) varied across selection and dispersal levels (Figure 3). Generally, the effects of the temporal scale increased as we incremented the dispersal rates (a), for both niche breadth levels (σ). These temporal scale effects raised the relevance of the temporal variables, and reduced the fractions explained by other factors. The shared fraction between space and time was negligible in all the scenarios, indicating pure temporal or spatial patterns in the metacommunity structure due to the design of the simulations (e.g., equal distribution of emigrants among the localities).
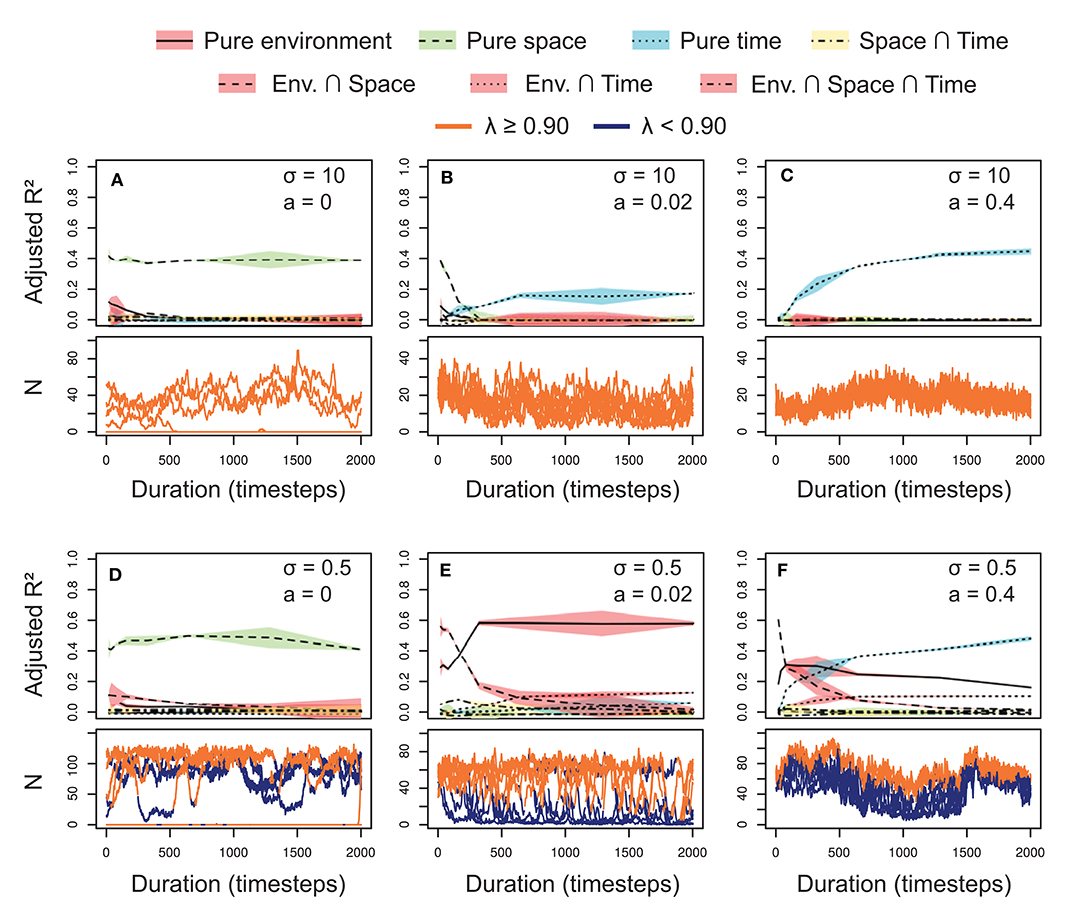
Figure 3. Relative importance (adjusted R2) of the explanatory sets on the variation of simulated metacommunities under different scenarios of niche differentiation (σ: broad in A–C vs. narrow in D–F) and dispersal rate (a: low in A,D, intermediate in B,E and high in C,F) in a gradient of study durations (top subpanels, A–F). The lines represent the mean, and the colored pattern the standard error of the adjusted R2 of the 10 replicated simulations. The bottom subpanels display the associated temporal changes in abundance (N) of one random species in 10 localities represented with different lines. The color of the lines depend on the environmental performance of the species in each locality through time, being orange under favorable and blue under unsuitable conditions (with a threshold of λ = 0.90).
With neutral conditions (σ = 10; Figures 3A–C, top subpanels), spatial variables dominated at low dispersal rates (a = 0), whereas temporal variables were prevalent at high dispersal rates (a = 0.4). At intermediate dispersal rates (a = 0.02), the pattern was a combination of the two extremes. Dispersal determined the main dimension (spatial or temporal) of change of the metacommunity. We can better understand this behavior if we observe the temporal dynamics of a single random species in each of the ten sites separately (Figures 2A–C, bottom subpanels). At low dispersal, spatial variation was high and maintained through time due to neutral dynamics. Therefore, space was relevant independently of the study duration. This spatial variation disappeared as we increased the dispersal rates (i.e., synchronizing the localities), until all the variation was concentrated in the temporal axis. However, the relevance of the temporal variables was not constant, increasing logarithmically with the study duration (Figures 3B,C).
When selection was included in the simulations by establishing narrower niches (σ = 0.5; Figures 3D–F) environmental effects appeared, and spatial and temporal variables exhibited a similar behavior to the neutral scenarios. However, the relevance of the environmental variable also depended on dispersal rate, accounting for larger fractions of metacommunity variation at intermediate dispersal rates (a = 0.02). Generally, the shared fraction between environment and space was higher at short study duration, whereas the shared fraction between environment and time slightly increased with the study duration (a pattern similar to pure spatial and temporal fractions). With low dispersal (a = 0), the species dynamics showed non-occupied suitable localities (λ ≥ 0.9; see the orange line for N = 0 in Figure 3D, bottom subpanel). In these conditions, the environmental variable was less relevant than the spatial variables, which captured this spatial variation in species distribution. At intermediate dispersal rates (a = 0.02), the species abundances fitted the environmental suitability through time, according to a constant dominant relevance of the environmental variable (Figure 3E). At high dispersal rates (Figure 3F) the represented species (lower subpanel) survived even under unsuitable conditions. However, its abundances were higher in the suitable than in the unsuitable conditions, showing an important role for environmental effects at least at short and intermediate study durations. We can also observe a synchronization of the local populations, increasing the relevance of the temporal effects as we extended the study duration.
When exploring the empirical data on aquatic invertebrate metacommunities, explanatory variables accounted only for a relatively low proportion of the metacommunity variation, compared with the simulated scenarios, and their relative role depending on time extent varied widely among groups (Figure 4). Generally, pure environmental fractions were more relevant than the others, explaining about 5–25% of the metacommunity variation, particularly for the ponds (Figures 4B,C). In these data, the spatio-temporal position of the samples were more complex than in the simulations, and we can observe some relevance of combined spatio-temporal effects (i.e., the shared fraction between space and time). Extending the analyses of the empirical data at different temporal scales, while keeping the number of temporal sampling points fixed, we can observe changes in the variation partitioning results, but the effects of the study duration were unclear (Figure 4). Extending the study duration seems to generally increase the relevance of the environmental variables and decrease the spatio-temporal fractions. However, the opposite was true in some cases, and anyway these changes were relatively very low compared with the simulations.
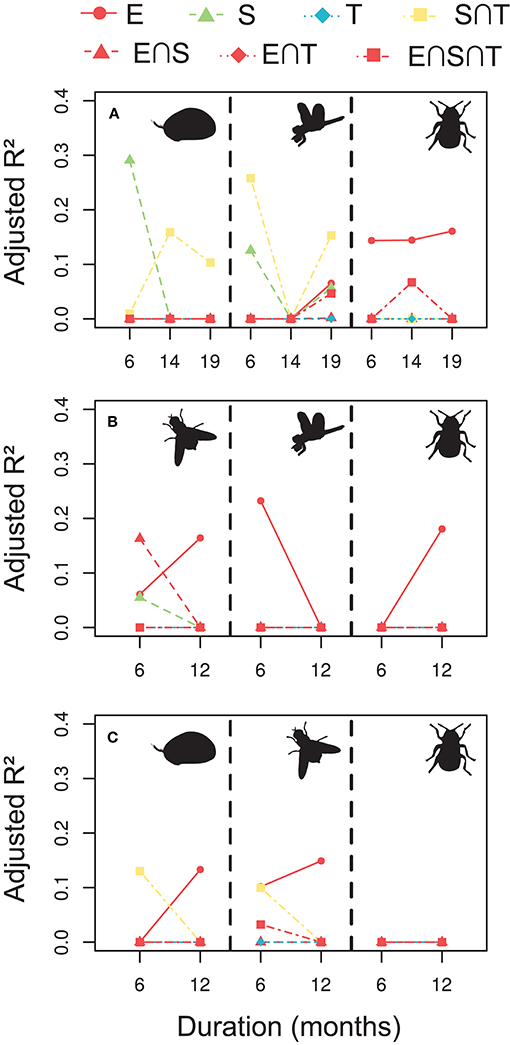
Figure 4. Relative importance (adjusted R2) of the explanatory sets on the variation of the empirical metacommunities in the Stream (A), Ponds 1 (B), and Ponds 2 (C) in a gradient of study durations from 6 to 19 months (A) or 6–12 months (B,C), with six temporal sampling points. In the Stream (A), we displayed ostracods (left), odonates (center), and coleopterans (right). In the Ponds 1 (B), we represented dipterans (left), odonates (center), and coleopterans, and in the Ponds 2 (C), ostracods (left), dipterans (center), and coleopterans (right).
Our results show that the temporal scale of observation affects our perception of the main processes contributing to metacommunity organization. Previous studies already highlighted the influence of spatial scale on the inference of these processes when analyzing communities sampled once (e.g., Condit et al., 2002; Heino et al., 2017; Viana and Chase, 2019), or comparing the spatial effects between several temporal points of the same metacommunity (e.g., Langenheder et al., 2012; Fernandes et al., 2014; Castillo-Escrivà et al., 2017). Other studies have focused on the effects of temporal scales on temporal turnover, but at one spatial point (e.g., Korhonen et al., 2010; Tomašových and Kidwell, 2010). Here, we integrated both perspectives, taking into account the spatio-temporal structure of the data as a whole and testing the influence of sampling period extent on the results of variation partitioning.
The simulations pointed out how dispersal and selection play a key role on metacommunity variation in both the spatial and temporal dimensions. Low dispersal rates allow maintaining the spatial variation through time, because local dynamics are spatially independent without a flux of organisms (Koelle and Vandermeer, 2004). In these cases, long study durations present the same results as short study durations in the simulations, suggesting to focus our sampling design only across space when dispersal is very limited (PD archetype), taking into account ranges of distributions and dispersal abilities of the organism studied (Wiens, 1989). On the other side, high dispersal reduces the spatial variation and temporally synchronizes all the local communities (Loreau et al., 2003; Gonzalez et al., 2009; Pandit et al., 2013). This synchronization implies that the whole metacommunity variation goes to the temporal axis (as expected with dispersal surplus in ME, and NT archetypes), and the longer the study duration, the higher the influence of time needed to capture these effects (e.g., ecological drift, progressive dispersal) on metacommunity variation.
The distribution of the environmental variation through time and space can also determine the importance of an adequate spatial or temporal scale of observation in niche-constrained metacommunities (SS archetype; Korhonen et al., 2010; Viana and Chase, 2019). In our simulations, the environmental variation was predominantly spatially distributed and the localities offered the whole environmental gradient at all the timesteps (even though the local environment was changing through time). Consequently, species always had available localities with suitable conditions when a locality became unsuitable; the key is an adequate dispersal to reach the optimal sites. Notwithstanding this environmental heterogeneity, extending the study duration affected the relevance of the shared fractions between environment and space-time, decreasing the fraction shared with space and slightly increasing the fraction overlapped with time. However, if the environmental variability would be expanded through time (as under climate change scenarios; Thompson et al., 2015), the temporal extent of observation would have a more important effect on detecting such environmental relevance.
In the empirical metacommunities, we observed relatively large differences when modifying the temporal scales of observation, usually increasing pure environmental effects and decreasing spatial pure and shared fractions. However, there was a large variation in this response among groups of organisms and landscape settings. According to the results of the simulations, the studied empirical metacommunities most probably rely on low to intermediate dispersal rates, combined with strong environmental filtering. However, the low explained proportion of metacommunity variation also suggests that fine-scale stochastic dynamics might have an important role in the empirical settings. Such low explained proportions are indeed very common in metacommunity studies (Cottenie, 2005), and may originate, among other sources, from the sampling design and methods used. First, the spatial and temporal scales could not be adequate to fully capture metacommunity variation, as we find in the simulations, emphasizing the importance of the sampling design (Viana and Chase, 2019). Second, we might have not acquired some relevant environmental information, failing to fully explain niche-related patterns and therefore increasing the unexplained fraction. Third, the statistical methods used might not be the best for the data being analyzed (e.g., linear models for non-linear environmental responses), although recent studies have developed new and promising methods (Clappe et al., 2018; Viana et al., 2019). Moreover, the large unexplained variation in empirical data demonstrates multiple and complex variation sources largely disregarded in the simulations, such as methodological errors when sampling or processing the samples, the influence of rare species (Magurran and Henderson, 2003) or trophic interactions (Guzman et al., 2019; García-Girón et al., 2020).
Previous empirical studies analyzing spatio-temporal patterns of metacommunities (Muylaert et al., 2000; Ysebaert and Herman, 2002; Padial et al., 2014) highlighted the relevance of the environment, even when environmental variables were temporally structured. According to our results, this also suggests a dependence on the temporal scale of observation, particularly whenever the environmental heterogeneity increases with the study duration. However, these studies only discussed pure spatial and temporal patterns, whereas we added explicitly mixed spatio-temporal patterns and the results could be different because of this combination (although some of the studies had indeed detected an overlap between space and time; Padial et al., 2014). Nevertheless, the spatio-temporal MEMs used here have some issues, such as their origin on symmetric connections, which may not be adequate for time (unlike AEMs, which consider an asymmetric relationship between points; Blanchet et al., 2008b).
In our empirical metacommunities, the shared fraction between space and time was important in some cases, indicating that the spatio-temporal variation in natural metacommunities might be more complex than that shown by our simulations. For example, ephemeral ponds do not disappear and appear always at the same time, creating spatio-temporal patterns in the data. The sampling design in these cases should take into account both spatial and temporal scales together. Therefore, the sampling design should be based on a previous knowledge of the temporal fluctuations of the landscape, this being important to find natural references of stable (such as tropical systems or stable interstitial zones; Hubbell, 2001; Dumas, 2002) and unstable landscapes (such as temporary ponds or intermittent rivers; Castillo-Escrivà et al., 2017; Cid et al., 2020) to test the theoretical predictions. This also encourages the use of more complex landscapes in the simulations for specific cases, taking into account different types of environmental variation (e.g., mosaic, gradient; Viana and Chase, 2019), the type of spatial distribution of localities (e.g., regular, random; Henriques-Silva et al., 2015), and regular or unexpected temporal events (e.g., droughts, seasonality; Tonkin et al., 2017).
We applied a basic model for the simulations that assumed that all the organisms of each metacommunity had the same population parameters. The study of metacommunity dynamics requires more complex models, considering the survival of the individuals through time (as a kind of temporal dispersal, such as diapause or lethargy) or the population structure (e.g., eggs, juveniles, adults). Simulating or monitoring metacommunities with different life-history strategies (Verberk et al., 2008) may allow comparisons at several temporal scales of observation among groups that differ in development time, synchronization in the reproduction, type of reproduction (e.g., semelparity or iteroparity) or with a population age-structure with changing dispersal capabilities among stages (e.g., juvenile and adult dimorphism). This type of comparison among organisms with different traits (e.g., body sizes and dispersal capabilities) has been a frequent approach in spatial studies of metacommunities (e.g., Soininen et al., 2011; Astorga et al., 2012; De Bie et al., 2012).
Another limitation of our simulations was to consider the same life-history traits (e.g., fecundity, survival, life cycle, dispersal capabilities) for all species. Natural communities are more complex, and variable life-history strategies within the community may allow the coexistence of species with similar trophic requirements (Amarasekare, 2003). For example, metacommunities could be composed by good competitors (with long life cycles, iteroparous, low dispersal rates, and niche dependence) and good colonizers (with short development times, semelparous, high dispersal rates, and low niche dependence; Chave et al., 2002). The prevalence of a trait could determine the relevance of the assembly processes in a metacommunity at different observational scales, whereas rare species may drive an increase in the amount of unexplained variation (Magurran and Henderson, 2003). Additionally, priority effects can also strongly influence the relevance of temporal factors in metacommunities (Fukami, 2015). As a process that is basically temporal, we can emulate historic and priority effects considering resistant stages to adverse transient environments (Wisnoski et al., 2019) and/or setting different inter-specific competition parameters for the modeled species (Thompson et al., 2020). Despite all these limitations, our model provides a general view of the effects of the temporal scale of observation on understanding metacommunity dynamics and methodological problems related to its study.
We focused on the temporal scale of observation using only one spatial scale, but the distribution of the metacommunity variation in the spatial and the temporal dimensions depends on both scales (increasing the extent of one of them decreases the relative relevance of the other). It is important to predict at which spatial and temporal scales the metacommunity variation is balanced in both dimensions, allowing to establish equivalences between spatial and temporal units (Adler and Lauenroth, 2003). We could find the equivalence by analyzing the data, but we need to develop deductive methods to estimate this equivalence taking into account the community structuring processes. This equivalence between space and time is crucial to plan research or conservation projects.
The inference of metacommunity structuring processes is influenced by the temporal scale of observation, depending on the distribution of the metacommunity variation between the spatial and the temporal dimensions. In our simulations, the variation was accumulated in the spatial dimension when dispersal rates were low, and in this case, an increase of the study duration did not have any effect on the inference of the underlying processes. On the other hand, high dispersal rates synchronized all the local communities, reducing the metacommunity variation to the temporal dimension. In this case, the study duration influenced our estimation of the metacommunity organization processes, logarithmically increasing the role of time-related effects (dispersal movements, ecological drift) when increasing the temporal extent of the study. In addition, we found the temporal scale effects to depend on the distribution of the environmental variation, which can generate more spatial or temporal variation in the metacommunity. In the empirical data, we observed only a slight influence of increasing temporal scale, mostly producing an increase of the role of environmental effects and decrease of spatial effects. This suggests metacommunity variation was rather distributed along the spatial axes and/or that the temporal scales considered were not adequate (maybe too short) to observe an increase in the role of time. However, the empirical data is expected to be more complex than the simulations, possibly including many unmeasured spatial, environmental, and stochastic effects. The present study highlights the importance of selecting an adequate observational scale to study or assess natural metacommunities, and the necessity to develop better methods to model and analyze spatio-temporal dynamics of natural systems.
All datasets generated for this study are included in the article/Supplementary Material.
FM-J, JR, and AC-E conceived the study. JR carried out the fieldwork and the identification of the organisms of the empirical data. JR and FM-J provided the empirical datasets. AC-E and FM-J designed the simulations. AC-E programmed the code and analyzed the data. AC-E wrote the first draft of the paper, with further revisions and contributions by FM-J. All authors approved the final version.
Partial funding has been provided by the METACOM-SET project (code CGL2016-78260-P), funded by the Spanish Ministry of Economy and Competitiveness (Agencia Española de Investigación, and FEDER).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We would like to thank Ramón Hernández and Luis Valls for their valuable contribution building the datasets of the Magre stream and the Racó de l'Olla. We are also grateful for the comments and suggestions of Miguel Cañedo-Argüelles, Alienor Jeliazkov and Victor Saito, which improved the present paper.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2020.561838/full#supplementary-material
Adler, P. B., HilleRisLambers, J., and Levine, J. M. (2007). A niche for neutrality. Ecol. Lett. 10, 95–104. doi: 10.1111/j.1461-0248.2006.00996.x
Adler, P. B., and Lauenroth, W. (2003). The power of time: spatiotemporal scaling of species diversity. Ecol. Lett. 6, 749–756. doi: 10.1046/j.1461-0248.2003.00497.x
Amarasekare, P. (2003). Competitive coexistence in spatially structured environments: a synthesis. Ecol. Lett. 6, 1109–1122. doi: 10.1046/j.1461-0248.2003.00530.x
Anderson, M. J., and Cribble, N. A. (1998). Partitioning the variation among spatial, temporal and environmental components in a multivariate data set. Aust. J. Ecol. 23, 158–167. doi: 10.1111/j.1442-9993.1998.tb00713.x
Astorga, A., Oksanen, J., Luoto, M., Soininen, J., Virtanen, R., and Muotka, T. (2012). Distance decay of similarity in freshwater communities: do macro-and microorganisms follow the same rules? Glob. Ecol. Biogeogr. 21, 365–375. doi: 10.1111/j.1466-8238.2011.00681.x
Azeria, E. T., and Kolasa, J. (2008). Nestedness, niche metrics and temporal dynamics of a metacommunity in a dynamic natural model system. Oikos 117, 1006–1019. doi: 10.1111/j.0030-1299.2008.16529.x
Bivand, R. S., and Wong, D. W. S. (2018). Comparing implementations of global and local indicators of spatial association. Test 27, 716–748. doi: 10.1007/s11749-018-0599-x
Blanchet, F. G., Legendre, P., and Borcard, D. (2008a). Forward selection of explanatory variables. Ecology 89, 2623–2632. doi: 10.1890/07-0986.1
Blanchet, F. G., Legendre, P., and Borcard, D. (2008b). Modelling directional spatial processes in ecological data. Ecol. Model. 215, 325–336. doi: 10.1016/j.ecolmodel.2008.04.001
Borcard, D., Legendre, P., and Drape, P. (1992). Partialling out the spatial component of ecological variation. Ecology 73, 1045–1055. doi: 10.2307/1940179
Cañedo-Argüelles, M., Gutiérrez-Cànovas, C., Acosta, R., Castro-López, D., Cid, N., et al. (2020). As time goes by: 20 years of changes in the aquatic macroinvertebrate metacommunity of mediterranean river networks. J. Biogeogr. 47, 1861–1874. doi: 10.1111/jbi.13913
Castillo-Escrivà, A., Valls, L., Rochera, C., Camacho, A., and Mesquita-Joanes, F. (2017). Metacommunity dynamics of ostracoda in temporary lakes: overall strong niche effects except at the onset of the flooding period. Limnologica 62, 104–110. doi: 10.1016/j.limno.2016.11.005
Chase, J. M., and Leibold, M. A. (2003). Ecological niches: linking classical and contemporary approaches. Chicago, IL: University of Chicago Press. doi: 10.7208/chicago/9780226101811.001.0001
Chave, J., Muller-Landau, H. C., and Levin, S. A. (2002). Comparing classical community models: theoretical consequences for patterns of diversity. Am. Nat. 159, 1–23. doi: 10.1086/324112
Chesson, P. (2000). Mechanisms of maintenance of species diversity. Annu. Rev. Ecol. Syst. 31, 343–366. doi: 10.1146/annurev.ecolsys.31.1.343
Cid, N., Bonada, N., Heino, J., Cañedo-Argüelles, M., Crabot, J., Sarremejane, R., et al. (2020). A metacommunity approach to improve biological assessments in highly dynamic freshwater ecosystems. Bioscience 70, 427–438. doi: 10.1093/biosci/biaa033
Clappe, S., Dray, S., and Peres-Neto, P. R. (2018). Beyond neutrality: disentangling the effects of species sorting and spurious correlations in community analysis. Ecology 99, 1737–1747. doi: 10.1002/ecy.2376
Condit, R., Pitman, N., Leigh, E. G., Chave, J., Terborgh, J., Foster, R. B., et al. (2002). Beta-diversity in tropical forest trees. Science 295, 666–669. doi: 10.1126/science.1066854
Cottenie, K. (2005). Integrating environmental and spatial processes in ecological community dynamics. Ecol. Lett. 8, 1175–1182. doi: 10.1111/j.1461-0248.2005.00820.x
Datry, T., Bonada, N., and Heino, J. (2016). Towards understanding the organisation of metacommunities in highly dynamic ecological systems. Oikos 125, 149–159. doi: 10.1111/oik.02922
De Bie, T., Meester, L., Brendonck, L., Martens, K., Goddeeris, B., Ercken, D., et al. (2012). Body size and dispersal mode as key traits determining metacommunity structure of aquatic organisms. Ecol. Lett. 15, 740–747. doi: 10.1111/j.1461-0248.2012.01794.x
Dornelas, M., Gotelli, N. J., McGill, B., Shimadzu, H., Moyes, F., Sievers, C., et al. (2014). Assemblage time series reveal biodiversity change but not systematic loss. Science 344, 296–299. doi: 10.1126/science.1248484
Dray, S., Bauman, D., Blanchet, G., Borcard, D., Clappe, S., Guenard, G., et al. (2020). Adespatial: Multivariate Multiscale Spatial Analysis. R package version 0.3-8.
Dray, S., Legendre, P., and Peres-Neto, P. R. (2006). Spatial modelling: a comprehensive framework for principal coordinate analysis of neighbour matrices (PCNM). Ecol. Model. 196, 483–493. doi: 10.1016/j.ecolmodel.2006.02.015
Dumas, P. (2002). Stability of interstitial crustacean communities in an isolated alluvial aquifer. Hydrobiologia 468, 63–76. doi: 10.1023/A:1015226423335
Fernandes, I. M., Henriques-Silva, R., Penha, J., Zuanon, J., and Peres-Neto, P. R. (2014). Spatiotemporal dynamics in a seasonal metacommunity structure is predictable: the case of floodplain-fish communities. Ecography 37, 464–475. doi: 10.1111/j.1600-0587.2013.00527.x
Fukami, T. (2015). Historical contingency in community assembly: integrating niches, species pools, and priority effects. Annu. Rev. Ecol. Evol. Syst. 46, 1–23. doi: 10.1146/annurev-ecolsys-110411-160340
García-Girón, J., Heino, J., García-Criado, F., Fernández-Aláez, C., and Alahuhta, J. (2020). Biotic interactions hold the key to understanding metacommunity organisation. Ecography 43, 1180–1190. doi: 10.1111/ecog.05032
Gonzalez, A., Mouquet, N., and Loreau, M. (2009). “Biodiversity as spatial insurance: the effects of habitat fragmentation and dispersal on ecosystem functioning,” in Biodiversity, Ecosystem Functioning, and Human Wellbeing, eds S. Naeem, D. E. Bunker, A. Hector, M. Loreau, and C. Perrings (New York, NY: Oxford University Press), 134–146. doi: 10.1093/acprof:oso/9780199547951.003.0010
Gravel, D., Canham, C. D., Beaudet, M., and Messier, C. (2006). Reconciling niche and neutrality: the continuum hypothesis. Ecol. Lett. 9, 399–409. doi: 10.1111/j.1461-0248.2006.00884.x
Guzman, L. M., Germain, R. M., Forbes, C., Straus, S., O'Connor, M. I., Gravel, D., et al. (2019). Towards a multi-trophic extension of metacommunity ecology. Ecol. Lett. 22, 19–33. doi: 10.1111/ele.13162
Heino, J., Melo, A. S., Siqueira, T., Soininen, J., Valanko, S., and Bini, L. M. (2015). Metacommunity organisation, spatial extent and dispersal in aquatic systems: patterns, processes and prospects. Freshw. Biol. 60, 845–869. doi: 10.1111/fwb.12533
Heino, J., Soininen, J., Alahuhta, J., Lappalainen, J., and Virtanen, R. (2017). Metacommunity ecology meets biogeography: effects of geographical region, spatial dynamics and environmental filtering on community structure in aquatic organisms. Oecologia 183, 121–137. doi: 10.1007/s00442-016-3750-y
Henriques-Silva, R., Boivin, F., Calcagno, V., Urban, M. C., and Peres-Neto, P. R. (2015). On the evolution of dispersal via heterogeneity in spatial connectivity. Proc. R. Soc. B Biol. Sci. 282:20142879. doi: 10.1098/rspb.2014.2879
Hubbell, S. P. (2001). The Unified Neutral Theory of Biodiversity and Biogeography. Princeton, NJ: Princeton University Press.
Huttunen, K.-L., Mykrä, H., Paavo, R., and Muotka, T. (2018). Estimates of benthic invertebrate community variability and its environmental determinants differ between snapshot and trajectory designs. Freshw. Sci. 37, 769–779. doi: 10.1086/700402
Koelle, K., and Vandermeer, J. (2004). Dispersal-induced desynchronization: from metapopulations to metacommunities. Ecol. Lett. 8, 167–175. doi: 10.1111/j.1461-0248.2004.00703.x
Korhonen, J. J., Soininen, J., and Hillebrand, H. (2010). A quantitative analysis of temporal turnover in aquatic species assemblages across ecosystems. Ecology 91, 508–517. doi: 10.1890/09-0392.1
Langenheder, S., Berga, M., Östman, O., and Székely, A. J. (2012). Temporal variation of β-diversity and assembly mechanisms in a bacterial metacommunity. ISME J. 6, 1107–1114. doi: 10.1038/ismej.2011.177
Legendre, P., de Cáceres, M., and Borcard, D. (2010). Community surveys through space and time: testing the space-time interaction in the absence of replication. Ecology 91, 262–272. doi: 10.1890/09-0199.1
Legendre, P., and Gallagher, E. D. (2001). Ecologically meaningful transformations for ordination of species data. Oecologia 129, 271–280. doi: 10.1007/s004420100716
Legendre, P., and Gauthier, O. (2014). Statistical methods for temporal and space-time analysis of community composition data. Proc. R. Soc. B Biol. Sci. 281:20132728. doi: 10.1098/rspb.2013.2728
Leibold, M. A., and Chase, J. M. (2017). Metacommunity Ecology. Princeton, NJ: Princeton University Press. doi: 10.2307/j.ctt1wf4d24
Leibold, M. A., Holyoak, M., Mouquet, N., Amarasekare, P., Chase, J. M., Hoopes, M. F., et al. (2004). The metacommunity concept: a framework for multi-scale community ecology. Ecol. Lett. 7, 601–613. doi: 10.1111/j.1461-0248.2004.00608.x
Lindholm, M., Alahuhta, J., Heino, J., and Toivonen, H. (2020). No biotic homogenisation across decades but consistent effects of landscape position and pH on macrophyte communities in boreal lakes. Ecography 43, 294–305. doi: 10.1111/ecog.04757
Loreau, M., Mouquet, N., and Gonzalez, A. (2003). Biodiversity as spatial insurance in heterogeneous landscapes. Proc. Natl. Acad. Sci. U.S.A. 100, 12765–12770. doi: 10.1073/pnas.2235465100
Magurran, A. E., and Henderson, P. A. (2003). Explaining the excess of rare species in natural species abundance distributions. Nature 422:714. doi: 10.1038/nature01547
Mesquita-Joanes, F., Smith, A. J., and Viehberg, F. A. (2012). “The ecology of ostracoda across levels of biological organisation from individual to ecosystem: a review of recent developments and future potential,” in Ostracoda as Proxies for Quaternary Climate Change, eds D. J. Horne, J. A. Holmes, J. Rodriguez-Lázaro, and F. A. Viehberg (Amsterdam: Elsevier), 15–35. doi: 10.1016/B978-0-444-53636-5.00002-0
Mezquita, F., Hernandez, R., and Rueda, J. (1999). Ecology and distribution of ostracods in a polluted mediterranean river. Palaeogeogr. Palaeoclimatol. Palaeoecol. 148, 87–103. doi: 10.1016/S0031-0182(98)00177-1
Mouquet, N., and Loreau, M. (2003). Community patterns in source sink metacommunities. Am. Nat. 162, 544–557. doi: 10.1086/378857
Muylaert, K., Sabbe, K., and Vyverman, W. (2000). Spatial and temporal dynamics of phytoplankton communities in a freshwater tidal estuary (Schelde, Belgium). Estuar. Coast. Shelf Sci. 50, 673–687. doi: 10.1006/ecss.2000.0590
Oksanen, J., Blanchet, F. G., Friendly, M., Kindt, R., Legendre, P., McGlinn, D., et al. (2019). vegan: Community Ecology Package. R package version 2.5-6.
Padial, A. A., Ceschin, F., Declerck, S. A. J., Meester, L. D., Bonecker, C. C., Lansac-Tôha, F. A., et al. (2014). Dispersal ability determines the role of environmental, spatial and temporal drivers of metacommunity structure. PLoS ONE 9:e111227. doi: 10.1371/journal.pone.0111227
Pandit, S. N., Kolasa, J., and Cottenie, K. (2013). Population synchrony decreases with richness and increases with environmental fluctuations in an experimental metacommunity. Oecologia 171, 237–247. doi: 10.1007/s00442-012-2407-8
Peres-Neto, P. R., Legendre, P., Dray, S., and Borcard, D. (2006). Variation partitioning of species data matrices: estimation and comparison of fractions. Ecology 87, 2614–2625. doi: 10.1890/0012-9658(2006)87[2614:VPOSDM]2.0.CO;2
R Core Team (2020). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Rueda, J. (2015). Biodiversidad y ecología de metacomunidades de macroinvertebrados acuáticos de las malladas de la Devesa y del Racó de l'Olla (PN de l'Albufera de Valencia) (Dissertation thesis). University of Valencia, Burjassot, Spain.
Rueda, J., Camacho, A., Mezquita, F., Hernández, R., and Roca, J. R. (2002). Effect of episodic and regular sewage discharges on the water chemistry and macroinvertebrate fauna of a mediterranean stream. Water Air Soil Pollut. 140, 425–444. doi: 10.1023/A:1020190227581
Sarremejane, R., Cañedo-Argüelles, M., Prat, N., Mykrä, H., Muotka, T., and Bonada, N. (2017). Do metacommunities vary through time? Intermittent rivers as model systems. J. Biogeogr. 44, 2752–2763. doi: 10.1111/jbi.13077
Schlather, M., Malinowski, A., Menck, P. J., Oesting, M., and Strokorb, K. (2015). Analysis, simulation and prediction of multivariate random fields with package randomfields. J. Stat. Softw. 63, 1–25. doi: 10.18637/jss.v063.i08
Schmidt-Kloiber, A., and Hering, D. (2015). www.freshwaterecology.info–an online tool that unifies, standardises and codifies more than 20,000 European freshwater organisms and their ecological preferences. Ecol. Indic. 53, 271–282. doi: 10.1016/j.ecolind.2015.02.007
Smith, T. W., and Lundholm, J. T. (2010). Variation partitioning as a tool to distinguish between niche and neutral processes. Ecography 33, 648–655. doi: 10.1111/j.1600-0587.2009.06105.x
Soininen, J., Korhonen, J. J., Karhu, J., and Vetterli, A. (2011). Disentangling the spatial patterns in community composition of prokaryotic and eukaryotic lake plankton. Limnol. Oceanogr. 56, 508–520. doi: 10.4319/lo.2011.56.2.0508
Sokol, E. R., Brown, B. L., and Barrett, J. E. (2017). A simulation-based approach to understand how metacommunity characteristics influence emergent biodiversity patterns. Oikos 126, 723–737. doi: 10.1111/oik.03690
Thompson, P. L., Beisner, B. E., and Gonzalez, A. (2015). Warming induces synchrony and destabilizes experimental pond zooplankton metacommunities. Oikos 124, 1171–1180. doi: 10.1111/oik.01945
Thompson, P. L., Guzman, L. M., De Meester, L., Horváth, Z., Ptacnik, R., Vanschoenwinkel, B., et al. (2020). A process-based metacommunity framework linking local and regional scale community ecology. Ecol. Lett. 23, 1314–1329. doi: 10.1111/ele.13568
Tilman, D. (2004). Niche tradeoffs, neutrality, and community structure: a stochastic theory of resource competition, invasion, and community assembly. Proc. Natl. Acad. Sci. U.S.A. 101, 10854–10861. doi: 10.1073/pnas.0403458101
Tomašových, A., and Kidwell, S. (2010). The effects of temporal resolution on species turnover and on testing metacommunity models. Am. Nat. 175, 587–606. doi: 10.1086/651661
Tonkin, J. D., Bogan, M. T., Bonada, N., Rios-Touma, B., and Lytle, D. A. (2017). Seasonality and predictability shape temporal species diversity. Ecology 98, 1201–1216. doi: 10.1002/ecy.1761
Valls, L., Rueda, J., and Mesquita-Joanes, F. (2013). Dynamics of ostracoda (crustacea) assemblages in a mediterranean pond system (racó de l'olla, albufera nat. park) with focus on the exotic species Candonocypris novaezelandiae (Baird, 1843). Ann. Limnol.-Int. J. Limnol. 49, 237–247. doi: 10.1051/limn/2013053
Vellend, M. (2010). Conceptual synthesis in community ecology. Q. Rev. Biol. 85, 183–206. doi: 10.1086/652373
Verberk, W. C. E. P., Siepel, H., and Esselink, H. (2008). Life-history strategies in freshwater macroinvertebrates. Freshw. Biol. 53, 1722–1738. doi: 10.1111/j.1365-2427.2008.02035.x
Viana, D. S., and Chase, J. M. (2019). Spatial scale modulates the inference of metacommunity assembly processes. Ecology 100:e02576. doi: 10.1002/ecy.2576
Viana, D. S., Keil, P., and Jeliazkov, A. (2019). Partitioning environment and space in species-by-site matrices: a comparison of methods for community ecology and macroecology. bioRxiv [Preprint]. doi: 10.1101/871251
Wagner, H. H., and Dray, S. (2015). Generating spatially constrained null models for irregularly spaced data using moran spectral randomization methods. Methods Ecol. Evol. 6, 1169–1178. doi: 10.1111/2041-210X.12407
Wisnoski, N. I., Leibold, M. A., and Lennon, J. T. (2019). Dormancy in metacommunities. Am. Nat. 194, 135–151. doi: 10.1086/704168
Wu, J., and Li, H. (2006). “Concepts of scale and scaling,” in Scaling and Uncertainty Analysis in Ecology, eds J. Wu, B. Jones, H. Li, and O. L. Loucks (Dordrecht: Springer), 3–15. doi: 10.1007/1-4020-4663-4_1
Keywords: temporal scale, selection, dispersal, ecological drift, metacommunity dynamics
Citation: Castillo-Escrivà A, Mesquita-Joanes F and Rueda J (2020) Effects of the Temporal Scale of Observation on the Analysis of Aquatic Invertebrate Metacommunities. Front. Ecol. Evol. 8:561838. doi: 10.3389/fevo.2020.561838
Received: 13 May 2020; Accepted: 19 August 2020;
Published: 22 October 2020.
Edited by:
Miguel Cañedo-Argüelles, University of Barcelona, SpainReviewed by:
Alienor Jeliazkov, Institut National de Recherche pour l'agriculture, l'alimentation et l'environnement (INRAE), FranceCopyright © 2020 Castillo-Escrivà, Mesquita-Joanes and Rueda. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andreu Castillo-Escrivà, YWNhc3RpbGxvZXNjcml2YUBnbWFpbC5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.