Uniting Community Ecology and Evolutionary Rescue Theory: Community-Wide Rescue Leads to a Rapid Loss of Rare Species

Most ecological communities are facing changing environments, particularly due to global change. When migration is impossible, adaptation to these altered environments is necessary to survive. Yet, we have little theoretical understanding how ecological communities respond both ecologically and evolutionarily to such environmental change. Here we introduce a simple eco-evolutionary model, the Community-Wide Rescue (CWR) model, in which a community faces environmental deterioration and each species within the community is forced to undergo adaptation or become extinct. We assume that all species in the community are equivalent except for their initial abundance. This individual based simulation model thus combines community ecology and evolutionary rescue theory. We show that under Community-Wide Rescue a rapid loss of rare species occurs. This loss occurs due to competition and a limited supply of beneficial mutations. The rapid loss of rare species provides a testable prediction regarding the impact of Community-Wide Rescue on species abundance distributions in ecological communities.

Introduction

Many ecosystems face abrupt human-induced environmental change and evolutionary adaptation might be the only way to avoid extinction when migration is difficult (Vitousek et al., 1997; IPCC, 2014). Understanding precisely how ecological communities respond to abruptly changing environments is therefore paramount. This calls for models that predict how an ecological community composed of many different species adapts to such a deteriorated environment (Hoffmann and Sgrò, 2011). Such models of community-wide adaptation are not only relevant from the perspective of global change, but they are also important to understand the response of any community to environmental change, such as the microbiome of a medical patient undergoing a prolonged treatment with antibiotics. In this case, not just a single pathogenic bacterium faces a changed environment, but a complex community consisting of many thousands of species (Arumugam et al., 2011; Cho and Blaser, 2012), must adapt to avoid extinction. Whilst many models exist that study how a population of a single species, or a community composed of two species, adapts to environmental change (Hoffmann and Sgrò, 2011; Martin et al., 2013; Northfield and Ives, 2013; Osmond and De Mazancourt, 2013; Cortez and Yamamichi, 2019), fewer models exist that describe the response of an entire community composed of multiple species to an altered environment, although there are some examples (De Mazancourt et al., 2008; Bell, 2017; Lasky, 2019). Furthermore, empirical results, describing community wide adaptation, such as those presented by Bell and Gonzalez (2011), Low-Décarie et al. (2015), Bell et al. (2019), and Roodgar et al. (2019), are clearly calling for such models.

Evolutionary rescue theory models situations in which a population can only escape extinction if it adapts. In a classical evolutionary rescue scenario, where the environment in which a population resides deteriorates, the population starts declining as a result. Extinction can then only be averted if a mutant establishes that has a positive growth rate in the new environment; i.e., the population is rescued. This process results in the well-known U-shaped curve of population size over time (Gomulkiewicz and Holt, 1995; Gonzalez et al., 2012; Orr and Unckless, 2014). Most models of evolutionary rescue focus on deriving the probability of the occurrence of such a rescue event given a certain initial population size, a rate of population decline, and a mutation rate. Evolutionary rescue theory could even be a useful tool to predict the emergence of antibiotic resistance (Martin et al., 2013; Alexander et al., 2014).

Here, we explore a new scenario in which not a single population, but a whole community composed of many different species faces a deteriorated environment, causing the populations of each species to decline. Only those species in which a rescue mutant with a positive growth rate establishes, remain in the community. In other words, evolutionary rescue occurs on a community-wide basis. We examine the effect of this process on species abundance distributions.

We present a parsimonious model of this Community-Wide Rescue (CWR) process. It describes the change in species abundances, during and after community-wide evolutionary rescue. We assume that all species are equivalent; they all start with the same negative growth rate and all have the same fixed mutation rate toward a phenotype with a positive growth rate. These assumptions are inspired by those made in the neutral model of biodiversity (Hubbell, 1997). The neutral model has been shown to be able to explain various patterns of species abundances, and has become a baseline model for community diversity patterns when species differences or species asymmetries are ignored (Alonso et al., 2006; Rosindell et al., 2011; Wennekes et al., 2012; Scheffer et al., 2018). However, because we include an explicit mutational process that introduces a different growth rate, our Community-Wide Rescue model is not strictly neutral. We compare our results with those of two null models: neutral models in which the community dynamics are solely governed by ecological drift. The first null model has a constant community size, whilst the second null model mimics the decrease in community size that occurs during Community-Wide Rescue.

The aim of this paper is to construct and explore a simple model for the CWR process, and to examine how under this model CWR affects the patterns of species abundances within a community. We quantify these patterns using Rank Abundance Curves (RAC, also known as rank abundance diagrams or distributions, RAD, McGill et al., 2007). It is well known that many different mechanisms can generate similar RACs, and hence RACs should be interpreted with caution (Chave et al., 2002). We aim to see if this general pattern also holds for our CWR model, or if perhaps RACs are informative about the (past) occurrence of CWR. We show that CWR causes a loss of rare species from the community, due to a limited supply of beneficial mutations and competition. In rare species, their low abundance limits their supply of beneficial mutations that can rescue them from extinction, whilst they face increased competition with more common species that have already undergone such beneficial mutations. However, RACs produced by the CWR process could equally well have been produced by a neutral model. In addition, as RACs proved uninformative, we also examined the rate at which CWR changes the relative species abundances (i.e., alters the RAC) and compare this to the rate at which ecological drift alters species abundance patterns. We show that CWR causes an extremely rapid loss of rare species. Such insights are crucial to understand the effects of environmental change on ecological communities.

Materials and Methods

Our model of the CWR process is a continuous-time individual-based stochastic model, where birth, death, and mutation events are simulated using the Doob-Gillespie algorithm (Gillespie, 1976). We assume that all species are equivalent except for their initial densities. This assumption is unlikely to hold in a natural community, but its simplicity allows us to focus on the key ingredients of the CWR process. Furthermore, we consider a single closed community, i.e., there is no immigration. It is worth noting that this implies that the observed dynamics are transient in nature, when time goes to infinity all species will eventually go extinct due ecological drift. This assumption of no migration allows us to more clearly see the effect of CWR in a single (local) community. In the CWR model, the community consists of several species, each with an initial abundance that is drawn using the sampling formula for standard neutral communities (Etienne, 2005). Initially, all individuals of each species have the same negative growth rate. We call an individual with this negative growth rate a “resident.” The initial community thus represents a community immediately after a drastic environmental change, in which the populations of all species are declining and unless adaptation occurs extinction is inevitable for all species. However, each resident individual can undergo a mutation to become a mutant individual, this occurs with a rate μ (note that this process implicitly assumes asexual inheritance). Again, the value for μ is the same, regardless of the species to which an individual belongs. All mutants have the same positive growth rate. Hence, we assume the simplest possible model of evolutionary rescue, as posited by Orr and Unckless (2008) and Martin et al. (2013): only a single mutational step is required to achieve a positive growth rate and this mutation has a constant fitness effect. μ could for example represent the mutation rate toward antibiotic resistance, see also Martin et al. (2013).

The growth rates of the residents and mutants are implemented as follows. The death rates for the residents and the mutants are equal and given by d. We assume that the birth rate for both mutants and residents depends on total community size (i.e., total number of individuals in the community of all species combined),

$$b=b_0(1-\frac{N_{tot}}{K})(1)$$

where b₀ is the rate of birth in a pristine community (no other individuals present). This parameter b₀ is different between residents and mutants (hence, we have b_0,res and b_0,mut). We assume that b_{0, res} < d so that the resident always has a negative growth rate and b_0,mut > d, so that the mutants always have a positive growth rate. Parameter K is the number of individuals at which the birth rate is equal to 0, and N_tot is the total number of individuals (summed across species, including both residents and mutants) in the community. It is important to note that K is not the sole parameter controlling the carrying capacity of the community; this is determined by the interplay of b₀, d, and K and is given by K (1- d/b₀). Our model deviates from standard neutral models in that we do not impose a zero-sum constraint (otherwise the community cannot decline), and that instead we have community-wide density-dependent birth. Haegeman and Etienne (2008) showed that community-level density-dependence in immigration and birth does not affect the predictions on the species abundance distributions, so we do not strongly deviate from a standard neutral model in this sense. The default parameter set for simulating the CWR model was b_0,res = 0.05, b_0,mut = 0.6, d = 0.1, K = 16000, and μ = 0.0005. The initial species abundances for all simulations were generated with the sampling formula for standard neutral communities as derived by Etienne (2005) using a community size of 16000, a fundamental biodiversity number, θ, of 200 and a migration parameter, I, of 40. In this neutral model, the fundamental biodiversity number controls the species abundance distribution in the regional species pool, whilst the migration parameter governs the frequency of migration from the regional species pool to the local species pool. For a more complete description the reader is referred to Etienne and Olff (2004) and Etienne (2005). Here this model is simply used to generate a reasonable initial species abundance distribution. The exact same initial species abundance distribution was used for all simulations, unless stated otherwise. All simulations, plots and analysis were performed using R version 3.5.1 (R Core Team, 2014). All new simulation code is provided in the CWERNI R-package that is available at: https://github.com/DeadParrot69/CWERNI.

To answer the question whether an endpoint RAC from a CWR community can be distinguished from a RAC generated by a neutral community, we used a simulation, fitting, and re-simulation approach. First, we simulated a community using CWR, with the default parameters. Subsequently, we fitted a neutral model to the RAC using the SADISA-package (Haegeman and Etienne, 2017). From this fit we obtain a log-likelihood, which in essence is a measure of the goodness of fit of the neutral model on the RAC generated using CWR. To generate a distribution of log-likelihoods with which to compare the log-likelihood of the neutral model fit on the CWR RAC, the parameters obtained from the neutral model fit were used to perform 500 neutral model simulations (Etienne, 2005). Then, the SADISA-package (Haegeman and Etienne, 2017) was used on each of these neutral simulations to fit a neutral model. This created a distribution of log-likelihoods for these neutral model simulations. Subsequently we determined whether the log-likelihood obtained from the neutral model fit on the CWR RAC falls outside or inside the distribution of the log-likelihoods obtained through neutral model fits on neutral model simulations. Instead of the log-likelihood we also looked at the distribution of two different diversity indices, the Shannon entropy (Rényi entropy, α = 1) and the collision entropy (Rényi entropy, α = 2) of the simulated communities. This process was repeated ten times each time with a newly drawn neutral starting community. We note that the model underlying the SADISA estimates is subtly different from that used to perform the re-simulations. The SADISA estimator makes an independent species assumption, whilst the code used for the simulations instead assumes a zero-sum assumption, but it has been shown that the RACs that these model produce are indistinguishable (Haegeman and Etienne, 2008, 2017).

In order to place the rate of rare species loss due to CWR into context, we compared it to the rate of rare species loss in a local community due to ecological drift in two truly neutral models. The first is a simple neutral model (SN) without a CWR process, where the birth and death rates are equal to those of the mutant in the CWR model. This model is thus a neutral model of the local community without immigration or speciation; it only describes the loss of species through ecological drift.

We expected the CWR model to show a decrease in total community size before recovery (due to the negative growth rate of the residents). Such a decrease in local community size, can accelerate the rate of rare species loss through ecological drift. Therefore, we also constructed a neutral model similar to SN, but where the basic birth rate for all species is set to a value less than the death rate for a predetermined time interval. This induces a steady decrease in total community size from the start of the simulation until the end of the interval. We chose the length of the interval, such that the community size decrease is similar to that observed during CWR. We call this model the variable-birth neutral model (VBN).

We simulated the three models (CWR, SN, and VBN) for 100 units of time. This was a sufficient number for all residents to go extinct in the CWR model, see also Supplementary Figure 6. When there are no more residents in the community the evolutionary rescue process is considered complete as all species have either undergone adaptation or gone extinct; hence we chose to simulate for 100 units of time. Each model was simulated 500 times. The SN model was simulated using the parameters b₀ = 0.6, d = 0.1, and K = 16000 (i.e., the same parameters as the mutants in the CWR model). For the VBN model we set the basic birth rate of all the species in the community (b₀) equal to b₀, _res, during the first twenty units of time. After this time interval, which was tuned so as to create a decrease in total community size similar or perhaps even slightly larger in nature than that in the CWR community, we set the basic birth rate equal to b₀,_mut. The other parameters were the same as in the SN model. To study the RAC of a community at different stages of CWR, we plotted the resulting RACs at different points in time: t = 15, t = 30, t = 50, t = 75, and t = 100.

In models examining evolutionary rescue, the mutation rate and the establishment probability of the mutant are known to determine the probability of evolutionary rescue (Martin et al., 2013). Therefore, to gain more insight into our CWR model, we wanted to examine the effect of the mutation rate (μ) and mutant birth rate (b_0,mut), on the CWR process. by respectively varying the mutation rates (μ = 0.00005, 0.0005, 0.005, 0.05) and the mutant birth rate (b_0,mut = 0.2, 0.4, 0.6, 0.8), and leaving all other parameters the same as in the default parameter set. Again, we ran 500 independent simulations for each set of parameters.

In our CWR model we assumed that b_0,res < d so that the resident always has a negative growth rate. If this condition is not satisfied, one is no longer modeling evolutionary rescue. However, one can imagine a scenario in which b_0,res > d, for example when a bacterial community is confronted with sub-inhibitory concentrations of antibiotics. In such a community the species are not doomed to go extinct, but residents are simply replaced by fitter mutants, in essence a community-wide selective sweep. Such situations might be much more common than strict evolutionary rescue scenarios, so examining this situation could extend the applicability of our model. Therefore, we also studied a selective sweep model, derived from our CWR model, in which the only difference is that b_0,res > d, resulting in both a resident and a mutant with a positive net growth rate, whilst the mutant still has a higher net growth rate than the resident. We performed 500 simulations of this model using the parameter set b_0,res = 0.3 and all other parameters the same as in the default CWR model parameter set.

Results

The loss of rare species in the CWR community (Figures 1A,B) is much faster than in the neutral (SN) community (Figures 1C,D). In other words, the CWR process causes a very rapid loss of rare species, when compared to the rate of rare species loss from a local community due to ecological drift. Furthermore, the rate of rare species loss in the CWR model is also much larger than in the VBN model (Figures 1E,F). Because the VBN model has a variable carrying capacity tuned to create a decrease in total community size similar to the one observed in the CWR model, we can conclude that the rapid loss of rare species in the CWR model is not just due to ecological drift being accelerated by a decrease in total community size. In addition, the observed rapid loss of rare species occurs consistently in a relatively wide range of community sizes (between K = 1000 and K = 16000, see Supplementary Figures 12–14).

FIGURE 1

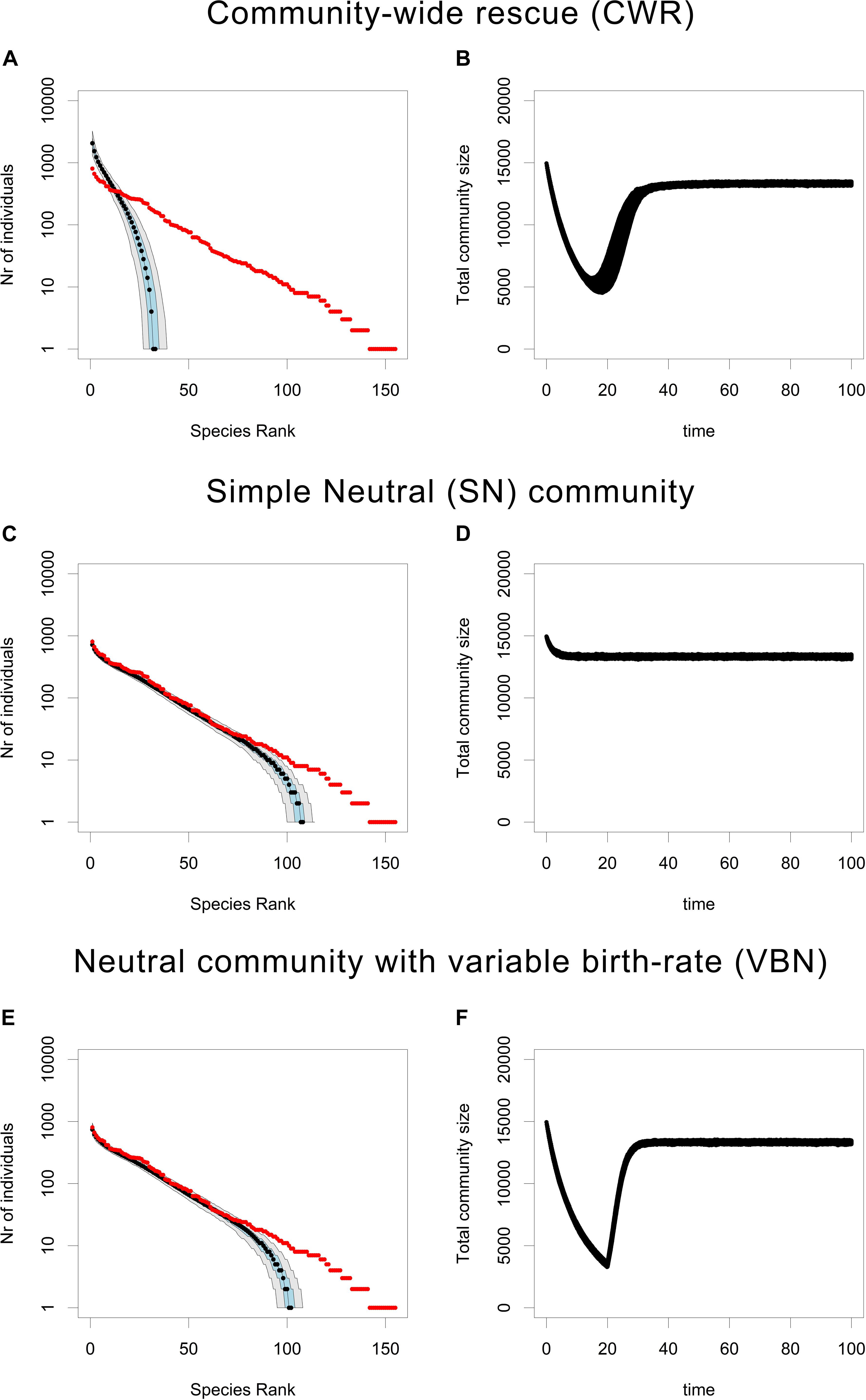
Figure 1. Rank Abundance Curves and total community size under the CWR, SN, and VBN models. (A,C,E) Show the RACs produced after 100 units of time by the CWR model, the SN model and the VBN model, where the median is shown in black, the 25th and the 75th percentile are shown in blue and the 5th and the 95th percentile are shown in gray, the initial community is plotted in red. (B,D,F) Show the accompanying trajectories of total community size for each simulation over time. All plots are based on 500 simulations. Parameters for (A,B): b_0,res = 0.05, b_0,mut = 0.6, d = 0.1, K = 16000, and μ = 0.0005, for (C,D): b₀ = 0.6, d = 0.1 and K = 16000, for (E,F): b₀ = 0.05 for t between 0 and 20, b₀ = 0.6 for t between 20 and 100, d = 0.1, and K = 16000.

The same pattern is evident if one examines the figures showing the RACs at different time points for each of the three models (Figure 2 and Supplementary Figures 7, 8). Furthermore, by closely examining Figure 2 one can see exactly at which point during the CWR process the loss of rare species occurs. During the first stage of CWR a community-wide decline occurs that does not greatly alter the shape of the RAC (Figure 2A). It is only as the first mutants begin to invade and the total community size starts to rebound (Figure 2F) that the shape of the RAC begins to change and that the loss of rare species starts to occur (Figure 2B). The loss of rare species continues after the community size has stabilized (Figures 2C,D). Once the residents have disappeared from the population, the shape of the RAC is fairly stable (Figures 2D–F).

FIGURE 2

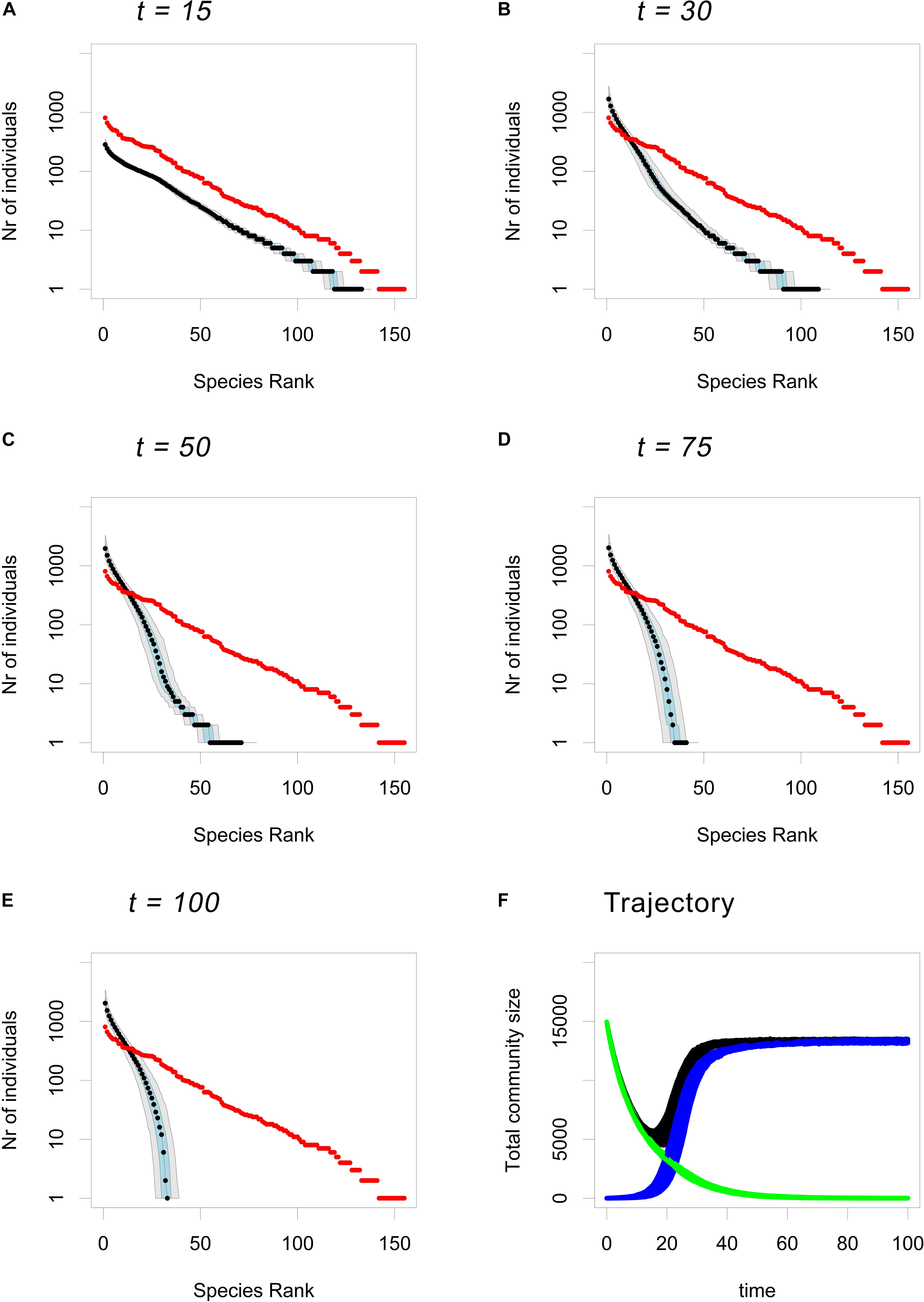
Figure 2. Time trajectory of the RAC under the CWR model. Plots based on 500 CWR simulations using the (default) parameters b_0,res = 0.05, b_0,mut = 0.6, d = 0.1, K = 16000 and μ = 0.0005. (A–E) Show the RAC of the community at t = 15, t = 30, t = 50, t = 75, and t = 100 respectively, were the median is shown in black, the 25th and the 75th percentile are shown in blue and the 5th and the 95th percentile are shown in gray, and the input community is plotted in red. (F) Shows the trajectories of the total community size (black), the total number of residents in the communities (green) and the total number of mutants in the community (blue).

The mutation rate has a strong influence on the results (Figure 3). If the mutation rate is very high, rescue becomes so likely that all species undergo rescue and there is no loss of rare species beyond the effects of normal ecological drift in a neutral community without speciation/immigration (Figures 3A,B). By contrast, if the mutation rate is very low, almost none of the species in the community undergo rescue (Figure 3E) and in some cases not a single rescue mutant manages to establish itself in the community (Figure 3F). Therefore, intermediate mutation rates seem to be required for CWR to impact the RAC and create a loss of rare species greater than that produced by ecological drift alone. In other words, the rate of rare species loss during CWR depends on the mutation rate.

FIGURE 3

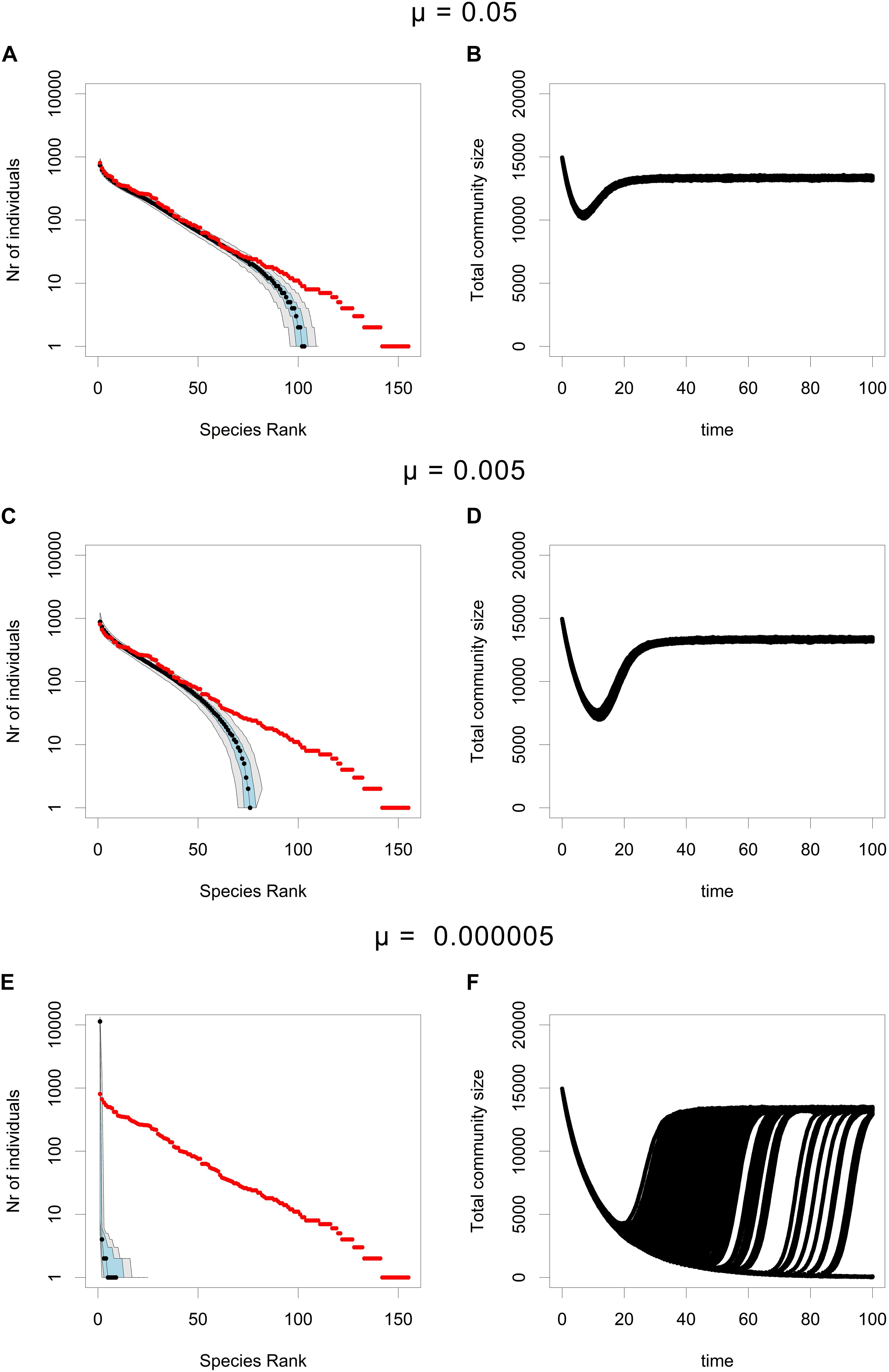
Figure 3. RACs (A,C,E) and total community size trajectories (B,D,F) under the CWR process, for different mutation probabilities (μ), for each different mutation rate 500 simulations were performed. In the RAC plots the median is shown in black, the 25th and the 75th percentile are shown in blue, the 5th and the 95th percentile are shown in gray and the initial community is plotted in red. Simulations were performed using the parameters b_0,res = 0.05, b_0,mut = 0.6, d = 0.1, and K = 16000. For (A,B) μ = 0.05, in (C,D) μ = 0.005, and in (E,F) μ = 0.000005. The total community size trajectories were plotted for of each of the 500 simulations, hence the separation of these trajectories at low mutation rates (F).

Increasing b_0,mut i.e., increasing the fitness advantage of the mutant, does not seem to influence the loss of rare species, as the RAC’s obtained after the CWR process, for different values of b_0,mut are indistinguishable (Figure 4). However, increasing b_0,mut does seem to increase the speed of the rescue process. In particular, if b_0,mut is higher, the recovery phase of the rescue process proceeds much faster, due to the higher maximal growth rate of the mutant. It should be noted that increasing b_0,mut also increases the net carrying capacity of the rescued population, because despite a constant K, the net carrying capacity, given by K (1- d/b₀), is the density where the net birth rate is equal to the death rate. Despite this increased carrying capacity, the recovery phase is still much faster in the simulations with a high b_0,mut.

FIGURE 4

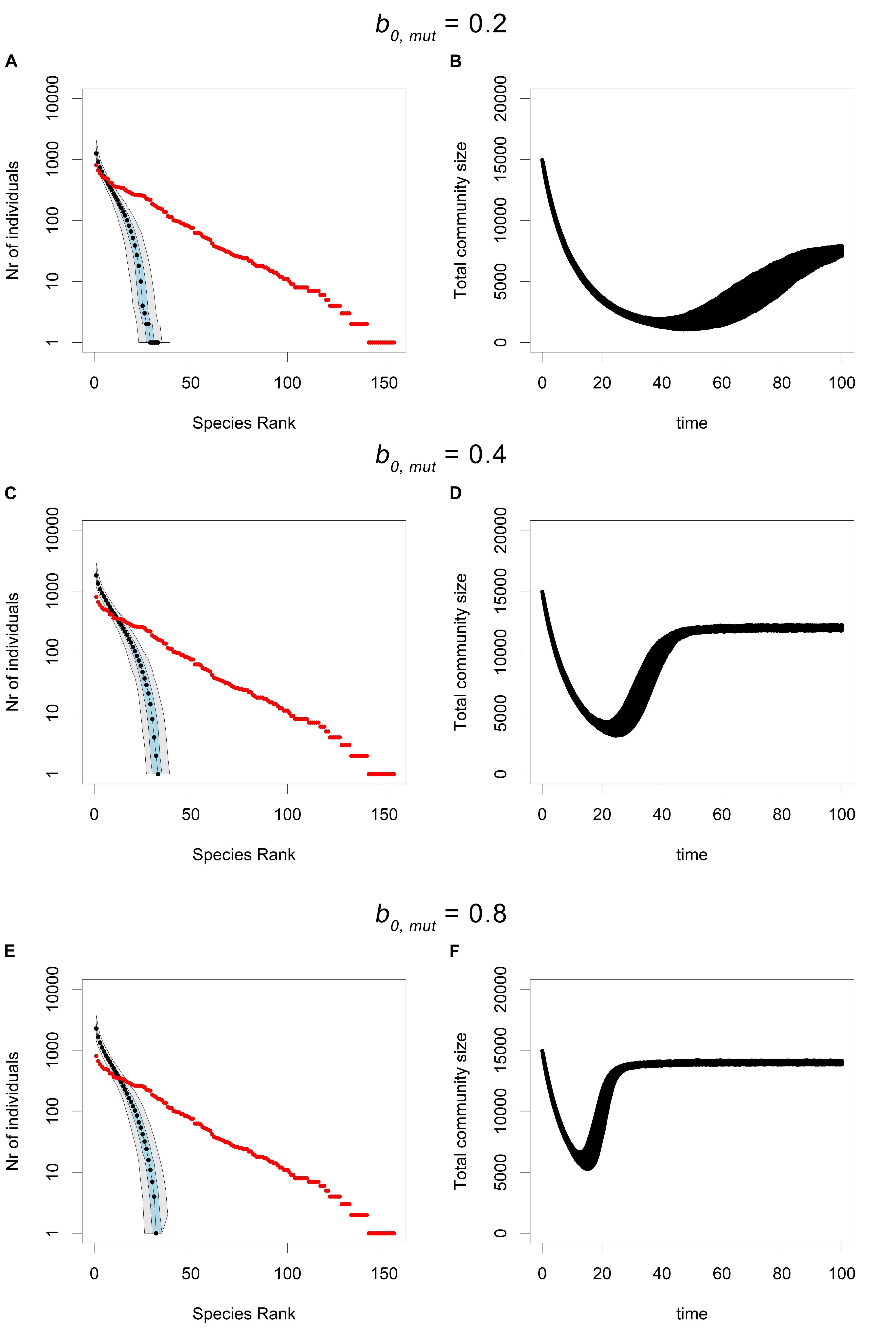
Figure 4. The RAC under CWR processes with different mutant birth probabilities (b_0,mut). All simulations were performed using the parameters b_0,res = 0.05, d = 0.1, K = 16000, and μ = 0.0005. In (A,B) b_0,mut = 0.2, for (C,D) b_0,mut = 0.4 and in (E,F) b_0,mut = 0.8. Panels (A,C,E) show the RAC’s after 100 units of time, where the median is shown in black, the 25th and the 75th percentile are shown in blue and the 5th and the 95th percentile are shown in gray, with the input community plotted in red. (B,D,F) Display the trajectories of total community size over time. All plots are based on 500 simulations.

In the selective sweep model, the residents have a positive net growth rate, i.e., instead of CWR, the resident with a positive growth rate is replaced by a mutant with an even higher growth rate. As can be seen in Figure 5B, there is only a very minor decrease in the total community size during this replacement process. However as can be seen in Figure 5A, the rate of rare species loss in the selective sweep model is much higher than in the neutral SN and VBN models. In other words, when compared to ecological drift, community wide adaptation can cause a very rapid loss of rare species, just like CWR.

FIGURE 5

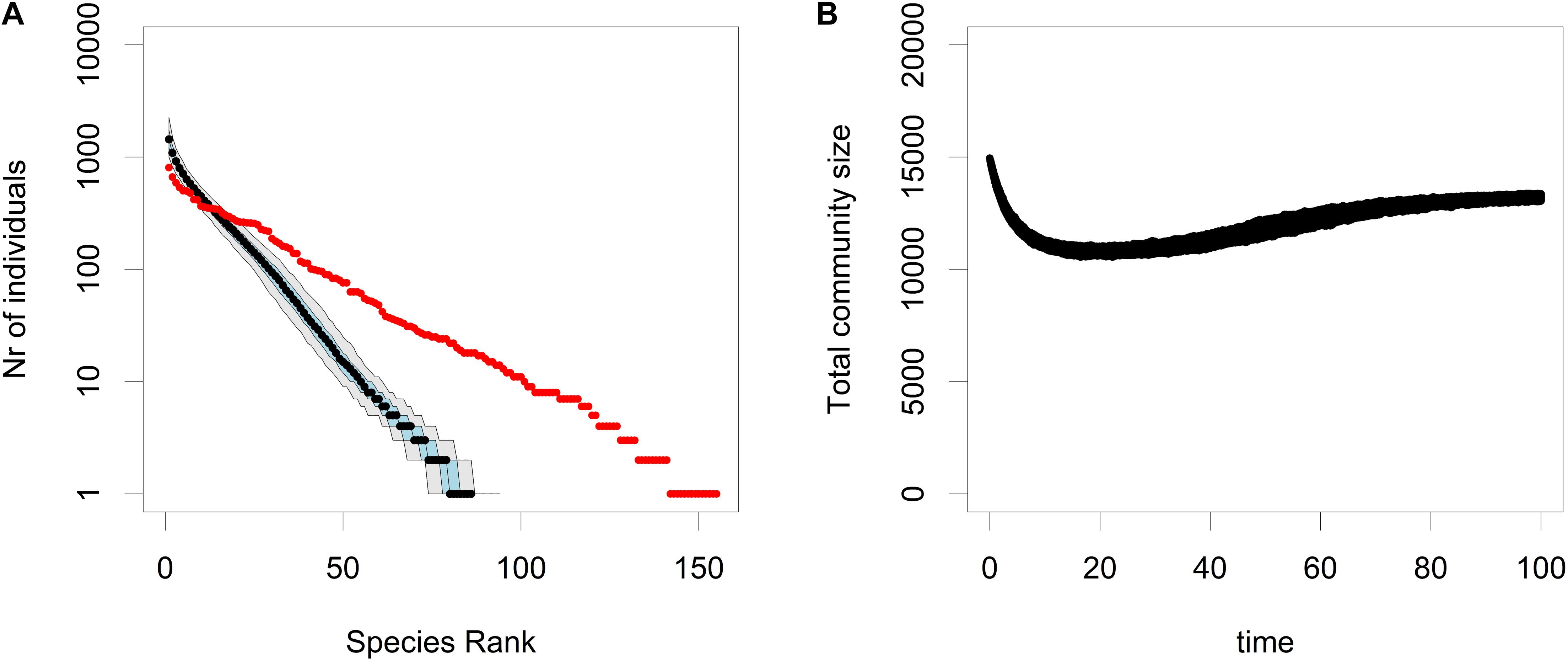
Figure 5. The RAC (A) and the total community size (B) for simulations of the CWR model where the strict conditions of CWR are relaxed and reflect a scenario where the net growth rate of the residents is positive, yet still lower than that of the mutants. This causes a selective sweep during which the residents are replaced by the mutants, because the mutants have a higher fitness. In the RAC plot the median is shown in black, the 25th and the 75th percentile are shown in blue and the 5th and the 95th percentile are shown in gray, and the input community is plotted in red. These plots are based on 500 simulations. The parameters used were b_0,res = 0.3, b_0,mut = 0.6, d = 0.1, K = 16000 and μ = 0.0005.

The fitting and re-simulation approach using the log-likelihoods of neutral model fits showed that the log-likelihood of a neutral model fit on the CWR model results consistently fell within the distribution of log-likelihoods obtained from neutral model simulations (Supplementary Figure 9A). A similar result was obtained when instead of log-likelihoods, the values of the Shannon entropy and the Rényi entropy of the RACs were used; the values of the Shannon entropy and the Rényi entropy estimated from the CWR RAC consistently fell inside those estimated on neutral model simulations simulated using neutral model parameters estimated from the CWR RACs (Supplementary Figures 9B,C). Both of these results imply that there is no information in an endpoint RAC alone that would allow one to determine whether that RAC had been created by a neutral process or a CWR process.

Discussion

We have shown that a single endpoint RAC does not allow one to determine whether that RAC had been created by a neutral process or a CWR process. This conclusion is in accordance with the general pattern in the literature; whilst some non-neutral processes, such as trait based environmental filtering (Jabot, 2010), can be detected by examining species abundances, many different non-neutral processes can generate surprisingly similar RACs (Chave et al., 2002).

The most striking outcome of our modeling effort is that CWR (Figures 1A,B) causes a very rapid loss of rare species, when compared to ecological drift (Figures 1C,D). This holds even if one accounts for the increase in ecological drift due to a decrease in total community size as in the VBN model (Figures 1E,F). Furthermore, this result is shown for a wide range of community sizes (between K = 1000 and K = 16000, see Supplementary Figures 12–14). In a neutral model governed by ecological drift, rare species are more likely to go extinct simply due to their lower abundance. However, in the CWR model rare species have a higher probability of going extinct, because their low abundance also means that they will have a lower probability of producing a beneficial mutant before going extinct. In other words, for rare species the supply of beneficial mutations is limited by their low abundance. This dependence of the probability of rescue on the initial population density is well characterized in standard models of evolutionary rescue and has also been demonstrated empirically (Holt, 1990; Bell and Gonzalez, 2009; Martin et al., 2013). Low abundance causes a low probability of a beneficial mutant occurring, because mutation occurs on a per-capita basis, i.e., the probability of a beneficial mutation arising during a certain time interval depends on the product of μ and the population size of the species, so during the same time interval a mutation is less likely to occur in a species with a small population size. Furthermore, the time to extinction for rare species is lower, so there is less time for a mutant to arise before the rare species goes extinct.

However, there is another effect, hypothesized by Bell (2017), which contributes to the loss of rare species: competition. This represents a crucial difference between our model and standard models of evolutionary rescue (Martin et al., 2013). In our model the birth rate of all species is governed by the total number of individuals in the community (regardless of their species), all species compete with each other (community-level density dependence). So, a species that has undergone rescue will increase the total number of individuals in the community. This causes the birth-rate of the remaining species to decrease. For the species that have not yet undergone rescue, this accelerates their decay, decreasing the time available to find a mutant before going extinct. In other words, the evolutionary rescue of one species, promotes the extinction of its competitors (Bell, 2017). Rare species that do manage to produce a mutant will tend to do so relatively late in the simulation, because their low abundance gives them a low probability of producing a mutant per unit of time. On the other hand, species with a high abundance that manage to produce a mutant will tend to do so relatively early on in the simulation, thereby promoting the extinction of the rare species through competition. It is interesting to contrast these results with those of De Mazancourt et al. (2008), who showed that on a community level biodiversity can inhibit adaptation, due to competitive interactions. In our model, the fact that rare species fail to adapt is also partly driven by competitive interactions, in that sense reaffirming the general result that competition can inhibit adaptation. However, the crucial difference is that in the model of De Mazancourt et al. (2008) these competitive interactions are driven by explicit assumptions about the ecology of each species, whilst in our model species are ecologically equivalent except for their initial abundance.

In our model, the limited supply of beneficial mutations at low abundance and competition between the species, together disproportionally promote the extinction of rare species during CWR. These two effects are also crucial to understand how changing the mutation rate impacts the CWR process (Figure 3). From standard models of evolutionary rescue it follows that a high mutation rate results in a high probability of rescue (Martin et al., 2013). Furthermore, in our model a high mutation rate implies that mutations occur at very similar times for different species, limiting the competitive advantage of common species that rescue early. Therefore, if the mutation rate is too high, almost all species undergo rescue and very little rare species loss occurs (Figures 3A,B). For very low mutation rates the opposite holds true and very few species undergo rescue (Figures 3E,F). It should be noted that at very low mutation rates, in some cases not even a single species undergoes rescue. So, in other words, a lower mutation rate causes a greater loss of rare species, yet if the mutation rate is too low no rescue occurs and the entire community goes extinct.

The influence of the mutant birth rate (b_0,mut) on the CWR process (Figure 4) is not as straightforward. Based on standard models of evolutionary rescue, increasing the mutant birth rate should increase the fixation probability of the mutant and thereby increase the probability of rescue. Furthermore, increasing the mutant birth rate should also increase the competitive advantage of those species that rescue early. However, contrary to our expectations, we observed that an increase in the mutant birth rate does not cause an increase in the loss of rare species. Instead, an increase in the mutant birth rate only seems to affect the speed of the CWR process. This is in part due to the fact that an increase in the mutant birth rate also increases the overall carrying capacity of the community. This increase could offset the competitive advantage of the species that rescue early. Because they grow faster, the equilibrium community size is also larger. However, this increase in the community size does not influence the fixation probability of the mutant as derived in classical models of evolutionary rescue. Therefore, the fact that increasing the mutant birth rate does not increase the loss of rare species indicates that competition between early and late rescuing species is the more dominant mechanism responsible for the loss of rare species. This emphasizes the added value of our current modeling approach for understanding evolutionary rescue in a multi-species context.

We also created a different model based on the CWR model where we allowed the residents to have a positive growth rate (b_0,res > d). Relaxing this assumption implies that this model does not reflect a strict evolutionary rescue scenario, as this requires a decaying resident population. This model represents a community-wide selective sweep, during which residents with a positive growth rate are replaced by mutants with an even higher growth rate. When comparing this selective sweep model (Figures 5A,B) to the neutral SN and VBN model it is evident that the community-wide selective sweep causes a rapid loss of rare species when compared to ecological drift. However, the rate of rare species loss is lower than in the CWR model. Hence, one might conclude that community-wide adaptation in general leads to a loss of rare species, implying that our findings from the CWR model are more generally applicable. Furthermore, as there is no evolutionary rescue process in our selective sweep model, the only mechanism responsible is the competition between species that have found the high fitness mutant and those that have not. Hence the fact that competition alone is enough to cause the rapid rare species loss in the selective sweep model also indicates that competition is a more dominant mechanism of rare species loss in the CWR model.

As emphasized before, our CWR model assumes a simple model of evolutionary rescue. Most notably, rescue requires only a single mutation step, with a fixed positive fitness effect. For some situations these assumptions should provide a reasonable approximation. For example, the evolution of resistance to certain antibiotics requires only a single or very few mutations. In addition, the mechanisms underlying resistance can be quite similar across different species (Hooper and Jacoby, 2015). However, obviously these simple assumptions do not hold under all biological circumstances. So how would a more complex assumptions regarding mutation affect the outcome of our CWR model? Allowing multiple mutational steps of varying fitness effects would serve to make the competition during the rescue process more asymmetrical. Therefore, this would be expected to cause an even greater loss of rare species compared to our current CWR model.

The CWR model presented here assumes that all species are (initially) equal, differing only in their initial abundances, an assumption inspired by the neutral theory of biodiversity. Evidently this assumption is unlikely to strictly hold in natural communities, yet it allows us to create a relatively simple model. Furthermore, our model does not consider immigration and speciation. Future CWR models could include mutation probabilities, birth probabilities, and death probabilities that differ across species, and include migration and speciation. It will be interesting to see whether demographic rescue, by immigration, will counteract or aid evolutionary rescue by mutation.

It is striking that the change in the shape of the RAC produced by the CWR process i.e., one devoid of rare species is a pattern commonly observed by ecologists in “stressed” or disturbed communities (Bazzaz, 1975; Halloy and Barratt, 2007; Webb and Leighton, 2011). Additionally, antibiotic treatment also seems to cause a similar loss of rare species in the microbiome of patients, which persists long after the treatment (Sommer and Dantas, 2011). Interestingly, a study of benthic foraminifera during the Paleocene–Eocene thermal maximum by Webb et al. (2009) showed a decrease in richness, an increase in kurtosis, and a decrease in evenness during the Paleocene–Eocene thermal maximum, i.e., a change in the shape of the RAC that would also be consistent with a CWR scenario.

However, it is important to realize that there are countless other ecological explanations that may account for the loss of rare species in stressed environments. For example, rare species tend to be more specialized and are hence more sensitive to disturbance (Davies et al., 2004). Or the loss of a single keystone species can in turn lead to the loss of many rare species that may depend on it (Rapport et al., 1985). Thus, if rapid loss of rare species is observed, that is much faster than would be expected due to ecological drift, this does not per se imply an underlying CWR process.

However, this does not mean that CWR is a hypothetical process with little relevance, to real ecological communities. Experimentalists are examining evolutionary rescue in a community context. The examples include microbiomes adapting to antibiotic treatment (Roodgar et al., 2019); soil microbial communities adapting to herbicides (Low-Décarie et al., 2015) and lacustrine plankton communities adapting to acidification (Bell et al., 2019). There are many more situations in which CWR could be considered as a potential mechanism for rare species loss, as many ecosystems face irreversible human induced environmental change on a community-wide level (Vitousek et al., 1997).

All in all, the current CWR model represents an initial exploration of CWR and could be considered as a baseline model regarding the effect of community-wide evolutionary rescue on species abundances. Yet, this simple model provides a clear testable prediction regarding the effect of CWR on species abundances: Community-Wide Rescue causes a very rapid loss of rare species.

Data Availability Statement

The simulation code presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/DeadParrot69/CWERNI.

Author Contributions

TE was primarily responsible for the conception of the idea, programming, simulation, analysis, and writing of this manuscript. KB contributed to the development of the ideas and provided extensive input regarding the writing of the manuscript. RE contributed to the development of the ideas, proposed modeling strategies, suggested analyses and provided extensive input regarding the writing of the manuscript.

Funding

TE wishes to thank the Erasmus Mundus Programme in Evolutonary biology (MEME) for the opportunities and funding provided. RE thanks the Netherlands Organisation for Scientfic Research (NWO) for funding through a VICI grant. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement No. 789240).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are greatly indebted to Pedro Neves, Inès Daras, and Richel Bilderbeek for their valuable comments on the model and the manuscript. Furthermore, Rixt Heerschop is thanked for a proofreading and her help in preparing the figures. F. J. Weissing is thanked for his continous support. Guillaume Martin and Yoann Anciaux are thanked for their valuable lessons and discussions regarding evolutionary rescue theory. In addition, we thank S. Panish-Inq. for her unexpected comments. We would also like to thank Mika van Eldijk for providing computational resources when they were most needed. Furthermore, we would like to thank François Massol and five reviewers for their valuable comments which greatly improved the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2020.552268/full#supplementary-material

References

Alexander, H. K., Martin, G., Martin, O. Y., and Bonhoeffer, S. (2014). Evolutionary rescue: linking theory for conservation and medicine. Evol. Appl. 7, 1161–1179. doi: 10.1111/eva.12221

PubMed Abstract | CrossRef Full Text | Google Scholar

Alonso, D., Etienne, R. S., and McKane, A. J. (2006). The merits of neutral theory. Trends Ecol. Evol. 21, 451–457. doi: 10.1016/j.tree.2006.03.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Arumugam, M., Raes, J., Pelletier, E., Le Paslier, D., Yamada, T., Mende, D. R., et al. (2011). Enterotypes of the human gut microbiome. Nature 473, 174–180.

Google Scholar

Bazzaz, F. A. (1975). Plant species diversity in old-field successional ecosystems in Southern Illinois. Ecology 56, 485–488. doi: 10.2307/1934981

CrossRef Full Text | Google Scholar

Bell, G. (2017). Evolutionary rescue. Annu. Rev. Ecol. Evol. Syst. 48, 605–627.

Google Scholar

Bell, G., Fugère, V., Barrett, R., Beisner, B., Cristescu, M., Fussmann, G., et al. (2019). Trophic structure modulates community rescue following acidification. Proc. R. Soc. B 286:20190856. doi: 10.1098/rspb.2019.0856

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, G., and Gonzalez, A. (2009). Evolutionary rescue can prevent extinction following environmental change. Ecol. Lett. 12, 942–948. doi: 10.1111/j.1461-0248.2009.01350.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, G., and Gonzalez, A. (2011). Adaptation and evolutionary Rescue in metapopulations experiencing environmental deterioration. Science 1327, 1327–1331. doi: 10.1126/science.1203105

PubMed Abstract | CrossRef Full Text | Google Scholar

Chave, J., Muller-Landau, H. C., and Levin, S. A. (2002). Comparing classical community models: theoretical consequences for patterns of diversity. Am. Nat. 159, 1–23. doi: 10.2307/3079311

CrossRef Full Text | Google Scholar

Cho, I., and Blaser, M. J. (2012). The human microbiome: at the interface of health and disease. Nat. Rev. Genet. 13, 260–270. doi: 10.1038/nrg3182

PubMed Abstract | CrossRef Full Text | Google Scholar

Cortez, M. H., and Yamamichi, M. (2019). How (co) evolution alters predator responses to increased mortality: extinction thresholds and hydra effects. Ecology 100:e02789.

Google Scholar

Davies, K. F., Margules, C. R., and Lawrence, J. F. (2004). A synergistic effect puts rare, specialized species at greater risk of extinction. Ecology 85, 265–271. doi: 10.1890/03-0110

CrossRef Full Text | Google Scholar

De Mazancourt, C., Johnson, E., and Barraclough, T. G. (2008). Biodiversity inhibits species’ evolutionary responses to changing environments. Ecol. Lett. 11, 380–388. doi: 10.1111/j.1461-0248.2008.01152.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Etienne, R. S. (2005). A new sampling formula for neutral biodiversity. Ecol. Lett. 8, 253–260. doi: 10.1111/j.1461-0248.2004.00717.x

CrossRef Full Text | Google Scholar

Etienne, R. S., and Olff, H. (2004). A novel genealogical approach to neutral biodiversity theory. Ecol. Lett. 7, 170–175. doi: 10.1111/j.1461-0248.2004.00572.x

CrossRef Full Text | Google Scholar

Gillespie, D. T. (1976). A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 22, 403–434. doi: 10.1016/0021-9991(76)90041-3

CrossRef Full Text | Google Scholar

Gomulkiewicz, R., and Holt, R. D. (1995). When does evolution by natural selection prevent extinction? Evolution 49, 201–207. doi: 10.2307/2410305

CrossRef Full Text | Google Scholar

Gonzalez, A., Ronce, O., Ferriere, R., and Hochberg, M. E. (2012). Evolutionary rescue: an emerging focus at the intersection between ecology and evolution. Philos. Trans. R. Soc. B 368:20120404. doi: 10.1098/rstb.2012.0404

PubMed Abstract | CrossRef Full Text | Google Scholar

Haegeman, B., and Etienne, R. S. (2008). Relaxing the zero-sum assumption in neutral biodiversity theory. J. Theor. Biol. 252, 288–294. doi: 10.1016/j.jtbi.2008.01.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Haegeman, B., and Etienne, R. S. (2017). A general sampling formula for community structure data. Methods Ecol. Evol. 8, 1506–1519. doi: 10.1111/2041-210x.12807

CrossRef Full Text | Google Scholar

Halloy, S. R. P., and Barratt, B. I. P. (2007). Patterns of abundance and morphology as indicators of ecosystem status: a meta-analysis. Ecol. Complexity 4, 128–147. doi: 10.1016/j.ecocom.2007.04.002

CrossRef Full Text | Google Scholar

Hoffmann, A. A., and Sgrò, C. M. (2011). Climate change and evolutionary adaptation. Nature 470, 479–485.

Google Scholar

Holt, R. D. (1990). The microevolutionary consequences of climate change. Trends Ecol. Evol. 5, 311–315. doi: 10.1016/0169-5347(90)90088-u

CrossRef Full Text | Google Scholar

Hooper, D. C., and Jacoby, G. A. (2015). Mechanisms of drug resistance: quinolone resistance. Ann. N.Y. Acad. Sci. 1354, 12–31. doi: 10.1111/nyas.12830

PubMed Abstract | CrossRef Full Text | Google Scholar

Hubbell, S. P. (1997). A unified theory of biogeography and relative species abundance and its application to tropical rain forests and coral reefs. Coral Reefs 16, S9–S21.

Google Scholar

IPCC (2014). Climate Change (2014): Synthesis Report. Geneva: IPCC.

Google Scholar

Jabot, F. (2010). A stochastic dispersal-limited trait-based model of community dynamics. J. Theor. Biol. 262, 650–661. doi: 10.1016/j.jtbi.2009.11.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Lasky, J. R. (2019). Eco-evolutionary community turnover following environmental change. Evol. Appl. 12, 1434–1448. doi: 10.1111/eva.12776

PubMed Abstract | CrossRef Full Text | Google Scholar

Low-Décarie, E., Kolber, M., Homme, P., Lofano, A., Dumbrell, A., Gonzalez, A., et al. (2015). Community rescue in experimental metacommunities. Proc. Natl. Acad. Sci. U.S.A. 112, 14307–14312. doi: 10.1073/pnas.1513125112

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, G., Aguilée, R., Ramsayer, J., Kaltz, O., and Ronce, O. (2013). The probability of evolutionary rescue: towards a quantitative comparison between theory and evolution experiments. Philos. Trans. R. Soc. B 368:20120088. doi: 10.1098/rstb.2012.0088

PubMed Abstract | CrossRef Full Text | Google Scholar

McGill, B. J., Etienne, R. S., Gray, J. S., Alonso, D., Anderson, M. J., Benecha, H. K., et al. (2007). Species abundance distributions: moving beyond single prediction theories to integration within an ecological framework. Ecol. Lett. 10, 995–1015. doi: 10.1111/j.1461-0248.2007.01094.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Northfield, T. D., and Ives, A. R. (2013). Coevolution and the effects of climate change on interacting species. PLoS Biol. 11:e1001685. doi: 10.1371/journal.pbio.1001685

PubMed Abstract | CrossRef Full Text | Google Scholar

Orr, H. A., and Unckless, R. L. (2008). Population extinction and the genetics of adaptation. Am. Nat. 172, 160–169. doi: 10.1086/589460

PubMed Abstract | CrossRef Full Text | Google Scholar

Orr, H. A., and Unckless, R. L. (2014). The population genetics of evolutionary rescue. PLoS Genet. 10:e1004551. doi: 10.1371/journal.pgen.1004551

PubMed Abstract | CrossRef Full Text | Google Scholar

Osmond, M. M., and De Mazancourt, C. (2013). How competition affects evolutionary rescue. Philos. Trans. R. Soc. B 368:20120085. doi: 10.1098/rstb.2012.0085

PubMed Abstract | CrossRef Full Text | Google Scholar

R Core Team (2014). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.

Google Scholar

Rapport, D. J., Regier, H. A., and Hutchinson, T. C. (1985). Ecosystem behavior under stress. Am. Nat. 125, 617–640. doi: 10.1086/284368

CrossRef Full Text | Google Scholar

Roodgar, M., Good, B. H., Garud, N. R., Martis, S., Avula, M., Zhou, W., et al. (2019). Longitudinal linked read sequencing reveals ecological and evolutionary responses of a human gut microbiome during antibiotic treatment. bioRxiv [Preprint]. doi: 10.1101/2019.12.21.886093

CrossRef Full Text | Google Scholar

Rosindell, J., Hubbell, S. P., and Etienne, R. S. (2011). The unified neutral theory of biodiversity and biogeography at age ten. Trends Ecol. Evol. 26, 340–348. doi: 10.1016/j.tree.2011.03.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Scheffer, M., van Nes, E. H., and Vergnon, R. (2018). Toward a unifying theory of biodiversity. Proc. Natl. Acad. Sci. U.S.A. 115, 639–641. doi: 10.1073/pnas.1721114115

PubMed Abstract | CrossRef Full Text | Google Scholar

Sommer, M. O. A., and Dantas, G. (2011). Antibiotics and the resistant microbiome. Curr. Opin. Microbiol. 14, 556–563. doi: 10.1016/j.mib.2011.07.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Vitousek, P. M., Mooney, H. A., Lubchenco, J., and Melillo, J. M. (1997). Human domination of earth’s ecosystems. Science 277, 494–499. doi: 10.1126/science.277.5325.494

CrossRef Full Text | Google Scholar

Webb, A. E., Leighton, L., Schellenberg, S., Landau, E., and Thomas, E. (2009). Impact of the Paleocene-Eocene thermal maximum on deep-ocean microbenthic community structure: using rank-abundance curves to quantify paleoecological response. Geology 37, 783–786. doi: 10.1130/g30074a.1

CrossRef Full Text | Google Scholar

Webb, A. E., and Leighton, L. R. (2011). “Exploring the ecological dynamics of extinciton,” in Quantifying the Evolution of Early Life, eds M. Laflamme and S. Q. Dornbos (Cham: Springer), 185–220.

Google Scholar

Wennekes, P. L., Rosindell, J., and Etienne, R. S. (2012). The neutral—niche debate: a philosophical perspective. Acta Biotheor. 60, 257–271. doi: 10.1007/s10441-012-9144-6

PubMed Abstract | CrossRef Full Text | Google Scholar