Avoiding Conceptual and Mathematical Pitfalls When Developing Indices to Inform Conservation

Introduction

Ecologists are increasingly turning to integrative indices in order to distill the many types of threats facing ecosystems into a simple score that can be used to prioritize conservation objectives and facilitate restoration efforts (e.g., Isaac et al., 2007; Halpern et al., 2012; Pimiento et al., 2020). Unfortunately, these indices have often been developed in an ad-hoc manner with little to no appreciation for the myriad conceptual and mathematical issues that can arise when forcing multiple variables into a single numerical score. Here, using a recent paper by Pimiento et al. (2020) as a case study, we demonstrate the critical problems that can emerge when creating an index that integrates different types of information from multiple distinct sources. We then develop better alternatives and describe how to avoid common pitfalls when creating an index.

The FUSE Index as a Case Study

Pimiento et al. (2020) created the FUSE index by combining information about a species' (i) specialization (FSp) and uniqueness (FUn) based on its functional traits and (ii) extinction risk inferred from its IUCN Red List status (GE) in order to inform conservation efforts. Although no explanation or derivation was presented for the FUSE index, it appears to have emerged as an attempt to extend the EDGE index (Isaac et al., 2007), which is defined as EDGE = log(1 + ED) + GE × log(2). The EDGE index thus sums the (natural) logarithm of a species' evolutionary distinctiveness score ED and its extinction risk as captured by GE, a discrete numerical variable between 0 and 4 that represents its IUCN Red List status. GE is further multiplied by the natural logarithm of 2 so that each incremental change in GE represents a doubling of extinction risk.

To adapt this index for their purposes, Pimiento et al. first rescaled species' specialization (FSp) and uniqueness (FUn) scores by dividing by their respective maximum values in order to ensure that they both varied between 0 and 1. They then multiplied these rescaled FSp and FUn scores by 4 in order to force them to have the same range as GE (0–4). Finally, they formed the FUSE index by summing (i) the log of the product of GE and FSp with (ii) the log of the product of GE and FUn:

$\text{FUSE}=log\left(1+4\frac{\text{FSp}}{\text{max}(\text{FSp})}\text{GE}\right)+log\left(1+4\frac{\text{FUn}}{\text{max}(\text{FUn})}\text{GE}\right)$

Although the steps involved in creating FUSE might seem reasonable when described in isolation, their combined effects produce a flawed index that is neither mathematically coherent nor parsimonious. To understand why, one merely needs to make use of the elementary mathematical identity by which the sum of logarithmic terms can be rewritten as the logarithm of their product (Martin-Gay and Greene, 2013). Using this identity, one can rewrite the FUSE index as:

$\begin{array}{l}\text{FUSE}=log(1+4\frac{\text{FSp}}{\text{max}(\text{FSp})}\text{GE}+4\frac{\text{FUn}}{\text{max}(\text{FUn})}\text{GE}\\ +16\frac{\text{FSp}}{\text{max}(\text{FSp})}\frac{\text{FUn}}{\text{max}(\text{FUn})}\text{G}{\text{E}}^2)\end{array}$

Expressing the FUSE index in this way exposes its many critical issues which, collectively, make it completely inscrutable. The most generous interpretation of the FUSE index that we can offer is that it represents the weighted sum of different powers of GE. Specifically, the rescaled FSp and FUn scores serve as additive weights for GE and the product of the rescaled FSp and FUn scores serves as a weight for GE². Hence, the FUSE index represents the sum of the “additive” and “multiplicative” effects of the rescaled FSp and FUn scores on different powers of GE (i.e., it contains a mixture of linear and quadratic terms of GE). This is clearly mathematically incoherent and ecologically unjustified. The FUSE index would be equally incoherent and nonsensical if it were interpreted as the sum of the rescaled FSp and FUn scores weighted by GE plus their product weighted by GE². Overall, these issues with FUSE emerged because of the incorrect and unnecessary use of the logarithmic function, adding to the growing body of evidence demonstrating that logarithms continue to baffle some ecologists (Menge et al., 2018).

Reverse Engineering FUSE and Developing Better Alternatives

Although no explanation was provided for combining FSp, FUn and GE in this incoherent manner, two potential motivations immediately come to mind. If the authors meant for the FUSE index to be a weighted sum of GE with weights FSp and FUn, but needed to take the logarithms of the terms for some reason, they could have done so as follows (Figure 1):

$\text{FUS}{\text{E}}^{\prime }=log\left(1+\frac{\text{FSp}}{\text{max}(\text{FSp})}\text{GE}+\frac{\text{FUn}}{\text{max}(\text{FUn})}\text{GE}\right)$

This alternative index FUSE′ is both more coherent and parsimonious than FUSE, as it represents (the logarithm of) the weighted sum of GE, with rescaled versions of FSp and FUn serving as weights. Unlike FUSE, FUSE′ does not combine the “additive” and “multiplicative” effects of FSp and FUn on different powers of GE. Additionally, because FSp and FUn serve as weights, ensuring that their range is identical by dividing by their respective maximum values is sufficient. They need not be multiplied by 4 to ensure that their range matches that of GE, as was unnecessarily done in FUSE. Similarly, there would be no need to multiply by 4 if FUSE′ were interpreted as the weighted sum of the rescaled FSp and FUn scores, with GE serving as the weight.

FIGURE 1

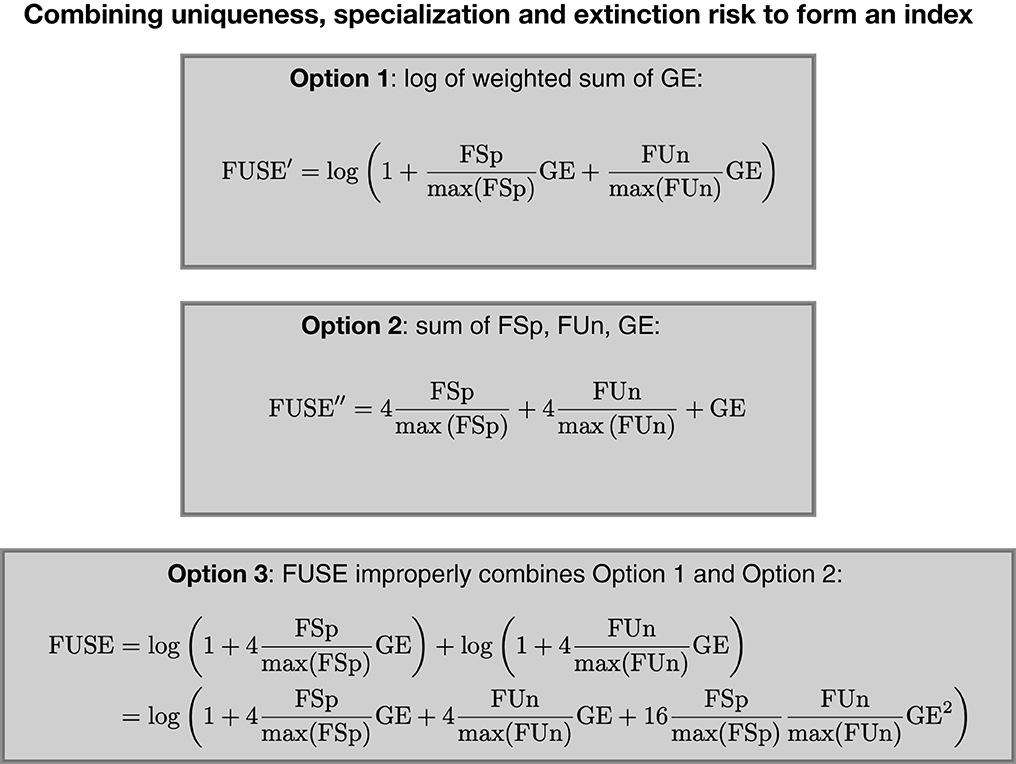
Figure 1. Combining uniqueness, specialization, and extinction risk to form an index. The FUSE index represents an improper combination of two more coherent and parsimoniuous indices based on (i) the log of the weighted sum of GE and (ii) the sum of FSp, FUn and GE.

If the authors intended for FUSE to represent the “additive” effects of FSp, FUn and GE they could have done so by using a much simpler and more coherent formula (Figure 1):

$\text{FUS}{\text{E}}^{″}=4\frac{\text{FSp}}{\text{max}(\text{FSp})}+4\frac{\text{FUn}}{\text{max}(\text{FUn})}+\text{GE}$

Here, unlike for FUSE, the rescaled versions of FSp and FUn must be multiplied by 4 in order to ensure that they have the same potential influence as GE on the FUSE″ index. The FUSE index thus appears to have arisen as an improper combination of these two more parsimonious and mathematically coherent indices. Because these different formulations were motivated by distinct goals, their combination in FUSE made the index incomprehensible.

The FUSE index not only fails to produce meaningful quantitative measures, but it cannot even provide useful qualitative information in the form of a properly ordered ranking of species based on extinction risk. This is because FUSE's mathematically incoherent formula prevents it from producing a ranking of species that is consistent with that of other coherent and more parsimonious formulas such as FUSE′. This can be demonstrated mathematically. If S is the set of species we wish to rank in terms of species priority or risk, then for a species s_i ∈ S we will let F_i = f(s_i) represent the FUSE value of species s_i, while $F_i^{\prime }=g(s_i)$ will represent the same species' FUSE′ value. Given that f:S → ℝ and g:S → ℝ, where ℝ is the set of real numbers, both f and g can be used to induce a (weak) linear order on the set of species S, such that the ranking s_i ≤ s_j will hold based on the “≤” relation among the corresponding elements in ℝ.

What we wish to show here is that for two arbitrary species, s₁ and s₂, it is possible to order species such that s₁ ≤ s₂ based on F₁ ≤ F₂, while at the same time obtaining the opposite order s₁ ≥ s₂ based on $F_1^{\prime }\ge F_2^{\prime }$. This will occur if both F₁ ≤ F₂ and $F_1^{\prime }\ge F_2^{\prime }$ hold simultaneously, resulting in two different species ordering or priority rankings, s₁ ≤ s₂ and s₁ ≥ s₂, respectively.

Given a species s_i, we will for simplicity use x_i as the discrete variable (between 0 and 4) that indicates species risk (i.e., GE above), and a_i and b_i as the aggregate or weighted parameters that quantify the functional uniqueness and functional specialization, respectively. Using the slightly more parsimonious FUSE′ formula to establish the condition $F_1^{\prime }\ge F_2^{\prime }$ we get

$\begin{array}{ll}0\ge F_2^{\prime }-F_1^{\prime }& (1)\end{array}$

$\begin{array}{ll}0\ge log(1+a_2{x}_2+b_2{x}_2)-log(1+a_1{x}_1+b_1{x}_1)& (2)\end{array}$

$\begin{array}{ll}0\ge (a_2{x}_2-a_1{x}_1)+(b_2{x}_2-b_1{x}_1).& (3)\end{array}$

At the same time using the FUSE formula to establish the condition for F₁ ≤ F₂ will yield

$\begin{array}{ll}0\le F_2-F_1& (4)\end{array}$

$\begin{array}{l}0\le log(1+a_2{x}_2+b_2{x}_2+a_2{b}_2{x}_2^2)\\ -log(1+a_1{x}_1+b_1{x}_1+a_1{b}_1{x}_1^2)& (5)\end{array}$

$\begin{array}{ll}0\le (a_2{x}_2-a_1{x}_1)+(b_2{x}_2-b_1{x}_1)+(a_2{b}_2{x}_2^2-a_1{b}_1{x}_1^2).& (6)\end{array}$

To simplify these two results, we will use μ_sp and μ_u to represent the factor by which both the effects of specialization and uniqueness for s₂ are greater than that of s₁, respectively, while λ will be the factor by which the extinction risk of s₂ is greater than that of s₁ (i.e., λ = x₂/x₁); and finally t will represent the scale of species 1's specialization value relative to its uniqueness value (t = b₁/a₁). We will also assume a₁ > 0, b₁ > 0 and x₁ > 0. This gives the following two conditions which must hold:

$\begin{array}{ll}{\mu }_u+{\mu }_{sp}t\le \frac{1+t}{\lambda }& (7)\end{array}$

$\begin{array}{ll}{\mu }_u+{\mu }_{sp}t\ge \frac{1+t}{\lambda }-{\displaystyle \underset{\text{due to the summation of }log\text{ terms in }\text{FUSE}}{{\displaystyle \underbrace{({\mu }_{sp}{\mu }_u{\lambda }^2-1)\frac{t{a}_1{x}_1}{\lambda }}}}}& (8)\end{array}$

Recall here that a₁ is an aggregate parameter representing the total effect of species s₁'s uniqueness, and x₁ is the IUCN status or GE value for species s₁. Condition (7) is derived from $F_1^{\prime }\ge F_2^{\prime }$, while (8) is the direct consequence of F₁ ≤ F₂. Both Condition (7) and Condition (8) must hold simultaneously for two different ordered relationships to exist. For this to be the case, the second term on the RHS of Condition (8) must be large enough that when subtracted from the first term on the RHS it will reverse the inequality sign in Condition (7). It is clear from visual inspection that both conditions can easily hold for a range of parameter values. The second term on the RHS of(8), which allows the order of species ranks to be reversed, is the unanticipated consequence of Pimiento et al. (2020) having arbitrarily, and in a mathematically unjustified manner, summed two logarithmic terms to obtain the FUSE formula. Overall, these mathematical conditions provide a general and dataset-agnostic proof of FUSE's critical flaws.

Discussion

Although our case study focused on FUSE, many of the issues that we described are universal and could thus potentially affect any integrative index. Unfortunately, this includes several indices that were developed for conservation or environmental planning purposes because they failed to ensure that the numerous criteria they combined were commensurable with each other, that is whether the different criteria being used to rank entities could be evaluated on the same ordinal scale. Even worse, the criteria included in some of these indices are often not even tangible because they do not allow entities to be meaningfully arranged on any (let alone the same) ordinal scale (see Chapters 4 and 7 in Sarkar, 2005, for a brief discussion). Although both tangibility and commensurability can be assumed to hold when all the relevant criteria can be measured on the same quantitative scale (e.g., market prices on a monetary scale), this is rarely the case for conservation and environmental indices.

For example, recent indices developed to quantify ocean health (Halpern et al., 2012) and beach quality (Ariza et al., 2010) treat their fundamentally different criteria or variables such as water quality, noise pollution and “sense of place” as comparable and exchangeable. This is deeply problematic because there is no objective way of determining whether a unit increase in “sense of place” can compensate for a unit decrease in water quality. Although surveys can be conducted to determine how to weight these different variables, the weightings will be subjective and vary over time—that is, for all practical purposes they are not even tangible. For instance, on a relatively pristine beach, the surveys are likely to ascribe a large weight to noise pollution and a small weight to water quality. However, if water quality on that same beach decreases markedly following the construction of a new sewage outfall nearby, subsequent surveys are likely to result in an inflation of the weight associated with water quality and a deflation of the weight associated with noise pollution. The inherent subjectivity of the weightings used to build integrative indices thus demonstrates that these scores do not quantify anything real or concrete in nature. Rather, indices are artificial constructs that can mislead, especially when they are built using incomparable and incommensurable criteria.

The FUSE index is particularly bad because it combines incomparable and incommensurable variables in a mathematically incoherent and non-parsimonious manner. We caution that although we developed and presented better alternatives to the FUSE index, we are in no way advocating for their use in conservation. Indeed, despite the fact that FUSE′ and FUSE″ address the most egregious mathematical issues with FUSE, they are still not justifiable because they forcibly combine variables that are fundamentally different and represent completely distinct types of rarity (i.e., rarity expressed in terms of low population size for GE vs. rarity expressed in terms of uniqueness and specialization in functional trait space for FUn and FSp).

For instance, the relationship between extinction risk and the IUCN Red List status embodied by GE is largely arbitrary, with FUSE assuming a linear increase and EDGE—the index that inspired FUSE—assuming a nonlinear increase (doubling). Such differences in assumptions can lead to very different scores and rankings of species vulnerability (Mooers et al., 2008). Additionally, the commingling of distinct types of rarity could lead to situations where species that are rare in functional trait space (i.e., very specialized with high FSp and very unique with high FUn) but not rare or endangered with respect to population size (e.g., GE = 1) receive a high FUSE score and are thus incorrectly designated as high-priority targets for conservation. Hence, there is simply no mathematical or ecological justification for mashing these fundamentally different variables into a single index.

Even when they make the same assumptions about how to quantify extinction risk and the variables they combine are commensurable, indices like EDGE, FUSE, and their variants can still produce very different species rankings and conservation priorities. This is because there are a quasi-infinite number of formulations that can be used to combine multiple variables into a single index in order to ascribe a metric structure to a given set of species. Because the metric space defined by formulas like FUSE allows one to explicitly assign numerical scores and thus quantify the purported differences between species, these values must be mathematically justified and analytically meaningful. However, this is impossible when multiple variables are arbitrarily forced into a single, non-parsimonious index without a clear rationale.

A much better solution would be to use a hierarchical approach in order to prioritize conservation efforts by first sorting species based on their degree of endangerment (i.e., using GE alone). Species characterized by the same degree of endangerment could then be ranked based on their specialization and uniqueness, as determined by their functional traits. This kind of hierarchical approach would avoid combining incommensurable measures of rarity into a common index and could thus never incorrectly identify species that are not endangered but have high specialization and uniqueness as conservation priorities. Similar approaches have been proposed in the past to “synchronize” distinct measures and criteria for prioritizing conservation efforts without shoehorning distinct variables into a single index (for example, see the use of multiple criterion synchronization in Sarkar and Garson, 2004).

FUSE clearly demonstrates that we are very much in the “Wild West” phase of index development, with ad-hoc numerical schemes being used to invent indices that are neither coherent nor parsimonious. It is important to note that these critical flaws should not be brushed aside simply because FUSE is able to produce numerical results that happen to be similar to those generated by more sensible formulas for any particular dataset. Doing so would be analogous to arguing for the non-parsimonious and now discredited geocentric model of the solar system because it produces predictions of planetary movement that are similar to those generated by the heliocentric model, even if the former requires unnecessary complications like epicycles. Overall, even when indices cannot be derived from first principles, they must still adhere to basic scientific tenets such as coherence and parsimony. Indices such as FUSE that fail on both accounts should thus be avoided in conservation biology.

Author Contributions

TG and PP conceived the project, developed the arguments, and co-wrote the paper.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge support from the National Science Foundation (OCE-1635989, OCE-1735743, and CCF-1442728).

References

Ariza, E., Jimenez, J. A., Sarda, R., Villares, M., Pinto, J., Fraguell, R., et al. (2010). Proposal for an integral quality index for urban and urbanized beaches. Environ. Manage. 45, 998–1013. doi: 10.1007/s00267-010-9472-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Halpern, B. S., Longo, C., Hardy, D., McLeod, K. L., Samhouri, J. F., Katona, S. K., et al. (2012). An index to assess the health and benefits of the global ocean. Nature 488, 615–620. doi: 10.1038/nature11397

PubMed Abstract | CrossRef Full Text | Google Scholar

Isaac, N. J. B., Turvey, S. T., Collen, B., Waterman, C., and Baillie, J. E. M. (2007). Mammals on the EDGE: conservation priorities based on threat and phylogeny. PLoS ONE 2:e296. doi: 10.1371/journal.pone.0000296

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin-Gay, E., and Greene, M. (2013). Intermediate Algebra: A Graphing Approach, 5th Edn. Boston, MA: Pearson.

Menge, D. N. L., MacPherson, A. C., Bytnerowicz, T. A., Quebbeman, A. W., Schwartz, N. B., Taylor, B. N., et al. (2018). Logarithmic scales in ecological data presentation may cause misinterpretation. Nat. Ecol. Evol. 2, 1393–1402. doi: 10.1038/s41559-018-0610-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Mooers, A. O., Faith, D. P., and Maddison, W. P. (2008). Converting endangered species categories to probabilities of extinction for phylogenetic conservation prioritization. PLoS ONE 3:e3700. doi: 10.1371/journal.pone.0003700

PubMed Abstract | CrossRef Full Text | Google Scholar

Pimiento, C., Leprieur, F., Silvestro, D., Lefcheck, J. S., Albouy, C., Rasher, D. B., et al. (2020). Functional diversity of marine megafauna in the Anthropocene. Sci. Adv. 6:eaay7650. doi: 10.1126/sciadv.aay7650

PubMed Abstract | CrossRef Full Text | Google Scholar

Sarkar, S. (2005). Biodiversity and Environmental Philosophy: An Introduction. Cambridge Studies in Philosophy and Biology. New York, NY: Cambridge University Press.

Google Scholar

Sarkar, S., and Garson, J. (2004). Multiple criterion synchronisation for conservation area network design: the use of non-dominated alternative sets. Conserv. Soc. 2, 433–488.

Google Scholar