Effect of the Reproduction Method in an Artificial Selection Experiment at the Community Level

Selection at the group level is proposed to be an evolutionary process occurring in the context of multilevel selection in natura. In artificial selection experiments, selecting at the community level can allow to find multispecies assemblages that are more efficient than a single species at solving a given problem. In such procedures, the main difficulty is to find a balance between variation and heritability, which are both essential for selection to act. The aim of our study was to determine if the way of creating offspring units of selection from parental units, called “reproduction method,” could influence artificial selection efficiency through a differential in the variation/heritability balance. Selecting microbial communities depending on their biomass production and propagating them either one by one or in a mix of three communities, we showed that the effect of the reproduction method was not maintained over time with a loss of the effect of artificial selection on community phenotype at certain cycles and a very low heritability. However, mixing parental communities was more efficient at increasing biomass production than using a single parental community (+5% of biomass). We discussed the role of differences in community richness and structure in explaining these results.

Introduction

From a theoretical standpoint, the three conditions stated by Lewontin (1970) for selection to occur, i.e., (i) the existence of phenotypic variation, (ii) the existence of a link between this variation and a differential in fitness, (iii) the heritability of the variation, can be completed at the group level. But group selection and its role as an evolutionary process in natura have been controversial especially because they are difficult to demonstrate (Okasha, 2006; West et al., 2007; Leigh, 2010). By contrast, artificial selection at the group level in experimental conditions has been proven effective in changing a phenotypic trait of the group but also in changing the fitness of the individuals composing this group (Goodnight and Stevens, 1997).

The first experimental results of group selection in beetle populations of Tribolium castaneum and in communities of T. castaneum and T. confusum, gave a stronger response to selection than predicted by modeling (Wade, 1978; Goodnight and Stevens, 1997). Indeed group selection may have an effect on variance components that are not involved at lower levels (e.g., individuals, genes). For example, if the considered selection unit is a population, genetically-based among-individuals interactions can be selected. If we consider higher levels such as communities, selection at higher levels than the population can occur through genetically-based between-species interactions, such as syntrophy (obligately mutualistic metabolism; Morris et al., 2013).

Artificial selection at the group level is of particular interest because it allows the selection of combinations of organisms, and hence indirectly combinations of genes, that would not have been discovered otherwise. Many applications could be considered, especially on microbial ecosystems for improving the degradation of toxic compounds, such as 3-chloroaniline (Swenson et al., 2000a), for which syntrophic interactions between species often take place. Other experiments of community level artificial selection have proven to be efficient for example at reducing CO₂ emissions (Blouin et al., 2015) or modifying the flowering date of Arabidopsis thaliana (Panke-Buisse et al., 2015). However, the long-term stability of the selected communities has not been investigated.

Usually in an artificial selection procedure, three successive steps take place: the identification of the units of interest according to the targeted phenotype, the selection of these units, and the creation of a new population of units from the selected ones. Then many questions arise about the efficiency of artificial selection as pointed out by Xie et al. (2019) when modeling artificial selection in a two-species community. Few of them have been addressed experimentally. Swenson et al. (2000b) investigated the effect of the size of the sample used to create a new population from the selected parents, and more recently, Wright et al. (2019) discussed the effect of the incubation time on the expression of the targeted phenotype. In this study, we investigated the effect of the reproduction method, which has been tackled in a model (Williams and Lenton, 2007), but not in experiments. By analogy with the artificial selection process on sexually reproducing organisms, the “reproduction method” refers here to the way of creating new experimental units from parental units. Because we work with microbial communities, we can consider two possibilities: (i) offspring units all derive from a unique parental unit, or (ii) they derive from the combination of several parental units. These two methods can, respectively be regarded as asexual and sexual reproduction, and are referred to as “propagule method” and “migrant pool method” in the literature (Wade, 1978; Williams and Lenton, 2007; Goodnight, 2011). Depending on the reproduction method, the efficiency of artificial selection (i.e., our ability to reach a targeted phenotype) might be impacted in ways that are difficult to predict.

Indeed, as group selection can act on intra- and interspecific genetically based interactions (Goodnight, 2000), one could expect that the most efficient reproduction method would be the one that best maintains the interactions responsible for the phenotype of interest. In other words, the genes responsible for these interactions must be preserved from one cycle to the other. This refers to the concept of heritability (h²) which is, in the narrow-sense, the proportion of total phenotypic variance related to additive genetic variance (i.e., not due to dominance, epistatic, or environmental variance; Visscher et al., 2008). A higher heritability is expected with the propagule method as offspring units are produced by a unique parental unit whereas the migrant pool method is more likely to disturb the among-individuals or between-species interactions potentially responsible for the community phenotype, thus leading to a decrease in selection efficiency (Williams and Lenton, 2007).

However, as exposed by Penn (2003), artificial selection efficiency depends not only on heritability but also on phenotypic variation and on the balance between both of them. Phenotypic variation between offspring and parental units and within offspring units is supposed to occur mainly through sampling effect and stochastic ecosystem dynamic (e.g., demographic and genetic drift) (Wade, 1978; Penn, 2003). It is expected that mixing several parental units (migrant pool method), thought to be different by the action of the two phenomena aforementioned, maintains a higher inter-, and intragroup diversity over time which could enhance selectable variation by group selection. On the contrary, the propagule method is thought to give rise to an erosion of diversity over time due to the use of a unique parental unit to produce a new offspring population. Thus, a different balance between phenotypic variation and heritability (i.e., different selection efficiency) is expected between the two reproduction methods. Because the effect of these methods could vary according to the target of the selection, i.e., a high, low or stable value of a community phenotype (Williams and Lenton, 2007), this hypothesis was tested in different selection contexts, using microbial communities as experimental units, and biomass production as targeted phenotype.

Materials and Methods

Experimental Selection

The microbial community providing the initial pool of communities selected in this experiment was extracted from a topsoil sample (a lawned area at the INRA centre in Dijon, France). We inoculated 1 g of soil in 10 ml of lysogeny broth (LB) medium diluted 1:5. After 24 h of cultivation (28°C, 130 rpm) and a decantation (30 s, 1 000 rpm), 1 ml of supernatant diluted in 100 ml of LB 1:5 was incubated at 28°C for 48 h (130 rpm) and a second incubation (48 h, 28°C) was conducted in a 96 well-microplate to allow the community to adapt to experimental conditions (200 μl per well). The content of this microplate was pooled and diluted 20 times. It corresponded to the initial material on which the artificial selection was conducted. The experiment ran over 14 cycles. A cycle is defined as the incubation time between two selection events, which occurred through the inoculation of three microplates and their incubation at 28°C for 48 h. The 48 h duration was experimentally determined to select the microbial communities once the stationary phase has been reached to maximize the probability of selecting complex and stable interactions instead of selecting individual traits (e.g., fast growing microorganisms).

Selection treatments were based on the estimation of biomass production by optical density measurements (λ = 595 nm) with a microplate reader (Thermomax, Molecular Devices^®, United States). Hereafter we will use “biomass production” to refer to the estimation of biomass production by optical density measurement. We considered three selection treatments. In two of them, we used directional artificial selection, targeting either an increase (High, H) or a decrease (Low, L) in biomass production. The third treatment corresponded to stabilizing selection, i.e., selection of communities with the closest biomass to the average (Stabilizing, S). In addition, communities were randomly chosen (Random, R) without any consideration of their biomass production as a control to assess the effect of experimental conditions on biomass production.

For each treatment aforementioned, the creation of a new cycle occurred through two different reproduction methods: once the parental communities have been selected, the offspring communities derived either from a single parental community (Propagule method, P) or from the mixing of three parental communities (Migrant pool method, M) (Figure 1). In the first case (P), the parental community was selected among ten, and this procedure was repeated three times (n = 30 per selection treatment, three distinct lines). With the second method (M), three parental communities were selected among 30 (n = 30 per selection treatment, one line).

FIGURE 1

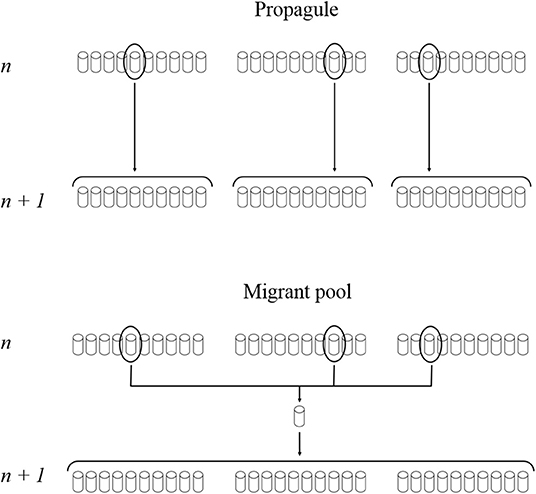
Figure 1. Reproduction methods. Propagule method corresponded to the selection of one parental community among ten at cycle n and the creation of ten new communities from this parental unit at cycle n+1. This protocol was repeated independently three times (n = 30, three distinct lines). Migrant pool method corresponded to the selection of three parental communities among thirty (one among ten, three times, to have a constant selection rate between the two reproduction methods; n = 30, one line). The three parental units were mixed and used to create thirty new communities at cycle n+1. The experiment ran over 14 cycles.

For each new experimental cycle, 120 μl were taken from the well(s) corresponding to the selected community(ies), pooled or not depending on the treatment, and diluted 20 times with LB 1:5 to inoculate the microplates of the next cycle (200 μl per well).

Combining the selection treatments and the reproduction methods, there were eight different treatments in total (RP, RM, LP, LM, SP, SM, HP, HM).

Microbial Community Analysis

A microbial diversity analysis was conducted on the initial community and on communities from cycles 3, 7, 10, and 14 by ARISA, a community fingerprinting method (Fisher and Triplett, 1999), using the primers 1522F and 132R. The pictures of the obtained gels were analyzed with ONE-Dscan (BD Biosciences^®, United States) giving a number of bands and the intensity of each band.

Heritability

In an artificial directional selection experiment, the heritability (h²) can be estimated by the slope of the regression of the cumulative selection response to the cumulative selection differential: this is called realized heritability (Falconer and Mackay, 1996 cited by Visscher et al., 2008; Roff, 2012). The selection response (R) is given by the difference between the mean phenotype of the offspring units and the mean phenotype of the parental unit(s). The selection differential, S, is given by the difference between the mean phenotype of the selected unit(s) (parent(s) of the next cycle) and the mean phenotype of the entire population of units (selected and unselected units). h² was calculated for each line independently and multiple testing was taken into account with Bonferroni correction (Bland and Altman, 1995). This calculation method was only proposed for directional selection (Roff, 2012) so it was not used to characterize Stabilizing lines in which the treatment consisted in the reduction of the selection differential thus making the regression of the cumulative selection response to the cumulative selection differential unsuitable. In order to characterize the degree to which the parental phenotype influenced the offspring phenotype for Stabilizing, and even for Random lines, we calculated the sum of squares of the difference between offspring biomass production and the respective parental biomass production depending on the reproduction method all cycles together.

Statistical Analyses

Considering a possible block effect due to the distribution of selection treatments onto three 96 well-microplates, we corrected for each cycle the biomass production values with the values of communities belonging to the same line that were present and repeated over the three microplates. Biomass production was analyzed using the following linear mixed model:

$\begin{array}{l}{\text{Y}}_{\text{ijkl}}=\mu +{\text{cycle}}_{\text{i}}+\text{ selection }{\text{treatment}}_{\text{j}}\\ +\text{ reproduction }{\text{method}}_{\text{k}}+{\left(\text{cycle x selection treatment}\right)}_{\text{ij}}\\ +{\left(\text{cycle x reproduction method}\right)}_{\text{ik}}\\ +{\left(\text{selection treatment x reproduction method}\right)}_{\text{jk}}\\ +{\left(\text{cycle x selection treatment x reproduction method}\right)}_{\text{ijk}}\\ +{\text{LINE}}_{\text{l}}+{\epsilon }_{\text{ijkl}}\end{array}$

where Y is biomass production, cycle is the effect of the experimental cycle (df = 13), selection treatment is the effect of the selection treatment (df = 3), reproduction method is the effect of the reproduction method (df = 1), (cycle x selection treatment), (cycle x reproduction method), (selection treatment x reproduction method) and (cycle x selection treatment x reproduction method) are interaction effects, LINE is the random effect of the line, ε_ijkl is the residual error. The analysis was performed with lmer function of lmerTest package (Kuznetsova et al., 2017) and r.squaredGLMM function of MuMin package (Barton, 2019) in R version 3.6.1. The anova function within the stats package (R Core Team, 2019) was used to describe the linear mixed model.

Biomass production, all cycles taken together, was analyzed with a two-way ANOVA (with selection treatment, reproduction method, and their interaction as factors) followed by a Tukey's HSD test (stats package in R version 3.6.1)

The ARISA data were analyzed using a non-metric multidimensionnal scaling (NMDS; vegan package in R version 3.6.1; Oksanen et al., 2018). A dissimilarity matrix was built with vegdist function and Bray-Curtis index, and NMDS was performed with metaMDS function.

Results

Biomass Variations Over Time

The linear mixed model showed that the cycle factor had a strong effect on biomass production (77% of the explained variance; mean square of the cycle factor divided by the total mean square excluding that of the residuals) as well as its interaction with the selection treatment (11%) and the three-way interaction: cycle-by-selection treatment-by-reproduction method (9%; Table S1). As shown in Figure S1, the effect of the cycle was not monotonic and a loss of the effect of artificial selection on community biomass was observed at certain cycles. A general decrease of biomass was observed at the beginning of the experiment in R, L and S lines and to a lesser extent in H lines (mean decrease of 28% between cycle one and six in R, L and S lines vs −11% in H lines).

Selection Treatment

Biomass production was not always changing in the expected direction (Figure 2A, Figure S1). All cycles taken together, L lines produced significantly less biomass than H and R lines (Figure S2, −5.1 and −3.9%, respectively, p < 2 × 10⁻¹⁶). Stabilizing selection was not effective in maintaining an absorbance value over time (Figure 2A), which gave rise to mean values (all cycles taken together) similar to those obtained in H lines in treatment M and to those obtained in L lines in treatment P (Figure 2B).

FIGURE 2

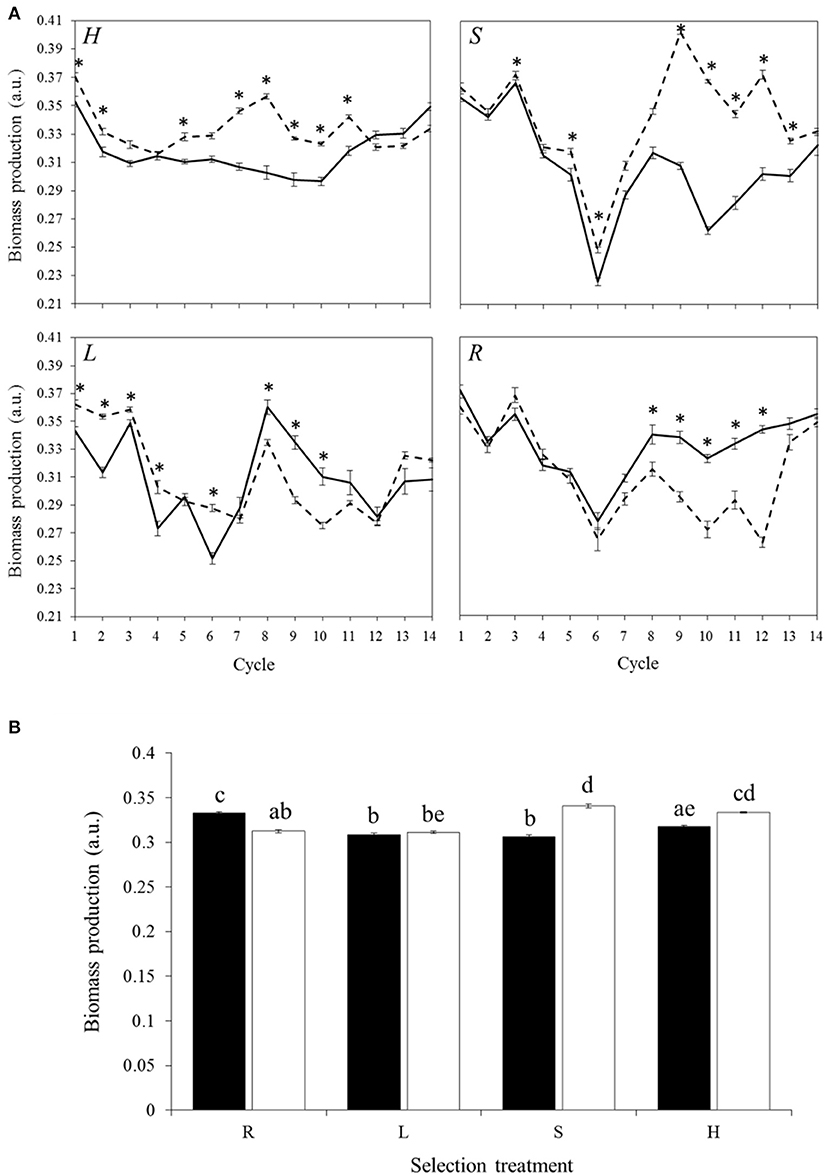
Figure 2. Biomass production (A) Over time. Mean biomass production of the 30 communities of propagule (solid lines) or migrant pool (dotted lines) reproduction method. Biomass production of the communities from propagule lines was averaged even if these communities belonged to three distinct lines as their profile were quite similar. Bars represent SE. Asterisks represent significant differences between the two reproduction methods in a given cycle and selection treatment (Tukey HSD test at each cycle; p < 0.05). Top left, High; top right, Stabilizing; bottom left, Low; bottom right, Random. (B) All cycles together. Mean biomass production depending on the selection treatment and the reproduction method (n = 420). Black, propagule; white, migrant pool. R, Random; L, Low; S, Stabilizing; H, High. Bars represent SE. Different letters represent significant differences (Tukey HSD test; p < 0.05).

Reproduction Method

Biomass production differed significantly between the two reproduction methods over time (Figure 2A, Table S1). Indeed there were transient phases of divergence during which HM and SM produced more biomass than HP and SP, respectively (difference of 4.48–17.75% between HM and HP and of 1.68–40.24% between SM and SP, depending on the cycle) and RM produced less biomass than RP (Figure 2A; difference of 7.22–23.54% between RM and RP depending on the cycle). LP and LM were quite close to each other in terms of biomass production over the course of the experiment.

Biomass was 5 and 11% higher using three parental communities (M) than a single one (P) with the selection treatments H and S, respectively (Figure 2B). However, the L selection treatment was not affected by the reproduction method (Figure 2B). In the Random lines (R), using a single parental community resulted in a higher biomass production than the one obtained when three parental communities were pooled.

Heritability

Our assessment of realized heritability suggested that h² depended on the selection treatment (H or L): in L lines, the slope of the regression of the cumulative selection response to the cumulative selection differential tended to be either positive or negative, depending on the line, but never significantly different from zero (Table S2). The slope was always positive in H lines, ranging from 0.02 to 0.15, although this was not significantly different from zero after correcting for multiple testing. Our results did not allow us to conclude on the effect of the reproduction method on h² because of a lack of statistical power (due to a low number of observations constrained by the number of cycles). However, all selection treatments taken together, the sum of the squares of the difference between parents and offspring biomass production was significantly higher in migrant pool lines than in propagule lines (0.05 and 0.02, respectively, on average; Mann-Whitney U test: W = 2,036, df = 1; p = 7.8 × 10⁻⁸).

Community Structure

Communities from the different lines were originating from the same initial pool and remained close from each other at the third cycle in terms of composition (Figure 3). Then, they diverged between cycles three and seven. At cycle 7, and to a lesser extent at cycle 10, the divergence of the microbial communities seemed to be mostly driven by the selection treatment (Figure 3). Moreover, the relative position of the centroids of the two reproduction methods tended to diverge over time, with no more overlap between the two ellipses at cycle 14 (Figure 3). For a given selection treatment, M communities were closer from each other than P communities as they were stemming from the same line of 30 communities. At the 14th cycle, P communities grouped at the center of the graph whereas M communities of the L, H and S selection treatments were located at the periphery, indicating a stronger divergence due to the selection treatment.

FIGURE 3

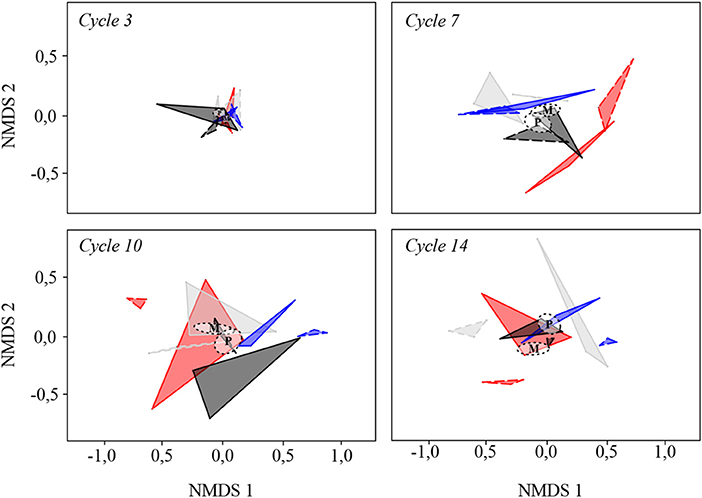
Figure 3. Non-metric multidimensional scaling of community structure over time. Polygons connect communities from the same selection treatment and reproduction method (three communities were analyzed per treatment and cycle). Black, Random; gray, Low; blue, Stabilizing; red, High. Polygons with solid borders: propagule; polygons with dotted borders: migrant pool. For each reproduction method, the centroid position (average position of the communities for a given reproduction method, taking SE into account) is represented by a dotted circle.

Richness was similar for every treatment at cycle 3 (between 34 and 37 OTUs) and underwent a significant decline over time until reaching values of 16 to 24 OTUs (Figure 4; F = 41.6; df = 31; p < 2 × 10⁻¹⁶). Interestingly, this decline occurred later in L lines whatever the sampling method, with no significant difference of richness between cycles 3 and 7 unlike all other treatments (Figure 4). In addition, in the treatment combining a high biomass selection and a migrant pool reproduction method (HM), the sharp decrease in richness between cycles 3 and 7 was followed by an unexpected regular increase in richness from cycle 7–14. This significant increase exhibited a small variance which suggests that this was not a random effect, for example due to a contamination, but rather a reliable change in community structure with an increase in abundance of species initially present at a level below the detection threshold of our molecular method.

FIGURE 4

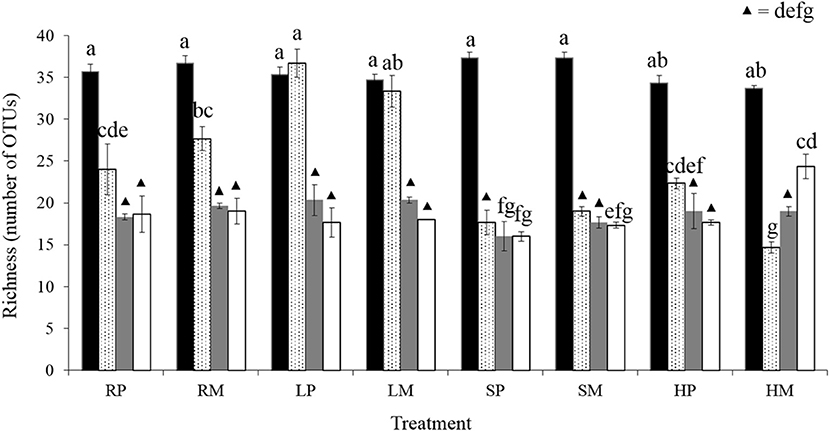
Figure 4. Community richness over time. Richness was assessed by ARISA on three communities per treatment and per cycle. Black, cycle 3; dotted, cycle 7; gray, cycle 10; white, cycle 14. Bars represent SE. Different letters represent significant differences (Tukey HSD test; p < 0.05). P, Propagule; M, Migrant pool; R, Random: L, Low; S, Stabilizing; H, High.

Discussion

One of the main issue in conducting efficient artificial selection on microbial community is to be able to preserve the entities responsible for the phenotype of interest (e.g., species, species-species interactions) from one cycle to the other (Arias-Sánchez et al., 2019). In this study, we experienced difficulties in reaching and fixing the targeted phenotypes. Indeed, only transient phases of divergence among the selected lines and between them and the randomly chosen lines were observed. This is in accordance with experiments by Swenson et al. (2000b). Very small initial differences in ecosystems, originating from variation in population size, or species composition, can be amplified by the complex dynamics of ecosystems through what is called the “butterfly effect” (Swenson et al., 2000b). More recently, an experiment demonstrated that the variance of the community property (CO₂ emission) and the heritability of this property declined along selection cycles, confirming the importance of the sampling effect in explaining differences in and collapse of the selected property (Blouin et al., 2015). This points out a paradox in community selection: a minimal variance resulting from community dynamics is necessary for selection to act (variation principle), but if this variance occurs through the butterfly effect, then it could prevent any heritability between parents and their offspring (Penn, 2003). This is consistent with our results which showed very low values of realized heritability. It indicated that only a small part of phenotypic variation, if any, was due to genetic additive variation which could explain our difficulties to maintain the effect of artificial selection over time. A modeling approach developed by Xie et al. (2019) suggested that artificial selection could be improved by lowering non-heritable variation (e.g., small variation in initial offspring community biomass). This could be done through the use of cell sorting instead of pipetting to create offspring communities and by extending the cycle duration to allow the communities to reach a stable state in which initial differences are compensated. It supposes that initial differences can be compensated contrary to what is expected under the butterfly effect hypothesis (the model developed by Xie et al. (2019) involved a two-species community whereas Swenson et al. (2000b) worked on complex microbial communities). Our experimental design probably induced too much non-heritable variation, which was a limitation in the parent/offspring resemblance and thus, in the selection treatment efficiency.

First of all, the effect of the selection treatments was confounded with a global decrease in biomass production at the beginning of the experiment which was probably due to a lack of adaptation and/or acclimatization of the microbial community (originated from the soil) to the experimental conditions despite the 48 h-cycle conducted in microplates before the start of the experiment. We cannot link this decrease in biomass production to a decrease in species richness, since in the L lines, the decrease in richness arose later (between cycles 7 and 10) than the decrease in biomass (from cycle 1 to 7). Interestingly, this initial decrease in biomass production tended to be shorter and less pronounced in H lines than in all other lines. Targeting a high biomass production, we probably selected the best-suited communities for the experimental conditions, at least at the beginning of the experiment.

The selection treatment influenced not only biomass production but also community structure. Even though we cannot assure that the observed changes in biomass production were not due to the increase in abundance of a unique microorganism, it is likely that the selection treatments have changed interaction patterns between members of the communities. Williams and Lenton (2007) proposed an ecosystem modeling approach to identify if interactions at the community level were necessary to explain some microbial ecosystem responses to artificial selection. They identified some cases in which the ecosystem response to selection was partly due to interactions between species, suggesting that these interactions can be under artificial selection pressure. The percentage of cases involving multiple species and interactions among them was higher in low lines than in high lines. Williams and Lenton argued that converging to a target (a fixed level of an abiotic factor in their study) is more difficult than diverging from it (which can be more easily achieved by a single microorganism). In our experiment, the targeted phenotypes did not correspond to fixed values so that, contrary to Williams and Lenton, our procedure did not involve converging to or diverging from a target. Despite this, our results showed that selecting for low biomass production preserved community richness longer than selecting for high biomass production. As pointed out by Day et al. (2011), whether or not the response to artificial selection involves several interacting species depends on the selection target and the existing solutions to reach it. Thus, multispecies solutions may be easier to find selecting on a low biomass production.

Our results suggested that the reproduction method in an artificial selection experiment can be responsible for different responses to selection. The propagule method was predicted to be more reliable but more detrimental to species richness than the migrant pool method. It is difficult to draw an overall conclusion about whether one reproduction method is more reliable to preserve the property than the other, because only transient phases of divergence between these two methods were observed and because of the three-way interaction between the reproduction method, the selection treatment and the cycle. Contrary to our results, Williams and Lenton (2007) did not notice any difference between the propagule and the migrant pool methods in the ecosystem response to selection (in silico selection on a level of abiotic factors). However, the probability that the evolution of the ecosystem property can be due to interactions among species was higher with the propagule (4 and 38% of the cases in High and Low lines, respectively) than with the migrant pool method (0 and 25% of the cases in High and Low lines, respectively) (Williams and Lenton, 2007). From this model, it can be concluded that the propagule method is likely to better conserve intra and inter-species interactions. In our experiment, it seemed that the migrant pool method was a better way of increasing biomass production considering H lines, but also S lines. This was in contradiction with the prediction that the best method would be the one that had the lower rate of reconfiguration of interactions network (i.e., propagule method) and suggested that it could depend on the targeted phenotype.

The migrant pool method is more often used than the propagule method in artificial selection experiments on microbial communities (Swenson et al., 2000a,b; Blouin et al., 2015; Panke-Buisse et al., 2015). This is mainly due to an expected decrease in richness stronger in the propagule than in the migrant pool method. Indeed, each sampling event at the origin of one community could be responsible for the loss of different species. With a regular pooling of several communities with different compositions, the experimenter can expect to prevent a decrease in richness. When the selection procedure is repeated several times as in our experiment, the migrant pool method was indeed more favorable to a recovery of specific richness (likely not previously detected with our molecular method) at least in the lines selected for a high biomass production. This reproduction method was also responsible for a higher level of variation than the propagule method, as indicated by the highest difference in parent-offspring biomass production and the highest divergence of community structure according to the selection treatment than with the propagule method. In our experimental conditions, it thus appeared that the variation brought by the migrant pool method was more favorable to artificial selection of high biomass lines than the propagule method.

In conclusion, preserving a microbial community phenotype over selection events is a key issue of artificial selection efficiency. Whether to mix several communities in selection procedures or not, or the number of communities to mix, are questions that need to be asked before conducting an artificial selection experiment. The reproduction method is of importance as it can play a role on community structure and diversity, and influence the targeted phenotype.

Data Availability Statement

The raw data supporting the conclusions of this manuscript will be made available by the authors, without undue reservation, to any qualified researcher.

Author Contributions

MB, MD, TR, and AS conceived the study. MD and TR conducted the experiments and AS and TR performed the statistical analyses. TR, MB, and AS wrote the article.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Jérémie Béguet for his help in ARISA analysis and members of the EMFEED team, Agroécologie laboratory, for discussions and advices.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2019.00416/full#supplementary-material

References

Arias-Sánchez, F. I., Vessman, B., and Mitri, S. (2019). Artificially selecting microbial communities: if we can breed dogs, why not microbiomes? PLOS Biol. 17:e3000356. doi: 10.1371/journal.pbio.3000356

CrossRef Full Text | Google Scholar

Barton, K. (2019). MuMin: multi-model inference. R Package Version 1.43.46.

Google Scholar

Bland, J. M., and Altman, D. G. (1995). Statistics notes: Multiple significance tests: the Bonferroni method. BMJ 310, 170–170. doi: 10.1136/bmj.310.6973.170

CrossRef Full Text | Google Scholar

Blouin, M., Karimi, B., Mathieu, J., and Lerch, T. Z. (2015). Levels and limits in artificial selection of communities. Ecol. Lett. 18, 1040–1048. doi: 10.1111/ele.12486

PubMed Abstract | CrossRef Full Text | Google Scholar

Day, M. D., Beck, D., and Foster, J. A. (2011). Microbial communities as experimental units. BioScience 61, 398–406. doi: 10.1525/bio.2011.61.5.9

PubMed Abstract | CrossRef Full Text | Google Scholar

Falconer, D. S., and Mackay, T. F. C. (1996). Introduction to Quantitative Genetics. Harlow: Longman

Google Scholar

Fisher, M. M., and Triplett, E. W. (1999). Automated approach for ribosomal intergenic spacer analysis of microbial diversity and its application to freshwater bacterial communities. Appl. Environ. Microbiol. 65, 4630–4636.

PubMed Abstract | Google Scholar

Goodnight, C. J. (2000). Heritability at the ecosystem level. PNAS 97, 9365–9366. doi: 10.1073/pnas.97.17.9365

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodnight, C. J. (2011). Evolution in metacommunities. Philos. Transac. R. Soc. 366, 1401–1409. doi: 10.1098/rstb.2010.0290

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodnight, C. J., and Stevens, L. (1997). Experimental studies of group selection: what do they tell us about group selection in nature? Am. Natural. 150, S59–S79. doi: 10.1086/286050

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuznetsova, A., Brockhoff, P., and Christensen, R. H. B. (2017). lmerTest package: tests in linear mixed effects models. J. Stat. Softw. 82, 1–26. doi: 10.18637/jss.v082.i13

CrossRef Full Text | Google Scholar

Leigh, E. G. Jr. (2010). The group selection controversy. J. Evolut. Biol. 23, 6–19. doi: 10.1111/j.1420-9101.2009.01876.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lewontin, R. (1970). The Units of Selection. Ann. Rev. Ecol. Systemat. 1, 1–18. doi: 10.1146/annurev.es.01.110170.000245

CrossRef Full Text | Google Scholar

Morris, B. E. L., Henneberger, R., Huber, H., and Moissl-Eichinger, C. (2013). Microbial syntrophy: interaction for the common good. FEMS Microbiol. Rev. 37, 384–406. doi: 10.1111/1574-6976.12019

PubMed Abstract | CrossRef Full Text | Google Scholar

Okasha, S. (2006). The levels of selection debate: philosophical issues. Philosophy Compass 1, 74–85. doi: 10.1093/acprof:oso/9780199267972.001.0001

CrossRef Full Text | Google Scholar

Oksanen, J., Blanchet, F. G., Friendly, M., Kindt, R., Legendre, P., McGlinn, D., et al. (2018). vegan: Community ecology package. R package version 2.5-3.

Google Scholar

Panke-Buisse, K., Poole, A. C., Goodrich, J. K., Ley, R. E., and Kao-Kniffin, J. (2015). Selection on soil microbiomes reveals reproducible impacts on plant function. ISME J. 9, 980–989. doi: 10.1038/ismej.2014.196

PubMed Abstract | CrossRef Full Text | Google Scholar

Penn, A. (2003) “Modelling artificial ecosystem selection: a preliminary investigation,” in Advances in Artificial Life. ECAL 2003. Lecture Notes in Computer Science Vol. 2801, eds W. Banzhaf, J. Ziegler, T. Christaller, P. Dittrich, and J. T. Kim (Berlin, Heidelberg: Springer), 659–666.

Google Scholar

R Core Team (2019). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria.

PubMed Abstract | Google Scholar

Roff, D. A. (2012). Evolutionary Quantitative Genetics. Dordrecht: Springer Science & Business Media.

Google Scholar

Swenson, W., Arendt, J., and Wilson, D. S.. (2000a). Artificial selection of microbial ecosystems for 3-chloroaniline biodegradation. Environ. Microbiol. 2, 564–571. doi: 10.1046/j.1462-2920.2000.00140.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Swenson, W., Wilson, D. S., and Elias, R. (2000b). Artificial ecosystem selection. PNAS 97, 9110–9114. doi: 10.1073/pnas.150237597

PubMed Abstract | CrossRef Full Text | Google Scholar

Visscher, P. M., Hill, W. G., and Wray, N. R. (2008). Heritability in the genomics era — concepts and misconceptions. Nat. Rev. Genet. 9, 255–266. doi: 10.1038/nrg2322

PubMed Abstract | CrossRef Full Text | Google Scholar

Wade, M. J. (1978). A critical review of the models of group selection. Quart. Rev. Biol. 53, 101–114. doi: 10.1086/410450

CrossRef Full Text | Google Scholar

West, S. A., Griffin, A. S., and Gardner, A. (2007). Social semantics: altruism, cooperation, mutualism, strong reciprocity and group selection. J. Evolut. Biol. 20, 415–432. doi: 10.1111/j.1420-9101.2006.01258.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, H. T. P., and Lenton, T. M. (2007). Artificial selection of simulated microbial ecosystems. PNAS 104, 8918–8923. doi: 10.1073/pnas.0610038104

PubMed Abstract | CrossRef Full Text | Google Scholar

Wright, R. J., Gibson, M., and Christie-Oleza, J. A. (2019). Understanding microbial community dynamics to improve optimal microbiome selection. Microbiome 7:85. doi: 10.1186/s40168-019-0702-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, L., Yuan, A. E., and Shou, W. (2019). Simulations reveal challenges to artificial community selection and possible strategies for success. PLOS Biol. 17:e3000295. doi: 10.1371/journal.pbio.3000295

PubMed Abstract | CrossRef Full Text | Google Scholar