
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Ecol. Evol., 16 October 2019
Sec. Conservation and Restoration Ecology
Volume 7 - 2019 | https://doi.org/10.3389/fevo.2019.00384
This article is part of the Research TopicNorth American Monarch Butterfly Ecology and ConservationView all 35 articles
The United States Fish and Wildlife Service is currently evaluating the monarch butterfly (Danaus plexippus) for listing under the Endangered Species Act and using the Species Status Assessment (SSA) framework to estimate and forecast drivers that impact the species' risk of extinction. To evaluate eastern and western monarch populations the monarch SSA built on a foundation of published population models and other literature to identify current growth rates and information on threats and conservation efforts. Here we present the resulting methodology, which aimed to explore the magnitude of monarch population responses to the aggregation of multiple drivers under various scenarios. Our methodology differs from previous research by developing a series of functional cause and effect relationships that link monarch population-specific responses to threats or conservation actions. We incorporated these population-specific responses into stochastic geometric growth models for both eastern and western populations to estimate the probability of quasi-extinction in 50 years. Our models were parameterized using previously estimated population-specific trend data (growth rates and environmental variability) and expert elicited estimates of population responses to multiple drivers (i.e., amount of available breeding and overwintering habitat, insecticide use, migration resource availability, and climate change). We explored plausible future scenarios with realistic place-holder data to evaluate how changes in these drivers influenced monarch quasi-extinction risk for each population. In addition, we captured uncertainty in quasi-extinction risk by calculating cumulative quasi-extinction risk over a full range of quasi-extinction threshold values which were sampled from a uniform distribution bounded by expert-elicited estimates. In both populations, our baseline for comparison was the “current” condition defined by population-specific growth rate and environmental stochasticity from previous research. The result of the methodology presented here is a novel and comprehensive tool that incorporates the impact of future stressors into projections of population numbers over time. The approach provides a tractable and updatable tool that includes multiple types of information and the associated uncertainty of drivers, population impacts, and risk of extinction. For monarchs, this tool will be critical for incorporating the best scientific and commercial information available in the upcoming listing decision.
Migratory monarch (Danaus plexippus) populations in North America are in decline and several population viability analyses (hereafter PVAs) predict the likelihood of monarch extinction or quasi-extinction in the near future (Flockhart et al., 2015; Semmens et al., 2016; Oberhauser et al., 2017; Schultz et al., 2017). Given the decreasing population trend of North American monarchs and subsequent extinction concern, monarchs are being evaluated for listing under the Endangered Species Act by the U.S. Fish and Wildlife Service (The Service). As part of this effort The Service conducts a species status assessment (SSA)–a scientifically rigorous framework designed to evaluate a species' status using the best available science to aid decision makers (U.S. Fish Wildlife Service, 2016). Within the SSA, analyses define a species' viability (the ability to sustain populations into the future given existing and future threats and conservation efforts) while also tracking key uncertainties and assumptions. For monarchs, most information available for evaluating population-level persistence exists for the North American eastern and western migratory populations through a suite of PVAs. Flockhart et al. (2015) focused solely on the eastern migratory population and used matrix modeling to address scenarios for changes in climate change and habitat and their effects on demographic rates into the future. Also using a matrix model, Oberhauser et al. (2017) focused on vital rate differences within geographic sub-regions of the breeding range of the eastern migratory population and future conservation scenarios that would increase population growth above the replacement rate. In a third matrix model for the eastern population, Hunt and Tongen (2017) explored the range in possible growth rates for monarchs under varying hypothetical seasonal and habitat effects (in both breeding areas and overwintering grounds). Semmens et al. (2016) and Schultz et al. (2017) explore quasi-extinction risk in the eastern and western populations, respectively, using threats implicit in the estimated population growth rate. These PVAs partially fill SSA requirements and are the foundation of the framework presented in this manuscript to assess both populations' resiliency (ability to sustain plausible expected changes in their environment and threats into the future).
The SSA must evaluate and incorporate information on current and future threats to accurately estimate future monarch population resiliency. Existing information on the threats to monarchs is mostly based in the eastern monarch population and reconstructs the patterns that lead to current declines (Flockhart et al., 2015; Oberhauser et al., 2017; Thogmartin et al., 2017b). These primary drivers of monarch population decline include the loss of breeding habitat (land conversion and adoption of glyphosate tolerant genetically-modified crops; Thogmartin et al., 2017b), the loss and degradation of overwintering habitat (Sáenz-Romero et al., 2012; Vidal et al., 2014; Honey-Rosés et al., 2018), climate change (Brower et al., 2012; Lemoine et al., 2015), insecticides (Belsky and Joshi, 2018), and threats faced during the annual migration (Inamine et al., 2016). The western population faces additional threats such as loss of overwintering or breeding habitat from climate-related fire and drought (Griffiths and Villablanca, 2015; Pelton et al., 2016). Furthermore, both populations face the threats of road kill mortality (Kantola et al., 2019; Mora Alvarez et al., 2019), diseases, parasitism, and predation (Altizer and de Roode, 2015; Oberhauser et al., 2015). Each of these threats contributes to the current and future resiliency of eastern and western monarch populations through population-specific responses that the SSA endeavors to make explicit.
In addition to threats, population projections of North American migratory monarchs should incorporate future conservation efforts, which may slow or potentially reverse declining population trends. Increasing the number of milkweed stems, for example, may overcome current monarch population declines (Nail et al., 2015; Thogmartin et al., 2017a). Furthermore, improving breeding habitat within specific sub-regions of migratory monarchs may increase population growth rates above the level of replacement (Oberhauser et al., 2017). In this manuscript, we seek to further define the degree to which conservation actions impact monarch populations by combining conservation efforts with a full suite of current and future threats.
Finally, the SSA endeavors to track key uncertainties when estimating extinction risk. Quasi-extension thresholds—the level at which a population is no longer viable—are one source of uncertainty for North American migratory monarchs. Quasi-extinction threshold estimates for the western migratory monarch population vary from as low as 20,000 butterflies (Schultz et al., 2017) to as high as 50,000 butterflies (Wells et al., 1990). Quasi-extinction thresholds for the eastern migratory monarch population range from 1,000 butterflies (Flockhart et al., 2015) to 0.25 hectares of occupied overwintering habitat (without reporting a density estimate for the number of butterflies per hectare; Semmens et al., 2016; Oberhauser et al., 2017). Because of this uncertainty, future monarch population projections should compare against a range of quasi-extinction thresholds.
Here, we describe a geometric growth model for eastern and western migratory monarch populations that incorporates population responses to future threats and conservation actions and addresses the uncertainty around quasi-extinction thresholds. We used formal expert elicitation to obtain a list of population-specific threats and quantify how changes in threats or conservation actions influenced monarch populations. We used additional expert elicitation to derive a range of quasi-extinction thresholds (highest, lowest, and most likely) that define a distribution of quasi-extinction thresholds. Relying on expert judgment is a common and necessary step to parameterize models (e.g., Canessa et al., 2018; Gerber et al., 2018). We believe this model fulfills the goals of the monarch SSA and provides unique insights into plausible future scenarios of monarch population trends over the next 50 years. This model also allows for the rapid and transparent integration of new information on population threats, growth, or quasi-extinction thresholds for future SSA analyses. We hope the inclusion of this model in peer-reviewed literature will invite feedback and additional testing that improves our SSA analyses and contributes to The Service's commitment to transparent and scientifically rigorous species evaluations.
The biology and migratory behavior of eastern and western monarch populations are comparable enough to allow for a similar modeling approach to project population growth. Adult monarchs in the eastern North American population migrate annually and in the spring move northward from Mexico to breed in the United States and Canada over several successive generations. At the end of the breeding season, the final generation of adults migrate back to Mexico to overwinter before starting the cycle again the next year (Malcolm et al., 1993; Solensky, 2004). The western North American monarch population disperses annually from overwintering sites along the California and northern Mexican coast to breeding grounds that expand as far east as the Rocky Mountains and northward to Canada. Similar to the eastern population, western monarchs have several successive generations before returning to overwinter in California (Solensky, 2004; Stevens and Frey, 2010).
The base population growth model for both the eastern and western monarch populations is based on the log-scale geometric growth model developed by Semmens et al. (2016) for t in 1, …, T discrete time steps:
In this model let Nt+1 be the log monarch population size in their wintering grounds at time t + 1, which is assumed to be a lognormal random variable such that the mean, μt, is composed of the log monarch population size in the current time-step, Nt, and their log population growth rate (λ):
The variance term in Equation (1), ε, is process noise (i.e., environmental stochasticity) which is assumed to be a gamma random variable with shape k and scale θ:
The gamma distribution is a continuous probability distribution that generates positive real numbers such as standard deviations for a random normal variable. The gamma distribution has an expected mean of k * θ and variance k * θ2.
To incorporate future threats and conservation actions into monarch population projections we modified Equation (2) by adding an additional term, δ, which represents a net change in population size (N) due to the both positive and negative drivers (i.e., δ is the summed effect of αi in 1, …, I influences on the monarch population):
Values for Nt, λ, k, and θ were derived from previous monarch research (Table 1), while the calculation of δ was derived through expert elicitation (Figure 1, described in more detail below).
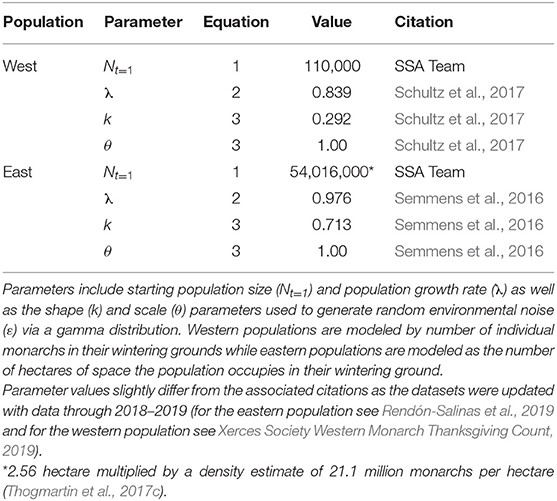
Table 1. Model parameters used to project monarch populations with the log-scale geometric growth model.
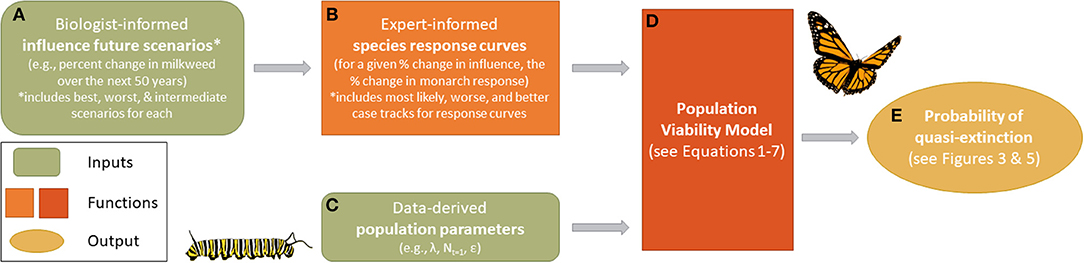
Figure 1. An overview of the monarch modeling framework. Biologist-informed scenarios (A) represent percent change in a given influence over the next 50 years and include best, worst, and intermediate scenarios for each. Expert-elicited population response curves (B) specific to each influence provide the proportional change in monarch response given a proportional change in the influence (including most likely, reasonable best, and reasonable worse case responses from experts). Population response curves differ by influence and region (Eastern and Western population). Population demographic data (C) were sourced from existing literature and used to initialize the model (D), which also received inputs from (B). Simulation outputs from the population viability analysis were compared against a range of quasi-extinction values (E) to estimate the cumulative probability of extinction in 50 years.
To incorporate future threats and conservation actions, δ, we first updated monarch population data (λ and ε, Table 1) from 2015 to 2019 for both the eastern and western populations to represent the “current” state of growth (λ) of the populations (Equation 2). Given this “current” state of growth, we characterized monarch population responses to expected future threats or conservation actions by two factors: (A) the magnitude of change in a threat or conservation action that happens over time and (B) the specific population responses, α (Equation 5), to that change in a threat or conservation action (Figures 1A,B).
Factor A was determined by developing a range of plausible future scenarios (see Future Scenarios below) with varying magnitudes of change in a threat or conservation action. These future scenarios represent the future state conditions and were derived by the SSA Team and based on published data, expert knowledge, and professional judgment (see Supplemental Material 1, Tables S2, S8). The data sources for each driver represent different time horizons that were converted to a per-year effect. For example, if η is the expected proportion of monarchs lost to a certain threat over 80 years the annual proportion that remained was calculated as (1 – η)1/80. To balance variations in the different time horizons associated with different drivers we modeled a 50-year time window into the future.
Factor B was determined by constructing “population-response curves” derived through expert elicitation in a series of separate expert elicitation workshops for eastern and western monarch populations (Figure 1B). We followed widely-accepted best practices to plan, prepare, elicit, and synthesize expert judgments (Hemming et al., 2017; see Supplemental Material 2 for information specific to our elicitation meetings). Experts identified the influences they believed drive monarch population dynamics. Using the top drivers (Table 2), we elicited the expected population response of monarchs (in terms of proportional change in population size) due to the proportional changes of a driver (e.g., a 2-fold increase or decrease in milkweed availability). This was necessary because relationships between a driver and monarch response may not be linear. For example, a 1.25 proportional increase of a threat does not necessarily represent a reduction of 1.25 in monarch populations as (B) may not have a 1:1 relationship with (A).
We elicited population responses to a full range of potential changes in the drivers. For example, experts described the expected proportional change in population size given a 1.10, 1.25, 1.50, 1.75, or 2.00-fold increase or decrease in nectar resources. Each expert was asked to provide a highest, lowest, and most likely response for each proportional change in the drivers, thereby producing three response curves per driver (these curves are denoted as the “most likely” track, “reasonable best” track, and “reasonable worst” track).
The relationship between factor A and B was often non-linear. To account for varying degrees of non-linearity, a smoothed loess curve (R Core Team, 2013) was applied to the median expert scores for each proportional change in threat or conservation action to generate a population-response-curve (See Supplemental Material 3 for the fitted loess curves to expert elicited population responses). This method allowed population response curves to be as linear or non-linear as necessary. For some drivers (insecticides and climate) population response curves were developed differently by inferring population response from historical information (Supplemental Material 1). Collectively, the monarch population response captures biological variability (the expert predicted possible outcomes in numbers of individuals) as well as variability in future state conditions (the scenarios developed by the monarch SSA Core team).
In our eastern model our expert elicitation yielded an additional nuance—that monarchs respond differently to milkweed and breeding range nectar for r in 1, …, 3 sub-regions, which differ in their relative contribution of individuals to the overall population (sub-regions were based on those used in Oberhauser et al., 2017). We incorporated these region-specific population growth responses in an approach similar to that of the region-specific matrix model projections in Oberhauser et al. (2017). To incorporate sub-regional effects, we introduce a proportional term to the model, ρr, which splits the population into the r sub-regions according to their expert elicited importance such that ∑ ρ = 1. While this sub-regional splitting does not explicitly account for the fact that the eastern monarch population breeds multiple times in each region, it accounts for the cumulative contribution of each region to the monarch population across the entire breeding season. Therefore, for the three sub-regions the population that arrives in Mexico is:
Ultimately, the drivers used in the eastern population model were similar to those of the west, the drivers or α values were related to habitat availability (milkweed and nectar), exposure to insecticides, climate variability, and overwintering conditions in Mexico where monarchs face threats due to deforestation and climate change. However, unlike the western model, the climate impacts in the eastern population only acted by impacting habitat (milkweed and nectar). Additionally, the eastern model included an additional driver (and response curve) for nectar along the migration route which represented changes in available nectar resources during the late summer and fall for migrating adult monarchs. Experts felt nectar availability for fall migrants was a limiting resource for the eastern population because migratory route and breeding range do not completely overlap (as it does in the Western population) and monarchs funnel through a smaller geographic area where spatially available nectar resources need to be distinguished.
Our methodology for calculating quasi-extinction deviates from other published monarch models in that the quasi-extinction threshold varies along a range of expert-elicited values. For the eastern population, we elicited estimates of the lowest, highest, and most likely threshold values for quasi-extinction. We defined the minimum value of our quasi-extinction threshold as the median “lowest” estimate across all experts (1 million butterflies; 0.05 ha given 21.1 million density). The maximum value of our quasi-extinction threshold was similarly created using the median “highest” quasi-extinction values (12.8 million butterflies; 0.61 ha given 21.1 million density). For the western population, we used quasi-extinction thresholds reported in the literature with the lowest quasi-extinction threshold of 20,000 individuals (Schultz et al., 2017) and highest value of 50,000 (Wells et al., 1990). Using these ranges in quasi-extinction, we calculated the cumulative probability of extinction in three steps. First, we ran the population model for 100,000 simulations. Next, to capture the range of uncertainty around the expert-elicited quasi-extinction thresholds, we approximated a uniform distribution of quasi-extinction values by generating an evenly spaced sequence of 500 numbers between the minimum and maximum values for each population. Following this, we compared the 100,000 simulations per population to each of the 500 quasi-extinction threshold values. Simulated populations went extinct if they fell below the selected quasi-extinction threshold (Figure 1). Once a population hit the quasi-extinction threshold it could not recover throughout our simulations (i.e., remained at zero for the rest of the simulation). The resulting 50 million values (100,000 sims * 500 qE values) were then used to calculate the cumulative probability of extinction per year (proportion that were quasi-extinct).
Our initial model lacked an upper bound for population size (i.e., carrying capacity), and consequently, our initial simulations occasionally resulted in unrealistically high population sizes (e.g., >800 million or 38 ha). To address this, we capped yearly population sizes to approximately twice the largest observed population size for eastern (36 hectares) and western (2.4 million individuals) populations. When a population trajectory crossed its carrying capacity the estimate for that year was replaced with the carrying capacity value. The growth rate for the following year was still drawn from the distribution of growth rates defined by lambda (λ) and process noise (ε).
Future projections of monarch populations included a baseline scenario (the “current” state of growth based only on updated λ and, Equation 2) and a number of future scenarios. A complete future scenario was a composite of various states of each threat or conservation action. For example, the most optimistic states for each threat or conservation action were combined to create a composite “Best-case” scenario. For the eastern monarch population, we defined five scenarios: Best-case, Worst-case, and three Intermediate scenarios. We defined four scenarios for the western monarch population: Best-case, Worst-case, and two Intermediate scenarios. For a complete list of all scenarios see Supplemental Material 1. The baseline comparison for all future scenarios is the population projections under the “current” state of growth. The “current” state of growth is the eastern and western PVAs projected into the future with only the impacts of λ and environmental stochasticity (ε; Table 1). This resulted in a total of eleven scenarios across the eastern and western monarch populations (Figure 1). For each scenario, we ran a set of simulations (100, 000 simulations) for each of the three separate response curves generated (i.e., most likely, reasonable best, and reasonable worst). Both the uncertainty in monarch response (through the expert-elicited “highest” to “lowest” response) and in the future state of the drivers (through SSA team's range of “best-case” to “worst-case” future scenarios) was captured in the analysis.
Under the “current” condition, the western population had a λ = 0.839 (0.47–1.51). This estimate served as the “baseline,” or zero-change value, for comparisons of future scenario results (Figure 2).
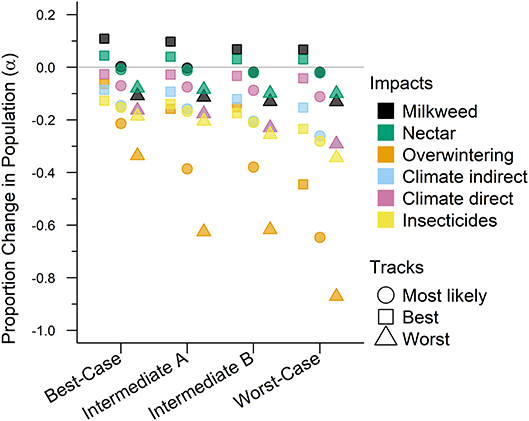
Figure 2. The impacts from future drivers in the western monarch population as predicted by our model. The impact is represented by a magnitude change above or below baseline lambda estimates and grouped by scenario along they x-axis. The colors represent the specific impacts and shapes represent the three expert elicited tracks created for each scenario (see legend).
The Best-case scenario for the western monarch population included the best plausible estimates for reductions in threats and increases in conservation efforts to combat the current declines in monarch numbers. These scenario inputs resulted in changes to λ that, once aggregated, ranged from a −0.003 decrease from the baseline λ estimate to a −0.193 decrease in λ after 50 years (Table 3). The range represents the multiple “tracks” of possible population response curves according to experts: most likely, reasonable best, and reasonable worst. The most likely track yielded a λ of 0.8283 (0.46–1.49; Table 3) or a decrease of 0.0107 from baseline λ. The individual drivers of milkweed and nectar caused positive proportional changes in population (α values) under the reasonable best tracks (proportional increases of 0.109 and 0.044, respectively, Figure 2) and even a small positive change under the most likely track for milkweed (proportional increase of 0.003, Figure 2). Alternatively, the reasonable worst tracks for milkweed and nectar estimated negative α values of −0.108 and −0.079, respectively (Figure 2). The largest α values were negative and were driven by overwintering habitat loss which predicted a most likely track value of −0.213 and a reasonable worst track value of −0.336 (Figure 2).
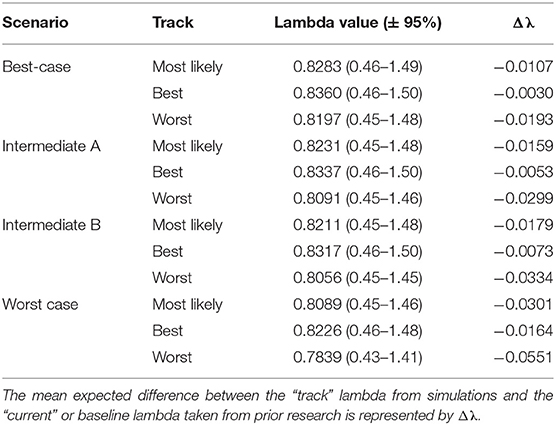
Table 3. Western population scenario specific λ values with 95% confidence intervals after incorporating scenario specific drivers.
Intermediate A for the western population represented a moderate reduction in the impact of threats and achieved only partial implementation of conservation efforts over the next 50 years. Intermediate A is less optimistic than the Best-case scenario but more optimistic than Intermediate B. Specifically, Intermediate A had lower rates of habitat loss in breeding and overwintering areas than Intermediate B as well as smaller population loss due to insecticides (Figure 2). These scenario inputs resulted in decreases ranging from −0.005 to −0.029 from the baseline λ estimate over 50 years (Table 3). The most likely track yielded a λ of 0.8231 (0.45–1.48; Table 3) or a −0.016 decrease from baseline λ. The reasonable best track for milkweed and nectar predicted α values of 0.097 and 0.040, respectively (Figure 2). However, all other tracks and drivers yielded zero changes in α or negative α values (Figure 2). Overwintering habitat loss drove the largest and most negative α values, predicting changes of −0.386 under the most likely track and −0.626 under the reasonable worst track (Figure 2).
Intermediate B for the western population represented a moderate reduction in the impact of threats and partial implementation of conservation over the next 50 years. Intermediate B is more pessimistic than Intermediate A in estimates of habitat loss and in population loss due to insecticides (Figure 2). These scenario inputs for Intermediate B resulted in decreases from the baseline estimate of λ ranging from −0.0073 to −0.0334 over 50 years (Table 3). The most likely track yielded a λ of 0.8211 (0.45–1.48; Table 3) or a −0.0179 decrease from baseline λ. The reasonable best track for milkweed and nectar predicted positive α values of 0.068 and 0.030, respectively (Figure 2). However, all other tracks and drivers yielded negative α values (Figure 2). Overwintering habitat loss drove the largest α values in population size predicting changes of −0.379 under the most likely track and −0.617 under the reasonable worst track (Figure 2).
The Worst-case scenario for the western monarch population included the plausible but reasonably pessimistic expectations for threats with minimal help from conservation efforts (Figure 2). These reasonably pessimistic expectations included a larger impact on monarch population decline from insecticides and climate (Figure 2). These scenario inputs for the Worst Case resulted in decreases from the baseline estimate of λ ranging from −0.0164 to −0.0551 over 50 years (Table 3). The most likely track yielded a λ of 0.8089 (0.45–1.46; Table 3) or a −0.0301 decrease from baseline λ. The reasonable best track for milkweed and nectar predicted α values of 0.067 and 0.029, respectively (Figure 2). However, all other tracks and drivers yielded negative α values (Figure 2). Overwintering habitat loss drove the largest α values predicting changes of −0.646 under the most likely track and −0.871 under the reasonable worst track (Figure 2).
Our quasi-extinction threshold collected from the literature ranged between 20,000 and 50,000 butterflies. Across this range, the probability of quasi-extinction for the western monarch population reached 99.99% (99.98–100.0) by 50 years in both the “current” or baseline model and all future scenarios tested (Figure 3). The differences between future scenario results are primarily in the times it took to reach 100% quasi-extinction. Relative to the “current” model, all future scenarios took shorter amounts of time to reach 100% probability of quasi-extinction. The baseline or “current” model took 33 years to reach 99.9% (99.58–99.94) while the Worst-case scenario under the reasonable worst track reached 99.9% (99.47–99.95) quasi-extinction within 20 years (Figures 3A,E). Our Best-case scenario under the reasonable best track reached 99.9% (99.51–99.94) quasi-extinction in 31 years while the most likely track reached 99.9% (99.49–99.94) quasi-extinction in 29 years (Figure 3B). Our Intermediate A and B scenarios both take 28 years to reach 99.9% (99.54–99.94) and 99.9% (99.59–99.95) probability of quasi-extinction, respectively, under their own most likely tracks (Figures 3C,D).
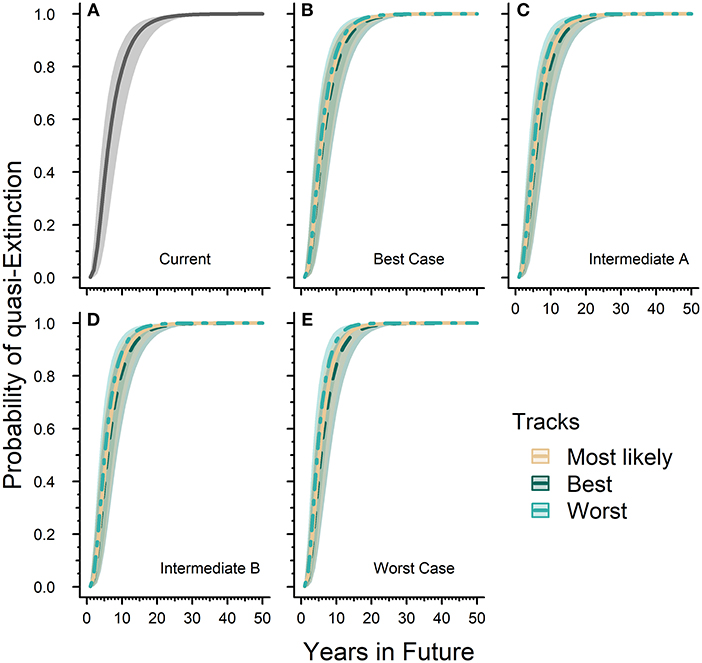
Figure 3. Western monarch population future risk of quasi-extinction. Sub-figure (A) represents the “current” projected probability of quasi-extinction with only the effects of lambda and environmental stochasticity and no threats where the solid line is mean estimate and the gray ribbon is the associated 95% confidence interval. The remaining sub-figures (B–E) represent the projected probability of quasi-extinction under varying future scenarios that include population responses to threats. Sub-figures (B–E) contain three tracks for each scenario, which are represented by different line types and colors (see legend). Lines represent mean estimates and shaded ribbons are 95% confidence intervals. For all sub-figures the 95% confidence intervals cover the full range of quasi-extinction thresholds (20,000–50,000 monarchs).
Under the “current” condition, growth rates varied slightly across the sub-regions North Central λ = 0.976 (0.24–4.02), North East λ = 0.975 (0.24–4.02), and South λ = 0.976 (0.24–4.02). These estimates served as the “baseline,” or zero-change value, for comparisons of future scenario results (Figures 4A–C).
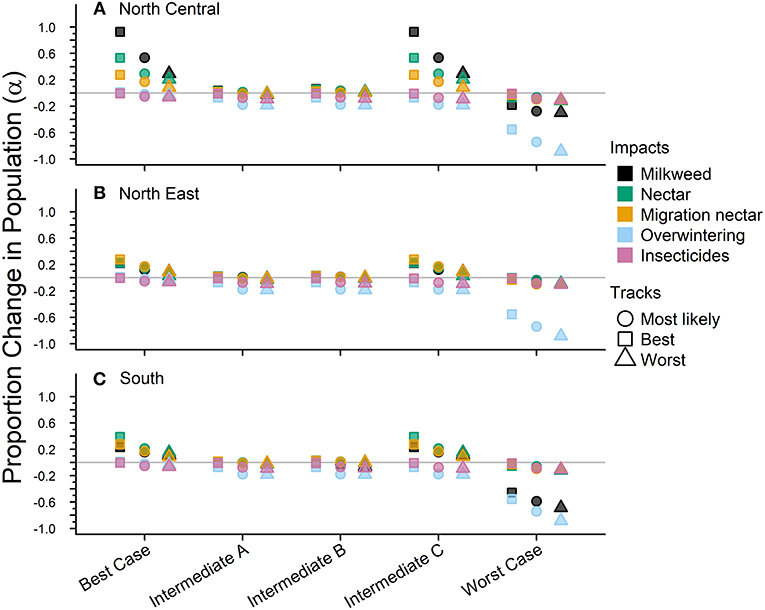
Figure 4. The impacts from future drivers in the eastern monarch population as predicted by our model. Impacts are split across the three sub-regions for this population (A–C). The impact is represented by a magnitude change above or below baseline lambda estimates and grouped by scenario along they x-axis. The colors represent the specific impacts and shapes represent the three expert elicited tracks created for each scenario (see legend).
The Best-case scenario for the eastern monarch population included the best plausible estimates for reductions in threats and maximum expected increases in conservation efforts to combat current monarch declines. These scenario inputs resulted in increases to λ in each sub-region, ranging from a 0.002 increase over baseline λ (reasonable worst, North East, Table 4) to the largest increase of 0.026 over baseline (reasonable best, North Central, Table 4). The range of changes in λ values represented the multiple “tracks” of possible population responses according to experts. The most likely tracks in all sub-regions yielded increases in λ of 0.9913 (0.24–4.09) in the North Central, 0.9827 (0.24–4.05) in the North East, and 0.9839 (0.24–4.06) in the South (Table 4). Under the Best case scenario, milkweed and nectar were predicted to yield positive α values of 0.93 and 0.54, respectively, in the North Central region over the next 50 years under the reasonable best tracks (Figure 4A) and also under the most likely tracks (0.54 for milkweed and 0.29 for nectar). However, plausible negative α values were still expected under the Best-case scenario for overwintering habitat (−0.018 to −0.036, most likely and reasonable worst tracks) and insecticides (−0.050 to −0.063, most likely and reasonable worst tracks; Figures 4A–C).
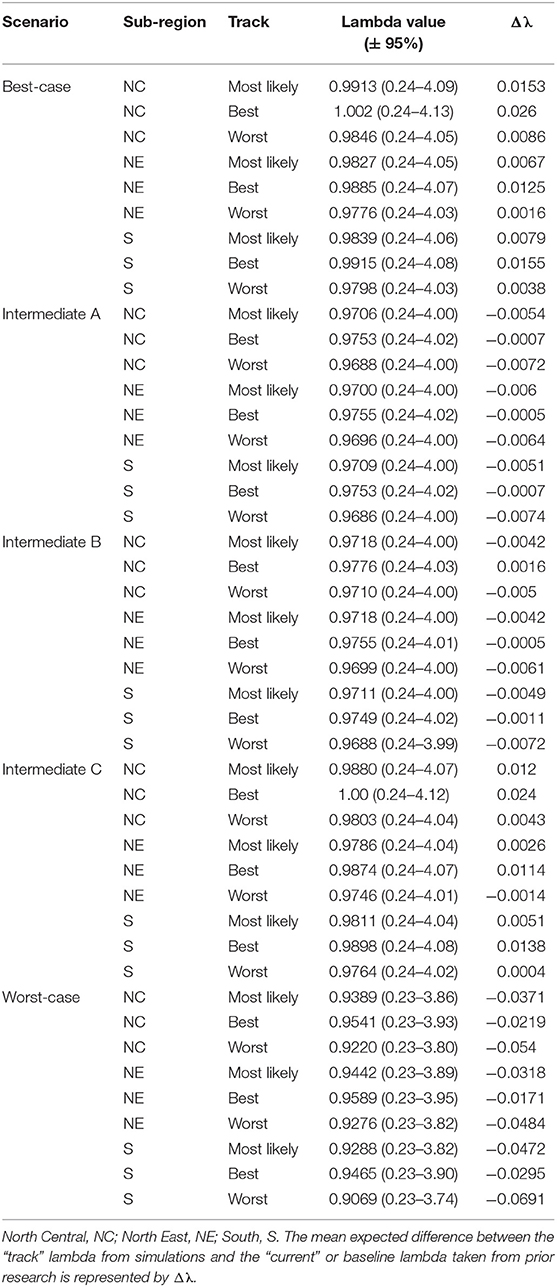
Table 4. Eastern population scenario specific λ values, per sub-region, with 95% confidence intervals after incorporating scenario specific drivers.
Intermediate A for the eastern population moderately reduced the impact of threats and achieved only partial implementation of conservation efforts over the next 50 years. Intermediate A is less reasonably optimistic than the Best-case scenario but more reasonably optimistic than Intermediate B. Notably, Intermediate A assumed no net change in habitat due to climate and balanced gains in habitat due to conservation with losses due to land-use changes (Figures 4A–C). Other drivers of insecticides and overwintering habitat continued at the same rate as historical estimates (Figures 4A–C). These scenario inputs resulted in either no changes in λ or very small declines from the baseline λ. The largest decline below baseline λ was a drop of 0.007 in the reasonable worst track in the South (Table 4). The most likely tracks in all regions yielded declines of only −0.005 to −0.006 in λ from baseline with 0.9706 (0.24–4.00) in the North Central, 0.9700 (0.24–4.00) in the North East, and 0.9709 (0.24–4.00) in the South (Table 4). Under the Intermediate A scenario, milkweed and nectar each were predicted to produce positive α values of 0.034 and 0.025, respectively, in the North Central over the next 50 years under the reasonable best track (Figure 4A). Across the reasonable best and worst tracks overwintering habitat changes yielded negative α values ranging from −0.070 to −0.182 and insecticides yielded negative α values of −0.01 to −0.09 (Figures 4A–C).
Intermediate B for the eastern population represented moderate changes in threats and conservation expectations over the next 50 years. Specifically, Intermediate B assumed two changes: (1) conservation efforts overcame continued losses of breeding habitat due to land-use changes and (2) climate change impacts could moderately decrease available habitat. Furthermore, insecticide use increased at a low rate of 5.0–10% per year. These scenario inputs resulted in zero change or very small increases or decreases from the baseline λ. The largest increase above baseline λ was a 0.002 increase in the reasonable best track of the North Central region (Table 4). The largest decline below baseline λ was −0.007 in the reasonable worst track of the South region (Table 4). The most likely tracks in all regions yielded −0.004 declines in λ from baseline with 0.9718 (0.24–4.00) in the North Central, 0.9718 (0.24–4.00) in the North East, and 0.9711 (0.24–4.00) in the South (Table 4). Under the Intermediate B scenario, milkweed and nectar each contributed positive α values of 0.003–0.062 for milkweed and 0.017–0.053 for nectar in the North Central over the next 50 years (Figure 4A). Plausible negative α values for the Intermediate B scenario under the reasonable best and worst tracks resulted from the drivers of overwintering habitat, a values of −0.07 to −0.182, and insecticides, α values of −0.01 to −0.093 (Figures 4A–C).
Intermediate C for the eastern population represented a combination of plausible but reasonably optimistic habitat gains and more moderate increases in threats over the next 50 years. Specifically, Intermediate C combined the assumptions of the Best-case scenario for habitat specific drivers (milkweed, nectar, and migration nectar) and the moderate changes in threats from Intermediates A and B for insecticides and overwintering (Figures 4A–C). These scenario inputs caused increases in λ across all regions except for track 3 in the North East where there was no change from baseline. Increases ranged from 0.004 to 0.024 over the baseline λ estimate over 50 years (Table 4). The most likely tracks in all regions yielded increases of 0.002–0.012 in λ from baseline with 0.9880 (0.24–4.07) in the North Central, 0.9786 (0.24–4.04) in the North East, and 0.9811 (0.24–4.04) in the South (Table 4). For the Intermediate C scenario under the most likely or reasonable best tracks, milkweed, and nectar yielded the same positive alpha values as the Best case scenario, with α values of 0.54 and 0.93 for milkweed and 0.29 and 0.54 for nectar (Figure 4C). Plausible negative α values under the Intermediate C scenario mirror the α values of Intermediate B for overwintering, ranging from of −0.07 to −0.182 (reasonable best to worst), and the α values for Intermediate A for insecticides, ranging from −0.01 to −0.09 (Figures 4A–C).
The Worst-case scenario for the eastern monarch population included reasonable pessimistic expectations for threats with minimal help from conservation efforts. These reasonable pessimistic expectations included monarch population losses from all drivers (no net gains from conservation actions) and a larger impact on monarch population decline from insecticides and overwintering habitat loss (Figures 4A–C). These scenario inputs resulted in declines across all regions ranging from −0.061 to −0.0171 below the baseline λ estimate over 50 years (Table 4). The most likely tracks in all regions yielded declines of −0.0318 to −0.0472 in λ from baseline with 0.9389 (0.23–3.86) in the North Central, 0.9442 (0.23–3.89) in the North East, and 0.9288 (0.23–3.82) in the South (Table 4). Under the Worst-case scenario, the driver of milkweed predicted larger negative α values than the drivers of nectar, migration nectar, and insecticides when comparing across all regions. The smallest α value from changes in milkweed was −0.181 under the reasonable best track in the North Central region (Figure 4A). The largest α value from change in milkweed was −0.686 under the reasonable worst track in the South region (Figure 4C). Nectar and migration nectar related α values were smaller than those of milkweed, but still negative, and ranged from −0.01 to −0.13 over all tracks and regions (Figures 4A–C). The loss of overwintering habitat drove the overall largest α values under the Worst-case scenario, up to −0.89 under the reasonable worst track over 50 years (Figures 4A–C).
Our expert elicited quasi-extinction threshold ranged between 0.05 and 0.61 hectares. The “current” or baseline probability of quasi-extinction for the eastern monarch population was 46.7% (17.0–62.2) in 50 years (Figure 5A). The inclusion of future scenarios would either increase or decrease this estimate over time depending on the scenario. The Best-case scenario reduced the probability of quasi-extinction estimate by 6.9–22.2% below the baseline for all three tracks of expert predicted responses (Figure 5B): the mostly likely track estimates the probability of quasi-extinction in 50 years as 40.8% (13.4–56.7), the reasonable best track estimates the probability of quasi-extinction as 36.3% (22.0–52.2), and reasonable worst track estimates the quasi-extinction probability as 43.5% (15.0–59.4). Our Worst-case scenario increased the baseline quasi-extinction estimate by a much greater magnitude than the reductions from Best-case, increasing the risk of quasi-extinction by 25.2–60.3% (Figure 5F). For the Worst-case scenario the probability of quasi-extinction in 50 years was, respectively, 66.7% (34.0–79.1), 58.5% (26.1–72.6), and 74.9% (44.2–85.2) for the most likely, reasonable best, and reasonable worst tracks (Figure 5F).
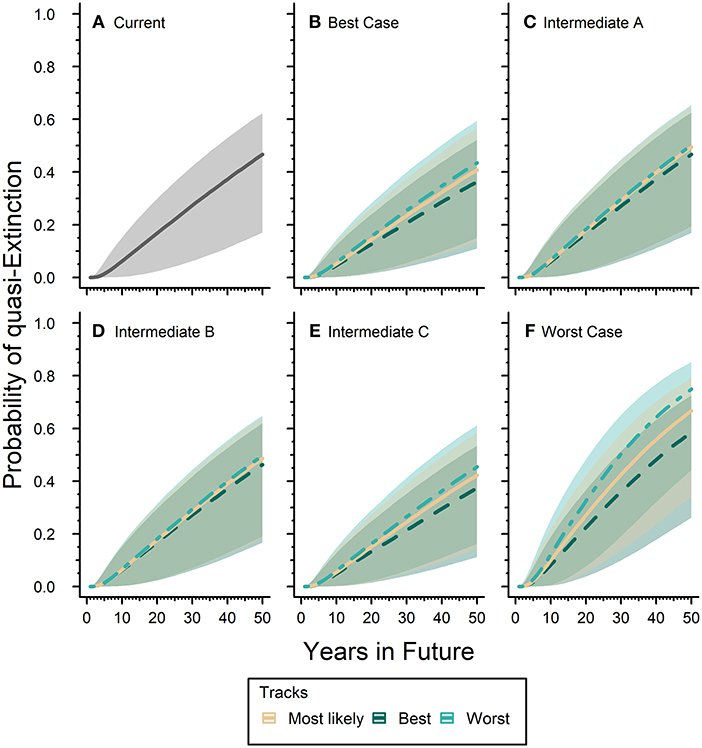
Figure 5. Eastern monarch population future risk of quasi-extinction. Sub-figure (A) represents the “current” projected probability of quasi-extinction with only the effects of lambda and environmental stochasticity and no threats where the solid line is mean estimate and the gray ribbon is the associated 95% confidence interval. The remaining sub-figures (B–F) represent the projected probability of quasi-extinction under varying future scenarios that include population responses to threats. Sub-figures (B–F) contain three tracks for each scenario, which are represented by different line types and colors (see legend). Lines represent mean estimates and shaded ribbons are 95% confidence intervals. For all sub-figures the 95% confidence intervals cover the full range of quasi-extinction thresholds (0.05–0.61 hectares).
The primary goal of this modeling effort was to create a rigorous, transparent, and re-usable tool that incorporates future threats and conservation actions and quantifies uncertainty around quasi-extinction thresholds for both the eastern and western migratory monarch populations. The challenges presented by the unique biology of migratory monarchs included: the need to represent multiple generations in the eastern migratory population, incorporating a mechanism for density dependence to better reflect population numbers, uncertainty around quasi-extinction levels, and a continuum of monarch responses to future state conditions of threats that could incorporate a range of scenarios for future projections. We believe incorporating expert elicitation in this framework allowed us to address many of these challenges through sub-regional growth responses in the eastern population, ranges in quasi-extinction thresholds that were used to test uncertainties around quasi-extinction risk, and population response curves that allowed multiple future state conditions to be tested under varying scenarios. We also addressed density dependence through introducing a carrying capacity to limit false resilience in population sizes. This modeling framework can be easily updated by the monarch SSA team as more information on threats and conservation actions become available. This tool also allows for seamless updates of population growth rates that vary each year with newly reported monarch overwintering numbers that will result in new population estimates and estimates of future quasi-extinction risk. Additionally, as more information becomes available on quasi-extinction thresholds for each population, the thresholds tested by this model can be modified to update future predictions.
These results provide novel insights into the relative magnitude of positive and negative drivers, based on the expert-elicited response curves. In our reasonable scenarios, the outcomes of the model yielded future state conditions where the effects of negative drivers outweighed the effects of positive drivers on population size. In the western population, each driver explored was associated with its own negative population response (Figure 2) which, when combined, resulted in growth rates that were anywhere from −0.003 to −0.0551 lower than current estimated growth rates (Table 3). Despite including conservation efforts for overwintering areas and breeding grounds, the plausible scenarios still resulted in continued monarch population declines and high risks of quasi-extinction into the future (Figure 3). The magnitude of change in driver-specific population responses between scenarios considered for the west were extremely similar (Figure 2) resulting in very little variation in population quasi-extinction risk under future scenarios (Figure 3).
In the eastern population there were more variable population growth rates and lower risks of quasi-extinction likely due to higher N, higher lambda, and a wider range of driver-specific population responses than in the west (Figures 4, 5). Drivers of milkweed, nectar, and overwintering habitat represented the largest sources of future changes in the eastern population (Figure 4A). The Best-case and Intermediates B and C scenarios in the eastern monarch population included large enough changes in habitat to result in larger monarch populations and lower probabilities of quasi-extinction. However, scenarios that did not include large conservation gains in habitat (Intermediate A and Worst-case) yielded probabilities of quasi-extinction equal to or higher than the baseline estimate (Figures 5C,D).
These results illustrate the sensitivity of the model to the inputs. Therefore, it is important to construct realistic projections of both threats and conservation actions. Furthermore, these results underscore the need for research to better understand how conservation efforts can be used to reduce or possibly counteract current monarch population declines. Because population drivers and responses are separated in our approach it is possible to consider the manipulation of drivers for the biggest benefit to the species. In the western population, further protecting overwintering grounds and nectar resources could cause a large and positive population response by the species. However, those changes would need to be greater in scope than what our analysis viewed as plausible. In the eastern population, gains in habitat drivers like milkweed and nectar may combat population losses from other drivers but only at high levels (Best-case scenario). Current large-scale, multi-state conservation efforts could be an excellent future test of this model prediction.
It is important to note that our model (similar to Flockhart et al., 2015; Semmens et al., 2016; Schultz et al., 2017) does not include parameters to address the uncertainty around a metapopulation-based link between eastern and western monarch populations. While there is evidence for exchange of individuals between the eastern and western populations (and the southern Florida non-migratory population), the specific rates and consistency of those exchange events are unknown (Brower and Pyle, 2004; Dingle et al., 2005; Knight and Brower, 2009; Morris et al., 2015). The inclusion of emigration and immigration, however, could possibly reduce our quasi-extinction estimates if immigration is large enough to allow a population to recover. Thus, further research is necessary to determine the magnitude of monarch immigration and emigration so that these rates may be included in future monarch PVAs.
There is also uncertainty around the accuracy of overwintering density estimates for the eastern monarch population. Because monarch overwintering population size in Mexico is measured in hectares, the density value determines the initial population size estimate, Nt, in our model. We chose one plausible density estimate—the median density of 21.1 million (Thogmartin et al., 2017c). Prior to Thogmartin et al. (2017c), published estimates of these densities range from 6.9 to 60.9 million monarchs per hectare (Calvert, 2004). In addition, experts who participated in the monarch expert elicitation reported density fluctuations within and among years. Our model did not include an underlying density function to allow for this possible fluctuation, but the effects of such uncertainty could be incorporated into future PVAs. Within the framework we developed, shifting density assumptions would alter the initial starting population size, Nt, thereby possibly affecting risk of quasi-extinction. Higher density values would equate to larger Nt, which would provide greater buffer against poor years and lower quasi-extinction risk over time. Lower density values would equate to opposite outcomes in Nt and quasi-extinction risk over time. Density estimates and assumptions could easily be updated in the future and tested with multiple values to better capture the developing knowledge on how density estimates translate hectare estimates to numbers of individuals.
We believe our model results build on previously published PVAs for the eastern and western migratory monarch populations. In the eastern monarch population, our “current” or baseline results are most equivalent to the future quasi-extinction estimates from models by Flockhart et al. (2015), Semmens et al. (2016), and Oberhauser et al. (2017). Our analysis updated the existing λ and ε for the eastern population from Semmens et al. (2016) (with overwintering data from 2017 to 2018 and 2018 to 2019) and forecasted monarch population trends into the future. In the western monarch population, our “current” or baseline analysis would be most equivalent to Schultz et al. (2017) with similar updates to the existing λ and ε. However, our future scenario results differ from these models as we incorporated population responses to changes in threats and conservation into the future. In addition, the use of a full range of quasi-extinction thresholds and a carrying capacity bring our modeling effort closer to the goals for assessing risk and uncertainty. Ultimately, these modifications build on published PVAs while also adding to the collective understanding of monarch risk into the future.
The PVA presented here is not the only factor included in The Service's process for evaluating the monarch for listing under the Endangered Species Act. There are additional influences and analyses for non-migratory monarchs and monarchs outside of North America considered within the SSA framework. Furthermore, this study does not explicitly test assumptions about population response to influences outside of those considered by our expert elicitation process, many of which require further study, nor does it take into account potential catastrophic events outside the scope of historical events (implicitly incorporated into λ). Future studies looking to incorporate threats for monarchs into the future may shed light into which drivers should or should not be included in this model or if the assumptions associated with a geometric growth model are valid. Our results show the potential of incorporating future threats and conservation actions into population projections for migratory monarchs, thereby making it easier to change which threats and conservation actions are included and to what degree they will change into the future. By doing so, we believe we have not only met the goals set by the SSA framework, but we have created a transparent and reproducible tool that will be repeatedly applied to exploring monarch population responses into the future.
The findings and conclusions in this article are those of the author(s) and do not necessarily represent the views of the U.S. Fish and Wildlife Service.
The datasets and R package generated for this study are available on request to the corresponding author.
KV, KN, and JS contributed to conception and design of the study. KV and MF designed the modeling framework and developed R code for this analysis. KV wrote the first draft of the manuscript. All authors helped with later drafts, manuscript revision, and read and approved the submitted version.
MF's work was supported by the Abra Prentice Foundation.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We would like to recognize the following experts for providing their monarch expertise and for participating in the formal expert elicitation process: Anurag Agrawal, Sonia Altizer, Linda Fink, Matt Forister, Jessica Griffiths, Pablo F. Jaramillo-López, Sarina Jepsen, Vera Krischik, Stephen Malcolm, Dan Meade, Gail Morris, Karen Oberhauser, Ian Pearse, Emma Pelton, John Pleasants, Cheryl Schultz, Chip Taylor, Francis Villablanca, and Louie Yang. Additionally, we would like to thank the following experts for their contributions to our analyses: Brice Semmens and Wayne Thogmartin. We thank all of the FWS biologists on the monarch SSA team for their help with scenario development and population response curves as well as and Nancy Golden, Dave Warburton, Sarah Warner, and Lisa Williams.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2019.00384/full#supplementary-material
Altizer, S., and de Roode, J. C. (2015). “Monarchs and their debilitating parasites: immunity, migration, and medicinal plant use,” in Monarchs in a Changing World: Biology and Conservation of an Iconic Insect, eds K. S. Oberhauser, K. R. Nail, and S. M. Altizer (Ithaca, NY: Cornell University Press, 83–93.
Belsky, J., and Joshi, N. K. (2018). Assessing role of major drivers in recent decline of monarch butterfly population in North America. Front. Environ. Sci, 6:86. doi: 10.3389/fenvs.2018.00086
Brower, L. P., and Pyle, R. M. (2004). “The interchange of migratory monarchs between Mexico and the Western United States, and the importance of floral corridors to the fall and spring migrations,” in Conserving Migratory Pollinators and Nectar Corridors in Western North America, ed G. P. Nabhan (Tucson, AZ: University of Arizona Press), 144–166.
Brower, L. P., Taylor, O. R., Williams, E. H., Slayback, D. A., Zubieta, R. R., and Ramirez, M. I. (2012). Decline of monarch butterflies overwintering in Mexico: is the migratory phenomenon at risk? Insect Conserv. Divers. 5, 95–100. doi: 10.1111/j.1752-4598.2011.00142.x
Calvert, W. H. (2004). “Two methods for estimating overwintering monarch population size in Mexico,” in The Monarch Butterfly: Biology and Conservation, eds K. S. Oberhauser and M. J. Solensky (Ithaca, NY; London: Cornell University Press, 121–127.
Canessa, S., Bozzuto, C., and Campbell Grant, E. H. (2018). Decision-making for mitigating wildlife diseases: from theory to practice for an emerging fungal pathogen of amphibians. J. Appl. Ecol. 55, 1987–1996. doi: 10.1111/1365-2664.13089
Dingle, H., Zalucki, M. P., Rochester, W. A., and Armijo-Prewitt, T. (2005). Distribution of the monarch butterfly, Danaus plexippus (L.) (Lepidoptera: Nymphalidae), in western North America. Biol. J. Linnean Soc. 85, 491–500. doi: 10.1111/j.1095-8312.2005.00512.x
Flockhart, D. T., Pichancourt, J.-B., Norris, D. R., and Martin, T. G. (2015). Unravelling the annual cycle in a migratory animal: breeding-season habitat loss drives population declines of monarch butterflies. J. Anim. Ecol. 84, 155–165. doi: 10.1111/1365-2656.12253
Gerber, B. D., Converse, S. J., Muths, E., Crockett, H. J., Mosher, B. A., and Bailey, L. L. (2018). Identifying species conservation strategies to reduce disease-associated declines. Conserv. Lett. 11, 1–10. doi: 10.1111/conl.12393
Griffiths, J., and Villablanca, F. (2015). Managing monarch butterfly overwintering groves: making room among the eucalyptus. Calif. Fish Game. 101, 40–50.
Hemming, V., Burgman, M. A., Hanea, A. M., McBride, M. F., and Wintle, B. C. (2017). A practical guide to structure expert elicitation using the IDEA protocol. Methods Ecol. Evol. 9, 169–180.
Honey-Rosés, J., Maurer, M., Ramírez, M. I., and Corbera, E. (2018). Quantifying active and passive restoration in central Mexico from 1986–2012: assessing the evidence of a forest transition. Restor. Ecol. 26, 1180–1189. doi: 10.1111/rec.12703
Hunt, E., and Tongen, A. (2017). A periodic matrix population model for monarch butterflies. Nat. Res. Model. 30:e12123. doi: 10.1111/nrm.12123
Inamine, H., Ellner, S. P., Springer, J. P., and Agrawal, A. A. (2016). Linking the continental migratory cycle of the monarch butterfly to understand its population decline. Oikos 125, 1081–1091. doi: 10.1111/oik.03196
Kantola, T., Tracy, J. L., Baum, K. A., Quinn, M. A., and Coulson, R. N. (2019). Spatial risk assessment of eastern monarch butterfly road mortality during autumn migration within the southern corridor. Biol. Conserv. 231, 150–160. doi: 10.1016/j.biocon.2019.01.008
Knight, A., and Brower, L. P. (2009). The influence of Eastern North American autumnal migrant monarch butterflies (Danaus plexippus L.) on continuously breeding resident monarch populations in Southern Florida. J. Chem. Ecol. 35, 816–823. doi: 10.1007/s10886-009-9655-z
Lemoine, N. P., Capdevielle, J. N., and Parker, J. D. (2015). Effects of in situ climate warming on monarch caterpillar (Danaus plexippus) development. PeerJ. 3:e1293. doi: 10.7717/peerj.1293
Malcolm, S. B., Cockrell, B. J., and Brower, L. P. (1993). “Spring recolonization of eastern North America by the monarch butterfly: successive brood or single sweep migration?,” in Biology and Conservation of the Monarch Butterfly, eds S. B. Malcolm and M. P. Zalucki (Los Angeles, CA: Natural History Museum of Los Angeles County, 253–267.
Mora Alvarez, B. X., Carrera-Treviño, R., and Hobson, K. A. (2019). Mortality of monarch butterflies (Danaus plexippus) at two highway crossing “Hotspots” during autumn migration in Northeast Mexico. Front. Ecol. Evol. 7:273. doi: 10.3389/fevo.2019.00273
Morris, G. M., Kline, C., and Morris, S. M. (2015). Status of Danaus plexippus population in Arizona. J. Lepid. Soc. 69, 91–107. doi: 10.18473/lepi.69i2.a10
Nail, K. R., Stenoien, C., and Oberhauser, K. S. (2015). Immature monarch survival: effects of site characteristics, density, and time. Ann. Entomol. Soc. Am. 108, 680–690. doi: 10.1093/aesa/sav047
Oberhauser, K., Wiederholt, R., Diffendorfer, J. E., Semmens, D., Ries, L., Thogmartin, W. E., et al. (2017). A trans-national monarch butterfly population model and implications for regional conservation priorities. Ecol. Entomol. 42, 51–60. doi: 10.1111/een.12351
Oberhauser, K. S., Anderson, M., Anderson, S., Caldwell, W., De Anda, A., Hunter, M., et al. (2015). “Lacewings, wasps, and flies—oh my: insect enemies take a bite out of monarchs,” in Monarchs in a Changing World: Biology and Conservation of an Iconic Insect, eds K. S. Oberhauser, K. R. Nail, and S. M. Altizer (Ithaca, NY: Cornell University Press, 71–82.
Pelton, E., Jepsen, S., Schultz, C., Fallon, C., and Black, S. H. (2016). State of the monarch butterfly overwintering sites in California. Portland, OR: The Xerces Society for Invertebrate Conservation.
R Core Team (2013). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Available online at: http://www.R-project.org/.
Rendón-Salinas, E., Martínez-Meza, F., Mendoza-Pérez, M., Cruz-Piña, M., Mondragon-Contreras, G., and Martínez-Pacheco, A. (2019). Superficie Forestall Ocupada por las Colonias de Mariposas Monarca en México Durante la Hibernación de 2018–2019. Available online at: http://d2ouvy59p0dg6k.cloudfront.net/downloads/2018_reporte_monitoreo_mariposa_monarca_mexico_2018_2019.pdf
Sáenz-Romero, C., Rehfeldt, G. E, Duval, P., and Lindig-Cisneros, R. A. (2012). Abies religiosa habitat prediction in climatic change scenarios and implications for monarch butterfly conservation in Mexico. Forest Ecol. Manag. 275, 98–106. doi: 10.1016/j.foreco.2012.03.004
Schultz, C. B., Brown, L. M., Pelton, E., and Crone, E. E. (2017). Citizen science monitoring demonstrates dramatic declines of monarch butterflies in western North America. Biol. Conserv. 214, 343–346. doi: 10.1016/j.biocon.2017.08.019
Semmens, B. X., Semmens, D. J., Thogmartin, W. E., Weiderholt, R., López-Hoffman, L., Diffendorfer, J. E., et al. (2016). Quasi-extinction risk and population targets for the Eastern, migratory population of monarch butterflies (Danaus plexippus). Sci. Rep. 6:23265. doi: 10.1038/srep23265
Solensky, M. J. (2004). “Overview of monarch migration,” in The Monarch Butterfly: Biology and Conservation, eds K. S. Oberhauser and M. J. Solensky (Ithaca, NY; London: Cornell University Press, 79–83.
Stevens, S. R., and Frey, D. F. (2010). Host plant pattern and variation in climate predict the location of natal grounds for migratory monarch butterflies in western North America. J. Insect Conserv. 14, 731–744. doi: 10.1007/s10841-010-9303-5
Thogmartin, W. E., Diffendorfer, J. E., López-Hoffman, L., Oberhauser, K., Pleasants, J., Semmens, B. X., et al. (2017c). Density estimates of monarch butterflies overwintering in central Mexico. PeerJ 5:e3221. doi: 10.7287/peerj.preprints.2832v1
Thogmartin, W. E., López-Hoffman, L., Rohweder, J., Diffendorfer, J., Drum, R., et al. (2017a). Restoring monarch butterfly habitat in the Midwestern US: ‘all hands on deck.' Environ. Res. Lett. 12:074005. doi: 10.1088/1748-9326/aa7637
Thogmartin, W. E., Wiederholt, R., Oberhauser, K., Drum, R. G., Diffendorfer, J. G., Altizer, S., et al. (2017b). Monarch butterfly population decline in North America: identifying the threatening processes. R. Soc. Open Sci. 4:170760. doi: 10.1098/rsos.170760
U.S. Fish and Wildlife Service (2016). USFWS Species Status Assessment Framework: an Integrated Analytical Framework for Conservation. Version 3.4 dated August 2016.
Vidal, O., López-García, J., and Rendón-Salinas, E. (2014). Trends in deforestation and forest degradation after a decade of monitoring in the Monarch Butterfly Biosphere Reserve in Mexico. Conserv. Biol. 28, 177–186.
Wells, H., P. H., and Cook, P. (1990). The importance of overwinter aggregation for reproductive success of monarch butterflies (Danaus plexippus L). J. Theor. Biol. 147, 115–131. doi: 10.1016/S0022-5193(05)80255-3
Xerces Society Western Monarch Thanksgiving Count (2019). Western Monarch Thanksgiving Count Data, 1997–2018. Available online at: www.westernmonarchcount.org
Keywords: monarch butterfly, Danaus plexippus, population viability analysis, quasi-extinction risk, threats, expert-elicitation
Citation: Voorhies KJ, Szymanski J, Nail KR and Fidino M (2019) A Method to Project Future Impacts From Threats and Conservation on the Probability of Extinction for North American Migratory Monarch (Danaus plexippus) Populations. Front. Ecol. Evol. 7:384. doi: 10.3389/fevo.2019.00384
Received: 02 May 2019; Accepted: 24 September 2019;
Published: 16 October 2019.
Edited by:
Wayne E. Thogmartin, United States Geological Survey (USGS), United StatesReviewed by:
Tyler Flockhart, University of Maryland Center for Environmental Science (UMCES), United StatesCopyright © 2019 Voorhies, Szymanski, Nail and Fidino. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kristen J. Voorhies, a3Jpc3Rlbl92b29yaGllc0Bmd3MuZ292; Jennifer Szymanski, amVubmlmZXJfc3p5bWFuc2tpQGZ3cy5nb3Y=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.