Effects of Natal Dispersal and Density-Dependence on Connectivity Patterns and Population Dynamics in a Migratory Network

Taylor, Caz M.

doi:10.3389/fevo.2019.00354

ORIGINAL RESEARCH article

Front. Ecol. Evol., 24 September 2019

Sec. Behavioral and Evolutionary Ecology

Volume 7 - 2019 | https://doi.org/10.3389/fevo.2019.00354

This article is part of the Research Topic Flexibility in the Migration Strategies of Animals View all 31 articles

Effects of Natal Dispersal and Density-Dependence on Connectivity Patterns and Population Dynamics in a Migratory Network

$\nCaz M. Taylor$ Caz M. Taylor^*

Department of Ecology and Evolutionary Biology, Tulane University, New Orleans, LA, United States

Migratory species can be visualized as occupying spatial networks with nodes representing regions and the populations that seasonally occupy them and links between seasonal subpopulations representing migratory connectivity. Connectivity is often regarded as a static property of a migratory network and visualized to evaluate the vulnerability of migratory populations to changes in specific regions. However, if the network itself is a dynamical system, its connectivity can be an output of the system that may be changed by perturbations to the network. I constructed a regulated, tripartite network population model with breeding, winter, and migration route nodes that also includes natal dispersal and in which connectivity goes to a dynamical equilibrium. I investigated how natal dispersal as well as the strength of density-dependent population regulation during breeding and non-breeding seasons affects connectivity patterns and the responses of the network population to simulated habitat loss. I found that when the population is primarily regulated by availability of habitat in only one season and natal dispersal was geographically constrained, connectivity patterns were unsymmetrical with weak (diffuse) connectivity from the non-regulating to regulating season and stronger connectivity in the other direction. Less-constrained natal dispersal always resulted in weak connectivity throughout. The overall magnitude of declines caused by habitat loss was determined by relative regulation and generally was not affected by natal dispersal although it was possible, with high natal dispersal, for loss of low-quality nodes in a non-regulating season to cause increases in network population size since the low-quality nodes were acting as an ecological trap. Although we expect that localness (i.e., the extent to which declines resulting from local winter habitat loss was concentrated in a small breeding area vs. spread across a larger area) should be predicted by connectivity, localness was in fact hugely variable and affected by both density-dependence and natal dispersal and generally quite difficult to predict from the connectivity pattern. In summary, the complexity of the system meant that visualization of a network by itself, without knowledge of the underlying processes causing connectivity patterns, often does not provide a good indication of the vulnerability of the network or individual node populations to habitat loss.

Introduction

In recent years, a great deal of research has used various tracking technologies to determine the migratory connectivity, i.e., the connections between breeding and non-breeding locations (Webster et al., 2002) of species of migratory animals, particularly birds. Migratory connectivity is referred to as strong when individuals from a single breeding location are close together during the winter and weak if they spread out over a large geographic distance and use multiple wintering locations (Webster et al., 2002). Most of the publications resulting from this work state that knowledge of migratory connectivity and/or its strength is essential for understanding declines and setting conservation priorities (e.g., Rushing et al., 2014; Trierweiler et al., 2014; Hallworth et al., 2015; El-Arabany et al., 2016; Dhanjal Adams et al., 2017; Knight et al., 2018). A few studies have found correlations between connectivity and declines which leads to the suggestion of causal relationships. For example, Hewson et al. (2016) suggests that connectivity plays a role in the declines of Common cuckoos (Cuculus canorus) in the U.K. since the proportion of birds that used one migration route correlated with the degree of population decline across nine breeding populations. In another example, Kramer et al. (2018) found that Golden-winged warblers (Vermivora chrysoptera) from declining breeding populations were spending the winter in South America, while birds from stable populations were wintering in Central America and suggest that this strong connectivity explains declines. In a review of 45 species of long-distance, terrestrial migrant landbird, Finch et al. (2017) found that connectivity is often weak and say that the conservation implications of weak connectivity are that the loss (or protection) of any non-breeding site will have a diffuse and widespread effect on many breeding populations.

The overall assumption here is that by visualizing or measuring connectivity in a population, we can make at least some general spatial recommendations for conservation. But, using connectivity information in this direct way makes an underlying (and usually unstated) assumption about the fixedness, at least over some period of time, of migratory connectivity. But we know that it is possible for connectivity to be the outcome of a migration system such that perturbations, such as habitat loss, that affect population size also change connectivity, and this raises the possibility that conservation actions will change connectivity and perhaps lead to unpredicted and unintended consequences. One approach to model dynamics of connectivity applied a maximum flow algorithm to several species of shorebirds moving through networks of non-breeding (winter and stopover sites). This model assumes that “population flow” can be modeled analogously to water flow in a pipe under the assumption is that the population will fill a network to capacity. Habitat loss (in this case due to sea level rise) caused a drop in capacity at some nodes in the network and therefore changed the overall capacity of the network and the connectivity in the network (Iwamura et al., 2013). Another approach, Migratory Flow Networks also use the analogy of water in pipes but model population flows as following general physical flux laws such that the movement between nodes depends on the attractiveness of source and destination nodes as well as the resistance to movement between them (Taylor et al., 2016). Changing the attractiveness or resistance in a migratory flow network results in altered connectivity.

Connectivity can also be determined by modeling the network as a dynamical system and solving for a steady-state equilibrium of the system. Taylor and Norris (2010) constructed a bipartite network model which had two set of nodes representing breeding and over-wintering locations where the population was regulated by density-dependent breeding success and winter survival while survival during migration declined with distance (or cost-distance) between nodes. With these assumptions, the connectivity in the migratory network goes to a stable steady state or equilibrium that is potentially altered by any change to any node or parameter. Simulated habitat loss at a single winter node showed that local winter habitat loss can cause declines even in unconnected breeding habitat regions (Taylor and Norris, 2010). This framework was used to predict the unmeasured migratory connectivity in Mexican free-tailed bats (Tadarida brasiliensis mexicana) (Wiederholt et al., 2013). The Taylor and Norris (2010) framework allows a continuum of relative strengths of density-dependence (affected by the amount of habitat/resources) in winter vs. breeding, such that the network population may be strongly winter-regulated, equally regulated by winter and breeding habitat, or strongly breeding-regulated. A version of the Taylor and Norris (2010) model was fitted to trend and tracking data for a migratory songbird, Wood thrush (Hylocichla mustelina), and found that the population was strongly winter-regulated and the pattern of declines across the breeding range could be explained primarily by habitat loss that has occurred in one winter region (Taylor and Stutchbury, 2016). Relative strength of regulation across seasons will clearly have consequences for the overall effects of habitat loss; in a strongly winter-regulated population, winter habitat loss will cause larger population declines than equivalent breeding habitat loss but how, or whether, regulation affects connectivity patterns in a network has not been explored.

One process that is certain to affect connectivity, but was not included in the modeling approaches described above, is dispersal. In migratory birds, two forms of dispersal have been described, natal dispersal is the displacement of first-time breeding birds from their natal location while breeding dispersal is the displacement of adults from their previous breeding location (Greenwood and Harvey, 1982). Cresswell (2014) put forward the hypothesis of serial residency, where offspring on their first migration move randomly (perhaps with some geographical constraints) to a non-breeding, then subsequently to a breeding location and, following those first two migrations, remain highly faithful to their selected winter and breeding locations for the rest of their lives. A great deal of evidence supports this hypothesis in migratory birds, including low juvenile natal site fidelity but high adult breeding-site fidelity to breeding as well as high adult fidelity to wintering and even staging or stopover locations. The consequence of serial residency will be to generally make connectivity patterns more diffuse (weaker), especially at small scales such that strong migratory connectivity will only be apparent at a large scale (Cresswell, 2014). How dispersal and serial residency affects the consequences of habitat loss has not been explored but, as discussed above, it is often assumed that when connectivity is weak, the loss (or protection) of any non-breeding site will have a diffuse and widespread effect on many breeding populations (Finch et al., 2017).

Here, I explore how natal dispersal (with serial residency) and the strength of density-dependent population regulation during breeding and non-breeding seasons affect connectivity and the consequences of local winter habitat loss. I explore both the trend, which is the magnitude of the species-level breeding decline resulting from winter habitat loss, as well as the localness of those declines, which is whether the declines are spatially localized vs. widespread across the breeding range. To do this, I use a version of the Taylor and Norris (2010) equilibrium network population model with several modifications. First, in order to explicitly include the migration seasons, I extended the model from a bipartite to a tripartite network with the inclusion of migration route nodes that represent, as single nodes, generalized routes that animals take to move from their breeding to winter regions and back (Cooke, 1905). Stopover sites are incorporated within a route rather than modeled as separate nodes. Migration survival is assumed to be negatively related to distance and positively related to the quality of the migration route used. Limited numbers of available routes of differing qualities is a move toward a more realistic representation of a migration system and routes can greatly affect connectivity patterns. Second, I added the process of natal dispersal under the assumption of serial residency. Natal dispersal can be constrained by distance and is controlled by a continuous parameter that varies from 0 (no dispersal) to 1 (offspring disperse everywhere in the network). Values between 0 and 1 are distance-constrained natal dispersal. Third, I vary the relative regulation in the network by changing the average carrying-capacity (which is inversely related to strength of density dependence) in nodes in each season. In a set of networks with randomly generated node locations and parameters, I vary the level of natal dispersal and relative regulation and measure how regulation and natal dispersal affect connectivity, the overall magnitude, and the localness of declines. I discuss to what degree visualization of connectivity in a migratory network allows us to predict the consequences of habitat loss or other changes in the network.

Quantifying Connectivity in a Migratory Network

To be able to summarize and compare connectivity across networks, we need to quantify connectivity. Metrics that have been developed that summarize the strength of connectivity are based on individual-level tracking data (Ambrosini et al., 2009; Cohen et al., 2017). As described above in the terminology of migratory connectivity, strong connectivity means individuals from a given location in one season are remaining close together in another season while weak (sometimes called diffuse) connectivity means they are spreading out and the metrics used to quantify strength of connectivity reflect this definition in that high values indicate strong connectivity (Webster et al., 2002; Ambrosini et al., 2009; Cohen et al., 2017). It has been pointed out, however, that migratory connectivity actually has multiple components that are often conflated. Finch et al. (2017) define two: population spread—the geographic distance over which individuals from a single breeding population spread out in the non-breeding season and inter-population mixing—the degree to which individuals from different breeding populations mix on the non-breeding grounds. It is possible for breeding populations to have high population spread but still have low mixing or overlap among wintering regions (Finch et al., 2017).

Describing a migratory system as a network leads to a somewhat different way of thinking about connectivity. The metrics mentioned above are based on measured geographic distances from tracking data on individual animals that have generally been tracked from the breeding to the non-breeding season and not often the other way around. In a network to quantify connectivity, we need graph-theoretical metrics (Rayfield et al., 2015) and we can separately quantify the strength of connectivity from a node in any season to nodes in any other season. In a bipartite network (e.g., Taylor and Norris, 2010), with breeding and winter seasons, there are two metrics of connectivity breeding-to-winter connectivity that could be calculated for any breeding node and winter-to-breeding connectivity that could be calculated for any winter node.

Here I develop a network-based season X-to-season Y connectivity metric based on the average diversity of connections from X to Y nodes. If animals from a single node in season X migrate to a large number of Y nodes then X-to-Y connectivity is weak but if animals from nodes in X are predominantly using one or a small number of Y nodes, X-to-Y connectivity will be strong. Network connectivities do not have to be symmetrical; it is possible for X-to-Y connectivity to be weak but Y-to-X connectivity to be strong. Breeding-to-winter and winter-to-breeding connectivity are related to the concepts of population spread and inter-population mixing, respectively (Finch et al., 2017) but the former are network or graph-theoretic metrics that assume a network or graph structure in which space has been discretized into nodes whereas the latter are geographic metrics that assume contiguous ranges. Weak breeding-to-winter connectivity corresponds to high population spread and weak winter-to-breeding connectivity corresponds to high inter-population mixing. With more than two seasons, there are other possible metrics. Cohen et al. (2018) measured breeding-to-winter, breeding-to-spring migration, and breeding-to-fall migration connectivity in Neotropical migratory birds. In general with k seasons, there are k! possible measures of the strength of connectivity.

Formally, following the terminology of other connectivity metrics, I define Network Migratory Connectivity NMC_XY, as the strength of connectivity from season X to season Y in a migratory network. NMC_XY is 1—the normalized Shannon diversity index, H2′ (Dormann et al., 2009) for the connections from nodes in X to Y averaged over nodes in season X,

\begin{array}{l} N M C_{X Y} = 1 - H 2_{X Y}^{'} = 1 - \frac{1}{N_{X}} \sum_{x = 1}^{N_{X}} \frac{H 2_{x Y}}{l o g (N_{Y})} . & (1) \end{array}

N_X and N_Y are the numbers of nodes in seasons X and Y, H2_xY is the Shannon Diversity index for node x with respect to connections to nodes in season Y (i.e., $H 2_{x Y} = - \sum_{y} p_{x y} l o g (p_{x y})$ where p_xy is the proportion of the population at node x that links to node y in season Y. NMC_XY takes into account the number and evenness of connections between X and Y and is normalized by the number of nodes so that it ranges between 0 (completely diffuse or weak connectivity; all possible connections are populated evenly) to 1 (strong connectivity; one connection between each node in X and Y).

Population Model Description

I developed a spatially structured, full annual-cycle population model of a migratory species. The annual cycle is comprised of four seasonal time-steps, Breeding, Fall migration, Wintering and Spring migration but space is modeled as a tripartite graph in which nodes, which represent spatial regions as well as the populations of animals that seasonally inhabit those regions, are classified into one of three types: breeding nodes occupied during the breeding season, winter nodes occupied during a stationary non-breeding period (referred to as “winter”), and migration route nodes which are used during both migration seasons. All nodes have a point location and an associated quality. Winter and breeding nodes also have a carrying capacity and density is defined as the population size at the node divided by carrying capacity. Fecundity is modeled as density-dependent and declines with density at the breeding node. Winter survival is also density-dependent and declines with density at the winter node. Migration route nodes do not have a carrying capacity since the model assumes no density-dependence in migration survival. Links represent movements between or through nodes. The model is an extension of the bipartite model presented in Taylor and Norris (2010). During a year, an individual moves through a cycle of 3 nodes: one breeding, one winter, and one route—for simplicity, one route node represents the geographic routes used by an individual during both migrations—and repeats the same cycle in the following year.

The “trick” to modeling population dynamics on such a network is to model the dynamics of each component of the global population that inhabits each cycle in the network. I use the notation $P = (b, w, r)$ to denote a “cycle subpopulation” $P$ that seasonally inhabits breeding node b, winter node w, and route node r. Nodes are not unique to cycles but are part of several cycles and so the cycle subpopulations overlap and compete with each other when there are density-dependent vital rates. Natal dispersal is modeled as displacement from one cycle subpopulation to another. In this model formulation, population dynamics, including natal dispersal, are completely deterministic. A cycle $P$ has a length, $L_{P}$ , which is the migration distance and is defined as the sum of the Euclidean distance from b to r plus r to w. The size of cycle subpopulation $P$ at the start of the breeding season in year t is $N_{P, t}$ and the population dynamics during the year from t to t + 1 are given by the following:

Breeding: During the breeding season, the number of offspring produced is given by,

\begin{array}{l} R_{P, t} = R_{max} (Q_{b}) e^{- (\frac{N_{b, t}}{K_{b}})} & (2) \end{array}

where R_max, maximum reproductive success, is a function of the quality, Q_b of the breeding node. Reproductive success declines with density ( $\frac{N_{b, t}}{K_{b}}$ ) at the breeding node, where N_b,t is the population size at node b obtained by summing over all cycles that include node b and K_b is the carrying capacity of breeding node b.

Natal Dispersal: Following the breeding season, offspring are redistributed uniformly among cycles according to the level of natal dispersal ND, which is a value between 0 and 1 that represents how far offspring will disperse. The distance between cycles (b1, r1, w1) and (b2, r2, w2) is defined as the sum of the Euclidean distances (w1 to w2) + (b1 to b2) + (r1 to r2). Offspring from any cycle $P$ will be distributed evenly to all cycles that are no farther than ND * D_max from $P$ , where D_max is the maximum distance between any two cycles in the network. So, the proportion of offspring that moves from cycle $Q$ to cycle $P$ , $f_{N D} (Q, P)$ , will be 1/(number of cycles that are no farther than ND.D_max from $Q$ ) if $P$ is within (ND.D_max), and 0 otherwise. If ND = 0, all offspring will stay on their natal cycle and if ND = 1, all offspring will be uniformly distributed among all cycles in the network. Natal dispersal is thus modeled here as a deterministic rather than stochastic process. ND is a dimensionless (unitless) parameter as it is expressed as relative to the maximum distance between cycles in the network.

All adults are assumed to survive through the breeding season and the distributed offspring are added into the cycle subpopulations to give the population sizes at the end of the breeding season,

\begin{array}{l} N_{P, t}^{'} = N_{P, t} + \sum_{Q} R_{Q, t} f_{N D} (Q, P) & (3) \end{array}

Fall Migration: Migration survival is not density dependent but declines with migration distance (i.e., cycle length, $L_{P}$ ) at rate α_r which is a decreasing function of the quality of the route node Q_r. Following Fall migration at the start of winter the population size is given by

\begin{array}{l} N_{P, t}^{″} = N_{P, t}^{'} e^{(- α_{r} (Q_{r}) L_{P})} & (4) \end{array}

Winter: Winter survival is density dependent and at the end of winter, the population size is given by

\begin{array}{l} N_{P, t}^{‴} = N^{″} S_{max} (Q_{w}) e^{- \frac{N_{w, t}^{″}}{K_{w}}} & (5) \end{array}

where the maximum survival, S_max,w is a is a function of the quality, Q_w of the winter node. $N_{w, t}^{″}$ is the population size at node w obtained by summing over all cycles that include node w and K_w is the carrying capacity.

Spring Migration: Survival during spring is assumed to be identical to fall migration survival and, following Spring migration, we have arrived back at the start of the next breeding season; the population size is given by,

\begin{array}{l} N_{P, t + 1} = N_{P, t}^{‴} e^{(- α_{r} (Q_{r}) L_{P})} & (6) \end{array}

Solving for Equilibrium

The model described above is a collection of deterministic processes and, for any given network configuration (including node parameter values), will go to the same fixed, equilibrium state from any starting point that has all cycles populated. This equilibrium solution of the model was obtained by starting with all cycles populated, $N_{P} > 0$ for all $P$ and simulating Equations (2)–(6) for multiple generations until the population stops changing $N_{P, t + 1} - N_{P, t} < 1 0^{- 8}$ for all $P$ (Taylor and Norris, 2010). From the solution, the total population size, the populations size at each node, and all 6 connectivity metrics were calculated, NMC_BW, NMC_WB, NMC_BR, NMC_RB, NMC_WR, and NMC_RW.

Network Parameterization

Networks were generated inside a region defined by a unit square using the following steps:

• 20 breeding nodes were located randomly within a horizontal rectangle occupying the top 20% of the region.

• 20 winter nodes were located randomly within a horizontal rectangle occupying the bottom 20% of the region.

• 5 route nodes were located randomly within a horizontal rectangle occupying the central 20% of the region.

• Node quality Q_i of any node i was randomly generated from a truncated normal distribution with mean 0, standard deviation 0.05, and limits (0.1).

• For each breeding node, b, the maximum number of offspring per individual, see Equation (2), was given by R_max,b = 1 + 2(Q_b) and is scaled to have a value between 1 and 3.

• For each route node, r, the rate at which survival declines with migration distance, Equations (4) and (6), is given by α_r = 0.1 + 1/(1 + 18Q_r), scaled to make migration survival between 0.3 and 0.78 for a migration distance of 1.

• For each winter node, w, the maximum survival, Equation (5), is given by S_max,w = (0.8 + 0.2Q_w), scaled to be between 0.8 and 1.0.

• Carrying capacities K_b, K_w for breeding and winter nodes were generated from zero-truncated normal distributions and no upper bounds with means $\bar{K_{B}}$ and $\bar{K_{W}}$ and standard deviations equal to the mean multiplied by 0.1. See below for values of $\bar{K_{B}}$ and $\bar{K_{W}}$ used.

• Natal dispersal is a network-level parameter, ND, which could take on any value between 0 and 1. See below for values of ND used.

Regulation

The relative regulation between breeding and winter in the network was quantified as a function of the ratio of the means of breeding $\bar{K_{B}}$ and winter $\bar{K_{W}}$ carrying capacity,

\begin{array}{l} r e g u l a t i o n = \frac{\sqrt{4 \bar{K_{B}} / \bar{K_{W}}}}{\sqrt{4 \bar{K_{B}} / \bar{K_{W}}} + 1} & (7) \end{array}

Because carrying capacities in the two seasons affect differently-scaled vital rates (reproductive success (0 to ∞) and survival (0 to 1), we found that when $\bar{K_{W}}$ was 4 times the size of $\bar{K_{B}}$ (regulation = 0.5), the population was equally regulated by winter and breeding. When $\bar{K_{W}} = \infty$ , regulation = 0 and the population is completely regulated by breeding. When $\bar{K_{B}} = \infty$ , regulation = 1 and the population is completely regulated by winter.

Model Runs

To explore the effects of natal dispersal and relative regulation on connectivity and on the consequences of winter habitat loss, $\bar{K_{B}}$ and $\bar{K_{W}}$ were set to 21 different values of regulation from 0 and 1 inclusive. Natal dispersal, ND, was set to one of 5 different values, which were: None: ND = 0, Low: ND = 0.05, Moderate: ND = 0.1, High: ND = 0.5, and Complete: ND = 1. For each combination of regulation and ND, 100 network configurations were generated using the steps above (resulting in 100 × 21 × 5 = 10,500 total model runs). Each network was solved for equilibrium and population sizes and connectivity metrics were calculated. One winter node was then randomly selected from all those that were occupied, i.e., population size at the node was at least 0.1% of the global population, and removed from the network. The network with the node removed was then re-solved for the new equilibrium value. The results of this perturbation were recorded as trend, the magnitude of the percentage decline (or increase) in the global breeding population size after node was removed. Also, the localness of the effect of habitat loss was measured as the diversity of individual breeding node trends measured as a normalized Shannon's index, the diversity among the proportions of the total population change that occurred at individual nodes. When localness is high, this means there is high variation in the effects of habitat loss, i.e., there are big changes in population size at a small number of nodes and no change or small changes at others. When localness is low, changes are more evenly distributed across the network.

Results

Connectivity Patterns

Density-dependence and natal dispersal interacted to affect connectivity patterns. When density-dependent regulation was skewed toward one season, this caused an asymmetry in connectivity but only when there was no or low natal dispersal. With low natal dispersal in a strongly winter-regulated network, several breeding nodes were unoccupied but all winter nodes were occupied which led to strong winter-to-breeding (and migration-to-breeding) connectivity and relatively weak breeding-to-winter (and migration-to-winter) connectivity (Figures 1A, 2). The asymmetry in connectivity lessened as the regulation because less winter-skewed and with equal regulation all breeding and winter habitat was occupied and winter-to-breeding and breeding-to-winter connectivity were the same strength (Figures 1D, 2). In a network that was breeding-regulated (still with no or low natal dispersal), the situation was reversed and there was unoccupied winter habitat, strong breeding-to-winter (and migration-to-winter) connectivity and relatively weak winter-to-breeding (and migration-to-breeding) connectivity (Figures 1G, 2).

FIGURE 1

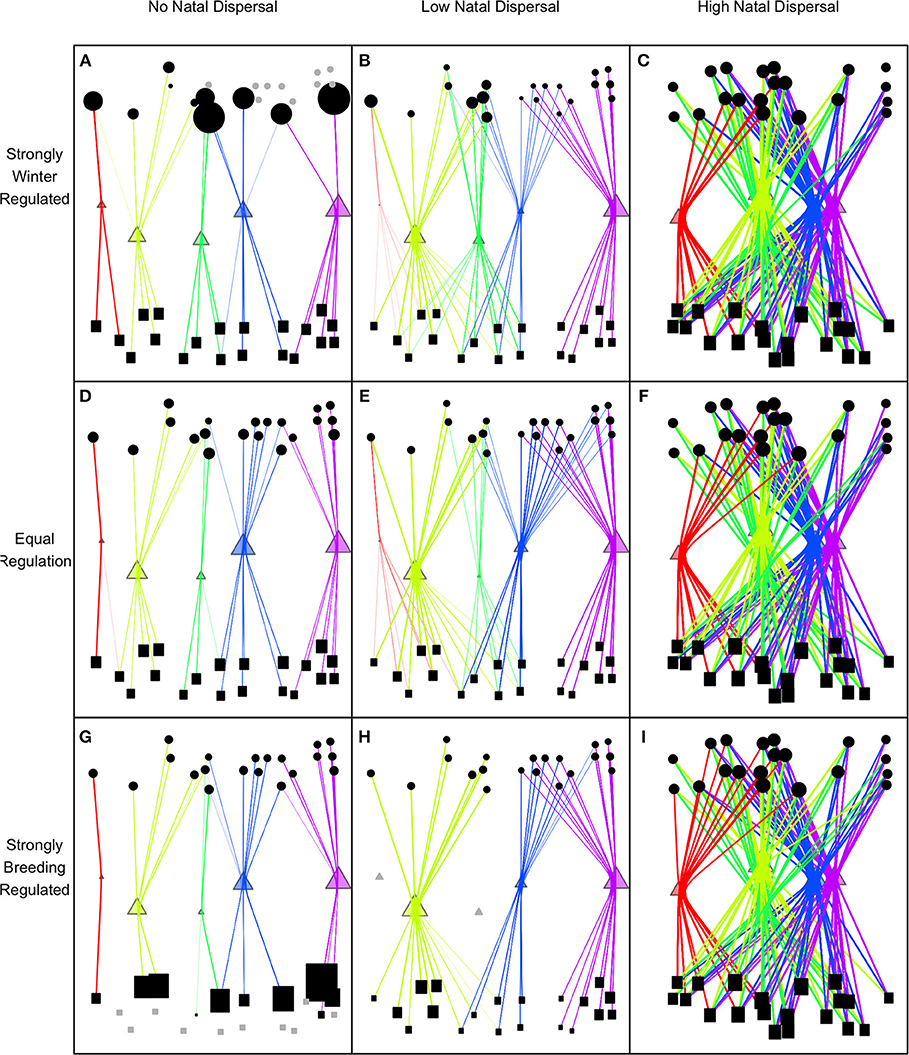
Figure 1. Equilibrium connectivity of network with randomly generated locations of breeding (circles), winter (rectangles), and route (triangles) nodes when there is no natal dispersal (ND = 0; A,D,G), low natal dispersal (ND = 0.05; B,E,H), or high natal dispersal (ND = 0.5; C,F,I), and when the network is strongly regulated by availability of habitat in winter (reg = 0.17; A,B,C), equally regulated by winter and breeding habitat (reg = 0.5; D,E,F), or strongly regulated by breeding habitat (reg = 0.83; G,H,I). The gray circles, triangles, and squares (e.g., in A,H,G) are unoccupied breeding, route, and winter nodes, respectively. The relative size of each node is proportional to the size of the node population to show the distribution of the population within each season.

FIGURE 2

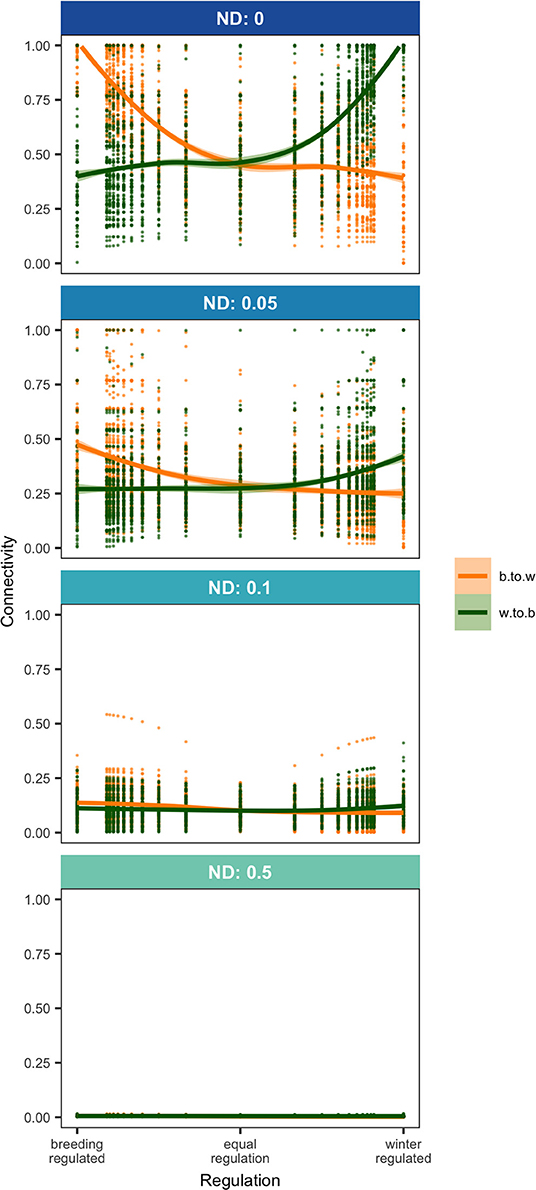
Figure 2. Breeding-to-winter (b.to.w; NMC_BW) and winter-to-breeding (w.to.b; NMC_WB; Equation 1) connectivity in networks where regulation (Equation 7) varies from 0 to 1 at four levels of natal dispersal, ND. Points show the results of model runs and trendlines are fitted locally weighted polynomial (loess) curves.

The spatial configuration of nodes, which was randomly generated, caused connectivity strengths and occupancy of nodes to be highly variable among networks with the same levels of ND and regulation but again only when there was low or no natal dispersal (Figure 2). Unoccupied nodes, which only occurred in networks with no or low natal dispersal and in seasons where regulation was relatively weak, tended to be lower quality than occupied nodes but occupancy also depended on the location of the node within the network. Since there is no regulation during migration season, occupancy and population size at route nodes were related to route node quality although location and distance from other routes also caused variation in route usage. High quality routes that were distant from others had high usage but nodes close to slightly higher quality routes had low usage (Figure 1).

Any amount of natal dispersal weakened connectivity overall in the network (Figures 1, 2) and narrowed the gap between winter-to-breeding and breeding-to-winter connectivity (Figure 2). Once natal dispersal became moderate or high, all connectivities were zero or close to zero for all values of regulation (Figures 1C,F,I, 2). High or moderate natal dispersal reduced the variation in the strengths of connectivities and also caused all nodes to be occupied irrespective of spatial location, quality, or season.

Effects of Winter Habitat Loss: Size of Declines

Winter habitat loss at a local scale, modeled as the removal of an occupied winter node, unsurprisingly led to a small population decline in a breeding-regulated network and large decline in winter-regulated network. The size of the decline was controlled almost entirely by the relative regulation of the network population and was largely unaffected by natal dispersal. There was one exception: in a strongly breeding-regulated network with no natal dispersal, winter habitat loss would cause small global declines but with high natal dispersal loss of winter habitat, in some cases, actually caused a small increase in overall population (Figure 3).

FIGURE 3

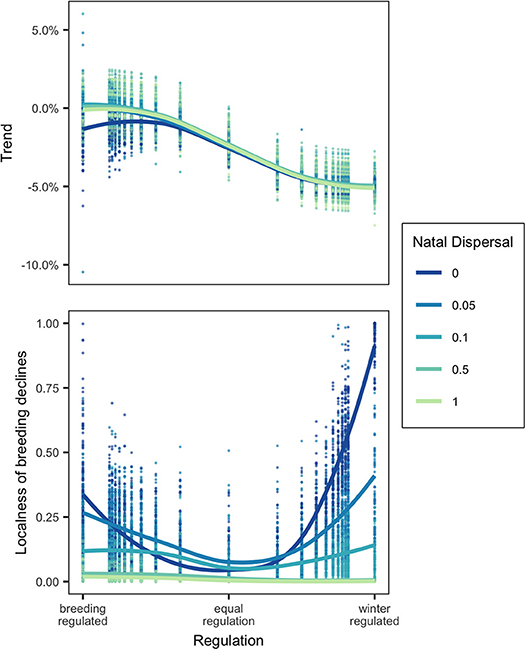
Figure 3. Top panel shows the Trend (% decline in population) and bottom panel shows the localness (as defined in text) of declines following removal of occupied winter node for networks in which regulation where regulation (Equation 7) varies from 0 to 1 at five levels of natal dispersal, ND. Points show the results of model runs and trendlines are fitted locally weighted polynomial (loess) curves.

Effects of Winter Habitat Loss: Localness of Declines

There was a large amount of variation in the distribution of declines, so much so that it is difficult to generalize results (Figure 3). When natal dispersal was high, declines caused by local winter habitat loss were always distributed throughout the breeding range (localness was low) as would be expected by the weak connectivity. With low natal dispersal, declines tended on average to be more localized when regulation was skewed toward one season and less localized when the network was equally regulated. The most localized declines were seen when there was no natal dispersal and strong winter-regulation. The most diffuse declines were either when natal dispersal was relatively unconstrained or when regulation was equal between breeding and winter. Figure 4 shows that although there are some cases where the network showed strong breeding-to-winter connectivity and localized declines due to habitat loss and other cases with weak connectivity and diffuse effects of habitat loss, there are also networks with strong connectivity where declines resulting from habitat loss were diffuse and localness was high.

FIGURE 4

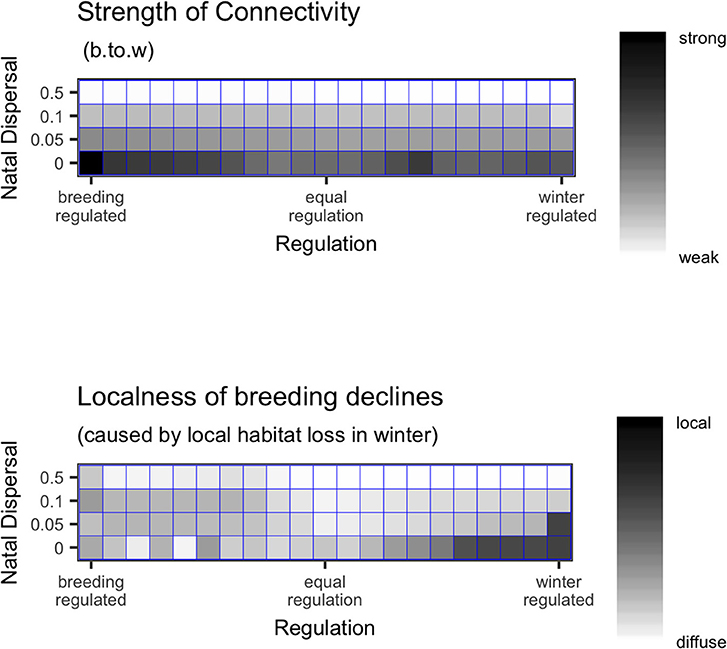
Figure 4. Top panel shows the breeding-to-winter (b.to.w; NMC_BW; Equation 1) connectivity, and bottom panel shows the localness (as defined in text) of declines, as they vary with natal dispersal, ND and regulation. The lack of correspondence between the top and bottom panels shows that connectivity is not a reliable predictor of localness.

Discussion

Both population regulation and natal dispersal affected connectivity in a migratory network and so the question arises as to what degree we can infer regulation or natal dispersal levels from connectivity patterns. When a network population was primarily regulated by one season, this caused an asymmetry in winter-to-breeding compared to breeding-to-winter connectivity (measured as the diversity of connection strengths) due to unoccupied habitat in seasons where regulation was relatively weak but natal dispersal wiped out this difference and generally made all connectivities weak. Rappole and McDonald (1994) suggested that observations of unoccupied habitat in one season could be used as indication of skewed regulation toward the opposite season so perhaps an asymmetry in connectivity could be used in the same way? However, studies that measure connectivity in both directions are rare since they involve tracking individuals from both breeding and winter locations. Stanley et al. (2015) did this for Wood thrushes and showed weak breeding-to-winter connectivity (i.e., non-breeding ranges from any breeding site were large and overlapping) and slightly stronger winter-to-breeding connectivity (breeding ranges from a given winter site were also large but there was less overlap among them), suggesting equal to winter regulation in this species. Two studies showed that Ovenbirds (Seiurus aurocapilla) exhibit weak breeding-to-wintering connectivity from individual breeding location (individuals tracked from 4 breeding locations had non-overlapping but large spread in non-breeding ranges) and similarly weak winter-to-breeding connectivity from three winter locations, suggesting equal, perhaps slightly skewed toward breeding, regulation in this species (Hallworth and Marra, 2015; Hallworth et al., 2015). Such inferences must be made with great caution, however, since even quite constrained natal dispersal tends to equalize season-to-season connectivities (Figure 2) and since the connectivity metrics depend on the geographic scales at which nodes are defined.

The overall pattern of connectivity could be an indicator of the level of natal dispersal as suggested by Cresswell (2014). One pattern that emerges from multiple avian tracking studies that we often see is strong connectivity in the network when measured at a large scale or coarse resolution (i.e., if we cluster nodes together within geographic regions) but weak connectivity at a small scale. This pattern, which is observed, for example, in Common nightingales (Luscinia megarhynchos) (Hahn et al., 2013), Ovenbirds (Hallworth and Marra, 2015; Hallworth et al., 2015), and Tree swallows (Tachycineta bicolor) (Knight et al., 2018), suggests that natal dispersal in these species is constrained since their connectivity resembles the networks in panels A, D, G, B, E, and H rather than panels C, F, or I of Figure 1.

The magnitude of declines in the species caused by local habitat loss was, as expected, strongly determined by the relative strength of density-dependence (Sherry and Holmes, 1996; Sutherland, 1996). Local winter habitat loss in a winter-regulated network population caused a large decline while the same loss caused only a small to zero decline in a breeding-regulated network population. Natal dispersal generally had no effect on the magnitude of declines with one surprising exception: in a strongly breeding-regulated network with some degree of natal dispersal, the removal of a winter node could cause the overall population size to increase. This occurred when the habitat lost was low quality and its removal causes a shift to higher quality habitat which supported a higher equilibrium cycle subpopulation size. In this case, natal dispersal could be said to be buffering the population from effects of habitat loss (Cresswell, 2014).

It is thought that if migratory animals show weak migratory connectivity then loss of habitat or other unfavorable localized events in the non-breeding season will have a diffuse effect on the size of the global breeding population and thus a small effect on any single breeding population, whereas breeding populations with strong connectivity will be more vulnerable to localized unfavorable events in the non-breeding area (Finch et al., 2017). I tested this by measuring “localness,” the diversity and evenness of declines across breeding nodes, following local winter habitat loss. While there were some general patterns, I found that localness was highly variable and difficult to predict. Natal dispersal did reduce localness (making breeding decline more diffuse) as well as making connectivity weak and thus if comparing two networks in which the connectivity difference was due to differences in natal dispersal, the relative localness of declines could be correctly inferred from the connectivity patterns. However, regulation had a non-linear effect on localness as well as affecting connectivity. With low or no natal dispersal, localness was lowest when the regulation was equal between winter and breeding and higher when skewed toward either season while breeding-to-winter connectivity decreased as winter-regulation increased. This means that if comparing two networks where the connectivity differences were due to different regulation, localness of declines would not be predictable from connectivity (Figures 3, 4). Even knowing the connectivity in a migratory network, we cannot be sure whether local habitat loss in a population will result in small or large declines or whether the declines will be localized vs. widespread unless we are also sure of the underlying processes that generate specific connectivity patterns.

The model developed here advances that presented in Taylor and Norris (2010) by demonstrating how to include natal dispersal, which has generally been overlooked in migration (Cresswell, 2014). As expected, natal dispersal had a large, easily-predictable effect on connectivity, a less-predictable but still large effect on the localness of declines resulting from habitat loss, and little-to-no effect on the magnitude of declines. Natal dispersal is modeled here as a deterministic (rather than stochastic) process in which offspring are uniformly distributed to all cycles that are within a distance threshold. The assumed dispersal kernel (the proportion or probability that an animal disperses a particular distance) is a step function with equal dispersal to all cycles closer than the threshold and no dispersal to cycles past the threshold. It would be straightforward to use a differently-shaped dispersal kernel, for example a function that declines exponentially with distance, and we might expect that this would affect the resulting connectivity patterns. However, since we know so little about natal dispersal in migratory animals, there does not appear to be a basis for assuming a different kernel shape. Natal dispersal and connectivity strength in this model are expressed as dimensionless metrics and are relative to the breeding and wintering range areas of the species. Across multiple species, high natal dispersal (ND ≈ 1.0) might be expected for a species with small breeding and winter ranges and low natal dispersal for wide-ranging species, although this pattern has not, to my knowledge, been demonstrated. The network model predicts weaker connectivity within its known range in a species with higher natal dispersal relative to its range. If it can be shown that species with smaller ranges do typically have higher relative natal dispersal, then the model predicts that, within their ranges, connectivity will typically be weaker in those species.

A second advance on Taylor and Norris (2010) is the extension to explicitly consider migration seasons, often believed to be the most critical seasons for migratory species although direct evidence for this is still rare (Sillett and Holmes, 2002; Newton, 2006; Klaassen et al., 2013). Other migratory network models have taken the approach of including stopover locations (places where animals stop to re-fuel during migration) as separate nodes in a migratory network (e.g., Iwamura et al., 2013; Knight et al., 2018). While this has the advantage of being able to examine the importance of individual stopover locations, and therefore is the appropriate approach for many questions, it complicates population modeling of these networks because individuals within the same migration route may stop at a variable number of locations. Instead, here I adopt the concept of migration routes, included in the model as single nodes. This idea follows from a long history of bird migration studies that describe routes of individual species and flyways used by multiple species (Cooke, 1905; Lincoln, 1935). Although the concept of flyways is a simplification, it has proved highly useful in regulation and conservation planning for migratory birds, including the management of migratory waterfowl and shorebirds by the U.S. Fish & Wildlife Service and its partners (https://www.fws.gov/birds/management/bird-management-plans.php) and conservation work by non-profit organizations (e.g., https://www.audubon.org/birds/flyways). Furthermore, several recent studies that track migratory birds from multiple sites have identified disjunct migration routes (e.g., Stanley et al., 2015; Brown et al., 2017; Hahn et al., 2019). The idea of migration routes, or corridors, is also important in describing the migration and planning conservation of non-avian species including elephants (Roever et al., 2013), sea turtles (Morreale et al., 1996), and ungulates (Berger and Cain, 2014; Coe et al., 2015). The simplification of route nodes allows a more general, compact, and tractable formulation of the population model as a tripartite migratory network. This model could be used to explore breeding-to-migration or winter-to-migration connectivity as well as the effects of loss or degradation of migration routes on population size. Preliminary investigations along these lines indicate that geography matters a great deal for predicting the effects of loss of migration routes. Loss of a route that is near to another of reasonably good quality (whether occupied or not) will have a small effect whereas loss of isolated routes can have large impacts. A very important assumption in this model is that the population depends on distance but is not regulated by the migration season, i.e., survival during migration depends on the quality of the route but is independent of the number or density of individuals occupying a route node. Inclusion of density-dependence in migration survival would likely have large effects on all the results presented here.

The network could easily be extended beyond tripartite to multipartite to include more seasons to represent the spring and fall migration separately or perhaps to divide the winter season to accommodate winter movements, etc. While resembling metapopulations in many ways, multipartite migratory networks function somewhat differently in that a subpopulation rather than occupying a single node is more properly thought of as occupying a set of spatial nodes (one for each season) and the links that connect them. Using graph-theory terminology, this would be termed a path or, in this case, a cycle, since the path connects back to the first node (for a general habitat network, this has also been termed a “pathway”; Wiederholt et al., 2017). I use the term cycle and the model describes population dynamics on each cycle. I modeled natal dispersal as flux between cycles. The results described above can be more deeply understood by realizing that, when not at equilibrium, some cycles are sources and some sinks. With no natal dispersal, at equilibrium, sink cycles become extinct and some nodes in a season where regulation is relatively weak are unoccupied. But with natal dispersal, there is continual dispersal into sink cycles so that, at equilibrium, most habitat in both seasons (all if natal dispersal is very high) remains occupied and connectivity is weakened.

Other possible future extensions to the model could introduce other processes that might affect connectivity or population dynamics including seasonal interactions (e.g., when quality of winter habitat affects breeding success (Norris and Taylor, 2006; Harrison et al., 2010), orientation processes, i.e., how animals orient themselves or choose routes (Thorup and Rabøl, 2001; Willemoes et al., 2014), and differential migration by sex (Briedis and Bauer, 2018), which might require coupled but separate networks for males and females. The ecological model presented here could be adapted to explore evolutionary dynamics, e.g., evolution of natal dispersal. One limitation of the multipartite network approach is that it does not consider within-year timing of processes and therefore is not perhaps the best approach to use to explore consequences of changes in phenology and mismatch. There are other network approaches, specifically migratory flow networks that can be used to explore this (Taylor et al., 2016).

In summary, the tripartite migratory network model presented here shows that the connectivity pattern in a migratory network is altered by both regulation and natal dispersal, especially the latter. Since regulation is the primary determinant of the effects of habitat loss and natal dispersal has the largest effect on connectivity, visualization of connectivity patterns is not a reliable predictor of whether declines caused by local habitat loss will be localized vs. diffuse and connectivity alone provides almost no information about the expected magnitude of declines following habitat loss. This does not mean that visualization of connectivity is not important—of course it is—but it is only the first step and understanding the processes that lead to different connectivity patterns is vital to understand population trends in migratory species.

Data Availability Statement

All datasets generated for this study are included in the manuscript/supplementary files.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This research was funded by a Scholar award from the James S. McDonnell Foundation.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ambrosini, R., Moller, A. P., and Saino, N. (2009). A quantitative measure of migratory connectivity. J. Theor. Biol. 257, 203–211. doi: 10.1016/j.jtbi.2008.11.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Berger, J., and Cain, S. L. (2014). Moving beyond science to protect a mammalian migration corridor. Ibis 28, 1142–1150. doi: 10.1111/cobi.12327

PubMed Abstract | CrossRef Full Text | Google Scholar

Briedis, M., and Bauer, S. (2018). Migratory connectivity in the context of differential migration. Biol. Lett. 14:20180679. doi: 10.1098/rsbl.2018.0679

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, S., Gratto-Trevor, C. L., Porter, R., Weiser, E. L., Mizrahi, D., Boldenow, M., et al. (2017). Migratory connectivity of Semipalmated Sandpipers and implications for conservation. Condor 119, 207–224. doi: 10.1650/CONDOR-16-55.1