- Department of Biology, Institute of Ecology and Evolution, University of Oregon, Eugene, OR, United States
Although most models conceptualize a metacommunity as a collection of habitat patches embedded in a matrix that is not hospitable to life, new applications of metacommunity theory to host-microbiome systems have shown this assumption to be flawed. Frequently the matrix is at least somewhat hospitable to the species that normally reside in the habitat patches. We modify an existing patch dynamic metacommunity model to incorporate the possibility of a hospitable matrix and expand the process of dispersal to include moving out of the patch, surviving/growing in the matrix, and moving into a new patch. With these alterations, we find that it is substantially harder for a dispersal specialist to persist in a system with a hospitable matrix compared to an inhospitable matrix. In addition, we find that the traits required to successfully disperse in the hospitable system are different from those required in the inhospitable system. The difference in dispersal traits in a hospitable environment vs. an inhospitable one could be especially of interest to host-microbiome systems where manipulation of the matrix is common practice. For example, ventilation or disinfection of built environments is a common way to change the matrix properties for metacommunities of human or animal-associated microbiomes. We conclude that the qualities of the matrix can have important effects on community assembly, and that relaxing matrix assumptions broadens the range of applications for metacommunity ecology, including its use for host-microbe systems.
Introduction
The metacommunity concept has had a wide-reaching impact on ecology (Leibold et al., 2004; Logue et al., 2011). Its central contribution has been to conceive of communities as being governed by both local and regional processes, connected by dispersal. This insight has allowed the synthesis of many disparate theoretical approaches under the umbrella of metacommunity ecology (Leibold and Chase, 2018). This synthesis has had a great influence on ecology generally, and has expanded our understanding of evolution (Urban et al., 2008), coexistence (Mouquet and Loreau, 2002), and community assembly (Mittelbach and Schemske, 2015). It has been especially influential on the emerging field of microbiome science, where it has provided a theoretical foundation for understanding microbiome variation, especially in host-microbe systems (Costello et al., 2012; Burns et al., 2017; Miller et al., 2018).
A great deal of theory has been developed around understanding the patterns expected with different metacommunity regimes defined by different levels of dispersal and patch heterogeneity. Almost all of this theory treats dispersal as direct (i.e., when colonists leave one patch they arrive instantaneously in another, with possible death along the way), and the matrix as inhospitable (i.e., no colonists remain in the matrix for the next generation or dispersal time step) (Levins and Culver, 1971; Fournier et al., 2016; Shoemaker and Melbourne, 2016; Sokol et al., 2017). Despite its prevalence, the assumption of an inhospitable matrix is not met in many ecological systems. This shortcoming (especially with regard to island biogeography) has been acknowledged in the conservation literature for years (Mendenhall et al., 2014). More recently, this assumption has been challenged by the application of metacommunity ecology to host-associated communities (i.e., the microbiomes of animals and plants; Miller et al., 2018), because a hospitable matrix is especially likely in such systems. Environmental reservoirs often play important roles in the transmission of microbiome members among animal and plant hosts, and this is likely to be true of humans as well. Most humans live in built environments that harbor microbiomes that are largely influenced by the microbiomes of the human inhabitants, which can in turn be influenced by the nature [and even the architecture (Kembel et al., 2012)] of the built environment.
Ignoring the ecology of the matrix could have important implications for our understanding of community assembly and dynamics. First, it may lead to misunderstandings about the provenance of community members if we do not take into account those that came from the matrix. Second, a hospitable matrix allows dispersal to occur over a much longer and more continuous timescale, which better captures the environment's role as a reservoir, which is commonly observed for micro-organisms. Finally, dispersal through a hospitable matrix opens up more complicated life history strategies for dispersing species. Instead of merely getting out of the old patch and into a new patch in a single step, colonists could specialize on any of the steps along the way. The traits that make a species readily able to leave a patch may not be the same as those traits that might enhance survival or growth in the matrix or even entrance into a new patch. For example, traits related to seed dispersal such as dandelion parachutes or burrs that attach to animal vectors may help get out of a patch but not be much use when it comes to getting established in a new patch. Such differences are especially apparent in host-microbiome systems where emigration and immigration often happen through entirely different routes.
Here we examine what happens when we incorporate a hospitable matrix into a metacommunity model. Instead of moving directly from patch to patch, some portion of the dispersing individuals will remain in the matrix and be eligible to complete the dispersal process in the future. We find that when the assumption of an inhospitable matrix is relaxed, it becomes clear that survival or growth in the matrix complicates the process of dispersal, and it becomes substantially harder for a dispersal specialist to persist. In addition, we find that the traits required to successfully disperse in the hospitable system are different from those required in the inhospitable system.
Materials and Methods
Patch Dynamics Framework
We set out to investigate the importance of the matrix and the strategies species employ to move through it using a simple patch dynamics model (Leibold et al., 2004). We utilize this modeling framework because it most clearly isolates the effect of dispersal on coexistence in the matrix and it is well-studied for the direct-dispersal case. The patch dynamics framework assumes identical habitat patches that are subject to random extinction events. Diversity in the system is maintained through a dispersal-competition tradeoff: one species is dominant in the patch (patch specialist) while the other species (dispersal specialist) can survive by being the first to colonize a newly empty patch. In modern coexistence parlance, this enables coexistence via the storage effect (Chesson, 2000; Shoemaker and Melbourne, 2016). Compared to other processes that promote coexistence in metacommunities, it is a weak mechanism (Shoemaker and Melbourne, 2016), but it is entirely dependent on the dispersal dynamics between patches and so it is ideal for exploring changes in dispersal within a metacommunity. There is recent evidence that a dispersal-competition tradeoff was an important factor in early microbial adaptation to dry land (Dini-Andreote et al., 2018), and it is likely to be especially important in the turbulent early days of host colonization in host-microbiome systems (Stewart et al., 2018). Therefore, we believe that this theoretical framework is ideal for examining the effect of a hospitable matrix on metacommunity processes.
To assess the effects of a hospitable matrix and an expanded range of dispersal traits on coexistence we constructed a patch-dynamic metacommunity model based on previous models that sought to understand coexistence in metacommunity processes (Shoemaker and Melbourne, 2016). This model, like the MCSim model (Sokol et al., 2017), employs a step-wise dispersal mechanism that is readily adapted to incorporate a hospitable matrix. We looked at the conditions for persistence of two competing species, one with a growth rate advantage in the patch (patch specialist) and one with a dispersal advantage (dispersal specialist). We investigated the potential for coexistence over a range of values for disturbance rate, tradeoff strength, number of patches, and mean dispersal rate in directly dispersing metacommunities, metacommunities where species could survive (but not grow) in the matrix, and metacommunities where growth was possible in the matrix.
In addition to changing the conditions of the metacommunity, we looked at the traits of the species. To be a dispersal specialist, a species must have an advantage at some point during the dispersal process to gain an overall dispersal advantage. There are three distinct methods of gaining such an advantage: a species could leave a patch at a relatively high rate compared to the patch specialist species, it could grow or survive in the matrix at a relatively high rate, or it could gain entry into a patch (from the matrix) at a relatively high rate. We call these different strategies “out trait,” “matrix growth,” and “in trait.” We alter which of these traits provide the dispersal advantage for the dispersal specialist to see whether the point at which the advantage is applied matters to the outcome of the model.
The Model
We adapted our metacommunity model from Shoemaker and Melbourne (2016). It is a discrete-time, stepwise model that keeps track of the populations of two species as they grow in and move between identical individual habitat patches. The two microbial species are differentiated by their traits at several points: growth rate in the patch (R), growth rate in the matrix (M), dispersal rate out of the patch (dout), and dispersal rate into the patch (din).
The model proceeds in a step-wise fashion: after initialization, species compete within a patch according to the Beverton-Holt model, commonly employed in metacommunity models and thus well-suited to our goal of relaxing matrix assumptions,
Here Ni, k(t) is the density of species i in patch k at time t, Ri indicates the growth rate of species i, and α is a parameter that sets the carrying capacity of a patch (see Table S1 for parameters). Competition and growth (if there is any) within the matrix happens similarly to and simultaneously with growth in the patch.
Where Ni, M is the density of species i in the matrix and Mi is the growth rate in the matrix of species i.
After a single time step in the patch, the dispersal step takes place. Species leave the patch according to their dispersal out trait, mi, k = Ni, k * dout, i, where mi, k is the migration density of species i out of patch k, and dout, i is the dispersal rate of species i out of a patch. The emigrants from all patches are combined in the matrix (with the residents in the matrix, or without for the inhospitable matrix case) and then are added back into the patches proportionally to their density in the matrix and their dispersal in trait din, i.
Finally, some patches are chosen at random for an extinction event (set by the “Patch Disturbance Rate” parameter). If a patch is disturbed, then the densities of both species in the patch are set to zero and they remain at zero until the immigration step of the next iteration.
We ran all simulations for 2,500 time steps, and because of the fluctuations inherent in the patch dynamic model we calculated final density as the average per-patch density over the last 50 time steps. We repeated each simulation 100 times and report the proportion of times a species was present at the end of the simulation. All model simulations were done using R statistical software.
Analyses
We explored the model in three ways. First, we determined the effect of a hospitable matrix by allowing persistence or growth in the matrix between time steps. Second, we examined the effect of different dispersal traits by conferring an advantage to the dispersal specialist in either dout, din, or M. Third, we confirmed that these effects were due to the matrix conditions and not merely the introduction of patch heterogeneity by adding a single matrix-like patch into a metacommunity with direct dispersal (and comparing the resulting dynamics to our original model).
In all cases, we determined the effect of altering the model by measuring persistence rates of the two species (patch specialist and dispersal specialist), across a range of number of patches and disturbance rates. There are four possible outcomes, patch specialist out-competes dispersal specialist, dispersal specialist out-competes patch specialist, coexistence, and total extinction. The prevalence of each of these outcomes is our main indicator of differential effects of survival and/or growth in the matrix.
Patch disturbance rate is a typical parameter investigated in patch-dynamic studies. It is a measure of the environmental variability and the prevalence of empty patches. In general, a higher disturbance rate should favor the dispersal specialist over the patch specialist because the dispersal specialist is better able to utilize newly emptied patches and the patch specialist is the one that primarily loses (because it is present) when a patch is destroyed. Number of patches is less well-addressed in patch dynamic studies [they often consider infinite or a very large number of patches; (Levins, 1979)] but it has the potential to greatly alter metacommunity dynamics (Burns et al., 2017).
Model Variants
We look first at the difference among a direct dispersal model, a model with a completely inhospitable matrix, a model where dispersal is indirect through a matrix where species can survive but cannot grow, and a model where all species can grow slowly and evenly in the matrix (Figure 1). We start by assuming that the dispersal specialist has the same advantage on the way in and on the way out (see Table S1 for parameter values and Figures S1–S3 for additional analyses).
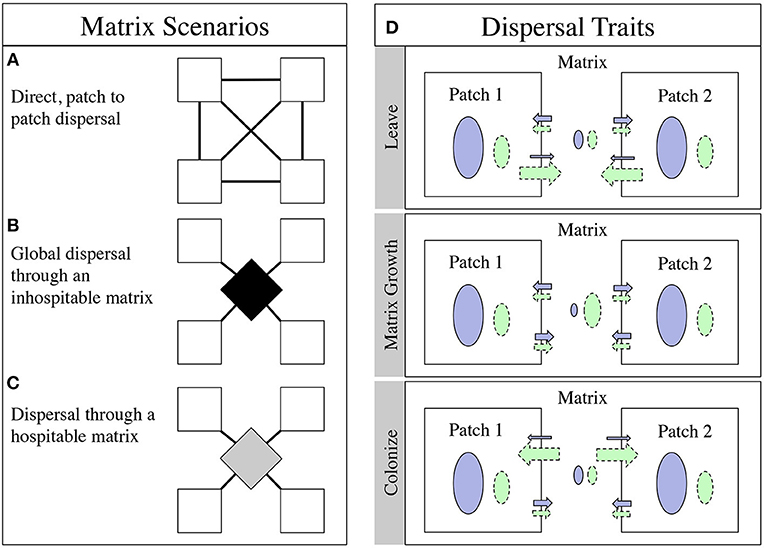
Figure 1. The alternative matrix scenarios and the different dispersal regimes. (A) The direct dispersal model, colonists from the patches move directly into another patch, symbolized by lines directly connecting the white boxes. (B) The global dispersal scenario, colonists move from the patches move into a common pool (symbolized by the black diamond) and then move back out to the patches, leaving nothing behind. (C) The hospitable matrix, colonists move from the white patches into the matrix (now a gray diamond) and back out to the patches, but some of them stay in the gray matrix to get another chance at dispersing the next timestep. (D) The dispersal scenarios. The dispersal specialist (green, dashed borders) has an advantage getting out in the Leave scenario, but no advantage getting back into the patch or growing in the matrix. The dispersal specialist has an advantage in growth in the matrix in the Matrix Growth scenario (symbolized by the ovals in the matrix), but no advantage getting out of or back into the patch. Finally, in the Colonize scenario, the dispersal specialist gets back into the patch at a higher rate, but has no advantage getting out or growing in the matrix. In all scenarios the patch specialist (blue, solid borders) has a growth advantage in the patch (symbolized by the ovals in the patches).
We begin with two variants of an inhospitable matrix. We first construct a model with direct dispersal where the emigrants from one patch are sent to another, randomly chosen patch (Figure 1A). This model has no matrix; immigrants from one patch move instantly and with their cohort to another patch. Although we call this a direct dispersal model, we maintain the stepwise process that creates an emigrant pool with the dout trait and then an immigrant pool with the din trait as described in section The Model. The patch connections are re-drawn each time step so the system becomes well-mixed. This one-to-one type of transmission may be analogous to vector-aided transmission in many systems: the duck foot theory of algae dispersal (Schlichting, 1960), for instance, or storm-driven dispersal between islands. Next, we look at a global dispersal model where all emigrants from all the patches are pooled and then evenly divided among all the patches (Figure 1B) (Shoemaker and Melbourne, 2016). The conditions of this matrix may seem somewhat artificial (global mixing, totally inhospitable matrix) but it is a commonly used approximation in the literature.
We also look at two variants of a hospitable matrix, both using the same approach as the global dispersal model (Figure 1C). First, we have a persistence model where some of the emigrants remain in the matrix but have no growth in the matrix between time steps. These residents of the matrix are then re-mixed with the dispersing cohort from the following time step and have another chance to successfully disperse to a patch. Finally, we have a low growth model where the emigrants from the patches that remain in the matrix have a low growth rate of 1.2, compared to 1.4 and 1.45 in the patches.
The choice of parameter values, as with any purely theoretical study, was not designed to exactly mimic a particular system, but to illustrate the maximum range of interesting behavior. In particular, the timescale is undefined so each time step could take a second or a year. It is important, however, to note that the rates are relevant to each other: the relative speed of growth and dispersal is fixed by the particular choice of values. To put our model in terms of host-microbiome systems, we could fix the timescale at 15 min per step. This would give our two species a doubling time in the host of about 30 min (~27 min for the patch specialist and ~30 for the dispersal specialist), slightly slower than that of some E. coli strains (~20 min) and about on par with other measured host-associated bacterial strains in zebrafish (~28 min) (Robinson et al., 2018). On this same timescale, our dispersal rate results in approximately 1 unit of density of colonists on average entering a given host in 6 time steps, or 1.5 h (at equilibrium conditions). Again, this is roughly on the same scale as we see in zebrafish systems, where researchers have measured successful colonization of a population of hosts on the order of 45 min to 5 h (Robinson et al., 2018).
Results
Inhospitable vs. Hospitable Matrix
Metacommunity Theory Expectations
As described above, we introduced a hospitable matrix into a patch dynamics model by allowing survival or growth in the matrix. From previous work (Levins and Culver, 1971) we expect there to be a range of parameter space where the dispersal specialist and the patch specialist can coexist. We also expect that an increase in the rate of disturbance will increase the advantage of the dispersal specialist relative to the patch specialist (Tilman et al., 1994). Finally, although patch number is not a well-studied parameter, we know from our own previous work (Burns et al., 2017) that increasing the number of patches can increase the relative advantage of the dispersal specialist. A simple argument that relies on the intermediate value theorem explains why, with only a single patch, the patch specialist by definition wins, and with multiple patches the dispersal specialist can persist, therefore there is an increasing function relating patch number to dispersal specialist persistence.
Effect of a Hospitable Matrix
The direct and global dispersal scenarios (Figures 1A,B) produce equivalent results (Figures 2A,B) and we will consider them together for the rest of the paper. Both of these models assume an inhospitable matrix, and the global dispersal model is often used in patch dynamics models as a short-hand for direct dispersal models. With the chosen parameter values, there is a sizeable range of coexistence (Figure 2A, Region IV), as expected. We also see that increasing the disturbance rate increases the persistence of the dispersal specialist and decreases the persistence of the patch specialist. Finally, when there are very few patches and/or very high disturbance, both species go extinct. If all patches experience a disturbance effect at the same time or in quick succession, it is likely that the entire system will go extinct.
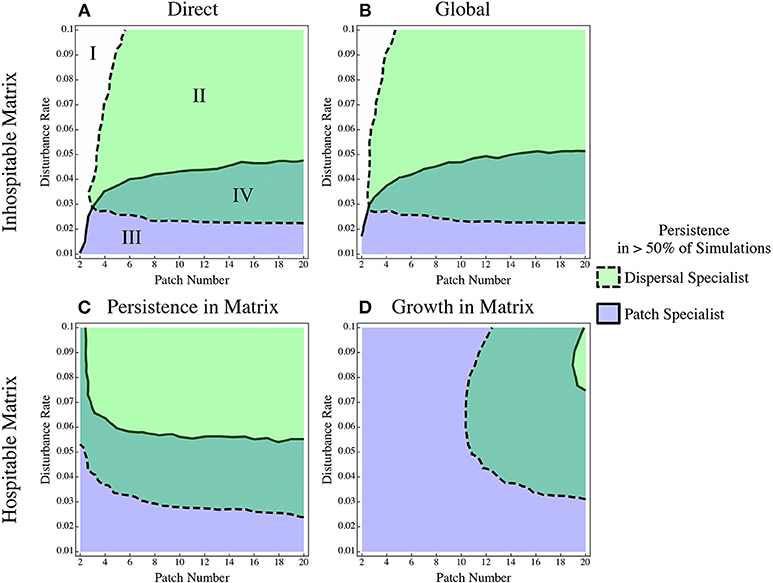
Figure 2. The persistence of a dispersal specialist and patch specialist when in competition under different dispersal regimes. The four possibilities are delineated in the first panel: I Extinction, II Dispersal specialist wins, III Patch specialist wins, IV Coexistence. Two inhospitable matrix scenarios: (A) direct dispersal and (B) the Global dispersal model, and two hospitable matrix scenarios (C) persistence in the matrix and (D) growth in the matrix. The region borders the 50% chance of persistence cline, this contour is the only plotted one for simplicity, it is a very sharp change (see Figure S4 for additional contour lines).
In the hospitable matrix scenarios, there are two main deviations from the inhospitable models. First, the region of extinction at low patch numbers disappears. The hospitable matrix provides a refuge that can maintain the population in the event of total extinction in the patches. The second main effect is that in both hospitable scenarios the dispersal specialist does worse than in the inhospitable matrix scenarios. The region of parameter space where it is able to coexist with or out-compete the patch specialist is smaller (Figure 2C). When the matrix allows growth, this effect is more pronounced (Figure 2D); the dispersal specialist loses out even when the disturbance rate is very high and can only out compete the patch specialist in a sliver of parameter space.
The dramatic shift in the dominance of the system is caused by the accumulation of patch specialists in the matrix (Figure 3). The patch specialist population in the matrix is bolstered by dispersal from patches that have not recently experienced a disturbance event. These patches have a high density of the patch specialist and nearly no dispersal specialists. Thus, even though the dispersal specialist delivers a larger proportion of its propagules to the next patch, it loses out when it comes to total biomass (Figure 3).
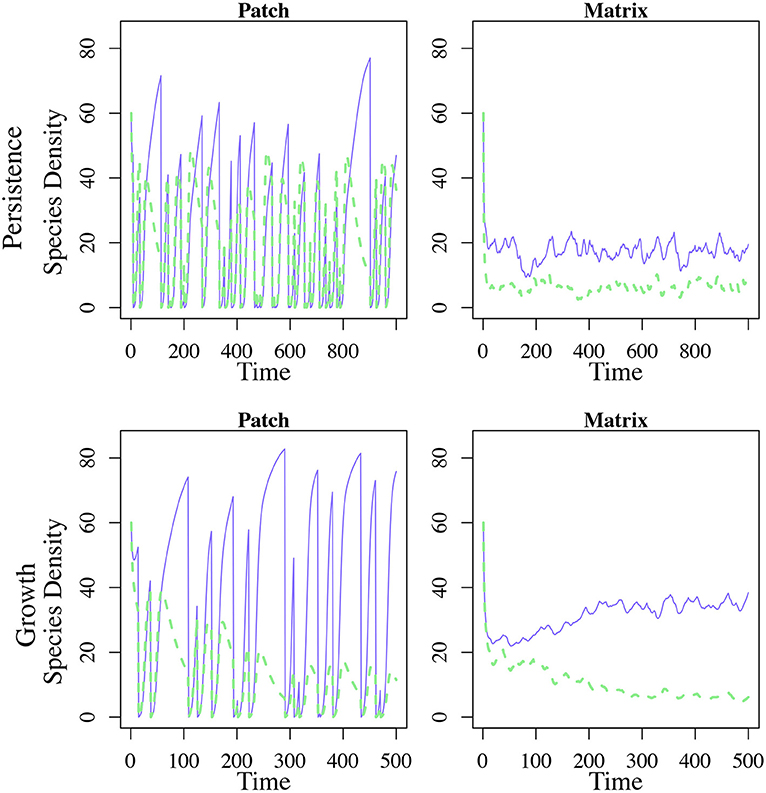
Figure 3. Population dynamics of patch and matrix with 10 patches and 0.05 disturbance. Blue, solid lines indicate the patch specialist species while green dotted lines indicate the dispersal specialist. The first row is one patch and the matrix from the persistence in the matrix model while the second row is one patch and the matrix from the growth in the matrix scenario. Only one patch from each model is shown for simplicity.
Trait Variation
Altering the Traits
To alter where in the dispersal process the dispersal specialist has an advantage over the patch specialist, we look at the three dispersal related traits dout, din, and M. In the models described in the previous section, dout and din were set so that they both conferred an equal advantage to the dispersal specialist, while M was set so that neither species had a growth advantage in the media. Now, we confer an advantage to the dispersal specialist in one of the traits at a time (Figure 1D). For the dout and din traits, when the dispersal specialist has an advantage, it has a 6-fold advantage over the patch specialist, when there is no advantage, both the disperser and the competitor have the same trait value (either dout = 0.01 or din = 0.1). By conferring the same relative advantage to each trait, we are able to directly compare the effect of specializing in one trait vs. the other. For the M trait, either the species have equal growth rates in the matrix (1 in the no growth or 1.2 in the low growth case) or the dispersal specialist has an M greater than that of the patch specialist.
dout vs. din
With an inhospitable matrix, the effects of an advantage on the way in or way out were subtle. When the dispersal specialist had an advantage on the way in Figure 4A, it did somewhat better than when it had the advantage on the way out (Figure 4B). This may be due to the effect on the patch specialist: when colonists move from the patch into the inhospitable matrix, any colonists that don't make it back into the patch are lost from the system. So, when the dispersal advantage to the dispersal specialist is in the out trait, the patch specialist by definition retains more of its population in the patch, sending out fewer colonists, and losing less of its population to the inhospitable matrix. When the surrounding matrix is deadly, it makes sense either to keep your propagules close or to equip them with the ability to move through the matrix to the next patch.
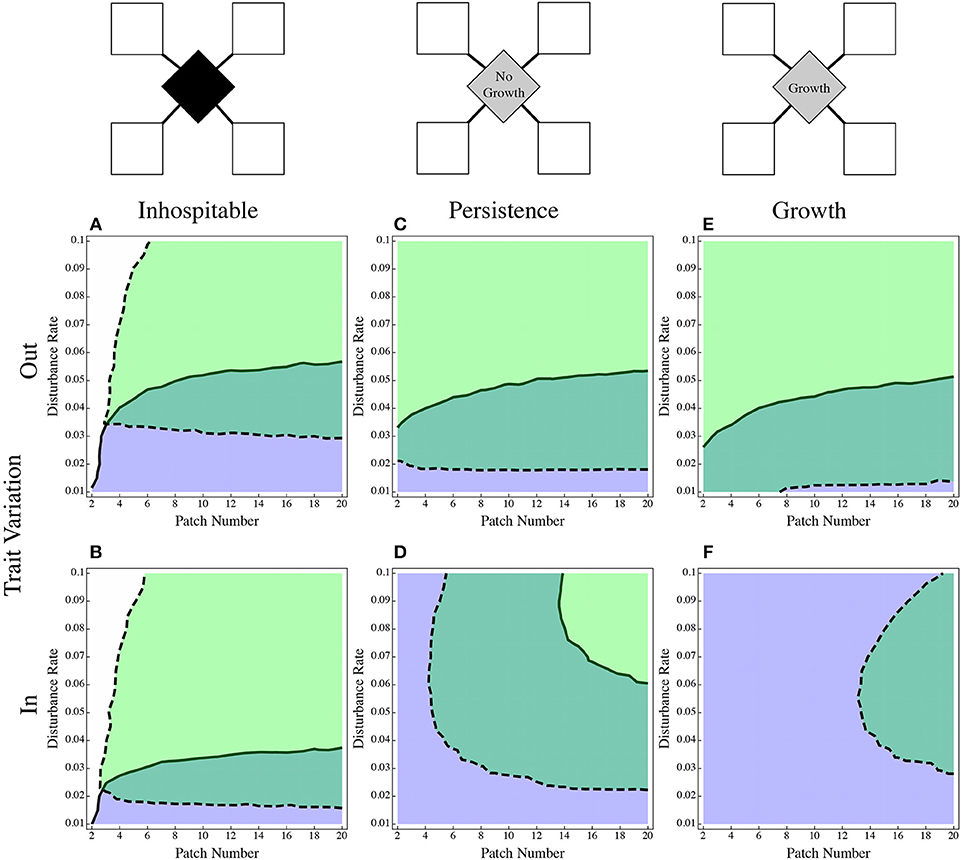
Figure 4. The effect of dispersal advantage applied on the way in vs. on the way out. The direct dispersal case (A,B) shows that the advantage being applied on the way out (A) is less advantageous for the dispersal specialist than when applied on the way in (B). The hospitable matrix scenarios (C–F) show the opposite effects, the range of the dispersal specialist is much smaller when the advantage is applied on the way into the patch (D,F) than it is on the way out of the patch (C,E). The coloring is as in Figure 1.
The opposite occurs when the matrix is more hospitable. In the persistence model (Figures 4C,D), the dispersal specialist did relatively better when its advantage was applied to the out trait (Figure 4C). Its persistence was dramatically reduced when it held an advantage only in the in trait (Figure 4D). The population is no longer lost to the matrix in this model, and as shown with (Figure 3), the composition of the matrix can alter the composition of the colonists that get moved back into the patches. The effect is even more pronounced in the model that allows growth in the matrix (Figures 4E,F), When the disperser's only advantage is in the in trait, there is no region where it excludes the patch specialist (Figure 4F).
Growth Advantage in the Matrix
Because there is by definition no growth in the matrix for the direct and global models, we cannot compare this to the inhospitable matrix as we did with the in and out traits above. Instead, we look at how much of a growth advantage the dispersal specialist needs in the matrix to overcome the growth advantage of the patch specialist in the patch (Figure 5). The nature of the matrix and the number of patches both have an effect. If the matrix is very resource poor and has depressed growth rate overall, the dispersal specialist needs a larger relative advantage to persist, but if growth is relatively fast in the matrix, it does not need such a large advantage to compensate for the patches. The number of patches contributing to the matrix has a similar effect; if there are more patches, the population in the matrix becomes dominated by emigrants, requiring more of an advantage for the dispersal specialist in the matrix. The difference in growth rates examined translates from a 25% faster doubling time in the water (top row, Figure 5) to a doubling time that is roughly twice as long in the water than in the fish (bottom row, Figure 5). This range of growth rates is consistent with measures in the zebrafish microbiome system (J. Lebov, personal communication).
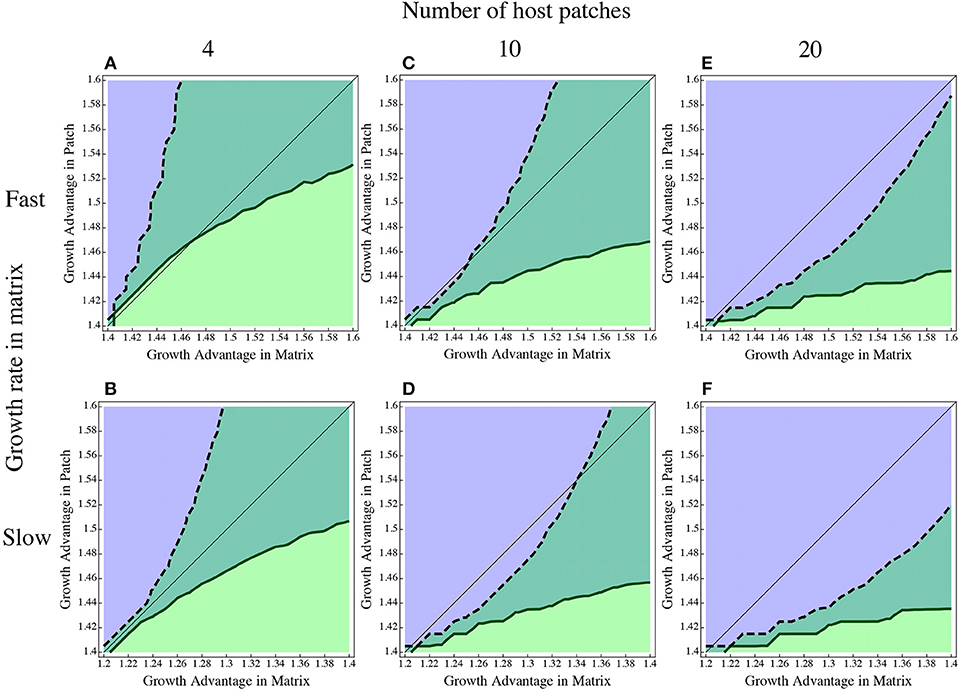
Figure 5. Dispersal advantage through growth in the matrix. The growth rate of the dispersal specialist in the patch is fixed at 1.4 and the growth rate of the patch specialist in the patch is varied along the y-axis. The growth rate of the patch specialist is fixed in the matrix at either 1.4 [top row (A,C,E)] or 1.2 [bottom row (B, D,F)] while the dispersal specialist's matrix growth is varied along the x-axis. The bottom left corner of each graph has both competitors equal in both locations. The region above the thin black line indicates more relative advantage for the patch specialist in the patch and the region below that line gives the region of more relative advantage for the disperser in the matrix.
Matrix or Patch Heterogeneity?
It is possible that these effects are a result not of the matrix, but of simply introducing patch heterogeneity into the patch dynamics model. To rule this out, we re-ran the original set of models with dispersal advantage in both traits but instead of having a hospitable matrix, we simply added another patch to the direct dispersal model with the same properties (carrying capacity and growth rate) as the matrix (Figure 6). Either we had a patch with no growth that only collected and emitted colonists (Figure 6B), or a patch with the same growth rate as the matrix in the low growth model (Figure 6C). All patches and the matrix have the same carrying capacity (results from the direct dispersal (Figure 6A) and hospitable matrix (Figures 6D,E) included for comparison). Making the matrix into just another patch retains the effect of having a refuge from disturbance and from strong competition in the patches, but it changes the flow of dispersal. A single patch does not experience dispersal in the same way that the matrix does, since all immigrants must pass through the matrix; any difference between the two models (hospitable matrix and matrix-like patch) comes from a change in the dispersal pattern. The matrix-like patch model is similar to the hospitable matrix models in that the dispersal specialist has a decreased range of persistence, but the effect is much less pronounced.
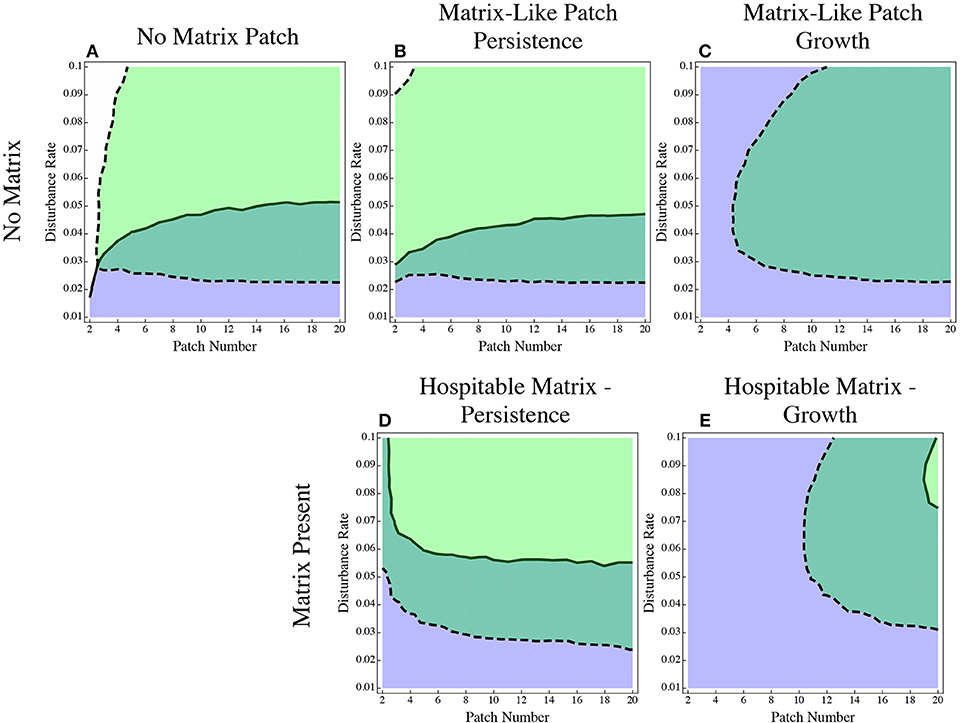
Figure 6. The effect of a matrix-like patch. In (A) there is only direct dispersal between identical patches as before. In (B) an additional patch is added to the direct dispersal model with the same properties as the matrix with no growth. In (C) an additional patch is added to the direct dispersal model with the same properties as a matrix with low growth. (D,E) are reproduced from Figure 1 for comparison. In (D) the matrix is the same as the matrix-like patch in (B,E) the matrix is the same as the matrix-like patch in (C).
Discussion
Metacommunity Theory Ignores Hospitable Matrices
The dominant theoretical approaches treat dispersal in metacommunities as a direct process, assuming a totally inhospitable matrix between the patches. This assumption is likely incorrect for many ecological systems. For example, seeds can at least survive (in dormant form) outside their preferred habitat patch. This is especially true for host-microbiome systems where many of the resident species in the host can be found living and growing in the surrounding environment. This mismatch between assumption and reality is likely to lead to incorrect conclusions about the effects of dispersal between patches and about the life history strategies that species employ to move through their environment.
We use a model that explicitly tests the impact of a hospitable environment on metacommunity processes in a patch dynamic framework. Despite the current emphasis on investigating synthesis between the metacommunity archetypes (Leibold and Chase, 2018), a purely patch dynamics model is optimal here because it allows us to manipulate dispersal in relative isolation. We look both at the effect that the characteristics of the matrix have on the outcome of competition between a dispersal specialist and a patch specialist and the effect of differing dispersal strategies that the dispersal specialist could employ. In general we find that a hospitable matrix makes it more difficult to persist as a dispersal specialist relative to an inhospitable matrix. In addition, the optimal dispersal strategies are different between the two matrix types; in an inhospitable matrix, it is best to specialize on getting into a patch, while with a hospitable matrix it is better to specialize on getting out of a patch.
What Does a Hospitable Matrix Do?
In this model and in many real-world systems, a hospitable matrix acts as a reservoir for the species in the patches, removing them from the threat of extinction when a given patch experiences disturbance. In any patchy environment where there is periodic disturbance, all populations within a patch are doomed; “dispersal is escape in space” (Levin et al., 1984). In the case of a hospitable environment, the “escape” is made by allowing individuals to leave a patch and move into the surrounding habitat. The hospitable matrix also introduces a time lag in the system: if a species goes extinct in all the patches it may still be present in the matrix at least temporarily (for an investigation of the effects of adding a time lag within a patch, see Wisnoski et al., 2019). A hospitable matrix also serves as a record of those communities that have come before. In host-microbe metacommunities, this property of the matrix has been used for such disparate applications as determining the previous inhabitants of a building (Hampton-Marcell et al., 2017) and designing optimal air flow in hospitals to cut down on hospital acquired infections (Arnold, 2014).
Community Effects
In general, a hospitable matrix makes it more difficult to be a dispersal specialist. The presence of an alternative patch, through which all dispersal flows, bolsters the dispersing populations of both species, decreasing the relative advantage of the dispersal specialist. The matrix population provides a stepping-stone for the patch specialist to gain early entrance into an empty patch, leading to an overall loss of dispersal advantage for the dispersal specialist. The dispersal strategy may also be more risky for a species in a hospitable matrix scenario, where there is a more complicated path to re-establishment in a new patch, decreasing the advantage of such a lifestyle. Thus, we might expect to see fewer “fugitive” species in systems with a hospitable matrix. The other main effect of a hospitable matrix is to provide a refuge against the stochastic extinction that occurs with direct dispersal at very low patch numbers. The hospitable matrix permits persistence and even coexistence with only a handful of patches where the direct dispersal model always eventually leads to total extinction.
Effect of Traits
How different life history strategies (reflected in dispersal traits) play out under different matrix conditions is indicative of the role of the hospitable matrix. As discussed above, exiting the patch is sufficient to bolster populations against patch disturbance with a hospitable matrix. In the inhospitable matrix case, leaving the patch is insufficient to ensure safety. This difference is reflected in the different effects of dispersal traits between the two cases. When the matrix is inhospitable, the best way to be a dispersal specialist is to be efficient at getting into a patch, whereas in the hospitable matrix it is better to be good at getting out of the patch. It is easy to imagine why this is so; an advantage in getting out of the patch in the inhospitable case would put a species at risk of loss to the surrounding matrix, but in the hospitable case, where loss to the matrix translates into a larger matrix population to colonize a new patch, the opposite is true. The mechanism works through an enhanced advantage to the dispersal specialist and also a cost to the patch specialist. If the competitor is equally good at getting out of the patch, then it loses population to the inhospitable matrix that might have otherwise stayed in the patch where it is more fit. Conversely, in the hospitable matrix case, the patch specialist (by virtue of its high population in the patch) can overcome its dispersal disadvantage if it can build up a large enough population in the matrix. This buildup of population in the matrix is evident in the population dynamics (Figure 3).
Of course, it would be possible to configure the parameters in such a way that in a hospitable system, a sufficiently high advantage in din could produce the same overall fitness advantage to the dispersal specialist as a smaller advantage in dout. The result still illustrates that specializing in getting out of the patch is a more effective strategy for the dispersal specialist in a hospitable matrix than specializing in getting in.
Trait Tradeoffs
A difference in the advantage conferred by alternative dispersal traits would be particularly dramatic if there is any sort of tradeoff between these two strategies. For example, previous work suggests that there is a negative correlation between planktonic behavior and clumping behavior among bacteria in the larval zebrafish gut, behaviors that may correspond to increased “in traits” and “out traits,” respectively (Wiles et al., 2016; Robinson et al., 2018; Schlomann et al., 2018). The tradeoff between seed number and seed size in plants may also reflect a trade-off between “in traits” and “out traits”; small seeds are produced in greater numbers than larger seeds, allowing more of them to get out of the patch (Smith and Fretwell, 1974), while larger seeds are superior at establishing in a new patch, giving them an advantage at getting in Westoby et al. (1996). The offspring quality-quantity tradeoff more generally might be another instance of this kind of tradeoff (Einum and Fleming, 2000). Whether it is better to simply send as many propagules as possible out into the environment or equip them more properly for the journey might depend on the hospitableness or deadliness of the surrounding matrix.
More Than Patch Heterogeneity
The comparison between the hospitable matrix and heterogeneous patches makes clear that the effect of a hospitable matrix goes beyond merely adding patch heterogeneity. Although, as expected, adding another patch where the patch specialist can avoid extinction in a patch decreases the advantage of the dispersal specialist, the results are much less pronounced than for the hospitable matrix. The implication is that the organization of the metacommunity dispersal network matters. The position of the matrix as “between” all other patches is crucial to its effect. To distinguish a hospitable matrix from already well-studied patch heterogeneity (e.g., via species sorting or mass effects), some degree of mixing in the matrix is necessary. Otherwise, the system reduces to a spatial model with two habitat types and source-sink dynamics. The mixing could be in the matrix itself, for example water may be reasonably well-mixed, or it could be a result of patch movement, as with mobile animal hosts and their associated microbiomes. The observed effect of disadvantaging the dispersing species is likely to be strongest when the matrix is more homogeneously mixed. In aquatic systems this is more likely to be the case than in terrestrial systems. But even in terrestrial systems, if the patches themselves are mobile (e.g., animals moving around, humans entering and exiting a building) the effect might be more like an aquatic than a terrestrial mixing of the matrix. Thus, we might expect to see dispersers in a built environment or in an aquatic environment at a greater disadvantage than in an explicitly spatial environment (e.g., the microbiome of downed logs in a forest or in pitcher plants).
Implications for Host-Associated Communities
Hospitable matrices are likely the norm in host-associated communities. It has long been known that human diseases can reside in the environment; such environmental reservoirs are called “fomites” in the literature (Boone and Gerba, 2007). Less is known about non-pathogenic human associated microbes, but there is evidence that our surrounding environment can be an important conduit for microbial dispersal influencing the composition of our gut microbiomes (Ruiz-Calderon et al., 2016; Stagaman et al., 2018). Houseplants, soil, and the surrounding environment have been shown to be proximal sources of the skin microbiome (Vandegrift et al., 2019). Conversely, the microbial cloud emitted from the human inhabitants of a room remain viable for long enough to be used for forensic purposes (Metcalf et al., 2017). In non-human primate systems there is evidence of microbiome members surviving for extended periods of time in the environment between hosts (Tung et al., 2015). In aquatic systems, the environment is often the means by which colonists move from host to host; research in aquaculture has shown that composition of the gut microbiome of fish is a subset of the community found in the surrounding water and sediments, implying that the environment provides a continuous reservoir for the microbiome (Wu et al., 2012) and that the conditions of this reservoir affects the function of the microbiome (Vadstein, 2018). The role of the matrix as a reservoir is even more obvious in plant-associated fungal communities, where the soil can retain microbial signatures of former plant microbiomes for up to 80 years after the plants have been removed (Bachelot et al., 2016). All in all, for host-microbiome systems, the hospitable matrix is the rule rather than the exception.
The hospitable matrix as a reservoir unites several concepts of species pools. Often, the species pool in ecological literature is envisioned as either the sum of all the species in all the patches (as is often the case in metacommunity models) or as some external entity (MacArthur and Wilson, 1963), uninfluenced by the events in the patches (Mittelbach and Schemske, 2015). The species pool in a system with a hospitable matrix does not reflect exactly the conditions of the patches (this is its role as a reservoir), but it is affected by colonists exiting those patches. The mix of independence and feedback between the species pool and the patches may need to be considered when applying methods to assess the neutrality of a system.
Because of the prevalence of hospitable matrices in host-microbiome systems, our results regarding traits may be particularly useful. In a system with a particularly hospitable matrix we would expect particularly transmissible microbes to specialize in getting out of the host. For example, many pathogens employ this strategy, getting themselves out of the host through sneezes and coughs. Microbes that specialize on transmission may invest more resources in surviving in the environment outside of the host; spore formation, or oxygen tolerance may be examples of this strategy. Movement through a less hospitable environment would require adaptations that ensure a quick arrival in the next host: sexual transmission that eliminates the need to persist in the environment or chemotaxis to quickly find a new host.
Manipulation of the matrix to alter the transmission of microbes is an important way that humans and other animals manipulate their microbiomes. Humans alter the transmission of pathogens through changing the ventilation and cleaning of our buildings, social insects imbue their nests with antimicrobial compounds (Turnbull et al., 2011), and birds build their nests out of antimicrobial plants (Ruiz-Castellano et al., 2016). Our results suggest that such matrix management can have different results for different species. Measures that decrease the hospitality of the environment may end up selecting for transmission specialists at the expense of host-specialist species. If it is the case that pathogenic bacteria tend to be better adapted for transmission than commensal strains that specialize in playing nice with the host, our efforts at cleaning and hygiene might be counterproductive.
Future Studies
We have only scratched the surface of the implications of matrix conditions for metacommunities. We highlight three important avenues for continuing research: evolutionary dynamics, patch heterogeneity, and experimental studies with model organisms. Our observation of differential advantages of different life history strategies under hospitable and inhospitable matrix conditions raises questions about how evolutionary dynamics would proceed in these systems. Our model incorporates traits but not trait change; what would an evolutionary stable dispersal strategy look like under different matrix types? Do we see differences in average seed mass and dispersal ability across landscapes with different matrix types? The possibility of tradeoffs between dout and din could lead to drastically different evolutionary endpoints.
This study also limits itself to the patch dynamic archetype; what would the role of the matrix be in a system that also included patch heterogeneity? Here, the recent work by Wisnoski et al. (2019) might provide a clue. They find that dormancy in a patch increases the overall diversity of the system; a hospitable matrix (which induces its own kind of time lag) could have a similar effect. Interest in bridging the gaps between different archetypes has been surging in metacommunity research. This could be another interesting avenue to pursue.
As always, our theoretical results must be tested empirically. In plant and animal systems, the relevant real-world tests might involve attempting to quantify species ability to survive in the matrix, and perhaps manipulating that ability. Using host-microbiome systems with model organisms might be particularly fruitful. With model organisms in laboratory settings, it would be possible to dial up or down the hospitableness of the matrix, either through sterilization or fertilization of the housing conditions. The way in which microbes move between hosts could also be manipulated: For example, one could prevent direct dispersal between hosts by physically separating the individuals, but allowing microbes to move between habitats. One could also directly manipulate the relative importance of dout and din, for example by adding microbes directly to the gut (e.g., via gavage).
Finally, because matrix management is so common in human systems, microbiome surveys of built environments might be an excellent source of real world data with which to test these ideas. If changing the matrix changes the composition of human microbiomes, we would expect to see a change in composition after changes in matrix properties (for example, before and after implementation of new cleaning procedures). We might also expect to see different microbiomes in people who live in more or less easily disinfected environments.
Conclusion
Metacommunity ecology has proven to be a useful framework for incorporating dispersal processes into our understanding of community assembly, but it has typically assumed that patches are separated by an inhospitable matrix. In this paper we expand the usefulness of the metacommunity framework to include systems where the matrix itself is a player. We find that there is a sizeable impact of the matrix on community outcomes, both in terms of coexistence and in terms of the most advantageous traits. It is becoming increasingly clear that the matrix cannot be excluded when considering host-microbiome metacommunities, but it is also likely that many plant and animal metacommunities do not meet the assumption of an inhospitable matrix. Thus, our expansion serves not only to broaden the application of metacommunity theory (e.g., to host-microbiome systems) but also to illuminate processes common to all of ecology.
Data Availability
The code used to generate the model for this study can be found on github https://github.com/bethmillery/hospitable-matrix.
Author Contributions
EM conducted the modeling and wrote the first draft of the manuscript. BB contributed substantially to the intellectual development of the ideas and revisions.
Funding
This work was supported by a grant from The National Institutes of Health #215220 and 217100.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2019.00276/full#supplementary-material
References
Arnold, C. (2014). Rethinking sterile: the hospital microbiome. Environ. Health Perspect. 122, 1–6. doi: 10.1289/ehp.122-A182
Bachelot, B., Uriarte, M., Zimmerman, J. K., Thompson, J., Leff, J. W., Asiaii, A., et al. (2016). Long-lasting effects of land use history on soil fungal communities in second-growth tropical rain forests. Ecol. Appl. 26, 1881–1895. doi: 10.1890/15-1397.1
Boone, S. A., and Gerba, C. P. (2007). Significance of fomites in the spread of respiratory and enteric viral disease. Appl. Environ Microb. 73, 1687–1696. doi: 10.1128/AEM.02051-06
Burns, A. R., Miller, E. T., Agarwal, M., Rolig, A. S., Milligan-Myhre, K., Seredick, S., et al. (2017). Inter-host dispersal overwhelms host factors in the assembly of host-associated microbial communities. Proc. Natl. Acad. Sci. U.S.A. 114, 11181–11186. doi: 10.1073/pnas.1702511114
Chesson, P. (2000). Mechanisms of maintenance of species diversity. Annu. Rev. Ecol. Syst. 31, 343–366. doi: 10.1146/annurev.ecolsys.31.1.343
Costello, E. K., Stagaman, K., Dethlefsen, L., Bohannan, B. J. M., and Relman, D. A. (2012). The application of ecological theory toward an understanding of the human microbiome. Science 336, 1255–1262. doi: 10.1126/science.1224203
Dini-Andreote, F., van Elsas, J. D., Olff, H., and Salles, J. F. (2018). Dispersal-competition tradeoff in microbiomes in the quest for land colonization. Sci. Rep. 8:9451. doi: 10.1038/s41598-018-27783-6
Einum, S., and Fleming, I. A. (2000). Highly fecund mothers sacrifice offspring survival to maximize fitness. Nature 405, 565–567. doi: 10.1038/35014600
Fournier, B., Mouquet, N., Leibold, M. A., and Gravel, D. (2016). An integrative framework of coexistence mechanisms in competitive metacommunities. Ecography 40, 630–641. doi: 10.1111/ecog.02137
Hampton-Marcell, J. T., Lopez, J. V., and Gilbert, J. A. (2017). The human microbiome: an emerging tool in forensics. Microb. Biotechnol. 10, 228–230. doi: 10.1111/1751-7915.12699
Kembel, S. W., Jones, E., Kline, J., Northcutt, D., Stenson, J., Womack, A. M., et al. (2012). Architectural design influences the diversity and structure of the built environment microbiome. Isme J. 6, 1469–1479. doi: 10.1038/ismej.2011.211
Leibold, M. A., Holyoak, M., Mouquet, N., Amarasekare, P., Chase, J. M., Hoopes, M. F., et al. (2004). The metacommunity concept: a framework for multi-scale community ecology. Ecol. Lett. 7, 601–613. doi: 10.1111/j.1461-0248.2004.00608.x
Levin, S. A., Cohen, D., and Hastings, A. (1984). Dispersal strategies in patchy environments. Theor. Popul. Biol. 26, 165–191. doi: 10.1016/0040-5809(84)90028-5
Levins, R. (1979). Coexistence in a variable environment. Am. Nat. 114, 765–783. doi: 10.1086/283527
Levins, R., and Culver, D. (1971). Regional coexistence of species and competition between rare species. Proc. Natl. Acad. Sci. U.S.A. 33, 1246–1248. doi: 10.1073/pnas.68.6.1246
Logue, J. B., Mouquet, N., Peter, H., and Hillebrand, H. (2011). Empirical approaches to metacommunities: a review and comparison with theory. Trends Ecol. Evol. 26, 482–491. doi: 10.1016/j.tree.2011.04.009
MacArthur, R. H., and Wilson, E. O. (1963). An equilibrium theory of insular zoogeography. Evolution 17, 373–387. doi: 10.1111/j.1558-5646.1963.tb03295.x
Mendenhall, C. D., Karp, D. S., Meyer, C. F. J., Hadly, E. A., and Daily, G. C. (2014). Predicting biodiversity change and averting collapse in agricultural landscapes. Nat. Commun. 509, 213–217. doi: 10.1038/nature13139
Metcalf, J. L., Xu, Z. Z., Bouslimani, A., Dorrestein, P., Carter, D. O., and Knight, R. (2017). Microbiome tools for forensic science. Trends Biotechnol. 35, 814–823. doi: 10.1016/j.tibtech.2017.03.006
Miller, E. T., Svanbäck, R., and Bohannan, B. J. M. (2018). Microbiomes as metacommunities: understanding host-associated microbes through metacommunity ecology. Trends Ecol. Evol. 33, 926–935. doi: 10.1016/j.tree.2018.09.002
Mittelbach, G. G., and Schemske, D. W. (2015). Ecological and evolutionary perspectives on community assembly. Trends Ecol. Evol. 30, 241–247. doi: 10.1016/j.tree.2015.02.008
Mouquet, N., and Loreau, M. (2002). Coexistence in metacommunities: the regional similarity hypothesis. Am. Nat. 159, 420–426. doi: 10.1086/338996
Robinson, C. D., Klein, H. S., Murphy, K. D., Parthasarathy, R., Guillemin, K., and Bohannan, B. J. M. (2018). Experimental bacterial adaptation to the zebrafish gut reveals a primary role for immigration. PLoS Biol. 16:e2006893. doi: 10.1371/journal.pbio.2006893
Ruiz-Calderon, J. F., Cavallin, H., Song, S. J., Novoselac, A., Pericchi, L. R., Hernandez, J. N., et al. (2016). Walls talk: Microbial biogeography of homes spanning urbanization. Sci. Adv. 2:e1501061–e1501068. doi: 10.1126/sciadv.1501061
Ruiz-Castellano, C., Tomás, G., Ruiz-Rodríguez, M., Martín-Gálvez, D., and Soler, J. J. (2016). Nest material shapes eggs bacterial environment. PLoS ONE 11:e0148894. doi: 10.1371/journal.pone.0148894
Schlichting, H. E. J. (1960). The role of waterfowl in the dispersal of algae. Trans. Am. Microsc. Soc. 79, 160–166. doi: 10.2307/3224082
Schlomann, B. H., Wiles, T. J., Wall, E. S., Guillemin, K., and Parthasarathy, R. (2018). Bacterial cohesion predicts spatial distribution in the larval zebrafish intestine. Biophys. J. 115, 2271–2277. doi: 10.1016/j.bpj.2018.10.017
Shoemaker, L. G., and Melbourne, B. A. (2016). Linking metacommunity paradigms to spatial coexistence mechanisms. Ecology 97, 2436–2446. doi: 10.1002/ecy.1454
Smith, C., and Fretwell, S. (1974). The optimal balance between size and number of offspring. Am. Nat. 108, 499–506. doi: 10.1086/282929
Sokol, E. R., Brown, B. L., and Barrett, J. E. (2017). A simulation-based approach to understand how metacommunity characteristics influence emergent biodiversity patterns. Oikos 126, 732–737. doi: 10.1111/oik.03690
Stagaman, K., Cepon-Robins, T. J., Liebert, M. A., Gildner, T. E., Urlacher, S. S., Madimenos, F. C., et al. (2018). Market Integration Predicts human gut microbiome attributes across a gradient of economic development. mSystems 3:e00122–17. doi: 10.1128/mSystems.00122-17
Stewart, C. J., Ajami, N. J., O'Brien, J. L., Hutchinson, D. S., Smith, D. P., Wong, M. C., et al. (2018). Temporal development of the gut microbiome in early childhood from the TEDDY study. Nat. Commun. 562, 583–588. doi: 10.1038/s41586-018-0617-x
Tilman, D., May, R. M., Lehman, C. L., and Nowak, M. A. (1994). Habitat destruction and the extinction debt. Nature 371, 65–66. doi: 10.1038/371065a0
Tung, J., Barreiro, L. B., Burns, M. B., Grenier, J.-C., Lynch, J., Grieneisen, L. E., et al. (2015). Social networks predict gut microbiome composition in wild baboons. Elife 4:e05224. doi: 10.7554/eLife.05224
Turnbull, C., Hoggard, S., Gillings, M., Palmer, C., Stow, A., Beattie, D., et al. (2011). Antimicrobial strength increases with group size: implications for social evolution. Biol. Lett. 7, 249–252. doi: 10.1098/rsbl.2010.0719
Urban, M. C., Leibold, M. A., Amarasekare, P., De Meester, L., Gomulkiewicz, R., Hochberg, M., et al. (2008). The evolutionary ecology of metacommunities. Trends Ecol. Evol. 23, 311–317. doi: 10.1016/j.tree.2008.02.007
Vadstein, O. (2018). K-selection as microbial community management strategy: a method for improved viability of larvae in aquaculture. Front. Microbiol. 9:2730. doi: 10.3389/fmicb.2018.02730
Vandegrift, R., Fahimipour, A. K., Muscarella, M., Bateman, A. C., Van Den Wymelenberg, K., and Bohannan, B. J. M. (2019). Moving Microbes: the Dynamics of Transient Microbial Residence on Human Skin. Available online at: https://www.biorxiv.org/content/10.1101/586008v1 (accessed April 9, 2019).
Westoby, M., Leishman, M., and Lord, J. (1996). Comparative ecology of seed size and dispersal. Philos. Trans. R. Soc. London B: Biol. Sci. 351, 1309–1318. doi: 10.1098/rstb.1996.0114
Wiles, T. J., Jemielita, M., Baker, R. P., Schlomann, B. H., Logan, S. L., Ganz, J., et al. (2016). Host gut motility promotes competitive exclusion within a model intestinal microbiota. PLoS Biol. 14:e1002517. doi: 10.1371/journal.pbio.1002517
Wisnoski, N. I., Leibold, M. A., and Lennon, J. T. (2019). Dormancy in metacommunities. Am. Nat. 194. doi: 10.1086/704168
Keywords: metacommunity, dispersal, patch dynamics, host-microbiome, modeling, theory
Citation: Miller ET and Bohannan BJM (2019) Life Between Patches: Incorporating Microbiome Biology Alters the Predictions of Metacommunity Models. Front. Ecol. Evol. 7:276. doi: 10.3389/fevo.2019.00276
Received: 25 April 2019; Accepted: 03 July 2019;
Published: 18 July 2019.
Edited by:
Marco A. Molina-Montenegro, University of Talca, ChileReviewed by:
Florence Anne Laure Gutzwiller, Center for Bioinformatics and Integrative Biology (CBIB), ChileSebastian Abades, Universidad Mayor, Chile
Copyright © 2019 Miller and Bohannan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Elizabeth T. Miller, ZW1pbGxlcjhAdW9yZWdvbi5lZHU=
 Elizabeth T. Miller
Elizabeth T. Miller Brendan J. M. Bohannan
Brendan J. M. Bohannan