Optimal Control of Rat-Borne Leptospirosis in an Urban Environment

Humans acquire leptospirosis through direct contact with animal reservoirs, or more commonly, contact with the environment contaminated with leptospires shed in animal urine. Reservoir populations can be difficult to control through rodenticide application, and resource reduction via habitat management is costly and logistically complicated to implement. When resources are limited, simulation of different combinations of control methods can inform their application in the field. Here we present a framework to find time-dependent control measures for rodent-borne leptospirosis using optimal control mathematical model theory. An age-structured model for leptospire infection in a Norway rat (Rattus norvegicus) population was developed, informed by empirical analyses of data from the city of Salvador, Brazil. We extended this model to include two temporary control measures, rodenticide, and resource reduction, and two permanent control measures, reducing rat carrying capacity and leptospire lifespan in the environment. Optimal control theory seeks the optimum time-dependent controls while taking into account both the cost of the control measures and the “cost” of infection. Multiple control scenarios and the predicted effect of the optimal controls on the population and infection dynamics are presented to illustrate the applications of combinations of temporary and permanent controls. Permanent controls lead to a reduction in prevalence of leptospiral carriage in the rodent population. However, temporary controls can also achieve a reduction in the number of infected rats low enough to reduce risk to humans. Although we focus our modeling on a well-studied species, the Norway rat, our approach can be applied to other disease systems with animal and environmental reservoirs to inform decisions to reduce the risk of human infection.

Introduction

Leptospirosis is one of the most widespread zoonoses, with over a million cases worldwide (Costa et al., 2015a). Generally, animals are ultimately responsible for the maintenance of zoonotic pathogens causing human disease, and control of the animal population is often the main target in reducing human infection. Removal of zoonotic reservoirs to reduce or prevent human risk of infection has previously been achieved for Hantavirus (Zhang et al., 2010) and visceral leishmaniasis (Ashford et al., 1998). However, while humans may acquire leptospire infection through direct contact with the animal reservoir, it more commonly occurs through contact with the environment (water and soil) contaminated with leptospires shed in animal urine. In the urban slums of Salvador, Brazil, the incidence of severe cases of human leptospirosis is high, 58.7 per 100,000 residents, with annual peaks in the rainy season (Reis et al., 2008). To prevent human infection, the cycle of infection must be broken. In terms of control, one crucial choice, therefore, is whether to target the animal or the environmental reservoir.

Typical of tropical urban slum environments world-wide, Norway rats, Rattus norvegicus, are the natural reservoir of leptospirosis in Salvador (Costa et al., 2014b). The high prevalence of infection in the rat population (Costa et al., 2014a), the high concentration of leptospires shed by the rats (Costa et al., 2015b), and an apparent lifetime of shedding following infection (Ellis, 2015) combine to make Norway rats a particularly effective reservoir. Indeed, in Salvador, an environmental reservoir of soil and water contaminated with leptospires appears to be maintained solely by the Norway rat population (Costa et al., 2015b; Minter et al., 2017). Human leptospirosis in Salvador appears to be solely caused by L. interrogans serogroup Icterohaemorrhagiae. Such pathogenic leptospires are not known to reproduce in the environment, and survival at least of the vast majority of the population is short (Evangelista and Coburn, 2011; Casanovas-Massanaa et al., 2018). Therefore, reduction in the rodent population will, in turn, reduce the environmental load of leptospires.

Indirect evidence suggests that humans acquire infection predominantly through contact with open sewers and annual flooding washing contaminated soil into areas of human use (Reis et al., 2008; Hagan et al., 2016). Nonetheless, the question remains as to whether control should target the ultimate source of infection (the rats) or the immediate threat (typically, the contaminated environment).

Environmental controls, such as closure of open sewers and improved drainage, would directly reduce risk of infection for humans, by limiting their exposure to a contaminated environment, but require large scale concerted effort, making them more difficult, and expensive to implement than animal control (Costa et al., 2017). However, Norway rat populations are themselves difficult to control as they are neophobic (Clapperton, 2006), reducing uptake of rodenticides, and rats can become resistant to rodenticides (Clapperton, 2006). Populations recover quickly after a population decrease (Shilova and Tchabovsky, 2009), as a result either of in situ survival with subsequent reproduction or immigration (Hein and Jacob, 2015). At best, therefore, rodenticide exerts only short-term population reduction.

Reducing the suitability of habitat by restricting access to food and refuges can itself reduce the carrying capacity of the rodent population (Lambert et al., 2008; Adrichem et al., 2013; Buckle, 2013). For example, in cities like Salvador, reducing access to food could be achieved by improving removal of garbage and reducing access of rats to houses, and available refuges could be reduced by clearing larger pieces of garbage, construction materials, and dense vegetation. Further, the reduction of suitable rodent habitat by, for example, closing open sewers, would at the same time increase the mortality of leptospires by decreasing moisture levels in the soil and exposing them to UV radiation (Lambert et al., 2008; Casanovas-Massanaa et al., 2018). Additional environmental controls exist, such as paving areas to improve drainage, which we anticipate would increase leptospire mortality.

Mathematical models can be used to test the effectiveness of control measures in an infected population (Hethcote, 2000). Optimal control theory seeks to identify optimum time-dependent controls, while considering both the cost of the control measures and the cost of having no control (in this case the cost of rats, or of a given level of environmental contamination). Time-dependent effects are important as, for example, control measures applied intermittently (such as rodenticides) may be wasteful if applied at the wrong time, and reactive measures generally should be sensitive to changes in rat populations and the environment (Traweger et al., 2006). Given restrictions on resources and time, it is of interest to find the optimal level and disposition of control efforts to inform intervention policies.

Here, an age-structured model for leptospire infection in the Norway rat population of Salvador is presented, informed by empirical analysis (Costa et al., 2015b; De Oliveira et al., 2016; Panti-May et al., 2016; Minter et al., 2017). This model is then extended to include time dependent rodent control measures integrating rodenticide applications and resource reduction. We present the predicted effects of the control measures on the total population size of rats, the population size of infected individuals, and the size of the environmental load of leptospires. In addition, we explore the effects of environmental controls that permanently change the carrying capacity of the rodent population, the environmental loads and the mortality of leptospires.

Estimates of the costs of control measures, and especially of not applying controls, are all approximate. Hence, the outputs of our analysis are not designed as the basis for management recommendations. Rather, they provide illustrations of how the key features a rodent-environment-zoonosis system, exemplified by urban leptospirosis carried by rats, may drive the generation of optimal control strategies. Thus, for example, we explore how the timing of temporary measures (such as direct rodent control) may interact with more permanent interventions (for example, modifying the environment), and the dependence of this on their relative costs. Such general patterns may themselves then identify where improved estimates of costs would be most valuable in the direct application of approaches such as this in developing management plans.

Materials and Methods

An Age Structured Model for Leptospire Infection in Rattus norvegicus

The model is based on that presented by Minter et al. (2018) with an age structure following Holt et al. (2006). The model is assumed to represent a population of rodents within the urban slums of Salvador, Brazil as described in Minter et al. (2018). The urban slums are comprised of valleys in which the trapped population of rodents surpasses 100. It comprises a system of seven differential equations representing the number of juveniles (J), sub-adults (W), and adults (A) as follows:

$\begin{array}{l}\frac{d{J}_X}{dt}=b(1-u(t))(A_X+(1-{\upsilon }_1)A_Y)exp(-\alpha (W+A))\hfill \\ - {\phi }_J{J}_X-m_J{J}_X\hfill & (1)\end{array}$

$\begin{array}{l}\frac{d{J}_Y}{dt}=b(1-u(t))A_Y{\upsilon }_{1}exp(-\alpha (W+A))\hfill \\ - {\phi }_J{J}_Y-m_J{J}_Y\hfill & (2)\end{array}$

$\begin{array}{ll}\begin{array}{l}\frac{d{W}_X}{dt}={\phi }_J{J}_X-{\upsilon }_2{W}_X(W_Y+A_Y)/(W+A)-{\upsilon }_3{W}_{X}L-{\phi }_W{W}_X\hfill \\ \begin{array}{c}- m_W{W}_X-p\tau (t)W_X\end{array}\hfill \end{array}& (3)\end{array}$

$\begin{array}{ll}\begin{array}{l}\frac{d{W}_Y}{dt}={\phi }_J{J}_Y+{\upsilon }_2{W}_X(W_Y+A_Y)/(W+A)+{\upsilon }_3{W}_{X}L-{\phi }_W{W}_Y\hfill \\ - m_W{W}_Y-p\tau (t)W_Y\hfill \end{array}& (4)\end{array}$

$\begin{array}{ll}\begin{array}{l}\frac{d{A}_X}{dt}={\phi }_W{W}_X-{\upsilon }_2{A}_X(W_Y+A_Y)/(W+A)-{\upsilon }_3{A}_{X}L\hfill \\ - m_A{A}_X-p\tau (t)A_X\hfill \end{array}& (5)\end{array}$

$\begin{array}{ll}\begin{array}{l}\frac{d{A}_Y}{dt}={\phi }_W{W}_Y+{\upsilon }_2{A}_X(W_Y+A_Y)/(W+A)+{\upsilon }_3{A}_{X}L\hfill \\ - m_A{A}_Y-p\tau (t)A_Y\hfill \end{array}& (6)\end{array}$

$\begin{array}{ll}\frac{dL}{dt}=l_W{W}_Y+l_A{A}_Y-\mu L& (7)\end{array}$

with subscripts X and Y indicating susceptible and infected individuals, respectively (see also Figure 1).

FIGURE 1

Figure 1. Flow diagram of the age structured model with self-regulation incorporated.

Rats are born into the juvenile class at a constant rate b throughout the year. All offspring of susceptible adults (A_X) are born susceptible, but infected adults (A_Y) “give birth” to a proportion (υ₁) of infected offspring. The offspring can be infected in utero, through perinatal infection or from environmental contamination in the nest. We cannot distinguish these routes as juvenile animals are confined to the nest. There is self-regulation of the birth rate, at intensity α, where all sub-adults and adults (W + A = (W_X + W_Y) + (A_X + A_Y)) are competing for resources, reducing the birth rate in the system, which in turn introduces an effective “carrying capacity” to the population. The parameter u relates to control and is described below.

Juveniles (J) are those individuals not yet able to exist independently outside the nest, suffering in-nest mortality at rate m_J. Juveniles mature into sub-adults at a rate φ_J. Sub-adults can become infected via direct contact with infected sub-adults or adults at rate (υ₂) or via contact with the environment (rate υ₃). Sub-adults suffer mortality at rate m_W. Sub-adults then mature into adults at a rate φ_W, where they are at risk of further direct and environmental transmission (at the same rates as the sub-adults, υ₂, υ₃). Adults suffer mortality at rate m_A.

Infected sub-adults and adults both shed into the population of free-living leptospires [L, Equation (7)], but at different rates (l_W, l_A) specified on a log10 scale. Infected juveniles may shed but if they do it will be in the nest, not into the environment as we have defined it here. Free-living leptospires suffer mortality at rate μ.

Parameter values were informed directly from field data or estimated based on field data. Table 1 provides details.

TABLE 1

Table 1. Parameter definitions and values for the age-structured model.

Control Measures

We investigate the effect of, in total, four control measures on the rodent infection dynamics and environmental load of leptospires. These are two-time dependent controls—rodenticide and resource reduction—and two permanent environmental controls: carrying capacity control and leptospire mortality control. It is worth noting that both rodenticide and resource reduction will target all rats, not just those that are infected. Resource reduction can be implemented after a rodenticide program, the aim being to prevent the population from recovering. The time-dependent controls are incorporated into the structure of the mathematical model. The two environmental controls are assumed to have a permanent effect and so are specified as permanent changes in the model parameter values.

Rodenticide is incorporated by assuming that a proportional number of susceptible and infected, sub-adults and adults are removed, according to the total target proportion at time t, τ(t), and the probability that a rat contacts the rodenticide, p, which is constant (Equations 1–7). We assume that if a rodent contacts rodenticide, then death is certain, since, for example, Mlynarèíková et al. (1999) found a mortality rate of 100% after 8 days when Norway rats consumed bromadiolone rodenticide. Rodenticide is placed outside houses and so animals that are confined to the nest (juveniles) will not be affected.

Resource reduction is assumed to affect the rodent population by reducing the effective birth rate either by decreasing suitable habitat for nesting or reducing the resources available for reproduction. The control is formulated in the model by assuming that the birth rate (b) is reduced by a proportion, 1 − u(t), at time t.

For the two permanent, environmental controls, we include, first, a carrying capacity control that permanently reduces habitat suitability for rats and hence affects the availability of the resources. This is specified as a reduction (ω₁) in the self-regulation parameter such that if we write α = 1/a then α^new = 1/(a(1 − ω₁)). The second environmental control permanently reduces the suitability of the environment for leptospires, and so reduces their lifespan. This control is specified as $\frac{1}{{\mu }^{new}}=\frac{1}{\mu }(1-{\omega }_2)$.

Given that there is no recovery, infection becomes endemic in the rodent population and the population sizes remain constant. When the model is run using the parameter values as specified in Table 1 with no control, and endemic low prevalence (17%) is observed in the juveniles as the only transmission route to them is vertical. Prevalence reaches 56% in the sub-adult population and 87% in the adult population. In the free roaming population (sub-adults and adults combined) the prevalence is 71%. The proportion of animals in each category was 0.32 juveniles, 0.23 sub-adults, and 0.45 adults of a total population of ~100. These endemic state values were used as the starting conditions for all control model simulations.

Optimal Control

Rats can be infected at any point in their lifetime, and so we wish to investigate the effect on the risk of human infection of reducing rat abundance overall. Hence, the time dependent control measures in the age-structured model (Equations 1–7) target all rats (susceptible and infected). Optimal control theory can be used to find the optimum amount of a time dependent control given restrictions on cost and on the length of the intervention programme (Sharomi and Malik, 2015). In the following sections, details of the optimal control problem are presented (see Supplementary Information for a brief introduction to optimal control and Sharomi and Malik, 2015 for examples in epidemiology).

The optimal control scheme is found by minimizing the so-called objective function. We aimed to reduce the total number of rats H(t) = J_X(t)+J_Y(t)+W_X(t)+W_Y(t)+A_X(t)+A_Y(t) and the number of leptospires (on the log10 scale) while simultaneously minimizing the control efforts used. Here, these are the proportion of the rodent population targeted with rodenticide (τ) and the proportional reduction in the birth rate (u). Hence the objective function includes the total number of rats and two controls,

$\begin{array}{ll}{\displaystyle {\int }_{t_0}^{t_f}{c}_{1}H(t)+c_{2}L(t)+\frac{c_3}{2}\tau {(t)}^2+\frac{c_4}{2}u{(t)}^2 dt}& (8)\end{array}$

where c₁, c₂, c₃, and c₄ are the weights which transform the component parts of the integral to the same monetary scale (Table 2). The weights are often specified in monetary terms, but given that the costs of these controls are unknown in absolute terms, we refer to the costs, for this initial exploration of this method, as “weights.”

TABLE 2

Table 2. Value of fixed weights of rats, leptospires and the control measures.

The weight c₁, associated with a rat of any age class or infection status, can be thought of as equivalent to a proportion of the cost of human infection, assuming that any rat has the potential to infect a human in its lifetime. The relationship between the number of rats and the risk of human infection is not well-understood, and so we assume a linear relationship between the “weight” of a rat and the number of rats, specified in the objective function in equation (8) as c₁H(t). We include quadratic terms for the control measures to account for the non-linear costs at high levels of control (Table 2) (Miller Neilan et al., 2010; Posny et al., 2015; Malik et al., 2016).

We investigate the optimal controls under the assumption that rodenticide control has the same weight (cost) per unit as resource reduction, and that the permanent environment controls are 10 times more expensive, but that both environment controls have the same weight (Table 2). We assigned weights to each rat and to each log10 leptospires in the environment. We assumed that if one rat had a rate of 1, then each log10 of leptospires had a relative weight of 0.1. Infected rats are the source of leptospires in the environment, are a pest species and once infected, shed for their entire lifetime. Hence, we assigned a higher weight to rats because we anticipate that rodent control well-received and potentially more effective.

The optimal controls are found by solving the age-structured model forward in time using initial values for the control measures. Then the adjoint equations are solved backward in time using the solutions of the age-structured model. The values of the control measures are then updated using Equations (9, 10). This process is repeated until the level of the control measures have converged. The convergence criterion used was that the values from subsequent iterations were the same to five decimal places.

We assume that the time-dependent control measures, rodenticide, and resource reduction, would at most be applied for a continuous period of 30 days (Pertile et al., unpublished; de Masi et al., 2009). Hence, we investigate the optimal temporary rodent controls (rodenticide and resource reduction) for a period of 30 days. In our study system, rodent population sizes remain relatively constant throughout the year (Panti-May et al., 2016), and so we did not investigate different timings of the controls throughout the year. We also find the optimal temporary controls assuming environmental controls had been applied 30 days beforehand. Given the optimal controls, the age structured model with control (Equations 1–8) was applied for the control period (60 days = 30 days permanent control effect +30 days of temporary control measures applied) and a period of no control (540 days) to investigate the longer term effect of these controls on infection dynamics. As measures of success of the control scenarios, we calculated the cumulative total number of rats, cumulative number of leptospires and the total weight of the different scenarios. Finally, given the uncertainties surrounding the weights assigned to the different controls, we present a sensitivity analysis of these weights.

Results

For contrasting levels (none and high) of the two permanent environmental controls, carrying capacity control and leptospire mortality control, there was no distinguishable difference in the optimal level of rodenticide application in a 30 day period (Figures 2A,B). For most of the control period, 100% of the rodent population needs to be targeted with rodenticide in order to reduce the total rodent population and the number of free living leptospires (Figures 2A,B). For resource reduction, when there is no additional permanent control, the birth rate should be reduced by 100% for most of the control period, though for a slightly shorter period than rodenticide (Figure 2A). However, as the reduction in carrying capacity, ω₁ increases, the optimal level of resource reduction is 0 in the first few days of the control program (Figure 2B).

FIGURE 2

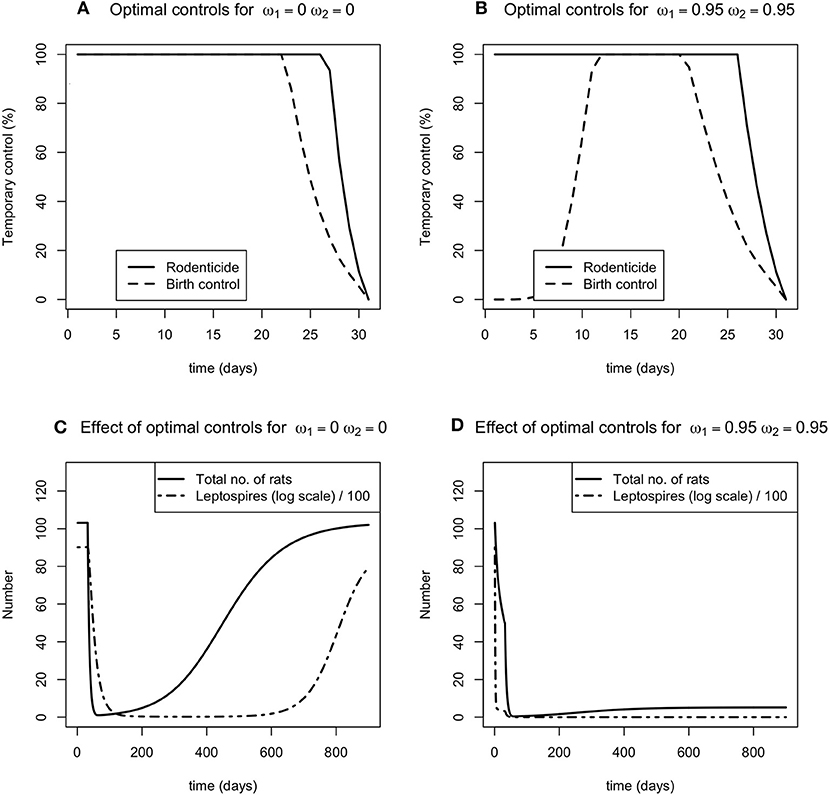
Figure 2. (A,B) The optimal level of the time dependent controls, rodenticide (solid line) and resource reduction (dashed line), when the environmental controls are a) not applied (ω₁ = 0, ω₂ = 0), (B) applied at a high level (ω₁ = 0.95, ω₂ = 0.95). (C,D) The effect of no and high control (C,D, respectively) on the total number of rats (solid line) and number of leptospires (dot dashed line).

These permanent controls reduce the number of infected rats and leptospires to new lower endemic equilibria. When the reduction in carrying capacity is at its highest, there is a sharp reduction in the number of rats in the population (Figures 2C,D). The temporary controls alone reduce the number of infected rats and leptospires to a low level for fixed period of time, following which the rodent population recovers and reaches its previous carrying capacity, accompanied by a delayed response from the number of leptospires.

The cumulative number of leptospires over the control and no control period was reduced both by high reductions in the carrying capacity and the leptospire mortality rate (Figure 3A). The cumulative number of rats, however, was only reduced only by the carrying capacity control (Figure 3B). The associated weights of the control scenarios were lowest when low levels of either of the permanent control were applied, but also when a very high level of carrying capacity reduction was applied (Figure 3C), since a high reduction in carrying capacity requires very little subsequent application of resource reduction (as also illustrated in Figure 2).

FIGURE 3

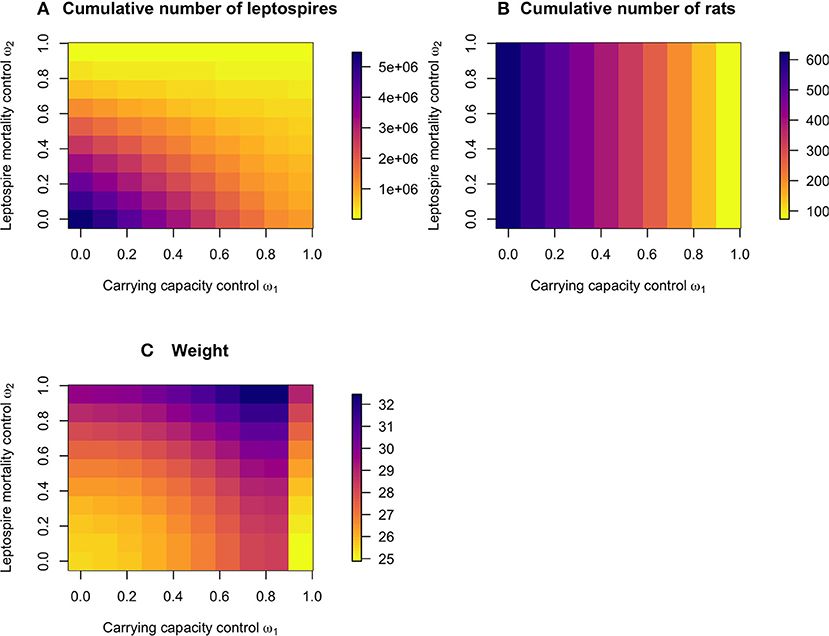
Figure 3. The predicted effect of the permanent and temporary controls on (A) the cumulative number of leptospires on the log10 scale, and (B) the cumulative number of rats over the 600 days period, with (C) the associated cumulative weights of the control measures.

The optimal controls of resource reduction and rodenticide were differentially sensitive to changes in the weights (Figure 4). When the resource reduction had a higher weight, the optimal level of resource reduction was much reduced, whereas the optimal level of rodenticide application was little affected (Figure 4B). The sensitivity was less to changes in rodenticide weights (Figures 4C,D). Higher weights led to a somewhat reduced period over which 100% control was optimal, but to little change in the optima for resource reduction.

FIGURE 4

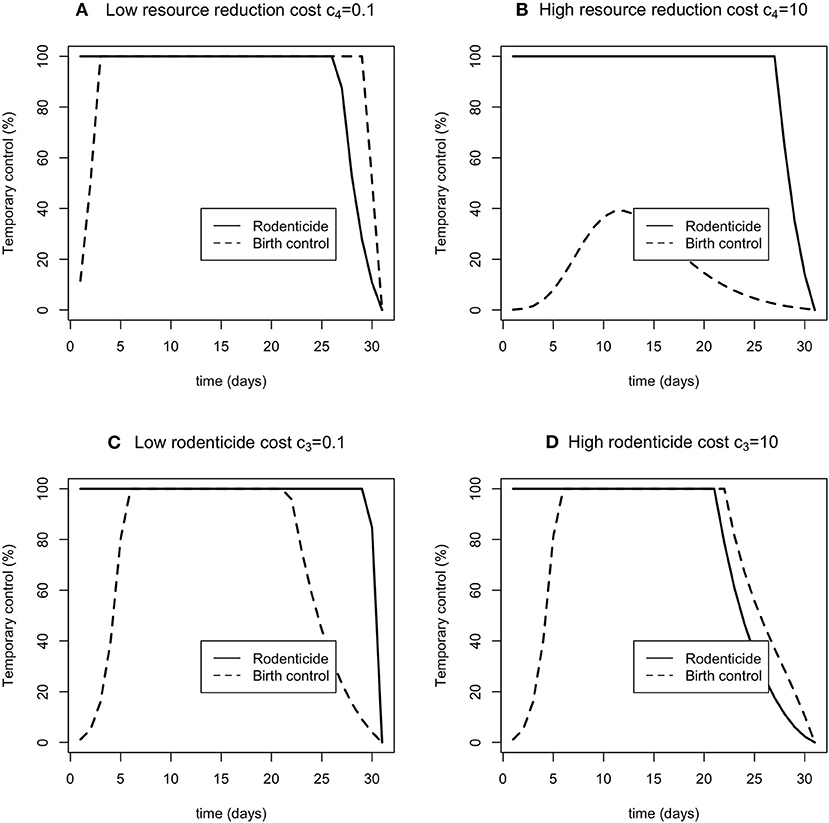
Figure 4. The sensitivity of the optimal time dependent controls rodenticide (solid line) and resource reduction (dashed line) for low and high costs of rodenticide (A,B) and resource reduction (C,D).

Discussion

Human zoonotic infections can be prevented by reducing the size of the reservoir population maintaining a pathogen, which, as in the case of leptospirosis, may also reduce the environmental load of pathogens, resulting in reduced intra- and inter-specific transmission. We present a framework to help identify and explore empirically an optimal mix of control measures to reduce the risk of human infection with leptospires. Application of temporary control measures following permanent changes to the environment is effective in reducing the rodent population size and the number of leptospires to a low level.

Permanently reducing the overall level of risk of exposure and infection among rats and humans would be effective in preventing human contact with open-sewer/contaminated water soil. Permanent controls have the added benefit of reducing risk of other diseases, especially diarrheal infections, and upgrading the urban slum environment. However, risk reduction may not be decreased sufficiently to significantly reduce cases of human leptospirosis during high risk periods, such as rainy seasons (Hagan et al., 2016). Though the temporary rodent controls result in an eventual return to the initial carrying capacity, the immediate effect of the controls could create a significant reduction in leptospires when humans are at highest risk of infection.

Control by rodenticide alone is never effective for Norway rat eradication as bait placement will not reach all rats and often, as in Salvador, rodenticide use is reactive, and placement is often focused around residents from which incident human leptospirosis cases have been recently identified. To further complicate this control, owner permission is required prior to placement, and when an adult home owner is unavailable at the first attempt follow-up attempts may not occur. Additionally, the neophobic behavior of rats ensures remnant populations remain, which is regarded as a major barrier to the success of rodenticide campaigns (Clapperton, 2006; Feng and Himsworth, 2014). Moreover, it is logistically difficult to design a rodenticide campaign targeting a pre-defined proportion of the rodent population, since consistently accessing the required number of households to apply rodenticide is difficult.

Habitat management reduces survival by eliminating refuges (Lambert et al., 2008; Buckle, 2013), but should be extensive enough to sufficiently cover the “typical” home range of rats. The home or activity range of urban rats is small: in the order of 10 s of meters in temperate urban locations (Feng and Himsworth, 2014) in contrast to rats inhabiting rural areas (Lambert et al., 2008). For rodents in urban settings, clearing garbage will reduce food, and in some cases, refuge sources, but data on empirical effects are unavailable and require pilot field studies (see below). In some cases, to clear garbage and other solid waste, there needs to be improvements in infrastructure, such as construction of roads and identifying local and city-level recycling centers that can take in the refuse. This complicates the logistics and cost calculations for habitat management interventions.

To that end, further complexities of the formulation of the control measures should be explored such as time dependent effectiveness of rodenticide and rodent behavior in response to population changes. Though death can be assumed upon ingestion of sufficient rodenticide, death does not occur instantaneously and takes up to 8 days following consumption and dose acquired (Mlynarèíková et al., 1999). This time lag may also apply to resource reduction (Williams, 2007) such as the removal of garbage influencing the population size and birth rates. Additionally, we assumed that juveniles would not be affected by application of rodenticide. Norway rats adopt communal nursing behavior, which leads to better survival of abandoned young, and these young, whose parents have been killed via rodenticide, may thereby survive (Meaney and Stewart, 1981; Butler and Whelan, 1994). If the population size becomes low enough, however, this nursing behavior cannot occur (Hein and Jacob, 2015), and it is expected that those animals in the nest will die as a result of a rodenticide campaign. This population size-dependent behavior has not been included in the modeling framework, which could lead to an underestimation of the effectiveness of rodenticide control.

Our model parameters were chosen to accurately predict leptospiral carriage prevalence among sub-adult and adult populations. However, model predictions of the effects of control measures have not been validated. To use this framework to plan control measures, the model framework for predicting prevalence should be validated using data from both successful and unsuccessful interventions (Joseph et al., 2013). Our analysis explored multiple control scenarios with different weights (costs), but the costs of the different controls, set against the cost of the existence of rats and leptospires in the environment, are not known. Estimating such costs is a priority.

Author Contributions

AM carried out the analyses and created the figures. All authors contributed to writing and editing the manuscript.

Funding

This work was supported by the Oswaldo Cruz Foundation and Secretariat of Health Surveillance, Brazilian Ministry of Health; the Wellcome Trust (102330/Z/13/Z); and a NSF-NIH grant from the Ecology and Evolution of Infection Diseases (EEID) program (1 R01 TW009504), NIH grants (5 R01 AI052473, 5 U01 AI088752, 1 R25 TW009338, and 1 R01 AI121207), and by the Research and Policy for Infectious Disease Dynamics (RAPIDD) program of the Science and Technology Directorate (US Department of Homeland Security).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2019.00209/full#supplementary-material

References

Adrichem, M. H. C., Van Buijs, J. A., Goedhart, P. W., and Verboom, J. (2013). Factors influencing the density of the brown rat (Rattus norvegicus) in and around Houses In- Amsterdam. J. Dutch Mamm. Soc. 56, 77–91.

Google Scholar

Ashford, D. A., David, J. R., Freire, M., David, R., Sherlock, I., Eulálio, M. C., et al. (1998). Studies on control of visceral leishmaniasis: impact of dog control on canine and human visceral leishmaniasis in Jacobina, Bahia, Brazil. Am. J. Trop. Med. Hyg. 59, 53–57. doi: 10.4269/ajtmh.1998.59.53

PubMed Abstract | CrossRef Full Text | Google Scholar

Buckle, A. (2013). Anticoagulant resistance in the United Kingdom and a new guideline for the management of resistant infestations of norway rats (Rattus norvegicus Berk.). Pest Manag. Sci. 69, 334–341. doi: 10.1002/ps.3309

PubMed Abstract | CrossRef Full Text | Google Scholar

Butler, F. T., and Whelan, J. (1994). Population-structure and reproduction in brown-rats (Rattus norvegicus) from Pig Farms, Co Kildare, Ireland. J. Zool. 233, 277–291. doi: 10.1111/j.1469-7998.1994.tb08588.x

CrossRef Full Text | Google Scholar

Calhoun, J. B. (1962). The Ecology and Sociology of the Norway Rat (US Public Health Service Publication No. 1008). Washington, DC: US Government Printing Office.

Casanovas-Massanaa, A., Pedra, G. G., Wunder, E. A. Jr., Diggle, P. J., Begon, M., and Albert, I, (2018). Quantitative survival of leptospira interrogans in soil and water microcosms. Am. Soc. Microbiol. 84, e00507–e00518. doi: 10.1128/AEM.00507-18

CrossRef Full Text

Clapperton, B. K. (2006). A Review of the Current Knowledge of Rodent Behavior in Relation to Control Devices. Wellington, NZ: Science & Technical Publishing Deptartment of Conservation, 1–55.

Costa, F., Carvalho-Pereira, T., Begon, M., Riley, L., and Childs, J. (2017). Zoonotic and vector-borne diseases in urban slums: opportunities for intervention. Trends Parasitol. 33, 660–662. doi: 10.1016/j.pt.2017.05.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Costa, F., Hagan, J. E., Calcagno, J., Kane, M., Torgerson, P., Martinez-Silveira, M. S., et al. (2015a). Global morbidity and mortality of leptospirosis: a systematic review. PLOS Negl. Trop. Dis. 9:e0003898. doi: 10.1371/journal.pntd.0003898

PubMed Abstract | CrossRef Full Text | Google Scholar

Costa, F., Porter, F. H., Rodrigues, G., Farias, H., de Faria, M. T., Wunder, E., et al. (2014a). Infections by leptospira interrogans, seoul virus, and Bartonella Spp. among Norway rats (Rattus norvegicus) from the urban slum environment in Brazil. Vector Borne Zoon. Dis. 14, 33–40. doi: 10.1089/vbz.2013.1378

PubMed Abstract | CrossRef Full Text | Google Scholar

Costa, F., Ribeiro, G. S., Felzemburgh, R. D. M., Santos, N., Reis, R. B., Santos, A. C., et al. (2014b). Influence of household rat infestation on leptospira transmission in the urban slum environment. PLoS Negl. Trop.Dis. 8:e3338. doi: 10.1371/journal.pntd.0003338

PubMed Abstract | CrossRef Full Text | Google Scholar

Costa, F., Wunder, E., De Oliveira, D., Bisht, V., Rodrigues, G., Reis, M. G., et al. (2015b). Patterns in leptospira shedding in Norway rats (Rattus norvegicus) from Brazilian slum communities at high risk of disease transmission. PLOS Negl. Trop. Dis. 9:e0003819. doi: 10.1371/journal.pntd.0003819

PubMed Abstract | CrossRef Full Text | Google Scholar

de Masi, E., Vilaça, P. J., and Razzolini, M. T. P. (2009). Evaluation on the effectiveness of actions for controlling infestation by rodents in Campo Limpo Region, São Paulo municipality, Brazil. Int. J. Environ. Health Res. 19, 291–304. doi: 10.1080/09603120802592723

PubMed Abstract | CrossRef Full Text | Google Scholar

De Oliveira, D., Figueira, C. P., Zhan, L., Pertile, A. C., Pedra, G. G., Gusmão, I. M., et al. (2016). Leptospira in breast tissue and milk of urban norway rats (Rattus norvegicus). Epidemiol. Infect. 144, 1–10. doi: 10.1017/S0950268816000637

PubMed Abstract | CrossRef Full Text | Google Scholar

Ellis, W. A. (2015). “Animal leptospirosis,” in Leptospira and Leptospirosis, ed B. Ellis-Adler (Berlin; Heidelberg: Springer), 99–137. doi: 10.1007/978-3-662-45059-8_6

CrossRef Full Text | Google Scholar

Evangelista, K. V., and Coburn, J. (2011). Leptospira as an emerging pathogen: a review of its biology, pathogenesis and host immune responses. Fut. Microbiol. 5, 1413–1425. doi: 10.2217/fmb.10.102

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, A. Y. T., and Himsworth, C. G. (2014). The secret life of the city rat: a review of the ecology of urban norway and black rats (Rattus norvegicus and Rattus Rattus). Urban Ecosyst. 17, 149–162. doi: 10.1007/s11252-013-0305-4

CrossRef Full Text | Google Scholar

Galef, B. G. (1981). “The ecology of weaning,” in Parental Care in Mammals, eds D. J. Gubernick and P. H. Klopfer (Boston, MA: Springer US), 211–241. doi: 10.1007/978-1-4613-3150-6_6

CrossRef Full Text | Google Scholar

Glass, G., Childs, J., Korch, G., and LeDuc, J. (1989). Comparative Ecology and Social Interactions of Norway Rat (Rattus norvegicus) Populations in Baltimore, Maryland. Occasional Papers of the Museum of Natural History. The University of Kansas, 1–33.

Google Scholar

Hagan, J. E., Moraga, P., Costa, F., Capian, N., Ribeiro, G. S., Wunder, E. A., et al. (2016). Spatiotemporal determinants of urban leptospirosis transmission: four-year prospective cohort study of slum residents in Brazil. PLoS Negl. Trop. Dis. 10:e0004275. doi: 10.1371/journal.pntd.0004275

PubMed Abstract | CrossRef Full Text | Google Scholar

Hein, S., and Jacob, J. (2015). Recovery of small rodent populations after population collapse. Wildlife Res. 42, 108–118. doi: 10.1071/WR14165

CrossRef Full Text | Google Scholar

Hethcote, H. (2000). The mathematics of infectious diseases. SIAM Rev. 42, 599–653. doi: 10.1137/S0036144500371907

CrossRef Full Text | Google Scholar

Holt, J., Davis, S., and Leirs, H. (2006). A Model of leptospirosis infection in an african rodent to determine risk to humans: seasonal fluctuations and the impact of rodent control. Acta Trop. 99, 218–225. doi: 10.1016/j.actatropica.2006.08.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Joseph, M. B., Mihaljevic, J. R., Arellano, A. L., Kueneman, J. G., Preston, D. L., Cross, P. C., et al. (2013). Taming wildlife disease: bridging the gap between science and management. J. Appl. Ecol. 50, 702–712. doi: 10.1111/1365-2664.12084

CrossRef Full Text | Google Scholar

Lambert, M. S., Quy, R. J., Smith, R. H., and Cowan, D. P. (2008). The effect of habitat management on home-range size and survival of rural Norway rat populations. J. Appl. Ecol. 45, 1753–1761. doi: 10.1111/j.1365-2664.2008.01543.x

CrossRef Full Text | Google Scholar

Malik, T., Imran, M., and Jayaraman, R. (2016). Optimal control with multiple human papillomavirus vaccines. J. Theor. Biol. 393, 179–193. doi: 10.1016/j.jtbi.2016.01.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Meaney, M. J., and Stewart, J. (1981). A descriptive study of social development in the rat (Rattus norvegicus). Anim. Behav. 29, 34–45. doi: 10.1016/S0003-3472(81)80149-2

CrossRef Full Text | Google Scholar

Miller Neilan, R. L., Schaefer, E., Gaff, H., Fister, K. R., and Lenhart, S. (2010). Modeling optimal intervention strategies for cholera. Bull. Math. Biol. 72, 2004–18. doi: 10.1007/s11538-010-9521-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Minter, A., Diggle, P. J., Costa, F., Childs, J., Ko, A. I., and Begon, M. (2017). Evidence of multiple intraspecific transmission routes for leptospira acquisition in Norway rats (Rattus norvegicus). Epidemiol. Infect. 145, 3438–3448. doi: 10.1017/S0950268817002539

PubMed Abstract | CrossRef Full Text | Google Scholar

Minter, A., Diggle, P. J., Costa, F., Childs, J., Ko, A. I., and Begon, M. (2018). A model for leptospire dynamics and control in the Norway rat (Rattus norvegicus) the reservoir host in urban slum environments. Epidemics 25, 26–34. doi: 10.1016/j.epidem.2018.05.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Mlynarèíková, H., Legáth, J., Molnár, L., and Kovalkovièová, N. (1999). “Study of effectiveness of anticoagulant rodenticides used in Slovak republic,” in Proceedings of 3rd Int Conf–Urban Pests, Prague, eds W. M. H. Robinson, F. Rettich, and G. W. Rambo (Hronov: Grafické Závody).

Panti-May, J. A., Carvalho-Pereira, T. S. A., Serrano, S., Pedra, G. G., Taylor, J., Pertile, A. C., et al. (2016). A two-year ecological study of Norway rats (Rattus norvegicus) in a Brazilian urban slum. PLoS ONE 11:e0152511. doi: 10.1371/journal.pone.0152511

PubMed Abstract | CrossRef Full Text | Google Scholar

Posny, D., Wang, J., Mukandavire, Z., and Modnak, C. (2015). Analyzing transmission dynamics of cholera with public health interventions. Math. Biosci. 264, 38–53. doi: 10.1016/j.mbs.2015.03.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Reis, R. B., Ribeiro, G. S., Felzemburgh, R. D. M., Santana, F. S., Mohr, S., Melendez, A. X. T. O., et al. (2008). Impact of environment and social gradient on leptospira infection in urban slums. PLoS Negl. Trop. Dis. 2:e228. doi: 10.1371/journal.pntd.0000228

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharomi, O., and Malik, T. (2015). Optimal control in epidemiology. Ann. Oper. Res. 251, 55–71. doi: 10.1007/s10479-015-1834-4

CrossRef Full Text | Google Scholar

Shilova, S. A., and Tchabovsky, A. V. (2009). Population response of rodents to control with rodenticides. Curr. Zool. 55, 81–91

Google Scholar

Traweger, D., Travnitzky, R., Moser, C., Walzer, C., and Bernatzky, G. (2006). Habitat preferences and distribution of the brown rat (Rattus norvegicus Berk.) in the city of Salzburg (Austria): implications for an urban rat management. J. Pest Sci. 79, 113–125. doi: 10.1007/s10340-006-0123-z

CrossRef Full Text | Google Scholar

Villafañe, I. E. G., Cavia, R., Victoria Vadell, M., Suárez, O. V., and Busch, M. (2013). Differences in Population parameters of Rattus norvegicus in urban and rural habitats of central Argentina. Mammalia 77, 187–193. doi: 10.1515/mammalia-2012-0075

CrossRef Full Text | Google Scholar

Williams, B. K. (2007). Optimal management of non-Markovian biological populations. Ecol. Model. 200, 234–242. doi: 10.1016/j.ecolmodel.2006.07.039

CrossRef Full Text | Google Scholar

Zhang, Y.-Z., Zou, Y., Fu, Z. F., and Plyusnin, A. (2010). Hantavirus infections in humans and animals, China. Emerg. Infect. Dis. 16, 1195–1203. doi: 10.3201/eid1608.090470

PubMed Abstract | CrossRef Full Text | Google Scholar