- 1Department of Natural Resource Ecology and Management, Iowa State University, Ames, IA, United States
- 2Department of Entomology, Iowa State University, Ames, IA, United States
Models are an integral part of the scientific endeavor, whether they be conceptual, mathematical, statistical, or simulation models. Models of appropriate complexity facilitate comprehension and improve understanding of the variables driving system processes. In the context of conservation planning decision-making or research efforts, a useful model can aid interpretation and avoid overfitting by including only essential elements. Models can serve two related, but different purposes: understanding and prediction of future system behavior. Predictive models can require several iterations of refinement and empirical data gathering to be useful for conservation planning. Models with less predictive ability can be used to enhance understanding of system function and generate hypotheses for empirical evaluation. Modeling monarch butterfly systems, whether it be landscape-scale movement in breeding habitats, migratory behavior, or population dynamics at monthly or yearly timeframes, is challenging because the systems encompass complex spatial and temporal interactions across nested scales that are difficult, if not impossible, to empirically observe or comprehend without simplification. We review mathematical, statistical, and simulation models that have provided insights into monarch butterfly systems. Mathematical models have provided understanding of underlying processes that may be driving monarch systems. Statistical models have provided understanding of patterns in empirical data, which may represent underlying mechanisms. Simulations models have provided understanding of mechanisms driving systems and provide the potential to link mechanisms with data to build more predictive models. As an example, recently published agent-based models of non-migratory eastern North American monarch butterfly movement and egg-laying may provide the means to explore how different spatial patterns of habitat, habitat quality, and the interaction of stressors can influence future adult recruitment. The migratory process, however, has not been addressed with agent-based modeling. Using western monarch migration as an example, we describe how modeling could be used to provide insights into migratory dynamics. Future integration of migratory models with non-migratory and population dynamics models may provide better understanding and ultimately prediction of monarch butterfly movement and population dynamics at a continental scale.
Introduction to Modeling
Models are an integral part of the scientific process. Models have been described as “a representation of reality” that serves a specified purpose (Webb, 2001) or a “description of a system” (Haefner, 2005). Models can be used for several purposes. A useful distinction is between models that help improve understanding and those that provide predictive capability. Better understanding of a system provides insights on key drivers and processes in a system that may otherwise be difficult to observe. Prediction is possible when drivers and processes are quantified so that future system states can be estimated. All models are simplified versions of reality that allow us to make inferences and conclusions about a system without unnecessary complexity. The art of modeling is to construct a model simple enough to make conclusions about a system but not so simple that all connection to reality is lost. This “sweet spot” has been termed the Medawar Zone (Figure 1; Grimm et al., 2005).
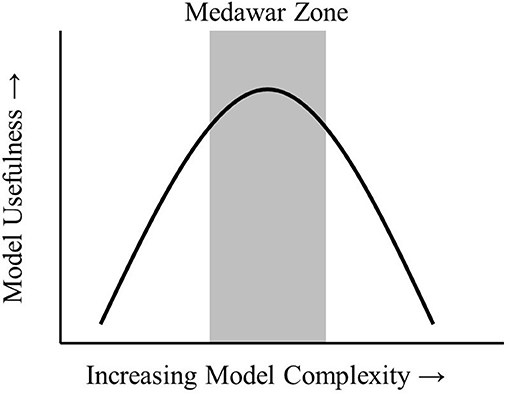
Figure 1. The Medawar Zone. As models increase in complexity, the Medawar Zone is the region of maximum usefulness. Adapted from Grimm et al. (2005) (permission granted).
Classes of models include conceptual, mathematical, statistical, and simulation/algorithmic models. Conceptual models are ideas or hypotheses of how a system functions. All research is based explicitly or implicitly upon conceptual models of how systems work and may be explicitly represented with flowcharts or other tools to communicate working hypotheses of a system (Heemskerk et al., 2003). Mathematical models represent a conceptual model of a system using analytical expressions and equations. They tend to be highly simplified expressions of system processes and are often used to explore general theory. Statistical modeling seeks to separate statistical noise from signal by modeling the probabilistic processes that are thought to have generated the observed data. Simulation models (which are a type of algorithmic models) use a series of rules to describe system behavior. Typically, they use programming code to simulate a system. While other authors describe more detailed taxonomies (see, for example, Hilborn and Mangel, 1997), and some models may not fit readily into one of these categories, all models simplify reality to make generalizable or comprehensible conclusions, and will be more or less appropriate for different purposes.
Conceptual and mathematical models typically increase our understanding of systems, but do not have the detail necessary to predict future system states. Mathematical models typically have poor predictive abilities in temporally and spatially explicit settings because they are simplified and designed to explore fundamental dynamics. Statistical and simulation models are often more suitable for prediction. In creating predictive models, one may be tempted to simply fit outputs to empirical data, with limited mechanistic rationale. Turchin (1998) p. 41–45 reviewed model development in the field of movement ecology and described curve-fitting models as empirical or phenomological models, which only consider the observed phenomenon, and no underlying processes. However, without a mechanistic rationale of system processes, no comparison can be made between predictive capability of different phenomological models. Over time empirical models have been abandoned in favor of models that can provide insight into system processes (Turchin, 1998). The goal of developing a predictive model is to balance internal mechanistic structure with fit of output to empirical data, consistent with the model's intended application.
Evaluating complex, predictive models may not be as simple as comparing outputs to field observations or experimental data (Rykiel, 1996; Batty and Torrens, 2005; Bennett et al., 2013). A complex model built from “the bottom up” may have many opportunities for error propagation that leads to invalid results. Consequently, complex simulation models may benefit from calibration against empirical data (Thiele et al., 2014), especially when used for predictive purposes. If empirical data is abundant, testing multiple endpoints over a range of variability can provide comprehensive model evaluation. Such evaluations may require complex analysis techniques (Marino et al., 2008).
Models are used extensively in monarch butterfly research and conservation planning. Modeled monarch butterfly systems include migration, population size, movement and egg-laying of non-migratory monarch butterflies, and developmental process from egg to adult. Of particular interest are population trends and causes of trends. Understanding or predicting movement of millions of individual monarchs at continental scales requires simplification of system processes. Determining the magnitude of population trends and causes of trends requires interpretation of variation in observed population measures. Many modeling approaches have been employed toward this end. Mathematical models such as matrix models and island chain models have been employed, as have statistical models such as Bayesian state-space models. In this review we describe the strengths and limitations of modeling approaches applied to monarch butterfly research and conservation issues. We synthesize findings of modeling efforts to date and provide suggestions to improve our understanding of monarch butterfly systems.
Approach
We reviewed the literature to provide an update on the state of the art in modeling monarch butterfly systems, with a focus on population dynamics and their unique migratory system. We reviewed papers covering eastern and western North American monarch butterfly populations. To find an illustrative suite of modeling papers, we searched Web of Science for the topic “monarch model,” which returned 570 results. From among these 570 results, we searched for papers that used a variety of modeling approaches to answer questions about monarch biology. We selected papers that provided insight into the history of modeling monarch systems, the variety of methods available, and future directions for monarch modeling. While we did not constrain our search to the eastern monarch population, there are comparatively fewer modeling papers for the western monarch population. In this review we also describe and evaluate model assumptions to help identify opportunities to link empirical studies with model development to further understanding and the means to predict future states of monarch systems (Restif et al., 2012).
We describe three classes of models: mathematical, statistical, and simulation. In addition to describing the models and their assumptions, we attempt to identify common conclusions across the modeling efforts. We highlight instances where similar conclusion are reached by different research teams using different models, which suggests higher confidence in understanding and/or predicting future conditions. We synthesize model findings in the areas of conceptual frameworks, population fluctuations, causes of population declines, empirical data needs, and migratory processes. We close by making recommendations for moving forward.
Modeling Eastern North American Monarch Populations
While a substantial body of research results is available for monarch butterflies, some authors have noted a need for modeling to help improve understanding and inform conservation options (Oberhauser, 2004; Dyer and Forister, 2016). Most field research is undertaken at patch scales, with conclusions extrapolated to larger spatial and temporal scales based on conceptual models of system function. Much of the literature makes implicit assumptions about how monarch systems function, but often those assumptions have not been explicitly stated and tested.
Mathematical Models
Yakubu et al. (2004) developed a spatially discrete advection model, which can also be characterized as an island chain model, where “islands” are generations of monarch butterflies. Heuristically, the events (births and death) that occur in one generation (island) are passed on to the next generation. The objective of the model was to understand the effects of migration and intraspecific competition on population dynamics. The model estimates population levels of four generations each year with a system of non-linear difference equations incorporating survival, migration, and fecundity. Since the fecundity function is not empirically known, Yakubu et al. (2004) tested compensatory and over-compensatory density dependence and documented the possibility of complex oscillatory behavior and or even chaos (unpredictable population fluctuations) under some conditions, which was not predicted in the modeling framework of (Flockhart et al., 2015; see below). Such dynamics could partly be responsible for the observed fluctuations in the overwintering monarch populations. This modeling effort does not include weather effects, spatial heterogeneity (except in the sense that different generations occupy different locations), or individual and spatio-temporal variation in survival or fecundity. Weather effects could potentially dampen or amplify oscillatory or chaotic behavior. This model advances a hypothesis that the system has the potential to demonstrate unpredictable oscillatory or chaotic behavior, even without drivers such as weather.
Periodic matrix projection models are very common in ecology (Caswell, 2001) and are based on several key assumptions. Matrix models require partitioning populations into separate spatio-temporal groups for which survival and fecundity are considered constant. Partitioning the population into many groups requires substantial effort to empirically estimate survival and fecundity for each group. Williams et al. (2002) note this as an important limiting factor in the development of complex matrix models. (Newman et al. (2014), pp.39) has some excellent discussion on the pros and cons of matrix models. The important distinction between matrix models and other models is that matrix models project the population size, they do not estimate the population size; thus matrix models are highly sensitive to the quality of the data used in their development. Except for matrix models, mathematical models of monarch systems are scarce.
Flockhart et al. (2015) created a matrix model incorporating stochasticity in parameters and density dependence. The model was spatially explicit in that the different migratory and non-migratory generations over the season were associated with different locations on the North American continent (a type of island chain model similar to that of Yakubu et al., 2004). Three hypotheses for the cause of the population decline were tested: habitat loss in the breeding grounds, habitat loss on overwintering grounds, and climate change on the overwintering grounds. The model predictions were compared with 19 years of adult overwintering monitoring data. While the projected population sizes were not significantly different from the monitored overwintering population size estimates, the projections did not exhibit observed overwintering population fluctuations. Insights from this model include an estimated decline of 14% in population size over the next 100 years, with the reduction in milkweed in the summer breeding range as the most significant driver of decline. As the model currently stands, nearly constant survival rates are used across years, which results in an exponential model with some variation from added stochasticity and density dependence [see Figure 3a of Flockhart et al. (2015)]. Because the variation in survival rates and fecundity that lead to the overwintering population size in Mexico are unknown, the matrix model is unable to capture the full range of population variability. If there was a desire to understand or predict population responses at finer temporal or spatial scales using a similar model, the population could be divided into smaller geographic regions and time periods. However, survival, fecundity, and migration would then need to be estimated for each region and time period.
Oberhauser et al. (2017) also created a matrix model using a Bayesian framework. In this framework the authors used overwintering population monitoring data to help estimate parameters in the matrix model. Because parameters were estimated, the model has statistical and mathematical facets, but is included here for comparison to the model developed by Flockhart et al. (2015). Model parameters were given informative priors developed from published data and expert elicitation. The data supplied to the model to estimate the posterior distributions was the overwintering population size and the Midwest USA egg production index (Pleasants and Oberhauser, 2013). The eastern North America population was divided into four regions and four generations (i.e., an island chain model). The mean of the population growth rate posterior distribution was 0.957. Sensitivity and elasticity analysis showed that, because the system is very complex, many parameters were important to population growth. The most important parameters were spring migration survival from overwintering sites in Mexico to the southern U.S., fecundity, and spring immature survival in the southern U.S. Among seven management scenarios, increasing breeding habitat in the south and north central regions were most important for increasing population growth rate. This matrix model assumed a stable-age distribution with density independent growth and did not include environmental factors. Because this model was tuned to the overwintering population data, it is likely much more realistic than other matrix models, though it still assumes constant survival rates.
Statistical Models
Many statistical models have increased our understanding of monarch population dynamics. Pleasants and Oberhauser (2013) regression model predicts the overwintering population, based on a Midwest egg production index, with an r2 = 0.47. The Midwest egg production index is based on surveys in Iowa agricultural fields as reported by the authors, Monarch Larval Monitoring Program data (MLMP; Prysby and Oberhauser, 2004; Stenoien et al., 2015) from non-agricultural locations in the Midwest, and surveys of milkweed in Iowa (Hartzler, 2010). Data from these sources is extrapolated to estimate egg production in the Midwest. The authors note four factors not incorporated into the model that may be associated with the unexplained variance: variability in survival from egg to adult; variability of contributions to the Mexico overwintering population from geographic regions other than the Midwest; variability in fall migration survival; and variability in the conversion factor used to calculate the number of eggs in the Midwest.
Zipkin et al. (2012) used a complex Bayesian Poisson regression model with 17 parameters to model monarch butterfly counts at 90 sites in Ohio from 1996 to 2008. The model's purpose was to further understanding of climatic effects on monarch butterflies during spring migration. This model involved a complex analysis of the correlation between abundance on breeding grounds and climactic factors. Four climate effects were included in the model (spring precipitation, spring growing degree days, summer growing degree days, and summer Palmer Drought Index), along with several interactions and quadratic effects. Wet Texas springs and average Texas spring temperatures produced the greatest monarch abundance in Ohio.
Saunders et al. (2016) advanced the approach used by Zipkin et al. (2012) to predict monarch abundance in Ohio and Illinois based on spring climatic conditions in Texas by testing model predictive ability. Of 16 years of data, they used subsets of 8–15 years of data to generate models and compare model outputs to the empirical data from years not included in model development. The difference between predicted and observed monarch counts was quantified using Bayesian p-values, where a p-value of 0.5 indicated good model fit and p-values < 0.3 or > 0.7 indicated poor fit (i.e., the model is either overestimating or underestimating parameters). The model had good predictive ability for years that had near average spring precipitation and temperatures, or when there was a year with similar spring precipitation and temperature values in the dataset. Model prediction was poor for years with weather parameters that were not similar to any other years in the dataset. The large numbers of parameters may have overfit the model to some degree, causing less predictive ability particularly for years with unusual weather. The model suggested spatial synchrony in Ohio and Illinois, with monarch abundance in the two states more dependent on climatic conditions in Texas than local Midwest conditions. While the models developed by Saunders et al. (2016) and Zipkin et al. (2012) may provide our best statistical evidence of climate effects on monarch butterfly population responses, these efforts also highlight the difficulty of modeling a continental-scale migratory system. Additional models could be tested for their predictive ability as in Saunders et al. (2016).
Semmens et al. (2016) fit a Bayesian state-space statistical model to egg counts and overwintering population size for the purpose of estimating extinction risk. The model was first-order auto-regressive, meaning the overwintering population from 1 year was estimated using the overwintering population from the previous year. The observed overwintering population and Midwest egg production index (Pleasants and Oberhauser, 2013) informed estimation of the true value of the overwintering population. This model quantified the variation and trends in observed overwintering population size using a normal distribution and no underlying mechanisms, and then projected trends into the future. This model estimated a mean population growth rate of 0.94, with a 66% probability of the average annual growth being below 1.0 and an 11–57% probability of quasi-extinction over 20 years. This model accounted for yearly variation in overwintering population size using a random deviate each year that was assumed to be normally distributed. No environmental covariates were used and the model did not include any demographic mechanics such as survival and fecundity.
Inamine et al. (2016) compared North American Butterfly Association1 (NABA) citizen science monitoring data from the eastern U.S. and historical counts from Cape May, New Jersey, and Peninsula Point, Michigan over different time periods and regions to link population dynamics across the annual migratory and breeding cycles to help elucidate causes of the population decline. They divided the yearly cycle into successive regions that represent the location of the monarchs over the year: Spring Mexico, Spring South, Midwest and Northeast, Fall South, and Fall Mexico. A string of regression analyses between each successive area were undertaken (i.e., an assumed donor-recipient relationship, similar to the island-chain model of Yakubu et al., 2004) to determine if the population counts in a region can be predicted from the counts in the previous spatio-temporal area. The Midwest summer NABA counts showed no statistical relationship with Mexico overwintering counts over the period of 1993–2014. Inamine et al. (2016) concluded that unknown factors must be increasing mortality rates during fall migration. Agrawal and Inamine (2018) restated the arguments in Inamine et al. (2016) that factors during fall migration may be partly driving population decline.
Ries et al. (2015) conducted an analysis similar to Inamine et al. (2016) using NABA data and linear regression between successive spatio-temporal stages of the annual monarch cycle. Their findings were similar to those of Inamine et al. (2016); however, Ries et al. (2015) and Pleasants et al. (2017) cautioned that bias in population count data could be causing the discontinuity between the U.S. Midwest summer population counts and the overwintering population size. While the modeling results of Inamine et al. (2016) and Ries et al. (2015) help form the basis of a migratory failure hypothesis (Agrawal and Inamine, 2018), other modeling efforts indicate loss of milkweed in the summer breeding range as the primary stressor, due to either Roundup Ready crops (e.g., Pleasants and Oberhauser, 2013; Flockhart et al., 2015) or modern agricultural practices since the 1950's (Boyle et al., 2019; but see Ries et al., 2019; Wepperich, 2019). Collectively, these models highlight uncertainty in data used to develop and evaluate models (e.g., the ability of current monitoring designs to quantify monarch migratory patterns across the eastern United States), as well as uncertainty in the independent or interacting roles of reduced nectar sources (Brower et al., 2015), road side mortality (Kantola et al., 2019), spatial-temporal climatic variability (Zalucki and Rochester, 2004), and reduced milkweed (Lemoine, 2015), in monarch population trends.
The environmental niche model of Batalden et al. (2007) used MLMP monitoring data on site occupancy status (whether a site had ≥ one egg or no eggs) to estimate the area of the monarch ecological niche in the eastern U.S. over successive generations. Geographic Information System raster data layers of climatic and topographic parameters were tested for correlation with occupied sites. The variables of maximum, minimum, and mean monthly temperatures; precipitation; elevation; and slope were correlated with occupied sites to predict month-specific models of the area in the eastern U.S. suitable for monarch occupation. The monthly niche models indicate that monarchs follow their preferred climatic niche during the breeding season, but switch climatic preferences during the winter months. Batalden et al. (2007) then looked at changes in the environmental niche using models of future climatic conditions. These models indicate that by 2055, more niche area will be available from March to June. The area of the monarch niche will be similar in July to August, but will extend farther north into Canada, nearly to Hudson Bay. The potential consequences for spatial discontinuity in monarch and milkweed range during July and August remains an unresolved issue.
Simulation Models
Simulation models attempt to create a simplified representation of a monarch butterfly system using algorithms (i.e., a set of rules). By manipulating the algorithms, researchers hope to gain insights on natural processes; e.g., movement behavior of adult monarchs. Models have been used to simulate movement at landscape scales and monarch development and colonization at continental scales. Adult butterflies are well-suited for agent-based modeling (also known as individual-based modeling), which is a type of simulation model. Adult butterflies were the subjects of some of the first agent-based models (because they move freely across the landscape, unlike terrestrial species whose movement paths are highly restricted by terrain; Jones, 1977; Jones et al., 1980). Insects are also thought to have limited capacity for memory (Collett et al., 2013); hence incorporating memory does not significantly increase model complexity. As a consequence, butterfly movement can often be simulated using random walk assumptions (Codling et al., 2008).
Pioneering efforts to simulate monarch butterfly movement and egg-laying in a spatially explicit environment were reported by Zalucki (1983). Zalucki's model incorporated movement, egg-laying, and immature survival to the adult stage in a spatially explicit environment. The environment was a 3.1 km2 circular area with large and small patches of milkweed with interspersed individual milkweed plants. Using a 1 s time step, the model included many biological processes, from male-female interactions to the time needed to lay eggs. Key findings were that low directionality of flight increased fitness when milkweed was spread out, while high directionality increased fitness when milkweed patches were more clumped.
More recently, Zalucki and Lammers (2010) and Zalucki et al. (2016) used agent-based models to explore the effect of reduced milkweed in the matrix (i.e., corn and soybean fields in the U.S. Midwest) between patches of milkweed. Zalucki and Lammers (2010) predicted that clearing milkweed from the matrix would result in ~20% reduction of eggs laid. Zalucki et al. (2016) presented a more detailed model to advance understanding of movement and egg laying in hypothetical 11.2 km2 landscape scenarios with the same area of milkweed distributed in different sizes of milkweed patches in varying spatial patterns. This model suggested a 30% decline in monarch lifetime egg production in a scenario when large milkweed patches were consolidated in space, as compared to a scenario where small patches were uniformly distributed in the landscape.
Grant et al. (2018) subsequently developed an agent-based model to predict movement of non-migratory, summer breeding female butterflies and egg-laying patterns in a spatially explicit Iowa USA agricultural landscape. Movement decisions were based on assumptions of monarch perceptual range for detecting milkweed and spatial memory. Monarchs probabilistically choose habitat patches with more milkweed and have a lower probability of returning to patches they have already visited. This movement algorithm was more complex than Zalucki et al. (2016) in that monarch agents could choose between multiple habitat types within their perceptual range. In assessing performance of the model algorithms, patterns that needed to be reflected in model outputs (sensu Grimm et al., 2005) included: female monarchs moving long distances (10 km/day); expressing vagile behavior, i.e., not remaining in a selected habitat patch; and laying eggs widely across the landscape. By tying monarch movement to habitat within their perceptual range substantial realism was added to the model. Random walk models are commonly used in biology (Codling et al., 2008), but in previous research, model agents have not responded to habitat heterogeneity (see review by Wallentin, 2017). The use of a spatial memory algorithm by Grant et al. (2018) was also a unique addition to agent-based modeling and contributed to the vagile behavior of the monarch agents. The model does include several assumptions and constraints. First, the minimum size of habitat patches is 50 × 50 m, consequently individual milkweed or very small patches of milkweed are not explicitly included in the model. Rather, milkweed stems are assumed to be homogeneous within habitat patches, though adjusting egg-laying probabilities can help account for habitat heterogeneity. Second, monarch movement is modeled as a fixed-length step of 20–50 m. The model could be improved and further evaluated with empirical research data on adult movement behavior, which could enhance the mechanistic basis for the movement algorithms. Survey data on milkweed and monarch egg density in different, adjoining landcover classes could also improve model calibration, as discussed below.
To calibrate the model described by Grant et al. (2018) requires empirical data that is difficult to obtain because it requires intensive and large-scale sampling. More specifically, egg densities in milkweed patches within adjoining landcover categories is needed. Subsequent to publication of Grant et al. (2018), information provided in Blader (2018) provided the means to calibrate model parameters to field data. Blader (2018) geolocated milkweed and monarch eggs in two 1.6-km rural roadsides in rural Story and Boone counties Iowa in 2017 (Figure 2). This data was converted to milkweed and eggs per ha to be compatible with the model input and output for estimates, respectively, for roadsides adjacent to corn and soybean fields. The calibration process first involved running the model using parameters in Grant et al. (2018) for these spatially explicit roadsides and comparing the predicted eggs laid to the observed eggs laid in the same roadsides. A model parameter that establishes a probability for an agent to lay an egg within a landcover type, which is based on the assumed milkweed density, was then adjusted such that subsequent model predictions of eggs laid in these landcover types are similar to the eggs observed in the monitored roadsides. Calibration substantially improved the predictive ability of the model (Figure 3). Prior to calibration, model predictions of egg densities when milkweed density was 20–240 milkweed/ha were approximately 2 to 5 times higher than reported by Blader (2018). After calibration, predicted egg densities were within a factor of 2 compared to the empirical densities. A more robust calibration data set would include measured milkweed and egg densities in the adjoining landcover types (e.g., crop fields, pastures, and restored prairies), as well as the roadsides.
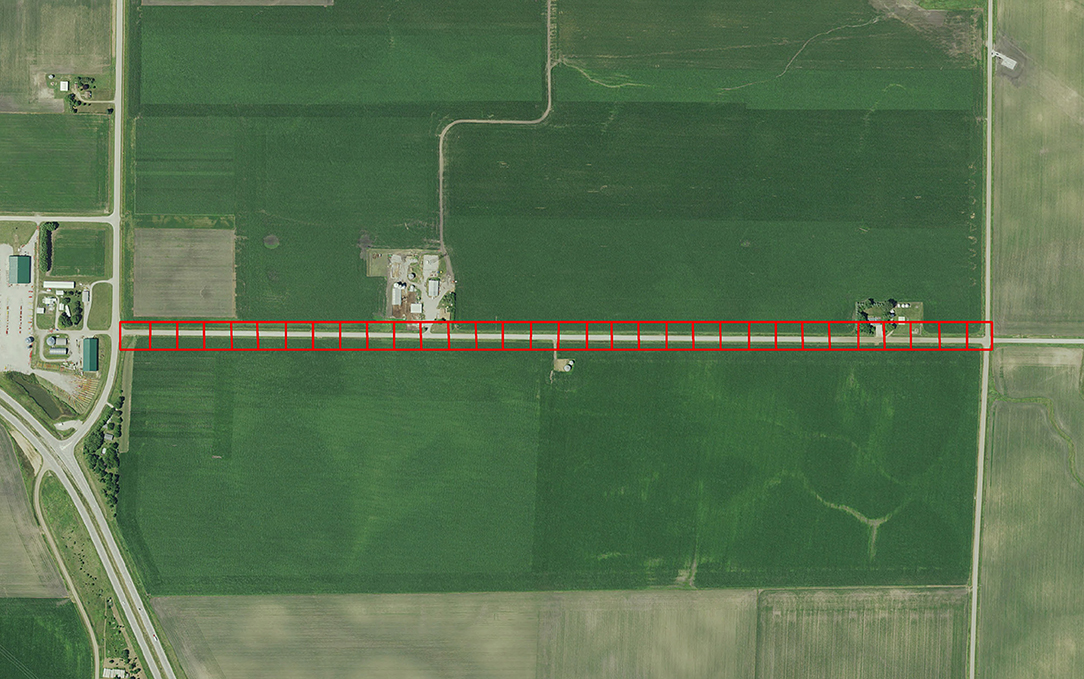
Figure 2. The rural road in Boone County in which egg density data was collected by Blader (2018). Red squares (50m X 50m) outline patches in the agent-based model developed by Grant et al. (2018). Empirically-measured egg density for each patch is compared to predicted egg density to calibrate the model.
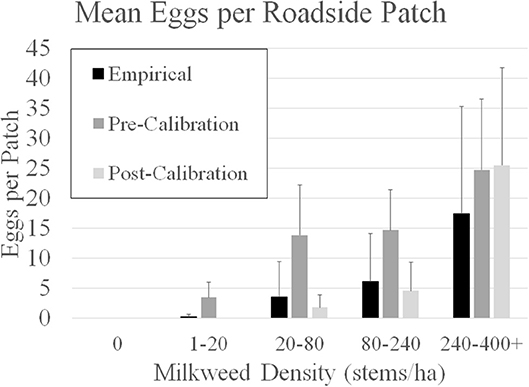
Figure 3. Comparison of model-predicted mean eggs per 50m X 50m patch in five categories of milkweed density in two 1.6 km roadsides in Boone and Story counties in Iowa, USA. Empirical data from Blader (2018). Pre- calibration estimates for the roadsides is based on the agent-based model assumptions in Grant et al. (2018). Post-calibration estimates are derived from the Grant et al. (2018) model after calibration with empirical milkweed density provided in Blader (2018). Error bars are 1 SD.
Zalucki and Rochester (2004) presented a Monte Carlo model of eastern North American monarch dynamics from spring colonization of the eastern U.S. until fall migration. This was the first model to explicitly include multiple generations, weather, and developmental dynamics in a single model. Probabilities were assigned to describe components of the system, including colonization probabilities, egg-laying probabilities, and probabilities of developing from egg, through 1st−5th instar, and adult, for each of the generations. Populations were simulated at 187 weather station locations where temperature and other climatic data defined colonization probabilities and developmental rates. A single simulated monarch was then run using a Monte Carlo approach. The proportion of times the monarch was found in a particular state was assumed to represent the proportion of the monarch population that would be at that location. The model explained only a very modest portion of the variation in the observed data (r2 = 0.12, p < 0.001), but provided key findings that climate is a powerful driver of yearly population dynamics and that breeding generations quickly overlapped, due to individual variation in stage duration.
Feddema et al. (2004) developed perhaps the most comprehensive model of spring migration and development. The eastern U.S. was divided into 50 square mile grids. Fifty miles was chosen to match the assumed daily movement of migrating monarchs. Occupancy status (occupied or not) and population size was calculated for each grid over the course of the year. The model queried National Climate Data Center2 databases from weather stations nearest to each grid cell. The model makes several assumptions. First, arrival time is defined by solar angle rather than distance from the overwintering site. Consequently, arrival date is determined by latitude. Second, once a grid cell becomes occupied, it stays occupied until fall migration. Third, daily movement is assumed to be 50 miles throughout the year; the authors note the movement step is not realistic. Fourth, only mortality due to temperature is included. Fifth, one new cohort is laid in a grid cell each day after the cell becomes occupied. While this is a unique modeling approach, the model failed to capture many patterns observed in the empirical data. Comparison of model results to Journey North3 datasets showed discrepancies between predictions and first observations of spring-migrating monarchs. Monarch production estimates from the model are not significantly correlated to empirical data. The model did show that natural variation in temperature can lead to different arrival times at more northerly latitudes.
Modeling Western North American Monarch Populations
There are comparatively fewer published population models of the western population. Espeset et al. (2016) used Bayesian hierarchical modeling and path analysis to estimate trends in western monarch populations and the effects of weather on those trends. The data for the analysis was from sites along a transect across Northern California which has been surveyed biweekly for monarch butterfly presence during flight season for 27–42 years, and publicly available overwintering population numbers. They included climate data as predictor variables to explore their effect on the population trend. The model estimated a continuing downward trend in western monarch populations on the Central Valley breeding grounds. A sliding-window regression analysis indicated that the largest decline in numbers occurred in spring months. The authors concluded that factors were mostly strongly affecting western monarchs during overwintering and spring, but that populations tended to rebound to normal levels during the summer. Warmer winter and spring temperatures and higher spring precipitation were correlated with more monarchs observed at the survey sites. However, the path analysis revealed that climate effects were not the strongest factor in the declining population. In other words, after accounting for climate effects, populations still trended downward. The cause of this downward trend is poorly understood, but because the downward trend is most pronounced in the spring, the authors recommend looking at overwintering sites for causes of losses. Poor years for western monarchs were not correlated with poor years for eastern monarchs, prompting the conclusion that the two populations are influenced by different factors.
Schultz et al. (2017) developed a multivariate auto-regressive state-space model using data collected on western monarch overwintering populations, which is similar in approach to that used by Semmens et al. (2016). Survey efforts varied substantially across overwintering sites. Some sites were surveyed every year for many years while some sites were surveyed intermittently over the years. The statistical framework employed in the model addressed data obtained through varying levels of monitoring effort for individual overwintering sites. Average population growth rate from 1981 to 2016 was estimated to be 0.927 and the estimated quasi-extinction risk within 20 years was 0.72. Schultz et al. (2017) noted high variation in annual population growth rates may be due to climate factors, which were not included in their models. They also note that vital rates, such as survival, are poorly understood for eastern and western monarchs.
Synthesis of Monarch Population Models
Significant effort has been invested in developing monarch butterfly models that can improve our understanding and means to predict population dynamics and trends in eastern North America. Nevertheless, there is no standard model framework of monarch population dynamics. Authors have repeatedly stated the need for a full model of the monarch annual demographic cycle that includes weather effects. As Zipkin et al. (2012) stated: “No modeling approach has yet captured the full complexity of how climate interacts with all the potential factors that influence monarch population growth, including the condition and number of incoming migrants from Mexico, milkweed growth and congruence with monarch arrivals, natural enemies, and appropriate climatic environments for activity and growth throughout each phase of their migratory cycle.” Inamine et al. (2016) stated: “Understanding the complex population dynamics of monarchs over space and time therefore remains an important ecological as well as conservation challenge.” Malcolm (2018), in the context of determining the risk monarchs suffer from anthropogenic factors, stated: “Risk for this highly mobile species has to be put into the context of a complex life history across relevant time and space for both eastern and western populations of monarchs in North America.”
Consistent with these observations, we attempt to synthesize several themes from the models summarized in this review.
Conceptual Frameworks Underlying Mathematical, Statistical, and Simulation Models
Conceptual models of monarch population dynamics implicitly or explicitly acknowledge that weather patterns influence continental to local patterns in system responses, yet few models have included weather effects. Many authors have noted that weather is needed to better predict observed population patterns (Zalucki and Rochester, 2004; Zipkin et al., 2012; Stenoien et al., 2015; Espeset et al., 2016; Semmens et al., 2016; Schultz et al., 2017). This indicates a significant discrepancy between what may be a critical driver of population dynamics and what we can currently model to improve understanding and predictions.
Monarch models tend to have a “top-down” perspective in exploring large-scale trends with uncertain empirical data. Top-down models look at broad scales, either national or continental and tend to be correlative and not mechanistic. For example, Oberhauser et al. (2017) is essentially a correlation between overwintering sites and breeding ground data, with matrix population mechanics constraining the relationship. Zipkin et al. (2012) and Saunders et al. (2016) are also correlative analyses between abundance on the breeding grounds and Texas climate data. Saunders et al. (2016) laudably tested the predictability of their model. These models do provide important advances to understanding the system, but the capacity to predict system responses remains challenging. The complexity of the system necessitates a correlative approach to begin improving understanding; however, development of simulation models including system mechanics may provide the best return on investment. The Zalucki and Rochester (2004) model included developmental mechanics in a national scale model. Zalucki et al. (2016) took the critical step of incorporating movement mechanics in their agent-based model, followed by inclusion of improved movement mechanics into Grant et al. (2018). Improving the mechanistic basis of our models, instead of using only a correlative approach, will likely improve understanding and prediction.
Most mathematical and statistical models use an “island chain” approach in which different generations and areas of the U.S. are modeled sequentially. After the first generation, however, monarch generations overlap and may become indistinguishable in late July and August (Zalucki and Rochester, 2004). Consequently, spatial areas in an “island chain” approach are most appropriate at large, regional scales (e.g., Midwest, Northeast). However, there is no standard definition of regions and different modelers have divided the eastern U.S. into “islands” of different areas. In theory, the island chain approach could provide greater insights using shorter timeframes and smaller geographical divisions; however, as islands become smaller, they become more artificial.
With increasing availability of high-performance computing, simulation modeling (e.g., agent-based modeling) may be a viable alternative to the island model approach to advance understanding and prediction. The process of parameterizing a simulation model would also help inform the lack of system understanding and identify high-priority research needs. A good example of this process in monarch butterfly research can be seen in the work of Drury and Dwyer (2005), who developed models and generated data to understand mechanisms behind spring monarch colonization of habitat patches. Developing a model for the entire eastern monarch population would be a challenging undertaking, spanning multiple nested spatio-temporal scales. To efficiently build the capability to model the annual monarch cycle with agent-based modeling, different modules would need to be developed that can be used concurrently. For example, migratory and non-migratory modules could be developed with the migratory module outputs serving as inputs for the non-migratory module.
Modeling Population Fluctuations
To date, published models have limited ability to predict annual fluctuations in overwintering population counts. Matrix models have not predicted population fluctuations because variability in survival rates from year to year is unknown (e.g., see Flockhart et al., 2015). Yakubu et al. (2004) showed that the system has the potential to generate fluctuations and chaotic trends without any explanatory variables. Semmens et al. (2016) modeled population dynamics using a first-order auto-regressive model to investigate population growth rate but modeled annual fluctuations as normally distributed with no mechanistic rationale. Weather patterns have been shown to influence the spring migration and define the monarch's environmental niche (e.g., see previous summaries of Zalucki and Rochester, 2004; Batalden et al., 2007; Zipkin et al., 2012; Saunders et al., 2016). Population fluctuations are likely driven by changes in survival and fecundity under different weather conditions. Improved methods for estimating demographic rates—survival, in particular—are needed to adequately model monarch population dynamics. It seems likely that weather patterns contribute to the overwintering population fluctuations as well; however, to date no attempts have been made to use weather patterns over the entire annual cycle to better understand or predict overwintering population levels. Without an improved understanding how weather drives fluctuations in the overwintering population, it will be difficult to predict how climate change will affect future monarch butterfly population dynamics.
Causes of Population Decline
Some modeling approaches support the hypothesis that milkweed decline within the summer breeding range is the primary cause for the decline in the eastern population (e.g., Pleasants and Oberhauser, 2013; Flockhart et al., 2015; Thogmartin et al., 2017; Malcolm, 2018; Stenoien et al., 2018). Other modeling efforts suggest that adverse effects during the fall migration have driven the decline (Ries et al., 2015; Inamine et al., 2016; Agrawal and Inamine, 2018; Saunders et al., 2019). Uncertainties in underlying empirical data and assumptions, combined with different approaches for including uncertainties in the modeling efforts, contribute to varying interpretations of the causes for the population decline.
The NABA data used by Inamine et al. (2016) and Ries et al. (2015) may be biased (see Ries et al. for discussion of potential bias). The NABA data are counts of adult monarchs at sites selected by citizen scientists and have two potential limitations. First, because detection probability is not estimated, the amount of bias in the counts is not known. Second, the sites are not chosen using a probabilistic sampling design; consequently, the relationship of the counts to the true monarch population is unknown. The limitations of using counts with no estimates of detection probability has been noted for numerous species (MacKenzie and Kendall, 2002), including butterflies (Kery and Plattner, 2007; Nowicki et al., 2008; Pellet, 2008; Pellet et al., 2012; Kral et al., 2018). One likely mechanism that would bias detection probability is monarch movement becoming more confined to NABA count locations as milkweed in agricultural fields decreased (Pleasants et al., 2017). There may be additional factors biasing counts; however, without empirical data on monarch densities, which currently seems difficult or impossible to obtain, it may be difficult to determine the presence and causes of bias. Estimating detection probability for adult monarchs in the near term seems unlikely because of their vagile behavior, though statistical methods to address this issue continue to advance (Rossman et al., 2016). The monarch research community is confronted with the difficult task of resolving the extent to which uncertainty in the NABA counts undermines the migration failure hypothesis. Exploration of hypothesized causes of mortality during migration, such as nectar source declines or roadkill mortality, could provide independent support for the migration failure hypothesis.
Other research groups have concluded that milkweed limitation is the primary driver of monarch decline (Pleasants and Oberhauser, 2013; Flockhart et al., 2015; Thogmartin et al., 2017; Malcolm, 2018; Stenoien et al., 2018). Additional potential factors for the decline, while acknowledged, have largely been considered insignificant. The Pleasants and Oberhauser (2013) model estimates that the Midwest egg production index accounts for 47% of the observed variation in overwintering population size. These researchers acknowledge that their model does not account for variability in survival from egg to adult; variability of contributions to the Mexico overwintering population from other geographic regions; variability in fall migration survival; and variability in the conversion factor used to calculate the number of eggs in the Midwest.
Ideally a model constructed to quantify variation in overwintering population due to these other factors would be helpful; however, there are limitations in current knowledge to support such a modeling effort:
1. Currently there is no statistically rigorous estimator for survival rates from egg to adult (Oberhauser et al., 2001; Flockhart et al., 2015) however, ad hoc estimates indicate that survival rates may be declining (Nail et al., 2015).
2. Site selection bias has an unknown effect on trend analyses. Subsampling or a rarefaction analysis could be utilized with existing NABA data to determine the effect of site-selection bias.
3. Flockhart et al. (2017) concluded that on average 40% of overwintering monarchs originate in the Midwest; Pleasants and Oberhauser (2013) contend that the contribution from the Midwest was likely higher before the advent of Roundup Ready crops in 1996. Contributions to the overwintering population from the regions associated with the count zones in Michigan and New Jersey suggest no declines (Davis, 2012). Trends in contributions from other regions to the overwintering populations are poorly or completely unknown.
4. Threats during the fall migration could include lack of nectar forage. Monarch butterflies need adequate lipid stores to survive the overwintering period in Mexico. Saunders et al. (2019) found that continental scale landscape greenness, which they used as an index of nectar forage, was positively correlated with overwintering population size. Brower et al. (2015) documented low lipid stores in some monarchs in Texas during fall peak migration; whether those monarchs reached the overwintering sites is unknown. These papers suggest that nectar source availability on breeding grounds and the migration route has the potential to have a negative effect on monarch populations.
5. Kantola et al. (2019) estimated that 3.6 and 1.1 million monarchs were killed along roads in Oklahoma and Texas during the 2016 and 2017 fall migrations, respectively. These mortality rates are approximately 4% and 2% of the overwintering population in Mexico in those years. Kantola et al. (2019) estimate the population declined on average 7% each year so a 2–4% roadside mortality rate could be an important part of the annual decline. These authors also note that a high level of roadkill could also be occurring in Mexico. In addition, McKenna et al. (2001) estimated 500,000 monarchs were killed in 1 week in Illinois during fall migration. If similar numbers of monarchs are killed during fall migration in other Midwestern, Northeastern, and Southern states, this factor could contribute substantially to mortality during fall migration. A useful exercise would be to determine if increases in traffic in different regions of the US correlates with monarch population decline.
6. Refining the conversion factor of Pleasants and Oberhauser (2013) for the Midwest would require more surveys from a broader area.
Perhaps a model could be constructed utilizing different data (e.g., NABA adult counts, MLMP egg and larval counts, milkweed density, roadkill mortality rates, etc.); however, such a model is more likely to be successful using monitoring data derived through a probabilistic survey design.
Empirical Data
Empirical survey data on monarch butterflies of all stages is limited and the inferential value of some of that data has been questioned (Pleasants et al., 2017). Most inferences on monarch butterfly populations come from a few sources: overwintering population size measurements, citizen science counts of adults (e.g., NABA, Illinois and Ohio programs), and citizen science counts of larval stages (e.g., MLMP).
Much of the monarch data available is from citizen science programs and it is difficult to imagine how substantial data could be collected on monarch populations without these efforts. Data from citizen science programs may have limitations due to spatial sampling bias, because volunteers choose the survey locations, and there are no estimates of detection probability. Other citizen science programs have recognized these limitations. eBird, perhaps the largest citizen science program in the world (Sullivan et al., 2009), has recognized the imperfect detection issue, among other potential limitations (Sullivan et al., 2014). However, it is encouraging that studies have shown that eBird data can provide very similar results to standardized shorebird surveys (Callaghan and Gawlik, 2015). Detection probability for monarch eggs and larvae could be determined experimentally. Detection probability for adult monarchs is a difficult problem because of their vagile behavior. Monarch butterfly modeling research would be well served by data from monitoring programs with probabilistic sampling. A monitoring program under development by Monarch Joint Venture, USGS, and USFWS will hopefully fill this need (Cariveau et al., 2019). Analysis of MonarchWatch4 mark-recapture data, another citizen science program, would also be a welcome addition to the monarch data available for modeling efforts.
More data would also be useful for refining and calibrating algorithms in simulation models. Data on monarch movement patterns and behavior could help improve the movement algorithm in Grant et al. (2018), which is the mechanistic basis for the model. Data on milkweed density and egg density in a diversity of adjoining landcover types would improve calibration of landscape-scale simulation models. Milkweed and egg survey design and model frameworks need to be reconciled to ensure spatial and temporal scale concordance.
Modeling Monarch Migration
Modeling monarch migration has generally proceeded with an island chain approach (e.g., Flockhart et al., 2015; Oberhauser et al., 2017). Zalucki and Rochester (2004) modeled colonization probability over time in at weather station locations in the eastern U.S. These approaches omit the mechanics of movement (Zalucki et al., 2016). An agent-based model of monarch migration could include the important mechanics of movement and treat monarchs as individuals rather than very large “islands” in which each individual is assumed to be the same. Modeling migration at continental scales is a non-trivial task. Perhaps modeling the migration of the smaller western North American monarch population may be a more tractable starting point.
Western monarchs are declining (Espeset et al., 2016; Schultz et al., 2017) and the 2018 Thanksgiving counts found only ~28,429 monarchs5 With so few monarchs spread over the entire western U.S., modeling may help interpret current information and predict future conditions because a limited amount of survey data can be obtained. Pattern-oriented modeling could be a viable option. Grimm et al. (2005) describe pattern-oriented modeling as an approach that incorporates important system patterns; patterns exhibited by systems are likely the result of underlying mechanisms. Grimm et al. (2005) give an example of patterns used to model spatio-temporal patterns in European beech forests. Important patterns were: (1) the spatial mosaic of forest patches at different successional patterns, (2) different successional stages had different forest structure, and (3) when large individual trees fell, they created canopy openings. After incorporating these patterns, the model of beech forest dynamics predicted age structure and distribution of large old trees well and led to new understanding and hypotheses about the system. Incorporating important patterns gives a model robustness under varying conditions, sometimes even without in-depth calibration or evaluation. Some considerations for a potential pattern-orientated model of the western monarch migration that could be used to assess different hypotheses of annual monarch movements are summarized below.
The western monarch population overwinters along central and southern coastal California and spreads throughout the U.S. west of the continental divide during the summer (Reppert and de Roode, 2018). The most important breeding habitat has not been identified (Jepsen and Black, 2015), though recent efforts to map milkweed in the west have been undertaken (Dilts et al., (In Prep)). Western monarchs are genetically very similar to eastern monarchs (Lyons et al., 2012) and may have navigation strategies similar to eastern monarchs, or may have strategies adapted to the west. The mountains and deserts of the western U.S. strongly constrain movement patterns (Dingle et al., 2005). Overwintering monarchs originate from a variety of places in the western U.S. Stable isotope ratios demonstrate that western monarchs originate from four isoscapes in the western U.S.: 40% originate from the “northern inland range,” 30% from the “southern coastal range,” 16% from the “central range,” and 12% from the “northern coast and southern inland range” (Yang et al., 2016).
Following Grimm et al. (2005), several patterns that are important in the yearly cycle of western monarch migration should be reflected in a pattern-oriented model:
1. Monarchs are primarily found in coastal California during the winter and can be found nearly anywhere from northern Baja California to Mendocino County, California. Monarch aggregations can ebb and flow in size over the winter (Frey and Schaffner, 2004; Jepsen and Black, 2015).
2. The proportion of overwintering western monarchs from different areas of the range should match proportions from radio-isotope studies (Yang et al., 2016).
3. Monarchs spread throughout the U.S. west of the Continental Divide in the summer (Dingle et al., 2005).
4. The dates of monarch records may indicate spring expansion first into Nevada and Oregon, then Washington, Utah, British Colombia, Alberta, and Saskatchewan. Records in Idaho were scarce, perhaps because of sampling effort. Most Arizona records were from fall months (Dingle et al., 2005).
5. Monarchs tagged in Arizona have been found in California and Mexican wintering sites (Morris et al., 2015).
6. Monarchs tend to follow riparian corridors and wetter areas where milkweed and nectar sources are more abundant (Dingle et al., 2005).
7. Monarchs tend to fly around mountains in the spring, following the foothills, rather than directly over mountains (Nagano et al., 1993).
8. There is significant individual variation in behavior in spring migration behavior (Dingle et al., 2005) and overwintering congregation locations, with some individuals overwintering in Arizona (Morris et al., 2015) and other locations where temperature does not exceed 4°C (Dingle et al., 2005).
We hypothesize that fine-scale monarch movement constrained by landscape and weather factors results in the observed patterns. Annual migration strategies are the primary driver of observed patterns. Testing different conceptual models of monarch movement and migration strategies for consistency with these patterns can determine which conceptual models of monarch movement are most accurate, providing inference on monarch migration strategies and improving model robustness. We propose several conceptual models of western monarch migration to test against these patterns. Some models are based on eastern monarch research, under the assumption that western monarchs may use the same migration strategies as eastern monarchs:
1. Western monarch distribution is simply a yearly range expansion and contraction with no directional movement and migration involved. Monarchs diffuse into the Great Basin during warm summer months, and are forced back to the coast by cold temperatures in the fall (Wenner and Harris, 1993). This would serve well as a null model.
2. Western monarch orientation rotates 360° over the year (Brower, 1996).
3. Western monarchs are “true navigators” that know where they are going and how to get there (Pyle, 1999;Oberhauser et al., 2013).
4. Western monarchs employ vector navigation wherein they have an instinct to travel in a certain direction until geography and weather shunt their movements (Mouritsen et al., 2013a;Mouritsen et al., 2013b).
In a simulation model, western monarch agents could be programmed with directionality according to the four conceptual models highlighted above. For example, monarch agents following strategy 4 would have a strong northeast directionality during the spring months, but would have a higher probability of staying at the same elevation instead of gaining altitude to maintain a base directionality. Individual variation in directionality (Froy et al., 2003) and probabilistic movement decisions would result in monarchs spreading over the landscape. For each movement step, agents would have a probability of laying eggs depending on the habitat. Each egg would be a new agent, with developmental rate dictated by temperature and survival rate. Eggs that survive would become adult monarch agents and begin moving across the landscape. As directionality fades over the summer, simple diffusion along riparian corridors would occur.
An agent-based model could test the proposed models of the western monarch annual movement cycle. Once a model is found that matches observed patterns, the model could identify which areas are most important to monarch migration and breeding. Modeling movement and demographics of monarchs over the year could increase understanding of important movement and migration corridors and increase understanding of important breeding habitat. Such a model could also address questions about the annual movements of western monarchs. Model results could be tested with empirical surveys and conservation steps could be prioritized accordingly.
Advancing Monarch Butterfly Modeling
While monarch modeling using mathematical, statistical and simulation approaches has greatly increased understanding of monarch butterfly systems, improved approaches are needed to understand the causes of monarch population trends, including the effects of climate change and other stressors, and to predict population responses as a function of alternate conservation plans. Most statistical modeling to date has been largely correlative with little mechanistic basis. Mathematical and statistical models have used an island chain conceptual framework, but new understanding and prediction may require an agent-based approach. Few models have incorporated weather effects, though most authors acknowledge that they believe weather to be a primary driver of population fluctuations. Agent-based modeling with built-in demographics and weather effects could address this need. Incorporating movement patterns and behavior in agent-based models provide an important mechanistic basis (Zalucki et al., 2016). A model of western monarch migration could serve as an important developmental step to advancing agent-based modeling of eastern monarch migration. A model of eastern monarch migration could incorporate existing agent-based models for non-migratory generations.
What are the challenges to advancing such a modeling effort? Mechanisms that need to be incorporated include movement behavior, developmental dynamics, density dependent effects, effects of nectar resources on movement behavior, spatial memory effects, behavioral interactions between individuals, predation dynamics, and land-use stressors, such as pesticides and mowing. It is not clear that all of these effects are possible or necessary to include in agent-based models, but a conceptual model could begin to address these factors systematically. Models could be developed with nested modules to address these issues and their interactions. Moving forward on collecting data to refine model algorithms and calibrate and evaluate models is a significant challenge. Advancing understanding and predictive capabilities of the monarch system will require well-planned collaboration between laboratory and field-based research and modeling teams. The continued existence of monarch butterflies as a migratory phenomenon will likely require new approaches to develop the necessary understanding and predictive capability to determine those conservation actions necessary to reverse population declines in eastern and western North America. International teams with a diversity of backgrounds are well positioned to develop new conceptual models of monarch systems to address these challenges.
Author Contributions
Many of the ideas in this paper have been developed over time by discussions between the authors. TG had primary responsibility reviewing the cited journal articles and wrote the initial draft. SB provided secondary reviews of articles, guidance, editing, and additional discussion and development of ideas for the manuscript.
Funding
This work was supported, in part, by the Agriculture and Food Research Initiative Pollinator Health Program (Grant No. 2018-67013-27541) from the USDA National Institute of Food and Agriculture. The authors also acknowledge support from the College of Agriculture and Life Sciences at Iowa State University and the Iowa Monarch Conservation Consortium.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Discussions with the Monarch Butterfly Working Group at Iowa State University and many monarch butterfly researchers aided in development of concepts in the manuscript.
Footnotes
References
Agrawal, A. A., and Inamine, H. (2018). Mechanisms behind the monarch's decline. Science 360, 1294–1296. doi: 10.1126/science.aat5066
Batalden, R. V., Oberhauser, K., and Peterson, A. T. (2007). Ecological niches in sequential generations of eastern North American monarch butterflies (Lepidoptera: Danaidae): the ecology of migration and likely climate change implications. Environ. Entomol. 36, 1365–1373. doi: 10.1603/0046-225X(2007)36[1365:ENISGO]2.0.CO;2
Batty, M., and Torrens, P. M. (2005). Modelling and prediction in a complex world. Futures 37, 745–766. doi: 10.1016/j.futures.2004.11.003
Bennett, N. D., Croke, B. F., Guariso, G., Guillaume, J. H., Hamilton, S. H., Jakeman, A. J., et al. (2013). Characterising performance of environmental models. Environ. Model. Softw. 40, 1–20. doi: 10.1016/j.envsoft.2012.09.011
Blader, T. R. (2018). Milkweed patch size effects on monarch butterfly oviposition within Iowa prairies and roadsides. (Master's thesis). Iowa State University, Ames, IA, United States.
Boyle, J. H., Dalgleish, H. J., and Puzey, J. R. (2019). Monarch butterfly and milkweed declines substantially predate the use of genetically modified crops. Proc. Natl. Acad. Sci. U.S.A. 116, 3006–3011. doi: 10.1073/pnas.1811437116
Brower, L. (1996). Monarch butterfly orientation: missing pieces of a magnificent puzzle. J. Exp. Biol. 199, 93–103.
Brower, L. P., Fink, L. S., Kiphart, R., Pocius, V. M., Zubieta-Hern'andez, R. R., and Ram'irez, M. I. (2015). “Effect of the 2010–2011 drought on the lipid content of monarch butterflies migrating through Texas to overwintering sites in Mexico,” in Monarchs in a Changing World: Biology and Conservation of an Iconic Butterfly, eds K. S. Oberhauser, K. R. Nail, and S. Altizer (Ithaca, NY: Cornell University Press), 117–129.
Callaghan, C. T., and Gawlik, D. E. (2015). Efficacy of eBird data as an aid in conservation planning and monitoring. J. Field Ornithol. 86, 298–304. doi: 10.1111/jofo.12121
Cariveau, A., Holt, H., Ward, J. P. Jr., Lukens, L., Kasten, K., Thieme, J., et al. (2019). The integrated monarch monitoring program: from design to implementation. Front. Ecol. Evol. 7:00167. doi: 10.3389/fevo.2019.00167
Codling, E. A., Plank, M. J., and Benhamou, S. (2008). Random walk models in biology. J. R. Soc. Interface 5, 813–834. doi: 10.1098/rsif.2008.0014
Collett, M., Chittka, L., and Collett, T. S. (2013). Spatial memory in insect navigation. Curr. Biol. 23, R789–R800. doi: 10.1016/j.cub.2013.07.020
Davis, A. K. (2012). Are migratory monarchs really declining in eastern North America? Examining evidence from two fall census programs. Insect Conserv. Divers. 5, 101–105. doi: 10.1111/j.1752-4598.2011.00158.x
Dilts, T., Steele, M., Engler, J. D., Pelton, E. M., Jepsen, S. J., McKnight, S., et al. (2019). Host plants and climate structure habitat associations of the western monarch butterfly. 7:00188. Front. Ecol. Evol. doi: 10.3389/fevo.2019.00188
Dingle, H., Zalucki, M. P., Rochester, W. A., and Armijo-Prewitt, T. (2005). Distribution of the monarch butterfly, Danaus plexippus (L.)(Lepidoptera: Nymphalidae), in western North America. Biol. J. Linn. Soc. 85, 491–500. doi: 10.1111/j.1095-8312.2005.00512.x
Drury, K. L., and Dwyer, G. (2005). Combining stochastic models with experiments to understand the dynamics of monarch butterfly colonization. Am. Nat. 166, 731–750. doi: 10.1086/497542
Dyer, L. A., and Forister, M. L. (2016). Wherefore and whither the modeler: understanding the population dynamics of monarchs will require integrative and quantitative techniques. Ann. Entomol. Soc. Am. 109, 172–175. doi: 10.1093/aesa/sav160
Espeset, A. E., Harrison, J. G., Shapiro, A. M., Nice, C. C., Thorne, J. H., Waetjen, D. P., et al. (2016). Understanding a migratory species in a changing world: climatic effects and demographic declines in the western monarch revealed by four decades of intensive monitoring. Oecologia 181, 819–830. doi: 10.1007/s00442-016-3600-y
Feddema, J. J., Shields, J., Taylor, O. R., and Bennett, D. (2004). “Simulating the development and migration of the monarch butterfly,” in The Monarch Butterfly: Biology and Conservation, eds K. S. Oberhauser and M. J. Solensky (Ithaca, NY: Cornell University Press), 229–240.
Flockhart, D. T., Brower, L. P., Ramirez, M. I., Hobson, K. A., Wassenaar, L. I., Altizer, S., et al. (2017). Regional climate on the breeding grounds predicts variation in the natal origin of monarch butterflies overwintering in Mexico over 38 years. Glob. Chang. Biol. 23, 2565–2576. doi: 10.1111/gcb.13589
Flockhart, D. T., Pichancourt, J. B., Norris, D. R., and Martin, T. G. (2015). Unravelling the annual cycle in a migratory animal: breeding-season habitat loss drives population declines of monarch butterflies. J. Anim. Ecol. 84, 155–165. doi: 10.1111/1365-2656.12253
Frey, D., and Schaffner, A. (2004). “Spatial and temporal pattern of monarch overwintering abundance in western North America,” in The Monarch Butterfly: Biology and Conservation, eds K. S. Oberhauser and M. J. Solenski (Ithaca, NY: Cornell University Press), 167–176.
Froy, O., Gotter, A. L., Casselman, A. L., and Reppert, S. M. (2003). Illuminating the circadian clock in monarch butterfly migration. Science 300, 1303–1305. doi: 10.1126/science.1084874
Grant, T. J., Parry, H. R., Zalucki, M. P., and Bradbury, S. P. (2018). Predicting monarch butterfly (Danaus plexippus) movement and egg-laying with a spatially-explicit agent-based model: the role of monarch perceptual range and spatial memory. Ecol. Model. 374, 37–50. doi: 10.1016/j.ecolmodel.2018.02.011
Grimm, V., Revilla, E., Berger, U., Jeltsch, F., Mooij, W. M., Railsback, S. F., et al. (2005). Pattern-oriented modeling of agent-based complex systems: lessons from ecology. Science 310, 987–991. doi: 10.1126/science.1116681
Haefner, J. W. (2005). Modeling Biological Systems: Principles and Applications. New York, NY: Springer Science and Business Media.
Hartzler, R. G. (2010). Reduction in common milkweed (Asclepias syriaca) occurrence in Iowa cropland from 1999 to 2009. Crop Prot. 29, 1542–1544. doi: 10.1016/j.cropro.2010.07.018
Heemskerk, M., Wilson, K., and Pavao-Zuckerman, M. (2003). Conceptual models as tools for communication across disciplines. Conserv. Ecol. 7:8. doi: 10.5751/ES-00554-070308
Hilborn, R., and Mangel, M. (1997). The Ecological Detective: Confronting Models with Data. Princeton, NJ: Princeton University Press.
Inamine, H., Ellner, S. P., Springer, J. P., and Agrawal, A. A. (2016). Linking the continental migratory cycle of the monarch butterfly to understand its population decline. Oikos 125, 1081–1091. doi: 10.1111/oik.03196
Jepsen, S., and Black, S. H. (2015). “Understanding and conserving the western North American monarch population,” in Monarchs in a Changing World. Biology and Conservation of an Iconic Butterfly, eds K. Oberhauser, K. Nail, and S. Altizer (Ithaca, NY: Cornell University Press), 147–156.
Jones, R. E. (1977). Movement patterns and egg distribution in cabbage butterflies. J. Anim. Ecol. 46, 195–212. doi: 10.2307/3956
Jones, R. E., Gilbert, N., Guppy, M., and Nealis, V. (1980). Long-distance movement of Pieris rapae. J. Anim. Ecol. 49, 629–642. doi: 10.2307/4268
Kantola, T., Tracy, J. L., Baum, K. A., Quinn, M. A., and Coulson, R. N. (2019). Spatial risk assessment of eastern monarch butterfly road mortality during autumn migration within the southern corridor. Biol. Conserv. 231:150–160. doi: 10.1016/j.biocon.2019.01.008
Kery, M., and Plattner, M. (2007). Species richness estimation and determinants of species detectability in butterfly monitoring programmes. Ecol. Entomol. 32, 53–61. doi: 10.1111/j.1365-2311.2006.00841.x
Kral, K., Harmon, J., Limb, R., and Hovick, T. (2018). Improving our science: the evolution of butterfly sampling and surveying methods over time. J. Insect Conserv. 22, 1–14. doi: 10.1007/s10841-018-0046-z
Lemoine, N. P. (2015). Climate change may alter breeding ground distributions of eastern migratory monarchs (Danaus plexippus) via range expansion of Asclepias host plants. PLoS ONE 10:e0118614. doi: 10.1371/journal.pone.0118614
Lyons, J. I., Pierce, A. A., Barribeau, S. M., Sternberg, E. D., Mongue, A. J., and de Roode, J. C. (2012). Lack of genetic differentiation between monarch butterflies with divergent migration destinations. Mol. Ecol. 21, 3433–3444. doi: 10.1111/j.1365-294X.2012.05613.x
MacKenzie, D. I., and Kendall, W. L. (2002). How should detection probability be incorporated into estimates of relative abundance? Ecology 83, 2387–2393. doi: 10.1890/0012-9658(2002)083[2387:HSDPBI]2.0.CO;2
Malcolm, S. B. (2018). Anthropogenic impacts on mortality and population viability of the monarch butterfly. Annu. Rev. Entomol. 63, 277–302. doi: 10.1146/annurev-ento-020117-043241
Marino, S., Hogue, I. B., Ray, C. J., and Kirschner, D. E. (2008). A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 254, 178–196. doi: 10.1016/j.jtbi.2008.04.011
McKenna, D. D., McKenna, K. M., Malcom, S. B., and Bebenbaum, M. R. (2001). Mortality of Lepidoptera along roadways in central Illinois. J. Lepid. Soc. 55, 63–68. Available online at: http://images.peabody.yale.edu/lepsoc/jls/
Morris, G. M., Kline, C., and Morris, S. M. (2015). Status of Danaus plexippus population in Arizona. J. Lepid. Soc. 69, 91–107. doi: 10.18473/lepi.69i2.a10
Mouritsen, H., Derbyshire, R., Stalleicken, J., Mouritsen, O. Ø., Frost, B. J., and Norris, D. R. (2013a). An experimental displacement and over 50 years of tag-recoveries show that monarch butterflies are not true navigators. Proc. Natl. Acad. Sci. U.S.A. 110, 7348–7353. doi: 10.1073/pnas.1221701110
Mouritsen, H., Derbyshire, R., Stalleicken, J., Mouritsen, O. Ø., Frost, B. J., and Norris, D. R. (2013b). Reply to Oberhauser et al.: the experimental evidence clearly shows that monarch butterflies are almost certainly not true navigators. Proc. Natl. Acad. Sci. U.S.A. 110:E3681. doi: 10.1073/pnas.1309282110
Nagano, C. D., Sakai, W. H., Malcolm, S. B., Cockrell, B. J., Donahue, J. P., and Brower, L. P. (1993). “Spring migration of monarch butterflies in California,” in Biology and Conservation of The Monarch Butterfly, eds S. B. Malcom and M. P. Zalucki (Los Angeles, CA: Natural History Museum of Los Angeles County; Science Series), 219–232.
Nail, K. R., Stenoien, C., and Oberhauser, K. S. (2015). Immature monarch survival: effects of site characteristics, density, and time. Ann. Entomol. Soc. Am. 108, 680–690. doi: 10.1093/aesa/sav047
Newman, K. B., Buckland, S. T., Morgan, B., King, R., Borchers, D. L., Cole, D., et al. (2014). Modelling Population Dynamics. New York, NY: Springer.
Nowicki, P., Settele, J., Henry, P. Y., and Woyciechowski, M. (2008). Butterfly monitoring methods: the ideal and the real world. Isr. J. Ecol. Evol. 54, 69–88. doi: 10.1560/IJEE.54.1.69
Oberhauser, K., Wiederholt, R., Diffendorfer, J. E., Semmens, D., Ries, L., Thogmartin, W. E., et al. (2017). A trans-national monarch butterfly population model and implications for regional conservation priorities. Ecol. Entomol. 42, 51–60. doi: 10.1111/een.12351
Oberhauser, K. S. (2004). “Modeling the distribution and abundance of monarch butterflies,” in The Monarch Butterfly: Biology and Conservation, eds K. S. Oberhauser and M. J. Solenski (Ithaca, NY: Cornell University Press), 199–202.
Oberhauser, K. S., Prysby, M. D., Mattila, H. R., Stanley-Horn, D. E., Sears, M. K., Dively, G., et al. (2001). Temporal and spatial overlap between monarch larvae and corn pollen. Proc. Natl. Acad. Sci. U.S.A. 98, 11913–11918. doi: 10.1073/pnas.211234298
Oberhauser, K. S., Taylor, O. R., Reppert, S. M., Dingle, H., Nail, K. R., Pyle, R. M., et al. (2013). Are monarch butterflies true navigators? The jury is still out. Proc. Natl. Acad. Sci. U.S.A. 110, E3680–E3680. doi: 10.1073/pnas.1308369110
Pellet, J. (2008). Seasonal variation in detectability of butterflies surveyed with Pollard walks. J. Insect Conserv. 12, 155–162. doi: 10.1007/s10841-007-9075-8
Pellet, J., Bried, J. T., Parietti, D., Gander, A., Heer, P. O., Cherix, D., et al. (2012). Monitoring butterfly abundance: beyond Pollard walks. PLoS ONE 7:e41396. doi: 10.1371/journal.pone.0041396
Pleasants, J. M., and Oberhauser, K. S. (2013). Milkweed loss in agricultural fields because of herbicide use: effect on the monarch butterfly population. Insect Conserv. Divers. 6, 135–144. doi: 10.1111/j.1752-4598.2012.00196.x
Pleasants, J. M., Zalucki, M. P., Oberhauser, K. S., Brower, L. P., Taylor, O. R., and Thogmartin, W. E. (2017). Interpreting surveys to estimate the size of the monarch butterfly population: pitfalls and prospects. PLoS ONE 12:e0181245. doi: 10.1371/journal.pone.0181245
Prysby, M. D., and Oberhauser, K. S. (2004). “Temporal and geographic variation in monarch densities: citizen scientists document monarch population patterns,” in The Monarch butterfly: Biology and Conservation, eds K. S. Oberhauser and M. J. Solenski (Ithaca, NY: Cornell University Press), 9–20.
Reppert, S. M., and de Roode, J. C. (2018). Demystifying monarch butterfly migration. Curr. Biol. 28, R1009–R1022. doi: 10.1016/j.cub.2018.02.067
Restif, O., Hayman, D. T., Pulliam, J. R., Plowright, R. K., George, D. B., Luis, A. D., et al. (2012). Model-guided fieldwork: practical guidelines for multidisciplinary research on wildlife ecological and epidemiological dynamics. Ecol. Lett. 15, 1083–1094. doi: 10.1111/j.1461-0248.2012.01836.x
Ries, L., Taron, D. J., and Rendón-Salinas, E. (2015). The disconnect between summer and winter monarch trends for the eastern migratory population: possible links to differing drivers. Ann. Entomol. Soc. Am. 108, 691–699. doi: 10.1093/aesa/sav055
Ries, L., Zipkin, E. F., and Guralnick, R. P. (2019). Tracking trends in monarch abundance over the 20th century is currently impossible using museum records: a response to Boyle et al. (2019). bioRχiv. doi: 10.1101/581801
Rossman, S., Yackulic, C. B., Saunders, S. P., Reid, J., Davis, R., and Zipkin, E. F. (2016). Dynamic N-occupancy models: estimating demographic rates and local abundance from detection-nondetection data. Ecology 97, 3300–3307. doi: 10.1002/ecy.1598
Rykiel, E. J. Jr. (1996). Testing ecological models: the meaning of validation. Ecol. Model. 90, 229–244. doi: 10.1016/0304-3800(95)00152-2
Saunders, S. P., Ries, L., Neupane, N., Ramirez, M. I., García-Serrano, E., Rendón-Salinas, E., et al. (2019). Multiscale seasonal factors drive the size of winter monarch colonies. Proc. Natl. Acad. Sci. U.S.A. 116, 8609–8614. doi: 10.1073/pnas.1805114116
Saunders, S. P., Ries, L., Oberhauser, K. S., and Zipkin, E. F. (2016). Evaluating confidence in climate-based predictions of population change in a migratory species. Glob. Ecol. Biogeogr. 25, 1000–1012. doi: 10.1111/geb.12461
Schultz, C. B., Brown, L. M., Pelton, E., and Crone, E. E. (2017). Citizen science monitoring demonstrates dramatic declines of monarch butterflies in western North America. Biol. Conserv. 214, 343–346. doi: 10.1016/j.biocon.2017.08.019
Semmens, B. X., Semmens, D. J., Thogmartin, W. E., Wiederholt, R., López-Hoffman, L., Diffendorfer, J. E., et al. (2016). Quasi-extinction risk and population targets for the Eastern, migratory population of monarch butterflies (Danaus plexippus). Sci. Rep. 6:23265. doi: 10.1038/srep23265
Stenoien, C., Nail, K. R., and Oberhauser, K. S. (2015). Habitat productivity and temporal patterns of monarch butterfly egg densities in the Eastern United States. Ann. Entomol. Soc. Am. 108, 670–679. doi: 10.1093/aesa/sav054
Stenoien, C., Nail, K. R., Zalucki, J. M., Parry, H., Oberhauser, K. S., and Zalucki, M. P. (2018). Monarchs in decline: a collateral landscape-level effect of modern agriculture. Insect Sci. 25, 528–541. doi: 10.1111/1744-7917.12404
Sullivan, B. L., Aycrigg, J. L., Barry, J. H., Bonney, R. E., Bruns, N., Cooper, C. B., et al. (2014). The eBird enterprise: an integrated approach to development and application of citizen science. Biol. Conserv. 169, 31–40. doi: 10.1016/j.biocon.2013.11.003
Sullivan, B. L., Wood, C. L., Iliff, M. J., Bonney, R. E., Fink, D., and Kelling, S. (2009). eBird: a citizen-based bird observation network in the biological sciences. Biol. Conserv. 142, 2282–2292. doi: 10.1016/j.biocon.2009.05.006
Thiele, J. C., Kurth, W., and Grimm, V. (2014). Facilitating parameter estimation and sensitivity analysis of agent-based models: a cookbook using NetLogo and R. J. Artif. Soc. Soc. Simul. 17:11. doi: 10.18564/jasss.2503
Thogmartin, W. E., López-Hoffman, L., Rohweder, J., Diffendorfer, J., Drum, R., Semmens, D., et al. (2017). Restoring monarch butterfly habitat in the Midwestern US: ‘all hands on deck'. Environ. Res. Lett. 12:074005. doi: 10.1088/1748-9326/aa7637
Wallentin, G. (2017). Spatial simulation: a spatial perspective on individual-based ecology—a review. Ecol. Model. 350, 30–41. doi: 10.1016/j.ecolmodel.2017.01.017
Webb, B. (2001). Can robots make good models of biological behaviour? Behav. Brain Sci. 24, 1033–1050. doi: 10.1017/S0140525X01000127
Wenner, A. M., and Harris, A. M. (1993). “Do California monarchs undergo long-distance directed migration?” in Biology and Conservation of The Monarch Butterfly, eds S. B. Malcom and M. P. Zalucki (Los Angeles, CA: Los Angeles County Museum, Science Series No. 38), 209–218.
Wepperich, T. M. (2019). Monarch butterfly declines reported in Boyle et al. (2019) are biased by unexamined changes in museum collections over time. bioRχiv doi: 10.1101/562314
Williams, B. K., Nichols, J. D., and Conroy, M. J. (2002). Analysis and Management of Animal Populations. San Diego, CA: Academic Press.
Yakubu, A. A., Sáenz, R., Stein, J., and Jones, L. E. (2004). Monarch butterfly spatially discrete advection model. Math. Biosci. 190, 183–202. doi: 10.1016/j.mbs.2004.03.002
Yang, L. H., Ostrovsky, D., Rogers, M. C., and Welker, J. M. (2016). Intra-population variation in the natal origins and wing morphology of overwintering western monarch butterflies Danaus plexippus. Ecography 39, 998–1007. doi: 10.1111/ecog.01994
Zalucki, M. P. (1983). Simulation of movement and egglaying in Danaus plexippus (Lepidoptera: Nymphalidae). Res. Popul. Ecol. 25:353. doi: 10.1007/BF02515609
Zalucki, M. P., and Lammers, J. H. (2010). Dispersal and egg shortfall in monarch butterflies: what happens when the matrix is cleaned up? Ecol. Entomol. 35, 84–91. doi: 10.1111/j.1365-2311.2009.01160.x
Zalucki, M. P., Parry, H. R., and Zalucki, J. M. (2016). Movement and egg laying in monarchs: to move or not to move, that is the equation. Austral Ecol. 41, 154–167. doi: 10.1111/aec.12285
Zalucki, M. P., and Rochester, W. A. (2004). “Spatial and temporal population dynamics of monarchs down-under: lessons for North America,” in The Monarch Butterfly: Biology and Conservation, eds K. S. Oberhauser and M. J. Solensky (Ithaca, NY: Cornell University Press), 219–228.
Keywords: modeling, monarch butterfly, agent-based modeling, population dynamics, migration
Citation: Grant TJ and Bradbury SP (2019) The Role of Modeling in Monarch Butterfly Research and Conservation. Front. Ecol. Evol. 7:197. doi: 10.3389/fevo.2019.00197
Received: 19 February 2019; Accepted: 13 May 2019;
Published: 31 May 2019.
Edited by:
Wayne E. Thogmartin, United States Geological Survey, United StatesReviewed by:
Matthew Forister, University of Nevada, Reno, United StatesFrancisco Botello, National Autonomous University of Mexico, Mexico
Copyright © 2019 Grant and Bradbury. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tyler J. Grant, dGdyYW50QGlhc3RhdGUuZWR1
 Tyler J. Grant
Tyler J. Grant Steven P. Bradbury
Steven P. Bradbury