- Department of Ecology and Evolutionary Biology, University of California, Los Angeles, Los Angeles, CA, United States
There is increasing evidence that climate warming is impacting biodiversity by disrupting species interactions. Trophic (consumer-resource) interactions, which comprise the fundamental units (modules) of food webs, are of particular importance because they have an intrinsic tendency to fluctuate in abundance, thus running to risk of stochastic extinction during periods of low abundances. Here I present a mathematical framework for predicting warming effects on consumer-resource interactions. This work differs from previous theory in two ways. First, it uses delay differential equations to realistically depict the developmental delays inherent in ectotherm life cycles, and incorporates mechanistic descriptions of phenotypic trait responses, derived from first principles of thermodynamics, into the dynamical delay model. Second, it tests the latest IPCC predictions on warmer-than-average winters and hotter-than-average summers. I investigate warming effects on three major axes: latitude (tropical vs. temperate), life stage attacked (juvenile vs. adult), and nature of consumer-resource dynamics in the absence of temperature variation (stable vs. complex). I report three findings. First, consumer-resource interactions in the tropics are more at risk of species losses due to warming while those in the temperate zone are more at risk of extreme fluctuations in species' abundances. Second, effects of warming are more detrimental when the consumer attacks the adult stage of the resource and when consumer-resource interactions exhibit complex dynamics. Third, hotter-than-average summers are more detrimental to consumer-resource interactions than warmer-than-average winters. I discuss implications of these results for biodiversity and biological pest control.
Introduction
Trophic interactions between consumers and resources (e.g., predator-prey, plant-herbivore, host-parasite) play a fundamental role in all communities, be they natural or managed. A unique property that distinguishes trophic interactions from other species interactions is the conflict of interest between species: the consumer benefits from the interaction while the resource is harmed by it. This leads to unique dynamical outcomes such as intrinsic oscillations in abundance, and coevolutionary arms races (Murdoch et al., 2002, 2003).
The majority of consumer-resource interactions in nature occur amongst ectotherms (e.g., microbes, invertebrates, fish, amphibians, and reptiles) whose body temperature depends on the environmental temperature (Brown et al., 2004; Angilletta, 2009). It is well-known that temperature variation (e.g., diurnal, seasonal) has a strong effect on consumer-resource dynamics and persistence. For instance, differential adaptability of prey species to seasonal temperature regimes can generate temporal refuges, which can reduce overexploitation by predators and dampen predator-prey oscillations (Murdoch et al., 2003); differential adaptability of natural enemies can achieve more effective pest control through complementary action (Takagi and Hirose, 1994; Rochat and Gutierrez, 2001; Hunt-Joshi et al., 2005; Tuda et al., 2006).
There is increasing evidence that climate warming is disrupting consumer-resource interactions, causing phenological shifts and increasing the likelihood of species extinctions (Dunn and Winkler, 1999; Walther et al., 2002; Root et al., 2003; Parmesan, 2006; Inouye, 2008; Miller-Rushing and Primack, 2008; Post et al., 2008). This has spurred a body of theory (Vasseur and McCann, 2005; van de Wolfshaar et al., 2008; OConnor et al., 2011; Ohlberger et al., 2011; Binzer et al., 2012; Dell et al., 2014; Gilbert et al., 2014; Amarasekare, 2015; Uszko et al., 2017), which has greatly enhanced our understanding of how temperature variation and climate warming influence the dynamics and persistence of consumer-resource interactions. There, however, remains two key gaps in our knowledge. The first is a biological one. No studies to date have incorporated the key feature that characterizes the complex life cycles of multicellular ectotherms: time delays induced by development from egg to adult. As we know from classical theory, developmental delays lead to types of complex dynamics (e.g., generation cycles, delayed feedback cycles) that are unobserved in models that do not account for the age/stage-structure (Gurney et al., 1983; Nisbet and Gurney, 1983; Murdoch et al., 2003). Importantly, such dynamics emerge even in the absence of temperature variation. A lack of knowledge on how temperature variation affects complex dynamics arising from developmental delays is one of the most crucial impediments to predicting how climate change will impact consumer-resource dynamics involving multicellular ectotherms. The second gap in our knowledge is a physical one. Existing studies do not incorporate recent IPCC predictions about warmer-than-average winters and hotter-than-average summers (IPCC, 2018).
Here I take a first step toward bridging these gaps. I develop a mathematical framework that realistically depicts the developmental delays that characterize ectotherm life cycles, and incorporates mechanistic descriptions of phenotypic trait responses to temperature into dynamical models of consumer-resource interactions. Its key feature is that it can predict population-level effects of warming at different latitudes based solely on trait response data, and completely independently of population-level information. This provides a powerful alternative to species distribution models that rely on population-level data to predict the effects of climate warming.
Mathematical Framework
Consider a consumer-resource interaction in which the resource and consumer species each has two stages in the life cycle (juvenile and adult), and the consumer exploits the juvenile or adult stage of the resource species. We would expect the resource species to experience intra-specific competition for its own limiting factors (e.g., food, space). Such self-limitation can occur via density-dependent fecundity or mortality. Common examples of such interactions involve insect parasitoids attacking nymphal/larval or adult stages of other insects, lizards and spiders feeding on insects, and lady beetles feeding on aphids (Murdoch et al., 2003). The dynamics of the stage-structured interaction are given by:
where J and A depict juvenile and adult stages of the resource species, and L and C, those of the consumer species. The functions and , (X = J, A) describe the joint effects temperature and density on per capita birth and mortality rates, g(X(t)) is the consumer's functional response, and dZ(t), Z = L, C depicts the density-independent mortality rates of the juvenile and adult consumer.
We consider g to be a saturating function of resource abundance given strong empirical evidence that saturating functional responses are the commonest observed in nature (Murdoch et al., 2003; Jeschke et al., 2004). Then, where a(T(t)) and h(T(t)) depict, respectively, the consumer's temperature-dependent attack rate and handling time. The stoichiometric properties underlying the consumer's conversion efficiency (f) makes it insensitive to temperature (Peters, 1983; Custer, 2005), and there is no empirical evidence suggesting systematic changes with temperature (Uszko et al., 2017). Density-dependent fecundity is typically depicted as (Murdoch et al., 2003; Amarasekare and Coutinho, 2014) where b(T(t)) is the temperature-dependent per capita birth rate, and q(T(t)), the temperature-dependent resource self-limitation strength. Density-dependent mortality is given by (Amarasekare and Coutinho, 2014).
The function MY(t) (Y = J, L) is the temperature-dependent recruitment rate, which is the product of the recruitment rate into the juvenile stage τY(t) time units ago and the fraction of juveniles (larvae) that survive to adulthood (SY(t)). The function mY(T(t)) (Y = J, L) depicts variation in the per individual maturation rate with time due to the temperature dependence of juvenile developmental delay (τY).
The population-level effects of climate warming we observe is the result of temperature effects on the underlying life history and consumption traits of consumers and resources. The first step therefore is to understand how temperature variation affects these traits.
Temperature Responses of Life History and Consumption Traits
Life history and consumption traits of ectotherms exhibit plastic temperature responses (reaction norms, Roff, 1992) that represent the phenotypic-level manifestations of temperature effects on underlying biochemical processes (e.g., reaction kinetics, hormonal regulation; Johnson and Lewin, 1946; Sharpe and DeMichele, 1977; Schoolfield et al., 1981; Nijhout, 1994; Van der Have and de Jong, 1996; Van der Have, 2002; Ratkowsky et al., 2005; Kingsolver, 2009; Kingsolver et al., 2011). Temperature effects on biochemical rate processes (e.g., reaction kinetics and enzyme inactivation) give rise to phenotypic-level responses that are left-skewed or monotonic increasing/decreasing (Van der Have and de Jong, 1996; Gillooly et al., 2001, 2002; Van der Have, 2002; Savage et al., 2004). Mortality and maturation rates exemplify such rate-controlled responses. This contrasts with temperature effects on on biochemical regulatory processes (e.g., neural and hormonal regulation; Nijhout, 1994; Hochachka and Somero, 2002; Long and Fee, 2008), which yield phenotypic-level responses that are symmetric unimodal (e.g., Gaussian). This is because regulatory processes are driven by negative feedbacks that push increasing and decreasing rate processes toward an intermediate optimum.
Temperature Response of Mortality
Density-independent per capita mortality rate of all ectotherms increases with temperature within the biologically relevant temperature range (Johnson and Lewin, 1946; Sharpe and DeMichele, 1977; Schoolfield et al., 1981; Ratkowsky et al., 2005), i.e., the temperature range between the lower threshold below which body fluids freeze and the upper threshold above which proteins denature (Gillooly et al., 2001, 2002; Savage et al., 2004). Below this range, mortality starts to increase with decreasing temperature due to the freezing of body fluids and other related phenomena (Van der Have and de Jong, 1996; Gillooly et al., 2001, 2002; Savage et al., 2004; Dell et al., 2011). The complete mortality response can be described by a modified version of the Boltzmann-Arrhenius function (Van der Have and de Jong, 1996; Gillooly et al., 2001, 2002; Savage et al., 2004):
where d(T) is the mortality rate at temperature T (in K), Ad is the Arrhenius constant, which quantifies how fast the mortality rate increases with increasing temperature, and TR is a reference (baseline) temperature. The mortality at this temperature, dTR, represents the species-specific intrinsic mortality rate. The parameter TL is the temperature threshold at which mortality starts to increase with decreasing temperature, and AL quantifies how quickly the mortality rate decreases with decreasing temperature. Note that Ad > 0 and AL < 0.
Temperature Response of Birth and Consumption Rates
A large number of studies spanning a range of ectothermic taxa show that per capita birth and consumption rates exhibit unimodal responses to temperature (Dreyer and Baumgartner, 1996; Carriere and Boivin, 1997; Morgan et al., 2001; Dannon et al., 2010; Hou and Weng, 2010; Jandricic et al., 2010; Dell et al., 2011; Englund et al., 2011; Amarasekare and Savage, 2012; Amarasekare, 2015). Both are well-described by a Gaussian function:
where Topta is the temperature at which the birth (consumption) rate is maximal (aTopt), and sa is a measure of the response breadth, the temperature range over which the species can reproduce and exploit resources.
Temperature Response of the Handling Time
Data from a number of ectotherm taxa spanning zooplankton to fish show that the handling time (inverse of the maximum uptake rate) exhibits a symmetric U-shaped response (Englund et al., 2011), which is well-described by an inverse Gaussian function:
where Topth is the temperature at which the handling time is minimal (hTopt), and sh depicts the temperature range over which a consumer can handle its resource/prey species.
Temperature Response of the Maturation Rate
Maturation rate of ectotherms exhibits a left-skewed temperature response (Sharpe and DeMichele, 1977; Schoolfield et al., 1981; Van der Have and de Jong, 1996; Van der Have, 2002; Kingsolver, 2009; Kingsolver et al., 2011) that results from the reduction in reaction rates at low and high temperature extremes due to enzyme inactivation. This response is well-described by a thermodynamic rate process model (Sharpe and DeMichele, 1977; Schoolfield et al., 1981; Ratkowsky et al., 2005):
where m(T) is the maturation rate at temperature T (in K), mTR is the maturation rate at the reference temperature TR at which the enzyme is 100% active, AmJ (enthalpy of activation divided by the universal gas constant R) quantifies temperature sensitivity, TL/2 and TH/2 are, respectively, the low and high temperatures at which the enzyme is 50% active, and AL and AH are the enthalpy changes associated with low and high temperature enzyme inactivation divided by R (Johnson and Lewin, 1946; Sharpe and DeMichele, 1977; Schoolfield et al., 1981; Van der Have and de Jong, 1996; Van der Have, 2002; Ratkowsky et al., 2005).
Temperature Response of Resource Self-Limitation
Self-limitation in the resource species arises from intra-specific competition. Experiments on temperature effects on competition in insects suggest that the temperature response of the per capita intra-specific coefficient (q(T)) can be monotonic or unimodal (Amarasekare and Coutinho, 2014; Amarasekare, 2015; Johnson et al., 2016). When the per individual demand for resources increases with temperature, due to higher activity levels at higher temperatures (Gillooly et al., 2001, 2002; Savage et al., 2004), self-limitation strength tends to increase monotonically with temperature. In this case, q(T) is given by the Boltzmann-Arrhenius relationship:
where q(T) is the self-limitation strength at temperature T, Aq is the Arrhenius constant, which quantifies how fast the competition strength increases with increasing temperature, and TR is a reference (baseline) temperature.
When the per-individual demand for resources is greatest during peak reproductive activity, which occurs at the optimal temperature for reproduction (Amarasekare and Coutinho, 2014; Amarasekare, 2015; Johnson et al., 2016), self-limitation strength exhibits a unimodal response with a maximum at the optimal temperature for reproduction. In this case q(T) is unimodal and well-described by a Gaussian function (Equation 3). I use the Gaussian form in our analyses because empirical evidence (Amarasekare and Coutinho, 2014; Amarasekare, 2015; Johnson et al., 2016; Uszko et al., 2017) suggests this to be more common than the monotonic form.
Predicting Warming Effects on Consumer-Resource Interactions
Several large-scale data analyses show that the qualitative nature of phenotypic trait responses described above is conserved across ectotherm taxa (Dell et al., 2011; Englund et al., 2011; Kingsolver et al., 2011; Amarasekare and Savage, 2012). This allows us to make general predictions about trait responses to climate warming that applies across ectotherm taxa, habitat, and latitudes. By mapping various climate warming scenarios on to the phenotypic trait responses and comparing the result with the species' typical thermal regime, we can predict the effect of warming on trait responses. We can also predict the potential consequences of warming-induced changes in trait responses for population dynamics and species interactions.
There are two important aspects of trait responses that allow us to predict which traits are likely to be the most strongly affected by warming. The first is the distinction between rate-controlled and regulatory responses. The second is latitudinal variation in thermal adaptation. I will discuss each on in turn.
We see from the previous section that rate-controlled responses tend to be more skewed than regulatory responses. Because regulatory responses are more symmetrically unimodal, a negative deviation from the optimum (i.e., cooler temperatures) has the same detrimental effect as a positive deviation (i.e., warmer temperatures). This is not the case for skewed responses. For instance, the maturation rate exhibits a left-skewed response, with a faster decline at temperatures above the optimum than below it (Johnson and Lewin, 1946; Sharpe and DeMichele, 1977; Schoolfield et al., 1981; Van der Have and de Jong, 1996; Van der Have, 2002; Ratkowsky et al., 2005). The mortality rate exhibits an inverted right-skewed response with mortality increasing rapidly with decreasing temperature at the low extreme (e.g., below freezing temperature) and increasing exponentially with increasing temperature above the low extreme (Johnson and Lewin, 1946; Sharpe and DeMichele, 1977; Schoolfield et al., 1981; Van der Have and de Jong, 1996; Gillooly et al., 2001, 2002; Savage et al., 2004; Ratkowsky et al., 2005). This difference suggests that warming may have more detrimental effects on maturation and mortality than it does on the resource birth rate, and the consumer's attack rate and handling times.
Turning now to latitudinal differences, tropical thermal regimes are characterized by high mean temperatures and low-amplitude seasonal fluctuations, while temperate thermal regimes are characterized by low mean temperatures and high-amplitude seasonal fluctuations. As a result, tropical ectotherms exhibit trait responses with narrow breadths and thermal optima that coincide with the mean habitat temperature, while temperate ectotherms exhibit trait responses with wider breaths and optima that well-exceed the mean temperature (Deutsch et al., 2008; Tewksbury et al., 2008; Amarasekare and Johnson, 2017; Scranton and Amarasekare, 2017).
Climate Change Scenarios
Climate warming is expected to manifest as an increase in the mean annual temperature and/or a change in the seasonal thermal regime with warmer winters and hotter summers (IPCC, 2018). I consider the following three scenarios:
1. Warmer winters: the minimum temperature increases faster than the maximum temperature, resulting in an increase in the mean temperature and a decrease in the amplitude.
2. Hotter summers: the minimum temperature increases more slowly than the maximum temperature, resulting in an increase in the mean and amplitude both.
3. Warmer winters and hotter summers: the minimum and maximum temperatures change at the same rate, resulting in an increase in the mean while the amplitude stays the same.
By mapping these scenarios onto resource and consumer trait responses, I obtain the following general results.
Trait-Based Predictions
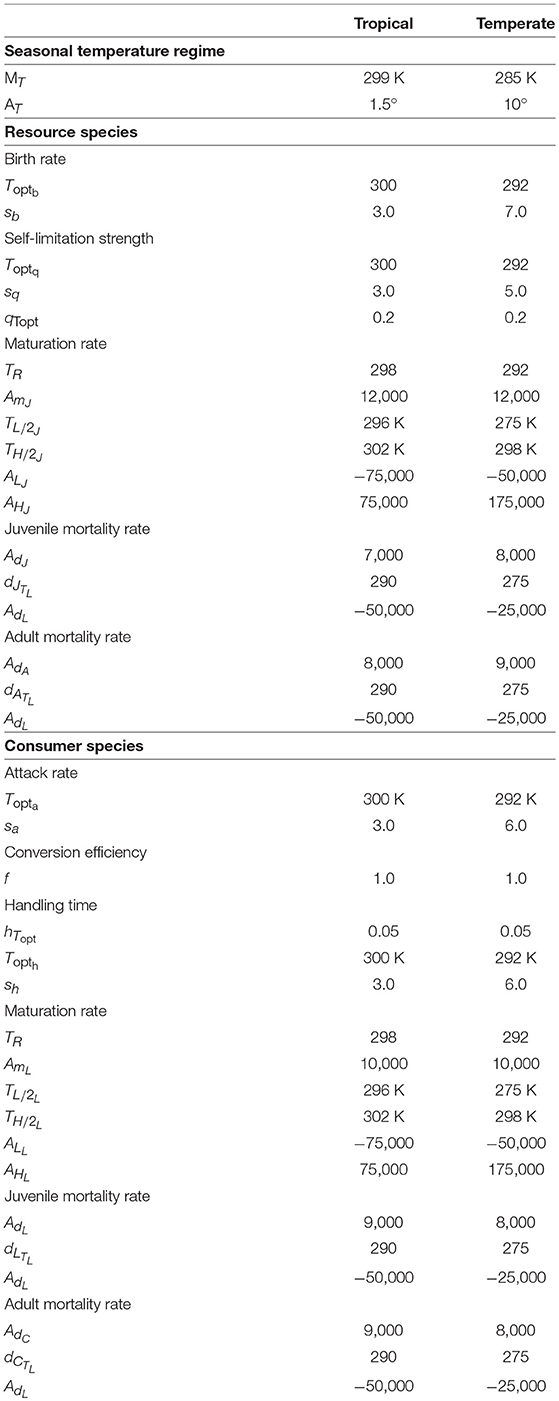
First, all warming scenarios lead to an increase in the mortality rate and a decrease in the maturation rate of both resource and consumer species. Because the maturation response is strongly left-skewed, the decrease in the maturation rate at high temperatures is much greater than those of birth and attack rates and self-limitation strength (Figure 1). This is significant because it means that species can develop faster and emerge earlier in the year because of warmer winter temperatures, but the decrease in the maturation rate during the hotter summers exceeds the increase in the maturation rate during warmer winters, resulting in a lower average maturation rate over the year.
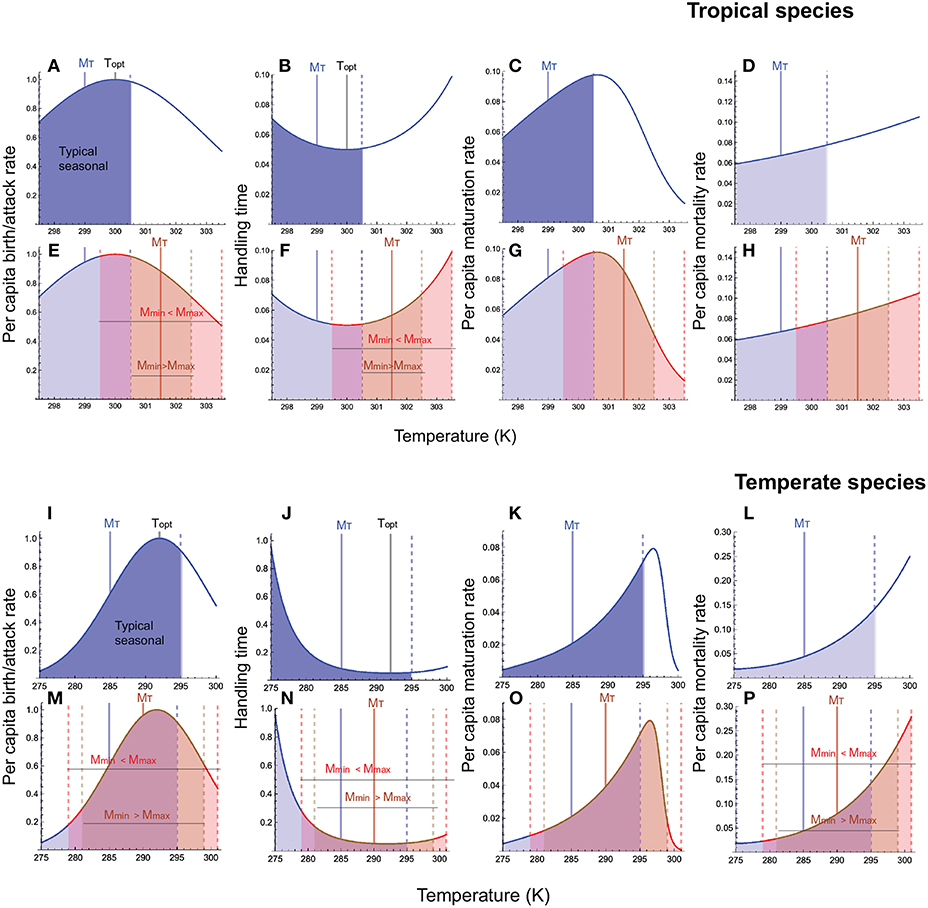
Figure 1. Temperature responses of resource and consumer traits under typical seasonal variation and warming. (A–H) are for tropical ectotherms, and (I–P), for temperate ectotherms. For each latitude, panels in the top row depict temperature responses under typical seasonal variation, and those in the bottom row, temperature responses under the two warming scenarios: minimum temperature increases faster than the maximum (MinT > MaxT) and minimum temperature increases slower than the maximum (MinT < MaxT). On panels in the bottom row for each species [(A–D) for tropical and (I–L) for temperate], the blue portion of the response curve depicts the response under seasonal variation, the brown portion of the curve when MinT > MaxT, and the red portion of the curve, MinT < MaxT. In each panel, the solid blue vertical line depicts the mean habitat temperature and the solid black line, the physiologically optimal temperature; the dashed vertical blue lines depict the temperature range experienced by species under typical seasonal variation, the dashed red lines depict the range when MinT < MaxT, and the dashed brown lines, when MinT > MaxT. For ease of comparison, increase in minimum and maximum temperature for the two scenarios are chosen such that the mean temperature (MT) is the same. Note that the temperature range on the x-axis is smaller in the for tropical species (297.5–303.5 K) than for the temperate species (275–301 K). Parameter values for the tropical species are: ToptX = 300, sX = 3.0(X=b, a, h, q), TRY = 297(Y=R, C), TLZ = 296, THZ = 302 (Z=J, L),MT = 299, AT = 1.5°,m = 3, a = 2 when the minimum temperature increases faster than the maximum and m = 2, a = 3 when the minimum increases more slowly than the maximum. Parameter values for the temperate species are: ToptX = 292, sX = 6.0(X=b, a, h, q), TRY = 292(Y=R, C), TL/2Z = 275, TH/2Z = 298(Z=J, L),MT = 285, AT = 10°,m = 6, a = 4 when the minimum temperature increases faster than the maximum and m = 4, a = 6 when the minimum increases more slowly than the maximum. Other parameters are: bTopt = aTopt = 1.0, hTopt = 0.05, qTopt = 0.2, f = 1.0, dYTR = 0.1, dZTR = 0.1, mZTR = 0.05, AdY = 10, 000, AdZ = 10, 000, AmZ = 10, 000, ALY = −25, 000, AL/2Z = −50, 000, AH/2Z = 100, 000.
Second, hotter-than-average summers are more detrimental to both tropical and temperate species compared to warmer-than-average winters. This is because maturation and mortality are most negatively affected by this warming scenario.
Third, all warming scenarios cause the mean habitat temperature to approach the physiologically optimal temperature in temperate ectotherms, and to exceed the optimal temperature in tropical ectotherms. Across all latitudes, this causes a decrease in the resource species' birth rate and self-limitation strength, and the consumer species' attack rate. The change in the mean temperature affects the consumer's handling time differentially depending on latitude, decreasing the handling time in temperate habitats and increasing it in tropical habitats. This is because the handling time exhibits a U-shaped response to temperature. The mean temperature becoming closer to the optimum in temperate habitats pushes the handling time toward its minimum, while the mean temperature exceeding the optimum pushes the handling time above the minimum (Figure 1).
Population-Level Predictions
The trait-based analysis suggests that maturation and mortality rates to be the most strongly affected by climate warming. If so, they should have a stronger detrimental effect on consumer-resource persistence in the face of climate warming. I explore this possibility by investigating consumer-resource coexistence in a constant thermal environment (i.e., the organism in question experiences the same temperature, on average, with few or no fluctuations around the mean), for which analytical expressions of resource and consumer persistence criteria can be derived.
Consider first the conditions for the resource and consumer species' viabilities when there is no developmental delay in either species (i.e., τJ = 0, τL = 0). When resource self-limitation affects fecundity and the consumer attacks the adult stage of the resource, the resource can maintain a viable population (i.e., R⋆ > 0) provided
and the consumer can persist on the resource (i.e., C⋆ > 0) provided
Note that when there are no developmental delays, the resource species' viability is determined by the consumer's temperature dependent attack and mortality rates [a(T) and dC(T)], its temperature-dependent handling time (h(T)), and conversion efficiency (f). Note that the product h(T)dC(T) is the fraction of the consumer's life span spent in handling food items at temperature T. The resource species' viability requires that the consumer species' efficiency in converting resources to consumer reproduction exceed the time it spends handling food items over its lifetime. Consumers with long handling times run the risk of driving their resources extinct.
When there are no developmental delays, the consumer species' viability is determined by the temperature responses of resource birth and death rates, resource self-limitation, the consumer's death rate and its consumption traits (conversion efficiency, attack rate, and handling time).
When both species exhibit developmental delays, the conditions for resource and consumer viabilities are, respectively:
and
where .
There are three key points to note. First, developmental delays cause a significant reduction in the upper temperature limit for viability in both resource and consumer species (Figure 2).
Figure 2. Resource and consumer species' viabilities as a function of temperature. In each panel, the gray curve depicts the temperature range over which each species has a positive abundance in the absence of developmental delays (Equations 7, 8), and the orange, green, and red curves, the temperature range for viability in the presence of delays (Equations 9, 10). In (A), the green, orange, and red curves represent, respectively, the resource species viability when the consumer's temperature sensitivities of maturation (AmL) and mortality (AdL) are the same (k1 = AdL−AmL = 0), mortality has greater temperature sensitivity than maturation (k1 = 8, 000), and vice versa (k1 = −8, 000). In (B), the green, orange, and red curves represent, respectively, the consumer species' viability when the resource and consumer species' temperature sensitivities of maturation are the same (k2 = AmJ−AmL = 0), resource's maturation has lower temperature sensitivity than consumer's (k2 = −4, 000) and vice versa (k2 = 4, 000). In (C), the curves depict depicts consumer viability the consumer species' viability when the resource and consumer species' temperature sensitivities of mortality are the same (k3 = AdJ−AdL = 0), resource's mortality has greater temperature sensitivity than consumer's (k3 = 2, 000) and vice versa (k3 = −2, 000). Other parameters are as in Figure 1.
Second, the resource species' developmental delay has a stronger effect on consumer viability than the consumer's delay on resource viability. This is because the resource species' developmental delay enters the consumer's viability criterion as an additive term, while the consumer's delay enters the resource species' viability criterion only as an exponential term (compare Equation 9 and Equation 10). The resource species' developmental delay therefore causes a stronger reduction in the consumer's viability than does the consumer's delay on resource viability.
Third, the resource species' developmental delay has a stronger effect on consumer viability than the consumer's developmental delay. To see this, consider the consumer's viability criterion when the resource species' developmental delay is long relative to that of the consumer (i.e., τJ > 0, τL → 0):
as opposed to when the resource species' developmental delay is short relative to that of the consumer (i.e., τJ → 0, τL > 0):
Comparing Equations (11) and (12) shows that the resource species' developmental delay has a stronger effect on consumer viability for the same reason as above, i.e., it enters the consumer's viability criterion as an additive term, while the consumer's delay enters the its viability criterion only as an exponential term.
Importantly, the effect of developmental delays on viability is mediated by the multiplicative effect of the temperature responses of maturation and mortality rates. Differences between the resource and consumer in their temperature sensitivities of mortality and maturation therefore play a key role in determining the lower and upper thermal limits to viability. For instance, the resource species' viability is affected by the multiplicative effect of the consumer's maturation and juvenile mortality rates. As noted in the trait-based analysis above, the maturation rate decreases and the mortality rate increases with increasing temperature. This leads to a steep decline in viability as temperatures increase above the physiologically optimal range. Resource viability is lower when the consumer's maturation rate is more temperature-sensitive that its mortality rate (Figure 2A). This is because lower mortality and faster development means a larger adult consumer population and hence greater exploitation of the resource.
As with the resource species, differential temperature sensitivities of maturation and mortality rates have a strong effect on consumer viability. Thermal limits to consumer viability are narrower when the resource species' maturation rate is more temperature-sensitive, and mortality rate less temperature-sensitive, than those of the consumer (Figures 2B,C). This is because when the decrease in the resource maturation rate with increasing temperature exceeds the increase in the mortality rate, the resource developmental delay increases at both low and high temperatures. This causes a reduction in the adult resource population at temperatures below and above the optimal temperature range, narrowing the consumer's thermal limits to viability.
Summary of Predictions
Taken together, the trait-based and viability analyses make three testable predictions. First, warming has its strongest impact on viability through its effects on maturation and mortality rates. Second, the resource species' developmental delay has a greater negative effect on the consumer's viability than the consumer's delay. Third, because of the conflict of interest between species, we expect the consumer to be more susceptible to warming than the resource. This is because the resource is negatively affected by warming, but is positively affected by negative warming effects on consumer, while the consumer is negatively affected by warming and the negative effects of warming on the resource. The next step is to test these predictions with the dynamical model (Equation 2).
Consumer-Resource Persistence in a Variable Thermal Environment
Equation (1) is non-autonomous (i.e., long-term outcomes are not independent of time) and cannot yield analytical results on long-term outcomes. I conduct numerical analyses to investigate the consumer-resource dynamics and long-term outcomes under both typical seasonal variation and climate warming.
Let seasonal temperature variation be depicted by the sinusoidal function T(t) = MT+ATS(t) where t is time in days, MT is the mean habitat temperature in K, AT is the amplitude of seasonal fluctuations (), and (or ) with yr = 365 days.
The change in the seasonal thermal regime under climate warming is given by T(t) = (MT+mt) + (AT+at)S(t) with m = (mhigh+mhigh)/2 and a = (mhigh−mhigh)/2 depicting respectively, the daily rate of increase in mean and amplitude. The quantities mlow = s1/(n * yr) and mhigh = s2/(n * yr) where s1 and s2 are, respectively, the number of degrees by which the minimum and maximum temperatures increase in n years. When the minimum and maximum temperatures increase at the same rate (s1 = s2), the mean temperature increases over time with no net change in the amplitude. When the minimum temperature increases faster than the maximum (warmer-than-average winters; s1 > s2), the mean increases over time while the amplitude decreases. When the maximum temperature increases faster than the minimum (hotter-than-average summers; s1 < s2), the mean and the amplitude both increase over time. I incorporate warming as a liner increase in the mean, minimum and maximum temperatures. The formulation, however, is general and can accommodate any form of empirically observed warming regime.
The nature of consumer-resource dynamics is an important axis of investigation because developmental delays can lead to complex dynamics even in the absence of temperature variation (Gurney et al., 1983; Nisbet and Gurney, 1983). In this case, the steady state outcomes of Equation (1) depend on the developmental delay relative to adult longevity (Murdoch et al., 2003). When the resource species' developmental delay is short relative to adult longevity but longer than the consumer's developmental delay, the outcome is a stable equilibrium (Murdoch et al., 2003). When the reverse is true, the ensuing delay in the operation of density-dependence can lead to delayed feedback cycles. When density-dependence operates through fecundity and the consumer attacks the juvenile stage, such delayed feedback is manifested as single generation cycles with a period approximately equal to the resource species' generation time; when the consumer attacks the adult stage, the feedback cycles have a delay equal to the resource species' developmental delay (Murdoch et al., 2003).
I ran the model (Equation 1) for a period of 100 years and recorded long-term abundances in the 101th year. I analyzed six cases along three axes of biological relevance: resource life stage attacked (juvenile vs. adult resource), latitudinal variation in temperature regime (tropical vs. temperate), and nature of consumer-resource dynamics in the absence of temperature variation (stable vs. complex). For each case analyzed, I checked for deterministic extinction of consumer and resource, and calculated the variability in abundances as the coefficient of variation (standard deviation of the time series of abundance in the 101th year scaled by the mean abundance). I used parameter values (Table 1) that are realistic for insect species in tropical and temperate habitats (Sharpe and DeMichele, 1977; Schoolfield et al., 1981; Kooijman, 1993; Van der Have and de Jong, 1996; Amarasekare and Savage, 2012; Amarasekare and Johnson, 2017; Scranton and Amarasekare, 2017). In accordance with empirical findings (Gao et al., 2013; Johnson et al., 2016), I considered the unimodal temperature response of competition to have the same parameter values as the temperature response of reproduction, i.e., competition is strongest at the temperature optimal for reproduction (Toptq = Toptb), and operates on the same temperature range within which the species can reproduce (sq ≤ sb).
Results
Analysis of the dynamical model both confirms predictions of the trait-based analysis and yields new insights. Three generalities emerge. First, consumer-resource interactions in the tropics are more at risk of species losses due to warming, while those in the temperate zone are more at risk of extreme fluctuations in species' abundances. Second, effects of warming are more detrimental when the consumer attacks the adult stage of the resource and when consumer-resource interactions exhibit complex dynamics. Third, hotter-than-average summers are more detrimental to consumer-resource interactions than warmer-than-average winters. Below I explain these results in detail.
First, as predicted by the trait-based analysis, warming poses a greater risk of deterministic extinction for tropical consumer-resource interactions. The consumer goes extinct once the minimum temperature exceeds 2° when the adult stage is attacked (Figures 3B,F,J,N,R,V), and 3° when the juvenile stage is attacked (Figures 4B,F,J,N,R,V); the resource goes extinct once the minimum temperature exceeds 3 and 4°, respectively, in these two cases (Figures 3, 4A,E,I,M,Q,U). In contrast, deterministic extinction of temperate resources and consumers does not occur until the maximum temperature increases by 6° (Figures 3, 4C,D,K,O,S,W for resource, Figures 3, 4D,H,L,P,T,X for consumer). However, both resource and consumer species exhibit large fluctuations in abundance (Figure 5). Fluctuations are more extreme when the consumer attacks the adult resource stage and consumer-resource dynamics are complex rather than stable (compare Figure 3 and Figure 4).
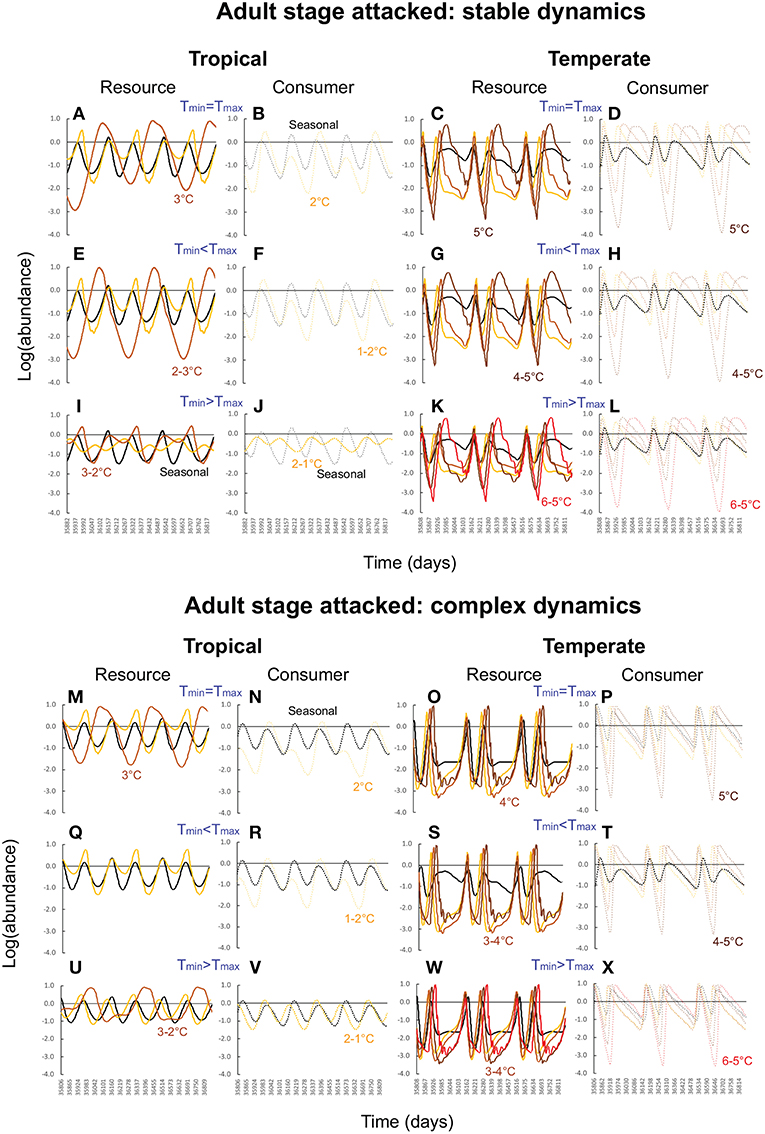
Figure 3. Consumer-resource dynamics in tropical and temperate habitats when the consumer attacks the adult stage and consumer-resource dynamics are stable (A–L) vs. complex (M–X). In all panels, the black curves (solid for resource, dashed for consumer) depict abundances under typical seasonal variation. Yellow, light brown, dark brown, and red curves depict progressively higher levels of warming (1–4°C for tropical habitats, 2–6°C for temperate habitats). For each latitude, the top row of panels depict effects of warming when the minimum and maximum temperatures increase at the same rate (mean increases, amplitude unchanged). The second row depicts warming effects when the maximum temperature increases faster than the minimum (mean and amplitude both increase), and the third row, when the minimum temperature increases faster than the maximum (mean increases, amplitude decreases). Parameter values for the tropical community are: bTopt = 5.0, mJTR = 0.05 (τJTR = 20), dJTR = 0.1, dATR = 0.05, aTopt = 1.0 for stable dynamics, and bTopt = 2.0, mJTR = 0.07 (τJTR = 15), dJTR = 0.05, dATR = 0.01, mLTR = 0.1 (τLTR = 10), dLTR = 0.1, dCTR = 0.01, aTopt = 0.5 for complex dynamics. Parameter values for the temperate community are: bTopt = 1.0, mJTR = 0.04 (τJTR = 25), dJTR = 0.1, dCTR = 0.1, aTopt = 0.5, mLTR = 0.1 (τJTR = 10), dLTR = 0.1, dCTR = 0.05for stable dynamics, and bTopt = 1.0, mJTR = 0.05 (τJTR = 20), dJTR = 0.05, dRTR = 0.01, dLTR = 0.1, dCTR = 0.05, mLTR = 0.1 (τJTR = 10) for complex dynamics. All other parameters values are as in Table 1.
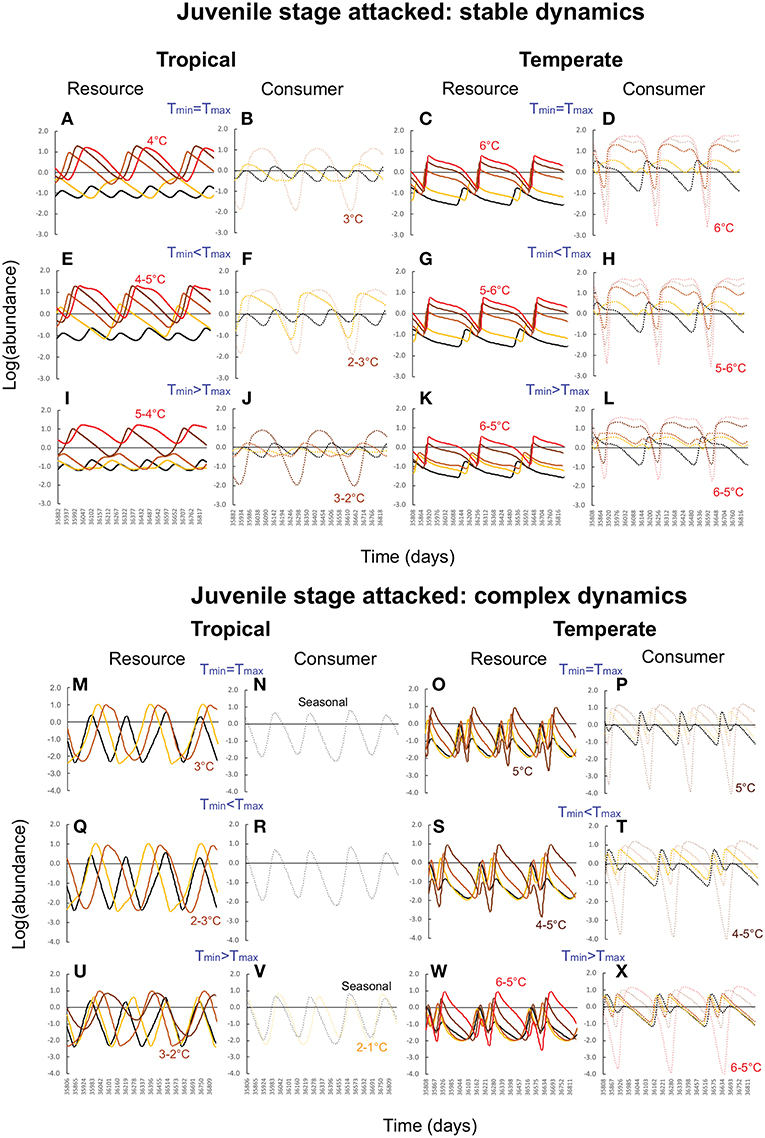
Figure 4. Consumer-resource dynamics in tropical and temperate habitats when when the consumer attacks the juvenile stage and consumer-resource dynamics are stable (A–L) vs. complex (M–X). In all panels, the black curves (solid for resource, dashed for consumer) depict abundances under typical seasonal variation. Yellow, light brown, dark brown, and red curves depict progressively higher levels of warming (1–4°C for tropical habitats, 2-6°C for temperate habitats). For each latitude, the top row of panels depict effects of warming when the minimum and maximum temperatures increase at the same rate (mean increases, amplitude unchanged). The second row depicts warming effects when the maximum temperature increases faster than the minimum (mean and amplitude both increase), and the third row, when the minimum temperature increases faster than the maximum (mean increases, amplitude decreases). Parameter values for the tropical community are: bTopt = 2.0, mJTR = 0.07 (τJTR = 15), dJTR = 0.05, dATR = 0.01, aTopt = 0.5, dLTR = 0.1, dP1TR = 0.05, mLTR = 0.1 (τLTR = 10)for stable dynamics, and bTopt = 2.0, mJTR = 0.05 (τJTR = 20), dJTR = 0.05, dATR = 0.05, aTopt = 0.5, dLTR = 0.1, dP1TR = 0.05, mLTR = 0.1 (τLTR = 10). Parameter values for the temperate community are: bTopt = 2.0, mJTR = 0.04 (τJTR = 25), dJTR = 0.1, dCTR = 0.01, dLTR = 0.1, dCTR = 0.05, mLTR = 0.1 (τJTR = 10) for stable dynamics and bTopt = 1.0, mJTR = 0.05 (τJTR = 20), dJTR = 0.05, dRTR = 0.05, dLTR = 0.1, dCTR = 0.05, mLTR = 0.07 (τJTR = 15) for complex dynamics. Other parameter values are as in Table 1.
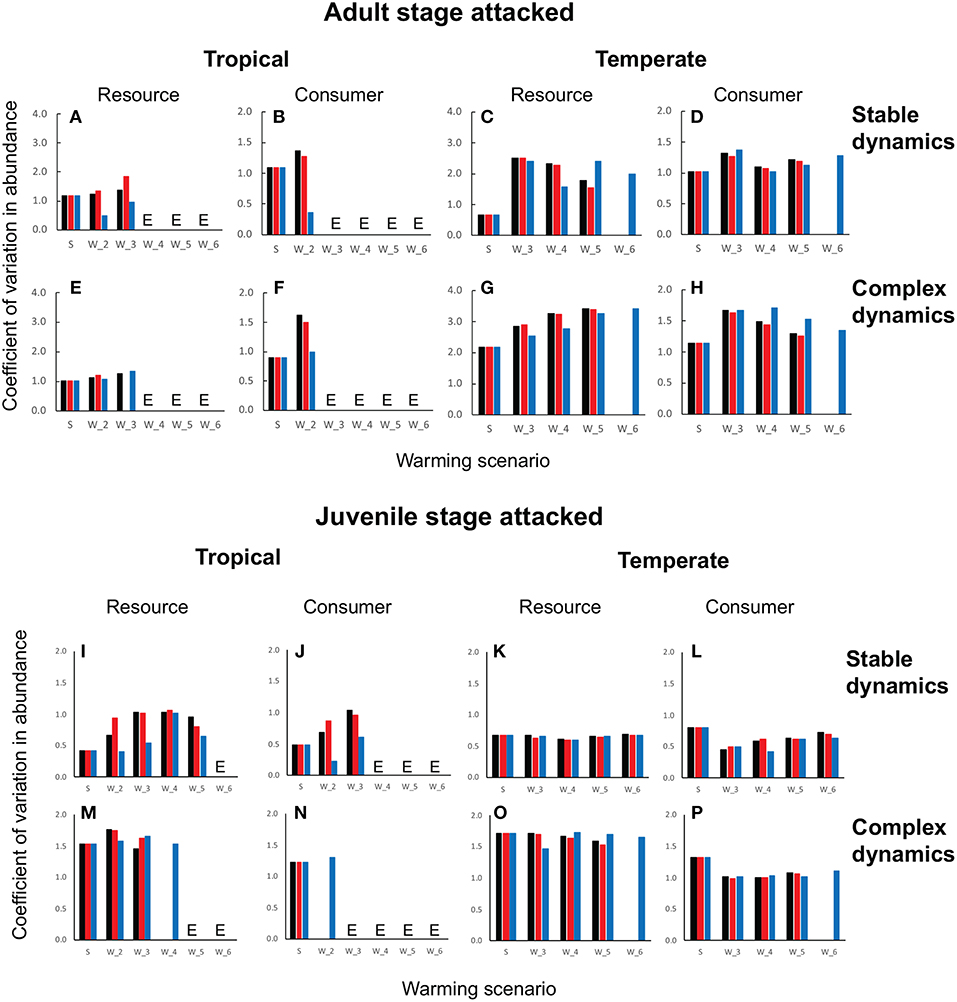
Figure 5. Coefficient of variation in resource and consumer abundances in tropical and temperate habitats when the consumer attacks the adult stage (A–H) vs. the juvenile stage (I–P). In all panels, the x-axis gives the CV in abundance under typical seasonal variation (S) and successively increasing levels of warming (W2⋯ , W6) where Wi (i = 1, 6) depicts a warming scenario in which the maximum temperature increases by i⋆ [e.g., W2 denotes W22 (black column), W12 (red column), and W21 (blue column). In each panel, the black column depicts warming effects when the minimum and maximum temperatures increase at the same rate, the red column depicts effects when the maximum increases faster than the minimum, and the blue column, when the maximum increases slower than the minimum. In each case (juvenile vs. adult), the top row of panels depicts stable dynamics (A–D) when the adult is attacked and (I–L) when the juvenile is attacked] and the bottom row, complex dynamics (E–H) for adult and [m-(p) for juvenile]. Cases marked with E depict warming-driven extinctions of resource and/or consumer. Parameter values are as in Figures 3, 4 and Table 1.
The second result involves two new insights that were not anticipated by the trait-based and analytical viability analyses. The first is that warming is more detrimental when the consumer attacks the adult stage of the resource. Not only does warming cause more extinctions when the adult stage is attacked compared to when the juvenile stage is attacked, but it also leads to greater variability in abundance in both resource and consumer species (compare Figure 3 and Figure 4). These outcomes ensue regardless of latitude or nature of consumer-resource dynamics (Figure 5).
The second insight is that warming has a greater detrimental effect when consumer-resource interactions exhibit complex dynamics. As noted in the previous section, when the juvenile developmental delay is long relative to adult longevity, delay in the operation of density-dependence can lead to delayed feedback cycles in the absence of temperature variation. When consumer-resource interactions exhibiting such cycles are subject to warming, the interplay between intrinsic non-linear dynamics and non-linear trait temperature responses to warming can predispose species to extinction. Indeed, when consumer-resource dynamics are complex, we see the deterministic extinction of resources and consumers at lower levels of warming than when dynamics are stable (compare Figure 3 and Figure 4). We also see greater variability in abundances (Figure 5).
The third result concerns the effect of warming scenario. As predicted by the trait-based analysis, hotter-than-average summers are more detrimental to consumer-resource interactions than warmer-than-average winters. It causes a greater number of resource and consumer extinctions across latitudes, and leads to greater variability in abundances. Greater variability in abundances is more clearly seen in the resource rather than in the consumer, in tropical rather than in temperate habitats, and when the consumer attacks the adult rather than the juvenile stage of the resource. Of note, as the strength of warming increases the difference between the two warming scenarios diminishes, as can be seen by the increasing similarity in the CVs of abundances between scenarios as warming proceeds from 1 to 6°. Interestingly, the effects of warming scenarios are more apparent when one examines the temporal trajectories of population trajectories rather than the summary measures of variability in abundances (CV). We see that, across the board, the dynamical effects of hotter summers alone are more similar to the scenario with warmer winters and hotter summers, indicating that hotter summers tend to override the effect of warmer winters. The reason for this can be seen by looking more closely at how phenology and population trajectories change over the year as a result of warming. Warming causes earlier emergence because winters are warmer. However, warming causes summers to also be hotter, causing a reduction in birth, attack and maturation rates and increasing mortality rates. This in turn leads to a lowering of summer abundance. As warming proceeds summer abundance declines further, causing population growth to be restricted to early spring and fall. When extinction occurs, it is because summer abundances fall too low for species to recover from.
Discussion
Evidence for the detrimental effects of climate warming on biodiversity is rapidly accumulating (Dunn and Winkler, 1999; Walther et al., 2002; Root et al., 2003; Parmesan, 2006; Inouye, 2008; Miller-Rushing and Primack, 2008; Post et al., 2008). An accurate gauge of these detrimental effects requires that we understand the effects warming has on key components of biodiversity. Consumer-resource interactions (e.g., predator-prey, plant-herbivore, host-parasite) constitute the fundamental building blocks of all communities. They therefore serve as a key indicator for gauging the effects of warming on biodiversity. Understanding how warming affects consumer-resource dynamics and persistence is therefore a key research priority.
Here I develop a mathematical framework for predicting the effects of warming on consumer-resource interactions. This framework, based on delay differential equations, realistically captures the developmental delays that characterize the life cycles of multicellular ectotherms. It also incorporates mechanistic descriptions of consumer and resource trait responses to temperature, and the latest IPCC predictions about warmer-than-average winters and hotter-than-average summers. I use a trait-based analysis to generate predictions about population-level consequences of warming, which I then test with the dynamical model. I report three key findings.
First, tropical consumer-resource interactions are more at risk of species losses due to warming, while temperate interactions are more at risk of extreme fluctuations. Second, warming is more detrimental when the consumer attacks the adult stage of the resource and when consumer-resource dynamics exhibit complex dynamics. Third, hotter-than-average summers are more detrimental than warmer-than-average winters.
The first finding, that tropical consumer-resource interactions are more prone to species losses while temperate interactions are more prone to extreme fluctuations, highlights the different challenges that climate warming poses to ectotherm communities inhabiting different latitudes. Since tropical ectotherms exhibit thermal optima that coincide with the mean habitat temperature (Deutsch et al., 2008; Tewksbury et al., 2008; Amarasekare and Savage, 2012; Amarasekare and Johnson, 2017), an increase in the mean temperature, regardless of whether it is through an increase in the minimum or maximum temperature, pushes the species into a thermal realm in which birth, attack and maturation rates decrease and mortality rates increase. The resulting negative per capita growth rate causes deterministic extinction. In contrast to the tropics, which see warming-induced extinctions, temperate habitats see an increase in the fluctuations of resource and consumer abundances. In all cases, the decrease in fluctuations are greater in magnitude than the increase, which means that species are less prone to outbreak densities in the face of warming than they are to stochastic extinction during periods of low abundances.
The expectation based on the trait-based analysis that warming is more detrimental to the consumer than to the resource is borne out by the dynamical model analysis. The tropics see more cases of consumer rather than resource extinction, while the temperate realm sees greater declines in consumer rather than resource abundance, and hence a greater risk of stochastic extinction. These outcomes ensue because of the conflict of interest between species inherent in consumer-resource interactions. The resource species is negatively affected by warming, but positively affected by warming effects on the consumer, while the consumer is negatively affected both by warming and the negative effects of warming on the resource species.
The second finding is that warming has a greater detrimental effect when the consumer attacks the adult stage of the resource and when consumer-resource interactions exhibit complex dynamics. The reason that warming has differential effects based on the life stage attacked can be explained as follows. Temperature affects juvenile development through the multiplicative effect of juvenile maturation and mortality. Warming both decreases the maturation rate and increases the mortality of the juvenile resource stage, resulting in a smaller adult resource population that the consumer then overexploits. Such overexploitation can lead to increasing consumer-resource fluctuations and eventual extinction, effects compounded by warming-induced reduction in consumer attack rate and increase in handling time. When the consumer attacks the juvenile stage of the resource, the invulnerable adult resource stage acts as a buffer (particularly when fecundity and adult longevity are high), making the consumer less resource-limited and reducing the tendency for extreme fluctuations and warming-induced extinction.
The reason why warming has a greater detrimental effect on consumer-resource interactions exhibiting complex dynamics is because the interplay between population cycles resulting from delayed density-dependent feedback and temperature variation can cause resource abundances to fall to levels at which the consumer cannot maintain itself. Even when deterministic extinction does not occur, this interplay can lead to large fluctuations in abundance that can predispose species to stochastic extinction.
The third result is that hotter-than-average summers is more detrimental to consumer-resource interactions than warmer-than-average winters. This is an interesting finding in light of the fact that it is the warmer-than-average winters that lead to advanced emergence and phenological asynchrony (Dunn and Winkler, 1999; Walther et al., 2002; Root et al., 2003; Parmesan, 2006; Inouye, 2008; Miller-Rushing and Primack, 2008; Post et al., 2008). The crucial insight to emerge from the comparative analysis of warming scenarios is that asynchrony in emergence is not the issue. It is what follows that matters. While warmer-than-average winters cause advanced emergence and higher spring abundance due to faster maturation rates and the concomitant reduction in juvenile mortality, hotter-than-average summers cause a steep decline in birth and maturation rates and a steep increase in the mortality rate. This is because maturation reaches its lowest and mortality its highest under this warming scenario. The population-level outcome is a large decline in abundance during summer. The hotter the summers become, the more difficult it is for species to recover from the large decline in summer abundance. Since the consumer is dependent on the resource, a large decrease in resource abundance makes recovery from low abundances an extra challenge for the consumer.
These findings have implications for both biodiversity and biological control. Regarding biodiversity, two general results emerge. The first concerns life history and consumption trait attributes that increase susceptibility to warming. Interactions in which resource species' maturation rate is more temperature-sensitive (i.e., large Arrhenius constants and narrower response breadths), and mortality rate less temperature-sensitive (smaller Arrhenius constants), than those of the consumer are more susceptible to the detrimental effects of warming, as are those in which consumer's maturation rate is more temperature-sensitive that its mortality rate. In the former, greater susceptibility to warming ensues because when the decrease in the resource maturation rate with increasing temperature exceeds the increase in the mortality rate, the resource developmental delay increases at both low and high temperatures. This causes a reduction in the adult resource population at temperatures below and above the optimal temperature range, narrowing the consumer's thermal limits to viability. In the latter, greater susceptibility to warming occurs because lower mortality and faster development of the juvenile resource stage means a larger adult consumer population and hence greater exploitation of the resource. Similarly, interactions in which the resource species has high fecundity and long developmental delays relative to adult longevity and the consumer has a long developmental delay relative to that of the resource are more at risk of extinction due to warming as are those in which the adult resource stage is attacked.
The second general result regarding biodiversity is that consumer-resource interactions in the tropics are more at risk of extinction due to warming while temperate interactions are more vulnerable to extreme fluctuations. This generates a latitudinal difference in the nature and timing of extinctions. Warming causes deterministic extinction of tropical resources and consumers, leading to immediate disruption of species interactions. In contrast, warming predisposes temperate resource and consumers to stochastic extinction during low abundances, which means that interaction disruptions are likely to occur with a time delay. Such extinction debts may lead to unexpected outcomes since it is difficult to predict a priori the order and timing of species losses. If the consumer goes extinct first, diversity may be recovered through natural recolonizations or reintroduction of the consumer; if the resource goes extinct first, the entire interaction will be lost and recovery would be much more challenging.
Regarding biological control, warming-induced loss of natural enemies that serve as biological control agents can cause pest outbreaks that can compromise the supply of essential food items, thus creating a significant threat to food security. Pests whose adult stages are attacked are more likely to lose their natural enemies, particularly in tropical climates where many important crops are grown, leading to greater pest damage. At the same time, pests with invulnerable adult stages are likely to benefit from warming and resist the effects of biological control. Warming-induced failure of biological control can lead to greater pesticide use and greater pollution, thus compounding existing environmental problems. One key finding of this study is that one can make predictions about population-level outcomes of warming based solely on how temperature affects ectotherms' phenotypic traits. When choosing natural enemy agents to attack a particular pest, it is crucial to compare their maturation and mortality responses to determine whether the enemy has greater tolerance of the high-temperature extremes projected for the region such that its maturation-mortality response allows for a sustainable adult population in the face of warming.
In this study I have focused on pairwise consumer-resource interactions, a necessary first step in developing a framework that incorporates developmental delays and mechanistic temperature response functions. Extending the framework to incorporate additional tropic levels and competition between species is an important future direction. While the results of the trait-based and analytical viability analyses are general and can apply across ectotherm taxa from any latitude or habitat type, the dynamical model was analyzed using parameter values realistic for insects and other terrestrial ectotherms. Determining whether the latitudinal, life stage, and warming-scenario effects found for terrestrial consumer-resource interactions generalize to aquatic ones is a fruitful future exercise.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This research was supported by a Complex Systems Scholar Grant from the James S. McDonnell Foundation and National Science Foundation grant DEB-1457815 to PA.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I thank two referees for constructive comments that greatly improved the manuscript.
References
Amarasekare, A., and Johnson, J. (2017). Evolution of thermal reaction norms in seasonally varying environments. Am. Nat. 189, E31–E45. doi: 10.1086/690293
Amarasekare, P. (2015). Temperature effects on consumer-resource interactions. J. Anim. Ecol. 84, 665–679. doi: 10.1111/1365-2656.12320
Amarasekare, P., and Coutinho, R. (2014). Effects of temperature on intra-specific competition in ectotherms. Am. Nat. 184, E50–E65. doi: 10.1086/677386
Amarasekare, P., and Savage, V. (2012). A mechanistic framework for elucidating the temperature dependence of fitness. Am. Nat. 179, 178–191. doi: 10.1086/663677
Angilletta, M. (2009). Thermal Adaption: A Theoretical and Empirical Synthesis. Oxford: Oxford University Press.
Binzer, A., Guill, C., Brose, Y., and Rall, B. (2012). The dynamics of food chains under climate change and nutrient enrichment. Philos. Trans. R. Soc. Biol. Sci. 367, 2935–2944. doi: 10.1098/rstb.2012.0230
Brown, J., Gillooly, J. F., Allen, A. P., Savage, V. M., and West, G. B. (2004). Toward a metabolic theory of ecology. Ecology 85, 1771–1789. doi: 10.1890/03-9000
Carriere, Y., and Boivin, G. (1997). Evolution of thermal sensitivity of parasitization capacity in egg parasitoids. Evolution 51, 2028–2032. doi: 10.1111/j.1558-5646.1997.tb05125.x
Custer, A. (2005). Stoichiometric estimates of the biochemical conversion efficiencies in tsetse metabolism. BMC Ecol. 5:6. doi: 10.1186/1472-6785-5-6
Dannon, E. A., Tamo, M., van Huis, A., and Dicke, M. (2010). Functional response and life history parameters of Apanteles taragamae, a larval parasitoid of Maruca vitrata. BioControl 55, 363–378. doi: 10.1007/s10526-009-9263-4
Dell, A., Pawar, S., and Savage, S. M. (2011). Systematic variation in the temperature dependence of physiological and ecological traits. Proc. Natl. Acad. Sci. U.S.A. 108, 10591–10596. doi: 10.1073/pnas.1015178108
Dell, A., Pawar, S., and Savage, S. M. (2014). Temperature dependence of trophic interactions are driven by asymmetry of species responses and foraging strategy. J. Anim. Ecol. 83, 70–84. doi: 10.1111/1365-2656.12081
Deutsch, C. J., Tewksbury, J., Huey, R. B., Sheldon, K., Ghalambor, C., Haak, D., and Martin, P. R. (2008). Impacts of climate warming on terrestrial ectotherms across latitude. Proc. Natl. Acad. Sci. U.S.A. 105, 6668–6672. doi: 10.1073/pnas.0709472105
Dreyer, H., and Baumgartner, J. (1996). Temperature influence on cohort parameters and demographic characteristics of the two cowpea coreids Clavigralla tomentosicollis and C. shadabi. Entomol. Exp. Appl. 78, 201–213. doi: 10.1111/j.1570-7458.1996.tb00783.x
Dunn, P. O., and Winkler, D. W. (1999). Climate change has affected the breeding date of tree swallows throughout north america. Proc. R. Soc. Lond. Ser. B 266, 2487–2490. doi: 10.1098/rspb.1999.0950
Englund, G., Öhlund, G., Hein, C. L., and Diehl, S. (2011). Temperature dependence of the functional response. Ecol. Lett. 14, 914–921. doi: 10.1111/j.1461-0248.2011.01661.x
Gao, G., Lu, Z., Xia, D., Sun, P., Ma, J., and Xu, Y. (2013). Effects of temperature and density on the mortality and reproduction of cotton aphid Aphis gossypii. Chin. J. Appl. Ecol. 24, 1300–1304.
Gilbert, B., Tunney, T., McCann, K., DeLong, J., Vasseur, D., Savage, V., et al. (2014). A bioenergetic framework for the temperature dependence oftrophic interactions. Ecol. Lett. 17, 902–914. doi: 10.1111/ele.12307
Gillooly, J. F., Brown, J. H., West, G. B., Savage, V. M., and Charnov, E. L. (2001). Effects of size and temperature on metabolic rate. Science 293, 2248–2251. doi: 10.1126/science.1061967
Gillooly, J. F., Charnov, E. L., West, G. B., Savage, V. M., and Brown, J. H. (2002). Effects of size and temperature on developmental time. Science 293, 2248–2251. doi: 10.1038/417070a
Gurney, W., Nisbet, R., and Lawton, J. (1983). The systematic formulation of tractable single-species population models incorporating age structure. J. Anim. Ecol. 52, 479–495. doi: 10.2307/4567
Hou, Y., and Weng, Z. (2010). Temperature-dependent development and life table parameters of Octodonta nipae (coleoptera: Chrysomelidae). Environ. Entomol. 39, 1676–1684. doi: 10.1603/EN10015
Hunt-Joshi, T. R., Root, R., and Blossey, B. (2005). Disruption of weed biological control by an opportunistic mirid predator. Ecol. Appl. 15, 861–870. doi: 10.1890/04-1336
Inouye, D. (2008). Effects of climate change on phenology, frost damage, and floral abundance of wildflowers. Ecology 89, 353–362. doi: 10.1890/06-2128.1
IPCC (2018). IPCC, 2018: An IPCC Special Report on the Impacts of Global Warming of 1.5°C Above Pre-industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty. Geneva: World Meteorological Organization.
Jandricic, S. E., Wraight, S. P., Bennett, K. C., and Sanderson, J. P. (2010). Developmental times and life table statistics of Aulacorthum solani (hemiptera: Aphididae) at six constant temperatures, with recommendations on the application of temperature-dependent development models. Environ. Entomol. 39, 1631–1642. doi: 10.1603/EN09351
Jeschke, J. M., Koop, M., and Tollrian, R. (2004). Consumer-food systems: why type i functional responses are exclusive to filter feeders. Biol. Rev. Cambrid. Philos. Soc. 79, 337–349. doi: 10.1017/S1464793103006286
Johnson, C., Coutinho, R., Berlin, E., Dolphin, K., Heyer, J., Kim, B., et al. (2016). Effects of temperature and resource variation on insect population dynamics: the bordered plant bug (Largus californicus) as a case study. Funct. Ecol. 30, 1122–1131. doi: 10.1111/1365-2435.12583
Johnson, F., and Lewin, I. (1946). The growth rate of E. coli in relation to temperature, quinine and coenzyme. J. Cell. Compar. Physiol. 28, 47–75. doi: 10.1002/jcp.1030280104
Kingsolver, J., Woods, A., Buckley, L. B., Potter, L., MacLean, H., and Higgins, J. (2011). Complex life cycles and the responses of insects to climate change. Integr. Compar. Biol. 51, 719–732. doi: 10.1093/icb/icr015
Kooijman, S. (1993). Dynamic Energy Budgets in Biological Systems. Cambridge, UK: Cambridge University Press.
Long, M., and Fee, M. (2008). Using temperature to analyse temporal dynamics in the songbird motor pathway. Nature 456, 189–194. doi: 10.1038/nature07448
Miller-Rushing, A., and Primack, R. (2008). Global warming and flowering times in thoreau's concord: a community persspective. Ecology 89, 332–341. doi: 10.1890/07-0068.1
Morgan, D., Walters, K. F. A., and Aegerter, J. N. (2001). Effect of temperature and cultivar on the pea aphid, Acyrthosiphon pisum (hemiptera: Aphididae) life history. Bull. Entomol. Res. 91, 47–52. doi: 10.1079/BER200062
Murdoch, W., and Briggs, C. J., and M. N. R (2003). Consumer Resource Dynamics. Princeton, NJ: Princeton University Press.
Murdoch, W., Kendall, B. E., Nisbet, R. M., Briggs, C., and McCauley, E., and R. B (2002). Single-species models for many-species food webs. Nature 417, 541–543. doi: 10.1038/417541a
Nisbet, R. M., and Gurney, W. (1983). The systematic formulation of population-models for insects with dynamically varying instar duration. Theor. Popul. Biol. 23, 114–135. doi: 10.1016/0040-5809(83)90008-4
OConnor, M., Gilbert, B., and Brown, C. (2011). Theoretical predictions for how temperature affects the dynamics of interacting herbivores and plants. Am. Nat. 178, 626–638. doi: 10.1086/662171
Ohlberger, J., Edeline, E., Vollestad, L. A., Stenseth, N., and Claessen, D. (2011). Temperature-driven regime shifts in the dynamics of size-structured populations. Am. Nat. 177, 211–223. doi: 10.1086/657925
Parmesan, C. (2006). Ecological and evolutionary responses to recent climate change. Annu. Rev. Ecol. Syst. 37, 637–669. doi: 10.1146/annurev.ecolsys.37.091305.110100
Post, E., Pedersen, C., Wilmers, C., and Forchhammer, M. C. (2008). Warming, plant phenology and the spatial dimension of trophic mismatch for large herbivores. Proc. R. Soc. B 275, 2005–2013. doi: 10.1098/rspb.2008.0463
Ratkowsky, D., Olley, J., and Ross, T. (2005). Unifying temperature effects on the growth rate of bacteria and the stability of globular proteins. J. Theor. Biol. 233, 351–362. doi: 10.1016/j.jtbi.2004.10.016
Rochat, J., and Gutierrez, A. (2001). Weather mediated regulation of olive scale by two parasitoids. J. Anim. Ecol. 70, 476–490. doi: 10.1046/j.1365-2656.2001.00505.x
Roff, D. (1992). The Evolution of Life Histories: Theory and Analysis. New York, NY: Chapman and Hall.
Root, T. L., Price, J. T., Hall, K. R., Schneider, S. H., Rosenzweig, C., and Pounds, J. A. (2003). Fingerprints of global warming on wild animals and plants. Nature 421, 57–60. doi: 10.1038/nature01333
Savage, V. M., Gillooly, J. F., Brown, J. H., West, G. B., and Charnov, E. L. (2004). Effects of body size and temperature on population growth. Am. Nat. 163, 429–441. doi: 10.1086/381872
Schoolfield, R., Sharpe, J., and Magnuson, C. (1981). Non-linear regression of biological temperature-dependent rate models based on absolute reaction-rate theory. J. Theor. Biol. 88, 719–731. doi: 10.1016/0022-5193(81)90246-0
Scranton, K., and Amarasekare, A. (2017). Predicting phenological shifts in a changing climate. Proc. Natl. Acad. Sci. U.S.A. 114, 13212–13217. doi: 10.1073/pnas.1711221114
Sharpe, P., and DeMichele, D. (1977). Reaction kinetics of poikilotherm development. J. Theor. Biol. 64, 649–670. doi: 10.1016/0022-5193(77)90265-X
Tewksbury, J. J., Huey, R. B., and Deutsch, C. (2008). Climate warming puts the heat on tropical ectotherms. Science 320, 1296–1297. doi: 10.1126/science.1159328
Tuda, M., Matsumoto, T., Itioka, T., Ishida, N., Takanashi, M., Ashihara, W., et al. (2006). Climatic and inter-trophic effects detected in 10-year population dynamics of biological control of the arrowhead scale by two parasitoids in Southwestern Japan. Popul. Ecol. 48, 59–70. doi: 10.1007/s10144-005-0243-y
Uszko, W., Diehl, S., Englund, G., and Amarasekare, P. (2017). Effects of warming on predator-prey interactions - a resource-based approach and a theoretical synthesis. Ecol. Lett. 20, 513–523. doi: 10.1111/ele.12755
van de Wolfshaar, K. E., de Roos, A., and Persson, L. (2008). Population feedback after successful invasion leads to ecological suicide in seasonal environments. Ecology 89, 259–268. doi: 10.1890/06-2058.1
Van der Have, T. (2002). A proximate model for thermal tolerance in ectotherms. Oikos 98, 141–155. doi: 10.1034/j.1600-0706.2002.980115.x
Van der Have, T. M., and de Jong, G. (1996). Adult size in ectotherms: temperature effects on growth and differentiation. J. Theor. Biol. 183, 329–340. doi: 10.1006/jtbi.1996.0224
Vasseur, D., and McCann, K. (2005). A mechanistic approach for modeling temperature-dependent consumer-resource dynamics. Am. Nat. 166, 184–198. doi: 10.1086/431285
Keywords: ectotherm, intra-specific competition, life history, latitude, traits, temperature variation
Citation: Amarasekare P (2019) Effects of Climate Warming on Consumer-Resource Interactions: A Latitudinal Perspective. Front. Ecol. Evol. 7:146. doi: 10.3389/fevo.2019.00146
Received: 17 December 2018; Accepted: 15 April 2019;
Published: 15 May 2019.
Edited by:
Diego Barneche, University of Exeter, United KingdomReviewed by:
John Paul DeLong, University of Nebraska-Lincoln, United StatesGuilherme Ortigara Longo, Federal University of Rio Grande do Norte, Brazil
Copyright © 2019 Amarasekare. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Priyanga Amarasekare, YW1hcmFzZWtAdWNsYS5lZHU=
 Priyanga Amarasekare
Priyanga Amarasekare