- School of Biological Sciences, University of Manchester, Manchester, United Kingdom
Developmental systems integrate inputs of variation from different origins into the observable variation of the resulting phenotype. Different components of phenotypic variation can be distinguished that correspond to those inputs, but the response of the system to each input factor can be modulated by other factors, so that there are interactions among the factors. This paper uses the concept of the target phenotype, introduced by Nijhout and Davidowitz to designate the expected phenotype for a given genotype and environment, to provide definitions and explanations of key concepts. This logic is put to use to explore the factors contributing to fluctuating asymmetry. To illustrate how genetic variation, phenotypic plasticity in response to temperature variation, and random developmental noise interact, this study uses computer simulations based on a simplified developmental model of a trait. The simulations show extensive interactions among the input factors, which can be explained by the non-linear nature of the developmental model. As a result, all the loci that control the developmental parameters end up affecting the resulting phenotypic trait, its reaction norm in response to temperature changes, and also its fluctuating asymmetry. Further, temperature (or possibly other environmental factors) can affect both trait values and the amount of fluctuating asymmetry without any involvement of stress. The model is broadly consistent with what is known from actual biological systems, and the results obtained from it have far-reaching implications for interpreting observations of the different types of phenotypic variation.
Introduction
Evolutionary biologists have extensively paid attention to genetic variation of phenotypic traits, as evidenced by the existence of an entire discipline of evolutionary quantitative genetics (e.g., Lynch and Walsh, 1998), but much less extensive efforts have been devoted to investigating non-genetic components of variation (but see e.g., Bradshaw, 1965; West-Eberhard, 2003; Herrera, 2009; Moczek et al., 2011). Often, several different components of non-genetic variation are lumped together in categories such as the “environmental variation” in quantitative genetics (Lynch and Walsh, 1998). Yet, this variation includes a number of components of non-genetic variation that differ fundamentally in their origin and in their biological significance, such as variation induced by variability in environmental factors and variation from inherent variability in developmental processes. To understand phenotypic variation and its different components, it is therefore important to define and distinguish concepts clearly, as well as to examine how they are related.
To appreciate how the different components of variation arise and how they are expressed in the phenotype, it is useful to consider them as the inputs and outputs of the developmental system (Figure 1; see also Félix and Barkoulas, 2015). Each component of variation has a direct cause or origin that constitutes the input of variation into the developmental system. These direct causes are inducing the differences between different instances of a phenotypic trait, which make up the respective component of variation. For instance, genetic variation originates from individuals that differ by carrying different alleles for relevant genes, phenotypic plasticity results from individuals experiencing different environmental conditions, and developmental instability results from random variation in developmental processes (developmental noise), which produce deviations in each developing structure from the norm expected for that genotype and environment. Such variation is the input for the developmental system, which translates it into the output of the observable phenotypic variation. The processes by which the input of variation is translated into phenotypic variation depend on the state of the developmental system, which in turn is influenced by the genotype and environment in which development takes place. For instance, genetic variation also depends on the environment in which organisms grow, phenotypic plasticity depends on the genotype under consideration, and developmental instability is contingent on both genotype and environment. The terminology to designate the different levels (Table 1) focuses on the direct causes of variation, but it is helpful to recall that other factors also have an effect.
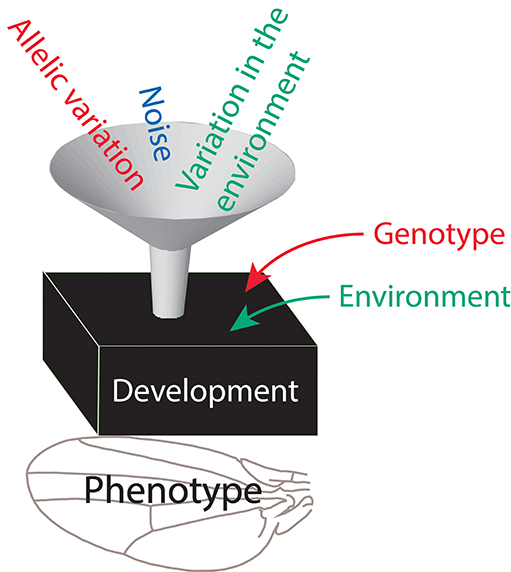
Figure 1. A cartoon view of how the developmental system mediates the effects of different inputs of variation to produce phenotypic variation. Note that genes and the environment have two possible roles each: as direct inputs of variation (in the funnel), when individuals differ in their genotypes or in the environments they experience and may differ in their phenotype as a result, and also as factors influencing the state of the developmental system (arrows from the right) and therefore possibly how it responds to the direct inputs.
There is not always a straightforward relation between the inputs of variation into the developmental system and the phenotypic outputs. For instance, some inputs of variation may produce only a small amount or no phenotypic variation at all—a phenomenon that has attracted considerable attention under the headings of buffering, canalization, and robustness (Waddington, 1942; Debat and David, 2001; Nijhout, 2002; Félix and Barkoulas, 2015; Hallgrimsson et al., 2018). Buffering can affect variation of a given trait from different sources, and there has been a continuing debate whether the buffering mechanisms are the same or differ between the different sources of variation (Debat et al., 2000; Debat and David, 2001; Hallgrímsson et al., 2002; Klingenberg, 2003b; Nijhout and Davidowitz, 2003; Breuker et al., 2006; Takahashi, 2018). There is even the question whether such buffering primarily relies on specific mechanisms, such as molecular chaperones or cell cycle regulators, or whether it is mostly an outcome of the architecture of the developmental system that generates the trait of interest (Klingenberg and Nijhout, 1999; Milton et al., 2003; Debat et al., 2011; Green et al., 2017).
This paper explores these issues from a conceptual viewpoint that differs from previous discussions of phenotypic plasticity and its developmental basis because it is based on the concept of at target phenotype, the expected phenotype for a given genotype and environment (Nijhout and Davidowitz, 2003). An important aim is to track how the developmental system converts the different inputs of variation into variation of the morphological trait and how different factors can modulate this process (Figure 1). This paper does this by using a simple numerical model of the development of a morphological trait, expanded from previous studies (Nijhout and Paulsen, 1997; Klingenberg and Nijhout, 1999) by adding a simple model of temperature dependence to incorporate phenotypic plasticity in the model. There are inherent limitations to the insights that can be drawn from theoretical models, because they inevitably are highly simplified representations of biological systems; nevertheless, such models can conclusively demonstrate conditions that are sufficient to generate a given phenomenon and therefore indicate that more complex explanations are not required. These considerations have significant implications for the understanding of phenotypic plasticity and developmental instability.
Concepts
The target phenotype is the phenotype expected for a specific genotype and under particular environmental conditions in the absence of any stochastic variation (Nijhout and Davidowitz, 2003). It is therefore a theoretical construct, but it can be highly useful for understanding many concepts relating to phenotypic variation (Table 1).
Most commonly, genotype and environment are specific to each individual in a population. This fact led Nijhout and Davidowitz (2003, p. 6) to characterize the target phenotype as a property of an individual. There are important theoretical and experimental situations, however, where multiple individuals share the same genotype and environment and therefore those individuals also share the same target phenotype. With modular organisms, such as plants, it may also be useful to apply the concept of target phenotype to discuss variation among repeated parts within an individual, e.g., variation among leaves or flowers in response to their position on the plant (Herrera, 2009). It therefore seems preferable not to tie the concept to a particular level, such as the individual.
Genetic variation of a trait in a given environment can be characterized as the variation among genotypes in their target phenotypes. Phenotypic plasticity of a trait is variation of the target phenotype for a given genotype in different environments. In particular, a reaction norm characterizes plasticity by describing how the target phenotype for a specific genotype varies as a function of an environmental variable. Finally, developmental instability is the deviation of particular instance of a trait (e.g., the trait value for the left wing of a particular Drosophila fly or for a particular petal of a flower) from the target phenotype for the genotype and environment.
These definitions based on target phenotype are compatible with the decomposition of variation in quantitative genetics (Falconer and Mackay, 1996; Lynch and Walsh, 1998). Also note that these definitions do not make any reference to the measurements that are needed to quantify the respective item. For instance, the definition of developmental instability does not refer to fluctuating asymmetry. In practice, of course, fluctuating asymmetry is used to quantify developmental instability in the overwhelming majority of studies (e.g., Polak, 2003), but the theoretical concept is not inevitably tied to this method for estimating it.
Inputs of Variation
For understanding the variation of target phenotypes and individual trait deviations from the target phenotype, it is necessary to consider the developmental system and how it produces variation in phenotypic traits. It is helpful to visualize the developmental system with various inputs and the phenotype as the output (Figure 1). Inputs of variation include genetic variation and environmental factors that affect development, but also random variation from within the developmental system itself. The degree to which the output of variation matches the input depends on the nature of the developmental system—there can be various interactions between inputs, potentially resulting in very complex behaviors of the system as a whole (Klingenberg and Nijhout, 1999).
Genetic variation of phenotypic traits originates from allelic differences in gene products that are involved in developmental processes or from differences in levels of gene expression. For both of these possibilities, different genotypes are associated with different activities of some developmental process, such as cell signaling, morphogenetic movements, or regulation of gene expression. The differences between alleles and their developmental consequences for phenotypic traits give rise to the visible differences in the target phenotype that can be quantified as genetic variation in phenotypic traits. Depending on the context of investigation, allelic differences can be minor, as it is often the case for the majority of alternative alleles segregating within populations, or conversely, they can be substantial differences resulting from mutations with large effects or that evolved over many generations and may have accumulated multiple mutations in this process. In the extreme, such large genetic effects may disrupt the developmental system so that, for some genotypes, the trait does not form at all or an entire structure is lost (examples include many of the classical mutants used in developmental genetics, e.g., various wingless alleles in Drosophila).
Environmental variation, as the term is commonly used especially in quantitative genetics, subsumes at least three different types of non-genetic variation: phenotypic variation induced by variation in environmental conditions (in the sense of a reaction norm), intra-individual variation in response to intrinsic organismal factors (e.g., ontogeny, side, position), and developmental instability that results from random variability in developmental processes themselves. What these three components of variation have in common is that they do not result from genotypic differences between individuals, hence they can be subsumed under the heading of non-genetic variation (Table 1). But otherwise, these categories differ fundamentally from each other in their origins and their implications, and need to be discussed separately.
Phenotypic variation induced by variation in environmental conditions is the component of variation usually referred to in discussions of phenotypic plasticity: the target phenotype changes as a function of one or more environmental parameters. This function is the reaction norm for the phenotypic trait with respect to the environmental parameters of interest. Its shape determines how readily the phenotypic trait responds to environmental variation. The amount of phenotypic variation produced in this way is determined jointly by these reaction norms and by the distribution of variation in the environmental conditions. The scale at which environmental variation occurs is sometimes used to distinguish macro- from microenvironmental variation, and canalization relating to it (Wu, 1997; Debat and David, 2001; Dworkin, 2005b; Takahashi, 2018). In the context of experimental studies, macro- and microenvironmental variation are often used to distinguish the effects of differences between treatments from the residual environmental variation within treatments (e.g., variation among Drosophila flies of the same genotype reared in the same vial, or among trees of the same genotype planted next to each other in the same experimental plot). At very large scales, phenotypic plasticity may contribute to the phenotypic differentiation among populations experiencing different environmental conditions. At smaller scales, it contributes to variation among individuals within populations. Environmental heterogeneity can even occur at a scale that is sufficiently small to cause differences between different parts of the same organism or structure, and phenotypic plasticity in response to such small-scale environmental variation may contribute to observable asymmetry of organisms (Palmer, 1996; Nijhout and Davidowitz, 2003; Tucić et al., 2018).
Intra-individual variation in response to intrinsic organismal factors is a heterogeneous category that encompasses a variety of factors in accordance with the organisms of interest and their body plans. One of the factors is ontogeny, the changes of a given part over time from its inception to maturity and on to senescence. Because all organisms and all their parts undergo ontogenetic changes, this is a very general factor and usually morphological studies take it into account, either by investigating it explicitly or by using a standard ontogenetic stage to eliminate it from the data. For organisms with a modular or metameric body plan, consisting of repeated parts arranged along some axis, there can be systematic variation among those parts according to their position. In metameric animals, this variation among parts that are serial homologs such as vertebrae and ribs in vertebrates or various segmental structures in arthropods, is being increasingly studied with the approaches of geometric morphometrics (Bruner and Bartolino, 2008; Böhmer et al., 2015; Savriama et al., 2016, 2017). Likewise, in plants, there is often pronounced variation among leaves or flowers associated with the position along the same shoot, which has been termed heteroblasty and is the subject of quantitative investigation (Jones, 1993; Bateman and Ruddall, 2006; Chitwood et al., 2014, 2016). There even can be systematic differences between the left and right sides of organisms or symmetric structures, and studies using geometric morphometrics have found such directional asymmetry to be widespread (Klingenberg et al., 1998; Chitwood et al., 2012; Klingenberg, 2015, p. 851 f.). All these factors, as different as they are from each other, are intrinsic to the organisms of interest and produce variation that is predictable in the respective context: there is a specific target phenotype for a structure at any given ontogenetic stage, at each particular position on the organism, or for each side.
Developmental instability, the final component of non-genetic variation, consists of random deviations of the actual phenotype from the target phenotype expected for the particular genotype and environmental conditions. Developmental instability is a consequence of developmental noise, that is, stochastic fluctuations in developmental processes. Such stochastic fluctuations exist, for instance, because developmentally important mRNA and protein molecules occur in limited numbers per cell (Elowitz et al., 2002; Albayrak et al., 2016) and because transcription tends to occur in intermittent bursts (McAdams and Arkin, 1997; Wang et al., 2018). The result is random variation in timings and rates of the processes in which the respective molecules are involved, and a degree of random variation among cells and in developmental processes even at a larger scale (Klingenberg, 2003b). How developmental noise is manifest in the phenotype depends on the developmental processes that produce the phenotype in question and how these processes mediate the expression of developmental noise in the phenotype, in other words, how sensitive or robust the developmental system is.
Although developmental noise is conceptually clear and distinct from other sources of variation, it is difficult or impossible to separate empirically from other components of the system and to quantify on its own. Developmental noise itself is not observable directly, but only manifest through its consequences on some trait, with the developmental system mediating the expression of noise as phenotypic variation in the trait. The same amount of phenotypic variation could result from a large input of noise attenuated by a robust developmental system or from very little noise amplified by a sensitive developmental system. The observed variation in a phenotypic trait is therefore the combined effect of the developmental noise and the sensitivity or robustness of the developmental system. This aggregate effect is developmental instability, the tendency of the developmental system to produce variation about the target phenotype.
Even developmental instability can be challenging to quantify. Empirical studies need to estimate it from measurements of multiple structures sharing the have target phenotype, which should differ from each other only by developmental instability. The most widely used approach to do this is to use fluctuating asymmetry, under the assumption that the left and right sides share the same genotype and environment and therefore also the same target phenotype, so that their difference indicates developmental instability (Klingenberg, 2003b; Nijhout and Davidowitz, 2003). There are a number of theoretical and technical challenges with using fluctuating asymmetry for estimating developmental instability of individuals (see also section What Fluctuating Asymmetry is Made of; Palmer and Strobeck, 1986, 2003; Whitlock, 1998; Van Dongen, 2006).
Buffering and Robustness
Not all inputs of variation produce a response in the phenotype. The absence of phenotypic change in the presence of variation in relevant input parameters indicates that developmental systems may have a capacity for buffering against internal or external variation or to be robust against such variation. This is biologically significant and has given rise to a variety of concepts such as canalization, robustness, and developmental stability (Waddington, 1942; Debat and David, 2001; Hallgrímsson et al., 2002; Nijhout and Davidowitz, 2003; Félix and Barkoulas, 2015).
The literature on canalization and related subjects has been rather confusing, with different and apparently conflicting definitions of concepts, even of canalization itself (e.g., Debat and David, 2001; Dworkin, 2005a). Buffering, canalization and robustness tend to be used as synonymous or at least nearly synonymous terms (buffering and canalization often are used to designate a process or activity, whereas robustness refers exclusively to the resulting state, i.e., a trait being buffered against the effects of some input factor). A degree of differentiation exists between the terms canalization and developmental stability: canalization is normally used for buffering against external inputs of genetic or environmental variation, whereas developmental stability is buffering against developmental noise (Debat et al., 2000; Debat and David, 2001; Hallgrímsson et al., 2002).
It is helpful to use the concept of the target phenotype for trying to clarify the concepts. Accordingly, canalization is the tendency for the target phenotype to remain unchanged even though there is variation in some genetic or environmental factor. A weaker version of this definition, allowing for degrees of canalization, stipulates that canalization implies that target phenotypes at different values of a specific genetic or environmental factor differ less than expected for some appropriate standard (that standard depends on the context of a given study). This definition makes it clear that canalization always relates to some specific input of variation. Also, the concept of canalization is generally used in relation to extrinsic factors (i.e., genetic or environmental variation from outside the organism). A trait may be canalized with respect to one environmental factor but not another, it may be genetically canalized concerning allelic variation at one locus but not another, or it may be canalized in relation to the total genetic variation in a population but not in relation to some environmental factor. Whether there is an association between the degrees of canalization of a particular trait in response to different inputs is an empirical question, and will depend on the trait, genotypes and environmental factors of interest.
Whereas canalization refers to buffering that maintains the same target phenotype despite variation in some genetic or environmental factors, developmental stability is the buffering that limits the variation about the target phenotype for a particular genotype and environment. It reflects the ability of the developmental system to limit random deviations of actual trait values from the expectation of the target phenotype. The variation responsible for those deviations is developmental noise, the random variation arising from within the developmental system. Yet, it is also the developmental system that attenuates and absorbs developmental noise to some extent and is therefore responsible for developmental stability. For instance, cell compartmentalization and autoregulatory switching mechanisms can help to stabilize concentrations of gene products and reduce their variation among cells (e.g., Battich et al., 2015; Papadopoulos et al., 2019). As mentioned above, developmental noise is not directly observable, but is only manifest in its phenotypic expression, and the same applies to developmental stability—the two are inextricably tied together and can only be seen in their joint effects on the final phenotype.
There has been a debate on whether the buffering processes involved in canalization and developmental stability are the same or whether they are distinct (Debat et al., 2000; Hallgrímsson et al., 2002; Breuker et al., 2006). This is debate addresses the question whether developmental buffering acting on inputs of variation from distinct origins, external genetic or environmental variation or intrinsic noise from developmental processes, relies on the same or separate mechanisms. In principle, one would want to know how variation from these distinct origins enters the developmental system and how it is cascaded through the system to generate the observable phenotypic outputs. The question then would be whether and how much the pathways involved in buffering variation from different sources overlap. Unfortunately, this approach is not practically feasible. Instead, empirical studies investigating the relationship between canalization and developmental stability have resorted to comparing the patterns of variation for fluctuating asymmetry and of variation among individuals. Such comparisons have provided somewhat mixed results: some studies found marked differences (e.g., Klingenberg et al., 2002; Santos et al., 2005; Breno et al., 2011; Webster and Zelditch, 2011), some even going as far as concluding that canalization and developmental stability are independent (Debat et al., 2000), whereas others found various degrees of agreement in patterns consistent with a shared buffering process (e.g., Klingenberg et al., 2001, 2010; Willmore et al., 2005; Breuker et al., 2006; Ivanović and Kalezić, 2010), and some obtained mixed results (for a more complete compilation of relevant studies, see Klingenberg, 2015, p. 893). These analyses all are based on a comparison of patterns in the outputs of variation from the developmental system. In order to use the similarity of patterns in the output of variation to answer the question whether the buffering processes are the same, the comparisons have to make the implicit assumption that the patterns in the inputs of variation are the same. Unfortunately, that assumption is problematic because the patterns in the inputs of variation, the total genetic and environmental variation for canalization and developmental noise for developmental stability, cannot be compared or quantified without the effects of the developmental system that inevitably include its buffering effects. For this reason, inferences about canalization and developmental stability from comparisons of patterns of variation among individuals and fluctuating asymmetry ought to be interpreted with some caution.
What Fluctuating Asymmetry Is Made Of
A good illustration of the different sources of variation and buffering is the question of what processes contribute to fluctuating asymmetry. This question is relevant because fluctuating asymmetry is widely used under the assumption that it originates as developmental instability, produced by random variation in the development of the structure under study (Palmer, 1996; Klingenberg, 2003b; Nijhout and Davidowitz, 2003). For this reason, fluctuating asymmetry is used widely as a measure of individual quality or of the effects of environmental stresses on organisms (Palmer and Strobeck, 1986; Parsons, 1990; Møller and Swaddle, 1997; Beasley et al., 2013) and also to investigate the developmental origins of morphological integration (Klingenberg, 2003a, 2015).
The justification for using fluctuating asymmetry to characterize developmental instability is that the left and right sides of an individual usually share the same genome and experience the same environment, and should therefore also have the same target phenotype. Because the two sides are separate realizations of the structure of interest, developmental noise arises independently on the two sides and produces different realizations of developmental instability, the deviations from the target phenotype. In computing the difference between the left and right sides, the target phenotype cancels out and leaves the observed asymmetry as a manifestation of developmental instability.
The phenotypic expression of this random variation is mediated by the developmental system, through both the input of developmental noise and any possible buffering of its effects. In fact, developmental noise and buffering are usually not observable in isolation, but only in their combined effect as developmental instability, the tendency of traits to deviate from their target phenotype. Whereas the origin of developmental noise is purely spontaneous, not caused by genetic or environmental variation, genetic and environmental factors can have an effect on developmental processes that mediate its expression and thus influence developmental instability (Klingenberg and Nijhout, 1999). The use of fluctuating asymmetry as a measure of stress uses this reasoning: if stress increases developmental noise or reduces developmental buffering, exposure to stress should increase developmental instability (Parsons, 1990; Beasley et al., 2013). Likewise, genetic quality of individuals might correlate with lower levels of developmental noise or better ability for buffering, and therefore with reduced developmental instability (Møller, 1997; Møller and Swaddle, 1997; Lens et al., 2002).
Developmental instability, however, is not necessarily the only contributor to fluctuating asymmetry. The reasoning that fluctuating asymmetry is an expression of developmental instability assumes that the left and right sides of each individual share the same target phenotype, which means that they must share the same genome and the same environment. The assumption of a shared genome is usually not problematic—even if somatic mutations are widespread, such as in plants, there is evidence that they are contributing at most a minor fraction of phenotypic variation within individuals (Herrera, 2009). The assumption that the two sides experience the same environment is more questionable because environmental factors can be heterogeneous and may differ between the sides of an individual. For motile organisms, such as most animals, this environmental heterogeneity is likely to average out so that, integrated over the period of development of the organism, the cumulative effect of the environmental factors on both sides is the same. For sessile organisms, however, this argument does not apply because they are consistently exposed to heterogeneity in their immediate surroundings. If, as a result, different parts of the same organism experience different environmental conditions, the assumption that they share the same target phenotype may no longer hold. Specifically, if there is phenotypic plasticity in response to an environmental factor that is heterogeneously distributed, it may produce a component of asymmetry that is not due to developmental instability, but which arises from plasticity in response to the heterogeneity in that factor. This has long been recognized and discussed theoretically in the literature on fluctuating asymmetry (Palmer, 1996; Nijhout and Davidowitz, 2003; Van Dongen, 2006; Klingenberg et al., 2012; Savriama et al., 2012; Klingenberg, 2015), but empirical evidence has been elusive.
The problem, for demonstrating that phenotypic plasticity in response to environmental heterogeneity contributes to fluctuating asymmetry, is that it is not known which factors may induce plasticity and that it is difficult or impossible to quantify how they are distributed in the surroundings of an organism. A recent study (Tucić et al., 2018) has partly overcome this problem by reasoning that solar irradiance, in temperate latitudes, forms a gradient where the amount of light differs with orientation (on the northern hemisphere, more light from southerly directions). Accordingly, if the associated differences in light or temperature elicit phenotypic plasticity, a component of asymmetry can be accounted by the compass orientation of parts. Tucić et al. (2018) tested this idea by studying flower parts of Iris pumila in an experimental garden and found significant differences in the shapes, but not the sizes, of floral parts according to orientation. This is the first evidence that a component of asymmetry in these flowers is due to phenotypic plasticity in response to a directed environmental factor, most likely solar irradiance. For the three different floral parts, orientation accounted for between 7.3 and 12.8% of the shape variation among parts within flowers (Tucić et al., 2018). This is a minimal estimate of the amount of floral asymmetry that is due to phenotypic plasticity in response to environmental heterogeneity. It leaves out any asymmetry due to a plastic response to factors that have irregular spatial patterns and therefore affect every flower differently. Quantifying that component of asymmetry will be more challenging and may be impossible (for a more detailed discussion, see Tucić et al., 2018). In conclusion, for the one instance where this has been studied, phenotypic plasticity in response to environmental heterogeneity accounts for an appreciable portion of fluctuating asymmetry. This phenomenon therefore needs to be taken seriously for studies of fluctuating asymmetry in plants and other sessile organisms and deserves further study.
Overall, therefore, the biological variation that manifests itself as fluctuating asymmetry is complex and influenced by multiple factors. Developmental noise, the main cause of fluctuating asymmetry, is itself neither genetic nor environmentally determined, but its phenotypic expression is mediated by genetic and environmental factors. Under some circumstances, for instance in plants and other sessile organisms, further asymmetry may arise through phenotypic plasticity in response to environmental heterogeneity. In practical applications, this is further complicated by measurement error, which is an important concern for asymmetry studies (Palmer and Strobeck, 1986, 2003; Palmer, 1994; Klingenberg, 2015).
Modeling Components of Variation and Their Interactions
To examine the interactions among factors contributing to phenotypic variation, I use a simple model of the development of a trait that can accommodate multiple inputs of variation. It is an extension of a model previously used for examining the inheritance of traits, particularly the origin of non-additive variation such as dominance and epistasis, as well as the origin and inheritance of fluctuating asymmetry (Nijhout and Paulsen, 1997; Klingenberg and Nijhout, 1999; Gilchrist and Nijhout, 2001). As an addition to the previous versions, phenotypic plasticity is incorporated into the model through a response to temperature. As a result, it is possible to examine reaction norms both for the target phenotype and for the variability of the trait, as well as genetic variation of reaction norms.
Model
The basic model presented in this study is the same as that used previously by Nijhout and Paulsen (1997) and Klingenberg and Nijhout (1999), implementing a diffusion–threshold process (Figure 2). In the model, a morphogen is released from a point source and also, at a lower background rate, from every other location in the linear array that represents a developing tissue. The morphogen can diffuse from the source through the surrounding tissue. The morphogen is subject to decay, reducing the concentration by a certain fraction per unit of time. After a set time, the resulting morphogen gradient is read by comparing the concentrations to a threshold value, and the trait value is taken as the distance from the source where the morphogen concentration exceeds the threshold value. Overall, this model is therefore controlled by six parameters: Source, Background, Decay, Diffusion, Time, and Threshold (Figure 2).
Figure 2. The developmental model of a simple trait, controlled by six parameters. A point source releases a morphogen at a specific concentration (Source), and additional morphogen is produced as a background concentration at every location (Background). The morphogen diffuses away from the point source according to a set diffusion rate (Diffusion), and it decays at another set rate (Decay). After a specific time has elapsed (Time), the morphogen concentration gradient (dark blue line) is compared to a set threshold value (Threshold). The trait value is the distance from the point source within which the morphogen concentration exceeds the threshold value.
For each of the parameters controlling the developmental model, there is a single locus with two alleles that determines the parameter value in a strictly additive manner (the parameter value for the heterozygous genotype is exactly intermediate between the values for the two homozygous genotypes). The genotypic values used here (Table 2) are the same as in the previous studies (Nijhout and Paulsen, 1997; Klingenberg and Nijhout, 1999), so that the results are directly comparable. For each locus, one allele tends to produce a smaller and the other a larger trait value, and the alleles are designated accordingly as the S and L alleles. Note that this designation according to the effects on the value of the trait does not agree for all loci with the respective values of the developmental parameters (for Source, Background, Diffusion, and Time, the L allele is associated with the greater value of the developmental parameter than the S allele, but for Decay and Threshold, the L allele is associated with a smaller value of the developmental parameter than the S allele).
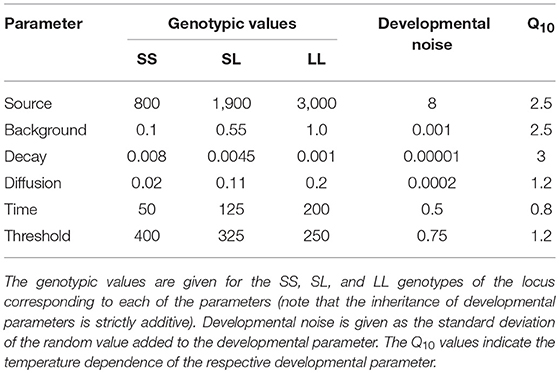
Table 2. Genotypic values, developmental noise and Q10 values for the parameters in the developmental model.
The model was used to obtain trait values numerically, as analytical solutions are not available for the model (Nijhout and Paulsen, 1997; Klingenberg and Nijhout, 1999). The concentration gradient was computed as a linear array with 50 intervals. For the readout of the location where the gradient intersects the threshold to obtain the trait value, linear interpolation was used. All calculations were conducted with custom-written R scripts (see Supplementary Materials).
Phenotypic plasticity in response to an environmental factor is implemented as variation in temperature and a response of the developmental parameters according to a Q10 rule. This is a simple and widespread form of the response of biological processes to variation in temperature: for every increase of the temperature by 10°, the rate of the process increases by the factor given by the Q10 index. The result is an exponential increase of the reaction rate with temperature, which is often found at relatively cool temperatures, where reaction rate is limited by chemical reaction rates. For many processes, higher temperatures produce a decline in the reaction rates because of denaturing or decay of key enzymes; this is beyond the dynamics included in this model and might lead to different results (see Discussion). Throughout this study, a reference temperature is used that provides the same results as the previous studies (Nijhout and Paulsen, 1997; Klingenberg and Nijhout, 1999), augmented by a temperature range of 5° below and above this temperature. Note that the reference temperature is not an optimal temperature, but it is simply intermediate in the range of temperatures considered in this study. It is not the aim of this study to model stressful temperatures, either low or high, which would require a different type of model for the dynamics of the system at more extreme temperatures.
Developmental noise is incorporated in the model by adding small random deviations to the values of the developmental parameters. The deviations are simulated as normally distributed random variables with zero means and standard deviations corresponding to the “Low” level of developmental noise in the study by Klingenberg and Nijhout (1999). These deviations are independent of all other factors such as genotype or environment. To assess the effects of developmental noise on the phenotypic trait, pairs of traits are simulated as the left and right sides of an individual and the difference between them is used as the fluctuating asymmetry of the trait (Klingenberg and Nijhout, 1999). As in the previous study, fluctuating asymmetry is quantified as the average of the absolute values of the differences between the two trait values in each pair, the FA1 index of Palmer and Strobeck (1986). For the simulations involving developmental noise, a sample size of 1,000 individuals (i.e., 2,000 trait values) is used per genotype and temperature.
Results
The target phenotype changes as a function of the developmental parameters in a moderately non-linear fashion (Figure 3). For the reference temperature, this is exactly the same that was shown before for this model (Figure 2 in Nijhout and Paulsen, 1997; Figure 1A in Klingenberg and Nijhout, 1999), but adding variation induced by temperature differences shows that the target phenotypes are plastic and that this plasticity itself acts in a moderately non-linear manner. This non-linearity is only moderately strong, as there is a substantial linear component in the dependency on temperature, which can be seen from the fact that all the curves for the low temperature (blue curves in Figure 3) are shifted downwards by comparison to the corresponding curves for the reference temperature (black curves), and that all but one of the curves for the high temperature (red curves) are shifted upwards, and even the one exception (the curve for Decay on an LL genetic background, upper-right panel in Figure 3) is shifted upwards for a substantial part of the parameter range. That the response is somewhat non-linear is evident because the curves for the high and low temperatures are not just shifted up and down precisely, but vary in slope and curvature as well, and because temperature affects different genotypes differently. Especially for the LL genetic backgrounds (top triplet of curves in each panel of Figure 3), the curves for the warm temperature (red curves) tend to be steeper than those for the reference temperature (black curves) or the cold temperature (blue curves). In particular, the curve for the Decay parameter on an LL genetic background at the high temperature intersects the curves for the reference and low temperatures (top three curves in the upper-right panel of Figure 3). In addition, the fact that the differences between the curves for the three temperatures are consistently larger for the LL genetic backgrounds than for the SS or SL backgrounds indicates that phenotypic plasticity in response to temperature is influenced by the genotype.
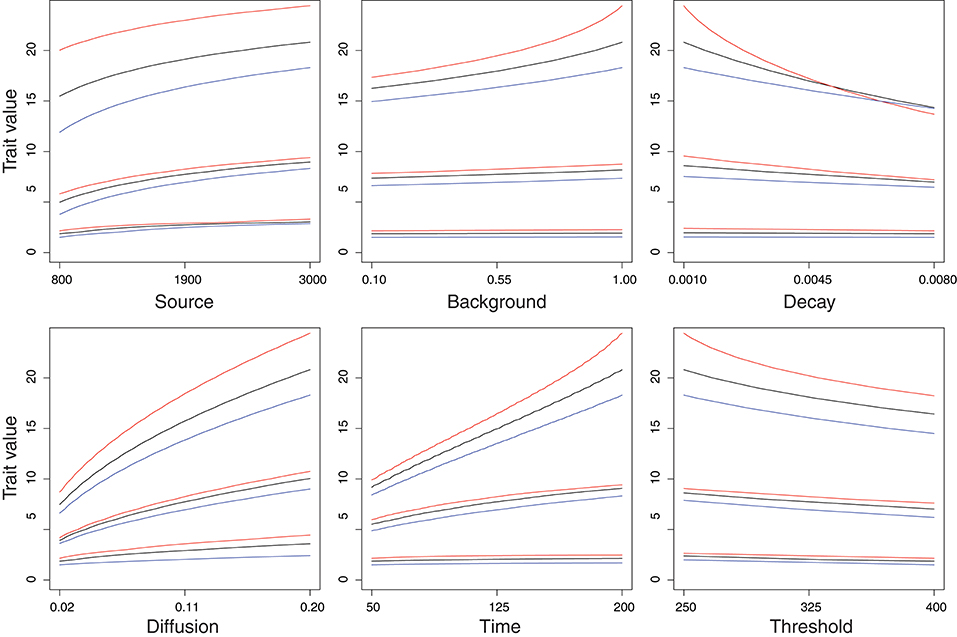
Figure 3. Effects of temperature and genetic background on the functions relating values of the developmental parameters to the target phenotypes. In each panel, the trait values (with no stochastic variation, thus these are the target phenotypes) are plotted as a function of one of the parameters in the developmental model. Each panel contains three groups of curves, corresponding to the genotype for loci controlling the five remaining parameters in the developmental model: for the group at the top, all five loci have the LL genotype, for the middle group, they have the SL genotype, and for the bottom group, they have the SS genotype. In each group, the black curve is the function at the reference temperature, the red curve is the function at the warm temperature (reference +5°) and the blue curve is the function at the cold temperature (reference −5°).
The reaction norms for different genotypes can be plotted as functions of the target phenotype vs. temperature (Figure 4). Again, there is a strong effect of the genotypes, as can be seen from the differences in the vertical positions of the curves. By comparison, most of the differences between the trait values at the low and high temperatures, the left and right sides of the curves, are smaller. Most of the curves in Figure 4 are slightly inclined, indicating reactions norms with higher trait values at warmer temperatures. The reaction norms also differ among genotypes. Above all, there is an obvious difference between the genetic backgrounds, with the reaction norms for SS backgrounds (green curves near the bottom of each panel) being relatively flat and nearly linear, those for SL backgrounds being intermediate (black curves), and those for the LL background (orange curves) being steeper and sometimes showing marked curvature. Also, the reaction norms for the LL genetic backgrounds differ the most between the three genotypes of the focal locus in each panel, in both the position and shape of the curve. At least for the LL backgrounds, there are clearly visible differences between the reaction norms for the three genotypes at each of the six loci controlling the developmental parameters in the model, showing that each of those loci has an effect on the reaction norms. For the Decay locus (upper right panel of Figure 4), the reaction norm for the LL genotype on LL background (top orange curve) has a positive overall slope, indicating that the trait value increases with increasing temperature, whereas the SS genotype on the same LL background (lowermost orange curve) produces a reaction norm with a very subtle negative overall slope, so that the trait value at the warmest temperatures in the range is lower than at the coldest temperatures. The genotypes also differ in the degree of curvature and in whether the curves are convex or concave.
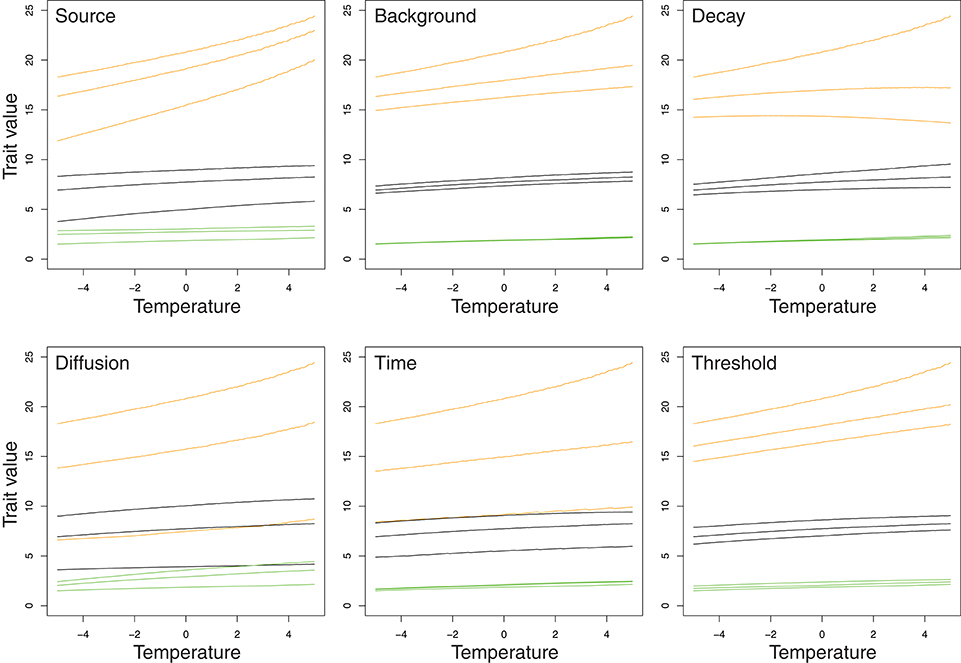
Figure 4. Reaction norms of the target phenotype of the trait vs. temperature for different genotypes in the loci controlling the developmental parameters. The reaction norms are drawn for a range of 5° above and below the reference temperature, which is designated by a value of zero. Each panel shows three groups of reaction norms according to the genetic background, that is the genotype in the five loci other than the focal locus of the respective panel: green curves are for the SS genotype in those five loci, black for the SL genotype, and orange for the LL genotype. Within each of those three groups, the curve at the top is for the LL genotype of the focal locus for the panel, the middle curve is for the SL genotype, and the curve at the bottom is for the SS genotype.
To examine the effects of temperature variation on fluctuating asymmetry, samples of 1,000 individuals were simulated and the FA1 index was computed for each of the 729 possible genotypes at the reference temperature and at colder and warmer temperatures (5° below and above the reference). The resulting reaction norms for fluctuating asymmetry (Figure 5) show that temperature has an effect for many of the genotypes. Many of the reaction norms show a decrease from colder to warmer temperatures. Also, most of the reaction norms are non-linear, often with the reference temperature with an FA1 index that is lower than the midpoint between the FA1 indices of the cold and warm extremes.
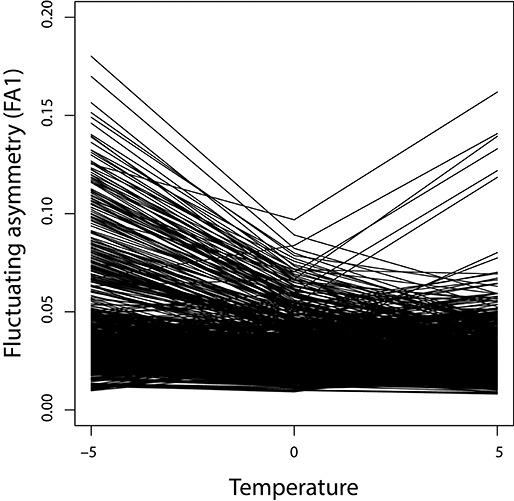
Figure 5. Reaction norms for fluctuating asymmetry. For each of the 729 possible genotypes, the lines connect the values of the FA1 index for the cold, reference and warm temperatures (with the reference temperature designated zero).
Discussion
The results of the model simulations are broadly consistent with and expand the findings of the preceding simulation study that focused on fluctuating asymmetry (Klingenberg and Nijhout, 1999). Just as that study found that all six loci controlling the developmental parameters in the model have not only an effect on the target phenotype, but also on the level of fluctuating asymmetry, the simulations presented here demonstrate that they also affect the reaction norms for the target phenotype (Figure 4) as well as the reaction norms for fluctuating asymmetry (Figure 5). Even in this simple developmental model of a phenotypic trait, the different inputs of variation from genetic and environmental factors as well as developmental noise interact with each other in complex ways to produce the observable phenotypic variation.
The interactions between the different factors are not built into the model as such, but are the outcome of how the developmental system functions, here as a simple diffusion–threshold mechanism (Figure 2), and of how it is affected by genetic and environmental variation as well as developmental noise. The key point in this is that the relations between the inputs and outputs of the system are non-linear, so that the functions relating input factors to the phenotypic output are curved lines, if a single factor is considered, or curved surfaces, if multiple input factors are considered simultaneously. As a result, the change in the phenotypic value per unit of increase in a specific factor changes with the value for that factor. This relationship can be further modified by changing the value for an additional factor. The consequence is that different input factors can act as modifiers of each other's relationships between input of variation and phenotypic output. That non-linear developmental processes have important implications for the expression of genetic variation, developmental buffering and robustness, as well as fluctuating asymmetry has long been recognized (e.g., Nijhout and Paulsen, 1997; Klingenberg and Nijhout, 1999; Gilchrist and Nijhout, 2001; Nijhout, 2002; Klingenberg, 2004; Green et al., 2017; Hallgrimsson et al., 2018).
To get a better understanding of how such interactions arise from non-linear developmental systems, it is easiest to look at a graphical example (Figure 6). The graph shows the curves of a phenotypic trait vs. the level of a developmental activity in two different environments. The level of developmental activity is influenced by a gene with two alleles a and A, and the levels of developmental activity for the resulting three genotypes are indicated by the vertical dotted lines in the graph. For simplicity, I assume that the gene acts in a perfectly additive manner, so the value of developmental activity for the heterozygous aA genotype is exactly intermediate between the values for two homozygous aa and AA genotypes. Due to the non-linear nature of the function translating the developmental activity into phenotypic values, the target phenotypes for the three genotypes are not equally spaced, but the aA phenotype is closer to the AA than the aa phenotype, so that the A allele is partially dominant over the a allele. Non-linear mapping from developmental parameters to phenotypic values has long been recognized as an explanation for non-additive genetic phenomena such as dominance and epistasis (Kacser and Burns, 1981; Nijhout and Paulsen, 1997; Klingenberg and Nijhout, 1999; Gilchrist and Nijhout, 2001; Klingenberg, 2004). In the example (Figure 6), the dominance of A over a holds within both environments, but it is evident that the differences between the target phenotypes for the different genotypes are considerably greater in the environment corresponding to the upper curve than in the environment corresponding to the lower curve. Therefore, it is clear that the additive and dominance effects of the A vs. a alleles differ between the two environments. And, vice versa, the reaction norms for the trait between the two environments would differ among the three genotypes because the difference between the target phenotypes in the two environments is clearly bigger in the AA and aA than in the aa genotype. It follows that there is an interaction between the genetic and environmental effects: because the mapping from developmental activity level to target phenotype is non-linear and because the curves for this mapping in the two environments differ by more than just a shift up or down along the phenotype axis, genetic effects differ between environments and environmental effects differ among genotypes. Such genotype-by-environment interactions have been extensively discussed and studied as part of evolutionary and applied quantitative genetics (Via and Lande, 1985; Lynch and Walsh, 1998, ch. 22; Saltz et al., 2018).
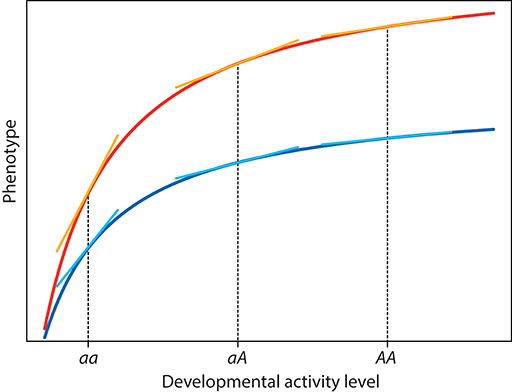
Figure 6. Developmental mapping of the level of some developmental activity to the phenotype in two different environments. For the curves corresponding to both environments, tangents are drawn at the developmental activity levels of the aa, aA, and AA genotypes to indicate the sensitivity to developmental noise for the six genotype–environment combinations.
There are yet more interactions contained in this example, if we consider the effects of developmental noise. Developmental noise adds small changes to the values of developmental parameters. Its phenotypic effects can be assessed by considering how the phenotype changes in response to a slight shift to the left or right along the mapping curve. Evidently, this depends on the slope of the curve in the vicinity of the mean value of the developmental parameter for the genotype in question: the greater the slope, the more will the phenotypic values deviate from the target phenotype for a given perturbation of the developmental parameter. Where the curve is steeper, a small deviation in the developmental activity will lead to a bigger phenotypic response than in a region where the curve is flatter (tangents to curves in Figure 6). Therefore, the slope of the developmental mapping curve is a measure of developmental instability (Klingenberg and Nijhout, 1999; Klingenberg, 2003b, 2004, 2015). A recent study that manipulated the expression of the Fgf8 signaling factor in mice provides experimental evidence consistent with this prediction (Green et al., 2017). The amount of variation in the slope is associated with the degree of curvature in the developmental mapping function. Accordingly, one can expect an association between the differences in developmental stability and the degree of curvature of the developmental mapping function, which in turn is related to non-additive genetic effects such as dominance and epistasis. This reasoning leads to the hypothesis that dominance and epistasis should be particularly important for the inheritance of fluctuating asymmetry (Klingenberg and Nijhout, 1999; Klingenberg, 2004; Leamy and Klingenberg, 2005). The relatively few empirical studies available to address this hypothesis, on the whole, are consistent with this hypothesis (Leamy et al., 2002, 2015; Leamy, 2003; Varón-González and Navarro, 2018).
Discussions on the genetic basis of particular phenotypic traits and of phenomena such as phenotypic plasticity and fluctuating asymmetry have tended to focus on specific “trait genes,” “reaction norm genes,” “canalization genes,” or “fluctuating asymmetry genes.” The model used here used no specific genes of this kind, but only the six loci that each determine one of the six developmental parameters. Yet, because the effects of all six loci are mediated through the developmental system, each of them affects the phenotypic trait and thus is a “trait gene” in that sense (Nijhout and Paulsen, 1997; Klingenberg and Nijhout, 1999), each of the also affects fluctuating asymmetry and thus is a “fluctuating asymmetry gene” (Klingenberg and Nijhout, 1999), and each of them also affects the reaction norm of the trait and is therefore a “reaction norm gene” (Figure 4). This is a reminder that genetic effects on different aspects of organisms may be connected in complex ways, and that the thinking about genes for particular traits or functions may be gross oversimplifications or misleading (Beurton et al., 2000; Keller, 2000; Lewontin, 2000).
There is a further lesson to be drawn from the observation that all loci in the simulation model affected the reaction norms and amount of fluctuating asymmetry (Figure 4; Klingenberg and Nijhout, 1999). Recent discussions on the genetic control of developmental buffering have often emphasized specific mechanisms such as molecular chaperones (Rutherford and Lindquist, 1998; Queitsch et al., 2002; Takahashi et al., 2010; Zabinsky et al., 2018) or cell cycle regulation (Debat et al., 2011). An alternative to such specialized processes for the control of developmental buffering is that the non-linear dynamics of the developmental processes that generate a trait also regulate its variability and its potential for response to environmental factors (Figures 4–6). There is experimental evidence demonstrating that variation in the expression levels of genes with key roles in developmental processes can also affect the variability of the resulting phenotypic traits (von Dassow et al., 2000; Eldar et al., 2002; Green et al., 2017; Hallgrimsson et al., 2018). As a consequence, there is a very large number of potential mechanisms for regulating traits, their variability and response to environmental factors. So far, many studies of developmental buffering have focused on a known target, such as the Hsp90 chaperone, and often were successful in finding effects for various traits in different taxa (Rutherford and Lindquist, 1998; Queitsch et al., 2002; Milton et al., 2003; Debat et al., 2006; Takahashi et al., 2010; Zabinsky et al., 2018). Investigating the role of the developmental system itself in the regulation of buffering is likely to be challenging because of the great number of potential targets that need to be investigated. To obtain an unbiased picture of the mechanisms modulating the variation in phenotypic traits, however, this effort is necessary and it is promising new insights.
The simulation results and the considerations above also have some important implications for analyses of the non-genetic component variation, especially fluctuating asymmetry. If a study finds differences in fluctuating asymmetry of some organism between two environments, the usual interpretation is that the environment with the higher amount of asymmetry is more stressful and thus produces higher developmental instability (Parsons, 1990; Hoffmann and Woods, 2003; Beasley et al., 2013; Lazić et al., 2015). In the simulation model of this study, many genotypes, when developing in environments with different temperatures, clearly differed in the amounts of fluctuating asymmetry (Figure 5). In the model, these temperature-induced differences in fluctuating asymmetry are based entirely on the Q10 dynamics of the response to temperature and do not involve any stress whatsoever. It follows that stress is not required for some environments to produce increased fluctuating asymmetry, and thus increased fluctuating asymmetry is not sufficient evidence for inferring the presence of stress. Differences in the amounts of fluctuating asymmetry between environments may be due to differences in stress, as is usually expected, but alternatively they may be due to the reaction norms of fluctuating asymmetry between those environments (Figure 5) or, for plants, due to differences in the degree of localized heterogeneity of relevant factors within the environments and in the asymmetry resulting from plastic responses to that heterogeneity (Tucić et al., 2018). Similarly, for differences in fluctuating asymmetry among genotypes within a single environment, a widespread assumption is that genotypes differ in their ability to cope with developmental perturbations and their overall genetic quality via genomic coadaptation or specific buffering mechanisms, which may be associated with overall genetic quality and fitness (Møller and Swaddle, 1997; Alibert and Auffray, 2003; Takahashi et al., 2010, 2011; Debat et al., 2011). Even though the developmental model contains no specific buffering mechanisms and no inherent differences in quality or fitness among individuals or genotypes, it produces substantial differences in fluctuating asymmetry among the genotypes at any particular temperature (Figure 5; Klingenberg and Nijhout, 1999). This is a reminder that inferences about genetic quality or fitness of individuals or genotypes are problematic if they are based solely on fluctuating asymmetry.
The model used in the computer simulations and the graphical model of Figure 6 are highly simplified representations of biological processes, which raises the question whether they are sufficiently realistic to draw biological conclusions. The reasoning above uses the models to show that they are sufficient to account for a range of phenomena that are also observed in real biological systems. For arguing that a simplified model is sufficient to account for a set of observed phenomena, the question about realism is not critical. The key point, in this context, is that the models are non-linear. It is the non-linearity of the developmental model that produces the interactions among the factors influencing the phenotypic trait and that is responsible for variation in developmental instability. Such non-linearity is the hallmark of actual developmental systems (Klingenberg and Nijhout, 1999; Nijhout, 2002; Klingenberg, 2003b; Green et al., 2017; Hallgrimsson et al., 2018), and thus the central criterion is met for biological inferences from the model to be valid.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I thank Alex Shingleton for inviting me to contribute to the Research Topic, which prompted me to return to this project, and for his editorial advice, patience and insistence. The initial ideas for the work presented in this paper originated when I was a postdoctoral fellow in the lab of Fred Nijhout at Duke University, 1997–1999. I would like to thank Fred, the members of his lab at the time, and to the members of the Duke population biology group, and two reviewers of an earlier version of this manuscript for critical discussions.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2019.00056/full#supplementary-material
References
Albayrak, C., Jordi, C. A., Zechner, C., Lin, J., Bichsel, C. A., Khammash, M., et al. (2016). Digital quantification of proteins and mRNA in single mammalian cells. Mol. Cell 61, 914–924. doi: 10.1016/j.molcel.2016.02.030
Alibert, P., and Auffray, J.-C. (2003). “Genomic coadaptation, outbreeding depression, and developmental instability,” in Developmental Instability: Causes and consequences, ed M. Polak (New York, NY: Oxford University Press), 116–134.
Bateman, R. M., and Ruddall, P. J. (2006). Evolutionary and morphometric implications of morphological variation among flowers within an inflorescence: a case study using European orchids. Ann. Bot. 98, 975–993. doi: 10.1093/aob/mcl191
Battich, N., Stoeger, T., and Pelkmans, L. (2015). Control of transcript variability in single mammalian cells. Cell 163, 1596–1610. doi: 10.1016/j.cell.2015.11.018
Beasley, D. A. E., Bonisoli-Alquati, A., and Mousseau, T. A. (2013). The use of fluctuating asymmetry as a measure of environmentally induced developmental instability: a meta-analysis. Ecol. Indic. 30, 218–226. doi: 10.1016/j.ecolind.2013.02.024
Beurton, P. J., Falk, R., and Rheinberger, H.-J. (eds.). (2000). The Concept of the Gene in Development and Evolution: Historical and Epistemological Perspectives. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511527296
Böhmer, C., Rauhut, O. W. M., and Wörheide, G. (2015). Correlation between Hox code and vertebral morphology in archosaurs. Proc. R. Soc. Lond. B Biol. Sci. 282:20150077. doi: 10.1098/rspb.2015.0077
Bradshaw, A. D. (1965). Evolutionary significance of phenotypic plasticity in plants. Adv. Genet. 13, 115–155. doi: 10.1016/S0065-2660(08)60048-6
Breno, M., Leirs, H., and Van Dongen, S. (2011). No relationship between canalization and developmental stability of the skull in a natural population of Mastomys natalensis (Rodentia: Muridae). Biol. J. Linn. Soc. 104, 207–216. doi: 10.1111/j.1095-8312.2011.01702.x
Breuker, C. J., Patterson, J. S., and Klingenberg, C. P. (2006). A single basis for developmental buffering of Drosophila wing shape. PLoS ONE 1:e7. doi: 10.1371/journal.pone.0000007
Bruner, E., and Bartolino, V. (2008). Morphological variation in the seahorse vertebral system. Int. J. Morphol. 26, 247–262. doi: 10.4067/S0717-95022008000200002
Chitwood, D. H., Headland, L. R., Ranjan, A., Martinez, C. C., Braybrook, S. A., Koenig, D. P., et al. (2012). Leaf asymmetry as a developmental constraint imposed by auxin-dependent phyllotactic patterning. Plant Cell 24, 2318–2327. doi: 10.1105/tpc.112.098798
Chitwood, D. H., Klein, L. L., O'Hanlon, R., Chacko, S., Greg, M., Kitchen, C., et al. (2016). Latent developmental and evolutionary shapes embedded within the grapevine leaf. N. Phytol. 210, 343–355. doi: 10.1111/nph.13754
Chitwood, D. H., Ranjan, A., Kumar, R., Ichihashi, Y., Zumstein, K., Headland, L. R., et al. (2014). Resolving distinct genetic regulators of tomato leaf shape within a heteroblastic and ontogenetic context. Plant Cell 26, 3616–3629. doi: 10.1105/tpc.114.130112
Debat, V., Alibert, P., David, P., Paradis, E., and Auffray, J.-C. (2000). Independence between developmental stability and canalization in the skull of the house mouse. Proc. R. Soc. Lond. B Biol. Sci. 267, 423–430. doi: 10.1098/rspb.2000.1017
Debat, V., Bloyer, S., Faradji, F., Gidaszewski, N., Navarro, N., Orozco-terWengel, P., et al. (2011). Developmental stability: a major role for Cyclin G in Drosophila melanogaster. PLoS Genet. 7:e1002314. doi: 10.1371/journal.pgen.1002314
Debat, V., and David, P. (2001). Mapping phenotypes: canalization, plasticity and developmental stability. Trends Ecol. Evol. 16, 555–561. doi: 10.1016/S0169-5347(01)02266-2
Debat, V., Milton, C. C., Rutherford, S., Klingenberg, C. P., and Hoffmann, A. A. (2006). Hsp90 and the quantitative variation of wing shape in Drosophila melanogaster. Evolution 60, 2529–2538. doi: 10.1111/j.0014-3820.2006.tb01887.x
Dworkin, I. (2005a). “Canalization, cryptic variation, and developmental buffering: a critical examination and analytical perspective,” in Variation: A Central Concept in Biology, eds B. Hallgrímsson and B. K. Hall (Burlington, MA: Elsevier Academic Press), 131–158.
Dworkin, I. (2005b). A study of canalization and developmental stability in the sternopleural bristle system of Drosophila melanogaster. Evolution 59, 1500–1509. doi: 10.1111/j.0014-3820.2005.tb01799.x
Eldar, A., Dorfman, R., Weiss, D., Ashe, H., Shilo, B.-Z., and Barkai, N. (2002). Robustness of the BMP morphogen gradient in Drosophila embryonic patterning. Nature 419, 304–308. doi: 10.1038/nature01061
Elowitz, M. B., Levine, A. J., Siggia, E. D., and Swain, P. S. (2002). Stochastic gene expression in a single cell. Science 297, 1183–1186. doi: 10.1126/science.1070919
Falconer, D. S., and Mackay, T. F. C. (1996). Introduction to Quantitative Genetics. Essex: Longman.
Félix, M.-A., and Barkoulas, M. (2015). Pervasive robustnes in biological systems. Nat. Rev. Genet. 16, 483–496. doi: 10.1038/nrg3949
Gilchrist, M. A., and Nijhout, H. F. (2001). Nonlinear developmental processes as sources of dominance. Genetics 159, 423–432.
Green, R. M., Fish, J. L., Young, N. M., Smith, F. J., Roberts, B., Dolan, K., et al. (2017). Developmental nonlinearity drives phenotypic robustness. Nat. Commun. 8:1970. doi: 10.1038/s41467-017-02037-7
Hallgrimsson, B., Green, R. M., Katz, D. C., Fish, J. L., Bernier, F. P., Roseman, C. C., et al. (2018). The developmental-genetics of canalization. Sem. Cell Dev. Biol. doi: 10.1016/j.semcdb.2018.05.019. [Epub ahead of print].
Hallgrímsson, B., Willmore, K., and Hall, B. K. (2002). Canalization, developmental stability, and morphological integration in primate limbs. Yearb. Phys. Anthropol. 45, 131–158. doi: 10.1002/ajpa.10182
Herrera, C. M. (2009). Multiplicity in Unity: Plant Subindividual Variation and Interactions With Animals. Chicago, IL: University of Chicago Press. doi: 10.7208/chicago/9780226327952.001.0001
Hoffmann, A. A., and Woods, R. E. (2003). “Associating environmental stress with developmental stability: problems and patterns,” in Developmental Instability: Causes and Consequences, ed M. Polak (New York, NY: Oxford University Press), 387–401.
Ivanović, A., and Kalezić, M. L. (2010). Testing the hypothesis of morphological integration on a skull of a vertebrate with a biphasic life cycle: a case study of the alpine newt. J. Exp. Zool. B Mol. Dev. Evol. 314, 527–538. doi: 10.1002/jez.b.21358
Jones, C. S. (1993). Heterochrony and heteroblastic leaf development in two subspecies of Cucurbita argyrosperma (Cucurbitaceae). Am. J. Bot. 80, 778–795. doi: 10.1002/j.1537-2197.1993.tb15294.x
Klingenberg, C. P. (2003a). “Developmental instability as a research tool: using patterns of fluctuating asymmetry to infer the developmental origins of morphological integration,” in Developmental Instability: Causes and Consequences, ed M. Polak (New York, NY: Oxford University Press), 427–442.
Klingenberg, C. P. (2003b). “A developmental perspective on developmental instability: theory, models and mechanisms,” in Developmental Instability: Causes and Consequences, ed M. Polak (New York, NY: Oxford University Press), 14–34.
Klingenberg, C. P. (2004). “Dominance, nonlinear developmental mapping and developmental stability,” in The Biology of Genetic Dominance, ed R. A. Veitia (Austin, TX: Landes Bioscience), 37–51.
Klingenberg, C. P. (2015). Analyzing fluctuating asymmetry with geometric morphometrics: concepts, methods, and applications. Symmetry 7, 843–934. doi: 10.3390/sym7020843
Klingenberg, C. P., Badyaev, A. V., Sowry, S. M., and Beckwith, N. J. (2001). Inferring developmental modularity from morphological integration: analysis of individual variation and asymmetry in bumblebee wings. Am. Nat. 157, 11–23. doi: 10.1086/317002
Klingenberg, C. P., Barluenga, M., and Meyer, A. (2002). Shape analysis of symmetric structures: quantifying variation among individuals and asymmetry. Evolution 56, 1909–1920. doi: 10.1111/j.0014-3820.2002.tb00117.x
Klingenberg, C. P., Debat, V., and Roff, D. A. (2010). Quantitative genetics of shape in cricket wings: developmental integration in a functional structure. Evolution 64, 2935–2951. doi: 10.1111/j.1558-5646.2010.01030.x
Klingenberg, C. P., Duttke, S., Whelan, S., and Kim, M. (2012). Developmental plasticity, morphological variation and evolvability: a multilevel analysis of morphometric integration in the shape of compound leaves. J. Evol. Biol. 25, 115–129. doi: 10.1111/j.1420-9101.2011.02410.x
Klingenberg, C. P., McIntyre, G. S., and Zaklan, S. D. (1998). Left-right asymmetry of fly wings and the evolution of body axes. Proc. R. Soc. Lond. B Biol. Sci. 265, 1255–1259. doi: 10.1098/rspb.1998.0427
Klingenberg, C. P., and Nijhout, H. F. (1999). Genetics of fluctuating asymmetry: a developmental model of developmental instability. Evolution 53, 358–375. doi: 10.1111/j.1558-5646.1999.tb03772.x
Lazić, M., Carretero, M. A., Crnobrnja-Isailović, J., and Kaliontzopoulou, A. (2015). Effects of environmental disturbance on phenotypic variation: an integrated assessment of canalization, developmental stability, modularity, and allometry in lizard head shape. Am. Nat. 185, 44–58. doi: 10.1086/679011
Leamy, L. J. (2003). “Dominance, epistasis, and fluctuating asymmetry,” in Developmental Instability: Causes and Consequences, ed M. Polak (New York, NY: Oxford University Press), 142–156.
Leamy, L. J., and Klingenberg, C. P. (2005). The genetics and evolution of fluctuating asymmetry. Annu. Rev. Ecol. Evol. Syst. 36, 1–21. doi: 10.1146/annurev.ecolsys.36.102003.152640
Leamy, L. J., Klingenberg, C. P., Sherratt, E., Wolf, J. B., and Cheverud, J. M. (2015). The genetic architecture of fluctuating asymmetry of mandible size and shape in a population of mice: another look. Symmetry 7, 146–163. doi: 10.3390/sym7010146
Leamy, L. J., Routman, E. J., and Cheverud, J. M. (2002). An epistatic genetic basis for fluctuating asymmetry of mandible size in mice. Evolution 56, 642–653. doi: 10.1111/j.0014-3820.2002.tb01373.x
Lens, L., Van Dongen, S., Kark, S., and Matthysen, E. (2002). Fluctuating asymmetry as an indicator of fitness: can we bridge the gap between studies? Biol. Rev. 77, 27–38. doi: 10.1017/S1464793101005796
Lewontin, R. C. (2000). The Triple Helix: Gene, Organism, and Environment. Cambridge, MA: Harvard University Press.
Lynch, M., and Walsh, B. (1998). Genetics and Analysis of Quantitative Traits. Sunderland, MA: Sinauer.
McAdams, H. H., and Arkin, A. (1997). Stochastic mechanisms in gene expression. Proc. Natl. Acad. Sci. U.S.A. 94, 814–819. doi: 10.1073/pnas.94.3.814
Milton, C. C., Huynh, B., Batterham, P., Rutherford, S. L., and Hoffmann, A. A. (2003). Quantitative trait symmetry independent of Hsp90 buffering: distinct modes of genetic canalization and developmental stability. Proc. Natl. Acad. Sci. U.S.A. 100, 13396–13401. doi: 10.1073/pnas.1835613100
Moczek, A. P., Sultan, S., Foster, S., Ledón-Rettig, C., Dworkin, I., Nijhout, H. F., et al. (2011). The role of developmental plasticity in evolutionary innovation. Proc. R. Soc. Lond. B Biol. Sci. 278, 2705–2713. doi: 10.1098/rspb.2011.0971
Møller, A. P. (1997). Developmental stability and fitness: a review. Am. Nat. 149, 916–932. doi: 10.1086/286030
Møller, A. P., and Swaddle, J. P. (1997). Asymmetry, Developmental Stability, and Evolution. Oxford: Oxford University Press.
Nijhout, H. F. (2002). The nature of robustness in development. Bioessays 24, 553–563. doi: 10.1002/bies.10093
Nijhout, H. F., and Davidowitz, G. (2003). “Developmental perspectives on phenotypic variation, canalization, and fluctuating asymmetry,” in Developmental Instability: Causes and Consequences, ed M. Polak. (New York, NY: Oxford University Press), 3–13.
Nijhout, H. F., and Paulsen, S. M. (1997). Developmental models and polygenic characters. Am. Nat. 149, 394–405. doi: 10.1086/285996
Palmer, A. R. (1994). “Fluctuating asymmetry analyses: a primer,” in Developmental Instability: Its Origins and Implications, ed T. A. Markow (Dordrecht: Kluwer), 335–364.
Palmer, A. R., and Strobeck, C. (1986). Fluctuating asymmetry: measurement, analysis, patterns. Annu. Rev. Ecol. Syst. 17, 391–421. doi: 10.1146/annurev.es.17.110186.002135
Palmer, A. R., and Strobeck, C. (2003). “Fluctuating asymmetry analyses revisited,” in Developmental Instability: Causes and Consequences, ed. M. Polak (New York, NY: Oxford University Press), 279–319.
Papadopoulos, D. K., Skouloudaki, K., Engström, Y., Terenius, L., Rigler, R., Zechner, C., et al. (2019). Control of Hox transcription factor concentration and cell-to-cell variability by an auto-regulatory switch. Development 146:dev168179. doi: 10.1242/dev.168179
Parsons, P. A. (1990). Fluctuating asymmetry: an epigenetic measure of stress. Biol. Rev. 65, 131–145. doi: 10.1111/j.1469-185X.1990.tb01186.x
Polak, M. (2003). Developmental Instability: Causes and Consequences. New York, NY: Oxford University Press.
Queitsch, C., Sangster, T. A., and Lindquist, S. (2002). Hsp90 as a capacitor of phenotypic variation. Nature 417, 618–624. doi: 10.1038/nature749
Rutherford, S. L., and Lindquist, S. (1998). Hsp90 as a capacitor for morphological evolution. Nature 396, 336–342. doi: 10.1038/24550
Saltz, J. B., Bell, A. M., Flint, J., Gomulkiewicz, R., Hughes, K. A., and Keagy, J. (2018). Why does the magnitude of genotype-by-environment interaction vary? Ecol. Evol. 8, 6342–6353. doi: 10.1002/ece3.4128
Santos, M., Iriarte, P. F., and Céspedes, W. (2005). Genetics and geometry of canalization and developmental stability in Drosophila subobscura. BMC Evol. Biol. 5:7. doi: 10.1186/1471-2148-5-7
Savriama, Y., Gerber, S., Baiocco, M., Debat, V., and Fusco, G. (2017). Development and evolution of segmentation assessed by geometric morphometrics: the centipede Strigamia maritima as a case study. Arthropod Struct. Dev. 46, 419–428. doi: 10.1016/j.asd.2017.03.002
Savriama, Y., Gómez, J. M., Perfectti, F., and Klingenberg, C. P. (2012). Geometric morphometrics of corolla shape: dissecting components of symmetric and asymmetric variation in Erysimum mediohispanicum (Brassicaceae). N. Phytol. 196, 945–954. doi: 10.1111/j.1469-8137.2012.04312.x
Savriama, Y., Vitulo, M., Gerber, S., Debat, V., and Fusco, G. (2016). Modularity and developmental stability in segmented animals: variation in translational asymmetry in geophilomorph centipedes. Dev. Genes Evol. 226, 187–196. doi: 10.1007/s00427-016-0538-3
Takahashi, K. H. (2018). Multiple modes of canalization: Links between genetic, environmental canalizations and developmental stability, and their trait-specificity. Sem. Cell Dev. Biol. doi: 10.1016/j.semcdb.2018.05.018. [Epub ahead of print].
Takahashi, K. H., Okada, Y., Teramura, K., and Tsujino, M. (2011). Deficiency mapping of the genomic regions associated with effects on developmental stability in Drosophila melanogaster. Evolution 65, 3565–3577. doi: 10.1111/j.1558-5646.2011.01400.x
Takahashi, K. H., Rako, L., Takano-Shimizu, T., Hoffmann, A. A., and Lee, S. F. (2010). Effects of small Hsp genes on developmental stability and microenvironmental canalization. BMC Evol. Biol. 10:284. doi: 10.1186/1471-2148-10-284
Tucić, B., Budečević, S., Manitašević Jovanović, S., Vuleta, A., and Klingenberg, C. P. (2018). Phenotypic plasticity in response to environmental heterogeneity contributes to fluctuating asymmetry in plants: first empirical evidence. J. Evol. Biol. 31, 197–210. doi: 10.1111/jeb.13207
Van Dongen, S. (2006). Fluctuating asymmetry and developmental instability in evolutionary biology: past, present and future. J. Evol. Biol. 19, 1727–1743. doi: 10.1111/j.1420-9101.2006.01175.x
Varón-González, C., and Navarro, N. (2018). Epistasis regulates the developmental stability of the mouse craniofacial shape. Heredity doi: 10.1038/s41437-018-0140-8. [Epub ahead of print].
Via, S., and Lande, R. (1985). Genotype-environment interaction and the evolution of phenotypic plasticity. Evolution 39, 505–522. doi: 10.1111/j.1558-5646.1985.tb00391.x
von Dassow, G., Meir, E., Munro, E. M., and Odell, G. M. (2000). The segment polarity network is a robust developmental module. Nature 406, 188–192. doi: 10.1038/35018085
Waddington, C. H. (1942). Canalization of development and the inheritance of acquired characters. Nature 150, 563–565. doi: 10.1038/150563a0
Wang, Y., Ni, T., Wang, W., and Liu, F. (2018). Gene transcription in bursting: a unified mode for realizing accuracy and stochasticity. Biol. Rev. 94, 248–258. doi: 10.1111/brv.12452
Webster, M., and Zelditch, M. L. (2011). Evolutionary lability of integration in Cambrian ptychoparioid trilobites. Evol. Biol. 38, 144–162. doi: 10.1007/s11692-011-9110-2
West-Eberhard, M. J. (2003). Developmental Plasticity and Evolution. New York, NY: Oxford University Press.
Whitlock, M. (1998). The repeatability of fluctuating asymmetry: a revision and extension. Proc. R. Soc. Lond. B Biol. Sci. 265, 1429–1431. doi: 10.1098/rspb.1998.0453
Willmore, K. E., Klingenberg, C. P., and Hallgrímsson, B. (2005). The relationship between fluctuating asymmetry and environmental variance in rhesus macaque skulls. Evolution 59, 898–909. doi: 10.1111/j.0014-3820.2005.tb01763.x
Wu, R. L. (1997). Genetic control of macro- and microevnvironmental sensitivities in Populus. Theor. Appl. Genet. 94, 104–114. doi: 10.1007/s001220050388
Keywords: canalization, developmental buffering, developmental instability, dominance, fluctuating asymmetry, non-linear developmental models, phenotypic plasticity, reaction norm
Citation: Klingenberg CP (2019) Phenotypic Plasticity, Developmental Instability, and Robustness: The Concepts and How They Are Connected. Front. Ecol. Evol. 7:56. doi: 10.3389/fevo.2019.00056
Received: 28 September 2018; Accepted: 15 February 2019;
Published: 07 March 2019.
Edited by:
Alexander William Shingleton, University of Illinois at Chicago, United StatesReviewed by:
Christian Braendle, Centre National de la Recherche Scientifique (CNRS), FrancePedro Martinez, University of Barcelona, Spain
Copyright © 2019 Klingenberg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Christian Peter Klingenberg, Y3BrQG1hbmNoZXN0ZXIuYWMudWs=
 Christian Peter Klingenberg
Christian Peter Klingenberg