Eco-Evolutionary Origins of Diverse Abundance, Biomass, and Trophic Structures in Food Webs

Organismal traits and their evolution can strongly influence food web structure and dynamics. To what extent the evolution of such traits impacts food web structure, however, is poorly understood. Here, we investigate a simple three-species omnivory food web module where the attack rates of all predators evolve as ecological dynamics unfold, such that predator trophic levels are themselves dynamic. We assume a timescale where other vital rates that govern population dynamics are constant and incorporate a well-known tradeoff between attack rates and the conversion of prey into predator biomass. We show that this eco-evolutionary model yields a surprisingly rich array of dynamics. Moreover, even small amounts of selection lead to important differences in the abundance, trophic, and biomass structure of the food web. Systems in which intermediate predators are strongly constrained by tradeoffs lead to hourglass-shaped food webs, where basal resources and top predators have large abundances, but intermediate predators are rare, like those observed in some marine ecosystems. Such food webs are also characterized by a relatively low maximum trophic level. Systems in which intermediate predators have weaker tradeoffs lead to pyramid-shaped food webs, where basal resources are more abundant than intermediate and top predators, such as those observed in some terrestrial system. These food webs also supported a relatively higher maximum trophic level. Overall, our results suggest that eco-evolutionary dynamics can strongly influence the abundance-, trophic-, and biomass-structure of food webs, even in the presence of small levels of selection, thus stressing the importance of taking traits and trait evolution into account to further understand community-level patterns and processes.

Introduction

Food webs often share structural similarities across ecosystems, such as the relationship between the number of species and the number of feeding interactions (Martinez, 1992; Williams and Martinez, 2004; Gravel et al., 2013), the existence of an upper limit to the number of trophic levels (Pimm et al., 1991; Williams and Martinez, 2004), and the prevalence of highly repeated structural modules (McCann et al., 1998; Milo et al., 2002; Williams et al., 2002; Paulau et al., 2015). Surprisingly, these characteristics are relatively conserved over both space and time (Lafferty et al., 2008; Dunne et al., 2014; Yeakel et al., 2014), although some of these structural patterns might have simple statistical underpinnings (Williams, 2010). Understanding the factors that determine these structural similarities, despite large differences in the identity of species and environments that give rise to these food webs has long been a central issue in ecology (May, 1973; Cohen and Newman, 1985; Pimm, 1991; Dunne, 2006; Dunne et al., 2008; Lafferty et al., 2008; McCann, 2011; Allesina and Tang, 2012; Gravel et al., 2013, 2016).

Multiple biotic and abiotic factors have been shown to influence food web structure. For example, the transfer of energy and matter across trophic levels is highly inefficient, which limits the number of trophic levels (Schoener, 1989; Arim et al., 2016). The quality of energy also changes across trophic levels: arthropods are richer in protein than in lipids as their trophic level increases (Wilder et al., 2013) which is why adaptive foraging (Kratina et al., 2012) and/or prey switching (Abrams and Matsuda, 2004) can lead to omnivory in food webs (Thompson et al., 2007). In addition, environmental variables often determine food web structure. For example, temperature may decrease the number of trophic levels (Petchey et al., 1999; Brose et al., 2012), influence the biomass distribution and body-size structure of food webs (Yvon-Durocher et al., 2011; Gibert and DeLong, 2014; Binzer et al., 2016), and alter the energetic structure and function of soil food webs (Schwarz et al., 2017) as well as the number of interactions between species in mountain communities (Lurgi et al., 2012).

Phenotypic traits, such as body size, have long been known to play an important role in determining food web structure through gape limitation in aquatic food webs (Arim et al., 2010, 2016) and thus, predator-prey interactions (Vucic-Pestic et al., 2010; DeLong and Vasseur, 2012; Schneider et al., 2012; Kalinkat et al., 2013; DeLong et al., 2014). In fact, larger body sizes often result in consumers that feed at higher trophic levels (Riede et al., 2011), thus playing a central role in determining food web trophic structure (Petchey et al., 2008; Iles and Novak, 2016; Barneche and Allen, 2018). The effect of traits other than body size, however, has long been overlooked, despite evidence that such traits can impact both vulnerability to predation (Black and Dodson, 1990; Hammill et al., 2010; Yin et al., 2011), as well as foraging rates (Gibert et al., 2017). Trait variation has been shown to strongly influence predator-prey dynamics (Bolnick et al., 2011; Schreiber et al., 2011; Vasseur et al., 2011; Gibert and Brassil, 2014; Gibert and DeLong, 2015; Gibert et al., 2015), which could in turn impact food web structure and dynamics. For example, genetic variation on host plants determines which herbivores feed on them (Barbour et al., 2016) through trait matching (Dehling et al., 2016), which determines food web structure from the bottom up. Phenotypic variation in predator traits, on the other hand, increases predator connectivity and reduces trophic level (Gibert and DeLong, 2017), which structures food webs from the top down. Together, these results suggest that evolutionary changes in traits controlling predator-prey interactions can have important but poorly understood impacts on food web structure and dynamics.

Indeed, ecological and evolutionary processes are increasingly recognized to operate at largely overlapping timescales (Thompson, 1998; Yoshida et al., 2003; Hairston et al., 2005; Jones et al., 2009; Cortez and Ellner, 2010; Vasseur et al., 2011; DeLong and Gibert, 2016; DeLong et al., 2016; Yeakel et al., 2018a), and the combined effects of these eco-evolutionary dynamics may have a large influence on food web structure (Allhoff et al., 2015). Given that genotypes and phenotypes as well as genetic and phenotypic variation, can all influence patterns of species interactions, evolutionary change occurring on ecological time-scales has the potential to impact ecological dynamics within food webs, thus leading to changes in abundances across trophic levels, which we refer to as abundance structure. Considering that biomass is the product of a species average mass and its abundance, changes in food web abundance structure may also lead to changes in the distribution of biomass across the food web, which we refer to as biomass structure. Last, because trophic levels also change as ecological dynamics unfold (Gibert and DeLong, 2017), how such changes in abundance and biomass structure impact the distribution of trophic levels throughout the food web, which we refer to as trophic structure, is largely unknown.

Here we assess the effects that low levels of evolutionary change in traits controlling predator-prey interactions can have on the abundance, biomass, and trophic structure of a simple food web. To do so, we investigate the steady state behavior of the omnivory trophic module (a resource, an intermediate consumer that eats the resource, and a top predator that eats both; Figure 1A) where the abundances and the parameters controlling each predator-prey interaction are subject to selection, and thus, change over time. We show that even small amounts of evolutionary change can lead to important differences in abundance and biomass structure, as well as maximum trophic level, underlining the potential importance of eco-evolutionary dynamics in shaping the structure of food webs.

FIGURE 1

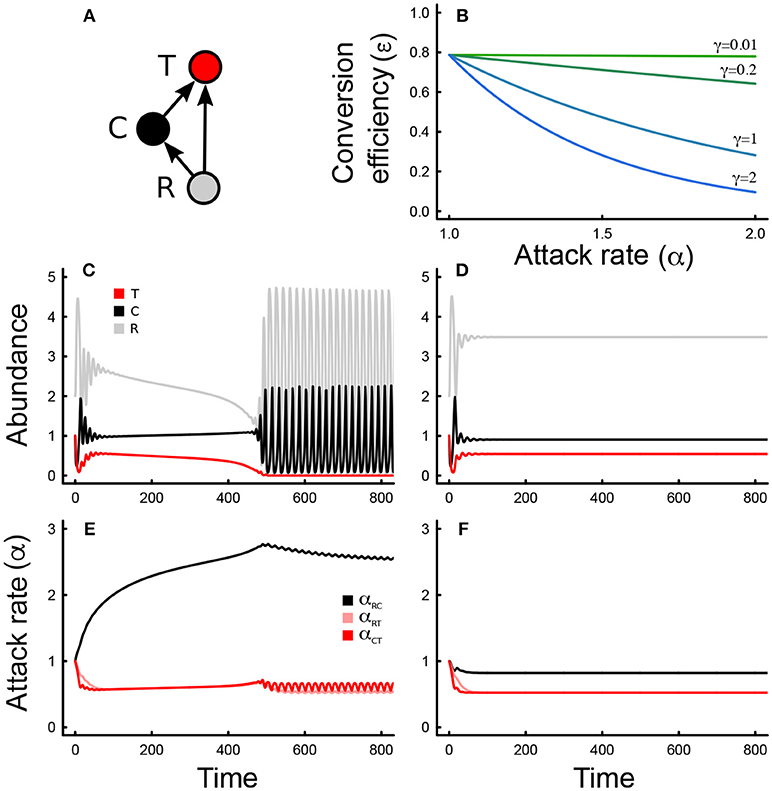
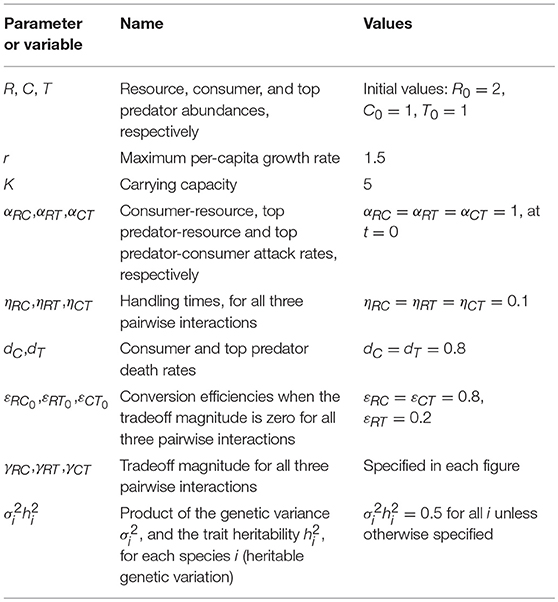
Figure 1. (A) Depiction of the omnivory food web module, where T is the top predator (red), C is the intermediate consumer (black), and R is the basal resource (gray). Colors are consistent across all figures. (B) Tradeoff between conversion efficiency (ε) and attack rate (α) for different levels of the tradeoff magnitude (γ). (C) Changes in abundance over time for all three species, and all evolving attack rates (E), for a low consumer tradeoff (γ_RC = 0.01). (D,F) Same as in (C,E) but for a large consumer tradeoff (γ_RC = 2). Parameter values in Table 1.

TABLE 1

Table 1. Model parameters and variables descriptions and values.

Methods

The Model

We model the eco-evolutionary dynamics of a three species omnivory module (Figure 1A) as it is the simplest system where the trophic level of the top predator can change over time. The underlying ecological model tracks the abundances of the top predator (T), the intermediate consumer (C), and the basal resource (R). We assume that all predator-prey interactions are controlled by a type-II functional response, determined by the attack rate (α), and the handling time (η) of the predator. Resources grow logistically, hence experience density-dependence, and predators die at constant per-capita rates (d_C and d_T). Together, our ecological dynamics are defined by the following system of differential equations:

$\begin{array}{llll}\frac{dR}{dt}& =& rR\left(1-\frac{R}{K}\right)-\frac{{\alpha }_{RC}RC}{1+{\alpha }_{RC}{\eta }_{RC}R}-\frac{{\alpha }_{RT}RT}{1+{\alpha }_{RT}{\eta }_{RT}R}& (1)\end{array}$

$\begin{array}{llll}\frac{dC}{dt}& =& {\epsilon }_{RC}\frac{{\alpha }_{RC}RC}{1+{\alpha }_{RC}{\eta }_{RC}R}-\frac{{\alpha }_{CT}CT}{1+{\alpha }_{CT}{\eta }_{CT}C}-d_{C}C& (2)\end{array}$

$\begin{array}{llll}\frac{dT}{dt}& =& {\epsilon }_{RT}\frac{{\alpha }_{RT}RT}{1+{\alpha }_{RT}{\eta }_{RT}R}+{\epsilon }_{CT}\frac{{\alpha }_{CT}CT}{1+{\alpha }_{CT}{\eta }_{CT}C}-d_{T}T,& (3)\end{array}$

were K is the carrying capacity of the resource, r is the maximal per-capita growth rate of the resource, ε_RC is the efficiency of resource biomass conversion into consumer biomass, ε_RT is the efficiency of resource conversion into top predator biomass, and ε_CT is the efficiency of consumer biomass conversion into top predator biomass.

To model the evolutionary component of the full eco-evolutionary omnivory module, we assume that only the traits controlling the attack rates of both predators can evolve over time. If large changes in important underlying traits, such as body size, were to occur over time, we would expect sweeping changes across all parameters (DeLong et al., 2014; DeLong and Gibert, 2016). Instead, we are implicitly assuming that the timescale is relatively short and selection by the environment is relatively weak such that the other vital rates in the model remain constant. Under these assumptions, we model the evolution of predator attack rates using the standard formulation (Lande, 1976; Kondoh, 2003; Ellner and Becks, 2010; Schreiber et al., 2011), where the rate of evolutionary change of the focal trait (here, the attack rates) is determined by the total amount of heritable genetic variation for that trait (or the product of the genetic variance, σ², with the heritability of the trait, h²), and the adaptive landscape, defined as the rate of change of the per-capita growth rate of the focal predator (i.e., its absolute fitness, $W_i=\frac{1}{N_i}\frac{d{N}_i}{dt}$) with respect to a change in the evolving trait:

$\begin{array}{ll}\frac{d{\alpha }_i}{dt}={\sigma }_i^2{h}_i^2\frac{\partial W_i}{\partial {\alpha }_i}.& (4)\end{array}$

We also assume the existence of a tradeoff between predator conversion efficiencies and attack rates following previous work (Mougi and Iwasa, 2010; Van Velzen and Gaedke, 2017), which leads to reduced conversion efficiencies with increased attack rates (Figure 1B):

$\begin{array}{ll}{\epsilon }_i={\epsilon }_{i_0}{e}^{-{\gamma }_i({\alpha }_0-{\alpha }_i),}& (5)\end{array}$

where ε_i0 is the maximum conversion efficiency, α₀ is the initial attack rate (at t = 0), and γ_i is the strength of the tradeoff. When the strength of the tradeoff, or tradeoff magnitude, is low, the attack rate and conversion efficiency of the consumer are relatively independent; when the tradeoff magnitude is high, low attack rates lead to high conversion efficiencies and vice versa (Figure 1B). The tradeoff magnitude can lead to differences in transient and steady state dynamics in abundance (Figures 1C,D), as well as trait evolution (Figures 1E,F). Different assumptions regarding this tradeoff are possible for different ecological contexts, though a thorough exploration of how these would play out is beyond the scope of the present paper [but see (Gounand et al., 2016) for examples of variation in such assumptions in a different context]. The starting parameter values of the model were chosen to allow species coexistence in the absence of evolution.

Food Web Structure

To address how eco-evolutionary dynamics may affect food web structure, we tracked equilibrium abundances for all three species across different combinations of the tradeoff magnitude associated with the attack rate of the intermediate consumer preying on the basal resource (γ_CR) and that of the tradeoff magnitude associated with the attack rate of the top predator preying on the consumer. The tradeoff magnitude associated with the attack rate of the top predator preying on the basal resource (γ_TR) was kept constant and equal to unity. Thus, we were able to examine how species abundances changed across trophic levels. The model can lead to oscillations in abundance in certain regions of parameter space, in which case we used a geometric mean over time as our measure of average species abundance.

To assess how trophic structure changed over time, we measured the maximum trophic level in the food web module over time, which has been shown to change dynamically with species abundance in the omnivory module (Gibert and DeLong, 2017). Using the standard definition of trophic level, $T{L}_i=1+\sum _{j=1}^n{p}_{ij}T{L}_j$, where TL_i is the trophic level of species i, and p_ij is the fractional contribution of species j to the diet of species i, it is possible to rewrite the p_ij as a function of predator foraging rates. The trophic level of the top predator, T, then becomes:

$\begin{array}{l}T{L}_T=1+\frac{1}{{\epsilon }_{RT}\frac{{\alpha }_{RT}RT}{1+{\alpha }_{RT}{\eta }_{RT}R}+{\epsilon }_{CT}\frac{{\alpha }_{CT}CT}{1+{\alpha }_{CT}{\eta }_{CT}C}}\\ \times \left(T{L}_R{\epsilon }_{RT}\frac{{\alpha }_{RT}RT}{1+{\alpha }_{RT}{\eta }_{RT}R}+T{L}_C{\epsilon }_{CT}\frac{{\alpha }_{CT}CT}{1+{\alpha }_{CT}{\eta }_{CT}C}\right),& (6)\end{array}$

where TL_R = 1 and TL_C = 2. Because the foraging rates are functions of time, the trophic level of the top predator, TL_T (i.e., the maximum trophic level of the omnivory module) will also be a function of time. The trophic level will approach a stable steady state as the abundances approach a stable steady state.

Last, we converted steady state abundances into biomass by multiplying steady state abundances by species body mass. We defined the mass of the basal resource to be equal to 1 unit of mass, and used well-known predator-prey body size scaling relationships (Layman et al., 2005; Brose et al., 2006; Riede et al., 2011) to obtain the mass of the intermediate consumer and that of the top predator. The scaling exponent between prey and predator mass varies widely in nature but has a mean of 1.16 (Brose et al., 2006). We examined three different scaling exponents to observe its influence on equilibrium biomass structure: 0.85, 1.16, and 1.5, while keeping the intercept constant and equal to 1.80 (Brose et al., 2006). These three scenarios impose different constraints on the biomass structure of the food web. A larger scaling exponent means that predators tend to be much larger than their prey compared to a scenario where the exponent is smaller. All analyses were performed in Julia v0.62 (Bezanson et al., 2014) using the DifferentialEquations package (Rackauckas and Nie, 2017). Julia code is available to download from https://github.com/JPGibert/Eco_evo_food_webs

Results

General Dynamics

The eco-evolutionary dynamics of the omnivory food web module are quite sensitive to changes in the tradeoff magnitude that controls the relationship between conversion efficiencies and attack rates when only one attack rate is allowed to evolve at any given time (Figures 1C–F, 2). We find that the tradeoff magnitude associated with the attack rate of the intermediate consumer on the resource mediates coexistence (red arrow, Figure 2A) in the parameter range that was analyzed. When the tradeoff magnitude is small, the consumer attack rate evolves to very large values, which leads to competitive exclusion of the top predator, and unstable consumer-resource dynamics. Intermediate values lead to stable coexistence (Figure 2A), whereas too large of a tradeoff magnitude leads to instability and fluctuations in both abundances and traits (Figure 2A). Steady state attack rates decrease with increasing tradeoff magnitudes throughout, although trait fluctuations are observed only at very large values of the consumer tradeoff magnitude (Figure 2B). Tradeoff magnitudes also impact steady state abundances, with intermediate consumer abundances being larger than top predator consumer abundances for low to moderate values of the tradeoff magnitude, and smaller for larger values (Figure 2A).

FIGURE 2

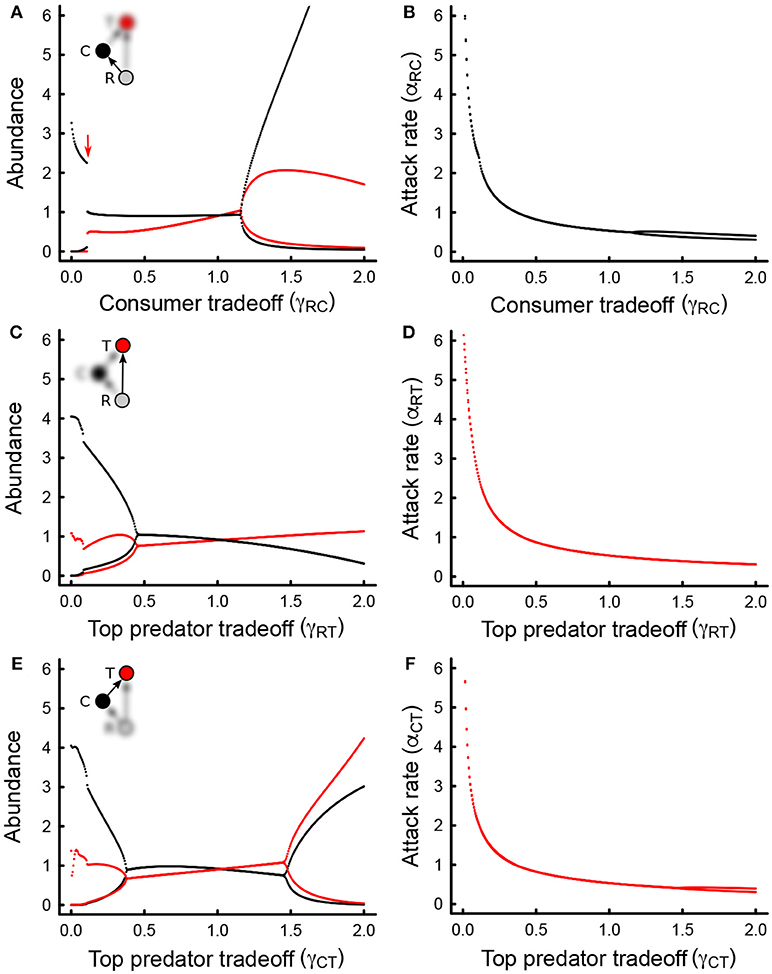
Figure 2. (A) Bifurcation plots (abundance minima and maxima at equilibrium) for the top predator (red) and intermediate consumer (black), across increasing levels of the consumer tradeoff (γ_RC). Only the attack rate between the consumer and the basal resource is allowed to evolve. Oscillatory behavior (instability) occurs whenever maxima and minima are not equal (there are two curves rather than one). The red arrow indicates the tradeoff value below which top predators cannot persist. (B) Same as in (A) but for the consumer attack rate instead of the abundance. (C) As in (A) but for the tradeoff associated with the attack rate between the top predator and the basal resource (γ_RT). (D) As in (B) but for the interaction depicted in (C). (E) As in (A,C), but for the cost associated with the attack rate between the top predator and the intermediate consumer (γ_CT). (F) As in (B,D) but for the interaction depicted in (E). In all cases, only the focal attack rate is allowed to evolve, and all other parameter values are as in Table 1.

These results largely hold for the tradeoff magnitude associated with the other interactions: the tradeoff magnitude of the top predator consuming the resource, and that of the top predator consuming the intermediate consumer (Figures 2C–F). However, neither the tradeoff magnitude of the top predator consuming the basal resource, or the intermediate consumer appear to affect persistence (Figures 2C,E), although both can impact stability: an increase in the tradeoff magnitude of the top predator-resource interaction leads to more stable dynamics (Figure 2C), and an increase in the tradeoff magnitude of the top predator-intermediate consumer interaction first stabilizes the system at lower values, and then destabilizes the system at larger values (Figure 2E). In all cases, steady state attack rates decline as the tradeoff magnitudes increase (Figures 2D,F). An increase in tradeoff magnitudes also leads to larger top predator abundance than intermediate consumer abundance (Figures 2C,E). Together, these results suggest that dynamically rich behaviors emerge from the eco-evolutionary dynamics of omnivory, even when selection is weak.

Impacts on Food Web Structure

Changes in steady state abundances with tradeoff magnitudes result in differences in the abundance structure of the food web (Figure 3A). The omnivory food web module can take on different shapes depending on which species (resource, intermediate consumer, top predator) has higher or lower abundances. Indeed, observed abundance structures in our model range from a top-heavy hour-glass food-web, when the intermediate consumer has a large tradeoff magnitude (Figure 3A, yellow), to a bottom-heavy pyramid when the intermediate consumer has a smaller tradeoff magnitude (Figure 3A, blue, green). When the intermediate consumer has a small to moderate tradeoff magnitude, several scenarios are possible. If the top predator has a smaller tradeoff magnitude, the abundance structure becomes a “bent pyramid”: consumer abundances are more similar to resource abundances than they are to top predator abundances, giving the pyramid a convex curvature (Figure 3A, blue). If the top predator has a moderate tradeoff magnitude, a pyramidal abundance structure is also possible, but consumer abundances are smaller and more similar to top predator abundances than they are to resource abundances, giving the pyramid a concave curvature (Figure 3A, green). Last, if the top-predator has a large tradeoff magnitude, the abundance structure of the food web is diamond-shaped, where intermediate consumers are the most abundant of all species (Figure 3A, orange).

FIGURE 3

Figure 3. (A) Plot of discretized changes in the abundance structure of the omnivory food web module assessed across all combinations of the consumer tradeoff (γ_RC), and the top predator tradeoff (γ_CT). A qualitative depiction of the abundance structure appears in black within each discrete region. (B) Discretized plot of the continuous changes in maximum trophic level (trophic level of the top predator, depicted in red), as the top predator and consumer tradeoffs change. Numbers indicate the trophic level of the top predator at each boundary. Gray areas indicate regions where coexistence is not feasible in (A,B). Parameter values as in Table 1.

Interestingly, all changes in abundance structure are accompanied by changes in the maximum trophic level of the food web: maximum trophic level ranges from low for the hour-glass abundance structure to high for the diamond abundance structure (Figure 3B). In other words, as eco-evolutionary dynamics unfold, hourglass food webs result in top consumers and intermediate consumers with similar trophic levels, and overall greater amounts of omnivory as the top predator relies more heavily on the basal resource (Figure 3B). On the other hand, diamond abundance structures result in top predators with a greater dietary reliance on intermediate consumers than on resources, resulting in a higher trophic level, which in turn leads to a more chain-like food web trophic structure (Figure 3B).

Taking into account three different scaling exponents for the predator-prey mass relationship (Figure 4A), the equilibrium biomass structure of the food web remains qualitatively similar to that of the abundance structure, but with some important quantitative differences (Figures 4B–D). First as the exponent increases such that predators are increasingly larger than their prey, the hourglass biomass structure becomes more prevalent (Figures 4B–D). Second, the size of parameter space that leads to diamond biomass structure appears to be unaffected by an increase in the steepness of the body size relationship, which suggests that other factors influence its occurrence (Figures 4B–D, orange). Third, bent pyramid biomass structures (Figure 4, blue) become more rare as the scaling exponent increases, while concave-pyramid biomass structure (Figure 4, green) becomes more common across the range of parameter values that we consider.

FIGURE 4

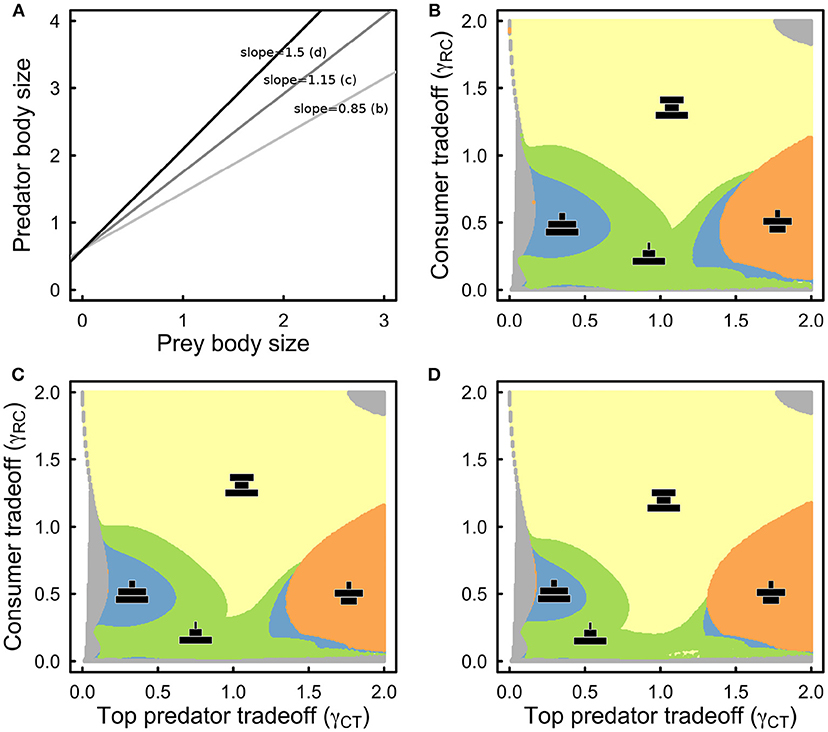
Figure 4. (A) Plot of the assumed predator-prey body-size scalings where only the scaling exponent was allowed to change. The middle line is the average taken across taxa (Brose et al., 2006). (B) Same as in Figure 3A, but with respect to biomass structure and assuming 0.85 as the slope of the predator-prey body size scaling. (C) As in (B) but for a slope of 1.15. (D) As in (B,C) but for a slope of 1.5. Color coding and qualitative biomass depictions (black) as in Figure 3. All other parameter values as in Table 1.

Discussion

The results of our model show that ecological and evolutionary processes can jointly determine food web abundance, trophic, and biomass structure. By modeling a simple tri-trophic system with omnivory, in which the maximum trophic level of the food webs can be accounted for explicitly, we have shown that most types of abundance and biomass food-web structures, namely, pyramid, hourglass, and diamond, can occur as the result of eco-evolutionary dynamics, even when selection is weak. As omnivorous interactions are ubiquitous in nature (Thompson et al., 2007), our theoretical predictions may be relevant for larger and more complex food webs. Together, our findings suggest that the dynamical and evolutionary constraints on food web structure are perhaps much greater than previously thought.

Evolutionary changes in attack rates, as ecological dynamics unfold, can impact species persistence (Figure 2), as well as steady state abundances and their stability (Figures 1, 2). Such impacts are mediated by the tradeoff between conversion efficiency and attack rates. This tradeoff is common in nature (Kiørboe, 2011). Increasing attack rates typically are the consequence of greater velocities for cursorial predators (Aljetlawi, 2004; Pawar et al., 2012). These greater velocities can in turn result in a higher metabolic cost (Carbone et al., 2007), which leads to lower net assimilation rates and, thus, conversion efficiency. Because of this, we posit that larger tradeoff magnitudes would be typically associated with increased metabolic costs and lower conversion efficiencies. We point out that larger tradeoff magnitudes could also be driven by concomitant changes in assimilation rates as attack rates evolve, provided that other physiological traits are also evolving. While we explicitly assume that this does not occur in our framework, we acknowledge that our results could be interpreted from this perspective, and the sensitivity of our model results to differences in the attack rate-conversion efficiency relationship suggests that this may be a fruitful area for additional empirical and theoretical work.

The magnitude of the metabolic costs associated with predation can strongly impact food web richness and stability, emphasizing the important role that this tradeoff plays in trophic interactions. Lower costs typically lead to less speciose, unstable systems (Figure 2A), intermediate costs lead to speciose, stable systems, and large costs lead to speciose, but unstable dynamics (Figure 2). Metabolic costs can in turn scale with phenotypic traits such as body size (Brown et al., 2004; DeLong et al., 2010; Barneche and Allen, 2018; Yeakel et al., 2018b) or depend on external environmental factors such as temperature (Gillooly et al., 2001; Savage et al., 2004). Larger organisms, or organisms that experience elevated temperatures, may thus have increased metabolic costs than do smaller species or species that live in colder climates. Ecosystems where intermediate predators are too small or live in colder climates may thus be less speciose and unstable, as is the case in high-latitude predator-prey systems involving rodents and raptors (Hanski et al., 1991, 1993; Brommer et al., 2010), while speciose but more stable systems may be more common in warmer climates (Ims et al., 2008).

The relationship between metabolic costs and steady state abundances and instability has consequences for different aspects of food web structure, as different abundance, and biomass distributions are possible for different values of the metabolic costs (Figures 2, 3). Indeed, as unstable dynamics typically occur at low and high values of the metabolic costs, we expect food webs occurring in those value ranges to experience fluctuations in predator-prey dynamics. If we further consider that large fluctuations can increase the chance of stochastic extinctions (May, 1973; Chesson, 1981; Fox and Kendall, 2002), then our results suggest that food-web structures that are composed of species with very low or very high metabolic costs may be prone to stochastic extinction. For example, it is possible that diamond food-web structures may be rare in nature, and perhaps more often exist in a transient state, as such structures appear to be associated with very large metabolic costs for the top predator, and hence, large fluctuations in abundance.

Albeit a minimal food web module, our model retains key features of large, complex food webs, such as the occurrence of omnivory and more than two trophic levels, features that are generally not included in models exploring eco-evolutionary dynamics [e.g., (Schreiber et al., 2011; Vasseur et al., 2011; DeLong and Gibert, 2016; Yeakel et al., 2018a)]. Interestingly, such a simple model yields a surprisingly rich array of possible food-web abundance and biomass structures and reveals important differences in the maximum trophic level as a function of metabolic costs. While there is variation in the types of biomass structures observed within different ecosystem types (Hatton et al., 2015), fully inverted or hourglass food webs may be more typical of marine ecosystems (Fath and Killian, 2007; Woodson et al., 2018) but see (Trebilco et al., 2013) for an alternative standpoint), pyramid food webs tend to be terrestrial (Hatton et al., 2015), while diamond food webs may be more common in ponds, lakes or other systems with very abundant intermediate consumers, and less common top predators (Polis, 1999).

Our model offers key insights into how differences in food-web structure across ecosystems may be influenced by the eco-evolutionary dynamics of attack rates and their associated metabolic costs. For example, our results suggest that marine ecosystems (hourglass-structured food webs) should have higher metabolic costs associated with intermediate predators, while top predators should generally have lower costs (Figures 3, 4). This may indeed be true: larger organisms suffer lower energetic penalties when swimming because of reduced drag, while smaller organisms spend more energy to overcome drag (Batchelor, 2000). Our results also suggest that terrestrial ecosystems (pyramid-structured food webs) occur whenever intermediate predators have lower metabolic costs, while top predators can be variable (Figures 3, 4). This prediction also appears to be supported by observations: energy expenditures associated with terrestrial cursorial locomotion scales with body size (Carbone et al., 2007), such that smaller organisms, typically occupying lower trophic levels [e.g., (Riede et al., 2011)], have lower costs than larger, higher trophic, organisms.

While direct empirical tests of these predictions may be challenging, it may be possible to assess the validity of some of these ideas using Daphnia sp. as a top predator. Daphnia can prey upon both meso and micro zooplankton (Wickham, 1998), and as such, can prey upon bacteria as well as their protist consumers. This would lead to an omnivory module with Daphnia as the top predator and omnivore, a bacterivore protist species as the intermediate consumer, and bacteria as the resource. Microcosms can be inoculated with clonal Daphnia, in which evolution is not possible because of the absence of variation, or non-clonal Daphnia, which will allow for eco-evolutionary dynamics to ensue (Fussmann et al., 2003). Over time, it would be possible to assess whether there are differences in abundance or biomass accumulation between the two treatments, and also assess whether parameters of the Daphnia functional response, such as attack rates or handling times, are diverging between the clonal and non-clonal lines. It would then be possible to examine whether changes in metabolic costs could lead to similar abundance and biomass accumulations by running the same experiment at two different temperatures. While these results would not be exactly replicating the assumptions of our toy model, they could shed light on whether eco-evolutionary dynamics can influence food web abundance and biomass structure.

Taking individual-level and trait variation into account has recently been shown to be important to fully understand population and community-level patterns (Bolnick et al., 2011; Violle et al., 2012; Gibert et al., 2015). Indeed, genetic variation in basal resources strongly determines which organisms can prey upon them, thus influencing food web structure from the bottom up (Barbour et al., 2016), while phenotypic variation in predator traits determines species-level connectivity (Gibert and DeLong, 2017), trophic level (Svanbäck et al., 2015; Gibert and DeLong, 2017), and can be used to predict multiple structural features in food webs (Gibert and DeLong, 2017). Our model only follows mean attack rates and disregards how joint changes in mean and variance could potentially influence food web structure through eco-evolutionary dynamics. Because both genetic and phenotypic variation can directly impact food web structure and the pace of evolutionary change, an extension of our initial exploration that includes the dynamics of trait variance as well as that of mean trait values may further illuminate how evolving traits may impact food web structure.

We show that even small amounts of evolutionary change for traits that determine the strength of predator-prey interactions may lead to dramatic differences in food web structure. We therefore anticipate that additional complexity, such as the simultaneous evolution of multiple traits [e.g., through ecological pleiotropic traits (Strauss and Irwin, 2004; DeLong and Gibert, 2016)], a larger number of species with highly heterogeneous interactions such as those observed in empirical food webs, the inclusion of changes in variation as well as mean trait values, as well as a broader exploration of parameter space, will provide additional insight into the fundamental eco-evolutionary drivers of the different types of large-scale structural attributes observed in food webs. As a case in point, differences in the functional form of imposed tradeoffs can lead to quantitative differences in model output in a model that tracks trait selection in food webs (Gounand et al., 2016). Moreover, in a tri-trophic model with explicit life-history stages tracking juvenile and adult biomass, differences in energy transfer leads to differential biomass accumulation across stages, including overcompensation (De Roos et al., 2007). In some cases, biomass accumulation is more likely for juveniles than for adults, and vice versa, which is analogous to our results that show the emergence of different abundance and biomass food web structures.

Despite the inherent simplicity of our approach, we show that an impressively diverse array of food web abundance, biomass, and trophic structures are possible when trait evolution is incorporated into a three-species omnivory model. Changes in metabolic costs (or assimilation rates) mediating trait evolution and energy transfers across species are partly responsible for resulting patterns of abundance and biomass accumulation across trophic levels, which leads to differences in trophic structure and trophic position. Our model reproduces most known types of abundance and biomass structure, i.e., concave and convex pyramidal structures, diamonds, and hourglasses, which suggests that even small levels of evolutionary changes in one trait can have important consequences on these large-scale structural characterizations of food webs.

Author Contributions

JPG conceived the study, JPG and JDY designed the analyses, and JPG implemented the modeling. JPG and JDY analyzed the results and wrote the manuscript.

Funding

JPG was funded by a James S. McDonnell Foundation Postdoctoral Fellowship in Complex Systems. JDY was supported by startup funds from the University of California, Merced.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Uttam Bhat, Ritwika VPS, and Taran Rallings for helpful discussions and comments, and we are indebted to two reviewers for their suggestions on a previous version of this manuscript.

References

Abrams, P. A., and Matsuda, H. (2004). Consequences of behavioral dynamics for the population dynamics of predator-prey systems with switching. Popul. Ecol. 46, 13–25. doi: 10.1007/s10144-003-0168-2

CrossRef Full Text | Google Scholar

Aljetlawi, A. (2004). Prey–predator size-dependent functional response: derivation and rescaling to the real world. J. Anim. Ecol. 73, 239–252. doi: 10.1111/j.0021-8790.2004.00800.x

CrossRef Full Text | Google Scholar

Allesina, S., and Tang, S. (2012). Stability criteria for complex ecosystems. Nature 483, 205–208. doi: 10.1038/nature10832

PubMed Abstract | CrossRef Full Text | Google Scholar

Allhoff, K. T., Ritterskamp, D., Rall, B. C., Drossel, B., and Guill, C. (2015). Evolutionary food web model based on body masses gives realistic networks with permanent species turnover. Sci. Rep. 5:10955. doi: 10.1038/srep10955

PubMed Abstract | CrossRef Full Text | Google Scholar

Arim, M., Abades, S. R., Laufer, G., Loureiro, M., and Marquet, P. A. (2010). Food web structure and body size: trophic position and resource acquisition. Oikos 119, 147–153. doi: 10.1111/j.1600-0706.2009.17768.x

CrossRef Full Text | Google Scholar

Arim, M., Borthagaray, A. I., and Giacomini, H. C. (2016). Energetic constraints to food chain length in a metacommunity framework. Can. J. Fish. Aquat. Sci. 73, 471–476. doi: 10.1139/cjfas-2015-0156

CrossRef Full Text | Google Scholar

Barbour, M. A., Fortuna, M. A., Bascompte, J., Nicholson, J. R., Julkunen-Tiitto, R., Jules, E. S., et al. (2016). Genetic specificity of a plant–insect food web: implications for linking genetic variation to network complexity. Proc. Natl. Acad. Sci. U.S.A. 113, 2128–2133. doi: 10.1073/pnas.1513633113

PubMed Abstract | CrossRef Full Text | Google Scholar

Barneche, D. R., and Allen, A. P. (2018). The energetics of fish growth and how it constrains food-web trophic structure. Ecol. Lett. 21, 836–844. doi: 10.1111/ele.12947

PubMed Abstract | CrossRef Full Text | Google Scholar

Batchelor, G. K. (2000). An Introduction to Fluid Dynamics. Cambridge, UK: Cambridge University Press.

Google Scholar

Bezanson, J., Edelman, A., Karpinski, S., and Shah, V. B. (2014). Julia: a fresh approach to numerical computing. SIAM 59, 65–98. doi: 10.1137/141000671

CrossRef Full Text

Binzer, A., Guill, C., Rall, B. C., and Brose, U. (2016). Interactive effects of warming, eutrophication and size structure: impacts on biodiversity and food-web structure. Glob. Chang. Biol. 22, 220–227. doi: 10.1111/gcb.13086

PubMed Abstract | CrossRef Full Text | Google Scholar

Black, A. R., and Dodson, S. I. (1990). Demographic costs of Chaoborus-induced phenotypic plasticity in Daphnia pulex. Oecologia 83, 117–122. doi: 10.1007/BF00324642

PubMed Abstract | CrossRef Full Text | Google Scholar

Bolnick, D. I., Amarasekare, P., Araújo, M. S., Bürger, R., Levine, J. M., Novak, M., et al. (2011). Why intraspecific trait variation matters in community ecology. Trends Ecol. Evol. 26, 183–192. doi: 10.1016/j.tree.2011.01.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Brommer, J. E., Pietiäinen, H., Ahola, K., Karell, P., Karstinenz, T., and Kolunen, H. (2010). The return of the vole cycle in southern Finland refutes the generality of the loss of cycles through “climatic forcing.” Glob. Chang. Biol. 16, 577–586. doi: 10.1111/j.1365-2486.2009.02012.x

CrossRef Full Text | Google Scholar

Brose, U., Dunne, J. A., Montoya, J. M., Petchey, O. L., Schneider, F. D., and Jacob, U. (2012). Climate change in size-structured ecosystems. Philos. Trans. R. Soc. Lond. B Biol. Sci. 367, 2903–2912. doi: 10.1098/rstb.2012.0232

PubMed Abstract | CrossRef Full Text | Google Scholar

Brose, U., Jonsson, T., Berlow, E. L., Warren, P., Banasek-Richter, C., Bersier, L.-F., et al. (2006). Consumer–resource body-size relationships in natural food webs. Ecology 87, 2411–2417. doi: 10.1890/0012-9658(2006)87[2411:CBRINF]2.0.CO;2

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, J. H., Gillooly, J. F., Allen, A. P., Savage, V. M., and West, G. B. (2004). Toward a metabolic theory of ecology. Ecology 85, 1771–1789. doi: 10.1890/03-9000

CrossRef Full Text | Google Scholar

Carbone, C., Teacher, A., and Rowcliffe, J. M. (2007). The costs of carnivory. PLoS Biol. 5:e22. doi: 10.1371/journal.pbio.0050022

PubMed Abstract | CrossRef Full Text | Google Scholar

Chesson, P. L. (1981). Models for spatially distributed populations: the effect of within-patch variability. Theor. Popul. Biol. 19, 288–325. doi: 10.1016/0040-5809(81)90023-X

CrossRef Full Text | Google Scholar

Cohen, J. E., and Newman, C. M. (1985). A stochastic theory of community food webs I. Models and aggregated data. Proc. R. Soc. B Biol. Sci. 224, 421–448. doi: 10.1098/rspb.1985.0042

CrossRef Full Text | Google Scholar

Cortez, M., and Ellner, S. P. (2010). Understanding rapid evolution in predator-prey interactions using the theory of fast-slow dynamical systems. Am. Nat. 176, E109–E127. doi: 10.1086/656485

PubMed Abstract | CrossRef Full Text | Google Scholar

De Roos, A. M., Schellekens, T., van Kooten, T., van de Wolfshaar, K., Claessen, D., and Persson, L. (2007). Food-dependent growth leads to overcompensation in stage-specific biomass when mortality increases: the influence of maturation versus reproduction regulation. Am. Nat. 170, E59–E76. doi: 10.1086/520119

PubMed Abstract | CrossRef Full Text | Google Scholar

Dehling, D. M., Jordano, P., Schaefer, H. M., Böhning-Gaese, K., and Scheuling, M. (2016). Morphology predicts species' functional roles and their degree of specialisation in plant-frugivore interactions. Proc. R. Soc. B Biol. Sci. 283:20152444. doi: 10.1098/rspb.2015.2444

PubMed Abstract | CrossRef Full Text | Google Scholar

DeLong, J. P., Forbes, V. E., Galic, N., Gibert, J. P., Laport, R. G., Phillips, J. S., et al. (2016). How fast is fast? Eco-evolutionary dynamics and rates of change in populations and phenotypes. Ecol. Evol. 6, 573–581. doi: 10.1002/ece3.1899

PubMed Abstract | CrossRef Full Text | Google Scholar

DeLong, J. P., and Gibert, J. P. (2016). Gillespie eco-evolutionary models (GEMs) reveal the role of heritable trait variation in eco-evolutionary dynamics. Ecol. Evol. 6, 935–945. doi: 10.1002/ece3.1959

PubMed Abstract | CrossRef Full Text | Google Scholar

DeLong, J. P., Hanley, T. C., and Vasseur, D. A. (2014). Predator-prey dynamics and the plasticity of predator body size. Funct. Ecol. 28, 487–493. doi: 10.1111/1365-2435.12199

CrossRef Full Text | Google Scholar

DeLong, J. P., Okie, J. G., Moses, M. E., Sibly, R. M., and Brown, J. H. (2010). Shifts in metabolic scaling, production, and efficiency across major evolutionary transitions of life. Proc. Natl. Acad. Sci. U.S.A. 107, 12941–12945. doi: 10.1073/pnas.1007783107

PubMed Abstract | CrossRef Full Text | Google Scholar

DeLong, J. P., and Vasseur, D. A. (2012). A dynamic explanation of size–density scaling in carnivores. Ecology 93, 470–476. doi: 10.1890/11-1138.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunne, J. A. (2006). “The network structure of food webs,” in Ecological Networks. Linking structure to dynamics in food webs, eds M. Pascual and J. A Dunne (New York, NY: Oxford University Press), 386.

Google Scholar

Dunne, J. A., Labandeira, C. C., and Williams, R. J. (2014). Highly resolved early Eocene food webs show development of modern trophic structure after the end-Cretaceous extinction. Proc. R. Soc. B Biol. Sci. 281:20133280. doi: 10.1098/rspb.2013.3280

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunne, J. A., Williams, R. J., Martinez, N. D., Wood, R. A., and Erwin, D. H. (2008). Compilation and network analyses of cambrian food webs. PLoS Biol. 6:e102. doi: 10.1371/journal.pbio.0060102

PubMed Abstract | CrossRef Full Text | Google Scholar

Ellner, S. P., and Becks, L. (2010). Rapid prey evolution and the dynamics of two-predator food webs. Theor. Ecol. 4, 133–152. doi: 10.1007/s12080-010-0096-7

CrossRef Full Text | Google Scholar

Fath, B. D., and Killian, M. C. (2007). The relevance of ecological pyramids in community assemblages. Ecol. Model. 208, 286–294. doi: 10.1016/j.ecolmodel.2007.06.001

CrossRef Full Text | Google Scholar

Fox, G. A., and Kendall, B. E. (2002). Demographic stochasticity and the variance reduction effect. Ecology 83, 1928–1934. doi: 10.1890/0012-9658(2002)083[1928:DSATVR]2.0.CO;2

CrossRef Full Text | Google Scholar

Fussmann, G. F., Ellner, S. P., and Hairston, N. G. Jr. (2003). Evolution as a critical component of plankton dynamics. Proc. Biol. Sci. 270, 1015–1022. doi: 10.1098/rspb.2003.2335

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibert, J. P., Allen, R. L., Hruska, R. J., and DeLong, J. P. (2017). The ecological consequences of environmentally induced phenotypic changes. Ecol. Lett. 20, 997–1003. doi: 10.1111/ele.12797

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibert, J. P., and Brassil, C. E. (2014). Individual phenotypic variation reduces interaction strengths in a consumer-resource system. Ecol. Evol. 4, 3703–3713. doi: 10.1002/ece3.1212

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibert, J. P., Dell, A. I., DeLong, J. P., and Pawar, S. (2015). Scaling-up trait variation from individuals to ecosystems. Adv. Ecol. Res. 52, 1–17. doi: 10.1016/bs.aecr.2015.03.001

CrossRef Full Text | Google Scholar

Gibert, J. P., and DeLong, J. P. (2014). Temperature alters food web body-size structure. Biol. Lett. 10:20140473. doi: 10.1098/rsbl.2014.0473

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibert, J. P., and DeLong, J. P. (2015). Individual variation decreases interference competition but increases species persistence. Adv. Ecol. Res. 52, 45–64. doi: 10.1016/bs.aecr.2015.01.002

CrossRef Full Text | Google Scholar

Gibert, J. P., and DeLong, J. P. (2017). Phenotypic variation explains food web structural patterns. Proc. Natl. Acad. Sci. U.S.A. 114, 11187–11192. doi: 10.1073/pnas.1703864114

PubMed Abstract | CrossRef Full Text | Google Scholar

Gillooly, J. F., Brown, J. H., West, G. B., Savage, V. M., and Charnov, E. L. (2001). Effects of size and temperature on metabolic rate. Science 293, 2248–2251. doi: 10.1126/science.1061967

PubMed Abstract | CrossRef Full Text | Google Scholar

Gounand, I., Kéfi, S., Mouquet, N., and Gravel, D. (2016). Trait selection during food web assembly: the roles of interactions and temperature. Theor. Ecol. 9, 417–429. doi: 10.1007/s12080-016-0299-7

CrossRef Full Text | Google Scholar

Gravel, D., Massol, F., and Leibold, M. A. (2016). Stability and complexity in model meta-ecosystems. Nat. Commun. 7:12457. doi: 10.1038/ncomms12457

PubMed Abstract | CrossRef Full Text | Google Scholar

Gravel, D., Poisot, T., Albouy, C., Velez, L., and Mouillot, D. (2013). Inferring food web structure from predator-prey body size relationships. Methods Ecol. Evol. 4, 1083–1090. doi: 10.1111/2041-210X.12103

CrossRef Full Text | Google Scholar

Hairston, N. G., Ellner, S. P., Geber, M. A., Yoshida, T., and Fox, J. A. (2005). Rapid evolution and the convergence of ecological and evolutionary time. Ecol. Lett. 8, 1114–1127. doi: 10.1111/j.1461-0248.2005.00812.x

CrossRef Full Text | Google Scholar

Hammill, E., Petchey, O. L., and Anholt, B. R. (2010). Predator functional response changed by induced defenses in prey. Am. Nat. 176, 723–731. doi: 10.1086/657040

PubMed Abstract | CrossRef Full Text | Google Scholar

Hanski, I., Hansson, L., and Henttonen, H. (1991). Specialist predators, generalist predators, and the microtine rodent cycle. J. Anim. Ecol. 60, 353–367. doi: 10.2307/5465

CrossRef Full Text | Google Scholar

Hanski, I., Turchin, P., Korpimäki, E., and Henttonen, H. (1993). Population oscillations of boreal rodents: regulation by mustelid predators leads to chaos. Nature 364, 232–235. doi: 10.1038/364232a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Hatton, I. A., McCann, K. S., Fryxell, J. M., Davies, T. J., Smerlak, M., Sinclair, A. R., et al. (2015). The predator-prey power law: Biomass scaling across terrestrial and aquatic biomes. Science 349:aac6284. doi: 10.1126/science.aac6284

PubMed Abstract | CrossRef Full Text | Google Scholar

Iles, A. C., and Novak, M. (2016). Complexity increases predictability in allometrically constrained food webs. Am. Nat. 188, 87–98. doi: 10.1086/686730

PubMed Abstract | CrossRef Full Text | Google Scholar

Ims, R. A., Henden, J.-A., and Killengreen, S. T. (2008). Collapsing population cycles. Trends Ecol. Evol. 23, 79–86. doi: 10.1016/j.tree.2007.10.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones, L. E., Becks, L., Ellner, S. P., Hairston, N. G. Jr, Yoshida, T., and Fussmann, G. F. (2009). Rapid contemporary evolution and clonal food web dynamics. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 364, 1579–1591. doi: 10.1098/rstb.2009.0004

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalinkat, G., Schneider, F. D., Digel, C., Guill, C., Rall, B. C., and Brose, U. (2013). Body masses, functional responses and predator-prey stability. Ecol. Lett. 16, 1126–1134. doi: 10.1111/ele.12147

PubMed Abstract | CrossRef Full Text | Google Scholar

Kiørboe, T. (2011). How zooplankton feed: mechanisms, traits and trade-offs. Biol. Rev. 86, 311–339. doi: 10.1111/j.1469-185X.2010.00148.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kondoh, M. (2003). Foraging adaptation and the relationship between food-web complexity and stability. Science 299, 1388–1391. doi: 10.1126/science.1079154

PubMed Abstract | CrossRef Full Text | Google Scholar

Kratina, P., LeCraw, R. M., Ingram, T., and Anholt, B. R. (2012). Stability and persistence of food webs with omnivory: is there a general pattern? Ecosphere 3, 1–18. doi: 10.1890/ES12-00121.1

CrossRef Full Text | Google Scholar

Lafferty, K. D., Allesina, S., Arim, M., Briggs, C. J., De Leo, G., Dobson, A. P., et al. (2008). Parasites in food webs: the ultimate missing links. Ecol. Lett. 11, 533–546. doi: 10.1111/j.1461-0248.2008.01174.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lande, R. (1976). Natural selection and random genetic drift in phenotypic evolution. Evolution 30, 314–334.

PubMed Abstract | Google Scholar

Layman, C. A., Winemiller, K. O., Arrington, D. A., and Jepsen, D. B. (2005). Body Size and trophic position in a diverse tropical food web. Ecology 86, 2530–2535. doi: 10.1890/04-1098

CrossRef Full Text | Google Scholar

Lurgi, M., López, B. C., and Montoya, J. M. (2012). Climate change impacts on body size and food web structure on mountain ecosystems. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 367, 3050–3057. doi: 10.1098/rstb.2012.0239

PubMed Abstract | CrossRef Full Text | Google Scholar

Martinez, N. D. (1992). Constant connectance in community food webs. Am. Nat. 139, 1208–1218. doi: 10.1086/285382

CrossRef Full Text | Google Scholar

May, R. M. (1973). Qualitative stability in model ecosystems. Ecology 54, 638–641. doi: 10.2307/1935352

CrossRef Full Text | Google Scholar

McCann, K. S. (2011). Food Webs. Princeton, NJ: Princeton University Press.

Google Scholar

McCann, K. S., Hastings, A., and Huxel, G. R. (1998). Weak trophic interactions and the balance of nature. Nature 395, 794–798. doi: 10.1038/27427

CrossRef Full Text | Google Scholar

Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chklovskii, D., and Alon, U. (2002). Network motifs: simple building blocks of complex networks. Science 298, 824–827. doi: 10.1126/science.298.5594.824

PubMed Abstract | CrossRef Full Text | Google Scholar

Mougi, A., and Iwasa, Y. (2010). Evolution towards oscillation or stability in a predator-prey system. Proc. Biol. Sci. 277, 3163–3171. doi: 10.1098/rspb.2010.0691

CrossRef Full Text | Google Scholar

Paulau, P. V., Feenders, C., and Blasius, B. (2015). Motif analysis in directed ordered networks and applications to food webs. Sci. Rep. 5:11926. doi: 10.1038/srep11926

PubMed Abstract | CrossRef Full Text | Google Scholar

Pawar, S., Dell, A. I., and Savage, V. M. (2012). Dimensionality of consumer search space drives trophic interaction strengths. Nature 486, 485–489. doi: 10.1038/nature11131

PubMed Abstract | CrossRef Full Text | Google Scholar

Petchey, O. L., Beckerman, A. P., Riede, J. O., and Warren, P. H. (2008). Size, foraging, and food web structure. Proc. Natl. Acad. Sci. U.S.A. 105, 4191–4196. doi: 10.1073/pnas.0710672105

PubMed Abstract | CrossRef Full Text | Google Scholar

Petchey, O. L., McPhearson, P. T., Casey, T. M., and Morin, P. J. (1999). Environmental warming alters food-web structure and ecosystem function. Nature 402, 69–72. doi: 10.1038/47023

CrossRef Full Text | Google Scholar

Pimm, S. L. (1991). The Balance of Nature? Ecological Issues in the Conservation of Species and Communities. Chicago, IL: The University of Chicago Press.

Google Scholar

Pimm, S. L., Lawton, J. H., and Cohen, J. E. (1991). Food web patterns and their consequences. Nature 350, 669–674. doi: 10.1038/350669a0

CrossRef Full Text | Google Scholar

Polis, G. A. (1999). Why are parts of the world green? Multiple factors control productivity and the distribution of biomass. Oikos 86, 3. doi: 10.2307/3546565

CrossRef Full Text | Google Scholar

Rackauckas, C., and Nie, Q. (2017). Differential equations.jl – a performant and feature-rich ecosystem for solving differential equations in julia. J. Open Res. Softw. 5:15. doi: 10.5334/jors.151

CrossRef Full Text | Google Scholar

Riede, J. O., Brose, U., Ebenman, B., Jacob, U., Thompson, R., Townsend, C. R., et al. (2011). Stepping in Elton's footprints: a general scaling model for body masses and trophic levels across ecosystems. Ecol. Lett. 14, 169–178. doi: 10.1111/j.1461-0248.2010.01568.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Savage, V. M., Gillooly, J. F., Brown, J. H., and Charnov, E. L. (2004). Effects of body size and temperature on population growth. Am. Nat. 163, 429–441. doi: 10.1086/381872

PubMed Abstract | CrossRef Full Text | Google Scholar

Schneider, F. D., Scheu, S., and Brose, U. (2012). Body mass constraints on feeding rates determine the consequences of predator loss. Ecol. Lett. 15, 436–443. doi: 10.1111/j.1461-0248.2012.01750.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Schoener, T. W. (1989). Food webs from the small to the large. Ecology 70, 1559–1589. doi: 10.2307/1938088

CrossRef Full Text | Google Scholar

Schreiber, S. J., Bürger, R., and Bolnick, D. I. (2011). The community effects of phenotypic and genetic variation within a predator population. Ecology 92, 1582–1593. doi: 10.1890/10-2071.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwarz, B., Barnes, A. D., Thakur, M. P., Brose, U., Ciobanu, M., Reich, P. B., et al. (2017). Warming alters the energetic structure and function but not resilience of soil food webs. Nat. Clim. Chang. 7, 895–900. doi: 10.1038/s41558-017-0002-z

CrossRef Full Text | Google Scholar

Strauss, S., and Irwin, R. (2004). Ecological and evolutionary consequences of multispecies plant-animal interactions. Annu. Rev. Ecol. Evol. Syst. 35, 435–466. doi: 10.1146/annurev.ecolsys.35.112202.130215

CrossRef Full Text | Google Scholar

Svanbäck, R., Quevedo, M., Olsson, J., and Eklöv, P. (2015). Individuals in food webs: the relationships between trophic position, omnivory and among-individual diet variation. Oecologia 178, 103–114. doi: 10.1007/s00442-014-3203-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Thompson, J. N. (1998). Rapid evolution as an ecological process. Trends Ecol. Evol. 13, 329–32.

PubMed Abstract | Google Scholar

Thompson, R. M., Hemberg, M., Starzomski, B. M., and Shurin, J. B. (2007). Trophic levels and trophic tangles: the prevalence of omnivory in real food webs. Ecology 88, 612–617. doi: 10.1890/05-1454

PubMed Abstract | CrossRef Full Text | Google Scholar

Trebilco, R., Baum, J. K., Salomon, A. K., and Dulvy, N. K. (2013). Ecosystem ecology: size-based constraints on the pyramids of life. Trends Ecol. Evol. 28, 423–431. doi: 10.1016/j.tree.2013.03.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Velzen, E., and Gaedke, U. (2017). Disentangling eco-evolutionary dynamics of predator-prey coevolution: the case of antiphase cycles. Sci. Rep. 7:17125. doi: 10.1038/s41598-017-17019-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Vasseur, D. A., Amarasekare, P., Rudolf, V. H., and Levine, J. M. (2011). Eco-Evolutionary dynamics enable coexistence via neighbor-dependent selection. Am. Nat. 178, E96–E109. doi: 10.1086/662161

PubMed Abstract | CrossRef Full Text | Google Scholar

Violle, C., Enquist, B. J., McGill, B. J., Jiang, L., Albert, C. H., Hulshof, C., et al. (2012). The return of the variance: intraspecific variability in community ecology. Trends Ecol. Evol. 27, 244–252. doi: 10.1016/j.tree.2011.11.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Vucic-Pestic, O., Rall, B. C., Kalinkat, G., and Brose, U. (2010). Allometric functional response model: body masses constrain interaction strengths. J. Anim. Ecol. 79, 249–256. doi: 10.1111/j.1365-2656.2009.01622.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Wickham, S. A. (1998). The direct and indirect impact of Daphnia and Cyclops on a freshwater microbial food web. J. Plankton Res. 20, 739–755. doi: 10.1093/plankt/20.4.739

CrossRef Full Text | Google Scholar

Wilder, S. M., Norris, M., Lee, R. W., Raubenheimer, D., and Simpson, S. J. (2013). Arthropod food webs become increasingly lipid-limited at higher trophic levels. Ecol. Lett. 16, 895–902. doi: 10.1111/ele.12116

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, R. J. (2010). Simple MaxEnt models explain food web degree distributions. Theor. Ecol. 3, 45–52. doi: 10.1007/s12080-009-0052-6

CrossRef Full Text | Google Scholar

Williams, R. J., Berlow, E. L., Dunne, J. A., Barabási, A.-L., and Martinez, N. D. (2002). Two degrees of separation in complex food webs. Proc. Natl. Acad. Sci. U.S.A. 99, 12913–12916. doi: 10.1073/pnas.192448799

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, R. J., and Martinez, N. D. (2004). Limits to trophic levels and omnivory in complex food webs: theory and data. Am. Nat. 163, 458–468. doi: 10.1086/381964

PubMed Abstract | CrossRef Full Text | Google Scholar

Woodson, C. B., Schramski, J. R., and Joye, S. B. (2018). A unifying theory for top-heavy ecosystem structure in the ocean. Nat. Commun. 9:23. doi: 10.1038/s41467-017-02450-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeakel, J. D., Gibert, J. P., Gross, T., Westley, P. A. H., and Moore, J. W. (2018a). Eco-evolutionary dynamics, density- dependent dispersal and collective behaviour: implications for salmon metapopulation robustness. Philos. Trans. R. Soc. B Biol. Sci. 373:20170018. doi: 10.1098/rstb.2017.0018

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeakel, J. D., Kempes, C. P., and Redner, S. (2018b). Dynamics of starvation and recovery predict extinction risk and both Damuth's law and Cope's rule. Nat. Commun. 9:657. doi: 10.1038/s41467-018-02822-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeakel, J. D., Pires, M. M., Rudolf, L., Dominy, N. J., Koch, P. L., Guimarães, P. R., et al. (2014). Collapse of an ecological network in Ancient Egypt. Proc. Natl. Acad. Sci. U.S.A. 111, 14472–14477. doi: 10.1073/pnas.1408471111

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, M., Laforsch, C., Lohr, J. N., and Wolinska, J. (2011). Predator-induced defense makes daphnia more vulnerable to parasites. Evolution 65, 1482–1488. doi: 10.1111/j.1558-5646.2011.01240.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoshida, T., Jones, L. E., Ellner, S. P., Fussmann, G. F., and Hairston, N. G. Jr. (2003). Rapid evolution drives ecological dynamics in a predator-prey system. Nature 424, 303–306. doi: 10.1038/nature01767

PubMed Abstract | CrossRef Full Text | Google Scholar

Yvon-Durocher, G., Montoya, J. M., Trimmer, M., and Woodward, G. (2011). Warming alters the size spectrum and shifts the distribution of biomass in freshwater ecosystems. Glob. Chang. Biol. 17, 1681–1694. doi: 10.1111/j.1365-2486.2010.02321.x

CrossRef Full Text | Google Scholar