An Online Experimental Framework for Cooperative Relationships With a Real-Time Decision-Making and Rewarding Environment

This paper investigates interactions between game theoretical strategies and social relationships in real-time decision-making and rewarding environments. We propose an experimental framework based on techniques of web-based multiplayer online games for this purpose. In our framework, multiple human players, represented as particles in a two-dimensional space of social interactions, can modify their positions and game strategies for the prisoner's dilemma in real time, and receive benefit or cost emerging from both game theoretical and social relationships with neighboring players. We report on experiments with human participants in different conditions of the payoff matrix, which reflects game structures, and the speed of each player, which reflects the ability to change her social relationship. We show that cooperative relationships emerge in real human groups regardless of experimental settings, and show their basic behavioral patterns. We further discuss relationships between behavioral characters of participants in the experiments and their psychological characters to see how their personalities can be reflected in their behavior in such a game theoretical framework, and show that a few psychological characters of participants might reflect their behavioral characters at least in part, but there were variations in these relationships between experimental groups.

Introduction

Understanding human behavior in real-time decision-making environments is getting much attention, because such situations are ubiquitous in both real-world activities (e.g., stock markets, team works, school activities) and social networks (e.g., Facebook, Twitter, Instagram). While traditional game theoretical approaches have mainly focused on discrete interactions (e.g., standard repeated games) (Maynard Smith, 1982; Hofbauer and Sigmund, 1998), recent studies have shown human behavior in real-time decision-making environments is different from that in cases with discrete interactions (Friedman and Oprea, 2012; Hawkins and Goldstone, 2016).

Hawkins and Goldstone (2016) conducted a version of two-player and asymmetric coordination game, termed the Battle of the Exes, in both real-time decision-making environments and traditional staged environments. In their environment, players were placed at opposite ends of the two-dimensional virtual world, and allowed to move toward one of the two destinations, each corresponds to the player's decision, with full freedom to change that destination at any time. They reported that players who were allowed to interact continuously within rounds achieved outcomes with greater efficiency and fairness than players who were forced to make simultaneous decisions. Friedman and Oprea (2012) also assumed a case of continuous interactions based on a prisoner's dilemma in which players can switch between cooperation and defection at any point in time and they receive the flow of payoffs that changes in continuous time according to the changes in their strategies. They showed that the proportion of cooperative behavior in this real-time decision-making and rewarding environment was much higher than that in a case with standard discrete and repeated interactions.

It has also been shown that structures of social networks can influence the emergence of cooperative behavior (Nowak and May, 1992; Nowak, 2006; Pinheiro et al., 2012), theoretically. Recent experimental studies with interaction networks of human populations based on repeated games suggested that the population structure can affect the evolution of cooperative behavior as theoretically expected (Rand et al., 2014), or may not affect so significantly than theoretically expected (Grujić et al., 2014) because they might adopt different strategy updating criterions (e.g., moody conditional cooperation Grujić et al., 2014, reinforcement learning Horita et al., 2017) rather than an imitation-based criterion (e.g., imitating the best), which is a common assumption in theoretical models.

In addition, theoretical studies showed that dynamic changes in network structures can affect the global dynamics of human behaviors (Zimmermann and Eguíluz, 2005; Pacheco et al., 2006; Suzuki et al., 2008), and recent experimental studies with human participants have also shown that cooperative clusters can emerge when participants could modify their network structure of interactions (Fehl et al., 2011; Rand et al., 2011; Wang et al., 2012; Antonioni et al., 2014; Yonenoh and Akiyama, 2014). This is because participants tend to keep cooperative relationships while severing connections with defectors, and thus form cooperative and highly connected clusters in general (Rand et al., 2011). Recently, Cuesta et al. (2015) showed the existence of reputation on neighbors (i.e., the history of their actions in the past a few rounds) can facilitate the emergence of cooperative clusters, and Antonioni et al. (2016) further showed there existed two types of participants who are reliable subjects and cheaters when cheating her own reputation with a cost was allowed.

There have also been studies that focused on effects of the mobility of agents on evolution of cooperation in spatial environments. Meloni et al. (2009) showed the intermediate speed of random movement on a continuous 2D space can facilitate the evolution of cooperation Sicardi et al. (2009) also showed that a random movement on a 2D diluted grid in which vacant cells are allowed to exist can affect differently different types of 2-person games. Antonioni et al. (2015) first conducted an experimental study with human participants in such a situation in which each participant can move toward a vacant neighboring cell, and showed that cooperative clusters formed temporally but dissolved due to invasion by defectors. Efferson et al. (2016) also showed that participant can establish cooperative clusters by running away from bad behavior even when they do not know much about the information of potential new neighbors.

However, these previous studies on the evolution of cooperation in dynamically networking or spatially interacting populations assumed discrete interactions between individuals in the sense that relationships between individuals are discrete (i.e., “connected or not” or “neighbor or not”) and their relationships also change in time in a discrete manner while real human relationships could be continuous and can change in continuous time, as described above.

Our purpose is to understand how both game theoretical strategies and social relationships among humans change in real time decision-making and rewarding environments. For this purpose, we are developing an experimental framework based on techniques of web-based multiplayer online games (Kodera et al., 2017).

We use a simple multi-player game that is adapted from Nishimoto et al.'s computational model for investigating dynamically changing social relationships termed social particle swarm (SPS) model (Nishimoto et al., 2013, 2014). See Nishimoto et al. (2013) for details. They assumed that individuals were in a two-dimensional and toroidal plane. This represents a social or psychological space in which the proximity between two individuals reflected their social or psychological closeness. Each particle has a strategy for the prisoner's dilemma (PD) game, and moves according to the force vector generated from the payoffs in the game. The behavior of the particles in each step consists of two sequential processes: First, all particles simultaneously decide whether to select cooperation or defection in the current step in a tit-for-tat fashion based on the proportion of cooperators among its neighboring agents within a fixed range in the previous time step. If this proportion is larger than an attribute value of each individual, termed cooperation threshold, the focal individual cooperates, and otherwise it defects. Second, each individual receives attractive (repulsive) force from each neighbor who gives a positive (negative) payoff according to the payoff matrix of the PD game, whose the magnitude is proportional to the payoff value and inversely proportional to the distance between the focal individual and the neighbor. Then, each individual moves toward the direction of the resultant vector of the all forces at a fixed speed. They observed repeated occurrences of explosive dynamics that consisted of a formation of an altruistic cluster followed by its collapse with explosive dispersal of defective particles. While Antonioni et al. (2015) showed formation and collapse of cooperative clusters in a 2D diluted grid environment, it is unclear how human groups behave under such a situation in which a lot of individuals continuously change their relationships in real time.

In our preliminary framework, multiple human players, represented as particles in a shared two-dimensional space of social interactions, can modify their positions and game strategies for the prisoner's dilemma in real time, and receive benefit or cost emerging from both game theoretical and social relationships with neighboring players. In preliminary experiments (Kodera et al., 2017), we did not observe stable emergence of cooperative relationships, and simple analyses showed that this could be due to several model settings such as no limitation of visibility of other players (i.e., all players can observe all others), and the lower limit of the accumulated score.

In this paper, we propose an updated framework to investigate dynamic changes in continuously changing social relationships in real time decision-making and rewarding environments by considering these factors that might negatively affect the emergence of cooperation in the previous one. We discuss benefits of this framework for this purpose by conducting several experiments with human participants, showing that cooperative relationships can emerge regardless of parameter settings relating to the game structure and the mobility of players, and analyzing their behavioral patterns.

We further discuss relationships between behavioral characters of participants in the experiments and their psychological characters to see if how their personalities can be reflected in their behavior in such a game theoretical framework. Relationships between behaviors in online social networks (e.g., Facebook) of users and their personality have been discussed (Gosling et al., 2011; Seidman, 2013). Gosling et al. (2011) found that several connections between the Big Five personality traits and self-reported Facebook-related behaviors, suggesting that the users extended their offline personalities into the domains of online social networks. We conducted a survey on the Big Five personality traits (Oshio et al., 2012) and the relational mobility of their social environments (Yuki et al., 2007) after experimental sessions. We analyzed the correlation among behavioral characters in experiments and these psychological characters, showing that a few psychological characters of participants might reflect their behavioral characters at least in part, but there were variations in these relationships between experimental groups.

Materials and Methods

A Multi-Player Online Game-Based Experimental Framework

We first introduce a multi-player game based on the SPS model to observe continuous and dynamic relationships. Then, we explain how we implemented this framework to simulate this game situation with human participants.

We assume that N human subjects (players) participate in an experimental trial. Each player is represented as a point and arranged in a 500 × 500 two dimensional and toroidal space. Figure 1A shows an example interface showing the distribution of 7 players in the neighboring area of a player in the plane.

FIGURE 1

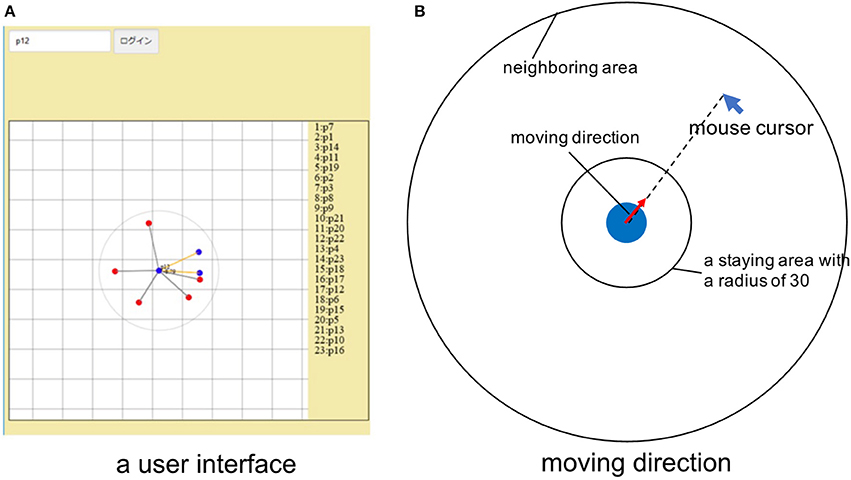
Figure 1. (A) A screenshot of a web-based user interface. A player is located at the center of the panel, and her neighbors within the range of R = 100 were shown. The color of each point represents her strategy (blue: cooperation, red: defection). The color and the thickness of the link reflects the payoff from a neighbor to the focal player. (B) The moving direction of a player. A player moves toward the direction of the mouse cursor with a speed V (pixel/step) if the cursor is outside of the staying area.

The position of each player represents her social state against the other players, which approximates her physical, social and psychological properties that may affect her interest against her neighbors. The proximity between two players reflects their social closeness. Each player can move freely in this space and change its strategy of the prisoner's dilemma (cooperate or defect) at arbitrary timing during a trial. The score arising from their social relationship with neighbors was accumulated through a session, and the objective of each player is to maximize her own accumulated score.

To simulate such a real-time decision-making and rewarding environment, we implemented a server-client framework using WebSocket and HTML5, which are used for developing Web-based online games.

Client Application

Figure 1A shows an example of the web-based client application for each human player. It enables a player to login to a server application with a handle name. During an experimental session, each player can see the current spatial distribution of neighboring players as shown in the square panel. The circle with a radius R = 100 in the plane represents the neighboring area. The focal player can observe other players within this area, and recognize them as neighbors. Cooperators are represented as blue points, and defectors are represented as red points. The focal player is always placed at the center of the panel, and she is connected to other neighboring players to emphasize the distance to the neighbors. The color of the connecting line represents the color of the other player (orange: cooperator, gray: defector) and its width is inversely proportional to the distance. The handle name and the current accumulated score of the focal player are indicated around the player in the plane. There is also a leaderboard showing the current ranking of all the players.

A player can specify each player's direction of movement using a mouse cursor (Figure 1B). If the focal player places a mouse cursor outside of the small staying area around her on the panel, she moves toward the cursor on the space. Note that her position on the space changes, but she is kept in the center of the panel, always showing her neighboring area. The strategy of the focal player is flipped when the “c” key is pressed. In addition, the strategy is also flipped with a small probability 0.2% at every time step to make players pay much attention to the strategy. Specifically, the client application sends the xy-coordinate of the mouse cursor on the window to a server application at every time step of 0.2 s asynchronously. It also sends a key event every time when “c” key was pressed.

Server Application

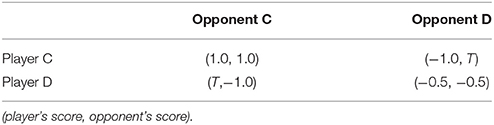
The server application conducts two procedures at every time step with a short time interval of DT = 0.5 s. First, it updates the accumulated scores of all players. The strategy of each player is updated using the information that was sent from client applications. Each player i gets a score depending on her current social relationships with all neighbors, which is defined by Table 1 and Equation (1):

$\begin{array}{ll}Score={\displaystyle \sum _{j\in neighborsofi}}\frac{{pd}_{i,j}}{d_{i,j}+1},& (1)\end{array}$

where pd_i,j represents a payoff, in Table 1, that the player i gets by playing a game with j. d_{i, j} represents the distance between i and j in the plane. This equation means that the basic game theoretical relationship between players is based on the prisoner' dilemma, but the net score is inversely proportional to the proximity between them, which reflects the effect of the social relationship between them. The score is accumulated over the whole game playing time.

TABLE 1

Table 1. Payoff matrix.

Then, the position of each player is updated according to the information that was from the corresponding client. Each player moves toward the direction specified by the mouse cursor by V pixels if she does, and thus can move with a speed of V/DT pixels per second. Finally, the state and position of all players and their accumulated scores are sent to the all clients and reflected in their interfaces.

Experimental Procedures

The experimental procedures with human participants have been approved by the planning and evaluation committee in the Graduate School of Information Science, Nagoya University (GSIS-H28-3). An informed consent was obtained from all participants before experiments. We recruited N = 23 undergraduate or graduate school students at Nagoya University as participants and conducted experiments (E1) on July 14th, 2017. All the participants were gathered in a computer room of our department. Each participant was assigned a standard desktop PC and asked to use an interface on a web-browser with a mouse and a keyboard. They were not allowed to talk with each other during the experiment. They were asked to maximize their own accumulated score regardless of the relative value from others', and told that they would receive 1,000 yen for taking part in an experiment and additional bonus at most 500 yen will be paid according to the accumulated score. However, all participants received 1,500 yen after the experiment.

After an introduction of the game and the user interface to participants, 23 participants participated in three experimental sessions (S1–S3) and 21 participants participated in one experimental session (S4) with different payoff matrices with a temptation to defect T = 1.5 (S1, S2) and 1.2 (S3, S4), and a different speed V = 3 (S1, S3), 6 (S2, S4), sequentially. The experimental instruction is shown as the Data sheet 1 in the Supplementary Materials. Each player was asked to maximize her own accumulated score. Each session lasted for about 10 min, but players were not informed of the exact time limit in advance. We used data for initial 265 s (i.e., 530 time steps) for analysis of each session, which is the minimal experimental duration among the all sessions. We also assumed a practice session (for 1 min) before S1, and a short break (for 2 min) between S2 and S3.

Two players did not participate in S4 and did not have a survey questionnaire (explained below). Another player participated in all the sessions but did not have a survey questionnaire. Thus, we used the data from all the 23 participants for the behavioral analysis in S1, S2, and S3, and used them from 21 participants in S4 in section Behavioral and psychological characteristics of players. We used the behavioral and personal data from 20 participants who answered questionnaires in the next section.

We also conducted another experiment (E2) on February 6th, 2018 with N = 13 undergraduate or graduate school students at Nagoya University, using a different order of experimental settings T = 1.5 (S1, S3) and 1.2 (S2, S4), and V = 3 (S1, S2), 6 (S3, S4). We conducted this experiment to grasp a general behavioral tendency that could be observed in both experiments. In this experiment, all participants participated in all the sessions and completed a survey questionnaire. We used data for initial 305 s (i.e., 610 time steps) for the analysis.

A Survey on the Big Five Traits and the Relational Mobility

After S4, we also conducted a survey questionnaire on Big Five personality traits and relational mobility of their social environments. Specifically, we conducted the Big Five personality (or Five-Factor Model) test on all participants using a Japanese version of Ten-Item Personality Inventory (TIPI-J) (Oshio et al., 2012), which is based on Ten Item Personality Inventory (TIPI) proposed by Gosling et al. (2003). TIPI is a 10-item (questions) measure of the Big Five dimensions, which is commonly used to describe personality according to five traits: openness (inventive/curious vs. consistent/cautious), conscientiousness (efficient/organized vs. easy-going/careless), extraversion (outgoing/energetic vs. solitary/reserved), agreeableness (friendly/compassionate vs. challenging/detached), and neuroticism (sensitive/nervous vs. secure/confident).

The relational mobility is the degree to which individuals in a given society have the option to form new relationships and end old relationships (Yuki et al., 2007). When an individual perceives their social environment to be low in relational mobility, they perceive it as difficult and costly to leave current relationships and to establish new ones. We focus on how the relational mobility of their local environments can affect their behaviors in our experiments. The relational mobility scale (Yuki et al., 2007; Schug et al., 2010), a 12-item measure, was used to assess the two components of the relational mobility of participants.

Participants were asked to rate 22 (10 for the Big Five and 12 for the relational mobility) statements using a 6 (the relational mobility scale) or 7 (the Big Five traits) -point scales (options ranged from: 1-strongly disagree, to 6/7-strongly agree). We then calculated scores of the Big Five personality traits (OPE: openness to experience, CON: conscientiousness, EXT: extraversion, AGR: agreeableness, and NEU: neuroticism) and two components of the relational mobility (MNP: meeting new people, and CIP: choosing one's own interaction partners) for each individual. The questionnaire is shown as the Data sheet 2 in the Supplementary Materials.

Results

General Behavioral Tendency

Figure 2A shows the temporal dynamics of the proportion of cooperators and the average number of neighbors in E1-S3. While both indices fluctuated through the session, we observed cooperative clusters emerged and collapsed locally. Figure 2B shows an example transition of the social dynamics in S3 that were often observed in all experimental sessions. We see that a cooperative cluster with a small number of players forms spontaneously (t = 25), and keeps or grows its size by increasing mutual benefit among players (t = 61). However, when some defectors find and approach them, or some players change their states from cooperative to defective, cooperative players escape from defectors and try to find other players to establish cooperative relationships (t = 90). Such an emergence and collapse of cooperative cluster occurred repeatedly in the all experimental sessions.

FIGURE 2

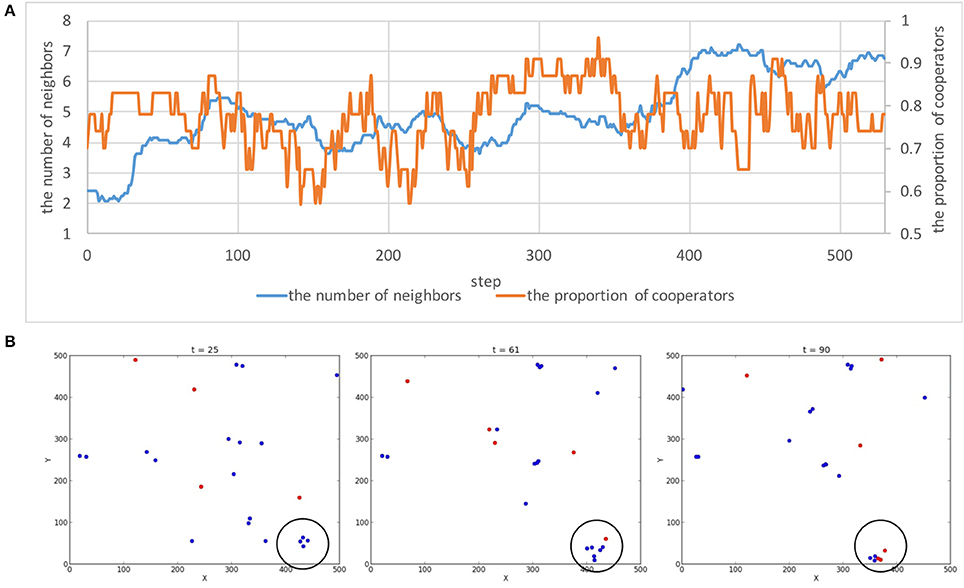
Figure 2. (A) The temporal dynamics of the proportion of cooperators and the average number of neighbors in E1-S3. (B) An example transition of the social dynamics in E1-S3 that were typically observed in the all experimental trials. Blue, cooperators; red, defectors. (Left) A spontaneous formation of cooperative cluster, (Center) a growing cluster, (Right) an escape from defectors. We can also see some other clusters of cooperators in the field.

Figure 3 shows the average proportion of cooperators and moving players (i.e., the proportion of players who decided to move toward any direction) among all players at each time step, in each session. It should be noted that the proportion of cooperation was between about 0.63 and 0.82, meaning that many individuals tended to be cooperative in this experimental framework.

FIGURE 3

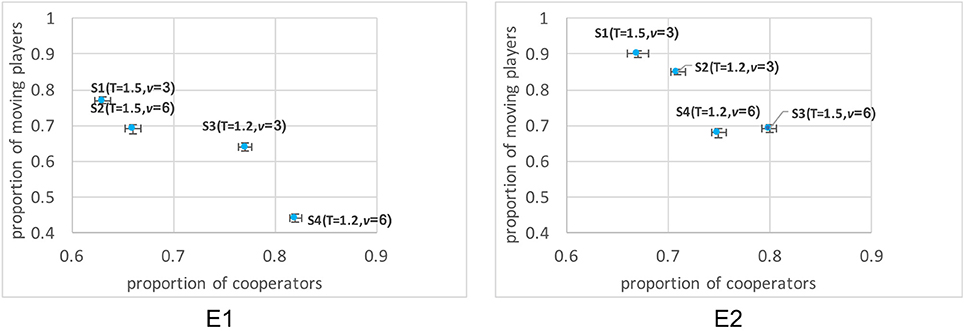
Figure 3. The average proportion of cooperators and moving players in each session. The error bar represents 95% confidence interval.

We also see that the proportion of cooperators increased as the experimental sessions proceeded from S1 to S4 (except for S3 and S4 in E2). It is highly possible that this trend is, at least in part, due to the effect of increased learning experience of game environments because experimental sessions were conducted sequentially. Having this in mind, we still observed a negative relationship between the proportion of cooperators and the proportion of moving players in both experiments. This implies that more successful cooperators tended to move less often. Also, the smaller temptation to defect (T) tended to contribute to the higher proportion of cooperation (except for S3 and S4 in E2), and the larger speed of movement (V) tended to contribute to the lower proportion of moving players. These might reflect the effect of the temptation to defect as expected, and also reflect that the ability to more quickly modify each player's social state contributed to form stable cooperative relationships.

Figure 4 shows the proportion of cooperative and moving players at step t when the proportion of cooperative neighbors was lower than 0.5 or not in the previous step t-1. In the all sessions, players tended to be more cooperative and tended to be less frequently moving when there were more than half of neighbors were cooperative (Kolmogorov-Smirnov test, p-value < 0.001). This simple rule is expected to be a basic mechanism that contributed to the emergence of stable cooperation in these experiments.

FIGURE 4

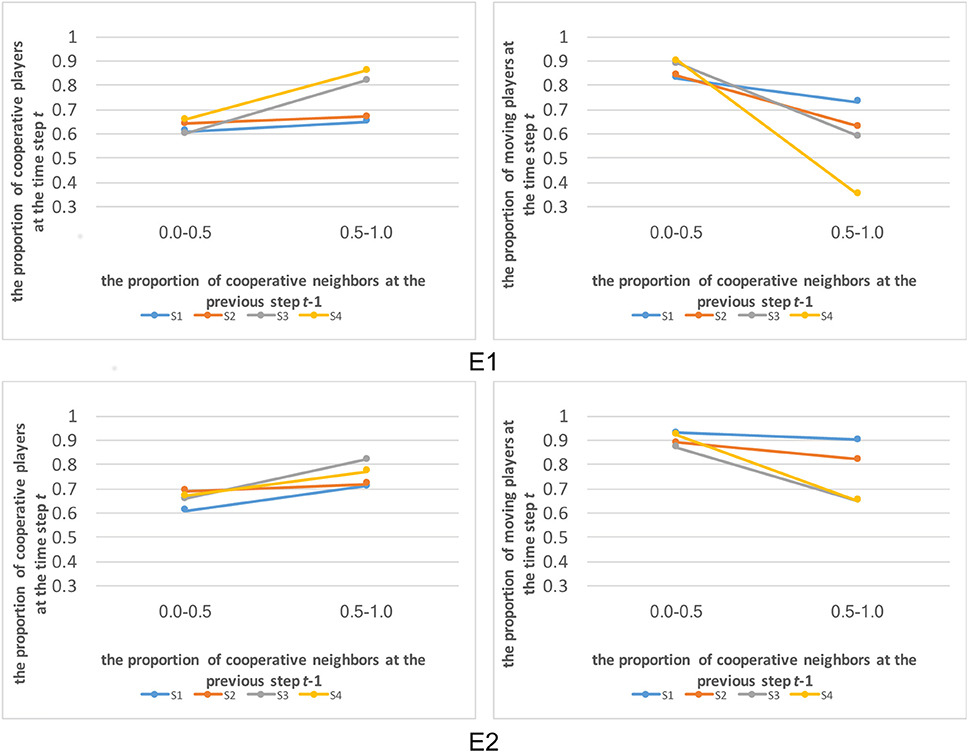
Figure 4. The proportion of cooperative and moving players at step t when the proportion of cooperative neighbors was lower than 0.5 or not in the previous step t-1.

Behavioral and Psychological Characteristics of Players

Next, we focus on relationships among behavioral and psychological characteristics of each participant in experimental sessions. Specifically, we defined 5 behavioral indices that represent different aspects of each individual's behavior as follows: COO: the ratio of a focal player's cooperation (i.e., the proportion of time during which her state was cooperative), NEI: the number of neighbors, MOV: the proportion of steps at which the focal player moved, CHA: the number of time steps in which the focal player changed her strategy, SCO: the total score that the focal player obtained, in each session.

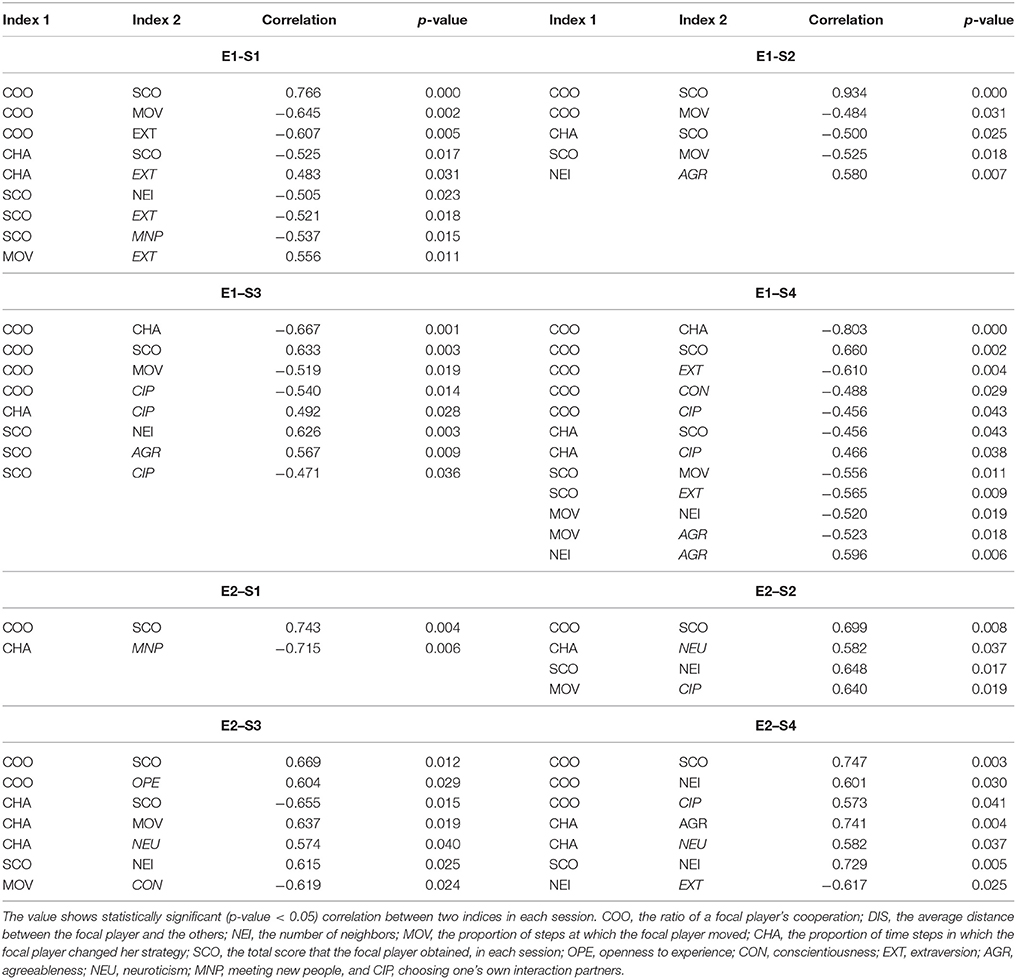
We conducted a correlation analysis (Spearman's rank correlation coefficient) among these 5 indices and scores of 7 components of psychosocial properties explained in section Server application to grasp overall correlation among behavioral and psychological characters. We focused on statistically significant (p-value < 0.05) pairs of these indices in each experimental session.

Table 2 shows results of the analysis in each experimental session. In E1, there is a strong correlation between SCO and COO in all the experimental sessions, meaning that more cooperative players obtained higher scores. This is because cooperative players successfully established stable cooperative relationships as discussed in the previous section.

TABLE 2

Table 2. Results of correlation analyses of indices (Spearman' s rank correlation coefficient).

There is also a negative relationship between “SCO or COO” and “MOV and CHA”, meaning that players who frequently changed their strategy and moved in the plane were less cooperative or obtained lower scores. This implies that defectors who were seeking and trying to exploit cooperative clusters were not successful probably because they were avoided by cooperators.

As for NEI, there were differences in their relationship with SCO among sessions. In S1, NEI had a negative relationship with SCO, respectively, and they had not so clear relationship with SCO in S2. This could be because smaller clusters of cooperators (e.g., two or three cooperators) were frequently invaded by defectors when the experimental setting was beneficial for defectors (S1 and S2) or players tended to be defectors due to the less game experience. On the other hand, NEI had a positive relationship with SCO in both S3 and S4, respectively. This means that players who tended to form large cooperative clusters obtained higher scores when the experimental setting was beneficial for cooperators (S3 and S4).

As for the relationship between these behavioral characters of players and their psychological characters, it was not easy to see general trends across all experimental sessions. However, it should be noticed that AGR had a positive relationship with NEI in S2 and S3, SCO in S3, and a negative relationship with MOV in S4. This implies that agreeable players tended to get clustered and less frequently moved, obtaining a higher score. In S3 and S4 in which there were the larger proportion of cooperators, COO had a negative relationship with CIP. This implies that players who do not have many chances to choose their own partners in their social environments tended to be cooperative.

In E2, we see the less number of significant correlations between indices than in E1, which is expected to be due to the small number of players. However, we still see a strong correlation between SCO and COO in all the experimental sessions, and the similar tendency of the correlation observed in E1 such as a positive relationship between “COO or SCO” and NEI in S2, S3, and S4. However, we observed different relationships between behavioral and psychological indices: there was a positive correlation between CHA and NEU, meaning that more sensitive players tended to change their strategy more frequently. We also see an opposite relationship such as the positive relationship between “COO and CIP” in S4. This implies that psychological characters of participants might reflect their behavioral characters at least in part, but there were variations in these relationships between experimental groups.

Discussion

We proposed and constructed an experimental framework to observe continuous and dynamic relationships in a group of human participants by applying techniques of web-based multiplayer online games. We implemented a multi-player game based on Nishimoto et al.'s SPS model in which human participants, represented as particles in a shared space, can change their positions and game theoretical strategies in real time, according to the benefits or costs arising from social relationships with neighboring players.

We found that cooperative clusters emerged in parallel in all experimental sessions, and found a strong positive assortativity between cooperators in some sessions. This is quite different from the cases in our preliminary experiments (Kodera et al., 2017). In these experiments, defectors dominated the population, chasing cooperators through experimental sessions. This is expected to be because each player could observe all the other players in these cases, and thus defector could exploit cooperators more easily. This implies that the spatial locality is an essential factor for the emergence of cooperation in our framework. The fact that there was no incentive to avoid mutual defections when their scores were the lower limit (0) could be another reason for defectors to successfully dominate the population.

We also found a general behavioral tendency of participants that they tend to be cooperative and tend not be moving when the proportion of neighboring cooperators were high. This fact supports the validity of the behavioral rule of particles adopted in the SPS model (Nishimoto et al., 2013), at least in part, in that their game strategy is based on the proportion of cooperators among neighbors and they tend to get close when they are cooperators.

It should be noted that psychological characters of participants reflected their behavioral characters in the three experimental sessions in E1, in part. That is, agreeable players established stable and cooperative clusters and obtained higher scores. Also, we found that players who have fewer chances to choose partners in their social environments tended to be cooperative. This may be due to the experimental settings in which cooperative clusters were easy to emerge. These results imply that our experimental framework can be a platform to conduct psychological experiments with many participants to see how psychological characters can affect global dynamics of social relationships emerging from interactions among them. However, at the same time, we also found that there were variations in these relationships between experimental groups. This implies that these relationships can be strongly affected by the social settings such as the number of participants and their distribution of psychological characters.

These results were from two small groups of participants, and the experiments were conducted in the sequential order, and thus there could be effects orders of sessions on the results. We believe that more detailed analysis with many groups can clarify general behavioral strategies of humans in real-time decision-making and rewarding environments.

Ethics Statement

This study was carried out in accordance with the recommendations of the planning and evaluation committee in the Graduate School of Information Science, Nagoya University, Japan with written informed consent from all subjects. All subjects gave written informed consent in accordance with the Declaration of Helsinki. The protocol was approved by the planning and evaluation committee in the Graduate School of Information Science, Nagoya University, Japan (GSIS-H28-3).

Author Contributions

RS, MI, and TA designed the experimental procedures, conducted experiments, and analyzed the results. KN constructed the original SPS model and SK constructed the web-based framework, and they advised on the experiments and analyses. RS and MI wrote the manuscript with support from all authors.

Funding

This work was supported in part by Japan Society for the Promotion of Science Grant-in-Aid for Scientific Research (JSPS KAKENHI) Grant number JP15K00335, JP15K00304, JP17KT0001 and JP17H06383 in #4903; and Topic-Setting Program to Advance Cutting-Edge Humanities and Social Sciences Research Grant number JP17J0011b.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2018.00074/full#supplementary-material

References

Antonioni, A., Cacault, M. P., Lalive, R., and Tomassini, M. (2014). Know thy neighbor: costly information can hurt cooperation in dynamic networks. PLoS ONE 9:e110788. doi: 10.1371/journal.pone.0110788

PubMed Abstract | CrossRef Full Text | Google Scholar

Antonioni, A., Sánchez, A., and Tomassini, M. (2016). Cooperation survives and cheating pays in a dynamic network structure with unreliable reputation. Sci. Rep. 6:27160. doi: 10.1038/srep27160

PubMed Abstract | CrossRef Full Text | Google Scholar

Antonioni, A., Tomassini, M., and Sánchez, A. (2015). Short-range mobility and the evolution of cooperation: an experimental study. Sci. Rep. 5:10282. doi: 10.1038/srep10282

PubMed Abstract | CrossRef Full Text | Google Scholar

Cuesta, J. A., Gracia-Lázaro, C., Ferrer, A., Moreno, Y., and Sánchez, A. (2015). Reputation drives cooperative behaviour and network formation in human groups. Sci. Rep. 5:7843. doi: 10.1038/srep07843

PubMed Abstract | CrossRef Full Text | Google Scholar

Efferson, C., Roca, C. P., Vogt, S., and Helbing, D. (2016). Sustained cooperation by running away from bad behavior. Evol. Hum. Behav. 37, 1–9. doi: 10.1016/j.evolhumbehav.2015.05.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Fehl, K., van der Post, D. J., and Semmann, D. J. (2011). Co-evolution of behavior and social network structure promotes human cooperation. Ecol. Lett. 14, 546–551. doi: 10.1111/j.1461-0248.2011.01615.x

CrossRef Full Text | Google Scholar

Friedman, D., and Oprea, R. (2012). A continuous dilemma. Am. Econ. Rev. 102, 337–363. doi: 10.1257/aer.102.1.337

CrossRef Full Text | Google Scholar

Gosling, S. D., Augustine, A. A., Vazire, S., Holtzman, N., and Gaddis, S. (2011). Manifestations of personality in online social networks: self-reported facebook-related behaviors and observable profile information. Cyberpsychol. Behav. Soc. Netw. 14, 483–488. doi: 10.1089/cyber.2010.0087

PubMed Abstract | CrossRef Full Text | Google Scholar

Gosling, S. D., Rentfrow, P. J., and Swann, W. B. Jr. (2003). A very brief measure of the big-five personality domains. J. Res. Personal. 37, 504–528. doi: 10.1016/S0092-6566(03)00046-1

CrossRef Full Text | Google Scholar

Grujić, J., Gracia-Lázaro, C., Milinski, M., Semmann, D., Traulsen, A., Cuesta, J. A, et al. (2014). A comparative analysis of spatial prisoner's dilemma experiment, conditional cooperation and payoff irrelevance. Sci. Rep. 4:4615. doi: 10.1038/srep04615

CrossRef Full Text | Google Scholar

Hawkins, R. X. D., and Goldstone, R. L. (2016). The formation of social conventions in real-time environments. PLoS ONE 11:e0151670. doi: 10.1371/journal.pone.0151670

PubMed Abstract | CrossRef Full Text | Google Scholar

Hofbauer, J., and Sigmund, K. (1998). Evolutionary Games and Population Dynamics. Cambridge: Cambridge University Press.

Google Scholar

Horita, Y., Takezawa, M., Inukai, K., Kita, T., and Masuda, N. (2017). Reinforcement learning accounts for moody conditional cooperation behavior: experimental results. Sci. Rep. 7:39275. doi: 10.1038/srep39275

PubMed Abstract | CrossRef Full Text | Google Scholar

Kodera, S., Suzuki, R., Nishimoto, K., and Arita, T. (2017). “A multiplayer online game-based experimental framework for observing continuous dynamics of human social relationships,” in Proceedings of the 22nd International Symposium on Artificial Life and Robotics (AROB2017) (Oita: ISAROB), 147–152.

Maynard Smith, J. (1982). Evolution and the Theory of Games. Cambridge: Cambridge University Press.

Google Scholar

Meloni, S., Buscarino, A., Fortuna, L., Frasca, M., Gómez-Gardeñes, J., Latora, V., et al. (2009). Effects of mobility in a population of prisoner's dilemma players. Phys. Rev. E 79:067101. doi: 10.1103/PhysRevE.79.067101

PubMed Abstract | CrossRef Full Text

Nishimoto, K., Suzuki, R., and Arita, T. (2014). “Where do the dynamics of social relationship come from? - An analysis based on social particle swarm,” in Proceedings of the 19th International Symposium on Artificial Life and Robotics (AROB2014) (Oita: ISAROB), 86–91.

Google Scholar

Nishimoto, K., Suzuki, R., and Arita, T. (2013). “Social particle swarm: explosiparticle dynamics based on cooperative/defective forces,” in Proceedings of 2013 IEEE Symposium on Artificial Life (IEEE ALIFE 2013) (New York, NY: IEEE), 134–139. doi: 10.1109/ALIFE.2013.6602442

CrossRef Full Text | Google Scholar

Nowak, M. A. (2006). Five rules for the evolution of cooperation. Science 314, 1560–1563. doi: 10.1126/science.1133755

PubMed Abstract | CrossRef Full Text | Google Scholar

Nowak, M. A., and May, R. M. (1992). Evolutionary games and spatial chaos. Nature 359, 826–829. doi: 10.1038/359826a0

CrossRef Full Text | Google Scholar

Oshio, A., Abe, S., and Cutrone, P. (2012). Development, reliability, and validity of the Japanese version of Ten Item Personality Inventory (TIPI-J). Jap. J. Personal. 21, 40–52. doi: 10.2132/personality.21.40

CrossRef Full Text | Google Scholar

Pacheco, J. M., Traulsen, A., and Nowak, M. A. (2006). Coevolution of strategy and structure in complex networks with dynamical linking. Phys. Rev. Lett. 97:258103. doi: 10.1103/PhysRevLett.97.258103

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinheiro, F. L., Pacheco, J. M., and Santos, F. C. (2012). From local to global dilemmas in social networks. PLoS ONE 7:e32114. doi: 10.1371/journal.pone.0032114

PubMed Abstract | CrossRef Full Text | Google Scholar

Rand, D. G., Nowak, M. A., Fowler, J. H., and Christakis, N. A. (2014). Static network structure can stabilize human cooperation. Proc. Natl. Acad. Sci. U.S.A. 111, 17093–17098. doi: 10.1073/pnas.1400406111

PubMed Abstract | CrossRef Full Text | Google Scholar

Rand, D. G., Arbesman, S., and Christakis, N. A. (2011). Dynamic social networks promote cooperation in experiments with humans. Proc. Natl. Acad. Sci. U S.A. 108, 19193–19198. doi: 10.1073/pnas.1108243108

PubMed Abstract | CrossRef Full Text | Google Scholar

Schug, J., Yuki, M., and Maddux, W. (2010). Relational mobility explains between- and within-culture differences in self-disclosure to close friends. Psychol. Sci. 21, 1471–1478. doi: 10.1177/0956797610382786

PubMed Abstract | CrossRef Full Text | Google Scholar

Seidman, S. (2013). Self-presentation and belonging on facebook: how personality influences social media use and motivations. Personal. Individ. Diff. 54, 402–407. doi: 10.1016/j.paid.2012.10.009

CrossRef Full Text | Google Scholar

Sicardi, E. A., Fort, H., Vainstein, M. H., and Arenzon, J. J. (2009). Random mobility and spatial structure often enhance cooperation. J. Theor. Biol. 256, 240–246. doi: 10.1016/j.jtbi.2008.09.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Suzuki, R., Kato, M., and Arita, T. (2008). Cyclic coevolution of cooperative behaviors and network structures. Phys. Rev. E 77:021911. doi: 10.1103/PhysRevE.77.021911

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Suri, S., and Watts, D. J. (2012). Cooperation and assortativity with dynamic partner updating. Proc. Natl. Acad. Sci. U.S.A. 109, 14363–14368. doi: 10.1073/pnas.1120867109

PubMed Abstract | CrossRef Full Text | Google Scholar

Yonenoh, H., and Akiyama, E. (2014). Selection of opponents in the prisoner's dilemma in dynamic networks: an experimental approach. J. Theor. Biol. 351, 25–36. doi: 10.1016/j.jtbi.2014.02.006

CrossRef Full Text | Google Scholar

Yuki, M., Schug, J., Horikawa, H., Takemura, K., Sato, K., Yokota, K., et al. (2007). Development of a Scale to Measure Perceptions of Relational Mobility in Society. Center for Experimental Research in Social Sciences Working Paper Series, (Hokkaido: Hokkaido University).

Zimmermann, M. G., and Eguíluz, V. M. (2005). Cooperation, social networks, and the emergence of leadership in a prisoner's dilemma with adaptive local interactions. Phys. Rev. E 72:056118. doi: 10.1103/PhysRevE.72.056118

PubMed Abstract | CrossRef Full Text | Google Scholar