- 1Natural Sciences and Engineering Research Council of Canada, Industrial Chair in Sustainable Forest Management, Forest Research Institute, Université du Québec en Abitibi-Témiscamingue, Québec, QC, Canada
- 2Centre D'ètude de La Forêt, Université du Québec à Montréal, Montréal, QC, Canada
- 3Life and Earth Sciences, École Pratique des Hautes Études, Paris Research University, Paris, France
- 4LEHNA (UMR5023, Centre National de la Recherche Scientifique), Université Lyon 1, Villeurbanne, France
- 5Natural Resources Canada, Canadian Forest Service, Laurentian Forestry Centre, Québec, QC, Canada
Tree species responses to climate change will be greatly influenced by their evolutionary potential and their phenotypic plasticity. Investigating tree-rings responses to climate and population genetics at the regional scale is crucial in assessing the tree behavior to climate change. This study combined in situ dendroclimatology and population genetics over a latitudinal gradient and compared the variations between the two at the intra- and inter-population levels. This approach was applied on the northern marginal populations of Thuja occidentalis (eastern white-cedar) in the Canadian boreal forest. We aimed first to assess the radial growth variability (response functional trait) within populations across the gradient and to compare it with the genetic diversity (microsatellites). Second, we investigated the variability in the growth response to climate at the regional scale through the radial growth-climate relationships, and tested its correlation with environmental variables and population genetic structure. Model selection based on the Akaike Information Criteria revealed that the growth synchronicity between pairs of trees of a population covariates with both the genetic diversity of this population and the amount of precipitation (inverse correlations), although these variables only explained a small fraction of the observed variance. At the regional scale, variance partitioning and partial redundancy analysis indicate that the growth response to climate was greatly modulated by stand environmental variables, suggesting predominant plastic variations in growth-response to climate. Combining in situ dendroclimatology and population genetics is a promising way to investigate species' response capacity to climate change in natural stands. We stress the need to control for local climate and site conditions effects on dendroclimatic response to climate to avoid misleading conclusions regarding the associations with genetic variables.
Introduction
Climate change will alter ecological gradients, notably via pole-ward shifts of isotherms and locally-dependent changes in precipitation patterns (IPCC, 2013). These modifications are likely to change the selection pressure patterns acting on plant distribution, such as cold temperatures and dryness (Gienapp et al., 2008; Chapin et al., 2011). Recent tree growth reductions in the boreal zone put into question species' capacity to cope with the rapid climate change (Beck et al., 2011; Berner et al., 2011). Induced impacts are expected to be most visible at the limits of a species distribution, where populations are further from the species optimum in ecological gradients (Guo et al., 2005; Sexton et al., 2009). It is now admitted that species response to climate change will combine migration with evolutionary and plastic responses (Davis and Shaw, 2001; Savolainen et al., 2007; Alberto et al., 2013). For long-lived sessile species such as trees, the local fate of a population will rely on its ability to either adapt or acclimate (Aitken et al., 2008). The evolutionary response of a population requires the existence of genetic variability for traits involved in responses to climate (Hartl and Clark, 1997; Savolainen et al., 2007; Polechová et al., 2009). Anticipating the impact of climate change on tree species therefore requires a good characterization of the spatial variations of those traits and of genetic features across large biogeographic gradients.
Tree radial growth is a functional trait that reflects trees' responses to climate. Cambial activity is an integrative indicator accounting for physiological mechanisms such as response to drought stress, dormancy phenology, and resistance to frost injuries (Schweingruber, 1996; Fritts, 2001). By investigating the relationships between climatic variability and annual radial growth, dendroclimatology precisely determines the past, and current local climatic constraints on trees (Fritts, 2001; Filion and Payette, 2010). Dendroclimatic studies conducted over large latitudinal transects are therefore a suitable tool to investigate the plastic response of trees to climate (Huang et al., 2010; Lapointe−Garant et al., 2010; Lloyd et al., 2011; Housset et al., 2015). However, extrapolating the current dendroclimatic response to future climate is impeded—among other challenges—by our lack of knowledge on the genetic control of cambial activity (e.g., Huang et al., 2013).
Consequently, there is a growing interest in research bridging tree-ring and genetic (Franks et al., 2014). A few dendroclimatic studies investigating the among-population variations in the growth-climate relationships in common-garden experiments evidenced genetic variation among provenances for the growth-climate relationships and a high plastic component (Savva et al., 2002, 2008; McLane et al., 2011; Taeger et al., 2013; Montwé et al., 2016). While transplant experiments in common gardens are the most direct way of controlling for environmental differences among populations, these experiments are not available for most non-commercial species. In such cases, investigations of tree responses to climate in natural stands are required. Moreover, investigation in natural stands brings complementary information to common-gardens, which are usually limited to even-aged and monospecific stands in a limited set of soil and climatic conditions.
Recent studies combined in situ genotyping and tree-rings data to test for genetic effects on synchronicity (e.g., King et al., 2013; Latutrie et al., 2015) or on growth-climate relationships (e.g., Bosela et al., 2016) across broad spatial transects. For instance, an effect of the postglacial genetic lineages on the growth-climate relationships for European silver fir (Abies alba Mill.) is reported (Bosela et al., 2016). However, this study did not control for the effect of possible confounding environment features (e.g., soil, elevation, etc). Comparing in situ genetic data and phenotypic data is very challenging because phenotypes results from a complex interplay between genetic control and plastic responses to environmental conditions over an ecological gradient (Gienapp et al., 2008; Franks et al., 2014). Numerous dendroclimatic studies report that growth-climate relationships are modulated by environmental variables such as regional precipitation or temperature regimes, soil variables and forest stands characteristics (e.g., Babst et al., 2013; Gewehr et al., 2014; Housset et al., 2015; Brienen et al., 2016). The effect of those ecological gradients could be confounded with a genetic effect on the growth responses to climate and need to be controlled.
In this study, we test for the correlation between population genetic structure and tree-rings responses to climate, while controlling for ecological gradients through an approach combining model selection and variance partitioning. To test this approach, we took advantage of two existing datasets on the boreal tree Thuja occidentalis L. (eastern white-cedar, hereafter “cedar”). The first dataset results from a study of stem annual radial growth carried out at its northern boreal margin evidencing an effect of tree size, soil, regional precipitation, and regional temperature (Housset et al., 2015). The second is a genetic study conducted in the same study area that investigated the cedar neutral genetic structure based on neutral markers (Xu et al., 2012). The objective is to test for a correlation between neutral population genetic structure and tree-rings, while accounting for environmental variables, at both the intra-population and the inter-population levels.
Materials and Methods
Study System
Cedar is an evergreen long-lived and shade-tolerant species native to North America, with a distribution (Figure 1) ranging from James Bay, Canada, in the north to the southern Great Lakes area, USA, in the south (Little, 1971). Our study area is located from the center to the northern leading edge of cedar distribution, in the eastern Canadian boreal zone (Figure 1B). A latitudinal transect was established from 47.3 to 50.0°N and divided into three zones based on cedar abundance: The continuous zone (CZ), where cedars are common, the discontinuous zone (DZ), which marks the northern edge of the continuous distribution where it becomes less common in the forest matrix and, the marginal zone (MZ) where only a few isolated stands were found (Figure 1A). The relative abundance of cedars in each zone was estimated at 55, 9, and 3%, respectively (Figure 1B; Xu et al., 2012; Beaudoin et al., 2014). A total of 24 cedar stands were sampled along this gradient, with 8 sites in the CZ, 7 in the DZ, and 9 in the MZ, with 4 in the east (MEZ) and 5 in the west (MWZ). Those 24 sampling sites will be referred to as populations in the following sections. Cedar species show plastic tolerance to moisture edaphic conditions by occupying poorly drained lowland sites to xeric or rocky sites (Hofmeyer et al., 2009). All cedar stands in the MZ were found in forest swamps or along lake and river shores. Consequently, to avoid sampling bias in the CZ and the DZ, trees were sampled in the same edaphic situations as in the MZ. Over the 1953–2010 period, climate was colder in the MZ, with a mean (±sd) annual temperature (MAT) of −0.03±0.37°C, than in the DZ and CZ, which had a MAT of 1.40 ± 0.25°C and 2.40 ± 0.33°C, respectively (Table 1). The annual sum of precipitation was on average (±sd) 908 ± 53 mm.year−1 in the MZ, 886 ± 27 mm.year−1 in the DZ and 937 ± 56 mm.year−1 in the CZ (Table 1).
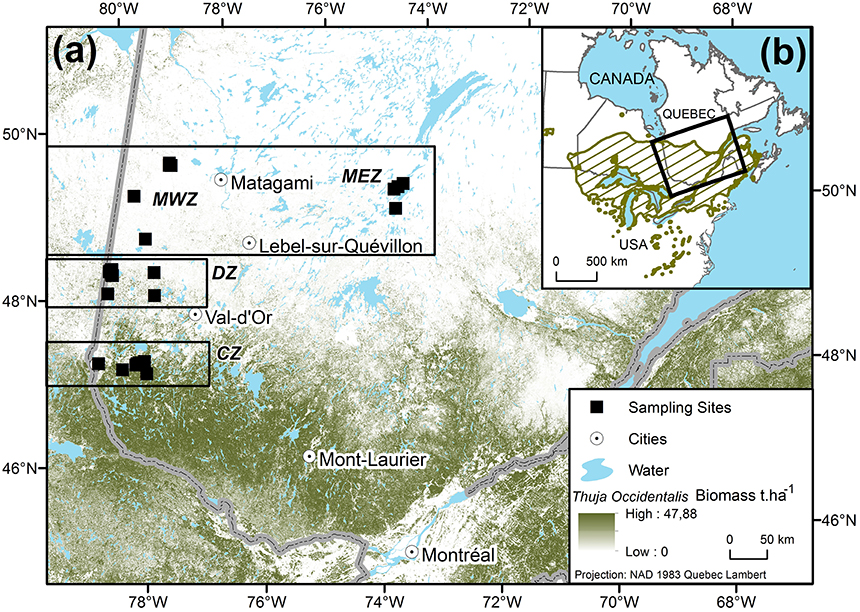
Figure 1. (A) Distribution of the Thuja occidentalis sampling sites (black squares, ■). The background shading illustrates cedar biomass in t.ha−1 (Beaudoin et al., 2014). Sampling was stratified between the continuous zone of distribution (CZ), the discontinuous zone (DZ), and the marginal zones (MWZ for west, MEZ for east). (B) Location of the study area (outlined area) relative to the species' range (hatched area, Little, 1971).
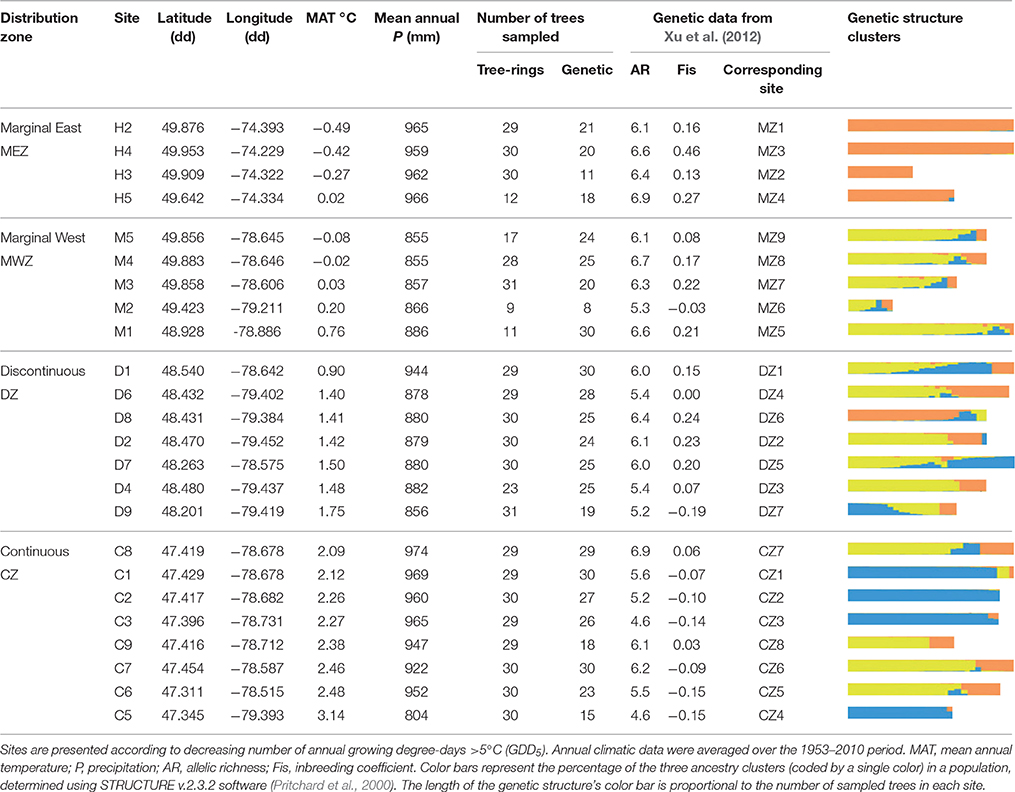
Table 1. Geographic, climatic, and neutral genetic features of the Thuja occidentalis sampling sites.
Genetic Data
Genetic structure variables were inferred from a recent study (Xu et al., 2012), which analyzed the cedar neutral genetic structure of our 24 populations. For each population, 15–30 trees (Table 1) were randomly selected and used for microsatellite genotyping. The genetic structure was assessed by genotyping at four polymorphic microsatellite loci derived from the phylogenetically closed species Thuja plicata Donn ex D. Don (TP9, TP10, TP11, and TP12). Xu et al. (2012) selected the optimal combination of markers (available at that time) delivering accurate estimates of cedar genetic diversity. The four microsatellite loci showed high discriminating power, with a combined probability of exclusion (PE) greater than 99% and a joint probability of genetic identity (PI) smaller than 10−5 (Peakall and Smouse, 2012).
Several indicators of intrapopulation genetic variability were used in this study. The expected heterozygoty (He) and the average within-population pairwise relatedness between each pair of trees in a population (Genrelatedness) statistics were computed with the software Genalex 6.5 (Peakall and Smouse, 2012). He is a proxy of gene diversity, with values ranging from 0 to 1 for low to high diversity. The allelic richness (AR), representing the alleles number corrected for sampled population size effect, was calculated using the software FSTAT2.9.3. The inbreeding coefficient (Fis) was calculated for each population using the software FSTAT2.9.3.
Genetic variability among populations at the landscape scale was analyzed through a clustering approach using the STRUCTURE v.2.3.2 software (Pritchard et al., 2000). Individuals were assigned to a number of assumptive clusters K, ranging from 1 to 15, with an admixture model and the option of correlated allele frequency (Falush et al., 2003). All parameters were set following the users' manual. To choose an appropriate run length, we performed a pilot run showing that burn-in and MCMC (Markov chain Monte Carlo) lengths of 300,000 each were sufficient to obtain consistent data. Increasing the burn-in or MCMC lengths did not improve the results significantly. Ten replicate runs for each value of K were performed. The most likely value of K was selected by plotting ΔK (see Supplementary Figure 2), following ad-hoc statistics (Evanno et al., 2005). This analysis identified three clusters (K = 3), which are hereafter depicted using three colors: Orange, yellow, and blue (Table 1). The average proportion of assignment of each individual to each cluster in a given population was used as a proxy to describe among population genetic differences at the regional scale.
Tree-Ring Data and Growth-Climate Relationships
The present study focused on the variability in growth sensitivity to climate among populations, but not on the growth itself. As response variables, we used the correlation matrix between climate and growth relationships described in Housset et al. (2015). This matrix was established on the correlations between monthly climatic variability and annual radial growth of cedar from 27 sampling sites, including the aforementioned 24 populations. Annual radial growth increments were obtained and analytical approaches were conducted using classical dendroclimatological procedures. The following paragraph summarizes Housset et al.'s approach used to derive the correlation matrix, and the main variables selected.
During summer 2010, up to 30 cedars were sampled in each site for dendroclimatic analysis. The genetic and dendrochronological samplings were conducted separately but on the exact same locations. Only dominant and codominant trees were sampled to lower the biases due to competition on tree-ring series. Two cores per tree were collected at 1.3 m above ground, sanded, measured, and cross-dated. To maximize the high-frequency growth responses associated with year-to-year climatic variability, each raw ring-width time-series was detrended using 60-year splines with a 50% frequency response (Cook and Kairiūkštis, 1990). After removing the first order autocorrelation, a mean Tree Growth Index (TGI) chronology was computed for each population using the R package “dplR” (Bunn, 2008). These residual chronologies were statistically tested against climatic time-series using bootstrapped correlation and response function analyses over the 1953–2010 period covered by meteorological observations (Biondi and Waikul, 2004). Correlation coefficients are computed between a site residual chronology and the matrix of monthly climatic data in order to represent the average relationship for the studied period. On the other hand, PCR (also known as response function analysis) is a multiple regression technique that uses the principal components of monthly climatic data to assess growth-climate relationships. Climatic time-series were monthly mean temperatures and total monthly precipitation, interpolated from Environment Canada meteorological records at each of the sampling sites using the software BioSIM for 1953–2010 (Régnière and Bolstad, 1994). This analysis revealed that cedar interannual growth variability was positively correlated with May temperature of the current year, but negatively correlated with June temperatures of the current year and with August temperatures of the year preceding ring formation. Climatic conditions of the previous year can affect tree growth, for instance through the process of carbohydrates reserve accumulation (Fritts, 2001). Precipitation also influenced annual radial growth, with a negative correlation with previous October and current-year May precipitation, and a positive correlation with previous June and current-year August precipitation. Figure 2 sums up the correlation scores of cedar radial growth with the seven monthly climatic variables, which will be referred to as the “growth-climate correlation matrix” in the following sections.
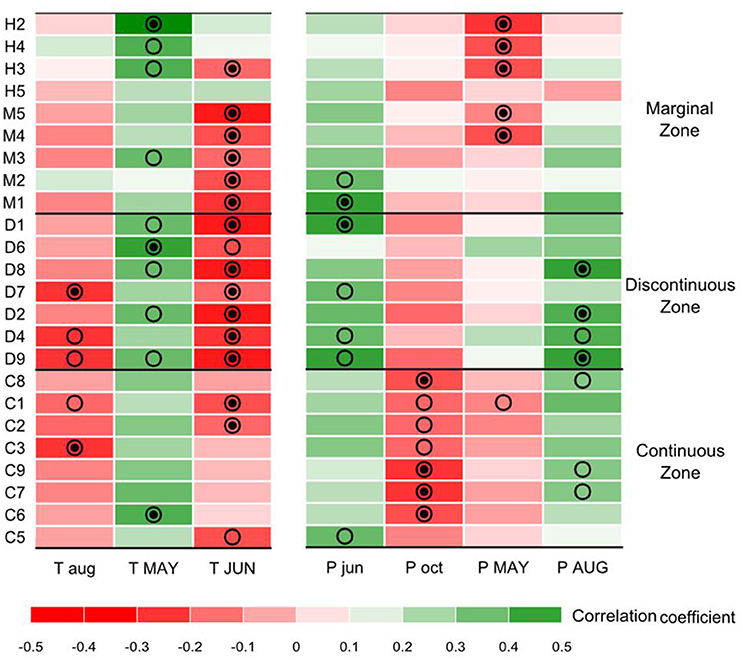
Figure 2. Growth-climate correlation matrix for the seven main monthly climatic drivers of radial growth interannual variations (columns) and the 24 sites (rows). Months in capital letters code for climate variables of the current year and, small letters for the year preceding ring formation. Colors represent the correlation coefficients scores computed between Thuja occidentalis residual tree-ring index chronologies and monthly mean temperature and monthly precipitation. Significant correlations are represented by dots (•) for the bootstrapped response function and by circles (○) for the correlation function. Sites are presented in order of increasing number of mean annual growing degree-days over the 1953–2010 period, the coldest sites being at the top.
Variability within a Population
Growth synchronicity was evaluated between the trees of each population. A mean chronology was computed for each tree from the spline-detrended chronologies of all its cores. The average pairwise correlation between single-tree chronologies within a population () was calculated (Cook and Kairiūkštis, 1990). This statistic, representing the average correlation between trees, was used as a proxy of growth synchronicity. It is inversely linked to growth variability. To remove biases due to population size differences, we resampled eight trees in each population and estimated this parameter by averaging it over 1000 repetitions. For each resampling, the was computed using the R package “dplR” (Bunn, 2008). Growth synchronicity between trees could be influenced by various factors such as differences in DBH or by genetic variability within a population. Variability in DBH was estimated using the standard deviation of tree DBH for each sampled population (sdDBH). Three complementary proxies of intrapopulation genetic diversity were used: Allelic richness (AR, see Supplementary Figure 1), expected heterozygoty (He), and average within-population pairwise relatedness (Genrelatedness). The inbreeding coefficient Fis (see Supplementary Figure 1) was also included in the model selection. The effects of regional climate on growth synchronicity along the latitudinal gradient was tested by adding the annual growing degree-days >5°C (GDD5) and the annual sum of precipitation from April to September (i.e., during the active vegetation stage) averaged over the 1953–2010 period.
We used model selection based on the corrected Akaike Information Criterion (AICc) statistic to determine which variable best explained growth synchronicity. In the model selection approach, each hypothesis is associated with a model that can be compared with other model hypotheses through AICc (Burnham and Anderson, 2010). The model with the lowest AICc is the one with the optimal trade-off between the best fit and the greatest parsimony. A model is considered to be more parsimonious when the number of estimated parameters k is lower. This method selects the hypothesis with the greatest likelihood to fit the observed data while avoiding the risk of overfitting them. A general rule of thumb is to consider only models with a difference in AICc lower than two as compared with the best model (Burnham and Anderson, 2010). Here, each model had growing variability as dependent variable and one of the following independent variables: sdDBH, AR, He, Genrelatedness, Fis, annual GDD1953−2010 or Seasonal P1953−2010.
Growth-Climate Relationships Variability among Populations
We performed another model selection procedure to test for covariation between the growth-climate relationships and among population genetic differences (STRUCTURE clustering) at the landscape scale. Sensitivity to climate is defined here as the coefficients of the aforementioned growth-climate correlation matrix. Alternatively, variability in sensitivity to climate may be due to the environmental conditions of each population. Therefore, the analysis included a model with genetic variables and a model with environmental variables having an effect on sensitivity to climate. A full model including both genetic and environmental variables was also included in the model selection. In the genetic model, we used the composition of each STRUCTURE groups (clusters) as explanatory variables to describe among population variations at the regional scale. Four environmental variables having an effect on variability among populations of the aforementioned growth-climate correlation values were identified in the Housset et al.' study (2015) and were included in the environmental model. Those four variables were: Mean DBH of the cored trees, carbon to nitrogen ratio (C:N) in the upper 50 cm, GDD5 and seasonal precipitation (mean sum of precipitation from April to September, i.e., during the current growing season) averaged over the 1953–2010 period. To sum up, the three following models were compared:
where ri is the correlation coefficient of growth with one of the aforementioned monthly climatic variables (columns in Figure 2). Furthermore, for each monthly correlation coefficients, a variance partitioning was computed between the three models to examine the amount of variability (adjusted R2) explained by each group of variables. The overall comparison of environmental vs. genetic variables was analyzed through the calculation of multivariate variance partitioning (Legendre and Legendre, 2012) on the seven monthly climatic variables using the R package “vegan” (Oksanen et al., 2013). Significance of the variance components were assessed through redundancy analysis (RDA) and partial redundancy analysis (pRDA) with 99 999 permutations (Legendre and Legendre, 2012). RDA are multivariate regressions where a set of response variables (here the growth-climate correlation matrix) are regressed against a set of explanatory variables. pRDA are RDA where the effect of the explanatory variables is assessed while controlling for another set of variables. pRDA can be particularly useful to test for the effect of genetic variables while controlling for the effect of local climate or soil conditions for example.
Results
Genetic Variability and Growth Synchronicity
The growth synchronicity between the trees of a given population () was smaller in the MZ than in the DZ (p = 0.025; Figure 3A). No statistical differences in were observed between the CZ and the DZ, nor between the CZ and the MZ. Genetic pairwise relatedness was smaller in the MZ than in the CZ (p = 0.049; Figure 3B). Based on model selection (Table 2), the best model to explain growth synchronicity between the trees of a population is the one with Seasonal P1953−2010 as an explanatory variable. Trees from a site receiving more precipitation had a lower synchronicity. Nevertheless, this relation was barely significant (p = 0.053) and poorly explains interindividual growth variability (adjusted R2 = 0.122). Four other models had a difference in AICc (Δ AICc) < 2, with the following explanatory variables: He, annual GDD1953−2010 (Δ AICc = 0.56), AR (1.39) and Genrelatedness (1.68). None of those models had a significant relation with . The major part of growth variability between trees was not captured by our variables.
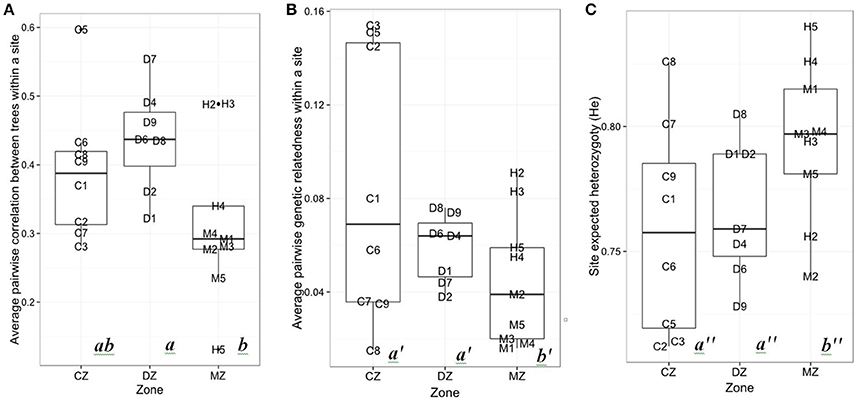
Figure 3. (A) Average pairwise growth correlation between trees within each site (), (B) average pairwise genetic relatedness, and (C) expected heterozygoty (He) for the continuous zone (CZ), discontinuous zone (DZ), and marginal zone (MZ). Different letters indicate a pairwise significant difference in the mean value between clusters (p < 0.05).
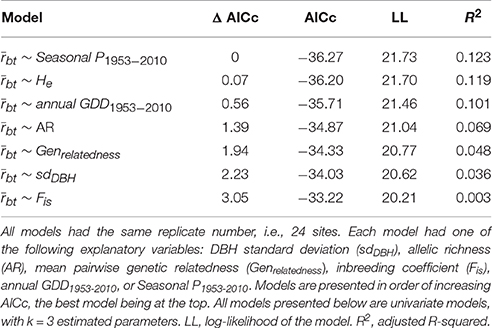
Table 2. Results of the linear model selection explaining the radial growth synchronicity between trees in a given site ().
Variability among Populations
Model selection revealed that the model including environmental variables best explained variability among populations in the correlation with temperatures of previous August and current June, as well as with precipitation of previous October, current May and current August (Table 3). According to variance partitioning, environmental variables captured most of the explained variance for those monthly climatic variables (Figure 4). Nevertheless, the genetic model (Equation 2) was the most likely to explain variations among populations in the correlation with current May temperature and previous June precipitation at the landscape scale (Table 3). Although this model was more parsimonious (k = 4) than the environmental one (k = 6), the Δ AICc (5.2 and 5.4, respectively) largely exceeded the difference in k. According to our data, populations with a greater percentage of trees from the blue genetic cluster were significantly (p = 0.019) less positively correlated with May temperature. A greater percentage of “blue” trees in the population was also significantly (p = 0.012) linked to a more positive correlation with previous June precipitation. The genetic structure accounted for the most important part of the explained variance for those two dependent variables (Figure 4), with an adjusted R2 of 0.17 for the correlation with May temperature and of 0.21 with previous June precipitation. The complete model with both the environmental and genetic variables was classified as the best model for none of the monthly climatic correlation coefficients included in the analysis (Table 3), although the adjusted R2 was greater (Figure 4). Overall, multivariate variance partitioning computed on the seven dependent variables (growth correlation with climate variables) revealed that environmental variables only explained 24% of the variance, while genetic structure only explained 5% (Figure 5). The part of variance that was jointly explained by both environmental and genetic data accounted for 43% of the total variance (with 13% overlap), while 57% of it remained unexplained.

Table 3. Results of the model selection explaining variability in growth-climate correlation coefficients among sites for each of the main climatic variables (columns from Figure 2).
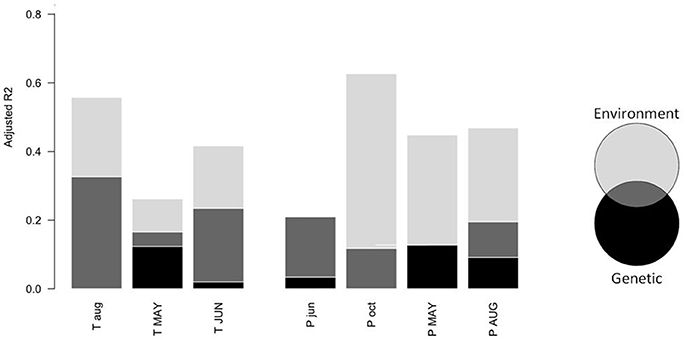
Figure 4. Univariate variance partitioning between environmental variables (Equation 1) and genetic variables (Equation 2) to explain variability in growth-climate correlation coefficient among sites for each monthly climatic variable of Figure 2. Black bars represent the percentage of variance explained by genetic variables only, dark gray bars represent the variance explained jointly by environmental and genetic variables, and pale gray bars represent the variance explained by environmental variables only. The sum of the three represents the total variance explained by all the variables (Equation 3).
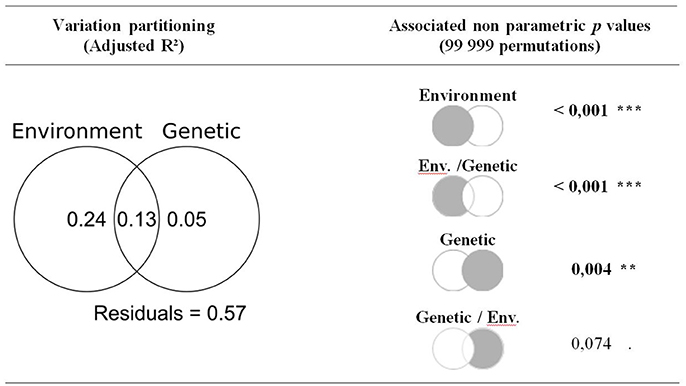
Figure 5. Multivariate variance partitioning of environmental variables (Equation 1) and genetic variables (Equation 2) to explain among-population variability in growth-climate relationships. Significance of each components of the variance partitioning were assessed through permutations (99 999) through redundancy analysis and partial redundancy analysis. Significant p-values are highlighted in bold.
Discussion
Our combined analysis of the association between population genetics and the dendroclimatic signal of cedar revealed a correlation between radial growth and genetics at both the intrapopulation (growth synchronicity) and the among-population levels (growth-climate relationships). However, our results evidenced a strong confounding effect by environmental variables in both cases, largely because environmental drivers and the neutral genetic structure are inter-correlated.
Intrapopulation Variability
Growth synchronicity between trees of a site () was lower in the MZ, meaning that cedar growth patterns were more variable from one tree to another toward the northern margin of its distribution. Based on model selection, this result was neither due to a greater spatial variability between the trees nor to size heterogeneity. Growth synchronicity was mostly influenced by seasonal precipitation (best model), a drier climate being associated with an increase in synchronicity. This finding is consistent with other studies showing that growth synchronicity was generally stronger under the most stressful climatic conditions (Schweingruber, 1996; King et al., 2013). It may seem surprising that precipitation exerts a common constraint on tree growth in our study system. However, although cedar is found in cold wetlands and shores, Housset et al. (2015) reported a growth limitation due to drought therein owing to the combination of a superficial root system and a lowering of the water table during the summer. Growth synchronicity between trees can be affected by stochastic processes such as abrupt change in competition, injuries or disturbances, especially in uneven aged natural stands, which could not be controlled in our study set and are thus accounted for as “noise.” Moreover, microtopographic variations among trees within a same site may cause differential responses to the same climatic conditions. It is therefore understandable that the explained variance is quite low (R2 = 0.122, p = 0.053) for the relation between and Seasonal P1953−2010. The model with the expected heterozygoty (He) had an AICc score very close to that of the model with Seasonal P1953−2010 (Δ AICc = 0.07). Both p (0.055) and R2 (0.119) values were also close to those of the first model. Higher He, meaning higher allelic diversity in the population, is negatively correlated with the intrapopulation growth synchronicity (). Growth synchronicity was generally negatively correlated with other indicators of genetic diversity (AR, which is in line with the findings of Latutrie et al., 2015) for Populus tremuloides Michaux. Disentangling the effects of environmental variables and genetics on growth synchronicity would require further investigations. Nevertheless, it remains that the amount of seasonal precipitation appears to primarily drive growth synchronicity, which supports the idea that plastic responses to environmental variables accounted for a great part of cedar intrapopulation growth variations across our transect.
Predominant Effect of the Environment on Growth-Climate Relationships
Model selection (Table 3) and variance partitioning (Figures 4, 5) conducted at the among-population level confirms the predominant effect of stand environmental conditions on growth response to climate. Environmental model had a better fit with the data for the correlation with summer temperatures (August of the previous year), with previous October precipitation and with current May and August precipitation. Unfortunately, there is no common garden for T. occidentalis cedar species to further experiment our empirical results. A provenance trial has shown that the height growth of T. plicata differed significantly among provenances (Jokela and Cyr, 1977; Russell et al., 2003). However, it did not test the effects of provenances on growth response to climate. Indeed, very few dendroclimatic studies have been conducted on trees in common gardens. For instance, a dendroclimatological study of different provenances of Pinus banksiana Lamb. in a common garden experiment in the eastern Canadian boreal forest concluded that there was no difference in the growth-climate relationships between provenances (Savva et al., 2008). In another common garden experiment conducted with Pinus sylvestris L. in Siberia, provenances accounted for only 15% of the explained variation in the dendroclimatic signal, while 85% was due to the environment (Savva et al., 2002). This is consistent with our results: Variance partitioning revealed that the variables of the environmental model accounted for 79% of the explained variance (Figure 5).
Genetic vs. Growth Climate Relationships
The multivariate analysis revealed that genetic variables were significantly associated with among-populations variations in the growth climate relationships (p = 0.004, Figure 5). Yet, the partial RDA revealed that, when controlling for the environmental variables, this relation was no longer significant (p = 0.074). When considering the growth-climate relationships independently, it appeared that the genetic model best fitted the variability in growth correlation with May and with previous June precipitation. According to variance partitioning, the genetic model's unique contribution exceeded that of the environmental model for those two growth-climate relationships (Figure 4). The genetic model was the second best model (Δ AICc < 2) to explain variations in the correlation with June temperature and with May and August precipitation. These findings suggest that environmental variables and the neutral genetic structure may be correlated, as was also suggested by the high amount of shared variance between the two (Figure 5).
Effect of Population Genetic Composition on Growth-Climate Relationships
We observed that the among-population variation in growth-responses to May temperature and to previous June precipitation (Δ AICc = 0) covariated with the genetic composition (K = 3 clusters) of cedar populations. This is convergent with the study of Bosela et al. (2016), who found contrasting growth responses to climate between two fir genetic lineages. Interestingly, those two growth-climate relationships are associated with mechanisms that are known to be under selection such as (1) dormancy phenology and (2) resistance to drought. First, it is generally accepted that dormancy phenology has a stronger genetic control than growth itself in several tree species (e.g., Howe et al., 2003; Alberto et al., 2013). The timing of growth initiation bears an important evolutionary signification, since there is a trade-off between the decreasing risk of frost damage and the optimization of the growing period length (Nienstaedt, 1974; Chuine, 2010). A common garden experiment evidenced a genetic variation in the date of radial growth initiation for Douglas fir Pseudotsuga menziesii (Mirb.) Franco (Li and Adams, 1994; Gould et al., 2012) and confirmed the existence of a genetic control of cambial reactivation to spring temperature. Second, for the response to drought stress, trees that use water more efficiently would be less affected by hydric stress the year before ring formation, because it allows them to store more carbohydrates or to build more cambial cells for the next growing year. Many experiments have already shown a genetic control for traits relative to drought resistance, such as hydraulic conductivity, stomatal number, stomatal density, and belowground/aboveground biomass ratio (Raj et al., 2011; Richter et al., 2012; Alberto et al., 2013; Moreira et al., 2014). Further, Fan et al. (2008) reported local adaptation to precipitation for T. plicata, for both height increments and transpiration efficiency traits. Because our genetic dataset only included neutral markers, (as in Bosela et al., 2016), further investigations including adaptive genetic markers are needed to test for causal relations between genetic and growth responses to climates. However, our findings provide interesting hypotheses to be tested in future research on cedar adaptation to climate.
Implications for Studies Combining Dendrochronology and Population Genetics
Combined in situ investigation of dendroclimatology and population genetics proved to be a promising approach to study the response to climate of tree species such as cedar, for which no common garden trial is available. It made it possible to estimate both the genetic and growth variabilities within natural populations, as well as differences in growth sensitivity to climate among populations at the landscape scale. Our approach based on variance partitioning and model selection evidenced that most of the current variability in growth response to climate was associated with site environmental conditions, suggesting predominant plastic variations across our latitudinal transect. Partial redundancy analysis revealed that the effects of genetic variables are confounded with environmental effects, although stronger correlation with genetic variables were observed for responses to summer drought and spring temperature. This study was an attempt to demonstrate that combining in situ population genetic variable and tree-rings data without controlling for environmental effects may bring to misleading results and ultimately affect studies' conclusions. We argue that combining tree-rings data and population genetics across vast ecological gradients should be developed to assess the influence of demographic and evolutionary histories of non-model tree species, and to anticipate their responses to climate change. Future efforts should include adaptive genetic markers to better capture signals of genetic control and should comprise relevant environmental descriptors that could blur the effects of genetic background on growth-climate relationships.
Author Contributions
JH, CC, MG, FT, and YB conceived the idea of this manuscript. JH and HX collected the data and conducted the lab measurements. JH and MG conducted the statistical analyses. All authors contributed to the interpretation. JH wrote the manuscript with the aid of all authors.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Aurélie Terrier and Nathalie Isabel for their useful comments on preliminary versions of this manuscript, as well as Cécile Leroy, Mélanie Desrochers, Danielle Charron, Véronique Paul, Pamela Cheers, Isabelle Lamarre, and Daniel Lesieur for their valuable help. This study was conducted with the financial support of the Natural Sciences and Engineering Research Council of Canada (NSERC) through its CREATE program in Forest Modeling Complexity and of the French program Paris Nouveau Monde of the heSam consortium (Ph.D. grants to JH). This research was also funded by a NSERC strategic grant (STPGP336871) to FT. The research was carried out within the framework of the MONTABOR International Associated Laboratory (LIA France-Canada CNRS-UM2-EPHE-UQAT-UQAM-UQAC) and the European Union IRSES NewForest program.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fevo.2016.00123/full#supplementary-material
References
Aitken, S. N., Yeaman, S., Holliday, J. A., Wang, T., and Curtis McLane, S. (2008). Adaptation, migration or extirpation: climate change outcomes for tree populations. Evol. Appl. 1, 95–111. doi: 10.1111/j.1752-4571.2007.00013.x
Alberto, F. J., Aitken, S. N., Alía, R., González-Martínez, S. C., Hänninen, H., Kremer, A., et al. (2013). Potential for evolutionary responses to climate change–evidence from tree populations. Global Change Biol. 19, 1645–1661. doi: 10.1111/gcb.12181
Babst, F., Poulter, B., Trouet, V., Tan, K., Neuwirth, B., Wilson, R., et al. (2013). Site- and species-specific responses of forest growth to climate across the European continent. Global Ecol. Biogeogr. 22, 706–717. doi: 10.1111/geb.12023
Beaudoin, A., Bernier, P. Y., Guindon, L., Villemaire, P., Guo, X. J., Stinson, G., et al. (2014). Mapping attributes of Canada's forests at moderate resolution through kNN and MODIS imagery. Can. J. For. Res. 44, 521–532. doi: 10.1139/cjfr-2013-0401
Beck, P. S. A., Juday, G. P., Alix, C., Barber, V. A., Winslow, S. E., Sousa, E. E., et al. (2011). Changes in forest productivity across Alaska consistent with biome shift. Ecol. Lett. 14, 373–379. doi: 10.1111/j.1461-0248.2011.01598.x
Berner, L. T., Beck, P. S. A., Bunn, A. G., Lloyd, A. H., and Goetz, S. J. (2011). High-latitude tree growth and satellite vegetation indices: correlations and trends in Russia and Canada (1982–2008). J. Geophys. Res. 116, G01015. doi: 10.1029/2010JG001475
Biondi, F., and Waikul, K. (2004). DENDROCLIM2002: a C++ program for statistical calibration of climate signals in tree-ring chronologies. Comput. Geosci. 30, 303–311. doi: 10.1016/j.cageo.2003.11.004
Bosela, M., Popa, I., Gömöry, D., Longauer, R., Tobin, B., Kyncl, J., et al. (2016). Effects of post-glacial phylogeny and genetic diversity on the growth variability and climate sensitivity of European silver fir. J. Ecol. 104, 716–724. doi: 10.1111/1365-2745.12561
Brienen, R. J. W., Gloor, M., and Ziv, G. (2016). Tree demography dominates long-term growth trends inferred from tree rings. Glob. Chang. Biol. doi: 10.1111/gcb.13410. [Epub ahead of print].
Bunn, A. G. (2008). A dendrochronology program library in R (dplR). Dendrochronologia 26, 115–124. doi: 10.1016/j.dendro.2008.01.002
Burnham, K. P., and Anderson, D. R. (2010). Model Selection and Multi-Model Inference: A Practical Information-Theoretic Approach. New York, NY: Springer-Verlag.
Chapin, F. S. I., Chapin, M. C., Matson, P. A., and Vitousek, P. (2011). Principles of Terrestrial Ecosystem Ecology. New York, NY: Springer-Verlag.
Chuine, I. (2010). Why does phenology drive species distribution? Philos. Trans. R. Soc. Lond. B Biol. Sci. 365, 3149–3160. doi: 10.1098/rstb.2010.0142
Cook, E., and Kairiūkštis, L. (1990). Methods of Dendrochronology: Applications in the Environmental Sciences. Dordrecht: Kluwer Academic Publishers.
Davis, M. B., and Shaw, R. G. (2001). Range shifts and adaptive responses to quaternary climate change. Science 292, 673–679. doi: 10.1126/science.292.5517.673
Evanno, G., Regnaut, S., and Goudet, J. (2005). Detecting the number of clusters of individuals using the software structure: a simulation study. Mol. Ecol. 14, 2611–2620. doi: 10.1111/j.1365-294X.2005.02553.x
Falush, D., Stephens, M., and Pritchard, J. K. (2003). Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics 164, 1567–1587.
Fan, S., Grossnickle, S. C., and Russell, J. H. (2008). Morphological and physiological variation in western redcedar (Thuja plicata) populations under contrasting soil water conditions. Trees 22, 671–683. doi: 10.1007/s00468-008-0225-8
Filion, L., and Payette, S. (2010). La Dendroécologie: Principes, Méthodes et Applications. Québec, QC: Les Presses de l'Universite Laval.
Franks, S. J., Weber, J. J., and Aitken, S. N. (2014). Evolutionary and plastic responses to climate change in terrestrial plant populations. Evol. Appl. 7, 123–139. doi: 10.1111/eva.12112
Gewehr, S., Drobyshev, I., Berninger, F., and Bergeron, Y. (2014). Soil characteristics mediate the distribution and response of boreal trees to climatic variability. Can. J. For. Res. 44, 487–498. doi: 10.1139/cjfr-2013-0481
Gienapp, P., Teplitsky, C., Alho, J. S., Mills, J. A., and Merilä, J. (2008). Climate change and evolution: disentangling environmental and genetic responses. Mol. Ecol. 17, 167–178. doi: 10.1111/j.1365-294X.2007.03413.x
Gould, P. J., Harrington, C. A., and Clair, J. B. S. (2012). Growth phenology of coast Douglas-fir seed sources planted in diverse environments. Tree Physiol. 32, 1482–1496. doi: 10.1093/treephys/tps106
Guo, Q., Taper, M., Schoenberger, M., and Brandle, J. (2005). Spatial-temporal population dynamics across species range: from centre to margin. Oikos 108, 47–57. doi: 10.1111/j.0030-1299.2005.13149.x
Hartl, D. L., and Clark, A. G. (1997). Principles of Population Genetics. Sunderland, MA: Sinauer associates Inc.
Hofmeyer, P. V., Kenefic, L. S., and Seymour, R. S. (2009). Northern white-cedar ecology and silviculture in the northeastern United States and southeastern Canada: a synthesis of knowledge. North. J. Appl. For. 26, 21–27.
Housset, J. M., Girardin, M. P., Baconnet, M., Carcaillet, C., and Bergeron, Y. (2015). Unexpected warming-induced growth decline in Thuja occidentalis at its northern limits in North America. J. Biogeogr. 42, 1233–1245. doi: 10.1111/jbi.12508
Howe, G. T., Aitken, S. N., Neale, D. B., Jermstad, K. D., Wheeler, N. C., and Chen, T. H. (2003). From genotype to phenotype: unraveling the complexities of cold adaptation in forest trees. Can. J. Bot. 81, 1247–1266. doi: 10.1139/b03-141
Huang, J.-G., Bergeron, Y., Berninger, F., Zhai, L., Tardif, J. C., and Denneler, B. (2013). Impact of future climate on radial growth of four major boreal tree species in the eastern Canadian boreal forest. PLoS ONE 8:e56758. doi: 10.1371/journal.pone.0056758
Huang, J., Tardif, J. C., Bergeron, Y., Denneler, B., Berninger, F., and Girardin, M. P. (2010). Radial growth response of four dominant boreal tree species to climate along a latitudinal gradient in the eastern Canadian boreal forest. Global Change Biol. 16, 711–731. doi: 10.1111/j.1365-2486.2009.01990.x
IPCC (2013). Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the IPCC. Cambridge University Press, Cambridge; New York, NY.
Jokela, J. J., and Cyr, C. L. (1977). “Performance of northern white-cedar in central Illinois,” in Proceedings of the Thirteenth Lake States Forest Tree Improvement Conference (St. Paul, MN: USDA Forest Service, North Central Forest Experiment Station), 100–106.
King, G. M., Gugerli, F., Fonti, P., and Frank, D. C. (2013). Tree growth response along an elevational gradient: climate or genetics? Oecologia 173, 1587–1600. doi: 10.1007/s00442-013-2696-6
Lapointe−Garant, M., Huang, J., Gea−izquierdo, G., Raulier, F., Bernier, P., and Berninger, F. (2010). Use of tree rings to study the effect of climate change on trembling aspen in Québec. Global Change Biol. 16, 2039–2051. doi: 10.1111/j.1365-2486.2009.02048.x
Latutrie, M., Mérian, P., Picq, S., Bergeron, Y., and Tremblay, F. (2015). The effects of genetic diversity, climate and defoliation events on trembling aspen growth performance across Canada. Tree Genet. Genomes 11, 96. doi: 10.1007/s11295-015-0925-3
Li, P., and Adams, W. T. (1994). Genetic variation in cambial phenology of coastal Douglas-fir. Can. J. For. Res. 24, 1864–1870. doi: 10.1139/x94-240
Little, E. L. J. (1971). Atlas of United States Trees, Vol. 1. Conifers and Important Hardwoods. Washington, DC: Miscellaneous Publication 1146. USDA Forest Service.
Lloyd, A. H., Bunn, A. G., and Berner, L. (2011). A latitudinal gradient in tree growth response to climate warming in the Siberian taiga. Global Change Biol. 17, 1935–1945. doi: 10.1111/j.1365-2486.2010.02360.x
McLane, S. C., Daniels, L. D., and Aitken, S. N. (2011). Climate impacts on lodgepole pine (Pinus contorta) radial growth in a provenance experiment. For. Ecol. Manag. 262, 115–123. doi: 10.1016/j.foreco.2011.03.007
Montwé, D., Isaac-Renton, M., Hamann, A., and Spiecker, H. (2016). Drought tolerance and growth in populations of a wide-ranging tree species indicate climate change risks for the boreal north. Global Change Biol. 22, 806–815. doi: 10.1111/gcb.13123
Moreira, B., Castellanos, M. C., and Pausas, J. G. (2014). Genetic component of flammability variation in a Mediterranean shrub. Mol. Ecol. 23, 1213–1223. doi: 10.1111/mec.12665
Nienstaedt, H. (1974). “Genetic variation in some phenological characteristics of forest trees,” in Phenology and Seasonality Modeling, ed H. Lieth (Berlin:Springer), 389–400.
Oksanen, J., Blanchet, F. G., Kindt, R., Legendre, P., Minchin, P. R., O'Hara, B., et al. (2013). vegan: Community Ecology Package. R Package Version 2.0-10. Available online at: http://CRAN.R-project.org/package=vegan
Peakall, R., and Smouse, P. E. (2012). GenAlEx 6.5: genetic analysis in Excel. Population genetic software for teaching and research—an update. Bioinformatics 28, 2537–2539. doi: 10.1093/bioinformatics/bts460
Polechová, J., Barton, N., and Marion, G. (2009). Species' range: adaptation in space and time. Am. Nat. 174, E186–E204. doi: 10.1086/605958
Pritchard, J. K., Stephens, M., and Donnelly, P. (2000). Inference of population structure using multilocus genotype data. Genetics 155, 945–959.
Raj, S., Bräutigam, K., Hamanishi, E. T., Wilkins, O., Thomas, B. R., Schroeder, W., et al. (2011). Clone history shapes Populus drought responses. Proc. Nat. Acad. Sci.U.S.A. 108, 12521–12526. doi: 10.1073/pnas.1103341108
Régnière, J., and Bolstad, P. (1994). Statistical simulation of daily air temperature patterns in Eastern North America to forecast seasonal events in insect pest management. Environ. Entomol. 23, 1368–1380. doi: 10.1093/ee/23.6.1368
Richter, S., Kipfer, T., Wohlgemuth, T., Calderón Guerrero, C., Ghazoul, J., and Moser, B. (2012). Phenotypic plasticity facilitates resistance to climate change in a highly variable environment. Oecologia 169, 269–279. doi: 10.1007/s00442-011-2191-x
Russell, J. H., Burdon, R. D., and Yanchuk, A. D. (2003). Inbreeding depression and variance structures for height and adaptation in self-and outcross Thuja plicata families in varying environments. For. Genet. 10, 171–184.
Savolainen, O., Pyhäjärvi, T., and Knürr, T. (2007). Gene flow and local adaptation in trees. Annu. Rev. Ecol. Evol. Syst. 38, 595–619. doi: 10.1146/annurev.ecolsys.38.091206.095646
Savva, Y., Bergeron, Y., Denneler, B., Koubaa, A., and Tremblay, F. (2008). Effect of interannual climate variations on radial growth of jack pine provenances in Petawawa, Ontario. Can. J. For. Res. 38, 619–630. doi: 10.1139/X07-178
Savva, Y., Schweingruber, F. H., Milyutin, L. I., and Vaganov, E. (2002). Genetic and environmental signals in tree rings from different provenances of Pinus sylvestris L. Planted in the southern taiga, central Siberia. Trees Struct. Funct. 16, 313–324. doi: 10.1007/s00468-001-0136-4
Sexton, J. P., McIntyre, P. J., Angert, A. L., and Rice, K. J. (2009). Evolution and ecology of species range limits. Annu. Rev. Ecol. Evol. Syst. 40, 415–436. doi: 10.1146/annurev.ecolsys.110308.120317
Taeger, S., Zang, C., Liesebach, M., Schneck, V., and Menzel, A. (2013). Impact of climate and drought events on the growth of Scots pine (Pinus sylvestris L.) provenances. For. Ecol. Manag. 307, 30–42. doi: 10.1016/j.foreco.2013.06.053
Keywords: climate change, dendrochronology, population genetics, marginal populations, radial growth
Citation: Housset JM, Carcaillet C, Girardin MP, Xu H, Tremblay F and Bergeron Y (2016) In situ Comparison of Tree-Ring Responses to Climate and Population Genetics: The Need to Control for Local Climate and Site Variables. Front. Ecol. Evol. 4:123. doi: 10.3389/fevo.2016.00123
Received: 05 August 2016; Accepted: 05 October 2016;
Published: 27 October 2016.
Edited by:
Marco A. Molina-Montenegro, University of Talca, ChileReviewed by:
Jesús Julio Camarero, Spanish National Research Council, SpainIan Sajid Acuña Rodriguez, Centro de Estudios Avanzados en Zonas Áridas (CEAZA), Chile
Copyright © 2016 Housset, Carcaillet, Girardin, Xu, Tremblay and Bergeron. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Christopher Carcaillet, Y2hyaXN0b3BoZXIuY2FyY2FpbGxldEBlcGhlLnNvcmJvbm5lLmZy
 Johann M. Housset
Johann M. Housset Christopher Carcaillet
Christopher Carcaillet Martin P. Girardin2,5
Martin P. Girardin2,5 Huaitong Xu
Huaitong Xu Yves Bergeron
Yves Bergeron