A novel inversion method of slope rock mechanical parameters using differential evolution gray wolf algorithm to optimize support vector regression

Introduction: The stability evaluation and deformation prediction in geotechnical engineering depend on accurate rock mass mechanical parameters (RMMPs). The selection of these parameters directly influences the reliability of analysis. The conventional techniques used to assess the RMMPs face considerable challenges in real-world applications, which necessitates the need to investigate novel approaches.

Methods: This paper proposes a displacement back-analysis (DBA) approach that utilizes support vector regression (SVR) optimized by differential evolution grey wolf algorithm (DE-GWO) to invert the RMMPs, which improves global optimization capability and inversion accuracy. Firstly, the uniform test design method is employed to outline the RMMPs for inversion, anddisplacement calculations are performed using FLAC^3D to generate learning and testing samples. Secondly, the DE-GWO, particle swarm optimization (PSO), genetic algorithm (GA), and SVR are integrated to identify the optimal superparameters, while the nonlinear mapping relationship between inversion parameters and displacements is established. Finally, the mechanical parameters to be measured are inversed based on field-measured displacements. This model is utilized to invert the RMMPs for a mining site located in Yunnan Province, and the inversed RMMPs are utilized for forward analysis. The results demonstrate that the DE-GWO-SVR method achieves the best results but requires the shortest inversion time.

Results: The inversed RMMPs fall within acceptable ranges, while the error between the forward and monitored displacements is less than 10%, with a maximum deviation of 9.52%. This research introduces an innovative approach for assessing the RMMPs.

1 Introduction

With the long-term exploitation of shallow mineral resources, numerous high and steep slopes have formed in open-pit mines worldwide. During the mining process, the study of slope stability and the analysis of support methods have become unavoidable technical requirements (Li et al., 2024). These tasks rely on precise mechanical parameters of slope rock masses as their foundation. Therefore, in slope remediation projects, accurately obtaining the mechanical parameters of slope rock masses is particularly critical. Prior to the construction of geotechnical engineering projects, scientific research institutions often create specific designs according to established specifications. In this context, the appropriate selection of RMMPs is crucial for assessing the stability and predicting the deformation of engineering structures (Liu et al., 2024; Zhou YJ. et al., 2024). Erroneous parameter values can indirectly lead to significant issues, such as structural collapse or resource wastage, due to overly conservative designs.

Traditional methods for determining the RMMPs include laboratory testing, empirical estimation, and in situ testing (Liu et al., 2022; Umbach and Middendorf, 2024). In-situ testing often requires substantial manpower and financial resources (Liu et al., 2023; Guo et al., 2021; Liu et al., 2020), resulting in lengthy testing cycles (Andhika, 2023). Given these constraints, researchers aim to identify reliable, convenient, and cost-effective techniques for evaluating the RMMPs while advancing traditional testing methodologies (Zhao et al., 2022; Li et al., 2023; Hu, 2023). Consequently, researchers closely pay attention to raw observation data related to undetermined mechanical parameters of rock masses and use them as a prototype for parameter inversion. Displacement monitoring, recognized as one of the most accessible and expedient forms of data, has garnered significant attention (Zhang et al., 2021). As a result, the back-analysis method that utilizes field-measured displacements has become a focal point of research in this field, as this method can compensate for the limitations of traditional methods, such as high variability and cost.

In recent years, rapid advancement of computer technology has led to the development of various machine-learning-based inversion methods (Wu et al., 2024; Pan B et al., 2024; Chen et al., 2024). Zhuang et al. (2019) proposed a DBA model based on SVR optimized by the Multi Strategy artificial fish swarm algorithm (MAFSA) for identifying mechanical parameters. The application of this method for the inversion of RMMPs in the Heshi Tunnel demonstrated significant effectiveness. Additionally, Zhang et al. (2021) developed an intelligent optimization algorithm that merges PSO technology with Gaussian process machine learning (GP) theory, and subsequently integrated this algorithm with the finite difference method (FDM) to develop a DBA method termed PSO-GP-FDM. This method was applied to the back-analysis of the RMMPs at the Tai’an pumped storage power station. The above inversion method ignores the problem that the optimization process can easily fall into local optimal solutions, which leads to poor stability in the optimization process and problematic inversion results (Luo et al., 2024; Wang et al., 2024; Zhou Y. et al., 2024). To this end Li et al. (2022) integrated the Grasshopper Optimization Algorithm (GOA), known for its superior global optimization capability, with Gaussian Process Regression (GPR), a machine learning with strong fitting capabilities, to tackle the challenges of time-intensive numerical calculations. The GOA-GPR-FLAC^3D approach that arises from this integration serves as a tool for DBA in underground engineering. Chong et al. (2018) introduced a DBA method based on a Gradient Boosting Regression Tree (GBRT) and Firefly Algorithm (FA), where GBRT serves as an example-based learning method to replace numerical modeling, and the algorithm is utilized for back-analysis. However, these methods require a relatively large number of samples, leading to slow inversion during the optimization process (Guo et al., 2022; Lin et al., 2023).

To address the challenge of large sample requirements, this study selects the SVR, which necessitates fewer samples for effective inversion. This algorithm is also adept at handling high-dimensional practical problems such as nonlinear issues. Furthermore, the rationality of parameter selection during the SVR inversion process significantly influences the practicability and reliability of the model. This paper employs a novel grey wolf algorithm (GWO) to optimize SVR parameters, which imitates the hierarchical structure of wolves and demonstrates a strong optimization potential (Shial and Sahoo, 2023). To mitigate the tendency for local optimization inherent in the algorithm, this study combines the differential evolution algorithm (DE) with the GWO to form a coupled differential evolution grey wolf optimization algorithm (DE-GWO). This algorithm enhances the global search capabilities through mutation, crossover, and selection to optimize efficient intelligent optimization algorithm of the support vector regression (SVR). Compared with the traditional Bayesian inversion method, which uses probabilistic sampling method and requires a large number of samples, DE-GWO-SVR uses populations for intelligent global search without a priori assumptions, dramatically improves the computational efficiency by parallel searching, and subsequently adopts SVR kernel function, which has a relatively small demand for samples, for regression, which has an obvious improvement in adaptability to nonlinear problems.

Herein, the DE-GWO-SVR algorithm for the inversion of RMMPs is established, and the training and testing samples are constructed in conjunction with FLAC^3D. The examination of three essential mechanical parameters—elastic modulus E, cohesion c, and internal friction angle φ—necessary for inversion design of field-measured displacement demonstrates the algorithm’s reduced computation time and enhanced inversion efficiency. The viability of this inversion approach is confirmed through back-analysis by comparing the results of numerical simulations with field-measured data.

2 Algorithm principle

2.1 SVR

SVR, proposed by Cortes and vapink V in the 1990s (Ajin and Segoni, 2024; Cortes and Vapnik, 1995), has emerged as a highly successful supervision technique in recent years. This learning model offers advantages such as lower sample requirements and the ability to handle nonlinear data. SVR, which serves as a branch of SVM, is specifically designed for fitting nonlinear data.

Given the training sample D = {(x1,y1), (x1,y1),…, (xm, ym)}, where yi∈R, the objective is to learn a regression model such that f(x) closely approximates y, with w and b as the model parameters to be determined.

SVR utilizes the regression function of Equation 1 to map the input space into a high-dimensional feature space for hyperplane establishment (Ren et al., 2023).

$f\left(x\right)=w^T\phi \left(x\right)+b(1)$

where w is the weight vector that controls smoothness, b is the offset parameter, and $\mathrm{\phi }\left(x\right)$ is the mapping function from low dimension to high dimension.

The goal of SVR is to minimize the distance between the hyperplane and the farthest sample point, so that the data can be fitted by the hyperplane (Dai and Hu, 2024; Wang et al., 2022). The SVR schematic is shown in Figure 1. To avoid excessive penalization, a threshold is set around the regression line of the model, which allows all data points within this threshold to incur no penalties for their errors (Qin et al., 2022).

Figure 1

Figure 1. Schematic representation of the SVR model.

The optimization objective of SVR is shown in Equation 2:

$\underset{w,b}{\mathit{min}}\frac{1}{2}{‖\omega ‖}^2(2)$

The insensitive loss function is Equation 3:

$l_{\epsilon }\left(z\right)\left\{\begin{array}{ll}0& \left|z\right|\le \epsilon \\ \left|z\right|-\epsilon & \left|z\right|>\epsilon \end{array}\right.(3)$

Consequently, the optimization problem for the SVR model can be articulated as in Equation 4:

$\underset{w,b}{\mathit{min}}\frac{1}{2}\parallel w{\parallel }^2+C{\displaystyle \sum _{I=1}^m}{l}_{\epsilon }\left(f\left(x_i\right)-y_i\right)(4)$

In practical applications, determining the appropriate $\mathrm{\epsilon }$ to ensure that the majority of data points are contained within the interval presents a significant challenge; thus, the relaxation variable ${\mathrm{\xi }}_i,{\widehat{\xi }}_i$ is introduced to relax the interval requirements of the function appropriately while allowing some samples not to be in the interval.

Equation 5 can be rewritten as:

$\left.\begin{array}{c}\underset{w,b,{\xi }_i,{\widehat{\xi }}_i}{\mathit{min}}\frac{1}{2}\parallel w{\parallel }^2+C{\displaystyle \sum _{I=1}^m}\left({\xi }_i,{\widehat{\xi }}_i\right)\\ s.t.f\left(x_i\right)-y_i\le \epsilon +{\xi }_i\\ y_i-f\left(x_i\right)\le \epsilon +{\widehat{\xi }}_i\\ {\xi }_i\ge 0,{\widehat{\xi }}_i\ge 0,i=1,2,\dots m\end{array}\right\}(5)$

Introducing Lagrange multiplier ${\mathrm{\mu }}_{\mathrm{i}},\mathrm{\alpha }$. As in Equation 6:

$\begin{array}{c}L\left(w,b,\alpha ,\widehat{\alpha },\xi ,\widehat{\xi },\mu ,\widehat{\mu }\right)=\frac{1}{2}\parallel w{\parallel }^2+C{\displaystyle \sum _{i=1}^m}\left({\xi }_i+{\widehat{\xi }}_i\right)-{\displaystyle \sum _{i=1}^m}{\xi }_i{\mu }_i-{\displaystyle \sum _{i=1}^m}{\widehat{\xi }}_i{\widehat{\mu }}_i\\ +{\displaystyle \sum _{i=1}^m}{\alpha }_i\left(f\left(x_i\right)-y_i-\epsilon -{\xi }_i\right)\\ +{\displaystyle \sum _{i=1}^m}{\widehat{\alpha }}_i\left(y_i-f\left(x_i\right)-\epsilon -{\widehat{\xi }}_i\right)\end{array}(6)$

The partial derivatives of α from b must be zero. This process adheres to the KKT condition, and we obtain Equation 7:

$\begin{array}{c}w={\displaystyle \sum _{i=1}^m}\left({\widehat{\alpha }}_i-{\alpha }_i\right)x_{i}s.t.\\ {\displaystyle {\alpha }_i}(f\left(x_i\right)-y_i-\epsilon -{\xi }_i=0\\ {\widehat{\alpha }}_i(y_i-f\left(x_i\right)-\epsilon -{\widehat{\xi }}_i=0\\ {\alpha }_i{\widehat{\alpha }}_i=0,{\xi }_i{\widehat{\xi }}_i=0\\ \left(C-{\alpha }_i\right){\xi }_i=0,\left(C-{\widehat{\alpha }}_i\right){\widehat{\xi }}_i=0\end{array}(7)$

The solution obtained is as in Equation 8:

$\begin{array}{c}f\left(x\right)={\displaystyle \sum _{i=1}^m}\left({\widehat{\alpha }}_i-{\alpha }_i\right)x_i^{T}x+b\\ b=y_i+\epsilon -{\displaystyle \sum _{j=1}^m}\left({\widehat{\alpha }}_j-{\alpha }_j\right)x_i^T{x}_i\end{array}(8)$

2.2 DE-GWO

2.2.1 Grey wolf algorithm

Sang-To et al. (2022) proposed the grey wolf optimizer (GWO) algorithm in 2014 to achieve optimization objectives. The GWO is characterized by fewer adjustable parameters and fast convergence speed (Zhu et al., 2024), and has attracted extensive attentions in parameter optimization process.

During hunting, the wolves follow a strict pyramid social hierarchy. The highest-ranking grey wolf, α, holds decision-making power. The remaining grey wolves who cooperate in predation are ranked as β, δ, and ω, respectively. Lower-ranked wolves serve their superiors and dominate the ranks below. The social hierarchy of wolves is shown in Figure 2.

Figure 2

Figure 2. Social hierarchy of wolves.

During the algorithm’s optimization stage, the population’s positions are updated by Equation 9:

$\begin{array}{c}D=\left|C•X_P^t-X^t\right|\\ X^{t+1}=X_P^t-A•D\end{array}(9)$

where D is the distance between grey wolf and prey; t is the number of iterations in the optimization process; X_p(t) and X(t) are the positions of the prey and the search individual after the t-th iteration, respectively; and A and C are the optimization process parameters. As shown in Equation 10.

$\begin{array}{c}a\left(t\right)=2\left(1-t/T_{\mathit{max}}\right)\\ A=2a{r}_1-aC=2r_2\end{array}(10)$

where T_max denotes the maximum number of iterations for the optimization process. Throughout this process, the parameter a gradually decreases from 2 to 0, while r1 and r2 are random values ranging from 0 to 1.

The three leading wolves, α, β and δ, are considered to have the best knowledge of prey locations. Therefore, during iterations, the top three optimal fitness values are assigned to these leading wolves, and then these wolves collectively determine their movement directions and automatically update their positions according to this information. This process is expressed in Equations 11, 12

$\left\{\begin{array}{c}{D}_{\alpha }=\left|C_1•X_{\alpha }^t-X^t\right|\\ D_{\beta }=\left|C_2•X_{\beta }^t-X^t\right|\\ D_{\delta }=\left|C_3•X_{\delta }^t-X^t\right|\end{array}\right.(11)$

$\left\{\begin{array}{l}{X}_1=X_{\alpha }^t-A_1•D_{\alpha }\\ X_2=X_{\beta }^t-A_2•D_{\beta }\\ X_3=X_{\delta }^t-A_3•D_{\delta }\\ X^{t+1}=\left(X_1+X2+X3\right)/3\end{array}\right.(12)$

where D_α, D_β, and D_δ are the distances between the remaining individuals in wolf pack ω and the three leading wolves α, β, and δ, respectively; X₁, X₂ and X₃ indicate the next movement directions of the remaining individuals in wolf pack ω under the leadership of the three leading wolves α, β, and δ, respectively; $X_{\beta }^t$ and $X_{\delta }^t$ are the control parameters after t iterations; A₂ and C₂ are the control parameters corresponding to the leading wolf β; A₃ and C₃ are the control parameters corresponding to the leading wolf δ.

2.2.2 DE algorithm

The DE algorithm follows three steps of mutation, crossover, and selection to enhance the global search capability. Its mathematical model is outlined in Table 1 (Zu et al., 2022). The tests demonstrate the algorithm’s effectiveness in addressing complex optimization challenges, including discontinuous and multi-peak problems.

Table 1

Table 1. Mathematical model of the DE algorithm.

2.2.2.1 Mutation operation

The fundamental principle involves calculating the vector difference between two randomly selected individuals from the population, which is subsequently combined with the individual that is being mutated. The mutation operation is pivotal to the DE algorithm’s robust global search capability.

2.2.2.2 Crossover operation

Exchange elements between the individual undergoing mutation and the new mutated individual from step (1).

2.2.2.3 Selection action

The algorithm retains the offspring when they outperform their parents; otherwise, the parents are carried forward to the next-generation.

2.2.3 Inversion of RMMPs based on DE-GWO-SVR

The following steps outline the proposed methodology, as illustrated in Figure 3:

Step 1: The inversion range of RMMPs is determined through a combination of laboratory rock mechanics tests and numerical simulations. A dataset is constructed using the orthogonal test method, and then it is divided into a training set and a testing set.

Step 2: The size and value range of parameters are set for the DE-GWO and SVR algorithms. Initialize the grey wolf population, including the parent, variation, and offspring populations. The values of $C,\phi$ that need to be optimized determine the position of each wolf.

Step 3: Execute the DE-GWO algorithm to update position of grey wolf in the main layer, and take the optimal solution of the updated position of the grey wolf in the main layer as the final solution.

Step 4: The model is developed using the optimally updated optimal parameters $C*,\phi *$ through iteration, and the SVR algorithm is utilized to invert the RMMPs.

Step 5: The inversed RMMPs are input into the three-dimensional numerical model for displacement forward analysis. The calculation results are compared with field-measured displacements for accuracy assessment (Wu et al., 2021).

Figure 3

Figure 3. Flow chart of mechanical parameter inversion of the DE-GWO-SVR model.

3 Engineering application

The study site is a metal mine located in Yunnan Province. The geographic location of the mine is shown in Figure 4, which is characterized by a combination of open-pit and underground mining. The upper section of the mine was mined through open-pit mining, with a designed bottom elevation of 1,384 m, a closed circle elevation of 1,834 m, a final boundary slope height of 120 m, a concave open-pit slope height of 420 m, and a tota. l slope height of 540 m. Following the completion of open-pit mining, ultrahigh slopes were formed. Currently, after optimizing the open-pit boundary, the western slope is in a state of expansion, which necessitates urgent stability analysis for both the slopes and underground mining. Accurate mechanical parameters of rock masses are essential for follow-up work. This study primarily focuses on determining the mechanical parameters for limestone and porphyry. Due to difficulties in accurately determining the mechanical parameter values of weak interlayers, these parameters are derived from relevant research findings.

Figure 4

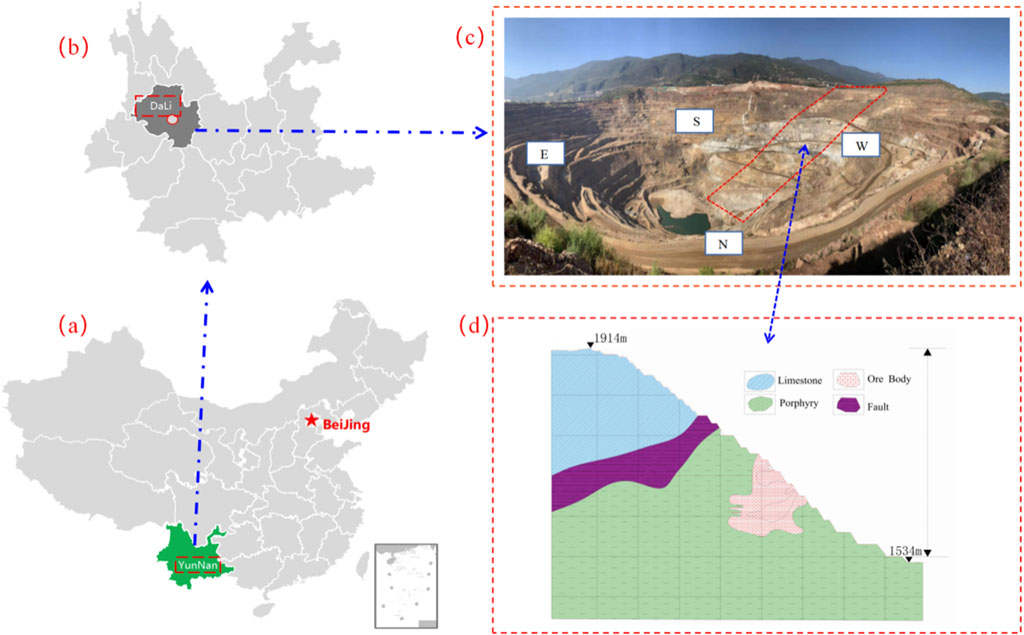
Figure 4. Geographic location of the mine. (a) Map of China; (b) Map of Yunnan Province; (c) Open pit mine slopes; (d) Slope inversion regional profiles.

3.1 Calculation model and layout of monitoring points

The 3D model uses the final open-pit bottom elevation as the coordinate origin, and the simulation range involves the western slope of the stope. The upper section of the slope consists of limestone, while the lower section comprises porphyry, which is intersected by the F6 fault. The peak of the slope reaches an elevation of 1,914 m, while the lowest elevation is recorded at 1,534 m. Monitoring points for slope displacement are arranged at the model elevation of 1,800 m, as illustrated in Figure 5. The model is comprised of 196,070 nodes and 241,272 elements, where the grids around the slope monitoring points are refined as Mohr Coulomb (Binaya et al., 2023) constitutive model.

Figure 5

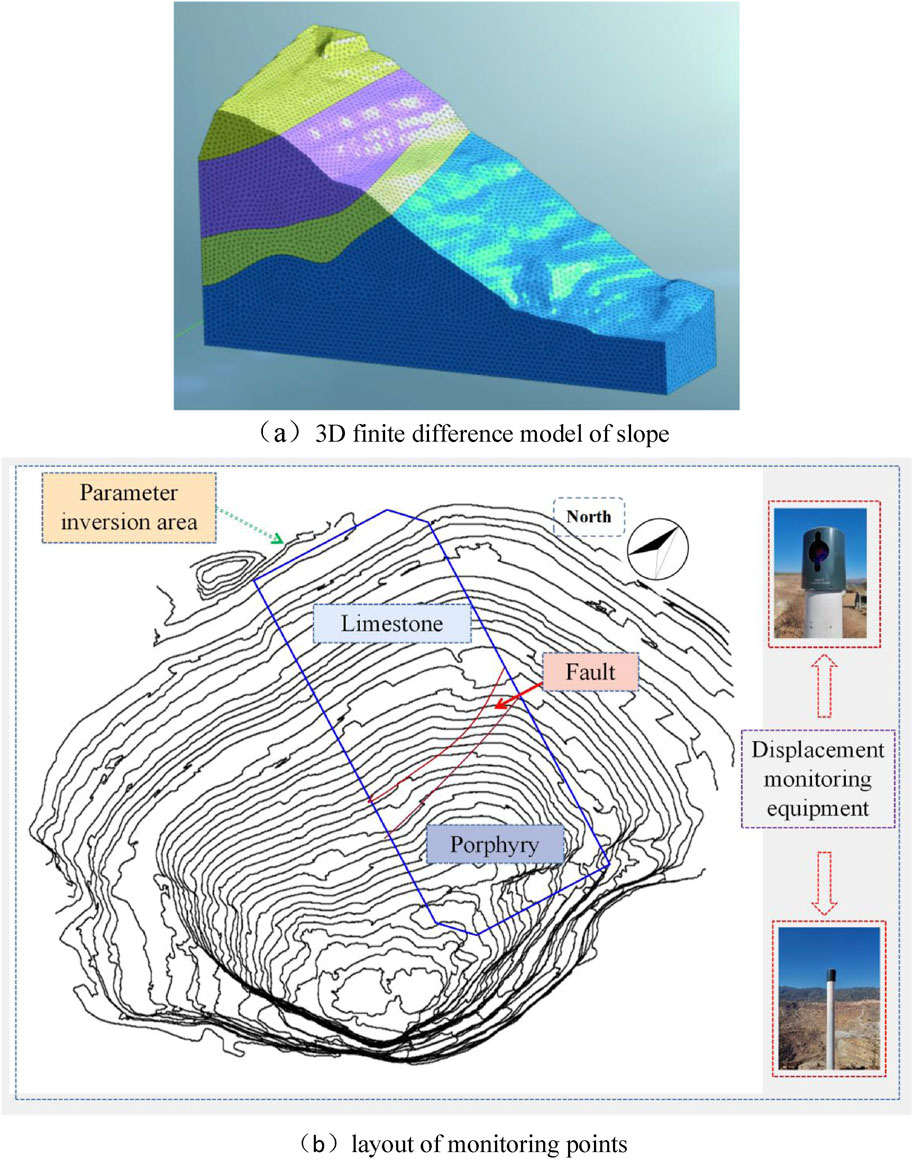
Figure 5. 3D finite difference model of slope and layout of monitoring points (a) 3D finite difference model of slope (b) layout of monitoring points.

3.2 Load application and excavation steps

The loads considered in the inversion calculation using FLAC^3D include initial self-weight stress resulting from the slope’s self-weight, tectonic stress induced by long-term crustal movements, and self-weight stress arising from equipment production and transportation.

Excavation is conducted progressively in accordance with the actual situation of the site during lateral expansion.

3.3 Determination of the parameter inversion range and test scheme

Given that Poisson’s ratio exhibits minimal variation during the mechanical parameter reduction process, it is not considered in the inversion. Instead, the inversion focuses on parameters sensitive to deformation, including the E, c, and φ, while the parameters of the fault are excluded from the inversion process.

The mechanical parameters of limestone and porphyry are obtained through laboratory rock mechanics tests and Hoek‒Brown strength criterion reduction. The rock specimens of limestone and porphyry were divided into two groups of five pieces each, which were immersed in water for 48 h, after which uniaxial compression tests were carried out, after which uniaxial compression tests were performed as depicted in Figure 6:

Figure 6

Figure 6. Laboratory uniaxial compression test.

Based on the field investigation and indoor uniaxial compression test results, the mechanical parameters of the rock mass are calculated by the Hooke Brown strength criterion (Table 2).

Table 2

Table 2. Calculation results of RMMPs.

Considering that the surrounding rock of the slope at the site is affected by weathering and other factors, the calculation results are different from the actual rock mass mechanical parameters, in order to derive the accurate mechanical parameters of the rock mass, the authors set the up and down ranges with each parameter as a benchmark on the basis of the calculation results, and finally determined the 21 group of parameters, see Table 3 for details.

Table 3

Table 3. Value range of RMMPs.

Uniform test design scientifically selects representative test combinations through orthogonal tables to cover the comprehensive information of multiple factors and levels with the least number of times, which is both efficient (reducing resource consumption), balanced (evenly distributing test points) and easy to analyze (clearly comparing the effects of the factors), and is widely used in the fields of industrial optimization, scientific research experiments, etc., which can significantly improve the research efficiency and reliability of multivariate problems (Wang, 2024). This approach not only significantly lowers the number of test points but also successfully achieves the intended test outcomes. By considering influencing factors and test levels, a uniform design table U₂^*(₁ 21⁷) is selected, with Columns 1, 3, and 4 utilized for scheme combinations. The test scheme is outlined in Table 4.

Table 4

Table 4. Orthogonal design table of inversion test scheme.

The inversion process is based on the DE-GWO-SVR model. The RMMPs in the aforementioned test scheme are assigned to the 3D slope model, and simulation calculations are conducted using FLAC^3D to determine the displacements at various monitoring points, so as to form the data samples required for the parameter inversion model, as illustrated in Table 5. A total of 21 combination schemes are utilized. All samples are employed in the training set, and from this set, 5 groups are randomly chosen to form the testing set.

Table 5

Table 5. Data samples range for the parameter inversion model.

4 Analysis of inversion results

Based on the data samples for inversion models, DE-GWO, PSO and BP are used to optimize the c and g of the SVR. The parameters for SVR optimized by DE-GWO are presented in Table 6.

Table 6

Table 6. Parameters for SVR after DE-GWO optimization.

The optimized parameters are input into the SVR, machine for model training, which establishes a nonlinear mapping relationship between the RMMPs, to be inverted and the simulated displacements. The comparison results between the inversed and original parameters of limestone and porphyry are displayed in Table 7.

Table 7

Table 7. Comparison between the inversed and original parameters of limestone and porphyry.

Table 7 reveal that the inversed parameter values are within the specified design ranges, which indicates their validity and effectiveness. The inversion accuracy of the three inversion models for the mechanical Figure 7 parameters of limestone and porphyry is elucidated through histograms and error bars. Among those, the DE-GWO-SVR model exhibits the highest inversion accuracy, followed by the PSO-SVR and GA-SVR models, with the PSO-SVR model outperforming the GA-SVR model. The training time consumption statistics of the three inversion models are shown in Figure 8, and it can be seen that the DE-GWO-SVR model used in this paper has the shortest time consumption compared to the other two models.

Figure 7

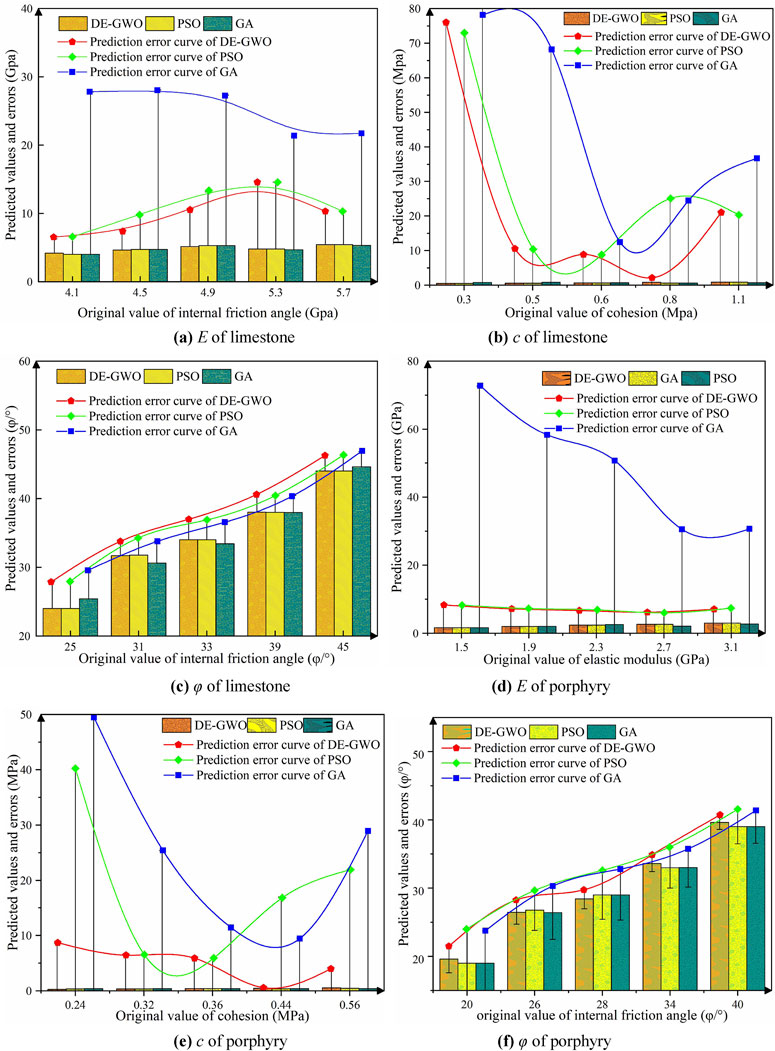
Figure 7. Analysis of inversion results. (a) E of limestone (b) c of limestone (c) ϕ of limestone (d) E of porphyry (e) c of porphyry (f) ϕ of porphyry.

Figure 8

Figure 8. Comparison of model training runtimes.

Finally, the DBA method utilizing the SVR optimized by the DE-GWO proposed in this study is employed to invert the RMMPs in the western slope of the mine. The measured displacements are substituted into the model, which focuses on analyzing the predicted internal friction angle of limestone. The comparison of predicted and expected values and the fitness curves are illustrated in Figures 9, 10, respectively.

Figure 9

Figure 9. Comparison between expected and predicted values.

Figure 10

Figure 10. Fitness curves.

The RMMPs are detailed in Table 8

Table 8

Table 8. Inversion values of mechanical parameters.

To further validate the accuracy and reliability of the DBA method, the inversed mechanical parameters are reassigned to FLAC^3D for forward analysis, and the simulated displacements are compared with the field-monitored displacements. This simulation incorporates both the gravity stress field of the overlying strata and the tectonic stress field to account for their combined effects on excavation.

The vertical stress at the top of the model reflects the stress generated by the self-weight of the overlying strata, with a unit of Pa. The calculation process is shown in Equation 13:

$\begin{array}{c}{S}_{zz}=\gamma h\\ \gamma =\rho g\end{array}(13)$

where S_ZZ represents the Z-direction gravitational stress; γ indicates the unit weight of the overlying strata; h denotes the distance from the bottom of the model to the surface. ;ρ denotes the density.

The tectonic stress fields are applied along the model’s X and Y directions, respectively, and they are assigned values based on the in situ stress measurement data from nearby mines as shown in Equations 14, 15 (Yuan et al., 2022):

${\sigma }_l=1.33+0.047H(14)$

${\sigma }_{h,\mathit{max}}=0.0401H+4.2364(15)$

The open-pit bottom elevation is 1,385 m, with a burial depth of approximately 500 m and a density of 2.68 g/cm³. The self-weight-induced vertical stress at the open-pit bottom is calculated to be 13.4 MPa, while the maximum horizontal tectonic stress is measured at 24.286 MPa.

The S-B method is employed to establish the initial geostress field of the model through gradient loading, and displacement constraints are applied to model boundaries.

Multiple monitoring points are arranged within the stope. The displacements of 10 monitoring points, which are arranged from high to low elevation, are selected for analysis.

The displacements at monitoring points are extracted from the numerical model, as illustrated in Figure 11. The inversed RMMPs are applied to the 3D model.

Figure 11

Figure 11. Displacement nephogram.

Upon completion of the slope expansion project at an elevation of 1850m, the displacements monitored at various measuring points presented in Table 9.

Table 9

Table 9. Comparison of measured and simulated slope displacements after slope expansion.

A comparison between Table 9 and Figure 12 reveals that the error between the measured and simulated displacements at each monitoring point is less than 10%, demonstrating the accuracy and reliability of this method.

Figure 12

Figure 12. Comparison between the measured and simulated displacements.

5 Discussion

This paper proposes a new inversion method of RMMPs of slope using differential evolutionary gray wolf algorithm to optimize the support vector regression, using displacement as the inversion means to link the intelligent algorithm, numerical simulation and the determination of the RMMPs, but the method also suffers from the limitations, the limitations are that the inversion accuracy of the rock mechanical parameters of the rock mechanical parameters of the hard rock slopes is high, and the accuracy of the inversion will be decreased if the slope contains multiple faults. Secondly, when creating the sample library, each set of data needs to be analyzed by numerical simulation once.

6 Conclusion

With the continuous advancement of artificial intelligence models, their roles in classification and regression prediction across various fields have become increasingly significant. However, many researchers have overlooked the challenges posed by local optimal solutions in optimizing intelligent models. This paper introduces an approach utilizing the DE-GWO algorithm to optimize the SVR, offering a new strategy for inverting the RMMPs.

(1) The value range of RMMPs is determined through field and laboratory tests. A parameter inversion design scheme is established utilizing the uniform test design method. The training and testing sets for the intelligent algorithm inversion model are constructed through numerical simulations.

(2) The DE-GWO algorithm is utilized to optimize the SVR by incorporating three processes—mutation, crossover, and selection—to boost its global search capability. This approach establishes a nonlinear mapping relationship between inversion parameters and the displacements, ultimately allowing for the prediction of RMMPs.

(3) a comparison of the inversion accuracy of DE-GWO, PSO, GA, and SVR for RMMPs reveals that the DE-GWO-SVR model achieves the highest accuracy, and the mechanical parameters are within the acceptable ranges, indicating the feasibility of this approach. The inversed mechanical parameters are incorporated into the 3D numerical model for forward analysis. The displacements calculated based on the inversed mechanical parameters match well with the field-monitored displacements, with an error of less than 10%.

Currently, there is no established standard for parameter optimization and inversion methodologies. The DE-GWO-SVR model proposed in this work is still in an exploration stage. Nevertheless, its reliability has been demonstrated by comparing it with the other two optimization models, which offers a new approach for ascertaining the RMMPs in geotechnical engineering.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

TH: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Validation, Writing – original draft. ZZ: Conceptualization, Methodology, Writing – review and editing. YZ: Data curation, Investigation, Writing – review and editing. JZ: Formal Analysis, Validation, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by grants from the National Natural Science Foundation of China (Grant no. 51864023), the National Natural Science Foundation of China (Grant no. 52264019) and the Yunnan Major Scientific and Technological Projects (Grant no. 202202AG050014) is gratefully acknowledged.

Conflict of interest

YZ was employed by the China Construction Eighth Engineering Division.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2025.1575194/full#supplementary-material

References

Ajin, R. S., Segoni, S., and Fanti, R. (2024). Optimization of SVR and CatBoost models using metaheuristic algorithms to assess landslide susceptibility. Sci. Rep. 14 (1), 24851. doi:10.1038/s41598-024-72663-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Andhika, S. (2023). In situ large scale direct shear test for evaluating compaction work of random material: case of construction failure in an Indonesia dam. Key Eng. Mater., 7060125–7060132. doi:10.4028/P-28QZDB

CrossRef Full Text | Google Scholar

Binaya, R. P., Helmut, K. G. Z., and Zenz, G. (2023). Slope stability evaluation due to reservoir draw-down using LEM and stress-based FEM along with mohr–coulomb criteria. Water 15 (22), 4022. doi:10.3390/w15224022

CrossRef Full Text | Google Scholar

Chen, Y. J., Yao, K., Zhu, B. B., Gao, Z. H., Xu, J., Li, Y. C., et al. (2024). Water quality inversion of a typical rural small river in southeastern China based on uav multispectral imagery: a comparison of multiple machine learning algorithms. Wate 16 (4), 553. doi:10.3390/w16040553

CrossRef Full Text | Google Scholar

Chong, C. Q., Andy, F., and Xu, Z. (2018). Back analysis method for stock displacements using gradient boosted regression tree and firefly algorithm. J. Comput. Civ. Eng. 32 (5).

Google Scholar

Cortes, C., and Vapnik, V (1995). Support vector networks. Mach. Learn. 20, 273–297. doi:10.1007/bf00994018

CrossRef Full Text | Google Scholar

Dai, X., and Hu, M. (2024). Traffic Flow prediction under emergency based on SVR classification regression, 39–50.

Google Scholar

Guo, X. T., Zhu, C. S., Hao, J., and Zhang, S. (2022). Multi-step wind speed prediction based on an improved multi-objective seagull optimization algorithm and a multi-kernel extreme learning machine. Appl. Intell. 53 (13), 16445–16472. doi:10.1007/s10489-022-04312-7

CrossRef Full Text | Google Scholar

Guo, Z. H., Jian, W. B., and Liu, Q. L. (2021). Rainfall infiltration analysis and infiltration model of slope based on in-situ tests, China. Geomechanics 42 (6), 1635–1647.

Google Scholar

Hu, Y. T. Z. Q. (2023). A hybrid CNN-LSTM machine learning model for rock mechanical parameters evaluation. Geoenergy Sci. Eng. 225, 211720. doi:10.1016/j.geoen.2023.211720

CrossRef Full Text | Google Scholar

Li, H., Chen, W. Z., Tan, X. Y., and Tan, X. J. (2023). Back analysis of geomechanical parameters for rock mass under complex geological conditions using a novel algorithm. Tunn. Undergr. Space Technol. incorporating Trenchless Technol. Res., 136. doi:10.1016/J.TUST.2023.105099

CrossRef Full Text | Google Scholar

Li, J. D., Yang, T. H., Liu, F. Y., Zhao, Y., Liu, H. L., Deng, W. X., et al. (2024). Modeling spatial variability of mechanical parameters of layered rock masses and its application in slope optimization at the open-pit mine. Int. J. Rock Mech. Min. Sci. 181, 181105859–105859. doi:10.1016/j.ijrmms.2024.105859

CrossRef Full Text | Google Scholar

Li, J. H., Sun, W. Z., Su, G. S., and Zhang, Y. (2022). An intelligent optimization back analysis method for geomechanical parameters in undergroundengineering. Appl. Sci. 12 (11), 5761. doi:10.3390/app12115761

CrossRef Full Text | Google Scholar

Lin, M., Fu, H. M., Wen, H. C., Lou, B., Luo, X., Li, Q., et al. (2023). A multi-strategy improved sooty tern optimization algorithm for concrete dam parameter inversion. Water 16 (1), 119. doi:10.3390/w16010119

CrossRef Full Text | Google Scholar

Liu, F. Y., Yang, T. H., Zhou, J. R., Deng, W. X., Yu, Q. L., Zhang, P. H., et al. (2020). Spatial variability and time decay of rock mass mechanical parameters: a landslide study in the dagushan open-pit mine. Rock Mech. Rock Eng. 53 (7), 3031–3053. doi:10.1007/s00603-020-02109-z

CrossRef Full Text | Google Scholar

Liu, G. F., Zhou, C., Feng, K., Jiang, Q., Li, S. F., Han, B., et al. (2024). Probabilistic evaluation method for the stability of large underground cavern considering the uncertainty of rock mass mechanical parameters: a case study of Baihetan underground powerhouse project. Eng. Geol. 340, 340107660–107660. doi:10.1016/j.enggeo.2024.107660

CrossRef Full Text | Google Scholar

Liu, G. F., Zhou, C., Li, Z. Q., and He, B. J. (2022). Sensitivity analysis on the estimation of mechanical parameters for rock mass around large cavern based on RMR and H-B criterion, China. J. Northeast. Univ. Nat. Sci. Ed. 43 (08), 1149–1158.

Google Scholar

Liu, J., Jiang, Q., Dias, D., and Tao, C. (2023). Probability quantification of GSI and D in Hoek–Brown criterion using bayesian inversion and ultrasonic test in rock mass. Rock Mech. Rock Eng. 56 (10), 7701–7719. doi:10.1007/s00603-023-03448-3

CrossRef Full Text | Google Scholar

Luo, M., Liu, M. C., Zhang, S. W., Gao, J., Zhang, X. J., Li, R. S., et al. (2024). Mining soil heavy metal inversion based on Levy Flight Cauchy Gaussian perturbation sparrow search algorithm support vector regression (LSSA-SVR). Ecotoxicol. Environ. Saf. 287, 287117295–117295. doi:10.1016/j.ecoenv.2024.117295

PubMed Abstract | CrossRef Full Text | Google Scholar

Pan, B. Z., He, H. C., and Fan, D. L. (2024). Inversion of sea surface ocean current in South China Sea, based on machine learning method, 13, doi:10.1117/12.302404412988129880E-129880E-6

CrossRef Full Text | Google Scholar

Qin, Y., Yu, H. G., Tao, J. F., Sun, H., and Liu, C. L. (2022). Advance rate optimization of earth pressure balance shield based on PSO-SVR, China. J. Zhejiang Univ. Eng. Ed. 56 (08), 1523–1532.

Google Scholar

Ren, J. H., Cui, J. Y., Dong, W., Xiao, Y. F., Xu, M. M., Liu, S. W., et al. (2023). Remote sensing inversion of typical offshore water quality parameter concentration based on improved SVR algorithm. Remote Sens. 15 (8), 2104. doi:10.3390/rs15082104

CrossRef Full Text | Google Scholar

Sang-To, T., Hoang, L.-M., Seyedali, M., Abdel, W. M., and Cuong-Le, T. (2022). A new movement strategy of grey wolf optimizer for optimization problems and structural damage identification. Adv. Eng. Softw., 173. doi:10.1016/J.ADVENGSOFT.2022.103276

CrossRef Full Text | Google Scholar

Shial, G., Sahoo, S., and Panigrahi, S. (2023). An enhanced GWO algorithm with improved explorative search capability for global optimization and data clustering. Appl. Artif. Intell. 37 (1). doi:10.1080/08839514.2023.2166232

CrossRef Full Text | Google Scholar

Umbach, C., and Middendorf, B. (2024). Investigations on lightweight concrete by in situ compression tests using high-resolution computed tomography (μ-CT). J. microscopy.wanshang 294, 177–190. doi:10.1111/jmi.13279

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, F., Song, R., Yu, H., Zhang, A., Wang, L., and Chen, X. (2024). Thermal parameter inversion of low-heat cement concrete for Baihetan arch dam. Eng. Appl. Artif. Intell. 131:107823, doi:10.1016/j.engappai.2023.107823

CrossRef Full Text | Google Scholar

Wang, F., Zhou, H. W., Zhou, Y. H., Zhao, C. J., Seman, E. A., and Gong, P. (2022). Thermal parameters inversion method for concrete dam based on optimal temperature measuring point selecting. Math. Problems Eng. 2022 (2022), 1–16. doi:10.1155/2022/4677344

CrossRef Full Text | Google Scholar

Wang, S. Y. (2024). Application of dynamic accuracy evaluation for press systems based on orthogonal design method. MethodsX 12, 12102568. doi:10.1016/j.mex.2024.102568

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, X. Z., Zhang, Z. C., Wang, K., and HanZH, W. L. J. (2021). Method for adjusting air volume of mine ventilation network based on DE-GWO algorithm, China. J. Central South Univ. Nat. Sci. Ed. 52 (11), 3981–3989.

Google Scholar

Wu, Z. J., Wu, Y., Weng, L., Li, M. Y., Wang, Z. Y., and Chu, Z. F. (2024). Machine learning approach to predicting the macro-mechanical properties of rock from the meso-mechanical parameters. Comput. Geotechnics 166, 105933. doi:10.1016/j.compgeo.2023.105933

CrossRef Full Text | Google Scholar

Yuan, L., Li, C., Li, S., Ma, X., Zhang, W., Liu, D., et al. (2022). Mine slope stability based on fusion technology of InSAR monitoring and numerical simulation. Sci. Program. 2022, 1–10. doi:10.1155/2022/8643586

CrossRef Full Text | Google Scholar

Zhang, Y. G., Tang, J., Liao, R. P., Zhang, M. f., Wang, X. m., et al. (2021). Application of an enhanced BP neural network model with water cycle algorithm on landslide prediction. Stoch. Environ. Res. Risk Assess. 35, 1273–1291. doi:10.1007/s00477-020-01920-y

CrossRef Full Text | Google Scholar

Zhao, H. B., Zhang, L., Ren, J. L., Wang, M., and Meng, Z. (2022). AdaBoost-based back analysis for determining rock mass mechanical parameters of claystones in goupitan tunnel, China. Buildings 12 (8), 1073. doi:10.3390/buildings12081073

CrossRef Full Text | Google Scholar

Zhou, Y., Li, C. Y., Pang, R., Li, Y. C., Xu, Y. S., and Chen, J. S. (2024b). A new approach for seepage parameter inversion of earth– rockfill dams based on an improved sparrow search algorithm. Comput. Geotechnics 167106036-, 106036. doi:10.1016/j.compgeo.2023.106036

CrossRef Full Text | Google Scholar

Zhou, Y. J., Feng, W. K., Hu, Y. P., Yi, X. Y., Ji, F., and Li, W. (2024a). Equivalent continuous numerical simulation of a large-scale underground powerhouse excavation considering the size effect of the jointed rock mass. Tunn. Undergr. Space Technol. incorporating Trenchless Technol. Res. 154, 154106058–106058. doi:10.1016/j.tust.2024.106058

CrossRef Full Text | Google Scholar

Zhu, A. F., Zhao, Q. C., Yang, T. L., Zhou, L., and Zeng, B. (2024). Wind speed prediction and reconstruction based on improved grey wolf optimization algorithm and deep learning networks. Comput. Electr. Eng. 114109074-, 109074. doi:10.1016/j.compeleceng.2024.109074

CrossRef Full Text | Google Scholar

Zhuang, D. Y., Ma, K., Tang, C. A., Liang, Z. Z., Wang, K. K., and Wang, Z. W. (2019). Mechanical parameter inversion in tunnel engineering using support vector regression optimized by multi-strategy artificial fish swarm algorithm. Tunneling Undergr. space Technol. incorporating trendless Technol. Res. 83, 425–436. doi:10.1016/j.tust.2018.09.027

CrossRef Full Text | Google Scholar

Zu, W. J., Wang, S. Q., Li, P., Li, H. X., Zhang, Y. H., and He, Z. (2022). Rural electricity demand forecast based on DE-GWO-SVR. J. Phys. Conf. Ser. 2401 (1), 012030. doi:10.1088/1742-6596/2401/1/012030

CrossRef Full Text | Google Scholar

Z, Y. (2020). Displacement back analysis of rock mass parameters for underground cavens using a novel intelligent optimization method. Int. J. geomechanics 20 (5), 04020035.

Google Scholar