Numerical simulation research on the micro failure mechanism of sandstone under freeze-thaw cycles

The process of micro crack formation in sandstone subjected to freeze-thaw cycles is pivotal for strip mine in cold regions. A discrete element numerical model considering the variation of frost heave force and water saturation during the freeze-thaw cycles is established by PFC3D in this paper. The results indicate that: (1) During freeze-thaw cycles, the development of cracks can be divided into three stages: stable, growth and explosive stage. The crack quantity in the stable and growth stage increases exponentially, while the quantity of cracks in the explosive stage increases linearly quickly. (2) Repeated freeze-thaws cause progressive damage to rocks from surface to interior. As the times of freeze-thaw increase, cracks gradually develop, and their distribution becomes more uniform on different angles. (3) Sandstone that have undergone freeze-thaw cycles is more prone to tensile failure, and the distribution of cracks becomes even more complex. These research findings provide a more accurate understanding of micro-fracture mechanisms in rocks in the freeze-thaw condition.

1 Introduction

The annual production of open-pit coal mines in China exceeds 1 billion tons, and these mines play a crucial role in ensuring China’s energy security. Open-pit coal mines are typical rock slopes, so the mechanical properties of rock have a significant impact on safe mining. The majority of China’s open-pit coal mines are nestled in the northern regions that extend beyond the 38°N latitude, characterized by their cold climates (Prischepa and Xu, 2025; Qingxiang and Yanlong, 2024), and one of the environmental characteristics of these cold regions is the large temperature fluctuation. Meanwhile the rock in open-pit coal mines have convenient access to water supply. When the temperature is below 0°C, the water within rocks freezes into ice, resulting in an increase in volume by about 9%. The repeated freeze-thaws cause cracks development within the rocks, leading to deterioration in their mechanical properties and subsequently affecting slope stability. Therefore, delving into the micro-fracture mechanisms of rocks amidst the cyclical freeze-thaw processes is of paramount importance.

At present, CT, NMR, and SEM have been widely used as non-destructive testing techniques in the field of rocks. Abdolghanizadeh et al. (2020) defined the damage coefficient of freeze-thawed rocks through CT numbers. Ju et al. (2024) explored the variation characteristics of the microstructure of frozen-thawed sandstone under different water saturation, and found that increasing water saturation during the freeze-thaw cycles leads to an enlargement in pore size. Xu et al. (2023) have elucidated the correlation between the microstructure of sandstone and its macroscopic mechanical properties, highlighting the substantial influence of rock microstructure on mining safety. With the help of NMR detection method, researchers have found that the expansion of macropores is the primary culprit in the degradation of sandstone’s mechanical properties over the course of freeze-thaw cycles, with the initiation of new pores emerging as a secondary factor (Li et al., 2018; Xie Haotian, 2024),the uniformity of pores continues to increase (Jia et al., 2020), and it is clear that freeze-thaw cycles result in progressive cumulative damage to sandstone (Gao et al., 2017; Liu et al., 2022a; Lu et al., 2023; Shi et al., 2023; Wu et al., 2022). CT and NMR detection are expensive and their accuracy heavily relies on algorithm precision. SEM is a direct detection method that allows for the observation of microscopic damage features in rocks. Researchers found that freeze-thaw cycles lead to the formation of pores and microcracks, and strength decrease between particles (Shi et al., 2024; Yang et al., 2019; Yin et al., 2023), particle loose or detach (Wu et al., 2020; Zhang et al., 2022a), the size of these pores increase, along with an increase in roughness (Liu et al., 2022b; Xu et al., 2022), and transgranular cracks become more prevalent (Zhang et al., 2022b). However, SEM can only detect specific areas of the specimen and cannot fully characterize the micro-damage mechanisms caused by freeze-thaw cycles on rocks as a whole. Furthermore, fixed point scanning techniques pose significant challenges. Therefore, SEM detection methods also have certain limitations (Wu et al., 2024).

Scholars, aiming to address the shortcomings of physical detection methods, have endeavored to probe the micro-damage mechanisms under freeze-thaw cycles through the application of numerical simulation techniques (Exadaktylos, 2006; Pu et al., 2020). Han and Li (2021) has conducted research on the impact of freeze-thaw cycles on the fracture toughness of sandstone, utilizing the finite element analysis software ANSYS to simulate and understand the behavior of rock under such conditions. Lv et al. (2022) has developed a thermo-mechanical coupling deformation model for porous rocks under low-temperature conditions, employing elastoplastic mechanics and finite element software to simulate the frost heave deformation of sandstone. Although significant progress has been made in studying the rock freezing-thawing process by finite element simulations, the limitations of continuum mechanics prevent freezing-thawing simulations based on finite element from capturing the evolution of internal cracks (Chao-jun et al., 2024). Therefore, Zhu et al. (2021) proposed a simulation method by water particle expansion using discrete element method to simulate the microscopic failure mechanism. However, the interaction between pore ice and rock and the water saturation degradation has not been considered during freezing and thawing in this study. Yong-jun et al. (2023a) introduced a freeze-thaw model in which the interaction between pore ice and rock is considered. However, the influence of rock mechanical property degradation and reduced water saturation on the growth of water particle radius during freeze-thaw cycles in PFC3D are not considered, which is extremely important (Tan et al., 2018).

In summary, a simulation method for freeze-thaw cycles in which the decrease in water saturation and mechanical property degradation are considered based on discrete element is proposed. By incorporating parameters provided by laboratory experiments, a discrete element-based numerical model for freeze-thaw is established, and the accuracy of the numerical model is verified by laboratory experiments results in this paper.

2 Laboratory tests

2.1 Experiment method

2.1.1 Specimen preparation

The specimens were taken from Inner Mongolia and the specimens were processed into diameter of 50 mm and height of 100 mm, as shown in Figure 1A. The basic mechanical parameters of sandstone are shown in Table 1.

Figure 1

Figure 1. Experimental facilities. (A) Specimen. (B) Dryer. (C) Vacuum Saturator. (D) Freeze-thaw machine. (E) Press machine.

Table 1

Table 1. Basic mechanical parameters of sandstone.

2.1.2 Experiment scheme

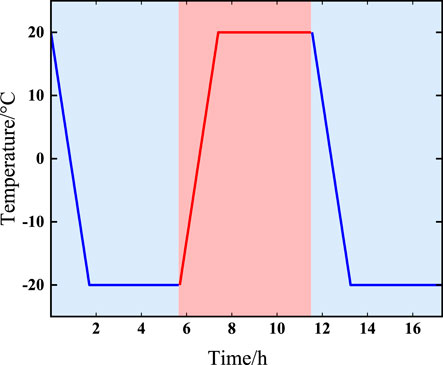
According to the relevant standards, the specimens underwent a drying and weighing process, followed by vacuum saturation in water. These saturated samples, enveloped in cling film, were then positioned within a freeze-thaw chamber, where they were subjected to temperatures alternating between + 20°C and −20°C, with each cycle lasting 4 hours, as illustrated in Figure 2. The number of freeze-thaw cycles N was set at intervals of 0, 10, 20, 30, and 40. The specimens' porosity was ascertained via Equation 1 the saturation method, and subsequently, the TAW-2000 pressure apparatus was utilized to perform uniaxial compression tests.

Figure 2

Figure 2. Temperature setting for freeze-thaw cycle.

2.2 Analysis of laboratory experiment

2.2.1 Sandstone porosity during freeze-thaw

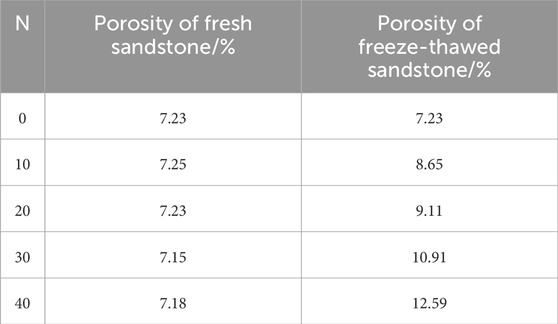
Porosity is the most direct macroscopic physical parameter for characterizing sandstone damage (Huang et al., 2021). The porosity before and after freeze-thaw of sandstones with similar initial porosity was determined by the mass method, as shown in Table 2.

$\varphi =\frac{{\mathrm{m}}_1-m_2}{{\rho }_w{V}_{ro}}(1)$

where $\varphi$ is porosity; $m_1$ is rock mass before freeze-thaw; $m_2$ is rock mass after freeze-thaw; ${\rho }_w$ is water density; $V_{ro}$ is rock volume.

Table 2

Table 2. Porosity of sandstone.

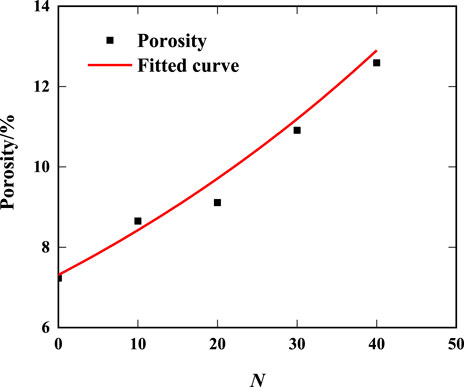
With the increasing times of freeze-thaw, the repeated migration and freezing of pore water inside rocks exacerbate the frost heave damage to the rocks. As shown in Figure 3 and Equation 2, the porosity of sandstone approximately exhibits exponential growth.

$\varphi =7.31e^{0.0142N}{R}^2=0.983(2)$

Figure 3

Figure 3. The variation curve of porosity with freezing-thawing times.

2.2.2 Strength and deformation of sandstone

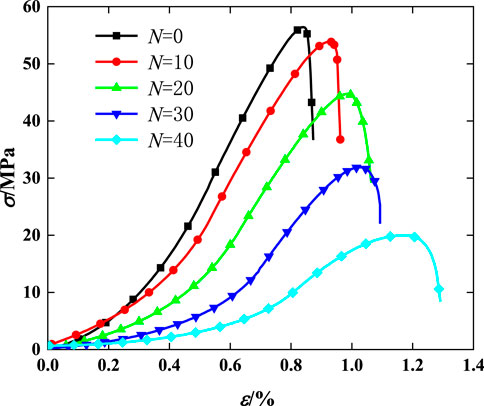
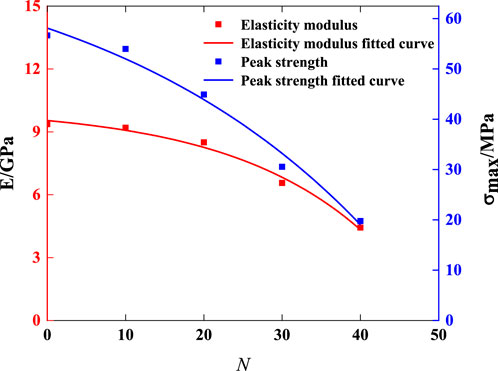
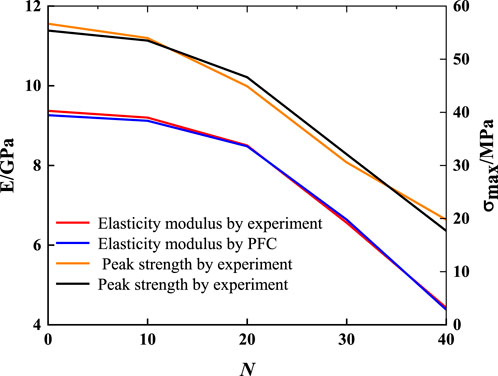
The stress-strain curve is shown in Figure 4, from which it can be observed that with an increase in freeze-thaw cycles, the compaction stage extends but the elastic stage shortens. Furthermore, as shown in Figure 5, Equations 3, 4, for 0 to 10 freeze-thaw cycles, there is only a slight deterioration in mechanical properties, and the peak strength decreases from an initial value of 56.67 MPa–53.98 MPa with a decrease rate of only 4.7%, while elastic modulus decreases from an initial value of 9.37 GPa–9.2 GPa with a decrease rate of only 1.8%. However, from 10 to 40 freeze-thaw cycles the sandstone is deteriorated severely, with peak strength decreasing from 53.98 MPa to 19.78 MPa, and the decreasing rate is up to 63.36%. The elastic modulu also decreases from 9.20 GPa to 4.43 GPa, and the decreasing rate is up to 51.85%. These experimental results are similar to those obtained by Khanlari et al. (2015).

$E\left(N\right)=10.16-{0.62}^{*}{e}^{\left({0.0056}^{*}N\right)}{R}^2=0.997(3)$

${\sigma }_{\max }=77.04-{18.92}^{*}{e}^{\left({0.028}^{*}N\right)}{R}^2=0.986(4)$

Figure 4

Figure 4. Stress-strain curve of freeze-thawed sandstone.

Figure 5

Figure 5. The curves of peak strength and elastic modulus with freeze-thaw times.

3 Numerical simulation for freeze–thaw cycles

3.1 Numerical model establishment

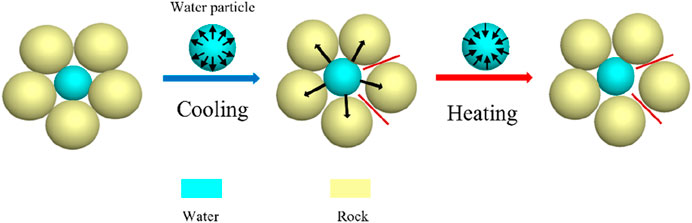
Subzero temperatures trigger the phase transition of pore water, causing volume expansion that increments porosity and advances crack propagation within the rock. This phenomenon erodes the matrix strength, identifying it as the predominant mechanism of damage during freeze-thaw cycles (Xianjun et al., 2011), as illustrated in Figure 6. Therefore, a numerical model for single freeze-thaw of rocks is established in this paper, based on the theory of volume expansion. Considering the characteristics of particle flow, the following assumptions are maded:

(1) The internal pores of the rocks are assumed to be spherical;

(2) The migration of water within rocks at low temperatures is not considered.

Figure 6

Figure 6. Schematic diagram of fracture caused by freeze-thaw cycles.

According to rock frost heaving model established by Quansheng et al. (2016), under the condition of ignoring the unfrozen water, the volume increment of water particles $\Delta V_w$ can be derived from Equations 5–9:

$\Delta V_w=\frac{4}{3}\pi \left({r_1}^3-{r_0}^3\right)(5)$

$r_1=r_0^{*}\left[1+\frac{p_i}{E_m}\frac{\left[1+{\upsilon }_m+2\left(1-2{\upsilon }_m\right)\varphi \right]}{2\left(1-\varphi \right)}\right](6)$

$p_i=\frac{0.029}{\frac{1}{E_m}\frac{1+2\varphi +\left(1-4\varphi \right){\upsilon }_m}{2\left(1-\varphi \right)}+1.029\frac{1-2{\upsilon }_i}{E_i}}(7)$

$E_m=\left[1+\frac{3\left(1-{\upsilon }_m\right)}{2\left(1-2{\upsilon }_m\right)}\varphi \right]E_s(8)$

${\upsilon }_s={\upsilon }_m(9)$

where $\Delta V$ is increment of water particle volume; $r_0$, $r_1$ are the water and ice particles radius; E_s(N), ${\upsilon }_s$ are the elastic modulus and Poisson’s ratio of rock, E_m, ${\upsilon }_m$ are the elastic modulus and Poisson’s ratio of rock matrix, and $\varphi$ is the porosity of rock. E_i, ${\upsilon }_i$ are the elastic modulus and Poisson’s ratio of pore ice, which are 9 GPa, 0.35 respectively (Quansheng et al., 2016).

The volume variation of individual water particles with temperature during freezing process can be expressed by Equations 10, 11 (Zhu et al., 2021):

$V=\left\{\begin{array}{l}{V}_0+V_w\left(1-w_u\right)T\le 0°\mathrm{C}\\ V_{0}T>0°\mathrm{C}\end{array}\right.(10)$

$w_u=\left\{\begin{array}{l}1-\left[1+0.139{\left(\frac{1}{\Delta T}\right)}^{1/3}\ln \left(\frac{1+e^{-0.268\Delta T}}{2}\right)\right]\left(1-e^{-0.268\Delta T}\right)\Delta T\le 0\\ 1\Delta T>0\end{array}\right.(11)$

where $V$ is the water particles volume; $V_0$ is initial water particle volume; $w_u$ is unfrozen water content, $\Delta T=T-T_1$, and the water freezing point is taken as 0 $°\mathrm{C}$.

Due to the instantaneous implementation of temperature in numerical model, maintaining a constant low temperature is not essential. When the temperature exceeds 0°C, water particle radius do not change anymore. Therefore, Equation 12 is the relationship between temperature and time.

$T=-\left|20\sin \left(\frac{\pi t}{30}\right)\right|(12)$

At present, the freeze-thaw cycle experiment only saturates the rocks initially and does not replenish water during the cycling process. As a result, the water saturation of the rocks gradually decreases,so the porosity filled with water is introduced (Huang et al., 2020), as show in Equation 13.

${\varphi }_{eN}={\varphi }_{N-1}-0.5\Delta {\varphi }_{N-1}(13)$

where ${\varphi }_{eN}$ is the porosity filled with water during the Nth rock freeze-thaw, ${\varphi }_{N-1}$ is the rock porosity after the (N-1) th freeze-thaw cycle, and $\Delta {\varphi }_{N-1}$ is the increment in cumulative porosity of rock after N-1 freeze-thaw cycles. The porosity of sandstone, which is filled with water during freeze-thaw cycles, can be obtained by substituting Equation 2 into Equation 13.

${\varphi }_e=7.27e^{0.0081N}(14)$

According to Equation 14, we continuously adjust the radius of water particles at the beginning of each cycle to simulate changes in porosity of frozen rock,and combining the mechanical parameters obtained from laboratory experiments results, rock particle radius increment are determined during each cycle. Due to the minimal impact of freeze-thaw cycles on rock Poisson’s ratio of, a constant value 0.22 for the rock Poisson’s ratio of is assumed.

Linear parallel bonding model in PFC3D is used, which can simulate the rock mechanical behavior (Yang et al., 2015). The numerical model has the same dimensions as the laboratory test, as shown in Figure 7. The particles in the model are divided into water and rock particles, with the volume ratio of water particles being equal to the water-filled porosity. The initial model consists of 68,463 particles, including 46,156 rock particles and 22,307 water particles. The rock particle size ranges from 0.9 to 1.1 mm, and the size of water particles ranges from 0.5 to 0.6 mm. After freeze-thaw cycles, a displacement loading of 0.05 m/s was applied after removing water particles from the specimen to ensure that sandstone strength is provided by its skeleton.

Figure 7

Figure 7. Numerical rock specimen.

3.2 Microscopic parameter calibration

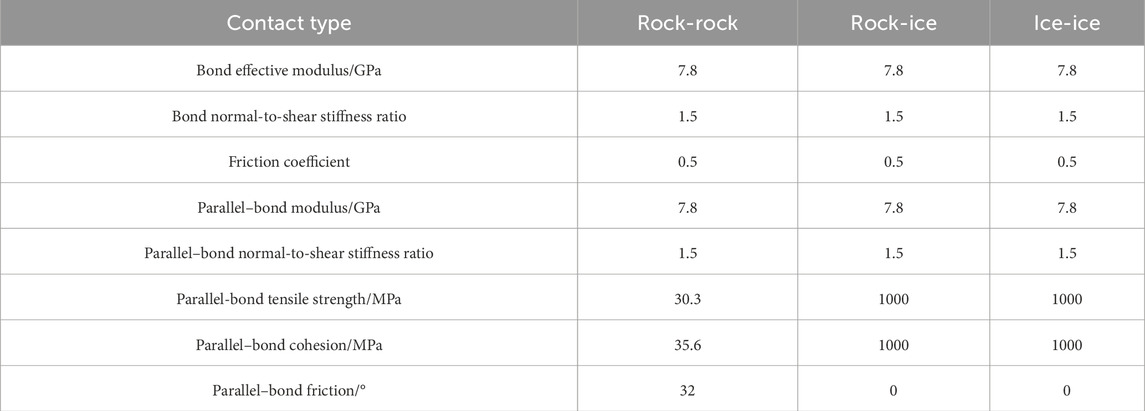
Combining the stress-strain curve of fresh sandstone, the micro-parameters of sandstone were calibrated by the trial-and-error method. The micro-parameters of the model are shown in Table 3, where the rock-ice particle and ice-ice particle contacts are large enough to ensure that cracks occur between rock particles. As shown in Figure 8, numerical calculations obtained a peak strength of 56.67 MPa and an elastic modulus of 9.36 GPa for the sandstone, and peak strength is 56.67 MPa and elastic modulus got by laboratory tests is 9.37 MPa. Except for the compaction stage, the stress-strain curves obtained from numerical calculations and laboratory tests are nearly identical, indicating that it is scientifical and reasonable to use the micro-parameters in Table 2 for numerical calculations.

Table 3

Table 3. Microscopic parameters of the model.

Figure 8

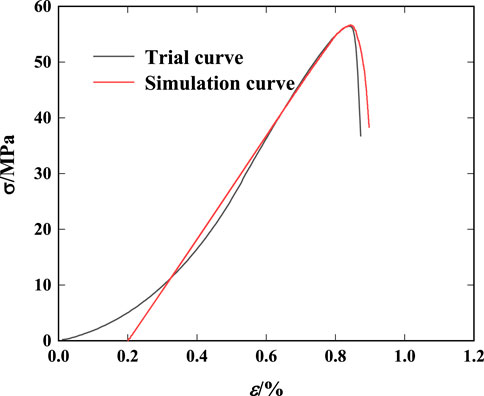
Figure 8. The stress-strain curves of fresh sandstone obtained by numerical simulation and laboratory experiment.

4 Analysis of simulation results

4.1 Sandstone micro damage during freeze-thaw cycles

4.1.1 Crack quantity characteristics

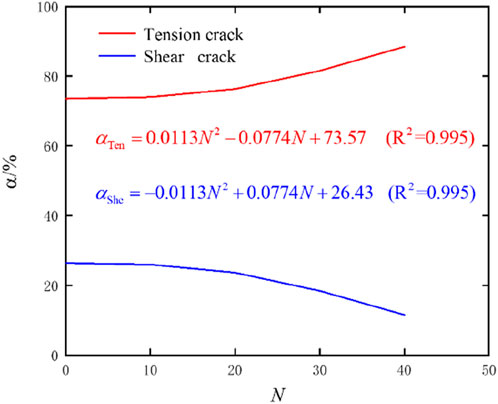
The quantity and proportion of shear cracks and tension cracks in sandstone during the freeze-thaw are shown in Figure 9. The data was fitted by Equation 15, revealing that as the freeze-thaw cycles increases, cracks continue to increase. Tensile cracks consistently remain dominant. This finding aligns with the results obtained by Liu et al. (2020) through CT. Based on the characteristics of crack quantity, crack development can be divided into three stages.

(1) When N < 5, it is the stable stage. During this stage, the porosity increases slowly and the frost heave force does not increase significantly. Therefore, there are only a few cracks, with tensile cracks accounting for more than 94.4%.

(2) When 5 < N < 25, it is growth stage of crack quantity. As the mechanical properties of sandstone gradually decrease and porosity continues to increase, the frost heave force acting on the sandstone keeps increasing. During this stage, the quantity of cracks increases exponentially with each cycle. The relative displacement between particles becomes more likely to occur, leading to a significant increase in shear cracks from 5.6% to 30.5%, which is a growth rate of 5.45 times, similar to the findings by Yong-jun et al. (2023b).

(3) When 25 < N < 40, it is explosive stage. Cracks penetrate through the sandstone gradually, significantly reducing its cementation strength. Therefore, the quantity of cracks in this stage increases rapidly in a linear form, while the proportion of tensile and shear cracks changes slightly.

Figure 9

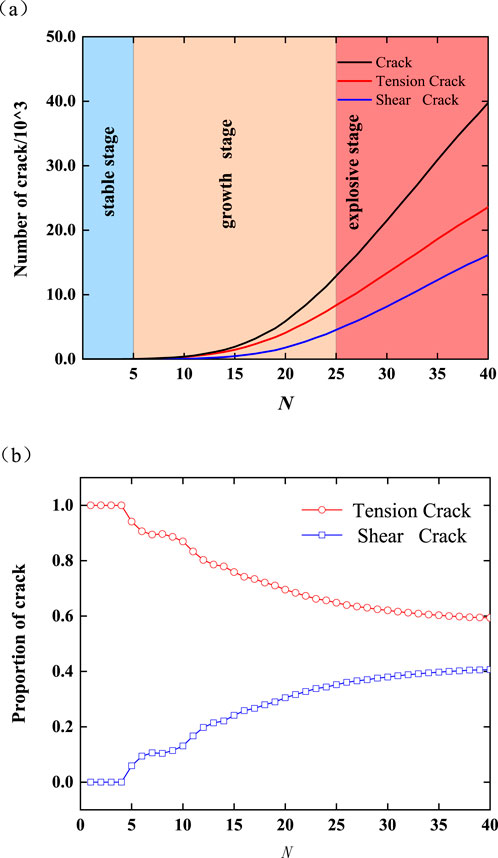
Figure 9. The variation curve of crack quantity and tension and shear crack proportion with freezing and thawing times. (A) The variation curve of cracks quantity with freezing and thawing times. (B) The variation curve of tension and shear crack proportion with freezing and thawing times.

In order to clarify the relationship between the quantity of cracks and freeze-thaw cycles more clearly, a fitting is performed on the data in Figure 9A, as shown in Equation 15. It can be observed that when the time of freeze-thaw is less than 25, crack quantity increases exponentially with freeze-thaw cycles. When the freeze-thaw cycles exceed 25, crack quantity increases linearly with freeze-thaw times. The determination coefficients R² are all greater than 0.99, indicating that this fitting formula reflects the relationship between crack quantity and freeze-thaw cycles effectively.

$K=\left\{\begin{array}{l}A{e}^{\left(B^{*}N\right)}-A0\le N<25\\ \lambda N+\mathrm{Q}25\le N<40\end{array}\right.(15)$

where K is crack quantity, and A, B, λ, Q are fitting parameters, which are shown in Table 4.

Table 4

Table 4. Fitting parameters for crack quantity.

4.1.2 Crack position distribution characteristics

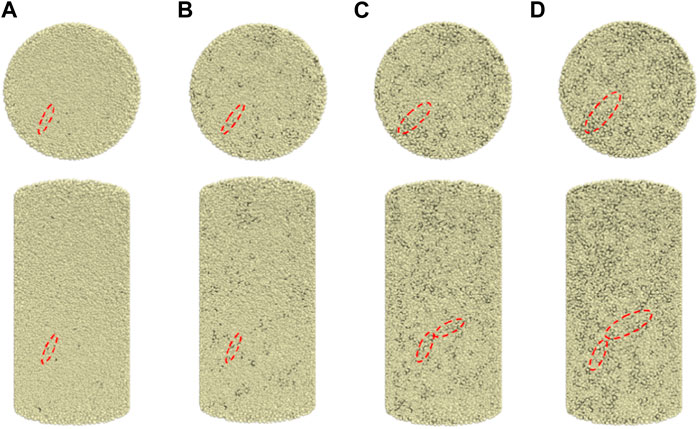
The distribution of freeze-thaw cracks is shown in Figure 10. It can be observed that when sandstone undergoes 10 cycles of freezethaw, only a small number of cracks appear on the sample surface. However, when sandstone undergoes 40 times freeze-thaw, crack connectivity occurs on the sample surface and the crack expanded into a fissure. According to Griffith’s strength theory, as the crack size increases, it becomes easier for cracks to propagate and the rock strength decreases. This result is consistent with laboratory test results.

Figure 10

Figure 10. Distribution of cracks in specimen. (A) N = 10. (B) N = 20. (C) N = 30. (D) N = 40.

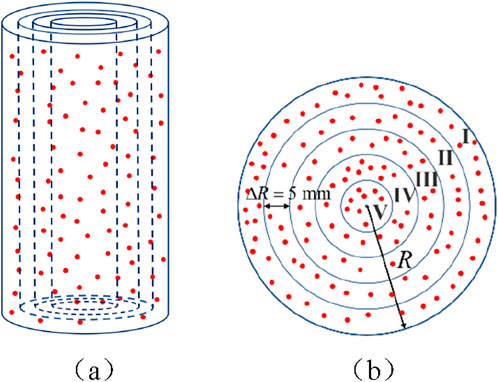
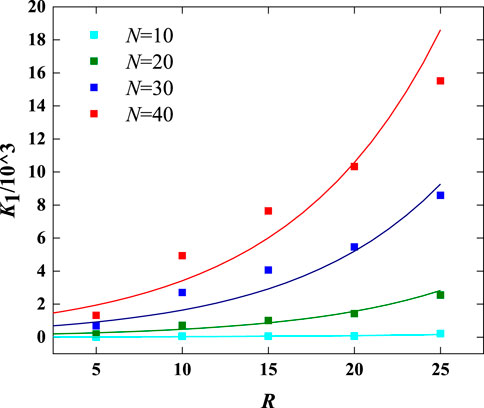
During the freeze-thaw cycles, it is a common phenomenon that rock spilling,and the specimen porosity of the surface layer is greater than the porosity of the interior, which indicates that freeze-thaw gradually damages rocks from the surface to interior. Therefore, the samples were divided into five regions with a radius interval of 5 mm, and a fitting analysis was conducted on the quantity of cracks within each region in relation to their positions (as shown in Figures 11, 12; Equation 16). It can be observed from the graph that due to greater constraint forces on internal particles compared to external ones, crack quantities follow this order: Region I > Region II > Region III > Region IV > Region V. Moreover, as R increases, crack quantities exhibit exponential growth. When sandstone undergoes 10 times freeze-thaw cycles, cracks in outermost region I account for 54.38% of all cracks; however, after 40 cycles, this proportion decreases to 39.04%, representing a decreasing amplitude of 28.21%. This result indicates that cracks continuously propagate towards the interior during freeze-thaw cycles.

$K_1=H{e}^{\left(lR\right)}(16)$

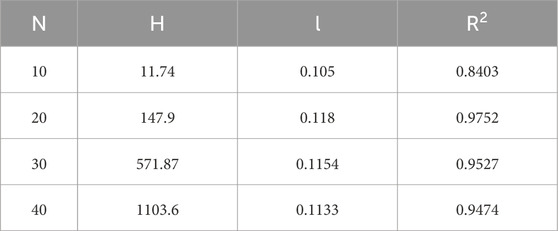
where K₁ is crack quantity in different region, R is the distance from the center of the circle to the outermost part of the region, and H and l are the fitting parameters, which are shown in Table 5.

Figure 11

Figure 11. Diagram of specimen area division. (A)Front View. (B)Top View.

Figure 12

Figure 12. The variation of the crack with distance from the center of the circle.

Table 5

Table 5. Fitting parameters for crack location.

4.1.3 Crack angle characteristics

The angles between tensile and shear cracks and the coordinate axis is extracted by Fish language, and a rose diagram showing the proportion of crack quantities in different angles is plotted, as shown in Figure 13. Because the cracks are mostly on the surface when sandstone undergoes 10 times freeze-thaw, it can be observed that the crack angles are chaotic. As sandstone undergoes 20–40 times freeze-thaw, the frost heave force increases continuously and the influence of internal constraint on cracks gradually decreases. Therefore, cracks are distributed more evenly in all directions.

Figure 13

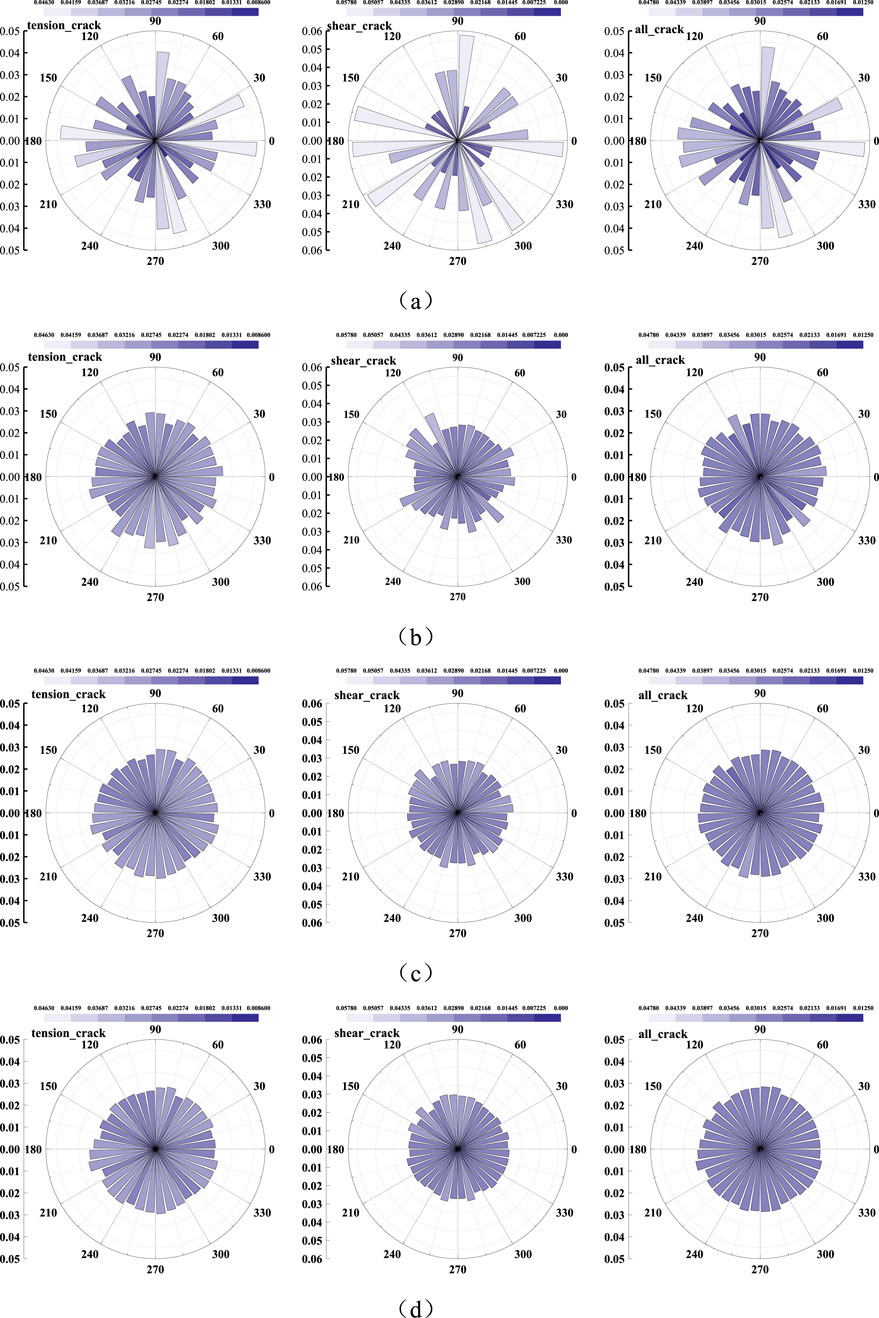
Figure 13. Proportion of crack angles under different freeze-thaw cycles. (A) N = 10. (B) N = 20. (C) N = 30. (D) N = 40.

4.2 Microscopic fracture of frozen-thawed sandstone under uniaxial compression

4.2.1 Crack development under uniaxial compression

The peak strength and elastic modulus of sandstone obtained from laboratory experiments and particle flow simulations are shown in Figure 14. It can be observed that the curves obtained from both methods have a high similarity, with a maximum error of 10.5%. Additionally, the failure modes are also similar (as shown in Figure 15), indicating the simulation results reliability.

Figure 14

Figure 14. Verification of numerical simulation.

Figure 15

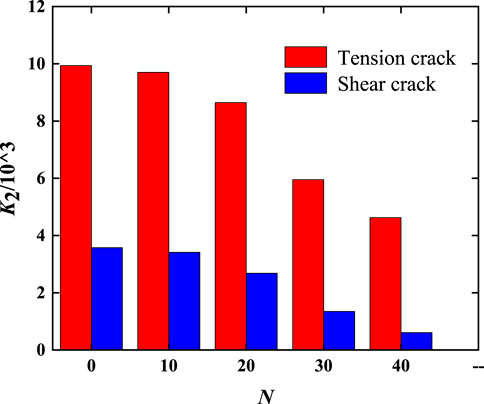
Figure 15. The crack quantity K₂ at the time of freeze-thawed specimen failure under uniaxial compression.

Freeze-thaw cycles cause a decrease in the intergranular bonding force, so the crack quantity decreases with the freeze-thaw cycles increase at point 4, as shown in Figure 15. As shown in Figure 16, when the specimen ruptures, tensile cracks accounts for more than 73%, which is the dominant factor for rock failure. Moreover, with the freeze-thaw times increasing, proportion of tensile cracks gradually increases. From 0 to 40 cycles, the proportion increases from 73.56% to 88.41%, with an increment rate of 20.19%. This conclusion is consistent with that obtained by Chao et al. (2023), Huang et al. (2018), which states that under uniaxial loading conditions, sandstone subjected to freeze-thaw cycles exhibits increased susceptibility to tensile failure.

Figure 16

Figure 16. The proportion of tension and shear crack at the time of freeze-thawed specimen failure.

4.2.2 Failure characteristics

The genesis of rock failure under stress is characterized by the evolution of crack initiation, propagation, and coalescence, which is a pivotal mechanism in the rock failure, as shown in Figure17A, characteristic points (1∼4) are selected at 70%, 85%, 100% of peak stress and at the end of curve to analyze the distribution of internal cracks and contact forces in rock samples under specific stress conditions. Figure 18 shows the process of sandstone failure, from which it can be observed that:

(1) When the axial stress reaches point 1 and 2, only a few of cracks appear.

(2) When the axial stress reaches point 3, cracks in the sample gather in some region and stress concentration occurs, leading to local failure. Freezing-thawing cycles reduce rock brittleness (Zhang et al., 2022a), so as the time of freezing-thawing increases, the crack accumulation decreases.

(3) When the axial stress reaches point 4, a large number of cracks gather, intensifying the phenomenon of stress concentration and forming a through-failure zone where the sandstone fractures. In the case of 0 and 10 freeze-thaw cycles, localized crack accumulation appears in the upper left corner of the sample but does not penetrate through. However, in instances of 20, 30, and 40 cycles of freeze-thaw, fractures within the upper left corner of the specimen coalesce with the principal region of failure, culminating in an interconnected zone of rupture. This outcome is in agreement with the findings by Zhu et al. (2021), which posit that an increment in the number of freeze-thaw cycles results in a more intricate pattern of crack distribution within sandstone.

Figure 17

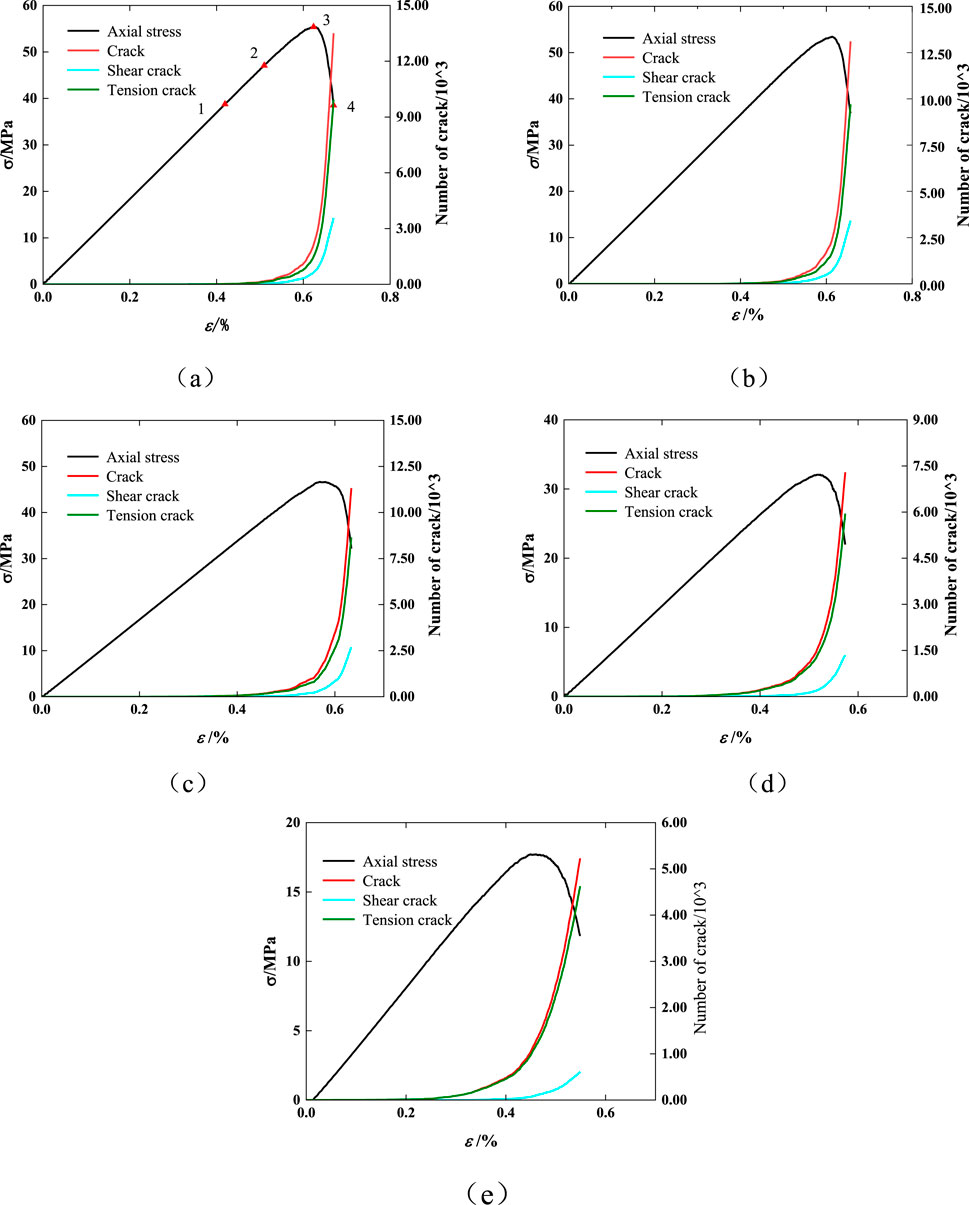
Figure 17. The crack quantity variation of freeze-thawed sandstone under uniaxial compression. (A) N = 0 (B) N = 10 (C) N = 20 (D) N = 30 (E) N = 40.

Figure 18

Figure 18. Failure process of freeze-thawed sandstone under uniaxial compression (characteristic points (1–4) are selected at 70%, 85%, 100% of peak stress and at the failure time). (A) N = 0 (B) N = 10 (C) N = 20 (D) N = 30 (E) N = 40.

5 Conclusion

The numerical model considering the frost heaving force increment and water saturation reduction during freeze-thaw cycles was constructed by combining laboratory experiments, frost heaving theory, and discrete element software PFC3D. This model can simulate crack evolution during freeze-thaw effectively and the fracture process of frozen-thawed sandstone under uniaxial loading is investigated further. This model capably simulates the progression of cracking throughout the freeze-thaw process, and it provides a deeper examination into the fracture mechanisms of sandstone when subjected to uniaxial stress after being frozen and thawed. The main conclusions are as follows:

(1) Compared with laboratory experimental results, the established numerical model for freeze-thaw process is effective within an acceptable range of error. The development of cracks within sandstone under freeze-thaw cycles typically evolves through a tripartite phase: stable phase (N < 5), growth phase (5 < N < 25), and explosive phase (N > 25). Furthermore, a relationship between crack quantity and freeze-thaw times has been established.

(2) Cracks distribute more uniformly at various angles, while cracks gradually develop towards the specimen interior during freeze-thaw cycles.

(3) The freeze-thaw cycles lead to an incresed proportion of tensile cracks under uniaxial loading, making the specimen more prone to tensile failure. Meanwhile, freeze-thaw cycles cause brittleness reduce in sandstone, resulting in a more complex distribution of internal cracks when sandstone fractures.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

LT: Conceptualization, Writing–original draft. WP: Conceptualization, Writing–original draft. HS: Methodology, Writing–review and editing. WB: Methodology, Writing–original draft. CZ: Conceptualization, Data curation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by National Natural Science Foundation of China (52304102) for experimental equipment and rock samples.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdolghanizadeh, K., Hosseini, M., and Saghafiyazdi, M. (2020). Effect of freezing temperature and number of freeze-thaw cycles on mode I and mode II fracture toughness of sandstone. Theor. Appl. Fract. Mech., 105. doi:10.1016/j.tafmec.2019.102428

CrossRef Full Text | Google Scholar

Chao, H., Xiaoguang, J., Jie, H. E., and Chi, Z. (2023). Research on damage model of rock under freeze-thaw cycles based on maximum tensile strain criterion. J. Southwest Jiaot. Univ. 58 (5), 1045–1055. doi:10.3969/j.issn.0258-2724.20210493

CrossRef Full Text | Google Scholar

Chao-jun, J., Rui-feng, P., Jun, Y. U., Ming-feng, L., and Zhong, L. I. (2024). Investigation on freeze-thaw damage mechanism of porous rock with discrete element method. Rock Soil Mech. 45 (2), 588–600. doi:10.16285/j.rsm.2023.0230

CrossRef Full Text | Google Scholar

Exadaktylos, G. E. (2006). Freezing-thawing model for soils and rocks. J. Mater. Civ. Eng. 18 (2), 241–249. doi:10.1061/(asce)0899-1561(2006)18:2(241)

CrossRef Full Text | Google Scholar

Gao, F., Wang, Q., Deng, H., Zhang, J., Tian, W., and Ke, B. (2017). Coupled effects of chemical environments and freeze–thaw cycles on damage characteristics of red sandstone. Bull. Eng. Geol. Environ. 76 (4), 1481–1490. doi:10.1007/s10064-016-0908-0

CrossRef Full Text | Google Scholar

Han, T., and Li, Z. (2021). Mechanical characteristics and failure modes for mode-I sandstone and rock-like cracked sample exposed to freeze thawing cycle. Bull. Eng. Geol. Environ. 80 (9), 6937–6953. doi:10.1007/s10064-021-02347-7

CrossRef Full Text | Google Scholar

Huang, S., Cai, Y., Liu, Y., and Liu, G. (2021). Experimental and theoretical study on frost deformation and damage of red sandstones with different water contents. Rock Mech. Rock Eng. 54 (8), 4163–4181. doi:10.1007/s00603-021-02509-9

CrossRef Full Text | Google Scholar

Huang, S., Liu, Q., Cheng, A., and Liu, Y. (2018). A statistical damage constitutive model under freeze-thaw and loading for rock and its engineering application. Cold Regions Sci. Technol. 145, 142–150. doi:10.1016/j.coldregions.2017.10.015

CrossRef Full Text | Google Scholar

Huang, S., Lu, Z., Ye, Z., and Xin, Z. (2020). An elastoplastic model of frost deformation for the porous rock under freeze-thaw. Eng. Geol. 278, 105820. doi:10.1016/j.enggeo.2020.105820

CrossRef Full Text | Google Scholar

Jia, H., Ding, S., Zi, F., Dong, Y., and Shen, Y. (2020). Evolution in sandstone pore structures with freeze-thaw cycling and interpretation of damage mechanisms in saturated porous rocks. Catena 195, 104915. doi:10.1016/j.catena.2020.104915

CrossRef Full Text | Google Scholar

Ju, X., Niu, F., Liu, M., He, J., and Luo, J. (2024). Impact of water saturation on the damage evolution characteristics of sandstone subjected to freeze–thaw cycles. Rock Mech. Rock Eng. 57 (3), 2143–2157. doi:10.1007/s00603-023-03663-y

CrossRef Full Text | Google Scholar

Khanlari, G., Sahamieh, R. Z., and Abdilor, Y. (2015). The effect of freeze-thaw cycles on physical and mechanical properties of Upper Red Formation sandstones, central part of Iran. Arabian J. Geosciences 8 (8), 5991–6001. doi:10.1007/s12517-014-1653-y

CrossRef Full Text | Google Scholar

Li, J., Kaunda, R. B., and Zhou, K. (2018). Experimental investigations on the effects of ambient freeze-thaw cycling on dynamic properties and rock pore structure deterioration of sandstone. Cold Regions Sci. Technol. 154, 133–141. doi:10.1016/j.coldregions.2018.06.015

CrossRef Full Text | Google Scholar

Liu, H., Yang, G., Yun, Y., Lin, J., Ye, W., Zhang, H., et al. (2020). Investigation of sandstone mesostructure damage caused by freeze-thaw cycles via CT image enhancement Technology. Adv. Civ. Eng. 2020 (1). doi:10.1155/2020/8875814

CrossRef Full Text | Google Scholar

Liu, T., Cui, M., Zhang, C., Zhou, K., Shi, W., and Cao, P. (2022a). Nuclear magnetic resonance analysis of the failure and damage model of rock masses during freeze‒thaw cycles. Bull. Eng. Geol. Environ. 81 (10), 445. doi:10.1007/s10064-022-02944-0

CrossRef Full Text | Google Scholar

Liu, X., Liu, Y., Dai, F., and Yan, Z. (2022b). Tensile mechanical behavior and fracture characteristics of sandstone exposed to freeze-thaw treatment and dynamic loading. Int. J. Mech. Sci. 226, 107405. doi:10.1016/j.ijmecsci.2022.107405

CrossRef Full Text | Google Scholar

Lu, H., Bao, W., Yin, Y., Sun, X., Li, H., Pan, Z., et al. (2023). Experimental study on multi-scale damage and deterioration mechanism of carbonaceous slate under freeze-thaw cycles. Bull. Eng. Geol. Environ. 82 (12), 458. doi:10.1007/s10064-023-03493-w

CrossRef Full Text | Google Scholar

Lv, Z., Luo, S., Xia, C., and Zeng, X. (2022). A thermal–mechanical coupling elastoplastic model of freeze–thaw deformation for porous rocks. Rock Mech. Rock Eng. 55 (6), 3195–3212. doi:10.1007/s00603-022-02794-y

CrossRef Full Text | Google Scholar

Prischepa, O. M., and Xu, R. (2025). Criteria for oil and gas bearing potential of jurassic continental sediments of the central part of junggarian sedimentary basin of the central part of junggarian sedimentary basin. Int. J. Eng. 38 (1), 223–235. doi:10.5829/ije.2025.38.01a.20

CrossRef Full Text | Google Scholar

Pu, Q., Huang, J., Zeng, F., Luo, Y., Li, X., Zhou, J., et al. (2020). Study on long-term dynamic mechanical properties and degradation law of sandstone under freeze-thaw cycle. Shock Vib. 2020, 1–10. doi:10.1155/2020/8827169

CrossRef Full Text | Google Scholar

Qingxiang, C., and Yanlong, C. (2024). Review of 70 years' achievements and high-quality development architecture system of surface coal mining in China. J. China Coal Soc. 49 (1), 235–260. doi:10.13225/j.cnki.jccs.2023.1479

CrossRef Full Text | Google Scholar

Quansheng, L., Shibing, H., Yongshui, K., and Yucong, P. (2016). Study of unfrozen water content and frost heave model for saturated rock under low temperature. Chin. J. Rock Mech. Eng. 35 (10), 2000–2012. doi:10.13722/j.cnki.jrme.2015.1157

CrossRef Full Text | Google Scholar

Shi, H., Wenlong, C., Zhang, H., Lei, S., Ming, L., Miaojing, W., et al. (2023). Dynamic strength characteristics of fractured rock mass. Eng. Fract. Mech. 292, 109678. doi:10.1016/j.engfracmech.2023.109678

CrossRef Full Text | Google Scholar

Shi, H., Zhang, H., Chen, W., Song, L., and Li, M. (2024). Pull-out debonding characteristics of rockbolt with prefabricated cracks in rock: a numerical study based on particle flow code. Comput. Part. Mech. 11 (1), 29–53. doi:10.1007/s40571-023-00607-9

CrossRef Full Text | Google Scholar

Tan, X., Chen, W., Liu, H., Wang, L., Ma, W., and Chan, A. H. C. (2018). A unified model for frost heave pressure in the rock with a penny-shaped fracture during freezing. Cold Regions Sci. Technol. 153, 1–9. doi:10.1016/j.coldregions.2018.04.016

CrossRef Full Text | Google Scholar

Wu, J., Jing, H., Gao, Y., Meng, Q., Yin, Q., and Du, Y. (2022). Effects of carbon nanotube dosage and aggregate size distribution on mechanical property and microstructure of cemented rockfill. Cem. and Concr. Compos. 127, 104408. doi:10.1016/j.cemconcomp.2022.104408

CrossRef Full Text | Google Scholar

Wu, J., Jing, H., Yin, Q., Yu, L., Meng, B., and Li, S. (2020). Strength prediction model considering material, ultrasonic and stress of cemented waste rock backfill for recycling gangue. J. Clean. Prod. 276, 123189. doi:10.1016/j.jclepro.2020.123189

CrossRef Full Text | Google Scholar

Wu, J., Wong, H. S., Zhang, H., Yin, Q., Jing, H., and Ma, D. (2024). Improvement of cemented rockfill by premixing low-alkalinity activator and fly ash for recycling gangue and partially replacing cement. Cem. and Concr. Compos. 145. doi:10.1016/j.cemconcomp.2024.105345

CrossRef Full Text | Google Scholar

Xie Haotian, X. Y. Z. Q. (2024). Experimental study on strength degradation and meso-structural characteristics of saturated sandstone under freeze-thaw cycles. Coal Sci. Technol., 1–10. doi:10.12438/cst.2023-1487

CrossRef Full Text | Google Scholar

Xianjun, T., Weizhong, C., Jianping, Y., and Junjie, C. (2011). Laboratory investigations on the mechanical properties degradation of granite under freeze–thaw cycles[J]. Cold. Reg. Sci. Techno. doi:10.1016/j.coldregions.2011.05.007

CrossRef Full Text | Google Scholar

Xu, J., Pu, H., and Sha, Z. (2023). Influence of microstructure on dynamic mechanical behavior and damage evolution of frozen–thawed sandstone using computed tomography. Materials 16 (1), 119. doi:10.3390/ma16010119

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Y., Chen, B., Wu, B., Chen, Z., Yang, L., and Li, P. (2022). Influence of freeze–thaw cycling on the dynamic compressive failure of rocks subjected to hydrostatic pressure. Bull. Eng. Geol. Environ. 81 (7), 276. doi:10.1007/s10064-022-02774-0

CrossRef Full Text | Google Scholar

Yang, S., Huang, Y., Ranjith, P. G., Jiao, Y., and Ji, J. (2015). Discrete element modeling on the crack evolution behavior of brittle sandstone containing three fissures under uniaxial compression. Acta Mech. Sin. 31 (6), 871–889. doi:10.1007/s10409-015-0444-3

CrossRef Full Text | Google Scholar

Yang, X., Jiang, A., and Li, M. (2019). Experimental investigation of the time-dependent behavior of quartz sandstone and quartzite under the combined effects of chemical erosion and freeze-thaw cycles. Cold Regions Sci. Technol. 161, 51–62. doi:10.1016/j.coldregions.2019.03.008

CrossRef Full Text | Google Scholar

Yin, T., Lu, J., Yu, Y., Wu, Y., Wang, J., and Men, J. (2023). Fracture behavior of yellow sandstone under freeze–thaw cycles with varied saturation states: an investigation of mode I fracture. Geomechanics Energy Environ. 36, 100502. doi:10.1016/j.gete.2023.100502

CrossRef Full Text | Google Scholar

Yong-jun, S., Yin-wei, S., Chen-jing, L. I., Hui-min, Y., Lei-tao, Z., and Li-jun, X. (2023a). Meso-fracture evolution characteristics of freeze-thawed sandstone based on discrete element method simulation. Rock Soil Mech. 44 (12), 3602–3616. doi:10.16285/j.rsm.2023.0448

CrossRef Full Text | Google Scholar

Yong-jun, S., Yin-wei, S., Chen-jing, L. I., Hui-min, Y., Lei-tao, Z., and Li-jun, X. (2023b). Study on meso-fracture evolution characteristics of sandstone after freeze-thaw cycles based on discrete element method simulation. Rock Soil Mech. 44 (12), 3602–3616. doi:10.13722/j.cnki.jrme.2018.1412

CrossRef Full Text | Google Scholar

Zhang, M., Fang, Z., Kang, Y., Wang, X., Huang, M., Li, D., et al. (2022a). Experimental investigation on the erosion behaviors of frozen-thawed sandstone under abrasive supercritical CO 2 jet impingement. Cold Regions Sci. Technol. 193. doi:10.1016/j.coldregions.2021.103423

CrossRef Full Text | Google Scholar

Zhang, Q., Liu, Y., Dai, F., and Jiang, R. (2022b). Experimental assessment on the fatigue mechanical properties and fracturing mechanism of sandstone exposed to freeze-thaw treatment and cyclic uniaxial compression. Eng. Geol. 306. doi:10.1016/j.enggeo.2022.106724

CrossRef Full Text | Google Scholar

Zhu, T., Chen, J., Huang, D., Luo, Y., Li, Y., and Xu, L. (2021). A DEM-based approach for modeling the damage of rock under freeze–thaw cycles. Rock Mech. Rock Eng. 54 (6), 2843–2858. doi:10.1007/s00603-021-02465-4

CrossRef Full Text | Google Scholar