Dynamic response and damage evolution characteristics of uniform rocky slopes with unstable rock masses based on shaking table tests

Seismic activities often trigger catastrophic events including collapses and rockfalls on rocky slopes. This research endeavors to understand the dynamic behavior and damage modes in uniform rocky slopes with unstable rock masses. To achieve this objective, the paper constructs a physical model of uniform rocky slope with unstable rock mass and performs triaxial loading shaking table tests. Subsequently, the seismo-dynamic responses and associated damage modes of the slope are scrutinized, and the initiation and deformation mechanisms of the hazardous rock are revealed. Further, we obtained the marginal spectral energy evolution characteristics of measurement points of both the unstable rock and bedrock. This deciphers the damage evolution characteristics of the weak structural plane. The results indicate that there are distinct elevation and surface amplification effects within the rock slopes, which systematically lessened with increasing seismic intensity. The vertical deformation of unstable rock mass is more sensitive to high seismic intensity. The seismic-induced initiation process of unstable rock masses is split into three stages: trailing edge tension cracking, sliding damage of structural planes, and a complete failure of structural plane shear capacity. It is also established that the Hilbert and marginal spectra effectively identified the damage process of unstable rock masses containing weak structural planes.

1 Introduction

Numerous slopes vary in complexity and steepness in the mountainous regions, posing significant threats to transportation, housing, and public buildings along the routes (Huang, 2011; Tang et al., 2010; Zheng et al., 2023). Collapses and rockfalls are important manifestations of the destruction of rocky slopes (Kusak, 2019; Macciotta et al., 2014; Moos et al., 2022; Yang et al., 2023; Zhan et al., 2022). Recent years have seen growing attention in the engineering community toward slope safety, leading to substantial research progress in understanding landslides, collapses, and other disasters under static conditions (Cheng et al., 2017; Istiyanti et al., 2021; Yang et al., 2022; Yun et al., 2023; Zhao et al., 2019), as well as advancements in slope protection engineering (Jiang et al., 2022; Wei et al., 2024). However, the western region is adjacent to the seismically active Qinghai-Tibet Plateau, characterized by numerous faults and fault zones, which predispose the area to frequent earthquakes (Ren et al., 2018). These seismic events significantly contribute to triggering collapses and rockfalls in the weathered rock layers of these slopes (Oswald et al., 2021; Valagussa et al., 2014; Zheng et al., 2022). Consequently, it becomes imperative to examine how rocky slopes, particularly those with unstable rock masses, behave and potentially fail when subjected to seismic activity. Such research could advance early detection of post-earthquake rockfall initiation and enhance the seismic resilience of slope engineering.

Under seismic loads, rocky slopes undergo elevation amplification effects, which directly affects the weak structural interfaces within the rock mass due to the bedrock’s thrust, causing surface cracking (Alfaro et al., 2012; Song et al., 2020). In this scenario, the slope acts as the disturbance object, the rock mass represents the impacted object, and the structural surfaces serve as the transmission medium. It can be seen that the triggering factor for rock mass sliding during seismic events is the structural surface’s load-bearing capacity failure post-seismic activity. Current scholarly work has yielded significant findings concerning the seismic stability of rocky slopes, focusing on risk assessment (Deng et al., 2020; Jeong et al., 2024; Yeznabad et al., 2021), multi-source coupling (Li et al., 2023; Martino et al., 2022), numerical analysis (Bouckovalas and Papadimitriou, 2005; Li H. et al., 2017), theoretical analysis (Zhang et al., 2022), and anchor destruction (Jia et al., 2024; Lin et al., 2017; Liu et al., 2016). Centrifuge modeling and shaking table tests are extensively utilized to examine the cumulative damage and failure mechanisms of seismic rocky slopes (Fang et al., 2023b; Song et al., 2021). Theoretical approaches such as acceleration response (Lin et al., 2017), Fourier transform spectrum (Li L.-Q. et al., 2017; Li et al., 2018), Hilbert-Huang Transform (HHT) (Fan et al., 2016), and transfer functions (Yang, 2013) are applied to investigate the gradual damage and instability of rocky slopes. Nonetheless, these studies predominantly focus on the seismic damage behavior of rocky slopes, with little consideration given to secondary disasters such as collapses and rockfalls triggered by the failure of rocky slopes with unstable rock masses. Microseismic signals are widely used in studying seismic rockfalls due to their effectiveness in providing information about surface processes (Feng et al., 2021). They serve as an efficient tool for early warning and localization of rockfalls. However, they are susceptible to disruption by external environmental factors and can be costly to implement. The seismic destruction of such slopes represents a complex dynamic coupling system (Chen et al., 2023), where the energy transfer between the slope and unstable rock, along with the condition of structural surfaces, is essential for evaluating rock stability. Furthermore, most research relies on uniaxial shaking table tests, neglecting multi-directional seismic forces' impact, which results in a gap with reality and an incomplete simulation of the seismic interaction between bedrock and unstable rocks.

To reveal the dynamic coupling mechanism of rock slopes and unstable rock mass systems, as well as the seismic damage behavior and damage evolution characteristics of weak structural planes, this paper simulates the dynamic behavior of uniform rocky slopes under seismic action using triaxial shake table tests, with a unstable rock mass containing weak structural planes set at the top of the slope. Analysis of monitored acceleration and displacement data reveals the initiation mechanism of the unstable rock mass. Utilizing the HHT method revealed the extent of damage to weak structural surfaces and the energy transfer dynamics. The results provide valuable insights for advancing engineering practices in rocky slope management.

2 Experimental study

2.1 Test equipment

The rock slope model featuring an unstable rock mass underwent shaking table tests at Southwest Jiaotong University. The table has size of eight by 10 m and supports a maximum load of 160 tons (see Figure 1). The system functions over a frequency range spanning 0.1–50 Hz, allowing it to replicate a broad spectrum of seismic loads across three dimensions and six degrees of freedom. It can achieve a peak horizontal acceleration of ±1.2 g and horizontal travel of up to 800 mm along the X and Y-axes.

Figure 1

Figure 1. Schematic diagram of shaking table.

2.2 Modeling

Materials that mimic the properties of soil or rock have been extensively utilized in physical modeling experiments to study slope dynamics. In shaking table tests for slopes, it is essential to maintain similarity between the prototype and the model. Due to the substantial geometric dimensions of actual slope engineering, achieving correspondence across all parameters within a single similarity system is challenging. This study establishes a similarity system utilizing 17 independent physical quantities commonly employed in shaking table tests. The model is constructed based on Buckingham’s π theorem and similarity theory (Yue et al., 2024). This theorem states that if phenomena are similar, the relationship describing various parameters can be transformed into a functional relationship between similarity criteria, and the functional relationship of the similarity criteria should be the same. Through analysis and organization, 17 independent physical quantities involved in this experiment are selected to establish a similarity system. These physical quantities must satisfy Equation 1:

$f\left(L,\gamma ,g,\phi ,E,\mu ,c,v_s,A,T_d,\omega ,\theta ,s,V,a,\sigma ,\epsilon \right)=0(1)$

Taking physical dimensions L, volumetric weight γ, and gravity acceleration g as control parameters, the similarity relationships among various physical quantities are established as shown in Table 1.

Table 1

Table 1. Similarity ratio of the model.

To simulate the rock mass for the study, a blend was selected comprising barite powder, quartz sand, gypsum, water, and glycerin, with a weight ratio of 31:60:20:10:1. For the simulation of weak structural planes, a blend consisting of loess, river sand, and water in a weight ratio of 4:7:1 was employed (Fan et al., 2025). In mixed material construction, manual compaction is performed every 20 cm to ensure uniformity and density. To verify the compaction effect, density measurements of the compacted soil samples are taken at various locations using a ring knife after each layer is compacted. Table 2 provides the mechanical parameters for both the model materials and the structural surfaces.

Table 2

Table 2. Physic-mechanical parameters of materials.

To accommodate the size and loading constraints of the shake table, a specially designed and constructed rigid model box was used for the tests, as depicted in Figure 2. Robust bolts firmly attached the box to the table, facilitating the efficient transfer of seismic waves to the internal slope model. This model had dimensions of 2.9 m in length, 1.0 m in width, and 2.3 m in height. To observe the slope’s dynamic response to different seismic forces, triaxial acceleration sensors and displacement sensors were strategically positioned along its central cross-section through the monitoring points marked on the foam boards on both sides of the model box. The location and side view of the model, as well as the sensor positions, are illustrated in Figure 3. The triaxial acceleration sensors had a measurement range of $\pm 2\mathrm{g}·s^{-2}$ and sensitivity of $42mV/m·s^{-2}$, while the displacement sensors had a range of $50cm$ and sensitivity of $0.0195mV/mm$. All sensors operated at a sampling rate of 1,000 Hz. In rock slope studies, the boundary condition is often considered a semi-infinite medium. As vibration waves propagate through the slope, they gradually attenuate, dissipating energy through radiation and damping. Polyethylene foam boards are used to reduce vibrational energy from boundary reflections, simulating the actual slope conditions of a “non-reflective” or “free field.” Within the model enclosure, a 10 cm thick layer of polyethylene foam acted as a padding to absorb and reduce the energy of vibrations caused by boundary reflections.

Figure 2

Figure 2. Rigid model box.

Figure 3

Figure 3. Sensors arrangement and model side view.

2.3 Test conditions

Based on the ATC-63 standards (Council, 2009), at least three seismic records, either artificial or actual, should be used for time-history analysis in shaking table tests. For this test, the seismic events selected as models were the typical Wolong, EL Centro, and Kobe earthquakes. These seismic waves were adjusted based on a time similarity ratio. After the adjustment, the durations for the Wolong, EL Centro, and Kobe seismic waves were reduced to approximately 36 s, 8 s, and 8 s, respectively. The seismic waves were applied in three different directions. Before application, each wave was normalized to achieve a peak amplitude of 0.1 g and subjected to baseline correction. Furthermore, varying vibration amplitudes were adjusted to mimic different seismic intensities. Before each seismic loading, the test model was subjected to frequency scanning using white noise to provide data for subsequent studies on how the rock-soil mass of slopes evolves in terms of damage following an earthquake. The selected white noise signal had low energy and frequency bandwidth (covering the resonant frequency band of the slope model at least three times). Specifically, the signal exhibited a vibration acceleration of 0.05 g and was characterized by a dominant frequency range spanning 0–150 Hz, as depicted in Figure 4. The sequence for applying the seismic waves is detailed in Table 3, while the time history curves and spectral characteristics of normalized waves in the X direction are depicted in Figure 5.

Figure 4

Figure 4. White noise time history curve.

Table 3

Table 3. Seismic wave loading sequence.

Figure 5

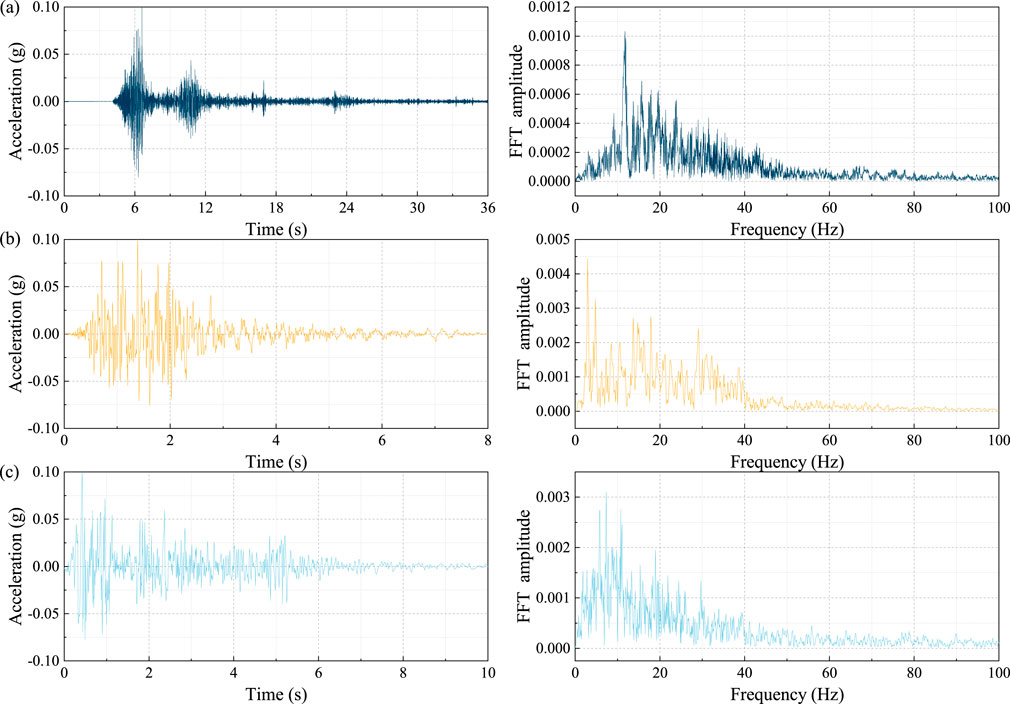
Figure 5. Acceleration curve and its spectral characteristics of normalized input waveforms in X-direction. (A) WL wave; (B) KB wave; (C) ELwave.

3 Dynamic response characterization

3.1 Accelerated response

The dynamic characteristics of slopes during seismic processes can be reflected by acceleration signals. To better understand the acceleration response of rocky slopes internally and on the surface at various depths along the free surface direction (X direction), two sets of monitoring points (A2, A3, A4) and (A5, A6, A4) under seismic excitation were selected for analysis, as depicted in Figure 6. Within the rock slope, elevational and surface amplification effects are apparent, and these effects intensify as the slope’s height increases. Moreover, as seismic intensity rises, the acceleration amplification effects at different depths gradually weaken and tend to equilibrium.

Figure 6

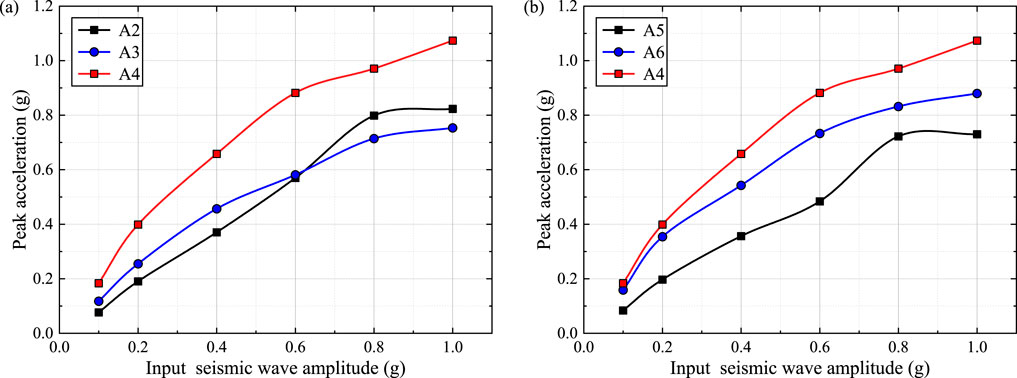
Figure 6. Evolutionary characteristics of acceleration response at different depths. (A) Measurement points A2, A3 and A4; (B) Measurement points A5, A6 and A4.

Wave effects such as reflection, transmission, and waveform transformation on the slope surface or interface can result in local acceleration distortion on the slope surface. Consequently, single-point acceleration values do not adequately represent the vibration response of the slope. To effectively examine the dynamic response of rocky slopes with unstable rock masses, it is vital to create contour maps illustrating the peak acceleration amplification factors during seismic events. The 0.8gKB wave condition resulted in a rock mass failure; therefore, for clarity and appropriate comparison, the KB seismic wave is employed as a case study in the paper. Utilizing data from seven effective triaxial acceleration sensors from the model test, contour maps of peak acceleration amplification factors have been presented in Figures 7, 8. In these figures, the X-direction denotes the slope surface’s free direction, while the Z-direction indicates its vertical orientation (see Figure 3).

Figure 7

Figure 7. Contour maps of peak acceleration amplification factors in X-direction.

Figure 8

Figure 8. Contour maps of peak acceleration amplification factors in Z-direction.

As seismic intensity increases, the vibration amplification region of rocky slopes expands from its top toward its interior. This expansion demonstrates that the plastic zone within the slope mass enlarges with increased seismic intensity. Under different seismic intensities, the peak acceleration exhibits significant elevation amplification effects, but the vibration field in two directions shows obvious differences. At low seismic intensities, the amplification of acceleration is more significant in the direction parallel to the free surface of the slope-rock mass system compared to the vertical direction. In contrast, during high-intensity seismic events, the amplification behavior is reversed, with the vertical direction experiencing greater acceleration amplification than the free surface direction. Figure 9 illustrates the amplification factors within the rock mass, depicting how these factors evolve with increasing seismic intensity. As seismic intensity escalates, the amplification factor at point A7 shows a rise in the Z direction while it diminishes in the X direction, indicating that vertical deformations of the rock mass are more sensitive to higher seismic intensities. Strong vertical vibrations are critical indicators of damage to the fragile structural planes in rocky slopes and unstable rock masses.

Figure 9

Figure 9. Evolution of the amplification factor for unstable rock mass.

3.2 Fourier spectrum evolution

To investigate the evolution of the Fourier spectrum characteristics of unstable rock masses and bedrock under various seismic intensities, this study analyzes the acceleration data recorded at the free surface at points A4 and A7, which flank the weak interface. Figure 10 illustrates the pertinent results. When peak seismic accelerations reach 0.1 and 0.2g, the fourier spectra of the unstable rock masses and bedrock are nearly identical, each displaying a distinct single peak. However, as seismic intensity increases to 0.4g, this single peak transforms into multiple peaks, with point A7 exhibiting notably higher amplitudes than point A4. This multi-peak pattern intensifies further with a seismic intensity of 0.6 g. These observations suggest that at lower seismic intensities, the bedrock-interface-unstable rock mass system behaves as a cohesive unit, undergoing collective movement with minimal damage at the weak interface. The sliding mass, in turn, attenuates high-frequency wave components while accentuating low-frequency components. Once the seismic intensity reaches 0.4g, the unstable rock mass undergoes substantial sliding and internal disruption. This results in a scattering effect as seismic waves traverse the interface, generating derived waves and a complex wave field that manifests as the observed multi-peak phenomena.

Figure 10

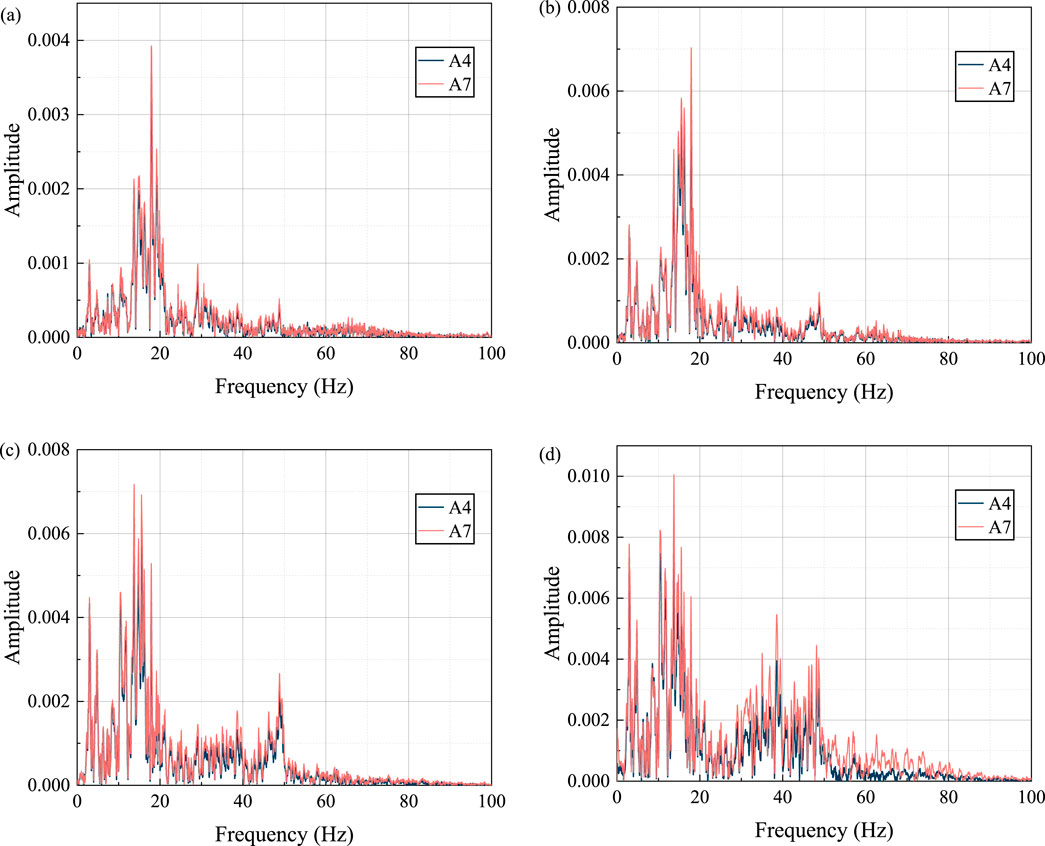
Figure 10. Fourier spectrum evolution of A4 and A7 measurement points under seismic loading. (A–D) represent the input 0.1 g, 0.2 g, 0.4 g, and 0.6 g KB seismic waves respectively.

3.3 Deformation response

The evolution curves of displacement increments monitored on the surface of the slope model under three seismic wave conditions are plotted in Figure 11. These increments reflect the slope’s permanent damage and deformation characteristics. Under these conditions, displacement increments at monitoring point D2 become pronounced starting from a seismic intensity of 0.4g, marking the development of elastoplastic zones in the slope’s upper region. In contrast, monitoring point D3 mainly notes displacement increments under a 0.6 g seismic wave, indicating substantial damage to the structural planes within the unstable rock mass. Therefore, it is deduced that noticeable slope damage initiates at a seismic intensity level of 0.4g, with significant cracking and propagation of the weak structural planes becoming apparent at a seismic intensity of 0.6 g.

Figure 11

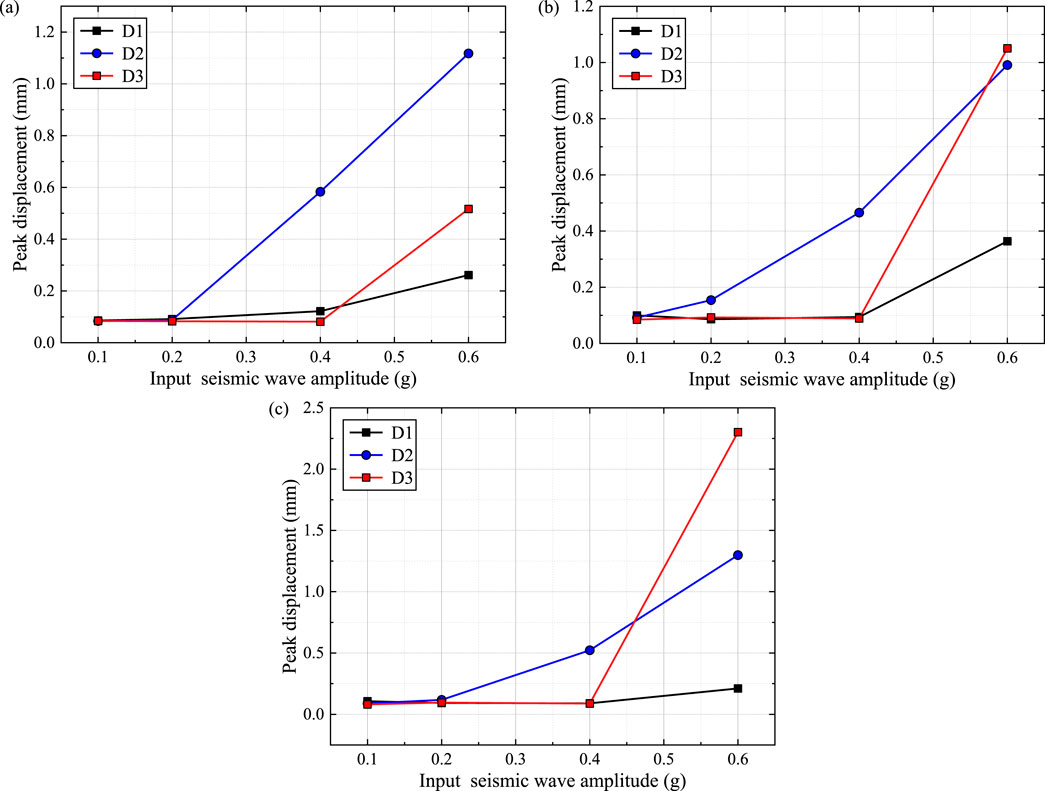
Figure 11. Evolution of displacement increment. (A–C) are the KB seismic wave, El seismic wave, and WL seismic wave respectively.

The time-history curve of slope surface displacement measurement points under a loading condition before rockfall (input of 0.6 g WL seismic wave) is plotted, as shown in Figure 12. Significant increments in displacement are recorded at all three points, with the least displacement at the slope’s toe (monitoring point D1). Notably, peak displacement occurs in the slope’s middle to rear part (monitoring point D2), where the unstable rock mass exhibits the most substantial permanent displacement. This observation suggests that the initial phases of seismic activity introduce cumulative damage to the structural planes within the unstable rock mass.

Figure 12

Figure 12. Displacement time-course curve with input 0.6 g WL seismic wave.

4 Mechanism of initiation and damage of unstable rock mass

4.1 Rockfall initiation process

Figure 13 depicts the triaxial acceleration time-history curves for the brief fall duration of the unstable rock mass under a 0.8 g seismic event. The acceleration curves show marked deviations from the initial waveform, including a pronounced increase in amplitude. Before the collapse, the acceleration in the X-direction spikes to 1.6 g. This suggests that the rock mass has lost intimate contact with the underlying bedrock and that the weak structural planes are heavily compromised, disrupting waveform transmission through the rock mass. Figure 14 provides real-time imagery capturing the onset of instability in the rock mass, taken with an industrial-grade camera, while Figure 15 presents the corresponding displacement time-history curve. Under the influence of the 0.8 g KB seismic wave, the initiation of the rock mass can primarily be divided into three stages: (1) Rear edge cracking: e previous 17 seismic events, the rear edge structural surface accumulated minor damage, which closed after the earthquakes ended. Under a horizontal seismic force of 0.8 g KB wave, the rear edge structural surface of the rock mass was the first to fail (during the 26.5s–27.3s period), resulting in approximately 4 mm of horizontal displacement. During this stage, the acceleration amplitude in the X direction peaked at 1.67 g. (2) Structural plane sliding damage: The significant horizontal displacement of the unstable rock mass rapidly led to the failure of the shear resistance at the bottom structural surface, causing the rock mass to slide (during the 27.3s–28.2s period). During this stage, the unstable rock mass experienced approximately 80 mm of horizontal displacement, and the acceleration amplitude in the X direction stabilized. (3) Total loss of shear capacity in structural planes: The bottom structural surface completely failed, losing its load-bearing capacity and resulting in the failure of the unstable rock mass. During this stage, 56 mm of deformation occurred within 0.4 s.

Figure 13

Figure 13. Acceleration time-history curves for the fall process of the unstable rock mass.

Figure 14

Figure 14. Record of unstable rock mass initiation.

Figure 15

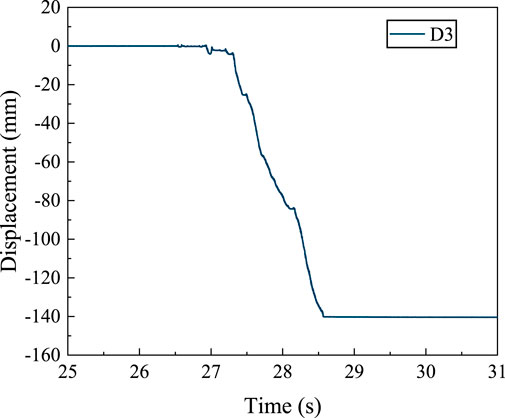
Figure 15. Time-displacement response curve of the unstable rock mass with input 0.8 g KB seismic wave.

4.2 Damage identification of structural plane of unstable rock mass

The Hilbert-Huang Transform is a commonly acknowledged technique for analyzing vibration signals, providing an effective depiction of the spectral features of seismic responses. It has been utilized by several researchers for structural damage identification. The HHT analysis method is primarily composed of two fundamental steps: Empirical Mode Decomposition (EMD) and Hilbert Spectrum Analysis (HSA) (Diao et al., 2021; Hamdi et al., 2013). The method unfolds in the following steps:

(1) From the monitored signal x(t), identify the upper envelope X_max(t) and lower envelope X_min(t) by pinpointing the local extreme points. Subtract the mean m₁(t) of these envelopes from x(t) to generate a new sequence h₁(t). Assess if h₁(t) meets the Intrinsic Mode Function (IMF) criteria. If it does, designate h₁(t) as the first IMF component. If not, substitute h₁(t) with x(t) and repeat until an IMF component is isolated.

(2) Subtract this IMF component from x(t) and treat the resultant sequence as the new original sequence. Continue to isolate subsequent IMF components until the residual sequence R_n(t) either becomes a monotonic function or decreases beneath a predefined threshold, culminating the process.

(3) Apply the convolution of the IMF component h₁(t) with 1/(πt) as in Equation 2:

$H\left[h\left(t\right)\right]=\frac{1}{\pi }{P}_v{\int }_{-\infty }^{+\infty }\frac{x\left(\tau \right)}{t-\tau }d\tau (2)$

Where $P_v$ represents the Cauchy principal value; $x\left(\tau \right)$ represents each order of IMF component; $\tau$ represents frequency.

In the amplitude-time plane, the original signal can be expressed as Equation 3.

$H\left(w,t\right)=\text{Re}{\displaystyle \sum _{j=1}^n}{a}_j\left(t\right)e^{i\int {\omega }_j\left(t\right)dt}\omega \left(t\right)(3)$

In the equation, n represents the number of IMF components; $a_j\left(t\right)$ and $\omega \left(t\right)$ respectively represents the instantaneous amplitude and frequency of IMF components.

The HHT offers a significant advantage by minimizing the fitting errors of the Fourier transform. This capability allows it to overcome the time-frequency correspondence challenges dictated by the Heisenberg uncertainty principle (Yue et al., 2024). HHT is especially effective for examining sudden signals, offering detailed insights into both the time-domain and frequency-domain responses observed during structural vibrations. Consequently, deploying the HHT method to investigate seismic responses in slopes can provide a more accurate representation of the evolving damage state in rock masses.

This study focuses on recognizing the damage patterns in the structural plane of unstable rock masses. By selecting monitoring points A4 and A7 as representative examples, the acceleration data oriented toward the free surface is analyzed using the HHT. This analysis is illustrated in Figure 16. The resulting Hilbert spectrum predominantly exhibits energy concentration across two frequency bands: low frequency (10–20 Hz) and high frequency (30–45 Hz), with the peak amplitudes chiefly within the low-frequency range. At an acceleration of 0.1g, the peak magnitudes corresponding to both the bedrock and the unstable rock mass are congruent, suggesting no apparent damage to the slope or rock mass, as corroborated by Section 3’s analysis. At 0.2 g acceleration, the bedrock’s peak amplitude surpasses that of the unstable rock mass, although both exhibit relatively subdued energy distributions in both frequency bands compared to the unstable rock mass, indicating damage to the weak structural planes. At 0.4 g, there is a marked escalation in energy distribution across both frequency bands, and the amplitude of the Hilbert Spectrum for the rock mass far exceeds that of the bedrock. At this time, both the slope and the rock mass experience a certain degree of damage. Concurrently, a decreasing trend in the dominant seismic energy frequency band within the unstable rock mass indicates diminished shear resistance along the weak structural planes. At 0.6 g, similar peak amplitudes are observed for the bedrock and the unstable rock mass, but the latter displays a pronounced increase in high-frequency energy.

Figure 16

Figure 16. Hilbert spectrum of slope A4/A7 monitoring point with input KB seismic wave.

The marginal spectrum assesses how much each frequency contributes to a signal’s total energy over its entire duration. The marginal spectrum traits derived from the Hilbert spectrum in Figure 16 are illustrated in Figure 17. When seismic waves travel through a slope, any damage at a specific location can lead to disrupted energy transmission, causing significant fluctuations and anomalies in the marginal spectrum. This behavior is reflected in the marginal spectrum characteristics of an unstable rock mass. Both the slope and the unstable rock mass primarily release energy in the low-frequency range. As the seismic intensity increases, displacement occurs between the bedrock and the unstable rock mass. The wave impedance of weak structural surfaces increases, amplifying low-frequency vibrations and attenuating high-frequency vibrations. This makes it difficult for high-frequency energy to transfer to the rock mass, resulting in the rock mass having less high-frequency energy than the bedrock. An increase in shear failure points lowers the main frequency band of the unstable rock mass. A reduction in low-frequency vibrations combined with an increase in high-frequency energy serves as critical indicators of impending failure along weak structural planes.

Figure 17

Figure 17. Marginal spectral curves. (A) A4 Monitoring point (B) A7 Monitoring point.

5 Discussion and limitations

Based on the method proposed by Fang et al. (2023b), a summarized protocol of the physical model tests is provided in Table 4, which directly presents the brief and essential information from the tests. Nevertheless, despite careful planning and execution, this study has limitations. The homogeneity of the materials used in the shaking table experiments may lead to idealized results that do not fully simulate actual site characteristics. Additionally, cost constraints limited the number of comparative tests. Factors such as the slope of weak structural surfaces and material strength may affect the outcomes. The potential impact of bedrock damage and cracking on unstable rock masses introduces further uncertainty.

Table 4

Table 4. Summarized protocol of the test.

Nevertheless, the findings provide valuable insights for assessing slope stability in engineering. Strong vertical acceleration can indicate damage to weak structural planes and unstable rock masses. Seismic damage also correlates with shifts in energy and frequency, aiding in the multi-field information monitoring of landslide deformation and failure (Fang et al., 2023a).

6 Conclusion

This study reveals the seismic damage patterns and dynamic response characteristics of uniform rocky slopes containing unstable rock masses through triaxial shaking table tests. The principal conclusions are:

(1) Within a rock slope, both elevation and surface amplification effects are notably significant, with their prominence escalating as the slope’s elevation rises. However, as seismic intensity grows, the acceleration amplification effect diminishes over time and eventually reaches a point of stabilization.

(2) The vertical deformation of unstable rock masses exhibits heightened sensitivity to elevated seismic intensities. Strong vertical acceleration shaking can serve as a key signal for damage to the weak structural planes of rock slopes and unstable rock masses. At lower seismic intensities, the acceleration amplification is notably more significant in the horizontal direction along the free surface compared to the vertical direction.

(3) The initiation process of unstable rock masses under seismic events is categorized into three stages based on experimental observations. Rear edge cracking: Horizontal seismic forces precipitate the initial failure of the rear structural planes, leading to notable horizontal displacement; Structural plane sliding damage: Excessive horizontal movement causes the rapid degradation of shear resistance along the lower structural planes, resulting in the rock mass sliding; Total loss of shear capacity in structural planes: A comprehensive failure of the load-bearing capability of the lower structural planes leads to the falling of the rock mass.

(4) Hilbert spectrum and marginal spectrum effectively identify the structural plane damage process of unstable rock masses. Energy distribution in rock slopes and unstable rock masses mainly concentrates within two frequency bands: 10–20 Hz and 30–45 Hz. Under low seismic intensity, the contact between the bedrock and unstable rock mass is relatively intact, and the Hilbert spectrum and the marginal spectrum exhibit comparable characteristics. Under high seismic intensity, there is significant energy loss that results in pronounced fluctuations and sudden changes within the marginal spectrum. This serves as an indicator of damage to structural planes. A notable reduction in low-frequency vibration frequencies, coupled with a rise in high-frequency vibration energy, are crucial signals pointing to the failure of these structural planes.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

DW: Conceptualization, Funding acquisition, Writing–original draft. HW: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was financially supported by the China Railway Group Limited Science and Technology Research and Development Program (2022-Major-01).

Conflict of interest

Author DW was employed by China Railway Eryuan Engineering Group Co. Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from China Railway Group Limited R&D Program (2022-Major-01). The funder had the following involvement in the study: decision to publish.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alfaro, P., Delgado, J., García-Tortosa, F. J., Giner, J. J., Lenti, L., López-Casado, C., et al. (2012). The role of near-field interaction between seismic waves and slope on the triggering of a rockslide at Lorca (SE Spain). Nat. Hazards Earth Syst. Sci. 12, 3631–3643. doi:10.5194/nhess-12-3631-2012

CrossRef Full Text | Google Scholar

Bouckovalas, G. D., and Papadimitriou, A. G. (2005). Numerical evaluation of slope topography effects on seismic ground motion. Soil Dyn. Earthq. Eng. 25, 547–558. doi:10.1016/j.soildyn.2004.11.008

CrossRef Full Text | Google Scholar

Chen, H., Zhu, H., and Zhang, L. (2023). Rock slope stability analysis incorporating the effects of intermediate principal stress. Rock Mech. Rock Eng. 56, 4271–4289. doi:10.1007/s00603-023-03277-4

CrossRef Full Text | Google Scholar

Cheng, X. S., Zheng, G., Diao, Y., Huang, T. M., Deng, C. H., Nie, D. Q., et al. (2017). Experimental study of the progressive collapse mechanism of excavations retained by cantilever piles. Can. Geotechnical J. 54, 574–587. doi:10.1139/cgj-2016-0284

CrossRef Full Text | Google Scholar

Council, A. T. (2009). Quantification of building seismic performance factors.

Google Scholar

Deng, Z., Liu, X., Liu, Y., Liu, S., Han, Y., Liu, J., et al. (2020). Model test and numerical simulation on the dynamic stability of the bedding rock slope under frequent microseisms. Earthq. Eng. Eng. Vib. 19, 919–935. doi:10.1007/s11803-020-0604-8

CrossRef Full Text | Google Scholar

Diao, Y., Jia, D., Liu, G., Sun, Z., and Xu, J. (2021). Structural damage identification using modified Hilbert–Huang transform and support vector machine. J. Civ. Struct. Health Monit. 11, 1155–1174. doi:10.1007/s13349-021-00509-5

CrossRef Full Text | Google Scholar

Fan, G., Zhang, J., Wu, J., and Yan, K. (2016). Dynamic response and dynamic failure mode of a weak intercalated rock slope using a shaking table. Rock Mech. Rock Eng. 49, 3243–3256. doi:10.1007/s00603-016-0971-7

CrossRef Full Text | Google Scholar

Fan, J., Yang, C., Yue, M., Luo, J., Lian, J., and Wei, P. (2025). Dynamic response of rock landslides and avalanche debris flows impacting flexible barriers based on shaking table tests. Soil Dyn. Earthq. Eng. 188, 109078. doi:10.1016/j.soildyn.2024.109078

CrossRef Full Text | Google Scholar

Fang, K., Miao, M., Tang, H., Jia, S., Dong, A., An, P., et al. (2023a). Insights into the deformation and failure characteristic of a slope due to excavation through multi-field monitoring: a model test. Acta Geotech. 18, 1001–1024. doi:10.1007/s11440-022-01627-0

CrossRef Full Text | Google Scholar

Fang, K., Tang, H., Li, C., Su, X., An, P., and Sun, S. (2023b). Centrifuge modelling of landslides and landslide hazard mitigation: a review. Geosci. Front. 14, 101493. doi:10.1016/j.gsf.2022.101493

CrossRef Full Text | Google Scholar

Feng, L., Intrieri, E., Pazzi, V., Gigli, G., and Tucci, G. (2021). A framework for temporal and spatial rockfall early warning using micro-seismic monitoring. Landslides 18, 1059–1070. doi:10.1007/s10346-020-01534-z

CrossRef Full Text | Google Scholar

Hamdi, S. E., Le Duff, A., Simon, L., Plantier, G., Sourice, A., and Feuilloy, M. (2013). Acoustic emission pattern recognition approach based on Hilbert–Huang transform for structural health monitoring in polymer-composite materials. Appl. Acoust. 74, 746–757. doi:10.1016/j.apacoust.2012.11.018

CrossRef Full Text | Google Scholar

Huang, R. (2011). Mechanisms of large-scale landslides in China. Bull. Eng. Geol. Environ. 71, 161–170. doi:10.1007/s10064-011-0403-6

CrossRef Full Text | Google Scholar

Istiyanti, M. L., Goto, S., and Ochiai, H. (2021). Characteristics of tuff breccia-andesite in diverse mechanisms of landslides in Oita Prefecture, Kyushu, Japan. Geoenvironmental Disasters 8, 4. doi:10.1186/s40677-021-00176-0

CrossRef Full Text | Google Scholar

Jeong, S., Moon, M., and Kim, D. (2024). Seismic wave amplification characteristics in slope sections of various inclined model grounds. Appl. Sciences-Basel 14, 9014. doi:10.3390/app14199014

CrossRef Full Text | Google Scholar

Jia, J., Gao, X., Bao, X., Xiang, X., Zhang, L., and Tu, B. (2024). Dynamic stability analysis method of anchored rocky slope considering seismic deterioration effect. Sci. Rep. 14, 7014. doi:10.1038/s41598-024-57413-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, X., Qian, Y., Yang, H., Xiao, Z., Fan, W., Zhu, Y., et al. (2022). Model test studies on slope supported by bamboo anchor and timber frame beam. Geotechnical Geol. Eng. 40, 4327–4344. doi:10.1007/s10706-022-02157-y

CrossRef Full Text | Google Scholar

Kusak, M. (2019). Key issues in 3D rockfall modeling, natural hazard and risk assessment for rockfall protection in Hrensko (Czechia). Acta Geodyn. Geomaterialia, 393–408. doi:10.13168/agg.2019.0033

CrossRef Full Text | Google Scholar

Li, H., Liu, Y., Liu, L., Liu, B., and Xia, X. (2017a). Numerical evaluation of topographic effects on seismic response of single-faced rock slopes. Bull. Eng. Geol. Environ. 78, 1873–1891. doi:10.1007/s10064-017-1200-7

CrossRef Full Text | Google Scholar

Li, L.-q., Ju, N.-p., Zhang, S., and Deng, X.-x. (2017b). Shaking table test to assess seismic response differences between steep bedding and toppling rock slopes. Bull. Eng. Geol. Environ. 78, 519–531. doi:10.1007/s10064-017-1186-1

CrossRef Full Text | Google Scholar

Li, L.-q., Ju, N.-p., Zhang, S., Deng, X.-x., and Sheng, D. (2018). Seismic wave propagation characteristic and its effects on the failure of steep jointed anti-dip rock slope. Landslides 16, 105–123. doi:10.1007/s10346-018-1071-4

CrossRef Full Text | Google Scholar

Li, Z., Yin, C., Tan, Z., Liu, X., Li, S., and Zhang, X. (2023). Rainfall-seismic coupling effect induced landslide hazard assessment. Nat. Hazards 118, 2123–2152. doi:10.1007/s11069-023-06084-w

CrossRef Full Text | Google Scholar

Lin, Y.-l., Li, Y.-x., Yang, G.-l., and Li, Y. (2017). Experimental and numerical study on the seismic behavior of anchoring frame beam supporting soil slope on rock mass. Soil Dyn. Earthq. Eng. 98, 12–23. doi:10.1016/j.soildyn.2017.04.008

CrossRef Full Text | Google Scholar

Liu, X., Liu, Y., He, C., and Li, X. (2016). Dynamic stability analysis of the bedding rock slope considering the vibration deterioration effect of the structural plane. Bull. Eng. Geol. Environ. 77, 87–103. doi:10.1007/s10064-016-0945-8

CrossRef Full Text | Google Scholar

Macciotta, R., Martin, C. D., and Cruden, D. M. (2014). Probabilistic estimation of rockfall height and kinetic energy based on a three-dimensional trajectory model and Monte Carlo simulation. Landslides 12, 757–772. doi:10.1007/s10346-014-0503-z

CrossRef Full Text | Google Scholar

Martino, S., Marmoni, G. M., Fiorucci, M., Ceci, A. F., Discenza, M. E., Rouhi, J., et al. (2022). Role of antecedent rainfall in the earthquake-triggered shallow landslides involving unsaturated slope covers. Appl. Sciences-Basel 12, 2917. doi:10.3390/app12062917

CrossRef Full Text | Google Scholar

Moos, C., Bontognali, Z., Dorren, L., Jaboyedoff, M., and Hantz, D. (2022). Estimating rockfall and block volume scenarios based on a straightforward rockfall frequency model. Eng. Geol. 309, 106828. doi:10.1016/j.enggeo.2022.106828

CrossRef Full Text | Google Scholar

Oswald, P., Strasser, M., Hammerl, C., and Moernaut, J. (2021). Seismic control of large prehistoric rockslides in the Eastern Alps. Nat. Commun. 12, 1059. doi:10.1038/s41467-021-21327-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, J., Xu, X., Zhang, S., Yeats, R. S., Chen, J., Zhu, A., et al. (2018). Surface rupture of the 1933 M 7.5 Diexi earthquake in eastern Tibet: implications for seismogenic tectonics. Geophys. J. Int. 212, 1627–1644. doi:10.1093/gji/ggx498

CrossRef Full Text | Google Scholar

Song, D., Chen, Z., Ke, Y., and Nie, W. (2020). Seismic response analysis of a bedding rock slope based on the time-frequency joint analysis method: a case study from the middle reach of the Jinsha River, China. Eng. Geol. 274, 105731. doi:10.1016/j.enggeo.2020.105731

CrossRef Full Text | Google Scholar

Song, D., Liu, X., Huang, J., Zhang, Y., Zhang, J., and Nkwenti, B. N. (2021). Seismic cumulative failure effects on a reservoir bank slope with a complex geological structure considering plastic deformation characteristics using shaking table tests. Eng. Geol. 286, 106085. doi:10.1016/j.enggeo.2021.106085

CrossRef Full Text | Google Scholar

Tang, H., Jia, H., Hu, X., Li, D., and Xiong, C. (2010). Characteristics of landslides induced by the great Wenchuan earthquake. J. Earth Sci. 21, 104–113. doi:10.1007/s12583-010-0008-1

CrossRef Full Text | Google Scholar

Valagussa, A., Frattini, P., and Crosta, G. B. (2014). Earthquake-induced rockfall hazard zoning. Eng. Geol. 182, 213–225. doi:10.1016/j.enggeo.2014.07.009

CrossRef Full Text | Google Scholar

Wei, Z., Li, Y., Dong, J., Cao, S., Ma, W., Wang, X., et al. (2024). The identification and influence factor analysis of landslides using SBAS-InSAR technique: a case study of Hongya Village, China. Appl. Sciences-Basel 14, 8413. doi:10.3390/app14188413

CrossRef Full Text | Google Scholar

Yang, C. (2013). Study on seismic dynamic characters of rock slopes and system including formation mechanism of landslides, stability discrimination of slope and assement of harzard scope of landslide for slope of bedrock and overburden layer. (Ph.D. thesis). Southwest Jiaotong University.

Google Scholar

Yang, H., Xing, B., He, J., Jiang, H., and Cheng, Q. (2022). The formation mechanism and failure mode of a talus slope induced by rockfalls in Nayong County, Southwest China. Front. Earth Sci. 10, 973528. doi:10.3389/feart.2022.973528

CrossRef Full Text | Google Scholar

Yang, Y., Zhang, Y., Teng, Z., Liu, P., and Qiao, L. (2023). Study on movement characteristics and numerical simulation of high-altitude rockfall in babao mountain in China. Front. Earth Sci. 11. doi:10.3389/feart.2023.1281364

CrossRef Full Text | Google Scholar

Yeznabad, A. F., Molnar, S., and El Naggar, M. H. (2021). Probabilistic solution for the seismic sliding displacement of slopes in Greater Vancouver. Soil Dyn. Earthq. Eng. 140, 106393. doi:10.1016/j.soildyn.2020.106393

CrossRef Full Text | Google Scholar

Yue, M., Qu, L., Zhou, S., Wu, D., Chen, Z., and Wen, H. (2024). Dynamic response characteristics of shaking table model tests on the gabion reinforced retaining wall slope under seismic action. Geotext. Geomembranes 52, 167–183. doi:10.1016/j.geotexmem.2023.10.001

CrossRef Full Text | Google Scholar

Yun, L., Zhang, X., Zheng, Y., Wang, D., and Hua, L. (2023). Enhance the accuracy of landslide detection in UAV images using an improved mask R-CNN model: a case study of sanming, China. Sensors 23, 4287. doi:10.3390/s23094287

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhan, J., Yu, Z., Lv, Y., Peng, J., Song, S., and Yao, Z. (2022). Rockfall hazard assessment in the Taihang grand canyon scenic area integrating regional-scale identification of potential rockfall sources. Remote Sens. 14, 3021. doi:10.3390/rs14133021

CrossRef Full Text | Google Scholar

Zhang, H., Wu, Y., Huang, S., Zheng, L., and Miao, Y. (2022). Analysis of flexural toppling failure of anti-dip rock slopes due to earthquakes. Front. Earth Sci. 9, 831023. doi:10.3389/feart.2021.831023

CrossRef Full Text | Google Scholar

Zhao, X., Hu, K., Burns, S. F., and Hu, H. (2019). Classification and sudden departure mechanism of high-speed landslides caused by the 2008 Wenchuan earthquake. Environ. Earth Sci. 78, 125. doi:10.1007/s12665-019-8083-9

CrossRef Full Text | Google Scholar

Zheng, B., Song, S., Cheng, X., Niu, R., Cheng, X., Ruan, H., et al. (2023). The influence of coal mining subsidence on the movement and deformation of loess slope in the loess gully area of Northern Shaanxi. Front. Earth Sci. 11. doi:10.3389/feart.2023.1273389

CrossRef Full Text | Google Scholar

Zheng, L., Wu, Y., Zhu, Z., Ren, K., Wei, Q., Wu, W., et al. (2022). Investigating the role of earthquakes on the stability of dangerous rock masses and rockfall dynamics. Front. Earth Sci. 9. doi:10.3389/feart.2021.824889

CrossRef Full Text | Google Scholar