Material point method for simulating strong mining pressure manifestation in multiple hard roof panels controlled by hydraulic fracturing

Ground hydraulic fracturing has emerged as an effective technique for mitigating strong mining pressure manifestations in longwall top coal caving (LTCC). However, the influence of different hydraulic fracture types on the strength characteristics of hard roofs (HR) remains unclear, as does their impact on the fracture process and stress redistribution characteristics of HR. In this study, a numerical simulation tool based on the material point method (MPM) and a strain-softening model was employed to construct a model for LTCC involving overburdened multi-layer HR panels. Furthermore, LTCC mining simulation research was conducted, encompassing prefabricated horizontal hydraulic fracturing, vertical fracturing, and non-fracturing models. The results revealed the following: 1) The fundamental mechanism of HR fracture involves tensile failure induced by the gravity load of the overburdened rock layer when suspended. Vertical cracks resulting from surface hydraulic fracturing significantly diminished the tensile strength of HR, thereby greatly reducing its collapse step distance. 2) In LTCC, the stress transfer dynamics within rock layers were characterized by the following: horizontal stress concentrated in the middle through bending deformation of the rock layer upon suspension. Furthermore, upon reaching its peak, the rock layer fractured and collapsed, thereby releasing horizontal stress. Hydraulic fracturing-induced reduction in HR tensile strength effectively mitigated horizontal stress concentration. 3) Vertical stress concentration occurred through the collapse of lower rock layers and the pressure exerted by suspended upper rock layers. The appearance of its peak represents the collapse of multiple rock layers, and through hydraulic fracturing, the collapse step distance was effectively shortened, weakening the concentration of vertical stress.

1 Introduction

Longwall top coal caving (LTCC) stands out as an efficient coal mining technology, extensively deployed across numerous mines (Das et al., 2023; Xia et al., 2017). However, as mining operations extend to greater depth and height, coal seams face escalating overburden rock pressure and structural stress (Le et al., 2017; Yu et al., 2022). The presence of a hard roof (HR), defined as a roof situated above a coal seam with substantial thickness, high strength, structural integrity, considerable collapse step distance, and hard lithology, significantly influences the movement of overburden strata in mining regions. The large suspended area of the HR amplifies high mining stress, thereby inducing strong mining pressure manifestation disasters (Li et al., 2020; Yang, 2015; Yu et al., 2015). The challenge of large-scale collapse of HRs emerges as a major threat to the secure and efficient operation of existing coal mines, underscoring the ongoing research focus on effective control measures (Ning et al., 2017; Xie and Xu, 2017).

Ground hydraulic fracturing emerges as an effective technique for addressing HR instability. Furthermore, by injecting high-pressure water into the HR, hydraulic fractures are induced, thereby reducing the integrity and strength of the HR, shortening its collapse step distance, and ultimately exerting control over strong mining pressure manifestations at the working face (Glubokovskikh et al., 2023; Huang et al., 2017; Liu et al., 2020). The different types of fracturing cracks exert distinct influences on the strength characteristics of the HR, while the interplay between these characteristics and the stress state during LTCC significantly impacts strong mining pressure manifestation (Konicek and Waclawik, 2018; Zhu et al., 2022). Therefore, investigating the fracture evolution and stress transfer characteristics of HRs under different types of ground fracturing control assumes paramount significance for strong mining pressure control and safe mining practices in coal mines.

To date, several scholars have conducted extensive experiments, simulations, and theoretical studies on the instability characteristics of HRs and the mechanisms underlying mining pressure during coal operations, yielding important results. Kang et al. (2018a), Kang et al. (2018b) studied large-scale roof collapse during longwall mining through comprehensive physical model experiments and corresponding numerical simulations. This further revealed roof collapse as a typical jumping failure phenomenon, with mid-span cross cracks in HRs and significant stress alleviation through hydraulic fracturing of the main roof. Pan et al. (2022) discussed the criterion for ground pressure behavior induced by high-level hard top plates, proposing load reduction via vertical fracturing of these plates. Yu et al. (2019) determined key formations for hydraulic fracturing through in-situ ground hydraulic action tests, presenting innovative solutions for breaking high-rise hard formations. Deng et al. (2023) conducted microseismic monitoring research on LTCC mining, identifying horizontal and vertical impact zones and proposing a key geological structure model to elucidate strong mining pressure behaviors. Eremin et al. (2020) employed a combination of finite difference and continuous damage mechanics methods to simulate the stress–strain evolution of rock mass during coal mining, determining the average advancing speed of the working face. Gao et al. (2021) utilized physical simulation methods to study the control effect of surface fracturing on formation structure and energy release. These significant contributions lay a solid foundation for this study.

However, this brief literature review indicates the paucity of reports on the impact of different types of fracturing cracks on the instability characteristics of HRs during the LTCC process, while the influence of ground hydraulic fracturing on the fracture process and stress redistribution characteristics of HRs remains unclear. Given the stress state of the hard top panel during the LTCC process is closely related to its instability characteristics, urgent attention is warranted in this regard.

In this study, the material point method (MPM) and the continuous medium strain-softening constitutive model were employed to construct an LTCC numerical model for the overlying multi-layer HRs. Subsequently, the calculation results were compared with similar physical simulation experimental results, verifying the applicability and capability of the model. Finally, leveraging this model, LTCC simulations were conducted using prefabricated horizontal fracturing cracks, vertical fracturing, and non-fracturing models. The study unveiled the controlled characteristics of strong mining pressure in multi-layer HRs through ground hydraulic fracturing from three perspectives: mining-induced overburden rock fractures evolution, stress transfer dynamics, and energy evolution, thereby offering theoretical support for engineering applications.

2 Simulation method

2.1 Governing equations

LTCC involves complex mechanical processes, including elastic-plastic deformation, rock damage, and fracture (Xiao et al., 2020). This study applied elastic theory to describe the dynamics and deformation of elastic objects. This theory comprises equations of motion (Equation 1), geometric equations (Equation 2), and elastic constitutive equations (Equation 3) (Ai and Gao, 2023).

$\nabla \sigma +\mathrm{\rho }\left(\mathbf{b}-\frac{\partial \mathbf{v}}{\partial \mathrm{t}}\right)=0(1)$

$∆\epsilon =\frac{1}{2}\left[\nabla \left(∆\mathbf{u}\right)+{\nabla }^T\left(∆\mathbf{u}\right)\right](2)$

$∆\sigma =\left(K-\frac{2}{3}G\right)∆{\epsilon }_{\mathrm{v}}+2G∆{\epsilon }_{\text{dev}}(3)$

where σ is the stress tensor (MPa), ε is the strain tensor, ε_v and ε_dev are the volumetric strain tensor and the deviator strain tensor, ρ is the density (kg/m³), b is the volumetric force (N/m³), v is the velocity (m/s), u is the displacement (m), K is the volumetric modulus (MPa), and G is the shear modulus (MPa).

The strain-softening constitutive model was utilized to simulate the evolution of rock damage, fracture initiation, and propagation. The Mohr–Coulomb criterion (Equation 4) and tensile failure criterion (Equation 5) were used to describe the shear and tensile yield strength, respectively.

$f_{\mathrm{s}}={\sigma }_1-N_{\mathrm{\phi }}{\sigma }_2+2c\sqrt{N_{\mathrm{\phi }}}(4)$

$f_{\mathrm{t}}={\sigma }_2-{\sigma }_{\mathrm{t}}(5)$

where f_s is the shear yield strength (MPa), f_t is the tensile yield strength (MPa), σ₁ is the maximum principal stress (MPa), σ₂ is the minimum principal stress (MPa), c is the cohesion (MPa), N_φ = (1+sin φ)/(1- sin φ), φ is internal friction (°), and σ_t is the tensile strength (MPa). The plastic deformation in the main direction is calculated using the orthogonal flow rule (Equation 6).

$∆{\epsilon }^p=\lambda \frac{\partial \mathrm{g}}{\partial \mathrm{\sigma }}(6)$

where ε^p is the plastic deformation, λ is the plastic correction coefficient, and g is the potential function.

It is crucial to describe the dynamic crack propagation in LTCC accurately. We employed a damage-softening constitutive model (Equations 7, 8) based on continuum mechanics to describe the deformation, damage, and softening of the target object. In this model, the accumulation of plastic strain causes the softening of the strength parameters. When the plastic strain reaches a threshold, the target object undergoes separation, and visible cracks are formed. No material points were removed during the mechanical process (Tang, 1997).

$\left\{\begin{array}{l}\begin{array}{l}\varphi ={\varphi }_{\mathrm{c}},{\epsilon }_{\mathrm{s}}^{\mathrm{p}}>{\epsilon }_{\mathrm{s},\max }^{\mathrm{p}}\\ c=0,{\epsilon }_{\mathrm{s}}^{\mathrm{p}}>{\epsilon }_{\mathrm{s},\max }^{\mathrm{p}}\end{array}\\ \begin{array}{l}\varphi =\frac{{\varphi }_0-{\varphi }_{\mathrm{c}}}{{\epsilon }_{\mathrm{s}0}^{\mathrm{p}}-{\epsilon }_{\mathrm{s},\max }^{\mathrm{p}}}\left({\epsilon }_{\mathrm{s}}^{\mathrm{p}}-{\epsilon }_{\mathrm{s},\max }^{\mathrm{p}}\right)+{\varphi }_{\mathrm{c}},{\epsilon }_{\mathrm{s}}^{\mathrm{p}}<{\epsilon }_{\mathrm{s},\max }^{\mathrm{p}}\\ c=\frac{c_0}{{\epsilon }_{\mathrm{s}0}^{\mathrm{p}}-{\epsilon }_{\mathrm{s},\max }^{\mathrm{p}}}\left({\epsilon }_{\mathrm{s}}^{\mathrm{p}}-{\epsilon }_{\mathrm{s},\max }^{\mathrm{p}}\right),{\epsilon }_{\mathrm{s}}^{\mathrm{p}}<{\epsilon }_{\mathrm{s},\max }^{\mathrm{p}}\end{array}\end{array}\right.(7)$

$\left\{\begin{array}{l}{\sigma }_{\mathrm{t}}=0,{\epsilon }_{\mathrm{t}}^{\mathrm{p}}>{\epsilon }_{\mathrm{t},\max }^{\mathrm{p}}\\ {\sigma }_{\mathrm{t}}=\frac{{\sigma }_{\mathrm{t}0}}{{\epsilon }_{\mathrm{t}0}^{\mathrm{p}}-{\epsilon }_{\mathrm{t},\max }^{\mathrm{p}}}\left({\epsilon }_{\mathrm{t}}^{\mathrm{p}}-{\epsilon }_{\mathrm{t},\max }^{\mathrm{p}}\right),{\epsilon }_{\mathrm{t}}^{\mathrm{p}}<{\epsilon }_{\mathrm{t},\max }^{\mathrm{p}}\end{array}\right.(8)$

where ${\epsilon }_{\mathrm{s}0}^{\mathrm{p}}$ and ${\epsilon }_{\mathrm{t}0}^{\mathrm{p}}$ are the initial shear and tensile plastic strains; and ${\epsilon }_{\mathrm{s},\max }^{\mathrm{p}}$ and ${\epsilon }_{\mathrm{t},\max }^{\mathrm{p}}$ the critical shear and tensile plastic strains; ${\varphi }_0$, $c_0$, and ${\sigma }_{\mathrm{t}0}$ the initial cohesion, MPa; initial friction angle, (°); initial tensile strength, MPa; ${\epsilon }_{\mathrm{s}}^{\mathrm{p}}$, ${\epsilon }_{\mathrm{t}}^{\mathrm{p}}$, $\varphi$, $c$, and ${\sigma }_{\mathrm{t}}$ the shear plastic strain, tensile plastic strain; cohesion, MPa; friction angle, (°); and tensile strength, MPa, in the current calculation step; and ${\varphi }_{\mathrm{c}}$ the residual friction angle, (°).

It is crucial to accurately describe the dynamic crack propagation in LTCC. In this study, a damage-softening constitutive model based on continuum mechanics was employed to describe the deformation, damage, and softening of the target object in simulating the process of rock fracture. In this model, the accumulation of plastic strain led to the deterioration of strength parameters. Furthermore, when the plastic strain reached the threshold, the material points automatically separated, and visible cracks appeared. Notably, throughout the entire mechanical process, no material points were removed.

2.2 MPM based on convective particle domain interpolation

The MPM is a mesh-free method that combines Lagrange and Euler methods. It discretizes an object into material points and uses a background mesh with linear functions (Kakouris and Triantafyllou, 2017; Ma et al., 2009). The motion equation was employed to analyze the Eulerian grid, and Lagrangian particles were utilized to assess the physical state (Kan et al., 2021; Sulsky et al., 1994). The physical quantities of the particles, such as density, velocity, and stress, were used to analyze the motions of these objects. The density of a continuum was approximated as (Equation 9):

$\rho \left(x_i\right)={\displaystyle \sum _{p=1}^{n_p}}{m}_p\delta \left(x_i-x_{ip}\right)(9)$

where n_p represents the total number of particles; m_p is the mass of particle p; δ is the Dirac delta function; and x_ip is the coordinate of particle p. A linear shape function with single point integration is typically used in the standard MPM. However, a single point (particle center) cannot describe the influence range of particles. Thus, the gradient of the linear shape function was not continuous at the boundary of the element, creating cross-element errors and unrealistic fractures.

The convective particle domain interpolation (CPDI) method was developed to overcome these challenges (Sadeghirad et al., 2011). Figure 1 illustrates the material point discretization and CPDI method during LTCC. The particles exhibited a rhomboid shape, with center position x_p and two configuration vectors r₁ and r₂. The configuration vector varied over time with the deformation gradient (Equation 10).

$\left\{\begin{array}{c}{r}_1^{n+1}={\mathit{F}}_p^{n+1}{r}_1^0\\ r_2^{n+1}={\mathit{F}}_p^{n+1}{r}_2^0\end{array}\right.(10)$

where r₁ and r₂ are the configuration vectors; ${\mathit{F}}_p^{n+1}=\left(\mathbf{I}+\nabla v_p^{n+1}∆t\right){\mathit{F}}_p^n$ is the deformation gradient matrix; I is the unit matrix; $\nabla v_p^{n+1}$ is the velocity gradient at the particle center; and Δt is the time increment during the calculation. The shape functions (Equation 11) and their gradients (Equation 12) at the particle center were averaged using the four corners of the particle domains.

$N_{Ip}^n=\frac{1}{4}{\displaystyle \sum _{i=1}^4}{N}_{{Ic}_i}^n(11)$

$\nabla N_{Ip}^m=\frac{1}{2V_p}\left\{\left(N_{{Ic}_1}^n-N_{{Ic}_3}^n\right)\left[\begin{array}{l}{r}_{1y}^n-r_{2y}^n\\ r_{2x}^n-r_{1x}^n\end{array}\right]+\left(N_{{Ic}_2}^n+N_{{Ic}_4}^n\right)\left[\begin{array}{l}{r}_{1y}^n+r_{2y}^n\\ {-r}_{2x}^n-r_{1x}^n\end{array}\right]\right\}(12)$

where V_p is the volume of a particle (m³); $N_{Ic}^n$ denotes the standard linear shape functions at the corner. The grid point velocity (Equation 13) and acceleration (Equation 14) were updated using the momentum theorem.

$v_I^{n+1}=\frac{M_I^n+∆t{f}_I^{n+1}}{m_I^n}(13)$

$a_I^{n+1}=\frac{f_I^{n+1}}{m_I^n}(14)$

where a is the acceleration (m/s²). The grid point velocity and acceleration were employed to compute the particle displacement (Equation 15), velocity (Equation 16), and strain increment (Equation 17) through interpolation.

$u_p^{n+1}=u_p^n+∆t{\displaystyle \sum _{I\epsilon p}}{N}_{Ip}^n{v}_I^{t+1}(15)$

$v_p^{n+1}=v_p^n+∆t{\displaystyle \sum _{I\epsilon p}}{N}_{Ip}^n{a}_I^{t+1}(16)$

$∆{\epsilon }_{p,ij}^{n+1}=∆t{\displaystyle \sum _{I\epsilon p}}\frac{1}{2}\left(\frac{\partial N_{Ip}^n}{\partial j}{v}_{I,i}^{n+1}+\frac{\partial N_{Ip}^n}{\partial i}{v}_{I,j}^{n+1}\right)(17)$

Figure 1

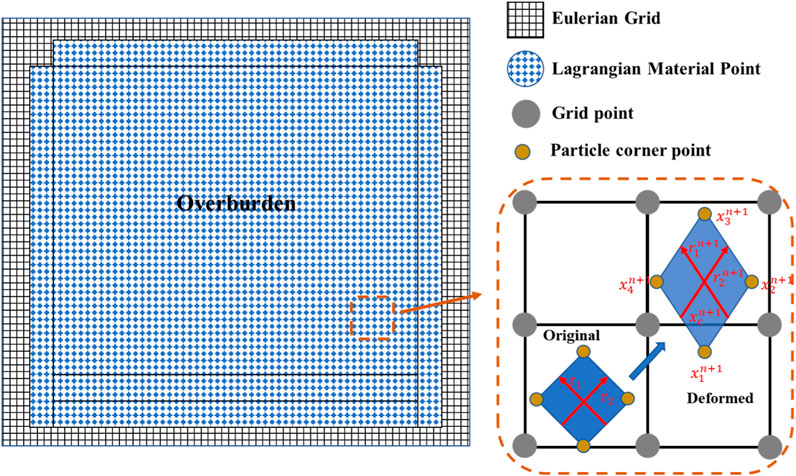
Figure 1. Discrete material points and convective particle domain interpolation (CPDI) method during LTCC.

The increment of the particle strain and the constitutive equation were used to determine the particle stress. The particle stress was updated using three steps (Zhou et al., 2023): 1) The study used the elastic constitutive equation (Equation 3) to calculate the elastic stress. 2) The study determined whether shear or tensile failure occurred (Equations 4, 5). 3) If a failure occurs, the stress is corrected using the flow rule (Equation 6). The final step consists of updating the position of the particles and storing historical information.

3 Model and verification

3.1 Physical model experiment

The physical simulation experiment described in this study adopts the research method of a similarity model, utilizing the 8101 working face of the Tashan coal mine in Datong City, Shanxi province, China as the modeling object. The roof of the coal mine is primarily composed of fine sandstone, medium sandstone, coarse sandstone, sandy mudstone, and more, with sandy lithology accounting for 90%–95%. Additionally, there are multiple layers of HRs, making it a typical coal mine with a HR in China. The 8101 working face measured 1,445 m in length and 231.4 m in width. LTCC was used to mine the ultra-thick coal seam, with a thickness range of 15.77 m–34.61 m, averaging 20.08 m. There were 5 HRs above the working face, and details regarding the lithology as well as physical and mechanical parameters of the working face strata can be found in reference (Lu et al., 2019).

In this study, a scaled-down similarity model was designed according to on-site observations and similarity theory (Kang et al., 2018a). The experimental equipment employed was the electro-hydraulic servo two-dimensional loading similarity simulation test system, independently developed by Chongqing University (Figure 2). The maximum size of the experimental model was 2.6 m × 2.0 m × 0.3 m (length × height × width). The data receiving system recorded the data monitored using pressure sensors during the excavation process of the model. The hydraulic servo control system applied vertical and horizontal loads to the model, simulating the effect of ground stress. An image acquisition device, comprising a video recorder, a camera, and a 3D laser scanner, captured images of rock mass movement during the model excavation, with a frame rate of 10 Hz for photography (Figure 2b).

Figure 2

Figure 2. Physical modeling system for LTCC. (a) Data acquisition system, (b) Overview of experimental equipment, (c) Monitoring scheme, and (d) Model construction and sensors.

The similarity coefficient designed using the similarity model met the basic conditions of similarity theory (Equation 18) (Kang et al., 2018a; Kang et al., 2018b):

$\frac{{\alpha }_{\mathrm{\sigma }}}{{\alpha }_{\mathrm{g}}\times {\alpha }_{\mathrm{\rho }}}=1(18)$

where α_σ is the stress similarity ratio; α_g is the geometric similarity ratio; and α_ρ is the density similarity ratio. Additionally, the following relationships need to be addressed (Equation 19):

${\alpha }_{\mathrm{g}}=\frac{{\mathrm{g}}_{\mathrm{p}}}{{\mathrm{g}}_{\mathrm{m}}},{\alpha }_{\mathrm{\rho }}=\frac{{\mathrm{\rho }}_{\mathrm{p}}}{{\mathrm{\rho }}_{\mathrm{m}}},{\alpha }_{\mathrm{\sigma }}=\frac{{\mathrm{\sigma }}_{\mathrm{p}}}{{\mathrm{\sigma }}_{\mathrm{m}}},{\alpha }_{\mathrm{t}}=\sqrt{{\alpha }_{\mathrm{g}}}(19)$

In the formula, the subscript p represents the prototype, m represents the model, g represents the length (m), σ Represents strength (MPa), and ρ indicates the bulk density (kg/m³). In this study, the stress similarity ratio α_σ = 250, geometric similarity ratio α_g = 200, density similarity ratio α_ρ = 1.25, and time similarity ratio α_t = 14.14.

In addition, the stress concentration factor can be calculated according to (Equation 20) (Kang et al., 2018a):

$C=\frac{{\sigma }_{\mathrm{c}}}{\sum {\gamma }_i{h}_i}(20)$

where $C$ is the stress concentration factor; ${\sigma }_{\mathrm{c}}$ the measured stress, Pa; ${\gamma }_i$ the bulk density of the ith overburden, kg/m³; and $h_i$ the thickness of the ith overburden, m.

The experimental steps are as follows:

1) Initially, create a similar model, place the uniformly mixed similar materials into the forming chamber of the experimental system, and compact them evenly. Spread mica sheets evenly on the surfaces of each layer to simulate the interface between rock layers (Figure 2d). Repeat this process for each rock layer and arrange pressure sensors at the designated measurement points (Figure 3), using tin foil to prefabricate hydrofracture cracks. After completing the construction of each layer, allow the model to solidify.

2) Subsequently, divide different rock layers and paste the positioning paper onto the surface of the model. The completed model is shown in Figure 2b. According to the actual in-situ stress and similarity coefficient, the vertical stress applied by the loading plate was 45.60 kPa, and the horizontal stress was 48.00 kPa.

3) Finally, the excavation simulation experiment was conducted according to the excavation mode of the on-site coal seam working face. In a similar model, the coal seam was excavated 40 cm away from the left boundary of the model. Given the loss of top coal, the excavation height was set to 7 cm. The actual working face of the Tashan coal mine advanced at ∼ 4.8 m per day. In this study, model excavation was conducted every 2 h, with each excavation reaching a length of 4 cm. After each excavation, photos were taken to record the entire process, and the entire excavation process was recorded in a video to collect data from pressure monitoring.

Figure 3

Figure 3. LTCC geometric model with multi-layer HRs.

3.2 Geometric models and ground fracturing schemes

The size of the numerical simulation model employed in this study was the same as that of physical experiments. Furthermore, when studying plane stress–strain challenges, the geometric model was abstracted and simplified as a two-dimensional model, loading the middle rock layer with a loading plate. The geometric model size of the rock layer was 2.60 m × 1.76 m. Discretize the entire geometric model into material points, containing ∼810,000 material points. The geometric model is shown in Figure 3.

The numerical simulation utilized geological information, material properties (Table 1), and boundary conditions from physical experiments. It is worth noting that similar materials are prepared according to the similarity coefficients, which are given in Section 3.1 Similar materials were prepared through laboratory experiments, and their mechanical properties were tested, as shown in Table 1. Additionally, we calibrated the critical shear strain and tensile strain of the rock and interlayer interface through trial calculations and comparisons between numerical and experimental results.

Table 1

Table 1. Mechanical parameters of overburden.

The interlayer was considered a material with relatively weak critical plastic strain. The mechanical parameters of the interlayer correlated with the adjacent rock layers, indicating that the mechanical parameters of the interlayer and the underlying rock layer were consistent (represented by “−” in Table 1). The residual internal friction angle was uniformly 30°

In the simulation of LTCC, based on the geometric similarity coefficient, the actual excavation length for each step was 8 m. Initially, the pre-mining stress distribution was calculated, and subsequently followed by the mining process. After each advancement, iterative calculations were conducted. At an allowable stress error of < 1e⁻⁵, the entire model attained force balance, terminating the rock movement. The calculation for the next mining step was conducted. It is worth noting that the MPM, as a Eulerian and Lagrange hybrid method, has lower computational efficiency. Therefore, we adopted a GPU parallel computing method to improve it.

To explore the effectiveness of different hydraulic fracturing crack types in controlling roof collapse during coal mining and their impact on the manifestation of mining pressure. Prefabricated horizontal fracturing (HF) cracks, vertical fracturing (VF), and non-fracturing (NF) models were employed. The study aimed to examine the effects of horizontal and vertical hydraulic fractures formed by surface hydraulic fracturing on several aspects: the damage of overlying rock, activation of hydraulic fractures, and disturbance of overlying rock stress distribution during the mining process.

By analyzing the relationship between the energy release events of rock layers and the peak stress at the working face, the target fracture layers were identified as NO.1 hard roof (HR1) and NO.2 hard roof (HR2) (Lu et al., 2019). The horizontal crack was located in the middle of the layer, with HR2 ranging from 188 m to 324 m and a length of 136 m. HR1 is located between 120 m and 400 m, with a length of 280 m. Vertical cracks run through the layers with intervals between them. HR2 exhibited three cracks with an interval of 68 m. HR1 exhibited five cracks spaced 70 m apart. The two fracturing schemes are shown in Figure 4.

Figure 4

Figure 4. Ground hydraulic fracturing scheme [(a) HF cracks; (b) VF cracks].

3.3 Verification

To assess the rationality and capability of the established numerical model, this section compared the physical experiments and numerical simulation results of different excavation lengths under horizontal crack conditions. Furthermore, it examined rock failure across three different excavation lengths (240 m, 300 m, and 360 m). Figures 5–7 show the movement of rock layers in both physical experiments and numerical simulations. It was observed that the collapse of the overburdened rock layer typically exhibited a trapezoidal shape, characterized by collapse height, collapse angle, and excavation length.

Figure 5

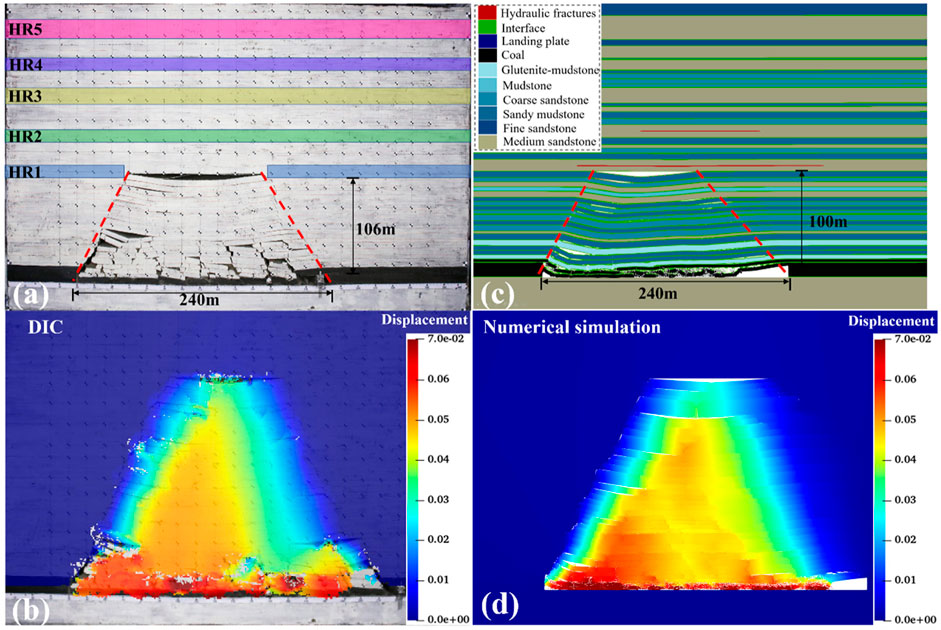
Figure 5. Rocks movement during 240 m in LTCC (a) Physical experiment layer motion, (b) numerical simulation layer motion, (c) physical model displacement results, and (d) numerical simulation displacement results.

Figure 6

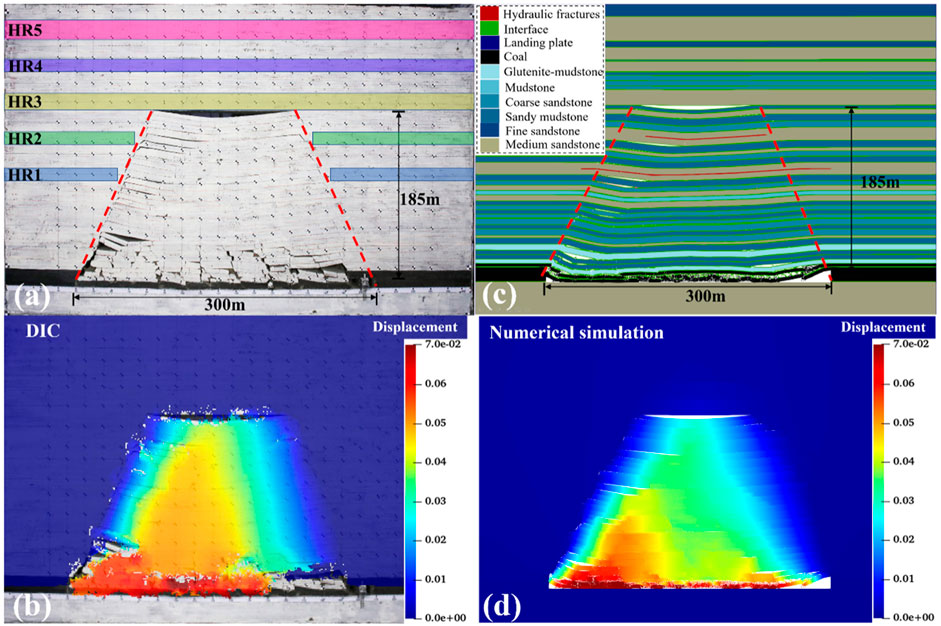
Figure 6. Rocks movement during 300 m in LTCC. (a) Physical experiment layer motion, (b) numerical simulation layer motion, (c) physical model displacement results, and (d) numerical simulation displacement results.

Figure 7

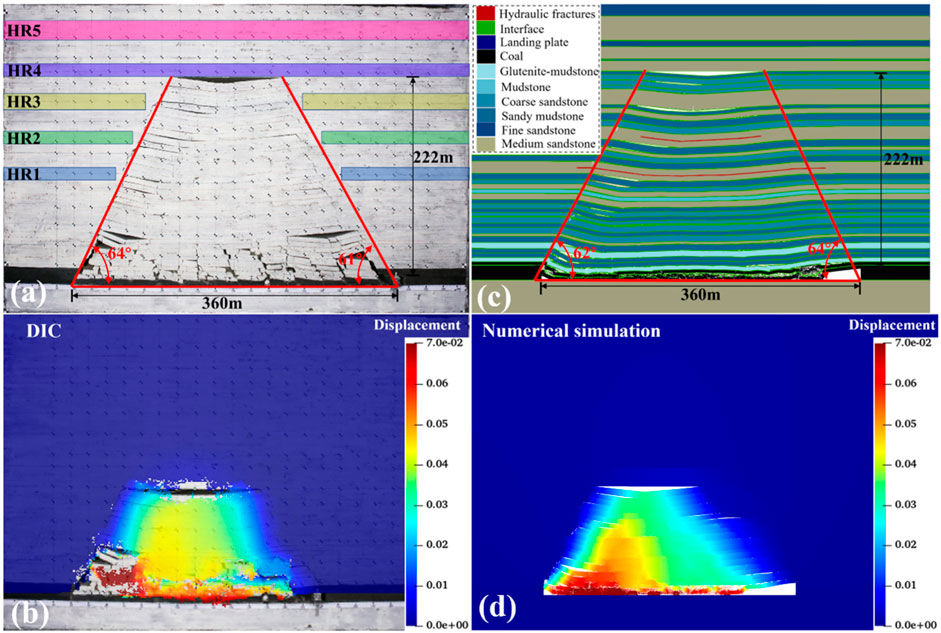
Figure 7. Rocks movement during 360 m in LTCC. (a) Physical experiment layer motion, (b) numerical simulation layer motion, (c) physical model displacement results, and (d) numerical simulation displacement results.

Under three excavation lengths, the experimental collapse heights were 106 m, 185 m, and 222 m, respectively. The MPM simulated collapse heights were 100 m, 185 m, and 222 m, respectively. In terms of collapse angle, when excavating 360 m, the experimental results of left and right collapse angles were 64° and 61°, and the MPM simulation results were 62° and 64°, respectively. Digital image correlation was employed in physical experiments to calculate the vertical displacement of rock layers. This method tracked the motion of pixels before and after deformation to describe the displacement field. Through the results, it was observed that there was a high degree of agreement between numerical simulation and experimental results in terms of collapse height, collapse angle, and rock displacement.

The abutment pressure of the working face was an important indicator reflecting whether the mining pressure manifestation was either strong or not. A stress concentration factor is defined as the ratio of the initial stress employed to adjacent stress along the coal seam floor (Figure 8). The maximum stress concentration factor obtained from experiments and numerical calculations was very close, and the trend was consistent.

Figure 8

Figure 8. Comparison of stress concentration factors for coal seam abutment pressure in models.

The above results indicated that the proposed numerical model and algorithm accurately simulated key behaviors such as roof settlement, layering, crack propagation, roof collapse, and the contact between collapsed roofs and crack blocks. It exhibited high applicability and can better describe the strong mining pressure manifestation characteristics of multi-layer HR underground fracturing control.

4 Results and discussion

4.1 Overburden fracture evolution induced through mining

This study simulated LTCC under NF, HF, and VF using established numerical models, and extracted the collapse situation of rock layers in each stage. Figure 9 shows the simulation of rock collapse in LTCC without hydraulic fracturing at an excavation distance range of 240 m–360 m.

Figure 9

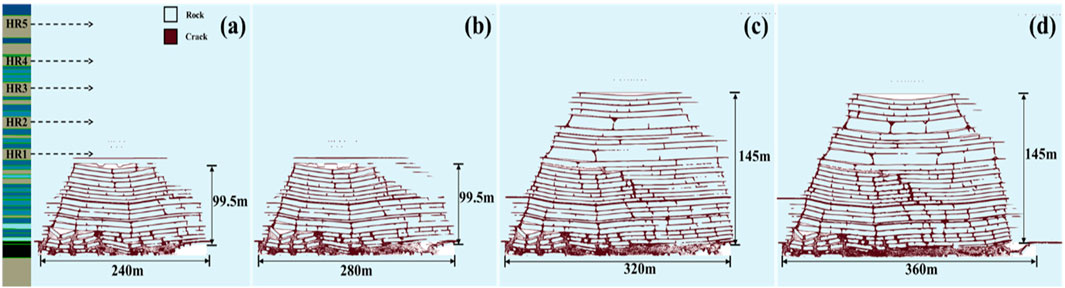
Figure 9. Overburden fractures evolution in NF. (a) Excavation distance 240 m, (b) excavation distance 280 m, (c) excavation distance 320 m, and (d) excavation distance 360 m.

As the working face continues to advance, the overhanging length of the roof increases, resulting in bending deformation, delamination, and damage to the roof. Furthermore, when excavating at distances of 240 m and 280 m, the height of the collapsed rock layer was 99.5 m, and the rock layer below HR1 was not broken. Additionally, when excavating at distances of 320 m and 360 m, the height of the collapsed rock layer was 145 m, and HR1 as well as HR2 were already broken. The collapsed layer reached the third hard roof (HR3), but it was not broken. The collapsed rock layers were more significantly compact compared with the previous stage.

Figure 10 shows the simulated rock collapse of ground fracturing horizontal cracks LTCC at an excavation distance range of 240 m–360 m. In comparison with hydraulic fracturing, under the influence of surface fracturing, the step distance of rock collapse was shortened. When excavating at distances of 240 m and 280 m, the height of the collapsed rock layer was 106 m. The rock layer below HR1 collapsed, but HR1 did not break. The excavation distance was 320 m, the collapse height was 145 m, and HR1 as well as HR2 was broken. The collapse layer reached HR3 and obvious cracks appeared, but they were not broken. The excavation distance was 360 m, the collapse height was 222 m, HR3 was broken, and the collapse area was significantly compacted.

Figure 10

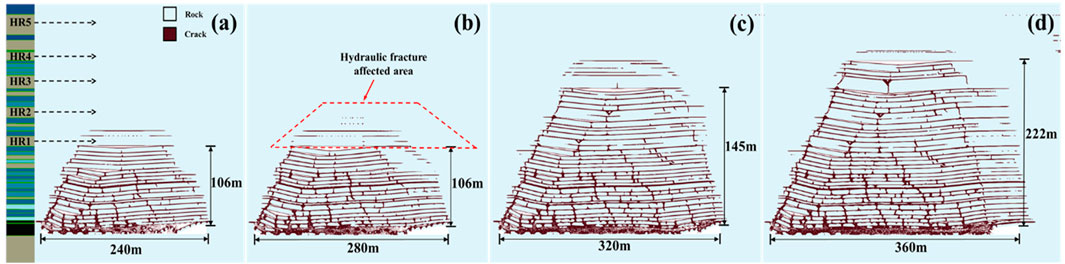
Figure 10. Overburden fractures evolution in HF. (a) Excavation distance 240 m, (b) excavation distance 280 m, (c) excavation distance 320 m, and (d) excavation distance 360 m.

Figure 11 shows the simulated rock collapse of ground fracturing vertical cracks LTCC at an excavation distance range of 240 m–360 m. In comparison with the previous two situations, the step distance of the collapsed rock was significantly reduced. Furthermore, when the excavation distance was 240 m, the height of the collapsed rock layer was 145 m, HR2, and the above rock layers were not broken, but a large number of cracks appeared. Additionally, when the excavation distance was 280 m, the collapse height was 185 m, and HR1 as well as HR2 were broken. The excavation distance was 320 m, the collapse height was 222 m, and the excavation was 360 m. The collapse height did not continue to increase, and the collapse area was further compacted.

Figure 11

Figure 11. Overburden fractures evolution in VF. (a) Excavation distance 240 m, (b) excavation distance 280 m, (c) excavation distance 320 m, and (d) excavation distance 360 m.

To further elucidate the impact of hydraulic fracturing on rock fracture in LTCC, the stress distribution in the collapse area of LTCC rock layers without hydraulic fracturing was extracted (Figure 12). The entire collapsed area was further divided into overburden rock layers, fractured areas, and compacted areas. The degree of overburden fracture correlated with gravity, and the fracture of the overburden rock layer started from the fracture zone, extracting three stages of fracture zone failure from (a) to (c).

Figure 12

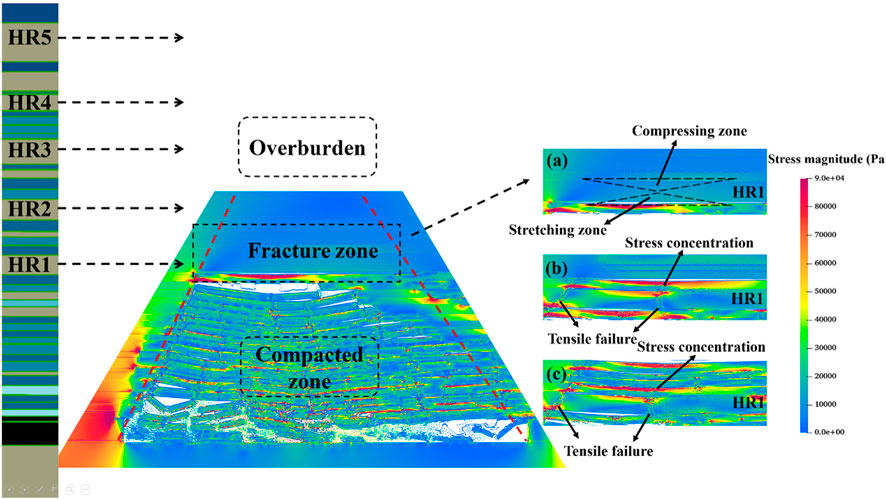
Figure 12. Stress distribution in the collapse area of LTCC rock layers without hydraulic fracturing. (a) Delam ination, (b) crack initiation, and (c) crack penetration.

As the working face advanced, the stress in the overburdened rock layer increased, and HR1 in the crack zone underwent downward bending deformation. The upper part of HR1 was compressed, while the lower part was stretched. Furthermore, due to the horizontal tensile force of the upper rock layer and the horizontal compressive force of the lower rock layer, adjacent rock layers exerted shear force on the interlayer interface, generating stress concentration at the interlayer interface. However, the strength of the interlayer interface was limited, damaging the interlayer interface. Thus, the overburden rock layer was suspended. The suspended overburden no longer bears the pressure of the upper rock layer but was affected by horizontal As the working face advanced, the span of the suspended overburden increased, leading to concentrated tensile stress in the middle and both ends of the span, resulting in tensile failure, which was the primary reason for the rupture of the overburden.

In summary, the essence of the fracture of the HR is the tensile damage caused by the gravity of the overburden rock layer when it is suspended. The vertical cracks caused by ground hydraulic fracturing can greatly weaken the tensile strength of the HR, thereby greatly reducing its collapse step distance. However, the short length of vertical cracks, coupled with the shielding effect of adjacent rock layers above and below the HR, as well as the compression of the maximum horizontal principal stress, correlated with the advance direction of the working face. This restrained crack propagation, thereby limiting damage progression. However, both horizontal and vertical cracks facilitated the damage and weakening of the HR, playing an important role in the early fracture of the HR.

4.2 Stress transfer characteristics

From the results in Section 4.1, it was observed that as the working face advanced, the interlayer stress of the overburdened rock layer continuously changed, particularly when the HR broke. To understand the stress transfer characteristics between layers in LTCC, four layers below HR1 (lower), four layers in the middle from HR1 to HR2 (middle), and four layers above HR2 (upper), totaling three layers were extracted. Figure 13 shows the perspectives of horizontal stress, vertical stress, and abutment stress on the working face.

Figure 13

Figure 13. Horizontal stress variation between LTCC layers in NF.

The horizontal stress value was negative, and the research object was subjected to horizontal compressive stress. The horizontal stress variation between LTCC layers without hydraulic fracturing shows three processes of the overburden layer from crack development to fracture, thereby completing collapse (Figure 13). In the initial phase, the horizontal stress within the three layers initially correlated with the ground stress. However, as the rock layers underwent suspension and layering, there was a subsequent decrease in horizontal stress. Figure 12 illustrates that the rock layer experienced horizontal compression before failure, resulting in concentrated compressive stress and crack formation. This phase was characterized by fluctuating stress levels, denoting the stage of crack development. The culmination of this process is marked by the fracture of the upper HR layer, exerting pressure on it, followed by the collapse of both the HR and lower rock layers, gradually releasing the horizontal stress.

The horizontal stress changes between the LTCC layers during HF (Figure 14) also show the same three processes, and fracture development (HF-upper) was observed before the HR3 fracture. Notably, hydraulic fracturing weakens HR1 and HR2, reducing the collapse step distance, and therefore shortening the crack development step distance. In a force balance system, the stress released by horizontal fractures during fracturing was transferred to other overburden layers, increasing their horizontal stress.

Figure 14

Figure 14. Horizontal stress variation between LTCC layers in HF.

In the horizontal stress variation between the LTCC layers of vertical fractures during fracturing (Figure 15), due to the stronger weakening ability of vertical fractures on the hard roof, further shortening the crack development step before HR1 fracture. Vertical cracks intermittently fracture the HR, causing a crack development step before each layer of HR fractures. Vertical cracks significantly weaken the tensile strength of the HR, preventing extensive suspension and decreasing compression on the lower rock layer, resulting in a relatively lower peak horizontal stress.

Figure 15

Figure 15. Horizontal stress variation between LTCC layers in VF.

Figure 16 shows the variation of interlayer vertical stress for three LTCC schemes. As the excavation distance increased and the overburden continuously collapsed, the vertical stress between layers decreased, but the fluctuation amplitude was different. Notably, there are four peak step distances, including three vertical cracks and one horizontal crack. In comparison with the vertical stress changes of LTCC rock layers with the entire process of crack evolution, it was observed that the appearance of the peak vertical stress was the result of stress transfer during rock collapse. Thus, each peak vertical stress represents a complete collapse of the rock layer. Furthermore, with a decrease in horizontal stress after the collapse of the lower rock layer, as well as a decrease in its own load-bearing capacity and vertical stress, the lower supporting stress on the overburden decreased, resulting in delamination, reduced load-bearing capacity, and a decrease in vertical stress. The collapse of the upper rock layer exhibited a repetitive phenomenon, thus all three layers exhibited vertical stress peak points at the same excavation distance.

Figure 16

Figure 16. Vertical stress variation between three LTCC schemes.

The peak value of advanced support pressure reflected the degree of mining pressure in the working face. Figure 17 shows the variation curves of the peak stress of advanced support for three LTCC schemes. As the working face advanced, overburdened rock layers collapsed, leading to fluctuations in the peak support pressure. To quantify and compare the changes in advanced support pressure, the root mean square (RMS) value throughout the entire propulsion process was calculated. Upon comparing HF and VF with the RMS of NF’s leading support pressure peak, it was observed that the RMS of VF’s leading support pressure peak decreased by 4.99%, while the RMS of HF’s leading support pressure peak decreased by 4.18%. After prefabricating hydrofracture cracks in the HR, the peak pressure of the advanced support in front of the coal wall was substantially reduced after the HR containing hydrofracture cracks broke, reducing the mining pressure manifestation of the working face.

Figure 17

Figure 17. Advanced abutment peak stress in three LTCC schemes.

In summary, as the working face advanced, overburden collapsed, and stress transfer dynamics within the rock layers exhibited distinct characteristics. Horizontal stress was concentrated in the middle through the bending deformation of the rock layer after it was suspended. Upon reaching its peak, the rock layer fractured and collapsed, thereby releasing horizontal stress. Reducing the tensile strength of HR through hydraulic fracturing effectively weakens horizontal stress concentration. The vertical stress was concentrated through the collapse of the lower rock layer and the suspended pressure of the upper rock layer. The appearance of its peak represents the collapse of multiple rock layers. Thus, upon shortening the collapse step distance, the concentration of vertical stress was effectively weakened.

4.3 Energy evolution characteristics

In this study, during the LTCC process, the energy of the strata was released, while the plastic deformation and fracture of the overburdened strata were accompanied by an increased dissipated energy. The accumulation of plastic strain in rocks led to rock degradation, which was attributable to rock failure. The damage stage of the rock layer was determined based on the characteristics of energy changes. The failure of rock layers during LTCC was divided into tensile failure and shear failure. The plastic tensile strain and plastic shear strain due to two failure modes constituted the plastic volumetric strain of the rock, which is calculated as (Equation 21) Sadeghirad et al. (2011):

${\epsilon }_v^p={\epsilon }_t^p+{\epsilon }_s^p\sin \theta (21)$

where ${\epsilon }_v^p$ is the plastic volumetric strain; ${\epsilon }_t^p$ is the tensile plastic strain; ${\epsilon }_s^p$ is the shear plastic strain, and θ is the shear expansion angle (°). Since the constitutive equation is based on the law of plastic flow, the shear expansion angle was the internal friction angle. The LTCC process was accompanied by the release of energy, and dissipated energy refers to the energy dissipated by rock elements during the failure and deformation process. This primarily led to damage and plastic deformation inside the rock. Therefore, based on elastic-plastic theory, plastic strain energy was utilized to calculate the energy released during the LTCC process. The calculation formula is (Equation 22) (Lan et al., 2010):

$E_p=\left|\frac{{\sigma }_1+{\sigma }_2+{\sigma }_3}{3}\cdot {\epsilon }_v^p\right|+\left|\frac{\sqrt{{\left({\sigma }_1-{\sigma }_2\right)}^2{+\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_3-{\sigma }_1\right)}^2}}{3}\cdot {\epsilon }_s^p\right|(22)$

In the interlayer dissipation energy variation of LTCC without hydraulic fracturing (Figure 18), all three layers exhibited S-shaped cumulative energy release curves, generating a large amount of dissipated energy from crack initiation to the crack penetration stage. Cracks development was accompanied by an increased energy at the second inflection point, upon HR1 fracturing. Additionally, during the period of energy increase, HR2 fractured in the central rock layer. Thus, as excavation continued, the accumulation of dissipated energy increased.

Figure 18

Figure 18. Interlayer dissipation energy of LTCC changes in NF.

In the variation of interlayer dissipation energy in hydraulic fracturing of LTCC horizontal fractures (Figure 19), as the hydraulic fracturing and weakening of hard top rock layers occurred, the fracture development interval shortened. Dissipation energy increased upon HR1 fracturing, decreased with HR2 fracturing, and resulting in a slight overall increase in total dissipation energy.

Figure 19

Figure 19. Interlayer dissipation energy of LTCC changes in HF.

In the variation of interlayer dissipation energy in the vertical fracture LTCC during fracturing (Figure 20), the fracture development interval was further reduced. The HR1 fracture step distance was significantly shortened, and the curve slope was also reduced. The dissipation energy significantly increased when HR2 and HR3 fractured. Thus, the total dissipated energy significantly increased.

Figure 20

Figure 20. Interlayer dissipation energy of LTCC changes in VF.

The above results indicated that hydraulic fracturing weakens the target formation, releasing energy in advance, and shortening the collapse step distance. As the reduction in the amplitude of energy release changes occurred, it led to plastic failure characteristics of the target layer. Moreover, with the increasing number of rock collapses, the total dissipated energy exhibited a more stable upward trend.

5 Conclusion

This study combined the MPM with the continuous medium strain-softening constitutive model to establish an LTCC numerical model for the overlying multi-layer HRs. Subsequently, the calculation results were compared with similar physical simulation experimental results, validating the applicability and capability of the model. Finally, LTCC simulation studies were conducted on prefabricated horizontal hydraulic fracturing, vertical hydraulic fracturing, and non-hydraulic fracturing models, leading to the following conclusion:

1) The essence of HR fracture lies in tensile damage due to the gravity of the overburdened rock layer when suspended. Vertical cracks resulting from ground hydraulic fracturing significantly weaken the tensile strength of the HR, thereby reducing its collapse step distance. Both vertical and horizontal water pressure cracks facilitated damage and weakening of the HR, playing crucial roles in its early fracture.

2) In LTCC, the stress transfer characteristics of rock layers are as follows: horizontal stress was concentrated in the middle through bending deformation of the rock layer after suspension, leading to fracture and collapse upon reaching its peak, and subsequent release of horizontal stress. Furthermore, reducing the tensile strength of HR through hydraulic fracturing effectively reduced horizontal stress concentration. The vertical stress was concentrated through the collapse of the lower rock layer and the suspended pressure of the upper rock layer. The appearance of its peak represents the collapse of multiple rock layers. Additionally, by shortening the collapse step distance, the concentration of vertical stress was effectively weakened.

3) Hydraulic fracturing weakens the target formation and shortened the collapse step distance, while also releasing energy in advance, reducing the amplitude of energy release changes, resulting in plastic failure characteristics of the target layer. As the number of rock collapses increased, the total dissipated energy exhibited a more stable upward trend.

This study analyzes the effects of different types of hydraulic fractures on the collapse of HR and their stress transfer characteristics. By understanding the impact of these fractures on hard roof structures, more effective mining strategies can be developed, thereby reducing the occurrence of mining accidents and enhancing operational safety. Additionally, this research provides a theoretical basis for the design of support structures in similar geological conditions.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XZ: Writing–original draft, Investigation, Conceptualization, Data curation. BX: Funding acquisition, Resources, Writing–original draft. NX: Methodology, Writing–review and editing, Supervision, Project administration. LZ: Software, Writing–review and editing. TG: Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was jointly supported by the Key R&D Program of Tibet Autonomous Region (grant number XZ202501ZY0099), the Key Technologies Research and Development Program of China (grant number 2023YFC3009005).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ai, S.-G., and Gao, K. (2023). Elastoplastic damage modeling of rock spalling/failure induced by a filled flaw using the material point method (MPM). Rock Mech. Rock Eng. 56, 4133–4151. doi:10.1007/s00603-023-03265-8

CrossRef Full Text | Google Scholar

Das, A. J., Mandal, P. K., Ghosh, N., Singh, A. P., Kumar, R., Tewari, S., et al. (2023). Evaluation of energy accumulation, strain burst potential and stability of rock mass during underground extraction of a highly stressed coal seam under massive strata-a field study. Eng. Geol. 322, 107178. doi:10.1016/j.enggeo.2023.107178

CrossRef Full Text | Google Scholar

Deng, G., Xie, H., Gao, M., Xie, J., Li, C., and He, Z. (2023). Fracture mechanisms of competent overburden under high stress conditions: a case study. Rock Mech. Rock Eng. 56, 1759–1777. doi:10.1007/s00603-022-03169-z

CrossRef Full Text | Google Scholar

Eremin, M., Esterhuizen, G., and Smolin, I. (2020). Numerical simulation of roof cavings in several Kuzbass mines using finite-difference continuum damage mechanics approach. Int. J. Min. Sci. Technol. 30, 157–166. doi:10.1016/j.ijmst.2020.01.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, R., Kuang, T., Zhang, Y., Zhang, W., and Quan, C. (2021). Controlling mine pressure by subjecting high-level hard rock strata to ground fracturing. Int. J. Coal Sci. Technol. 8, 1336–1350. doi:10.1007/s40789-020-00405-1

CrossRef Full Text | Google Scholar

Glubokovskikh, S., Sherman, C. S., Morris, J. P., and Alumbaugh, D. L. (2023). Transforming microseismic clouds into near real-time visualization of the growing hydraulic fracture. Geophys. J. Int. 234, 2473–2486. doi:10.1093/gji/ggad248

CrossRef Full Text | Google Scholar

Huang, B., Chen, S., and Zhao, X. (2017). Hydraulic fracturing stress transfer methods to control the strong strata behaviours in gob-side gateroads of longwall mines. Arab. J. Geosci. 10, 236. doi:10.1007/s12517-017-3024-y

CrossRef Full Text | Google Scholar

Kakouris, E. G., and Triantafyllou, S. P. (2017). Phase-field material point method for brittle fracture. Numer. Meth Eng. 112, 1750–1776. doi:10.1002/nme.5580

CrossRef Full Text | Google Scholar

Kan, L., Liang, Y., and Zhang, X. (2021). A critical assessment and contact algorithm for the staggered grid material point method. Int. J. Mech. Mater Des. 17, 743–766. doi:10.1007/s10999-021-09557-7

CrossRef Full Text | Google Scholar

Kang, H., Lou, J., Gao, F., Yang, J., and Li, J. (2018a). A physical and numerical investigation of sudden massive roof collapse during longwall coal retreat mining. Int. J. Coal Geol. 188, 25–36. doi:10.1016/j.coal.2018.01.013

CrossRef Full Text | Google Scholar

Kang, H., Lv, H., Gao, F., Meng, X., and Feng, Y. (2018b). Understanding mechanisms of destressing mining-induced stresses using hydraulic fracturing. Int. J. Coal Geol. 196, 19–28. doi:10.1016/j.coal.2018.06.023

CrossRef Full Text | Google Scholar

Konicek, P., and Waclawik, P. (2018). Stress changes and seismicity monitoring of hard coal longwall mining in high rockburst risk areas. Tunn. Undergr. Space Technol. 81, 237–251. doi:10.1016/j.tust.2018.07.019

CrossRef Full Text | Google Scholar

Lan, H., Pan, J., and Peng, Y. (2010). Numerical simulation for energy mechanism of underground dynamic disaster. J. China Coal Soc. 35, 10–14. doi:10.13225/j.cnki.jccs.2010.s1.008

CrossRef Full Text | Google Scholar

Le, T. D., Mitra, R., Oh, J., and Hebblewhite, B. (2017). A review of cavability evaluation in longwall top coal caving. Int. J. Min. Sci. Technol. 27, 907–915. doi:10.1016/j.ijmst.2017.06.021

CrossRef Full Text | Google Scholar

Li, C., Xie, H., Gao, M., Xie, J., Deng, G., and He, Z. (2020). Case study on the mining-induced stress evolution of an extra-thick coal seam under hard roof conditions. Energy Sci. and Eng. 8, 3174–3185. doi:10.1002/ese3.733

CrossRef Full Text | Google Scholar

Liu, J., Liu, C., Yao, Q., and Si, G. (2020). The position of hydraulic fracturing to initiate vertical fractures in hard hanging roof for stress relief. Int. J. Rock Mech. Min. Sci. 132, 104328. doi:10.1016/j.ijrmms.2020.104328

CrossRef Full Text | Google Scholar

Lu, Y., Gong, T., Xia, B., Yu, B., and Huang, F. (2019). Target stratum determination of surface hydraulic fracturing for far-field hard roof control in underground extra-thick coal extraction: a case study. Rock Mech. Rock Eng. 52, 2725–2740. doi:10.1007/s00603-018-1616-9

CrossRef Full Text | Google Scholar

Ma, S., Zhang, X., and Qiu, X. M. (2009). Comparison study of MPM and SPH in modeling hypervelocity impact problems. Int. J. Impact Eng. 36, 272–282. doi:10.1016/j.ijimpeng.2008.07.001

CrossRef Full Text | Google Scholar

Ning, J., Wang, J., Jiang, L., Jiang, N., Liu, X., and Jiang, J. (2017). Fracture analysis of double-layer hard and thick roof and the controlling effect on strata behavior: a case study. Eng. Fail. Anal. 81, 117–134. doi:10.1016/j.engfailanal.2017.07.029

CrossRef Full Text | Google Scholar

Pan, C., Xia, B., Zuo, Y., Yu, B., and Ou, C. (2022). Mechanism and control technology of strong ground pressure behaviour induced by high-position hard roofs in extra-thick coal seam mining. Int. J. Min. Sci. Technol. 32, 499–511. doi:10.1016/j.ijmst.2022.01.006

CrossRef Full Text | Google Scholar

Sadeghirad, A., Brannon, R. M., and Burghardt, J. (2011). A convected particle domain interpolation technique to extend applicability of the material point method for problems involving massive deformations. Numer. Meth Eng. 86, 1435–1456. doi:10.1002/nme.3110

CrossRef Full Text | Google Scholar

Sulsky, D., Chen, Z., and Schreyer, H. L. (1994). A particle method for history-dependent materials. Comput. Methods Appl. Mech. Eng. 118, 179–196. doi:10.1016/0045-7825(94)90112-0

CrossRef Full Text | Google Scholar

Tang, C. (1997). Numerical simulation of progressive rock failure and associated seismicity. Int. J. Rock Mech. Min. Sci. 34, 249–261. doi:10.1016/S0148-9062(96)00039-3

CrossRef Full Text | Google Scholar

Xia, B., Jia, J., Yu, B., Zhang, X., and Li, X. (2017). Coupling effects of coal pillars of thick coal seams in large-space stopes and hard stratum on mine pressure. Int. J. Min. Sci. Technol. 27, 965–972. doi:10.1016/j.ijmst.2017.06.020

CrossRef Full Text | Google Scholar

Xiao, F., Jiang, D., Wu, F., Zou, Q., Chen, J., Chen, B., et al. (2020). Effects of prior cyclic loading damage on failure characteristics of sandstone under true-triaxial unloading conditions. Int. J. Rock Mech. Min. Sci. 132, 104379. doi:10.1016/j.ijrmms.2020.104379

CrossRef Full Text | Google Scholar

Xie, J.-L., and Xu, J.-L. (2017). Effect of key stratum on the mining abutment pressure of a coal seam. Geosci. J. 21, 267–276. doi:10.1007/s12303-016-0044-7

CrossRef Full Text | Google Scholar

Yang, J. X. (2015). Mechanism of complex mine pressure manifestation on coal mining work faces and analysis on the instability condition of roof block. Acta Geodyn. Geomaterialia, 104–108. doi:10.13168/AGG.2015.0003

CrossRef Full Text | Google Scholar

Yu, B., Gao, R., Kuang, T., Huo, B., and Meng, X. (2019). Engineering study on fracturing high-level hard rock strata by ground hydraulic action. Tunn. Undergr. Space Technol. 86, 156–164. doi:10.1016/j.tust.2019.01.019

CrossRef Full Text | Google Scholar

Yu, B., Zhao, J., Kuang, T., and Meng, X. (2015). In situ investigations into overburden failures of a super-thick coal seam for longwall top coal caving. Int. J. Rock Mech. Min. Sci. 78, 155–162. doi:10.1016/j.ijrmms.2015.05.009

CrossRef Full Text | Google Scholar

Yu, M., Zuo, J., Sun, Y., Mi, C., and Li, Z. (2022). Investigation on fracture models and ground pressure distribution of thick hard rock strata including weak interlayer. Int. J. Min. Sci. Technol. 32, 137–153. doi:10.1016/j.ijmst.2021.10.009

CrossRef Full Text | Google Scholar

Zhou, L., Li, X., Peng, Y., Xia, B., and Fang, L. (2023). Material point method with a strain-softening model to simulate roof strata movement induced by progressive longwall mining. Int. J. Rock Mech. Min. Sci. 170, 105508. doi:10.1016/j.ijrmms.2023.105508

CrossRef Full Text | Google Scholar

Zhu, Z., Wu, Y., and Liang, Z. (2022). Mining-induced stress and ground pressure behavior characteristics in mining a thick coal seam with hard roofs. Front. Earth Sci. 10, 843191. doi:10.3389/feart.2022.843191

CrossRef Full Text | Google Scholar